Next Article in Journal
Seasonal Comparison of the Wildfire Emissions in Southern African Region during the Strong ENSO Events of 2010/11 and 2015/16 Using Trend Analysis and Anomaly Detection
Previous Article in Journal
Hydrological Modeling for Determining Flooded Land from Unmanned Aerial Vehicle Images—Case Study at the Dniester River
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 4
10.3390/rs15041072
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Framework for High-Resolution Mapping of Soil Organic Matter (SOM) by the Integration of Fourier Mid-Infrared Attenuation Total Reflectance Spectroscopy (FTIR-ATR), Sentinel-2 Images, and DEM Derivatives

by
Xuebin Xu
1,
Changwen Du
1,2,*,
Fei Ma
1,
Zhengchao Qiu
1 and
Jianmin Zhou
1
1
The State Key Laboratory of Soil and Sustainable Agriculture, Institute of Soil Science Chinese Academy of Sciences, Nanjing 210008, China
2
College of Advanced Agricultural Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(4), 1072; https://doi.org/10.3390/rs15041072
Submission received: 30 December 2022 / Revised: 1 February 2023 / Accepted: 14 February 2023 / Published: 15 February 2023
Browse Figures
Versions Notes

Abstract

:
Soil organic matter (SOM), as the greatest carbon storage in the terrestrial environment, is inextricably related to the global carbon cycle and global climate change. Accurate estimation and mapping of SOM content are crucial for guiding agricultural output and management, as well as controlling the climate issue. Traditional chemical analysis is unable to satisfy the dynamic estimation of SOM due to its low timeliness. Remote and proximal sensing have significant advantages in terms of ease of use, estimation accuracy, and geographical resolution. In this study, we developed a framework based on machine learning to estimate SOM with high accuracy and resolution using Fourier mid-infrared attenuation total reflectance spectroscopy (FTIR-ATR), Sentinel-2 images, and DEM derivatives. This framework’s performance was evaluated on a regional scale using 245 soil samples from northeast China. Results indicated that the calibration size could be shrunk to 50% while achieving a fair prediction performance for SOM content. The Lasso, partial least squares (PLS), support vector regression (SVR), and convolutional neural networks (CNN) performed well in predicting SOM from FTIR-ATR spectra, and the performance was enhanced further by using Sentinel-2 images and DEM derivates. The PLS, SVR, and CNN models created SOM maps with higher spatial resolution and variation than the Kriging approach. The PLS and SVR models provided enough variety and were more realistic in the local SOM map, making them usable at the field scale, and the suggested framework took a fresh look at high-resolution SOM mapping.

1. Introduction

Soil organic matter (SOM) is the foremost carbon stock in terrestrial ecosystems, storing nearly three times the carbon of the vegetation carbon pool and twice the carbon of the atmosphere carbon pool [1]. SOM has a significant impact on soil chemical and physical processes, as well as the global carbon cycle [2,3]. Furthermore, the quantity, quality, and dynamics/turnover of SOM are crucial to soil health because they are related to soil structure, water-retention capacity, nutrient cycling, and biological activity [4], and so they have a significant impact on global food and nutritional security [5]. Continuous cropping and tillage in northeastern China have resulted in a loss of SOM, endangering food security as well as the ecological environment. [6]. As a result, to guide scientific and successful agricultural production and land management, dynamic monitoring of the spatial distribution of SOM is essential.
Conventional chemical analysis for SOM is laborious, expensive, damaging to the sample being tested, and time-consuming, which makes it challenging to meet the demands of dynamic monitoring for SOM [7]. With a portable spectrometer, proximal spectroscopy is a quick and practical way to measure SOM content both in the lab and outdoors [2]. According to the distinctive response of chemical bonds and functional groups in SOM to the infrared waves, Fourier-transform mid-infrared spectroscopy (FTIR) has been frequently utilized to assess SOM content. For instance, mid-infrared photoacoustic spectroscopy, which produced higher accuracy than near-infrared (NIR) spectroscopy, was used by Peltre et al. [8] to quantify the soil organic carbon (SOC). The labile percentage of SOC was found by Huang et al. [9] using mid-infrared photoacoustic spectroscopy. Xu, Du, Ma, Shen, Wu, Liang, and Zhou [7] applied FTIR-ATR in conjunction with atomic spectroscopy to estimate SOM content in saliferous soil with high accuracy (R2 > 0.800). These studies demonstrated the effectiveness of the FTIR technique for quantifying SOM.
Quantifying the SOM of a sampling site is insufficient; the spatial distribution of SOM must be analyzed to study the dynamics changes. The spatial distribution of SOM has been extensively predicted and described using digital soil mapping [10]. Anthropogenic and environmental factors such as drainage, topography, and climate all have a strong influence on SOM content. As a result, these environmental covariates are commonly used in SOM-based on-point information mapping and machine learning algorithms [11]. Goydaragh et al. [12] reviewed current research and applications of different machine learning methods and covariates for mapping SOC concentrations and stocks. They discovered that the most popular approaches were multiple linear regression (MLR), random forest (RF), Cubist, Regression Tree (RT), neural network (NN), and support vector machine (SVM) and that covariates such as parent material, climate, organic activity, topography, and existing soil information were frequently used for modeling.
The availability of environmental covariate data is frequently questioned, particularly at the regional level. The spectral reflectance of soil-related information may be directly recorded by optical remote sensing satellites [13]. Another advantage of optical remote sensing satellites is their excellent temporal-spatial resolution. The European Space Agency’s Sentinel-2 satellite, for example, provides outstanding views of land with spatial resolutions of 10–60 m and a minimum global revisit period of five days [14]. A rising number of studies have begun to quantify the geographical distribution of SOM using satellite remote sensing images. Gholizadeh et al. [15] compared the accuracy of SOC mapping using Sentinel-2 images to that of airborne hyperspectral images and laboratory spectroscopy and discovered that the SOC map created by Sentinel-2 showed lower precision than lab spectroscopy but higher precision than airborne hyperspectral images. Zhou et al. [16] examined the performance of Sentinel-2, Sentinel-3, and Landsat-8 images for SOC prediction and reported that Landsat-8 performed the best for SOC content. The ancillary and MODIS Normalized Difference Vegetation Index (NDVI) imagery triumphantly produced a high-quality SOC map with a spatial resolution of 250 m [17]. Furthermore, Nguyen et al. [18] obtained excellent prediction performance for SOC by combining the Sentinel-1 radar data and Sentinel-2 multi-spectral data, with R2 of 0.870 and RMSE of 1.818 ton C ha−1. High-resolution topography data are currently accessible and have enormous potential for mapping SOM [19,20]. Zhou et al. [21] improved SOC mapping accuracy by combining Digital Elevation Models (DEM) and Sentinel-1 and Sentinel-2 data with machine learning. The DEM derivatives were discovered to be the primary explanatory variables for SOC estimation, accounting for more than half of the total relative importance.
The successful application of these environmental covariates in SOM mapping opens up new avenues for improving proximal sensing-based spatial estimation in SOM. Rial et al. [22] attempted to reduce analytical costs and time efforts by incorporating environmental covariates (climate, land use, and geology) into predictive models based on FTIR spectra. Goydaragh et al. [23] combined remote sensing data, DEM data, and FTIR spectra with the Cubist and Bat model to improve SOC prediction accuracy. Moura-Bueno et al. [24] also demonstrated that the environmental covariates that correlated with SOC (e.g., elevation, clay content) improved the prediction accuracy of Vis-NIR spectroscopy models. Nonetheless, these studies depended heavily on environmental covariates for SOM prediction alone rather than digital soil mapping of SOM. It is still unknown whether the satellite images and DEM data, when combined with FTIR-ATR spectra, could be used as predictors to predict SOM and as covariates to estimate the SOM distribution map. Therefore, it is necessary to design a framework for SOM mapping in which remote sensing data and proximal sensing data can coexist harmoniously.
As we know, digital soil mapping (DSM) is a complex and ordered process, including the generation of environmental covariates, soil sampling design, modeling or mapping, and validation. Although these processes significantly influence the mapping performance, the selection of environmental covariates that is usually proceeded with before soil sampling is a key step in DSM. Differently, the collection of proximal sensing data is completed after or during soil sampling. Therefore, the primary objective of integrating proximal sensing and remote sensing data to improve SOM prediction and mapping is the construction of data fusion models. We hypothesize that the fusion of remote sensing data and proximal sensing data can improve the prediction accuracy of SOM and thus contribute to the generation of a SOM distribution map. Based on this, we placed emphasis on the fusion and modeling processes in DSM and developed a new framework for SOM mapping based on machine learning, which includes Lasso, PLS, support vector regression (SVR), and convolutional neural networks (CNN). Based on prediction performance, the Kennard–Stone algorithm was used to optimize the calibration size. After that, soil samples were divided into calibration and validation sets. Predictors from Sentinel-2 images and DEM derivatives were extracted and then incorporated with FTIR-ATR spectra using a machine learning model to obtain a robust prediction of SOM content for validation samples. The mapping model was created by combining the measured SOM content in the calibration set and the predicted SOM content of validation samples. To map the spatial distribution of SOM, the entire Sentinel-2 image set and DEM derivatives in the study area were used as covariates. The primary objectives of this study were to (i) determine the optimal calibration size for SOM prediction using FTIR-ATR spectra; (ii) evaluate the performance of the fusion of Sentinel-2 images, DEM derivatives, and FTIR-ATR spectra in predicting SOM content; and (iii) validate the feasibility of the proposed framework as an important segment for high-resolution SOM mapping.

2. Materials and Methods

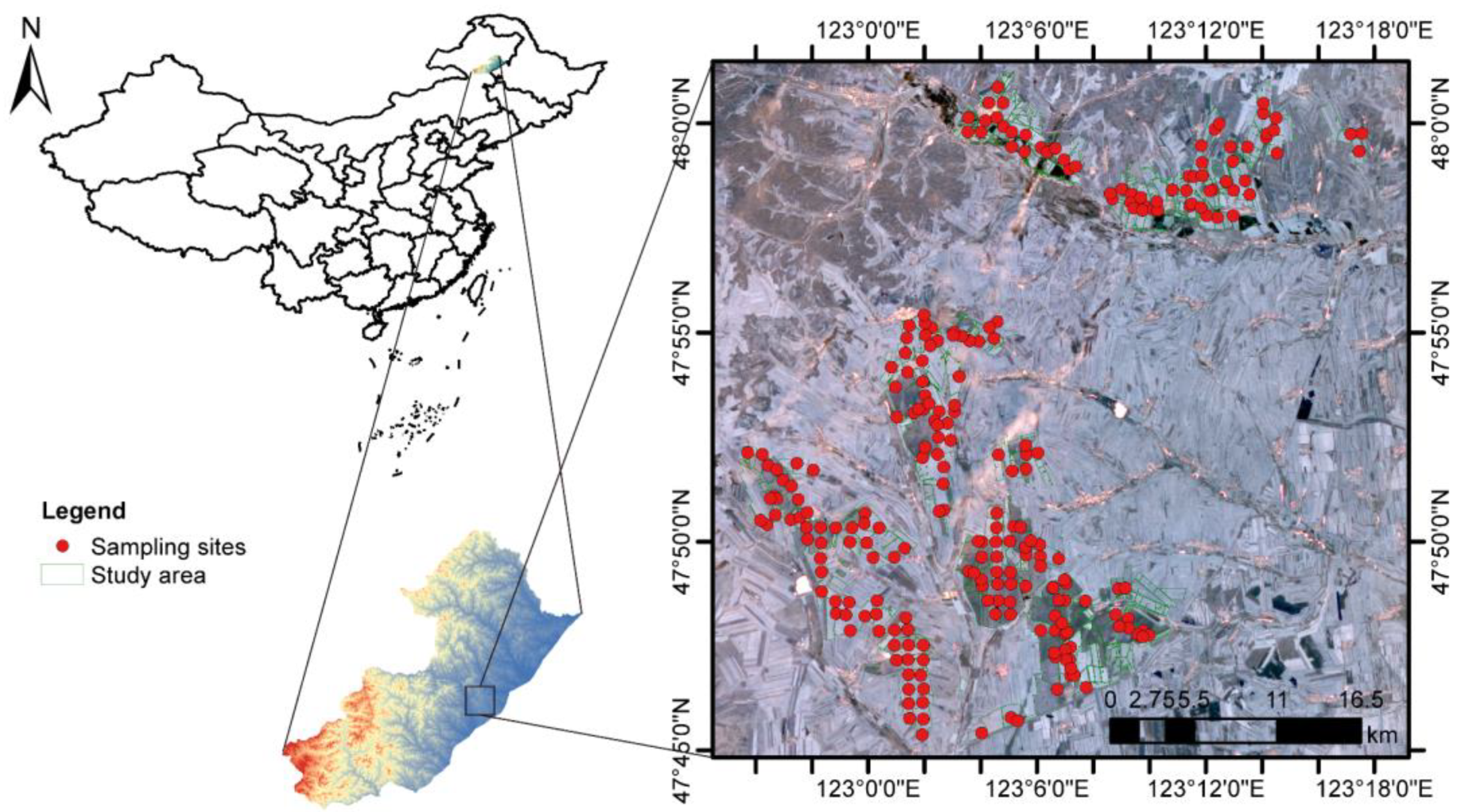
2.1. Study Area

The study area is located in Zalantun city and Arun Banner (122°56′–123°18′E, 47°45′–48°02′N), in the Inner Mongolia Autonomous Region (Figure 1). It has a warm temperate continental monsoon climate, with a daily average air temperature of 3.4 °C and annual average precipitation of 450–550 mm. The study area is overseen by the Dahewan Farm, which mostly cultivates maize (Zea mays L.) and soybean (Glycine max (L.) Merr.). Maize and soybeans are typically planted in early May and harvested in the middle of October. The soil in this study is classified as Phaeozem according to the World Reference Base (WRB) for soil resources [25].

2.2. Soil Sampling and Chemical Analysis

In late April 2021, 246 soil samples were collected using a regular grid sampling approach. Four samples were collected at a depth of 0–20 cm and thoroughly mixed across a 10 × 10 m area. A handheld GPS device was used to record the geographic coordinate information. The detailed sampling sites are shown in Figure 1. The air-dried soils were crushed and sieved through a 0.15 mm sieve a before being placed in disposable sampling bags for analysis. The potassium dichromatic oxidation technique was used to determine SOC content [26,27]. The SOC content was converted to SOM content by the conversion factor of 1.724. Duplicate measurements of some selected samples were used to control lab measurement errors.

2.3. FTIR-ATR Spectra Acquisition and Preprocessing

A handheld attenuated total reflectance infrared spectrophotometer was used to measure soil FTIR-ATR spectra (Agilent 4300, Agilent Technologies Inc., Santa Clara, CA, USA). Before sample screening, an air background spectrum was measured to correct the soil spectra. Following that, approximately 2 g of sieved soil was placed on the FTIR-ATR crystal and squeezed for measurement. Each spectrum was eventually recorded by averaging 64 sequential scans with a resolution of 0.466 cm−1 between the wavenumbers 4000 and 650 cm−1. Soil FTIR-ATR spectra were smoothed by a zero-phase digital filtering algorithm and then normalized in MATLAB R2020b (The Math Works, Natick, MA, USA).

2.4. Preprocessing of Sentinel-2 Images and DEM

Sentinel-2 featured two polar-orbiting satellites (A/B), each with a 100 min orbital period and a 786 km orbital height. It has four bands with a 10 m spatial resolution, six bands with a 20 m spatial resolution, and two bands with a 60 m spatial resolution (Table 1). Four cloud-free Sentinel-2 Level-1C images were obtained from the ESA Sentinels Scientific Data Hub (https://scihub.copernicus.eu/dhus/) (accessed on 4 January 2022) based on the closest field sampling date. Level-2A images were created by radiometrically calibrating and atmospherically correcting the Level-1C images with EAS’s Sen2Cor processor [28]. The Level-2A images were then mosaiced and clipped by region of interest to obtain a homogenous image with a spatial resolution of 10 m in ENVI 5.3 software (ESRI, Redlands, CA, USA). A total of 12 bands, comprising 3 visible bands, 3 vegetation red edge bands, 2 near-infrared (NIR) bands, 3 short-wave infrared (SWIR) bands, and 1 coastal aerosol band, were acquired (Table 1). We selected the spectral indices that were widely used as covariates to assess soil properties according to previous studies [13,15,18,20]. Thirty-four spectral indices were calculated (Table S1, Supplementary Materials). As the period of soil sampling was the dry season, it was very likely that the spatial variation in soil moisture was very limited. Therefore, we did not consider the difference in soil moisture among different samples. The 30 m spatial resolution DEM data (Aster GDEM v3) covering the study area were collected from Geospatial Data Cloud in China (http://www.gscloud.cn/search/) (accessed on 30 December 2021). The DEM raster image was resampled to a 10 m spatial resolution using the ‘NEAREST’ method in ArcGIS 10.3 software (ESRI, Redlands, CA, USA). Seventeen DEM derivatives (Table 2) were calculated as covariates in SAGA GIS software (http://www.saga-gis.org/en/) (accessed on 4 January 2022).

2.5. Framework

In our framework, soil samples were firstly collected. Then, the proximal sensing spectra were obtained in the laboratory after the soil was air-dried and ground. The Kennard–Stone technique was used to separate the 245 soil samples into a calibration set and a validation set according to the ideal calibration size [30]. There were two major topics in this study: prediction and mapping of SOM. The first was the prediction of the validation samples. The SOM content of the calibration samples was measured using the chemical method. Principal component analysis was used to minimize the dimensionality of the FTIR-ATR spectra and variables. To predict SOM content, the main component scores (X1) inside the top 98% explained variables were fused. The covariates (X2) used to estimate SOM content were extracted according to the geographic coordinates of the sampling sites in ArcGIS 10.3. The X1 and X2 were fused to build and optimize the machine learning model. The SOM of validation samples was predicted using the well-trained model. The best predictors were selected according to the importance of the variable. Then, the chemical-measured SOM of the calibration set and the model-predicted SOM of the validation samples were converged for SOM mapping. In SOM mapping, the models built between the SOM content and selected covariates were used to map the SOM spatial distribution. The detailed framework flow is shown in Figure 2. In this study, the best size of the calibration set was optimized. Prediction performances were tested with individual FTIR-ATR, covariates, and with their fused data.

2.6. Machine Learning Models

In this study, four machine learning models were carried out for SOM prediction and mapping in Python v3.8.3 using Scikit-learn v2.24.1 [31] and TensorFlow v2.4.1 backend [32].

2.6.1. Lasso Regression

Lasso regression is derived by adding an L1 penalty term into the ordinary linear model. It prefers solutions with fewer non-zero coefficients, lowering the number of characteristics on which a particular solution depends [33]. The objective function to minimize is:
J w = 1 2 n ‖ X w − y ‖ 2 2 + α ‖ w ‖ 1 ,
where w is the coefficient vector, α is a parameter that should be optimized, and ‖ w ‖ 1 is the L1 norm of the coefficient vector.

2.6.2. Partial Least Squares

To reduce duplicate information, PLS combines features from principal component analysis and multiple linear regression [34]. PLS generates score matrices T and U by projecting the independent variable (X) and the dependent variable (Y) to a new plane. The maximal covariance and linear connection between T and U are then discovered.
X = TP T + E ,
Y = UQ T + F ,
where P and Q are the loading matrices and E and F are the matrix of residuals.

2.6.3. Support Vector Regression

The SVM works on the premise of nonlinear mapping to make samples in low-dimensional space linear and then uses linear techniques to classify samples in a high-dimensional space [35]. The optimal classification plane is called a hyperplane. SVR, like SVM, is supposed to locate a line so that all points are as close to it as is feasible for regression. As a result, the goal optimization function now includes a relaxation variable.
J w = 1 2 ‖ w ‖ 2 + C ∑ i = 1 l ξ i ,                 s . t .     y i w T x i + b ≥ 1 − ξ i
where w is weight, C is the coefficient, and ξ i is a relaxation variable.

2.6.4. Convolutional Neural Networks

Convolution layers are added to the feedforward artificial neural network to create a CNN. As a result, a typical CNN design includes an input layer, a convolution layer, an activation layer, a pooling layer, a flatten layer, a fully connected layer, and an output layer [36]. To accept independent variables, the input layer whose size is compatible with the number of variables is employed. Filters are used to extract abstract information from one or more convolution layers. The activation layer is used to incorporate nonlinear components via an activation function to boost the neural network’s nonlinear expressiveness. After the activation layer, the pooling layer is used to lower the dimensionality of the feature map while maintaining information from the input feature map. The features are flattened into a vector using the flattening layer. The fully connected layer is used to remove the effect of feature placement on prediction and to establish the link between the output and the features. In a single regression task, the output layer with a neuron is coupled with the fully connected layer, which is followed by a linear function. We created a shallow CNN architecture with two convolution layers in this study. A leaky ReLU function was used to activate all of the output feature maps of the convolution layers.

2.7. Model Evaluation

The coefficient of determination (R2), mean absolute error (MAE), root mean square error (RMSE), and residual prediction deviation (RPD) were applied to evaluate the model performance.
R 2 = ∑ i = 1 n y ^ i − y ¯ 2 ∑ i = 1 n y i − y ¯ 2 ,
MAE = ∑ i = 1 n y ^ i − y i n
RMSE = ∑ i = 1 n y ^ i − y i 2 n
RPD = SD RMSE
where y i and y ^ i are measured and predicted SOM of the ith sample, respectively, y ¯ is the averaged SOM of n samples, and SD is the standard deviation of SOM. The variable importance of the model was assessed using Permutation Feature Importance, a model-testing technique that can be used for any fit estimation and is particularly useful for nonlinear or opaque estimators. The importance of permutation features is defined as the reduction of model scores when single feature values are randomly scrambled. This process breaks the relationship between feature and goal, so the decline in model scores indicates how much the model depends on this feature. In the ranking feature importance method, the jth feature is randomly scrambled to obtain a new feature variable. The model predicts the effect under the new feature variable, and the significance of the jth feature is calculated through the following formula:
i j = s − 1 K ∑ k = 1 K s k , j
where i j is the importance of the jth feature, s is the prediction score of the original feature construction model, and s k , j is the prediction score of the model constructed after the k repetition of the jth feature.

3. Results

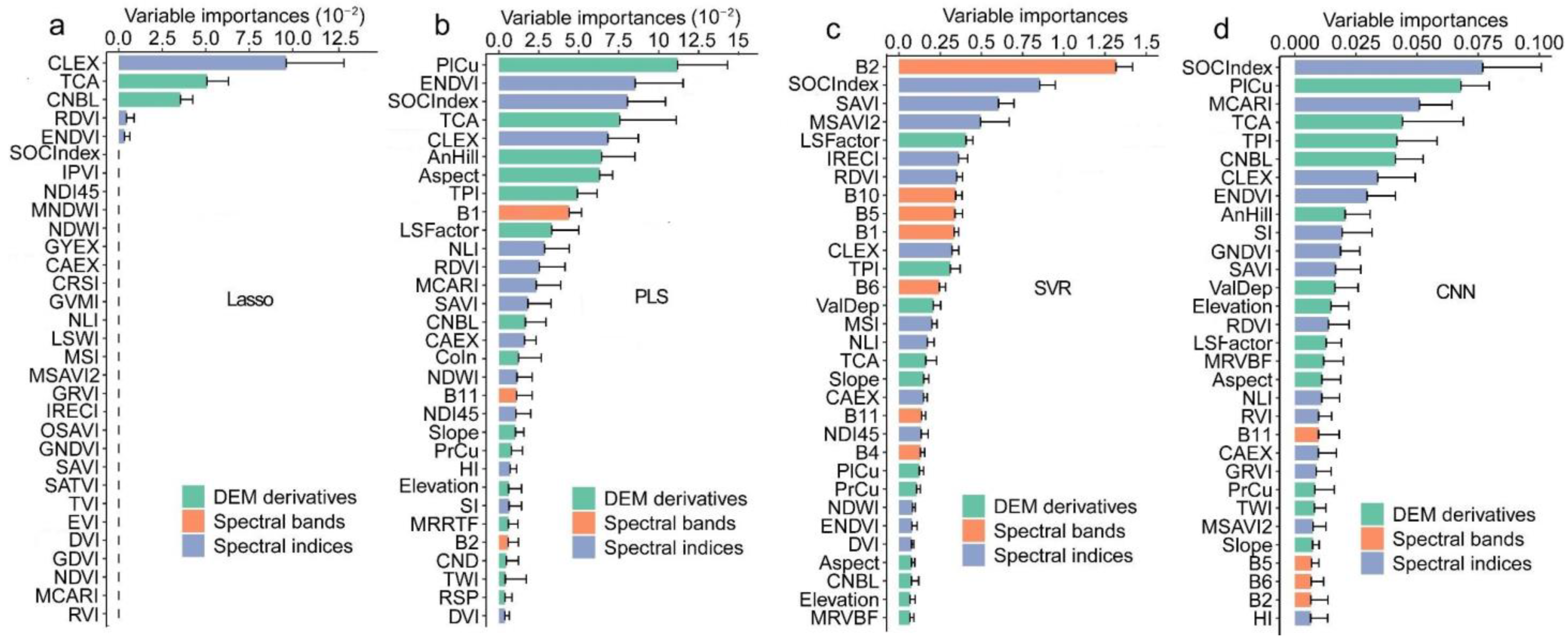
3.1. Correlation between SOM and Predictors

The SOM content in this area varied from 12.1 to 133.1 g kg−1 with a mean of 40.0 g kg−1, median of 38.9 g kg−1, and standard deviation of 10.8 g kg−1. The SOM had a skewness of 3.1 g kg−1, which was very high. The coefficient of variation of SOM was 27.0%, showing that the topsoil SOM varies somewhat in this region. The abnormal sample with SOM of 133.1 g kg−1 was abandoned because the value was scarcely more than the mean + 6SD (104.8 g kg−1). Therefore, 245 soil samples were used for the subsequent analysis. Pearson correlations between SOM content and predictors such as FTIR-ATR spectra, Sentinel-2 spectral bands and indices, and DEM derivatives are shown in Figure 3. The SOM content was inversely correlated with the stretching vibration (ν) of O–H at 4000–3550 cm−1, quartz overtone at 2000−1790 cm−1, bending vibration (δ) of Al–OH at 915 cm−1, and C–O out of the plane at 875 cm−1, respectively (Figure 3a). The νO–H at 4000−3550 cm−1 was potentially derived from clay minerals and water [37,38], the δAl–OH at 915 cm−1 was derived from kaolinite and smectite [39], and C–O out of the plane at 875 cm−1 was derived from carbonates (Table 3). The SOM content, however, revealed strong correlations with the FTIR-ATR bands of νC–H at 3000−2800 cm−1, νC=O/νC=C at 1720–1600 cm−1, νN–H, νC–N in the plane at 1570–1540 cm−1, νC=C at 1515 cm−1, νC–H at 1445–1350 cm−1, νC–O at 1160 cm−1, and δC–O at 1050 cm−1 (Figure 3a). Alcohols, phenols, carboxyl and hydroxyl groups, amides, amide II, aliphatic methyl and methylene groups, carbohydrates, aromatics, methyls, polysaccharides, nucleic acids, and proteins were the main constituents of these spectra lines (Table 3). SOM content had no significant relationship with Sentinel-2 spectral bands, but there were strong relationships with spectral indices and DEM derivatives (Figure 3b). SOM content, for example, correlated significantly positively with TCA, TWI, ValDep, MRVBF, RVI, DVI, NDVI, ENDVI, GDVI, EVI, TVI, OSAVI, IPVI, GRVI, RDVI, and CLEX and significantly negatively with Elevation, CNBL, and CAEX.

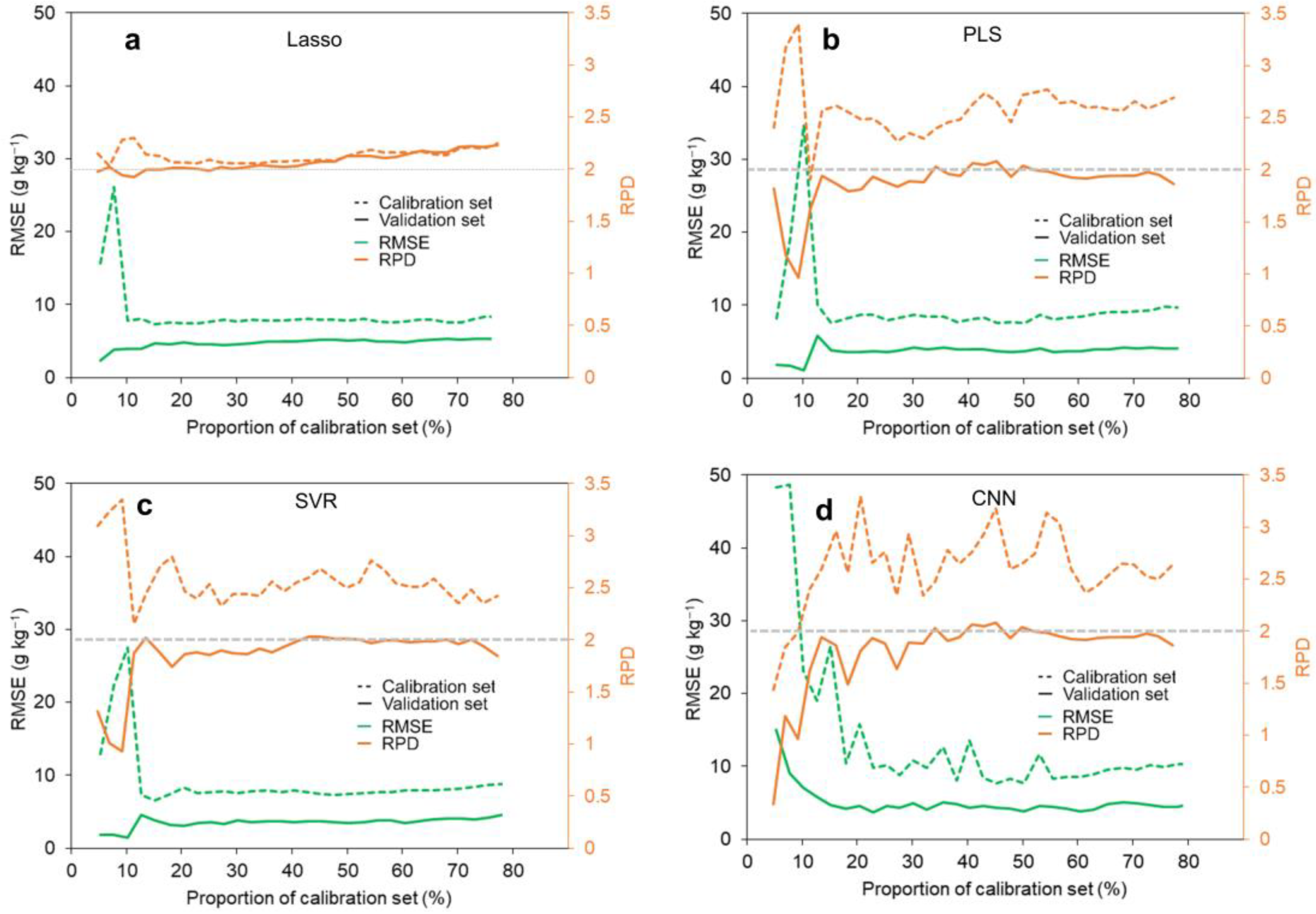
3.2. Optimal Calibration Size

In general, the model’s prediction performance decreases exponentially as the calibration size increases, whereas the difficulty of soil chemical analysis increases linearly. In four models, we investigated how the calibration size affected SOM prediction performance (Figure 4). As the proportion of the calibration set rose in the four models, there were apparent exponential declining trends in RMSE in both the calibration and validation sets. When the fraction of calibration size was greater than 40% in the PLS, SVR, and CNN models, the SOM prediction exhibited no improvement with increasing calibration size (Figure 4a–c). However, when the fraction of the calibration size was greater than 40% in the Lasso model, the RPD in the validation set continued to increase, suggesting the absence of resilience for a small calibration size. We picked 50% of the soil samples as a calibration set using the Kennard–Stone technique.

3.3. SOM Prediction Using FTIR-ATR Spectra

Figure 5 depicts the performance of four models with optimal model parameters (Table S2, Supplementary Materials) in terms of SOM prediction. The four models had a good quantitative performance for SOM prediction. The Lasso model had slight over-fitting, as SOM prediction performance for the calibration set (RMSEC = 2.8 g kg−1, RC2 = 0.845, and RPDC = 2.54) was better than the validation set (RMSEV = 7.6 g kg−1, RV2 = 0.651, and RPDV = 1.92). Over-fitting was also found in the CNN model, as SOM prediction performance in the calibration set (RMSEC = 3.1 g kg−1, RC2 = 0.813, and RPDC = 2.31) was superior to that in the validation set (RMSEV = 7.6 g kg−1, RV2 = 0.635, and RPDV = 1.77). The PLS model showed well-fitting, as the validation set (RMSEV = 7.1 g kg−1, RV2 = 0.701, and RPDV = 2.08) showed close performance compared to the calibration set (RMSEC = 3.680 g kg−1, RC2 = 0.738, and RPDC = 1.95). The SVR also had over-fitting because the calibration set (RMSEC = 3.3 g kg−1, RC2 = 0.795, and RPDC = 2.21) outperformed that the validation set (RMSEV = 7.4 g kg−1, RV2 = 0.643, and RPDV = 1.98). We also applied permutation feature importance, which calculated the feature importance of models for a given dataset to assess the importance of FTIR-ATR spectra (Figure S1, Supplementary Materials). The four models presented higher importance values at the bands of vO–H, vO–H/vC–H, overtone vCOH, vC=C/vC=O, vN–H/vC–N, and vC–H. The difference was that the Lasso and PLS models showed the highest positive important values at the overtone bands of vCOH and vC–H/vCOO−, whereas the SVR and CNN models had the highest positive importance value at the band of vN–H/vC–N. These findings supported the previously discovered link between spectral intensity and SOM content.

3.4. SOM Prediction Incorporating Satellite and DEM Data

Table 4 shows the prediction results of SOM from optimized models based on individual satellite and DEM data, as well as the fused data of FTIR-ATR, Sentinel-2, and DEM data. Individual Sentinel-2 bands and indices, as well as DEM derivatives, performed comparatively poorly in terms of SOM prediction as compared with FTIR-ATR spectra, owing to the limited link between SOM content and Sentinel-2 indices and DEM derivatives. In the validation set, the Lasso model produced the worst prediction result for SOM, which was predicted with an RMSE of 13.0 g kg−1, R2 of 0.121, and RPD of 1.12 using individual Sentinel-2 bands, indices, and DEM derivatives. Among the four models, the SVR model provided the best prediction performance for SOM (RMSE = 11.9 g kg−1, R2 = 0.299, and RPD = 1.23). The PLS and CNN models achieved considerable SOM prediction performance with an R2 of 0.215 and 0.204, respectively. This variation in prediction performance might be caused by the different learning abilities of models to abstract data. Only CLEX, TCA, and CNBL were significant in the Lasso model, indicating that the simplest linear model failed to acquire abstract characteristics in Sentinel-2 bands, indices, and DEM derivatives, as illustrated in Figure 6. The ranking of variables in the remaining three predictive models also changed noticeably. PLS and CNN models, for example, were sensitive to Sentinel-2 spectral indices and DEM derivatives, whereas the SVR model was impressed by Sentinel-2 spectral bands and indices. PlCu, ENDVI, SOC index, TCA, and CLEX were the five most important variables in the PLS model. The five most important variables in the SVR model were the B2, SOC index, SAVI, MSAVI2, and LS Factor. The CNN model’s five most important variables were the SOC index, PlCu, MCARI, TCA, TPI, and CNBL. The SOC index was one of the top five essential variables in three models, indicating that these three models were interpretable.
Nonetheless, combining Sentinel-2 and DEM data with FTIR-ATR spectra improved the prediction performance for SOM in four models (Table 4). In the Lasso model, incorporating Sentinel-2 and DEM sharply increased the R2 from 0651 to 0.700 and decreased the RMSE from 7.6 to 7.1 g kg−1. Furthermore, the over-fitting problem was avoided by combining Sentinel-2 and DEM data with FTIR-ATR spectra, as the value of RV2/RC2 increased from 0.77 to 1.13. For PLS and SVR models, combining Sentinel-2 and DEM data with FTIR-ATR spectra not only improved the prediction performance but also prevented over-fitting. The fusion of Sentinel-2 and DEM data with FTIR-ATR spectra did not improve the prediction performance of the CNN model but did prevent over-fitting.

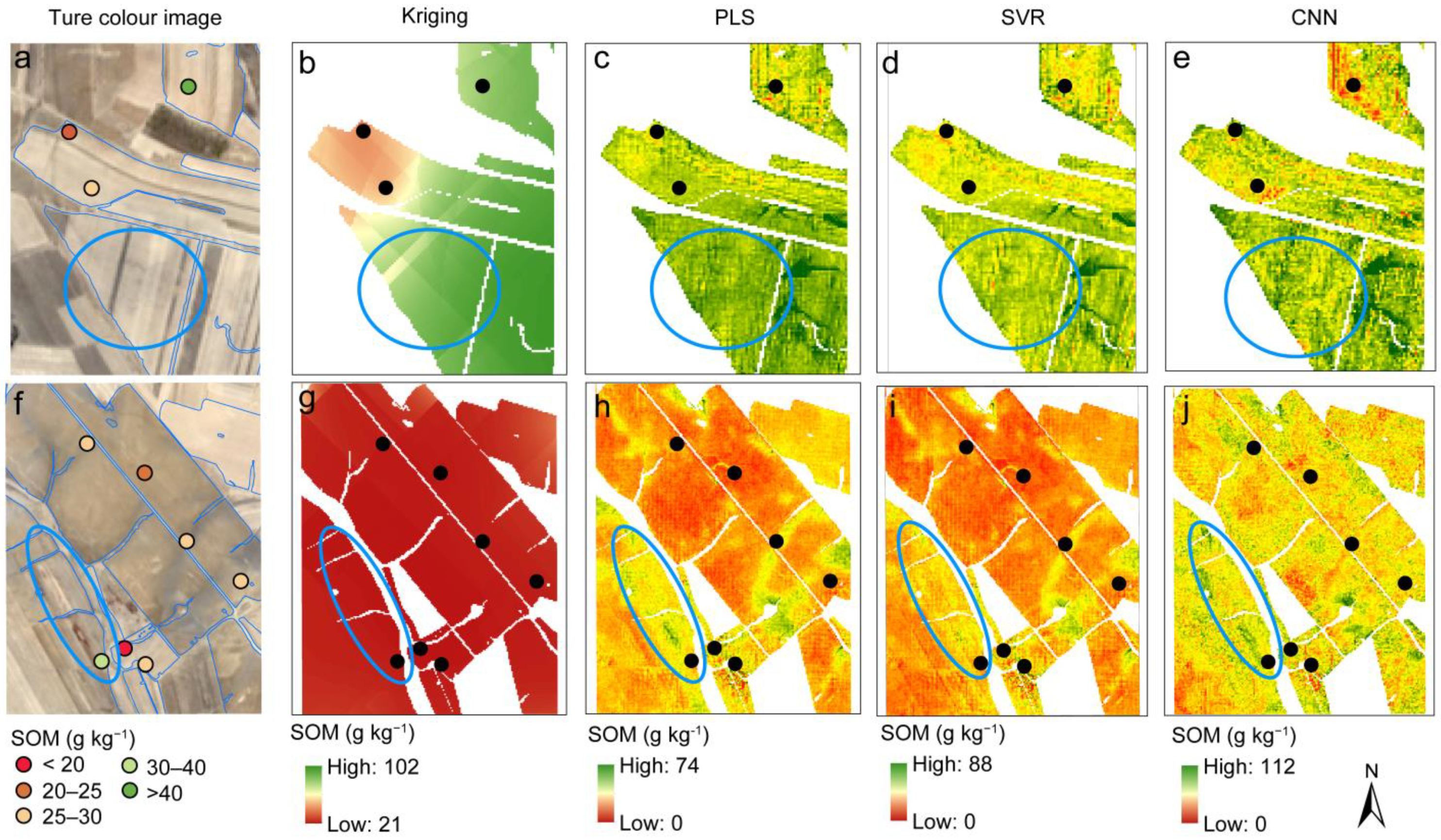
3.5. Digital Mapping of SOM

The first 10 important Sentinel-2 indices and DEM derivatives were selected to build PLS, SVR, and CNN models for the mapping of SOM according to the Permutation Feature Importance. SOM maps with 10 m spatial resolutions based on PLS, SVR, and CNN models were compared to SOM maps produced by Kriging interpolation (Figure 7). The correlation between predicted and measured SOM of the sampled soils revealed that the CNN model performed better than other models (Figure S2). Furthermore, in terms of SOM prediction, the PLS and SVR models outperformed the Kriging approach. Different machine learning models produced spatial distribution maps of SOM content that were comparable to Kriging interpolation on the global scale but differed in detail (Figure 7). The predicted SOM content was higher in the northern part of the study area, which had a lower elevation, than in the other parts. The northwestern part of the study area with the highest elevation had the lowest SOM contents. The highest elevation in the northwestern region of the study area had the lowest SOM content. This finding was also consistent with a strong negative correlation between SOM concentration and elevation (Figure 3). SOM maps with higher spatial resolution and diversity were produced using machine learning methods rather than Kriging interpolation (Figure 8).

4. Discussion

4.1. Optimization of Calibration Size Promoted Analysis Efficiency

When a field-scale FTIR-ATR spectra database is not available, the SOM content of some collected samples is analyzed using a chemical technique and used to construct a prediction model for the other samples using soil FTIR-ATR spectra to improve analysis efficiency. As a result, the calibration size is a critical aspect in defining the model’s prediction performance and the complexity of soil chemical analysis. According to Ma et al. [52], adequate calibration samples determine prediction accuracy; however, the inclusion of heretical cases decreases the model’s prediction capacity. In general, a large calibration size improves model performance, which plateaus when the calibration size is reduced to an appropriate level [53]. For example, Lucà et al. [54] investigated the influence of calibration size on the prediction performance of soil carbon in an independent validation set by Vis-NIR spectroscopy. According to the validation results, the optimum calibration sizes for PCR, SVR, and PLS were found to be 29 (17.9%), 72 (44.4%), and 115 (71.0%) samples, respectively. Ramirez-Lopez et al. [55] optimized the calibration size for the prediction of soil properties by Vis-NIR spectroscopy according to the mean squared Euclidean distance (MSD) values and found that the differences between the calibration sets in their MSD values were marginal beyond 180 samples, which was roughly 40% of the total sample size. According to Chen et al. [56], the prediction performance for calibration to validation ratios of 2:1, 4:1, and 9:1 using vis-NIR spectroscopy was relatively close, regardless of the influence of the calibration sample and validation techniques. In this study, we found slight promotion of the SOM prediction performance with increasing calibration size when the number of calibration samples was over 100 (40%), which was consistent with the previous study that 100–200 calibration samples were sufficient for spectral predictive modeling at a field scale [56]. When employing small calibration samples, the prediction performance was steady since the Euclidean distances between the spectra were considered and the calibration set and the unknown sample had comparable distribution characteristics [55]. As a consequence, fewer soil samples were needed for chemical analysis, and SOM analysis became more effective while maintaining the reliability of predictions.

4.2. Integration of Satellite and DEM Data Enhanced Prediction Performance

Previous studies had successfully reported reliable and accurate estimates of SOM using FTIR spectra [7,8,57,58]. Our study’s good prediction performance for SOM content in all four models was due to the excellent correlation between FTIR-ATR spectral intensity and SOM content (Figure 3a). The vibration lines obtained from the functional groups of organic matter were favorably associated with the SOM concentration, demonstrating that the FTIR-ATR approach captured SOM characteristics. However, the SOM presented a negative correlation with the vibration of minerals. This is due to a trade-off between the mineral and organic contents in soil, with soil with low SOM content having higher mineral content. These linear features were easily learned by the four models, resulting in reasonably accurate estimates of SOM. The capacity of various models to learn linear or abstract characteristics drove the disparities in SOM prediction performance. The linear models including Lasso, PLS, and SVR performed better than the CNN model, indicating their higher capacity for linear features. CNN is capable of dealing with abstract structures [59] because its multi-layer processing can transform a feature from the raw spectra into a higher-level representation of abstraction [60].
When using remote sensing data, several indicators demonstrated a good linear association with SOM content. For the same moisture content and parental material, dark-colored soils contain more SOC than pale-colored soils [61], which makes sense given the negative correlation of SOM content with SI and HI. The SOM content showed a negative correlation with land elevation, which was consistent with the previous study [62]. They also suggested that the SOM might be more stable at lower altitudes. The inverse relationship between soil carbonate and SOM content accounted for the negative correlation between CAEX and SOM content, as shown by FTIR-ATR spectral analysis. Individual remote sensing data had a relatively poorer performance than FTIR-ATR spectra. The relationship between SOM content and remote sensing data was critical for the model to estimate accurately. Previous studies had indicated that the types of remote sensing data, the choice of prediction models, and even the location of the study area all influenced prediction accuracy [21,63,64]. There was no omnipotent predictive model under all circumstances [12]. The comparison of prediction performance using satellite and DEM data in this study revealed that the types of machine learning had a significant impact on the SOM prediction accuracy (Table 4). The Lasso model, as a linear model, successfully captured the linear correlated predictors due to their high variable importance (Figure 6). However, these linear features were insufficient to predict SOM well, resulting in poor prediction performance for the Lasso model. The SVR model outperformed the other models with an RMSE of 11.9 g kg−1 and R2 of 0.299. This was also caused by the difference in the capability of these models to learn the features from remote sensing data. The SVR model was more sensitive to the Sentinel-2 bands and indices which were not linearly correlated with SOM content. This finding, when combined with the FTIR-ATR result, demonstrated that the SVR model could adapt to both linear and nonlinear features. Because CNN is a very data-hungry approach [65], it did not perform well on the calibration set of only 123 samples and 63 variables.
Integration of environmental variables into proximal sensing is an effective way to improve prediction accuracy. Goydaragh, Taghizadeh-Mehrjardi, Jafarzadeh, Triantafilis, and Lado [23] evaluated the performance of combining environmental variables and FTIR spectra as predictors in the prediction of SOC content. They found that a combination of environmental variables and FTIR spectra with the Cubist and Bat model was outperformed. In this study, the Sentinel-2 bands, indices, and DEM derivatives were used to improve the SOM prediction performance of FTIR-ATR. By incorporating Sentinel-2 bands, indices, and DEM derivatives, the Lasso, PLS, and SVR models were slightly improved, whereas the CNN model was not improved. Furthermore, the incorporation of Sentinel-2 bands, indices, and DEM derivatives prevented the four models from under-fitting. These findings suggested that incorporating environmental variables and proximal spectra could significantly improve model accuracy and robustness. As we all know, some of these remote sensing and DEM data are publicly available. As a result, incorporating these data into the model is extremely cost-effective, as it only requires a small amount of time and resources to improve the model’s accuracy. To improve prediction accuracy, future studies should include more environmental variables, data fusion approaches, and models. In addition, the quality of satellite imagery is related to the calibration, which converts the original satellite data into the radiation amount of the Earth’s atmosphere. Transfer of satellite data needs the support of ground spectral data. However, ground labs cannot fully simulate the orbiting environment, which influences the accuracy of the satellite image. If the problem of satellite calibration technology is not solved, the development of remote sensing satellites in digital soil mapping will also be restricted.

4.3. Machine Learning Model Improved Mapping Accuracy and Resolution

Similar geographical distribution in the global SOM content was obtained by three machine learning models as compared to the Kriging approach. The region with high SOM content was placed in the north while that with low SOM was located in the northwestern area. The regional distributions of SOM content as determined by Kriging and three machine learning techniques were significantly correlated with the elevation distribution. The relevance of elevation in estimating SOM has been proven in recent studies [12,66]. These findings suggested the robustness of the SOM mapping framework based on FTIR-ATR spectra, Sentinel-2, and DEM data. In comparison with other models, the CNN model had a better estimation of the spatial SOM content, which was different from the SOM prediction outcome. However, the CNN model overestimated some regions, as the predicted highest value (112 g kg−1) was higher than the actual one. The PLS and SVR models predicted more realistic highest values, indicating that the PLS and SVR models were more robust than CNN. In summary, the PLS and SVR models provided enough variety and were more realistic in the local SOM map.
Another benefit of using machine learning in digital soil mapping is its high precision and capacity to convey variance. Figure 8 shows that the PLS, SVR, and CNN models revealed more information about the spatial distribution of SOM than the Kriging method. The soil RGB colors of Sentinel-2, for example, were highly variable in Figure 8a, but the Kriging method failed to provide this local spatial variability. The PLS, SVR, and CNN models all demonstrated significant local spatial variability, but the CNN model performed the best, followed by PLS and SVR. Similarly, the Kriging method was incapable of displaying the local high SOM content in a large region surrounded by low SOM content. Surprisingly, as evidenced by the sampled soil in this region, the PLS, SVR, and CNN models were able to provide high SOM content in a low SOM region. The high-resolution variables of remote sensing were primarily responsible for the three models’ strong variation expression. In a nutshell, our findings show that combining FTIR-ATR spectra and remote sensing data improves not only the prediction performance of SOM content but also the mapping accuracy and robustness of spatial distribution.
Although we only focus on the modeling process in DSM by integrating remote sensing data and proximal sensing data, considering the environmental covariates in soil sampling design also influences the SOM mapping performance. For DSM, the mapping precision is significantly influenced by the distributions of sampling sites in the feature space and geographical space, as well as the distribution of point pairs at different distances [67,68]. For proximal sensing, the understanding of the impact of soil sampling design on prediction accuracy is still limited. Recently, a study indicated that it cannot absolutely provide definitive indications of either the effects of the study area size or soil sampling density in the prediction of SOC by vis-NIR spectroscopy [69]. Therefore, whether the inclusion of environmental covariates in soil sampling design can affect the accuracy of proximal sensing is still unknown and deserves further study. However, it is foreseeable that the consideration of environmental covariates will improve the accuracy of SOM mapping, so it is possible to further improve the accuracy and convenience of SOM mapping by incorporating soil sampling design into this framework in the future.

5. Conclusions

Soil FTIR-ATR spectra were integrated with remote sensing data to offer a framework for SOM mapping. This framework included optimization of calibration size, prediction of SOM content for sampled sites based on the fusion of FTIR-ATR spectra, Sentinel-2 bands, indices, and DEM derivates, and generation of a SOM map by machine learning. With a modest calibration size (50%), an acceptable prediction performance for SOM content based on FTIR-ATR spectra was obtained by partitioning the dataset using the Kennard–Stone algorithm, which significantly decreased the cost of SOM chemical analysis and increased efficiency. Predictive models were enhanced with Sentinel-2 bands, indices, and DEM derivates to improve forecast accuracy and prevent the over-fitting issue. The most effective model, PLS, performed admirably for SOM prediction, with an RMSE of 6.9 g kg−1, an R2 of 0.713, and an RPD of 2.25. The SOM maps generated by machine learning based on Sentinel-2 bands, indices, and DEM derivates showed higher spatial resolution and variation than the Kriging method. The PLS and SVR models achieved the more accurate and robust estimation for spatial SOM among the three machine learning models. In conclusion, this framework provides a detailed flowchart for mapping high-resolution SOM maps by integrating FTIR-ATR spectra and remote sensing data, thereby assisting in rapid soil assessment and tillage management.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs15041072/s1, Figure S1: Variable importance of FTIR-ATR spectra for SOM prediction in Lasso (a), PLS (b), SVR (c), and CNN (d); Figure S2: Density distribution of measured and estimated SOM contents by Kriging (a), PLS (b), SVR (c), and CNN (d) mapping models; Table S1: Derived indices from Sentinel-2 bands; Table S2: Optimized parameters of models for SOM prediction and mapping used in this study [70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96].

Author Contributions

Conceptualization, X.X. and C.D.; methodology, X.X. and Z.Q.; software, X.X.; validation, F.M. and X.X.; formal analysis, X.X.; investigation, F.M.; resources, C.D.; data curation, X.X.; writing—original draft preparation, X.X.; writing—review and editing, X.X., F.M. and C.D.; visualization, X.X.; supervision, C.D. and J.Z.; project administration, C.D.; funding acquisition, C.D. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA28040500, XDA28120400) and the R & D Project for Promoting Mongolia (NMKJXM202107).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Guo, L.; Zhang, H.; Shi, T.; Chen, Y.; Jiang, Q.; Linderman, M. Prediction of soil organic carbon stock by laboratory spectral data and airborne hyperspectral images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
  2. Gomez, C.; Viscarra Rossel, R.A.; McBratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and field vis-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar] [CrossRef]
  3. Luo, C.; Zhang, X.; Meng, X.; Zhu, H.; Ni, C.; Chen, M.; Liu, H. Regional mapping of soil organic matter content using multitemporal synthetic Landsat 8 images in Google Earth Engine. Catena 2022, 209, 105842. [Google Scholar] [CrossRef]
  4. Lal, R. Societal value of soil carbon. J. Soil Water Conserv. 2014, 69, 186A–192A. [Google Scholar] [CrossRef] [Green Version]
  5. Lal, R. Soil health and carbon management. Food Energy Secur. 2016, 5, 212–222. [Google Scholar] [CrossRef]
  6. Wang, S.; Zhao, Y.; Wang, J.; Gao, J.; Zhu, P.; Cui, X.A.; Xu, M.; Zhou, B.; Lu, C. Estimation of soil organic carbon losses and counter approaches from organic materials in black soils of northeastern China. J. Soil. Sediment. 2020, 20, 1241–1252. [Google Scholar] [CrossRef]
  7. Xu, X.; Du, C.; Ma, F.; Shen, Y.; Wu, K.; Liang, D.; Zhou, J. Detection of soil organic matter from laser-induced breakdown spectroscopy (LIBS) and mid-infrared spectroscopy (FTIR-ATR) coupled with multivariate techniques. Geoderma 2019, 355, 113905. [Google Scholar] [CrossRef]
  8. Peltre, C.; Lucas, S.; Du, C.; Thomsen, I.K.; Jensen, L.S. Assessing soil constituents and labile soil organic carbon by mid-infrared photoacoustic spectroscopy. Soil Biol. Biochem. 2014, 77, 41–50. [Google Scholar] [CrossRef]
  9. Huang, J.; Rinnan, Å.; Bruun, T.B.; Engedal, T.; Bruun, S. Identifying the fingerprint of permanganate oxidizable carbon as a measure of labile soil organic carbon using Fourier transform mid-infrared photoacoustic spectroscopy. Eur. J. Soil Sci. 2021, 72, 1831–1841. [Google Scholar] [CrossRef]
  10. McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
  11. Wadoux, A.M.J.C.; McBratney, A.B. Hypotheses, machine learning and soil mapping. Geoderma 2021, 383, 114725. [Google Scholar] [CrossRef]
  12. Goydaragh, S.; Kumar, L.; Wilson, B. Digital soil mapping algorithms and covariates for soil organic carbon mapping and their implications: A review. Geoderma 2019, 352, 395–413. [Google Scholar] [CrossRef]
  13. Wang, N.; Peng, J.; Xue, J.; Zhang, X.; Huang, J.; Biswas, A.; He, Y.; Shi, Z. A framework for determining the total salt content of soil profiles using time-series Sentinel-2 images and a random forest-temporal convolution network. Geoderma 2022, 409, 115656. [Google Scholar] [CrossRef]
  14. Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
  15. Gholizadeh, A.; Žižala, D.; Saberioon, M.; Borůvka, L. Soil organic carbon and texture retrieving and mapping using proximal, airborne and Sentinel-2 spectral imaging. Remote Sens. Environ. 2018, 218, 89–103. [Google Scholar] [CrossRef]
  16. Zhou, T.; Geng, Y.; Ji, C.; Xu, X.; Wang, H.; Pan, J.; Bumberger, J.; Haase, D.; Lausch, A. Prediction of soil organic carbon and the C:N ratio on a national scale using machine learning and satellite data: A comparison between Sentinel-2, Sentinel-3 and Landsat-8 images. Sci. Total Environ. 2021, 755, 142661. [Google Scholar] [CrossRef]
  17. Gardin, L.; Chiesi, M.; Fibbi, L.; Maselli, F. Mapping soil organic carbon in Tuscany through the statistical combination of ground observations with ancillary and remote sensing data. Geoderma 2021, 404, 115386. [Google Scholar] [CrossRef]
  18. Nguyen, T.T.; Pham, T.D.; Nguyen, C.T.; Delfos, J.; Archibald, R.; Dang, K.B.; Hoang, N.B.; Guo, W.; Ngo, H.H. A novel intelligence approach based active and ensemble learning for agricultural soil organic carbon prediction using multispectral and SAR data fusion. Sci. Total Environ. 2022, 804, 150187. [Google Scholar] [CrossRef]
  19. Wang, B.; Waters, C.; Orgill, S.; Gray, J.; Cowie, A.; Clark, A.; Liu, D.L. High resolution mapping of soil organic carbon stocks using remote sensing variables in the semi-arid rangelands of eastern Australia. Sci. Total Environ. 2018, 630, 367–378. [Google Scholar] [CrossRef]
  20. Minhoni, R.T.d.A.; Scudiero, E.; Zaccaria, D.; Saad, J.C.C. Multitemporal satellite imagery analysis for soil organic carbon assessment in an agricultural farm in southeastern Brazil. Sci. Total Environ. 2021, 784, 147216. [Google Scholar] [CrossRef]
  21. Zhou, T.; Geng, Y.; Chen, J.; Pan, J.; Haase, D.; Lausch, A. High-resolution digital mapping of soil organic carbon and soil total nitrogen using DEM derivatives, Sentinel-1 and Sentinel-2 data based on machine learning algorithms. Sci. Total Environ. 2020, 729, 138244. [Google Scholar] [CrossRef]
  22. Rial, M.; Cortizas, A.M.; Rodríguez-Lado, L. Mapping soil organic carbon content using spectroscopic and environmental data: A case study in acidic soils from NW Spain. Sci. Total Environ. 2016, 539, 26–35. [Google Scholar] [CrossRef]
  23. Goydaragh, M.G.; Taghizadeh-Mehrjardi, R.; Jafarzadeh, A.A.; Triantafilis, J.; Lado, M. Using environmental variables and Fourier Transform Infrared Spectroscopy to predict soil organic carbon. Catena 2021, 202, 105280. [Google Scholar] [CrossRef]
  24. Moura-Bueno, J.M.; Dalmolin, R.S.D.; Horst-Heinen, T.Z.; Grunwald, S.; ten Caten, A. Environmental covariates improve the spectral predictions of organic carbon in subtropical soils in southern Brazil. Geoderma 2021, 393, 114981. [Google Scholar] [CrossRef]
  25. IUSS Working Group WRB. World Reference Base for Soil Resources; IUSS Working Group WRB: Rome, Italy, 2014. [Google Scholar]
  26. Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and a proposed odification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
  27. Van Bemmelen, J.M. Über die Bestimmung des Wassers, des Humus, des Schwefels, der in den colloïdalen Silikaten gebundenen Kieselsäure, des Mangans u. s. w. im Ackerboden. Landwirthschaftlichen Vers. Station. 1890, 37, 279–290. [Google Scholar]
  28. Shoko, C.; Mutanga, O. Examining the strength of the newly-launched Sentinel 2 MSI sensor in detecting and discriminating subtle differences between C3 and C4 grass species. ISPRS J. Photogramm. 2017, 129, 32–40. [Google Scholar] [CrossRef]
  29. European Space Agency. Sentinel-2 MSI User Guide. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi (accessed on 4 January 2022).
  30. Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
  31. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
  32. Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.s.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on heterogeneous Distributed Systems. Available online: https://www.tensorflow.org/ (accessed on 12 January 2022).
  33. Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B. 1996, 58, 267–288. [Google Scholar] [CrossRef]
  34. Shetty, N.; Gislum, R. Quantification of fructan concentration in grasses using NIR spectroscopy and PLSR. Field Crop. Res. 2011, 120, 31–37. [Google Scholar] [CrossRef]
  35. Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
  36. Ng, W.; Minasny, B.; Montazerolghaem, M.; Padarian, J.; Ferguson, R.; Bailey, S.; McBratney, A.B. Convolutional neural network for simultaneous prediction of several soil properties using visible/near-infrared, mid-infrared, and their combined spectra. Geoderma 2019, 352, 251–267. [Google Scholar] [CrossRef]
  37. Churchman, G.J.; Foster, R.C.; D’Acqui, L.P.; Janik, L.J.; Skjemstad, J.O.; Merry, R.H.; Weissmann, D.A. Effect of land-use history on the potential for carbon sequestration in an Alfisol. Soil Tillage Res. 2010, 109, 23–35. [Google Scholar] [CrossRef]
  38. Xing, Z.; Tian, K.; Du, C.; Li, C.; Zhou, J.; Chen, Z. Agricultural soil characterization by FTIR spectroscopy at micrometer scales: Depth profiling by photoacoustic spectroscopy. Geoderma 2019, 335, 94–103. [Google Scholar] [CrossRef]
  39. Viscarra Rossel, R.A.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
  40. Xu, X.; Du, C.; Ma, F.; Shen, Y.; Zhou, J. Forensic soil analysis using laser-induced breakdown spectroscopy (LIBS) and Fourier transform infrared total attenuated reflectance spectroscopy (FTIR-ATR): Principles and case studies. Forensic Sci. Int. 2020, 310, 110222. [Google Scholar] [CrossRef]
  41. Pedersen, J.A.; Simpson, M.A.; Bockheim, J.G.; Kumar, K. Characterization of soil organic carbon in drained thaw-lake basins of Arctic Alaska using NMR and FTIR photoacoustic spectroscopy. Org. Geochem. 2011, 42, 947–954. [Google Scholar] [CrossRef]
  42. Ellerbrock, R.H.; Gerke, H.H. Characterizing organic matter of soil aggregate coatings and biopores by Fourier transform infrared spectroscopy. Eur. J. Soil Sci. 2004, 55, 219–228. [Google Scholar] [CrossRef]
  43. Soriano-Disla, J.M.; Janik, L.J.; Viscarra Rossel, R.A.; Macdonald, L.M.; McLaughlin, M.J. The performance of visible, near-, and mid-infrared reflectance spectroscopy for prediction of soil physical, chemical, and biological properties. Appl. Spectrosc. Rev. 2014, 49, 139–186. [Google Scholar] [CrossRef]
  44. Janik, L.J.; Skjemstad, J.O.; Shepherd, K.D.; Spouncer, L.R. The prediction of soil carbon fractions using mid-infrared-partial least square analysis. Soil Res. 2007, 45, 73–81. [Google Scholar] [CrossRef] [Green Version]
  45. Du, C.; Goyne, K.W.; Miles, R.J.; Zhou, J. A 1915–2011 microscale record of soil organic matter under wheat cultivation using FTIR-PAS depth-profiling. Agron. Sustain. Dev. 2014, 34, 803–811. [Google Scholar] [CrossRef]
  46. Du, C.; Linker, R.; Shaviv, A. Characterization of soils using photoacoustic mid-infrared spectroscopy. Appl. Spectrosc. 2007, 61, 1063–1067. [Google Scholar] [CrossRef]
  47. Calderón, F.; Haddix, M.; Conant, R.; Magrini-Bair, K.; Paul, E. Diffuse-reflectance fourier-transform mid-infrared spectroscopy as a method of characterizing changes in soil organic matter. Soil Sci. Soc. Am. J. 2013, 77, 1591–1600. [Google Scholar] [CrossRef] [Green Version]
  48. Leifeld, J. Application of diffuse reflectance FT-IR spectroscopy and partial least-squares regression to predict NMR properties of soil organic matter. Eur. J. Soil Sci. 2006, 57, 846–857. [Google Scholar] [CrossRef]
  49. Movasaghi, Z.; Rehman, S.; ur Rehman, D.I. Fourier transform infrared (FTIR) dpectroscopy of biological tissues. Appl. Spectrosc. Rev. 2008, 43, 134–179. [Google Scholar] [CrossRef]
  50. Madejová, J. FTIR techniques in clay mineral studies. Vib. Spectrosc. 2003, 31, 1–10. [Google Scholar] [CrossRef]
  51. Nayak, P.S.; Singh, B.K. Instrumental characterization of clay by XRF, XRD and FTIR. Bull. Mater. Sci. 2007, 30, 235–238. [Google Scholar] [CrossRef] [Green Version]
  52. Ma, F.; Du, C.; Zhou, J.; Shen, Y. Optimized self-adaptive model for assessment of soil organic matter using Fourier transform mid-infrared photoacoustic spectroscopy. Chemometr. Intell. Lab. Syst. 2017, 171, 9–15. [Google Scholar] [CrossRef]
  53. Kuang, B.; Mouazen, A.M. Influence of the number of samples on prediction error of visible and near infrared spectroscopy of selected soil properties at the farm scale. Eur. J. Soil Sci. 2012, 63, 421–429. [Google Scholar] [CrossRef] [Green Version]
  54. Lucà, F.; Conforti, M.; Castrignanò, A.; Matteucci, G.; Buttafuoco, G. Effect of calibration set size on prediction at local scale of soil carbon by Vis-NIR spectroscopy. Geoderma 2017, 288, 175–183. [Google Scholar] [CrossRef]
  55. Ramirez-Lopez, L.; Wadoux, A.M.J.C.; Franceschini, M.H.D.; Terra, F.S.; Marques, K.P.P.; Sayão, V.M.; Demattê, J.A.M. Robust soil mapping at the farm scale with vis–NIR spectroscopy. Eur. J. Soil Sci. 2019, 70, 378–393. [Google Scholar] [CrossRef] [Green Version]
  56. Chen, S.; Xu, H.; Xu, D.; Ji, W.; Li, S.; Yang, M.; Hu, B.; Zhou, Y.; Wang, N.; Arrouays, D.; et al. Evaluating validation strategies on the performance of soil property prediction from regional to continental spectral data. Geoderma 2021, 400, 115159. [Google Scholar] [CrossRef]
  57. Du, C.; Zhou, J.; Wang, H.; Chen, X.; Zhu, A.; Zhang, J. Determination of soil properties using Fourier transform mid-infrared photoacoustic spectroscopy. Vib. Spectrosc. 2009, 49, 32–37. [Google Scholar] [CrossRef]
  58. Xing, Z.; Du, C.; Tian, K.; Ma, F.; Shen, Y.; Zhou, J. Application of FTIR-PAS and Raman spectroscopies for the determination of organic matter in farmland soils. Talanta 2016, 158, 262–269. [Google Scholar] [CrossRef]
  59. Ni, W.; Nørgaard, L.; Mørup, M. Non-linear calibration models for near infrared spectroscopy. Anal. Chim. Acta 2014, 813, 1–14. [Google Scholar] [CrossRef]
  60. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
  61. Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]
  62. Bangroo, S.A.; Najar, G.R.; Achin, E.; Truong, P.N. Application of predictor variables in spatial quantification of soil organic carbon and total nitrogen using regression kriging in the North Kashmir forest Himalayas. Catena 2020, 193, 104632. [Google Scholar] [CrossRef]
  63. Beguin, J.; Fuglstad, G.A.; Mansuy, N.; Paré, D. Predicting soil properties in the Canadian boreal forest with limited data: Comparison of spatial and non-spatial statistical approaches. Geoderma 2017, 306, 195–205. [Google Scholar] [CrossRef]
  64. Castaldi, F.; Hueni, A.; Chabrillat, S.; Ward, K.; Buttafuoco, G.; Bomans, B.; Vreys, K.; Brell, M.; van Wesemael, B. Evaluating the capability of the Sentinel 2 data for soil organic carbon prediction in croplands. ISPRS J. Photogramm. 2019, 147, 267–282. [Google Scholar] [CrossRef]
  65. Padarian, J.; Minasny, B.; McBratney, A.B. Using deep learning to predict soil properties from regional spectral data. Geoderma Reg. 2019, 16, e00198. [Google Scholar] [CrossRef]
  66. Song, X.D.; Brus, D.J.; Liu, F.; Li, D.C.; Zhao, Y.G.; Yang, J.L.; Zhang, G.L. Mapping soil organic carbon content by geographically weighted regression: A case study in the Heihe River Basin, China. Geoderma 2016, 261, 11–22. [Google Scholar] [CrossRef]
  67. Li, X.; Gao, B.; Pan, Y.; Bai, Z.; Gao, Y.; Dong, S.; Li, S. Multi-objective optimization sampling based on Pareto optimality for soil mapping. Geoderma 2022, 425, 116069. [Google Scholar] [CrossRef]
  68. Wadoux, A.M.J.C.; Brus, D.J.; Heuvelink, G.B.M. Sampling design optimization for soil mapping with random forest. Geoderma 2019, 355, 113913. [Google Scholar] [CrossRef]
  69. Conforti, M.; Buttafuoco, G. Insights into the effects of study area size and soil sampling density in the prediction of soil organic carbon by vis-NIR diffuse reflectance spectroscopy in two forest areas. Land 2023, 12, 44. [Google Scholar] [CrossRef]
  70. Escadafal, R. Remote sensing of arid soil surface color with Landsat thematic mapper. Adv. Space Res. 1989, 9, 159–163. [Google Scholar] [CrossRef]
  71. Srisomkiew, S.; Kawahigashi, M.; Limtong, P.; Yuttum, O. Digital soil assessment of soil fertility for Thai jasmine rice in the Thung Kula Ronghai region, Thailand. Geoderma 2022, 409, 115597. [Google Scholar] [CrossRef]
  72. Metternicht, G.I.; Zinck, J.A. Remote sensing of soil salinity: Potentials and constraints. Remote Sens. Environ. 2003, 85, 1–20. [Google Scholar] [CrossRef]
  73. Yu, H.; Liu, M.; Du, B.; Wang, Z.; Hu, L.; Zhang, B. Mapping soil salinity/sodicity by using Landsat OLI imagery and PLSR algorithm over semiarid west Jilin Province, China. Sensors 2018, 18, 1048. [Google Scholar] [CrossRef] [Green Version]
  74. Wang, F.; Shi, Z.; Biswas, A.; Yang, S.; Ding, J. Multi-algorithm comparison for predicting soil salinity. Geoderma 2020, 365, 114211. [Google Scholar] [CrossRef]
  75. Wang, F.; Yang, S.; Wei, Y.; Shi, Q.; Ding, J. Characterizing soil salinity at multiple depth using electromagnetic induction and remote sensing data with random forests: A case study in Tarim River Basin of southern Xinjiang, China. Sci. Total Environ. 2021, 754, 142030. [Google Scholar] [CrossRef] [PubMed]
  76. Wu, W.; Al-Shafie, W.M.; Mhaimeed, A.S.; Ziadat, F.; Nangia, V.; Payne, W.B. Soil salinity mapping by multiscale remote sensing in Mesopotamia, Iraq. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 4442–4452. [Google Scholar] [CrossRef]
  77. Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
  78. Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
  79. Nellis, M.D.; Briggs, J.M. Transformed vegetation index for measuring spatial variation in drought impactedbiomass on Konza Prairie, Kansas. Trans. Kans. Acad. Sci. 1992, 95, 93–99. [Google Scholar] [CrossRef]
  80. Marsett, R.C.; Qi, J.; Heilman, P.; Biedenbender, S.H.; Carolyn Watson, M.; Amer, S.; Weltz, M.; Goodrich, D.; Marsett, R. Remote sensing for grassland management in the arid southwest. Rangeland Ecol. Manag. 2006, 59, 530–540. [Google Scholar] [CrossRef]
  81. Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
  82. Qi, J.; Kerr, Y.; Chehbouni, A. External factor consideration in vegetation index development. In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, Val d’Isere, France, 17–21 January 1994. [Google Scholar]
  83. Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
  84. Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
  85. Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
  86. Goffart, D.; Curnel, Y.; Planchon, V.; Goffart, J.-P.; Defourny, P. Field-scale assessment of Belgian winter cover crops biomass based on Sentinel-2 data. Eur. J. Agron. 2021, 126, 126278. [Google Scholar] [CrossRef]
  87. Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
  88. Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
  89. Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1: Theoretical approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar] [CrossRef]
  90. Scudiero, E.; Skaggs, T.H.; Corwin, D.L. Regional scale soil salinity evaluation using Landsat 7, western San Joaquin Valley, California, USA. Geoderma Reg. 2014, 2–3, 82–90. [Google Scholar] [CrossRef]
  91. Thaler, E.A.; Larsen, I.J.; Yu, Q. A new index for remote sensing of soil organic carbon based solely on visible wavelengths. Soil Sci. Soc. Am. J. 2019, 83, 1443–1450. [Google Scholar] [CrossRef]
  92. Taghizadeh-Mehrjardi, R.; Minasny, B.; Sarmadian, F.; Malone, B.P. Digital mapping of soil salinity in Ardakan region, central Iran. Geoderma 2014, 213, 15–28. [Google Scholar] [CrossRef]
  93. Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
  94. Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 red-edge bands for empirical estimation of green LAI and chlorophyll content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef] [Green Version]
  95. Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. 2013, 82, 83–92. [Google Scholar] [CrossRef] [Green Version]
  96. Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
Remotesensing 15 01072 g001 550
Figure 1. The geographic location of the study area and the distribution of the soil sampling sites.
Figure 1. The geographic location of the study area and the distribution of the soil sampling sites.
Remotesensing 15 01072 g001
Remotesensing 15 01072 g002 550
Figure 2. Detailed flowchart of the framework for data obtaining, processing, and modeling.
Figure 2. Detailed flowchart of the framework for data obtaining, processing, and modeling.
Remotesensing 15 01072 g002
Remotesensing 15 01072 g003 550
Figure 3. Pearson correlation between SOM content and FTIR-ATR spectral intensity (a) and Sentinel-2 spectral bands, indices, and DEM derivatives (b). The interpretation of the abbreviations can be found in Table 1 and Table 2, and Table S1. Significance levels are denoted with * p < 0.05 and ** p < 0.01, respectively.
Figure 3. Pearson correlation between SOM content and FTIR-ATR spectral intensity (a) and Sentinel-2 spectral bands, indices, and DEM derivatives (b). The interpretation of the abbreviations can be found in Table 1 and Table 2, and Table S1. Significance levels are denoted with * p < 0.05 and ** p < 0.01, respectively.
Remotesensing 15 01072 g003
Remotesensing 15 01072 g004 550
Figure 4. The root mean squared error (RMSE) and residual predictive deviation (RPD) were computed based on different calibration sizes in Lasso (a), partial least squares (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)) models.
Figure 4. The root mean squared error (RMSE) and residual predictive deviation (RPD) were computed based on different calibration sizes in Lasso (a), partial least squares (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)) models.
Remotesensing 15 01072 g004
Remotesensing 15 01072 g005 550
Figure 5. Scatter plots of measured and predicted SOM contents by Lasso (a), partial least square (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)) models based on FTIR-ATR spectra.
Figure 5. Scatter plots of measured and predicted SOM contents by Lasso (a), partial least square (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)) models based on FTIR-ATR spectra.
Remotesensing 15 01072 g005
Remotesensing 15 01072 g006 550
Figure 6. Variable importance of Sentinel-2 bands, indices, and DEM derivatives for SOM prediction in Lasso (a), partial least square (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)). The interpretation of the abbreviations can be found in Table 1 and Table 2, and Table S1.
Figure 6. Variable importance of Sentinel-2 bands, indices, and DEM derivatives for SOM prediction in Lasso (a), partial least square (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)). The interpretation of the abbreviations can be found in Table 1 and Table 2, and Table S1.
Remotesensing 15 01072 g006
Remotesensing 15 01072 g007 550
Figure 7. Estimated spatial distribution of SOM content in the study area using Kriging (a), partial least square (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)) models.
Figure 7. Estimated spatial distribution of SOM content in the study area using Kriging (a), partial least square (PLS, (b)), support vector regression (SVR, (c)), and convolutional neural network (CNN, (d)) models.
Remotesensing 15 01072 g007
Remotesensing 15 01072 g008 550
Figure 8. Subareas of the spatial distribution of SOM content in high (a–e) and low (f–j) SOM estimated by Kriging ((b) and (g)), partial least square (PLS, (c) and (h)), support vector regression (SVR, (d) and (i)), and convolutional neural network (CNN, (e) and (j)) methods. Subplots show the zooms of areas in Figure 7. The blue circle areas indicate that machine learning models show abundant and realistic local spatial variability than the Kriging method.
Figure 8. Subareas of the spatial distribution of SOM content in high (a–e) and low (f–j) SOM estimated by Kriging ((b) and (g)), partial least square (PLS, (c) and (h)), support vector regression (SVR, (d) and (i)), and convolutional neural network (CNN, (e) and (j)) methods. Subplots show the zooms of areas in Figure 7. The blue circle areas indicate that machine learning models show abundant and realistic local spatial variability than the Kriging method.
Remotesensing 15 01072 g008
Table
Table 1. Details of Sentinel-2 bands used in this study.
Table 1. Details of Sentinel-2 bands used in this study.
BandCentral Wavelengths (nm)Bandwidth (nm)Spatial Resolution (m)SNR 1 (at Lref)Description
B14432060129Coastal aerosol
B24906510154Blue
B35603510168Green
B46653010142Red
B57051520117Vegetation red edge
B6740152059Vegetation red edge
B77832020105Vegetation red edge
B884211510172NIR
B8A865202072Narrow NIR
B101375306050SWIR-Cirrus
B111610902010SWIR1
B1221901802010SWIR2
1 SNR refers to the signal-to-noise ratio. Referenced by European Space Agency [29].
Table
Table 2. Terrain attributes derived from Digital Elevation Model (DEM).
Table 2. Terrain attributes derived from Digital Elevation Model (DEM).
AttributesDefinition
ElevationElevation
SlopeSlope
AspectAspect
AnHillAnalytical Hillshading
LSFactorLS Factor
TCATotal catchment area
TWITopographic wetness index
CoInConvergence index
RSPRelative slope position
PrCuProfile curvature
PlCuPlan curvature
CNDChanel network distance
ValDepValley depth
TPITopographic position index
CNBLChanel network base level
MRRTFMulti-resolution of ridge top flatness index
MRVBFMulti-resolution of valley bottom flatness index
Table
Table 3. Assignment of the characteristic bands in FTIR-ATR spectra.
Table 3. Assignment of the characteristic bands in FTIR-ATR spectra.
Wavenumber (cm−1)VibrationFunctional Group or Component
620νO–HClay minerals [40]
3600–3000νO–H, N–HWater, alcohols, and phenols; carboxyl and hydroxyl groups, amides [41,42]
3000–2800νC–HAliphatic methyl and methylene groups [42,43]
2200–2000Overtone νCOHCarbohydrates [44]
1720–1600νC=O, νC=CCarboxylic acids; amides; Aromatics [45,46]
1570–1540νN–H, νC–N in planeAmide II [47,48]
1515νC=CAromatics [47]
1500–1300νCO32−Carbonates [39]
1445–1350νC–HMethyls [44,39]
1160νC–OPolysaccharides, nucleic acids, proteins [47]
1050δC–OCarbohydrates [39,49]
990νSi–OClay minerals [50]
915δAl–OHKaolinite and smectite [39]
875C–O out of planeCarbonates
770NH2 out of planePrimary amine [51]
where ν and δ denote stretching vibration and bending vibration, respectively.
Table
Table 4. Performance of SOM prediction by different models and data.
Table 4. Performance of SOM prediction by different models and data.
ModelSpectraSatellite and DEM DataFused
RMSER2RPDRv2/Rc2RMSER2RPDRv2/Rc2RMSER2RPDRv2/Rc2
Lasso7.60.6511.9210.77013.00.1211.1230.9517.10.7002.0561.132
PLS7.10.7012.0560.95012.00.2151.2170.9146.90.7132.1161.021
SVR7.40.6431.9730.80911.90.2991.2320.9317.20.6882.0281.010
CNN7.70.6351.8960.78112.10.2041.2050.8967.50.6321.9470.996
PLS, partial least square; SVR, support vector regression; CNN, convolutional neural network; MAE, mean absolute error; RMSE, root mean square error; and RPD, residual prediction deviation.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xu, X.; Du, C.; Ma, F.; Qiu, Z.; Zhou, J. A Framework for High-Resolution Mapping of Soil Organic Matter (SOM) by the Integration of Fourier Mid-Infrared Attenuation Total Reflectance Spectroscopy (FTIR-ATR), Sentinel-2 Images, and DEM Derivatives. Remote Sens. 2023, 15, 1072. https://doi.org/10.3390/rs15041072

AMA Style

Xu X, Du C, Ma F, Qiu Z, Zhou J. A Framework for High-Resolution Mapping of Soil Organic Matter (SOM) by the Integration of Fourier Mid-Infrared Attenuation Total Reflectance Spectroscopy (FTIR-ATR), Sentinel-2 Images, and DEM Derivatives. Remote Sensing. 2023; 15(4):1072. https://doi.org/10.3390/rs15041072

Chicago/Turabian Style

Xu, Xuebin, Changwen Du, Fei Ma, Zhengchao Qiu, and Jianmin Zhou. 2023. "A Framework for High-Resolution Mapping of Soil Organic Matter (SOM) by the Integration of Fourier Mid-Infrared Attenuation Total Reflectance Spectroscopy (FTIR-ATR), Sentinel-2 Images, and DEM Derivatives" Remote Sensing 15, no. 4: 1072. https://doi.org/10.3390/rs15041072

APA Style

Xu, X., Du, C., Ma, F., Qiu, Z., & Zhou, J. (2023). A Framework for High-Resolution Mapping of Soil Organic Matter (SOM) by the Integration of Fourier Mid-Infrared Attenuation Total Reflectance Spectroscopy (FTIR-ATR), Sentinel-2 Images, and DEM Derivatives. Remote Sensing, 15(4), 1072. https://doi.org/10.3390/rs15041072

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop