Abstract
The raindrop size distribution (DSD) is vital for applications such as quantitative precipitation estimation, understanding microphysical processes, and validation/improvement of two-moment bulk microphysical schemes. We trace the history of the DSD representation and its linkage to polarimetric radar observables from functional forms (exponential, gamma, and generalized gamma models) and its normalization (un-normalized, single/double-moment scaling normalized). The four-parameter generalized gamma model is a good candidate for the optimal representation of the DSD variability. A radar-based disdrometer was found to describe the five archetypical shapes (from Montreal, Canada) consisting of drizzle, the larger precipitation drops and the ‘S’-shaped curvature that occurs frequently in between the drizzle and the larger-sized precipitation. Similar ‘S’-shaped DSDs were reproduced by combining the disdrometric measurements of small-sized drops from an optical array probe and large-sized drops from 2DVD. A unified theory based on the double-moment scaling normalization is described. The theory assumes the multiple power law among moments and DSDs are scaling normalized by the two characteristic parameters which are expressed as a combination of any two moments. The normalized DSDs are remarkably stable. Thus, the mean underlying shape is fitted to the generalized gamma model from which the ‘optimized’ two shape parameters are obtained. The other moments of the distribution are obtained as the product of power laws of the reference moments M3 and M6 along with the two shape parameters. These reference moments can be from dual-polarimetric measurements: M6 from the attenuation-corrected reflectivity and M3 from attenuation-corrected differential reflectivity and the specific differential propagation phase. Thus, all the moments of the distribution can be calculated, and the microphysical evolution of the DSD can be inferred. This is one of the major findings of this article.
1. Introduction
The drop size distribution (DSD) is central to the formulation of radar algorithms that estimate the quantitative precipitation estimate (QPE) which is a separate article in this Special Issue [1,2] and to understanding the ongoing microphysical processes that control the evolution of DSDs in certain environments [3]. The DSD measured at an ‘instant’ of time at a certain location on the ground is a result of many drop–drop interactions that occur in the warm cloud and below cloud base often referred to as ‘warm rain’ processes. Each binary process results in a break up or coalescence event—neither of which are well understood [4]. In the case of virga, evaporation below the cloud base dominates causing cooling and possibly strong downdrafts [5]. Up/downdrafts, sedimentation and/or drop sorting is the result of cloud kinematic scales that are not resolvable by the usual bulk microphysics. The stronger updrafts loft the raindrops into the ‘cold’ regions of the cloud where they freeze and further grow by diffusional growth [6]. Similar to collision-coalescence, ice crystals grow rapidly by riming and aggregation. As the particles grow, their terminal fall speed exceeds the updraft speeds, leading to falling snow particles. Finally, snow particles melt as passing 0 °C melting layer [7,8,9,10] and further grow by the aforementioned warm rain processes, leading to a ‘cold rain’ precipitation shaft with large drops. It should be obvious by now that the DSD measured by a disdrometer is the end result of a torturous sequence of events.
The description and understanding of DSDs go back to the late nineteenth century. The development of ground-based disdrometers such as filter paper [11], Joss-Waldvogel Disdrometer [12], Parsivel (Particle Size and Velocity) [13], POSS (Precipitation Occurrence Sensor Systems) [14], 2DVD (2-Dimensional Video Distrometer) [15,16], HVSD (Hydrometeor Velocity and Size Detector) [17], MASC (Multi-Angle Snowflake Camera) [18,19], PIP (Precipitation Imaging Package) [20,21], etc., was a long-lasting issue for the accurate observation of DSDs. Several uncertainty issues existed in observed DSDs and their significance and filtering techniques were proposed to avoid misinterpretating these DSDs, thus the misunderstanding of naturally occurring microphysical processes [22,23,24,25]. Thus, the description of minute-by-minute observed DSDs requires special attention, in particular, functional fitting to find an exact form of DSD and to use fitted parameters to describe the natural variability of DSDs.
Nevertheless, early studies focused on the functional fit of observed DSDs with specific functions such as exponential, gamma, log-normal, etc. One of the rare studies that avoided fitting individual observed DSD was the description of observed DSDs averaged over the similar rainfall intensity R [11]. The exponential function was sufficient to describe the variability of DSDs with a single control parameter R in stratiform rain in Montreal. However, the individual observed DSDs exhibited large variation from the perfect single parameter exponential and attracted researchers to use two parameters exponential function [26] and/or three-parameter gamma function [27,28] to account for time scales in the order of minute (O (min)).
On the other hand, the idea of [11] further pushed for the normalization of DSDs. The demand of two parameters led to the two-parameter normalization by [26,29] who used the 3rd and 6th moment of DSDs. Later, this approach was revisited and finally applied to radar retrieval techniques [30]. Testud et al. [30] showed a “remarkable stability of shape” when the N(D) is normalized by Nw and the diameter is normalized by Dm. This particular form of the double moment normalization using the 3rd and 4th moments of the DSD compressed the scatter of N(D) vs. D substantially to the extent that 80–85% of the variability of the DSD can be attributed to variations in Nw and Dm with the intrinsic shape playing a much smaller role [31,32,33].
However, this favorable normalization is an outcome of scaling DSDs. The scaling concept was ubiquitous in nature. Sempere-Torres et al. [34,35] first described DSDs with the scaling concept, the power law between two moments of DSDs. This power law assumption led a single parameter (known as the reference variable by [34]) normalization and the two scaling parameters are linearly related. This scaling concept was extended into the double-moment scaling normalization [31]. The scaling normalization of [34] was a particular case of the double moment normalization, and furthermore, early works by [11,26,30] were outcomes of the selection of different moments. The theoretical underpinnings of double moment normalization, the choice of moments, and its generalization will be discussed later.
The polarimetric radar retrieval of the DSD has a root in the description and their models. Typically, the parameters of DSD models were derived from a combination of measured dual-polarimetric variables. As originally proposed by [36], ZDR is related to a mean size of DSD and while Zh is number concentration. This has been the basis of DSD retrieval up to now. In terms of DSD models, there are diverse trials with described DSD models. In general, the specific DSD model with assumptions were used for the retrieval of parameters earlier and normalized DSDs were commonly used as well. Since there are a substantial number of articles dealing with the subject of polarimetric radar retrieval of the DSD, we can only focus on a small number of seminal articles that have influenced the field. We borrowed heavily from a recent review by [37] that gives a more personal and reflective point of view. In addition, recent trails of moment estimation and then DSD retrieval will be discussed.
Section 2 mentions the description of DSDs and their models that are commonly used. The description of DSDs in diameter and moment space is discussed and several DSD models including scaling normalization is presented. The state-of-the-art retrieval of DSDs is explained in Section 3 as well. Section 4 describes the results of DSD retrievals with various methods. Furthermore, the application of DSD retrieval and the remaining issues are discussed in Section 5.
2. DSD Description and Models
2.1. Description of DSDs
2.1.1. DSDs in Diameter Space
DSDs are commonly expressed in the number concentration as functions of diameters, that is, the number of drop per unit volume per unit diameter interval in [m−3 mm−1]. The number of drops was counted for pre-determined diameter intervals and normalized with a measured volume and diameter interval.
Figure 1 showed 60 one-minute observed DSDs during a quasi-homogeneous microphysical process. Nevertheless, observed DSDs are quite noisy due to observational noise, such as drop sorting, and instrumental uncertainty which is poorly known [23]. Lee and Zawadzki [23] nicely illustrated that the drop sorting introduced random and systematic fluctuations of DSDs and the measurement noise should be reduced by the sequential intensity filter technique (SIFT). An extension of this filter, sorting and averaging procedure based on two parameters (SATP) was proposed by [25] to further reduce noise and to retain microphysical characteristics.

Figure 1.
60 one min observed DSDs by the Precipitation Occurrence Sensor System (POSS) on 5 May 1998 in Montreal. The x-axis is diameter in linear scale and the y-axis is number concentration in logarithmic scale.
Filtered DSDs should be used for describing the processes involved. Traditionally, a functional fitting is commonly applied for parameterizing DSDs. The most popular approach is the exponential fitting to observe DSDs (M-P DSDs) [11]. Ref. [11] was aware of the measurement noise. Instead of fitting individual observed DSDs, DSDs of similar rainfall intensity (R) were grouped for a few seasons and then averaged. This was repeated for different rainfall intensities and averaged DSDs were derived. This procedure eliminates some degree of noise in the observed DSDs by assuming that the noise is random in a given interval of R. Then, the averaged DSDs maintain the physical variation of DSDs. This is a similar filtering as SIFT but some significant physical variation is removed due to the physical variation of DSDs in similar Rs from different rain regimes [23]. Finally, the averaged DSDs were fitted with the exponential functions as follows:
where N(D) is number concentration [m−3 mm−1], D is diameter [mm]. The N0 is an intercept parameter and λ is the slope as shown in Equation (2). As shown by Figure 2, the N0 is a constant (=8 × 103 m−3 mm−1) and the slope [mm−1] is dependent on rainfall intensity (R):
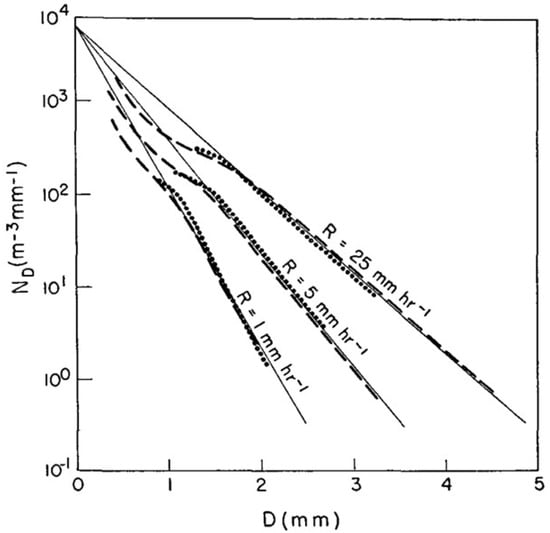
Figure 2.
Average DSDs (dotted lines) for different rainfall intensities and exponential fits (solid lines) introduced by [11]. Published 1948 by the American Meteorological Society.
Thus, Marshall and Palmer’s DSD requires a single parameter, either λ or R, to describe the full DSD spectra. It is important to note that the results are an outcome of a careful analysis of the observed DSDs from stratiform rainfall in summer. The measurement noise in DSDs is significantly eliminated by averaging DSDs, and in addition, the average is performed in similar rainfall intensity (R), thus effectively removing noise [23]. Although significant physical variation is reduced, recent analyses show similar M-P DSDs. In addition, the N(D) drops significantly around 1~2 mm diameters and then [11] extrapolates N(D) at sizes smaller than these diameters. This trend is repeatedly shown in the recently observed DSDs with advanced distrometers and their normalized DSDs (shown in later in Figures 5 and 6).
However, observed DSDs in nature vary with microphysical processes and their variation goes beyond the change of the slope in the exponential DSD. Their variation is linked with a change in mean diameter, spectral width, the total number concentration, and the shape of the DSD. Waldvogel [26] showed a systematic change of N0 within a widespread rain event due to change in the convective activity and used two parameters (N0 and λ) exponential DSD to explain DSD variation. In this expression, the N0 is a variable, and N0 and λ are defined as the intercept and slope parameters of exponential DSD that have the same liquid water content and radar reflectivity factor as the observed DSD. Thus, the derived N0 and λ are not the same as the directly fitted variables in the observed DSD.
In fact, when we examine the individual observed DSDs, the functional fitting does not fully describe the observed DSD. As shown in Figure 1, it is difficult to fit observed DSDs with two parameters exponential function and often attract further parameters. Instead of the two parameters of exponential DSD, the three parameters of the gamma function are used to describe the observed DSDs [27,28]:
where μ is the shape parameter. The shape of DSD is, however, constrained due to μ. That is, its shape is concave with negative μ and vice versa with positive μ. Thus, the general variation of the DSD shape is not fully described with the three parameters gamma function. In addition, the unit of N0 [m−3 mm−1−μ] varies with the value of the shape parameter μ and does not have the same physical meaning as in the exponential function.
The attempt of the functional fit with the gamma function applied to the observed DSDs from JWD (Joss Waldvogel disdrometer) that were affected by the deadtime. Thus, the shape of observed DSDs was biased (convex shape with low number concentration in smaller sizes). Furthermore, the variation of parameters was derived from Z-R relationships in the literature by comparing the derived Z-R power law from the gamma function [27]. This was mathematically incorrect and the uncertainty in the Z-R relationships due to DSD measurement noise and fitting methods was not properly considered [23]. Nevertheless, the gamma DSD is commonly applied to the bulk microphysical schemes in numerical weather prediction models, mostly fixed μ.
To better describe complex DSDs of different shape, the generalized gamma distribution (GG) is proposed [38,39,40,41]. A probability density function of GG [42] is
with positive parameters μ, c, λ. Then, the DSD is expressed as the product of 0th moment of the DSD (total number concentration) and p(D).
This includes the DSD models mentioned previously. The exponential distribution is a special case of c = 1 and μ = 1 and the gamma function is a special case of c = 1. The Weibull distribution (μ = 1) is a better assumption than the gamma distribution in terms of more flexibility of DSD shape.
Figure 3 showed the flexibility of shapes that can be represented by GG [31]. A mono-disperse shape is well presented with different skewness. Exponential and gamma shapes are shown with diverse curvature. In particular, the “S” shape (abundant smaller size drops, modal distribution in medium-size drops, and lower number concentration in larger size), so-called equilibrium DSDs [33], is presented with c = 3 and cμ − 1 = −2.
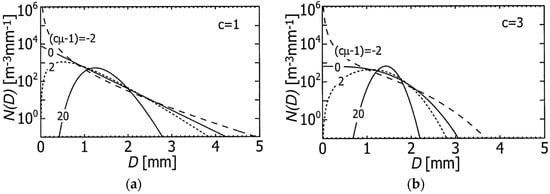
Figure 3.
(a,b) Sample DSDs of different shapes that are generated by the generalized gamma distribution. The liquid water content (LWC) and characteristic diameter (Dm’) are fixed as 0.5 g m−3 and 1.5 mm. Adapted from [31]. © American Meteorological Society. Used with permission.
The various DSD models (exponential, gamma, generalized gamma) were represented as a proxy of observed DSDs. These models mostly fit observed DSDs with predefined functions with direct least-square fit or a combination of moments. Thus, the existing noise in observed DSDs can be critical to mislead true parameters and should be removed prior to fitting. This approach has the advantage of presenting full spectra of DSDs with a few parameters and is commonly used in NWP parameterization.
2.1.2. DSDs in Moment Space
As shown in Figure 1, the observed DSDs were affected by a measurement noise, such as observational and instrumental uncertainties, which led to wiggly and diverse shapes. It is certain that some wiggles and variation in observed DSDs originated from the noise that was not related to the physical processes. In particular, a sudden change from one drop category to the other and rapid variation from one minute to the other in smaller and larger sizes are likely controlled by measurement noise.
Figure 4 showed different samples of one-minute DSDs observed by POSS in Montreal. Five DSDs were highlighted with different colors to show a narrow DSD (green), a broad gamma DSD (blue), a bimodal DSD (red), an exponential DSD (magenta), and a super-exponential DSD (orange). All these representative DSDs showed fine details. In fact, the traditional exponential or gamma model cannot perfectly describe these DSDs. The generalized gamma model will fit these DSDs better but fine details will be never explained.
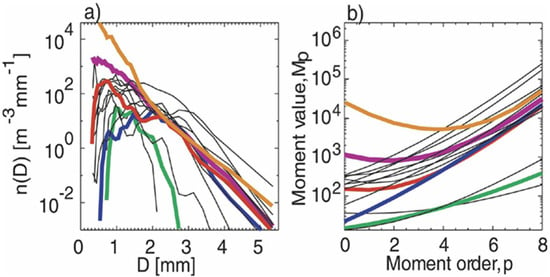
Figure 4.
(a) Samples of observed one-minute DSDs from POSS in Montreal. (b) Their moment values with moment order. Five DSDs were highlighted by different colors. Adapted from [43]. © American Meteorological Society. Used with permission.
However, all fine details are gone in a moment distribution (Figure 4b). Those wiggly shapes are gone and moment distributions straighten up. A monodisperse N(D) with a lower number concentration showed lower values of Mn and the bimodality of N(D) was gone (red). The gamma N(D) changed to nearly linear Mn, and an exponential or super-exponential N(D) showed a concave shape of Mn with increasing curvature when a higher concentration in smaller size drops. The change of slope and pivoting of Mn distribution can be explained by two parameters, that is, two moments [31,43]. An optimal choice of two moments can explain most of other moments [31]. However, its curvature is likely explained by an additional moment and three moments are sufficient to estimate other moments [43]. Thus, the description of DSDs in moment space has definite advantages in terms of (1) a better representation of observed DSDs and (2) minimal effect of measurement noise in DSD description.
Furthermore, bulk quantities (moments) are fields of interest in most cases. In the bulk microphysics scheme of NWP, the moments are predicted instead of DSDs and DSDs are diagnosed with predicted moments. Finally, other moments are derived from diagnosed DSDs. In this aspect, the relationships among moments can directly be used without knowing DSDs. In radar rain estimation, similar power-law relationships, such as R-Zh, R-KDP, R-(Zh, ZDR), etc., are used for estimating one moment from the other moments. When a multiple power law is used, that is, the third moment estimated from the other two moments, the estimation error can be lower than 30% for most of the cases and this error can be below 10% when three moments are used to estimate the fourth moment [43].
Instead of describing DSDs directly, N0 and λ are derived from a combination of two moments (3rd and 4th or 3rd and 6th moments) [26,29]. The derived N0 and λ were used to monitor the change in processes. Furthermore, DSDs were normalized with these two derived parameters [29,44] and the stability of normalized DSD was investigated. Normalization has an advantage in minimizing the effects of measurement noise since it is performed by integral moments which are less affected. In addition, the shape change became less significant as the overall slope change and pivoting were taken into account by normalization parameters. Thus, variation was reduced significantly in normalized DSDs.
The normalization is revisited by the concept of scaling law. When the Mi (i-th moment) of DSDs is used as a normalization parameter (or reference variable), normalized DSD can be expressed as
where g(x1) is called the generic shape in this normalization and x1 = [31]. The β is the scaling exponent. The power law between n-th and i-th moment exists:
where the coefficient, , is the n-th moment of g(x) in a single-moment normalization. Thus, the scaling law of DSDs represents self-similarity of distribution that is independent of Mi. The rainfall intensity R is commonly used as the reference variable in [34,35]. A similar concept was applied in the field of aerosol [45].
In a single-moment scaling normalization, the scatter around g(x) is significant. That is, a single parameter cannot fully describe the variability of DSDs. This requires the necessity of the second parameter. Similar to the single-moment scaling, if there exists the multiple power law among moments as below
The normalized DSD can be expressed as
where h(x2) is the generic DSD and subscript 2 indicates the double moment normalization. is the nth moment of h(x2). The and are the characteristic number concentration and characteristic diameter, respectively, and are defined by a combination of two reference variables (Mi and Mj) in the generalized double-moment scaling normalization [31]. Testud et al. [30] normalization is a particular case with i = 3 and j = 4 and Waldvogel [26] with i = 3 and j = 6. Testud et al. [30] found that h(x) was remarkably stable and all variability of DSDs was controlled by and .
A similar stability was found in many parts of the world [31,32,33,46]. Figure 5 showed the frequency distribution of normalized DSDs with the 3rd and 4th moments from climatological data of DSDs in two regions (South Korea and Oklahoma) [33]. Average h(x)s (solid lines in Figure 5c) were almost identical. This average h(x) was fitted with the generalized gamma (GG) function:
where , . The fitted GGs are almost identical with similar c and μ. Thus, most discernible variability is contained in the two parameters, either two moments or and . Thus, a fixed h(x) and two moments estimated from dual-polarimetric variables can be used to retrieve DSDs [32,47].

Figure 5.
Frequency distribution of normalized DSDs in (a) South Korea and (b) Oklahoma. (c) Average h(x)s and (d) fitted h(x) with the generalized gamma function. Adapted from [33]. © American Meteorological Society. Used with permission.
Furthermore, the general double-moment normalization or normalization with GG functions was used in the microphysical scheme in NWP. Szyrmer et al. [43] expanded the double-moment normalization into a three-moment scheme in which the rate of change of Mm (prognostic moment) was expressed as the function of Mm and non-reference moments (see Equation (3.3) in [43]). Thus, non-explicit functional forms of DSDs are required. Morrison et al. [48] also estimated arbitrary moments with multiple power law from one, two, and three reference moments and concluded that three reference moments well characterized most of DSD variability. Similar to [43], Morrison et al. [49] expressed the microphysical process rate with generalized multivariate power expressions to build flexible microphysical schemes.
2.2. Observation of DSDs
Most DSD measurements so far have used 2DVD, Parsivel, and MRR (Micro-Rain Radar). They differ in terms of their operational physical principles, resolution, sensitivity (truncation) to small drops, the sampling error for large drops, etc. [15,23,50]. Fundamentally, the N(D) from these instruments generally disagrees for D < 0.8 mm and D > 4 mm but tends to agree well in the mid-range of 0.8–4 mm [51,52]. They showed comparisons of N(D) measured using (Meteorological Particle Spectrometer (MPS) and 2DVD) vs. 2DVD alone in many different rain types and rain rates. They found that the ‘drizzle’ mode was ubiquitous and could not be captured by any single instrument (Figure 6, [52]). By combining DSDs from MPS and 2DVD, the complete DSDs clearly showed a drizzle mode and a precipitation mode (Figure 6). Further, the low-order moments important for the microphysical parameterizations of processes, such as evaporation and accretion, could not be estimated with 2DVD alone.
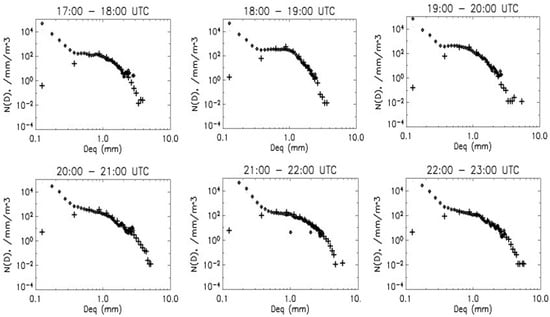
Figure 6.
Hourly DSDs from the 2DVD (plus signs) and 2DVD–MPS combined (open diamonds) adapted from Figure 11 of [52]. DSDs show the so-called “S-shape” with higher number concentration in smaller and medium sizes. © American Meteorological Society. Used with permission.
Wen et al. [53] intercompared 2DVD, Parsivels, and MRR in terms of spectral agreement and effects on evaporation and accretion during the 2014–2015 Mei-Yu season in east China. They found that only the 2DVD was accurate enough to measure the N(D), fall speeds, and lower-order moments (even without the optical array probe). Wen et al. [53] concluded that “while previous studies demonstrated that the microphysical parameterization has pronounced effects on numerically simulated storms, our study reveals that the instrumental differences and/or error have substantial impacts on the tuning of model microphysics. Therefore, to improve the accuracy of microphysical parameterization and ultimately the accuracy of storm simulations, obtaining more accurate DSDs from observations is critical and essential”.
The mean axis ratio vs. D is also one of the key observations that are required to parameterize DSDs with dual-polarimetric radar variables. The most frequently used mean axis ratio vs. D relation is from [54] who used the least squares fit the axis ratio vs. D from the literature, e.g., wind-tunnel data, airborne optical probe data, laboratory data of [55], etc., with different errors in these methods, the hypothesis being that the random errors will cancel and the mean of the fit will be close to reality. It is not entirely clear why the fit of [54] is so universally popular when the definitive 80 m water-fall experiment with 2DVD disdrometer [51] has proven to be the ‘best’ so far when compared with wind-tunnel measurements [56,57,58]. The data showed that the drops oscillate in the oblate-(slightly) prolate fundamental mode with a small component of the transverse mode mixed in.
In the wind tunnel experiments from [57], single drops were imaged using high-speed video cameras. Thus, the oscillation of a single drop was observed over several cycles and the time-averaged axis ratio was computed. The oscillation amplitude of individual drops in the wind tunnel and the increasing amplitude with an increase in equivolume D was in good agreement with the increase in the standard deviation of the axis ratio based on hundreds of the equisized drops from the 2DVD. The 80 m fall experiment data together with analysis of drop contours in two orthogonal planes showed that the canting angle distribution is approximately Gaussian with mean 0 deg. and standard deviation of 7 deg. A new understanding of drop shapes and oscillations by [59] synthesizes the knowledge of many years of laboratory measurements along with 2D-video measurements of natural raindrops. With such a solid base of theory and measurements, it is indeed surprising that the mean axis ratio from diverse measurements fitted with a polynomial fit to D is still the choice in papers as recent as (e.g., [53]).
3. Linkage between DSD Models and Dual-Polarimetric Parameters
There are a number of methods for the estimation of DSD parameters such as the two parameters [N0, D0] for the exponential, three parameters [N0, λ, μ] for the gamma, the two parameters that empirically constrained gamma [N0, λ, μ = f(λ)], and the four-parameter generalized gamma [N0′, Dm′, μ, c] with two shape parameters [μ, c]. In literature, the median mass or volume diameter, Dm or D0, is often used instead of Dm′ and normalized intercept parameter, NW for N0′. The most frequently used distribution in practice is the three-parameter gamma with one fixed-shape parameter μ = constant, or the constrained two-parameter gamma with variable μ = f(λ) in spite of the controversy surrounding its use. The most flexible is the four-parameter generalized gamma with the most flexibility in shape with μ controlling the small drop end (the so-called “drizzle” mode D ≤ 200 μm).
3.1. The First Ansatz: Exponential DSD
The first attempt at retrieving the parameters (N0, D0) of an exponential distribution using radar-measured Zh and Zdr was a concept paper introduced by [36]. They used the results in two published articles, (i) McCormick et al. [60] who showed that raindrops are oblate spheroids with their axis of symmetry aligned along the vertical and, (ii) the wind-tunnel experiments of Pruppacher and Beard [61] who showed that the axis ratio of the drops was nearly a linear function of the equivolume sphere diameter (for D > 1.0 mm). Combining these two inferences and Gan’s Rayleigh scattering, it was straightforward to compute Zdr and to relate it to D0 whilst the parameter N0 was estimated by relating log [N0/Zh] and D0. Note that this was a theoretical paper without any supporting measurements. It was a UK team at Appleton Laboratories led by Martin Hall and Steve Cherry who were the first to measure Zdr and use it to estimate N0 and D0 of an exponential DSD to estimate rapid attenuation fading at S-band at a high resolution along slanted earth–space paths [62]. Their goal was to use frequency scaling to estimate attenuation at X- and higher bands or directly integrate the product of the extinction coefficient with the exponential or gamma distributions.
3.2. The Second Ansatz: Exponential DSD
The second concept paper by [63] (henceforth SB) was related to finding another differential measurement to replace Zh as the measurement uncertainty could be large (±1 to 2 dB). Humphries [64] gave an insight as he computed the differential propagation phase shift between H and V-polarized waves in a highly oriented oblate rain medium to document the depolarization of an initial circularly polarized wave as it penetrated the rain medium. However, he failed to relate the differential propagation phase shift to the rain rate. His calculations led [63] to use the differential propagation phase shift (ΔHV) per unit distance along the beam when normalized by N0 could be related to D0. This was the second differential measurement that SB [63] were looking for to eliminate the use of Zh. However, there were no measurements of ΔHV available at that time using the available S-band radars (there were several in the USA) whose pulsing schemes were not suitable. In a ground-breaking article, Sachidananda and Zrnic [65] came up with an algorithm to estimate ΔHV (which they termed Φdp) which led to an explosion in the field. The microphysical implications of Zdr and Kdp were given in two seminal articles by [66,67], (a) Zdr could be related to M7/M6 where M is the moment of the DSD (for DSDs of the gamma family, Zdr can be related to Dm = M4/M3 where Dm is the mass-weighted mean diameter), (b) the Kdp is proportional to LWC (1-rm) where rm is the mass-weighted mean axis ratio and LWC is the liquid water content.
3.3. The Constrained Gamma Drop Size Distribution
The most widely used analytical DSD is the un-normalized gamma distribution with three parameters, N0, D0 and μ [27]. This has been utilized to derive N0 and D0 from the combination of [Zh, Zdr] [68], but because of the additional shape parameter, μ, there has been a need to assume a fixed value for μ to estimate R. An alternate way was proposed by Vivekanandan et al. [69] who used a 2D-video distrometer measured N(D) to estimate μ, N0, and D0 using the method of truncated moments. However, using simulations of a ‘perfect gamma’ DSD, Smith et al. [70] have written a number of articles on the errors of using moments to estimate [NW, Dm, μ] and pressed hard that a large number of drops are needed O(1000) to reduce the errors. They recommend maximum likelihood or L-moments [71] with the caveat that small drop truncation is not an issue. However, most commercial disdrometers, (a) cannot measure the small drop end (D < 0.5 mm) truncation and, (b) have a sampling problem due to a lack of statistical significance of the few large drops that are detected. The consensus opinion was that moments M2,4,6 would probably give the least error provided the number of drops was in the thousands every few minutes. However, Handwerker and Straub [72] differ from this opinion based on their own simulations of ‘perfect’ gamma DSD. Their contention was that it was ‘easier’ to approximate the truncated small drop concentration as opposed to “sampling adjustment” of the very noisy and few large drops. Their recommendation was that M0,1,2 may be the optimal combination of moments.
Vivekanandan et al. [69] found a high Pearson correlation between estimated values of μ and λ. An empirical least square fit of μ as a quadratic function of λ was obtained. This reduced the three-parameter to a two-parameter one. However, Mallet and Barthes [73], using simulations of gamma DSDs with fixed parameters [NW, Dm, μ] (typical of medium rain rates), found that using the method of truncated moments to estimate and based on 50 realizations of the selected medium rain rate parameters found a correlation of 0.98 between estimate and . This correlation is purely statistical with no physics. It also follows estimate and from the measured DSDs representing a variety of rain rates will show a high correlation irrespective of the instrument type used. Similarly, the negative correlation between log(NW) and Dm was also very evident (around −0.8).
Even modelers have started to adapt μ as a function of λ (and even rain rate, henceforth R) to improve the R from bulk microphysical schemes with constant μ. Nevertheless, constrained gamma continues to be used as it offers a way to estimate N0, D0, and μ using only two radar measurables Zh and Zdr [53,54,74]. Modelers have started to adapt μ as a function of rain rate and season in double-moment schemes, e.g., Morrison's two-moment bulk microphysical scheme. The goal is to improve the R from the Morrison gamma DSD with adaptive μ in terms of rain rate and season. They found that rain rate error statistics (rmse) for the adaptive μ = f(R) was 20% lower than μ = 0. However, they could not find physical reasons for the adaptive μ method.
In contrast, Schinagl et al. [75] used the microphysical parameterizations in two-moment bulk schemes μ = f(Dm′) which is a non-linear relation where Dm′ is the mean-mass diameter, to avoid excessive size sorting [76]. Seifert [77], on the other hand, simulated sedimentation, evaporation, coalescence and breakup, and derived a diagnostic non-linear μ-Dm′ relation which is implemented in the Consortium for Small-Scale Modeling (COSMO). The authors’ goal was to compare the polarimetric quantity (graph of Zdr vs. Dm′) from the model against the same graph derived from the empirical disdrometer-measured -λ quadratic. Schinagl et al. [75] comment “Our study calls for a thorough assessment of uncertainties in DSD parameter estimation which is prerequisite for any successful assimilation of polarimetric data in numerical weather prediction model”.
3.4. Testud’s Normalization
Testud et al. [30] used the normalization of Willis [44] to come up with a normalized form of the gamma distribution based on the premise that the LWC should not be dependent on μ. They defined the normalized intercept parameter NW = LWC/Dm4 and mass-weighted mean diameter Dm = M4/M3 which can be computed for any measured N(D). When the N(D) is scaled-normalized, the distribution in compact form can be written as Equation (9) or N(D) = Nw h(x) where x = D/Dm and h(x) can be any function (not necessarily in the gamma family). Testud et al. [30] and Lee et al. [31] wrote about the ‘remarkable stability’ of the intrinsic shape of h(x) even in convective and stratiform rain. This shape invariance implies that the variability of the observed N(D) due to the many microphysical and kinematic up/down-drafts and drop sedimentation processes is not controlled by h(x) but rather by fluctuations in Nw and Dm. It follows that the constrained gamma does not fall within this representation. The estimate of Nw, Dm, and the shape parameter μ from measured N(D) was used by Bringi et al. [78]. The method estimates Nw and Dm as defined by their moments while the estimation of μ is a one-dimensional non-linear minimization problem with the cost function being the absolute difference between the measured log N(D) and the desired log N(D). It is sometimes referred to as a least square [72]. However, one should keep in mind that log Nw and Dm are based on moments and there will be a negative correlation between them [73] in the range of −0.7 to −0.95 purely due to statistics. The optimal method of estimating the DSD parameters is that of maximum likelihood estimate (MLE) but for truncation at the low drop size end (D < 0.5 mm) which is common to disdrometers, the MLE does not perform as well [71] as the method of truncated moments.
One way to overcome the small drop truncation [46,52] is to use two different disdrometers, (a) a high resolution (50 μm) optical array probe used on aircraft and, (b) 2DVD with 200 μm resolution. The array probe is accurate from 100 μm to 1.5 mm whilst the 2D video is accurate for D > 0.7 mm. Thus, a composite spectrum can be defined as “use N(D) from optical array probe when D < 0.8 mm else use N(D) from the 2DVD.” Such composite spectra can be used to compare the performance of instruments (without the optical array probe), i.e., 2DVD alone, MRR, and Parsivel. There are only two permanent sites in the US (University of Alabama in Huntsville and Wallops Is, Huntsville, AL, USA) that have a collocated optical array and 2D-video inside a double fence intercomparison reference (DFIR).
4. Retrieval of DSD Parameters
4.1. Retrieval Algorithms for Parameters of the Normalized Gamma Distribution
The estimation of [Nw, Dm, μ] using the Testud normalization was developed by [79]. They used a linear relation of axis ratio vs. D with a slope of β (i.e., b/a =1 − βD) along with theoretical gamma DSDs covering a wide range of [log Nw, Dm, μ] based on [27]. Their goal was to first estimate β as the hypothesis that abs[β] decreased from mid-latitude rain (0.063 per mm) to tropical rain (0.045 per mm) to account for large amplitude oscillations due to the collisional processes which collide with collisional energy [80] insufficient to break up in the warm rain as opposed to damped oscillations due to rain forming from melting graupel/small hail. A complicated nonlinear regression was used to develop an algorithm for β in terms of Zh, Zdr, and Kdp which involved products of power laws, e.g., β = 2.08 Zh−0.365 Kdp0.38Zdr0.965 where Zh is mm6 m−3, Kdp in deg km−1 and differential reflectivity expressed as a ratio. In retrospect, Gorgucci’s ansatz must be considered remarkable. For example, Dm is retrieved using Dm = a Zhb Zdrc where a = 0.56, b = 0.064, c = 0.024 β−124. The total error (sum of parameterization and signal fluctuation errors) are quoted as 20% for the normalized standard deviation (or, NSD) when Zdr is around 2 dB. Similarly, the NSD of log NW is 16% when NW ≈ 8000 mm−1 m−3. These low NSDs are based on disdrometer-measured DSDs but no comparison with radar was given.
The first paper to quantify the use of the Gorgucci et al. method [79] appeared in Bringi et al. [78] who used radar data from SPOL and a dense gage network (10 gages in a square area of ≈ 20 m2). The details are many and cannot be explained in this review; nevertheless, the concept of an “effective” β introduced in this article has merit. However, this methodology did not appeal to the wider meteorological community since the bias errors in Zh, Zdr have to be low, respectively, ±1 dBZ and ±0.1 dB which is exceedingly difficult for research radars let alone the Operational Network of radars. Since Kdp is also involved, the errors will be high when Kdp is low (<0.2 deg km−1) which precludes the calculation of β unless the ZH > 35 dBZ. The above method has been used in a number of articles, including Bringi et al. [78], who were able to draw regions of stratiform, tropical convective, and continental convective in the log NW vs. Dm plane using Joss and 2DVD from a variety of locations ranging Papua New Guinea, Puerto Rico to Colorado. This article has been used extensively as a reference for other methods.
One of the accepted methods [78,81] for the retrieval of [Nw, Dm] is (a) access a large database of measured DSDs representative of the climatology of the region or from many regions; (b) use these measured DSDs and average them to a time resolution of 1–3 min; (c) the input to the T-matrix code is the measured DSD, frequency, mean axis ratio vs. D, temperature, mean, and standard deviation of the canting angle distribution. The integration range is given by the DSD data itself. (d) The T-matrix outputs [Zh, Zdr, Kdp, Ah, Adp and ρhv] for each measured DSD at a time resolution of 1–3 min; (e) simulate signal fluctuations or noise in Zh, Zdr, and Kdp by adding, for example, standard deviations of 1 dBZ, 0.25 dB and 0.3 deg km−1, respectively; (f) from the measured DSDs use moments M3, M4 to estimate [NW, Dm]; (g) use non-linear least squares fit of Dm (for example) as a 4th order polynomial in Zdr, and for NW a power law fit of the form M3/Dm4 and are defined by a combination of two reference variables (Mi and Mj) in the generalized double-moment scaling normalization [31]. The goal is to minimize the sum of the algorithm error and the radar measurement error. The value of β = 7 (for Rayleigh scattering), thus, the var(NW) is amplified by the factor β2. This is one reason why it is very difficult to validate radar estimates of NW against surface disdrometers.
The largest DSD database using multiple (3–7) third-generation 2DVDs was collected by the NASA ground validation program. The datasets were collected during relatively short field campaigns (around 2 months) as well as from more permanent sites (multiple years). The climatology included mid-latitude regimes including deep convection (field campaign in Oklahoma), frontal and mesoscale convective systems (field campaign in Iowa), warm-season orographic effects (field program in the Appalachians), cold-rain, coastal, and orographic effects (Washington State), as well as the multi-year sampling of sub-tropical convection (Alabama) and multi-year coastal mid-Atlantic region (Wallops Is, VA). The number of 1 min DSDs was over 204,000. The main difference is in step (c) where the fit to the laboratory measurement of transverse mode oscillations [82] was used for D < 6 mm and the equilibrium axis ratios of [59] for D > 6 mm. However, the largest drop generated in the laboratory (by [82]) was only 4 mm; in addition, three other smaller sizes were chosen. Beard et al. [83] in a reexamination of these data were convinced that the drop generator used by [82] for generating the 4 mm drops was, in fact, imparting the transverse mode oscillation which did not die down as the drop reached its terminal fall speed. In spite of this, Tokay et al. [81] chose to use the Andsager et al. fit [82] (for D < 6 mm) and the equilibrium Beard and Chuang fit [59] for D > 6 mm to retrieve Dm as a third-order polynomial in powers of Zdr, and NW as αZh/(Dm)β. The normalized standard error quoted by [81] is about 10% for Dm (for true Dm of 1.3 dB; it varies with a true value of Dm) and normalized standard error of log NW is about 6% (for true log Nw = 3.5; varies with a true value of log NW). Gorgucci et al. [79] get similar values. However, the Tokay et al. [81] quoted errors do not include radar measurement errors. Gorgucci et al. [79] estimated the sum of the two (uncorrelated) errors to be 18% for Dm and 15% for log Nw. The measurement error for log NW is seen to be a major component of the total error which can be reduced by spatial averaging or longer dwell times.
As an alternative to (a) above, the normalized gamma parameters can be uniformly distributed (for example) in the range 103 < NW < 105 mm−1 m−3; 0.5 < Dm < 3.5 mm, −1 < μ < 5. These ranges from [79] are based on [27] and appear to be representative of tropical climates. The input (c) above needs the upper limit of integration, e.g., Dmax = min [3 ∗ Dm, Dm= 8 mm] [84]. The rest of the steps are the same but it is not clear what physical meaning can be given to such a gamma distribution with random parameters. However, when R/NW is plotted vs. Dm, the median curve representing the 2D-histogram of [R/Nw; Dm] cannot be distinguished from the same using measured DSDs by 2DVDs in a large variety of climates. This is also true for other normalized plots [85].
4.2. Non-Parametric Methods
4.2.1. Variational Method
There have been several other (non-parametric) approaches to the estimation of the DSD of which the variational approach is the most common. The recent article by [86] is among the few we found that explicitly describes an optimized retrieval of DSD, attenuation-correction of Zh and Zdr, and R (simultaneously) from polarimetric radar measurements [Zh, Zdr, Φdp]. The measurement set includes ; ; where “n” refers to the nth range gate. The state vector is [Dm, W] where W is the rainwater content. The DSD is assumed to be constrained by μ = quadratic function of λ. The results based on one sweep of one C-band and one S-band radar data are very impressive when compared to the parametric methods described earlier. Nevertheless, some ad hoc assumptions have to be made regarding the measurement fluctuation errors for Zh, Zdr, and Φdp (all measured). The errors must be larger than the usually assumed values of 1 dBZ, 0.2 dB, and 0.35 deg km−1. The measurement errors are dependent on Doppler spectral width, number of samples, dwell time, SNR, etc. For Kdp, the error variance estimation depends on the path and several other factors [79]. The spatial correlation of the observational vector is largely unknown and must be assumed. The forward observational operator is not linear. In spite of these unknowns, the variational method involving the minimization of the cost function to yield the optimized [Dm, W] using the observational vector needs to be pursued to the point where the operational agencies will pursue it.
4.2.2. Inverse Method
Wen et al. [87] describe a different non-parametric method based on an inverse model where the input is {Zdr, Kdp/Zh} and the output is {μ, Dmax}, where Dmax is the maximum diameter of the retrieved gamma DSD. The choice of the ratio Kdp/Zh is based on the simple fact that the total number concentration clearly cancels out so the variability of both Dm and Kdp/Zh is fairly low. The choice of μ is based on the fact that the DSD is constrained gamma with μ being empirically linked to a quadratic in λ (using a large database of disdrometer measurements). The choice of Dmax (maximum drop diameter) is not typical since it is a random variable and reflects the variation of Zdr to the large drops in the tail of the distribution. Their approach is based on the k-nearest-neighbor (k-NN) classification from the pattern recognition literature [88]. This algorithm stores all 2DVD input–output correlations from the available data as a “training” set. When a new {Zdr, Kdp/Zh} input is presented, the {μ, Dmax} output class that is the most common amongst the k nearest (training set) neighbors of the new input is selected. The k-NN is particularly suitable when large training data are available (e.g., numerous 2DVD DSDs are now available through NASA ~1,000,000 1 min DSDs [89]).
Wen et al. [87] used the Euclidean distance to define the closeness of neighbors. They applied an empirical μ = quadratic in λ relation based on 2DVD data, while N0 is obtained after the fact using Zh, μ, λ, and Dmax. Their training set comprising Zdr and Kdp∕Zh was generated using a polynomial function whose inputs μ and Dmax are drawn from 10-year 2DVD DSD data with constraints μ ∈ [−3:20], Dmax ∈ [1.7; 8 mm], and Dmax > Dm. The test stage used S-band radar data from a WSR-88D located in Oklahoma City, OK. The moments M0, M2, M4, and M6 were computed from {N0, μ, Λ, Dmax}. The validation results in terms of what they define as the relative absolute error (RAE) ranged from 0.986 (or 98.6%) for M0 to 0.455 (or 45.5%) for M6, while Pearson’s correlation coefficient between radar-based M0 and 2DVD M0 “truth” was 0.651 (the maximum correlation coefficient for other moments was <0.7). The predictive performance of k-NN was quantified through root relative squared error (RRSE), which computes the difference between the k-NN-predicted values with the actual ones relative to when a simple predictor is used. More than characterizing the accuracy of the computation of moments, both RAE and RRSE give an indication of the efficacy of k-NN-based prediction over the most basic mean-value prediction method. Wen et al. [87] reported low RRSE for M2, M4, and M6, whereas it was large (>1) for M0. They commented that “both the inverse model and Bayesian approach produced DSD retrievals with large uncertainties due to the measurement errors, noise, and sampling problems of the instruments”.
5. Applications
5.1. DSDs in Light Rainfall
The drop size distributions in light rainfall (defined here as rates <1 mm h−1) arguably show the highest variability for a given rain rate (R) due to large variations in the “normalized” intercept parameter (NW) which is negatively correlated with the mass-weighted mean diameter (Dm), whereas the scaled-normalized shape is remarkably stable. Recent observations of the DSD using collocated high-resolution optical array probe for drizzle and small drops (D < 1 mm) and 2DVD for larger sizes (>0.75 mm) have shown that normalizing N(D) by Nw and scaling D by Dm (or in compact notation N(D) = NW h(x) where x = D/Dm), leads to the generalized gamma model as a good “climatological” fit for h(x) describable by two shape parameters (μ, c) (see Equation (12) and Figure 5).
The main problem associated with light-rain DSD retrievals from polarimetric radars stems from the fact that these events are dominated by small and tiny drops which have near-spherical shapes. As a result, the polarimetric parameters such as Zdr (and Kdp) will be very close to zero in these regions. To illustrate this, we show the measured Zdr and Zh from the CSU CHILL S-band radar during a light rain event period on 17 April 2015 in Greeley, Colorado (Figure 7). Radar scans were made at regular and closely spaced time intervals over a ground instrumentation site located at a 13 km range. The ground instruments included an MPS and a 2DVD both inside a 2/3rd scaled DFIR double wind fence. The disdrometer data were used to construct the full DSD spectra ranging down to 200 microns.
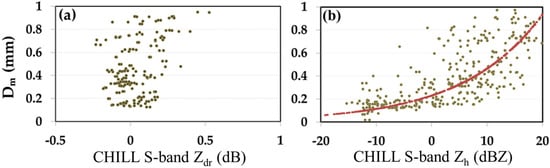
Figure 7.
Dm from the full DSD spectra at the ground instrumentation site vs. (a) the measured Zdr and (b) the measured Zh from the CSU CHILL S-band radar over the disdrometer location, during a light rain event period on 17 April 2015 in Greeley, Colorado.
Figure 7a shows the variation of Dm computed from the full DSD spectra vs. the measured Zdr from the S-band radar. Values of Dm (note the y-axis is on a log scale) range from 0.2 to 1 mm but Zdr can be seen to be around 0 dB, sometimes even negative (due to noise fluctuations). On the other hand, the S-band Zh shows more variation with Dm. The red dotted line represents the fitted equation. Although there is a considerable amount of scatter, the fitted equation seems a better way to estimate Dm (but with significant uncertainties). The equation will be tested for other light-rain events, e.g., in Wallops Island, a mid-latitude coastal region, where a large set of disdrometers and other instruments are located within the coverage of the S-band NPOL radar [90].
5.2. DSD-Based Classification of Stratiform and Convective Rain Regions
There have been a number of studies relating to the separation of stratiform and convective rain in terms of their DSD parameters. To begin with, DSD data analyses from [31] (see panel (a) of their Figure 8) show that the two rain types have a clear separation in the N0′ vs. Dm’ domain. Their results also show that for stratiform rain, the variation of N0′ shows an almost linear variation with Dm’, whereas convective rain does not show any correlation with Dm’. Note that the DSD data analysis used i = 3 and j = 4 for this particular case, hence, Dm’ will be the same as Dm.
Bringi et al. [78] examined the Nw vs. Dm for several locations in various climatic locations. Based on the standard deviation of the 1 min rain rate with time, the data points were classified separately into (i) stratiform rain, (ii) tropical-convective, and (iii) continental-convective rain. Later, Thurai et al. [91] collated all data points and showed that stratiform-convective separation can be made in the Nw vs. Dm domain. The separation technique was also tested using disdrometer data in Wallops Island (a mid-latitude coastal region, as mentioned earlier) and found to be applicable for several events. RHI scans from the S-band NPOL radar made over the disdrometer site were used for validation.
The separation method was tested with gridded data constructed from NPOL volume scans. The pixel-by-pixel classification based on the retrieved [Nw, Dm] was compared with the output from the ‘texture-based’ method of [92]. One example, taken from [93], is shown in Figure 8. The event occurred on 30 April 2020 which had a somewhat organized line of strong convection embedded within a larger system. Figure 8a shows the gridded reflectivity data, Figure 8b shows the DSD-based classification using the retrieved [Nw, Dm], panel (c) shows the classification according to the texture-based method and Figure 8d shows the match/mismatch between the two methods. Note the DSD-based classification in Figure 8b has an extra category representing mixed/transition/uncertain rain type (purple regions).
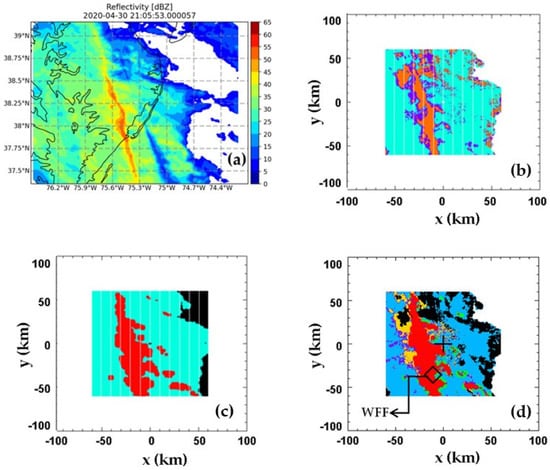
Figure 8.
(a) Reflectivity from the NPOL gridded data for the 30 April 2020 event at 21:06 UTC; (b) DSD-based rain type classification (orange: convective, cyan: stratiform, purple: mixed); (c) Texture-based classification (red: convective, cyan: stratiform); (d) matched and mismatched rain-types (see text for details), with the ground instrumentation site marked as WFF. Adapted from [93]. © American Meteorological Society. Used with permission.
For Figure 8d, the colors represent the following: (i) Light blue/cyan—when both methods classify as stratiform rain; (ii) Red—when both methods classify as convective rain; (iii) Orange—when DSD-based methods classify as convective rain whereas the texture method classifies as stratiform rain; (iv) Green—when DSD-based methods classify as stratiform rain whereas the texture methods classify as convective rain; (v) Purple—when DSD-based methods classify as mixed type; (vi) Black—when Zdr is < 0 dB, which is not included in the classification procedure.
In terms of percentages, the comparison between the DSD-based classification and the texture-based classification resulted in (i) 56% of the radar pixels being categorized as stratiform rain by both methods; (ii) 21% as convective rain by both methods; and (iii) a further 11% as the ‘mixed’ category from the DSD-based method. For the remaining 12% of the pixels, there was disagreement between the two methods which largely occurred in regions around the convective rain areas. Similar comparisons have been made earlier using the C-band CPOL gridded data (CAPPIs) in [94] which had also shown good agreement between the two methods. Thus, it appears that the DSD retrieval methods for polarimetric radars have the additional advantage of identifying stratiform and convective rain regions.
5.3. Retrievals of DSD Moments from Polarimetric Radars
The feasibility of retrieving the DSD moments from X-band polarimetric radars was demonstrated by [32] using data from several campaigns including IFloodS [95,96] conducted in Iowa, USA, and HyMEx [97,98] in the Mediterranean region. The proposed retrieval method entails the estimation of two ‘chosen’ reference moments, Mi and Mj, and a function h(x) which represents the underlying shape function after double-moment normalization [32] represented by the generalized gamma model [31]. The third and the sixth moments, M3 and M6, were chosen as the reference moments. M6 was estimated from the attenuation corrected reflectivity, Zh, and M3 was estimated from the attenuation-corrected differential reflectivity, Zdr, and the specific differential propagation phase, Kdp.
The method was tested later by [47] using the X-band radar from a campaign conducted in Greeley, Colorado. They also used the attenuation-corrected Zh to estimate M6 but made a slight adjustment for estimating M3, viz. instead of using Zdr and Kdp, they used Zdr and the specific attenuation Ah for horizontal polarization.
We have applied the same approach to XYOU (XYOU is an acronym for X-band radar located at Yonsei University, Seoul) X-band radar data from a pure warm-rain event during the 2020 summer field observation campaign in South Korea. After establishing the correct calibration factors for Zh and Zdr, attenuation correction procedures were applied in the same way as in [47], followed by the estimation of M3 and M6 again in the same way. Figure 9a–c show the attenuation corrected Zh, attenuation corrected Zdr and Ah, respectively. The intensity of the storm can be seen from the high values of Zh within the core of the storm reaching 60 dBZ. In that region, Zdr was around 3 dB and Ah was ~1.6 dB km−1.
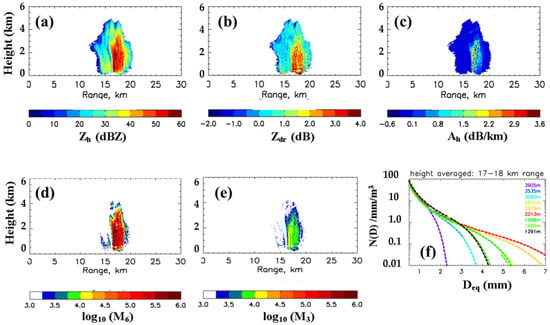
Figure 9.
(a) Attenuation corrected Zh, (b) attenuation corrected Zdr, and (c) Ah for a warm rain event which occurred on 10 August 2020; (d) retrieved M6; (e) retrieved M3; (f) DSDs derived from the retrieved moments averaged over 17–18 km range interval and averaged over various height intervals centered around the following: (purple—3.9 km; blue—3.5 km; cyan—3.1 km; yellow–green: 2.84 km; orange: 2.6 km; red—2.2 km; green—1.97 km; light-green: 1.69 km; black—1.29 km).
The retrieved M6 and M3 are shown in panels (d) and (e) of Figure 9. Note that the units are different for the moments. Panel (f) shows examples of the DSDs derived from all the retrieved moments, averaged over 1 km height intervals and 17–18 km range intervals. The heights range from 1.3 km to 4 km above ground level. As can be seen, the ‘growth’ is very significant and rapid from 4 km down to 2.2 km, and below that, the opposite happens, probably due to drop break-up being the dominant process.
To double-check the retrievals, the DSDs derived from the retrieved moments were used as an input to T-matrix-based scattering calculations at X-band to determine the Zh, Zdr, Kdp, and Ah at each of the pixels, which were then compared with the radar data. The procedure is shown in Figure 10. Figure 11 shows the vertical profiles of the output of the scattering calculations and the radar-data (after attenuation correction) within a very narrow radar range interval, 17.7 to 17.8 km. The comparisons are very good, especially for Zh, Zdr, and Ah. The extra parameter used for comparison, Kdp, shows more scatter, but the larger scatter is evident in both the scattering calculations and the radar-derived values.
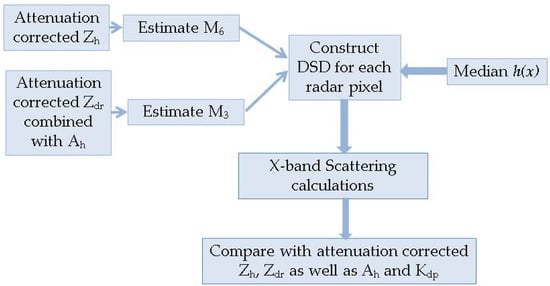
Figure 10.
Block diagram outlining the DSD estimation procedure and comparing with radar data.
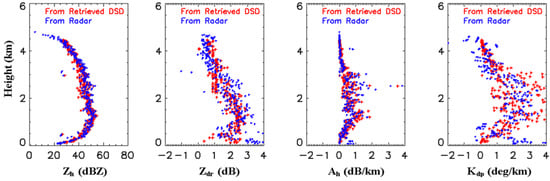
Figure 11.
Vertical profiles of radar data compared with those recalculated using DSDs derived from the retrieved moments: From the left to right, Zh, Zdr, Ah, and Kdp in the 17.7 to 17.8 km radar-range.
6. Conclusions
The principal objective of this article is to provide a review of the main assumptions and DSD representations that are used to retrieve the parameters of the DSD using polarimetric radar. While the optimal DSD representation is not known, it appears that the generalized gamma distribution (with four parameters of which two are shape parameters μ, c) is probably a good candidate for this using maximum entropy [99]. The μ value typically controls the curvature at the small drop end (generally concave up) while c controls the slope of log N(D) vs. D at the large drop end. In particular, when the concept of scaling DSDs with two moments is applied, the two parameters among the four parameters of generalized gamma distribution are replaced with the two characteristics parameters (characteristics number concentration and characteristic diameter which are expressed with two moments. These two parameters control the most discernable variability of DSDs and the remaining variability is contained in the scaling normalized DSD, h(x; μ, c), which is the function of the remaining two parameters, μ and c [31]. The mean h(x) is remarkably stable at the different climate regimes [31,32,33,46]. The important message is that all moments from M0 to M7 can be expressed as a product of power laws of the reference moments together with average h(x; μ, c). Note that h(x) need not be within the generalized gamma family or any pdf form as long as the moments are finite.
An important theme has been the remarkable stability of the generic shape of h(x; μ, c) across different rain types, intensities, and climate regimes. This stability is not manifested in the gamma unless μ = constant. However, the μ–λ relation (or, constrained gamma) based on disdrometer data is gaining wide acceptance since it offers a direct method of using radar data [ZH, ZDR]. One caveat is that use of the method of moments or truncated moments (truncation of tiny drops) due to disdrometer limitations together with small sample sizes (~100 or less) can cause significant bias and variance errors in N0 and λ. In addition, there is a strong negative Pearson correlation coefficient between log N0 and D0 of approximately −0.8 due purely to statistics with zero physics. There is also a strong positive correlation between μ and λ as well as N0−μ. The one reason why even recent research articles use the constrained gamma is that radar measured [ZH and ZDR] are used to estimate [N0, λ] without using KDP which, in spite of its many advantages, is noisy and the choice of smoothing interval can be subjective.
The Testud et al. [31] double-moment normalization of the gamma [NW, Dm, μ] based on reference moments [M3, M4] appears now to be the method most used in recent articles [78,81]. The estimation errors [79] were quantified by the normalized standard error inclusive of parameterization and measurement errors are <20% for D0 and <15% for log NW under ideal conditions, e.g., steady rain. Gorgucci et al. [79] did not use measured DSDs rather they used theoretical ranges for NW, Dm and μ uniformly distributed (random gamma). The estimator of μ is biased and the uncertainty is high so no standard error is quoted. The largest set of 1 min measured DSDs using a network of seven third-generation 2D-video disdrometers [81] was acquired by the GPM ground validation program held in a variety of climatic regimes. Their normalized standard error (parameterization errors only) for D0 < 10% whereas for log NW it was <16%.
A major caveat with respect to DSD measurements is that commercial disdrometers (e.g., 2DVD, Parsivel) do not have high enough resolution to measure drizzle drops (D < 100 μm) so the curvature at the small drop end is convex down. To measure the drizzle drops, an optical array probe (Meteorological Particle Spectrometer, MPS, manufactured by Droplet Measurement Systems, Longmont, CO, USA) with 50 μm resolution collocated with a 2DVD disdrometer gives the ‘complete’ drop spectra from D = 100 μm to precipitation-sized large drops. Without the MPS, the μ from Testud et al.’s gamma [31] will be positive and apparently stable but with the wrong shape and the number density would be biased low by an order of magnitude.
The retrieval of DSD parameters with the polarimetric radar requires an understanding of equilibrium drop shapes, orientations, and oscillation modes. The review article by [83] gives a new understanding of the laboratory measurements by [55,82], the wind tunnel measurements of [57], and the 2D-video measurements of drop contours in two orthogonal planes and their orientation distribution. It is rather a mystery that nearly all articles use the [54] mean axis ratio vs. D relation based on the fit to data from different methods with unknown errors the idea being that the random errors will cancel out on average leaving the mean values intact. Whereas, the 80 m fall bridge measurements with (frequently calibrated) 2DVD images in two orthogonal planes analyzed by [51] resulting in their fitted mean axis ratio vs. D relation has been cited but dismissed by ‘the Brandes et al. [68] fit that is very close to Thurai and Bringi [51]’. The review by [83] also clears up the dominance of transverse oscillations of 4 mm drops as being due to the ‘Initial condition’ of the particular type of drop generation which imparted transverse oscillations that did not decay with a fall distance of about 20 m when the fall speed reached its terminal velocity. Similar initial condition problems were also found to explain inconsistent transverse modes in 2–2.5 mm drops. The net effect is an upward shift in axis ratios (ratio of the minimum vertical chord to maximum) towards sphericity that was not found in either the 2DVD data or the wind tunnel data.
The most important application of the double-moment scaling normalization is the estimation of moments (M0–M7) using polarimetric radar, and a stable h(x; μ, c) representative of the climatology. The reference moments (M3, M6) are estimated from the attenuation-corrected differential reflectivity, Zdr and the specific differential propagation phase, and from the attenuation-corrected reflectivity, Zh. The two reference moments are used to estimate moments of DSDs with multiple power laws and, subsequently, a complete DSD can be derived. Thus, the complete DSD and different moments of DSDs can be used to investigate the microphysical evolution in space and time. DSD retrieval using advanced disdrometers, micro-rain radar, and vertical pointing Doppler X-band radars can be used to constrain the DSD retrievals at the surface and at intermediate heights. Another application is radar hydrology where the estimation of rain accumulation using corrected reflectivity and the specific attenuation (dB/km) which is constrained by the differential propagation phase leads to accurate estimates over large watersheds and smaller urban flooding.
The three operational radar wavelengths (λ) are S-, C-, and X-bands though X-band radars have a short maximum unambiguous range as well as the Nyquist frequency is ( which is a factor of 3 less than at S-band (for pulse repetition time, Ts = 1 ms). This makes the signal processing much more complicated with overlaid echoes or 2nd trip echoes. The clutter cancellation algorithms at X-band are also difficult to optimize relative to S-, and C-bands primarily because X-band radar transmitters are generally magnetrons whose phase stability is poor relative to S-band transmitters which are linear power amplifiers, e.g., Klystron while C-band radars (largely) use either Magnetrons or rarely Klystrons. High phase coherence is important in the measurement of differential phase. The specific differential phase shift (KDP) can be estimated with much more accuracy at S- as opposed C- and X-bands. The KDP is important for DSD parameter retrieval.
It is true that calibration and quality control of the radar is one of the prime requirements for DSD parameter retrieval and for QPE. Many operational agencies have their own methods with the NEXRAD probably having the most complete procedures to calibrate reflectivity to within an uncertainty of ±1 dBZ and differential reflectivity to within ±0.1 dB. These two measurements are primary in the retrieval of DSD parameters, shown repeatedly by [79] since the mid-1980s. The achievement of such low uncertainty errors is very difficult to achieve across large numbers of radars in the network which is not really frequency dependent. Nevertheless, S-band system networks have the best performance.
The most important drawback of the X-band is signal attenuation caused by rain along the path of about 0.25 dB/km. At C-band, the similar value is 0.07 and at S-band 0.017. While attenuation–correction algorithms have been developed at X-band and C-bands, their accuracy cannot be determined. This correction is vital for DSD parameter retrieval. There are differences between S- and X-bands generally when radar reflectivity is larger than 40 dBZ. In ice regions of convection, the differences can be 3–30 dBZ for hail sizes > 1″. The S- and X-band reflectivities have been compared in [100].
Reference [87] described estimating the parameters of the gamma distribution and the lower-order moments based on an inverse model where the input is {Zdr, KDP/Zh} and the output is {μ, Dmax}, where Dmax is the maximum diameter of the retrieved gamma DSD. Their approach follows the well-known k-nearest-neighbor (k-NN) classification from the pattern recognition literature. In principle, the method could be used to estimate the parameters of any DSD model provided the number of parameters is less than the number of available radar measurements. The DSD model should be a positive definite without any discontinuous. Ref. [87]'s approach is based on a truncated gamma DSD and several ‘tricks’ are used, e.g., μ–Λ polynomial using disdrometer data. The details are many and at times difficult to decipher. The final accuracies they obtain using the IM on real radar data for the important quantities such as R, and moments M0–M6 did not meet their expectations and quoting from their article, “the inverse model […] produced DSD retrievals with large uncertainties due to the measurement errors, noise, and sampling problems of the instruments.” Further, their results do not show that deep learning is immune to noise.
Author Contributions
Conceptualization, G.L., V.B. and M.T.; methodology, G.L., V.B. and M.T.; software, M.T.; validation, V.B. and M.T.; formal analysis, M.T.; investigation, G.L., V.B. and M.T.; resources, G.L. and V.B.; writing—original draft preparation, G.L., V.B. and M.T.; writing—review and editing, G.L., V.B. and M.T.; visualization, M.T.; project administration, G.L. and V.B.; funding acquisition, G.L. and V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Korea Meteorological Administration Research and Development Program under Grant KMI2021-02411. This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2021R1A4A1032646). VNB was funded by the National Science Foundation, grant number AGS-1901585 to Colorado State University and MT by NASA’s Atmospheric Dynamics Program via Grant Award Number 80NSSC20K0893.
Data Availability Statement
Data are available upon requests to the authors.
Acknowledgments
We would like to thank to Kyuhee Shin for editing this manuscript. We were very saddened by the demise of Isztar Zawadzki. He left a vast legacy for future students. I (GYL) was privileged to work and interact with him at McGill University. He was always helping PhD students reach their full potential and he freely shared his considerable knowledge with many post-doctoral researchers who made their way to McGill. We shall miss him dearly.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ryzhkov, A.; Zhang, P.; Bukovčić, P.; Zhang, J.; Cocks, S. Polarimetric Radar Quantitative Precipitation Estimation. Remote Sens. 2022, 14, 1695. [Google Scholar] [CrossRef]
- Germann, U.; Boscacci, M.; Clementi, L.; Gabella, M.; Hering, A.; Sartori, M.; Sideris, I.V.; Calpini, B. Weather Radar in Complex Orography. Remote Sens. 2022, 14, 503. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Prat, O.P.; Reimel, K.J.; van Lier-Walqui, M.; Morrison, H.C. Dual-Polarization Radar Fingerprints of Precipitation Physics: A Review. Remote Sens. 2022, 14, 3706. [Google Scholar] [CrossRef]
- Morrison, H.; Lier-Walqui, M.; Fridlind, A.M.; Grabowski, W.W.; Harrington, J.Y.; Hoose, C.; Korolev, A.; Kumjian, M.R.; Milbrandt, J.A.; Pawlowska, H.; et al. Confronting the Challenge of Modeling Cloud and Precipitation Microphysics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001689. [Google Scholar] [CrossRef]
- Srivastava, R.C. A simple model of evaporatively driven downdraft: Application to microburst downdraft. J. Atmos. Sci. 1985, 42, 1004–1023. [Google Scholar] [CrossRef]
- Rogers, R.R.; Yau, M.K. A Short Course in Cloud Physics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1996; ISBN 0-08-057094-1. [Google Scholar]
- Fabry, F.; Zawadzki, I. Long-term radar observations of the melting layer of precipitation and their interpretation. J. Atmos. Sci. 1995, 52, 838–851. [Google Scholar] [CrossRef]
- Bellon, A.; Lee, G.W.; Zawadzki, I. Error statistics of VPR corrections in stratiform precipitation. J. Appl. Meteorol. 2005, 44, 998–1015. [Google Scholar] [CrossRef]
- Garcia-Benadí, A.; Bech, J.; Gonzalez, S.; Udina, M.; Codina, B. A New Methodology to Characterise the Radar Bright Band Using Doppler Spectral Moments from Vertically Pointing Radar Observations. Remote Sens. 2021, 13, 4323. [Google Scholar] [CrossRef]
- Lee, J.-E.; Jung, S.-H.; Kwon, S. Characteristics of the Bright Band Based on Quasi-Vertical Profiles of Polarimetric Observations from an S-Band Weather Radar Network. Remote Sens. 2020, 12, 4061. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Joss, J.; Waldvogel, A. Ein Spektrograph für Niederschlagstropfen mit automatischer Auswertung. Pure Appl. Geophys. 1967, 68, 240–246. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Joss, J. An optical disdrometer for measuring size and velocity of hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Sheppard, B.E. The measurement of raindrop size distributions using a small Doppler radar. J. Atmos. Ocean. Technol. 1990, 7, 255–268. [Google Scholar] [CrossRef]
- Kruger, A.; Krajewski, W.F. Two-dimensional video disdrometer: A description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Schönhuber, M.; Lammer, G.; Randeu, W.L. The 2D-Video-Distrometer. In Precipitation: Advances in Measurement, Estimation and Prediction; Michaelides, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Barthazy, E.; Göke, S.; Schefold, R.; Högl, D. An optical array instrument for shape and fall velocity measurements of hydrometeors. J. Atmos. Ocean. Technol. 2004, 21, 1400–1416. [Google Scholar] [CrossRef]
- Garrett, T.J.; Fallgatter, C.; Shkurko, K.; Howlett, D. Fall speed measurement and high-resolution multiangle photography of hydrometeors in free fall. Atmos. Meas. Tech. 2012, 5, 2625–2633. [Google Scholar] [CrossRef]
- Praz, C.; Roulet, Y.-A.; Berne, A. Solid hydrometeor classification and riming degree estimation from pictures collected with a Multi-Angle Snowflake Camera. Atmos. Meas. Tech. 2017, 10, 1335–1357. [Google Scholar] [CrossRef]
- Pettersen, C.; Bliven, L.F.; von Lerber, A.; Wood, N.B.; Kulie, M.S.; Mateling, M.E.; Moisseev, D.N.; Munchak, S.J.; Petersen, W.A.; Wolff, D.B. The Precipitation Imaging Package: Assessment of Microphysical and Bulk Characteristics of Snow. Atmosphere 2020, 11, 785. [Google Scholar] [CrossRef]
- Pettersen, C.; Bliven, L.F.; Kulie, M.S.; Wood, N.B.; Shates, J.A.; Anderson, J.; Mateling, M.E.; Petersen, W.A.; von Lerber, A.; Wolff, D.B. The Precipitation Imaging Package: Phase Partitioning Capabilities. Remote Sens. 2021, 13, 2183. [Google Scholar] [CrossRef]
- Joss, J.; Gori, E.G. Shapes of raindrop size distribution. J. Appl. Meteorol. 1974, 17, 1054–1061. [Google Scholar] [CrossRef]
- Lee, G.W.; Zawadzki, I. Variability of drop size distributions: Noise and noise filtering in disdrometric data. J. Appl. Meteorol. 2005, 44, 634–652. [Google Scholar] [CrossRef]
- Lee, G.W.; Zawadzki, I. Variability of drop size distributions: Time-scale dependence of the variability and its effects on rain estimation. J. Appl. Meteorol. 2005, 44, 241–255. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G.; Brandes, E.; Schuur, T.; Ryzhkov, A.; Ikeda, K. Analysis of video disdrometer and polarimetric radar data to characterize rain microphysics in Oklahoma. J. Appl. Meteorol. 2008, 47, 2238–2255. [Google Scholar] [CrossRef]
- Waldvogel, A. The N0 jump of raindrop spectra. J. Atmos. Sci. 1974, 31, 1067–1078. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. Rainfall microphysics and radar properties: Analysis methods for drop size spectra. J. Appl. Meteorol. 1998, 37, 912–923. [Google Scholar] [CrossRef]
- Sekhon, R.S.; Srivastava, R.C. Doppler radar observations of drop-size distributions in a thunderstorm. J. Atmos. Sci. 1971, 28, 983–994. [Google Scholar] [CrossRef]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The concept of “normalized” distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Lee, G.; Zawadzki, I.; Szyrmer, W.; Sempere-Torres, D.; Uijlenhoet, R. A General Approach to Double-Moment Normalization of Drop Size Distributions. J. Appl. Meteorol. 2004, 43, 264–281. [Google Scholar] [CrossRef]
- Raupach, T.H.; Berne, A. Retrieval of the raindrop size distribution from polarimetric radar data using double-moment normalization. Atmos. Meas. Tech. 2017, 10, 2573–2594. [Google Scholar] [CrossRef]
- Bang, W.; Lee, G.; Ryzhkov, A.; Schuur, T.; Lim, K.-S.S. Comparison of Microphysical Characteristics between the Southern Korean Peninsula and Oklahoma Using Two-Dimensional Video Disdrometer Data. J. Hydrometeorol. 2020, 21, 2675–2690. [Google Scholar] [CrossRef]
- Sempere Torres, D.; Porrà, J.M.; Creutin, J.-D. A general formulation for raindrop size distribution. J. Appl. Meteorol. 1994, 33, 1494–1502. [Google Scholar] [CrossRef]
- Sempere Torres, D.; Porrà, J.M.; Creutin, J.-D. Experimental evidence of a general description of raindrop size distribution properties. J. Geophys. Res. 1998, 103, 1785–1797. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N. Potential Use of Radar Differential Reflectivity Measurements at Orthogonal Polarizations for Measuring Precipitation. J. Appl. Meteorol. 1976, 15, 69–76. [Google Scholar] [CrossRef]
- Bringi, V.; Zrnic, D. Polarization Weather Radar Development from 1970–1995: Personal Reflections. Atmosphere 2019, 10, 714. [Google Scholar] [CrossRef]
- Amoroso, L. Ricerche intorno alla curva dei redditi (Research regarding income curves). Ann. Math. Pura Appl. 1925, 2, 123–159. [Google Scholar] [CrossRef]
- Suzuki, E. Hyper gamma distribution and its fitting to rainfall data. Pap. Meteor. Geophys. 1964, 15, 31–51. [Google Scholar] [CrossRef]
- Uijlenhoet, R. Parameterization of Rainfall Microstructure for Radar Meteorology and Hydrology. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 1999. [Google Scholar]
- Auf der Maur, A.N. Statistical tools for drop size distribution: Moments and generalized gamma. J. Atmos. Sci. 2001, 58, 407–418. [Google Scholar] [CrossRef]
- Stacey, E.W. A Generalization of the Gamma Distribution. Ann. Math. Stat. 1962, 33, 1187–1192. Available online: http://www.jstor.org/stable/2237889 (accessed on 23 August 2022). [CrossRef]
- Szyrmer, W.; Laroche, S.; Zawadzki, I. A microphysical bulk formulation based on scaling normalization of the particle size distribution. Part I: Description. J. Atmos. Sci. 2005, 62, 4206–4221. [Google Scholar] [CrossRef]
- Willis, P.T. Functional fits to some observed drop size distributions and parameterization of rain. J. Atmos. Sci. 1984, 41, 1648–1661. [Google Scholar] [CrossRef]
- Friedlander, S.K.; Wang, C.L. The self-preserving particle size distribution for coagulation by brownian motion. J. Colloid Interface Sci. 1966, 22, 126–132. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N. Application of the Generalized Gamma Model to Represent the Full Rain Drop Size Distribution Spectra. J. Appl. Meteorol. Climatol. 2018, 57, 1197–1210. [Google Scholar] [CrossRef]
- Bringi, V.; Mishra, K.V.; Thurai, M.; Kennedy, P.C.; Raupach, T.H. Retrieval of lower-order moments of the drop size distribution using CSU-CHILL X-band polarimetric radar: A case study. Atmos. Meas. Tech. 2020, 13, 4727–4750. [Google Scholar] [CrossRef]
- Morrison, H.; Kumjian, M.R.; Martinkus, C.P.; Prat, O.P.; Van Lier-Walqui, M. A general N-moment normalization method for deriving raindrop size distribution scaling relationships. J. Appl. Meteorol. Climatol. 2019, 58, 247–267. [Google Scholar] [CrossRef]
- Morrison, H.; van Lier-Walqui, M.; Kumjian, M.R.; Prat, O.P. A Bayesian approach for statistical–physical bulk parameterization of rain microphysics. Part I: Scheme description. J. Atmos. Sci. 2019, 77, 1019–1041. [Google Scholar] [CrossRef]
- Chang, W.-Y.; Lee, G.; Jou, B.J.-D.; Lee, W.-C.; Lin, P.-L.; Yu, C.-K. Uncertainty in measured raindrop size distributions from four types of collocated instruments. Remote Sens. 2020, 12, 1167. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N. Drop axis ratios from a 2d video disdrometer. J. Atmos. Ocean. Technol. 2005, 22, 966–978. [Google Scholar] [CrossRef]
- Thurai, M.; Gatlin, P.N.; Bringi, V.N.; Petersen, W.A.; Notaros, B.; Carey, L.D.; Kennedy, P.; Notaroš, B.; Carey, L.D. Towards completing the rain drop size spectrum: Case studies involving 2D-video disdrometer, droplet spectrometer, and polarimetric radar measurements. J. Appl. Meteorol. Climatol. 2017, 56, 877–896. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, K.; Zhang, G.; Xue, M.; Zhou, B.; Liu, S.; Chen, X. Statistical characteristics of raindrop size distributions observed in East China during the Asian summer monsoon season using 2-D video disdrometer and Micro Rain Radar data. J. Geophys. Res. Atmos. 2016, 121, 2265–2282. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment. J. Appl. Meteorol. 2002, 41, 674–685. [Google Scholar] [CrossRef]
- Beard, K.V.; Kubesh, R.J.; Ochs, H.T. Laboratory measurements of small raindrop distortion. Part I: Axis ratios and fall behavior. J. Atmos. Sci. 1991, 48, 698–710. [Google Scholar] [CrossRef]
- Thurai, M.; Szakáll, M.; Bringi, V.N.; Beard, K.V.; Mitra, S.K.; Borrmann, S. Drop shapes and axis ratio distributions: Comparison between 2d video disdrometer and wind-tunnel measurements. J. Atmos. Ocean. Technol. 2009, 26, 1427–1432. [Google Scholar] [CrossRef]
- Szakáll, M.; Mitra, S.K.; Diehl, K.; Borrmann, S. Shapes and oscillations of falling raindrops—A review. Atmos. Res. 2010, 97, 416–425. [Google Scholar] [CrossRef]
- Szakáll, M.; Kessler, S.; Diehl, K.; Mitra, S.K.; Borrmann, S. A wind tunnel study of the effects of collision processes on the shape and oscillation for moderate-size raindrops. Atmos. Res. 2014, 142, 67–78. [Google Scholar] [CrossRef]
- Beard, K.V.; Chuang, C. A new model for the equilibrium shape of raindrops. J. Atmos. Sci. 1987, 44, 1509–1524. [Google Scholar] [CrossRef]
- McCormick, G.C.; Hendry, A.; Barge, B.L. The Anisotropy of Precipitation Media. Nature 1972, 238, 214–216. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Beard, K.V. A Wind Tunnel Investigation of the Internal Circulation Shape of Water Drops Falling at Terminal Velocity in Air. Q. J. R. Meteorol. Soc. 1970, 96, 247–256. [Google Scholar] [CrossRef]
- Hall, M.P.M.; Cherry, S.M.; Goddard, J.W.F.; Kennedy, G.R. Raindrop Sizes and Rainfall Rate Measured by Dual-Polarization Radar. Nature 1980, 285, 195–198. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N. Differential Reflectivity and Differential Phase Shift: Applications in Radar Meteorology. Radio Sci. 1978, 13, 271–275. [Google Scholar] [CrossRef]
- Humphries, R.G. Observations and Calculations of Depolarization Effects at 3 GHz due to Precipitation. J. Rech. Atmos. 1974, 8, 151–161. [Google Scholar]
- Sachidananda, M.; Zrnic, D.S. Differential Propagation phase-shift and rainfall rate estimation. Radio Sci. 1986, 21, 235–247. [Google Scholar] [CrossRef]
- Jameson, A.R. Microphysical Interpretation of Multi-Parameter Radar Measurements in Rain. Part I: Interpretation of Polarization Measurements and Estimation of Raindrop Shapes. J. Atmos. Sci. 1983, 40, 1792–1802. [Google Scholar] [CrossRef]
- Jameson, A.R. Microphysical Interpretation of Multiparameter Radar Measurements in Rain. Part III: Interpretation and Measurement of Propagation Differential Phase Shift between Orthogonal Linear Polarizations. J. Atmos. Sci. 1985, 42, 607–614. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. An evaluation of a drop distribution–based polarimetric radar rainfall estimator. J. Appl. Meteorol. 2003, 42, 652–660. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zhang, G.; Brandes, E. Polarimetric radar rain estimators based on constrained gamma drop size distribution model. J. Appl. Meteorol. 2004, 43, 217–230. [Google Scholar] [CrossRef]
- Smith, P.L.; Kliche, D.V.; Johnson, R.W. The bias and error in moment estimators for parameters of drop size distribution functions: Sampling from gamma distributions. J. Appl. Meteorol. Climatol. 2009, 48, 2118–2126. [Google Scholar] [CrossRef]
- Johnson, R.W.; Kliche, D.V.; Smith, P.L. Comparison of estimators for parameters of Gamma distributions with left-truncated samples. J. Appl. Meteorol. Climatol. 2011, 50, 296–310. [Google Scholar] [CrossRef]
- Handwerker, J.; Straub, W. Optimal Determination of Parameters for Gamma-Type Drop Size Distributions Based on Moments. J. Atmos. Ocean. Technol. 2011, 28, 513–529. [Google Scholar] [CrossRef]
- Mallet, C.; Barthes, L. Estimation of gamma raindrop size distribution parameters: Statistical fluctuations and estimation errors. J. Atmos. Ocean. Technol. 2009, 26, 1572–1584. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G.; Brandes, E.A.; Schuur, T.J. Polarimetric Radar Rain Estimation through Retrieval of Drop Size Distribution Using a Bayesian Approach. J. Appl. Meteorol. Climatol. 2010, 49, 973–990. [Google Scholar] [CrossRef]
- Schinagl, K.; Friederichs, P.; Trömel, S.; Simmer, C. Gamma Drop Size Distribution Assumptions in Bulk Model Parameterizations and Radar Polarimetry and Their Impact on Polarimetric Radar Moments. J. Appl. Meteorol. Climatol. 2019, 58, 467–478. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part II: A Proposed Three-Moment Closure and Scheme Description. J. Atmos. Sci. 2005, 62, 3065–3081. [Google Scholar] [CrossRef]
- Seifert, A. On the Shape–Slope Relation of Drop Size Distributions in Convective Rain. J. Appl. Meteorol. 2005, 44, 1146–1151. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop Size Distribution in Different Climatic Regimes from Disdrometer and Dual-Polarized Radar Analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Gorgucci, E.; Scarchilli, G.; Chandrasekar, V.; Bringi, V.N. Rainfall estimation from polarimetric radar measurements: Composite algorithms immune to variability in raindrop shape–size relation. J. Atmos. Ocean. Technol. 2001, 18, 1773–1786. [Google Scholar] [CrossRef]
- Johnson, D.B.; Beard, K.V. Oscillation energies of colliding raindrops. J. Atmos. Sci. 1984, 41, 1235–1241. [Google Scholar] [CrossRef]
- Tokay, A.; D’Adderio, L.P.; Wolff, D.B.; Petersen, W.A. Development and Evaluation of the Raindrop Size Distribution Parameters for the NASA Global Precipitation Measurement Mission Ground Validation Program. J. Atmos. Ocean. Technol. 2020, 37, 115–128. [Google Scholar] [CrossRef]
- Andsager, K.; Beard, K.V.; Laird, N.F. Laboratory measurements of axis ratios for large raindrops. J. Atmos. Sci. 1999, 56, 2673–2683. [Google Scholar] [CrossRef]
- Beard, K.V.; Bringi, V.N.; Thurai, M. A new understanding of raindrop shape. Atmos. Res. 2010, 97, 396–415. [Google Scholar] [CrossRef]
- Carey, L.D.; Petersen, W.A. Sensitivity of C-band polarimetric radar–based drop size estimates to maximum diameter. J. Appl. Meteorol. Climatol. 2015, 54, 1352–1371. [Google Scholar] [CrossRef]
- Bringi, V.; Grecu, M.; Protat, A.; Thurai, M.; Klepp, C. Measurements of Rainfall Rate, Drop Size Distribution, and Variability at Middle and Higher Latitudes: Application to the Combined DPR-GMI Algorithm. Remote Sens. 2021, 13, 2412. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, K.; Zhang, G.; Hu, D.; Yang, Z. Optimized raindrop size distribution retrieval and quantitative rainfall estimation from polarimetric radar. J. Hydrol. 2020, 580, 124248. [Google Scholar] [CrossRef]
- Wen, G.; Chen, H.; Zhang, G.; Sun, J. An Inverse Model for Raindrop Size Distribution Retrieval with Polarimetric Variables. Remote Sens. 2018, 10, 1179. [Google Scholar] [CrossRef]
- Shakhnarovich, G.; Darrell, T.; Indyk, P. Nearest-Neighbor Methods in Learning and Vision: Theory and Practice; MIT Press: Cambridge, MA, USA, 2006; ISBN 9780262195478. [Google Scholar]
- Gatlin, P.N.; Petersen, W.A.; Pippitt, J.L.; Berendes, T.A.; Wolff, D.B.; Tokay, A. The GPM Validation Network and Evaluation of Satellite-Based Retrievals of the Rain Drop Size Distribution. Atmosphere 2020, 11, 1010. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.; Wolff, D.; Marks, D.; Pabla, C.; Kennedy, P. Drop size distribution retrievals for light rain and drizzle from S-band polarimetric radars. In Proceedings of the 5th International Electronic Conference on Atmospheric Sciences, Basel, Switzerland, 16–31 July 2022. [Google Scholar] [CrossRef]
- Thurai, M.; Gatlin, P.N.; Bringi, V.N. Separating stratiform and convective rain types based on the drop size distribution 30 characteristics using 2D video disdrometer data. Atmos. Res. 2016, 169, 416–423. [Google Scholar] [CrossRef]
- Steiner, M.; Houze, R.A.; Yuter, S.E. Climatological Characterization of Three-Dimensional Storm Structure from Operational Radar and Rain Gauge Data. J. Appl. Meteorol. 1995, 34, 1978–2007. [Google Scholar] [CrossRef]
- Thurai, M.; Wolff, D.; Marks, D.; Pabla, C.; Bringi, V. Separation of Stratiform and Convective Rain Types Using Data from an S-Band Polarimetric Radar: A Case Study Comparing Two Different Methods. Environ. Sci. Proc. 2021, 8, 1. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; May, P.T. CPOL radar-derived drop size distribution statistics of stratiform and convective rain for two regimes in Darwin, Australia. J. Atmos. Ocean. Technol. 2010, 27, 932–942. [Google Scholar] [CrossRef]
- Petersen, W.; Krajewski, W.F. Special Collection of the Journal of Hydrometeorology, IFloodS 2013: A Field Campaign to Support the NASA-JAXA Global Precipitation Measurement Mission. 2013. Available online: https://journals.ametsoc.org/collection/IFloodS2013 (accessed on 23 August 2022).
- Mishra, K.V.; Krajewski, W.F.; Goska, R.; Ceynar, D.; Seo, B.-C.; Kruger, A.; Niemeier, J.J.; Galvez, M.B.; Thurai, M.; Bringi, V.N.; et al. Deployment and performance analyses of high-resolution Iowa XPOL radar system during the NASA IFloodS campaign. J. Hydrometeorol. 2016, 17, 455–479. [Google Scholar] [CrossRef]
- Drobinski, P.; Ducrocq, V.; Alpert, P.; Anagnostou, E.; Béranger, K.; Borga, M.; Braud, I.; Chanzy, A.; Davolio, S.; Delrieu, G.; et al. HyMeX: A 10-Year Multidisciplinary Program on the Mediterranean Water Cycle. Bull. Amer. Meteorol. Soc. 2014, 95, 1063–1082. [Google Scholar] [CrossRef]
- Caldas-Alvarez, A.; Khodayar, S. Assessing atmospheric moisture effects on heavy precipitation during HyMeX IOP16 using GPS nudging and dynamical downscaling. Nat. Hazards Earth Syst. Sci. 2020, 20, 2753–2776. [Google Scholar] [CrossRef]
- Wu, W.; McFarquhar, G.M. Statistical Theory on the Functional Form of Cloud Particle Size Distributions. J. Atmos. Sci. 2018, 75, 2801–2814. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Cifelli, R.; Kennedy, P.C.; Nesbitt, S.W.; Rutledge, S.A.; Bringi, V.N.; Martner, B.E. A Comparative Study of Rainfall Retrievals Based on Specific Differential Phase Shifts at X- and S-Band Radar Frequencies. J. Atmos. Ocean. Technol. 2006, 23, 952–963. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).