Next Article in Journal
Designing the Signal Quality Monitoring Algorithm Based on Chip Domain Observables for BDS B1C/B2a Signals under the Requirements of DFMC SBAS
Next Article in Special Issue
Hybrid BBO-DE Optimized SPAARCTree Ensemble for Landslide Susceptibility Mapping
Previous Article in Journal
Validation of Nadir SWH and Its Variance Characteristics from CFOSAT in China’s Offshore Waters
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 4
10.3390/rs15041007
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

GIS-Based Landslide Susceptibility Modeling: A Comparison between Best-First Decision Tree and Its Two Ensembles (BagBFT and RFBFT)

by
Jingyun Gui
1,2,*,
Leandro Rafael Alejano
2,
Miao Yao
3,
Fasuo Zhao
1 and
Wei Chen
4
1
Department of Geological Engineering, College of Geological Engineering and Geomatics, Chang’An University, Xi’an 710064, China
2
GESSMin Group, CINTECX, Department of Natural Resources and Environmental Engineering, University of Vigo, 36310 Vigo, Spain
3
China Information Industry Engineering Investigation and Research Institute, Xi’an 710001, China
4
College of Geology and Environment, Xi’an University of Science and Technology, Xi’an 710054, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(4), 1007; https://doi.org/10.3390/rs15041007
Submission received: 7 January 2023 / Revised: 6 February 2023 / Accepted: 9 February 2023 / Published: 11 February 2023
(This article belongs to the Special Issue Assessing Natural Hazards through Advanced Machine Learning Methods and Remote Sensing Technology II)
Browse Figures
Review Reports Versions Notes

Abstract

:
This study aimed to explore and compare the application of current state-of-the-art machine learning techniques, including bagging (Bag) and rotation forest (RF), to assess landslide susceptibility with the base classifier best-first decision tree (BFT). The proposed two novel ensemble frameworks, BagBFT and RFBFT, and the base model BFT, were used to model landslide susceptibility in Zhashui County (China), which suffers from landslides. Firstly, we identified 169 landslides through field surveys and image interpretation. Then, a landslide inventory map was built. These 169 historical landslides were randomly classified into two groups: 70% for training data and 30% for validation data. Then, 15 landslide conditioning factors were considered for mapping landslide susceptibility. The three ensemble outputs were estimated with a receiver operating characteristic (ROC) curve and statistical tests, as well as a new approach, the improved frequency ratio accuracy. The areas under the ROC curve (AUCs) for the training data (success rate) of the three algorithms were 0.722 for BFT, 0.869 for BagBFT, and 0.895 for RFBFT. The AUCs for the validating groups (prediction rates) were 0.718, 0.834, and 0.872, respectively. The frequency ratio accuracy of the three models was 0.76163 for the BFT model, 0.92220 for the BagBFT model, and 0.92224 for the RFBFT model. Both BagBFT and RFBFT ensembles can improve the accuracy of the BFT base model, and RFBFT was relatively better. Therefore, the RFBFT model is the most effective approach for the accurate modeling of landslide susceptibility mapping (LSM). All three models can improve the identification of landslide-prone areas, enhance risk management ability, and afford more detailed information for land-use planning and policy setting.

1. Introduction

Natural hazards jeopardize infrastructure, human security, and properties. Landslides are one of the most common geological hazards, threatening the safety of people all over the world. Multiple factors control landslide events [1], including natural factors (crustal movement), human engineering activities (construction, mining, and farming), and groundwater. The damage caused by landslides to humans cannot be ignored and may be severe; it is, therefore, necessary for policymakers to control and mitigate regional landslides to safeguard the sustainable development of mountainous areas and hilly terrains. For instance, the direct and indirect economic losses caused by landslides can reach as much as CNY 2 billion every year in China, which severely impedes the economic development of disaster-stricken areas [2]. Around the world, almost 66.3 million people live in areas with a high risk of landslides [3]. The key is to work out a regional landslide control and prevention plan. In any of these cases, it is vital to be able to conduct landslide susceptibility mapping (LSM) of a certain area, which is considered a worthwhile countermeasure to reduce and mitigate the impact of landslide hazards [4,5].
In recent decades, many models have been proposed and applied to landslide susceptibility based on Geographic Information Systems (GISs) and data mining technology. In the early stages, many researchers adopted statistical analysis [6,7]. Statistical models are based on the connections between factors causing landslides and existing hazards [8,9]. Currently, bivariate and multivariate statistical analyses are most commonly applied in statistical approaches for landslide susceptibility mapping. For instance, frequency ratio [10,11], statistical index [12,13], weight of evidence [14,15], index of entropy [16,17], evidential belief function [18,19], certainty factor [20,21], and logistic regression [19,22] models have been widely used in LSM.
However, carrying out landslide susceptibility mapping in a specific region is not an easy task, since it is a relatively complex non-linear issue. Therefore, models with higher accuracy need to be created. Most recently, with advances in various software programs based on machine learning (ML) and data mining (DM), various models have been designed for LSM, including artificial neural networks [23,24], Bayesian logistic regression [25], multivariate adaptive regression spline [26,27], decision tree [28,29], support vector machine [30,31], adaptive neuro-fuzzy inference system [32,33], random forest [34,35,36], logistic model tree [23,37], and alternate decision tree [38,39]. These models produced different results with various data types in a specific study area. Each model has its advantages and disadvantages. Therefore, the best method to map landslide susceptibility is currently under discussion.
Although these models generated by machine learning and data mining have enabled researchers to identify landslide-prone areas, the complexity of landslide formation has led to the exploration of more accurate and efficient integrated models. A literature review of recent publications reveals some ensemble frameworks such as function tree with random subspace and bagging [40], alternating decision tree with AdaBoost and bagging [38], multiboosting with credal decision tree and radial basis function network [41], multiple perception neural networks with AdaBoost, bagging, dagging, multiboosting, rotation forest, random subspace [42], and Bayesian optimization [43]. More recently, some researchers have also proposed more advanced boosting algorithms, such as categorical boosting, light gradient boosting, extreme gradient boosting [44,45,46], and natural gradient boosting [47,48]. All these studies have demonstrated that hybrid and ensemble frameworks tend to generate more reliable and accurate LSM than individual machine learning techniques in a specific region. Despite such promising results, there remains no agreement on the optimum hybrid or ensemble method for regional landslide susceptibility prediction. Therefore, efforts to develop more hybrid/ensemble models are essential for different areas.
Decision tree is among the most widely used classification algorithms in machine learning and data mining, and is regarded as a potentially powerful predictor. A decision tree classifier can explicitly reflect the structure of a dataset. Best-first decision tree (BFT) is built based on the decision tree [49]. Unlike standard decision tree classifiers such as the C5.0 which expands nodes in depth-first order, the BFT classification algorithm first expands the ‘best’ node in the splitting process. This algorithm is effective in decreasing overfitting and variance problems. With this advantage, BFT has been utilized by some researchers for landslide and flood susceptibility assessment, such as a solely used BFT model in LSM [50] and BFT integrated with bagging, decoration, and a random subspace in flood susceptibility mapping (FSM) [51]. All these works have denoted that BFT is a superior approach for landslide susceptibility prediction.
It is relevant to note that, although various landslide susceptibility hybrid/ensemble models have been proposed, there is a gap in integrating advanced rotation forest and BFT. RFBFT is a novel ensemble model in landslide prediction analysis. BagBFT has only been used to predict flood susceptibility, as mentioned in [51], and its application remains poorly constrained and requires further investigation. Therefore, BFT is selected as the base classifier, combined with bagging [52] and rotation forest [53], to predict landslide susceptibility in Zhashui County, where landslides frequently occur. No related studies have been performed in this area, making it a meaningful case to carry out LSM. More specifically, this study aims to survey and evaluate the performance of BFT, BagBFT, and RFBFT for identifying landslide-prone areas on a regional scale. The results of the three models are assessed and analyzed thoroughly through operating characteristic curves (ROCs), the area under the curve (AUC), the improved frequency ratio accuracy method, and statistical tests.

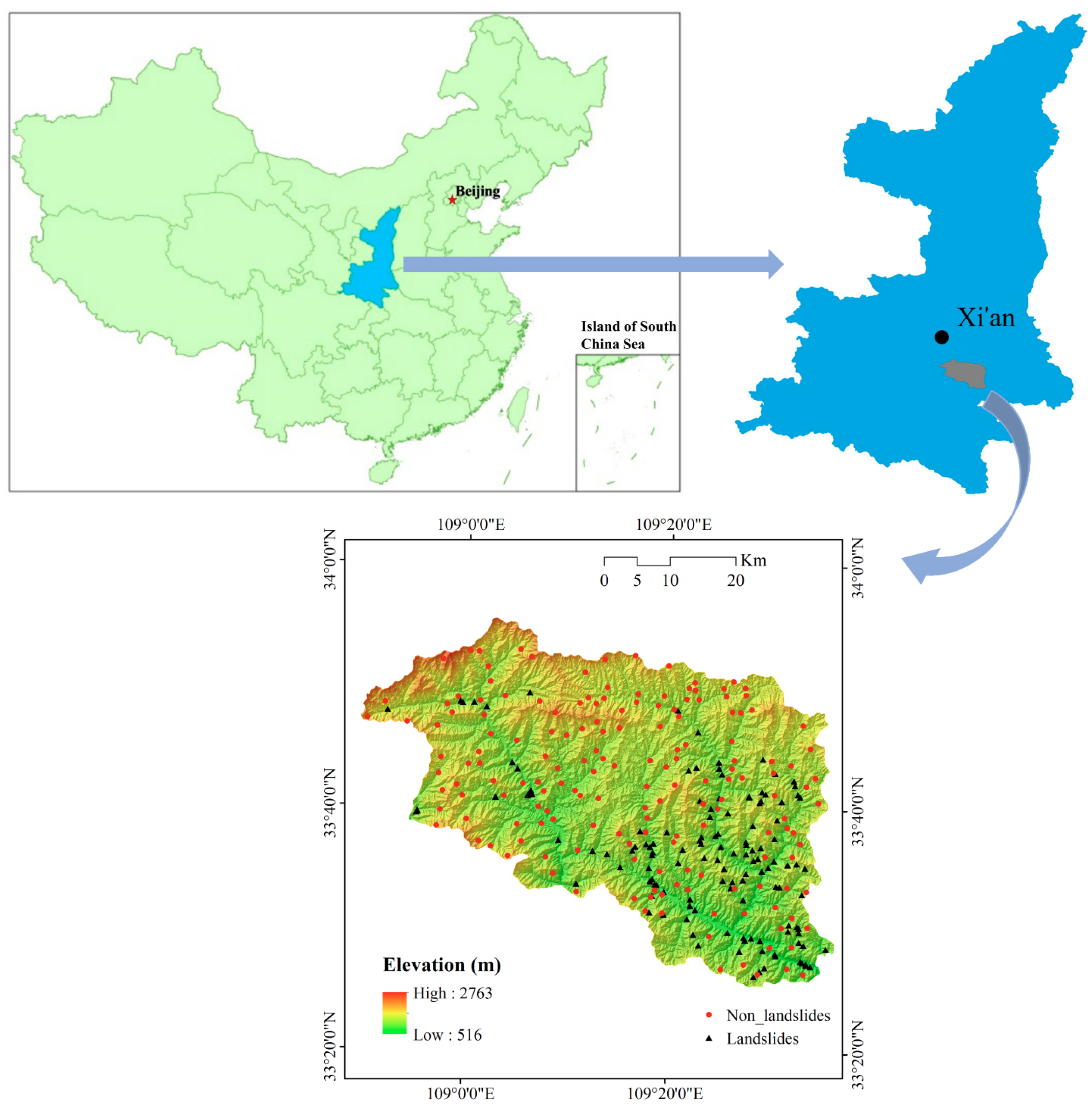
2. Study Area

The geographic coordinates of Zhashui County are between 108°50′E and 109°36′E and between 33°25′N and 33°56′N, with an area of 2322 km2, located in Shaanxi Province, China (Figure 1). The study area is a transitional climate region between the warm temperature region and the cool subtropical region, and the mean annual rainfall is 759.4 mm. Most precipitation in the area occurs from summer to autumn, with a seasonal precipitation of 276.7 mm and 334.2 mm, respectively. It is relevant to note that precipitation is one of the main factors triggering geological disasters (mainly landslides), which mostly occur in August and September. Therefore, Zhashui County indeed requires evaluation of landslides, and is thus a good case for LSM. Topographically, Zhashui County is part of the Qinba Mountain region. The general trend is high in the northwest and low in the southeast. The elevation varies from 516 m to 2763 m above sea level.

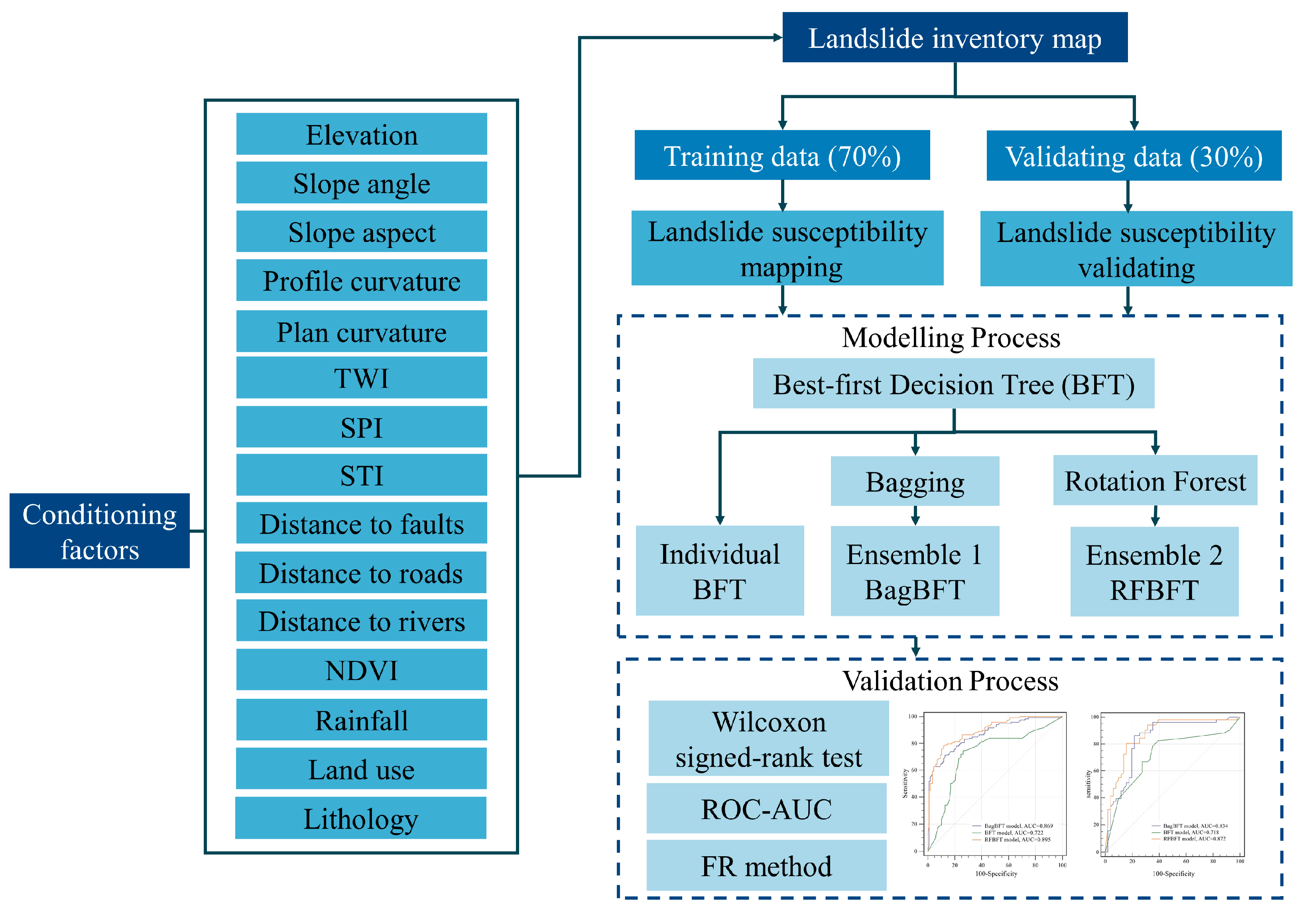
3. Materials and Methodologies

3.1. Data Preparation

Three separate activities were included: (1) mapping landslides; (2) modeling landslides based on BFT, BagBFT, and RFBFT methods; and (3) validating the modeling methods. The details of these steps are shown in Figure 2.
Landslide inventories are important for determining the relationship between landslide areas and landslide-prone areas. The distribution of past and recent landslides is the fundamental unit for landslide forecasting. In the study area, 169 landslide locations were identified from field investigations of geological hazards and image interpretation at a scale of 1:50,000, which then were randomly bifurcated into two groups, namely 118 (70%) for training and 51 (30%) for validation [14,54]. Therefore, a landslide-inventory map of the study area was produced, as shown in Figure 1.

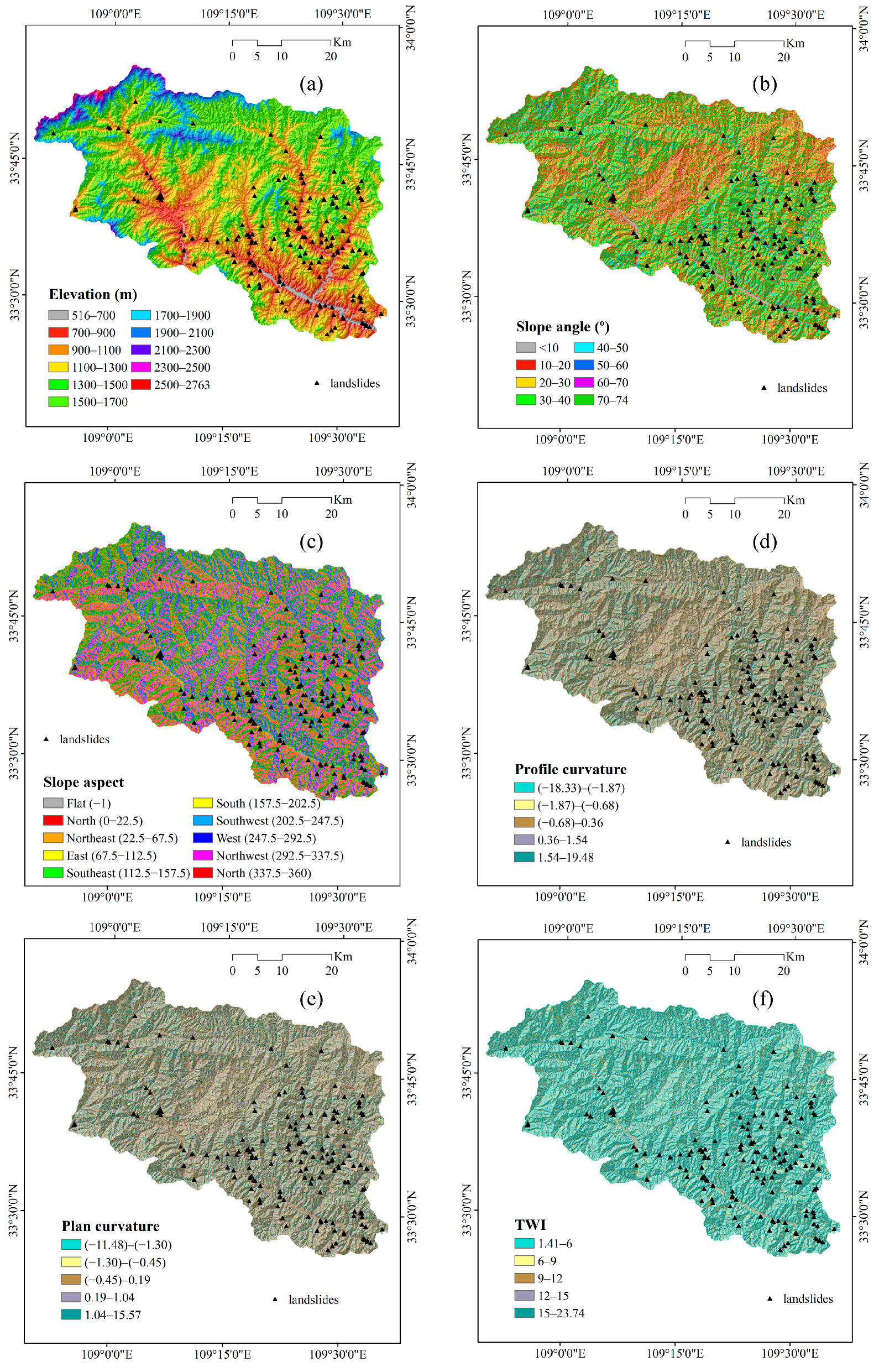
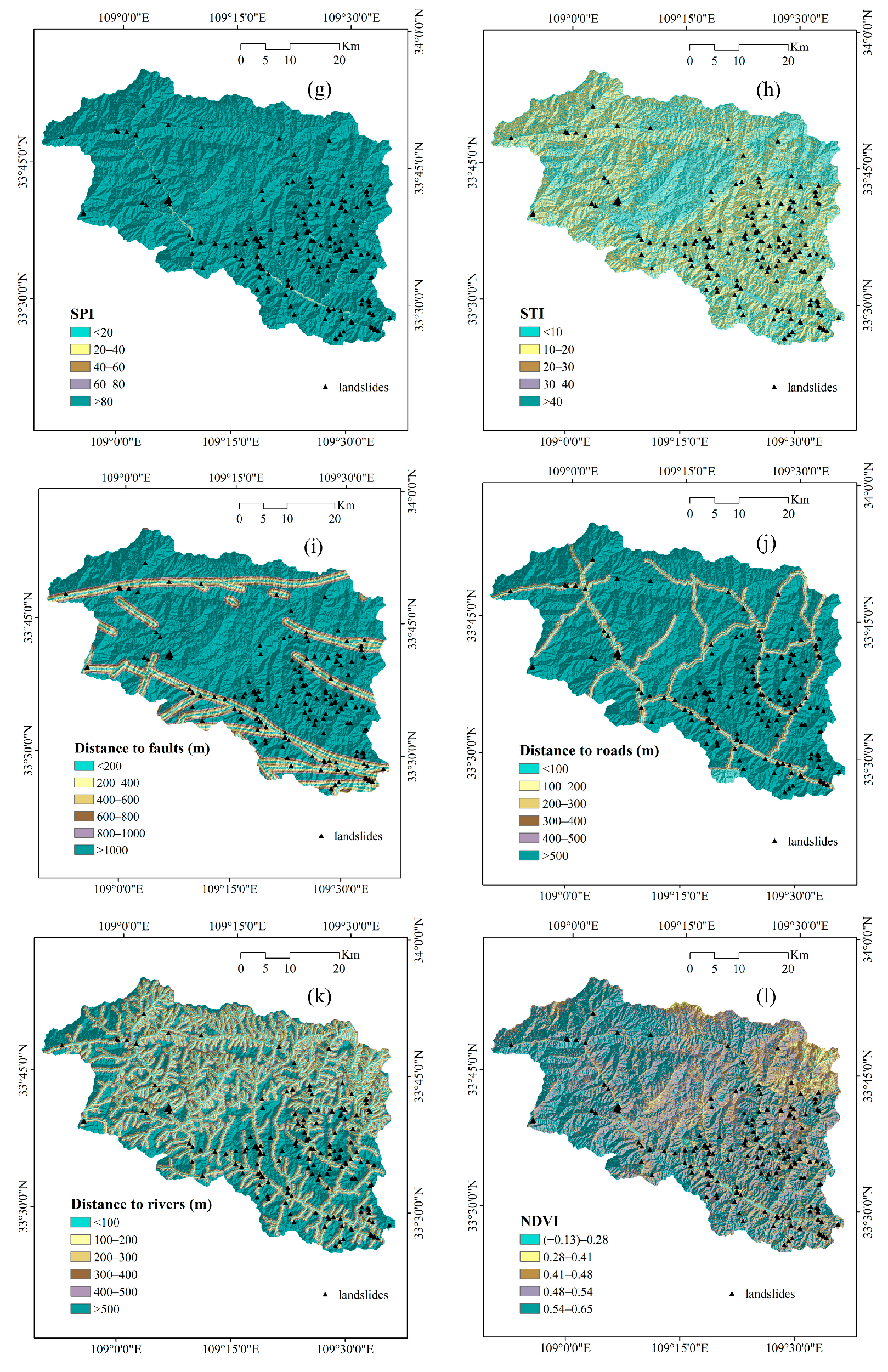
3.2. Landslide Conditioning Factors

Geological, topographic, hydrological, and environmental factors can trigger a landslide. Fifteen specific factors were selected as the most relevant factors leading to landslide occurrence: elevation, slope angle, slope aspect, profile curvature, plan curvature, topographic wetness index (TWI), stream power index (SPI), sediment transport index (STI), distance to faults, distance to roads, distance to rivers, normalized difference vegetation index (NDVI), rainfall, land use, and lithology.
Elevation is a key landslide conditioning factor, which is highly relevant to landslide occurrence [35,55]. It is relevant to note that landslides are more likely to form in high-elevation areas than in low-elevation areas [56]. In Figure 3a, the elevation was reclassified into eleven classes with a defined interval of 200 m: 516–700 m, 700–900 m, 900–1100 m, 1100–1300 m, 1300–1500 m, 1500–1700 m), 1700–1900 m, 1900–2100 m, 2100–2300 m, (2300–2500 m, and 2500–2763 m.
Slope angle may be the foremost landslide conditioning factor, dominating the concentration of surface flow and surface runoff [57]. Zhashui County has a steep terrain with a slope of 0–74° (Figure 3b), which was further classified into eight categories with a defined interval of 10°, i.e., 0–10°, 10–20°, 20–30°, 30–40°, 40–50°, 50–60°, 60–70°, and 70–74°.
Slope aspect is another significant topographic parameter, which plays a key part in the formation of landslides by affecting vegetation coverage, soil water retention, and soil strength [58]. Therefore, slope aspect is considered a conditioning factor and is obtained from the digital elevation model (DEM) within ArcGIS 10.5. In this paper, the slope aspect was divided into nine groups, including flat, north, northeast, east, southeast, south, southwest, west, and northeast (Figure 3c).
Profile curvature indicates the slope morphology, which can control the surface hydrological conditions, erosion, sedimentation rate, and soil characteristics of the slope, and all of these elements are relevant to slope stability [59]. In this study, profile curvature was calculated and grouped into five classes with the natural breaks (Jenks) method (Figure 3d).
Plan curvature is another index that embodies topographic characteristics and the steepness of the slope. The interrelation of plan curvature and profile curvature is close-knit, and both of them control the acceleration or deceleration of surface flow, which can influence the process of land sliding [60]. Here, the plan curvature values were reclassified into five groups based on the natural breaks (Jenks) method (Figure 3e).
The Topographic Wetness Index (TWI) is also an important landslide conditioning factor, which is utilized to measure the topographic domination over hydrological processes [61]. The TWI values of Zhashui County can be derived from DEM data, ranging from 1.41 to 23.74, which were then further manually reclassified into the following categories: 1.41–6, 6–9, 9–12, 12–15, and 15–23.74 (Figure 3f).
The Stream Power Index (SPI) expresses the erosion capacity of the concentrated flow. The higher the SPI value, the stronger the erosion caused by the flow. It can be computed as [14,62]:
S P I = A S × tan β
where As is the slope contributing area and β represents the slope angle (radian) [63]. The SPI values were computed by ArcGIS 10.5 and classified into five categories with a defined interval of 20, i.e., <20, 20–40, 40–60, 60–80, >80, as shown in Figure 3g.
Similarly, the sediment transport index (STI) measures the erosive force of the surface flow. Equation (2) calculates the sediment transport caused by the slope angle on the basis of As and β [64]. Here, STI values included five groups with an equal interval of 10, as illustrated in Figure 3h.
S T I = ( A S 22.13 ) 0.6 ( sin β 0.0896 ) 1.3
The three distance-related factors, namely distance to faults (Figure 3i), roads (Figure 3j), and rivers (Figure 3k), are also prominent conditioning factors for LSM [65]. The distribution of landslides can be affected by fault structure in a specific region. Additionally, in mountainous areas, road construction activities commonly generate engineering loads and wreck the integrity of the slope structure, which can lead to slope instability [66]. Rivers commonly have a negative impact on slope stability by eroding the foot of a slope and affecting the water content distribution [67,68]. These three distance-related conditioning factors were divided into five categories with equal intervals of 200 m, 100 m, and 100 m, respectively.
It is relevant to note that vegetation is vital for maintaining slope stability, especially in mountainous areas [69]. By means of root reinforcement, vegetated regions have advantageous mechanical effects on the shear strength of soil, thereby decreasing the possibility of slope instability. Therefore, a vegetation-covered slope tends to be more stable than a barren one. NDVI indicates the vegetation characteristics and can be acquired from Landsat 8 Operational Land Imager (OLI) images. NDVI can be defined as [14]:
N D V I = NIR − R NIR + R
where NIR is the near-infrared band and R is the red band of the electromagnetic spectrum. The values of NDVI vary from −1 to 1. A negative value indicates water bodies or barren rocks and sand, while a positive one denotes that the corresponding area is covered by vegetation. The NDVI values of the study area were further reclassified into five classes through the natural breaks (Jenks) method (Figure 3l).
In the Qinba Mountain region, geological hazards are closely related to rainfall, especially landslides. Herein, rainfall is a crucial conditioning factor for landslide occurrence [4]. It needs to be noted that long-term or heavy rainfall raises the groundwater level, increases pore water pressure, reduces the effective stress of soil, and then accelerates slope instability, which increases the possibility of landslides. A rainfall map was drawn using the meteorological data with a defined interval of 20 mm/y (Figure 3m).
Land use is another conditioning factor frequently utilized to create landslide susceptibility maps [70]. In some agricultural areas, landslides frequently occur due to long-term irrigation, such as in Jingyang County (China) [71]. The land-use types of the study area included farmland, garden land, forestland, commercial land, and industrial and mining storage land (Figure 3n).
Lithology is another key factor that directly controls slope stability [72]. Usually, landslides hit lithological units with lower strength and higher water content. The lithology of the study area was redivided into ten lithological units accounting for their lithofacies and geological ages. The detailed distribution of lithological units is shown in Figure 3o. Table 1 describes the lithological categories in the study area. Table 2 lists the information on the source and scale of the fifteen selected conditioning factors.

3.3. Best-First Decision Trees (BFT)

BFT was initially introduced by Friedman, Hastie, and Tibshirani [73]. It is a decision tree based on a learning algorithm, which utilizes multiple classifiers to create a classification that can optimize results, making it superior to models with a sole classifier. Structurally, BFT includes three kinds of nodes: a root node (topmost node), internal nodes (decision nodes), and leaf nodes (terminal nodes). When processing a standard divide-and-conquer classification, a decision tree algorithm starts with a root code with no incoming branches; then, branches from the root node enter internal nodes; next, with the available features, node types, are evaluated to form homogeneous subsets, which are represented by leaf nodes. Leaf nodes illustrate every possible result in the dataset. The decision-making process is repeated until no code can be spilled anymore and a terminal node is reached.

3.4. Bagging

Bagging, proposed by Breiman [52], comes from bootstrap aggregation [73]. Bagging serves to reduce the variability of data based on the use of bootstrapping together with a regression or classification model, such as a decision tree. Bagging is a straightforward and intuitive algorithm. With the training data, we can train a model that is be used to make a prediction. The process of averaging all previous predictions has two advantages: simplifying the solution and reducing the variance. For regression trees, many trees are grown (without pruning) and the mean of the predictions is calculated. In the case of classification trees, the simplest thing is to substitute the mean for the mode and use the majority vote criterion. Additionally, bagging allows the prediction error to be estimated directly, without the need to use a test sample or to apply cross-validation or, again, resampling [74].

3.5. Rotation Forest

Rotation forest was initially developed by Rodriguez, Kuncheva, and Alonso [53], using principal component analysis (PCA) [75]. This approach extracts the features from learning sets. Training sets are generated for learning base classifiers. Based on feature transformation, rotation forest focuses on improving the discrepancy and accuracy of the base classifiers. Before each sub-sample is drawn, the sample attribute set is randomly divided and combined, and the principal component analysis method is used to perform feature transformation on the data between the divided groups of sub-attribute sets. Processing the sub-sample data in this way not only makes the sub-samples different but also plays a role in data preprocessing, thereby improving the accuracy and difference of each base classifier. The calculation process of PCA can be expressed as transforming a set of observed variables into a set of uncorrelated variables through linear transformation and at the same time, keeping the total variance of the original variables unchanged. The standard error (generalization error) can be computed as follows:
G E = P x , y ( m g ( x , y ) < 0 )
m g ( x , y ) = a v k I ( h k ( x ) = y ) − m a x j ≠ y a v k I ( h k ( x ) = j )
where x and y are related factors representing the spatial of x and y, and I and mg are indicators and marginal functions, respectively [76].

4. Results

4.1. Spatial Relationship

The spatial relationship between the selected fifteen conditioning factors and historical landslides was measured and quantified through the frequency ratio (FR) method [10,29,51]. The corresponding FR values denoted the relationship between the subclasses of each factor and the landslide occurrence (Supplementary Table S1). Table S1 shows that the most landslide-prone parts of the study area have an elevation of 516–700 m, with a highest FR value of 22.86. Among other conditioning factors, the areas with higher FR values are those with an SPI of 60–80 (FR = 15.73), commercial land use (FR = 9.04), an NDVI of −0.13–0.28 (FR = 6.55), a TWI of 15–23.74 (FR = 6.48), a distance to a road of 0–100 m (FR = 4.06), a distance to a river of 0–100 m (FR = 2.64), a lithology of group 9 (FR = 2.20), a distance to a fault of 400–600 m (FR = 1.98), and rainfall of 693–713 mm/y (FR = 1.25), respectively. All these areas were identified as the landslide-susceptible portions of the study area.
More specifically, for the elevation factor, the FR values drop dramatically with the elevation increase. When the elevation is higher than 1500 m, the FR value is equal to 0, showing that these areas are assessed as landslide-proof portions of the study area. In terms of the land-use factor, the subclass of commercial land has the third-largest FR value of 9.04, followed by farmland (FR = 1.93). The FR values of other land-use type are smaller than 1. For the factor of distance to roads and rivers, the smaller the distance to a road, the higher the occurrence of landslides. From the aforementioned analysis, it can be noted that human activities play a crucial role in landslide occurrence since people tend to carry out activities in low-altitude areas and live close to water bodies. Another important factor is NDVI, demonstrating high FR values for the −0.13–0.28 (FR = 6.55) and 0.28–0.41 (FR = 5.47) subclasses, indicating poor vegetation coverage in these areas, which justifies NDVI as a vital conditioning factor since it is highly related to landslide occurrence. For the factor of TWI, as the value rank increases, the corresponding FR values grow. The results of SPI illustrate that it is highly related to landslide occurrence. The subclass of 60–80 has the second largest FR value among all the subclasses, 15.73, followed by 0–20 (FR = 7.50), 20–40 (FR = 6.77), 40–60 (FR = 2.41), and >80 (FR = 0.86), which is consistent with the study [14], showing that SPI is also an important factor. In terms of slope, as reported in [58], slope angle is closely related to landslides. A slope of 0–10° has an FR value of 3.50, followed by 50–60° (FR = 3.11), indicating that human activities tend to be performed in areas with gentle slopes, and steep slopes are more prone to instability. As stated in [72], lithology plays a role in landslide occurrence. In the study area, landslides frequently occurred in groups 4 (FR = 1.87) and 9 (FR = 2.20), in which sandstones developed. The rainfall in the study area was concentrated, and landslides occurred frequently in the rainy season. Generally, FR values grow with increasing rainfall, which implies that rainfall is also an important factor.

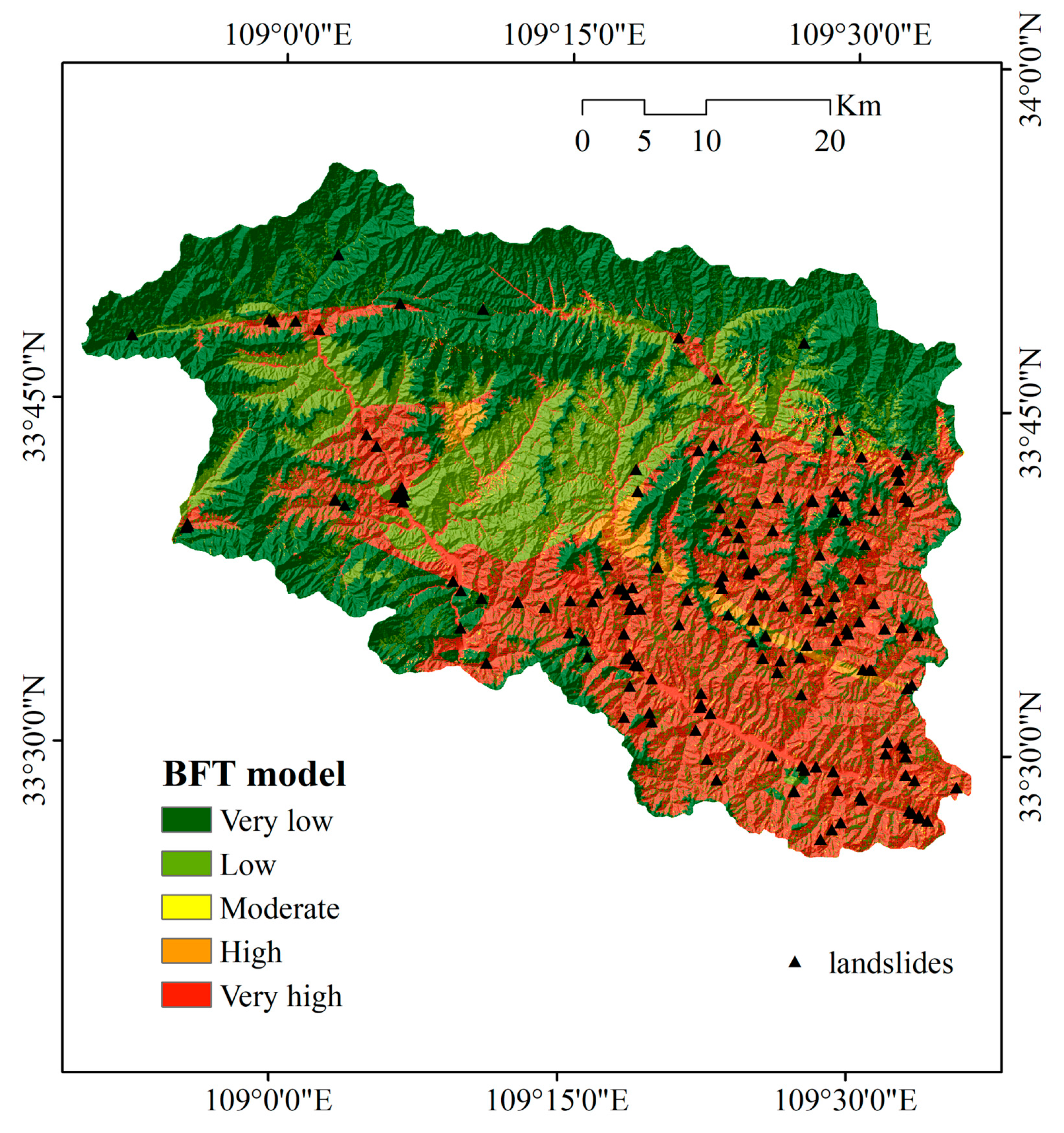
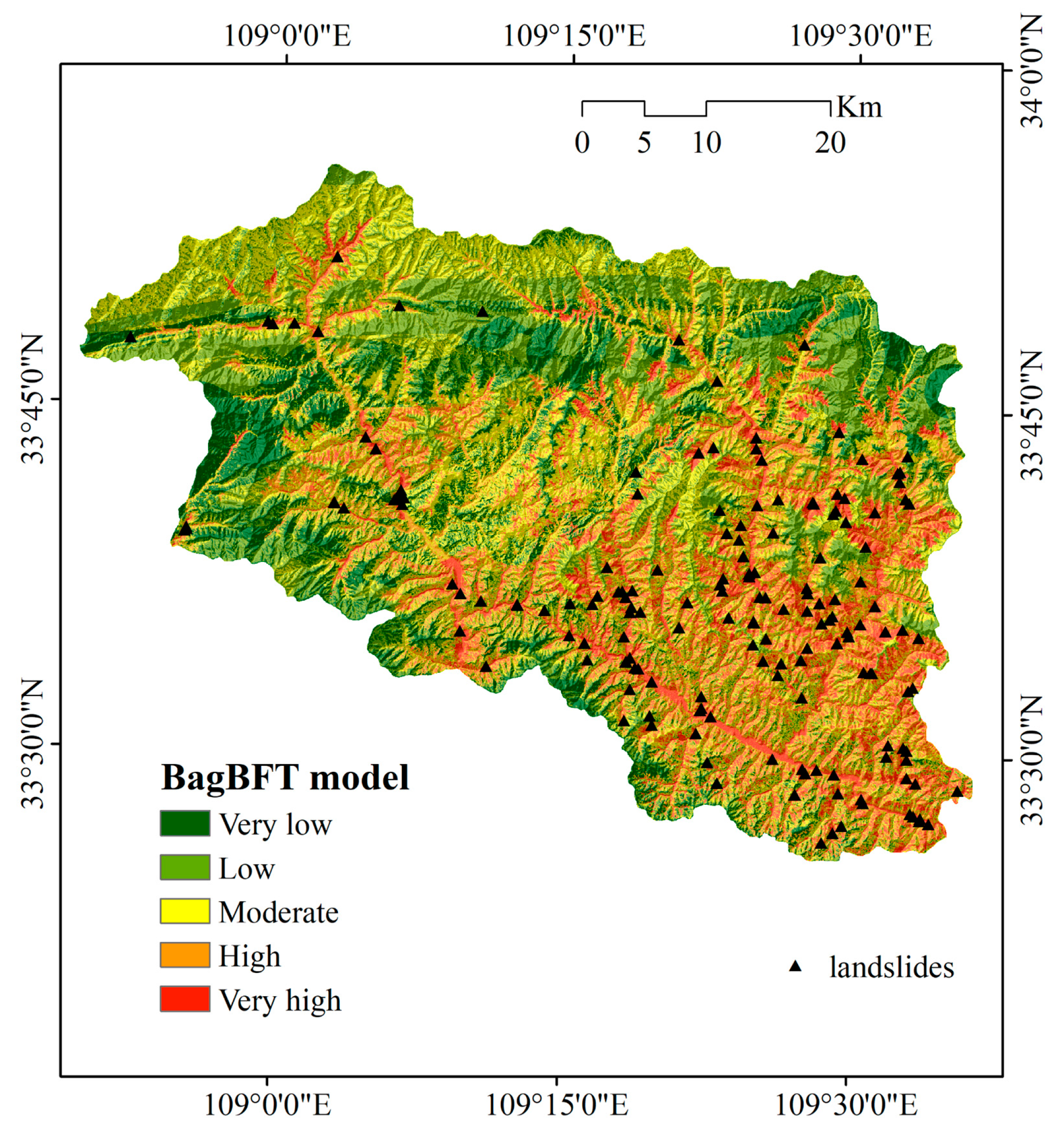
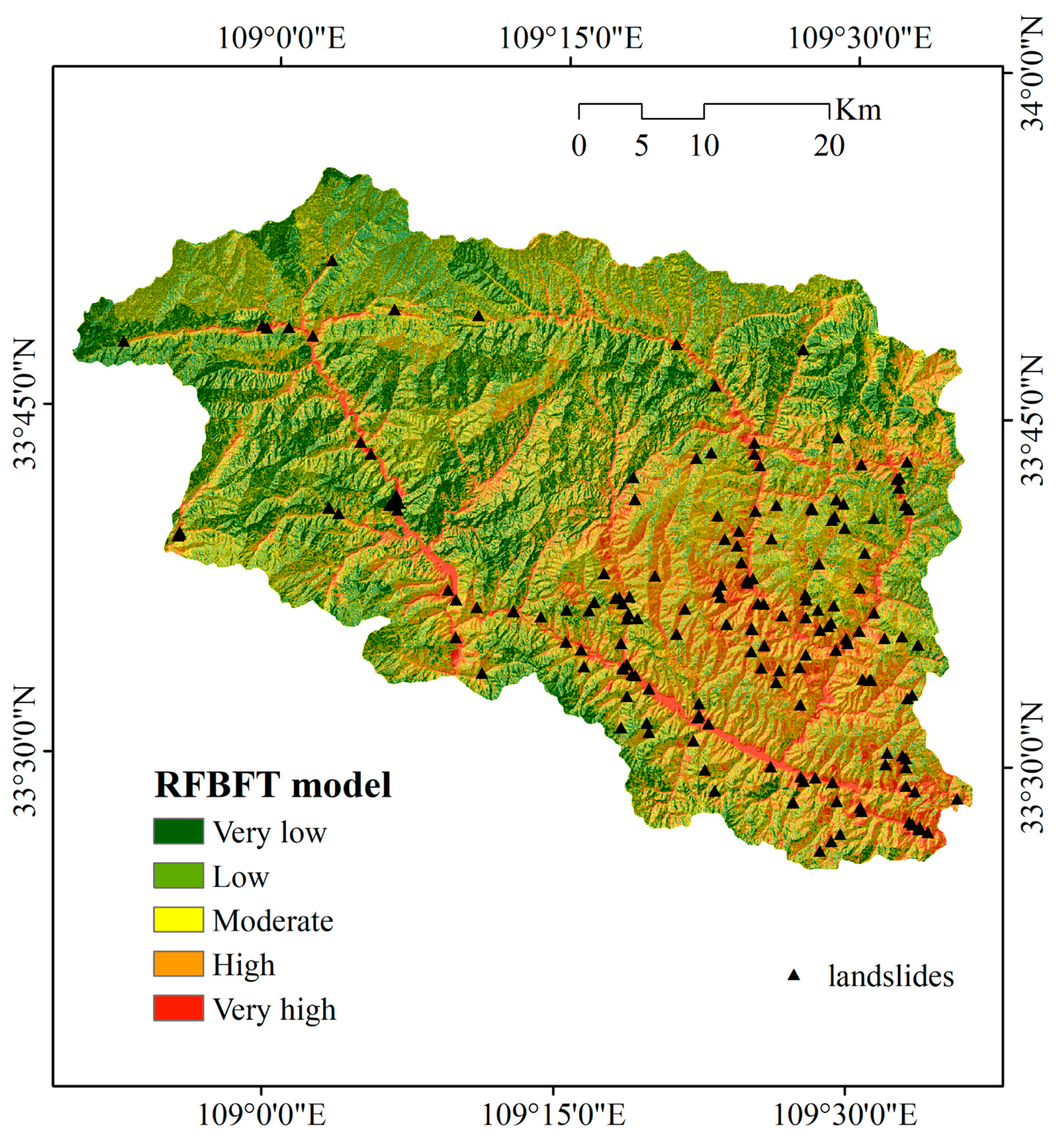
4.2. Constructing Landslide Susceptibility Maps

The selected conditioning factors strictly control the accuracy of the landslide susceptibility map. The fifteen factors used in this paper are typically chosen by other researchers and are also highly related to the landslides in Zhashui County. The value of the landslide susceptibility index (LSI) is computed by analyzing the spatial connections of historical landslides and every conditioning factor. After normalization, LSI values between 0 and 1 are obtained. Then, a stepwise forward process is applied to reclassify the LSI values into five classes from very low susceptibility to very high susceptibility on the basis of the natural break classification method [77]. The application of BFT, BagBFT, and RFBFT is summarized in Figure 4, Figure 5 and Figure 6, where each susceptibility map is demonstrated. The area percentage of each class within the three models is illustrated in Figure 7. For the BFT model, the raster pixels are distributed in 54.76%, 9.39%, 1.61%, 0.88%, and 33.35% of the area for the very low, low, moderate, high, and very high classes, respectively. The low class output from the BagBFT accounts for the highest percentage (28.69%) of the pixels. The very low, moderate, high, and very high classes cover 14.26%, 27.33%, 17.63%, and 12.08% of the area, respectively. Additionally, the RFBFT model classifications are 18.96%, 27.55%, 25.30%, 20.91%, and 7.28%, respectively.

4.3. Validation of the LSM

4.3.1. AUC-ROC Analysis

In the present study, BFT and two hybrid models (BagBFT and RFBFT) are employed to model landslide susceptibility. The datasets are divided into two parts, namely the training data and validation data, to evaluate the performance of each model. Presently, the receiver operating characteristic curve (ROC) and the area under the ROC curve (AUC) are typically applied to assess the accuracy of landslide susceptibility models [78]. Each model’s performance is assessed by the success rate curve in the training data, and the corresponding predictive capability is measured using the prediction rate curve in the validation data. Therefore, in order to evaluate the performance of the BFT, BagBFT, and RFBFT models, the ROC curves of these three models with training and validation datasets are illustrated in Figure 7.
The AUC values for the BFT, BagBFT, and RFBFT models generated by the training dataset are 0.722, 0.869, and 0.895, respectively (Figure 8a and Table 3). It is relevant to note that the RFBFT model has the lowest standard error (0.0199). Thus, both the BagBFT and RFBFT models can improve the accuracy of the base classifier BFT, and the integrated ensemble RFBFT model shows an outstanding performance.
In general, the optimal model is the model with the highest prediction rate. The AUC values of the validation data are 0.718, 0.834, and 0.872 for the BFT, BagBFT, and RFBFT models, respectively (Figure 8b and Table 4). It is relevant to note that the AUC values of the three models decrease slightly when compared with the training ones. In terms of standard error, the RFBFT is 0.0362, which is the lowest, followed by the BagBFT model (0.0424) and the BFT model (0.0521). The thorough results show that the RFBFT model has an outstanding predictive ability for landslide susceptibility mapping.

4.3.2. Improved Frequency Ratio Accuracy Analysis

In order to further estimate the results of the landslide susceptibility mapping produced by the three models, the authors applied a new approach [78]. For each class from very low to very high, the numbers of rasters and corresponding landslides are calculated. Then, the raster and landslide ratios are computed and compared (Table 5).
As can be seen from Table 5, with the increase in the landslide susceptibility grade, the ratio of landslide frequency in each class increases. The frequency ratio accuracy of the landslide susceptibility results can be obtained by dividing the frequency ratio of the extremely high and high classes by the sum of the frequency ratios for each model. For the BFT model, the sum of the frequency ratio for very high and high classes is 5.699, and for all five classes it is 7.482, meaning the frequency ratio accuracy of the BFT model is 0.76163. Similarly, we can compute these values for the BagBFT and RFBFT models, demonstrating that the frequency ratio accuracy of BagBFT and RFBFT is 0.92220 and 0.92224, respectively.

4.3.3. Statistical Significance Test

Assessment of the proposed models’ prediction accuracy is vital in LSM. Hence, Wilcoxon signed-rank [79] statistical tests were applied in this study to evaluate the models’ prediction capability (Table 6). Applying the Wilcoxon signed-rank tests at a 5% significance level, the Z and p values were utilized to identify whether to accept the hypothesis. In the present study, the Z values and p values for each pairwise comparison of BFT~BagBFT and BFT~RFBFT exceeded the critical values of ±1.96 and 0.05, respectively, denoting significant differences between these models. In contrast, the Z values and p values of BagBFT~RFBFT illustrate no significant differences between these two models. The results show that BFT is significantly different from the other two models.
Consequently, by means of AUC-ROC, the improved frequency ratio accuracy, and statistical significance analysis, the results of these three approaches show good consistency. BagBFT and RFBFT are acceptable for LSM in this study, and BFT performs worst among the three models. Therefore, we can finally obtain the most effective model, RFBFT, for mapping the landslide susceptibility in Zhashui County.

5. Discussions

With increasing human production activities and some environmental factors, the frequency of geological hazards, especially landslides, has been increasing in recent decades. These hazards can jeopardize infrastructure or even human security and property. Therefore, it is necessary to figure out novel and efficient techniques for spatially evaluating landslide occurrence. The ensemble-learning methods are regarded as excellent tools for optimizing LSM ability. The aim of this study is to introduce and compare three ensembles in predicting the spatial probability of landslide occurrence. Finally, integrated ensemble BFT models with rotation forest and bagging are proposed and utilized to model and anticipate landslide occurrence spatially. In this study, fifteen conditioning factors are selected due to their strong association with landslide formation.
The proposed ensemble frameworks significantly outperformed the individual base model, which is an important indicator and confirmation of how machine learning techniques can improve the base classifier’s flexibility and efficiency. Among the three models, they all have their advantages as widely used approaches in various publications. The BFT model was initially proposed to solve problems involving classification. It is a supervised learning classifier and is easy to implement, which allows the best node to be extended first. This advantage allows for exploring new pruning approaches to identify the number of expansions on the basis of cross-validation steps. The BFT model has been successfully used for flood susceptibility prediction integrated with bagging, decoration, and random subspace techniques [51]. For the Bagging-BFT (BagBFT) ensemble method, bagging can combine different base classifiers. Therefore, bagging is advantageous in reducing the classification variance to enhance the model’s performance. The application of bagging integrated with other models, such as the LogitBoost alternating decision trees and penalizing attributes, has justified its ability to improve the base model’s performance. The rotation forest classifier has been highlighted as being a strong tool to boost the base model’s performance [51]. It is an efficient method to improve wear classifiers based on feature extraction. The randomly split feature set leads to different rotations and generates diverse classifiers, which enable one to build more diverse and accurate individual classifiers. Additionally, rotation forest can be combined with any basic classifier, making it a promising machine-learning approach.
The FR approach was used to measure and quantify the spatial relationship between the selected fifteen conditioning factors and historical landslides. In this study, the most landslide-susceptible areas display an elevation of 516–700 m (FR = 22.86), an STI of 60–80 (FR = 15.73), commercial land use (FR = 9.04), an NDVI of −0.13–0.28 (FR = 6.55), a TWI of 15–23.74 (FR = 6.48), a distance to a road of 0–100 m (FR = 4.06), a distance to a river of 0–100 m (FR = 2.64), a lithology of group 9 (FR = 2.20), a distance to a fault of 400–600 m (FR = 1.98), and rainfall of 693–713 mm/y (FR = 1.25), respectively. This analysis shows the effect of each factor on landslide occurrence.
To evaluate the performance of BFT, BagBFT, and RFBFT in LSM, ROC curves and AUC values are obtained. The AUC values justify that all three of these models are efficient for LSM. The RFBFT model (AUC = 0.895 for training data; AUC = 0.872 for validating data) serves as the best performer, meaning that the rotation forest algorithm integrates well with the BFT model, followed by BagBFT (AUC = 0.869 for training data; AUC = 0.834 for validating data), and both outperform the BFT model (AUC = 0.722 for training data; AUC = 0.718 for validating data) for spatial model accuracy. Among the ensemble methods, the RFBFT performed slightly better than the BagBFT, making the RFBFT algorithm the most reliable model for the present case. In previous studies, rotation forest has also been shown to be among the most outstanding available classification algorithms, and enhances the performance models with a sole classifier as well [53]. The reason for the less optimal performance of BagBFT may be that the distribution of the data subset extracted by the bagging approach is similar to that of the original dataset, making the discrepancy between the base classifiers not as distinct, leading to the accuracy of the ensemble frameworks becoming dependent on the selected base classifiers.
In addition, statistical tests and a novel approach are utilized further to estimate the accuracy rate of the three proposed methods. All three models produce satisfactory landslide susceptibility prediction for the improved frequency ratio accuracy approach. The frequency ratio accuracy of the BagBFT (0.92220) and RFBFT (0.92224) models is much higher than that of the BFT (0.76163) model, which shows good consistency with the results of the ROC curves, also implying that the RFBFT model works slightly better than the BagBFT model. Additionally, in Figure 5 and Figure 6, it can be noted that LSMs of the BagBFT and RFBFT ensemble models are similar on the whole. Therefore, the LSM generated by the RFBFT ensemble model indicates a better prediction for the spatial aggregation characteristics and distribution of regional landslides in Zhashui County.
According to the literature review, most ML-based models were proven to have promising prediction abilities, but may also have certain limitations or challenges involving hyperparameter tuning [80]. Discussions on hyperparameter optimization are commonly performed in computer science, while few studies on machine learning-based landslide susceptibility have been carried out involving hyperparameter optimization [31]. Most LSM models need to generate a non-landslide dataset [81]. When we use machine learning methods to assess landslide susceptibility, the ratio of landslide (or positive) to non-landslide (or negative) input data is significant with regard to the models’ prediction accuracy. Therefore, an appropriate positive/negative (P/N) ratio is required for ML-based landslide prediction. This ratio is thought to be a hyperparameter of ML-based LSM models. In this regard, most researchers tend to adopt the same number of non-landslide samples as landslide ones [14], namely P/N is equal to 1:1, which is also the value we used in this study. However, some researchers pointed out that this equal ratio may lead to the overstatement of the proportion of landslide data in the corresponding area. Hence, different P/N ratios were tried, such as 1:1, 1:2, and 1:3 [82]. Overusing non-landslide samples may cause data pollution, which deteriorates the model’s performance. Most recently, to overcome the limitation of parameter settings, some researchers have tried to optimize this hyperparameter with different methods [83], including the support vector regression model [84], the whale optimization algorithm [85], and the Bayesian optimization algorithm [86]. Hyperparameter tuning of ML-based models for the best output varies from one issue to another, and so further studies are needed to aid in the ML model selection process.
Consequently, the results verify that the rotation forest model shows outstanding performance in improving the generalization ability and accuracy of the base classifier. Accordingly, the LSMs developed by the RFBFT and BagBFT models, to a certain extent, indicate a reference meaning to the study area. Identification of landslide-prone areas are significant and meaningful for land use and planning [87], and advanced techniques are efficient for this kind of study. The process of factor selection and ensemble model building has a certain value for similar studies. However, as these various models are applied in a specific region, the applicability of the models should be tested and varied in other mountainous areas.

6. Conclusions

Spatial modeling of landslides is a common and hot topic, and many researchers have studied this kind of study. The classic statistical approaches solely applied by many researchers show non-optimal accuracy; however, the mapping capability can be improved if they are integrated with artificial intelligence algorithms. In this paper, the aim is to build a new hybrid model to map landslide susceptibility in Zhashui County, China. A best-first decision (BFT) classifier with bagging (BagBFT) and rotation forest (RFBFT) ensembles are employed to figure out multi-dimensional and non-linear issues involving landslide hazards. The prediction ability of fifteen conditioning factors is estimated for the modeling process with these three models. Finally, a landslide susceptibility map is constructed. The ROC curve, improved frequency ratio accuracy, and Wilcoxon signed-rank tests are utilized to assess and compare the performance and accuracy of the three algorithms. The results illustrate that the RFBFT model has superior sensitivity. Accordingly, the RFBFT model is the best optimization ensemble for the study area, and it can also be utilized as a promising approach for spatially modeling the occurrence of landslides. This study ultimately contributes to providing valuable information for land-use planning and policymakers in the study area and other similar areas vulnerable to landslides.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15041007/s1, Table S1: Spatial relationship between conditioning factors and historical landslides using frequency ratio method.

Author Contributions

Conceptualization, J.G. and W.C.; methodology, L.R.A.; software, M.Y.; validation, J.G. and W.C.; formal analysis, L.R.A.; investigation, M.Y.; resources, M.Y.; data curation, W.C.; writing—original draft preparation, J.G.; writing—review and editing, L.R.A.; visualization, F.Z.; supervision, M.Y.; project administration, F.Z.; funding acquisition, F.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (No. 41977228), and Key Research Program of Shaanxi (Program No. 2022SF-335).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
  2. Han, J.; Wu, S.; Wang, H. Preliminary Study on Geological Hazard Chains. Earth Sci. Front. 2007, 14, 11–20. [Google Scholar] [CrossRef]
  3. Sassa, K.; Canuti, P. Landslides-Disaster Risk Reduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
  4. Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide Susceptibility Modeling Based on GIS and Novel Bagging-Based Kernel Logistic Regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
  5. Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
  6. Smith, H.G.; Spiekermann, R.; Betts, H.; Neverman, A.J. Comparing methods of landslide data acquisition and susceptibility modelling: Examples from New Zealand. Geomorphology 2021, 381, 107660. [Google Scholar] [CrossRef]
  7. Zhao, Y.; Wang, R.; Jiang, Y.; Liu, H.; Wei, Z. GIS-based logistic regression for rainfall-induced landslide susceptibility mapping under different grid sizes in Yueqing, Southeastern China. Eng. Geol. 2019, 259, 105147. [Google Scholar] [CrossRef]
  8. Pourghasemi, H.R.; Teimoori Yansari, Z.; Panagos, P.; Pradhan, B. Analysis and evaluation of landslide susceptibility: A review on articles published during 2005–2016 (periods of 2005–2012 and 2013–2016). Arab. J. Geosci. 2018, 11, 193. [Google Scholar] [CrossRef]
  9. Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
  10. Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
  11. Shu, H.; Guo, Z.; Qi, S.; Song, D.; Pourghasemi, H.R.; Ma, J. Integrating Landslide Typology with Weighted Frequency Ratio Model for Landslide Susceptibility Mapping: A Case Study from Lanzhou City of Northwestern China. Remote Sens. 2021, 13, 3623. [Google Scholar] [CrossRef]
  12. Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
  13. Coco, L.; Macrini, D.; Piacentini, T.; Buccolini, M. Landslide Susceptibility Mapping by Comparing GIS-Based Bivariate Methods: A Focus on the Geomorphological Implication of the Statistical Results. Remote Sens. 2021, 13, 4280. [Google Scholar] [CrossRef]
  14. Chen, W.; Sun, Z.; Han, J. Landslide Susceptibility Modeling Using Integrated Ensemble Weights of Evidence with Logistic Regression and Random Forest Models. Appl. Sci. 2019, 9, 171. [Google Scholar] [CrossRef]
  15. Zhipeng, L.; Yong, X.; Sheng, F.; Lixia, C.; Lei, L. Landslide susceptibility assessment based on multi-model fusion method: A case study in Wufeng County, Hubei Province. Bull. Geol. Sci. Technol. 2020, 39, 178–186. (In Chinese) [Google Scholar] [CrossRef]
  16. Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.B.; Panahi, M.; Hong, H.; et al. Landslide Detection and Susceptibility Mapping by AIRSAR Data Using Support Vector Machine and Index of Entropy Models in Cameron Highlands, Malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
  17. Jaafari, A.; Najafi, A.; Pourghasemi, H.R.; Rezaeian, J.; Sattarian, A. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, northern Iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef]
  18. Pradhan, A.M.S.; Kim, Y.-T. Spatial data analysis and application of evidential belief functions to shallow landslide susceptibility mapping at Mt. Umyeon, Seoul, Korea. Bull. Eng. Geol. Environ. 2017, 76, 1263–1279. [Google Scholar] [CrossRef]
  19. Zhao, X.; Chen, W. Optimization of Computational Intelligence Models for Landslide Susceptibility Evaluation. Remote Sens. 2020, 12, 2180. [Google Scholar] [CrossRef]
  20. Chen, W.; Li, W.; Chai, H.; Hou, E.; Li, X.; Ding, X. GIS-based landslide susceptibility mapping using analytical hierarchy process (AHP) and certainty factor (CF) models for the Baozhong region of Baoji City, China. Environ. Earth Sci. 2015, 75, 63. [Google Scholar] [CrossRef]
  21. Zhao, X.; Chen, W. GIS-Based Evaluation of Landslide Susceptibility Models Using Certainty Factors and Functional Trees-Based Ensemble Techniques. Appl. Sci. 2020, 10, 16. [Google Scholar] [CrossRef] [Green Version]
  22. Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid Integration Approach of Entropy with Logistic Regression and Support Vector Machine for Landslide Susceptibility Modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef] [PubMed]
  23. Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
  24. Chen, W.; Pourghasemi, H.R.; Zhao, Z. A GIS-based comparative study of Dempster-Shafer, logistic regression and artificial neural network models for landslide susceptibility mapping. Geocarto Int. 2017, 32, 367–385. [Google Scholar] [CrossRef]
  25. Rong, G.; Alu, S.; Li, K.; Su, Y.; Zhang, J.; Zhang, Y.; Li, T. Rainfall Induced Landslide Susceptibility Mapping Based on Bayesian Optimized Random Forest and Gradient Boosting Decision Tree Models—A Case Study of Shuicheng County, China. Water 2020, 12, 3066. [Google Scholar] [CrossRef]
  26. Pham, B.T.; Tien Bui, D.; Pourghasemi, H.R.; Indra, P.; Dholakia, M.B. Landslide susceptibility assesssment in the Uttarakhand area (India) using GIS: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
  27. Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
  28. Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. GIS-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, Naïve-Bayes tree, and alternating decision tree models. Geomat. Nat. Haz. Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
  29. Gui, J.; Pérez-Rey, I.; Yao, M.; Zhao, F.; Chen, W. Credal-Decision-Tree-Based Ensembles for Spatial Prediction of Landslides. Water 2023, 15, 605. [Google Scholar] [CrossRef]
  30. Liu, R.; Peng, J.; Leng, Y.; Lee, S.; Panahi, M.; Chen, W.; Zhao, X. Hybrids of Support Vector Regression with Grey Wolf Optimizer and Firefly Algorithm for Spatial Prediction of Landslide Susceptibility. Remote Sens. 2021, 13, 4966. [Google Scholar] [CrossRef]
  31. Can, Y.; Lei, L.; Yili, Z.; Wenqing, Z.; Shaohe, Z. Machine learning based on landslide susceptibility assessment with Bayesian optimized the hyperparameters. Bull. Geol. Sci. Technol. 2022, 41, 228–238. (In Chinese) [Google Scholar] [CrossRef]
  32. Arabameri, A.; Roy, J.; Saha, S.; Blaschke, T.; Ghorbanzadeh, O.; Tien Bui, D. Application of probabilistic and machine learning models for groundwater potentiality mapping in Damghan sedimentary plain, Iran. Remote Sens. 2019, 11, 3015. [Google Scholar] [CrossRef]
  33. Saadat, H.; Bonnell, R.; Sharifi, F.; Mehuys, G.; Namdar, M.; Ale-Ebrahim, S. Landform classification from a digital elevation model and satellite imagery. Geomorphology 2008, 100, 453–464. [Google Scholar] [CrossRef]
  34. Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.X. GIS-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. CATENA 2018, 164, 135–149. [Google Scholar] [CrossRef]
  35. Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. CATENA 2017, 151, 147–160. [Google Scholar] [CrossRef]
  36. Zheng, Y.; Chen, J.; Wang, C.; Cheng, T. Application of certainty factor and random forests model in landslide susceptibility evaluation in Mangshi City, Yunnan Province. Bull. Geol. Sci. Technol. 2022, 39, 131–144. (In Chinese) [Google Scholar] [CrossRef]
  37. Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance evaluation of GIS-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (ANFIS) with genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) for landslide spatial modelling. CATENA 2017, 157, 310–324. [Google Scholar] [CrossRef]
  38. Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. CATENA 2020, 187, 104396. [Google Scholar] [CrossRef]
  39. Arabameri, A.; Karimi-Sangchini, E.; Pal, S.C.; Saha, A.; Chowdhuri, I.; Lee, S.; Tien Bui, D. Novel Credal Decision Tree-Based Ensemble Approaches for Predicting the Landslide Susceptibility. Remote Sens. 2020, 12, 3389. [Google Scholar] [CrossRef]
  40. Peng, T.; Chen, Y.; Chen, W. Landslide Susceptibility Modeling Using Remote Sensing Data and Random SubSpace-Based Functional Tree Classifier. Remote Sens. 2022, 14, 4803. [Google Scholar] [CrossRef]
  41. Wang, G.; Lei, X.; Chen, W.; Shahabi, H.; Shirzadi, A. Hybrid Computational Intelligence Methods for Landslide Susceptibility Mapping. Symmetry 2020, 12, 325. [Google Scholar] [CrossRef] [Green Version]
  42. Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. CATENA 2017, 149, 52–63. [Google Scholar] [CrossRef]
  43. Xie, W.; Nie, W.; Saffari, P.; Robledo, L.F.; Descote, P.-Y.; Jian, W. Landslide hazard assessment based on Bayesian optimization–support vector machine in Nanping City, China. Nat. Hazards 2021, 109, 931–948. [Google Scholar] [CrossRef]
  44. Sahin, E.K. Comparative analysis of gradient boosting algorithms for landslide susceptibility mapping. Geocarto Int. 2022, 37, 2441–2465. [Google Scholar] [CrossRef]
  45. Sahin, E.K. Assessing the predictive capability of ensemble tree methods for landslide susceptibility mapping using XGBoost, gradient boosting machine, and random forest. SN Appl. Sci. 2020, 2, 1308. [Google Scholar] [CrossRef]
  46. Wang, L.; Wu, J.; Zhang, W.; Wang, L.; Cui, W. Efficient Seismic Stability Analysis of Embankment Slopes Subjected to Water Level Changes Using Gradient Boosting Algorithms. Front. Earth Sci. 2021, 9, 807317. [Google Scholar] [CrossRef]
  47. Kavzoglu, T.; Teke, A. Predictive Performances of Ensemble Machine Learning Algorithms in Landslide Susceptibility Mapping Using Random Forest, Extreme Gradient Boosting (XGBoost) and Natural Gradient Boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar] [CrossRef]
  48. Zhang, S.; Wang, Y.; Wu, G. Earthquake-Induced Landslide Susceptibility Assessment Using a Novel Model Based on Gradient Boosting Machine Learning and Class Balancing Methods. Remote Sens. 2022, 14, 5945. [Google Scholar] [CrossRef]
  49. Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
  50. Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
  51. Pham, B.T.; Jaafari, A.; Phong, T.V.; Yen, H.P.H.; Tuyen, T.T.; Luong, V.V.; Nguyen, H.D.; Le, H.V.; Foong, L.K. Improved flood susceptibility mapping using a best first decision tree integrated with ensemble learning techniques. Geosc. Front. 2021, 12, 101105. [Google Scholar] [CrossRef]
  52. Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
  53. Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
  54. Costache, R. Flood Susceptibility Assessment by Using Bivariate Statistics and Machine Learning Models–A Useful Tool for Flood Risk Management. Water Resour. Manag. 2019, 33, 3239–3256. [Google Scholar] [CrossRef]
  55. Chen, Q.; Yan, E.; Huang, S.; Wang, X. Susceptibility evaluation of geological disasters in southern Huanggang based on samples and factor optimization. Bull. Geol. Sci. Technol. 2020, 39, 175–185. (In Chinese) [Google Scholar] [CrossRef]
  56. Huang, F.; Li, J.; Wang, J.; Mao, D.; Sheng, M. Modelling rules of landslide susceptibility prediction considering the suitability of linear environmental factors and different machine learning models. Bull. Geol. Sci. Technol. 2022, 41, 44–59. (In Chinese) [Google Scholar] [CrossRef]
  57. Vijith, H.; Krishnakumar, K.N.; Pradeep, G.S.; Ninu Krishnan, M.V.; Madhu, G. Shallow landslide initiation susceptibility mapping by GIS-based weights-of-evidence analysis of multi-class spatial data-sets: A case study from the natural sloping terrain of Western Ghats, India. Georisk Assess. Manag. Risk. Eng. Syst. Geohazards 2014, 8, 48–62. [Google Scholar] [CrossRef]
  58. Chahal, P.; Rana, N.; Champati ray, P.K.; Bisht, P.; Bagri, D.S.; Wasson, R.J.; Sundriyal, Y. Identification of landslide-prone zones in the geomorphically and climatically sensitive Mandakini valley, (central Himalaya), for disaster governance using the Weights of Evidence method. Geomorphology 2017, 284, 41–52. [Google Scholar] [CrossRef]
  59. Kayastha, P.; Dhital, M.R.; De Smedt, F. Application of the analytical hierarchy process (AHP) for landslide susceptibility mapping: A case study from the Tinau watershed, west Nepal. Comput. Geosci. 2013, 52, 398–408. [Google Scholar] [CrossRef]
  60. Moosavi, V.; Niazi, Y. Development of hybrid wavelet packet-statistical models (WP-SM) for landslide susceptibility mapping. Landslides 2016, 13, 97–114. [Google Scholar] [CrossRef]
  61. Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology / Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrolog. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
  62. Moore, I.D.; Grayson, R.; Ladson, A. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrolog. Pprocess. 1991, 5, 3–30. [Google Scholar] [CrossRef]
  63. Ge, Y.; Chen, H.; Zhao, B.; Tang, H.; Lin, Z.; Xie, Z.; Lv, L.; Zhong, P. A comparison of five methods in landslide susceptibility assessment: A case study from the 330-kV transmission line in Gansu Region, China. Environ. Earth Sci. 2018, 77, 662. [Google Scholar] [CrossRef]
  64. Wu, Z.; Wu, Y.; Yang, Y.; Chen, F.; Zhang, N.; Ke, Y.; Li, W. A comparative study on the landslide susceptibility mapping using logistic regression and statistical index models. Arab. J. Geosci. 2017, 10, 187. [Google Scholar] [CrossRef]
  65. Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B.B. Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. CATENA 2019, 172, 212–231. [Google Scholar] [CrossRef]
  66. Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, Turkey. Landslides 2012, 9, 93–106. [Google Scholar] [CrossRef]
  67. Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. CATENA 2008, 72, 1–12. [Google Scholar] [CrossRef]
  68. Gorum, T.; Fan, X.; van Westen, C.J.; Huang, R.Q.; Xu, Q.; Tang, C.; Wang, G. Distribution pattern of earthquake-induced landslides triggered by the 12 May 2008 Wenchuan earthquake. Geomorphology 2011, 133, 152–167. [Google Scholar] [CrossRef]
  69. Prasannakumar, V.; Vijith, H. Evaluation and validation of landslide spatial susceptibility in the Western Ghats of Kerala, through GIS-based Weights of Evidence model and Area Under Curve technique. J. Geolog. So. India 2012, 80, 515–523. [Google Scholar] [CrossRef]
  70. Hosseinalizadeh, M.; Kariminejad, N.; Chen, W.; Pourghasemi, H.R.; Alinejad, M.; Mohammadian Behbahani, A.; Tiefenbacher, J.P. Spatial modelling of gully headcuts using UAV data and four best-first decision classifier ensembles (BFTree, Bag-BFTree, RS-BFTree, and RF-BFTree). Geomorphology 2019, 329, 184–193. [Google Scholar] [CrossRef]
  71. Cui, S.-H.; Pei, X.-J.; Wu, H.-Y.; Huang, R.-Q. Centrifuge model test of an irrigation-induced loess landslide in the Heifangtai loess platform, Northwest China. J. Mt. Sci. 2018, 15, 130–143. [Google Scholar] [CrossRef]
  72. Fan, Y.; Fan, X.; Fang, C. County comprehensive geohazard modelling based on the grid maximum method. Bull. Geol. Sci. Technol. 2022, 41, 197–208. (In Chinese) [Google Scholar] [CrossRef]
  73. Freedman, D.A. Bootstrapping regression models. Ann. Statist. 1981, 9, 1218–1228. [Google Scholar] [CrossRef]
  74. Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Chen, W.; Clague, J.J.; Geertsema, M.; Jaafari, A.; Avand, M.; Miraki, S.; Talebpour Asl, D. Shallow landslide susceptibility mapping by random forest base classifier and its ensembles in a semi-arid region of Iran. Forests 2020, 11, 421. [Google Scholar] [CrossRef]
  75. Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
  76. Masetic, Z.; Subasi, A. Congestive heart failure detection using random forest classifier. Comput. Methods Progr. Biomed. 2016, 130, 54–64. [Google Scholar] [CrossRef] [PubMed]
  77. Naghibi, S.A.; Pourghasemi, H.R. A Comparative Assessment Between Three Machine Learning Models and Their Performance Comparison by Bivariate and Multivariate Statistical Methods in Groundwater Potential Mapping. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
  78. Faming, H.; Songyan, H.; Xueya, Y.; Ming, L.; Junyu, W.; Wenbin, L.; Zizheng, G.; Wenyan, F. Landslide susceptibility prediction and identification of its main environmental factors based on machine learning models. Bull. Geol. Sci. Technol. 2022, 41, 79–90. (In Chinese) [Google Scholar] [CrossRef]
  79. Wang, G.; Chen, X.; Chen, W. Spatial Prediction of Landslide Susceptibility Based on GIS and Discriminant Functions. ISPRS Int. J. Geo-Inf. 2020, 9, 144. [Google Scholar] [CrossRef]
  80. Al-Najjar, H.A.H.; Pradhan, B.; Kalantar, B.; Sameen, M.I.; Santosh, M.; Alamri, A. Landslide Susceptibility Modeling: An Integrated Novel Method Based on Machine Learning Feature Transformation. Remote Sens. 2021, 13, 3281. [Google Scholar] [CrossRef]
  81. Li, X.; Cheng, J.; Yu, D.; Han, Y. Research on Non-Landslide Selection Method for Landslide Hazard Mapping. 2021; preprint. [Google Scholar] [CrossRef]
  82. Palau, R.M.; Hürlimann, M.; Berenguer, M.; Sempere-Torres, D. Influence of the mapping unit for regional landslide early warning systems: Comparison between pixels and polygons in Catalonia (NE Spain). Landslides 2020, 17, 2067–2083. [Google Scholar] [CrossRef]
  83. Xia, D.; Tang, H.; Sun, S.; Tang, C.; Zhang, B. Landslide Susceptibility Mapping Based on the Germinal Center Optimization Algorithm and Support Vector Classification. Remote Sens. 2022, 14, 2707. [Google Scholar] [CrossRef]
  84. Balogun, A.-L.; Rezaie, F.; Pham, Q.B.; Gigović, L.; Drobnjak, S.; Aina, Y.A.; Panahi, M.; Yekeen, S.T.; Lee, S. Spatial prediction of landslide susceptibility in western Serbia using hybrid support vector regression (SVR) with GWO, BAT and COA algorithms. Geosci. Front. 2021, 12, 101104. [Google Scholar] [CrossRef]
  85. Chen, W.; Hong, H.; Panahi, M.; Shahabi, H.; Wang, Y.; Shirzadi, A.; Pirasteh, S.; Alesheikh, A.A.; Khosravi, K.; Panahi, S.; et al. Spatial Prediction of Landslide Susceptibility Using GIS-Based Data Mining Techniques of ANFIS with Whale Optimization Algorithm (WOA) and Grey Wolf Optimizer (GWO). Appl. Sci. 2019, 9, 3755. [Google Scholar] [CrossRef]
  86. Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
  87. Skilodimou, H.D.; Bathrellos, G.D. Natural and Technological Hazards in Urban Areas: Assessment, Planning and Solutions. Sustainability 2021, 13, 8301. [Google Scholar] [CrossRef]
Remotesensing 15 01007 g001 550
Figure 1. Location of the study area.
Figure 1. Location of the study area.
Remotesensing 15 01007 g001
Remotesensing 15 01007 g002 550
Figure 2. Flowchart of the landslide susceptibility modeling.
Figure 2. Flowchart of the landslide susceptibility modeling.
Remotesensing 15 01007 g002
Remotesensing 15 01007 g003a 550Remotesensing 15 01007 g003b 550Remotesensing 15 01007 g003c 550
Figure 3. Thematic maps: (a) elevation; (b) slope angle; (c) slope aspect; (d) profile curvature; (e) plan curvature; (f) TWI; (g) SPI; (h) STI; (i) distance to faults; (j) distance to roads; (k) distance to rivers; (l) NDVI; (m) rainfall; (n) land use; (o) lithology.
Figure 3. Thematic maps: (a) elevation; (b) slope angle; (c) slope aspect; (d) profile curvature; (e) plan curvature; (f) TWI; (g) SPI; (h) STI; (i) distance to faults; (j) distance to roads; (k) distance to rivers; (l) NDVI; (m) rainfall; (n) land use; (o) lithology.
Remotesensing 15 01007 g003aRemotesensing 15 01007 g003bRemotesensing 15 01007 g003c
Remotesensing 15 01007 g004 550
Figure 4. Landslide susceptibility map using the BFT model.
Figure 4. Landslide susceptibility map using the BFT model.
Remotesensing 15 01007 g004
Remotesensing 15 01007 g005 550
Figure 5. Landslide susceptibility map using the BagBFT model.
Figure 5. Landslide susceptibility map using the BagBFT model.
Remotesensing 15 01007 g005
Remotesensing 15 01007 g006 550
Figure 6. Landslide susceptibility map using RFBFT model.
Figure 6. Landslide susceptibility map using RFBFT model.
Remotesensing 15 01007 g006
Remotesensing 15 01007 g007 550
Figure 7. Distribution of landslide susceptibility zones.
Figure 7. Distribution of landslide susceptibility zones.
Remotesensing 15 01007 g007
Remotesensing 15 01007 g008 550
Figure 8. ROC curves of the models: (a) training dataset, (b) validation dataset.
Figure 8. ROC curves of the models: (a) training dataset, (b) validation dataset.
Remotesensing 15 01007 g008
Table
Table 1. Description of the groups of lithologies.
Table 1. Description of the groups of lithologies.
GroupCodeLithologyGeological Age
1J2Monzonitic granite, quartz monzonite, granodiorite, quartz dioriteMiddle Jurassic
2T2, T3Quartz monzonite, monzonitic granite, granodioriteMiddle and late Triassic
3C1, C2Lower: carbonaceous phyllite; middle: siltstone, gray-green phyllite; upper: medium-thin bedded limestone; carbonaceous slate with quartz sandstone,
carbonaceous slate, slate sandwiched sandstone, quartz conglomerate and limestone, breccia limestone		Early and middle Carboniferous
4D1, D2, D3Lower: sandstone sandwiches slate, sandy argillaceous limestone, and local siderite sandwiches; upper: slate and phyllite-sandwich-sandstone. dolomite, limestone, sandstone, siltstone with a small amount of slate, locally
intercalated argillaceous limestone, slate mixed with fine sandstone		Devonian
5SGraniteSilurian
6OQuartz diorite, diorite, gabbro, gabbro-norite, alaskiteOrdovician
7Є1Lower: black carbonaceous slate and siliceous rock; upper: variegated (dark gray, gray-purple, light gray, gray-white) limestone, dolomitic limestone;
dolomite with flint		Cambrian
8Z1, Z2Lower: conglomerate, sandstone, shale with limestone; upper: dolomite, marl with sandstone, shaleEarly and middle Sinian
9Pz2Lower: mainly metamorphic quartz sandstone, meta granulite with mica-quartz schist; upper: sandy conglomerate, meta-sandstone, mica-quartz schist with a few marble layers from bottom to topUpper paleozoic
10Pt1, QnBiotite schist, graphite marble, clastic rock interbedded with basic lava, volcanic rock with marble, clastic rock with basic lava, volcanic rock with carbonaceous phyllite, marble, and siliceous rockLower Proterozoic, Qingbaikouan
Table
Table 2. Source and scale of conditioning factors.
Table 2. Source and scale of conditioning factors.
FactorsData SourceFormat Resolution/Scale
Elevation, slope angle, slope aspect, plan curvature, profile curvature, SPI, STI, TWI, distance to faults, distance to roads, distance to riversASTER GDEMRaster, 30 m
NDVILandsat 8 operational land imagerRaster, 30 m
RainfallNational Earth System Science Data CenterRaster, 30 m
Land use/coverLand use/cover mapsPolygon, 1:100,000
LithologyGeological mapsPolygon, 1:200,000
Table
Table 3. Parameters of ROC curves with the training dataset.
Table 3. Parameters of ROC curves with the training dataset.
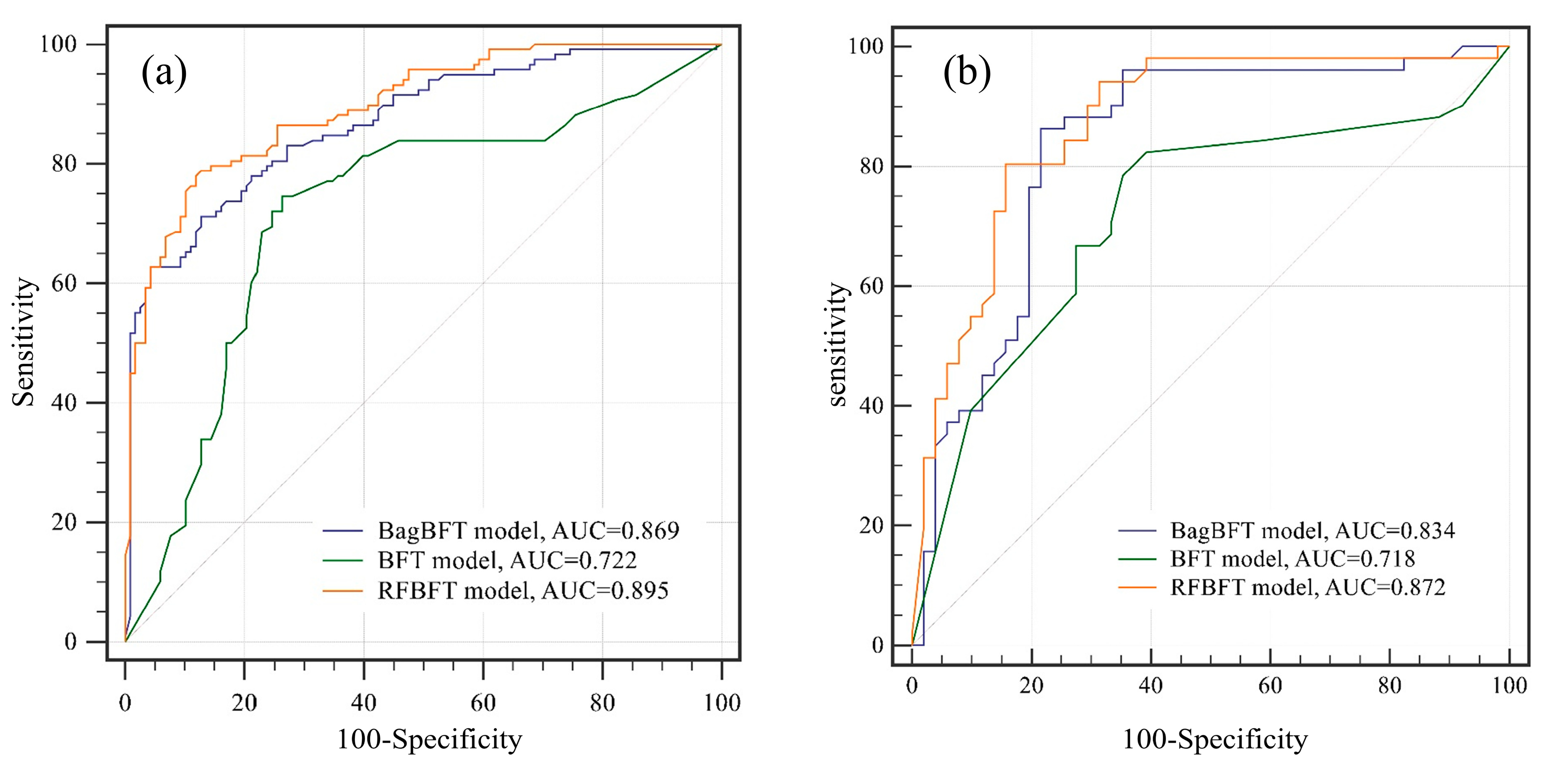
ModelAUCStandard Error95% Confidence Interval
BFT0.7220.03470.660 to 0.778
BagBFT0.8690.02310.819 to 0.909
RFBFT0.8950.01990.849 to 0.931
Table
Table 4. Parameters of ROC curves with the validation dataset.
Table 4. Parameters of ROC curves with the validation dataset.
ModelAUCStandard Error95% Confidence Interval
BFT0.7180.05210.620 to 0.803
BagBFT0.8340.04240.747 to 0.900
RFBFT0.8720.03620.791 to 0.930
Table
Table 5. Frequency ratio accuracy analysis of susceptibility figures of BFT, BagBFT, and RFBFT models.
Table 5. Frequency ratio accuracy analysis of susceptibility figures of BFT, BagBFT, and RFBFT models.
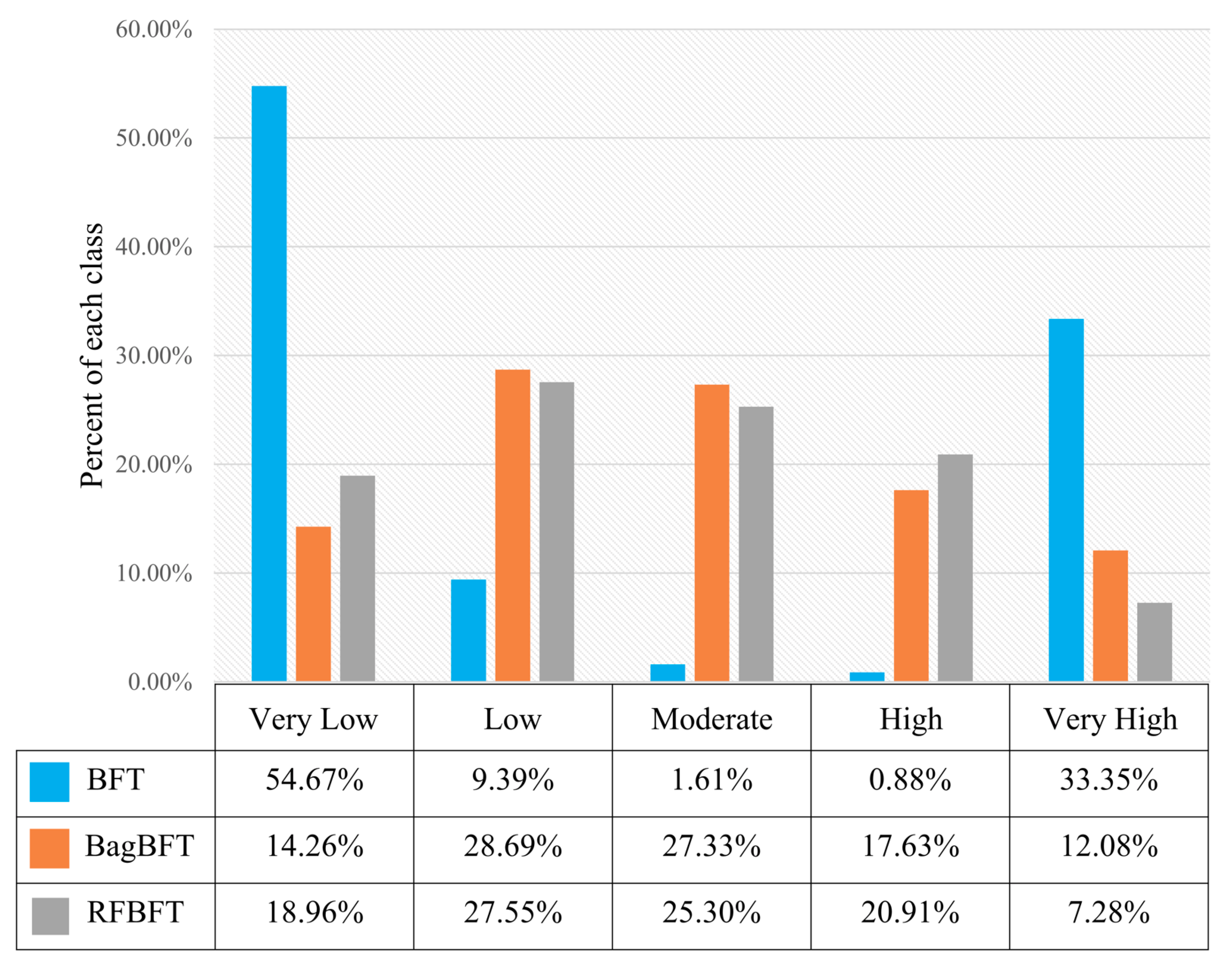
ModelSusceptibility LevelRasterRaster Ratio (%)Landslides QuantityRatio of Landslides Quantity (%)Frequency Ratio
BFTVery Low1,443,87854.762213.020.238
Low247,6579.3974.140.441
Moderate42,3621.6131.781.105
High23,2370.8852.963.357
Very High879,38833.3513278.112.342
BagBFTVery Low375,84414.2621.180.083
Low756,52728.6921.180.041
Moderate720,67527.331911.240.411
High464,92617.635230.771.745
Very High318,54912.089455.624.604
RFBFTVery Low499,85518.9600.000.000
Low726,28527.5595.330.193
Moderate667,08225.302112.430.491
High551,33320.916035.501.698
Very High191,9667.287946.756.420
Table
Table 6. Wilcoxon signed-rank test of the models with the training dataset.
Table 6. Wilcoxon signed-rank test of the models with the training dataset.
Pairwise ComparisonZ StatisticpSignificance
BFT~BagBFT2.3570.0184Yes
BFT~RFBFT3.1480.0016Yes
BagBFT~RFBFT1.6100.1073No
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gui, J.; Alejano, L.R.; Yao, M.; Zhao, F.; Chen, W. GIS-Based Landslide Susceptibility Modeling: A Comparison between Best-First Decision Tree and Its Two Ensembles (BagBFT and RFBFT). Remote Sens. 2023, 15, 1007. https://doi.org/10.3390/rs15041007

AMA Style

Gui J, Alejano LR, Yao M, Zhao F, Chen W. GIS-Based Landslide Susceptibility Modeling: A Comparison between Best-First Decision Tree and Its Two Ensembles (BagBFT and RFBFT). Remote Sensing. 2023; 15(4):1007. https://doi.org/10.3390/rs15041007

Chicago/Turabian Style

Gui, Jingyun, Leandro Rafael Alejano, Miao Yao, Fasuo Zhao, and Wei Chen. 2023. "GIS-Based Landslide Susceptibility Modeling: A Comparison between Best-First Decision Tree and Its Two Ensembles (BagBFT and RFBFT)" Remote Sensing 15, no. 4: 1007. https://doi.org/10.3390/rs15041007

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop