1. Introduction
With rapid developments of communication technologies, satellite communications have attracted a lot of attention in academia and industry. Especially, with the advent of many commercial satellite constellations, e.g., Starlink, OneWeb and O3b, many topics of satellite technologies have become the key research of 6G communications [
1,
2]. Compared with the terrestrial-network, the non-terrestrial-satellite-network (NTSN) has many advantages, such as global coverage and network security. These features can make up for the shortcomings of the traditional mobile communication.
Numerous studies imply that the non-terrestrial-network (NTN) contains Geo-synchronous Earth Orbit (GEO), Medium Earth Orbit (MEO), Low Earth Orbit (LEO) and High Altitude Platform (HAP) [
3]. GEO and MEO apply a higher altitude orbit. They can not only realize the data transfer function, but also realize the network management function. HAP is applied as an auxiliary platform for LEO. As the primary data transfer medium, LEO can realize both access services and data bearer services. All data flows are processed and transmitted by LEO nodes. Low orbit satellite behaves many special characteristics: frequent topology variation, dynamic link state and limited power resources [
4]. In particular, the lack of energy would lead to not only mission failure but also devastating damage to satellites. By a lot of research, many scholars indicate that an excellent routing strategy can solve those problems [
5]. In order to achieve load balancing and energy optimization, routing strategies are an important research direction. In addition, the routing strategy is also a key technology to improve network performance.
From the basic principle, NTSN routing strategies can be divided into centralized routing and distributed routing. In the former, the calculation of the routing path is concentrated in a single satellite node, e.g., the source node and the head of satellites cluster. Zhiguo Liu [
6] proposed a satellite network task deployment method based on the information centric network (ICN). The specific routing strategy is based on source routing architecture. P. Kumar [
7] proposed a centralized quality-of-service (QoS)aware routing algorithm for beyond 5G NTN. A modified Bresenham’s algorithm and Dijkstra’s algorithm are running in a calculating node. However, all centralized routing schemes suffer from sudden failure and congestion, because the centralized routing calculation cannot be changed once finished. In addition, the resource balancing also cannot be achieved by it. Xinran Fang [
8] present three basic cooperative models about the hybrid satellite–terrestrial network (HSTN). In it, a survey of the state-of-the-art technologies is provided. However, the relevant content of the energy balance is not covered. In the latter, each satellite node calculates the next hop node independently, according to the least state. Shiyue Dai [
9] proposed a distributed congestion control routing protocol based on traffic classification in LEO satellite networks. A low-overhead distributed scheme was used to compute the routing. Quan Chen [
10] proposed a distributed routing algorithm for the mega satellite constellation network. A Longer Side Priority strategy aims at maximizing the path searching space. Although the recovery of failure can be achieved in the above distributed schemes, they are difficult to take into account in resource balancing at the same time.
With the gradual increase in traffic density, network congestion and energy shortage cause the network performance to drop sharply. A lot of novel QoS-oriented routing schemes have been developed to improve the network performance. Cui-Qin Dai [
11] proposed a QoE-aware algorithm to enhance the user satisfaction by constructing QoE factors. A taboo list is introduced to optimize the latency. Yeqi LIU [
12] proposed a bee colony algorithm optimization based on the link cost. Many constraints are taken into account, e.g., Doppler wavelength drift, transmission delay, wavelength consistency and continuity. Load balancing and energy shortage problem have become research hotspots, because of the massive user in mega NTSN. Wei Liu [
13] proposed a pre-balancing shortest path algorithm to alleviate congestion in the heavy load zone. A congestion index is the key of this algorithm. Houtian Wang [
14] proposed a multi-objective optimization model in the congestion prediction. An ant colony algorithm is applied in it. This routing scheme performs well in balancing the traffic load and throughput. Jiang Liu [
15] proposed a selective iterative Dijkstra algorithm to reduce the congestion rate. It is a distributed strategy, which diverts the traffic flow of congestion nodes to neighboring nodes. Although the above routing scheme alleviates the congestion caused by high traffic density, the energy sensitive problem is ignored.
Due to the symmetric structure of NTSN, each satellite is in the ‘night side’ for about a half cycle. This feature poses a great challenge to energy supply capability, especially for communication satellites. Linchun Hao [
16] proposed an energy-aware traffic classification routing algorithm based on traffic characteristics. The key technology is to select different network metrics for route calculation according to service characteristics. However, there is no real energy control strategy and energy model in it. Yang Wu [
17] proposed a multi-QoS routing strategy for the software-defined satellite network. However, the energy balance is only introduced as an optimization condition, not an optimization goal.
In order to increase satellite efficiency, some scholars have carried out research on the satellite power system. Mengqiu Wang [
18] proposed an autonomous fault diagnosis for satellite power system to improve the capability of satellite to perform its on-orbit performance. Azmat Sher [
19] proposed a simulation of the power subsystem of small satellites by Simulink/Matlab. It includes the models of solar cell array, DC/DC converters, battery charge/discharge controller, power control distribution unit and payload. These studies increase system performance by optimizing the satellite power systems, but do not consider the characteristics of mega satellite constellations. The relationship between symmetrical constellations and energy balance is ignored. An energy model that takes into account both the satellite power system and the constellation energy balance is necessary.
Based on the above analysis, an energy model is proposed firstly in this paper. A tubular sliding time window (TSTW) model is proposed, which consists of the satellite power model and constellation solar model. Based on it, an energy sensitive and congestion balance (ESCB) routing scheme is proposed, secondly. A multi-objective optimization algorithm is implemented to find the routing path. Lastly, in order to more realistically verify the specific scheme, a reasonable traffic model is proposed. Two different services are contained in it, namely: access services and bearer services. A lot of simulations by the System Tool Kit (STK) and Network X packets indicate that the ESCB routing scheme achieves excellent communication performance and energy balance ability [
20,
21].
2. Energy Model
2.1. Constellation Topology
There are two commonly symmetric constellation topologies, namely the walker-delta and walker-polar. Due to the stability and periodicity, they are particularly suitable for NTSN applications. In former topology, there are multiple inclined orbits distributed evenly over the equator. The low and mid latitudes regions are covered better by it, but the pole regions are missed. Starlink is the most typical application. In the later topology, there are multiple vertical orbits distributed over a half equator. The global coverage can be achieved by it, but the traffic hotspot problem cannot be solved. OneWeb and Iridium are the most typical applications.
To study mega NTSN and routing scheme, a walker-delta constellation is the best research object. A walker-delta constellation consisting of 48 orbits and 1152 satellites is proposed, as shown in
Figure 1. In this constellation, there are four connectable satellites for a single ground user at any time. Two of them are ascent links (the connected satellites move from South Pole to North Pole) and other two are descent links (the connected satellites move from North Pole to South Pole).
The basic parameters of the specific constellation are inclination and altitude. They are defined as 55 degrees and 550 km in this paper. The orbit period is about 90 min. To simplify the research objectives, a satellite can be defined as (O, S), where O is the orbit factor and S is the satellite phase factor. The range of O is from 1 to 48, and the range of S is from 1 to 24. There are four inter-satellite-links (ISL) for each satellite.
2.2. Solar Power Model
For a satellite, energy is the basic guarantee of normal operation. Especially for communication satellites, the energy problem is particularly important, since the transmission power is related to the data rate. Carrier-noise-ratio (
CNR) is another important indicator of the communication system. It determines not only the capability of receiver but also the output power of the transmitter.
CNR [
22] can be described as
where
pt and
gt are the output power and antenna gain of transmitter,
gr and
ts are the antenna gain and noise temperature of receiver.
l is the path loss in space;
k is Boltzmann constant.
BW is the bandwidth of the channel, which can be described as:
where
α is the roll-off factor of the pattern filter;
Rd is the data rate of the system.
For a particular communication mode, CNR is determined by requirements. In order to increase the data rate, it is necessary to provide higher output power. Therefore, under a fixed traffic density, the energy balance and routing paths are closely related.
Solar energy system is the power provider for a satellite. There are two different orbit states, namely: “day side” and “night side” for walker-delta constellations. In the former, the satellite charges in sunlight; in the latter, the satellite discharges in shadow, as shown in
Figure 2.
In “day side”, charging power (
CP) is related to satellite solar panel design and relative attitude; it can be described as:
where
θ is the angle between the light line and the vertical line,
S is the area of the solar panel,
η is the energy conversion efficiency and
SC is the solar constant.
According to the public information of some commercial constellations, the charging power of Starlink and OneWeb can be obtained, as shown in the
Table 1 [
23].
Starlink apply a bigger solar panel to increase the charging power. However, this will cause a lot of occlusion issues. OneWeb applied a solar array drive assembly (SADA) to increase the energy conversion efficiency. A smaller solar panel can reduce manufacturing and carrying costs, but suffers from a lack of power. Therefore, an efficient energy balance strategy is very important for NTSN.
2.3. TSTW Model
To increase the energy balance performance of the NTSN system, a satellite illumination model is necessary. UsingSTK to simulate the above walker-delta constellation, it can be indicated that 40% of the orbit cycle is the “night side” and 60% of the orbit cycle is the “day side” for a satellite. In an orbit, a part of satellites are in the “day side”, and the rest are in the “night side”, as shown in
Figure 3. Each point represents a satellite, and different orbital planes are represented by different colors.
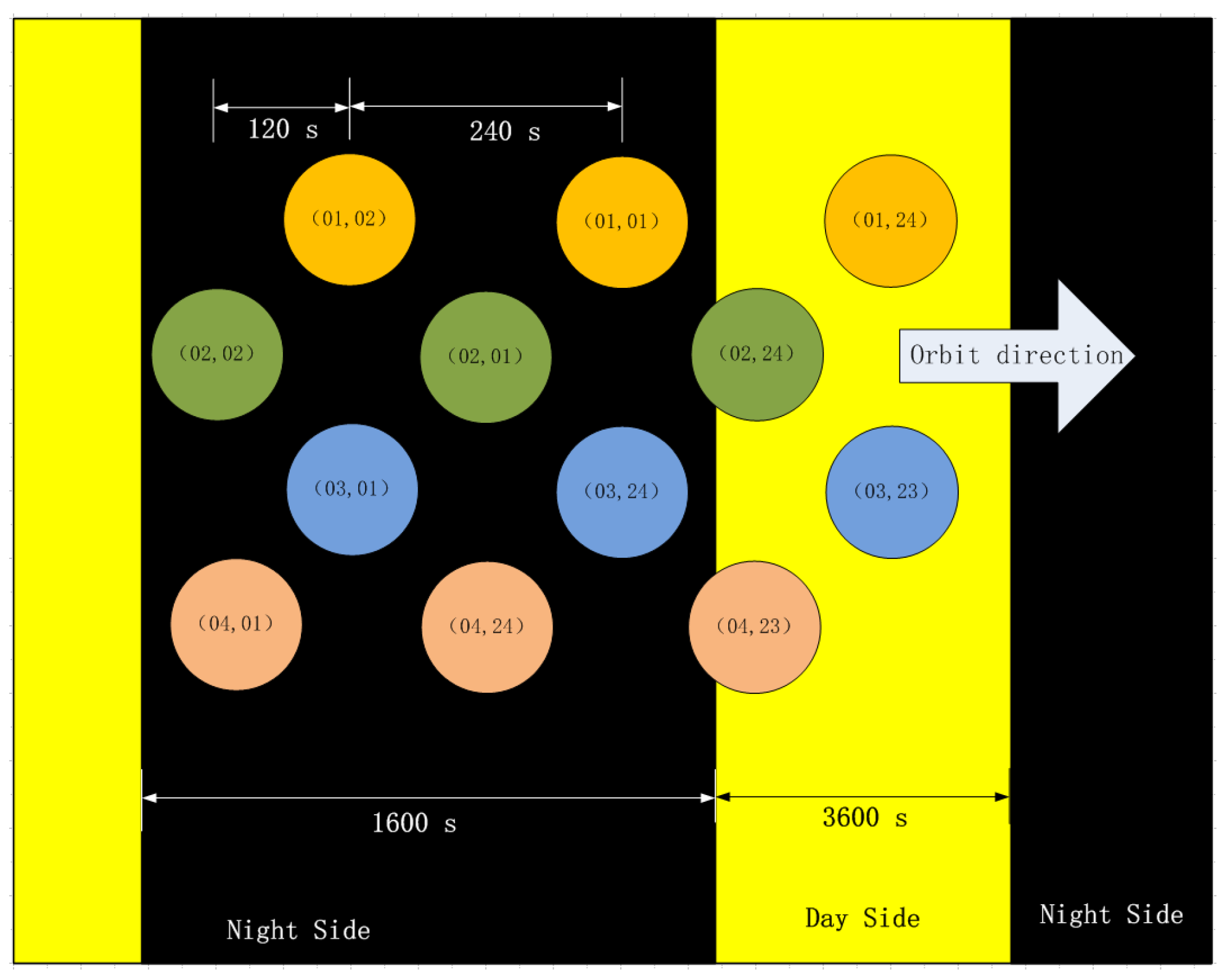
It can be calculated by the “Light Time” function in STK that satellites will enter “day side” in turn. On one hand, the charging interval between two adjacent satellites in an orbit is about 240 s. The average charging duration is about 3600 s, and the average umbra duration is about 1600 s. On other hand, the charging interval between two adjacent satellites in adjacent orbits is about 120 s. As shown in
Figure 4, satellites enter the “day side” from “night side” in tune. For a satellite, the “day side” and “night side” alternate periodically. This figure shows the chargeable time and non-chargeable time, respectively. However, there is about 400 s of fuzzy duration between the alternations. In this duration, the charging power rating fluctuates with orbital status, solar storms, etc. Therefore, the role of this region is ignored in the theoretical model.
In order to introduce the energy balance into the optimization objective, an energy prediction model is necessary. According to “Light Time” analysis, 13 adjacent satellites are in the “day side” for any orbit. A satellite remains in the fuzzy duration and the charging state is ignored. A tubular sliding time window model (TSTW) can imply this property, as shown in
Figure 5. In this model, a ring represents 24 satellites in an orbit, and a tubular sliding window represents the light duration. All satellites in the “day side” are surrounded by tubes. The tube will rotate clockwise. By rotating at a specific angle, the illuminating state of the satellite can be predicted.
The illuminating state of an orbit can be represented by a single ring. A constellation applies 48 rings, and there is a one-bit delay between adjacent rings, as shown in
Figure 6. With the tube rotating clockwise, satellites in different orbits are surrounded in order.
The main function of the model is an energy balance data structure suitable for NTSN. Utilizing the compass model with cyclic coverage, the state information can be obtained efficiently when the node energy changes. This information can include the past, present and predicted remaining energy. Especially for mega satellite constellations, efficient management of node information is always a key technology for on-orbit processing. In the routing algorithm, the node energy prediction hash table is periodically maintained. This table is updated synchronously with the charge prediction model. At the same time, we use the pointer address to select the charging node. Regular node charge and discharge information can be automatically completed by the model. The updated information between nodes only needs to contain the energy consumption and failure of each node.
As shown in
Figure 7, the data structure of the model is a hash table. Hash function and TSTW synchronous cycle transformation. Both node update and routing information are completed through the key-value pairs of the hash table. Based on the above satellite power model and constellation energy model, the prediction of residual energy can be introduced in the next chapter.
3. ESCB Routing Scheme
An energy sensitive and load balance (ESCB) routing scheme algorithm is proposed in this chapter. Some key performance indicators (KPI), such as latency, congestion and residual energy are considered in the algorithm. The adjusted parameters about satellite design are also considered in it, such as charging power and relative attitude between the satellite and sunlight.
In order to increase the system efficiency, each traffic service is equipped with an on-orbit buffer space, respectively. A congestion function (
CF) can be described as:
where
queueACC is the number of packets waiting in the buffer for access services;
queueBER is the number of packets waiting in the buffer for bearer services.
bufferACC and
bufferBER are the buffer space for two traffic services.
β and
χ are adjustment factors, and
β +
χ = 1. In addition to
CF, congestion is also an important constraint to routing policies. The congestion state (
CS) can be described as:
If a satellite is in the idle state, all data packets can be received arbitrarily. If in the busy state, the number of received packets will be decreased. If in the occupy state, satellite will forbid receiving packets.
In addition to congestion avoidance, energy balance is another important optimization objective. Energy factor (
EF) is an important indicator to measure energy balance, which can be described as:
where
RE(
t) is the residual energy of the satellite at the current moment,
CEpre(
t) is the predictive charging power in the current.
δ,
ε and
γ are adjustment factors, and
δ +
ε +
γ = 1.
CEpre(
t) can also be predicted by the TSTW model. When the tube rotates Ω degrees clockwise, the charging duration can also be calculated.
where Δ
t is the basic time slot, and
n is the number of time slots for the prediction. A latency can be described as:
where
delaypro-ber is the propagation delay,
delayqueue-ber is the queue delay,
c is the speed of light,
lv is the distance between adjacent satellites in the same orbit,
lh is the distance between neighbor satellites in the adjacent orbits,
queueACC is the number of packets waiting in the buffer for ISL transmission,
D is the size of the packet, and
BW is the bandwidth of the ISL channel.
For a link between (
O1,
S1) and (
O2,
S2) in NTSN, an objective function can be defined as:
where
η,
κ and
ν are adjustment factors for different services, and
η +
κ +
ν = 1. The objective function of a path can be described as:
where
path(
k) is one of the multiple candidate paths. The boundary conditions of optimization are described as:
where
BWrestrication and
Delayrestrication are restrictions for a specific service.
In this algorithm, congestion state can be calculated by Equations (6)–(9); energy state can be calculated by Equations (10) and (11); latency state can be calculated by Equations (12)–(14). A taboo list is made by Equations (6), (7), (17) and (18). Defining Equation (16) as the optimization goal, NTSN can be traversed to find the optimal routing path.
During actual operation, all node parameters are propagated through SIP signaling It broadcasts the status of the local node to neighbors at a fixed period. In addition, each node calculates the validity period of the neighbor information to perceive the status of the other node. The algorithm needs to traverse all the node information in the initialization phase. Once the status table is generated, the neighbor node status can be updated through the SIP signaling. Distributed routing computing only needs to be performed on the nodes whose status is updated, and do not need to traverse all the nodes every time. In order to reduce the computing burden of the nodes, the initial computing can be conducted by the ground station. Subsequent information updates can be conducted by each node individually.
The main algorithm runs as follows in
Figure 8.
Through the above scheme, the optimal solution and the sub-optimal solution can be found simultaneously as multiple paths. The specific algorithm takes into account both the congestion and energy balance together. The network performance can be greatly improved by it.
4. Traffic Model
To verify the effectiveness of this scheme, a reliable simulation is essential. As a condition of simulations, the traffic model must be realistic and reasonable. By the analysis of the requirements, it can be known that NTSN is a supplementary technology for terrestrial networks. NTSN mainly provides two services, namely the access services and bearer services. The former service is responsible for the Internet access of remote areas, oceans and mountains. The latter service provides a device-to-device (D2D) dedicated connection for special applications. The access services require ground-satellite-link (GSL), and bearer services require both the GSL and inter-satellite-link (ISL).
The traffic models of two services are related to population distributing, time period and the size of the constellation. In order to match the actual application, two independent traffic models are defined for two different services. There are three parameters defined in the traffic model, namely: the number of data flows (
NF), the allocation of data flows (
AF) and traffic density (
TD). NF determines the number of flows generated in a contribution cycle,
AF determines the position of flows and the
TD determines the number of packets generated in a flow. They are described as:
where
Poson[·] is a Poisson distribution function;
λ is the expectation and variance of distribution.
RS[
A,
B] is a random selection function. The return value of this function is a node table. The number of nodes in this table is B and they are randomly selected from network A.
Dt(
t) and
Dp(
lat) are time and position distribution correction factors.
α is an adjustment factor and
l is the mean of the traffic density.
NS is the total number of satellites.
NTE is the network topology of the NTSN constellation.
During the simulation, the traffic flow is periodically generated according to the above traffic model. Two independent traffic models are introduced for two different services. Both routing algorithm and simulation statistics are based on the above models.
5. Verification
To verify the performance of ESCB, a lot of simulations are finished. The basic scenario of the simulation is constructed by STK and Network X packets.
A walker delta constellation can be described as T/P/F, T is the total number of satellites, P is the number of orbital planes and F is the phase factor. In order to more effectively verify this scheme, a constellation with 1152/48/24 is introduced as an orbit topology.
In addition to the orbit scenario, the simulation settings are also very important, as shown in
Table 2.
In order to evaluate the performance of ESCB routing scheme, some key performance comparisons are performed with the virtual-topology-based Dijkstra shortest path routing (VT-SPR) algorithm [
23,
24]. At the same time, it also made a comprehensive performance comparison with Load-Balancing Routing Algorithm (LBRA), hybrid routing algorithm (HRA), Joint Depth-First-Search and Dijkstra algorithm (JDDA) and Q-learning-based dynamic distributed Routing scheme (QRLSN).
When the update period of SIP signaling is set to 30 s, it can be known that the update time of the node status is less than 5 s. The routing path selection of each data packet can be guaranteed within 10 milliseconds. Distributed routing operations can ensure that the node status is updated in time.
These parameters have been optimized a series of times during simulation and debugging. Finally, the most stable and globally optimal result is selected as the adjustment parameter.
As shown in
Figure 9, the congestion parameters of two different traffics will have a certain impact on the packet loss rate. In order to take into account the two traffic models at the same time, the global optimal parameters are selected as seat adjustment factors.
Similarly,
δ,
ε and
γ are introduced to adjust past, present and forecast energy factors. They are defined as memory factors for residual energy. As shown in
Figure 10, it is the optimization curve of the memory factor. They will affect the remaining energy of the system. Higher and more stable residual energy is the optimization goal of them.
In the optimization objective function,
η,
κ and
ν are used to balance different optimization objectives. Different businesses require different QoS requirements. Congestion, energy balance and delay can be controlled separately to match different business needs. For common applications, these parameters can be evenly distributed. The final parameter selection is shown in
Table 3.
To more realistically verify the routing scheme, two different traffic services are contributed separately. The delivery loss ratio (DLR) for access services (AS) is shown in
Figure 11. The maximum DLR of ESCB is below 0.5%. The traffic density l is set as 28, 29 and 30. The results indicate that the routing scheme maintains effective data transmission and keeps high delivery success ratio with the traffic density increases. Its DLR performance is much better than VT-SP.
The delivery loss ratio (DLR) for bearer services (BS) is shown in
Figure 12. The maximum DLR of ESCB is below 0.5%. The traffic density
l is defined as 28, 29 and 30. The results indicate that the routing scheme maintains effective data transmission and keeps high delivery success ratio as the traffic density increases. The comparing results also show the superiority of the specific scheme.
To verify the load balance performance of the specific scheme, the number of average queue packets are simulated, as shown in
Figure 13. The mean of average queue packets of ESCB is below 15. This result indicates that the routing scheme maintains stable load state. It achieves better load balance than VT-SP.
Energy sensitive properties are reflected in the residual energy performance, as shown in
Figure 14. Under high traffic density
l = 30, the residual energy remains above 33%. The results indicate that the specific routing scheme largely improve the limited energy.
In order to verify the energy balance performance, a residual energy jitter is simulated in
Figure 15. The difference between the residual energy of different nodes is measured by this performance. The uniformity of energy can also be reflected by it. The average residual energy jitter of ESCB is about 15%. The results indicate that the routing scheme maintains good energy balance.
In order to more clearly reflect the effectiveness of this paper, we compared the performance of various algorithms. We chose LBRA, HRA, JDDA and QRLSN as comparison objects [
25,
26]. As shown in
Figure 16, the average delivery loss rates of different algorithms are compared. During the simulation, a high-density flow was introduced. At the same time, packet loss caused by energy failure is considered. ESCB shows better delivery performance in simulations.
Similarly,
Figure 17 shows the latency performance comparison results. In the case of considering energy efficiency, the load balancing of the entire satellite network can be better balanced. Average latency performance can also be optimized. ESCB shows better latency performance in simulations.
Through the above simulations, the performance of the specific routing scheme is verified. The comparative analysis shows that the comprehensive performance of ESCB is much better than VT-SP. The comprehensive performance comparison with LBRA, HRA, JDDA and QRLSN also reflects the superiority of ESCB.