Multi-Sensor Observations Reveal Large-Amplitude Nonlinear Internal Waves in the Kara Gates, Arctic Ocean
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Background Conditions in the Kara Gates
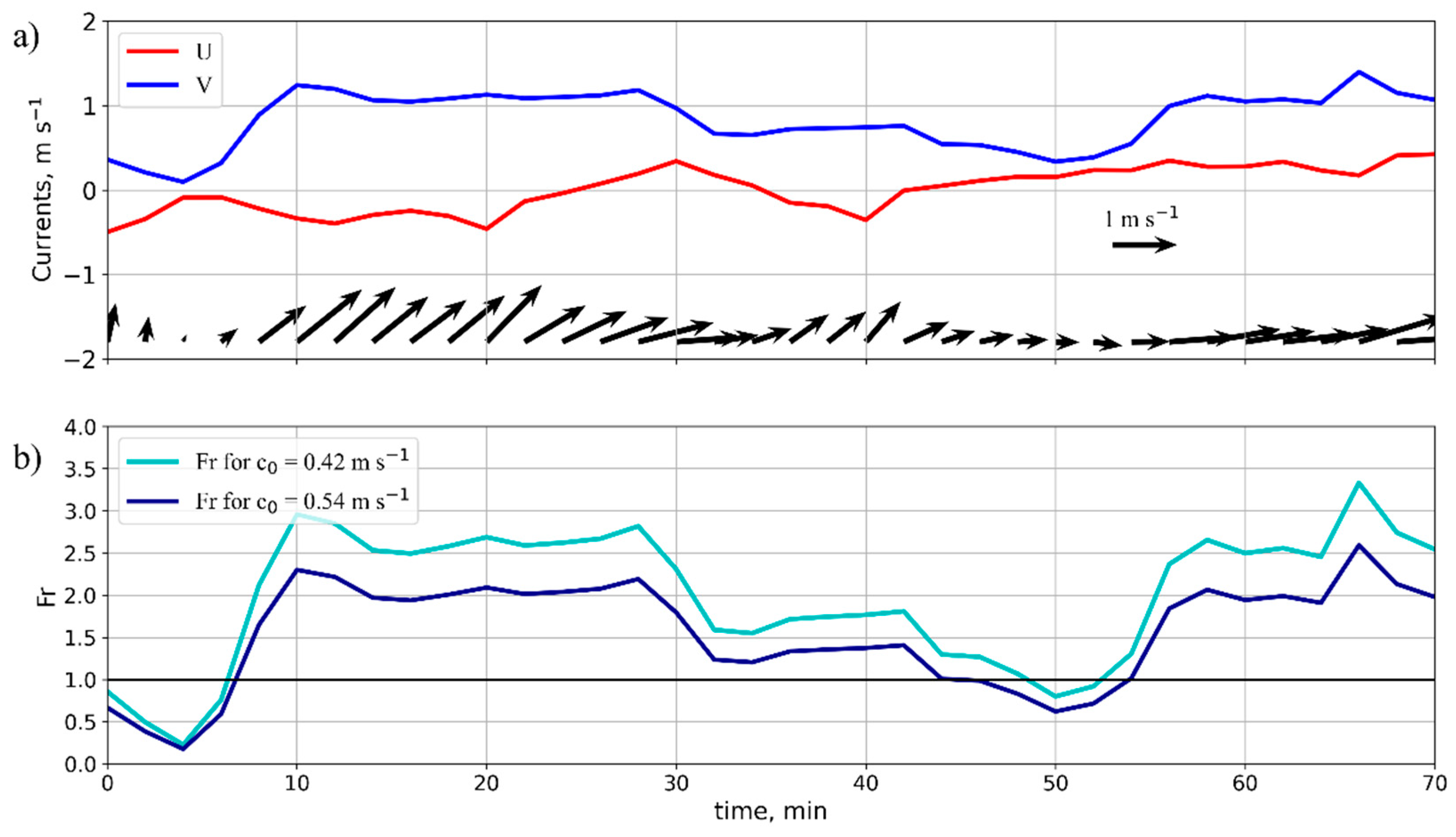
3.1.1. Tidal Conditions
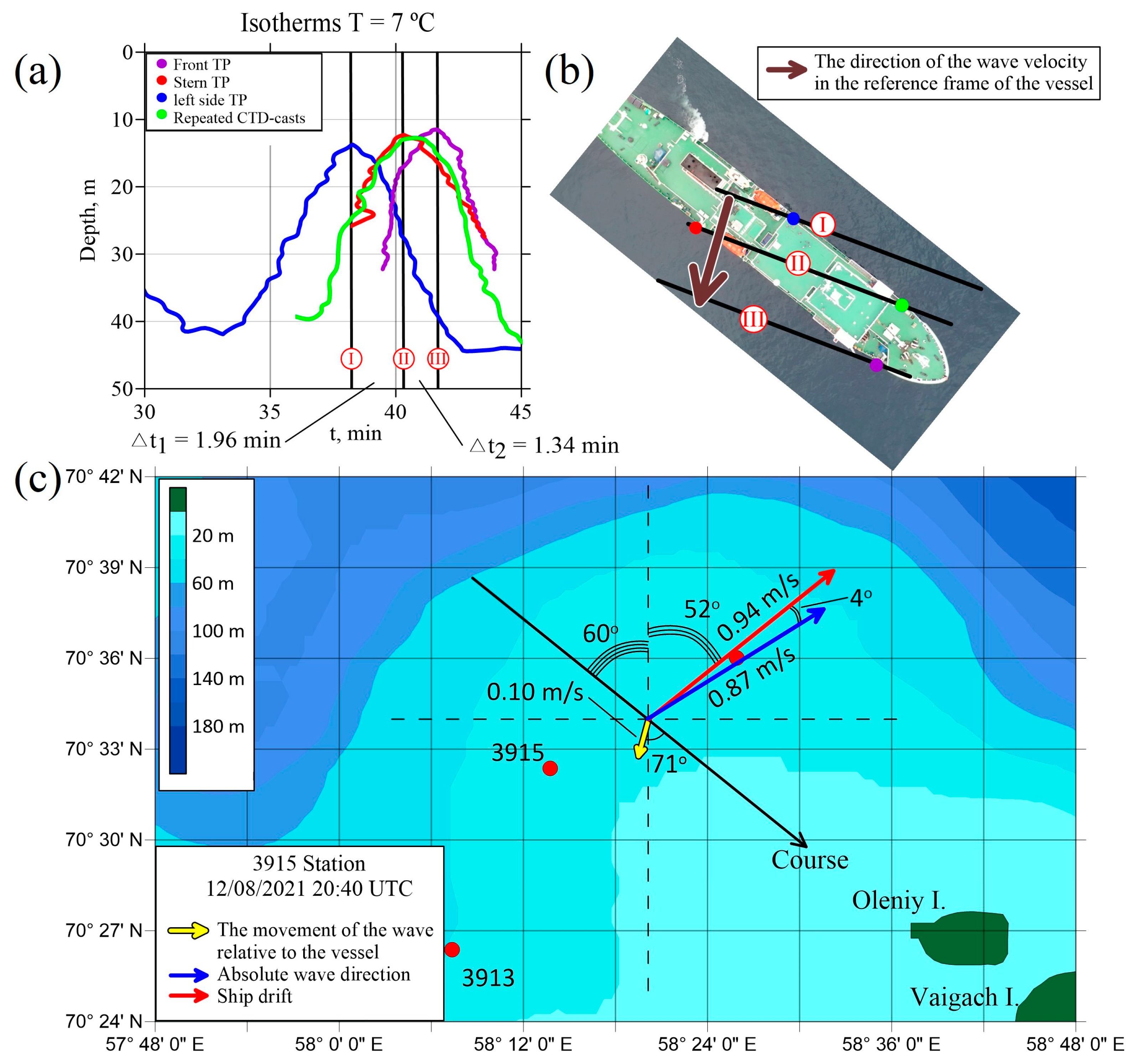
3.1.2. Surface Signatures of NLIWs in Satellite Data
3.2. Vertical Thermohaline Measurements at Stations
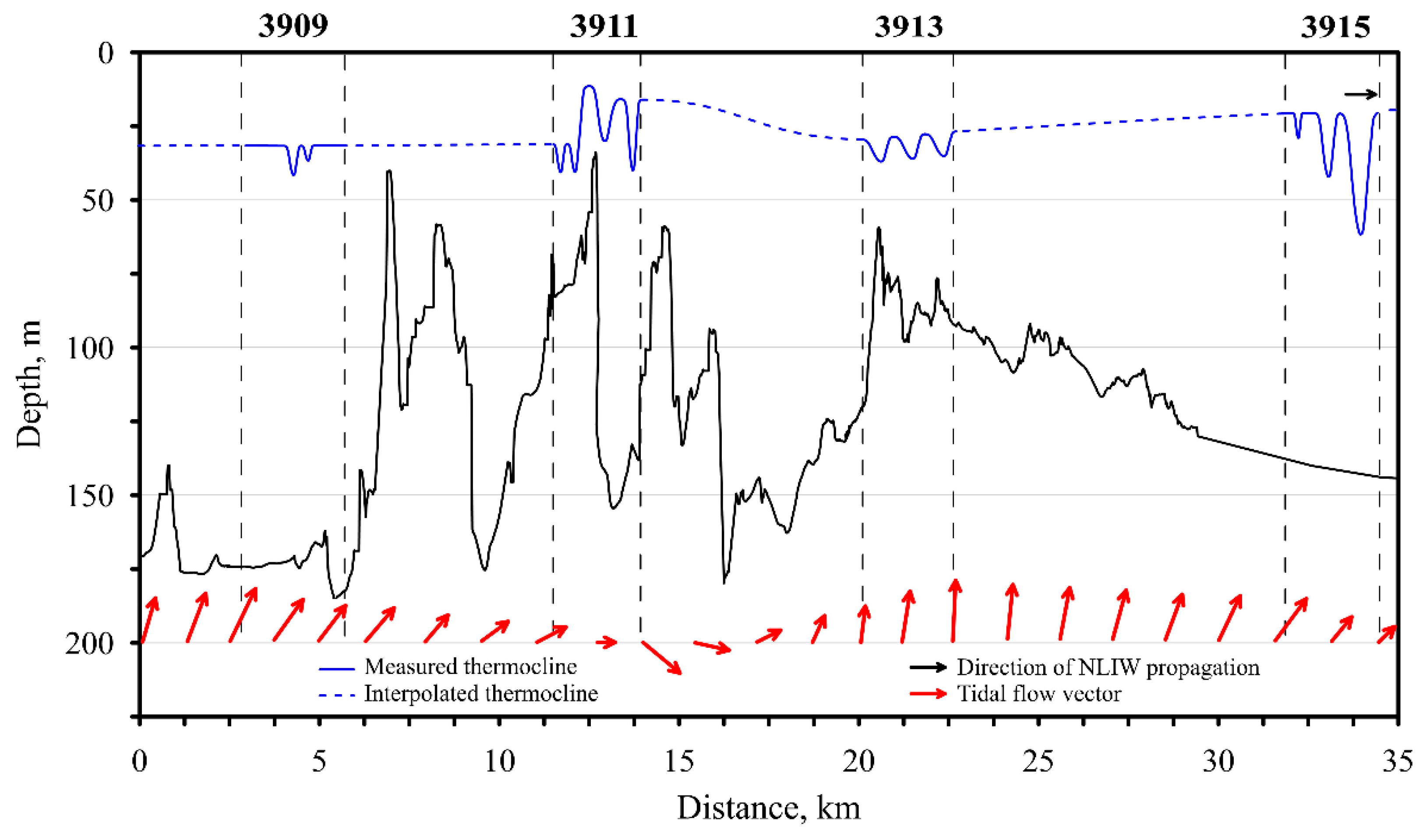
3.2.1. Station #3909
3.2.2. Station #3911
3.2.3. Station 3913
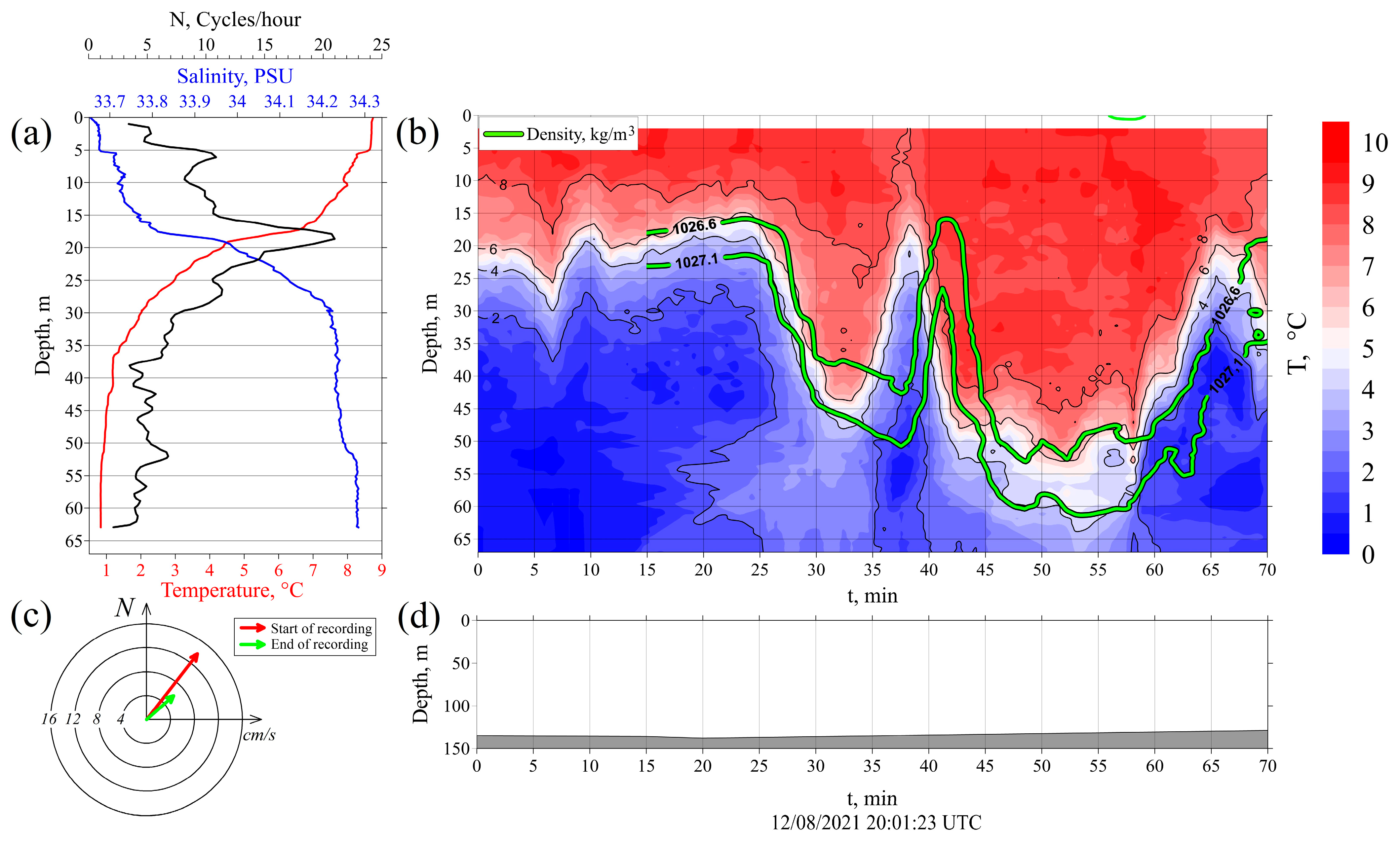
3.2.4. Station 3915
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pineda, J. Predictable upwelling and the shoreward transport of planktonic larvae by internal tidal bores. Science 1991, 253, 548–549. [Google Scholar] [CrossRef] [PubMed]
- Moum, J.N.; Farmer, D.M.; Smyth, W.D.; Armi, L.; Vagle, S. Structure and Generation of Turbulence at Interfaces Strained by Internal Solitary Waves Propagating Shoreward over the Continental Shelf. J. Phys. Ocean. 2003, 33, 2093–2112. [Google Scholar] [CrossRef]
- Boegman, L.; Stastna, M. Sediment Resuspension and Transport by Internal Solitary Waves. Ann. Rev. Fluid Mech. 2019, 51, 129–154. [Google Scholar] [CrossRef]
- Padman, L.; Dillon, T.M. Turbulent mixing near the Yermak Plateau during the coordinated Eastern Arctic Experiment. J. Geophys. Res. Oceans 1991, 96, 4769–4782. [Google Scholar] [CrossRef]
- Rippeth, T.P.; Vlasenko, V.; Stashchuk, N.; Scannell, B.D.; Green, J.A.M.; Lincoln, B.J.; Bacon, S. Tidal conversion and mixing poleward of the critical latitude (an Arctic case study). Geophys. Res. Lett. 2017, 44, 12349–12357. [Google Scholar] [CrossRef]
- Fer, I.; Koenig, Z.; Kozlov, I.E.; Ostrowski, M.; Rippeth, T.P.; Padman, L.; Bosse, A.; Kolas, E. Tidally forced lee waves drive turbulent mixing along the Arctic Ocean margins. Geophys. Res. Lett. 2020, 47, e2020GL088083. [Google Scholar] [CrossRef]
- Kozlov, I.E.; Atadzhanova, O.A.; Zimin, A.V. Internal solitary waves in the White Sea: Hot-spots, structure, and kinematics from multi-sensor observations. Remote Sens. 2022, 14, 4948. [Google Scholar] [CrossRef]
- Kozlov, I.; Romanenkov, D.; Zimin, A.; Chapron, B. SAR observing large-scale nonlinear internal waves in the White Sea. Remote Sens. Environ. 2014, 147, 99–107. [Google Scholar] [CrossRef]
- Zimin, A.V.; Kozlov, I.E.; Atadzhanova, O.A.; Chapron, B. Monitoring short-period internal waves in the White Sea. Izv. Atmos. Ocean. Phys. 2016, 52, 951–960. [Google Scholar] [CrossRef]
- Marchenko, A.V.; Morozov, E.G.; Kozlov, I.E.; Frey, D.I. High-amplitude internal waves southeast of Spitsbergen. Cont. Shelf Res. 2021, 227, 104523. [Google Scholar] [CrossRef]
- Morozov, E.G.; Pisarev, S.V. Internal Waves in the Region of the Akselsundet Strait of Western Spitsbergen Island. Izv. Atmos. Ocean. Phys. 2023, 59, 432–442. [Google Scholar] [CrossRef]
- Morozov, E.G.; Paka, V.T.; Bakhanov, V.V. Strong internal tides in the Kara Gates Strait. Geophys. Res. Lett. 2008, 35, L16603. [Google Scholar] [CrossRef]
- Kozlov, I.E.; Kudryavtsev, V.N.; Zubkova, E.V.; Zimin, A.V.; Chapron, B. Characteristics of short-period internal waves in the Kara Sea inferred from satellite SAR data. Izv. Atmos. Ocean. Phys. 2015, 51, 1073–1087. [Google Scholar] [CrossRef]
- Morozov, E.G.; Kozlov, I.E.; Shchuka, S.A.; Frey, D.I. Internal tide in the Kara Gates Strait. Oceanology 2017, 57, 8–18. [Google Scholar] [CrossRef]
- Harms, I.H.; Karcher, M.J. Modeling the seasonal variability of hydrography and circulation in the Kara Sea. J. Geophys. Res. 1999, 104, 13431–13448. [Google Scholar] [CrossRef]
- Morozov, E.G.; Parrilla-Barrera, G.; Velarde, M.G.; Scherbinin, A.D. The Straits of Gibraltar and Kara Gates: A comparison of internal tides. Oceanol. Acta 2003, 26, 231–241. [Google Scholar] [CrossRef]
- Boylan, B.M. Increased maritime traffic in the Arctic: Implications for governance of Arctic sea routes. Mar. Pol. 2021, 131, 104566. [Google Scholar] [CrossRef]
- Gunnarsson, B. Recent ship traffic and developing shipping trends on the Northern Sea Route—Policy implications for future arctic shipping. Mar. Pol. 2021, 124, 104369. [Google Scholar] [CrossRef]
- Kagan, B.A.; Timofeev, A.A. Modeling of the Stationary Circulation and Semidiurnal Surface and Internal Tides in the Strait of Kara Gates. Fund. Appl. Hydrophys. 2015, 8, 72–79. (In Russian) [Google Scholar]
- Kozlov, I.; Kudryavtsev, V.; Zubkova, E.; Atadzhanova, O.; Zimin, A.; Romanenkov, D.; Myasoedov, A.; Chapron, B. SAR observations of internal waves in the Russian Arctic seas. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 947–949. [Google Scholar]
- Kagan, B.A.; Sofina, E.V. Surface and internal semidiurnal tides and tidally induced diapycnal diffusion in the Barents Sea: A numerical study. Cont. Shelf Res. 2014, 91, 158–170. [Google Scholar] [CrossRef]
- Li, Q.; Wu, H.; Yang, H.; Zhang, Z. A numerical simulation of the generation and evolution of nonlinear internal waves across the Kara Strait. Acta Oceanol. Sin. 2019, 38, 1–9. [Google Scholar] [CrossRef]
- Morozov, E.G.; Pisarev, S.V. Internal tides at the Arctic latitudes (numerical experiments). Oceanology 2002, 42, 153–161. [Google Scholar]
- Vlasenko, V.; Stashchuk, N.; Hutter, K.; Sabinin, K. Nonlinear internal waves forced by tides near the critical latitude. Deep Sea Res. Part I 2003, 50, 317–338. [Google Scholar] [CrossRef]
- Ermoshkin, A.; Molkov, A. High-Resolution Radar Sensing Sea Surface States During AMK-82 Cruise. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2660–2666. [Google Scholar] [CrossRef]
- Gaisky, P.V.; Kozlov, I.E. Thermoprofilemeter for Measuring the Vertical Temperature Distribution in the Upper 100-Meter Layer of the Sea and its Testing in the Arctic Basin. Ecol. Saf. Coast. Shelf Zones Sea 2023, 1, 137–145. Available online: http://ecological-safety.ru/en/repository/issues/2023/01/11/ (accessed on 21 October 2023).
- Sandven, S.; Johannessen, O.M. High-frequency internal wave observations in the marginal ice zone. J. Geophys. Res. 1987, 92, 6911–6920. [Google Scholar] [CrossRef]
- Silvestrova, K.; Myslenkov, S.; Puzina, O.; Mizyuk, A.; Bykhalova, O. Water Structure in the Utrish Nature Reserve (Black Sea) during 2020–2021 According to Thermistor Chain Data. J. Mar. Sci. Eng. 2023, 11, 887. [Google Scholar] [CrossRef]
- Erofeeva, S.; Egbert, G. Arc5km2018: Arctic Ocean Inverse Tide Model on a 5 Kilometer Grid; Dataset, Arctic Data Center. 2020. Available online: https://arcticdata.io/catalog/view/doi%3A10.18739%2FA21R6N14K (accessed on 20 November 2022).
- Rogozhin, V.; Osadchiev, A.; Konovalova, O.P. Structure and variability of the Pechora plume in the southeastern part of the Barents Sea. Front. Mar. Sci. 2023, 10, 1052044. [Google Scholar] [CrossRef]
- Aleskerova, A.A.; Kubryakov, A.A.; Stanichny, S.V. A two-channel method for retrieval of the Black Sea surface temperature from Landsat-8 measurement. Izv. Atm. Ocean. Phys. 2017, 52, 1155–1161. [Google Scholar] [CrossRef]
- Korotaev, G.K.; Huot, E.; Le Dimet, F.X.; Herlin, I.; Stanichny, S.V.; Solovyev, D.M.; Wu, L. Retrieving ocean surface current by 4-D variational assimilation of sea surface temperature images. Remote Sens. Environ. 2008, 112, 1464–1475. [Google Scholar] [CrossRef]
- da Silva, J.C.B.; Ermakov, S.A.; Robinson, I.S.; Jeans, D.R.G.; Kijashko, S.V. Role of surface films in ERS SAR signatures of internal waves on the shelf: 1. Short-period internal waves. J. Geophys. Res. 1998, 103, 8009–8031. [Google Scholar] [CrossRef]
- Zhao, Z.; Klemas, V.; Zheng, Q.; Li, X.; Yan, X.-H. Estimating parameters of a two-layer stratified ocean from polarity conversion of internal solitary waves observed in satellite SAR images. Remote Sens. Environ. 2004, 92, 276–287. [Google Scholar] [CrossRef]
- Helfrich, K.R.; Melville, W.K. Long nonlinear internal waves. Annu. Rev. Fluid Mech. 2006, 38, 395–425. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Stepanyants, Y.A. Internal solitons in laboratory experiments: Comparison with theoretical models. Chaos Interdisc. J. Nonlin. Sci. 2005, 15, 03711. [Google Scholar] [CrossRef] [PubMed]
- Grue, J.; Jensen, A.; Rusas, P.; Sveen, J. Properties of large-amplitude internal waves. J. Fluid Mech. 1999, 380, 257–278. [Google Scholar] [CrossRef]
- Kao, T.W.; Pan, F.-S.; Renouard, D. Internal solitons on the pycnocline: Generation, propagation, and shoaling and breaking over a slope. J. Fluid Mech. 1985, 159, 19–53. [Google Scholar] [CrossRef]
- Gerkema, T.; Zimmerman, J.T.F. An Introduction to Internal Waves; Lecture Notes, Royal NIOZ, Texel, 2008. Available online: https://core.ac.uk/download/pdf/92866879.pdf (accessed on 1 October 2023).
- Ostrovsky, L.A.; Irisov, V.G. Strongly nonlinear internal solitons: Models and applications. J. Geophys. Res. Oceans 2017, 122, 3907–3916. [Google Scholar] [CrossRef]
- Peng, P.; Xie, J.; Du, H.; Wang, S.; Xuan, P.; Wang, G.; Wei, G.; Cai, S. Analysis of the Differences in Internal Solitary Wave Characteristics Retrieved from Synthetic Aperture Radar Images under Different Background Environments in the Northern South China Sea. Remote Sens. 2023, 15, 3624. [Google Scholar] [CrossRef]
- Zheng, Q.; Yan, X.-H.; Klemas, V. Statistical and dynamical analysis of internal waves on the continental shelf of the Middle Atlantic Bight from space shuttle photographs. J. Geophys. Res. 1993, 98, 8495–8504. [Google Scholar] [CrossRef]
- Joseph, R.I. Solitary waves in a finite depth fluid. J. Phys. A Mark. Gen. 1977, 10, L225–L227. [Google Scholar] [CrossRef]
- Benjamin, T.B. Internal waves of finite amplitude and permanent form. J. Fluid Mech. 1966, 25, 241–270. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean, 2nd ed.; Cambridge University Press: Cambridge, UK, 1980; 336p. [Google Scholar]
- Osborne, A.R.; Burch, T.L. Internal solitons in the Andaman Sea. Science 1980, 208, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Leppäranta, M. The Drift of Sea Ice, 2nd ed.; Springer Praxis Books; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Czipott, P.V.; Levine, M.D.; Paulson, C.A.; Menemenlis, D.; Farmer, D.M.; Williams, R.G. Ice flexure forced by internal wave packets in the Arctic Ocean. Science 1991, 254, 832–835. [Google Scholar] [CrossRef] [PubMed]
- Kowalik, Z.; Proshutinsky, A.Y. “The Arctic Ocean Tides” in the Polar Oceans Their Role Shaping Global Environment; Johannessen, O.M., Muench, R.D., Overland, J.E., Eds.; AGU: Washington, DC, USA, 1994; pp. 137–158. [Google Scholar]
- Padman, L.; Erofeeva, S. A barotropic inverse tidal model for the Arctic Ocean. Geophys. Res. Lett. 2004, 31, 19003. [Google Scholar] [CrossRef]
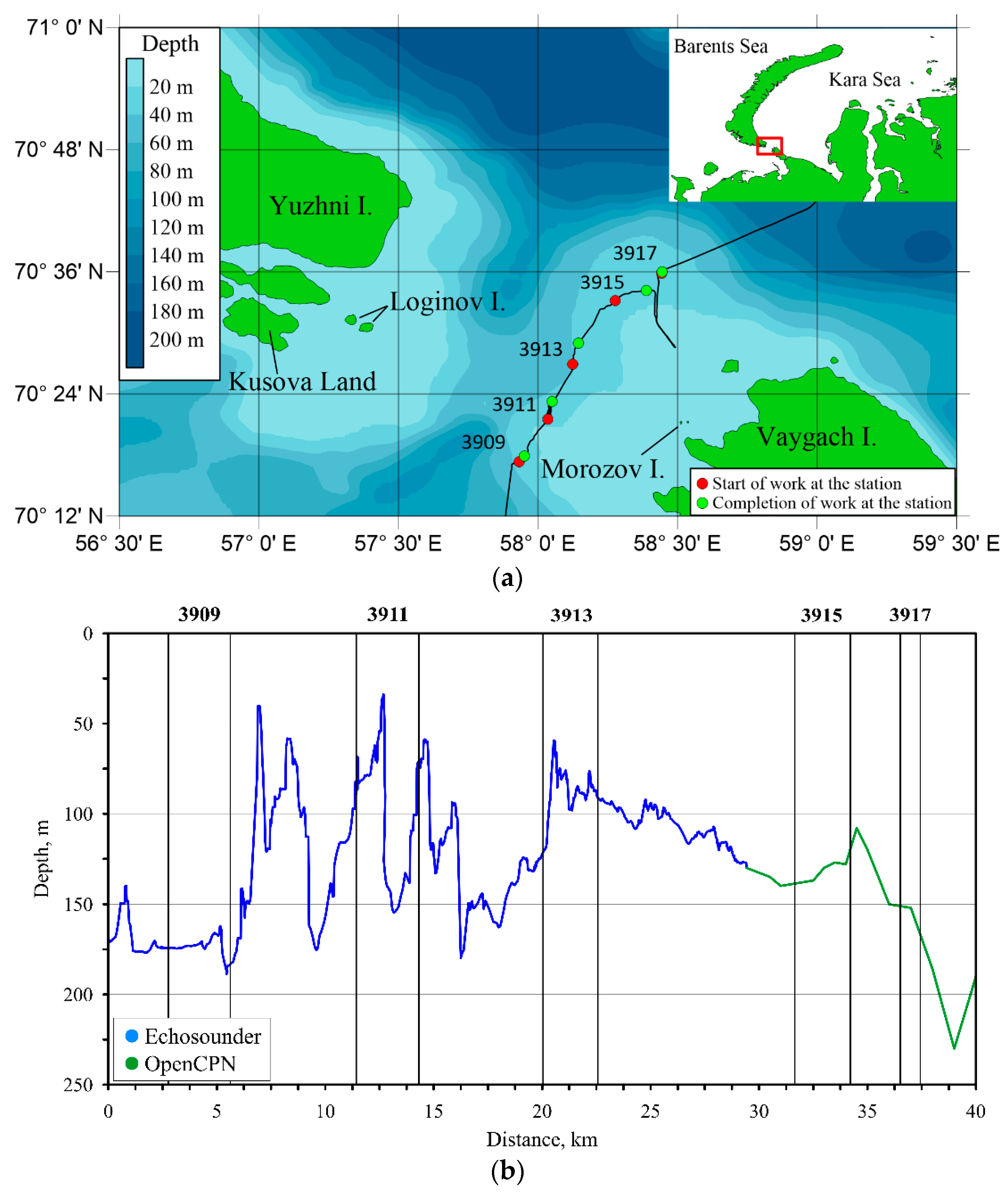

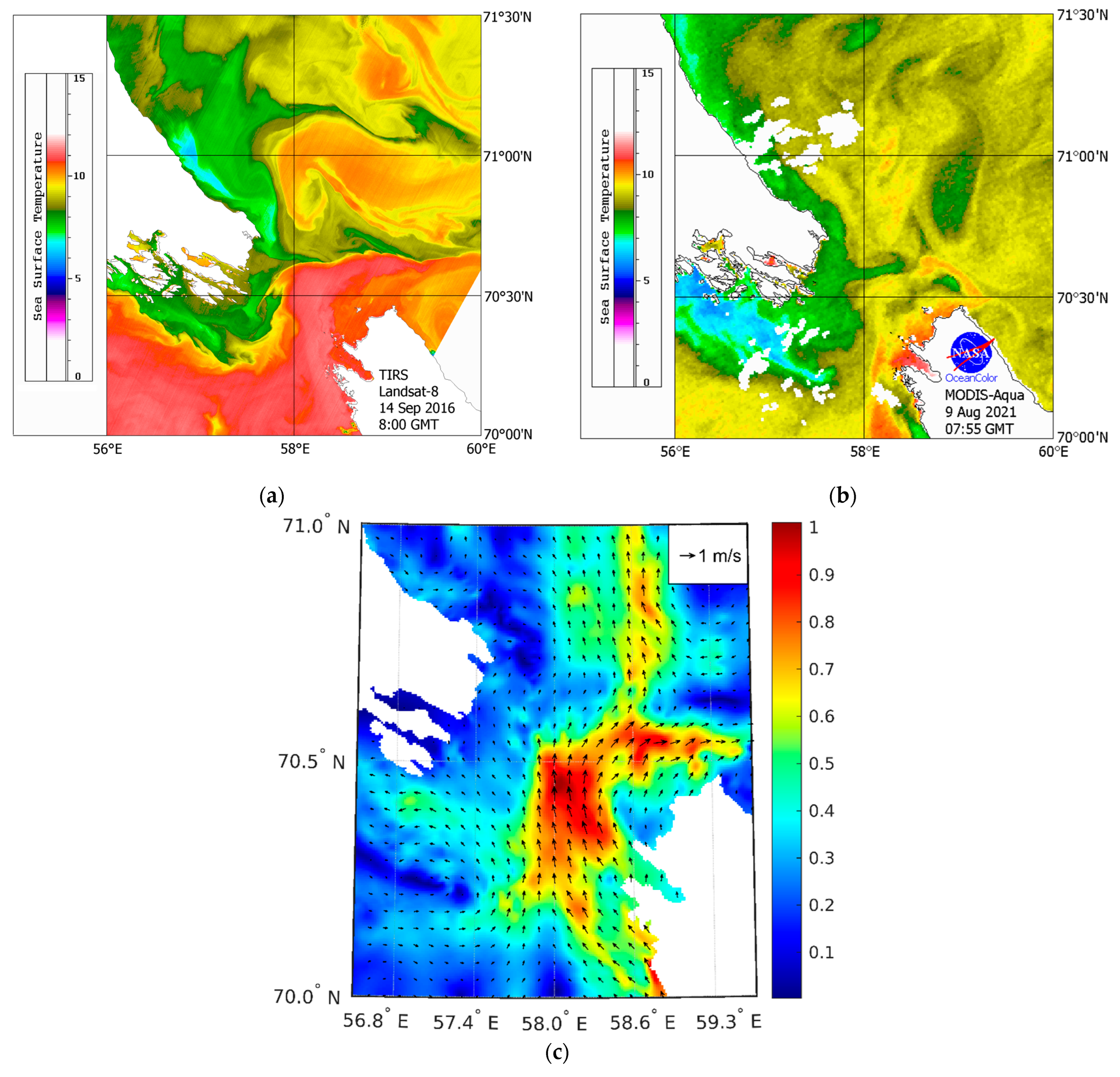
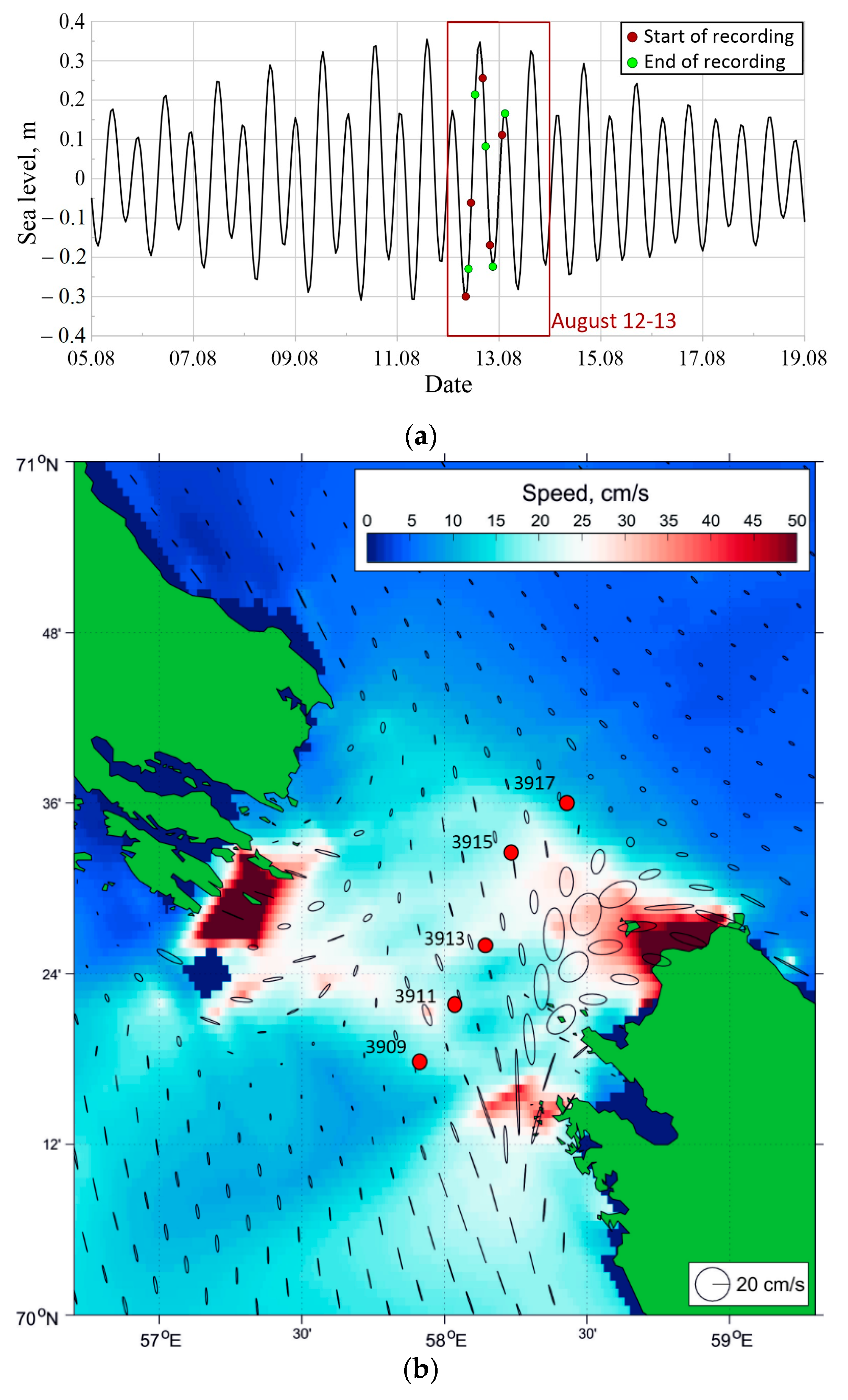
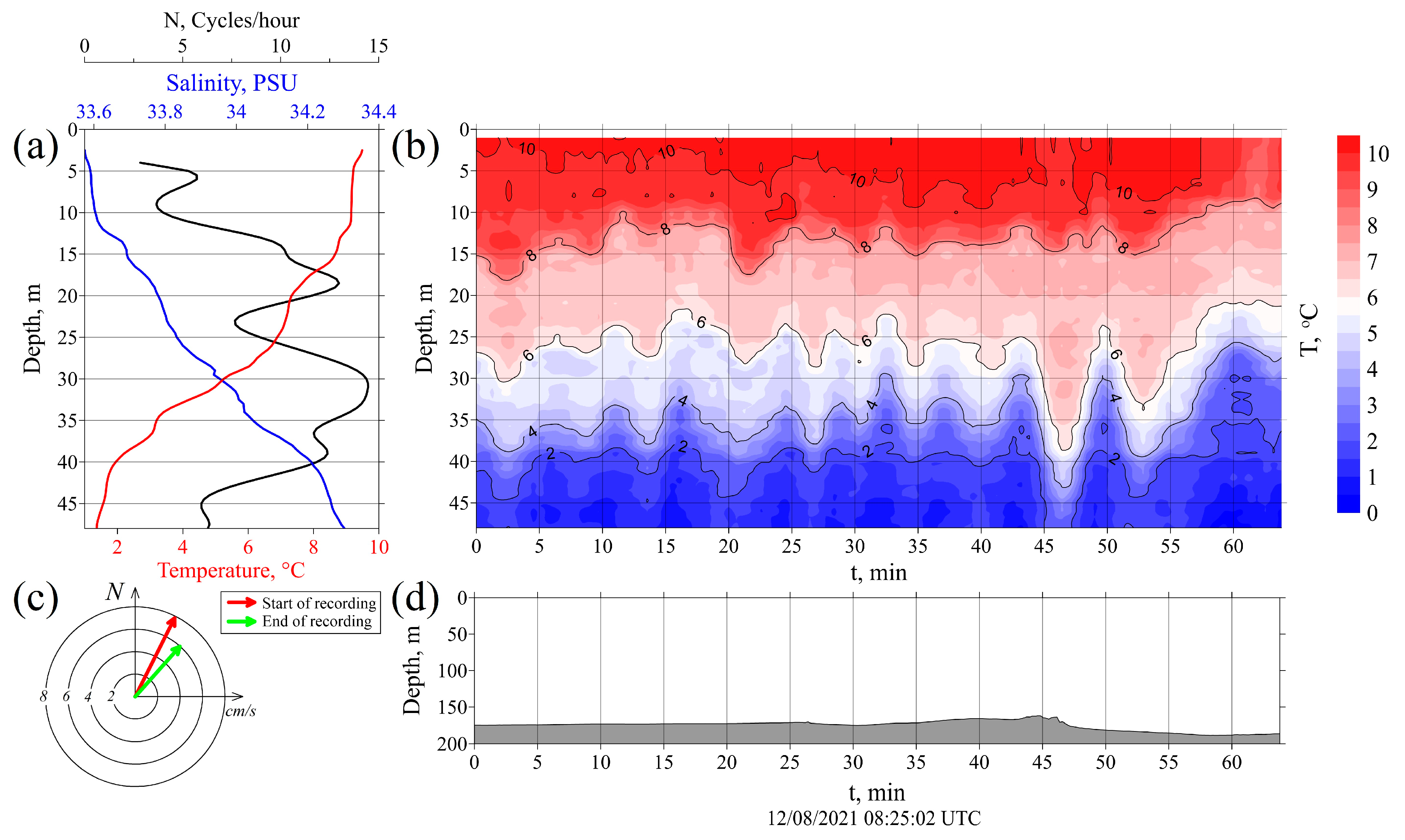
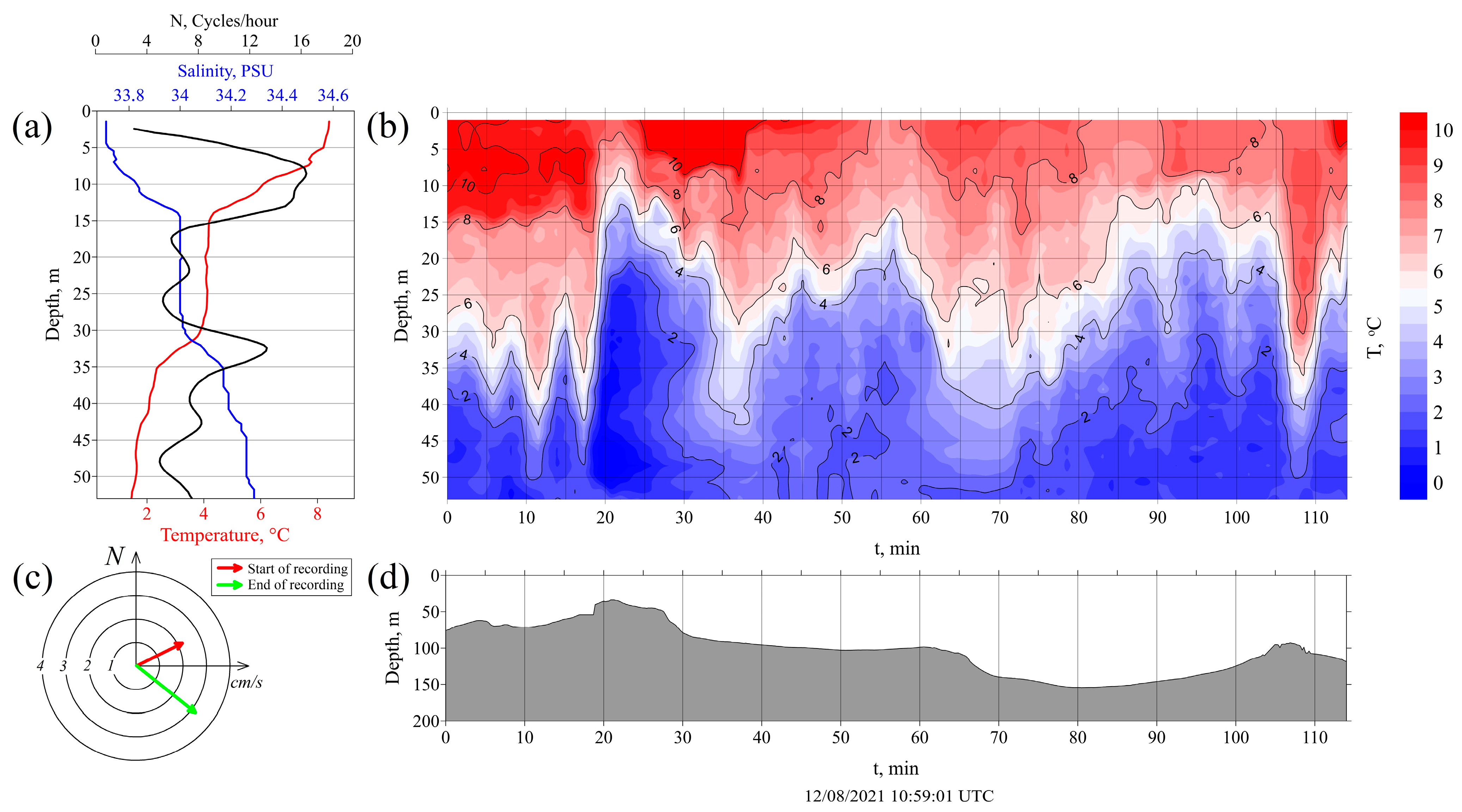

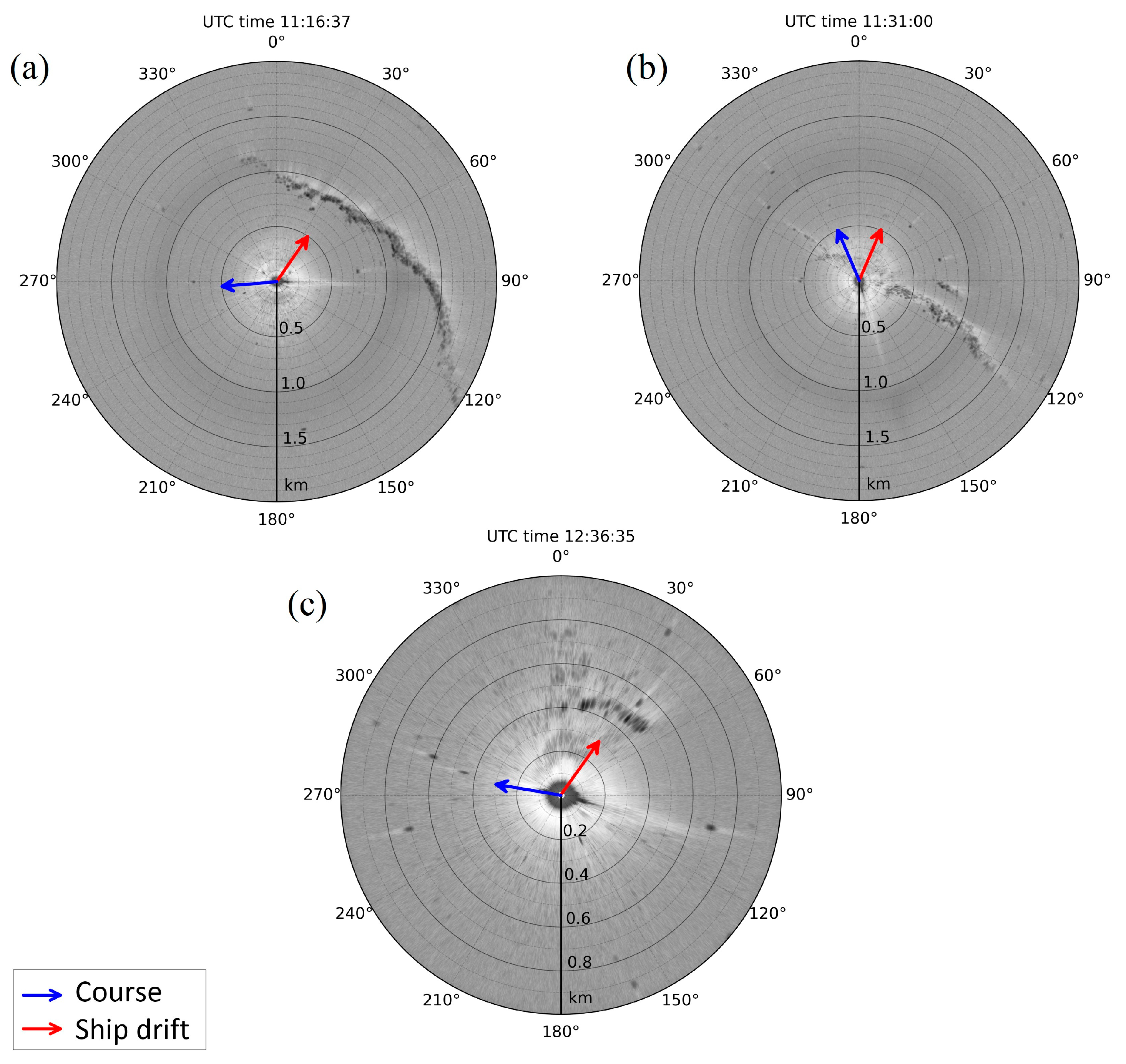
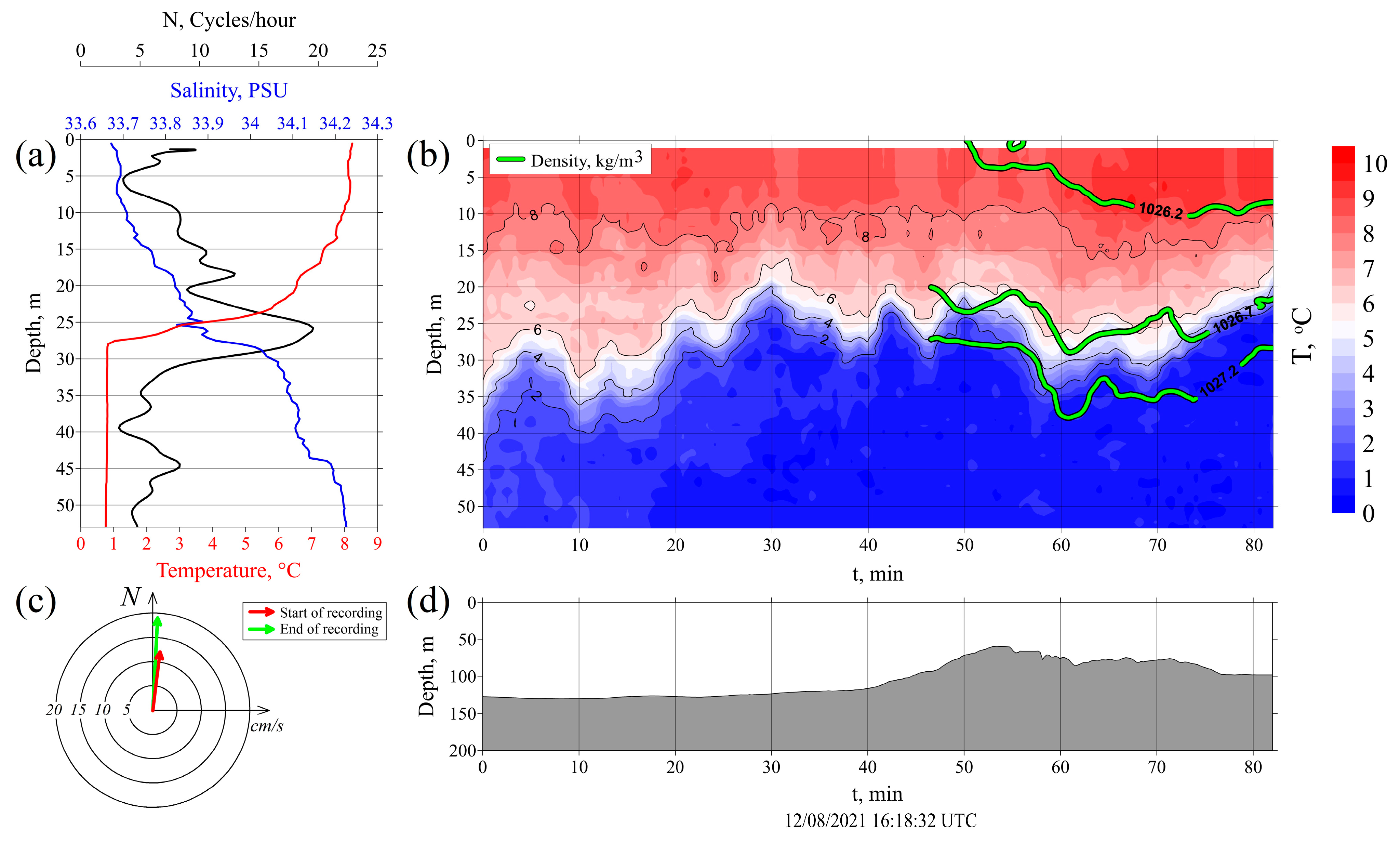
| Station | Time (UTC) | Length of Measurements, h | Start Latitude | Start Longitude | Start Depth, m |
|---|---|---|---|---|---|
| 3909 | 08:25 | 1.1 | 70°17.292′ | 57°55.797′ | 176 |
| 3911 | 10:59 | 1.9 | 70°21.540′ | 58°02.117′ | 82 |
| 3913 | 16:18 | 1.4 | 70°26.882′ | 58°07.401′ | 131 |
| 3915 | 20:01 | 1.2 | 70°33.275′ | 58°16.586′ | 127 |
| 3917 | 01:15 | 0.9 | 70°35.894′ | 58°25.495′ | 148 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Equation nos | - | (3) and (6) | (3) and (4) | (5) and (6) | (5) and (7) | (5) and (9) |
| [m/s] | 0.42 | 0.42 | 0.54 | 0.54 | 0.54 | |
| [m/s] | 0.86 | 0.62–0.7 | 0.62–0.69 | 0.87–0.98 | 0.71–0.72 | 0.73–0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozlov, I.E.; Kopyshov, I.O.; Frey, D.I.; Morozov, E.G.; Medvedev, I.P.; Shiryborova, A.I.; Silvestrova, K.P.; Gavrikov, A.V.; Ezhova, E.A.; Soloviev, D.M.; et al. Multi-Sensor Observations Reveal Large-Amplitude Nonlinear Internal Waves in the Kara Gates, Arctic Ocean. Remote Sens. 2023, 15, 5769. https://doi.org/10.3390/rs15245769
Kozlov IE, Kopyshov IO, Frey DI, Morozov EG, Medvedev IP, Shiryborova AI, Silvestrova KP, Gavrikov AV, Ezhova EA, Soloviev DM, et al. Multi-Sensor Observations Reveal Large-Amplitude Nonlinear Internal Waves in the Kara Gates, Arctic Ocean. Remote Sensing. 2023; 15(24):5769. https://doi.org/10.3390/rs15245769
Chicago/Turabian StyleKozlov, Igor E., Ilya O. Kopyshov, Dmitry I. Frey, Eugene G. Morozov, Igor P. Medvedev, Arina I. Shiryborova, Ksenya P. Silvestrova, Aleksandr V. Gavrikov, Elizaveta A. Ezhova, Dmitry M. Soloviev, and et al. 2023. "Multi-Sensor Observations Reveal Large-Amplitude Nonlinear Internal Waves in the Kara Gates, Arctic Ocean" Remote Sensing 15, no. 24: 5769. https://doi.org/10.3390/rs15245769
APA StyleKozlov, I. E., Kopyshov, I. O., Frey, D. I., Morozov, E. G., Medvedev, I. P., Shiryborova, A. I., Silvestrova, K. P., Gavrikov, A. V., Ezhova, E. A., Soloviev, D. M., Plotnikov, E. V., Zhuk, V. R., Gaisky, P. V., Osadchiev, A. A., & Stepanova, N. B. (2023). Multi-Sensor Observations Reveal Large-Amplitude Nonlinear Internal Waves in the Kara Gates, Arctic Ocean. Remote Sensing, 15(24), 5769. https://doi.org/10.3390/rs15245769






