Fast Solution of Scattering and Micro-Doppler Features from Moving Target Using a Tailored Shooting and Bouncing Ray Method
Abstract
:1. Introduction
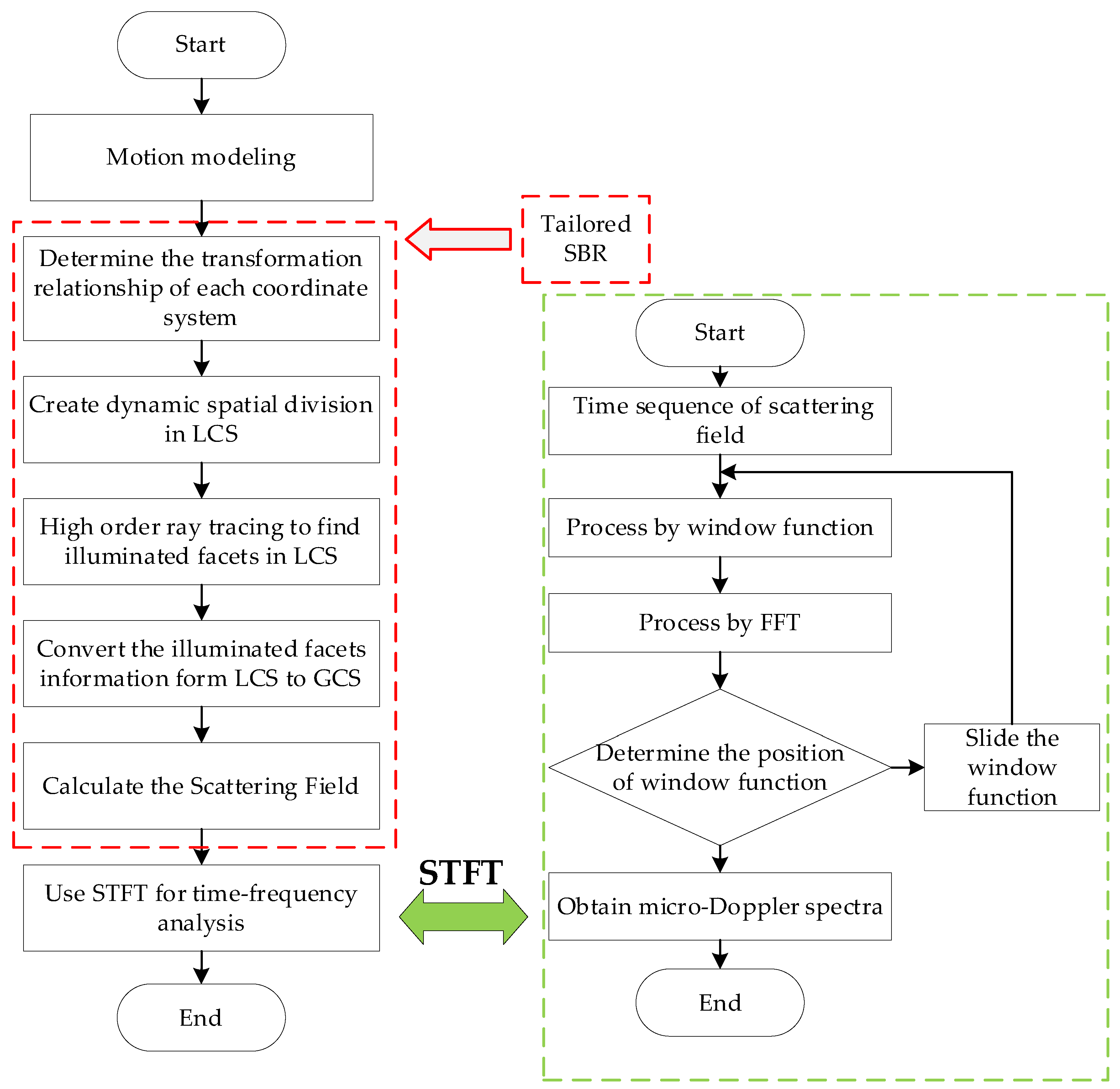
2. Fast Solution for EM Scattering and the Micro-Doppler of the Moving Target
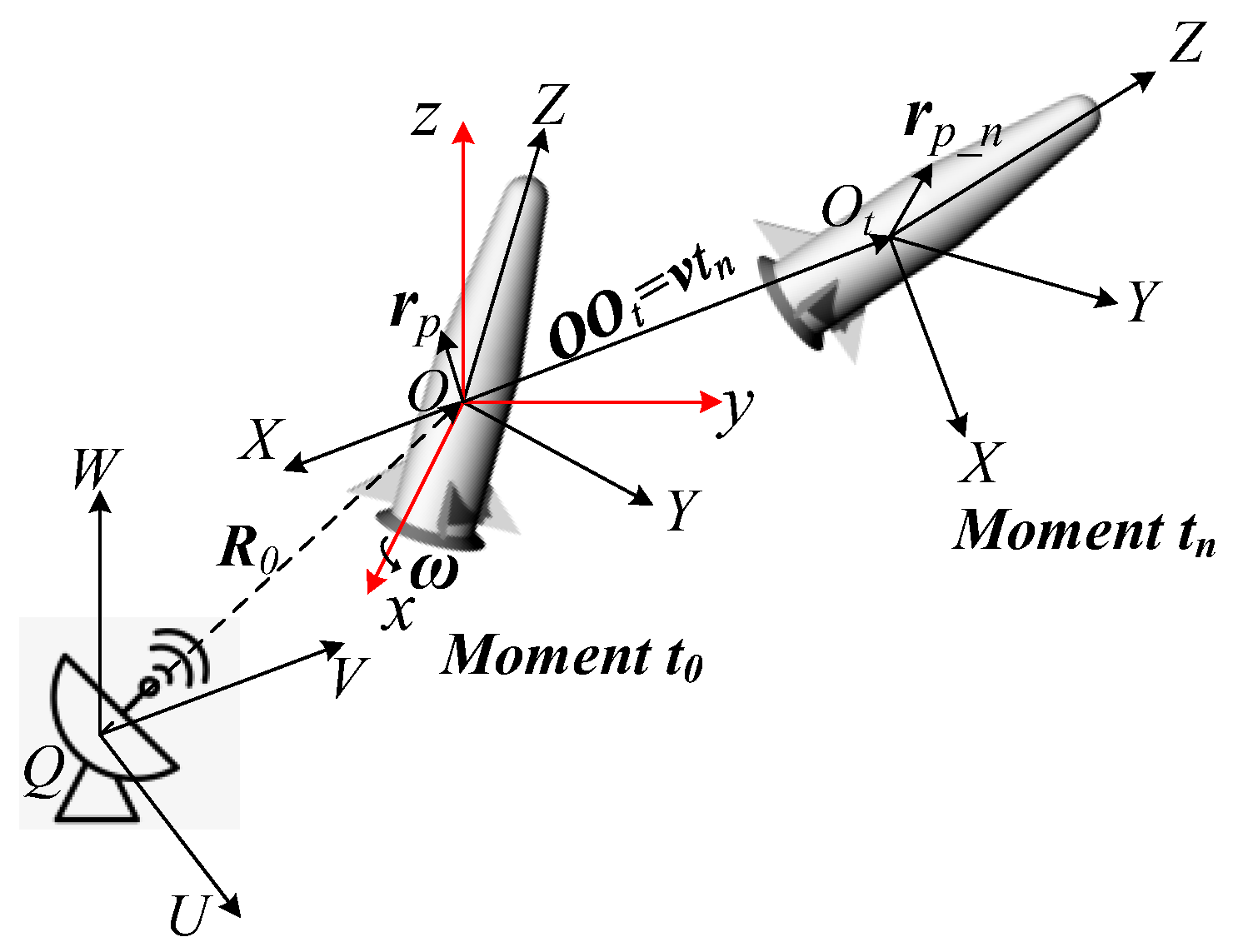
2.1. Motion Modeling of the Target
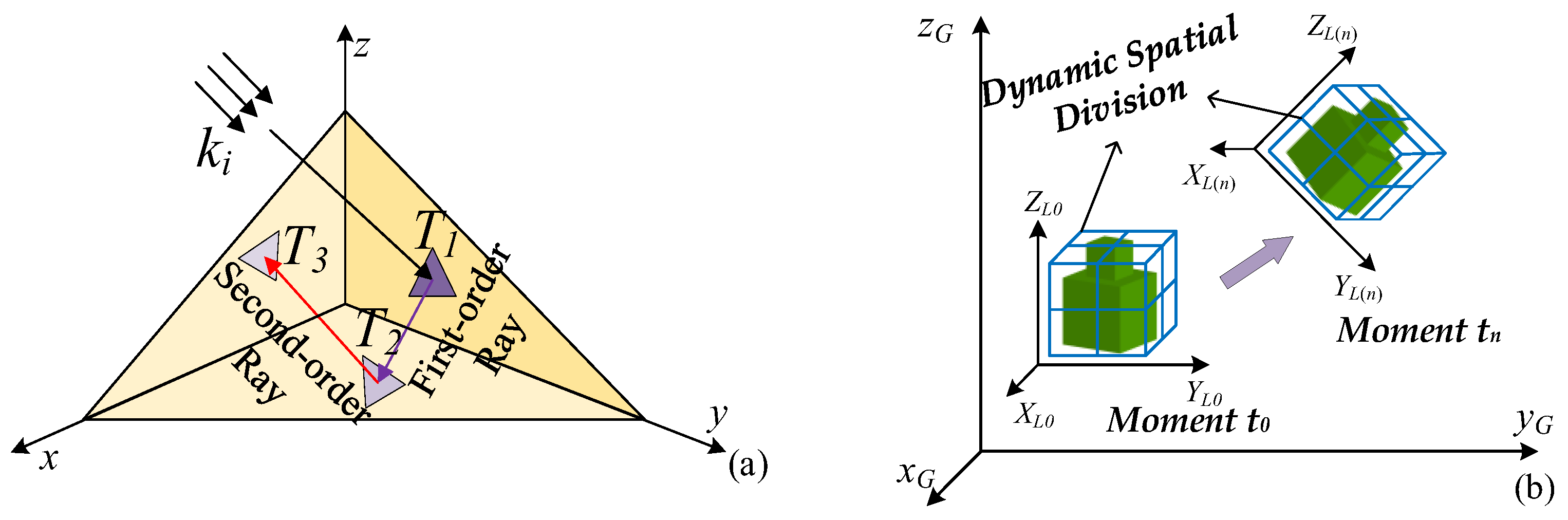
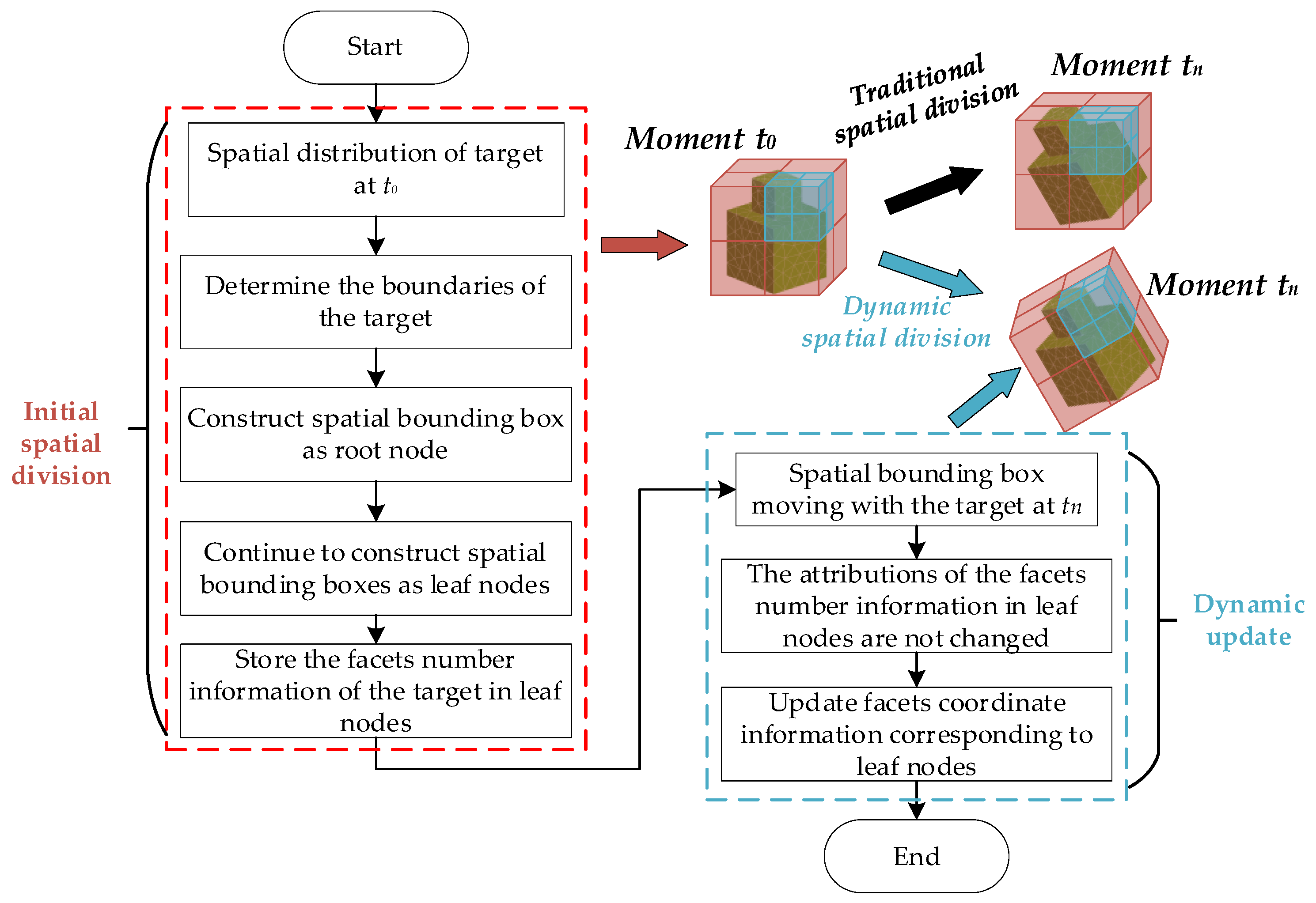
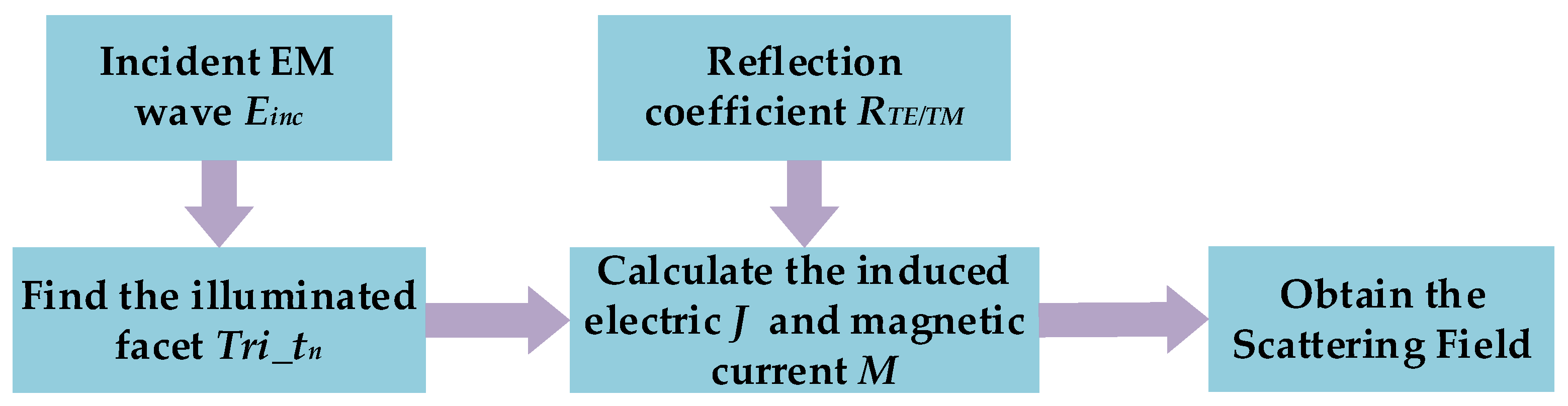
2.2. Fast Solution for EM Scattering of the Moving Target Using the Tailored SBR Method
2.3. Time-Frequency Analysis for the Micro-Doppler
- Step 1: The window function is moved to the starting position of the time sequence . At this time, the center position of is at , and the scattering field sequence is processed by the window function
- Step 2: The fast Fourier transform (FFT) is performed on a small sequence covered by the window function to obtain the Doppler shift of this sequence and it can be expressed aswhere represents the FFT operation;
- Step 3: After completing the FFT of the first sequence, the center of the window function is moved to . The moving distance should be less than the width of the window function, to ensure that there is an overlap between the two windows;
- Step 4: Repeat the above operation as shown in Figure 7, continuously slide the window function and process the sequence using FTT, and finally get the Doppler frequency spectra of all segments on .
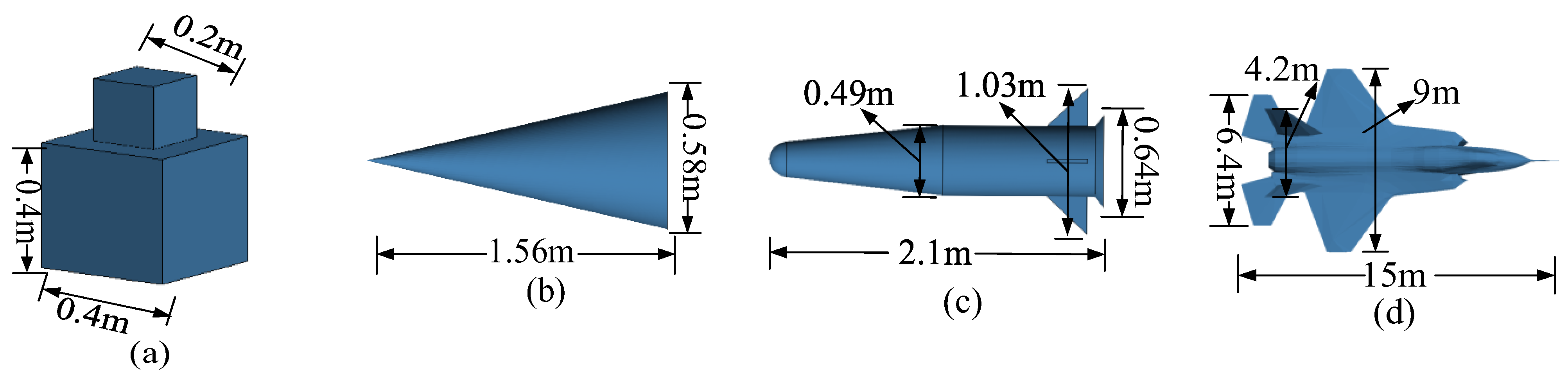
3. Simulation Results and Discussion
3.1. EM Scattering of the Moving Target
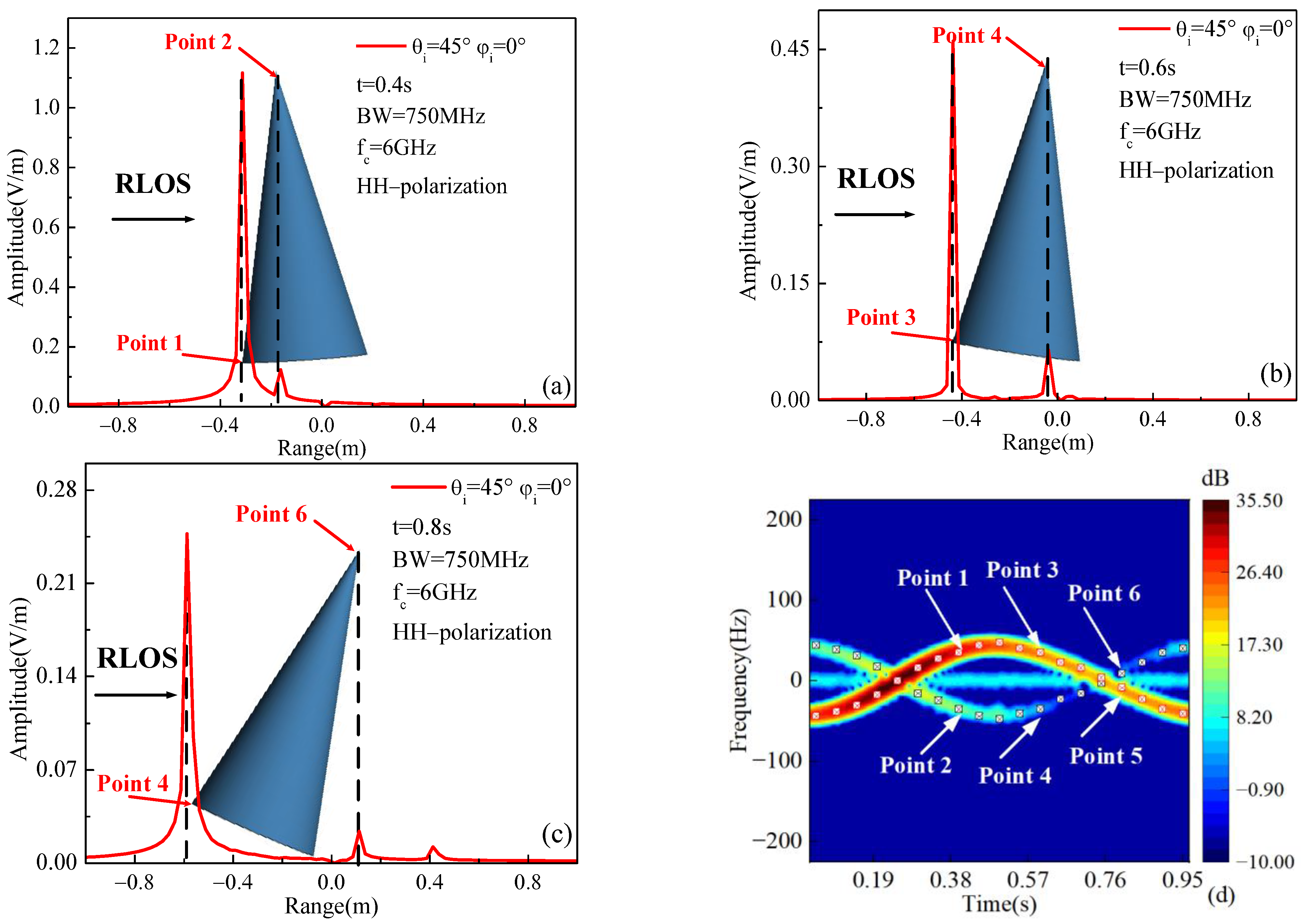
3.2. Micro-Doppler of the Wingless Missile
3.3. Micro-Doppler of the Winged Missile
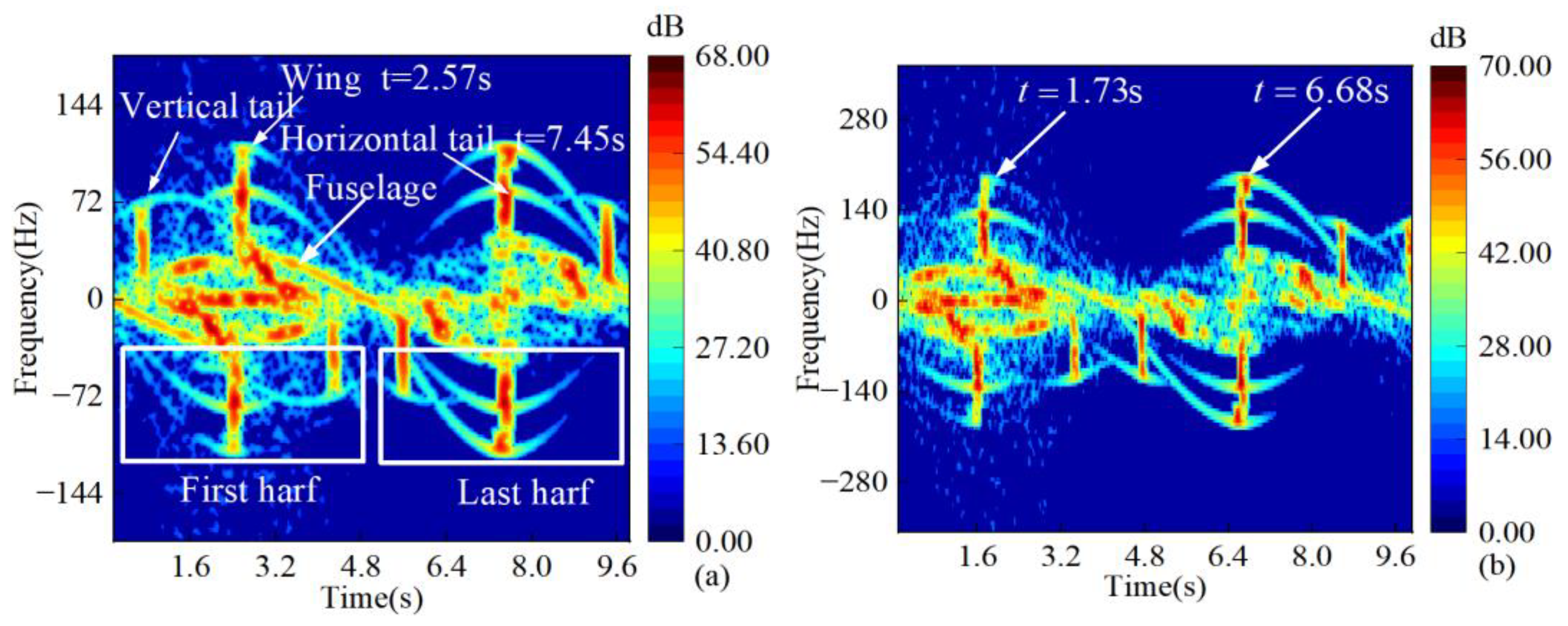
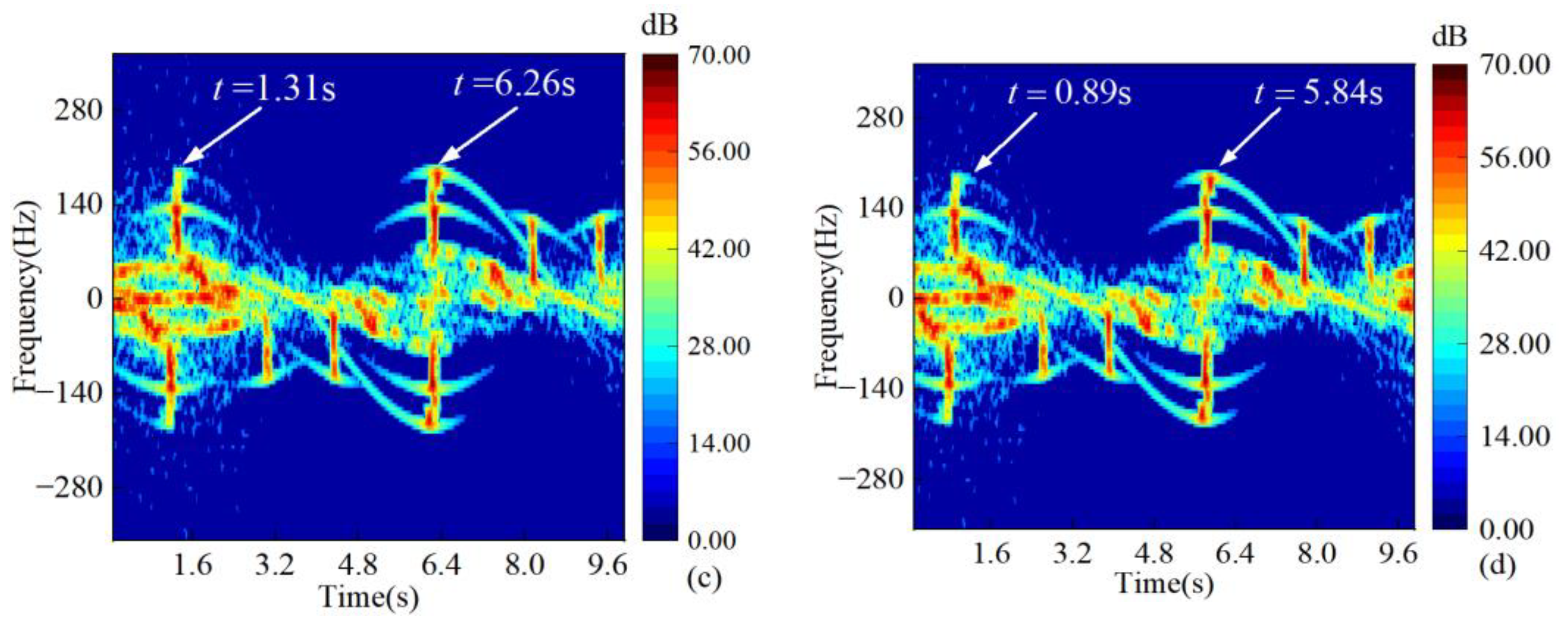
3.4. Micro-Doppler of the Aircraft
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rao, S.; Wilton, D.; Glisson, A. Electromagnetic scattering by surfaces of arbitrary shape. IEEE Trans. Antennas Propag. 1982, 30, 409–418. [Google Scholar] [CrossRef]
- Kuang, L.; Jin, Y.Q. Bistatic Scattering from a Three-Dimensional Object Over a Randomly Rough Surface Using the FDTD Algorithm. IEEE Trans. Antennas Propag. 2007, 55, 2302–2312. [Google Scholar] [CrossRef]
- Kong, W.B.; Zhou, H.X.; Zheng, K.L.; Hong, W. Analysis of Multiscale Problems Using the MLFMA With the Assistance of the FFT-Based Method. IEEE Trans. Antennas Propag. 2015, 63, 4184–4188. [Google Scholar] [CrossRef]
- Aguilar, A.G.; Jakobus, U.; Longtin, M.; Schoeman, M.; Strydom, W.; Tonder, J.J.V. Summary of the latest extensions to the electromagnetic field solver package FEKO. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium—Italy (ACES), Florence, Italy, 26–30 March 2017; pp. 1–2. [Google Scholar]
- Ling, H.; Chou, R.C.; Lee, S.W. Shooting and bouncing rays: Calculating the RCS of an arbitrarily shaped cavity. IEEE Trans. Antennas Propag. 1989, 37, 194–205. [Google Scholar] [CrossRef]
- Li, J.; Zhao, L.; Guo, L.-X.; Li, K.; Chai, S.-R. Hybrid PO-SBR-PTD method for composite scattering of a vehicle target on the ground. Appl. Opt. 2021, 60, 179–185. [Google Scholar] [CrossRef]
- Huang, W.F.; Zhao, Z.; Zhao, R.; Wang, J.Y.; Nie, Z.; Liu, Q.H. GO/PO and PTD With Virtual Divergence Factor for Fast Analysis of Scattering from Concave Complex Targets. IEEE Trans. Antennas Propag. 2015, 63, 2170–2179. [Google Scholar] [CrossRef]
- Bang, J.K.; Kim, B.C.; Suk, S.H.; Jin, K.S.; Kim, H.T. Time Consumption Reduction of Ray Tracing for Rcs Prediction using Efficient Grid Division and Space Division Algorithms. J. Electromagn. Waves Appl. 2007, 21, 829–840. [Google Scholar] [CrossRef]
- Feng, T.T.; Guo, L.X. An Improved Ray-Tracing Algorithm for SBR-Based EM Scattering Computation of Electrically Large Targets. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 818–822. [Google Scholar] [CrossRef]
- Wang, H.; Wei, B.; Liu, H. A Fast Method for SBR-Based Multiaspect Radar Cross Section Simulation of Electrically Large Targets. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1920–1924. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, J.Y.; Yu, W.M.; Cui, T.J. Time-Domain Shooting and Bouncing Rays Method Based on Beam Tracing Technique. IEEE Trans. Antennas Propag. 2015, 63, 4037–4048. [Google Scholar] [CrossRef]
- Dong, C.-L.; Guo, L.-X.; Meng, X.; Wang, Y. An Accelerated SBR for EM Scattering from the Electrically Large Complex Objects. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2294–2298. [Google Scholar] [CrossRef]
- Zou, G.; Tong, C.; Zhu, J.; Sun, H.; Peng, P. Study on Composite Electromagnetic Scattering Characteristics of Low-Altitude Target Above Valley Composite Rough Surface Using Hybrid SBR-EEC Method. IEEE Access 2020, 8, 72298–72307. [Google Scholar] [CrossRef]
- Lan, L.; Marino, A.; Aubry, A.; Maio, A.D.; Liao, G.; Xu, J.; Zhang, Y. GLRT-Based Adaptive Target Detection in FDA-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 597–613. [Google Scholar] [CrossRef]
- Lan, L.; Xu, J.; Liao, G.; Zhang, Y.; Fioranelli, F.; So, H.C. Suppression of Mainbeam Deceptive Jammer With FDA-MIMO Radar. IEEE Trans. Veh. Technol. 2020, 69, 11584–11598. [Google Scholar] [CrossRef]
- Kang, M.S.; Baek, J.M. Efficient SAR Imaging Integrated with Autofocus via Compressive Sensing. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Kang, M.S.; Baek, J.M. SAR Image Reconstruction via Incremental Imaging with Compressive Sensing. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4450–4463. [Google Scholar] [CrossRef]
- Shi, F.; Li, Z.; Zhang, M.; Li, J. Analysis and Simulation of the Micro-Doppler Signature of a Ship with a Rotating Shipborne Radar at Different Observation Angles. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Amiri, R.; Shahzadi, A. Micro-Doppler based target classification in ground surveillance radar systems. Digit. Signal Process. 2020, 101, 102702. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, Y.; Li, K.; Yuan, H.; Zhang, Q. Micro-Doppler Parameters Extraction of Precession Cone-Shaped Targets Based on Rotating Antenna. Remote Sens. 2022, 14, 2549. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Huang, Y.; Liu, N.; He, Y. Radon-Linear Canonical Ambiguity Function-Based Detection and Estimation Method for Marine Target with Micromotion. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2225–2240. [Google Scholar] [CrossRef]
- Chen, V.C.; Li, F.; Ho, S.S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Chen, V.C. Joint time-frequency analysis for radar signal and imaging. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 5166–5169. [Google Scholar]
- Gao, H.; Xie, L.; Wen, S.; Kuang, Y. Micro-Doppler Signature Extraction from Ballistic Target with Micro-Motions. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1969–1982. [Google Scholar] [CrossRef]
- Gong, J.; Yan, J.; Li, D.; Chen, R.; Tian, F.; Yan, Z. Theoretical and Experimental Analysis of Radar Micro-Doppler Signature Modulated by Rotating Blades of Drones. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1659–1663. [Google Scholar] [CrossRef]
- Li, T.; Wen, B.; Tian, Y.; Li, Z.; Wang, S. Numerical Simulation and Experimental Analysis of Small Drone Rotor Blade Polarimetry Based on RCS and Micro-Doppler Signature. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 187–191. [Google Scholar] [CrossRef]
- Chen, V.C. Spatial and temporal independent component analysis of micro-doppler features. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 348–353. [Google Scholar]
- Fan, T.-Q.; Guo, L.-X.; Lv, B.; Liu, W. An Improved Backward SBR-PO/PTD Hybrid Method for the Backward Scattering Prediction of an Electrically Large Target. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 512–515. [Google Scholar] [CrossRef]
- Gordon, W. Far-field approximations to the Kirchoff-Helmholtz representations of scattered fields. IEEE Trans. Antennas Propag. 1975, 23, 590–592. [Google Scholar] [CrossRef]



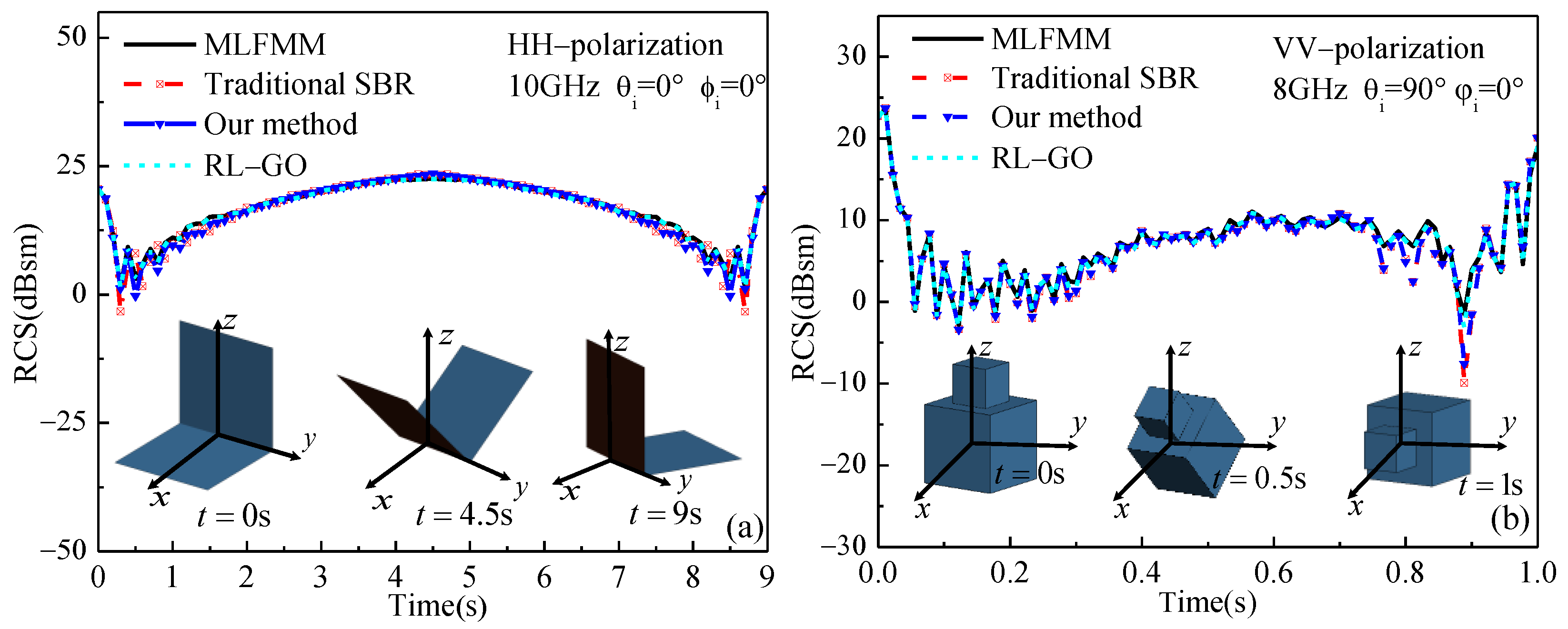
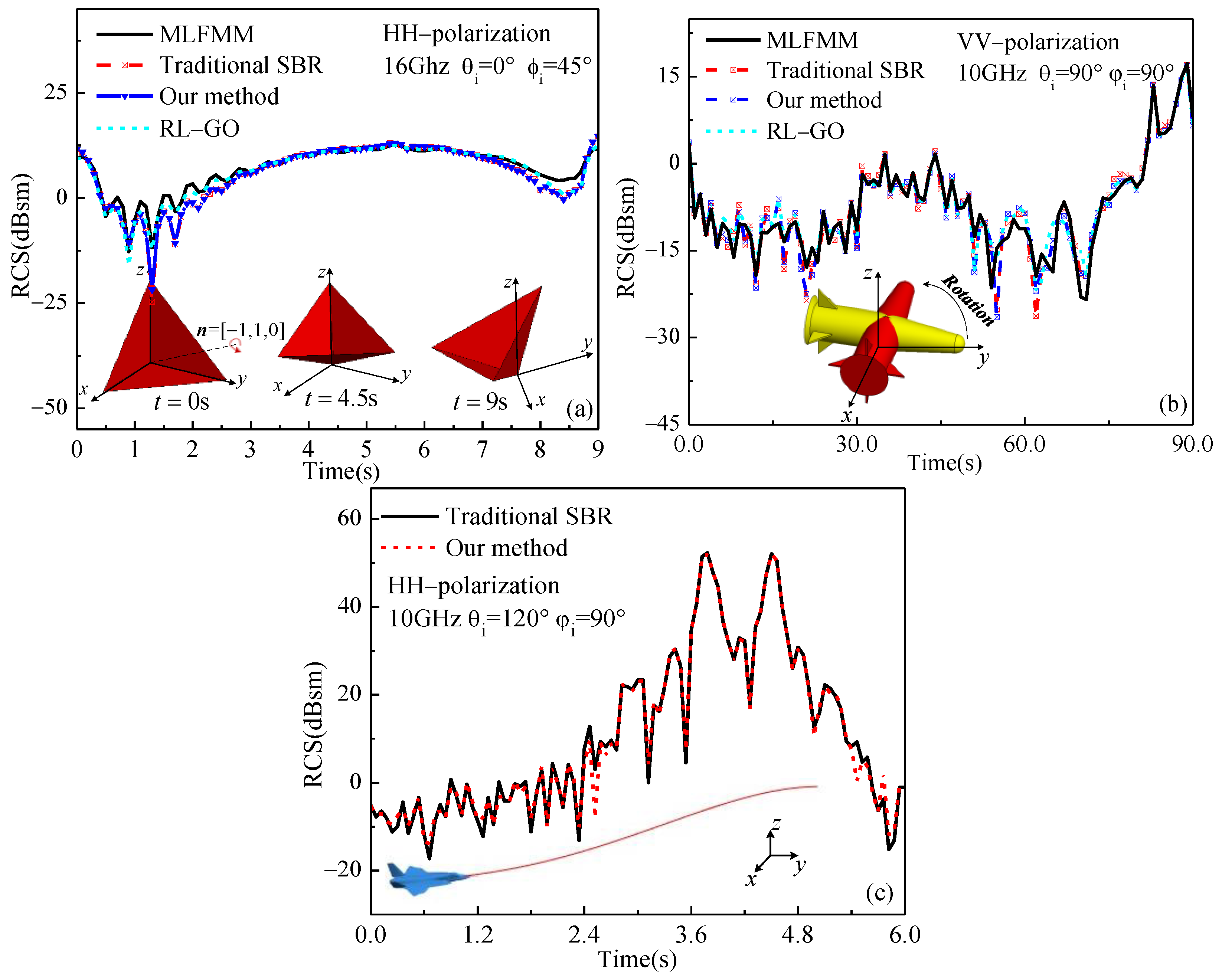


| MLFMM and Our Method | RL-GO and Our Method | |||
|---|---|---|---|---|
| Figure 10a | 0.41 | 2.11 | 0.36 | 2.10 |
| Figure 10b | 0.58 | 2.15 | 0.46 | 1.99 |
| Figure 11a | 0.88 | 2.17 | 0.53 | 1.81 |
| Figure 11b | 0.78 | 2.81 | 0.57 | 1.67 |
| Number of Facets | MLFMM (8 Threads) | RL-GO (8 Threads) | Traditional SBR (1 Thread) | Our Method (1 Thread) | Speedup | |
|---|---|---|---|---|---|---|
| Figure 10a | 16,492 | 6.74 min | 1.93 min | 1.01 min | 0.63 min | 1.60 |
| Figure 10b | 71,560 | 306.6 min | 13.83 min | 7.47 min | 3.22 min | 2.32 |
| Figure 11a | 12,786 | 4.81 min | 1.27 min | 0.96 min | 0.56 min | 1.71 |
| Figure 11b | 148,552 | 488.3 min | 34.16 min | 29.2 min | 6.31 min | 4.63 |
| Figure 11c | 248,880 | / | / | 41.97 min | 7.49 min | 5.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Y.; Li, J.; Guo, L.; Meng, W.; Wen, S. Fast Solution of Scattering and Micro-Doppler Features from Moving Target Using a Tailored Shooting and Bouncing Ray Method. Remote Sens. 2023, 15, 5724. https://doi.org/10.3390/rs15245724
Xi Y, Li J, Guo L, Meng W, Wen S. Fast Solution of Scattering and Micro-Doppler Features from Moving Target Using a Tailored Shooting and Bouncing Ray Method. Remote Sensing. 2023; 15(24):5724. https://doi.org/10.3390/rs15245724
Chicago/Turabian StyleXi, Yongji, Juan Li, Lixin Guo, Wei Meng, and Shunkang Wen. 2023. "Fast Solution of Scattering and Micro-Doppler Features from Moving Target Using a Tailored Shooting and Bouncing Ray Method" Remote Sensing 15, no. 24: 5724. https://doi.org/10.3390/rs15245724
APA StyleXi, Y., Li, J., Guo, L., Meng, W., & Wen, S. (2023). Fast Solution of Scattering and Micro-Doppler Features from Moving Target Using a Tailored Shooting and Bouncing Ray Method. Remote Sensing, 15(24), 5724. https://doi.org/10.3390/rs15245724







