SSCNet: A Spectrum-Space Collaborative Network for Semantic Segmentation of Remote Sensing Images
Abstract
:1. Introduction
- (1)
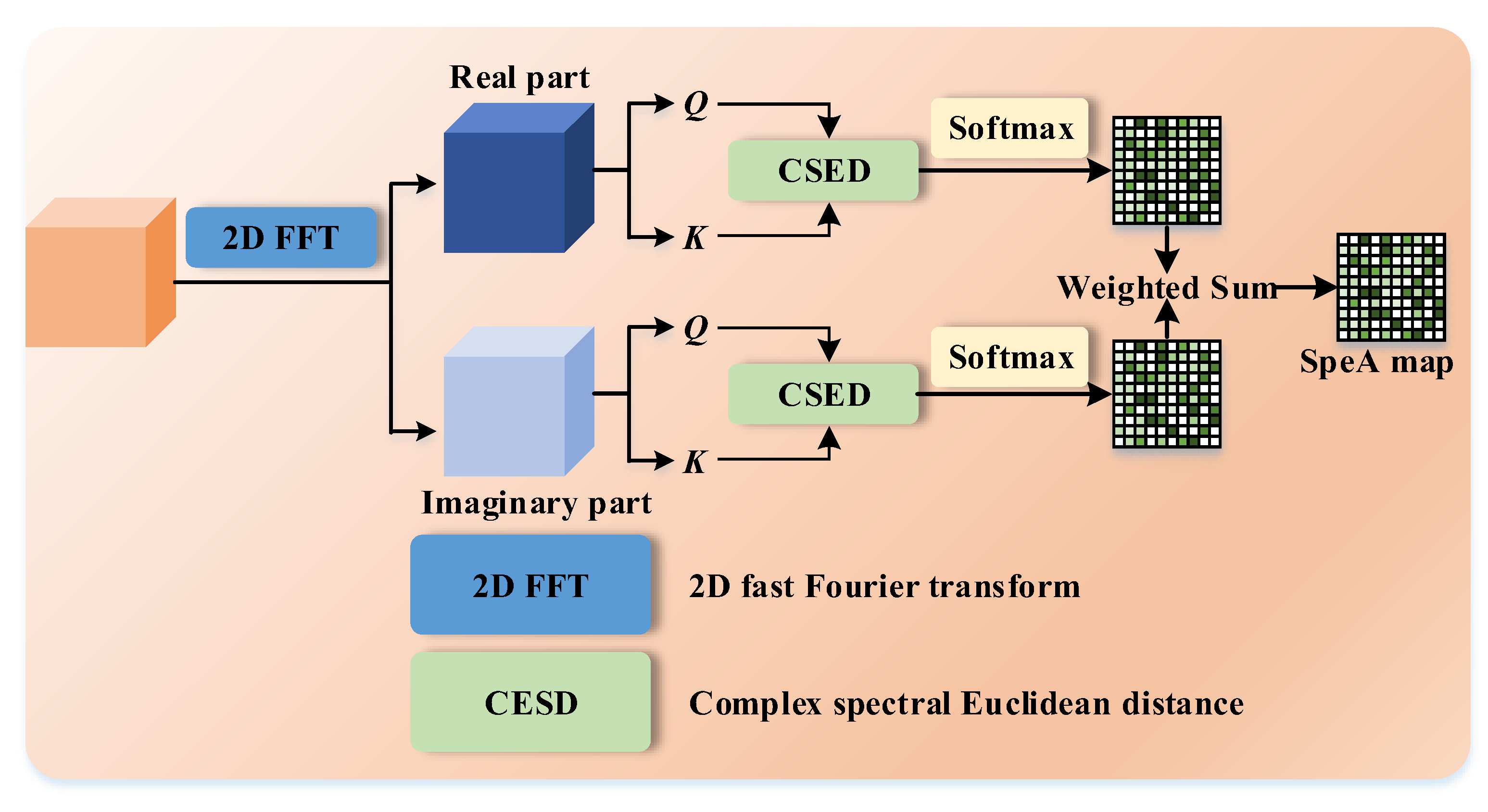
- We propose a SpeA for capturing the spectral context in the frequency domain. SpeA first maps the feature map into the frequency domain using a 2D fast Fourier transform (2D FFT) layer. Considering that the transformed features may be complex, we compute pairwise similarity by measuring the complex spectral Euclidean distance (CSED) of the real and imaginary parts. Subsequently, we create SpeA maps by weighted summation, enabling the prioritization of spectral features in attention modeling.
- (2)
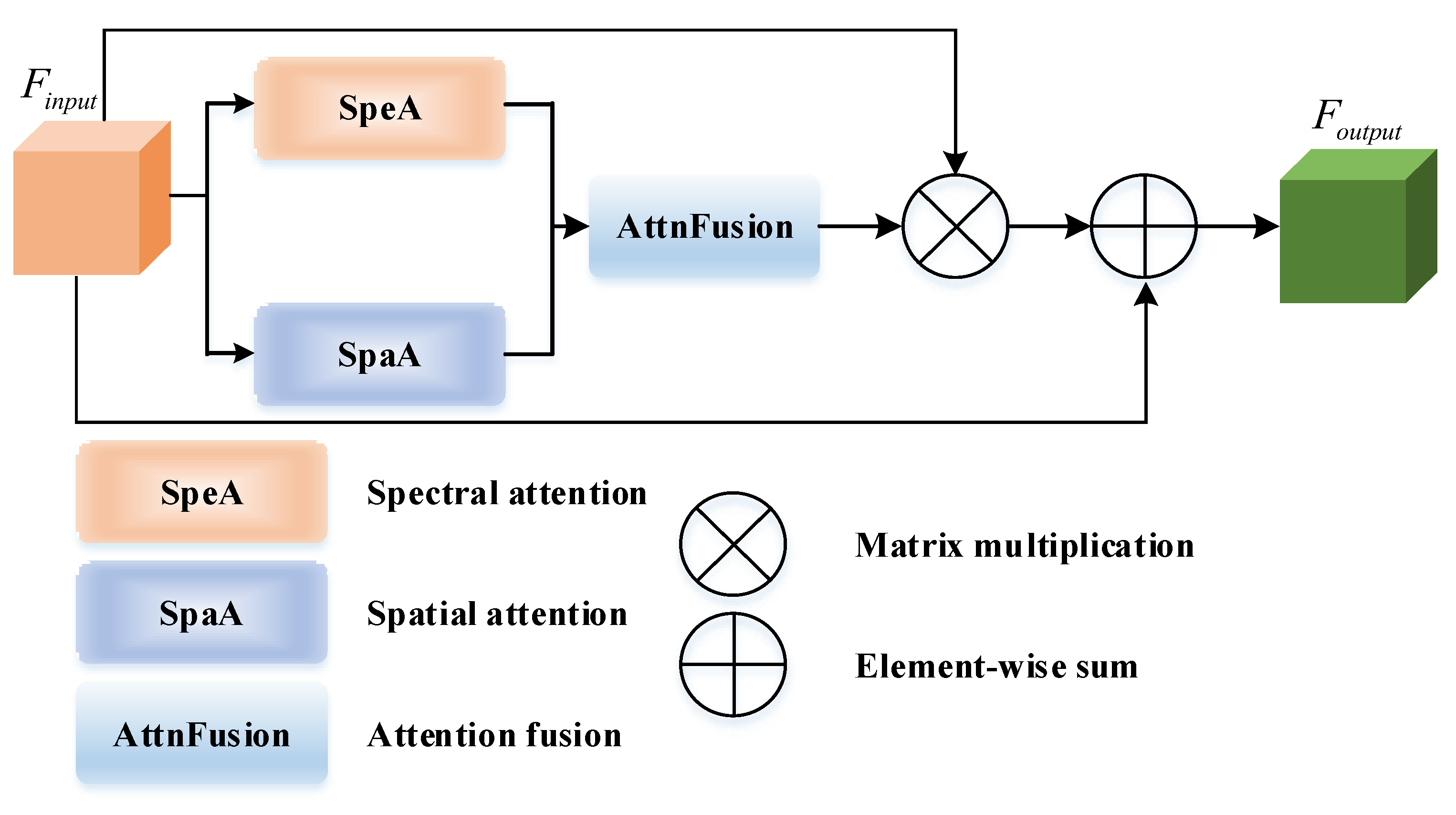
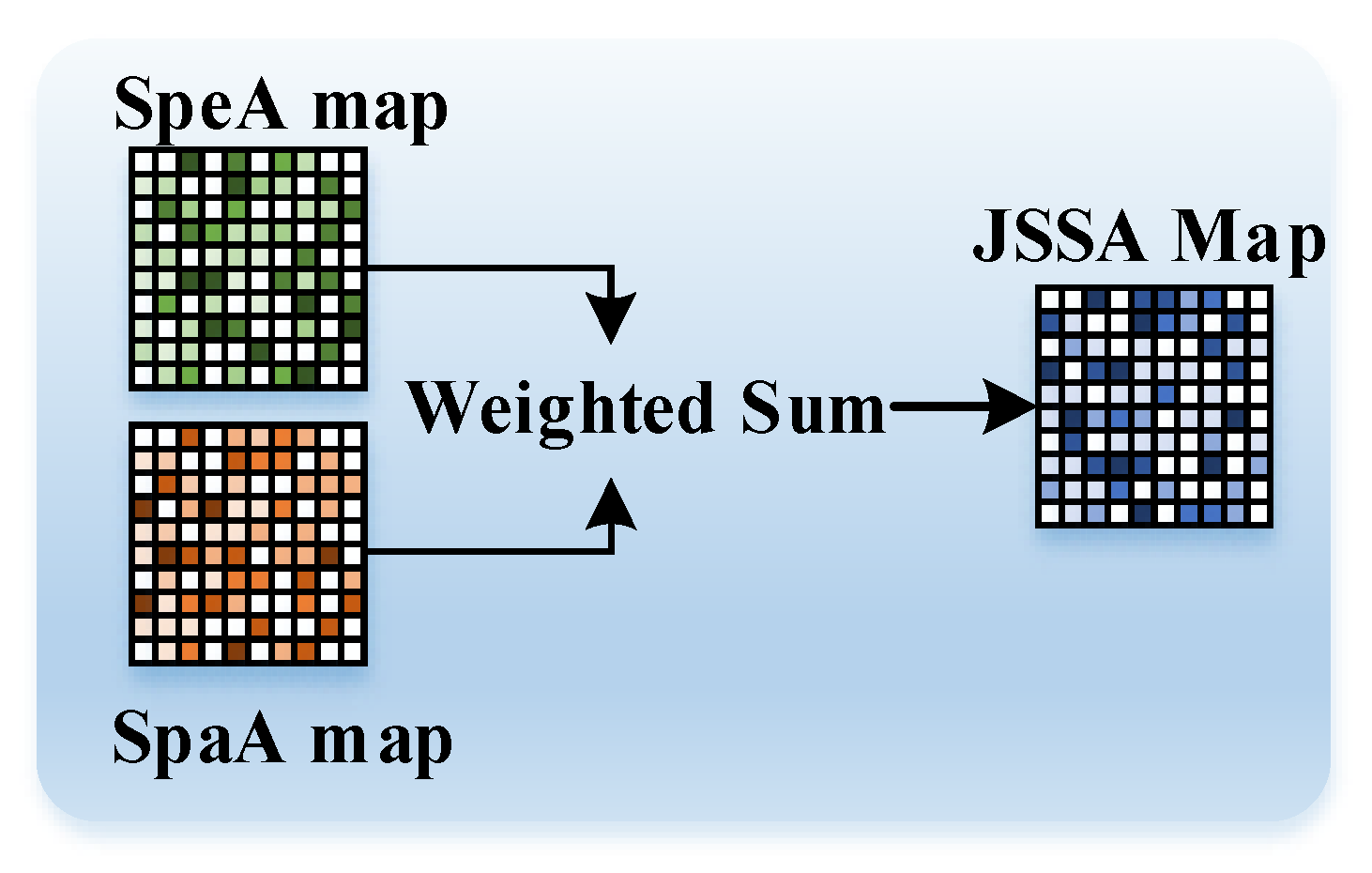
- To comprehensively model and utilize contexts that span spectral and spatial domains, we present the JSSA module. For spatial contexts, we incorporate position-wise self-attention as a parallel SpaA branch. Through an attention fusion (AttnFusion) module, we merge the attention maps obtained from SpeA and SpaA. This results in JSSA producing an attention map that considers both spectral and spatial contexts simultaneously.
- (3)
- We formulate a hybrid loss function (HLF) that encompasses both spectral and spatial losses. Concerning the high-frequency components, we calculate edge loss. While promoting the inner consistency of objects, mainly represented by low-frequency components, we introduce Dice loss to compensate. Simultaneously, we employ cross-entropy loss to supervise the spatial aspects. By combining these losses with appropriate weights, we establish a hybrid loss function that facilitates the network in learning discriminative representations within both the frequency and spatial domains.
- (4)
- Complementing the above-mentioned designs, we propose the SSCNet, a semantic segmentation network for remote sensing images. Thorough experimentation demonstrates its superior performance compared with other state-of-the-art methods. Furthermore, an ablation study corroborates the efficacy of the SpeA component.
2. Related Works
2.1. Semantic Segmentation for RSIs
2.2. Learning in Frequency Domain
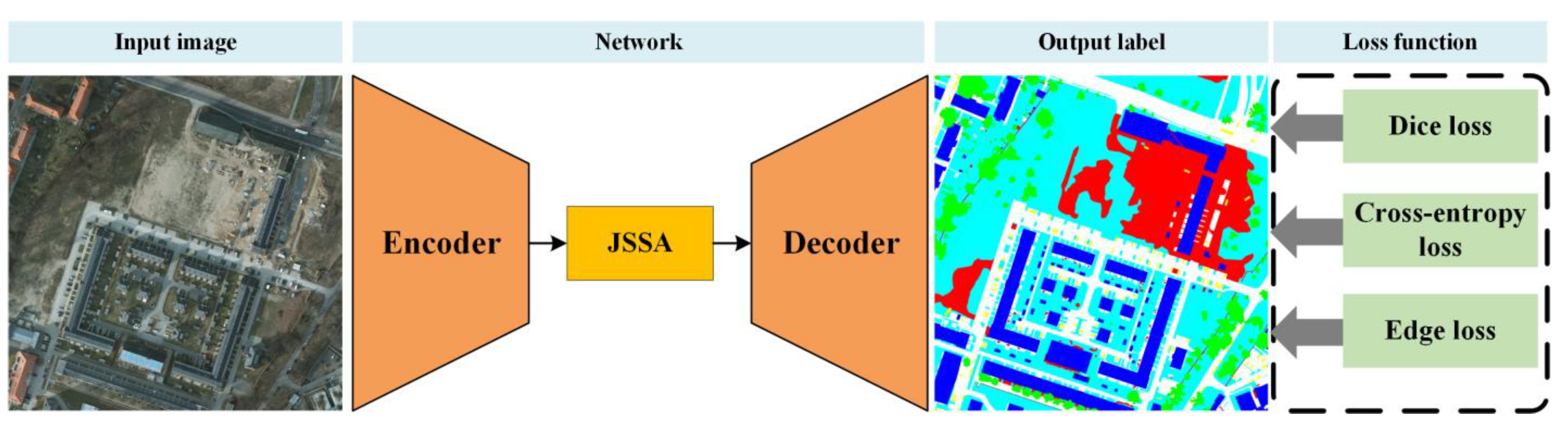
3. The Proposed Method
3.1. Overall Framework
3.2. Joint Spectral–Spatial Attention
3.3. Hybrid Loss Function
4. Experiments and Discussion
4.1. Datasets
4.1.1. ISPRS Potsdam Dataset
4.1.2. LoveDA Dataset
4.2. Implementation Details
4.3. Evaluation Metrics
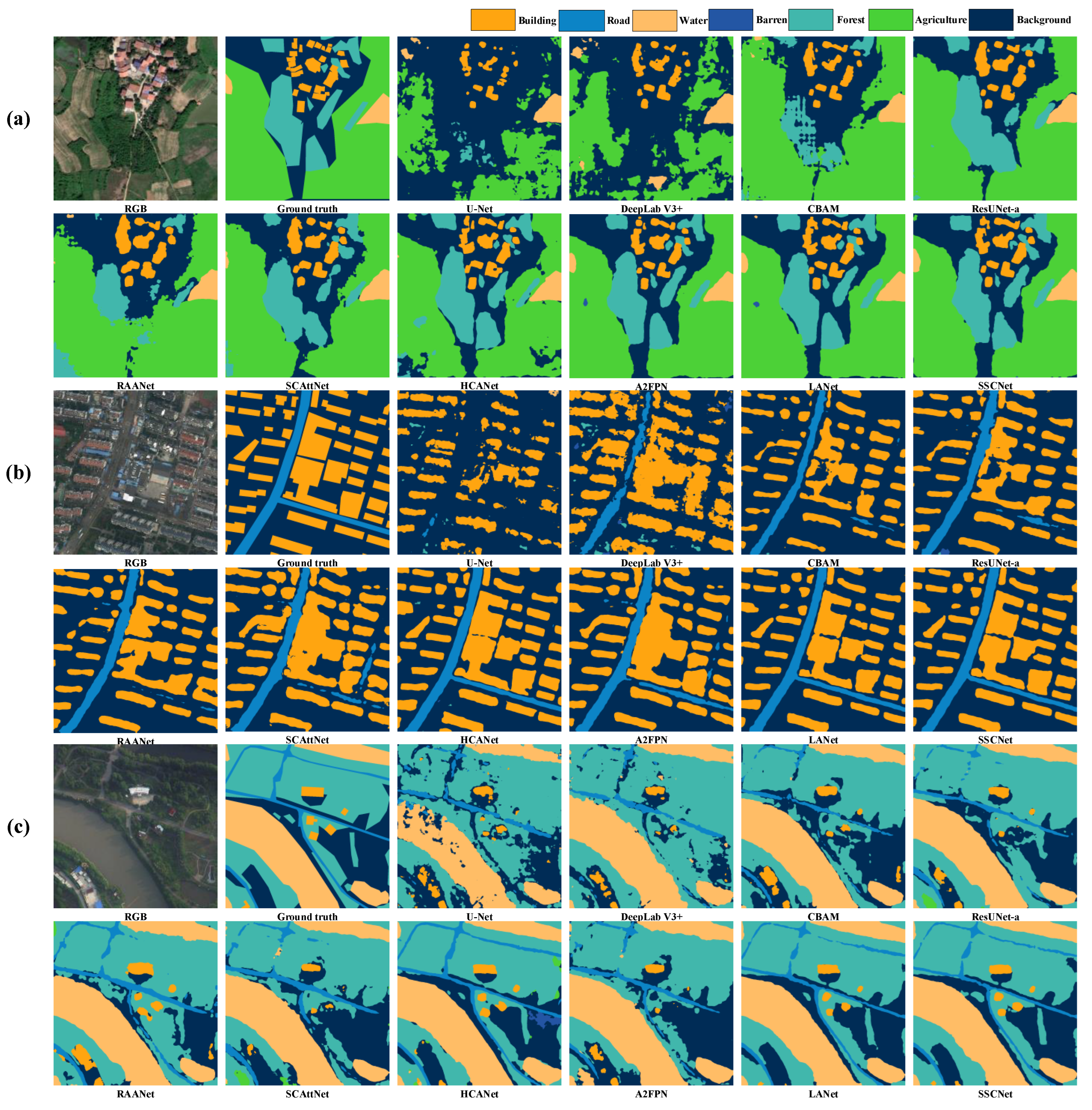
4.4. Comparison with State-of-the-Art Methods
4.4.1. Results on ISPRS Potsdam Dataset
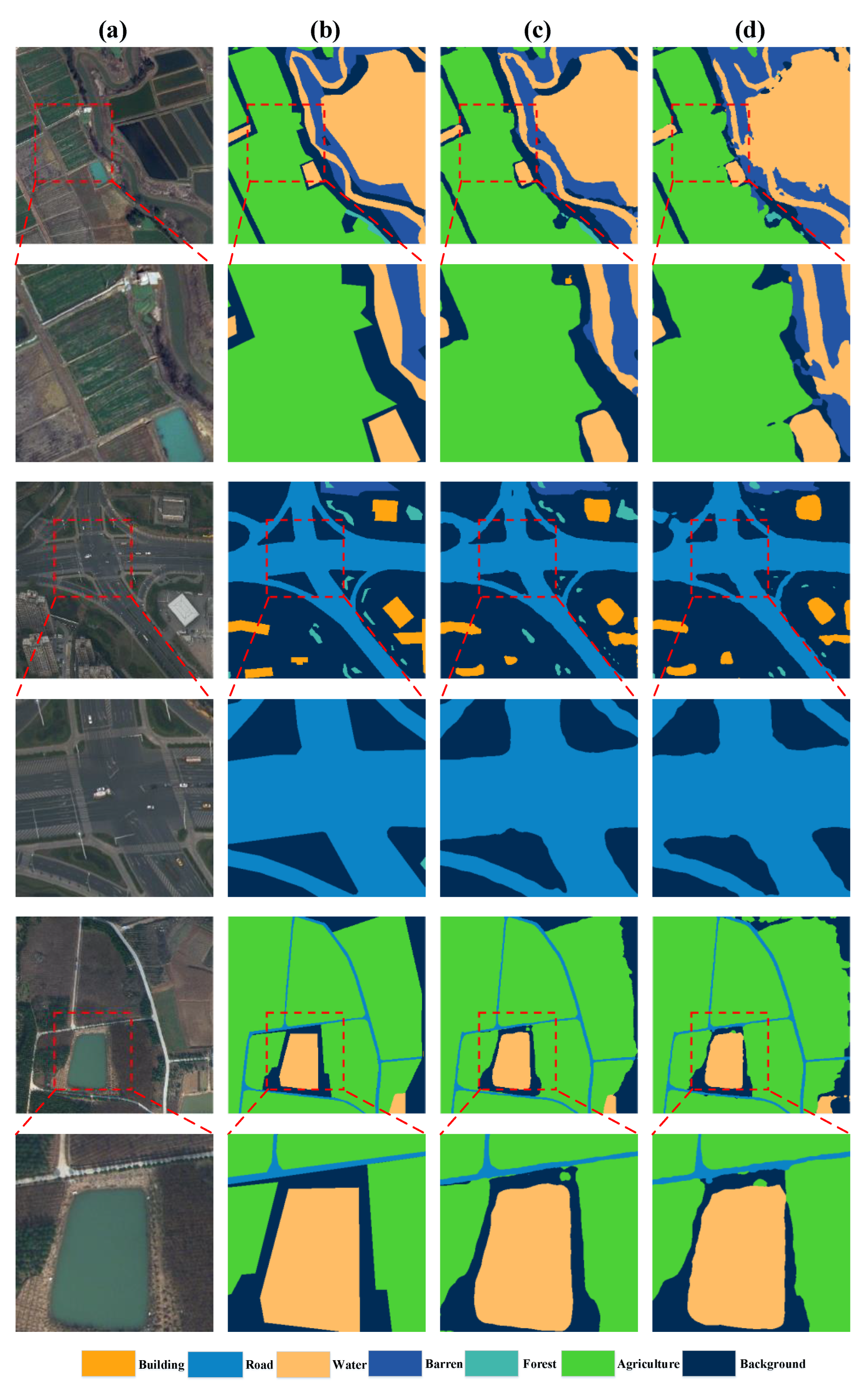
4.4.2. Results on LoveDA Dataset
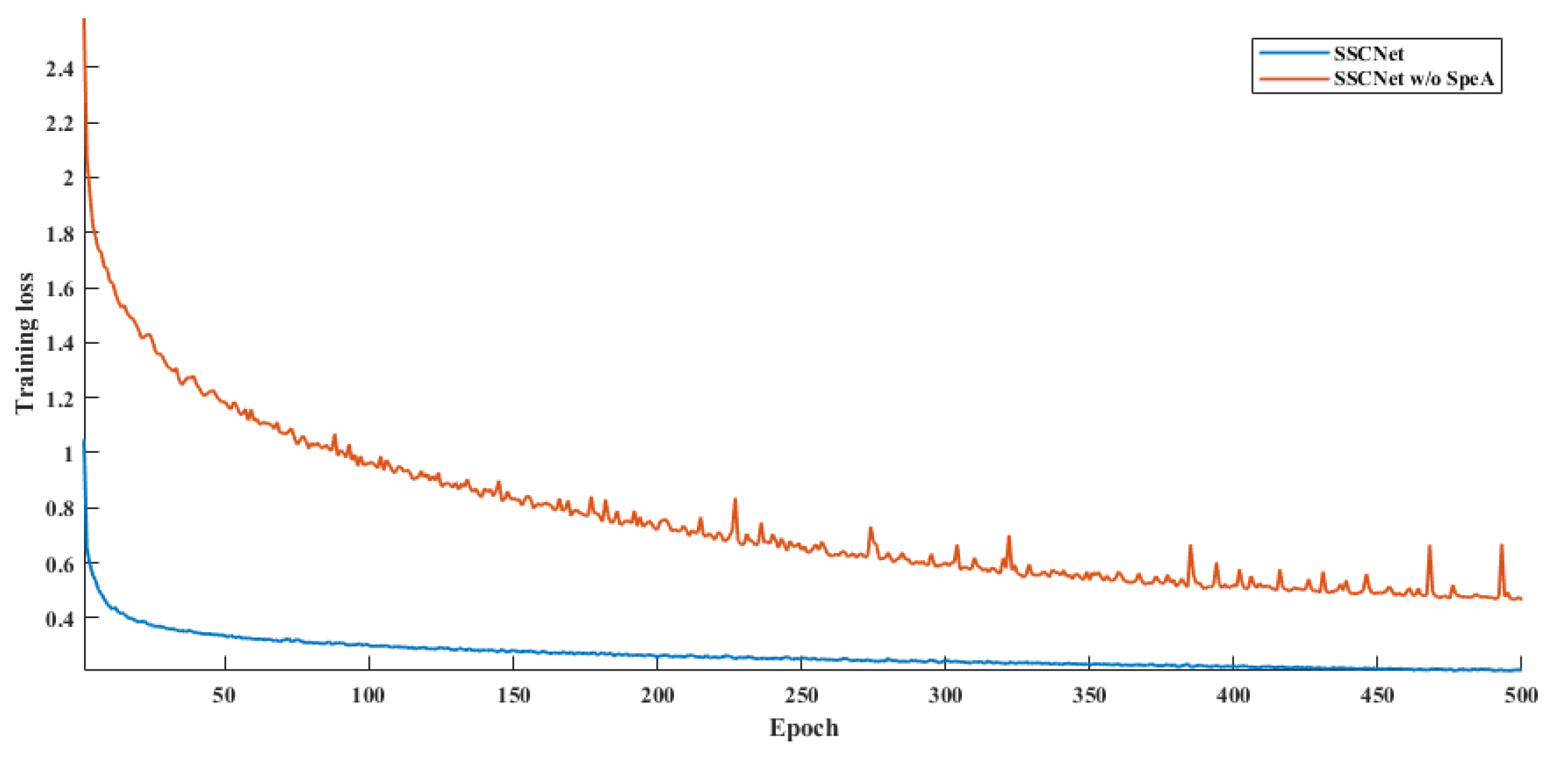
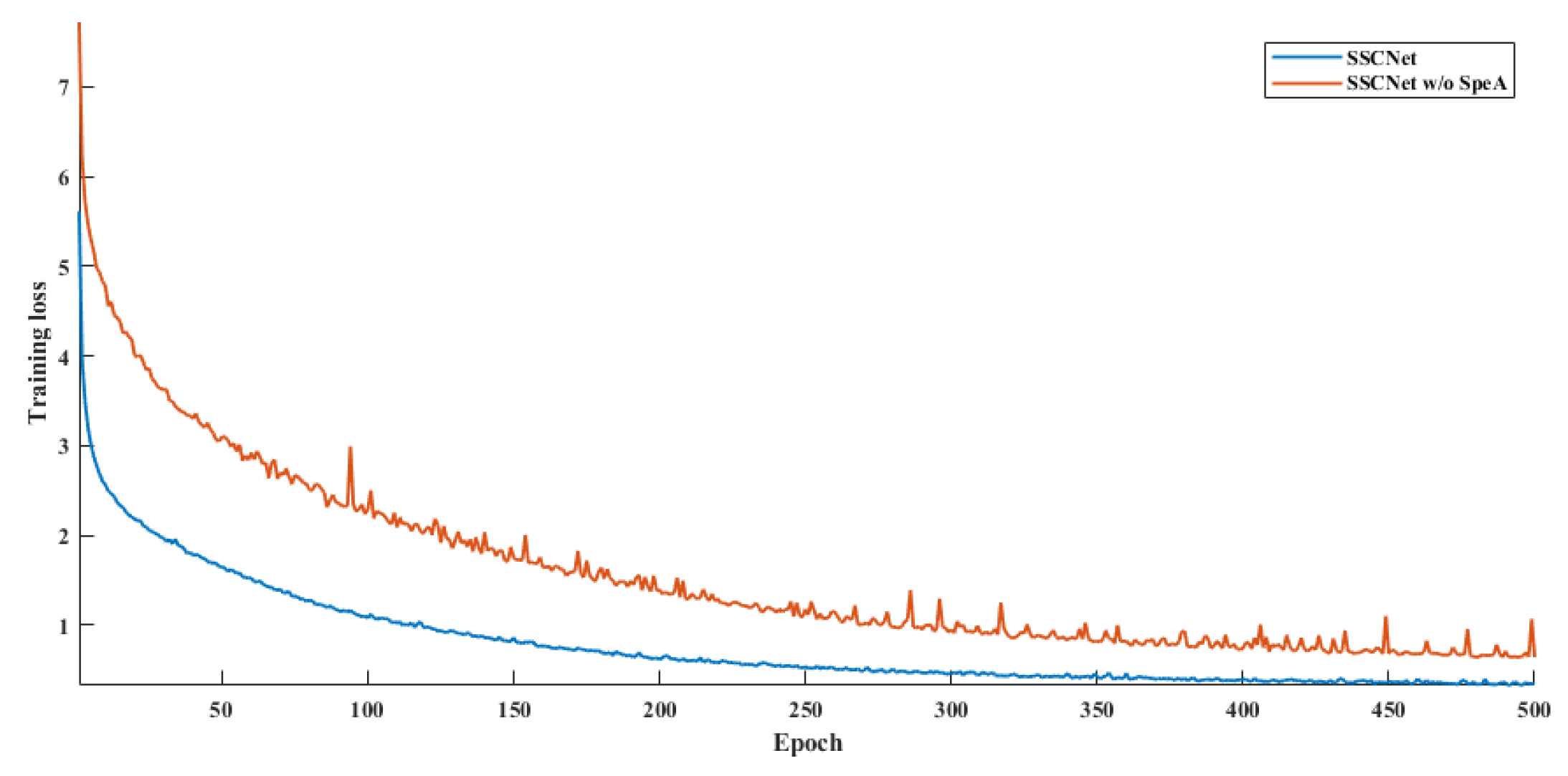
4.5. Ablation Study on SpeA
4.6. Effects of the Value of
4.7. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, W.; Chen, C.; Liu, W.; Yang, G.; Meng, X.; Wang, L.; Ren, K. Coastline extraction using remote sensing: A review. GIScience Remote Sens. 2023, 60, 2243671. [Google Scholar] [CrossRef]
- Saeid, A.A.A. Remote Sensing in Water Quality and Water Resources Management. Int. J. Res. Appl. Sci. Biotechnol. 2022, 9, 163–170. [Google Scholar] [CrossRef]
- Li, X.; Lyu, X.; Tong, Y.; Li, S.; Liu, D. An object-based river extraction method via optimized transductive support vector machine for multi-spectral remote-sensing images. IEEE Access 2019, 7, 46165–46175. [Google Scholar] [CrossRef]
- Qin, R.; Liu, T. A review of landcover classification with very-high resolution remotely sensed optical images—Analysis unit, model scalability and transferability. Remote Sens. 2022, 14, 646. [Google Scholar] [CrossRef]
- Lv, Z.; Huang, H.; Li, X.; Zhao, M.; Benediktsson, J.A.; Sun, W.; Falco, N. Land cover change detection with heterogeneous remote sensing images: Review, progress, and perspective. Proc. IEEE 2022, 110, 1976–1991. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Y.; Zhang, Y.; Zhong, L.; Wang, J.; Chen, J. DKDFN: Domain knowledge-guided deep collaborative fusion network for multimodal unitemporal remote sensing land cover classification. ISPRS J. Photogramm. Remote Sens. 2022, 186, 170–189. [Google Scholar] [CrossRef]
- Bai, H.; Li, Z.; Guo, H.; Chen, H.; Luo, P. Urban green space planning based on remote sensing and geographic information systems. Remote Sens. 2022, 14, 4213. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, L.; Luo, Y.; Li, D.; Junior, J.M.; Gonçalves, W.N.; Nurunnabi, A.A.M.; Li, J.; Wang, C.; Li, D. Road extraction in remote sensing data: A survey. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102833. [Google Scholar] [CrossRef]
- Bitala, W.; Johnima, A.; Junta, U.; Browndi, I. Predictive Analysis Towards Integration of Urban Planning and GIS to Manage Health Care Organization. Int. J. Sci. Adv. Technol. 2022, 36, 81–87. [Google Scholar]
- Román, A.; Tovar-Sánchez, A.; Roque-Atienza, D.; Huertas, I.E.; Caballero, I.; Fraile-Nuez, E.; Navarro, G. Unmanned aerial vehicles (UAVs) as a tool for hazard assessment: The 2021 eruption of Cumbre Vieja volcano, La Palma Island (Spain). Sci. Total Environ. 2022, 843, 157092. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Shao, Z.; Aslam, R.W.; Ahmad, I.; Liao, M.; Li, X.; Song, Y. Landslide hazard, susceptibility and risk assessment (HSRA) based on remote sensing and GIS data models: A case study of Muzaffarabad Pakistan. Stoch. Environ. Res. Risk Assess. 2022, 36, 4041–4056. [Google Scholar] [CrossRef]
- Yuan, X.; Shi, J.; Gu, L. A review of deep learning methods for semantic segmentation of remote sensing imagery. Expert Syst. Appl. 2021, 169, 114417. [Google Scholar] [CrossRef]
- Gonzalez-Diaz, I.; Diaz-de-Maria, F. A region-centered topic model for object discovery and category-based image segmentation. Pattern Recognit. 2013, 46, 2437–2449. [Google Scholar] [CrossRef]
- Anand, T.; Sinha, S.; Mandal, M.; Chamola, V.; Yu, F.R. AgriSegNet: Deep aerial semantic segmentation framework for IoT-assisted precision agriculture. IEEE Sens. J. 2021, 21, 17581–17590. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Yang, H. Self-adaptive mutation differential evolution algorithm based on particle swarm optimization. Appl. Soft Comput. 2019, 81, 105496. [Google Scholar] [CrossRef]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. Joint Deep Learning for land cover and land use classification. Remote Sens. Environ. 2019, 221, 173–187. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Liu, Y.; Piramanayagam, S.; Monteiro, S.T.; Saber, E. Semantic segmentation of multisensor remote sensing imagery with deep ConvNets and higher-order conditional random fields. J. Appl. Remote Sens. 2019, 13, 016501. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Elngar, A.A.; Arafa, M.; Fathy, A.; Moustafa, B.; Mahmoud, O.; Shaban, M.; Fawzy, N. Image classification based on CNN: A survey. J. Cybersecur. Inf. Manag. 2021, 6, 18–50. [Google Scholar] [CrossRef]
- Arkin, E.; Yadikar, N.; Xu, X.; Aysa, A.; Ubul, K. A survey: Object detection methods from CNN to transformer. Multimed. Tools Appl. 2023, 82, 21353–21383. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Lyu, X.; Tong, Y.; Chen, Z.; Li, S.; Liu, D. A remote-sensing image pan-sharpening method based on multi-scale channel attention residual network. IEEE Access 2020, 8, 27163–27177. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Liu, F.; Xia, R.; Tong, Y.; Li, L.; Xu, Z.; Lyu, X. Hybridizing Euclidean and Hyperbolic Similarities for Attentively Refining Representations in Semantic Segmentation of Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Q.; Zhang, G. MLCRNet: Multi-Level Context Refinement for Semantic Segmentation in Aerial Images. Remote Sens. 2022, 14, 1498. [Google Scholar] [CrossRef]
- ISPRS Potsdam 2D Semantic Labeling Dataset. [Online]. Available online: http://www2.isprs.org/commissions/comm3/wg4/2d-sem-label-potsdam.html (accessed on 22 December 2022).
- ISPRS Vaihingen 2D Semantic Labeling Dataset. [Online]. Available online: http://www2.isprs.org/commissions/comm3/wg4/2d-sem-label-vaihingen.html (accessed on 22 December 2022).
- Shang, R.; Zhang, J.; Jiao, L.; Li, Y.; Marturi, N.; Stolkin, R. Multi-scale Adaptive Feature Fusion Network for Semantic Segmentation in Remote Sensing Images. Remote Sens. 2020, 12, 872. [Google Scholar] [CrossRef]
- Du, S.; Du, S.; Liu, B.; Zhang, X. Mapping large-scale and fine-grained urban functional zones from VHR images using a multi-scale semantic segmentation network and object based approach. Remote Sens. Environ. 2021, 261, 112480. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Aleissaee, A.A.; Kumar, A.; Anwer, R.M.; Khan, S.; Cholakkal, H.; Xia, G.S.; Khan, F.S. Transformers in remote sensing: A survey. Remote Sens. 2023, 15, 1860. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. CCNet: Criss-Cross Attention for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 6896–6908. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Lyu, X.; Gao, H.; Tong, Y.; Cai, S.; Li, S.; Liu, D. Dual attention deep fusion semantic segmentation networks of large-scale satellite remote-sensing images. Int. J. Remote Sens. 2021, 42, 3583–3610. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Zhang, C.; Duan, C.; Su, J.; Wang, L.; Atkinson, P.M. Multiattention network for semantic segmentation of fine-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Xia, R.; Lyu, X.; Gao, H.; Tong, Y. Hybridizing Cross-Level Contextual and Attentive Representations for Remote Sensing Imagery Semantic Segmentation. Remote Sens. 2021, 13, 2986. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Chen, Z.; Zhang, K.; Xia, R. Attentively Learning Edge Distributions for Semantic Segmentation of Remote Sensing Imagery. Remote Sens. 2022, 14, 102. [Google Scholar] [CrossRef]
- Ding, L.; Tang, H.; Bruzzone, L. LANet: Local attention embedding to improve the semantic segmentation of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 426–435. [Google Scholar] [CrossRef]
- Jin, J.; Zhou, W.; Yang, R.; Ye, L.; Yu, L. Edge detection guide network for semantic segmentation of remote-sensing images. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L. Artificial intelligence for remote sensing data analysis: A review of challenges and opportunities. IEEE Geosci. Remote Sens. Mag. 2022, 10, 270–294. [Google Scholar] [CrossRef]
- Richards, J.A.; Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 2022; Volume 5. [Google Scholar]
- Pastorino, M.; Moser, G.; Serpico, S.B.; Zerubia, J. Semantic segmentation of remote-sensing images through fully convolutional neural networks and hierarchical probabilistic graphical models. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Tao, C.; Meng, Y.; Li, J.; Yang, B.; Hu, F.; Li, Y.; Cui, C.; Zhang, W. MSNet: Multispectral semantic segmentation network for remote sensing images. GIScience Remote Sens. 2022, 59, 1177–1198. [Google Scholar] [CrossRef]
- Yin, P.; Zhang, D.; Han, W.; Li, J.; Cheng, J. High-Resolution Remote Sensing Image Semantic Segmentation via Multiscale Context and Linear Self-Attention. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9174–9185. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Zhang, A.; Liu, Y. Semantic Segmentation of Hyperspectral Remote Sensing Images Based on PSE-UNet Model. Sensors 2022, 22, 9678. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Liu, Y.; Li, M.; Huang, H.; Zheng, X.; Guan, L. DCCaps-UNet: A U-Shaped Hyperspectral Semantic Segmentation Model Based on the Depthwise Separable and Conditional Convolution Capsule Network. Remote Sens. 2023, 15, 3177. [Google Scholar] [CrossRef]
- Liu, R.; Tao, F.; Liu, X.; Na, J.; Leng, H.; Wu, J.; Zhou, T. RAANet: A residual ASPP with attention framework for semantic segmentation of high-resolution remote sensing images. Remote Sens. 2022, 14, 3109. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, W.; Zhang, Y.; Wang, W.; Zhao, Q.; Wang, C. Transformer and CNN hybrid deep neural network for semantic segmentation of very-high-resolution remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–20. [Google Scholar] [CrossRef]
- Li, R.; Wang, L.; Zhang, C.; Duan, C.; Zheng, S. A2-FPN for semantic segmentation of fine-resolution remotely sensed images. Int. J. Remote Sens. 2022, 43, 1131–1155. [Google Scholar] [CrossRef]
- Sun, L.; Cheng, S.; Zheng, Y.; Wu, Z.; Zhang, J. SPANet: Successive pooling attention network for semantic segmentation of remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4045–4057. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Liu, F.; Lyu, X.; Tong, Y.; Xu, Z.; Zhou, J. A Synergistical Attention Model for Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Long, W.; Zhang, Y.; Cui, Z.; Xu, Y.; Zhang, X. Threshold Attention Network for Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Gueguen, L.; Sergeev, A.; Kadlec, B.; Liu, R.; Yosinski, J. Faster neural networks straight from jpeg. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 3–8 December 2018; pp. 3933–3944. [Google Scholar]
- Ehrlich, M.; Davis, L.S. Deep residual learning in the jpeg transform domain. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3483–3492. [Google Scholar]
- Xu, K.; Qin, M.; Sun, F.; Wang, Y.; Chen, Y.K.; Ren, F. Learning in the frequency domain. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1740–1749. [Google Scholar]
- Qin, Z.; Zhang, P.; Wu, F.; Li, X. Fcanet: Frequency channel attention networks. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 763–772. [Google Scholar]
- Wang, J.; Zheng, Z.; Ma, A.; Lu, X.; Zhong, Y. LoveDA: A remote sensing land-cover dataset for domain adaptive semantic segmentation. arXiv 2021, arXiv:2110.08733. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention (MCCAI), Munich, Germany, 5–9 October 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional block attention module. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Li, H.; Qiu, K.; Chen, L.; Mei, X.; Hong, L.; Tao, C. SCAttNet: Semantic Segmentation Network with Spatial and Channel Attention Mechanism for High-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2021, 18, 905–909. [Google Scholar] [CrossRef]



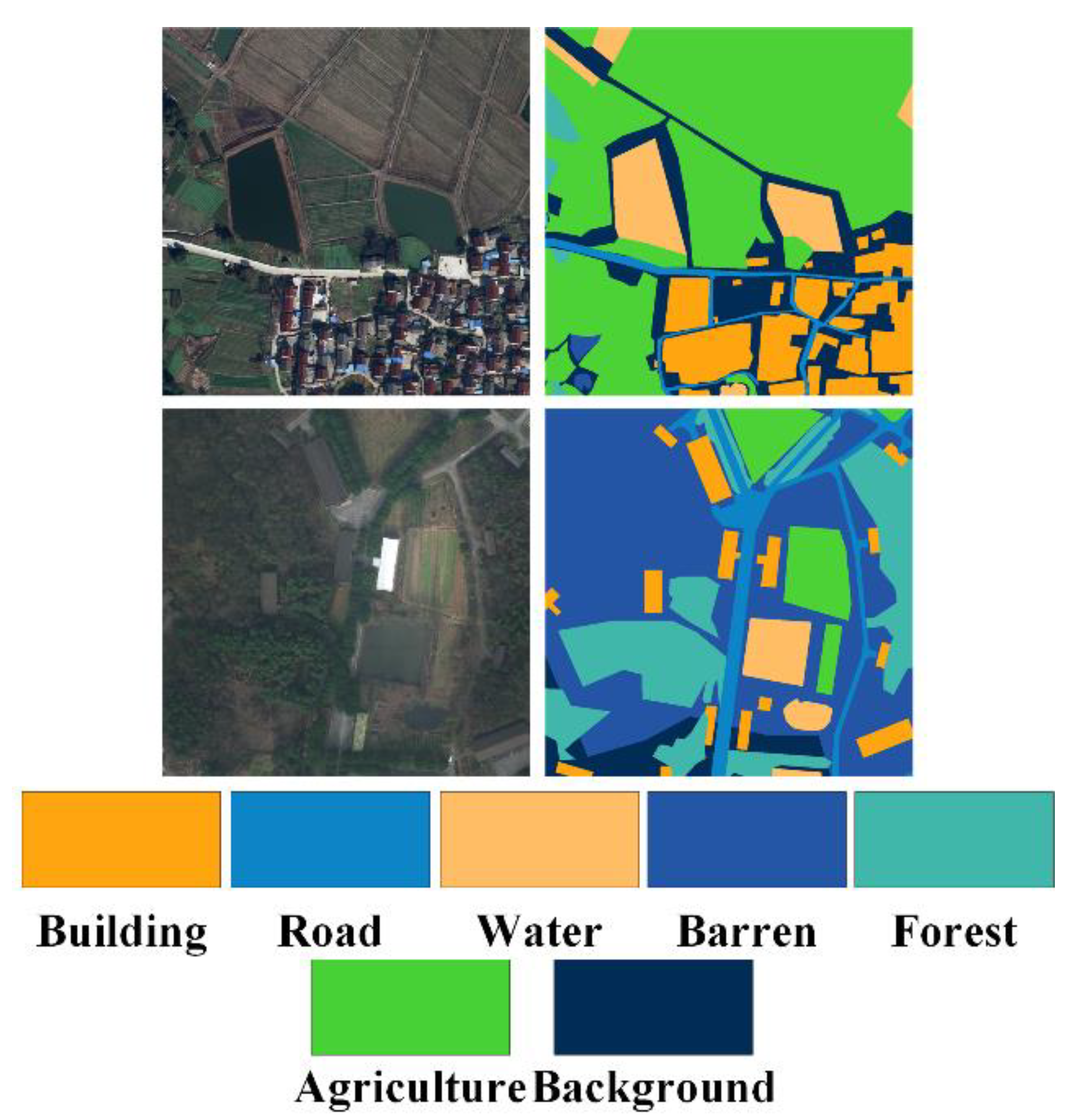


| Items | ISPRS Potsdam | LoveDA |
|---|---|---|
| Bands used | R, G, NIR | R, G, B |
| Spatial resolution | 5 cm | 0.3 m |
| Number of available images | 38 | 4191 |
| Spatial size | 6000 × 6000 | 1024 × 1024 |
| Imaging sensors | Airborne | Satellite |
| Sub-patch size | 256 × 256 | 256 × 256 |
| Training set (number of images) | 17 | 1677 |
| Validation set (number of images) | 2 | 419 |
| Test set (number of images) | 19 | 2095 |
| Test set (number of images) | Rotate 90, 180, and 270 degrees; horizontally and vertically flip | |
| Items | Settings |
|---|---|
| Learning strategy | ResNet 50 |
| Initial learning rate | 0.02 |
| Loss function for comparative methods | Cross-entropy |
| Max epoch | 500 |
| GPU memory | 48 GB |
| Batch size | 32 |
| Methods | Impervious Surfaces | Building | Low Vegetation | Tree | Car | AF | OA | mIoU |
|---|---|---|---|---|---|---|---|---|
| U-Net [57] | 86.92 | 88.71 | 73.48 | 86.43 | 47.86 | 76.68 | 75.31 | 69.54 |
| DeepLabV3+ [58] | 83.91 | 85.54 | 76.84 | 76.84 | 84.88 | 81.61 | 80.27 | 73.09 |
| CBAM [59] | 86.36 | 91.41 | 79.59 | 79.40 | 88.75 | 85.10 | 83.42 | 76.60 |
| ResUNet-a [43] | 91.35 | 96.35 | 84.75 | 86.55 | 92.25 | 90.25 | 88.55 | 80.37 |
| RAANet [46] | 89.89 | 95.16 | 86.70 | 81.33 | 77.16 | 86.05 | 84.73 | 77.51 |
| SCAttNet [60] | 88.66 | 92.23 | 86.30 | 82.55 | 78.80 | 85.71 | 85.41 | 77.55 |
| HCANet [34] | 92.35 | 96.35 | 86.75 | 87.65 | 93.35 | 91.29 | 90.15 | 81.45 |
| A2FPN [48] | 89.24 | 94.18 | 84.19 | 84.09 | 90.10 | 88.36 | 86.86 | 79.40 |
| LANet [36] | 91.88 | 95.83 | 86.33 | 87.27 | 92.91 | 90.84 | 89.75 | 80.73 |
| SSCNet (ours) | 93.19 | 97.16 | 89.50 | 91.41 | 93.26 | 92.90 | 91.03 | 82.55 |
| Methods | Background | Building | Road | Water | Barren | Forest | Agriculture | AF | OA | mIoU |
|---|---|---|---|---|---|---|---|---|---|---|
| U-Net [57] | 49.99 | 54.50 | 56.14 | 76.79 | 18.01 | 48.72 | 65.76 | 52.84 | 51.59 | 47.63 |
| DeepLabV3+ [58] | 52.06 | 54.75 | 56.91 | 77.62 | 16.04 | 47.97 | 67.50 | 53.27 | 52.07 | 47.41 |
| CBAM [59] | 54.23 | 60.76 | 63.10 | 78.83 | 26.51 | 52.05 | 69.72 | 57.89 | 54.41 | 49.96 |
| ResUNet-a [43] | 65.76 | 71.68 | 76.82 | 86.36 | 50.65 | 61.02 | 81.77 | 70.58 | 67.12 | 60.92 |
| RAANet [46] | 54.86 | 62.01 | 65.39 | 80.80 | 29.17 | 53.96 | 73.86 | 60.01 | 58.79 | 53.78 |
| SCAttNet [60] | 58.99 | 63.90 | 66.54 | 80.78 | 32.14 | 55.65 | 75.57 | 61.94 | 59.48 | 54.01 |
| HCANet [34] | 66.20 | 70.56 | 74.90 | 88.04 | 50.99 | 63.74 | 80.84 | 70.75 | 69.27 | 62.59 |
| A2FPN [48] | 65.66 | 71.57 | 76.71 | 86.24 | 50.57 | 60.93 | 81.65 | 70.47 | 67.02 | 60.83 |
| LANet [36] | 68.13 | 75.39 | 78.80 | 88.96 | 53.08 | 65.83 | 82.11 | 73.18 | 70.23 | 63.17 |
| SSCNet (ours) | 70.80 | 76.36 | 81.91 | 91.10 | 56.66 | 69.95 | 85.35 | 76.02 | 72.01 | 65.91 |
| Models | ISPRS Potsdam | LoveDA |
|---|---|---|
| SSCNet | 92.90/91.03/82.55 | 76.02/72.01/65.91 |
| SSCNet w/o SpeA | 87.92/87.62/79.55 | 62.65/60.16/54.62 |
| Values | ISPRS Potsdam | LoveDA |
|---|---|---|
| 87.92/87.62/79.55 | 62.65/60.16/54.62 | |
| 89.90/88.11/80.91 | 74.75/70.26/64.51 | |
| 92.90/91.03/82.55 | 76.02/72.01/65.91 | |
| 88.02/86.27/79.23 | 73.60/72.11/65.96 | |
| 84.02/83.73/76.02 | 59.14/56.79/51.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xu, F.; Yong, X.; Chen, D.; Xia, R.; Ye, B.; Gao, H.; Chen, Z.; Lyu, X. SSCNet: A Spectrum-Space Collaborative Network for Semantic Segmentation of Remote Sensing Images. Remote Sens. 2023, 15, 5610. https://doi.org/10.3390/rs15235610
Li X, Xu F, Yong X, Chen D, Xia R, Ye B, Gao H, Chen Z, Lyu X. SSCNet: A Spectrum-Space Collaborative Network for Semantic Segmentation of Remote Sensing Images. Remote Sensing. 2023; 15(23):5610. https://doi.org/10.3390/rs15235610
Chicago/Turabian StyleLi, Xin, Feng Xu, Xi Yong, Deqing Chen, Runliang Xia, Baoliu Ye, Hongmin Gao, Ziqi Chen, and Xin Lyu. 2023. "SSCNet: A Spectrum-Space Collaborative Network for Semantic Segmentation of Remote Sensing Images" Remote Sensing 15, no. 23: 5610. https://doi.org/10.3390/rs15235610
APA StyleLi, X., Xu, F., Yong, X., Chen, D., Xia, R., Ye, B., Gao, H., Chen, Z., & Lyu, X. (2023). SSCNet: A Spectrum-Space Collaborative Network for Semantic Segmentation of Remote Sensing Images. Remote Sensing, 15(23), 5610. https://doi.org/10.3390/rs15235610






