Polar Cloud Detection of FengYun-3D Medium Resolution Spectral Imager II Imagery Based on the Radiative Transfer Model
Abstract
:1. Introduction
2. Study Area and Data
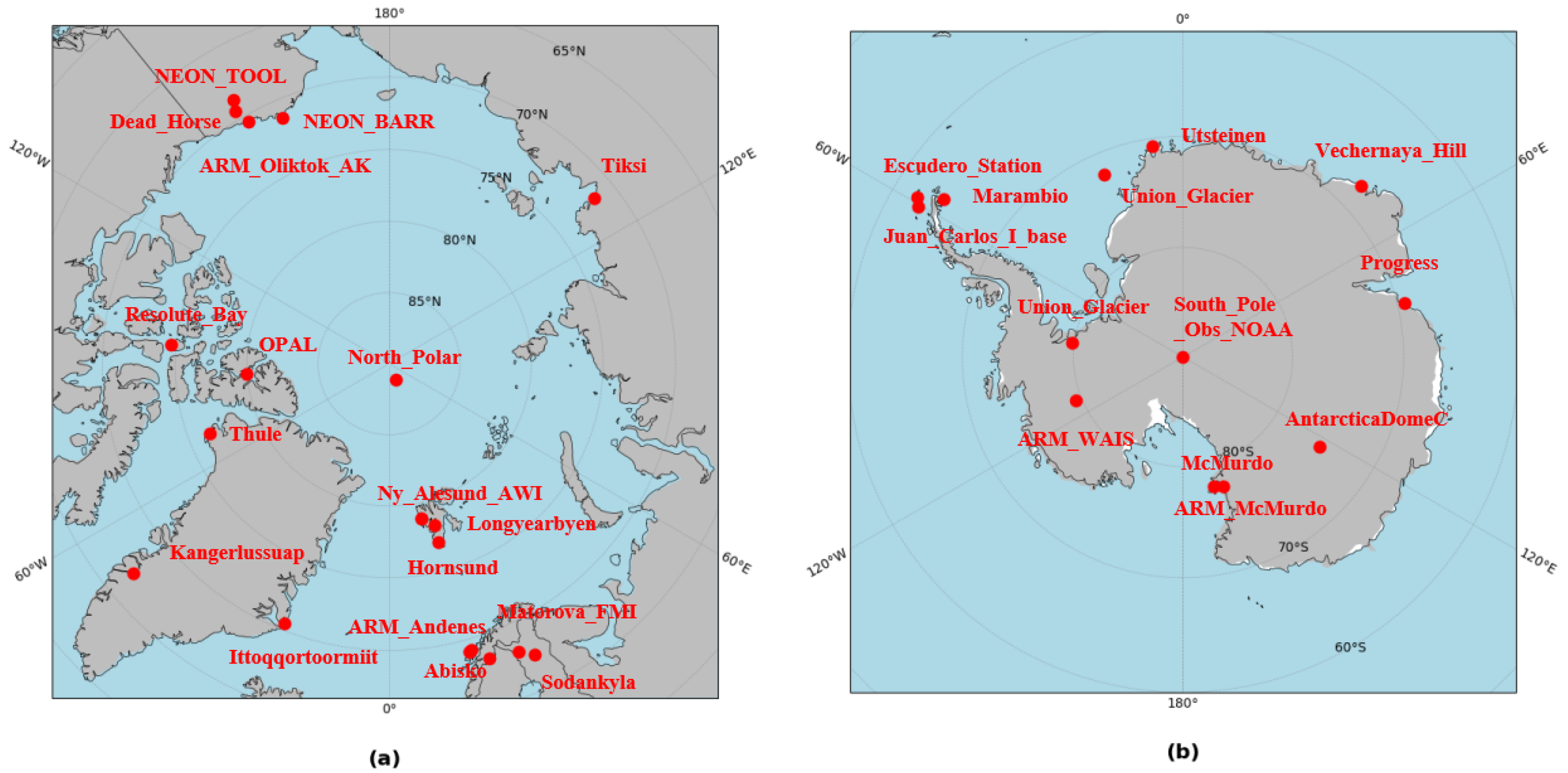
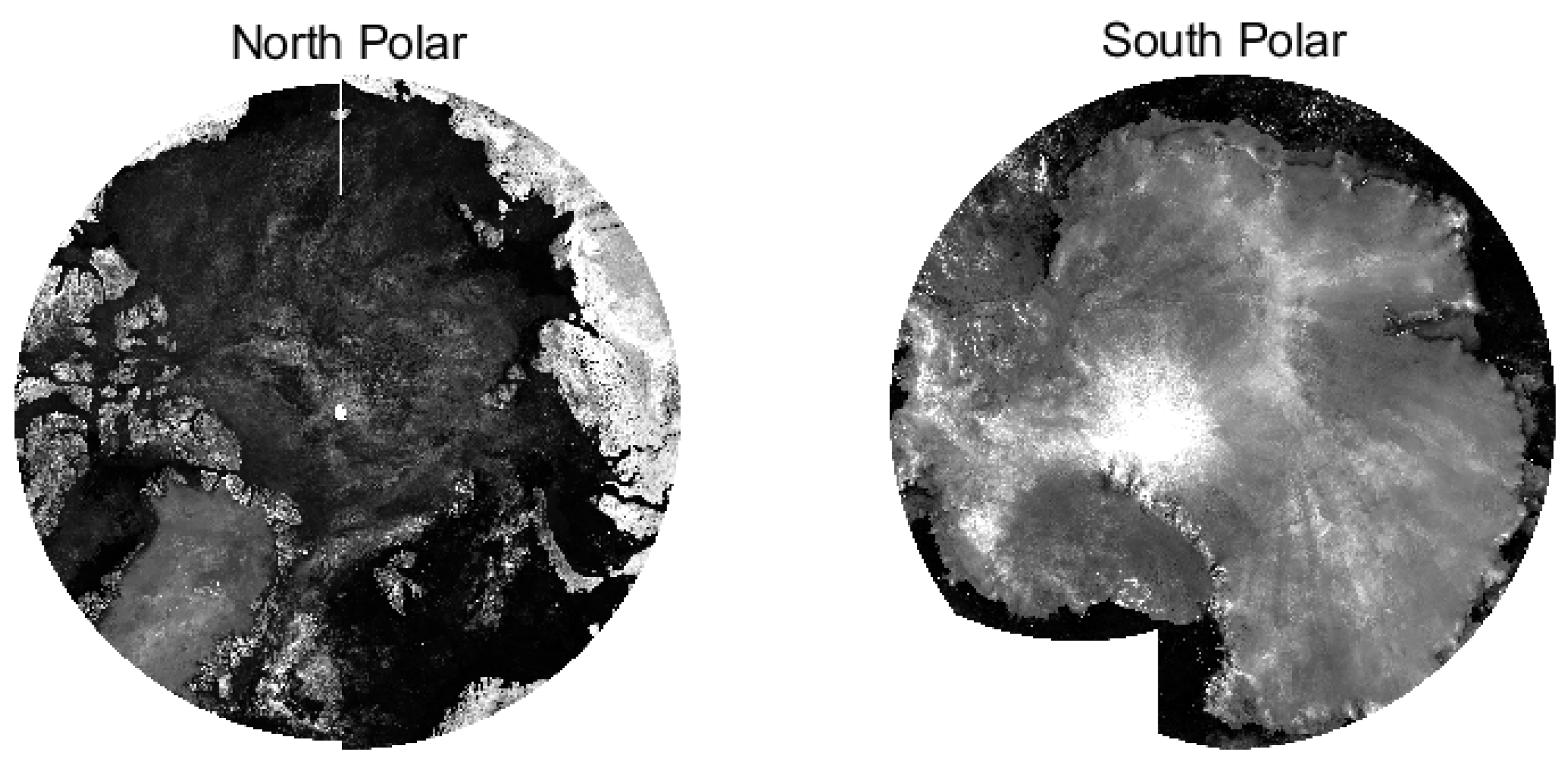
2.1. Study Area
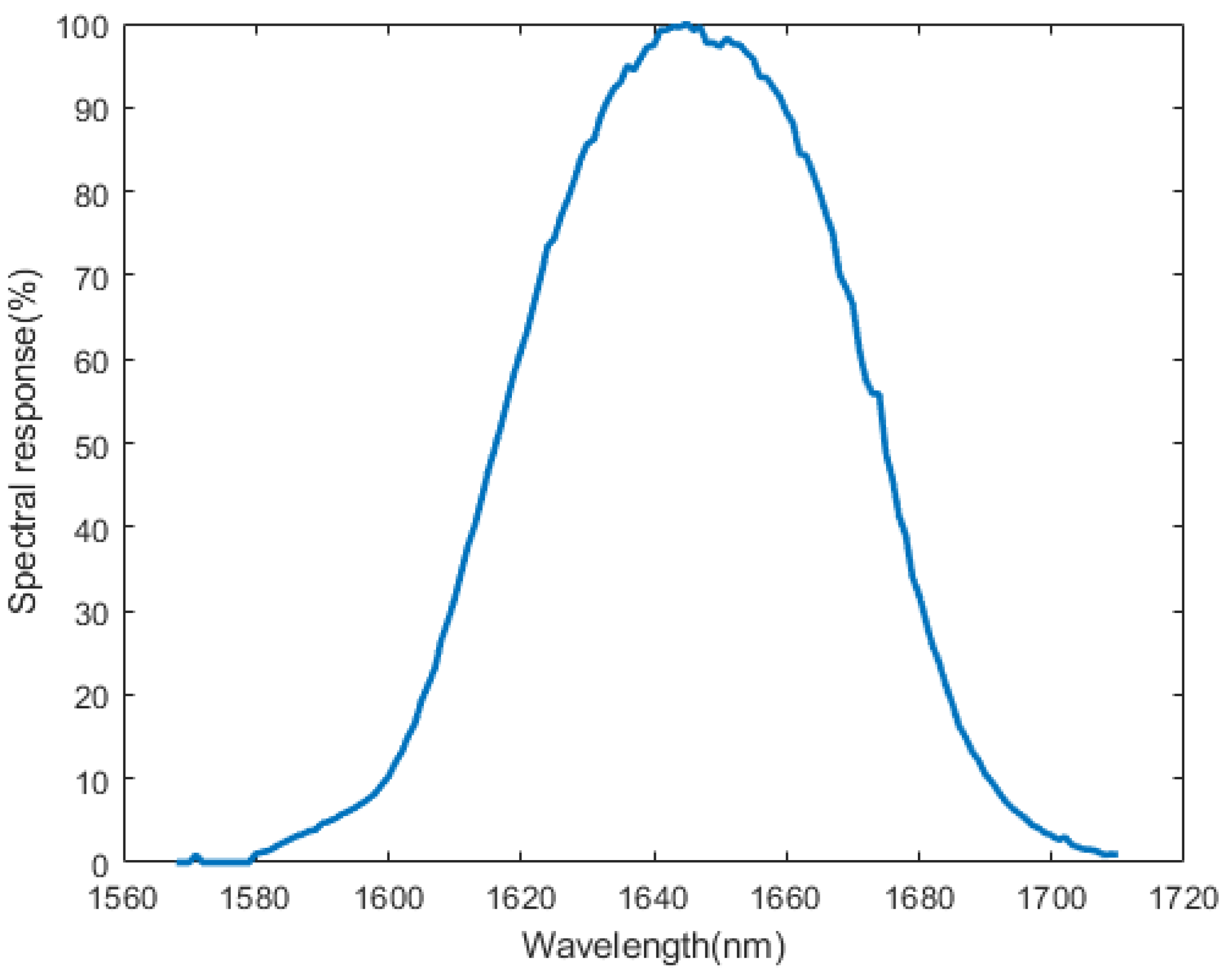
2.2. FY-3D MERSI-II Imagery
2.3. MODIS Surface Reflectance Products
2.4. MODIS Cloud Mask Products
2.5. Aerosol Robotic Network (AERONET)
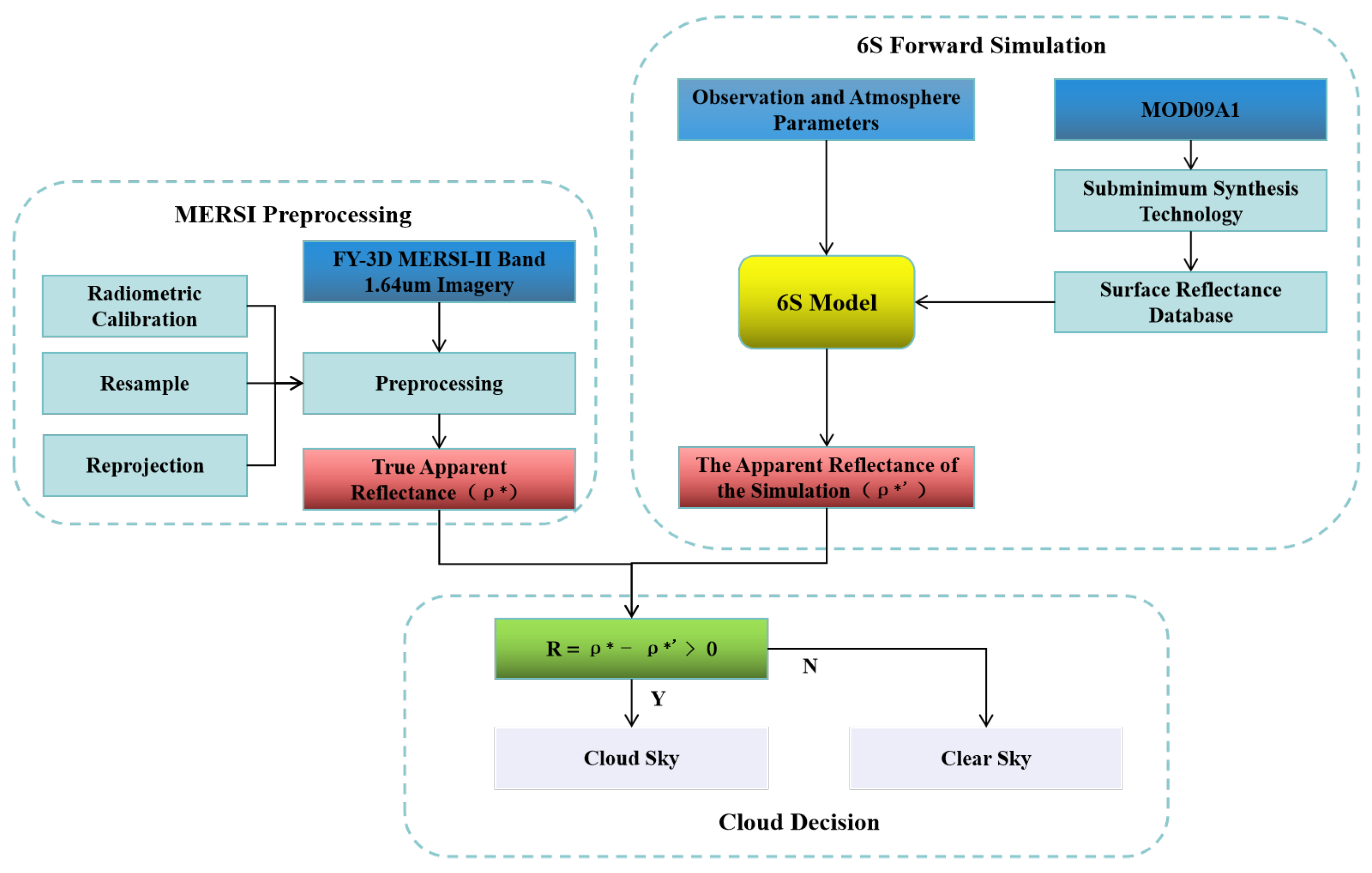
3. Methods
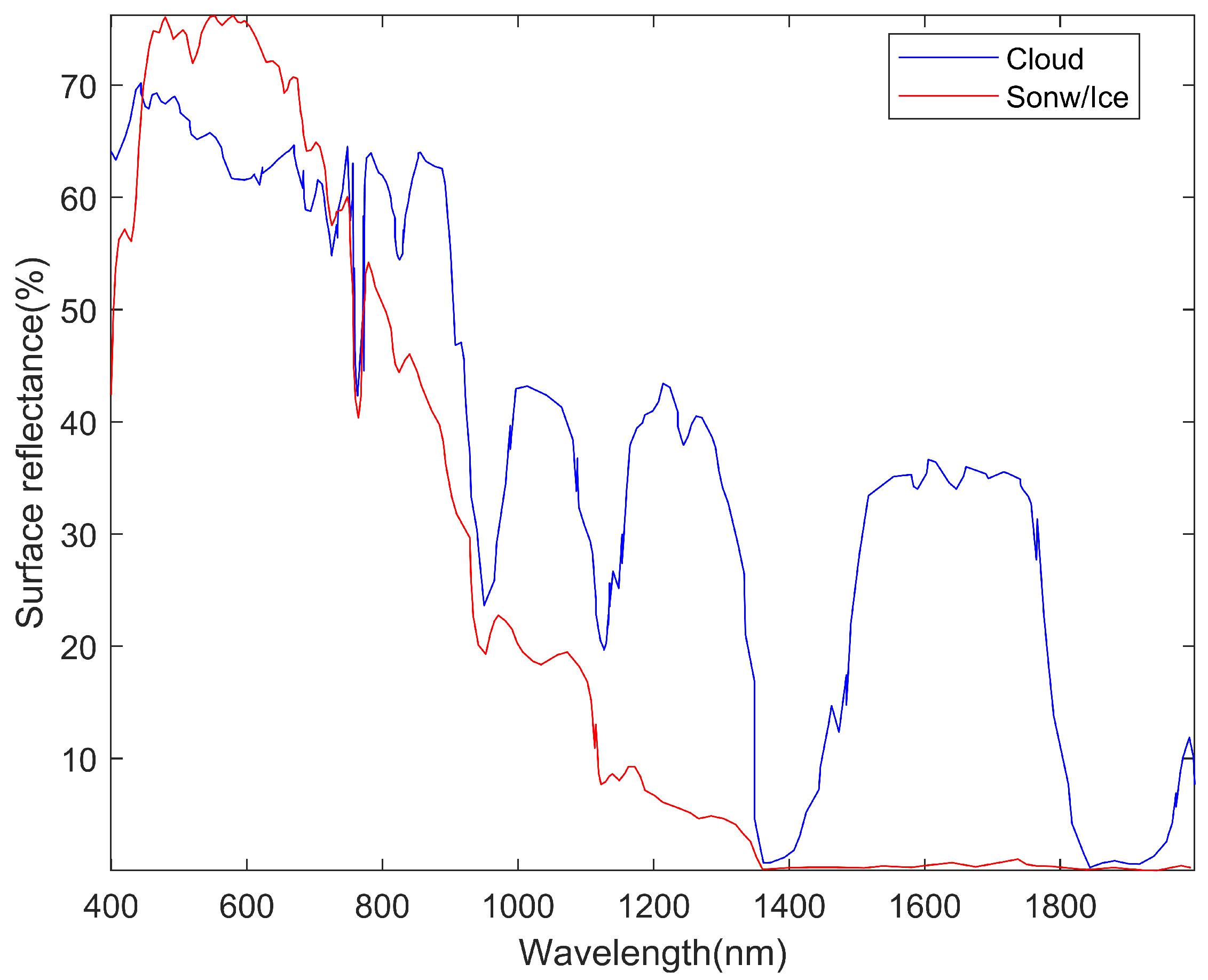
3.1. Theoretical Foundation
3.2. Construction of Polar Cloud Detection Model
3.2.1. Polar Surface Reflectance Database Construction
3.2.2. 6S Model Forward Simulation
3.2.3. Cloud Detection Model
3.2.4. Evaluation Methods
4. Results
4.1. Dataset and Experimental Setup
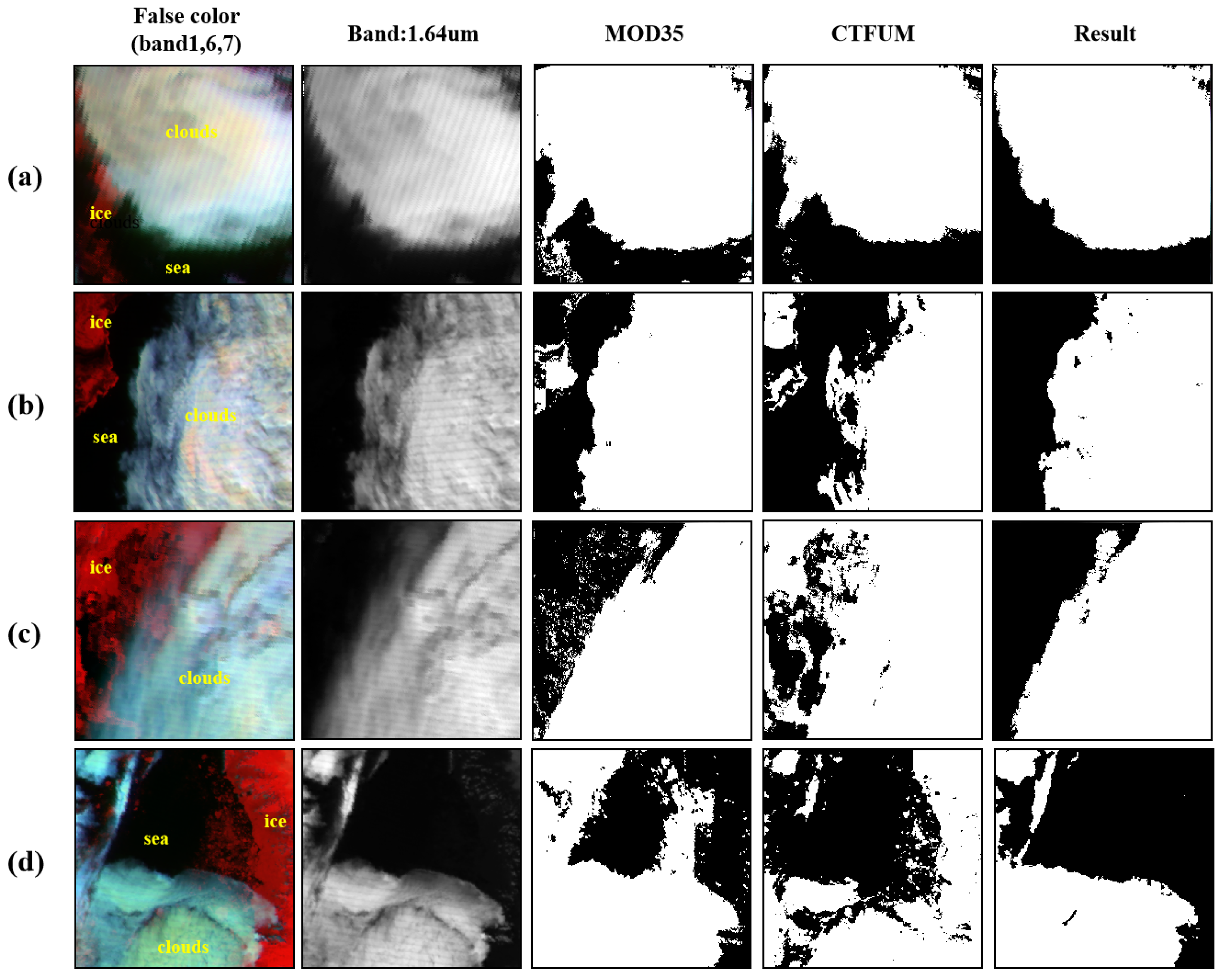
4.2. Comparative Analysis of Proposed Algorithm with Machine Learning Algorithms and MOD35
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahajan, S.; Fataniya, B. Cloud detection methodologies: Variants and development—A review. Complex Intell. Syst. 2020, 6, 251–261. [Google Scholar] [CrossRef]
- Zhang, Y.; Rossow, W.B.; Lacis, A.A.; Oinas, V.; Mishchenko, M.I. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Automated cloud, cloud shadow, and snow detection in multitemporal Landsat data: An algorithm designed specifically for monitoring land cover change. Remote Sens. Environ. 2014, 152, 217–234. [Google Scholar] [CrossRef]
- Zihan, L.; Yanlan, W. A review of cloud detection methods in remote sensing images. Remote Sens. Nat. Resour. 2017, 29, 6–7. [Google Scholar]
- Chandran, G.; Jojy, C. A survey of cloud detection techniques for satellite images. Int. Res. J. Eng. Technol. (IRJET) 2015, 2, 2485–2490. [Google Scholar]
- Li, Z.; Shen, H.; Weng, Q.; Zhang, Y.; Dou, P.; Zhang, L. Cloud and cloud shadow detection for optical satellite imagery: Features, algorithms, validation, and prospects. ISPRS J. Photogramm. Remote Sens. 2022, 188, 89–108. [Google Scholar] [CrossRef]
- Hughes, M.J.; Kennedy, R. High-quality cloud masking of Landsat 8 imagery using convolutional neural networks. Remote Sens. 2019, 11, 2591. [Google Scholar] [CrossRef]
- Zhan, Y.; Wang, J.; Shi, J.; Cheng, G.; Yao, L.; Sun, W. Distinguishing cloud and snow in satellite images via deep convolutional network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1785–1789. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J.; Wang, W.; Shi, Z. Cloud detection methods for remote sensing images: A survey. Chin. Space Sci. Technol. 2023, 43, 1. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Normalized-difference snow index (NDSI). In Encyclopedia of Snow, Ice and Glaciers; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Chen, G.; E, D. Support vector machines for cloud detection over ice-snow areas. Geo-Spat. Inf. Sci. 2007, 10, 117–120. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Bian, J.; Li, A.; Liu, Q.; Huang, C. Cloud and snow discrimination for CCD images of HJ-1A/B constellation based on spectral signature and spatio-temporal context. Remote Sens. 2016, 8, 31. [Google Scholar] [CrossRef]
- Screen, J.A.; Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 2010, 464, 1334–1337. [Google Scholar] [CrossRef] [PubMed]
- Zhu, A.J.; Hu, X.Q.; Lin, M.Y.; Jia, S.; Ma, Y. Global data acquisition methods and data distribution for FY-3D meteorological satellite. J. Mar. Meteorol. 2018, 38, 1–10. [Google Scholar]
- Vermote, E.; Vermeulen, A. Atmospheric correction algorithm: Spectral reflectances (MOD09). ATBD Version 1999, 4, 1–107. [Google Scholar]
- Roger, J.; Vermote, E.; Ray, J. MODIS Surface Reflectance User’s Guide; NASA: Washington, DC, USA, 2015. [Google Scholar]
- Chander, G.; Markham, B.L.; Barsi, J.A. Revised Landsat-5 thematic mapper radiometric calibration. IEEE Geosci. Remote Sens. Lett. 2007, 4, 490–494. [Google Scholar] [CrossRef]
- Ackerman, S.; Strabala, K.; Menzel, P.; Frey, R.; Moeller, C.; Gumley, L.; Baum, B.; Schaaf, C.; Riggs, G. Discriminating Clear-Sky from Clouds with MODIS: Algorithm Theoretical Basis Document (MOD35); University of Wisconsin-Madison: Madison, WI, USA, 2006. [Google Scholar]
- Remer, L.; Mattoo, S.; Levy, R.; Heidinger, A.; Pierce, R.; Chin, M. Retrieving aerosol in a cloudy environment: Aerosol product availability as a function of spatial resolution. Atmos. Meas. Tech. 2012, 5, 1823–1840. [Google Scholar] [CrossRef]
- Levy, R.; Mattoo, S.; Munchak, L.; Remer, L.; Sayer, A.; Patadia, F.; Hsu, N. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Hsieh, P.F.; Lee, L.C.; Chen, N.Y. Effect of spatial resolution on classification errors of pure and mixed pixels in remote sensing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2657–2663. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, F.J., Jr. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef] [PubMed]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Kang, X.; Gao, G.; Hao, Q.; Li, S. A coarse-to-fine method for cloud detection in remote sensing images. IEEE Geosci. Remote Sens. Lett. 2018, 16, 110–114. [Google Scholar] [CrossRef]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond accuracy, F-score and ROC: A family of discriminant measures for performance evaluation. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Hobart, Australia, 4–8 December 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1015–1021. [Google Scholar]
- Pang, S.; Sun, L.; Tian, Y.; Ma, Y.; Wei, J. Convolutional Neural Network-Driven Improvements in Global Cloud Detection for Landsat 8 and Transfer Learning on Sentinel-2 Imagery. Remote Sens. 2023, 15, 1706. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]




| Band | Central Wavelength (m) | Spatial Resolution (m) | SNR NET (K) | Dynamic Range |
|---|---|---|---|---|
| 1 | 0.470 | 250 | 100 | 90% |
| 2 | 0.550 | 250 | 100 | 90% |
| 3 | 0.650 | 250 | 100 | 90% |
| 4 | 0.865 | 250 | 100 | 90% |
| 5 | 1.38 | 1000 | 60/100 | 90% |
| 6 | 1.64 | 1000 | 200 | 90% |
| 7 | 2.13 | 1000 | 100 | 90% |
| 8 | 0.412 | 1000 | 300 | 30% |
| 9 | 0.443 | 1000 | 300 | 30% |
| 10 | 0.490 | 1000 | 300 | 30% |
| 11 | 0.555 | 1000 | 500 | 30% |
| 12 | 0.670 | 1000 | 500 | 30% |
| 13 | 0.709 | 1000 | 500 | 30% |
| 14 | 0.746 | 1000 | 500 | 30% |
| 15 | 0.865 | 1000 | 500 | 30% |
| 16 | 0.905 | 1000 | 200 | 100% |
| 17 | 0.936 | 1000 | 100 | 100% |
| 18 | 0.940 | 1000 | 200 | 100% |
| 19 | 1.03 | 1000 | 100 | 100% |
| 20 | 3.8 | 1000 | 0.25 K | 200–350 K |
| 21 | 4.050 | 1000 | 0.25 K | 200–380 K |
| 22 | 7.2 | 1000 | 0.30 K | 180–280 K |
| 23 | 8.550 | 1000 | 0.25 K | 180–300 K |
| 24 | 10.8 | 250 | 0.4 K | 180–330 K |
| 25 | 12.0 | 250 | 0.4 K | 180–330 K |
| Product ID | Product Name | Terra Prod ID | Terra Prod ID |
|---|---|---|---|
| Surface Reflectance 8-Day L3 Global 500 m | MOD09A1 | MYD09A1 | |
| Surface Reflectance 8-Day L3 Global 250 m | MOD09Q1 | MYD09Q1 | |
| MOD09 | Surface Reflectance Daily L2G Global 1 km and 500 m | MOD09GA | MYD09GA |
| Surface Reflectance Daily L2G Global 250 m | MOD09GQ | MYD09GQ | |
| Surface Reflectance Daily L3 Global 0.05Deg CMG | MOD09CMG | MYD09CMG |
| Band | Band Range (m) | SNR | Absolute Error | Relative Error (%) |
|---|---|---|---|---|
| 1 | 0.620–0.670 | 128 | 0.005 | 10–33 |
| 2 | 0.841–0.876 | 201 | 0.014 | 3–6 |
| 3 | 0.459–0.479 | 243 | 0.008 | 50–80 |
| 4 | 0.545–0.565 | 228 | 0.005 | 5–12 |
| 5 | 1.230–1.250 | 74 | 0.012 | 3–7 |
| 6 | 1.628–1.652 | 275 | 0.006 | 2–8 |
| 7 | 2.105–2.155 | 110 | 0.003 | 2–8 |
| Confusion Matrix | Predict | ||
|---|---|---|---|
| Positive | Negative | ||
| Real | Positive | TP | FN |
| Negative | FP | TN | |
| Figure | Date | Extents |
|---|---|---|
| Figure 8a | 18 July 2022 | (76°134.76N,67°018.27E)–(74°463.03N,78°926.48E) |
| Figure 8b | 25 June 2022 | (69°2955.69N,19°1537.65W)–(72°1656.96N,14°4734.53W) |
| Figure 8c | 2 August 2021 | (75°1857.67N,15°4858.67W)–(78°278.31N,6°3744.72W) |
| Figure 8d | 7 July 2022 | (69°2955.69N,19°1537.65W)–(72°1656.96N,14°4734.53W) |
| Figure 9a | 12 December 2020 | (76°5042.56S,132°3225.04E)–(76°919.45S,116°4054.09E) |
| Figure 9b | 25 November 2022 | (77°4013.89S,152°3259.73E)–(78°142.26S,134°3841.80E) |
| Figure 9c | 12 December 2021 | (85°424.77S,128°373.41E)–(83°2659.76S,93°1530.55E) |
| Figure 9d | 5 January 2021 | (80°275.82S,90°4235.74W)–(82°2340.10S,73°4613.62W) |
| Figure 10a | 26 December 2022 | (80°588.06S,144°493.99E)–(80°4849.85S,120°4634.46E) |
| Figure 10b | 9 January 2021 | (70°4243.70S,90°591.58W)–(73°3158.23S,80°1446.92W) |
| Figure 10c | 2 December 2020 | (83°5826.98S,117°4449.30E)–(81°5845.39S,90°4823.09E) |
| Figure | CAreal (%) | Cloud Product | CAproduct (%) | CAE (%) | Accuracy (%) | Precision (%) | Recall (%) | F1 (%) |
|---|---|---|---|---|---|---|---|---|
| Figure 8a | 74.62 | MOD35 | 77.91 | 3.29 | 93.13 | 91.21 | 99.96 | 95.39 |
| SVM | 77.15 | 2.53 | 88.69 | 85.37 | 99.96 | 92.09 | ||
| Result | 72.53 | −2.09 | 99.53 | 99.63 | 99.72 | 99.67 | ||
| Figure 8b | 71.44 | MOD35 | 73.63 | 2.19 | 95.67 | 94.14 | 99.98 | 96.97 |
| SVM | 73.62 | 2.18 | 95.68 | 94.14 | 99.98 | 96.97 | ||
| Result | 68.97 | −2.46 | 98.68 | 98.13 | 99.96 | 99.03 | ||
| Figure 8c | 74.60 | MOD35 | 72.05 | −2.55 | 95.15 | 94.42 | 98.79 | 96.56 |
| SVM | 72.04 | −2.56 | 95.15 | 94.42 | 98.80 | 96.56 | ||
| Result | 69.80 | −4.80 | 98.32 | 97.65 | 99.94 | 98.78 | ||
| Figure 8d | 45.08 | MOD35 | 61.41 | 16.33 | 84.94 | 75.63 | 99.80 | 86.05 |
| SVM | 54.78 | 9.7 | 84.10 | 78.73 | 91.04 | 84.44 | ||
| Result | 42.34 | −2.74 | 98.94 | 97.57 | 99.93 | 98.73 | ||
| Figure 9a | 72.98 | MOD35 | 28.49 | −44.48 | 62.41 | 99.20 | 43.07 | 60.06 |
| SVM | 58.01 | −14.97 | 60.83 | 69.52 | 65.24 | 67.31 | ||
| Result | 73.51 | 0.54 | 97.99 | 97.29 | 99.98 | 98.62 | ||
| Figure 9b | 57.38 | MOD35 | 10.12 | −47.26 | 48.07 | 98.64 | 16.16 | 27.78 |
| SVM | 79.66 | 22.28 | 66.84 | 72.12 | 83.99 | 77.60 | ||
| Result | 59.15 | 1.77 | 98.30 | 98.69 | 98.44 | 98.56 | ||
| Figure 9c | 75.42 | MOD35 | 81.91 | 6.49 | 82.23 | 80.86 | 96.93 | 88.17 |
| SVM | 69.11 | −6.31 | 84.67 | 87.90 | 89.72 | 88.80 | ||
| Result | 83.17 | 7.76 | 94.96 | 96.70 | 97.22 | 96.96 | ||
| Figure 9d | 48.53 | MOD35 | 5.19 | −43.34 | 26.83 | 88.48 | 5.94 | 11.14 |
| SVM | 46.02 | −2.51 | 86.44 | 84.31 | 85.95 | 85.12 | ||
| Result | 45.07 | −3.46 | 94.23 | 90.69 | 96.30 | 93.41 | ||
| Figure 10a | 54.49 | MOD35 | 20.74 | −33.75 | 36.32 | 99.44 | 24.50 | 39.31 |
| SVM | 42.81 | −11.68 | 73.85 | 84.27 | 65.02 | 73.40 | ||
| Result | 47.20 | −7.29 | 91.89 | 98.39 | 87.36 | 92.55 | ||
| Figure 10b | 92.78 | MOD35 | 11.66 | −81.12 | 23.68 | 98.62 | 13.12 | 23.16 |
| SVM | 54.70 | −38.08 | 59.94 | 99.40 | 57.78 | 73.08 | ||
| Result | 93.88 | 1.10 | 96.82 | 96.77 | 99.83 | 98.28 | ||
| Figure 10c | 70.80 | MOD35 | 7.01 | −63.78 | 24.01 | 98.77 | 8.36 | 15.42 |
| SVM | 44.54 | −26.26 | 66.05 | 77.75 | 59.03 | 67.71 | ||
| Result | 69.80 | −0.98 | 93.93 | 98.52 | 93.18 | 95.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Gong, C.; Hu, Y.; Zheng, F.; He, Z. Polar Cloud Detection of FengYun-3D Medium Resolution Spectral Imager II Imagery Based on the Radiative Transfer Model. Remote Sens. 2023, 15, 5221. https://doi.org/10.3390/rs15215221
Dong S, Gong C, Hu Y, Zheng F, He Z. Polar Cloud Detection of FengYun-3D Medium Resolution Spectral Imager II Imagery Based on the Radiative Transfer Model. Remote Sensing. 2023; 15(21):5221. https://doi.org/10.3390/rs15215221
Chicago/Turabian StyleDong, Shaojin, Cailan Gong, Yong Hu, Fuqiang Zheng, and Zhijie He. 2023. "Polar Cloud Detection of FengYun-3D Medium Resolution Spectral Imager II Imagery Based on the Radiative Transfer Model" Remote Sensing 15, no. 21: 5221. https://doi.org/10.3390/rs15215221
APA StyleDong, S., Gong, C., Hu, Y., Zheng, F., & He, Z. (2023). Polar Cloud Detection of FengYun-3D Medium Resolution Spectral Imager II Imagery Based on the Radiative Transfer Model. Remote Sensing, 15(21), 5221. https://doi.org/10.3390/rs15215221






