Abstract
The coming years will see the launch of several missions (TRISHNA, LSTM, SBG), which will acquire images in four or more spectral bands in thermal infrared (TIR) at high spatial resolution (~50–60 m) and with high temporal revisit (~2–3 days). The derivation of surface temperature and emissivity values from top-of-atmosphere radiances is not straightforward, as it is a non-deterministic process requiring additional information. In this paper, we propose the algorithm DirecTES to efficiently separate surface temperature and emissivity. This algorithm is based on the use of a comprehensive spectral database of emissivity, resulting in a well-posed deterministic problem while not assuming strong hypotheses. The algorithm can also benefit from non-TIR information, such as the acquisitions from the same satellite but in the visible and near-infrared domains, or exogenous data—land/sea mask or soil-occupation map. These would help identify the nature of the surface and therefore improve the temperature and emissivity retrievals. After the complete description of the method, we evaluate the performances of DirecTES on theoretical landscapes in TRISHNA’s context under a large range of atmospheric conditions. The retrievals of surface temperature reach RMSEs of 0.8 K over vegetation and 0.5 K over water, including both sensor and atmospheric uncertainties. We then evaluate DirecTES on ECOSTRESS images on sites where the ECOSTRESS Land Surface Temperature (LST) performance has been documented; DirecTES surface temperature retrievals are consistent with the ECOSTRESS LST product and the in-situ data.
1. Introduction
Land and sea surface temperature (LST and SST) have been identified by the Global Climate Observing System as two of the essential climate variables [1]. Surfaces temperature knowledge is essential to determine the Earth’s surface radiative budget [2]. In particular, in land surface energy balance models, LST is the key factor to estimate evapotranspiration, the largest water loss component of continental surfaces [3] and the most efficient way to dissipate energy from the surface. Surface temperatures are widely used for monitoring surfaces trends, inland water bodies, oceans and urban areas. Therefore, spatially distributed and continuous daily estimates of LST as a plot scale are needed. These requirements cannot be easily met by existing in-situ flux measurements, hence the need for remote sensing approaches to monitor LST over space and time.
The thermal infrared (TIR) domain (8–14 μm) is commonly used to assess LST, as the maximum radiometric emission for typical Earth surface temperatures (around 300 K) occurs in that specific window.
In the TIR, the radiation measured at the sensor level is composed of multiple terms coming from the surface, atmospheric emissions, and absorption. The surface-emitted radiation is a function of its temperature and emissivity. Land Surface Emissivity (LSE) is an intrinsic property of the surface and is defined as the ratio of the actual emitted radiation to the radiation emitted from a black body at the same thermodynamic temperature. For most natural Earth surfaces in the TIR domain and for a sensor with spatial scales < 100 m, the emissivity varies from ~0.7 to close to 1.0. The emissivity of vegetation, water, and ice cover are generally greater than 0.95 and spectrally flat in the 8–12 μm range [4]. The surface temperature varies with irradiation and local atmospheric conditions.
On its path to the satellite, the surface-emitted radiation gets attenuated by the atmosphere, which also emits radiation. Some of it directly reaches the sensor—the upwelling atmospheric intrinsic radiation—while some gets radiated downward to the surface and reflected back to the sensor: the reflected downwelling atmospheric radiation. The clear-sky at-sensor radiation can be written as three terms: the Earth-emitted radiation, described by Planck’s Law and weighted by the emissivity; the reflected downwelling radiation; and the upward atmospheric intrinsic radiation.
Even if the atmospheric properties (water vapor and air temperature) are well known and can be removed from the clear-sky at-sensor radiation equation, the problem of retrieving surface temperature and emissivity from multispectral measurements is still a non-deterministic process. Indeed, the total number of measurements available (N radiation in N spectral bands) is always lower than the number of variables to be solved for (N emissivity in N bands and one surface temperature). The temperature and emissivity problem is then solved using an additional constraint to retrieve the surface temperature and emissivity from remotely sensed acquisitions.
Among existing methods for LST retrieval [5,6], the empirical split window (SW) method derives surface temperature from measurements in two adjacent TIR channels, preferentially placed in the 10–12.5 μm interval. SW is based on the hypothesis that most natural surfaces have a flat emissivity spectrum in that TIR domain, which would imply that the brightness temperatures measured in the two selected channels are nearly equal. If a difference is measured between those brightness temperatures, it is fully attributed to atmospheric absorption. Therefore, the atmospheric effects can be directly corrected via an empirically determined formulation, which depends on both measured brightness temperatures. This approach is commonly used over oceans to compute the SST [7], as the emissivity of water is well known [8]. Several validation exercises reported accuracies better than 1 K, but it usually requires local information on surface conditions for emissivity effects [5]. The lack of such information can significantly enhance errors. A second commonly used method is the TES algorithm [9], which was initially developed by the ASTER Temperature Emissivity Working Group in order to efficiently tackle the issue of surface temperature/emissivity separation. The TES algorithm is a hybrid algorithm that capitalized on the strengths of previous algorithms; it is based on the hypothesis that over N ≥ 3 channels in the TIR domain, the TIR emissivity spectrum of a natural surface is composed of at least one value close to unity. Numerical simulation and some field validations have demonstrated that the TES can retrieve the LST to within about ±1.5 K, when the atmospheric effects are accurately corrected [9,10,11]. In different studies, the TES method shows significant errors in the LST, especially for surfaces with low spectral contrast emissivity (e.g., water, snow, vegetation) and under hot and wet atmospheric conditions [10,11,12,13,14,15].
The DirecTES algorithm, presented in this paper, relies on a spectral database of emissivity to add an additional equation and resulting in a well-posed deterministic problem. The principle is to calculate the LST corresponding to the radiation measured by the satellite for each pixel and for each material (or family of materials) of the emissivity spectral library. If the temperatures found for a given material in the N spectral bands are consistent within a given precision, the material is considered valid, and so is the corresponding LST.
After a complete description of the algorithm, this paper evaluates its performance in a theoretical study designed in the configuration of the upcoming TRISHNA mission. The algorithm is then applied to ECOSTRESS level 1 images in order to evaluate its potential to retrieve LST in a concrete and operational process.
2. DirecTES Algorithm Principle
The top-of-atmosphere (TOA) radiation reaching the satellite in the thermal infrared (TIR) can be written using the radiative transfer equation for each band k of a multi-spectral sensor:
with:
- : the TOA radiation reaching the satellite,
- : surface emissivity, which depends on the surface material,
- and are the downwelling and upwelling atmospheric radiations, respectively,
- : the upward atmospheric transmittance,
- : the emitted surface radiation, expressed as by the Planck’s Law, which depends on the surface temperature .
All terms of the equation above depend on the wavelength, as noted by the exponent k, which represents any spectral band k of a given sensor in the TIR.
The atmospheric variables , and can be calculated using a radiative transfer code such as MODTRAN [16] or RTTOV [17] using meteorological data—mainly vertical profiles of water vapor and temperature—available from the ECMWF ERA5, for example [18]. As mentioned above, the derivation of (1) for surface temperature and emissivity is not possible without additional information, as there are more unknowns than equations.
Our solution to this problem is to use brute force and to use a spectral library of emissions, for example from the ECOSTRESS spectral database [19].
For each material of the spectral library and each spectral band k of a given sensor, it is possible to “directly” derive the emitted surface radiation from (1):
and then derive the surface temperature by inverting Planck’s Law:
with:
- : Planck’s constant
- : Boltzmann’s constant
- : light speed in a vacuum
- : wavelength of the spectral band
For a given material of the spectral library, there are as many retrieved temperatures as there are sensor bands.
If these retrieved temperatures are not consistent with one another, it means that the selected material does not correspond with the material observed by the satellite, as the actual surface temperature obviously does not depend on the spectral band.
The consistency of the retrieved temperatures is estimated by comparing their span to a given threshold :
where and are the lower and upper quartile of temperatures for all spectral bands for the material .
If the spectral library is representative of all surface conditions—see the discussion about this topic later in the article—there is at least one material which fits the criterion of (4), which means the ensemble of potential surface materials is not empty:
The retrieved temperature is then expressed as the median value over all spectral bands and over all materials of :
The surface emissivity in each spectral band can then be calculated by reformulating (1):
The above algorithm principle is the basis for a sensor with spectral bands in only the thermal infrared or during nighttime. For missions such as TRISHNA, LSTM, SBG, Sentinel3 and others, which also have imaging capabilities in the visible, near-infrared and short-wave infrared (VNIR-SWIR), the identification of potential materials can be improved using this spectral information. The atmospheric corrections in the reflective range are of a different nature than those in the TIR and are not in the scope of this article, but have been described in the literature [20,21]. Assuming the surface reflections in a number of VNIR-SWIR spectral bands have been calculated prior to the application of DirecTES in the TIR, these values can be used to reduce the number of potential materials by replacing (5) to only consider the materials which are also consistent with the measured reflections in the VNIR-SWIR; for example, with the following criteria:
3. Application to TRISHNA
3.1. TRISHNA Mission
The TRISHNA mission (Thermal Infrared Imaging Satellite for High-Resolution Natural Resource Assessment) is a cooperation between the French (CNES) and Indian (ISRO) space agencies [22]. The chosen orbit has a cycle of 8 days at an altitude of 761 km, which allows a global coverage with a full resolution of 57 m at nadir over all continental land surfaces (including inland waters) and coastal waters. The large swath of +/−34° gives access to a revisit frequency of at least 3 acquisitions per 8-day period, depending on the latitude.
The spectral domain covers 11 bands from visible to thermal infrared, which are distributed over two instruments: the VNIR-SWIR Indian instrument and the TIR French instrument (Table 1). The four thermal infrared bands of the TIR instrument are used for emissivity and surface temperature retrieval and are candidates to be used in DirecTES.

Table 1.
TRISHNA spectral bands.
The VNIR-SWIR data will be processed to derive surface reflections. A candidate algorithm for this level 2 processing is MACCS-ATCOR Joint Algorithm—MAJA [20]. MAJA uses both multi-spectral and multi-temporal criteria to detect clouds and estimate aerosol contents—assuming that the land surface reflection changes more slowly than the atmospheric effects—and has been successfully applied to Sentinel2, Venμs or Landsat [23,24].
The performances of the TIR instrument were evaluated during the TRISHNA’s system preliminary design review (PDR), which was successfully held in June 2022 [25]. The relevant performance capacities for the evaluation of DirecTES in TRISHNA’s context are detailed hereafter. The total noise of the instrument, expressed in noise equivalent differential temperature (NEDT), is estimated as the linear sum of the temporal noise, caused by the detector chain, and the spatial noise, mostly caused by calibration and spectral response data uncertainties. The total noise is below 200 mK (TIR1&2) and 175 mK (TIR3&4) for all temperatures, which is below the goal specification (Figure 1).
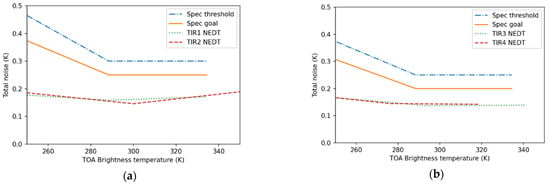
Figure 1.
Total noise equivalent differential temperature (NEDT) for TIR1&2 (a) and TIR3&4 (b) and comparison with the specifications, as a function of TOA brightness temperature.
The absolute radiometric accuracy (ARA) expresses the uncertainty of the instrument measurement over an ideal, uniform infinite scene when considering a large number of pixels; i.e., it is not affected by the temporal noise or non-uniformity within realistic earthly landscapes. Figure 2 shows the compliance with the goal ARA specification, with margin.
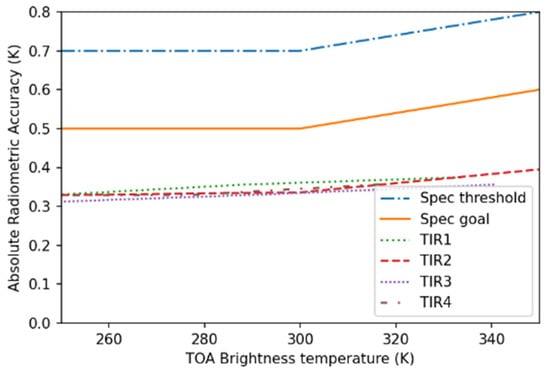
Figure 2.
Absolute radiometric accuracy (ARA) for all bands and comparison with the specifications, as a function of TOA brightness temperature.
The spectral knowledge of each pixel is estimated to be known with an uncertainty below 0.08% (specified at 0.1%). The spectral variability specification states that all pixels in the same spectral band shall measure the same radiation within 0.2%; the instrument is compliant with margin for TIR1 and TIR2 bands, and marginally compliant for TIR3 and TIR4, taking into account the pixel selection and the TDI summation.
The overall uncertainty over the radiation at level 1, which would affect any given pixel on a representative scene of the TRISHNA mission, has been evaluated over a set of representative landscapes and atmospheric conditions and is illustrated in Figure 3. At this level of the project, some posts have not been measured yet and are still allocations, often representative of worst-case scenarios. This uncertainty budget is therefore currently expected to be a worst-case scenario and will be reevaluated after full ground characterization in the coming years.
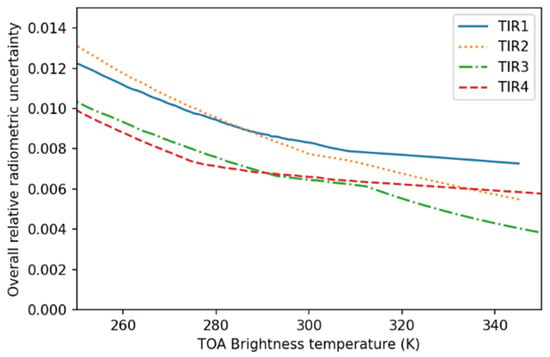
Figure 3.
Overall radiometric accuracy of a given pixel over representative scenes, expressed in relative to the TOA radiation for each TRISHNA band.
3.2. Spectral Library
The spectral library on which the algorithm is based is constituted by the association of three different datasets: 179 vegetation spectra, 6 water spectra, and 121 “urban” spectra. All these datasets cover both the TIR and VNIR-SWIR domains.
The vegetation spectra are based on the theoretical computation of 100,068 soil and vegetation spectra using the SAIL-Thermique model [26,27] with different types of soil, 11 spectra; and canopy, 22 leaf spectra; associated with distributions of leaf area index, leaf angle distributions, etc., and the reduction of the number of spectra down to 179 using a spectral angle mapper [28]. This dataset of vegetation over soil, representative of landscapes, pursues one of the core objectives of the mission (ecosystem stress, water resource management and agriculture) and is illustrated in Figure 4. This dataset will be referred as “SAIL179 Vegetation” throughout the document.
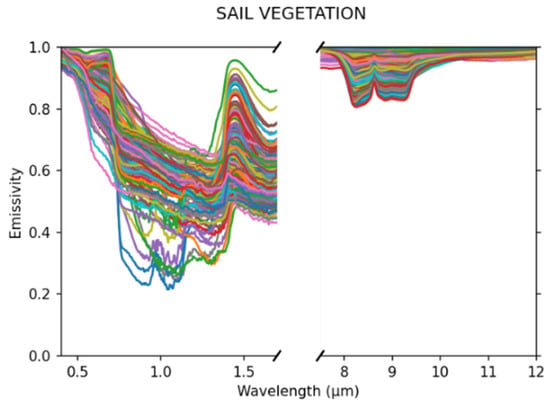
Figure 4.
VNIR-SWIR (left) and TIR (right) Emissivity of the SAIL179 vegetation database.
The water dataset consists in all the 6 water (liquid, snow, ice) spectra from ECOSTRESS database [19]. This dataset, illustrated in Figure 5, is representative of the landscapes pursued by of one of the core objectives of the mission (inland and coastal water), while the study of the cryosphere is a secondary objective of the mission. This dataset will be referred as “ECO6 Water” throughout the document.
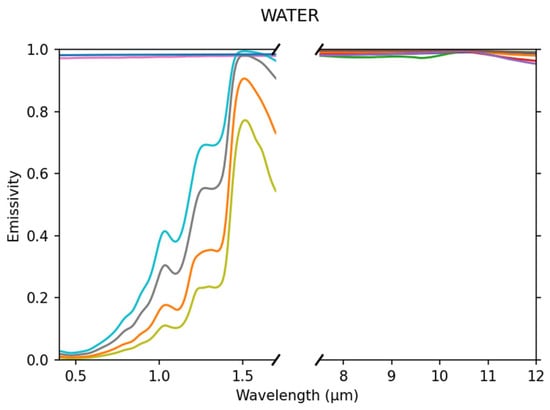
Figure 5.
VNIR-SWIR (left) and TIR (right) Emissivity of the ECO6 water database.
A significant area covered by the TRISHNA mission will be constituted by urban or semi-urban areas. These areas will be imaged by TRISHNA at a minimum resolution of 57 m, which means that there will be a mixture of several materials within one TRISHNA pixel most of the time. However, spectral libraries are usually constituted by spectra of pure materials, which will not be observed directly. The so-called “urban” dataset has been generated by combining all the spectra covering both VNIR-SWIR and TIR domains from the ECOSTRESS database [19] in the soil (41 spectra) and manmade (45 spectra) categories. The combination of all soil and surface spectra was performed, assuming a coverage percentage of the soil pixel with manmade material (20% and 50%) in order to be “representative” of the TRISHNA resolution. This yields 3690 spectra, which can be reduced using a spectral angle mapper and a 2° threshold down to 121 for computation purposes. These spectra constitute the “ECO121 Urban” dataset throughout the document (Figure 6). This dataset only addresses a secondary objective of the TRISHNA mission (urban areas), and there might be algorithms other than DirecTES to properly retrieve the land surface temperature over these areas [29,30]. Therefore, the performance of DirecTES for this dataset is only indicative.
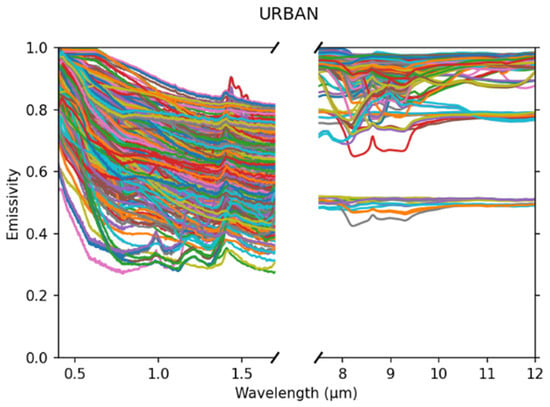
Figure 6.
VNIR-SWIR (left) and TIR (right) Emissivity of the ECO121 urban database.
4. DirecTES Theoretical Performance for TRISHNA
The evaluation of DirecTES performance can be done using end-to-end simulations (Figure 7). The simulations consist in the following steps:
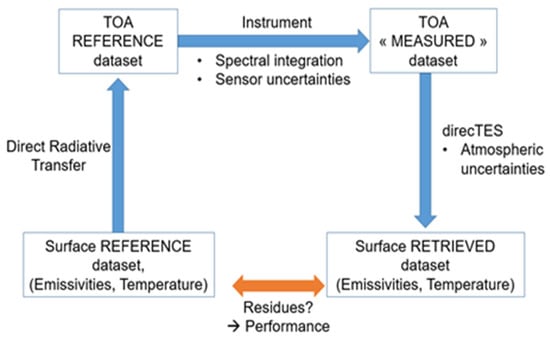
Figure 7.
Principle of end-to-end simulations to establish the theoretical performance of DirecTES.
- Suppose a surface reference dataset, i.e., temperature and emissivity in the TIR.
- This dataset is transposed to the top of the atmosphere using direct radiative transfer with representative atmospheric data, which yields a top-of-atmosphere (TOA) reference dataset.
- This TOA reference dataset is processed by an instrument module, which performs the spectral integration in TRISHNA bands and may apply an uncertainty, leading to a TOA dataset which is representative of the future TRISHNA measurements.
- DirecTES is applied on this TOA “measured” dataset to retrieve surface temperature and emissivity values.
The comparison of the reference and retrieved datasets at surface level and the analysis of its residuals provides the performance of DirecTES.
Throughout this section, the performances will be established on three ground datasets, which are the three spectral libraries presented in Section 3.2: SAIL179 (Vegetation), ECO6 (Water), and ECO121 (Urban). They will be considered separately to determine the performance of DirecTES on each of these typical landscapes. However, the DirecTES spectral library will always—unless specifically mentioned in Section 4.3.—contain the union of these three spectral libraries in order to be representative of operational conditions where the nature of each pixel is not known a priori.
The atmospheric conditions are derived from the TIGR database, which contains 2311 atmospheric profiles of gas content and temperatures, which are representative of the global atmospheric conditions [31]. A random selection of 75 spectra among the initial 2311 has been performed in order to reduce the number of simulations while trying to preserve the representativeness of the initial dataset in terms of atmospheric water vapor content (AWVC) and temperature distributions. This selection of profiles constitutes the TIGR75 database (Figure 8).
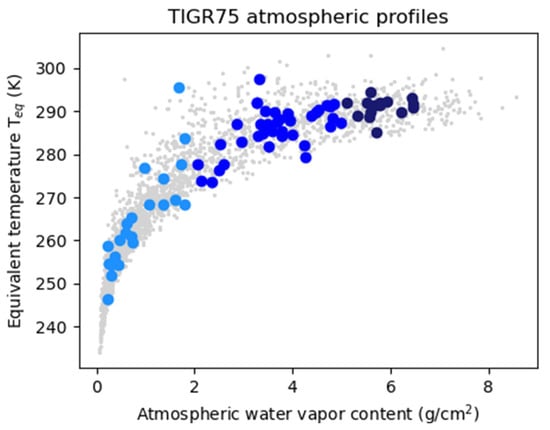
Figure 8.
Distribution in the equivalent temperature () and AWVC plan of the TIGR profiles. The grey dots show the original 2311 TIGR profiles, and the blue ones the 75 used in this study. The three shades of blue show water vapor contents in three different categories: AWVC < 2 g/cm2, 2 g/cm2 < AWVC < 5 g/cm2, and AWVC > 5 g/cm2.
The reference surface temperatures of the ground are different for each of the TIGR75 atmospheric profiles for the sake of consistency, and are chosen in relative to the lowest atmospheric level temperature for each profile :
Overall, for each ground dataset containing materials, the TOA reference dataset will therefore correspond to these materials, 5 different ground temperatures, and 75 atmospheric profiles, i.e., M × 75 × 5 simulations.
Finally, the performance of DirecTES will be tested in the presence of no additional uncertainty—this represents the intrinsic performance of the method, with sensor uncertainty only—applying an uncertainty as illustrated in Figure 3 in the instrument module, with atmospheric uncertainty only, or with the combination of both sensor and atmospheric uncertainties. For atmospheric uncertainty, we add to the atmospheric temperature a white Gaussian noise with a standard deviation of 0.8 K to each level of the atmospheric profile, as suggested by [32]. For ozone concentration and relative humidity, we add white Gaussian noise with standard deviations of 20% and 10%, respectively, as suggested by [33].
4.1. Performance with TIR Bands Only
Surface temperatures were retrieved with DirecTES for each element of the three different TOA reference datasets (vegetation, water and urban materials). The effect of instrumental and/or atmospheric sources of uncertainty was also assessed. Figure 9 shows the obtained biases (retrieved value minus reference value) as a function of DirecTES intrinsic parameter , and Figure 10 shows the obtained RMSE in the same cases.
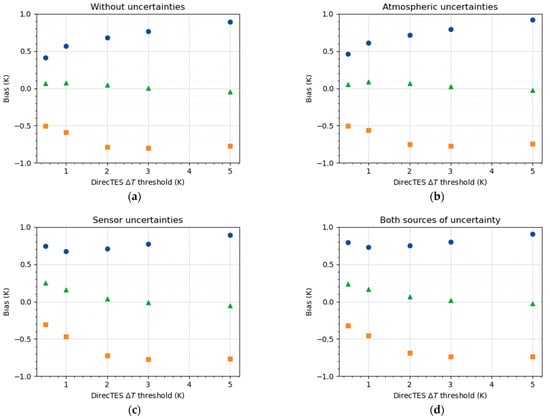
Figure 9.
Bias in DirecTES retrieved temperature as a function of DirecTES threshold , for each kind of material (green triangle: vegetation; blue dot: water; orange square: urban materials) in the presence of no uncertainty (a), atmospheric (b), sensor (c) and both sources of uncertainty (d).
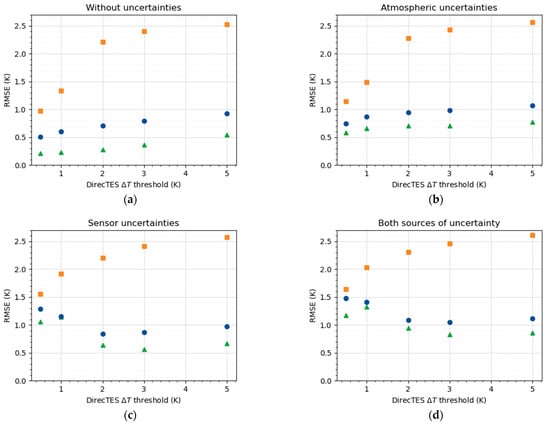
Figure 10.
RMSE in DirecTES retrieved temperature as a function of DirecTES threshold , for each kind of material (green triangle: vegetation; blue dot: water; orange square: urban materials) in the presence of no uncertainty (a), atmospheric (b), sensor (c) and both sources of uncertainty (d).
We note that even without uncertainty sources, temperature errors are generally not zero (Figure 9a and Figure 10a). These errors arise from the selection from the emissivity spectral library given as an input to DirecTES. For each pixel, emissivity spectra that are the most likely to lead to the measured radiations are selected for the rest of the algorithm (see Section 2 for more details). Generally, several emissivity spectra fit, and the associated temperatures vary accordingly, leading to the same measured radiations by design of the method. As a result, the median of all retrieved temperatures is not necessarily the exact temperature.
The temperature errors also come from the selection of . When is low, fewer spectra are selected for each pixel. This tends to lower the temperature errors when no uncertainty sources are added. When there are no sources of uncertainty, being almost equal to 0 (not shown here) leads to finding only the appropriate material for each case, then resulting in zero temperature error. However, this makes the inversion problem more sensitive to uncertainties—especially to sensor uncertainties in our case (Figure 9c and Figure 10c). A good compromise seems to be a high enough to avoid sensitivity to the uncertainties, yet not so high that it selects irrelevant emissivity spectra. In Figure 10d, we can see that a minimum in the RMSE is reached around a value of 3 K for water and vegetation, in the presence of both sources of uncertainty.
As stated above, a lower value leads to fewer spectra being selected for each pixel. Consequently, it is possible that no spectrum is selected, particularly in the presence of uncertainty sources. In this case, the algorithm cannot compute a temperature for the considered pixel without somehow releasing the constraint on . Figure 11 shows the percentage of pixels for which a temperature is retrieved by the algorithm with both uncertainty sources. As expected, this percentage increases with . For , it is around 99.8%, which makes this value a good compromise. For the remaining 0.2% cases where no temperature can be retrieved, an option may be to consider the material which has the smallest , even if it is greater than In the following sections, a value of is chosen. With this value, generating the synthetic image and running DirecTES on 75 atmospheric profiles multiplied by 25 combinations of sensor uncertainties takes 1′34″ for images made with SAIL179 (resp. 12.6″ for ECO6WATER and 1′03″ for ECO121URBAN), using 9 CPU.
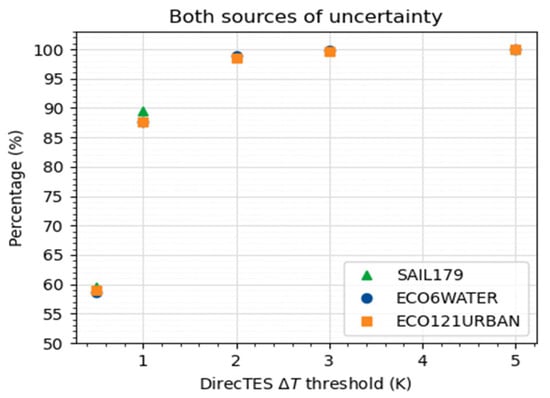
Figure 11.
Percentage of pixels for which a temperature is retrieved by DirecTES with both uncertainty sources.
Figure 9 and Figure 10 show different temperature error behaviors for each kind of tested material. It is particularly clear in Figure 9d, in the presence of both sources of uncertainty where vegetation materials have a low bias (~0.02 K), water materials have a high positive bias (~0.8 K) and urban materials have a high negative bias (~ −0.8 K). These behaviors are explained by the emissivity spectral library content. Water materials have a very high emissivity compared with the other materials. If lower emissivity spectra are also considered valid for DirecTES over water, their associated temperature will necessarily be higher to match the measured radiation, thus leading to an overestimated temperature. Similarly, urban materials have a lower emissivity than the other materials, leading to an underestimated temperature. This issue will be further discussed in Section 6.
The overall performance of the temperature retrievals using DirecTES with only TIR spectral bands is expressed in Figure 10d, in the presence of both sources of uncertainty and for , by the RMSE values of 0.82 K, 1.05 K, and 2.45 K for vegetation, water and urban landscapes, respectively (Figure 10d).
The TRISHNA’s implementation of the TES algorithm has also been evaluated over the same end-to-end simulation setup. The TES temperature retrievals show RMSE values of 1.02 K, 0.89 K, and 3.32 K for vegetation, water and urban landscapes, respectively.
In order to reduce the temperature errors and biases, one lever is the emissivity spectral library content and the selection of relevant spectra. The Section 4.2 aims at improving DirecTES accuracy for daytime images by selecting the emissivity spectra using VNIR-SWIR information.
4.2. Performance with Both TIR and VNIR-SWIR Bands
During daytime, TRISHNA will acquire VNIR-SWIR images simultaneously with TIR images. As explained earlier, TRISHNA VNIR-SWIR level 2 products (surface reflectance) will be available at level 2 with MAJA. Therefore, we can use this information to select relevant emissivity spectra from our library. The reflectance uncertainty corresponding to MAJA performances has been assessed on instrumented sites for Sentinel-2 and is around 0.01 to 0.02, depending on the studied VNIR-SWIR spectral band [24]. Hence, we add uniform random values between −0.02 and 0.02 to model reflectance uncertainty.
We consider only the case where atmospheric and instrument uncertainties are taken into account, as it is the most representative of a real case. To adapt the content of the emissivity spectral library, we compare the VNIR-SWIR component of these spectra with the reflectance in each pixel of the synthetic image and each considered VNIR-SWIR band, as in (8).
Figure 12 shows the bias, the RMSE, and the percentage of retrieved temperatures for different values of the reflectance threshold . The last points on the right of each plot represent the results without taking VNIR-SWIR into account, i.e., results from the Section 4.1. Apart from vegetation, which already had a low bias and RMSE, we observe a strong reduction of the bias and RMSE when decreases, together with a limited reduction of the number of retrieved temperatures. This is with the exception for , where too few emissivity spectra match the criterion, and the percentage of retrieved temperatures (not shown in the graph) are 40.04%, 29.92% and 34.01% for vegetation, water and urban materials, respectively. Note that a bias close to −0.1 K can be observed for a small value.
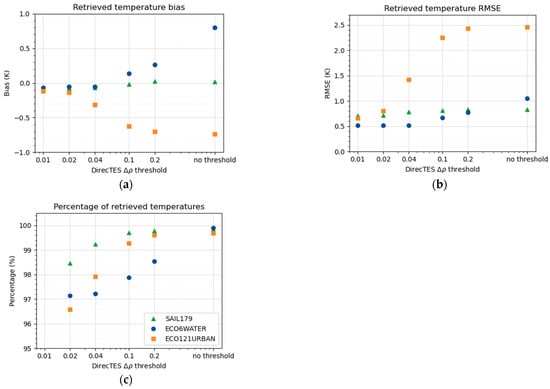
Figure 12.
Bias (a), RMSE (b) and retrieved percentage (c) obtained with DirecTES and , adding VNIR-SWIR information. These results are given as a function of the reflectance threshold to select emissivity spectra based on their VNIR-SWIR behavior.
In our case, values around 0.04 to 0.1 seem to be a good compromise, favoring lower temperature errors with a high percentage of retrieved materials. To maximize this, we will set to 0.1 in the following. This threshold seems relatively high compared to VNIR-SWIR retrieval uncertainties (~0.02, [24]) and therefore can be seen as a means for discriminating obvious misfits, which happens when using DirecTES with only TIR bands. As mentioned, the performance of DirecTES for vegetation when adding the VNIR-SWIR information does not change much—from an RMSE of 0.82 K to 0.8 K—as the performance with TIR-only bands was already good. The composition of our spectral library is indeed advantageous for vegetation, as it contains a lot of spectra from black-body-like materials (see Section 3.2). Since the majority of vegetation emissivity spectra are black-body-like, taking the median of the spectral library mechanically leads to adequate results for vegetation, even if some misfit materials might be present when using only TIR bands.
The improvement of DirecTES performance when adding VNIR-SWIR information is much more important for water (especially) and urban materials, with a bias from 0.8 K to 0.14 K and from −0.8 K to −0.52 K, respectively, and RMSEs from 1.05 K to 0.55 K and from 2.45 K to 2.25 K, respectively. This improvement comes with the cost of dealing with more information, and with and , generating the synthetic image and running DirecTES on 75 atmospheric profiles multiplied by 25 combinations of sensor uncertainties takes 2′01″ for images made with SAIL179 (resp. 18.9″ for ECO6WATER and 1′34″ for ECO121URBAN) using 9 CPU.
The results shown here for water are rather optimistic, as we only test 6 emissivity spectra from pure materials that are in the spectral library. For example, water turbidity could strongly affect the VNIR-SWIR reflectance while barely affecting the TIR emissivity [34]. In this case, pure water would be ruled out by information coming from VNIR-SWIR bands, although its TIR emissivity spectrum would be adapted to retrieve the temperature. To improve the results even more, it is possible to add any kind of information regarding the nature of the surface as shown in Section 4.3.
Figure 13 shows the bias, the RMSE, and the percentage of retrieved temperatures when using DirecTES with both TIR and VNIR-SWIR information, with and and as a function of atmospheric water vapor content for three different categories: dry (AWVC < 2 g/cm2), medium (2 g/cm2 < AWVC < 5 g/cm2) and humid atmospheric conditions (AWVC > 5 g/cm2). As seen in Figure 8, the AWVC correlates well with the atmospheric temperature: dry profiles correspond to cold ones, and humid profiles to warm ones. We can note that the evolution of the retrieved temperature bias is limited for vegetation and water within +/− 0.1 K for all atmospheric conditions (Figure 13a). Urban materials show more significant variations, as the atmospheric downwelling radiation plays a more important role for low emissivity materials. The retrieved temperature RMSE increases slightly between dry and medium AWVC for vegetation (+0.2 K) and water (+0.1 K), and more importantly between medium and humid conditions: + 0.6 K and 0.3 K for vegetation and water, respectively (Figure 13b). A similar behavior can be observed for the percentage of retrieved temperatures, which significantly decreases for very humid conditions (Figure 13c). This decrease of LST retrieval performance for high AWVC atmospheres was expected, as a higher AWVC implies a lower atmospheric transmission, which reduces the surface’s emitted radiation proportion with respect to the TOA signal. This has been observed in other studies [10,11,12,13,14,15]. Future improvements of the method could be to adapt the parameterization of the algorithm with regards to atmospheric conditions.
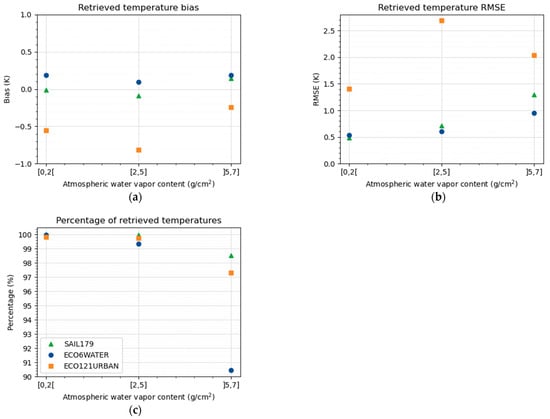
Figure 13.
Bias (a), RMSE (b), and retrieved percentage (c) obtained with DirecTES and , with VNIR-SWIR information. These results are given as a function of the atmospheric water vapor content in three categories: dry: AWVC < 2 g/cm2, medium: 2 g/cm2 < AWVC < 5 g/cm2, and humid: AWVC > 5 g/cm2.
4.3. Performance on Water Using Water Spectra
Aquatic environments and the cryosphere are essential components of the TRISHNA mission. To improve the results with these materials, it is possible to rely on water masks or surface knowledge that is generally available. In this case, the emissivity spectral library could be reduced to water spectra only.
A run with all 75 atmospheres, all 6 water materials, 5 tested temperatures, and sensor and atmospheric uncertainties yields the following results:
- Bias: −0.025 K
- RMSE: 0.55 K
- Percentage of retrieved temperatures: 98.0%
The absolute bias is lower than the one seen in the Section 4.2 with VNIR-SWIR (0.14 K with ), the RMSE is also reduced (0.65 K) and the percentage is equivalent (97.9%). DirecTES thus shows improved performance with a water mask. Moreover, computations are faster with a water-only spectral library. Generating the synthetic image and running DirecTES on 75 atmospheric profiles multiplied by 25 combinations of sensor uncertainties takes 10.5″ using 9 CPU (as a reminder, it was 12.9″ with TIR only, and 18.9″ with TIR and VNIR-SWIR).
Note that the RMSE value around 0.5 K mostly comes from atmospheric and instrument noise sources; indeed, a test with tap water only in both the synthetic image and in the emissivity spectral library leads to RMSE values of 0.047 K, 0.46 K, 0.30 K, and 0.57 K for no uncertainties, atmospheric uncertainties only, sensor uncertainties only, and both uncertainty sources, respectively.
4.4. Estimated Emissivity
Once a surface temperature is retrieved, it is possible to determine an equivalent emissivity value for each spectral band, thanks to TOA measurements in each band and available knowledge of atmospheric conditions (see (7)).
Note that for all sources of uncertainty—sensor and atmospheric noise and also errors in retrieved temperature—it is possible to obtain emissivity values which are not strictly in the interval. As a remedy, all values below 0 have been set to 0 and all values above 1 have been set to 1.
Other methodologies could be proposed to retrieve an emissivity value; for instance, a mean of all spectra of the emissivity spectral library that have been selected by the algorithm. This would avoid having values outside of the [0,1] interval. The advantage of the chosen method is that retrieved emissivity values are consistent with measured radiation and retrieved temperatures.
We have studied the three following cases:
- TIR bands only, sensor and atmospheric noise, , all materials in the emissivity spectral library;
- TIR and VNIR-SWIR bands, sensor and atmospheric noise, , , all materials in the emissivity spectral library;
- TIR bands and only water in the emissivity spectral library (water mask).
The obtained biases and RMSE are shown in Table 2.

Table 2.
Retrieved emissivity errors.
We observe that the retrieved emissivity values are lower for water (negative bias −0.027 for TIR only, to −0.0041 for TIR and water mask), which is in agreement with previous observations on positive temperature biases. A sensitivity analysis shows that a 1 K error in the retrieved temperature can lead to a several-hundredth error in the retrieved emissivity, which is what we have for all three kinds of materials with TIR only.
As expected from results regarding temperature retrievals, adding VNIR-SWIR information reduces the bias and the RMSE, especially for water (RMSE from 0.041 to 0.027). Adding a water mask also improves the results (bias from −0.0087 to −0.0041, with little impact on the RMSE). The emissivity retrieval performance of DirecTES using TIR and VNIR-SWIR bands give RMSE of 0.030, 0.027 and 0.064 for vegetation, water and urban datasets, respectively.
4.5. Discussion on the Spectral Library
The previous results have been obtained providing all emissivity spectra in the spectral library to the algorithm. This means that the tested materials in the synthetic scenes have (among other spectra) their exact emissivity spectrum tested to retrieve a temperature. Even though we have seen that, in the presence of uncertainty, it does not ensure retrieving a temperature (Figure 11, where the percentages of retrieved temperatures are strictly below 100%), this may produce optimistic results compared with real applications where the emissivity spectra of the different scene components are generally not known, and the spectral library might not be representative enough.
Moreover, even if some of our emissivity spectra are not pure materials (SAIL 179 Vegetation, ECO121 Urban as seen in Section 3.2), TRISHNA’s spatial resolution—57 m—implies that most scenes will be composites of several materials within a given pixel. As DirecTES intrinsic parameter is relatively high (3 K), it allows for the method to find a list of materials which are valid for DirecTES and are representative of these heterogeneous pixels. The representativeness of the spectral library against real data will be evaluated in Section 5 using ECOSTRESS images.
In the meantime, in order to assess the impact of using the same data in the spectral library and in the synthetic images, we ran several simulations of some of the previous cases with random divisions of the spectral library, such that materials in the synthetic images do not have their emissivity spectrum in the spectral library (pessimistic case). The synthetic scenes are composed of half the vegetation (89 spectra), half the water material (3 spectra) and half the urban materials (60 spectra), chosen randomly in 500 runs. For each run, the remaining spectra (154 spectra) compose the spectral library. Figure 14 shows the bias, RMSE, and retrieval percentage distributions for each kind of material when only TIR bands are used. The values obtained with all the 306 spectra in the spectral library are plotted with a dashed line (values obtained in Section 4.1). We observe that taking the whole library is very similar to what happens when dividing the set of emissivity spectra. The variations around this value for RMSE are of the order of 0.05 K for vegetation, 0.1 K for water, and 1 K for urban materials. As expected, the percentage of retrieved temperatures is generally lower, since the spectral library contains fewer emissivity spectra. However, it remains superior to 99% (96.5% for urban materials), which means that half the spectral library is representative enough to describe the other half, with the selection .
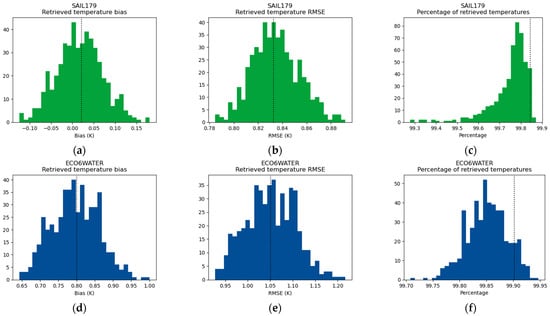
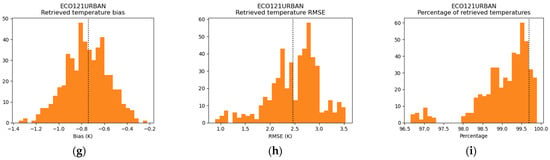
Figure 14.
Bias, RMSE, and retrieved percentage obtained with DirecTES and , with TIR information only, both sources of uncertainty, and 500 random divisions of the spectral library for vegetation (a–c), water (d–f) and urban materials (g–i). The dashed line represents the value obtained without dividing the spectral library.
Figure 15 shows the results obtained adding VNIR-SWIR information (as in Section 4.2) with . The bias obtained with the whole library is still quite representative of the results with the division of the library (with variations of a few tenths of a degree). Yet, we note that the percentage of retrieved temperatures is significantly lower with the divided library than with the whole library. This is particularly clear with water materials. Indeed, we have only six spectra for water materials, and adding VNIR-SWIR information rules out a lot of non-water material in the library. Consequently, since we have a smaller spectral library that does not contain the observed material, it is more likely that no temperature is retrieved. This means that half the spectral library is not rich enough to describe the other half when adding information for five other bands in order to discriminate materials, with selected and .
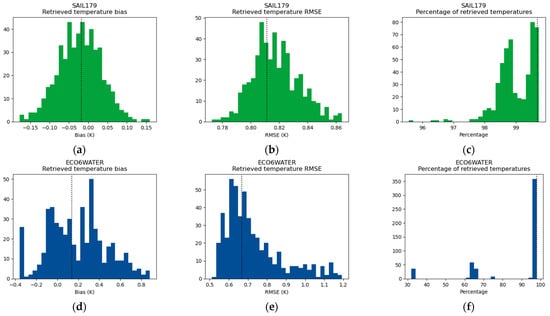
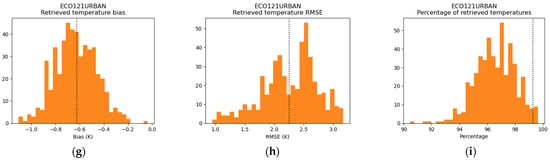
Figure 15.
Bias, RMSE, and retrieved percentage obtained with DirecTES, and with TIR and VNIR-SWIR information, both sources of uncertainty, and 500 random divisions of the spectral library for vegetation (a–c), water (d–f), and urban materials (g–i). The dashed line represents the value obtained without dividing the spectral library.
5. Application of DirecTES to ECOSTRESS Images
In addition to the theoretical analysis described in Section 4, DirecTES has also been tested on real TIR images from the ECOsystem Spaceborne Thermal Radiometer Experiment on Space Station (ECOSTRESS) mission. ECOSTRESS has been operating from the International Space Station (ISS) since July 2018 and has a multispectral whiskbroom scanner, originally possessing five spectral bands in the TIR centered on 8.29, 8.78, 9.20, 10.49, and 12.09 μm at 38 m × 69 m resolution [35]. Unfortunately, from May 2019, mass storage failures led to the elimination of the 8.29 and 9.2 μm channels to maximize the downlink capacity [35]. The temperature and emissivity separation can be performed with either five or the remaining three spectral bands, and its performance has been established in both cases on temperature-based or emissivity and radiation-based validation sites [36].
To evaluate the performance of DirecTES, we downloaded ECOSTRESS Level 1 products on five of these sites (Lake Tahoe, Russell Ranch, Gobabeb, Texas Grassland and Redwood Forest), associated with ERA5 atmospheric data from the Copernicus climate data store [37], which was then processed in the radiative transfer code MODTRAN6 [16]. DirecTES was applied to these data, and we compared the DirecTES-retrieved surface temperature with that from ECOSTRESS Level 2 products, which has itself been compared with in-situ data [36].
First, we estimated the theoretical performance using DirecTES for ECOSTRESS in the 3 or 5 spectral bands setup compared with TRISHNA (Section 4) using the same setup, spectral libraries, surface temperatures, atmospheric data and both sources of uncertainty, except for the sensor spectral configuration (Table 3). For the sake of comparison, we assumed the same sensor uncertainties for both TRISHNA and ECOSTRESS (Figure 3).

Table 3.
Comparison of DirecTES usage on ECOSTRESS (3 or 5 bands) or TRISHNA (4 bands) using the TIR information only and both atmospheric and sensor uncertainties.
We can see that the results are quite similar between TRISHNA and ECOSTRESS for the 5 spectral bands configuration, and that there is a significant decrease of performance when only using 3 bands, especially in terms of RMSE, as the mean bias is not really affected by the spectral configuration. This may be due to the fact that the sensor uncertainties are quite large (worst case scenario) and having only 3 bands, instead of 4 or 5, exacerbates their significance.
The dates of the ECOSTRESS acquisitions considered in this study and the sites and associated uncertainties (adapted from [36]) are detailed in Table 4. These dates have been chosen in order to have Sentinel2 acquisitions acquired at almost the same time as the ECOSTRESS acquisition (<100 min), in order to grant the possibility of using DirecTES with solely the ECOSTRESS TIR bands and also with the VNIR-SWIR information, derived from Sentinel2 L1C products processed to level 2 with MAJA [24]. Unfortunately, for these matchups, all ECOSTRESS images only contain the 3 distributed spectral bands (8.78, 10.49 and 12.09 μm), which are not ideal conditions for DirecTES, as shown in Table 3. All the ECOSTRESS scenes have been extracted to match the Sentinel2 tiles geometry, which produces images of ~1500 × 1500 pixels. Table 4 presents the ECOSTRESS LST bias (ECOSTRESS LST minus in-situ LST) documented by [36] on the 5 selected sites. Biases for DirecTES are calculated as the sum of the ECOSTRESS documented bias and the difference between DirecTES LST and ECOSTRESS LST, in order to represent the bias between DirecTES and the in-situ data. ECOSTRESS and DirecTES biases in Table 4 are then directly comparable.

Table 4.
Retrieved bias for L2 ECOSTRESS LST product and for DirecTES TIR and DirecTES TIR + VNIR-SWIR LST on the 5 selected sites. The documented ECOSTRESS bias has been adapted from [36].
Figure 16 accounts for the biases between ECOSTRESS and DirecTES retrieved LST over the 5 selected sites. Except for the specific site of Gobabeb, where the results are poor, DirecTES using TIR only shows good performances for LST retrievals, compared with the ECOSTRESS LST products. Moreover, biases are reduced below +/− 0.5 K for 12 over 19 acquisitions while using the VNIR-SWIR version of DirecTES.
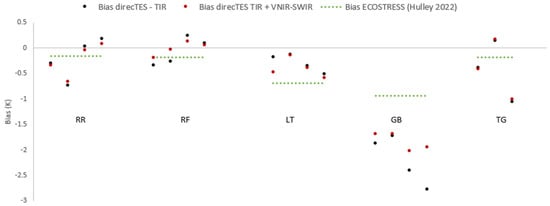
Figure 16.
Retrieved bias for L2 ECOSTRESS LST product [36] and for DirecTES TIR and DirecTES TIR + VNIR-SWIR LST on the 5 selected sites.
Table 5 and Figure 17 show the statistics of DirecTES retrievals compared to ECOSTRESS over the whole images (~1500 × 1500 pixels) containing the location where ECOSTRESS LST is evaluated [36]. As the validation results for ECOSTRESS over in-situ data revealed a cold bias for the retrieved LST, one can assume that a hot bias of DirecTES LST compared with ECOSTRESS is relevant for good LST estimations (while absolute bias stays lower than ECOSTRESS absolute bias).

Table 5.
Bias and RMSE of DirecTES LST retrievals compared with ECOSTRESS LST on the whole images containing the selected instrument sites.
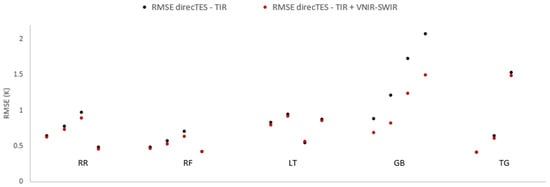
Figure 17.
RMSE between ECOSTRESS and DirecTES TIR and DirecTES TIR + VNIR-SWIR LST on the whole images containing the 5 selected sites.
RMSE obtained on ECOSTRESS data processed with DirecTES TIR only and DirecTES TIR + VNIR-SWIR are in the range of the uncertainties reported by [36], except for 3 images: GB_2020/07/13, GB_2020/10/01 and TG_2020/06/24 (Table 5, Figure 16). Adding VNIR-SWIR information in DirecTES reduces both RMSE and bias for Gobabeb, where the results are the poorest. For all other images, biases were reduced by 0.1 K at most, and RMSEs were reduced up to 0.6 K when adding VNIR-SWIR information.
Even if DirecTES LST are in quite good agreement with ECOSTRESS products, these results need to be put into perspective. On the one hand, the availability of only 3 ECOSTRESS bands is not ideal for DirecTES usage. We can then assume better retrievals in a more favorable setup using 4 bands in the TRISHNA case (Table 3). On the other hand, the critical point of the method lies in the constitution of the provided spectral library. The spectral library (constituted by the association of three different datasets: 179 vegetation spectra, 6 water spectra, and 121 “urban” spectra) provided to the algorithm was not efficiently calibrated in order to ensure good performances on bare soil or desert surfaces, which explains the poor results on Gobabeb. Moreover, the use of the urban spectral library, along with the vegetation and water libraries, on real images at the ECOSTRESS resolution is not relevant and leads to confusion between many materials. The constitution of a worst-case scenario in the theoretical analysis seems not to be adapted for practical usage, especially if the VNIR-SWIR component is not available. While using DirecTES with TIR bands only, many materials of the spectral library can lead to consistent retrieved temperatures within the given threshold = 3 K for each of the three spectral bands. As these materials could be very different, the retrieved temperatures could also be significantly different between one material and another. As illustrated by the outliers on Figure 18a, these multiple and different materials lead to a strong overestimation in the retrieved DirecTES temperatures, particularly due to the presence of low emissivity materials in the spectral library that fit the threshold criteria. Adding VNIR-SWIR information allows the algorithm to get rid of the obviously inconsistent materials, as illustrated on the scatter plot in Figure 18b. Nevertheless, using VNIR-SWIR information increases the computing time that goes from 32″ to process an image of 1570 × 1570 pixels with DirecTES TIR, to 45″ to process the same image of 1570 × 1570 pixels with DirecTES TIR + VNIR-SWIR using 48 CPU. An illustration of the retrieved direcTES LST compared to ECOSTRESS LST is shown on Figure 19.
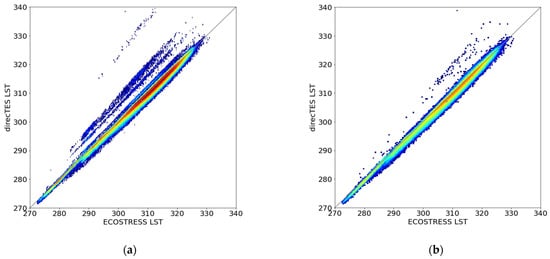
Figure 18.
Comparison of ECOSTRESS and DirecTES TIR (a) and DirecTES TIR + VNIR-SWIR (b) LST on whole image over Russell Ranch (9 June 2019). The black line is the identity curve.
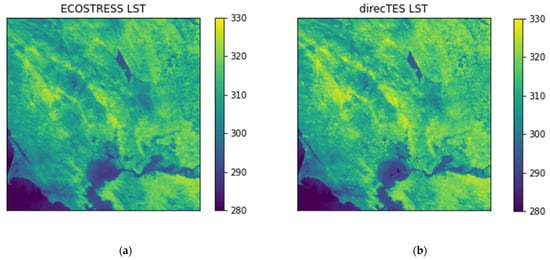
Figure 19.
Illustration of ECOSTRESS (a) and DirecTES TIR + VNIR-SWIR (b) LST maps over Russell Ranch (9 June 2019).
Finally, we compared the ECOSTRESS LSE with those retrieved using DirecTES with TIR and VNIR-SWIR spectral bands. Results are presented in Table 6 for each ECOSTRESS spectral band. The mean bias in emissivity is small for each site and spectral band, and is generally lower than 0.004 in absolute value, except for Gobabeb in bands 4 and 5. As mentioned above, the current spectral library is not sufficiently calibrated to ensure good performance on bare soil or desert surfaces, which explains the poor results on Gobabeb. The RMSEs are about 0.01 for all sites and spectral bands, which shows very good agreement between the ECOSTRESS LSE and those obtained with DirecTES. The differences between the two algorithms are significantly lower than the ones evaluated in the theoretical study (~0.03 for the TIR-VNIR-VSWIR configuration, Table 2).

Table 6.
Bias and RMSE of DirecTES TIR + VNIR-SWIR LSE retrievals compared with ECOSTRESS LSE on the whole images containing the selected instrument sites.
6. Discussion
We have seen in Section 4 that water materials have a high positive bias and urban materials a high negative bias, which is a consequence of their specific emissivity (high for water and low for urban materials) compared with the materials contained in the full spectral library. More importantly, it is in fact a consequence of the temperature–emissivity separation being underdetermined. Hot materials with low emissivity can be mistaken for cold materials with high emissivity. Figure 20 illustrates this effect when applying DirecTES on liquid water, without adding any source of uncertainty, and with . It shows all the emissivity spectra in the spectral library, positioned according to their equivalent TIR1 and TIR4 emissivity values. The tested liquid water spectrum is the black star. Each point is colored according to its associated span (see (4)), black points being the spectra for which , i.e., invalid ones. We observe that many spectra lead to a span smaller than 3 K, i.e., for each of these materials, there exists a temperature for which these materials would correspond to the measured radiations in the 4 TRISHNA spectral bands, even though the temperatures computed for them are disparate (see Figure 21 that shows the temperature for each selected spectrum).
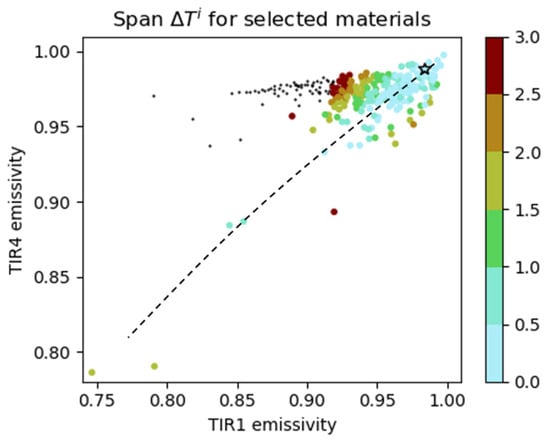
Figure 20.
Temperature span for all emissivity spectra in the spectral library, for a synthetic image made of one liquid water pixel, for a single atmosphere, and with no source of uncertainty. The black star represent the test liquid water spectrum. Black dots represent spectra with . The dashed line shows spans with a low value.
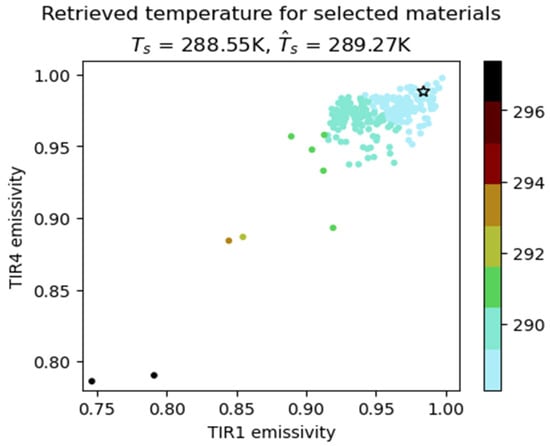
Figure 21.
Temperature for all selected emissivity spectra in the spectral library, for a synthetic image made of one liquid water pixel, for a single atmosphere, and with no source of uncertainty. The black star represents the test liquid water spectrum.
In Figure 20, we can see an “ambiguity valley” (materialized by a dashed line) where temperature spans are all very low, which means that finding the right spectrum only by modifying the threshold in this valley is hard, if not impossible, as soon as uncertainty sources are taken into account. This issue is intrinsic to the underdetermined nature of the temperature and emissivity separation problem. To improve DirecTES performances, additional information coming from VNIR-SWIR or a water mask thus offers better results, as it helps preselect only the relevant spectra in the spectral library. Hence, the valley becomes smaller and the impact of irrelevant spectra is reduced.
Over water areas, the problem of separating the emissivity and the temperature for thermal infrared measurements is not as critical as for land surfaces, since the emissivity of water is very well known and the variations due to to turbidity or wind speed and directionality, for example, are limited [34,38]. The atmospheric data from NWP, on the other hand, have an uncertainty compared with the actual conditions of the measurement, requiring spatial and temporal interpolations [32,33]. In this case, DirecTES can be adapted in order to separate surface temperature and atmospheric effects instead of emissivity. Instead of considering the radiative terms from one set of atmospheric conditions and searching for the appropriate material emissivity values and temperatures which would fit the satellite Level 1 measurements, the over-water adaptation considers only the water emissivity and searches for the atmospheric conditions and temperatures which would fit the satellite data.
Section 4 and Section 5 have shown the strong advantage of additional information, such as that provided by VNIR-SWIR channels, to properly discriminate materials from the spectral library in order to get rid of obvious misfits which may be considered when using TIR only, therefore improving the surface temperature retrievals. During nighttime or for TIR-only sensors, this information is not available simultaneously; however, several strategies can be used to mitigate this issue. VNIR-SWIR information can be retrieved either from a different sensor—as we did for ECOSTRESS using Sentinel2 in Section 5—or from the same sensor using one of the previous daytime acquisitions, as the surface reflectance evolves relatively slowly in time. A soil-occupation map could also provide the necessary additional information.
In general, atmospheric corrections are performed in equivalent quantities, i.e., integrated and averaged over the sensor spectral responses; as the sensor measures radiations in spectral bands, the radiative transfer terms and the temperature/emissivity separation are calculated for each spectral band, and Planck’s Law is inverted for each band’s equivalent wavelength. As the sensor bands have a certain non-zero bandwidth, this is an approximation. For TRISHNA bands, we evaluated the error associated with an integrated approach versus using the hyperspectral signal on the full spectral library and atmospheric conditions used in this paper. If the emissivity is known, i.e., there is no atmospheric correction, this error shows a bias from 0.02 to 0.13 K in absolute value and a standard deviation from 0.02 K to 0.09 K, depending on the spectral band.
In DirecTES, it is possible to bypass this issue by replacing (2) and (3) and calculating a look-up table of TOA radiations for each material, spectral band, and for a range of surface temperatures. The look-up table is then used to determine the surface temperature associated to each measured TOA radiation for each material and band, and then proceed with DirecTES processing. This approach does not make any approximations, but is more demanding in terms of computer resources. We can then compare DirecTES using equivalent quantities versus hyperspectral quantities using these look-up tables in TRISHNA’s case. The presence of both sensor and atmospheric uncertainties limits the impact of difference between the two approaches: there is a difference in bias of about 0.05–0.08 K and a smaller or similar one in RMSE for all materials, which seems negligible compared with the overall performance of the method. It might, however, be different for other sensors with larger spectral bands or overlapping bands for atmospheric transmission features.
7. Conclusions
DirecTES is a direct method for land and sea surface temperature and emissivity separation for infrared sensors. The algorithm relies on a spectral database of emissivity to add an additional equation and results in a well-posed deterministic problem. The theoretical performance of DirecTES has been evaluated over a synthetic database made from three spectral libraries and atmospheric conditions derived from the TIGR database. On that synthetic database, and for the TRISHNA sensor, DirecTES allowed LST retrievals within 0.8 K RMSE on vegetation scenes, 1 K RMSE on water scenes and 2.5 K RMSE on urban scenes using TIR spectral bands only. However, the identification of potential materials can be improved using spectral information in the VNIR-SWIR domain. Then, apart from vegetation (which already had a low bias and RMSE), we observe a strong reduction of the bias and RMSE when taking VNIR-SWIR into account. In addition to the theoretical analysis, DirecTES has also been tested on real TIR images. Over ECOSTRESS images, DirecTES LST retrievals were consistent with the ECOSTRESS LST product and in-situ data, even if the availability of only three ECOSTRESS bands is not favorable for DirecTES usage, which performs better with at least a four-band configuration.
The critical point of the method lies in the use of the provided spectral library. In this paper, results have been obtained using all emissivity spectra in the spectral library provided to the algorithm. With no supplementary information helping the identification of the ground nature, an “ambiguity valley” is observed. This means that different materials can be relevant for the algorithm criteria (similar LST in the TIR bands), even if the temperatures computed for them are disparate. To try and avoid these ambiguities, VNIR-SWIR information offers the algorithm an opportunity to get rid of some of the obviously inconsistent materials and yields better results, as it helps preselect only the relevant spectra in the spectral library.
Improvements of the method can then be considered and will be at the heart of future works. The first potential improvement is to use a land-cover mask that should be helpful to preselect the relevant spectral library data and may also decrease the computing time. Another perspective is to use the method in a multi-temporal configuration. With the hypothesis that surface emissivity changes slowly compared with temperatures, many views from the same scene could be treated simultaneously in order to avoid ambiguities, as the retrieved LST must be relevant between the different TIR bands while the retrieved emissivity values must be relevant between the different images.
Author Contributions
Conceptualization S.M., Data processing, data analysis and results interpretation: S.M., M.C., E.D. and T.H.G.V., Writing: S.M., M.C. and E.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been performed using CNES funding.
Data Availability Statement
The data is not publicly available.
Acknowledgments
The authors would like to thank S. Nativel for his work on preliminary versions of DirecTES and the early analysis of the ambiguity valley, and S. Coustance for her help on the parameterization of MAJA and its documented performance for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Belward, A. The Global Observing System for Climate: Implementation Needs, GCOS Steering Committee, Guayaquil, Ecuador. 2016. Available online: https://library.wmo.int/doc_num.php?explnum_id=3417 (accessed on 1 June 2022).
- Zhou, L.; Dickinson, R.E.; Tian, Y.; Jin, M.; Ogawa, K.; Yu, H.; Scmugge, T. A sensitivity study of climate and energy balance simulations with use of satellite-derived emissivity data over Northern Africa and the Arabian Peninsula. J. Geophys. Res. 2003, 108, 4795. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Jacob, F.; Schmugge, T.; Olioso, A.; French, A.; Courault, D.; Ogawa, K.; Petitcolin, F.; Chehbouni, G.; Pinheiro, A.; Privette, J. Modeling and inversion in thermal infrared remote sensing over vegetated land surfaces. In Advances in Land Remote Sensing; Springer: Berlin, Germany, 2008; pp. 245–291. [Google Scholar] [CrossRef]
- Brown, O.B.; Minnett, P.J.; Evans, R.; Kearns, E.; Kilpatrick, K.; Kumar, A.; Sikorski, R.; Závody, A. MODIS Infrared Sea Surface Temperature Algorithm Algorithm Theoretical Basis Document Version 2.0. 1999. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod25.pdf (accessed on 1 June 2022).
- Masuda, K.; Takashima, T.; Takayama, Y. Emissivity of pure and sea waters for the model sea surface in the infrared window regions. Remote Sens. Environ. 1988, 24, 313–329. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.J.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Gillespie, A.; Matsunaga, T.; Rokugawa, S.; Hook, S.J. Temperature and Emissivity Separation from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Images. In Proceedings of the SPIE’s 1996 International Symposium on Optical Science, Engineering, and Instrumentation, Infrared Spaceborne Remote Sensing IV, Denver, CO, USA, 5–9 August 1996. [Google Scholar] [CrossRef]
- Sawabe, Y.; Matstunaga, T.; Rokugawa, S.; Hoyano, A. Temperature and emissivity separation for multi-band radiometer and validation ASTER TES algorithm. J. Remote Sens. Soc. Jpn. 2003, 23, 364–375. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Valor, E.; Niclòs, R.; Sánchez, J.M.; Galve, J.M.; Mira, M. Temperature and emissivity separation from ASTER data for low spectral contrast surfaces. Remote Sens. Environ. 2007, 110, 162–175. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Abbott, E.; Gilson, L.; Hulley, G.; Jiménez-Muñoz, J.; Sobrino, J.A. Residual errors in ASTER temperature and emissivity standard products AST08 and AST05. Remote Sens. Environ. 2011, 115, 3681–3694. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. The North American ASTER Land Surface Emissivity Database (NAALSED) Version 2.0. Remote Sens. Environ. 2009, 113, 1967–1975. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. Generating consistent land surface temperature and emissivity products between ASTER and MODIS data for earth science research. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1304–1315. [Google Scholar] [CrossRef]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN6: A major upgrade of the MODTRAN radiative transfer code. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model. Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis, Q.J.R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Meerdink, S.K.; Hook, S.J.; Roberts, D.A.; Abbot, E.A. The ECOSTRESS Spectral library version 1.0. Remote Sens. Environ. 2019, 1230, 111196. [Google Scholar] [CrossRef]
- Hagolle, O.; Huc, M.; Villa Pascual, D.; Dedieu, G. A Multi-Temporal and Multi-Spectral Method to Estimate Aerosol Optical Thickness over Land, for the Atmospheric Correction of FormoSat-2, LandSat, VENμS and Sentinel-2 Images. Remote Sens. 2015, 7, 2668–2691. [Google Scholar] [CrossRef]
- Vermote, E.F.; El Saleous, N.Z.; Justice, C.O. Atmospheric correction of MODIS data in the visible to middle infrared: First results. Remote Sens. Environ. 2002, 83, 97–111. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Bhattacharya, B.K.; Crébassol, P.; Gamet, P.; Babu, S.S.; Boulet, G.; Briottet, X.; Buddhiraju, K.M.; Cherchali, S.; Dadou, I.; et al. The Indian-French Trishna Mission: Earth Observation in the Thermal Infrared with High Spatio-Temporal Resolution. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: Piscataway, NY, USA, 2018; pp. 4078–4081. [Google Scholar] [CrossRef]
- Hagolle, O.; Colin, J.; Coustance, S.; Kettig, P.; D’Angelo, P.; Auer, S.; Doxani, G.; Desjardins, C. Sentinel2 surface reflectance products generated by CNES and DLR: Methods, Validation and Applications. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 51, 9–15. [Google Scholar] [CrossRef]
- Colin, J.; Hagolle, O.; Landier, L.; Coustance, S.; Kettig, P.; Marcq, S.; Meygret, A.; Ossman, J.; Vermote, E. Assessment of the performance of the atmospheric correction algorithm MAJA for Sentinel-2 surface reflectance estimates. 2023; (in preparation). [Google Scholar]
- Charvet, D.; Gnata, X.; Toulemont, A.; Rizzolo, S.; Clénet, A.; Litouban, C.; Gossant, A.; Chassat, F.; Buffet, L.; Salcedo, C.; et al. TRISHNA TIR instrument development and performance status. In Proceedings of the International Conference on Space Optics—ICSO, Nice, France, 3–7 October 2022. [Google Scholar]
- Olioso, A. Simulating the relationship between thermal emissivity and the normalized difference vegetation index. Int. J. Remote Sens. 1995, 16, 3211–3216. [Google Scholar] [CrossRef]
- Olioso, A.; Jacob, F.; Weiss, M. First evaluation of land surface emissivity spectra simulated with the sail-thermique model. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3951–3954. [Google Scholar] [CrossRef]
- Neyret, A. Evaluation de différentes approaches visant à estimer l’émissivité de surface à partir d’informations du domaine visible, internal internship report. ISAE-CESBIO 2021, unpublished. [Google Scholar]
- Michel, A.; Roupioz, L.; Granero-Belinchon, C.; Briottet, X. Land Surface Temperature Retrieval over Urban areas from simulated TRISHNA data. In Proceedings of the 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, France, 22–24 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, S.; Ren, H.; Ye, X.; Dong, J.; Zheng, Y. Geometry and adjacency effects in urban land surface temperature retrieval from high-spatial-resolution thermal infrared images. Remote Sens. Environ. 2021, 262, 112518. [Google Scholar] [CrossRef]
- Chevallier, F.; Chédin, A.; Chéruy, F.; Morcrette, J.J. TIGR-like atmospheric-profile databases for accurate radiative-flux computation, Q.J.R. Meteorol. Soc. 2000, 126, 777–785. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An atmospheric correction parameter calculator for a single thermal band earth-sensing instrument. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; pp. 3014–3016. [Google Scholar] [CrossRef]
- Palluconi, F.; Hoover, G.; Alley, R.; Jentoft-Nilsen, M.; Thompson, T. An Atmospheric Correction Method for ASTER Thermal Radiometry Over Land, Algorithm Theoretical Basis Document. 1999. Available online: https://lpdaac.usgs.gov/documents/1153/AST_09T_User_Guide_V4.pdf (accessed on 1 June 2022).
- Wei, J.A.; Wang, D.; Gong, F.; He, X.; Bai, Y. The Influence of Increasing Water Turbidity on Sea Surface Emissivity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3501–3515. [Google Scholar] [CrossRef]
- Hook, S.J.; Cawse-Nicholson, K.; Barsi, J.; Radocinski, R.; Hulley, G.C.; Johnson, W.R.; Rivera, G.; Markham, B. In-flight validation of the ECOSTRESS, Landsats 7 and 8 thermal infrared spectral channels using the Lake Tahoe CA/NV and Salton Sea CA automated validation sites. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1294–1302. [Google Scholar] [CrossRef]
- Hulley, G.C.; Göttsche, F.M.; Rivera, G.; Hook, S.J.; Freepartner, R.J.; Martin, M.A.; Cawse-Nicholson, K.; Johnson, W.R. Validation and Quality Assessment of the ECOSTRESS Level-2 Land Surface Temperature and Emissivity Product. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–23. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Pressure Levels from 1959 to Present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.bd0915c6?tab=overview (accessed on 1 June 2022).
- Niclòs, R.; Caselles, V.; Valor, E.; Coll, C.; Sanchez, J.M. A simple equation for determining sea surface emissivity in the 3–15 μm region. Int. J. Remote Sens. 2009, 30, 1603–1619. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).