Abstract
Synthetic aperture radar (SAR) image change detection is one of the most important applications in remote sensing. Before performing change detection, the original SAR image is often cropped to extract the region of interest (ROI). However, the size of the ROI often affects the change detection results. Therefore, it is necessary to detect changes using local information. This paper proposes a novel unsupervised change detection framework based on deep learning. The specific method steps are described as follows: First, we use histogram fitting error minimization (HFEM) to perform thresholding for a difference image (DI). Then, the DI is fed into a convolutional neural network (CNN). Therefore, the proposed method is called HFEM-CNN. We test three different CNN architectures called Unet, PSPNet and the designed fully convolutional neural network (FCNN) for the framework. The overall loss function is a weighted average of pixel loss and neighborhood loss. The weight between pixel loss and neighborhood loss is determined by the manually set parameter . Compared to other recently proposed methods, HFEM-CNN does not need a fragment removal procedure as post-processing. This paper conducts experiments for water and building change detection on three datasets. The experiments are divided into two parts: whole data experiments and random cropped data experiments. The complete experiments prove that the performance of the method in this paper is close to other methods on complete datasets. The random cropped data experiment is to perform local change detection using patches cropped from the whole datasets. The proposed method is slightly better than traditional methods in the whole data experiments. In experiments with randomly cropped data, the average kappa coefficient of our method on 63 patches is over 3.16% compared to other methods. Experiments also show that the proposed method is suitable for local change detection and robust to randomness and choice of hyperparameters.
1. Introduction
Change detection using multi-temporal remote sensing images is one of the most important applications of remote sensing technology [1,2,3,4]. Change detection analysis is applied for land use and land cover monitoring [5,6], natural disaster assessment, urban management [7,8,9] and monitoring [10,11,12].
Change detection techniques fall into two categories according to the existence of additional ground reference data: supervised methods and unsupervised methods [13,14]. Supervised methods require ground truth to be given for a big training dataset [15], which is labor-intensive and time-consuming [3,16]. In this paper, we mainly focus on unsupervised change detection methods. Early unsupervised SAR image change detection methods are mainly traditional change detection methods based on probabilistic models, multi-resolution analysis and clustering methods. Rignot et al. [17] assume multi-look SAR intensities to be gamma distribution and use image differencing method for change detection. Bruzzone et al. [18] use Markov random fields to model the relationships between adjacent pixels. Bovolo et al. [19] utilize stationary wavelet decomposition to extract the multi-resolution features. Aiazzi et al. [20] extract change features based on information theory. Zhang et al. [21] proposed a novel Contourlet fusion clustering algorithm for unsupervised change detection.
In the past decade, deep learning has made unprecedented development. Due to its powerful feature extraction ability, deep learning has been widely used in the field of SAR image change detection [4,13,22,23,24,25,26]. Since the change detection data of SAR have fewer labels, methods based on semi-supervised learning and unsupervised learning have been widely used in the field of SAR change detection. In the field of semi-supervised learning, Wang et al. proposed a graph-based knowledge supplement network, which can suppress the adverse effects of noisy samples by adding discriminative information from a labeled dataset [27]. Zhao et al. proposed a semi-supervised SAR image change detection method based on a siamese variational autoencoder [28]. In the field of unsupervised change detection, since there are no labels, how to train a neural network becomes a key issue. At present, there are mainly two types of solutions, as shown in Figure 1a,b. The first is to use the existing pre-training model and the model parameters are used for feature extraction without modification [13]. The pretrained model is trained using external large datasets. Essentially, this method transfers the trained model on the semantic segmentation task to the change detection task. If the model is trained on an optical image dataset and the datasets to be tested are SAR images, image style transfer for SAR and optical images was considered [16,29]. The second method does not use any other dataset. Only two registered SAR images obtained at different times are needed. First, the pseudo-labels are generated using traditional methods, such as FCM clustering. Second, some reliable pseudo-labels are selected to train the neural network. Finally, the original images are inputted into the model and the change detection results are acquired [4,23,24,25,30,31], as shown in Figure 1b. For example, Qu et al. [31] proposed a dual-domain network (DDNet) using discrete cosine transform (DCT) for unsupervised SAR image change detection. Gao et al. [25] proposed a siamese adaptive fusion network (SAFNet) for unsupervised change detection. The pseudo-labels of DDNet and SAFNet are generated by the hierarchical FCM algorithm [32]. Each method yields good results [25,31].

Figure 1.
The three frameworks of the unsupervised change detection method using deep learning. (a) Pretrained model and change vector analysis [13]. (b) Using pseudo label selection for training and then test [4,23,24,30,31]. (c) The proposed framework using multi-objective optimization.
However, both methods have their own shortcomings. With the first method, it is difficult to adaptively process various real data due to the fixed network parameters. For the second method, it is necessary to manually design the criteria for sample selection. These selected samples are used to train the model. This is computationally expensive due to the time-consuming training process before testing. Furthermore, nearly all unsupervised methods need image binarization. Saha et al. [13] use the OTSU method for thresholding. Shen et al. [23] and Qu et al. [31] use the FCM method for pre-classification. Tang et al. [33] generate pseudo labels using the expectation-maximization (EM) algorithm. However, the traditional thresholding methods cannot handle regions with very little change [34].
This paper studies local change detection. We break up the image into small patches to test the performance of the method using only local information processing. Traditional segmentation methods may lead to many false alarms if only locally cropped images are processed. If the original images are cropped into small patches, the final change detection results will be very different from the results using full images. In order to solve this problem, in our previous work [34], we proposed a novel thresholding method called histogram fitting error minimization (HFEM) for a little-changed area. After the thresholding using HFEM, conditional random fields (CRFs) are used to model the relationships between the neighborhood pixels. Finally, the small fragments are removed. The fragment removal procedure was called post-processing in our previous work [34]. If the area of the fragment is less than a given value , it will be removed; otherwise, it will be retained. This procedure has been proven to be a very effective way to improve accuracy [31,34,35]. However, needs to be set manually. If is set too large, some truly changed area will be removed. If it is set too small, some larger false alarms will not be removed. Therefore, the post-processing procedure is essentially a supervised manual trial-and-error procedure (MTEP). As for the subject of image binarization, many excellent adaptive binarization methods have been proposed to replace MTEP [1,36,37]. It is meaningful to find a processing method that is not based on manual settings to replace post-processing.
In summary, there are currently two problems. First, existing methods do not perform well for local region change detection. Second, in our previous work, accuracy improvement largely depended on the fragment removal procedure. In order to solve these two problems, we proposed a novel unsupervised change detection framework called HFEM-CNN. Different from the above two frameworks based on unsupervised deep learning, this paper proposes a new end-to-end deep learning-based unsupervised change detection method, as shown in Figure 1c. This framework does not need to select training samples. The training and testing are carried out at the same time and it can also learn parameters adaptively. Compared to Figure 1b, the three procedures, including sample selection, training and testing, are combined into one step: multi-objective learning. Compared to our previous work [34], we use CNN to replace CRF and post-processing. The CNN-based method does not require manual setting of fragment size threshold. Although there are also some hyperparameters, such as the learning rate, momentum and the number of iterations, these three hyperparameters are the same as in [38]. This shows that such a setting is satisfactory for different tasks. Furthermore, the change detection results are also improved compared to the combination of CRF and the fragment removal procedure. This framework has the ability to detect cropped regions. The proposed method outperforms previous methods on the task of change detection for locally cropped regions.
In general, the contributions of this paper can be summarized as follows:
- 1.
- We first consider local change detection. Local change detection is a challenge for unsupervised change detection. We find that the proposed method has great advantages in local change detection.
- 2.
- This paper proposes a novel unsupervised change detection framework called HFEM-CNN. This framework combines sample selection, training and testing into one step: multi-objective learning. The parameters of the network are learned adaptively. Compared with our previous work, the method proposed in this paper is more automatic. It does not require fragment removal as the post-processing to achieve decent results.
- 3.
- The experiments are conducted on both whole images and cropped images. The encouraging results demonstrate that the proposed method is effective for the local change detection task.
It should be noted that the specific structure of the CNN is not our particular concern. In this work, we design a simple fully convolutional neural network (FCNN) for the experiments. It should be noted that the structure of FCNN is different from the famous FCN [39]. To facilitate the distinction, we use FCNN to refer to the fully convolutional network designed in this paper. Furthermore, the classic Unet [40] and PSPNet [41] are also used for unsupervised learning. In this paper, HFEM-FCNN, HFEM-Unet and HFEM-PSPNet are collectively referred to as HFEM-CNNs. The experiments demonstrate that simple neural networks such as FCNN and Unet perform better in this situation. As for the HPF, there are also many specific forms of HPF, such as difference operator, Sobel operator and Laplace operator. This paper uses difference operators as the specific forms of HPF for its simple practicality.
This paper is organized into six sections. Section 2 presents the definition of local change detection and the problem formulation of the proposed method. Section 3 elaborates the proposed method. The Experimental results on real multi-temporal SAR images are reported in Section 4, which also contains the experimental design and evaluation criteria. Discussions concerning the proposed method are presented in Section 5. Finally, conclusions are drawn in Section 6.
2. Local Change Detection
Let us first consider whether the change detection information relies on local or global information. Figure 2 shows a natural optical image and a remote sensing image. For natural optical images, patch one and patch two must be related because they both represent a part of the cat. Patch one represents the cat’s head and patch two represents one of the cat’s paws. That is, for ordinary optical images, a deeper neural network is necessary to increase the receptive field to obtain sufficient information. For remote sensing images, Patch one and patch two illustrate different buildings at a distance, respectively. Therefore, we make reasonable assumptions that patch one and patch two are uncorrelated.

Figure 2.
(a) Ordinary optical image; (b) Remote sensing image.
Let represent two single-polarization SAR images acquired from different times. Let represent a certain pixel. represents the area around the pixel and indicates whether the pixel changes, where 0 indicates no change and 1 indicates change. The mathematical expression for change detection relying only on local information is as follows:
Equation (1) represents the mathematical model of local change detection. Local change detection describes whether a pixel change depends only on its adjacent area and the other pixels are irrelevant. Based on the locality assumption, we design experiments with cropped regions. The original image is randomly cropped and then the cropped patches are used for change detection. We hope to design an unsupervised change detection algorithm that achieves good accuracy on both whole and cropped images.
3. Methods
Let and represent the SAR amplitude images, respectively. The two images were acquired from different moments in the same area. Change detection output is a binary map, with 1 representing changing regions and 0 representing unchanged regions.
The framework of this method is shown in Figure 3. In general, the proposed method has three steps: 1. Calculate the difference map and use HFEM for pixel-level segmentation. 2. Input the difference image into CNN and then perform high-pass filtering to obtain high-frequency components. We consider that for a good segmentation result, adjacent pixels tend to be assigned the same label. Based on the above principle, we feed the output of the CNN into a high-pass filter. 3. Calculate the weighted sum of the pixel loss and the neighborhood loss. The pixel loss is calculated between the output of the CNN and the pixel-level segmentation result. The neighborhood loss is calculated using the high-frequency component and the all-zero map. Finally, perform backpropagation to update CNN parameters. Compared with other deep learning-based unsupervised methods, our method combines sample selection, training and testing into one step, which greatly reduces the computation time.

Figure 3.
The framework of the proposed change detection method.
The remainder of this section describes each part of the proposed method.
3.1. Difference Image Calculation
The difference map can be generated using the classical change vector analysis method or the log-ratio method. Generally, the log-ratio method is very effective for detecting the change of pixels with low amplitude [1] but it is not very effective for pixels with high amplitude. In the SAR amplitude image, the amplitude of water is the lowest, the amplitude of land is medium and the amplitude of buildings is the highest. For water change detection, the log-ratio method is very effective and for building change detection, we choose the image differencing method. In this paper, the log-ratio method is applied to the change detection of water and the image difference method is applied to building change detection. Appendix A gives the explanation of why we adopted the image differencing approach for building change detection.
In this paper, the log-ratio method adds a normalization factor and the mathematical expression is shown in Equation (2):
The mathematical expression of the image differencing method is shown in Equation (3):
HFEM requires that the theoretical maximum value of the difference map is 255, so is the difference map using the log-ratio method, due to the normalization factor, for an 8-bit encoded input image. The theoretical maximum value of is 255. In this article, unless otherwise specified, and are collectively referred to as the difference image (DI).
3.2. The Review of HFEM
Let us first review the HFEM method [34]. HFEM is based on the assumption that the unchanged pixels in DI follow the half-normal distribution and the changed pixels in the DI follow the normal distribution. The reasonability of this assumption is explained in Appendix B. Let z denote the pixel of DI, and the following two equations are used to calculate the probability of the unchanged and the changed pixels in the DI:
where is the probability density function of the unchanged pixels, is the probability density function of the changed pixels, is the standard deviation of the unchanged pixels, is the standard deviation of the changed pixels, is the mean of the changed pixels and is the unchanged pixels.
Let denote the probability density function under the condition that changes exist in the region. represents the probability density function that there is no change in the region.
Let represent the histogram of . The optimization goal is to minimize the fitting error while ensuring the above two conditions. So the optimization model of the algorithm for solving the threshold is:
where represents the tolerance of the optimization.
Readers can refer to [34] for details.
3.3. CNN and Loss Function Design
In this paper, the CNN framework is different from the traditional deep learning-based change detection methods. The traditional deep learning unsupervised change detection methods contain three steps, sample selection, supervised training and testing, as shown in Figure 1b. The method in this paper does not require sample selection and supervised training. The network is directly optimized according to the thresholding result and the all-zero map, which is similar to the pixel energy and neighborhood energy in the CRF model [34]. The total loss function is the weighted sum of pixel loss and neighborhood loss, where represents pixel loss, represents neighborhood loss and represents the weight coefficient.
3.3.1. CNN Design
In this work, we test three different structures of CNN. First, we design FCNN, a simple fully convolutional network. Second, we test two classic semantic segmentation networks, called Unet [40] and PSPNet [41].
There are two primary considerations for the design of CNN in this paper. First, the CNN in this paper takes on the rule of filtering and denoising rather than the role of feature extraction in traditional CNNs. It should be noted that the denoising ability of CNN is different from despeckling. The denoising mentioned here mainly includes two points. The first is to remove small fragments in the thresholding result. The second is to connect some homogeneous changing areas. That is, it has a smoothing effect on the thresholding result, as shown in Figure 4. Second, for change detection using remote sensing images, this paper hopes to reduce the influence of the detection results by the ROI selection scale. Therefore, regarding the network depth, this paper uses a shallow convolutional neural network with less than 10 layers. A deeper neural network will make the results too smooth and blurred. This work does not use a downsampling or pooling layer in the network because the downsampling layer will reduce the resolution. On the one hand, more high-resolution information should be preserved. On the other hand, the receptive field of the network should be reduced to meet the assumption that different regions of the image are irrelevant. In summary, the design of FCNN is shown in Figure 5. FCNN contains convolution layers. The number of convolutional layer equals and the number of convolutional layer equals one. In this work, we set . The parameter is set to 1 for each convolution layer in order to maintain the image size.

Figure 4.
The performance of CNN to remove small fragments and smoothing. (a) HFEM thresholding result; (b) the output of CNN.

Figure 5.
The CNN structure of the proposed change detection method. A cyan rectangle in the figure represents the side view of a tensor and the number above the rectangle represents the number of channels. FCNN contains convolution layers. The number of convolutional layer equals and the number of convolutional layer equals one. In this work, we set .
The structure of Unet is shown in Figure 6a. Slightly different from the original Unet network, the parameter in order to maintain the image size before and after the convolution layer. The batchnorm (BN) layer [42] is used after the ReLU layer to accelerate the convergence.
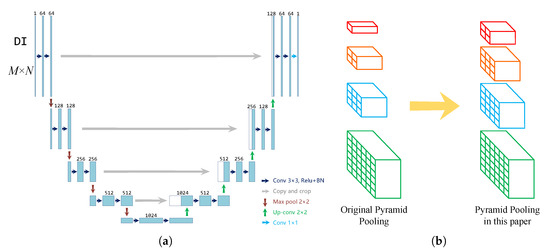
Figure 6.
The Unet and PSPNet tested in this paper. (a) The Unet structure used in the proposed change detection method. This figure is adapted from [40]. A cyan rectangle in the figure represents the side view of a tensor and the number above the rectangle represents the number of channels. (b) The pyramid pooling module of PSPNet used in the original paper and in this paper. This figure is adapted from [41]. The pyramid pooling module in the original paper is a four-level one with bin sizes of , , and , respectively [41]. In this paper, we change these sizes to , , and , respectively.
The structure of PSPNet is also slightly different from the original one. In this work, the batch size equals 1 because there is only one difference image fed into the neural network. However, if we use the original PSPNet, the batch normalization does not support the tensor because BN requires more than one value per channel [42]. Therefore, we slightly modify the pyramid pooling module in the original paper. We change the pyramid pooling sizes to , , and , respectively, as shown in Figure 6b. We avoid the inability to batch normalize. Other than that, no major modifications are made to the original network. ResNet-50 [43] is used as the backbone of PSPNet. Both pretrained and randomly initialized backbones are tested in Section 4.
3.3.2. Loss Function Design
Let represent the output of the convolutional neural network; represents the segmentation result of the HFEM algorithm. Among them, C represents the number of channels. If the classic cross entropy Loss is used, the number of output channels is equal to the number of categories. In this paper, there are only two categories of categories—changed class and unchanged class—so . Nevertheless, Binary Cross Entropy Loss (BCELoss) is a loss function specially designed for the two-class problem, which is suitable for change detection problems. If BCELoss is used, then the number of output channels . Each pixel of the output image represents the probability of change. At this time .
Let represent the row and column coordinates of the image, respectively, where , . Since change detection is a binary classification problem, BCELoss is used in this paper. Before calculating BCELoss, it is necessary to normalize the output Y to through the sigmoid function layer. The sigmoid function is as follows:
Let represent the output of the sigmoid function, where the element can be considered as the probability of the change of the th element. The larger the value, the greater the probability of change. The loss function BCELoss is as follows:
where is the th element in .
The L1Loss is adopted as the neighborhood loss function. The reason why BCEloss is not used is that BCELoss has a necessary premise that each pixel of the output image represents the probability of belonging to a certain class. After high-pass filtering, each pixel denotes the smoothness of the output image rather than the probability. So BCELoss cannot be used. In this paper, we adopt L1Loss as the neighborhood loss function. Obviously, the optimal solution is not the one where is zero, because even the ground truth, after high-pass filtering, is not an all-zero map. Therefore, in our consideration, the gradient near the optimal point cannot be too small to escape the area where approaches zero. The gradient of L1 loss has the same gradient everywhere except the zero point, so we choose L1loss as the neighborhood loss. The L1loss is also selected for spatial continuity in [38]:
Let represent the output of the high-pass filter, and represent an all-zero map. The all-zero map denotes a matrix with all zero elements. The L1Loss, which is used as the neighborhood loss, is expressed as follows:
It is worth noting that the specific form of the neighborhood loss will vary slightly depending on different high-pass filters. Correspondingly, the all-zero map also has different sizes.
3.3.3. High Pass Filter
In this paper, we use the difference operator as HPF. The difference operator is described below. The reason why we choose the all-zero map for calculating is also discussed.
For the difference operator, the output of the high-pass filter is divided into two parts, the row difference and the column difference, respectively. Let represent the column difference image. Let represent the row difference image. Then, each element in the matrix is calculated as follows:
When the difference operator is used as a high-pass filter, the outputs of the high-pass filter contain two items, namely and . The size of and is not the same as the output image, so the loss function at this time is calculated as follows:
For the output of the high-pass filter, it will be used to compare the all-zero map to calculate the loss. Let us discuss why the all-zero map is chosen as the target for learning. Let us look at a simple test. The Ottawa dataset is used for this test. First, we generate the DI using the log-ratio method and the original HFEM is used for image thresholding. The thresholding result and the label are put into the difference operator. The inputs and the outputs of the filter are shown in Figure 7. The result is processed by taking the absolute value.
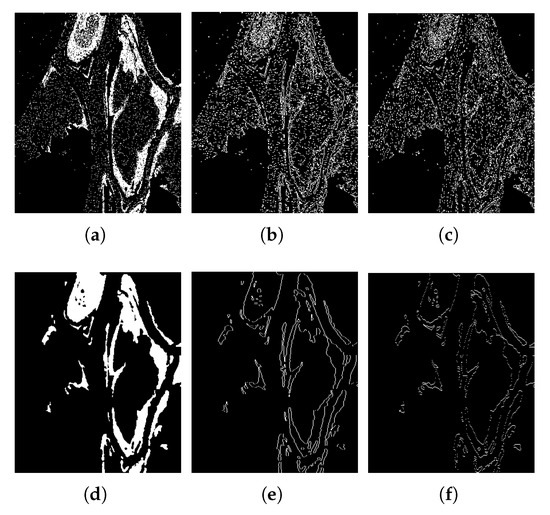
Figure 7.
The thresholding results and the label of Ottawa datasets, as well as the output of the high pass filter. (a) The thresholding result; (b) The row difference image of (a); (c) The column difference image of (a); (d) label; (e) The column difference image of (d); (f) The row difference image of (d).
It can be seen intuitively from Figure 7b,c that there are many non-zero pixels in the high-pass filtering result of (a). The high-pass filtering result of the label is only the edge of the changed area and the number of non-zero pixels is relatively low, as shown in Figure 7e,f. The numbers of non-zero pixels of (b) (c) (e) and (f) are 11922, 10394, 3282 and 1743. We calculate for thresholding result and label using Equation (15). For the thresholding result, and for the label. Therefore, we make an assumption that a good change detection result should be relatively smooth; that is, the result after passing through the high-pass filter is closer to the all-zero map. Based on this idea, we use an all-zero map as the label for training. Obviously, the result after high-pass filtering cannot be an absolute all-zero map unless there is no change at all. Therefore, both and must be taken into account, so we designed such a multi-objective learning framework, as shown in Figure 3.
4. Experiment
In this section, we implement experiments to demonstrate the effectiveness of the proposed framework. First, we describe the datasets and the evaluation criteria used in this experiment. Then, the experiment design is specified. The detailed experimental results are displayed in the final parts. In this experiment, the weight coefficient is set to for water change detection and to for building change detection. The number of convolution layers L in Figure 5 is set to 8. The difference operator is used as the high-pass filter, as shown in Equation (15). The proposed method and DDNet method are implemented using Pytorch 1.11 and CUDA 11.3 on a single NVIDIA RTX 3090 GPU. The FCMMRF, PCA-kmeans and HFEMCRF are implemented using MATLAB R2022a on AMD Ryzen 9 5900X CPU. We choose the stochastic gradient descent (SGD) method as the optimizer. The learning rate is set to and the momentum is set to . The number of iterations is set to 200.
For comparison, we experimented with four contrasting methods, called DDNet [31], SAFNet [25], FCMMRF [44] and HFEMCRF [34]. All four contrasting methods use the fragment removal procedure as postprocessing. Generally speaking, the parameter in the fragment removal procedure is generally set between 20 and 30. is set to 20 in the public code of SAFNet [25,45] and DDNet [31,46]. In our previous work, is set to 25 for HFEMCRF [34]. In order to maintain uniformity, we set to 20 for all four contrasting methods in this experiment. The implementation of the DDNet method is to use the code published by the original authors. The other methods we implemented ourselves according to the original papers. We test four HFENCNNs, including HFEM-Unet, HFEM-FCNN, HFEM-PSPNet and HFEM-PSPNet using pretrained backbone (HFEM-PSPNet-Pre).
4.1. Dataset Descriptions
We use three real SAR datasets in the experiment. The real datasets are Bern dataset, Ottawa dataset and Tongzhou dataset.
Bern dataset includes two SAR images, which were acquired by the European Remote Sensing Satellite 2 (ERS 2) SAR satellite covering Bern city. The two images were acquired in April and May 1999. Between these two moments, the waters of the Aare River flooded parts of the cities of Thun and Bern, including Bern Airport. The two images of Bern dataset are illustrated in Figure 8. The ground truth of Bern dataset is from [1].

Figure 8.
Bern dataset. (a) ; (b) ; (c) ground truth.
Ottawa dataset, which is shown in Figure 9 was acquired by the RADARSAT SAR sensor in the Ottawa region. Two images () were acquired in May and August 1997, respectively. During this time, the area suffered from flooding. The ground truth of Ottawa dataset is from [44].

Figure 9.
Ottawa dataset. (a) ; (b) ; (c) ground truth.
Tongzhou dataset contains two SAR images acquired by TerraSAR-X. These two images are cropped from two large SAR amplitude images without multi-look operation, which means the range resolution is equivalent to m and the azimuth resolution equals m. The size of the cropped image is . There were numerous newly built houses in this area between January 2014 and August 2015, so this dataset is used by us for building change detection. The ground truth of Tongzhou dataset is manually marked with reference to the optical images from Google Earth. However, two images of Tongzhou data are single-look images with greater speckle noise. Therefore, the multi-temporal SAR block-matching 3D (MSAR-BM3D) method [47] is used to remove the speckle noise for Tongzhou dataset. The original and despeckled images of Tongzhou dataset are depicted in Figure 10, respectively.

Figure 10.
Tongzhou datasets before and after despeckling. The despeckled images are used in the experiments. (a) without despeckling; (b) without despeckling; (c) after despeckling; (d) after despeckling; (e) ground truth.
We did not perform despeckling on the Bern dataset and the Ottawa dataset because these two datasets are relatively less noisy. To illustrate this and also to evaluate the effect of despeckling, we select the homogeneous areas and calculate the equivalent number of looks (ENL) of each dataset. The image of each dataset is selected to calculate the ENL. The selected patches of each image are shown in Figure 11a–c. The selected patch of the original Tongzhou image is the same as that of the despeckled image. It can be seen from Table 1 that the Bern dataset and the Ottawa dataset have relatively high ENL and do not require additional despeckling. However, two images of Tongzhou data are single-look images with greater speckle noise. Therefore, the multi-temporal SAR block-matching 3D (MSAR-BM3D) method [47] is used to remove the speckle noise for Tongzhou dataset. The original and despeckled images of Tongzhou dataset are depicted in Figure 10, respectively. The ENL of the despeckled image increased a lot, as shown in Table 1.

Figure 11.
The selected patches of image of each dataset used for calculating the ENL. (a–c) illustrate the selected regions of Bern, Ottawa and Tongzhou despeckled data, respectively. The selected patch of the original Tongzhou image is the same as that of the despeckled image.

Table 1.
The ENL of each dataset.
4.2. Evaluation Criteria
The confusion matrix is used for the evaluation criteria. For binary classification problems, the size of the confusion matrix is . The four elements in the confusion matrix are , , , . The definitions of these four variables are the same as [34].
In this paper, we consider four evaluation criteria—overall accuracy (OA), precision, recall, mIOU and kappa coefficient (KC)—which are defined as follows:
The kappa coefficient is defined as follows:
where
4.3. Experimental Design
In this work, we implement real data experiments to demonstrate the effectiveness of our method. The real data experiment includes two parts. In the first part, the three whole datasets are used to demonstrate that the proposed method is suitable for whole datasets. The second part is the core part of the experiment. We randomly crop the raw images and labels. Each image is cropped into 20 small patches with size . The number of changes in the cropped area is very small. Experiments prove that our method is superior to other algorithms in this extreme case. The datasets in this experiment contain a total of 63 image pairs, of which the first three pairs of images are images of the complete data and the last 60 pairs are randomly cropped images. We use all 63 pairs of patches to perform the experiment in the second part. The purpose is to examine the algorithm’s average performance in various scenarios.
The method of the whole data and the cropped data experiments is shown in Figure 12. The first line illustrates the experiment on whole datasets and the second line illustrates the experiment on the cropped datasets.
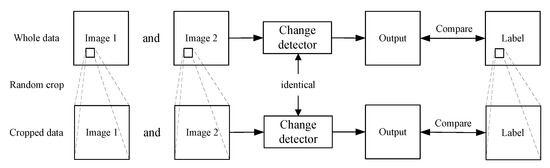
Figure 12.
Schematic diagram of two parts of real data experiment. The first row indicates the experiment using the complete data and the second row indicates that we use the cropped images from the complete data.
4.4. Experiment on Whole Datasets
In experiment 1, the datasets contain numerous changed pixels. The results of three whole datasets are shown in Figure 13, Figure 14 and Figure 15. We can see that HFEM-PSPNet does not perform well in three datasets. PSPNet uses ResNet as the backbone. Since the ResNet network is relatively deep, the denoising ability of the model is too strong, so the output image is too smooth. Therefore, relatively shallow networks are better suited for unsupervised SAR change detection; previous research [23,31] also supports our view.

Figure 13.
The results of Experiment 1 using Bern dataset. (a) DDNet. (b) DDNet(WP). (c) HFEMCRF. (d) HFEMCRF(WP). (e) FCMMRF. (f) FCMMRF(WP). (g) SAFNet. (h) HFEM-PSPNet. (i) HFEM-PSPNet-Pre. (j) HFEM-FCNN. (k) HFEM-Unet. (l) ground truth.

Figure 14.
The results of Experiment 1 using Ottawa dataset. (a) DDNet. (b) DDNet(WP). (c) HFEMCRF. (d) HFEMCRF(WP). (e) FCMMRF. (f) FCMMRF(WP). (g) SAFNet. (h) HFEM-PSPNet. (i) HFEM-PSPNet-Pre. (j) HFEM-FCNN. (k) HFEM-Unet. (l) ground truth.

Figure 15.
The results of Experiment 1 using Tongzhou dataset. (a) DDNet. (b) DDNet(WP). (c) HFEMCRF. (d) HFEMCRF(WP). (e) FCMMRF. (f) FCMMRF(WP). (g) SAFNet. (h) HFEM-PSPNet. (i) HFEM-PSPNet-Pre. (j) HFEM-FCNN. (k) HFEM-Unet. (l) ground truth.
The numerical results of evaluation criteria are illustrated in Table 2, Table 3 and Table 4. In this case, the traditional methods work well. The proposed method also obtains a good change detection performance. According to mIoU and the kappa coefficient, the proposed HFEM-FCNN performs the best on Bern dataset and Tongzhou dataset. However, from the three datasets, HFEM-CNNs did not show a significant advantage. The DDNet method performs the best on Ottawa dataset. Nonetheless, The accuracy of HFEM-CNNs is at the top of the three datasets. We do not prove that HFEM-CNNs are far superior to other methods on the whole datasets. We just need to prove that HFEM-CNNs can also achieve similar results with other excellent methods in ordinary cases. Experiment 1 aims to prove that HFEM-CNNs are suitable for normal datasets.

Table 2.
The numerical results of Bern dataset.

Table 3.
The numerical results of Ottawa dataset.

Table 4.
The numerical results of Tongzhou dataset.
4.5. Experiment on Whole and Cropped Datasets
Both whole datasets and cropped datasets are used in experiment 2. The aim of experiment 2 is to test the overall performance of the algorithm in various situations. The total number of pairs of images is 63, including three whole datasets and 60 cropped datasets. In order to better evaluate the performance, We first calculate the mean value of each criterion, then we give visualized results of six selected different patches.
The mean values of numerical results are shown in Table 5. The kappa coefficients of each dataset are shown in Figure 16. The acronym ’WP’ means ’without post-processing’. The meaning of post-processing is fragment removal procedure, which is explained in Section 1. The proposed method is compared with other methods, respectively. As can be seen from Figure 16, HFEM-Unet and HFEM-FCNN are better than DDNet, FCMMRF and HFEMCRF. Even though HFEMCRF greatly improves accuracy through post-processing, the proposed HFEM-Unet is still 3.16 % higher than HFEMCRF in kappa coefficient and 2.87 % than in mIoU. If HFEMCRF has no post-processing, the performance of HFEM-CNNs is much stronger than that of HFEMCRF. Therefore, the proposed framework is a good substitute for CRF and fragment removal procedure.

Table 5.
The average numerical results of all 63 datasets.
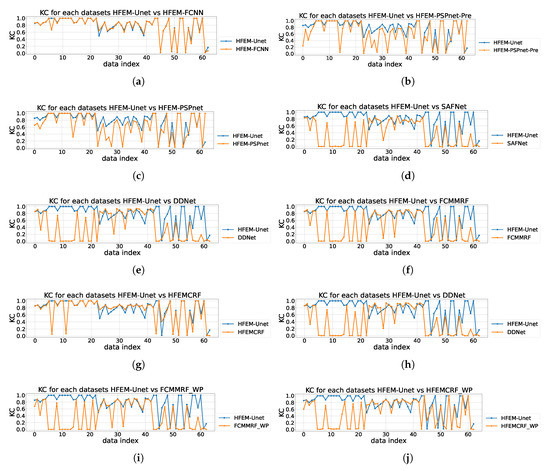
Figure 16.
The kappa coefficient of different methods on all 63 datasets. (a) HFEM-Unet vs HFEM-FCNN. (b) HFEM-Unet vs. PSPNet-Pre. (c) HFEM-Unet vs. PSPNet. (d) HFEM-Unet vs. SAFNet. (e) HFEM-Unet vs. DDNet. (f) HFEM-Unet vs. FCMMRF. (g) HFEM-Unet vs. HFEMCRF. (h) HFEM-Unet vs. DDNet(WP). (i) HFEM-Unet vs. FCMMRF(WP). (j) HFEM-Unet vs. HFEMCRF(WP).
For a subset of patches, our detection results have high kappa coefficients. However, for some special patches, the kappa coefficient value of HFEM-CNNs is very small. In order to visually demonstrate the effect of our method on different patches, we deliberately select eight patches. Four of them have good results and the results of the other four patches are not good. The indices of the four patches with good results are 8, 11, 30 and 43, respectively. The indices of the three patches with poor results are 23, 39 and 45, respectively. Figure 17 illustrates the selected patches. The blue dots represent the patches with good results and the red dots represent the patches with poor results. We give the visualized results and analysis of these selected patches.
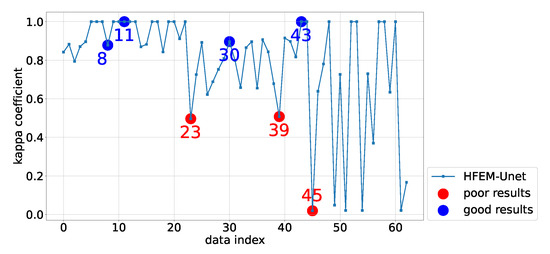
Figure 17.
The indices of the selected patches for visualization. Seven patches are selected, including four patches with good results and three patches with poor results. The indices of the four patches with good results are 8, 11, 30 and 43, which are represented by blue dots. The indices of the three patches with poor results are 23, 39 and 45, which are represented by red dots.
In our subsequent analysis, if there is no clear explanation, we use the row number in Figure 18 or Figure 19 to represent the patch number. For example, patch 1 in Figure 18 represents the patch results shown in the first row in Figure 18.

Figure 18.
The four lines represent the 16th, 19th, 38th and 43rd patches with good detection results. (a) . (b) . (c) DDNet. (d) FCMMRF. (e) HFEMCRF without post-processing. (f) HFEMCRF. (g) SAFNet. (h) HFEM-FCNN. (i) HFEM-Unet. (j) ground truth.

Figure 19.
The three lines represent the 23rd, 39th and 53rd patches with poor detection results. (a) . (b) . (c) DDNet. (d) FCMMRF. (e) HFEMCRF without post-processing. (f) HFEMCRF. (g) SAFNet. (h) HFEM-FCNN. (i) HFEM-Unet. (j) ground truth.
Figure 18 illustrates the results of four cropped patches with good results. Each line of Figure 18 represents the data and detection results of a patch. Patch 1 and patch 2 are cropped from Bern dataset. Patch 3 is cropped from Ottawa dataset and Patch 4 is cropped from Tongzhou dataset. The selected patches include no change areas as well as changed areas. As can be seen from Figure 18, for those patches with significant changes, our method performs well, as shown in patch 1 and patch 3 in Figure 18. Not only our method, but nearly all methods also perform well on the patches with a lot of change. However, for those patches without change, such as patch 2 and patch 4 in Figure 18, traditional methods do not perform well. The HFEM-CNN method can better avoid false alarms.
However, the proposed method can also lead to some unsatisfactory results, as shown in Figure 19. We select three patches with poor results. From Figure 19, we can clearly see that the proposed approach leaves out some of the details of the change. This is the reason for the low kappa coefficient in these patches. Nevertheless, from the effect point of view, our method greatly avoids false alarms at the cost of missing some details and we think it is still a good method. From the overall average kappa coefficient, the proposed method performs better than other methods. Due to the strong denoising ability of CNN, some tiny changes will be removed as noise.
5. Discussion
In this section, we first discuss the effect of random initialization. We do not fix the random seed and repeat the experiment 15 times. The hyperparameter is set to . These repeated experiments are intended to illustrate that the proposed method is less affected by randomness. Then, we discuss the influence of the hyperparameter , which aims to demonstrate the proposed method is robust with respect to the selection of the hyperparameter . The Unet is used as the CNN structure. Finally, we summarize the strengths and weaknesses of the proposed method.
5.1. The Effect of Random Initialization
We set the same hyperparameter and repeated experiments 15 times on the three datasets, respectively, to see how much performance is affected by randomness. The purpose of this experiment is to demonstrate that the performance of our method is reproducible and less affected by randomness. Let R represent the difference between the maximum value and the minimum value of the kappa coefficient in multiple experiments. As we can see from Figure 20, for Bern dataset, , for Ottawa dataset, , and for Tongzhou dataset, . The values in Table 2, Table 3 and Table 4 are the results of setting the random seed to 2022 for repeatability. Compared with the results in Table 2, Table 3 and Table 4, the proposed method is relatively stable and less affected by randomness.
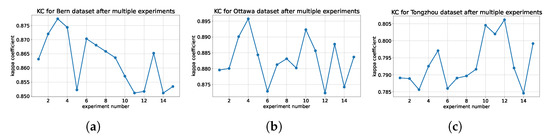
Figure 20.
The effect of random initialization on three datasets. (a) Bern dataset. (b) Ottawa dataset. (c) Tongzhou dataset.
5.2. The Effect of
In the experiment, the weight coefficient is set to . If is too large, the final output would be very close to HFEM. This means that the neighborhood information is not considered. In order to quantitatively discuss the influence of , we show the effect of different lambdas on the final output using three whole datasets, as shown in Figure 21. In order to ensure that the performance of the algorithm is not greatly affected by randomness, we do not fix the random seed. The performance shown in the Table 2, Table 3 and Table 4 is one of the results of multiple experiments, so it is slightly different from the result in Figure 21, but the error will not exceed one percent.
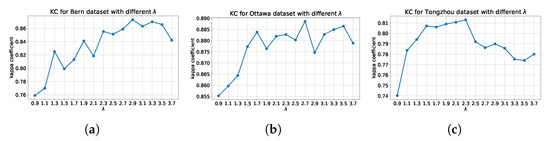
Figure 21.
The influence of on three datasets. (a) Bern dataset. (b) Ottawa dataset. (c) Tongzhou dataset.
It can be seen from Figure 21 that the setting of parameter does affect the detection accuracy. Because of this, in the cropped data experiment, we uniformly set the parameter to for all cropped datasets. If is too small, the output of the CNN will appear as an all-zero map. From the point of view of optimization, that the output is an all-zero map means in Equation (10) is approaching zero. Because of the small weight of , the overall loss is mainly dominated by . So it falls into a locally optimal solution.
Furthermore, as long as is set to about 2 to 3, the basic performance of the algorithm can still be guaranteed. We calculated the difference between the maximum and minimum kappa coefficients of the detection results when lambda equals . Let R denote the difference between the maximum value and the minimum value of the kappa coefficient using different . For Bern dataset, , for Ottawa dataset, and for Tongzhou dataset, . The difference is , and on Bern, Ottawa and Tongzhou datasets. Considering the impact of random initialization, the impact of changes in is even more negligible. For the Ottawa dataset, the influence of on the kappa coefficient is even lower than the influence of randomness on the kappa coefficient, which shows that the influence of lambda on the result is completely submerged in random noise. This shows that in such an interval, the effect of the method is relatively robust with respect to the selection of parameter .
Experiments prove that the proposed method is of great help in reducing false alarms. The proposed method has only one main hyperparameter . It can also be shown from the above two discussions that HFEM-Unet has little impact on random initialization. When is between 2 and 3, it has little impact on the final performance of the method. Therefore, HFEM-Unet is a relatively stable method that does not rely too much on hyperparameters. However, our previous work, HFEMCRF, is greatly affected by post-processing. Not only that, even if HFEMCRF uses post-processing, HFEM-CNN still slightly outperforms HFEMCRF on all 63 datasets. The proposed method is superior to HFEMCRF. Compared with the work of other scholars, such as DDNet, FCMMRF and SAFNet, the proposed method shows a great advantage in reducing the false alarm rate due to HFEM. However, the proposed method also has shortcomings. That is, the change detection of details needs to be improved. In order to reduce false alarms, the proposed method ignores some changes in details. This leads to the fact that the change detection results of the proposed method are not as good as other methods for some images with detailed changes.
6. Conclusions
This paper proposed the concept of local change detection. Local change detection describes whether a pixel change depends only on its adjacent area, while the other pixels are irrelevant. Based on the locality assumption, it is possible to implement change detection only using local patches. For better local change detection, we develop a novel change detection framework for local change detection, called HFEM-CNNs. We tested three different CNN architectures, namely Unet, PSPNet and our own designed FCNN. The experiments were conducted using both whole datasets and cropped datasets. Experiments show that simple shallow convolution networks such as Unet and FCNN are more suitable for the proposed framework.
The fragment-removal procedure is generally used as a post-processing step for traditional methods. However, this procedure is basically an MTEP process. The performance of the HNCRF method decreases rapidly without post-processing. So it is meaningful to find a processing method that is not based on manual settings to replace post-processing. The proposed CNN-based framework can solve this problem.
Experiments show that the proposed method performs a little better than other methods on the whole datasets. This demonstrates that HFEM-CNNs are suitable for normal change detection. Furthermore, the second part of the experiment demonstrates that the proposed method is effective with regard to the local change detection task. We can see from Section 5 that the proposed method is robust with regard to randomness and choice of hyperparameters.
Author Contributions
Conceptualization, K.Z. and X.L.; methodology, K.Z.; software, K.Z.; validation, K.Z. and X.L.; formal analysis, K.Z.; investigation, K.Z. and X.L.; resources, K.Z.; data curation, K.Z. and B.G.; writing—original draft preparation, K.Z.; writing—review and editing, X.L. and H.C.; visualization, K.Z. and H.C.; supervision, X.L.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by LuTan-1 L-Band Spaceborne Bistatic SAR data processing program, grant number E0H2080702, in part by the China Academy of Railway Sciences Fund, grant number 2019YJ028.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SAR | Synthetic aperture radar |
| HFEM | Histogram fitting error minimization |
| DI | Difference image |
| CNN | Convolutional neural network |
| CRF | Conditional random fields |
| FCM | Fuzzy c-means |
| EM | Expectation maximization |
| MTEP | Manual trial-and-error procedure |
| FCNN | full convolutional neural network |
| HPF | High-pass filters |
| HN | half-normal distribution |
Appendix A. The Choice of DI
In this appendix, we give the explanation of why we adopted the image differencing approach for building change detection. The previous studies have shown that the log-ratio method is more advantageous than the difference method [1,48]. If the log-ratio method is used, changes will be detected in the same manner both in high and low intensity regions [1].

Figure A1.
The comparison between optical and SAR image, as well as the comparison between log-ratio map and image differencing map. (a) optical image cropped from Google Earth; (b) SAR images. (c) log-ratio map. (d) image differencing map. (e) HFEM thresholding result of log-ratio map. (f) HFEM thresholding result of image differencing map.
In SAR images, buildings are usually strong scatterers and usually appear as high-brightness areas in SAR images. Due to specular reflection, water areas appear as areas of lower brightness in the SAR magnitude image, as shown in Figure A1a,b. The brightness of vegetation and land is between that of buildings and water.
There may be different kinds of changes in an area, such as changes in buildings, changes in water bodies or changes in vegetation. If the log-ratio method is performed, almost all change types will be detected, as shown in Figure A1c. Compared with the log-ratio map, the building change areas in the difference map are highlighted, while the vegetation and water change areas are relatively dark, as shown in Figure A1d. If we use the HFEM method to binarize the log-ratio map and the image differencing map separately, the results obtained are shown in Figure A1e,f. It can be seen from Figure A1e that some areas of vegetation change and water body change are segmented. In Figure A1f, the corresponding changes in water body and vegetation were not detected.
In this paper, we use Tongzhou data for building change detection and we hope to avoid other types of changes as much as possible. Therefore, we choose the image differencing method to generate difference map.
Appendix B. The Distribution of Changed and Unchanged Areas in DI
HFEM is based on the assumption that the unchanged pixels in DI follow the half-normal distribution and the changed pixels in the DI follow the normal distribution. In Appendix B, we show the reasonability of the assumption of HFEM.
We show the reasonability of this assumption with the histogram fit effect of the DI. In actual processing, the half-normal distribution can also obtain a good fitting effect. Figure A2 shows the histogram fitting results of the absolute value log-ratio (LR) map and image differencing (ID) map, respectively. LR and ID are defined by Equation (2) and Equation (3), respectively. is defined by Equation (6). As can be seen from Figure A2, The overall fitting effect is satisfactory and the assumption of HFEM is relatively reasonable.
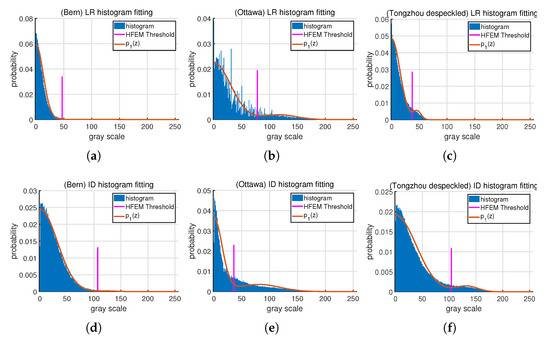
Figure A2.
Histogram fitting of LR and ID for three datasets. (a–c) illustrate the histogram of LR for Bern, Ottawa and Tongzhou datasets, respectively. (d–f) illustrate the histogram of ID for Bern, Ottawa and Tongzhou datasets, respectively.
References
- Bazi, Y.; Bruzzone, L.; Melgani, F. An unsupervised approach based on the generalized Gaussian model to automatic change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef]
- Gong, M.; Li, Y.; Jiao, L.; Jia, M.; Su, L. SAR change detection based on intensity and texture changes. ISPRS J. Photogramm. Remote Sens. 2014, 93, 123–135. [Google Scholar] [CrossRef]
- Zhang, X.; Su, H.; Zhang, C.; Gu, X.; Tan, X.; Atkinson, P.M. Robust unsupervised small area change detection from SAR imagery using deep learning. ISPRS J. Photogramm. Remote Sens. 2021, 173, 79–94. [Google Scholar] [CrossRef]
- Gong, M.; Yang, H.; Zhang, P. Feature learning and change feature classification based on deep learning for ternary change detection in SAR images. ISPRS J. Photogramm. Remote Sens. 2017, 129, 212–225. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, Y. An automatic approach for land-change detection and land updates based on integrated NDVI timing analysis and the CVAPS method with GEE support. ISPRS J. Photogramm. Remote Sens. 2018, 146, 347–359. [Google Scholar] [CrossRef]
- Chen, X.; Chen, J.; Shi, Y.; Yamaguchi, Y. An automated approach for updating land cover maps based on integrated change detection and classification methods. ISPRS J. Photogramm. Remote Sens. 2012, 71, 86–95. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, P.; Feng, X.; Yuan, M. Separate segmentation of multi-temporal high-resolution remote sensing images for object-based change detection in urban area. Remote. Sens. Environ. 2017, 201, 243–255. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Du, P.; Liang, H.; Xia, J.; Li, Y. Object-based change detection in urban areas from high spatial resolution images based on multiple features and ensemble learning. Remote. Sens. 2018, 10, 276. [Google Scholar] [CrossRef]
- Zhang, K.; Fu, X.; Lv, X.; Yuan, J. Unsupervised Multitemporal Building Change Detection Framework Based on Cosegmentation Using Time-Series SAR. Remote. Sens. 2021, 13, 471. [Google Scholar] [CrossRef]
- Anniballe, R.; Noto, F.; Scalia, T.; Bignami, C.; Stramondo, S.; Chini, M.; Pierdicca, N. Earthquake damage mapping: An overall assessment of ground surveys and VHR image change detection after L’Aquila 2009 earthquake. Remote. Sens. Environ. 2018, 210, 166–178. [Google Scholar] [CrossRef]
- Janalipour, M.; Taleai, M. Building change detection after earthquake using multi-criteria decision analysis based on extracted information from high spatial resolution satellite images. Int. J. Remote Sens. 2017, 38, 82–99. [Google Scholar] [CrossRef]
- Washaya, P.; Balz, T.; Mohamadi, B. Coherence change-detection with sentinel-1 for natural and anthropogenic disaster monitoring in urban areas. Remote Sens. 2018, 10, 1026. [Google Scholar] [CrossRef]
- Saha, S.; Bovolo, F.; Bruzzone, L. Unsupervised deep change vector analysis for multiple-change detection in VHR images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3677–3693. [Google Scholar] [CrossRef]
- Geng, J.; Ma, X.; Zhou, X.; Wang, H. Saliency-guided deep neural networks for SAR image change detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7365–7377. [Google Scholar] [CrossRef]
- Zhou, Z.H. A brief introduction to weakly supervised learning. Natl. Sci. Rev. 2018, 5, 44–53. [Google Scholar] [CrossRef]
- Saha, S.; Bovolo, F.; Bruzzone, L. Building Change Detection in VHR SAR Images via Unsupervised Deep Transcoding. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1917–1929. [Google Scholar] [CrossRef]
- Rignot, E.J.; Van Zyl, J.J. Change detection techniques for ERS-1 SAR data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 896–906. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. A detail-preserving scale-driven approach to change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2963–2972. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Zoppetti, C. Nonparametric change detection in multitemporal SAR images based on mean-shift clustering. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2022–2031. [Google Scholar] [CrossRef]
- Zhang, W.; Jiao, L.; Liu, F.; Yang, S.; Liu, J. Adaptive Contourlet Fusion Clustering for SAR Image Change Detection. IEEE Trans. Image Process. 2022, 31, 2295–2308. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Dong, J.; Li, B.; Xu, Q. Automatic change detection in synthetic aperture radar images based on PCANet. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1792–1796. [Google Scholar] [CrossRef]
- Shen, F.; Wang, Y.; Liu, C. Change Detection in SAR Images Based on Improved Non-Subsampled Shearlet Transform and Multi-Scale Feature Fusion CNN. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12174–12186. [Google Scholar] [CrossRef]
- Li, L.; Ma, H.; Jia, Z. Change Detection from SAR Images Based on Convolutional Neural Networks Guided by Saliency Enhancement. Remote Sens. 2021, 13, 3697. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, F.; Dong, J.; Du, Q.; Li, H.C. Synthetic aperture radar image change detection via siamese adaptive fusion network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10748–10760. [Google Scholar] [CrossRef]
- Zhang, W.; Jiao, L.; Liu, F.; Yang, S.; Song, W.; Liu, J. Sparse Feature Clustering Network for Unsupervised SAR Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Gao, F.; Dong, J.; Zhang, S.; Du, Q. Change Detection From Synthetic Aperture Radar Images via Graph-Based Knowledge Supplement Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1823–1836. [Google Scholar] [CrossRef]
- Zhao, G.; Peng, Y. Semisupervised SAR image change detection based on a siamese variational autoencoder. Inf. Process. Manag. 2022, 59, 102726. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar] [CrossRef]
- Gao, F.; Wang, X.; Gao, Y.; Dong, J.; Wang, S. Sea ice change detection in SAR images based on convolutional-wavelet neural networks. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1240–1244. [Google Scholar] [CrossRef]
- Qu, X.; Gao, F.; Dong, J.; Du, Q.; Li, H.C. Change detection in synthetic aperture radar images using a dual-domain network. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Gao, F.; Dong, J.; Li, B.; Xu, Q.; Xie, C. Change detection from synthetic aperture radar images based on neighborhood-based ratio and extreme learning machine. J. Appl. Remote Sens. 2016, 10, 046019. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, H.; Mou, L.; Liu, F.; Zhang, X.; Zhu, X.X.; Jiao, L. An unsupervised remote sensing change detection method based on multiscale graph convolutional network and metric learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Zhang, K.; Lv, X.; Chai, H.; Yao, J. Unsupervised SAR Image Change Detection for Few Changed Area Based on Histogram Fitting Error Minimization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Xiao, P.; Yuan, M.; Zhang, X.; Feng, X.; Guo, Y. Cosegmentation for object-based building change detection from high-resolution remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1587–1603. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Kittler, J.; Illingworth, J. Minimum error thresholding. Pattern Recognit. 1986, 19, 41–47. [Google Scholar] [CrossRef]
- Kim, W.; Kanezaki, A.; Tanaka, M. Unsupervised learning of image segmentation based on differentiable feature clustering. IEEE Trans. Image Process. 2020, 29, 8055–8068. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Gong, M.; Su, L.; Jia, M.; Chen, W. Fuzzy clustering with a modified MRF energy function for change detection in synthetic aperture radar images. IEEE Trans. Fuzzy Syst. 2013, 22, 98–109. [Google Scholar] [CrossRef]
- Gao, F. SAFNet. Available online: https://github.com/summitgao/SAR_CD_SAFNet/blob/main/SAFNet.ipynb (accessed on 12 December 2022).
- Gao, F. DDNet. Available online: https://github.com/summitgao/SAR_CD_DDNet (accessed on 12 December 2022).
- Chierchia, G.; El Gheche, M.; Scarpa, G.; Verdoliva, L. Multitemporal SAR image despeckling based on block-matching and collaborative filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5467–5480. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B. Generalized minimum-error thresholding for unsupervised change detection from SAR amplitude imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2972–2982. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).