Spatiotemporal Variations of Soil Temperature at 10 and 50 cm Depths in Permafrost Regions along the Qinghai-Tibet Engineering Corridor
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area
2.2. Data
2.3. Methods
3. Results
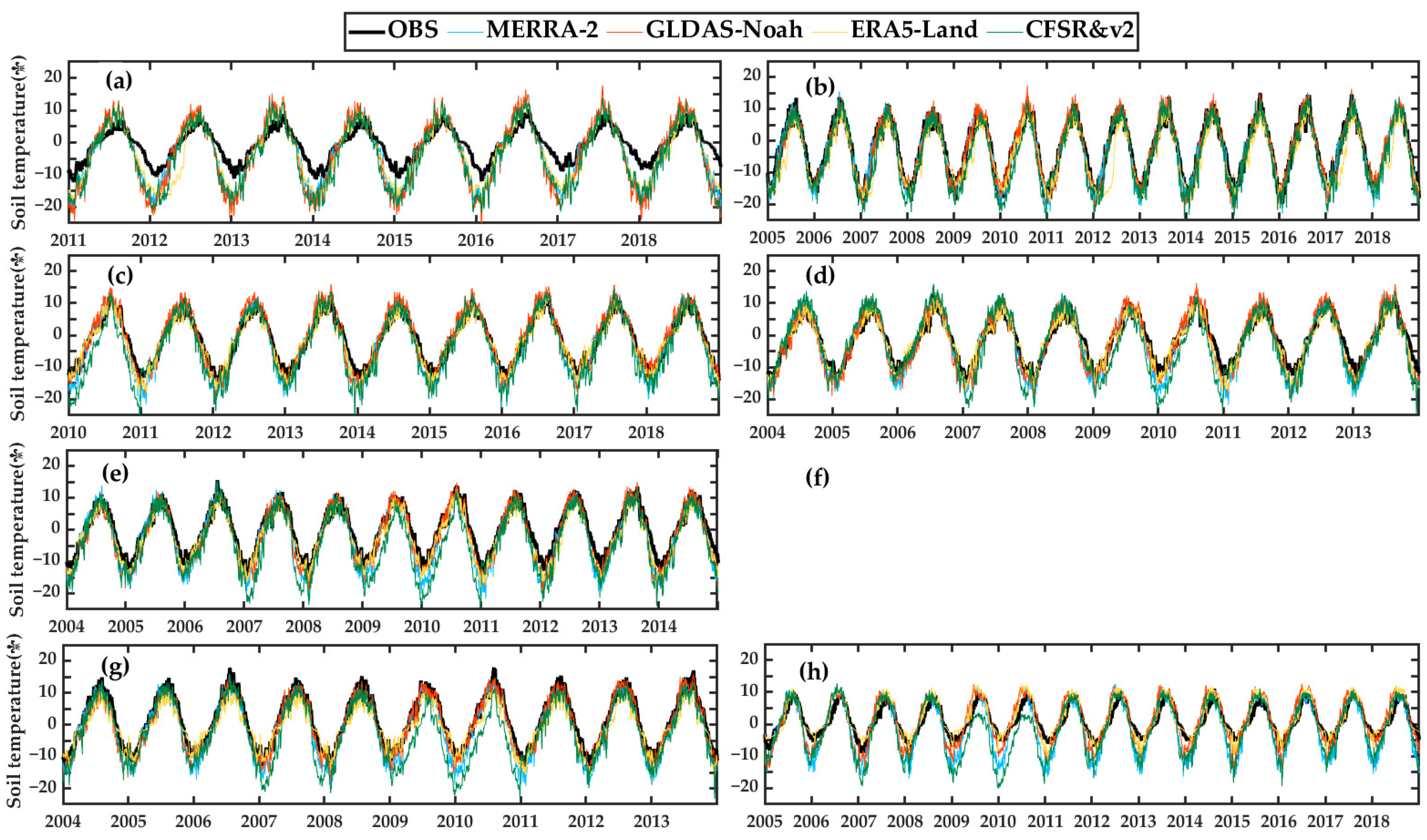
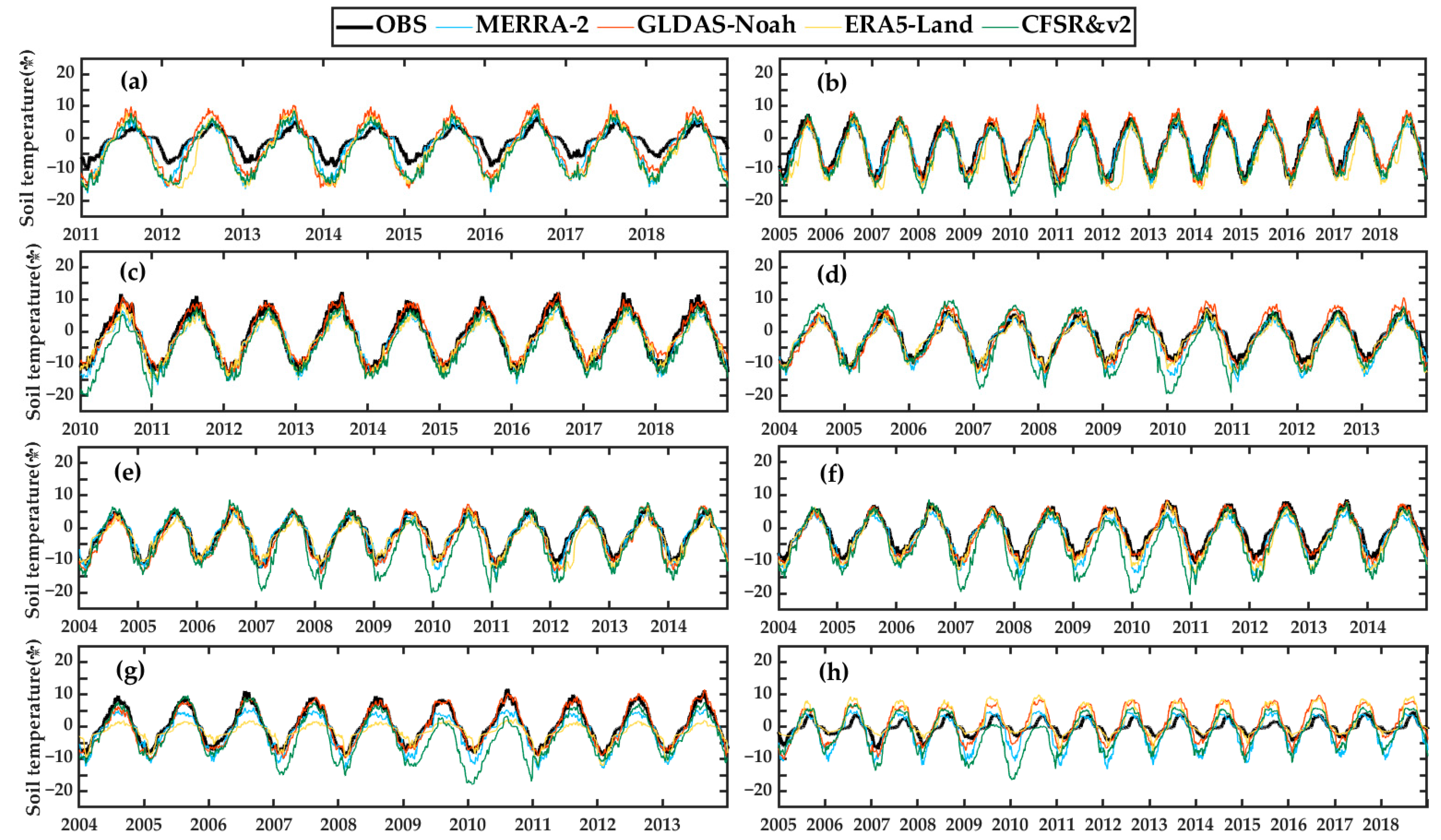
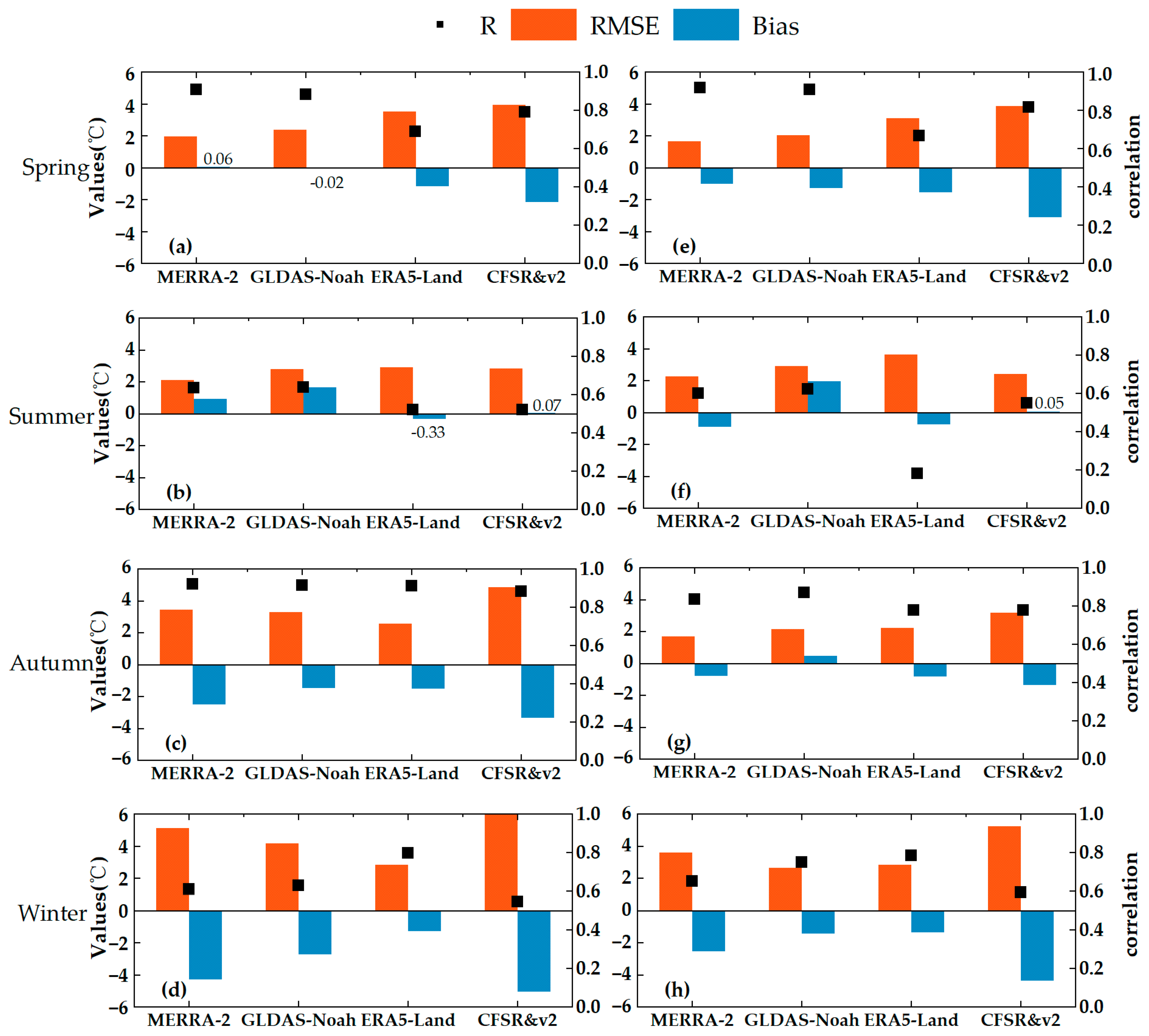
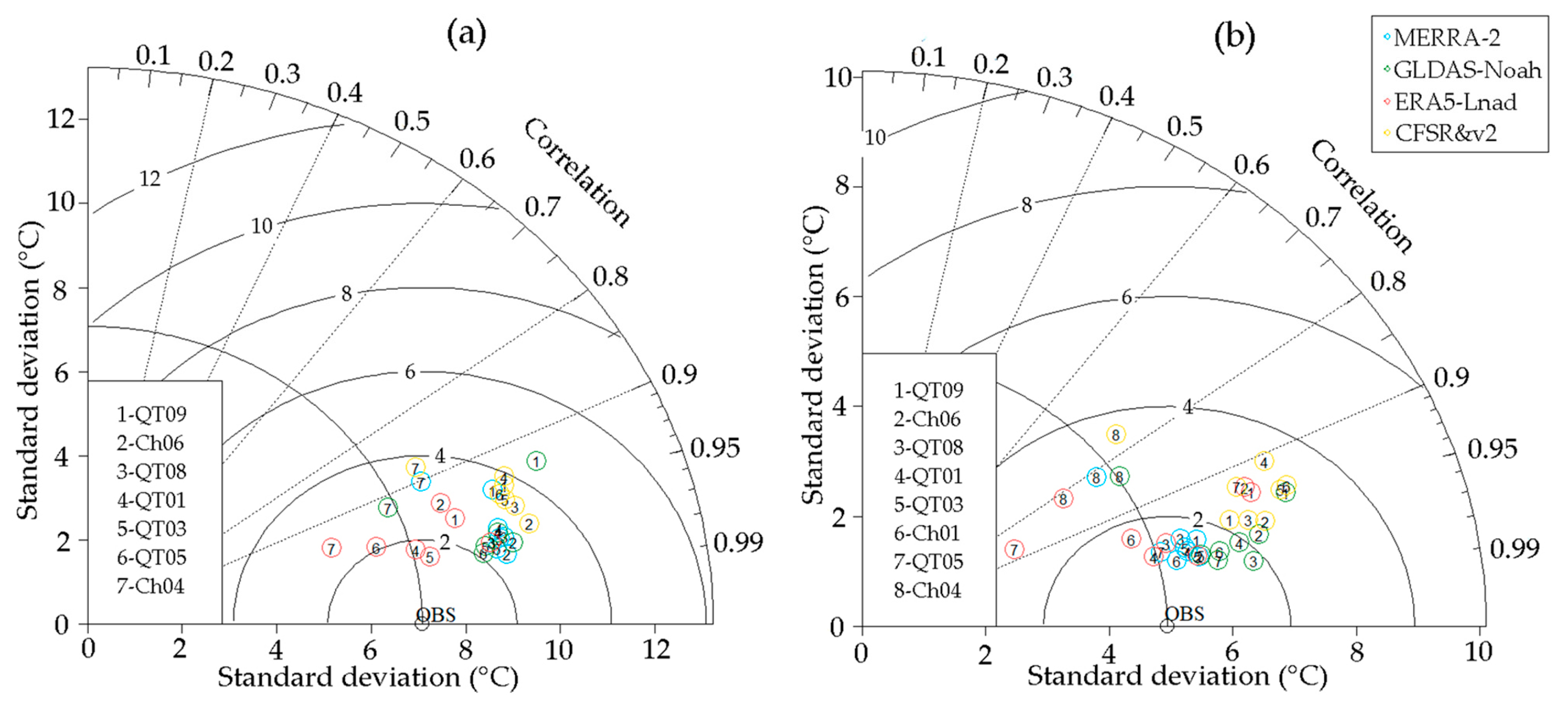
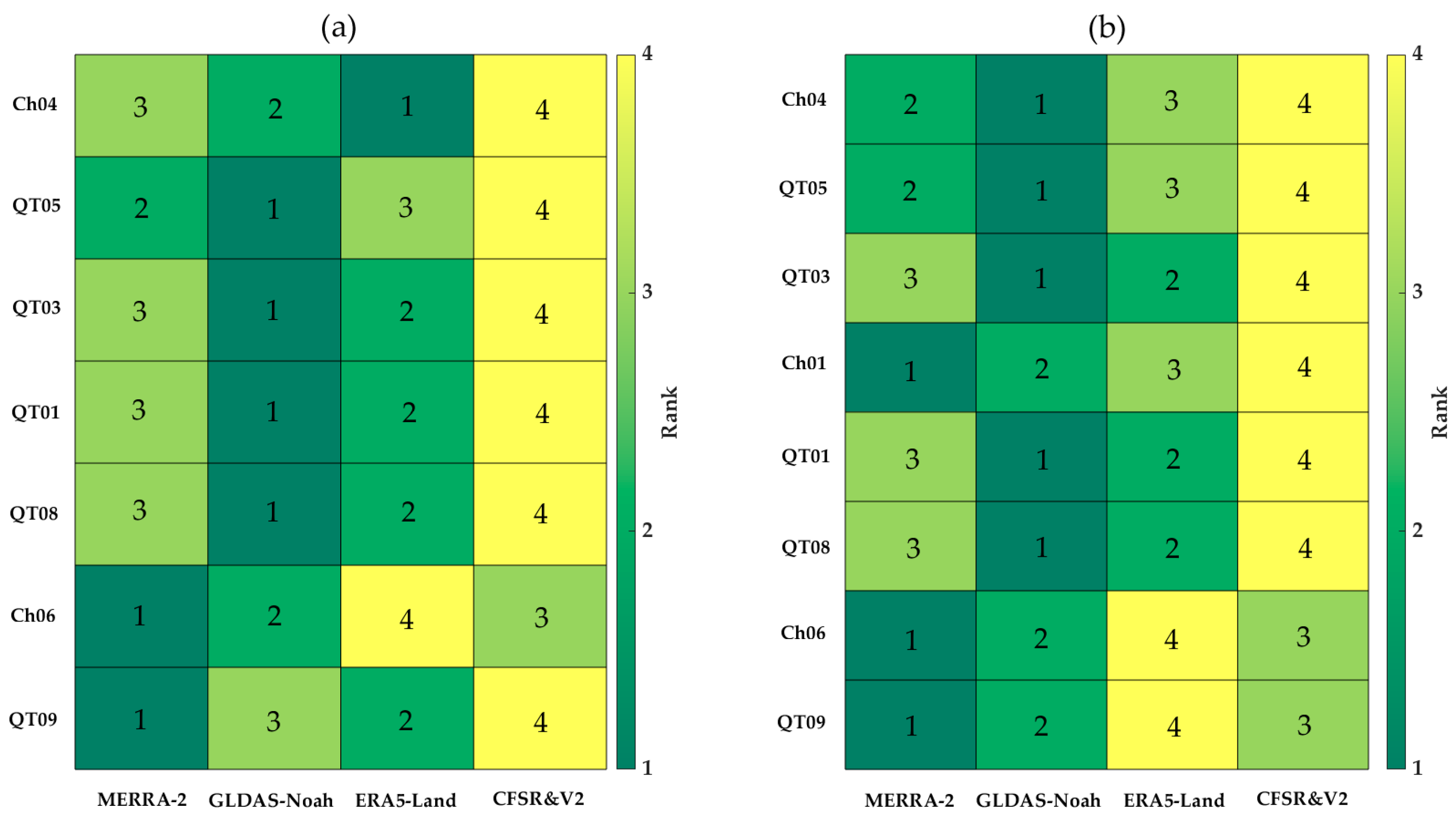
3.1. The Applicability of Reanalysis Data Products
3.2. Calibration of Reanalysis Data Products
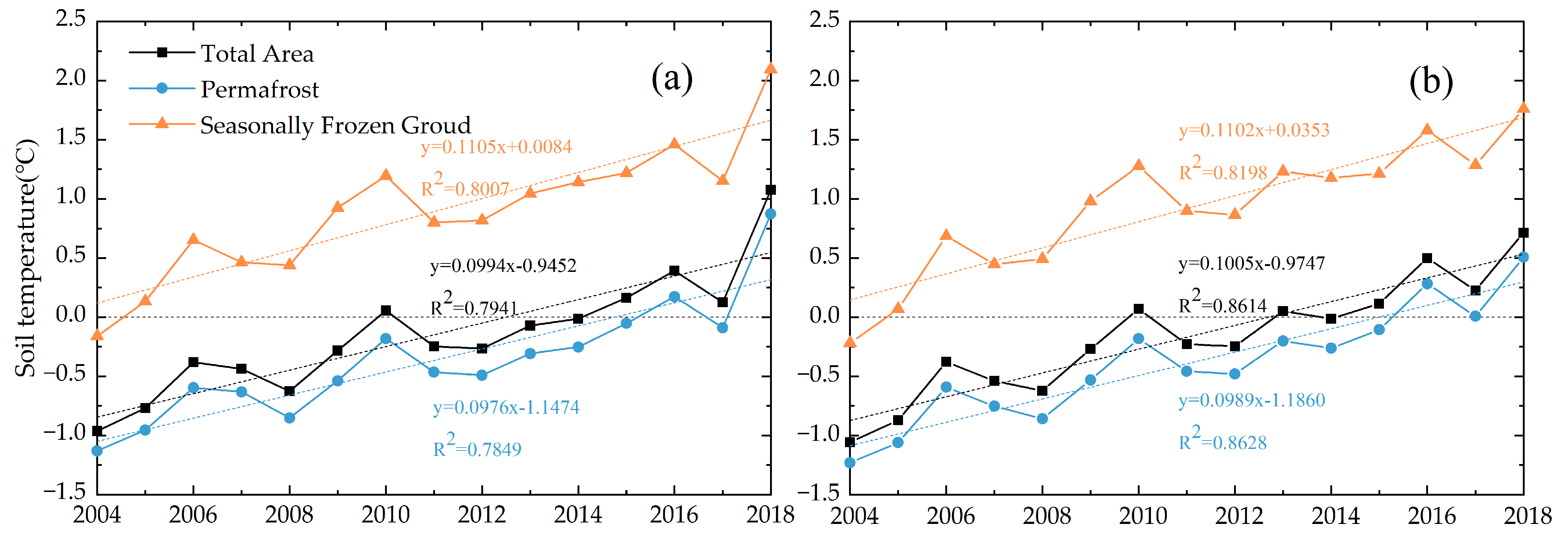
3.3. Temporal and Spatial Variation of Soil Temperature in the Shallow Layer
4. Discussion
4.1. The Applicability of the Different Reanalysis Soil Temperature Datasets
4.2. The Difference in Spatiotemporal Variations of Soil Temperature
4.3. The Limitation and Uncertainty of Soil Temperature
5. Conclusions
- (1)
- The four reanalysis datasets underestimated soil temperature the most in winter. The applicability of the four reanalysis datasets was higher at 50 cm. GLDAS-Noah had the lowest bias (Bias = −0.43 °C) from the measured data at all sites. Overall, the applicability of the GLDAS-Noah data was higher in this study area.
- (2)
- The multiple linear regression and random forest methods improved the accuracy of the GLDAS-Noah data to some extent. GLDAS-Noah corrected by the random forest model was more consistent with the measured data. The RMSE and bias of the random forest model were lower than those of the multiple linear regression model.
- (3)
- The soil temperature was in a warming state from 2004 to 2018, and the warming rate of the soil temperature at 50 cm depth is slightly higher than that of 10 cm. The warming rate of soil in the seasonally frozen ground regions is higher than that in the permafrost regions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, X.; Lai, X.; Fan, G.; Wen, J.; Yuan, Y.; Wang, X.; Wang, Z.; Zhu, L.; Zhang, Y.; Wang, B. Analysis on the applicability of reanalysis soil temperature and moisture datasets over Qinghai-Tibetan plateau. Plateau Meteorol. 2018, 37, 626–641. [Google Scholar]
- Lin, Z.; Ren, L.I.; Ding, Y.; Xiao, Y.; Sun, L.; Yang, L. Soil thermal regime in Qinghai-Tibet Plateau and its adjacent regions during 1977–2006. Adv. Clim. Change Res. 2011, 7, 307. [Google Scholar]
- Decharme, B.; Martin, E.; Faroux, S. Reconciling soil thermal and hydrological lower boundary conditions in land surface models. J. Geophys. Res. Atmos. 2013, 118, 7819–7834. [Google Scholar] [CrossRef]
- Cuo, L.; Zhang, Y.; Bohn, T.J.; Zhao, L.; Li, J.; Liu, Q.; Zhou, B. Frozen soil degradation and its effects on surface hydrology in the northern Tibetan Plateau. J. Geophys Res. Atmos. 2015, 120, 8276–8298. [Google Scholar] [CrossRef]
- Onwuka, B.; Mang, B. Effects of soil temperature on some soil properties and plant growth. Adv. Plants Agric. Res. 2018, 8, 34–37. [Google Scholar] [CrossRef]
- Turetsky, M.R.; Abbott, B.W.; Jones, M.C.; Anthony, K.W.; Olefeldt, D.; Schuur, E.A.; Grosse, G.G.; Kuhry, P.; Hugelius, G.; Koven, C.; et al. Carbon release through abrupt permafrost thaw. Nat. Geosci. 2020, 13, 138–143. [Google Scholar] [CrossRef]
- Cheng, G.; Zhao, L.; Li, R.; Wu, X.; Sheng, Y.; Hu, G.; Zou, D.; Jin, H.; Xin, L.; Wu, Q. Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau. Chin. Sci. Bull. 2019, 64, 2783–2795. [Google Scholar]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H.; Li, D. A projection of permafrost degradation on the Tibetan Plateau during the 21st century. J. Geophys. Res. Atmos. 2012, 117, D05106. [Google Scholar] [CrossRef]
- Fang, X.; Luo, S.; Lyu, S. Observed soil temperature trends associated with climate change in the Tibetan Plateau, 1960–2014. Theor. Appl. Climatol. 2019, 135, 169–181. [Google Scholar] [CrossRef]
- Yang, M.; Nelson, F.E.; Shiklomanov, N.I.; Guo, D.; Wan, G. Permafrost degradation and its environmental effects on the Tibetan Plateau: A review of recent research. Earth Sci. Rev. 2010, 103, 31–44. [Google Scholar] [CrossRef]
- Genxu, W.; Yuanshou, L.; Yibo, W.; Qingbo, W. Effects of permafrost thawing on vegetation and soil carbon pool losses on the Qinghai–Tibet Plateau, China. Geoderma 2008, 143, 143–152. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, Z.; Xie, Z.; Ma, W.; Wang, B.; Chen, X.; Li, M.; Zhong, L.; Sun, F.; Gu, L.; et al. A long-term (2005–2016) dataset of hourly integrated land–atmosphere interaction observations on the Tibetan Plateau. Earth Syst. Sci. Data 2020, 12, 2937–2957. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, P.; Liu, W.; Guo, Z.; Xue, S. The application of elevation corrected MERRA2 reanalysis ground surface temperature in a permafrost model on the Qinghai-Tibet Plateau. Cold Reg. Sci. Technol. 2020, 175, 103067. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, H.; Wang, M.; Liu, X.; Chen, Q.; Wang, C.; Zhang, H. A Review of Satellite Synthetic Aperture Radar Interferometry Applications in Permafrost Regions: Current Status, Challenges, and Trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 93–114. [Google Scholar] [CrossRef]
- Gao, H.; Nie, N.; Zhang, W.; Chen, H. Monitoring the spatial distribution and changes in permafrost with passive microwave remote sensing. ISPRS J. Photogramm. Remote Sens. 2020, 170, 142–155. [Google Scholar] [CrossRef]
- Tian, H.; Liu, L.; Zhang, Z.; Chen, H.; Zhang, X.; Wang, T.; Kang, Z. Spatiotemporal diversity and attribution analysis of land surface temperature in China from 2001 to 2020. J. Geogr. Sci. 2022, 77, 1713–1729. [Google Scholar]
- Liangpei, Z.; Jiang, H.E.; Qianqian, Y.; Yi, X.; Yuan, Q. Data-driven multi-source remote sensing data fusion: Progress and challenges. Acta Geod. Et Cartogr. Sin. 2022, 51, 1317. [Google Scholar]
- Dan, S.; Shi, C.; Shen, R.; Lei, B. Evaluation of ERA70, CLDAS, and ERA-Interim Reanalysis Surface Soil Temperatures Across China. Meteorol. Sci. Technol. 2021, 49, 830–837. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, L.; Wu, X.; Li, R.; Wu, T.; Su, Y.; Hao, J. Evaluation of reanalysis air temperature products in permafrost regions on the Qinghai-Tibetan Plateau. Theor. Appl. Climatol 2019, 138, 1457–1470. [Google Scholar] [CrossRef]
- Huang, X.; Han, S.; Shi, C. Evaluation of Three Air Temperature Reanalysis Datasets in the Alpine Region of the Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 4447. [Google Scholar] [CrossRef]
- Yang, S.; Li, R.; Wu, T.; Hu, G.; Xiao, Y.; Du, Y.; Zhu, X.; Jie, N.; Ma, J.; Zhang, Y. Evaluation of reanalysis soil temperature and soil moisture products in permafrost regions on the Qinghai-Tibetan Plateau. Geoderma 2020, 377, 114583. [Google Scholar] [CrossRef]
- Ramakrishna, A.; Tam, H.M.; Wani, S.P.; Long, T.D. Effect of mulch on soil temperature, moisture, weed infestation and yield of groundnut in northern Vietnam. Field Crops Res. 2006, 95, 115–125. [Google Scholar] [CrossRef]
- Hu, Q.; Feng, S. A daily soil temperature dataset and soil temperature climatology of the contiguous United States. J. Appl. Meteorol. 2003, 42, 1139–1156. [Google Scholar] [CrossRef]
- Jung, C.; Lee, Y.; Cho, Y.; Kim, S. A study of spatial soil moisture estimation using a multiple linear regression model and MODIS land surface temperature data corrected by conditional merging. Remote Sens. 2017, 9, 870. [Google Scholar] [CrossRef]
- Shen, Y.; Ruijsch, J.; Lu, M.; Sutanudjaja, E.H.; Karssenberg, D. Random forests-based error-correction of streamflow from a large-scale hydrological model: Using model state variables to estimate error terms. Comput. Geosci. 2022, 159, 105019. [Google Scholar] [CrossRef]
- Zarei, M.; Mohsen, N.; Mastouri, R. Bias correction of global ensemble precipitation forecasts by Random Forest method. Earth Sci. Inform. 2021, 14, 677–689. [Google Scholar] [CrossRef]
- He, Y.; Chen, C.; Li, B.; Zhang, Z. Prediction of near-surface air temperature in glacier regions using ERA5 data and the random forest regression method. Remote Sens. Appl. Soc. Environ. 2022, 28, 100824. [Google Scholar]
- Song, Y.; Zhou, D.; Zhang, H.; Li, G.; Jin, Y.; Li, Q. Effects of vegetation height and density on soil temperature variations. Chin. Sci. Bull. 2013, 58, 907–912. [Google Scholar] [CrossRef]
- Park, H.; Sherstiukov, A.B.; Fedorov, A.N.; Polyakov, I.V.; Walsh, J.E. An observation-based assessment of the influences of air temperature and snow depth on soil temperature in Russia. Environ. Res. Lett. 2014, 9, 064026. [Google Scholar] [CrossRef]
- Bennie, J.; Huntley, B.; Wiltshire, A.; Hill, M.O.; Baxter, R. Slope, aspect and climate: Spatially explicit and implicit models of topographic microclimate in chalk grassland. Ecol. Model. 2008, 216, 47–59. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, D.; Hu, G.; Wu, T.; Du, E.; Liu, G.; Yao, X.; Ren, L.; Pang, Q.; Qiao, Y.; et al. A synthesis dataset of permafrost thermal state for the Qinghai–Tibet (Xizang) Plateau, China. Earth Syst. Sci. Data 2021, 13, 4207–4218. [Google Scholar] [CrossRef]
- Wang, Z.W.; Wang, Q.; Zhao, L.; Wu, X.; Yue, G.; Zou, D.; Nan, Z.; Liu, G.; Pang, Q.; Fang, H.; et al. Mapping the vegetation distribution of the permafrost zone on the Qinghai-Tibet Plateau. J. Mt. Sci. 2016, 13, 1035–1046. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Peters-Lidard, C.; Kato, H.; Kumar, S.; Gottschalck, J.; Mitchell, K.; Meng, J. NASA/NOAA’s global land data assimilation system (GLDAS): Recent results and future plans. In Proceedings of the ECMWF/ELDAS Workshop on Land Surface Assimilation, Reading, UK, 8–11 November 2004; pp. 61–68. [Google Scholar]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data Discuss. 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Yan, D.; Ma, N.; Zhang, Y. Development of a fine-resolution snow depth product based on the snow cover probability in the Tibetan Plateau: Validations and spatial-temporal analyses. J. Hydrol. 2022, 604, 127027. [Google Scholar] [CrossRef]
- Yan, D.; Ma, N.; Zhang, Y. A daily, 0.05° Snow depth dataset for Tibetan Plateau (2000–2018). Natl. Tibet. Plateau Data Cent. 2022. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.; Nelson, A.; Edith, G. Hole-Filled Seamless SRTM Data V4, Tech. Rep. International Centre for Tropical Agriculture (CIAT), Cali, Columbia. Available online: http://srtm.csi.cgiar.org (accessed on 5 April 2022).
- Bakar, N.M.A.; Tahir, I.M. Applying multiple linear regression and neural network to predict bank performance. Int. Bus. Res. 2009, 2, 176–183. [Google Scholar] [CrossRef]
- Dong, H.; Wang, Y.; Li, L. A Review of Random Forest Optimization Algorithms. China Comput. Commun. 2021, 33, 34–37. [Google Scholar]
- Li, T.; Tian, Y.; Wu, L.; Liu, L. Landslide Susceptibility Mapping Using Random Forest. Geogr. Geo Inf. Sci. 2014, 30, 25–30+2. [Google Scholar]
- Brunke, M.A.; Fairall, C.W.; Zeng, X.; Eymard, L.; Curry, J.A. Which Bulk Aerodynamic Algorithms are Least Problematic in Computing Ocean Surface Turbulent Fluxes. J. Clim. 2003, 16, 619–635. Available online: https://journals.ametsoc.org/view/journals/clim/16/4/15200442_2003_016_0619_wbaaal_2.0.co_2.xml (accessed on 13 July 2022). [CrossRef]
- Brunke, M.A.; Wang, Z.; Zeng, X.; Bosilovich, M.; Shie, C. An Assessment of the Uncertainties in Ocean Surface Turbulent Fluxes in 11 Reanalysis, Satellite-Derived, and Combined Global Datasets. J. Clim. 2011, 24, 5469–5493. Available online: https://journals.ametsoc.org/view/journals/clim/24/21/2011jcli4223.1.xml (accessed on 13 July 2022). [CrossRef]
- Hu, G.; Zhao, L.; Li, R.; Wu, X.; Wu, T.; Xie, C.; Zhu, X.; Su, Y. Variations in soil temperature from 1980 to 2015 in permafrost regions on the Qinghai-Tibetan Plateau based on observed and reanalysis products. Geoderma 2019, 337, 893–905. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Y.; Chen, J.; Zhai, X.; Hu, Q. Performance of multiple machine learning model simulation of process characteristic indicators of different flood types. Progress in Geography 2022, 41, 1239–1250. [Google Scholar] [CrossRef]
- Zhu, F.; Cuo, L.; Zhang, Y.; Luo, J.J.; Lettenmaier, D.P.; Lin, Y.; Liu, Z. Spatiotemporal variations of annual shallow soil temperature on the Tibetan Plateau during 1983–2013. Clim. Dyn. 2018, 51, 2209–2227. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Ding, Y.; Wu, T.; Xiao, Y.; Du, E.; Liu, G.; Qiao, Y. Temporal and spatial variations of the active layer along the Qinghai-Tibet Highway in a permafrost region. Chin. Sci. Bull. 2012, 57, 2864–2871. [Google Scholar] [CrossRef]
- Nan, Y.; Fan, G. Analysis of Soil Temperature Variation over the Qinghai-Xizang Plateau from 2000 to 2016. J. Southwest Univ. 2019, 41, 40–51. [Google Scholar]
- Qin, Y.; Wu, T.; Li, R. The applicability of ERA-Interim land surface temperature dataset to map the permafrost distribution over the Tibetan Plateau. J. Glaciol. Geocryol. 2015, 37, 1534–1543. [Google Scholar]
- Bi, H.; Ma, J.; Zheng, W.; Zeng, J. Comparison of soil moisture in GLDAS model simulations and in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 2658–2678. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, W.; Guo, Z.; Xue, S. Spatial and temporal variations in soil temperatures over the Qinghai–Tibet Plateau from 1980 to 2017 based on reanalysis products. Theor. Appl. Climatol. 2020, 140, 1055–1069. [Google Scholar] [CrossRef]
- Yuan, L.; Zhao, L.; Hu, G.; Lu, M.; Zhou, H.; Liu, S.; Qiao, Y. Hydro-thermal dynamic and soil thermal diffusivity characteristics of typical active layer on the central Tibetan Plateau. J. Glaciol. Geocryol. 2020, 42, 378–389. [Google Scholar]
- Ma, J.; Li, R.; Liu, H.; Wu, T.; Yao, X.; Du, Y.; Yang, S.; Shi, J.; Qiao, Y. A review on the development of study on hydrothermal characteristics of active in permafrost areas in permafrost areas in Qinghai-Tibet Plateau. J. Glaciol. Geocryol. 2020, 42, 195–204. [Google Scholar]
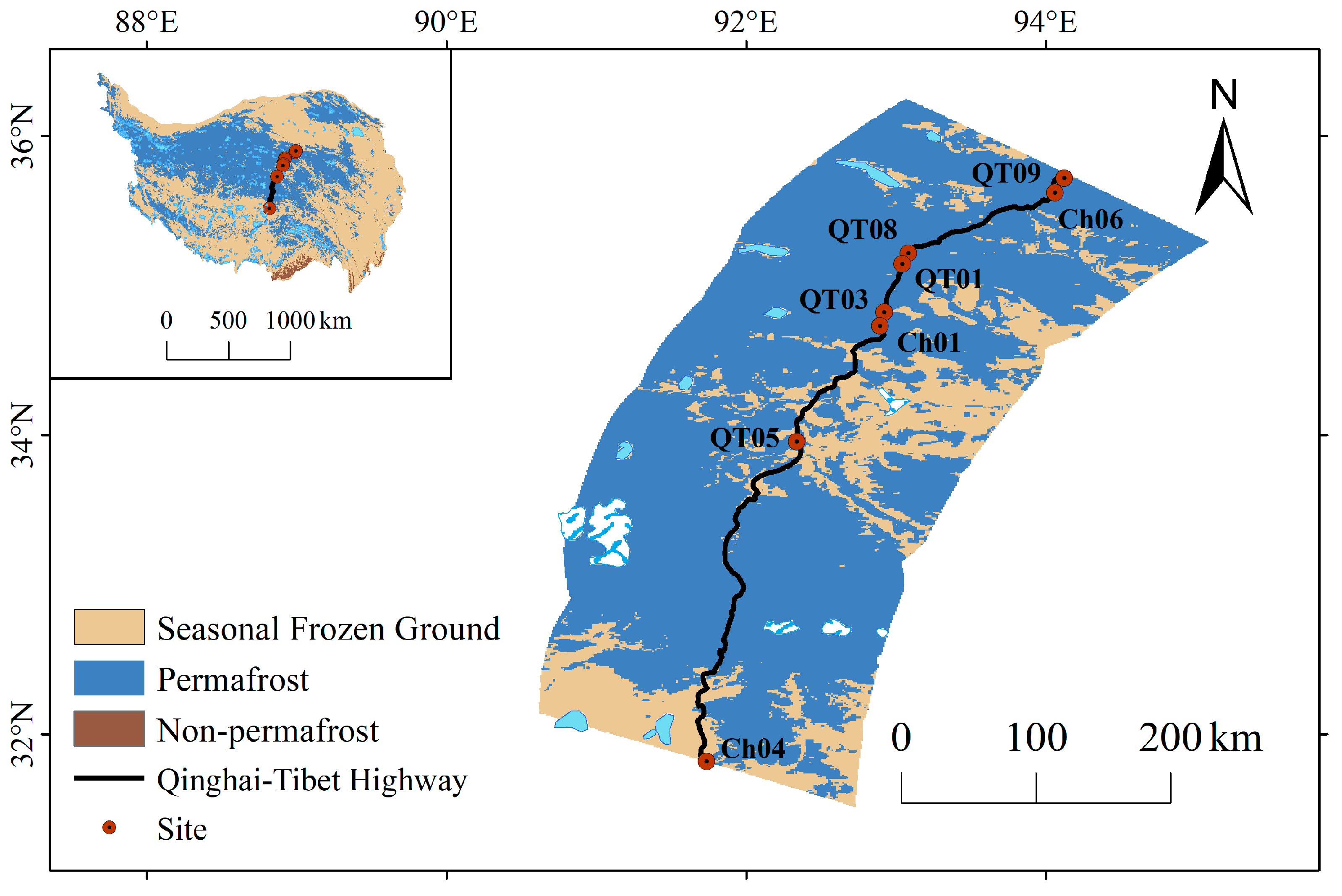

| Sites | Location | Longitude (°E) | Latitude (°N) | Altitude (m) | Time Period | Soil Temperature Depth/cm | Vegetation Type |
|---|---|---|---|---|---|---|---|
| QT09 | Xidatan | 94.1 | 35.7 | 4538 | 2011–2018 | 10, 40, 120, 160 | Alpine meadows |
| Ch06 | Kunlun Pass | 94.0 | 35.6 | 4746 | 2005–2018 | 10, 50, 100, 180 | Alpine grassland |
| QT08 | Wudaoliang | 93.0 | 35.2 | 4783 | 2010–2018 | 10, 40, 120, 200, 240 | Alpine meadows |
| QT01 | Hoh Xil | 93.0 | 35.1 | 4734 | 2004–2013 | 10, 50, 100, 180 | Alpine meadows |
| QT03 | Beiluhe | 92.9 | 34.8 | 4656 | 2004–2014 | 10, 50, 90, 200, 240 | Alpine meadows |
| Ch01 | Wind volcano | 92.8 | 34.7 | 4896 | 2005–2014 | 10, 50, 100, 160 | Alpine meadows |
| QT05 | Kaixinling | 92.3 | 33.9 | 4652 | 2004–2013 | 10, 50, 90, 210, 315 | Alpine grassland |
| Ch04 | Liangdaohe | 91.7 | 31.8 | 4808 | 2005–2018 | 15, 50, 95, 120 | Alpine meadows |
| Data Name | Temporal Resolution | Spatial Resolution | Time Period | Soil Temperature Depth/cm |
|---|---|---|---|---|
| MERRA-2 | 1 h | 0.5° × 0.625° | 1980–2021 | 9.88, 19.52, 38.59, 76.27, 150.7, 1000 |
| GLDAS-Noah | 3 h | 0.25° × 0.25° | 2000–2021 | 0–10, 10–40, 40–100, 100–200 |
| ERA5-Land | 1 h | 0.1° × 0.1° | 1950–2021 | 0–7, 7–28, 28–100, 100–200 |
| CFSR | 6 h | 0.312° × 0.312° | 1979–2010 | 0–10, 10–40, 40–100, 100–200 |
| CFSv2 | 6 h | 0.205° × 0.204° | 2011–2021 | 0–10, 10–40, 40–100, 100–200 |
| Depth | Model | R2 | RMSE (°C) | Bias (°C) |
|---|---|---|---|---|
| 10 cm | original | 0.89 | 3.23 | −0.62 |
| MLR | 0.91 | 2.14 | −0.82 × 10−2 | |
| RF | 0.95 | 1.74 | −0.55 × 10−2 | |
| 50 cm | original | 0.86 | 2.47 | −0.06 |
| MLR | 0.88 | 1.72 | −0.64 × 10−2 | |
| RF | 0.95 | 1.19 | 0.26 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, M.; Zhao, L.; Wang, C.; Hu, G.; Li, Y.; Zhao, J.; Zou, D.; Xing, Z.; Qiao, Y.; Liu, G.; et al. Spatiotemporal Variations of Soil Temperature at 10 and 50 cm Depths in Permafrost Regions along the Qinghai-Tibet Engineering Corridor. Remote Sens. 2023, 15, 455. https://doi.org/10.3390/rs15020455
Jiao M, Zhao L, Wang C, Hu G, Li Y, Zhao J, Zou D, Xing Z, Qiao Y, Liu G, et al. Spatiotemporal Variations of Soil Temperature at 10 and 50 cm Depths in Permafrost Regions along the Qinghai-Tibet Engineering Corridor. Remote Sensing. 2023; 15(2):455. https://doi.org/10.3390/rs15020455
Chicago/Turabian StyleJiao, Mengdi, Lin Zhao, Chong Wang, Guojie Hu, Yan Li, Jianting Zhao, Defu Zou, Zanpin Xing, Yongping Qiao, Guangyue Liu, and et al. 2023. "Spatiotemporal Variations of Soil Temperature at 10 and 50 cm Depths in Permafrost Regions along the Qinghai-Tibet Engineering Corridor" Remote Sensing 15, no. 2: 455. https://doi.org/10.3390/rs15020455
APA StyleJiao, M., Zhao, L., Wang, C., Hu, G., Li, Y., Zhao, J., Zou, D., Xing, Z., Qiao, Y., Liu, G., Du, E., Xiao, M., & Hou, Y. (2023). Spatiotemporal Variations of Soil Temperature at 10 and 50 cm Depths in Permafrost Regions along the Qinghai-Tibet Engineering Corridor. Remote Sensing, 15(2), 455. https://doi.org/10.3390/rs15020455







