Abstract
Convolutional neural networks (CNNs) have demonstrated impressive performance and have been broadly applied in hyperspectral image (HSI) classification. However, two challenging problems still exist: the first challenge is that redundant information is averse to feature learning, which damages the classification performance; the second challenge is that most of the existing classification methods only focus on single-scale feature extraction, resulting in underutilization of information. To resolve the two preceding issues, this article proposes a multiscale cross interaction attention network (MCIANet) for HSI classification. First, an interaction attention module (IAM) is designed to highlight the distinguishability of HSI and dispel redundant information. Then, a multiscale cross feature extraction module (MCFEM) is constructed to detect spectral–spatial features at different scales, convolutional layers, and branches, which can increase the diversity of spectral–spatial features. Finally, we introduce global average pooling to compress multiscale spectral–spatial features and utilize two fully connection layers, two dropout layers to obtain the output classification results. Massive experiments on three benchmark datasets demonstrate the superiority of our presented method compared with the state-of-the-art methods.
1. Introduction
A hyperspectral image (HSI) consists of hundreds of narrow spectral bands providing a detailed spectrum regarding the physical properties of materials and abundant spatial information enhancing the characterization of HSI scenes. Benefiting from affluent spectral and spatial features, HSI has been widely applied in numerous fields, such as military detection [1], change detection [2], and environmental monitoring [3]. Recently, HSI classification is one of the most popular technologies in the field of hyperspectral remote sensing. However, HSI classification also struggles with many challenges, such as lack of labeled samples, curse of dimension, and large spatial variability in spectral signatures. Therefore, it is still a relevant but challenging research topic in remote sensing.
Incipiently, many scholars focus on utilizing spectral information to settle “the curse of dimension” problem. Representative algorithms included band selection [4], linear discriminant analysis [5], collaborative representation classifier [6], maximum likelihood [7], etc. In addition to spectral features, spatial dependency was also incorporated into many classification frameworks, such as Markov random field [8], superpixel segmentation [9], 3-D morphological profile [10], and multiple kernel learning [11]. Although the abovementioned methods obtained good classification accuracy, they did not incorporate spectral features. Consequently, a promising method was presented to combine spatial and spectral information for classification. Li et al. proposed a spectral–spatial kernel SVM to obtain spectral and spatial features [12]. According to the structural similarity, a nonlocal weighted joint SRC method was built [13]. The above classification approaches, whether based on spatial features, spectral features, or spectral–spatial joint features, all relied on prior knowledge and lacked robust representation and generalization ability.
Of late, due to powerful feature extraction capacity, deep learning (DL) has shown promising performance and has been gradually introduced into HSI classification. Hu et al. first applied the concept of CNN to HSI classification [14]. Li et al. designed a CNN to extract pixel-pair features to obtain the correlation between hyperspectral pixels [15]. However, these methods need to transform the input data into a 1-D vector, resulting in loss of rich spatial information. To further improve classification accuracy, many classification approaches based on 2-D CNNs and 3-D CNNs had been developed to extract spectral and spatial information. Cao et al. built a compressed convolutional neural network, which was composed of a teacher model and a student model, for HSI classification [16]. Roy et al. employed 2-D CNN and 3-D CNN to excavate spatial–spectral joint features [17]. Zhang et al. presented a novel CNN exploiting diverse region inputs to capture contextual interactional information [18]. To extract quality feature maps, Ahmad devised a fast 3-D CNN [19]. To address the fixed problem of traditional convolutional kernels, Zhu et al. constructed a deformable CNN for HSI classification [20]. Li et al. trained a 3-D CNN model superior to traditional classification methods utilizing 2-D CNN, which can directly extract spatial–spectral joint information from the original HSI [21].
With the breakthrough of DL, some auxiliary technologies have emerged, such as residual learning, dense connection, multiscale feature extraction, and multilevel feature fusion. For example, considering the strong complementarity among different layers, Xie et al. proposed a multiscale densely connected convolutional network, which could make full use of information at diverse scales for HSI classification [22]. To eliminate redundant information and improve processing efficiency, Xu et al. designed a multiscale spectral–spatial CNN based on a novel image classification framework [23]. Zhang et al. presented a spectral–spatial fractal residual CNN to effectively excavate the spectral–spatial features [24]. Gao et al. devised a multiscale dual-branch feature fusion and attention network, which integrated the feature reuse property of residual learning and the feature exploration capacity of dense connection [25]. Song et al. improved the classification performance by introducing a deep residual network [26]. To obtain spectral-, spatial-, and multiscale-enhanced representations, Li et al. built a long short-term memory neural network for classification tasks [27].
To further obtain more discriminative and representative features, the attention mechanism is also applied to CNNs. To highlight the validity of sensitive pixels, Zhou et al. developed an attention module [28]. Yang et al. utilized a cross-spatial attention block to generate spatial and spectral information [29]. Hang et al. adopted a spectral attention subnetwork to classify spectral information and a spatial attention subnetwork to classify spatial information; then, the adaptive weighted summation approach was utilized to aggregate spectral and spatial classification results [30]. To boost the classification accuracy, Xiang et al. constructed a multilevel hybrid attention end-to-end model to acquire spatial–spectral fusion features [31]. Tu et al. designed a local–global hierarchical weighting fusion network, which was composed of a spectral subnetwork and a spatial subnetwork, including a pooling strategy based on local attention [32].
Inspired by the abovementioned advanced approaches, in this article, we propose a multiscale cross interaction attention network (MCIANet) for HSI classification. First, we design an interaction attention module (IAM) to highlight the distinguishability of HSI by learning the importance of different spectral bands, spatial pixels, and cross dimensions and to dispel redundant information. Then, the obtained interaction attention-enhanced features are fed into a multiscale cross feature extraction module (MCFEM), which is constructed to extract spectral–spatial features at different convolutional layers, scales, and branches. Finally, we introduce global average pooling to compress multiscale spectral–spatial features and utilize two dropout layers, two fully connected layers, and a SoftMax layer to obtain the output classification results.
The main contributions of this article are summarized as follows:
- (1)
- To strengthen the distinguishability of HSI and dispel the interference of redundant information, we design an interaction attention module (IAM). IAM can highlight spectral–spatial features favorable for classification by learning the importance of different spectral bands, spatial contexts, and cross dimensions.
- (2)
- To enrich the multiformity of spectral–spatial information, we devise a multiscale cross feature extraction module (MCFEM) based on an innovative multibranch lower triangular fusion structure. For one thing, MCFEM utilizes multiple available receptive fields to extract multiscale spectral–spatial features. For another thing, MCFEM introduces “up-to-down” and “down-to-up” fusion strategies to maximize use of information flows between different convolutional layers and branches.
- (3)
- IAM and MCFEM constitute the proposed HSI classification method. Compared with the state-of-the-art results of DL methods, the experimental results on three benchmark datasets show competitive performance, which indicates the proposed method exhibits potential to capture more discriminative and representative multiscale spectral–spatial features.
The remainder of this article is organized as follows. In Section 2, the related works on development of HSI classification are described. In Section 3, the overall framework of our designed model is presented. In Section 4, we provide the experimental results, with an analysis on three benchmark datasets. Finally, Section 5 provides conclusions.
2. Related Works
HSI classification methods are generally classified into two categories: machine learning (ML)-based and deep learning (DL)-based methods. Classification methods based on ML usually design features manually and then send these features into classifiers for training. Representative algorithms are principal components analysis (PCA) [33], support vector machine (SVM) [34], and 3-D Gabor filters [35]. These methods rely on handcrafted features with insufficient generalization ability, leading to an unsatisfactory classification result. In contrast, DL-based approaches can not only spontaneously capture high-level features in a hierarchical extraction way but also provide excellent classification performance. The DL-based methods include stack autoencoders (SAEs) [36], recurrent neural networks (RNNs) [37], convolutional neural networks (CNNs) [38], deep belief networks (DBNs) [39], generation adversarial network (GANs) [40], and graph convolutional networks (GCNs) [41]. Among the various DL algorithms, CNNs-based classification methods exhibit outstanding capability for HSI classification.
Numerous existing HSI classification networks are devoted to extracting spectral–spatial features at different scales to boost the classification performance. Many multiscale-features-based classification methods have been developed. For example, to capture complex multiscale spatial–spectral features, Wang et al. presented a multiscale dense connection network for HSI classification [42]. Yu et al. built a dual-channel convolutional network that not only learned global features but also took full advantage of spectral–spatial features at different scales [43]. Gao et al. constructed a multiscale feature extraction module to obtain granular level features [25]. Lee et al. placed a multiscale filter bank on the first layer of the developed contextual deep CNN, aiming to achieve multiscale feature extraction [44]. To learn spectral–spatial features at different scales, Li et al. devised a multiscale deep middle-level feature fusion network [45]. Zhao et al. trained a multiscale CNN to extract contextual information at different scales for HSI classification [46]. To reduce parameters and obtain the contextual features at different scales, Xu et al. constructed a multiscale octave 3-D CNN [47]. Fu et al. designed a segmentation model utilizing the multiscale 2-D-singular spectrum analysis method to capture joint spectral–spatial features [48]. Most existing multiscale-features-based HSI classifications utilize a functional module to obtain spectral–spatial features with different scales. The functional module usually can be divided into two main categories: one is that first adopting multiple available receptive fields to capture spectral–spatial features with diverse scales, respectively, then utilizing a concatenated operation to aggregate these features to obtain multiscale spectral–spatial features. The other is that exploiting multibranch strategy to extract spectral–spatial features with different scales, where each branch uses diverse receptive fields, then utilizing a concatenated operation to aggregate these features to obtain multiscale spectral–spatial features. However, these methods only utilize an easy concatenated operation to integrate features from different receptive fields or branches and do not explore the cross interaction of different receptive fields or branches, which results in spectral–spatial information loss, and they are averse to classification accuracy.
The attention mechanism has been successfully used in various visual tasks, such as salient object detection [49,50], super-resolution reconstruction [51,52,53], and semantic segmentation [54,55,56]. Due to the abilities of substantial information locating and extraction from input data, the attention mechanism is also applied to remote sensing problems. Guo et al. combined a spatial attention module with a spectral attention module, which can enhance the distinguishability of spatial and spectral information [57]. Xiong et al. utilized the dynamic routing between attention initiation modules to adaptively learn the proposed architecture [58]. To facilitate classification accuracy, Mou et al. introduced an end-to-end spectral attention block [59]. An end-to-end attention recurrent CNN was developed to classify high-resolution remote sensing scenes [60]. Aiming to enhance the discriminative capacity of spectral–spatial features, Xue et al. used the attention mechanism to adaptively weight spectral-wise and spatial-wise responses [21]. Xi et al. designed a hybrid residual attention to settle the overfitting problem [61]. To better characterize spectral–spatial data, attention mechanisms were incorporated into ResNet [62]. Most existing HSI classification approaches usually utilize spectral attention mechanisms, spatial attention mechanisms, or spectral–spatial joint attention mechanisms to enhance the HSI’s representation ability. However, these approaches rarely consider the close interdependencies between the and dimensions of HSI.
3. Method
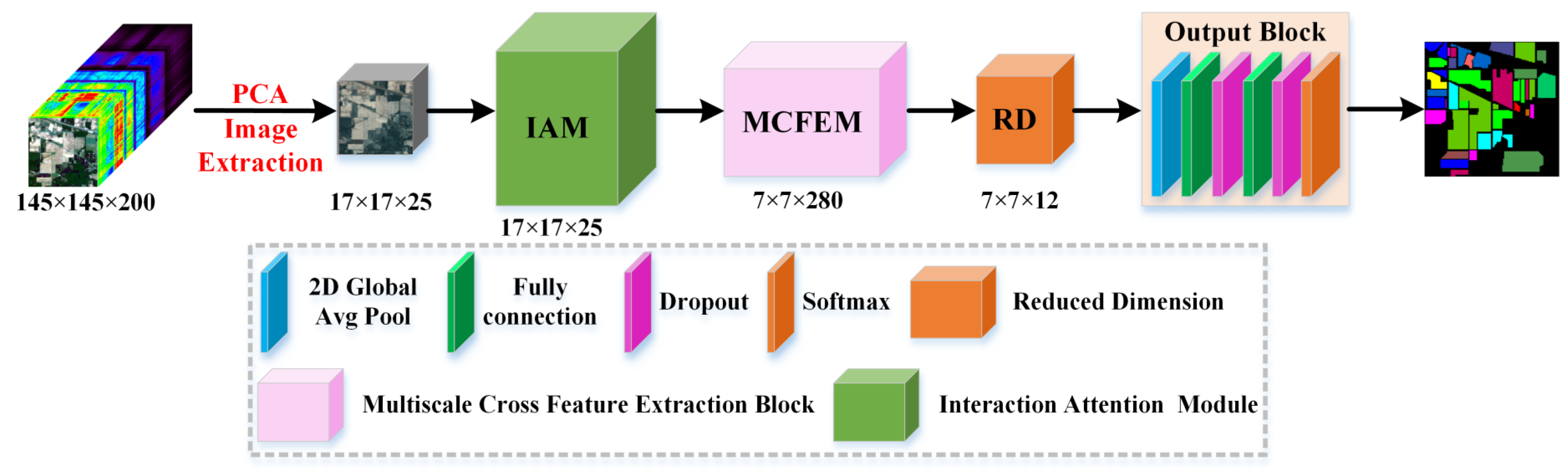
To graphically illustrate the working process of our proposed MCIFNet, we use the Indian Pines dataset as an example, as exhibited in Figure 1. According to Figure 1, the designed network is composed of two submodules: an interaction attention module (IAM) to strengthen the distinguishability of HSI and dispel the interference of redundant information, and a multiscale cross feature extraction module (MCFEM) to detect spectral–spatial features at different convolutional layers, scales, and branches while further enriching the multiformity of spectral–spatial information.
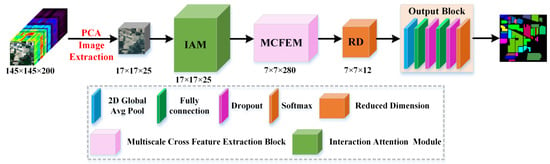
Figure 1.
Architecture of the designed MCIANet model.
3.1. Interaction Attention Module
By mimicking the perception system of humans, the attention mechanism can adaptively focus on parts of the visual space that are more relevant to classification results and weaken unserviceable ones to enhance the classification performance. Common attention mechanisms chiefly involve the spectral attention mechanism, spatial attention mechanism, and joint spectral–spatial attention mechanism. The spectral attention mechanisms are devoted to reassigning weights to each spectral band. For example, SENet [63] performed a global average pooling on spectral bands and then employed two fully connected layers to calculate weights. ECANet was constructed based on local 1-D convolutions [64]. The spatial attention mechanisms aim to emphasize the spatial portions that are more crucial in feature maps. One representative block was GE [65], which used spatial attention to better learn feature context. The co-attention network encoded the commonsense between text sequences and visual information, followed by an attention reduction module for redundant information filtering [66]. To obtain the long-range interdependency of spatial and spectral information, many studies fused spectral attention and spatial attention, such as BAM [67], scSE [68], and CBAM [69].
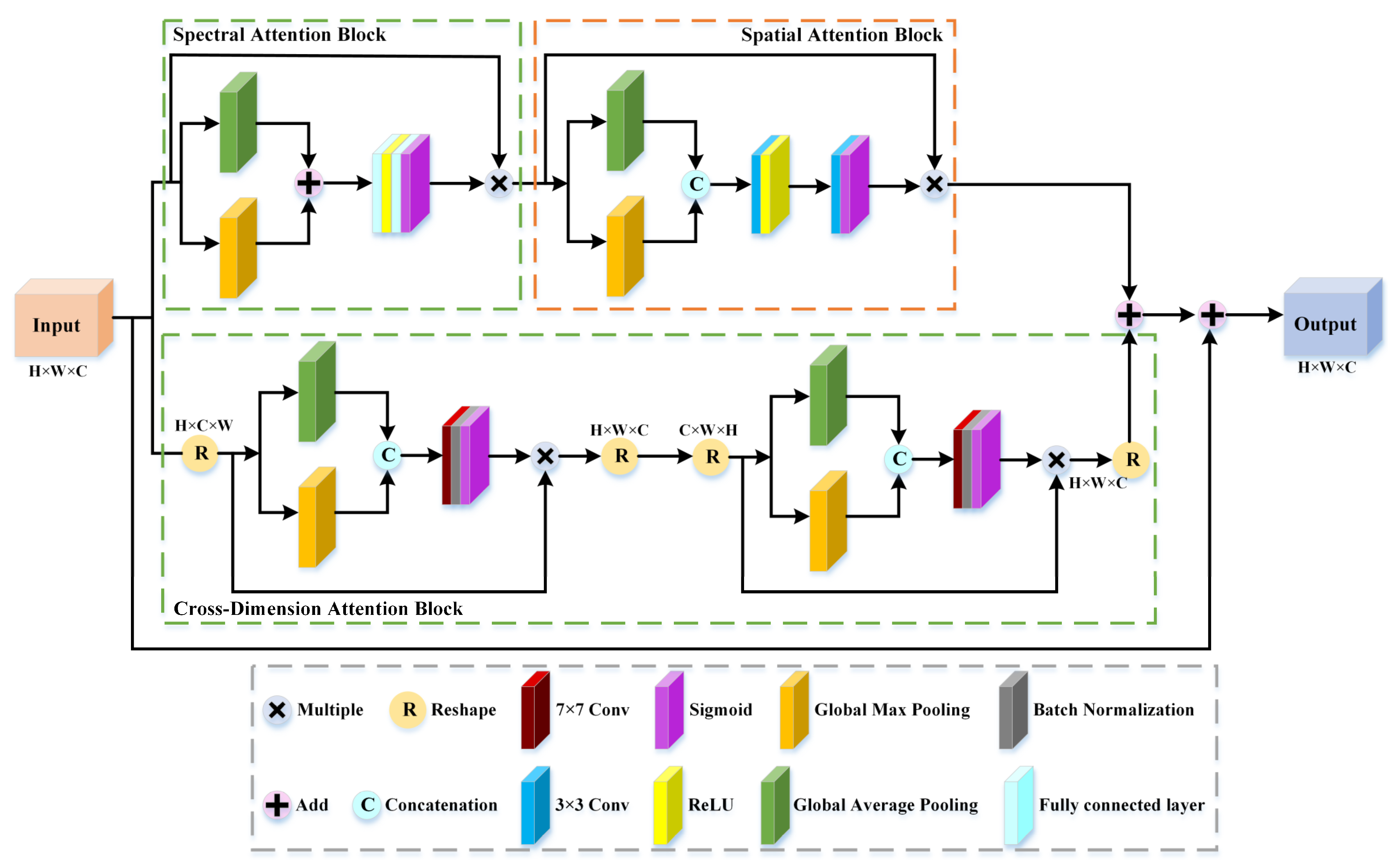
Inspired by the above successful attention mechanism applications and considering the 3-D characteristics of HSI, this article designs an improved attention mechanism module named interaction attention module (IAM). IAM includes a spectral attention block, a spatial attention block, and a cross dimension attention block, which can enhance informational features favorable for classification and suppress useless information by capturing the corresponding importance of spectral bands, spatial regions, and cross dimensions. The diagram of IAM is provided in Figure 2. The input feature map of IAM is denoted as , where and denote the height and width, and is the number of spectral bands.
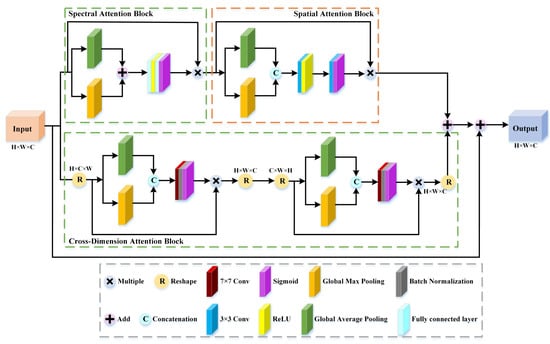
Figure 2.
The diagram of interaction attention module (IAM).
3.1.1. Spectral Attention Block
The spectral attention block can obtain different spectral weight feature maps in the spectral domain. First, global average pooling (GAP) and global max pooling (GMP) are performed to generate two 1-D vectors with a size of : average pooling feature and max pooling feature . Then, we use elementwise summation to integrate and . Next, the aggregated features are sent into a shared network composed of two fully connected layers (FCs) for training. The first FC is utilized to reduce the dimension with a reduction ratio . The second FC is dimensionality increasing. The whole process is summarized as follows:
where refers to the rectified linear unit (ReLU) activation function. is the sigmoid activation function. and denote the weights of the two FCs. Finally, the raw input data are multiplied by spectral attention map to acquire the spectral attention features .
3.1.2. Spatial Attention Block
The spatial attention module can provide different spatial weight feature maps in the spatial domain. Specifically, to fully exploit the input data information, GAP and GMP are employed to generate 2-D feature maps: average pooling feature and max pooling feature . Then, and are aggregated by a concatenation operation and sent to a convolutional layer with kernels. Moreover, to make the spatial attention feature map consistent with the spectral attention map, we utilize a convolutional layer with 1 kernel and set “padding = 1”. The whole process is summarized as follows:
where and denote the weights of the two convolutional layers. is the concatenation operation. Finally, the raw input data are multiplied by spatial attention map to acquire the spatial attention features .
3.1.3. Cross Dimension Attention Block
The cross dimension attention block can give higher weights to discriminative features in cross dimensions. This block is divided into two parts: one to capture the corresponding feature information between and , and the other to extract the importance between and . Similar to the aforementioned two attention blocks, we first transform to and . Then, these feature maps are transmitted to GAP and GMP and concatenated to obtain the reduced-dimension feature maps and , which are of shapes and . Subsequently, and are entered into a convolutional layer with 1 filter to obtain the intermediate feature maps of shapes and . Furthermore, we employ a sigmoid function to generate cross dimension attention maps and . The whole process is summarized as follows:
where represents the dimension transformation. and denote the weights of two convolutional layers. Finally, the obtained cross dimension attention maps and are multiplied by and and are changed the same shape as the raw input data to obtain cross dimension attention features and , respectively.
3.1.4. IAM
The IAM is composed of two parallel branches. One includes spatial attention block and spectral attention block, which is designed to not only learn the importance of spectral bands and spatial contexts but also obtain the large-term interdependency of spatial and spectral information. The other is constructed to obtain the cross dimension importance between and and between and . We transmit the spectral attention features to the spatial attention block to obtain the large-term spectral–spatial interdependency. We send the attention feature weights between and to the attention block between and to capture the cross importance of different dimensions. The obtained large-term spectral–spatial interdependency and cross dimension importance are combined to obtain the interaction attention-enhanced features . In addition, to avoid reasonable information loss and strengthen feature propagation, we also introduce skip transmission [70] into our proposed IAM. The whole process is summarized as follows:
3.2. Multiscale Cross Feature Extraction Module
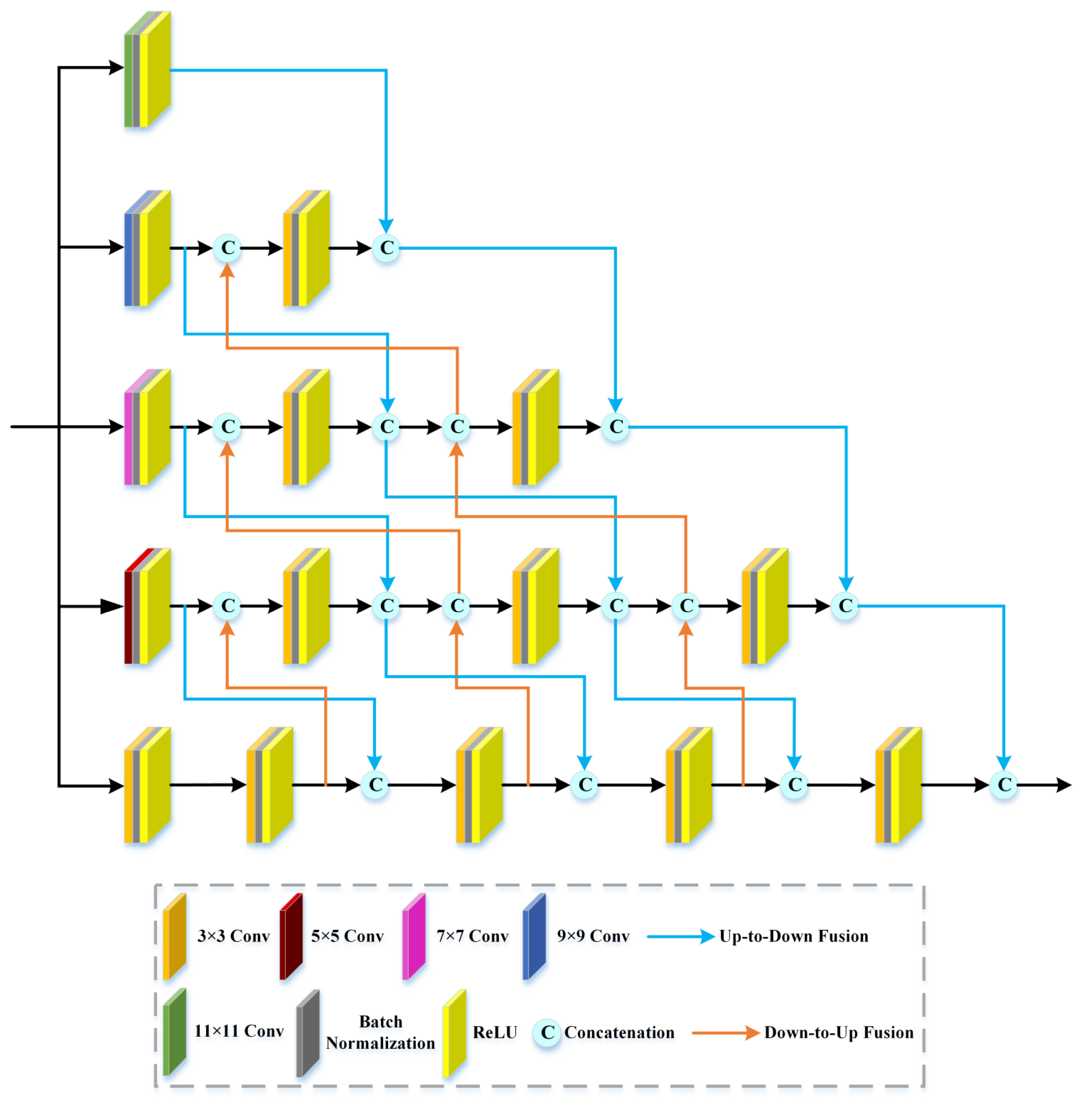
Many HSI classification studies utilizing a single-scale convolutional kernel have a common phenomenon in which the luxuriant spatial–spectral information of HSI cannot be adequately extracted, which impairs the classification performance. Therefore, to improve the classification accuracy, numerous works presented multiscale strategies to share features at different scales and promote information flow. In this article, we construct a multiscale cross feature extraction module (MCFEM). We introduce the multibranch strategy to capture spectral–spatial features at different scales, which employs different convolutional kernels to obtain different receptive fields. Additionally, we apply “up-to-down” and “down-to-up” fusion approaches to aggregate spatial–spectral features at different convolutional layers, scales, and branches to boost the representation ability of multiscale spatial–spectral information. The diagram of the MCFEM is provided in Figure 3.
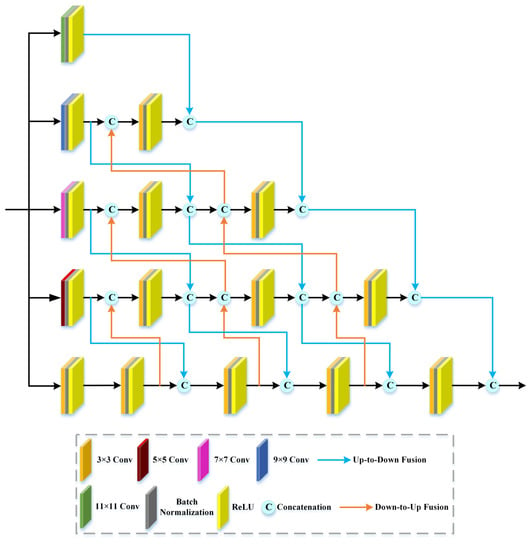
Figure 3.
The diagram of multiscale cross feature extraction module (MFEM).
As shown in Figure 3, the MCFEM is composed of five parallel branches, and the first convolutional layer of each branch uses different convolutional kernels to acquire spectral–spatial features with different receptive fields, involving , , , , and . In addition, the other convolutional layers of each branch are 2-D convolutions. The small-size convolutional kernels capture detailed information, while large-size convolutional kernels cover most spatial scales. Specifically, low-level features include more details but lack semantic information and are filled with noise. Compared with low-level features, high-level features possess strong semantics but inaccurate location information. Therefore, to enhance the classification results, “up-to-down” and “down-to-up” fusion methods are employed to integrate spatial–spectral features at different convolution layers, scales, and branches to make the multiscale features more abundant and stronger.
Concretely, in the “up-to-down” method, the output feature maps of the first convolution layer in each branch are fused with the output feature maps of the second convolution layer in next branch by a concatenation operation. The fused feature maps of the second convolution layer in each branch are connected with the output feature maps of the third convolution layer in the next branch. The rest is similar to the above operations. In the “down-to-up” method, the input feature maps of the final convolution layer in each branch are a combination of the output feature maps of the penultimate convolution layer in the next branch and the fused feature maps of the previous convolution layer in the current branch. The input feature maps of the penultimate convolution layer in each branch are a combination of the output feature maps of the antepenultimate convolution layer in the next branch and the fused feature maps of the previous convolution layer in the current branch. The rest is similar to the above operations. Furthermore, multiscale feature information at different branches is fused by a concatenation operation. Although the spatial–spectral features acquired at this time are more discriminative and multifarious, the dimension is high. Therefore, to achieve dimension reduction, we also built a reduction dimension block composed of convolutional layer following a batch normalization layer and ReLU, respectively.
4. Experiments and Discussion
4.1. Experimental Datasets
To prove the validity of our developed MCIANet, three benchmark datasets are utilized: Botswana dataset (BOW), Indian Pines (IP), and Houston 2013.
The BOW dataset [25] was gathered by the NASA EO-1 Hyperion sensor over the Okavango Delta. It is composed of pixels and 14 land-cover categories. The spatial resolution is 30 m per pixel. After eliminating noisy and uncalibrated bands, 145 bands remained at a range from 0.4 to 2.5 um.
The IP dataset [47] was collected by the airborne visible/infrared imaging spectrometer (AVIRIS) in northwestern Indiana. This scene has 16 different land-cover categories and pixels. After removing noisy bands, it contains 200 spectral bands from 0.4 to 2.5 um with a 20 m per pixel spatial resolution.
The Houston 2013 dataset [71] was provided by the 2013 IEEE GRSS Data Fusion Competition. It is composed of 15 land-cover categories and pixels with a 2.5 m per pixel spatial resolution. This scene involves 144 spectral bands, and the wavelength range is from 0.38 to 1.05 um.
Table 1, Table 2 and Table 3 list the land-cover categories, testing sample numbers, and training samples numbers of three benchmark datasets, respectively.

Table 1.
The information of sample numbers of the BOW dataset.

Table 2.
The information of sample numbers of the IP dataset.

Table 3.
The information of sample numbers of the Houston 2013 dataset.
4.2. Experimental Setup
All experiments are performed on a system with an NVIDIA GeForce RTX 2060 SUPER GPU and 6 GB of RAM. The software environment of the system is TensorFlow 2.3.0, Keras 2.4.3, and Python 3.6.
Considering the different sample numbers and the unbalanced class, diverse training sample ratios are employed for different benchmark datasets to demonstrate the performance of our presented network. For the IP dataset, 20% labeled samples are chosen as the training set and the remaining 80% labeled samples are chosen as the testing set at random. For the BOW and Houston 2013 datasets, we select 10% labeled samples for training and 90% labeled samples for testing at random. This article adopts cross entropy as a loss function to conduct the HSI classification task. Adam is adopted to optimize the parameters. First, the gradient information of the loss function at each parameter is calculated. Then, the learning rate is set to 0.001 according to the set learning rate; the subtraction strategy is utilized to update the parameters. Finally, when the network structure is arranged reasonably and each hyperparameter is set correctly, the loss value will show an overall decline trend with the training, and, when it becomes stable, the best training model can be obtained. In addition, the batch size and epochs are 16 and 400, respectively.
The average accuracy (AA), overall accuracy (OA), and Kappa coefficient (Kappa) are utilized to measure the classification results quantitatively. Notably, if three evaluation metrics are closer to 1, the classification result will be better.
4.3. Comparison Methods
In this section, we compare our presented MCIANet with eleven representative classification approaches, which are broadly split into two categories: one is based on traditional ML, including SVM, RF, KNN, and GaussianNB; another is based on DL, including HybridSN [17], MSRN_A [72], 3D_2D_CNN [73], RSSAN [74], MSRN_B [75], DMCN [31], and MSDAN [42]. To be fair, in comparative experiments, 10% and 90% labeled samples are randomly selected as the training set and testing set for the BOW and Houston 2013 datasets, respectively. Homoplastically, 20% and 80% labeled samples are assigned to the training set and testing set for the IP dataset, respectively. Table 4, Table 5 and Table 6 exhibit the quantization comparison accuracies of diverse classification methods on three benchmark datasets, reporting class-wise accuracy, OA, AA, and Kappa.

Table 4.
The classification results on the BOW dataset.

Table 5.
The classification results on the IP dataset.

Table 6.
The classification results on the Houston 2013 dataset.
First, as shown in Table 4, Table 5 and Table 6, it can be clearly seen that, compared with eight DL-based classification approaches, SVM, RF, KNN, and GaussianNB have low classification accuracies. This is because four ML-based methods only extract features in the spectral domain and ignore abundant contextual spatial features. Meanwhile, they need to rely on prior experience, leading to poor generalization ability. In contrast, due to a hierarchical structure, eight DL-based approaches can capture high-level features from the data automatically and obtain good classification results. Among all the classification approaches, our developed MCIANet obtains terrific classification results on three benchmark datasets. One possible reason for this is that our designed IAM can highlight the distinguishability of HSI by extracting the significance of different spectral bands, spatial pixels, and cross dimensions and let us know the “what”, “where”, and “cross dimension” that need to be emphatically learned. Another point is that our constructed MCFFM can extract multiscale spectral–spatial features to increase the diversity of spectral–spatial information.
Second, MARN_A, MSRN_B, MSDAN, and our proposed MCIANet construct functional modules to capture multiscale features. MSRN_A utilizes filters with sizes of , , and to extract multiscale spectral features and filters with sizes of , , and to extract multiscale spatial features. MSRN_B designs a multiscale residual block to perform lightweight and efficient multiscale feature extraction. MSDAN adopts multiscale dense connections to capture feature information at different scales. From Table 4, Table 5 and Table 6, it is clear that our developed method is remarkably superior to those of MARN_A, MSRN_B and MSDAN on three benchmark datasets. The possible reason for this is that our devised MCFEM uses filters with sizes of , , , , and to extract multiscale spectral–spatial features while introducing “up-to-down” and “down-to-up” fusion strategies to maximize use of information flow of different branches. Hence, different from the above three multiscale extraction strategies, our MCFEM can capture spectral–spatial features at various scales, convolutional layers, and branches.
Furthermore, from different perspectives, eight classification approaches based on DL can be divided into two categories: one uses attention functional modules, including MSRN_A, RSSAN, DMCN, MSDAN, and our proposed MCIANet; another does not utilize attention functional modules, including HybridSN, 3D_2D_CNN, and MSRN_B. According to Table 4, Table 5 and Table 6, the attention modules can improve the classification performance. For example, MSRN_A uses a spatial–spectral attention block and a spatial attention block to pay attention to the salient spatial regions and valid spectral bands. For the BOW dataset, three evaluation indices of MSRN_A are 99.01%, 99.12%, and 98.92%, which are 2.06%, 3.25%, and 2.23% higher than those of HybridSN and 7.6%, 6.91%, and 8.11% higher than those of MSRN_B. However, it can also be clearly observed that three evaluation indices of some classification methods that do not introduce attention modules are superior to those of some classification methods that utilize attention modules. The possible reason for this is that the former may have a neat model architecture for training and testing, which achieves good classification accuracies and robustness. The latter may increase the complexity of models and acquire more parameters for the training process. For example, for the Houston 2013 dataset, 3D_2D_CNN obtained 98.41% OA, 98.03% AA, and 98.28% Kappa, which are 2.1%, 1.66%, and 2.27% higher than those of RSSAN and are 1.59%, 2.15%, and 1.72% higher than those of DMCN. It is worth noting that our proposed method performs best overall. This is because our built IAM can enhance informational features favorable for classification and suppress useless information by capturing the corresponding importance of spectral bands, spatial regions, and cross dimensions, and the presented MCIANet requires relatively few parameters for the training process.
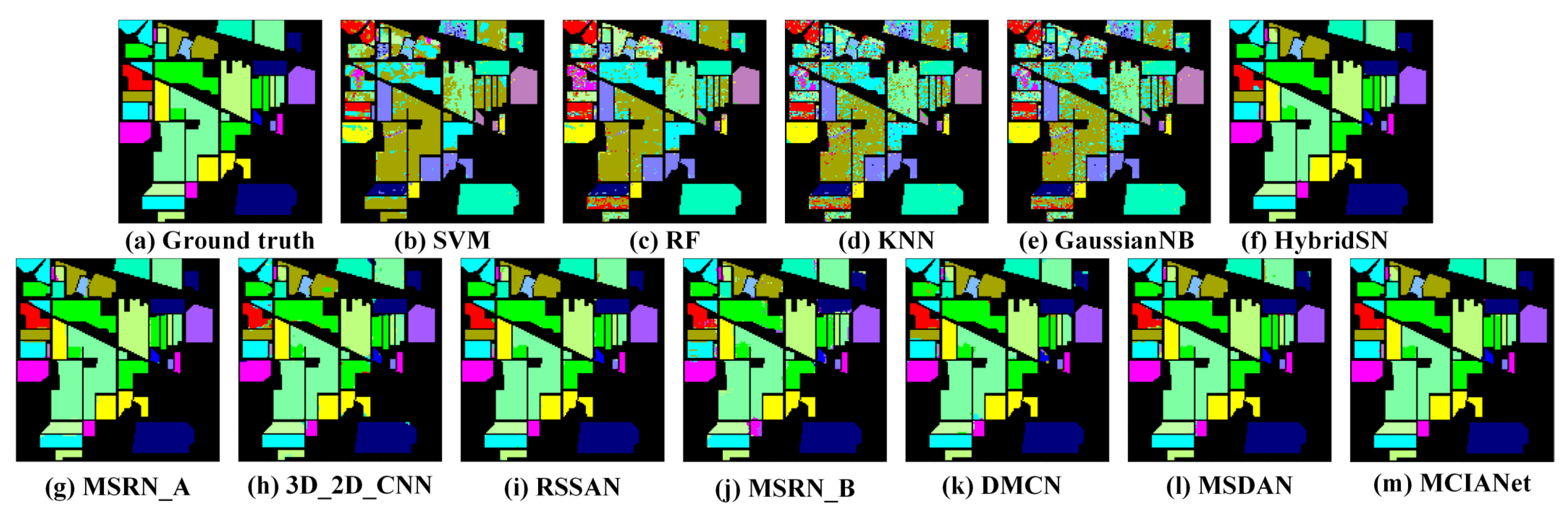
Moreover, Figure 4, Figure 5 and Figure 6 provide the corresponding visual images of each approach on three benchmark datasets. The visual image of the GuassianNB is the coarsest and has the most misclassified pixels. The probable explanation for this is that the classification methods based on traditional DL cannot fully extract features and lack robust representation. The visual images obtained by HybridSN, MSRN_A, 3D_2D_CNN, RSSAN, MSRN_B, DMCN, and MSDAN exhibit less noise and are relatively smooth. In contrast, the proposed MCIANet can generate better classification maps. We also change the training sample ratios of eight classification methods based on DL, including 1%, 3%, 5%, 7%, and 10%. Figure 7 shows the corresponding results. The classification performance gap between diverse methods gradually narrows as the number of training samples increases. Our proposed method still obtains excellent classification accuracies and shows robust generalization performance.

Figure 4.
The classification visual maps on BOW dataset.
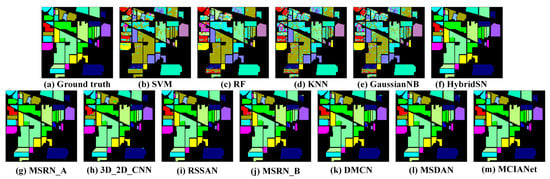
Figure 5.
The classification visual maps on IP dataset.

Figure 6.
The classification visual maps on Houston 2013 dataset.

Figure 7.
Generalization performance.
4.4. Discussion
4.4.1. Influence of Different Spatial Sizes
Different spatial sizes have different effects on classification results. Therefore, choosing a proper spatial size for our proposed MCIANet is vital. We analyzed the sensitivity of spatial size on three benchmark datasets with spatial sizes set to , , , , , , , and . Figure 8 provides the classification accuracies of the proposed model under different spatial sizes. For the BOW dataset, it is easy to find that, when the spatial size is , three evaluation indices are best. For the IP dataset, it can be noticed clearly that, when the spatial size is , the three evaluation indices are superior. For the Houston 2013 dataset, the three evaluation indices increase at first and then decrease as the spatial size is . Because HSI contains intricate topographic features and different HSIs have various feature distributions, different experimental datasets may require various spatial sizes. Therefore, we set the spatial size of , , and as the input of our designed framework to three benchmark datasets.

Figure 8.
The classification results of different spatial sizes.
4.4.2. Influence of Diverse Training Percentage
Number of training samples has a significant impact on classification accuracies of our proposed method. To explore the influence of different training sample percentages on classification accuracies, we chose 1%, 3%, 5%, 7%, 10%, 20%, and 30% of the available labeled samples for training and the remaining labeled samples for testing at random. Figure 9 provides classification accuracies of the built model with different training sample percentages. We can observe that three evaluation indices rise considerably and then grow slowly as the training sample percentage increases. For the BOW and Houston 2013 datasets, 10% labeled samples are assigned to the training set and the corresponding remaining 90% labeled samples are assigned to the testing set. For the IP dataset, we select 20% available data as the training samples and the corresponding remanent 80% available data as the testing samples.

Figure 9.
The classification results of diverse training ratios.
4.4.3. Influence of Different Numbers of Principal Components
HSI is composed of multitudinous continuous spectral bands, and these spectral bands are highly correlated with each other. To eliminate abundant redundant information and downsize the computational expense, we execute a PCA on the original HSI. The number of principal components is empirically adjusted to 5, 10, 15, 20, 25, 30, 35, and 40 to analyze the sensitivity of the principal component numbers on three benchmark datasets. Figure 10 provides the classification accuracies of the developed model under different principal component numbers. For the BOW dataset, it can be observed clearly that, when the principal component number is 40, three evaluation indices are best. For the IP dataset, it can be seen that the three evaluation indices increase at first and then plateau at 25. As the principal component number is over 25, the three evaluation indices begin to decline. For the Houston 2013 dataset, it can be found that the three evaluation indices rise at first and then plateau at 30. As the principal component number is over 30, the three evaluation indices begin to decline. These phenomena indicate to a certain extent that the principal component numbers are greater, and our proposed method can capture representative spectral–spatial features from these principal components. As the number of principal components continues to rise, the three evaluation indices decline due to interference of redundant information and noise. Hence, we set the principal component numbers to 40, 25, and 30 for three benchmark datasets.

Figure 10.
The classification results of different principal component numbers.
4.4.4. Influence of Diverse Compressed Ratio in the IAM
The compressed ratio determines the number of neurons in the FC layer. We discuss the impact of on three benchmark datasets and is set to 1, 2, 3, 4, 5, and 6. Figure 11 provides the classification accuracies of our presented model under different compressed ratios . According to the experimental observation, for the BOW dataset, the most appropriate is 3. For the IP dataset, the best is 2. For the Houston 2013 dataset, we choose a compressed ratio of 6.

Figure 11.
The classification results of diverse compressed ratios.
4.4.5. Influence of Various Numbers of Branches in the MCFEM
To analyze the influence of different branch numbers on the classification performance of our proposed method, different branch numbers are set to 1, 2, 3, 4, 5, and 6. Figure 12 provides the classification accuracies of the proposed model under different branch numbers. It is easy to notice that the three evaluation indices rise at first and then plateau at 5. As the branch number exceeds 5, the three evaluation indices begin to decline for three common datasets. This phenomenon indicates to a certain extent that, as the number of parallel branches increases, our devised MCFEM can learn more discriminative and richer multiscale spectral–spatial features and obtain better classification results. However, the greater parallel branch number will make the model more complicated and aggravate the computational burden, leading to poor classification results. Therefore, to achieve superior classification results, the number of parallel branches is set to 5 for three benchmark datasets.

Figure 12.
The classification results of various branch numbers.
4.5. Ablation Study
4.5.1. Effect of IAM
To prove the effectiveness of our constructed IAM, we performed seven comparative experiments on three benchmark datasets: only using spectral attention block (named case 1), only using spatial attention block (named case 2), only using cross dimension block (named case (3), using spectral and spatial attention blocks (named case 4), using spectral and cross dimension attention blocks (named case 5), using spatial and cross dimension attention blocks (named case 6), and our constructed IAM (named case 7). Figure 13 exhibits the corresponding results on three benchmark datasets.

Figure 13.
The ablation study of IAM.
From Figure 13, we can obviously find that comparative experiments on three benchmark datasets have different experimental results. For example, for case 1, three evaluation indices on BOW and IP datasets are good, but they are poor on the Houston 2013 dataset. For case 5, three evaluation indices on BOW and Houston 2013 datasets are good, but they are poor on the IP dataset. For case 2, three evaluation indices on three benchmark datasets have poor performance. These may be because HSI contains intricate topographic features and different HSIs have various feature distributions. The BOW and Houston 2013 datasets contain many smaller areas of the species; only using spatial or cross dimension block may not obtain good classification accuracies. Meanwhile, the IP dataset includes many large and continuous areas of the species; only using spatial block may obtain decent classification results. Compared with the other six experimental conditions, three benchmark datasets have superior three evaluation indices and outstanding classification results. This indicates that our constructed IAM is effective, which can highlight the distinguishability of HSI and dispel interference of redundant information by learning the importance of different spectral bands, spatial pixels, and cross dimensions.
4.5.2. Effect of the Presented Method
To further demonstrate and analyze the importance of IAM and MCFEM of our proposed MCIANet, we conducted comparative experiments on three benchmark datasets under three different conditions: only using IAM (named network 1), only using MCFEM (named network 2), using IAM and MCFEM (our proposed method, named network 3). Figure 14 exhibits the corresponding results on three benchmark datasets.

Figure 14.
The ablation study of proposed MCIANet.
According to Figure 14, it is clear that the three evaluation indices of network 1 are the lowest on three benchmark datasets. For example, for the BOW dataset, the three evaluation indices are 2.02%, 1.86%, and 1.84% lower than those of network 3. For the IP dataset, the three evaluation indices are 3.05%, 6.81%, and 3.47% lower than those of network 3. For the Houston 2013 dataset, the three evaluation indices are 4.31%, 4.09%, and 4.65% lower than those of network 3. These results prove that our constructed MCFFM is beneficial for our proposed MCIANet to fully extract spectral–spatial at different scales, convolutional layers, and branches, which further increases the diversity of spectral–spatial information. Compared with network 1, three evaluation indices of network 2 obviously increase. For example, for the BOW dataset, OA and AA are 0.31% and 0.26% lower than those of network 3. For the IP dataset, the three evaluation indices are 0.17%, 1.7%, and 0.19% lower than those of network 3. For the Houston 2013 dataset, the three evaluation indices are 0.32%, 0.59%, and 0.34% lower than those of network 3. These results indicate that IAM can strengthen the distinguishability of HSI and dispel the interference of redundant information. Therefore, to a certain extent, the IAM and MCFFM in our presented method considerably enhance classification performance.
5. Conclusions
In this article, a multiscale cross interaction attention network (MCIANet) for HSI classification is presented. First, the interaction attention module (IAM) can strengthen the distinguishing ability of HSI by learning the importance of different spectral bands, spatial contexts, and cross dimensions and dispelling the interference of redundant information. Then, the attention-enhanced spectral–spatial features from IAM are sent to a multiscale cross feature extraction module (MCFEM) to increase the diversity of spectral–spatial information, which utilizes an innovative multibranch lower triangular structure with different fusion strategies to extract multiscale spectral–spatial features while maximizing use of spectral–spatial information flows between different convolutional layers and branches. The experimental results on three benchmark datasets can not only demonstrate the effectiveness and superiority of our proposed method but also exhibit competitive performance compared with the state-of-the-art classification approaches.
However, there is still room for further study in the future. The effectiveness of CNNs heavily relies on the number of training samples. Additionally, the number of branches and network layers are selected by a manual setting. Therefore, adaptively choosing framework parameters and integrating unsupervised training methods into our designed model is another research direction to study.
Author Contributions
Conceptualization, D.L.; validation, P.L., H.Y., and G.H.; formal analysis, D.L.; investigation, D.L., P.L., H.Y., and G.H.; original draft preparation, D.L.; review and editing, D.L., Y.W., P.L., Q.L., H.Y., D.C., Z.L., and G.H.; funding acquisition, G.H. and D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Department of Science and Technology of Jilin Province under grant number 20210201132GX.
Data Availability Statement
The data presented in this study are available in this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, Z.; Zhu, W.; Chanussot, J.; Xu, Y.; Osher, S. Hyperspectral Anomaly Detection via Global and Local Joint Modeling of Background. IEEE Trans. Signal Process. 2019, 67, 3858–3869. [Google Scholar] [CrossRef]
- Du, B.; Ru, L.; Wu, C.; Zhang, L. Unsupervised Deep Slow Feature Analysis for Change Detection in Multi-Temporal Remote Sensing Images. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 9976–9992. [Google Scholar] [CrossRef]
- Laurin, G.V.; Chan, J.C.-W.; Chen, Q.; Lindsell, J.; Coomes, D.A.; Guerriero, L.; Del Frate, F.; Miglietta, F.; Valentini, R. Biodiversity Mapping in a Tropical West African Forest with Airborne Hyperspectral Data. PLoS ONE 2014, 9, e97910. [Google Scholar] [CrossRef]
- Du, H.; Qi, H.; Wang, X.; Ramanath, R.; Snyder, W. Band selection using independent component analysis for hyperspectral image processing. In Proceedings of the 32nd Applied Imagery Pattern Recognition Workshop, Washington, DC, USA, 15–17 October 2003. [Google Scholar]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Joint Within-Class Collaborative Representation for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2014, 7, 2200–2208. [Google Scholar] [CrossRef]
- Uss, M.L.; Vozel, B.; Lukin, V.V.; Chehdi, K. Maximum likelihood estimation of spatially correlated signal-dependent noise in hyperspectral images. Opt. Eng. 2012, 51, 111712. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Z.; Jiao, L.; Zhou, H. Multifeature hyperspectral image classification with local and nonlocal spatial information via Markov random field in semantic space. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1409–1424. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Liao, W.; Zhang, B.; Pizurica, A.; Philips, W. Multiscale superpixel-level subspace-based support vector ma-chines for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2142–2146. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, J.; Jia, S.; Jia, X.; Li, Q. Multiple 3-D Feature Fusion Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1873–1886. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized Composite Kernel Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]
- Li, L.; Ge, H.; Gao, J. A spectral-spatial kernel-based method for hyperspectral imagery classification. Adv. Space Res. 2017, 59, 954–967. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.; Huang, Y.; Zhang, L. A Nonlocal Weighted Joint Sparse Representation Classification Method for Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2014, 7, 2056–2065. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sensors 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Cao, X.; Ren, M.; Zhao, J.; Li, H.; Jiao, L. Hyperspectral Imagery Classification Based on Compressed Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1583–1587. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q. Diverse Region-Based CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M. A Fast 3D CNN for Hyperspectral Image Classification. arXiv 2020, arXiv:2004.14152. [Google Scholar] [CrossRef]
- Zhu, J.; Fang, L.; Ghamisi, P. Deformable Convolutional Neural Networks for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1254–1258. [Google Scholar] [CrossRef]
- Xue, A.; Yu, X.; Liu, B.; Tan, X.; Wei, X. HResNetAM: Hierarchical Residual Network with Attention Mechanism for Hyper-spectral Image Classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2021, 14, 3566–3580. [Google Scholar] [CrossRef]
- Xie, J.; He, N.; Fang, L.; Ghamisi, P. Multiscale Densely-Connected Fusion Networks for Hyperspectral Images Classification. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 246–259. [Google Scholar] [CrossRef]
- Xu, Z.; Yu, H.; Zheng, K.; Gao, L.; Song, M. A Novel Classification Framework for Hyperspectral Image Classification Based on Multiscale Spectral-Spatial Convolutional Network. In Proceedings of the 2021 11th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, Netherlands, 24–26 March 2021; pp. 1–5. [Google Scholar]
- Zhang, X.; Wang, Y.; Zhang, N.; Xu, D.; Luo, H.; Chen, B.; Ben, G. Spectral–Spatial Fractal Residual Convolutional Neural Network With Data Balance Augmentation for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10473–10487. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Chen, Z.; Li, C. A Multiscale Dual-Branch Feature Fusion and Attention Network for Hyperspectral Images Classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2021, 14, 8180–8192. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification With Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Li, H.-C.; Hu, W.-S.; Li, W.; Li, J.; Du, Q.; Plaza, A. A3 CLNN: Spatial, Spectral and Multiscale Attention ConvLSTM Neural Network for Multisource Remote Sensing Data Classification. IEEE Trans. Neural Networks Learn. Syst. 2020, 33, 747–761. [Google Scholar] [CrossRef]
- Zhou, Q.; Bao, W.; Zhang, X.; Ma, X. A Joint Spatial-Spectral Representation Based Capsule Network for Hyperspectral Image Classification. In Proceedings of the 2021 11th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, Netherlands, 24–26 March 2021; pp. 1–5. [Google Scholar]
- Yang, K.; Sun, H.; Zou, C.; Lu, X. Cross-Attention Spectral–Spatial Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 3133582. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Liu, Q.; Ghamisi, P.; Bhattacharyya, S.S. Hyperspectral Image Classification With Attention-Aided CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2281–2293. [Google Scholar] [CrossRef]
- Xiang, J.; Wei, C.; Wang, M.; Teng, L. End-to-End Multilevel Hybrid Attention Framework for Hyperspectral Image Classi-fication. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Tu, B.; He, W.; He, W.; Ou, X.; Plaza, A. Hyperspectral Classification via Global-Local Hierarchical Weighting Fusion Net-work. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2022, 15, 184–200. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-Based Edge-Preserving Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Mercier, G.; Lennon, M. Support vector machines for hyperspectral image classification with spectral-based kernels. Proc. IEEE Int. Geosci. Remote Sens. Symp. 2003, 6, 288–290. [Google Scholar]
- Shen, L.; Jia, S. Three-Dimensional Gabor Wavelets for Pixel-Based Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 5039–5046. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Liu, Q.; Xiao, L.; Yang, J. C Content-Guided Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6124–6137. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Liu, L.; Li, W.; Shi, Z.; Zou, Z. Physics-Informed Hyperspectral Remote Sensing Image Synthesis With Deep Conditional Generative Adversarial Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3173532. [Google Scholar] [CrossRef]
- Wang, S.; Gong, G.; Zhong, P.; Du, B.; Zhang, L.; Yang, J. Multiscale Dynamic Graph Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3162–3177. [Google Scholar]
- Wang, X.; Fan, Y. Multiscale Densely Connected Attention Network for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1617–1628. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Liu, Y.; Zheng, K.; Xu, Z.; Xiao, C. Dual-Channel Convolution Network With Image-Based Global Learning Framework for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper with Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Huang, L.; He, J. A Multiscale Deep Middle-level Feature Fusion Network for Hyperspectral Classification. Remote Sens. 2019, 11, 695. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Learning multiscale and deep representations for classifying remotely sensed imagery. ISPRS J. Photogramm. Remote Sens. 2016, 113, 155–165. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, Y.; Wang, D.; Luo, B. CSA-MSO3DCNN: Multiscale Octave 3D CNN with Channel and Spatial Attention for Hyperspectral Image Classification. Remote Sens. 2020, 12, 188. [Google Scholar] [CrossRef]
- Fu, H.; Sun, G.; Ren, J.; Zhang, A.; Jia, X. Fusion of PCA and Segmented-PCA Domain Multiscale 2-D-SSA for Effective Spec-tral-Spatial Feature Extraction and Data Classification in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2020, 60, 5500214. [Google Scholar]
- Zhou, L.; Yang, Z.; Yuan, Q.; Zhou, Z.; Hu, D. Salient Region Detection via Integrating Diffusion-Based Compactness and Local Contrast. IEEE Trans. Image Process. 2015, 24, 3308–3320. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Ji, W.; Piao, Y.; Li, J.; Zhang, Y.; Xu, S.; Lu, H. LFNet: Light Field Fusion Network for Salient Object Detection. IEEE Trans. Image Process 2020, 29, 6276–6287. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Song, R.; Xie, W.; Ge, C.; Li, B.; Li, Y. Hybrid 2-D–3-D Deep Residual Attentional Network With Structure Tensor Constraints for Spectral Super-Resolution of RGB Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2321–2335. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Xu, J.; Yang, J.; Tai, Y.-W. An Accurate and Lightweight Method for Human Body Image Super-Resolution. IEEE Trans. Image Process. 2021, 30, 2888–2897. [Google Scholar] [CrossRef]
- Chen, L.; Liu, H.; Yang, M.; Qian, Y.; Xiao, Z.; Zhong, X. Remote Sensing Image Super-Resolution via Residual Aggregation and Split Attentional Fusion Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9546–9556. [Google Scholar] [CrossRef]
- Liu, Q.; Su, H.; El-Khamy, M. Deep Guidance Decoder with Semantic Boundary Learning for Boundary-Aware Semantic Segmentation. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 7–9 January 2022. [Google Scholar]
- Zhang, R.; Chen, J.; Feng, L.; Li, S.; Yang, W.; Guo, D. A Refined Pyramid Scene Parsing Network for Polarimetric SAR Image Semantic Segmentation in Agricultural Areas. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 3086117. [Google Scholar] [CrossRef]
- Li, G.; Li, L.; Zhang, J. Hierarchical Semantic Broadcasting Network for Real-Time Semantic Segmentation. IEEE Signal Process Lett. 2022, 29, 309–313. [Google Scholar] [CrossRef]
- Guo, W.; Ye, H.; Cao, F. Feature-Grouped Network With Spectral–Spatial Connected Attention for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 3051056. [Google Scholar] [CrossRef]
- Xiong, Z.; Yuan, Y.; Wang, Q. AI-NET: Attention Inception Neural Networks for Hyperspectral Image Classification. In Proceedings of the GARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Mou, L.; Zhu, X.X. Learning to Pay Attention on Spectral Domain: A Spectral Attention Module-Based Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 110–122. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, S.; Chanussot, J.; Li, X. Scene Classification With Recurrent Attention of VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1155–1167. [Google Scholar] [CrossRef]
- Xi, B.; Li, J.; Li, Y.; Song, R.; Shi, Y.; Liu, S.; Du, Q. Deep Prototypical Networks with Hybrid Residual Attention for Hyper-spectral Image Classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2020, 13, 3683–3700. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Visual Attention-Driven Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8065–8080. [Google Scholar] [CrossRef]
- Jie, H.; Li, S.; Gang, S. Squeeze-and-excitation networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Vedaldi, A. Gather-excite: Exploiting feature context in convolutional neural networks. In Adv. Neural Inform. arXiv 2018, arXiv:1810.12348. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, W.; Yu, Y.; Turner, K.; Derr, T.; Wang, M.; Ntoutsi, E. Interpretable Visual Understanding with Cognitive Attention Network. arXiv 2021, arXiv:2108.02924. [Google Scholar] [CrossRef]
- Park, J.; Woo, S.; Lee, J.-Y.; Kweon, I.S. Bam: Bottleneck attention module. arXiv 2018, arXiv:1807.06514. [Google Scholar]
- Roy, A.G.; Navab, N.; Wachinger, C. Recalibrating Fully Convolutional Networks With Spatial and Channel “Squeeze and Excitation” Blocks. IEEE Trans. Med. Imaging 2018, 38, 540–549. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Acito, N.; Matteoli, S.; Rossi, A.; Diani, M.; Corsini, G. Hyperspectral Airborne “Viareggio 2013 Trial” Data Collection for Detection Algorithm Assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2365–2376. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, T.; Yang, Y. Hyperspectral image classification based on multi-scale residual network with attention mechanism. arXiv 2020, arXiv:2004.12381. [Google Scholar] [CrossRef]
- Ahmad, M.; Shabbir, S.; Raza, R.A.; Mazzara, M.; Distefano, S.; Khan, A.M. Hyperspectral Image Classification: Artifacts of Dimension Reduction on Hybrid CNN. arXiv 2021, arXiv:2101.10532. [Google Scholar] [CrossRef]
- Zhu, M.; Jiao, L.; Liu, F.; Yang, S.; Wang, J. Residual Spectral–Spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 449–462. [Google Scholar] [CrossRef]
- Gao, H.; Yang, Y.; Li, C.; Gao, L.; Zhang, B. Multiscale Residual Network with Mixed Depthwise Convolution for Hyper-spectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3396–3408. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).