Search for Electron Bursts in the Inner Van Allen Belts with the CSES and NOAA POES Satellites
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
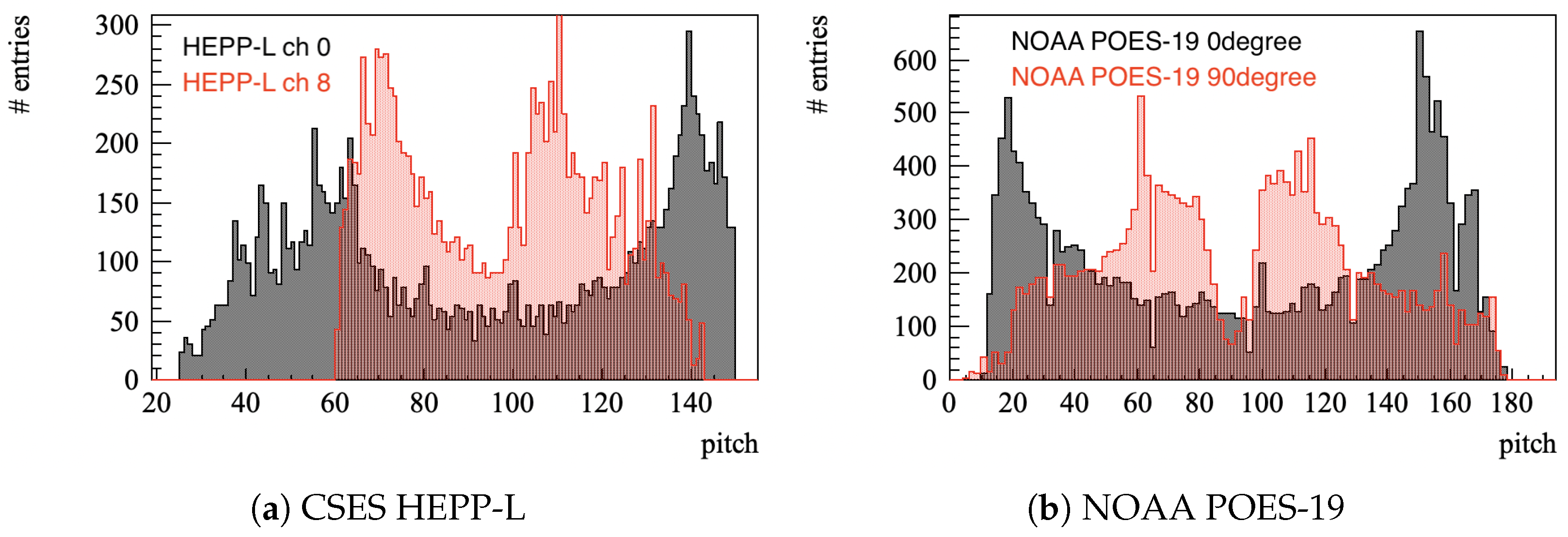
2.1.1. HEPP-L on CSES-01
2.1.2. NOAA POES-19 MEPED
2.2. Data Preparation
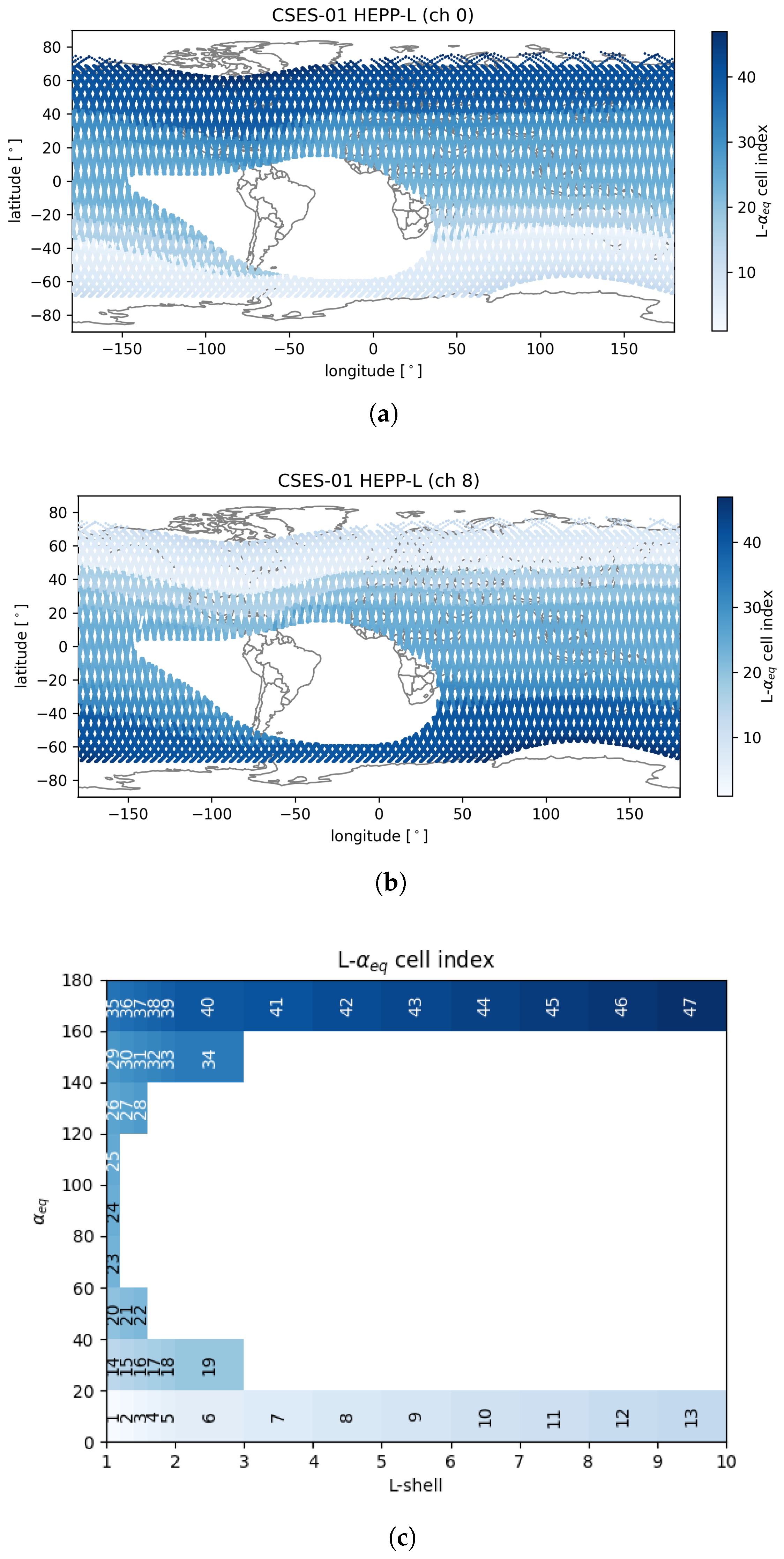
2.2.1. Study of Fluxes in the Invariant Phase Space
2.2.2. Time Integration
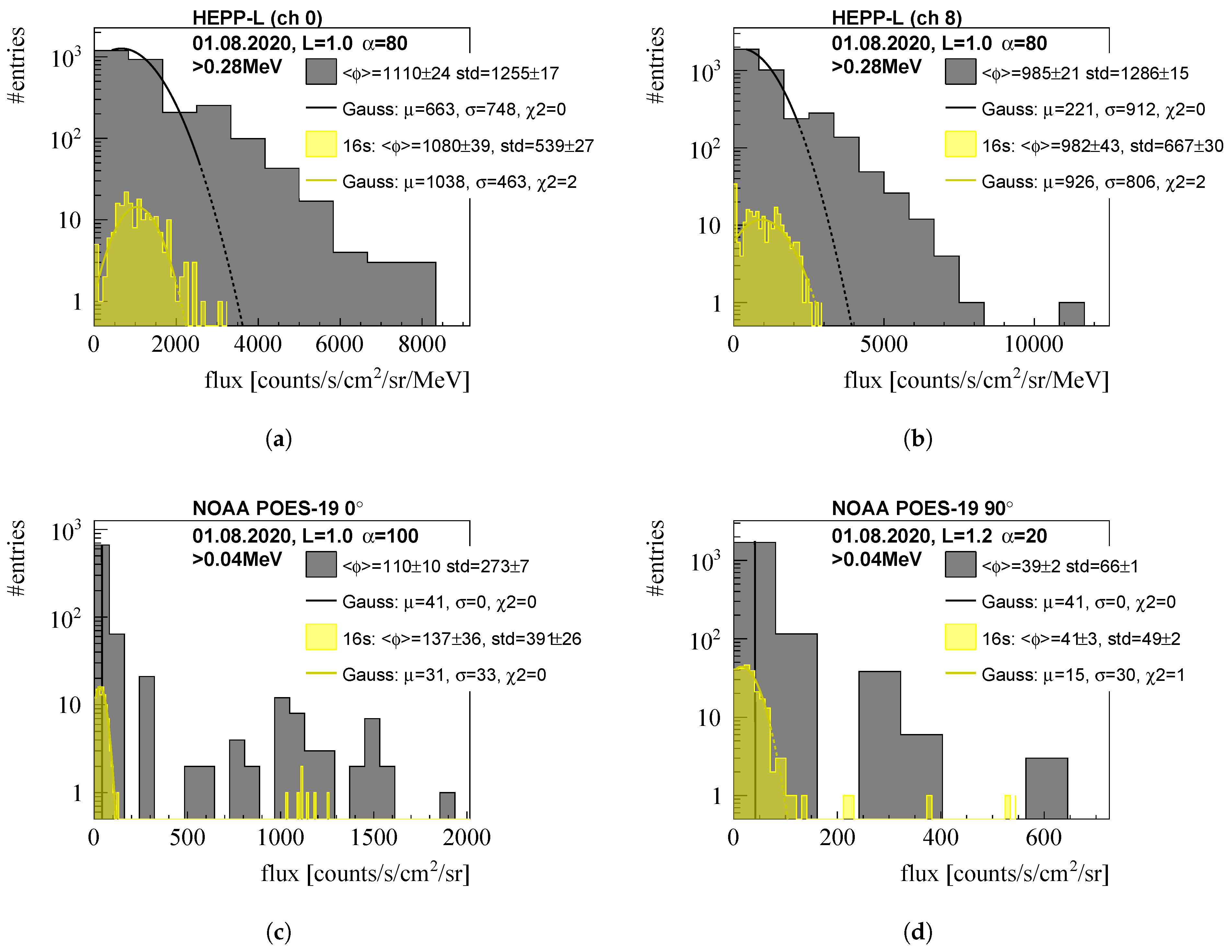
2.3. Daily Background Estimates
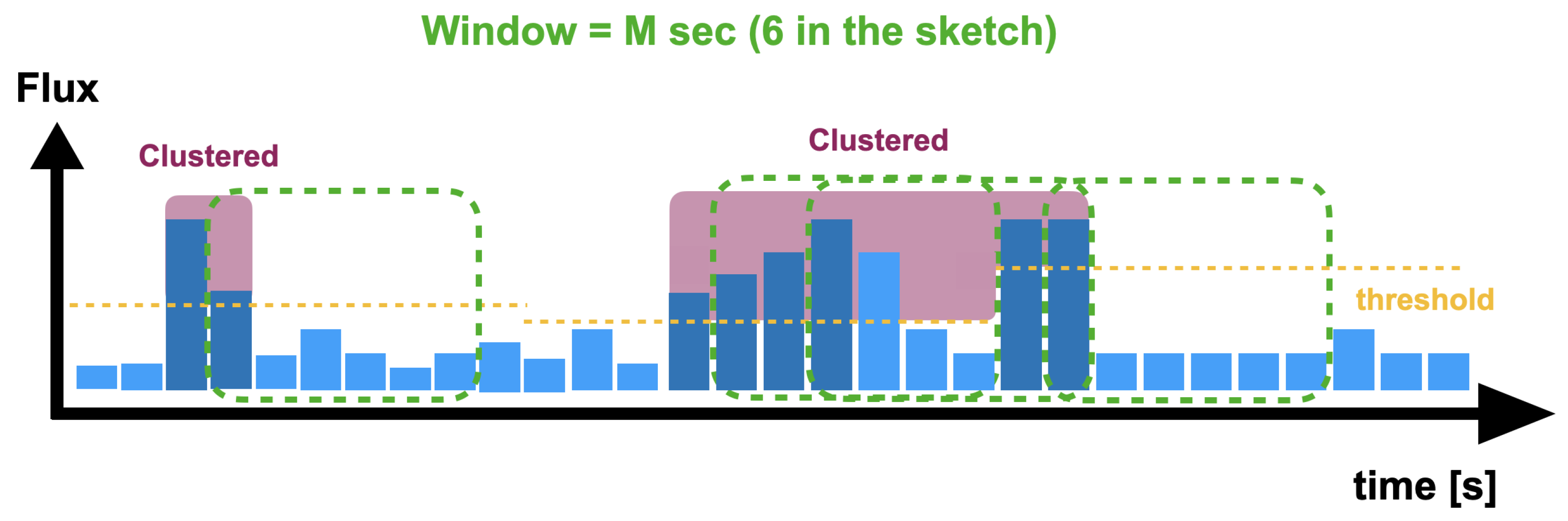
2.4. Clustering
- The time sequence is scanned to find events above the threshold (one of the four defined before). These events are called “seeds”.
- If two subsequent flux measurements are seeds, then a time window is opened. The window starts at the time of the second seed and extends for the next M seconds.
- If another pair of subsequent seeds is found in the time window, another window is opened, and the seed search continues. This procedure is iterated until no more pairs of subsequent seeds are found within M seconds from the previous.
- After the stop of the iterative procedure, the measurements within half a window from the first and last seed are added to the cluster.
2.5. Testing of Sensitivity and Efficiency
- (1)
- The time of the artificial signal is randomly chosen within the available time period (i.e., outside the SAA and within an L-shell range from 1 to 5).
- (2)
- Within that time period, the artificial signal replaces the original measurement with a value based on the average and standard deviation from the background estimation in that L- cell.
- (3)
- The background estimation is repeated on the new dataset, which includes the artificial signals.
- (4)
- The flux selection based on the new background estimation (with a threshold of ) is applied, and the number of artificial signals that are identified is counted and compared to the total number of introduced artificial signals.
3. Results
3.1. Efficiency and Sensitivity
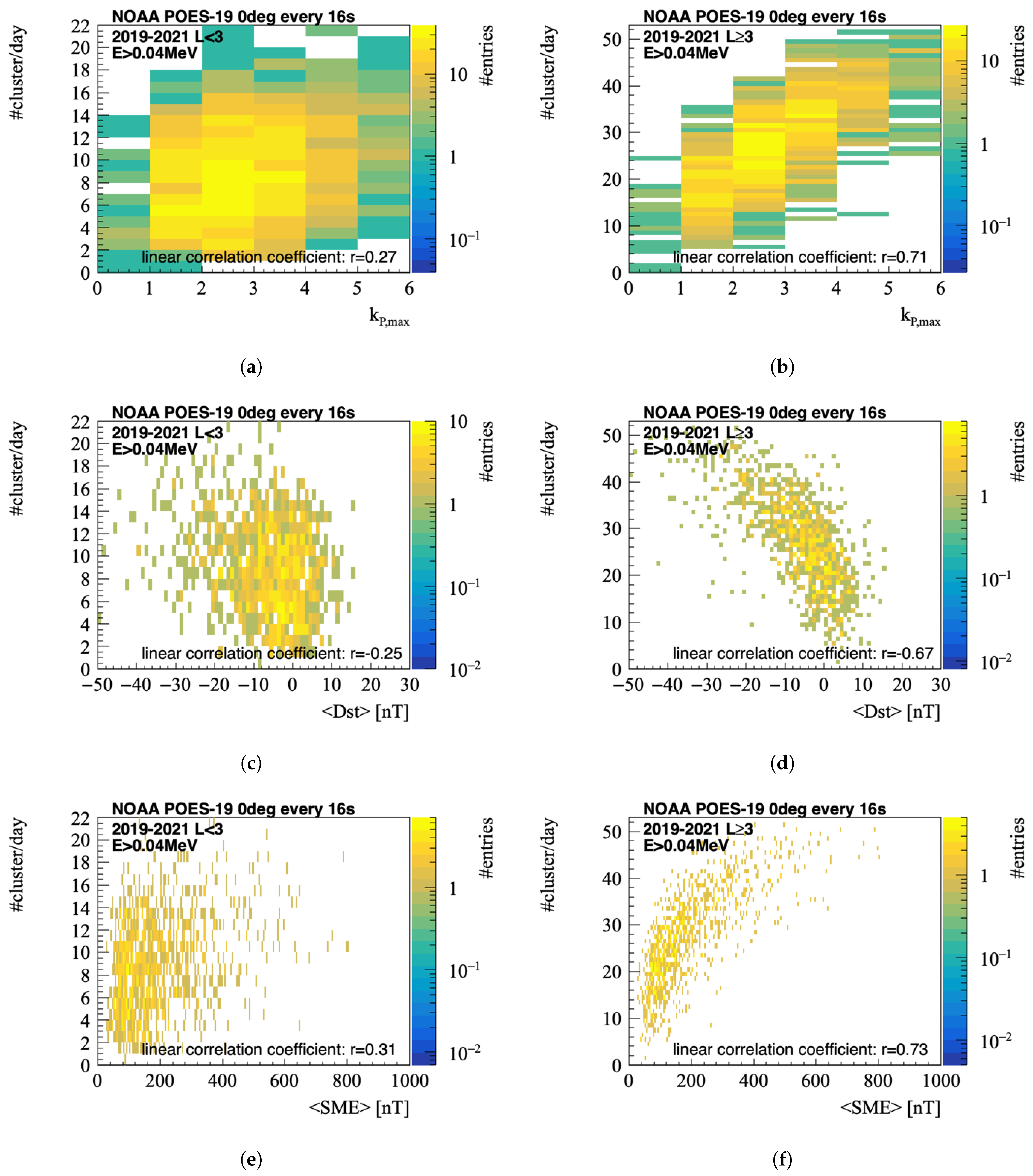
3.2. Correlation of Particle Bursts and Geomagnetic Indices
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aleksandrin, S.Y.; Galper, A.M.; Grishantzeva, L.A.; Koldashov, S.V.; Maslennikov, L.V.; Murashov, A.M.; Picozza, P.; Sgrigna, V.; Voronov, S.A. High-energy charged paricle burst in near-Earth space as earthquake precursors. Ann. Geophys. 2003, 21, 597–602. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Sgrigna, V.; Carota, L.; Conti, L.; Corsi, M.; Galper, A.; Koldashov, S.; Murashov, A.; Picozza, P.; Scrimaglio, R.; Stagni, L. Correlations between earthquakes and anomalous particle bursts from SAMPEX/PET satellite observations. J. Atmos. Sol. Terr. Phys. 2005, 67, 1448–1462. [Google Scholar] [CrossRef]
- Battiston, R.; Vitale, V. First evidence for correlations between electron fluxes measured by NOAA-POES satellites and large seismic events. Nucl. Phys. Proc. Suppl. 2013, 243–244, 249–257. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sasmal, S.; Basak, T.; Chakrabarti, S.K. Comparative study of charged particle precipitation from Van Allen radiation belts as observed by NOAA satellites during a land earthquake and an ocean earthquake. Adv. Space Res. 2019, 64, 719–732. [Google Scholar] [CrossRef]
- Brice, N. Fundamentals of very low frequency emission generation mechanisms. J. Geophys. Res. 1964, 69, 4515–4522. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Mazhaeva, O.A.; Goliavin, A.N.; Hayakawa, M. Observation by the Intercosmos-24 satellite of ELF-VLF electromagnetic emissions associated with earthquakes. Ann. Geophys. 1993, 11, 431–440. [Google Scholar]
- Imhof, W.L.; Reagan, J.B.; Voss, H.D.; Gaines, E.E.; Datlowe, D.W.; Mobilia, J.; Helliwell, R.A.; Inan, U.S.; Katsufrakis, J.; Joiner, R.G. Direct observation of radiation belt electrons precipitated by the controlled injection of VLF signals from a ground-based transmitter. Geophys. Res. Lett. 1983, 10, 361–364. [Google Scholar] [CrossRef]
- Voss, H.D.; Imhof, W.L.; Walt, M.; Mobilia, J.; Gaines, E.E.; Reagan, J.B.; Inan, U.S.; Helliwell, R.A.; Carpenter, D.L.; Katsufrakis, J.P.; et al. Lightning-induced electron precipitation. Nature 1984, 312, 740–742. [Google Scholar] [CrossRef]
- Parrot, M. Special issue of Planetary and Space Science ‘DEMETER’. Planet. Space Sci. 2006, 54, 411–412. [Google Scholar] [CrossRef]
- Sauvaud, J.-A.; Maggiolo, R.; Jacquey, C.; Parrot, M.; Berthelier, J.-J.; Gamble, R.J.; Rodger, C.J. Radiation belt electron precipitation due to VLF transmitters: Satellite observations. Geophys. Res. Lett. 2008, 35, 9. [Google Scholar] [CrossRef]
- Graf, K.L.; Inan, U.S.; Piddyachiy, D.; Kulkarni, P.; Parrot, M.; Sauvaud, J.A. DEMETER observations of transmitter-induced precipitation of inner radiation belt electrons. J. Geophys. Res. Space Phys. 2009, 114, A7. [Google Scholar] [CrossRef]
- Inan, U.S.; Piddyachiy, D.; Peter, W.B.; Sauvaud, J.A.; Parrot, M. DEMETER satellite observations of lightning-induced electron precipitation. Geophys. Res. Lett. 2007, 34, 7. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.C.; Vassiliadis, E.; Pulinets, S. Characteristics of flux-time profiles, temporal evolution, and spatial distribution of radiation-belt electron precipitation bursts in the upper ionosphere before great and giant earthquakes. Ann. Geophys. 2012, 55, 21–36. [Google Scholar]
- Shen, X.; Zong, Q.-G.; Zhang, X.M. Introduction to special section on the China Seismo-Electromagnetic Satellite and initial results. Earth Planet. Phys. 2018, 2, 439. [Google Scholar] [CrossRef]
- Huang, J.; Lei, J.; Li, S.; Zeren, Z.; Li, C.; Zhu, X.; Yu, W. The Electric Field Detector (EFD) onboard the ZH-1 satellite and first observational results. Earth Planet. Phys. 2018, 2, 469. [Google Scholar] [CrossRef]
- Zong, J.; Tao, D.; Shen, X. Possible ELF/VLF Electric Field Disturbances Detected by Satellite CSES before Major Earthquakes. Atmosphere 2022, 13, 1394. [Google Scholar] [CrossRef]
- Li, X.Q.; Xu, Y.B.; An, Z.H.; Liang, X.H.; Wang, P.; Zhao, X.Y.; Wang, H.Y.; Lu, H.; Ma, Y.Q.; Shen, X.H.; et al. The high-energy particle package onboard CSES. Radiat. Detect. Technol. Methods 2019, 3, 22. [Google Scholar] [CrossRef]
- Green, J. NOAA NESDIS-NGDC MEPED Telescope Data Processing; Technical Report; NOAA: Washington, DC, USA, 2013. [Google Scholar]
- Yando, K.; Millan, R.M.; Green, J.C.; Evans, D.S. A Monte Carlo simulation of the NOAA POES Medium Energy Proton and Electron Detector instrument. J. Geophys. Res. 2011, 116, A10231. [Google Scholar] [CrossRef]
- Zhang, Z. (Institute of Crustal Dynamics, China Earthquake Administration, Beijing 100085, China). 2022; Private Communication.
- Thébault, E.; Finlay, C.C.; Beggan, C.; Alken, P.; Aubert, J.; Barrois, O.; Bertrand, F.; Bondar, T.; Boness, A.; Brocco, L.; et al. International Geomagnetic Reference Field: The 12th generation. Earth Planets Space 2015, 67, 79. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The thirteenth generation. Earth Planets Space 2021, 73, 1–25. [Google Scholar] [CrossRef]
- McIlwain, C.E. Magnetic coordinates. Space Sci. Rev. 1966, 5, 585–598. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xiaowei, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Technical Report CONF-960830-TRN: 96:005928-0038, 2. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. ACM Trans. Database Syst. 2017, 42, 19. [Google Scholar] [CrossRef]
- Sklearn. Sklearn Implementation of DBSCAN Algoritm. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html (accessed on 18 November 2021).
- Wang, X.; Zhang, L.; Zhang, X.; Xie, K. Application of Improved DBSCAN Clustering Algorithm on Industrial Fault Text Data. In Proceedings of the 2020 IEEE 18th International Conference on Industrial Informatics (INDIN), Warwick, UK, 20–23 July 2020; Volume 1, pp. 461–468. [Google Scholar] [CrossRef]
- Zhang, M. Use Density-Based Spatial Clustering of Applications with Noise (DBSCAN) Algorithm to Identify Galaxy Cluster Members. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 042033. [Google Scholar] [CrossRef]
- Nakamura, R.; Kamei, K.; Kamide, Y.; Baker, D.N.; Blake, J.B.; Looper, M. SAMPEX observations of storm-associated electron flux variations in the outer radiation belt. J. Geophys. Res. Space Phys. 1998, 103, 26261–26269. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The Geomagnetic Kp Index and Derived Indices of Geomagnetic Activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Despirak, I.V.; Lyubchich, A.A.; Kleimenova, N.G.; Gromova, L.I.; Gromov, S.V.; Malysheva, L.M. Geomagnetic Effects of the Supersubstorms during the Magnetic Storm of March 9, 2012. Bull. Russ. Acad. Sci. Phys. 2021, 85, 246–251. [Google Scholar] [CrossRef]
- Newell, P.T.; Gjerloev, J.W. Evaluation of SuperMAG auroral electrojet indices as indicators of substorms and auroral power. J. Geophys. Res. Space Phys. 2011, 116, A12211. [Google Scholar] [CrossRef]
- Love, J. Magnetic monitoring of earth and space. Phys. Today 2008, 61, 31. [Google Scholar] [CrossRef]





| Instrument | Telescope | (cms·sr) | Measurement Rate (Hz) | (MeV) | |
|---|---|---|---|---|---|
| MEPED | 0 | [19] | 1/2 | 0.04/0.13/0.29/0.61 | |
| 90 | |||||
| HEPP-L | narrow channels: 0, 2, 4, 6, 8 | [21] | 1 | 0.1/0.28/0.46 | |
| wide channels: 1, 3, 5, 7 | |||||
| Dataset | L- Coverage (%) | Flux Losses (%) |
|---|---|---|
| NOAA POES-19 0 | 76.5 | 4.8 |
| NOAA POES-19 90 | 64.5 | 5.9 |
| HEPP-L channel 0 | 60.8 | 6.6 |
| HEPP-L channel 8 | 59.9 | 7.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neubüser, C.; Battiston, R.; Burger, W.J.; Follega, F.M.; Vitale, V. Search for Electron Bursts in the Inner Van Allen Belts with the CSES and NOAA POES Satellites. Remote Sens. 2023, 15, 411. https://doi.org/10.3390/rs15020411
Neubüser C, Battiston R, Burger WJ, Follega FM, Vitale V. Search for Electron Bursts in the Inner Van Allen Belts with the CSES and NOAA POES Satellites. Remote Sensing. 2023; 15(2):411. https://doi.org/10.3390/rs15020411
Chicago/Turabian StyleNeubüser, Coralie, Roberto Battiston, William Jerome Burger, Francesco Maria Follega, and Vincenzo Vitale. 2023. "Search for Electron Bursts in the Inner Van Allen Belts with the CSES and NOAA POES Satellites" Remote Sensing 15, no. 2: 411. https://doi.org/10.3390/rs15020411
APA StyleNeubüser, C., Battiston, R., Burger, W. J., Follega, F. M., & Vitale, V. (2023). Search for Electron Bursts in the Inner Van Allen Belts with the CSES and NOAA POES Satellites. Remote Sensing, 15(2), 411. https://doi.org/10.3390/rs15020411








