Abstract
Knowledge of the precise water depth in shallow areas of the ocean is of great significance to the safe navigation of ships and hydrographic surveying. Compared with traditional bathymetry, satellite remote sensing for water depth determination makes it possible to cover large areas by dynamic observation. In this paper, we conducted an optically shallow water bathymetric inversion study using a Stumpf empirical model, random forest model, neural network model, and support vector machine model based on Sentinel-2 satellite images and Ganquan Dao measured bathymetry data. We compared and analyzed the inversion results based on the empirical model and different machine learning models. The results show that the Stumpf empirical and machine learning models are capable of inverting optically shallow water depth. Moreover, the machine learning models had better fitting ability than the Stumpf empirical model with a sufficient number of samples, especially when the water depth was greater than 15 m. In addition, the random forest model had the highest overall accuracy among these models, with a root mean square error (RMSE) of 1.41 m and a regression coefficient (R2) of 0.96 for the test data.
1. Introduction
China has a long coastline, vast sea area, abundant marine resources, and coral reefs, representing some of the most productive and biologically diverse ecosystems on earth, and are mostly distributed in shallow waters [1]. Access to water depth of coral reefs aids in protecting and managing coral reefs. Furthermore, obtaining information on shallow water depth is critical for shipping management and marine resource development. The traditional methods of bathymetric measurement employ multibeam echosounders or bathymetric sonars [2,3,4]. This method of field sounding, however, is associated with significant labor costs, time-consuming operations, and difficult implementation in shallow water and disputed sea areas [5].
Remote sensing makes it possible to carry out large-scale dynamic shallow water depth monitoring [6]. Studies focusing on water depth retrieval using multi-spectral satellite images have been carried out in various countries since the 1970s and in China since the 1980s [3,7]. Due to correlation between exponential attenuation of energy and water depth, there is a quantitative relationship between water depth and remote sensing image data (e.g., digital quantization value, radiance, and reflectivity) [7]. Therefore, we can use remote sensing images and other auxiliary data (e.g., measured water depth and optical water parameters) to build water depth retrieval models. At present, three methods are mainly used for water depth retrieval using passive optical remote sensing: theoretical analytical models based on radiative transfer equation, semi-theoretical and semi-empirical models, and statistical models.
The theoretical analytical model was first established in 1978 by Lyzenga et al. based on the classical radiative transfer theory of double-layer flow [8], which used analysis of water reflectivity to retrieve water depth. The analytical expression of radiance received by the optical remote sensor as a function of water depth and bottom reflection is established by neglecting the reflection effect inside the water body [9]. In the absence of measured water depth data, the water depth can be retrieved from the image [10]. However, as the parameters involved are complex, it is necessary to determine the optical model parameters of the water body in the study area and iteratively calculate them to obtain the estimated water depth [11].
The semi-theoretical and semi-empirical model (also called empirical model) is based on the theory of light radiation attenuation in the water and uses the combination of a theoretical model and empirical parameters to determine the water depth using passive optical remote sensing [12]. The radiance received by the optical remote sensor is expressed as the sum of deep-water area radiance and bottom reflected radiance. In 1973, the log-linear model was proposed by Polcyn et al. [13], and became the more widely used model, and it was later simplified by Tanis et al. to derive a single-band model in 1986 [14]. As shown by Paredes et al., assuming that the reflectance ratio of each band on different substrate types is constant, a dual-band model is derived, which can also be developed into a multi-band model [15]. In order to avoid a situation where the difference between the radiance received by the optical remote sensor and the radiance in the deep-water area is negative in the log-linear model, Stumpf et al. proposed a log-transformed ratio model in 2003 [16]. In 2015, Sarah et al. compared the empirical and optimization methods on the Great Barrier Reef: Lizard Island (a continental island fringing reef) and Sykes Reef (a planar platform reef) [17]. Many domestic scholars have also studied the semi-theoretical and semi-empirical models. For example, in 2007, Tian et al. used Landsat-TM data to derive the remote sensing bathymetry equation, constructed a waveband ratio model to remove the deep bathymetric reflectivity, and completed the remote sensing mapping of the near-coastal bathymetry in Jiangsu [18]. In 2003, Dang et al. later used Landsat-TM data to build a bathymetric inversion model of the sea area near Yongshu Reef in the South China Sea by combining wavebands, and they also improved the accuracy of the estimated inversion bathymetry by adopting the method of dividing the substrate types [19]. In 2019, Lu et al. established the band ratio model by using measured points and three multispectral images of Landsat-8, SPOT-6, and WorldView-2 [20]. The semi-theoretical and semi-empirical model is widely used due to its simple parameters and optimizability to different study areas using only measured bathymetry data [21].
The statistical model directly establishes the statistical relationship between the radiance of the remote sensing image and the measured water depth without considering the physical mechanism of water depth remote sensing. The traditional statistical model expressions include the linear function, logarithmic function, and power function, although their accuracy is not high. In 1998, Zhang et al. showed that, using linear regression, the water depth can be inversed by adding a nonlinear correction term in the form of a power function [22]. In 2009, the water depths of the radial sand ridges in the South Yellow Sea off the coast of Jiangsu Province were retrieved by Zhang (using linear, exponential, reciprocal, and quadratic regression), as well as other types of water depth remote sensing models, and the average relative errors based on the traditional statistical models were mostly between 30% and 45% [23]. Machine learning is a statistical method that uses self-learning, self-organization, self-adaptation, and nonlinear dynamic processing [24,25]. The accuracy of machine learning is affected by the sample data. When there is a certain number of measured water depth data, the fitting effect is significantly better than with the two models described above. In 2005, Wang et al. used a BP neural network to invert the bathymetry of the Nangang section of the Yangtze River Estuary [26]. In 2018, Wang et al. used support vector machines to perform bathymetric inversions of the North Island in the Xisha Islands [27]. In 2019, Qiu et al. used the random forest algorithm to invert the bathymetry of Ganquan Dao in Xisha Islands and found that the machine learning-based bathymetry inversion is more accurate than that obtained using the traditional statistical model, with an average relative error of 10% to 20% [28]. In 2020, Bo et al. proposed a model based on a convolutional neural network which used different remote sensing images in four spectral bands, red, green, blue, and near-infrared, to retrieve the water depth. The accuracy of the convolutional neural network model was better than traditional neural network [29]. Moreover, when a sufficient number of measured water depth data from different areas can be obtained, the robustness of the machine learning model can be improved, making this method suitable for different water bodies and areas with highly transparent water.
In summary, many scholars have thus far conducted remote sensing shallow bathymetry inversion experiments using different methods. However, comparative analyses between different methods are still rare, especially regarding the widely used semi-theoretical, semi-empirical, and machine learning methods. Comparative research between machine learning methods and empirical methods for different quantities of measured water depth samples is absent, and the results of comparative analyses of machine learning methods and empirical methods in different water depth ranges are inconclusive. Therefore, in this paper, the accuracy and applicability of machine learning and semi-theoretical, semi-empirical model-based methods for bathymetric inversion in clean shallow water areas were compared and evaluated based on Sentinel-2 satellite images and measured bathymetric data of the optical shallow waters around the Ganquan Dao study area. The empirical models included the Stumpf empirical model, which is one of the most widely used models, and machine learning models included the random forest, neural network, and support vector machine models.
2. Study Area and Data
2.1. Study Area
The study area is located in the waters surrounding Ganquan Dao, Xisha Islands, China (Figure 1). The island is oval, 700 m long from north to south, 500 m wide from east to west, and covers an area of approximately 0.3 km2, with mixed sand and coral reef sediment. The waters around the island are clear and the water depth varies gently (mostly within 30 m) [30], which makes the area suitable for a remote sensing bathymetry inversion study.
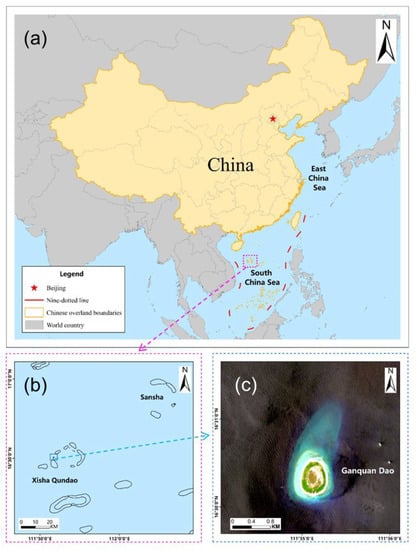
Figure 1.
(a) Location of the area shown in (b); (b) location of Xisha Qundao, blue rectangle represents the location of Ganquan Dao; and (c) true color image derived from a Sentinel-2 image of Ganquan Dao.
2.2. Data
Sentinel-2A data were downloaded from the European Space Agency (ESA) website (https://scihub.copernicus.eu/dhus/#/home, accessed on 12 August 2022) (Sensing date: 28 July 2020, at 10:55 a.m). The geographic coordinate system was WGS-84, the projection was UTM transverse Mercator projection, and the central meridian was 111 °E. The resolution and band information of the image are shown in Table 1.

Table 1.
Sentinel-2A band information.
The measured water depth data were obtained using LiDAR measurements. The horizontal and elevation accuracy were reliable and were considered suitable for use as the actual water depth data for water depth inversion research. The geodetic coordinate system was CGCS-2000 with Gauss-Kruger projection, the central meridian was 111 °E, and the elevation datum was the 1985 national elevation datum. The average water surface elevation 200 m from the land was used as the actual water surface elevation and actual water depth was obtained by subtracting the water surface elevation from the point elevation. Figure 2 shows a schematic diagram of the data distribution obtained by randomly selecting 10% of the measured water depth data (the small yellow triangles in the figure represent the measured water depth points).
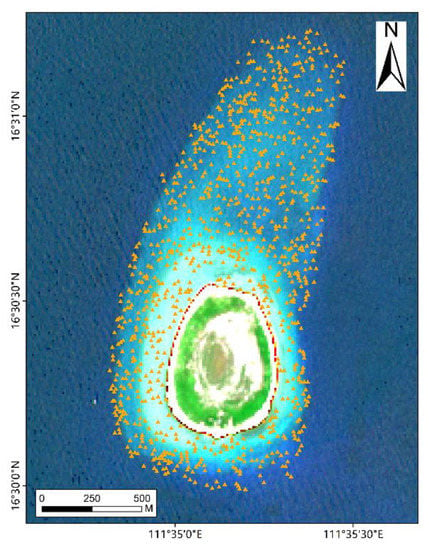
Figure 2.
Distribution diagram of measured water depth data.
The quality level of image data was Level-2A, and as the data had already undergone the steps of atmospheric and radiation correction by ESA, the pre-processing of the image in this paper mainly included water body extraction, sun-glint correction, and tidal correction for the measured bathymetry data.
2.2.1. Water Extraction
The normalized water body index (NDWI) proposed by McFeeters et al. was used for water body extraction around Ganquan Dao based on the green and near-infrared bands [31], and the specific calculation formula was as follows:
2.2.2. Sun-Glint Correction
The sun-glint phenomenon refers to the Fresnel reflection of sunlight on a rough sea surface caused by wind and waves in ocean remote sensing, which is manifested as a white flare in optical remote sensing images. As this is a strong reflection phenomenon with a strong effect on image radiance and the accuracy of bathymetry inversion, it was necessary to perform sun-glint correction in data pre-processing. In this paper, we adopted the correction scheme proposed by Hedley et al. [32]. The principle was to assume that the near-infrared band is completely absorbed by the water body, and so the brightness variation caused by solar flares in the visible band is linearly correlated with the variation in the near-infrared band, based on which the information in the near-infrared band can be used for sun-glint correction in the visible band. First, we extracted the grayscale values of certain image elements in the optical deep-water region of the image, determined the minimum value of its NIR band (RNIR-min), and then calculated the slope coefficients (Bi) of the NIR band and each visible band using the least-squares method. The regression coefficients were calculated by substituting the minimum values of the NIR bands into the following equation:
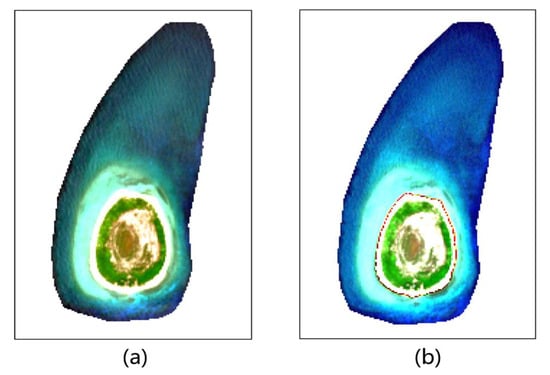
Figure 3.
Comparison before (a) and after (b) sun-glint correction.
2.2.3. Tidal Correction
Since the water depth measurement and remote sensing image acquisition times differed, the water surface elevation was also different due to tide influence, and it was necessary to implement a tidal correction for the measured water depth data. As a result, the water depth at the time of image = measured water depth + (tide height at the time of image − tide height at the measurement time). By querying the tide table, we determined that the tide height of Ganquan Dao at the time of image acquisition was 1.0 m and the tide height at the time of water depth data measurement was 0.7 m, meaning that the water depth at the image acquisition time was the measured water depth minus 0.3 m.
3. Methods
3.1. Stumpf Empirical Method
The Stumpf model was developed by Stumpf et al. as an empirical model [16] which can efficiently eliminate the influence of sediment, has simple parameters, and is suitable for a wide range of water transparencies. The model expression is:
3.2. Random Forest Method
Random forest is a machine learning algorithm formed by the combination of classification and regression tree (CART) algorithms, which performs well in various scenarios [34]. Random forest regression first uses the bootstrap sampling method (a sampling method with put-back) to randomly extract the sample data with the same total amount of K from the original sample with a total amount of K. This process is repeated N times. If the sample size is large enough, approximately 36.8% of the data will not be selected each time, which helps to avoid overfitting the model [35]. A decision tree is then constructed based on the sample dataset obtained by each extraction, and finally, N decision trees are obtained.
Secondly, for the construction of each regression decision tree, random forest needs to randomly select X feature attributes (X < the total number of features) from the attribute set of the sample and determine the optimal features according to the minimum root mean square error of node splitting, which ensures the diversity of the regression decision tree to the greatest extent. The random forest regression algorithm is based on the idea of ensemble learning, and the final prediction result is the average of all decision tree results.
3.3. Neural Network Method
A BP (Back-Propagation) neural network is a type of multilayer feedforward neural network which is trained according to error back-propagation. The network consists of two processes: the forward propagation of signals and the backward feedback of error [36]. In forward propagation, the input signal first completes the nonlinear transformation in the input layer through the hidden layer to generate the output signal. The neuron state of each layer only affects the neuron state of the next layer. If the actual output is not consistent with the expected output, the feedback is switched to the reverse feedback, the output error is reversed layer by layer from the hidden layer to the input layer, the error is distributed to all neurons of each layer, the network weights and thresholds are adjusted by the error signals obtained from each layer, and a predicted output value similar to the expected value is obtained through continuous training. Theoretically, a neural network with a single hidden layer can be infinitely close to any continuous nonlinear curve, but overfitting will also lead to a poor generalization ability of the model.
3.4. Support Vector Machine Method
The support vector machine (SVM) was first proposed to solve the binary classification problem, and its principle is to find an optimal classification hyperplane to meet the requirements, so that the hyperplane maximizes the blank area on both sides while ensuring classification accuracy [37]. In theory, SVM can achieve optimal classification of linearly separable data. It has shown many unique advantages in solving small sample, nonlinear, and high-dimensional pattern recognition problems, and has overcome the “curse of dimensionality” and “over-learning” problems to a large extent.
The basic aim of support vector machine regression is to find a function to construct a regression plane in the error channel (ε) with majority data points in range, achieving the minimized confidence range value [38]. For the nonlinear associations, the support vector machine maps the sample data to the feature space with high or infinite dimensions through the nonlinear function and constructs the regression estimation function in this linear space with infinite dimensions.
3.5. Water Depth Inversion Experiment
3.5.1. Correlation Analysis and Evaluation Index
Before the construction of the model, the correlation between the band information and the measured water depth was analyzed. The Pearson correlation coefficient was used for analysis and calculation and the highly correlated bands and band combinations are listed in Table 2.

Table 2.
Correlation analysis.
As shown in Table 2, the bands with high correlation are mainly the blue and green bands, as well as the ratio of the blue-green band to the green-red band. The poor correlation between the red band and the unlisted infrared band is caused by the gradually decreasing transmission capacity of light in water in response to an increase in wavelength, which is also the reason why most empirical models use the blue-green band as the independent variable.
We used R2, RMSE, and mean absolute error (MAE) as the evaluation index, and the calculation formula was as follows:
3.5.2. Model Construction
We selected 6586 measured water depth data points with tidal correction and water depth ranging from 0 to 25 m to construct the model. Stratified sampling was carried out at an interval of 5 m according to the 7:3 ratio of training samples to test samples, resulting in 4610 training samples and 1976 test samples.
We used Python to read the image and measured bathymetry data, and applied coordinate conversion to achieve geographic alignment between measured bathymetry data and remote sensing image elements. Subsequently, the reflectivity of each band of the corresponding pixel of the measured water depth point on the image was extracted and the water depth and reflectivity data of the training set were inserted into the model. In the process of building multiple machine learning models, we found that the accuracy of the final model did not change significantly when the reflectance value of a single band was used as the independent variable and the reflectance ratio of the band was used as the independent variable for model training. Therefore, in the machine learning model, the reflectance of the individual bands B2, B3, and B4 was used to construct the water depth prediction, whereas the Stumpf model takes the blue band (B2) and the green band (B3) as the model inputs. All the machine learning models were constructed using the scikit-learn package.
Firstly, for the Stumpf empirical model, when the Levenberg-Marquardt optimization algorithm was used for iterative optimization, the initial values of the parameters were in accordance with the literature [39]. After adjusting the settings, using a higher number of iterations, and specifying the optimal parameters, the accuracy of the model appeared stable. For the BP neural network model, many experiments are needed to determine the parameters of the model, including the number of hidden layers, the number of neurons in each layer, the learning rate, and the number of iterations. Through continuous adjustment, the final model was set as follows: four hidden layers with 64, 32, 16, and 8 neurons in each, respectively, a learning rate of 0.00001, an Adam optimizer based on a stochastic gradient, 200 samples selected each time (batch_size), and the number of iterations set to 200.
Random forest and support vector machine can automatically adjust the optimal parameters based on the training samples using cross-validation and the grid search method. In the random forest model, the number of decision trees was 350, the minimum number of samples in leaf nodes was 3, the maximum number of features considered when branching the decision tree was 2, and the maximum depth of the decision tree was 30. The radial basis function (RBF) was used for the support vector machine model, the penalty coefficient (C) was set to 90, and the gamma parameter of the kernel function was set to 0.5.
4. Results
4.1. Overall Model Accuracy
For model accuracy evaluation, the test data were inserted into the trained model, the water depth inversion results were obtained, the error of each model was calculated, and the inversion accuracy of the model was determined as shown in Table 3. A scatter diagram shown in Figure 4 displays the measured water depth and the predicted values. As seen in Table 3, the overall order of the models based on accuracy from highest to lowest was random forest, neural network model, support vector machine model, and Stumpf model.

Table 3.
Overall accuracy of the models.
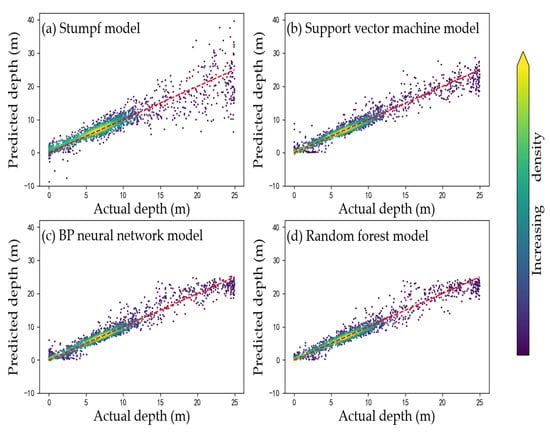
Figure 4.
(a–d) Scatter diagram of water depth inversion values and measured values.
As shown in Figure 4, the Stumpf empirical model performed well when the water depth was approximately 0 to 15 m, and the trends in the measured data were mostly consistent with those of the predicted data. However, when the water depth was shallow, the predicted values of some water depth points were negative and the deviation was large. The reason for this was that the water depth points near the shore were located in the wave-breaking zone, where the surface is very rough. At the same time, the concentration of suspended sediment was high, and the change in reflectance did not meet the inference of the Stumpf model (that the logarithmic ratio of blue and green bands gradually increases with an increase in water depth), resulting in some water depth predictions being negative. When the water depth was more than 15 m, there were obvious deviations between predicted values and measured values. This was caused by visible light being absorbed by the water body, resulting in a poor correlation between image reflectance and water depth, and low model accuracy.
Comparing the Stumpf empirical model and machine learning model, the accuracies of the random forest model, the neural network model, and the support vector machine model were higher than that of the Stumpf empirical model. The distributions of predicted and measured data in the scatter plot were more convergent, which shows that machine learning has advantages in solving nonlinear problems and its fitting ability is significantly better than that of the empirical model. Especially when the water depth was greater than 15 m, the machine learning model displayed good performance and the accuracy of the model was higher than that of the empirical model. However, there was a significant amount of noise that affected the accuracy of the model.
Further comparative analysis of the three machine learning models showed that the prediction accuracy of the random forest model was the highest, and its RMSE and MAE were lower than those of the support vector machine and neural network (RMSE = 1.41 m, MAE = 0.95). However, the random forest model also had limitations. In the random forest regression model, its output is the average of all the regression decision tree results in the model, and for each regression decision tree, its output is the average of the leaf nodes at the end of the tree. Consequently, the final output of the model is limited by the distribution range of the input data. For example, when the training data of the model only included the water depth data of 0–5 m, the random forest model could only invert the water depth in the range of 0–5 m.
4.2. Model Error Analysis
In order to compare the water depth inversion error in different water depth ranges, the root mean square error and mean absolute error of the inversion water depth in different ranges were determined (Table 4). As shown in Table 4, the accuracy of the machine learning models was higher than that of the empirical model in all water depth ranges, especially in the water depth range of 15 to 25 m. Among the three machine learning models, the random forest model had the highest accuracy in the water depth range of 0 to 10 m (RMSEs for ranges 0–5 m and 5–10 m were 0.82 m and 1.0 m, respectively). The accuracy of the support vector machine model was optimal in the water depth range of 10 to 20 m (RMSEs for ranges 10–15 m and 15–20 m were 1.9 m and 2.53 m, respectively). The accuracy of the neural network model was optimal in the water depth range of 20 to 25 meters (RMSE for range 20–25 m was 2.32 m).

Table 4.
Water depth range subsection accuracy.
The error distribution of each model is shown in Figure 5. The histogram in Figure 5 shows that the error distribution of each model conformed to the normal distribution, indicating that the models were reliable and had certain generalizations. Comparing the machine learning models and the empirical model, we found that the error distribution of the machine learning models was more concentrated and the number of points with large errors was significantly lower compared to the empirical model.
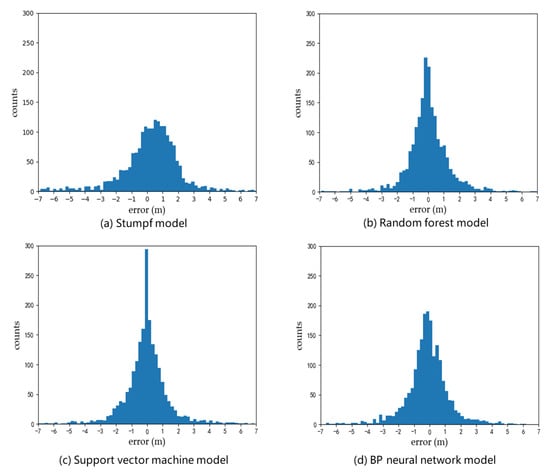
Figure 5.
(a–d) Model error distribution histograms.
Further comparison of the error histograms of each machine learning model showed that the number of data points distributed in the small error range of the support vector machine model was higher than that of the random forest and neural network models. This was caused by the vector machine regression building the regression hyperplane in the error band when constructing the regression function, in order to include as many data points as possible within the range of ε. For the data points that do not satisfy the error constraints, a slack variable and a penalty coefficient were introduced [40]. The data points on or beyond the error boundary are called support vectors, whereas points on the error boundary are usually called standard support vectors. The optimization goal is to maximize the distance from the support vector to the hyperplane. The data points within the error boundary (non-support vectors) will not affect the model construction, and therefore, the distribution of the SVM was concentrated within a small error range, although the overall accuracy of its model was lower than that of random forest and neural network models.
4.3. Influence of Sample Number on Model Accuracy
As the accuracy of the machine learning models was greatly affected by the number of samples, in order to evaluate the impact of the number of samples on the accuracy of the model, R2 was used as the accuracy index. The model training and test accuracies obtained by training on datasets of different sizes are shown in Figure 6.
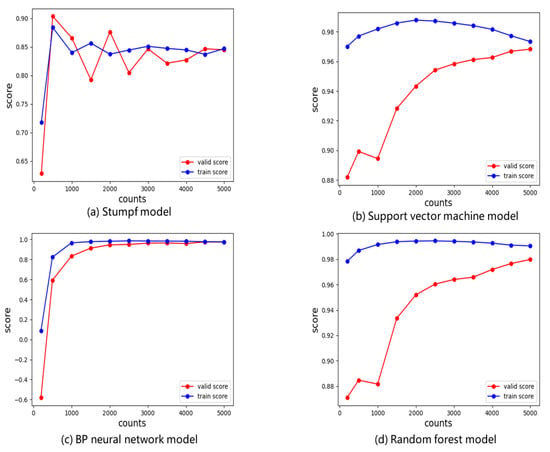
Figure 6.
Model accuracy response to different numbers of samples.
Firstly, the accuracy of the Stumpf empirical model in training data and test data improved with an increase in sample size, However, training accuracy did not change significantly with a change in the number of samples when the number of samples was sufficient. Test accuracy changed greatly, but the change was irregular, which indicates that the accuracy of the Stumpf empirical model was not affected by the number of samples, and besides, the model had poor stability and weak generalization ability. When the sample size was sufficient, the accuracy of the model was greatly affected by the quality of the data.
In the three machine learning models, the training accuracy of the model was improved with an increase in the number of samples when the number of samples was small. Due to the complexity of the neural network model parameters, when the number of samples was small, the fitting accuracy was poor, and the regression coefficient was negative. When the number of samples reached a certain number, the accuracy of the neural network and random forest models displayed no significant change with a further increase in the number of samples, while the training accuracy of the support vector machine decreased, because the support vector machine takes the training error as a constraint for the optimization problem and the minimization of the confidence range as the optimization goal [38]. With an increase in samples, in order to improve the generalization ability of the model, the error increased. Random forest and neural network displayed better fitting ability than the support vector machine.
The test accuracy of the three machine learning models was improved with an increase in the number of samples, which indicates that, with an optimal number of samples, machine learning can find potential nonlinear relationships between water depth and reflectivity.
4.4. Inversion Result
In order to evaluate the inversion accuracy of the models, the four trained models were used to invert the water depth around the study area. As shown in Figure 7, the prediction results of each model and the measured data were mostly consistent with the general trend of water depth change in each region.
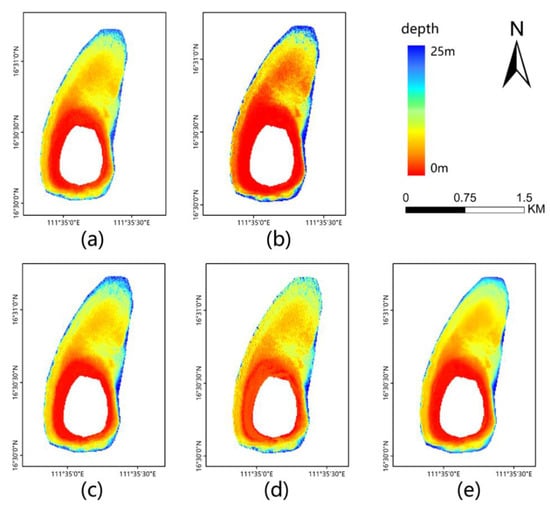
Figure 7.
(a–d) Bathymetric inversion results of the random forest model, the neural network model, the support vector machine model, and the Stumpf model. (e) Actual water depth.
By comparing the inversion results of the four models, we found that the water depth inversion results of the random forest model reflected the actual change in the water depth with higher accuracy. The neural network model underestimated water depth in shallow water areas and overestimated water depth when the actual depth was approximately 20 m. The support vector machine model was able to predict the trend of the true water depth change in general, but the inversion accuracy was lower than that of the random forest when the changes were small. The inversion accuracy of the Stumpf model was not ideal when the water was either shallow or deep.
5. Discussion
The overall accuracy of the model indicates that the errors of different models were consistent with change in water depth. The penetration of visible light decreases with a gradual increase in water depth, leading to increased errors. Therefore, the applicable depth range of multispectral remote sensing bathymetry inversion was within 25 m for both the machine learning methods and empirical methods. Inappropriate water depth range can affect inversion accuracy [41].
Compared with the empirical method, the machine learning method could achiever higher accuracy of water depth inversion with a sufficient number of samples, especially when the water depth is greater than 15m. The random forest model had the highest overall accuracy among the models, with a root mean square error (RMSE) of 1.41 m and a regression coefficient (R2) of 0.96 on the test data. This demonstrated that the random forest method can create more flexible and accurate models based on real data [42]. In the accuracy results of the water depth range segmentation, the machine learning algorithms had higher accuracy than the Stumpf empirical algorithm in each water depth range, which demonstrated the excellent fitting capability of machine learning in water depth inversion. However, the performance of individual machine learning models varied for different water depth ranges, with the random forest model more suitable for water depths below 10 m. The support vector machine model and neural network model were more applicable to water depth ranges from 10 m to 20 m and 20 m to 25 m, respectively.
With regard to the effect of different sample sizes on the accuracy of the model, machine learning methods require a certain sample size compared to empirical methods, otherwise the model would present lower accuracy. Stumpf empirical methods do not require large sample datasets; however, they are influenced significantly by sample data quality. Therefore, the Stumpf empirical method could be used when the quantity or distribution range of water depth is low. When sufficient water depth samples are available, the support vector machine method had an advantage for small sample data; conversely, the random forest and neural network methods had an advantage for large sample data.
Finally, the results of the model-based inversion of the water depth around the island using measured water depth data and multi-spectral remote sensing showed that it is possible to invert the real water depth trend; nevertheless, numerous factors influence the accuracy of water depth inversion, including suspended solids, sea floor type, and remote sensing image quality. Therefore, such factors should be included in water depth inversion models to enhance the accuracy of the inversion.
6. Conclusions
In the present study, the Stumpf empirical model, random forest model, neural network model, and support vector machine model for water depth inversion were established using Sentinel-2 satellite images and measured water depth data. The accuracy of each model was compared and analyzed, and the following conclusions were obtained.
- (1)
- Stumpf empirical and machine learning models are capable of inverting optically shallow water depth based on multispectral images and measuring bathymetry data, and the inversion results can reflect the real water depth trends.
- (2)
- The machine learning model displayed excellent nonlinear fitting ability, and its overall accuracy of water depth inversion was higher than that of the Stumpf empirical model, especially when the water depth was greater than 15 m. Among the random forest model, the neural network model, and the support vector machine model, the random forest model performed optimally.
- (3)
- When the water depth was less than 15 m, the accuracy of the Stumpf empirical model was not significantly different from that of the machine learning-based models. Additionally, its parameters were simple because only the reflectance of blue and green bands are required, and the model was not sensitive to the number of samples, and required only a small number to complete the construction of the model, which highlights the potential wide application of the Stumpf empirical model.
- (4)
- The machine learning model was greatly affected by the number of samples and model parameters, indicating that these parameters need to be adjusted for different experiments. In addition, the accuracy of the model could be improved by a sufficient number of data samples. As an additional requirement, the distribution range of the training dataset should be larger than the inversion range to improve the applicability and generalization ability of the model.
Based on the conclusions above, this study can provide a reference for bathymetric inversion in the clean optical shallow water region based on multispectral imagery and measured bathymetry data, mainly with regard to the selection and construction of models for different numbers of measured water depth samples and water depth ranges.
However, the relationship between water depth and remote sensing image reflectance is ultimately a complex nonlinear relationship, and the accuracy of bathymetry inversion is affected by suspended sediment, water substrate, and remote sensing image quality. Moreover, there are obvious differences in different regions of water bodies. Therefore, it is necessary to perform bathymetric inversion experiments for different optically shallow water regions and add more influencing factors as independent variables (e.g., suspended sediment concentration and substrate type). The accuracy of different methods in bathymetric inversion can be further evaluated and analyzed, and such aspects will be examined in our subsequent research.
Author Contributions
Conceptualization, Y.T.; data curation, Y.T.; methodology, W.Z.; project administration, Y.L.; resources, Y.L.; supervision, W.J., W.Z. and Y.D.; writing—review and editing, Y.T., W.Z. and Y.L.; visualization, J.Y., W.J. and Y.Z.; writing—original draft preparation, Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China: 41976190;41976189; the Science and Technology Program of Guangdong: 2021B1212100006, the GDAS Project of Science and Technology Development: 2022GDASZH-2022010202,2022010111,2022020402-01, the Science and Technology Key R&D Program Project of Guangxi: Gui Ke AB20297037.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goodman, J.A.; Purkis, S.J.; Phinn, S.R. Coral Reef Remote Sensing: A Guide for Mapping, Monitoring and Management; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Abdallah, H.; Bailly, J.-S.; Baghdadi, N.N.; Saint-Geours, N.; Fabre, F. Potential of Space-Borne LiDAR Sensors for Global Bathymetry in Coastal and Inland Waters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 202–216. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, W.; Zhang, P.; Yan, F. Progress in Water Depth Mapping from Visible Remote Sensing Data. Mar. Sci. Bull. 2007, 26, 92–101. [Google Scholar]
- Pydyn, A.; Popek, M.; Kubacka, M.; Janowski, L. Exploration and reconstruction of a medieval harbour using hydroacoustics, 3-D shallow seismic and underwater photogrammetry: A case study from Puck, southern Baltic Sea. Archaeol. Prospect. 2021, 28, 527–542. [Google Scholar] [CrossRef]
- Huang, W.; Su, F.; Yang, X.; Zhang, Y. Techniques of Water Depth Remote Sensing Retrieval and Underwater Obstacle Detection. Hydrogr. Surv. Charting 2015, 35, 16–19. [Google Scholar]
- Dang, F.; Ding, Q. A Study of shallow water depth extraction using Landsat imagery. Remote Sens. Land Resour. 2001, 13, 53–58. [Google Scholar]
- Teng, H.; MA, F.; LI, H.; YE, Q.; Xin, X. The Development and Model Analysis of The Retrieving Sounding Technology Using Satellite Remote Sensing. In Proceedings of the 21st Comprehensive Symposium on Ocean Surveying and Mapping, Chengdu, China, 12–17 September 2009. [Google Scholar]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, J.; Zhang, J.; Zhang, Z.; Wang, J. Progress in Shallow Water Depth Mapping from Optical Remote Sensing. Adv. Mar. Sci. 2018, 36, 331–351. [Google Scholar]
- Liu, Y.; Deng, R.; Qin, Y.; Cao, B.; Liang, Y.; Liu, Y.; Tian, J.; Wang, S. Rapid estimation of bathymetry from multispectral imagery without in situ bathymetry data. Appl. Opt. 2019, 58, 7538–7551. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, R.; Li, J.; Qin, Y.; Xiong, L.; Chen, Q.; Liu, X. Multispectral Bathymetry via Linear Unmixing of the Benthic Reflectance. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4349–4363. [Google Scholar] [CrossRef]
- Wang, H.; Huang, W.; Wu, D.; Cheng, Y. Bathymetry Inversion Method Based on Adaptive Empricial Semi-Analytical Model without in situ Data-A Case Study in South China Sea. Acta Opt. Sin. 2022, 42, 87–98. [Google Scholar]
- Polcyn, F.C.; Lyzenga, D.R. Calculations of Water Depth from ERTS-MSS Data; Environmental Research Institute of Michigan: Ann Arbor, MI, USA, 1973. [Google Scholar]
- Tanis, F.J.; Byrnes, H.J. Optimization of multispectral sensors for bathymetry applications. In Proceedings of the 19th International Symposium on Remote Sensing of Enviroment, Ann Arbor, MI, USA, 21–25 October 1985; pp. 865–874. [Google Scholar]
- Paredes, J.M.; Spero, R.E. Water depth mapping from passive remote sensing data under a generalized ratio assumption. Appl. Opt. 1983, 22, 1134–1135. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Hamylton, S.M.; Hedley, J.D.; Beaman, R.J. Derivation of High-Resolution Bathymetry from Multispectral Satellite Imagery: A Comparison of Empirical and Optimisation Methods through Geographical Error Analysis. Remote Sens. 2015, 7, 16257–16273. [Google Scholar] [CrossRef]
- Tian, J.; Wang, J.; Du, X. Study on Water Depth Extraction from Remote Sensing Imagery in Jiangsu Coastal Zone. Natl. Remote Sens. Bull. 2007, 11, 373–379. [Google Scholar]
- Dang, F.; Ding, Q. A Technique for Extracting Water Depth Information from Multispectral Scanner Data in the South China Sea. Mar. Sci. Bull. 2003, 22, 55–60. [Google Scholar]
- Lu, T.; Chen, S.; Tu, Y.; Yu, Y.; Cao, Y.; Jiang, D. Comparative Study on Coastal Depth Inversion Based on Multi-source Remote Sensing Data. Chin. Geogr. Sci. 2019, 29, 192–201. [Google Scholar] [CrossRef]
- Casal, G.; Monteys, X.; Hedley, J.; Harris, P.; Cahalane, C.; McCarthy, T. Assessment of empirical algorithms for bathymetry extraction using Sentinel-2 data. Int. J. Remote Sens. 2019, 40, 2855–2879. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Wang, W. Establishment of a RS-Fathoming Correlation Model. J. Hohai Univ. 1998, 26, 98–102. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Zhang, D.; Qian, Y. An underwater bathymetry reversion in the radial sand ridge group region of the southern Huanghai Sea using the remote sensing technology. Acta Oceanol. Sin. 2009, 31, 39–45. [Google Scholar]
- Ao, Y.; Li, H.; Zhu, L.; Ali, S.; Yang, Z. The linear random forest algorithm and its advantages in machine learning assisted logging regression modeling. J. Pet. Sci. Eng. 2018, 174, 776–789. [Google Scholar] [CrossRef]
- Cheng, K.; Zhu, Y. A Summary of Machine Learning and Related Algorithms. Stat. Inf. Forum. 2007, 22, 105–112. [Google Scholar]
- Wang, Y.; Zhang, Y. Study on remote sensing of water depth based on BP artificial neural networks. Ocean. Eng. 2005, 23, 37–42. [Google Scholar]
- Wang, J.; Ma, Y.; Zhang, J. Multiple kernel support vector regression based on fuzzy membership for remote sensing water depth fusion detection. Mar. Environ. Sci. 2018, 37, 130–136. [Google Scholar]
- Qiu, Y.; Shen, W.; Hui, X.; Zhang, H. Satellite-Derived Bathymetry Using Random Forest Model. J. Ocean. Technol. 2019, 34, 75–79. [Google Scholar]
- Ai, B.; Wen, Z.; Wang, Z.; Wang, R.; Su, D.; Li, C.; Yang, F. Convolutional Neural Network to Retrieve Water Depth in Marine Shallow Water Area From Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2888–2898. [Google Scholar] [CrossRef]
- Zhu, W.; Ye, L.; Qiu, Z.; Luan, K.; He, N.; Wei, Z.; Yang, F.; Yue, Z.; Zhao, S.; Yang, F. Research of the Dual-Band Log-Linear Analysis Model Based on Physics for Bathymetry without In-Situ Depth Data in the South China Sea. Remote Sens. 2021, 13, 4331. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Technical note: Simple and robust removal of sun glint for mapping shallow-ater benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Fan, J.; Pan, J. A note on the Levenberg–Marquardt parameter. Appl. Math. Comput. 2009, 207, 351–359. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Wang, M. Water Depth Inversion based on Landsat-8 Date and Random Forest Algorithm. J. Phys. Conf. Ser. 2020, 1437, 012073. [Google Scholar] [CrossRef]
- Lai, W.; Lee, Z.; Wang, J.; Wang, Y.; Garcia, R.; Zhang, H. A Portable Algorithm to Retrieve Bottom Depth of Optically Shallow Waters from Top-Of-Atmosphere Measurements. J. Remote Sens. 2022, 2022, 1–16. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Du, X.; Wu, T. Support Vector Machines for Regression. J. Syst. Simul. 2003, 11, 1580–1585. [Google Scholar]
- Qi, J.; Zhang, D.; Ren, Z.; Cui, A.; Yin, F.; Qin, J.; Zhan, J.; Zhu, J. Determination of the initial value ranges of nonlinear solutions for a log ratio bathymetric inversion model and bathymetry retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10875–10888. [Google Scholar] [CrossRef]
- Ding, S.; Qi, B.; Tan, H. An Overview on Theory and Algorithm of Support Vector Machines. J. Univ. Electron. Sci. Technol. China 2011, 40, 2–10. [Google Scholar]
- Li, J.; Knapp, D.E.; Schill, S.R.; Roelfsema, C.; Phinn, S.; Silman, M.; Mascaro, J.; Asner, G.P. Adaptive bathymetry estimation for shallow coastal waters using Planet Dove satellites. Remote Sens. Environ. 2019, 232, 111302. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite Derived Bathymetry Using Machine Learning and Multi-Temporal Satellite Images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).