Abstract
Among the current methods of synthetic aperture radar (SAR) automatic target recognition (ATR), unlabeled measured data and labeled simulated data are widely used to elevate the performance of SAR ATR. In view of this, the setting of semi-supervised few-shot SAR vehicle recognition is proposed to use these two forms of data to cope with the problem that few labeled measured data are available, which is a pioneering work in this field. In allusion to the sensitivity of poses of SAR vehicles, especially in the situation of only a few labeled data, we design two azimuth-aware discriminative representation (AADR) losses that suppress intra-class variations of samples with huge azimuth-angle differences, while simultaneously enlarging inter-class differences of samples with the same azimuth angle in the feature-embedding space via cosine similarity. Unlabeled measured data from the MSTAR dataset are labeled with pseudo-labels from categories among the SARSIM dataset and SAMPLE dataset, and these two forms of data are taken into consideration in the proposed loss. The few labeled samples in experimental settings are randomly selected in the training set. The phase data and amplitude data of SAR targets are all taken into consideration in this article. The proposed method achieves 71.05%, 86.09%, and 66.63% under 4-way 1-shot in EOC1 (Extended Operating Condition), EOC2/C, and EOC2/V, respectively, which overcomes other few-shot learning (FSL) and semi-supervised few-shot learning (SSFSL) methods in classification accuracy.
1. Introduction
As a longstanding and challenging problem in Synthetic Aperture Radar (SAR) imagery interpretation, SAR Automatic Target Recognition (SAR ATR) has been an active research field for several decades. SAR ATR plays a fundamental role in various civil applications including prospecting and surveillance, and military applications such as border security [1]. (Armored) vehicle recognition [2,3,4] in SAR ATR aims at giving machines the capability of automatically identifying the classes of interested armored vehicles (such as tank, artillery and truck), which is the focus of this work. Recently, high-resolution SAR images are increasingly easier to produce than before, offering great potential for studying fine-grained, detailed SAR vehicle recognition. Despite decades of effort by researchers, including the recent successful preliminary attempts presented by deep learning [5,6,7,8], as far as we know, the problem of SAR vehicle recognition remains an underexploited research field with the following significant challenges [9].
- The lack of large, realistic, labeled datasets. Existing SAR vehicle datasets, i.e., the Moving and Stationary Target Acquisition and Recognition (MSTAR) dataset [10], are too small and relatively unrealistic, and cannot represent the complex characteristics of SAR vehicles [1] including imaging geometry, background clutter, occlusions, and speckle noise and true data distributions, but are very easy for many machine-learning methods to achieve high performance with abundant training samples. Certainly, such SAR vehicle datasets are hard to create due to the non-cooperative application scenario and the high cost of expert annotations. Therefore, label-efficient learning methods deserve attention in such a context. In other words, in the recognition missions of SAR vehicle targets, labeled SAR images of armored vehicles are usually difficult to obtain and interpret in practice, which leads to an insufficient sample situation in this field [11].
- Large intra-class variations and small inter-class variations. Variations in imaging geometry, such as the imaging angle including azimuth angle and depression angle, imaging distance and background clutter, lead to remarkable effects on the vehicle appearance in SAR images (examples shown in Figure 1), causing large intra-class variation. The aforementioned variations in imaging conditions can also cause vehicles of different classes to manifest highly similar appearances (examples shown in Figure 1), leading to small inter-class variations. Thus, SAR vehicle recognition demands robust yet highly discriminative representations that are difficult to learn, especially from a few labeled samples.
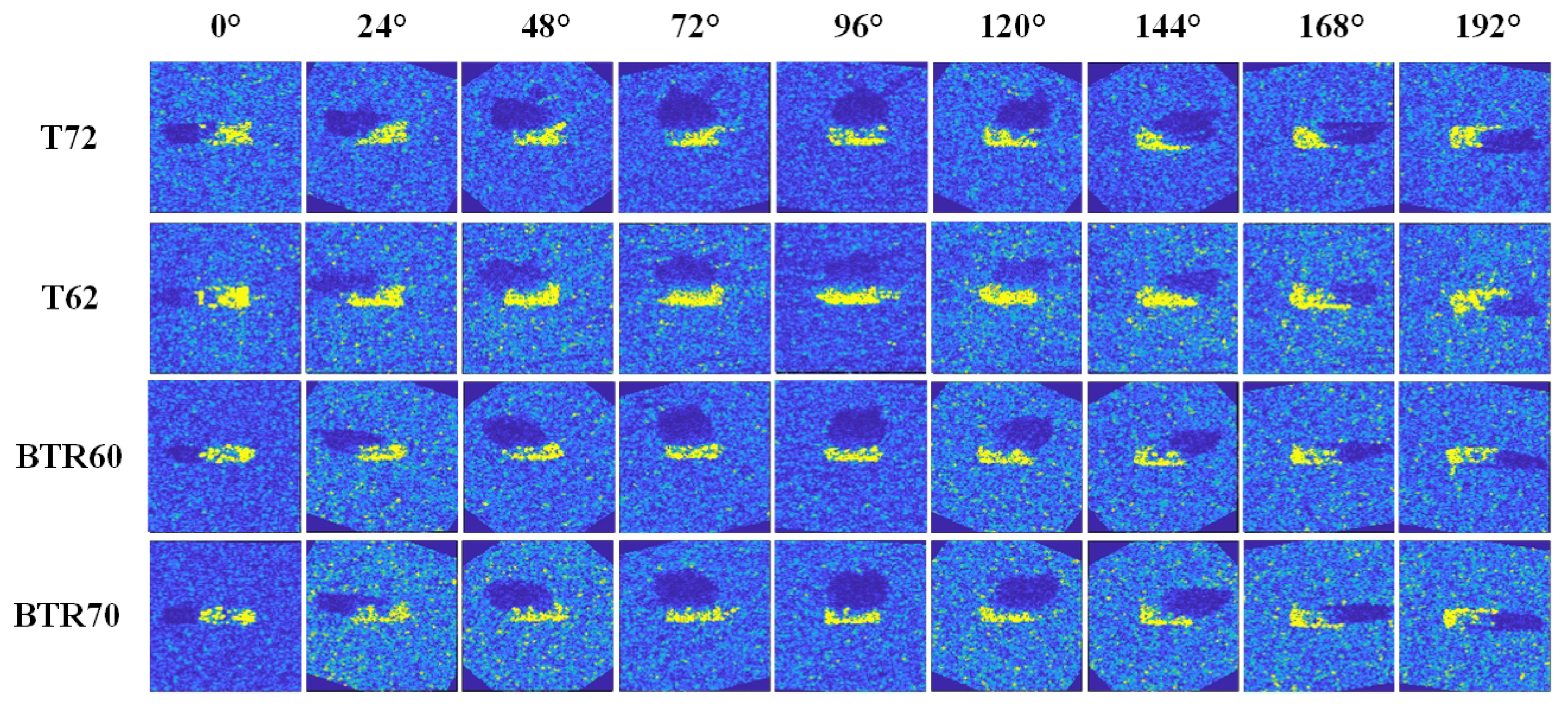
 Figure 1. The samples of four categories among the MSTAR SOC under the azimuth-angle normalization. According to its azimuth angle, the SAR image from each category is selected every 24 degrees. To ensure the continuity of the samples based on azimuth angles, the image of an adjacent azimuth angle is chosen if there is a vacancy of the particular degree value.
Figure 1. The samples of four categories among the MSTAR SOC under the azimuth-angle normalization. According to its azimuth angle, the SAR image from each category is selected every 24 degrees. To ensure the continuity of the samples based on azimuth angles, the image of an adjacent azimuth angle is chosen if there is a vacancy of the particular degree value. - The more difficult recognition missions among extended standard operation (EOCs). In MSTAR standard operation condition (SOC), the training samples and testing samples are only different in the depression angles, which are and . When it comes to EOCs, different from the SOC, the variations in the depression angles and the configuration or versions of targets lead to obvious imaging behaviors among SAR targets. Thus, the recognition missions among EOCs are much more difficult than SOC in the MSTAR dataset. This phenomenon also exists in the few-shot recognition missions.
Recently, in response to the aforementioned challenges, FSL [12] has been introduced to recognition missions of SAR ATR, aiming to elevate the recognition rate through a few labeled data. The lack of training data suppresses the performance of those CNN-based SAR target classification methods, which achieve a high recognition accuracy when the labeled data are sufficient [2]. To handle this challenge, simulated SAR images generated from auto-CAD models and the mechanism of electromagnetic scattering are introduced into the SAR ATR to elevate the recognition accuracy [13,14,15]. Although some common information can be transferred from labeled simulated data, there still exists huge differences between simulated data and measured data. The surroundings of the imaging target, the disturbance of the imaging platform, and even the material of vehicles make it hard to simulate the samples in the real environment. Because of this, some scholars are willing to leverage unlabeled measured data, instead of simulated data, in their algorithms, which launches the settings of semi-supervised SAR ATR [16,17,18,19].
Building upon our previous study in [11], this paper presents the first study of SSFSL in the field of SAR ATR, aiming to improve the model by making use of labeled simulated data and unlabeled measured data. Besides leveraging these data, information on azimuth angle is regarded as a kind of significant knowledge in digging discriminative representation in this paper.
When there are enough labeled SAR training samples, the feature-embedding space based on the azimuth angle of a category is approximately complete from to . Hence, under this situation, the influence of a lack of several azimuth angles on recognition rate is limited. Nevertheless, if there are only an extremely small number of labeled samples, their azimuth angle will dominate the SAR vehicle recognition results. Figure 1 shows four selected categories of SAR images from the MSTAR SOC within the azimuth-angle normalization [11]. It is obvious that the SAR vehicle images with huge differences in azimuth angles from the same category own quite different backscattering behaviors, which can be considered to be high intra-class diversity. When the difference of the azimuth angles of samples is over 50 degrees, the backscattering behaviors, including the shadow area and target area of the target, are dissimilar in accordance with the samples in the same row of Figure 1. In the meantime, the SAR vehicle images with the same or adjacent azimuth angles from different categories share similar backscattering behaviors, which is the inter-class similarity. The samples in the same column in Figure 1 are homologous in the appearance of the target area and shadow area, especially when vehicle types are approximate; for instance, the group of BTR60 and BTR70, and T62 and T72. These two properties among SAR images cause confusion in representation learning and mistakes in classification results.
To solve this problem, an azimuth-aware discriminative representation (AADR) learning method is proposed, and this algorithm can grasp the distinguishable information through azimuth angles among both labeled simulated data and unlabeled measured data. The motivation of the method is to design a specific loss to let the model study not only the category information but also the azimuth-angle information. For suppressing the intra-class diversity, the pairs of SAR samples from the same category within huge azimuth-angle differences are selected, and their absolute value of cosine similarity of representations will be adjusted from zero-near value to one-near value. Simultaneously, to enlarge inter-class differences, samples from different categories with the same azimuth angle are selected and their feature vectors will be pulled from approximately overlap to near orthogonality in the metric manner of cosine similarity. Following this idea, the azimuth-aware regular loss (AADR-r) and its variant azimuth-aware triplet loss (AADR-t) are proposed, and the details will be introduced in Section 3. Furthermore, the cross-entropy loss from the labeled simulated datasets and the KL divergence of pseudo-labels from the unlabeled measured dataset (MSTAR) are also considered in the proposed loss. After experiencing the modification through the proposed loss, the algorithm is used to learn the discriminative representation from the few-shot samples and be tested among the query set.
Based on the baseline in SSFSL, there is no overlap between categories among the source domain and the target domain. The number of simulated data in the source domain is abundant, whereas there are an extremely small number of measured samples with labels and enough unlabeled measured data in the target domain. According to the settings of SSFSL, samples from the support and query sets are distinguished by different depression angles, and the unlabeled data are only chosen from the samples in the support set.
Extensive contrast experiments and ablation experiments were carried out to show the performance of our method. In general, the three contributions of the paper are summarized below:
- Due to the lack of large and realistic labeled datasets among SAR vehicle targets, for the first time, we propose the settings of semi-supervised few-shot SAR vehicle recognition, which takes both unlabeled measured data and labeled simulated data into consideration. In particular, simulated datasets act as the source domain in FSL, while the measured dataset MSTAR serves as the target domain. Additionally, the unlabeled data in MSTAR dataset are available in the process of model training. This configuration is really close to the active task in few-shot SAR vehicle recognition that labeled simulated data, and unlabeled measured data can be obtained easily.
- An azimuth-aware discriminative representation loss is proposed to learn the similarity of representations of intra-class samples with large azimuth-angle differences among the labeled simulated datasets. The representation pairs are considered to be feature vector pairs, which are pulled close to each other in the direction of the vector. Meanwhile, the inter-class differences of samples with the same azimuth angle are also expanded by the proposed loss in the feature-embedding space. The well-designed cosine similarity works as the distance to make representation pairs in the inter-class be orthogonal to each other.
- tlo information and phase data knowledge are adopted in the stage of SAR vehicle data pre-processing. Moreover, the variants of azimuth-aware discriminative representation loss achieve 47.7% (10-way 1-shot SOC), 71.05% (4-way 1-shot EOC1), 86.09% (4-way 1-shot EOC2/C), and 66.63% (4-way 1-shot EOC2/V), individually. Plenty of contrast experiments with other FSL methods and SSFSL methods prove that our proposed method is effective, especially in three EOC datasets.
There are five sections in this paper. In Section 2, the semi-supervised learning and its applications in SAR ATR, FSL and its applications in SAR ATR, and SAR target recognition based on azimuth angle are introduced in the related work. The settings of SSFSL among SAR target classification is presented in Section 3.1. Then, in Section 3.2, the whole framework of the proposed AADR-r is shown. After that, AADR-t is described in Section 3.3. Then, in Section 4, experimental results among SOC and three EOCs are demonstrated in diagrams and tables. Sufficient contrast experiments, ablation experiments, and implementation details are introduced and analyzed in Section 5. Finally, this paper is concluded, and future work is designed in Section 6.
2. Related Work
2.1. Semi-Supervised Learning and Its Applications in SAR Target Recognition
(1). Semi-supervised learning: Semi-supervised learning uses both labeled and unlabeled data to perform certain learning tasks. In contrast to supervised learning, it permits the harnessing of large amounts of unlabeled data available in many cases [20]. Generally, there are three representative approaches for semi-supervised learning—generative models [21,22], conditional entropy minimization [23], and pseudo-labeling [24]. Among the methods of generative models, various auto-encoders [25,26] were proposed by adding consistency regularization losses computed on unlabeled data. However, all unlabeled examples were encouraged to make confident predictions on some classes in the approaches of conditional entropy minimization [27]. The means of pseudo-labeling [28], which was adopted in this article, imputes approximate classes on unlabeled data by making predictions from a model trained only on labeled data.
(2). Semi-supervised SAR target recognition: According to the classification of methods in semi-supervised learning, the methods of semi-supervised SAR target recognition can also be divided into three parts. A symmetric auto-encoder was used to extract node features and the adjacency matrix is initialized using a new similarity measurement method [16]. The methods with generative adversarial networks were also popular in solving the semi-supervised SAR target recognition [29]. In [30], the pseudo-labeling and the consistency regularization loss were both adopted, and these unlabeled samples with pseudo-labels were mixed with the labeled samples and trained together in the designed loss to improve recognition performance. Multi-block mixed (MBM) in [31], which could effectively use the unlabeled samples, was used to interpolate a small part of the training image to generate new samples. In addition, semi-supervised SAR target recognition under limited data was also studied in [18,19]. Kullback–Leibler (KL) divergence was introduced to minimize the distribution divergence between the training and test data feature representations in [18]. The dataset attention module (DAM) was proposed to add the unlabeled data into the training set to enlarge the limited label training set [32].
2.2. Few-Shot Learning and Its Applications in SAR Target Recognition
(1). Few-shot learning: Currently, few-shot learning is proposed to learn a classifier from the base dataset and adapt with extremely limited supervised information of each class. The methods to solve the few-shot learning problems are generally divided into metric-based and optimization-based. The metric-based methods tend to classify the samples by judging the distance between the query-set image and the support-set image, such as matching networks [33], prototypical networks [34], deep nearest-neighbor neural network (DN4) [35]. Optimization-based algorithms designed novel optimization functions [36], better initialization of training models [37] and mission-adapted loss [38] to improve the rapid adaptability to new tasks, which could be regard as common solutions in few-shot learning methods.
(2). Semi-supervised few-shot learning: When there are only a few labeled examples among novel classes, it is intuitive to use extra unlabeled data to improve the learning [39]. This leads to the setting of semi-supervised few-shot learning. Prototypical networks were improved by Ren et al. [40] to produce prototypes for the unlabeled data. Liu et al. [41] constructed a graph between labeled and unlabeled data and used label propagation to obtain the labels of unlabeled data. By adding the confident prediction of unlabeled to the labeled training set in each round of optimization, Li et al. [42] applied self-training in semi-supervised few-shot learning. In [43], a simple and effective solution was proposed to tackle the extreme domain gap by self-training a source domain representation on unlabeled data from the target domain.
(3). Few-shot SAR target recognition: Few-shot SAR target recognition [44,45,46,47,48,49,50,51,52,53] has had more and more emphasis placed on it in recent years. An AG-MsPN [9] was proposed to consider both complex-value information of SAR data and the prior attribute information of the targets. The connection-free attention module and Bayesian-CNN were proposed to transfer common features from the electro-optical domain to the SAR domain for SAR image classification in the extreme few-shot case [54]. The Siamese neural network [55] was also ameliorated to cope with the problems of few-shot SAR target recognition [51]. The MSAR [45] with a meta-learner and a base-learner could learn a good initialization as well as a proper update strategy. The inductive inference and the transductive inference were adopted in the hybrid inference network (HIN) [49] to distinguish the samples in the embedding space. These methods divided the MSTAR dataset into query set and support set and the performance is not reflected on the whole MSTAR dataset. DKTS-N was proposed to take SAR domain knowledge into consideration and evaluated among the whole categories in the MSTAR dataset, but the performance of DKTS-N among MSTAR EOCs was not pleasant according to [11].
2.3. SAR Target Recognition Based on Azimuth Angle
The information on azimuth angle, which is a kind of important domain knowledge in SAR images, has been applied in the algorithms for a long time. Usually, a series of SAR images with regular azimuth angles are input into the network, which is named multiview or multi-aspect [56,57,58,59,60]. In [56], every input multiview SAR image was first examined by sparse representation-based classification to evaluate its validity for multiview recognition. Then, the selected views were jointly recognized with joint sparse representation. Multiview similar-angle target images were used to generate a joint low-rank and sparse multiview denoising dictionary [57]. MSRC-JSDC learned a supervised sparse model from training samples by using sample label information, rather than directly employing a predefined one [61]. A residual network (ResNet) and bidirectional long short-term memory (BiLSTM) network was proposed to learn the azimuth-angle information among SAR images [58]. However, to exploit the spatial and temporal features contained in the SAR image sequence simultaneously, this article proposed a sequence SAR target classification method based on the spatial-temporal ensemble convolutional network (STEC-Net) [59]. The authors in [60] adopted a parallel network topology with multiple inputs and the features of input SAR images from different azimuth angles would be learned layer by layer. Although these above-mentioned methods made full use of the azimuth angles, a certain number of SAR images with different azimuth angles were required, which was impossible in extremely few-shot SAR target recognition. In this article, the discriminative representation information among different samples is refined from specially designed loss during model training.
3. Proposed Method
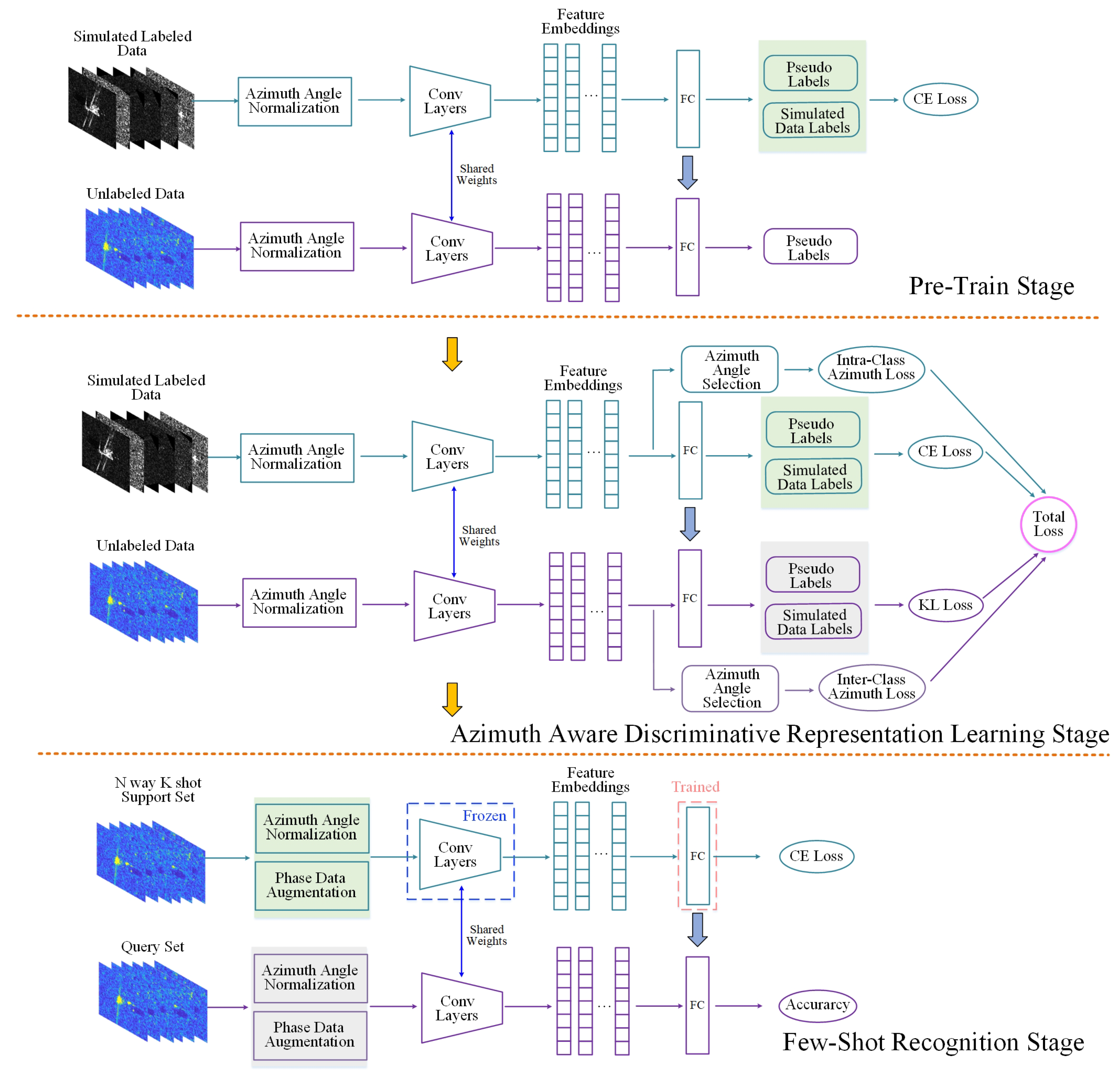
To cope with the challenge of semi-supervised few-shot SAR target recognition, the AADR framework is proposed within three stages in Figure 2. In this section, the settings of SSFSL are illustrated first. Then, the whole framework of AADR-r is introduced. Finally, the variant loss AADR-t will be described in detail.
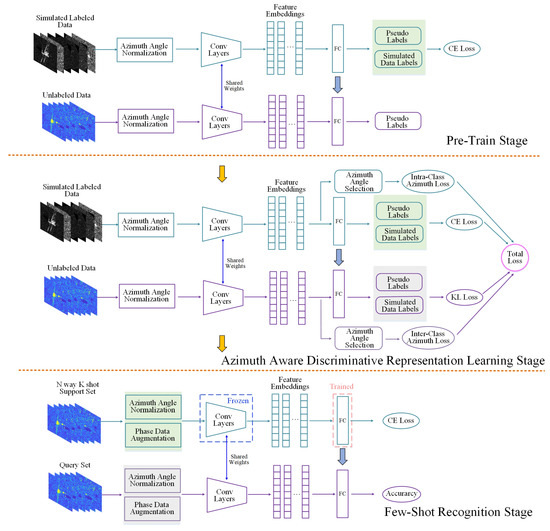
Figure 2.
The whole framework of the azimuth-aware discriminative representation framework with regular loss.
3.1. Problem Setting
Initially, the definition of terminology used in semi-supervised few-shot SAR target recognition can be written as follows: a huge labeled simulated dataset . is the image in the labeled simulated dataset . is the label of and the is the azimuth angle of the . is the categories among the simulated dataset. The measured MSTAR datasets are divided into and , according to the popular baseline. The train dataset and test dataset can be formulated by
, , are the image, label and azimuth angle of the image among the training measured dataset, respectively, while , , are the image, label and azimuth angle of the image among the testing measured dataset. and are the categories in the training and testing dataset and satisfy the relationship of . Actually, in the experiment settings of MSTAR SOC and EOC1, the relationship between categories among training and testing sets is , while in the experimental settings of EOC2/C and EOC2/V, there are more categories in the training set than categories in the testing set, so the relationship changes to . The unlabeled measured dataset is the same dataset as the without the label information, .
N-way K-shot indicates that there are N categories and each category contains K labeled samples. In most times, K is set to 1 or 5 in the experiments of MiniImageNet [36] and Ominiglot [62]. At the pre-train stage, all the labeled data are sampled from the , and the unlabeled data are the same samples as the but without the labels. In addition, and are involved in the azimuth-aware discriminative representation learning stage. It should be noted that there is not any FSL setting at either the first or the second stages. At the few-shot recognition stage, N-way K-shot samples are randomly selected from the , which act as the support set. All the data in compose the query set.
3.2. The Whole Framework with AADR-r
The whole framework of the azimuth-aware discriminative representation method is illustrated in Figure 2. At the pre-training stage, after the processing of azimuth-angle normalization, the simulated labeled data are fed into the deep neural network [6] within cross-entropy loss.
In Formula (3), a trained model with parameters and classifier are achieved. Due to the plenty of labeled data in the labeled simulated dataset, the recognition accuracy among is perfect, which is shown in the first row in the pre-training stage in Figure 2. embeds the input image x into . The input dim of the classifier is d, and the output dim is the number of classes among labeled simulated dataset . Then, the trained model with parameters and the classifier is adopted to classify the unlabeled data in with the pseudo-labels . After that, the pseudo-label of each unlabeled data are achieved, which is shown in Formula (4) and described in the second row in Figure 2. Every pseudo-label of the unlabeled image is fixed thorough the whole azimuth-aware discriminative representation learning stage. Formula (5) describes the process of feature extraction and classification, which appears many times in the training stage with the changing parameters .
The azimuth-aware discriminative representation learning module works at the second stage. Both simulated labeled data and unlabeled measured data experience azimuth-angle normalization before being fed into the network. Among the simulated labeled data, the information on labels and azimuth angles is accessible, so it is feasible to calculate the difference in azimuth angles between the samples from the same category. In the article, the gap is set to 50 degrees. The selected pair of samples among simulated labeled datasets obeys the rule according to Formula (6). The number of pairs in is , which is involved in Formula (7). The distance restricts the directions among representations of selected pairs. Before optimization, the distance of samples from the same category with huge differences in azimuth angle is relatively close to zero. However, through the designed azimuth-aware discriminative representation learning regular loss in simulated labeled dataset modules, the above-mentioned situation can be alleviated and the result of distance is guided to one. The cross-entropy loss of recognition among simulated labeled datasets is also taken into consideration to restrict the adaptation of in the whole optimization.
When it comes to the unlabeled measured dataset , although the samples are selected from the , only the pseudo-labels from the pre-training stage can be achieved, which is in Formula (8). The azimuth angles of samples are known. It is worth noting that, among the MSTAR dataset, the azimuth angles of any two samples in one category are different. Therefore, in , if there are two samples with the same azimuth angle, then these two samples must come from two different categories. Actually, before optimization, the distance of these two samples may be closer to 1 than 0, because of the similar backscattering behaviors. The purpose of the designed loss in Formula (9) is to make the model distinguish data from various categories within the same azimuth angle, through which the proposed loss enlarges the inter-class differences of samples and lets the feature vectors of these sample pairs be orthogonal to each other as far as possible. The selected samples pair is described in Formula (8) and the number of pairs in is . is the hyper-parameter in the loss. The KL loss introduces noise during training by encouraging the model to learn the representations that emphasize the groupings induced by the pseudo-labels among the unlabeled measured samples. The total loss of the second stage is shown in Formula (10). In ablation experiments, the effects of different parts of loss will be discussed and the results are shown in the corresponding tables.
In terms of the few-shot recognition stage, it is composed of a training and testing process, as shown in Figure 2. N way K shot labeled samples are randomly selected from the , acting as the support set, and all the samples in comprise the query set. The parameters are reserved from the second stage and frozen in this stage. Because the output categories in the fully connected classifier are different between the second stage and the third stage, the parameter of the classifier needs adapting through the few labeled data. After that, the feature extractor and the fully connected classifier are tested through the query set. The operation in the third stage is repeated 600 times and the average recognition rate and variance are recorded.
3.3. The Variants of AADR-t
In fact, the motivation of our designed AADR-r is similar to the triplet loss but without the anchor samples. To compare with the standard triplet loss, the AADR-t is designed to minimize the distance between an anchor sample and a positive sample with the same category, and maximize the distance between the anchor sample and a negative sample of a different category [63]. The differences between AADR-r and AADR-t are the selection rules of sample pairs and the loss function, which all exist in the second stage. It is worth noticing that, in this article, the selection of anchor sample , its hard negative sample and its hard positive sample take the azimuth angle into consideration. The hard negative sample shares the same azimuth angle as the anchor samples, but they are from different categories. The hard positive sample is the same class as the anchor sample but with a huge difference in azimuth angle. The details of selection rules are shown in Formulas (11) and (12). The categories among unlabeled samples are from pseudo-labels in the simulated dataset. The numbers of the triplet group in and can be expressed through and . Unlike the max operation and settings of margin in the raw triplet loss, the proposed AADR-t expands the cosine distance among the anchor sample and hard negative sample, and pulls in the cosine distance between the anchor sample and hard positive sample in both simulated dataset and unlabeled dataset, as shown in Formulas (13) and (14). The total triplet loss is composed of the loss in the simulated dataset and the unlabeled dataset, which is similar to Formula (10).
4. Experiments
To test the validity of AADR for semi-supervised few-shot SAR vehicle classification, extensive experiments were performed under the experimental settings that the public simulated SARSIM dataset and the simulated part of Synthetic and Measured Paired Labeled Experiment (SAMPLE) dataset were combined as the . The public MSTAR dataset was recognized as the . Actually, the few-shot labeled data are sampled from , and the data in the query set are from different depression angles or different types. The unlabeled data are all from . Take MSTAR SOC (Standard Operating Condition) as an example: the few-shot labeled data comprise the support set, while the unlabeled measured data are selected from the set of depression angle in MSTAR SOC, while the samples within depression angle in MSTAR SOC compose the query set. Contrast experiments with traditional classifiers, other advanced FSL approaches, and semi-supervised learning approaches were conducted. Additionally, ablation experiments with different dimensions of features, various base datasets, and errors in azimuth-angle estimation are also involved in our work.
Without the phase data, the data in the SAMPLE dataset and the SARSIM dataset only experience the gray-image adjustment and azimuth-angle normalization. However, the samples in the MSTAR database experience the phase data augmentation as in [11].
The feature extractor network in Figure 2 contains four fully convolutional blocks [64], which own a 3 × 3 convolution layer with 64, 128, 256 and 512 filters, relatively, 2 × 2 max-pooling layer, a batch-normalization layer, and a RELU (0.5) nonlinearity layer. We use the SGD with momentum optimizer with momentum 0.9 and weight decay . All experiments were run on a PC with an Intel single-core i9 CPU, four Nvidia GTX-2080 Ti GPUs (12 GB VRAM each), and 128 GB RAM. The PC operating system was Ubuntu 20.04. All experiments were conducted using the Python language on the PyTorch deep-learning framework and CUDA 10.2 toolkit.
4.1. Datasets
(1). SARSIM: The public SARSIM dataset [15] contains seven kinds of vehicles (humvee 9657 and 3663, bulldozer 13,013 and 8020, tank 65,047 and 86,347, bus 30,726 and 55,473, motorbike 3972 and 3651_Suzuki, Toyota car and Peugeot 607, and truck 2107 and 2096). Every image is simulated in the identical situation to MSTAR and for azimuth-angle interval at the following depression angles (, , , , , , and ), so there are 72 samples in each category under a certain depression angle.
(2). SAMPLE: The public SAMPLE dataset [65,66] is released by Air Force Research Laboratory with both measured and simulated data in 10 sorts of armored vehicle (tracked cargo carrier: M548; military truck: M35; wheeled armored transport vehicle: BTR70; self-propelled artillery: ZSU-23-4; tanks: T-72, M1, and M60; tracked infantry fighting vehicle: BMP2 and M2; self-propelled howitzer: 2S1). The azimuth angles of the samples, which are 128 × 128 pixel, in the SAMPLE dataset are from to and their depression angles are from to . For every measured target, a corresponding synthetic image is created with the same sensor and target configurations, but with totally different background clutter. In order to make the categories in the few-shot recognition stage and pre-training stage different, in most experiment settings in this article, only the synthetic images in the SAMPLE dataset are leveraged and combined with the SARSIM dataset to expand the richness of categories in the base dataset.
(3). MSTAR: In recent years, the MSTAR SOC dataset [10], including ten kinds of military vehicles during the Soviet era (military truck: ZIL-131; tanks: T-72 and T-62; bulldozer: D7; wheeled armored transport vehicle: BTR60 and BTR70; self-propelled howitzer: 2S1; tracked infantry fighting vehicle: BMP2; self-propelled artillery: ZSU-23-4; armored reconnaissance vehicle: BRDM2), was remarkable for verifying the algorithm performance among SAR vehicle classification missions. Imaged under the airborne X-band radar, the samples in this dataset were HH polarization mode within the resolution of 0.3 × 0.3 m. Targets, whose depression angles were , were for the support set and consisted of the unlabeled measured data, and were for testing, whose numbers among each category were shown in Table 1. The EOC1 (large depression variation) contained four kinds of target (ZSU-23-4, T-72, BRDM-2 and 2S1). The depression angle of the training and testing set were and , relatively. The targets in the EOC2/C (configuration variation) were various in parts of the vehicle, including explosive reactive armor (ERA) and an auxiliary gasoline tank. The EOC2/V (version variation) corresponded to the target version variation and shared the identical support set to the EOC2/C, but with a different query set, which is displayed in Table 2.

Table 1.
Categories among MSTAR SOC.

Table 2.
Categories among MSTAR EOCs.
4.2. Experimental Results
4.2.1. Experiments in SOC
Comparative experiments including classical classifiers (CC), FSL methods and SSFSL methods are shown in Table 3, under the FSL setting among 10-way K-shot (). The average recognition rate and variance of 600 random experiments for each setting are displayed in Table 3. CC algorithms include LR (logistic regression) [67], DT (decision tree) [68], SVM (support vector machine) [69], GBC (gradient-boosting classifier) [70] and RF (random forest) [71]. These methods share the same feature extractors as the AADR with individual classifiers. The average recognition rate of algorithms in SSFSL is higher than in FSL and CC in Table 3. Although the recognition rates of classical classifiers are unsatisfactory in few-shot conditions, some of them achieve a higher result than SSFSL in the settings of 10-way 10-shot. Our proposed AADR-r and AADR-t obtain a relatively better recognition rate in few-shot settings (), which are only a little lower than DKTS-N. The DKTS-N outstrips all the other methods in the settings of both few-shot and limited data in SOC for the following reason. The advantage of DKTS-N is learning the global and local features. The samples in training and testing sets in MSTAR SOC are similar because of the approximate depression angle and . Hence, the global and local features between the two sets are close and easy to be matched through Earth’s mover distance and nearest-neighbor classifiers in DKTS-N. However, highly different configurations and versions of armored vehicle lead to huge discrepancies in local features, which influence the scattering characteristics among SAR images. Therefore, the performance in the EOCs of DKTS-N decreases, which is the restriction of this metric-learning-based algorithm. The proposed AADR, an optimization-based method, overcomes the difficulties and shows an overwhelming performance in EOCs.

Table 3.
Few-shot classification accuracy of SOC among CC, FSL and SSFSL algorithms.
4.2.2. Experiments in EOCs
Due to the huge differences among SAR vehicle images, the FSL missions are harder in EOCs than in SOC. However, most of the SSFSL methods are better than FSL methods in the results of both SOC setting and EOCs settings, which means the usage of unlabeled data is beneficial for the FSL among SAR vehicles. In addition, the awareness of the azimuth angle also helps the model to grasp the important domain knowledge among SAR vehicles and overcome the intra-class diversity and inter-class similarity in few-shot conditions. From Table 4, it is obvious that our proposed AADR-r and AADR-t do a good job in EOCs, and the recognition results are much higher than other FSL methods and SSFSL methods. Instead of comparing the metric distances between the features, the model optimization through designed loss performs well in a large difference in depression angle, vehicle version, and configuration.

Table 4.
Few-shot classification accuracy of EOCs.
A similar process with different losses causes different results such that the accuracy of AADR-r exceeds AADR-t in most times. In fact, the categories of the anchor sample, hard negative sample, and hard positive sample among unlabeled data are generated by the trained model in the pre-training stage, according to Figure 2. Thus, the pseudo-labels participate in the loss and influence the result. For instance, the anchor sample and its hard negative sample are from the different categories, which are the pseudo-labels among the simulated data. However, if these two samples are from the same actual category in , this will lead to the wrong training in the second stage. Therefore, the results of AADR-t contain more uncertainties than AADR-r.
5. Discussion
In this section, the value of hyper-parameter in the total loss is discussed, which determines the proportion of the azimuth-aware discriminative representation learning loss. Then, the influence of different compositions of categories among base datasets is analyzed in this subsection. Moreover, the dimension configuration of the feature extractor is also discussed. The azimuth angles are accurate in the processing of normalization, but in this subsection, the angle errors are taken into account in both MSTAR SOC and EOCs.
5.1. The Influence of Loss Modules
In Table 5 and Table 6, the influence of different loss modules and their parameters on the recognition rate is shown, and other experiment settings are the same. Both 10-way recognition in SOC and 4-way recognition in EOCs are conducted. Azimuth-aware in the table is the proposed module in this article, which uses azimuth angle to suppress intra-class diversity of samples with huge azimuth-angle differences and enlarged inter-class differences of samples. The × in the table means that the related loss is not in the total loss. The SimCLR module is proposed in [23] and widely leveraged in semi-supervised learning. It encourages augmentations such as cropping, adding noise, and flipping. KL and CE indicate the Kullback–Leibler divergence and the cross-entropy loss, respectively. “-r” and “-t” represent the “AADR-r” and “AADR-t” and the hyper-parameter ranges from 0.1 to 0.7.

Table 5.
Influence of different loss module among SOC (10-way).

Table 6.
Influence of different loss module among EOCs (4-way).
The loss in the first row in each experiment setting is the result of STARTUP [43] and the loss in the second row is the result of STARTUP (no SS) [43]. Although the SimCLR module is beneficial to the classification rate in optical image datasets, it is obvious that the total loss without SimCLR (no SS) shows a better performance. Actually, the targets are in the center of the images and with the behaviors of backscatterings, which is different from the optical images. The operations in the SimCLR module, such as cropping, adding noise, and flipping, are not suitable for the SAR vehicle images. For instance, the crop operation may cut the key part of the SAR vehicles and the added noise is not reasonable according to the SAR imaging mechanism. The AADR-r is more stable than its variants AADR-t because the anchor samples among AADR-t, involving the pseudo-labels, which are the classification results of the unlabeled data, participate in the triplet loss. Every unlabeled sample actually owns its real label. If different unlabeled samples, which are from the same real category, are classified into different pseudo-labels, the results of AADR-t will be poorly influenced. The indicates the proportion of the azimuth-aware module in the total loss, and a fixed cannot be competent to all experimental settings. Comparatively, the result of in AADR-r is better. When it comes to the contribution of KL divergence, which is an important part of the semi-supervised learning with pseudo-labeling, it is easy to see that the absence of KL in the AADR-r with decreases a lot, compared to the raw contrast version.
5.2. Estimation Errors of Azimuth Angle
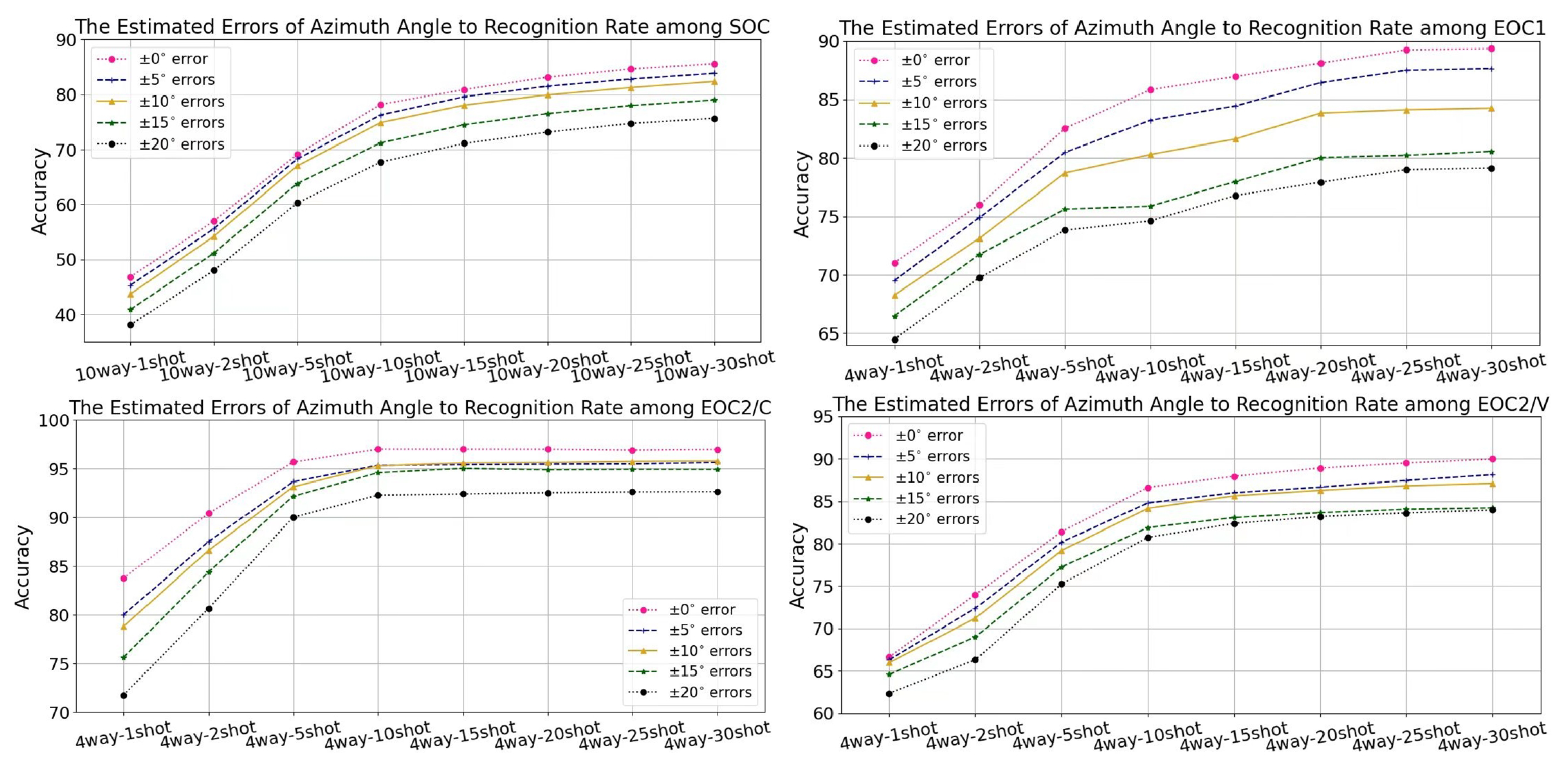
Figure 3 illustrates the accuracy of SOC and EOCs with various azimuth-angle estimation errors from 1-shot to 30-shot in 10-way and 4-way. The five-set of experiments shares the same configurations and parameters but with random estimation errors within a given range. The given range indicates that the estimation errors of azimuth-angle range from to . shows that the estimation error of azimuth angle is approximate to zero and achieves the highest recognition rate in the figure, which is regarded as the baseline. From the figure, when the estimation azimuth-angle errors are less than , there are almost 1% decreases in comparison to the baseline in SOC, EOC1, and EOC2/V. This demonstrates that our AADR is impressive under low estimated errors of azimuth angle. If the random errors ascend to , the recognition rates will witness a nearly 10% drop in SOC and EOC1. However, in the result of EOC2/C and EOC2/V, within the changes among weapon configurations and versions, the impact of estimated azimuth error on the accuracy is relatively tiny. According to these results, the estimated errors of azimuth angle have a more marked influence on the large variation of depression angle between the source tasks and the target tasks, than the changes in version or weapon configuration.
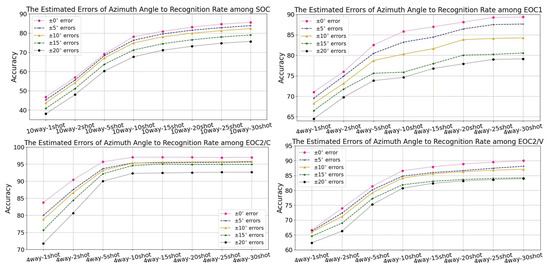
Figure 3.
The line charts of estimated azimuth-angle errors to the accuracy among SOC and EOCs.
6. Conclusions
To sum up, we put forward the AADR to deal with the task of few-shot SAR target classification, especially in the situations of a huge difference between support sets and query sets. The use of unlabeled measured data and labeled simulated data are one of the key means to elevate the recognition rate in a fresh semi-supervised manner. Additionally, azimuth-aware discriminative representation learning is also an available way to cope with the intra-class diversity and inter-class similarity among vehicle samples. In general, a large number of experiments showed that AADR was more impressive than other FSL algorithms.
There are still some flaws in the proposed methods. First, due to the optimization-based design, the classifier of the fully connected layer in AADR is not pleasant when the number of labeled data is over 10. According to Figure 3, as the number increases, the elevation of performance is limited. Hence, how to use more labeled data is significant to making the AADR powerful in situations of both few-shot and limited data. Second, the hyper-parameter in the loss, which indicates the proportion of azimuth-aware module, is fixed in the current algorithm. From the results, it is hard to determine a certain value of that can fit four experiments. Thus, a self-adaptation in the loss, related to the training epochs and learning rate, can guide the gradient descent in a better way.
Author Contributions
Conceptualization, L.Z., X.L. and L.L.; methodology, L.Z.; software, L.Z.; validation, L.Z., S.F. and X.M.; resources, K.J.; data curation, L.Z.; writing—original draft preparation, L.Z.; writing—review and editing, L.L.; visualization, L.Z.; supervision, L.L.; project administration, K.J. and G.K.; funding acquisition, X.L., K.J., G.K. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China grant number 2021YFB3100800 and the National Natural Science Foundation of China under Grant 61872379, 62001480 and Hunan Provincial Natural Science Foundation of China under Grant 2018JJ3613, 2021JJ40684.
Data Availability Statement
MSTAR dataset used in this work can be downloaded at https://www.sdms.afrl.af.mil/index.php?collection=registration (accessed on 28 December 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SAR | Synthetic Aperture Radar |
| ATR | Automatic Target Recognition |
| AADR | Azimuth-Aware Discriminative Representation |
| EOC | Extended Operating Condition |
| SOC | Standard Operating Condition |
| FSL | Few-shot Learning |
| SSFSL | Semi-supervised Few-shot Learning |
| MSTAR | Moving and Stationary Target Acquisition and Recognition |
| KL | Kullback–Leibler |
| MBM | Multi-block mixed |
| DAM | Dataset attention module |
| DN4 | Deep Nearest-Neighbor Neural Network |
| HIN | Hybrid Inference Network |
| ResNet | Residual Network |
| BiLSTM | Bidirectional Long Short-term Memory |
| STEC-Net | Spatial-temporal Ensemble Convolutional Network |
| SAMPLE | Synthetic and Measured Paired Labeled Experiment |
References
- Kechagias-Stamatis, O.; Aouf, N. Automatic target recognition on synthetic aperture radar imagery: A survey. IEEE Aerosp. Electron. Syst. Mag. 2021, 36, 56–81. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y. Target classification using the deep convolutional networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Tian, Z.; Zhan, R.; Hu, J.; Zhang, J. SAR ATR based on convolutional neural network. J. Radars 2016, 5, 320–325. [Google Scholar]
- Guo, W.; Zhang, Z.; Yu, W.; Sun, X. Perspective on explainable sar target recognition. J. Radars 2020, 9, 462–476. [Google Scholar]
- Liu, L.; Ouyang, W.; Wang, X.; Fieguth, P.; Chen, J.; Liu, X.; Pietikainen, M. Deep learning for generic object detection: A survey. Int. J. Comput. Vis. 2019, 128, 261–318. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Wang, S.; Wang, Y.; Liu, H.; Sun, Y. Attribute-guided multi-scale prototypical network for few-shot SAR target classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12224–12245. [Google Scholar] [CrossRef]
- Keydel, E.R.; Lee, S.W.; Moore, J.T. MSTAR extended operating conditions: A tutorial. In Algorithms for Synthetic Aperture Radar Imagery III. Proc. SPIE. 1996. Available online: https://www.sdms.afrl.af.mil/index.php?collection=registration (accessed on 28 December 2022).
- Zhang, L.; Leng, X.; Feng, S.; Ma, X.; Ji, K.; Kuang, G.; Liu, L. Domain knowledge powered two-stream deep network for few-shot SAR vehicle recognition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Lake, B.M.; Salakhutdinov, R.; Tenenbaum, J.B. Human-level concept learning through probabilistic program induction. Science 2015, 350, 1332–1338. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Zhao, L.; Ji, K.; Kuang, G. SAR target recognition based on task-driven domain adaptation using simulated data. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Liu, H.; Sun, Y.; Hu, L. SAR target recognition using only simulated data for training by hierarchically combining CNN and image similarity. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Malmgren-Hansen, D.; Kusk, A.; Dall, J.; Nielsen, A.A.; Engholm, R.; Skriver, H. Improving SAR automatic target recognition models with transfer learning from simulated data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1484–1488. [Google Scholar] [CrossRef]
- Wen, L.; Huang, X.; Qin, S.; Ding, J. Semi-supervised SAR target recognition with graph attention network. In Proceedings of the EUSAR 2021; 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021; VDE: Frankfurt, Germany, 2021; pp. 1–5. [Google Scholar]
- Liu, X.; Huang, Y.; Wang, C.; Pei, J.; Huo, W.; Zhang, Y.; Yang, J. Semi-supervised SAR ATR via conditional generative adversarial network with multi-discriminator. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2361–2364. [Google Scholar]
- Wang, N.; Wang, Y.; Liu, H.; Zuo, Q. Target discrimination method for SAR images via convolutional neural network with semi-supervised learning and minimum feature divergence constraint. Remote Sens. Lett. 2020, 11, 1167–1174. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, X.; Ren, H.; Li, L. Multi-view classification with semi-supervised learning for SAR target recognition. Signal Process. 2021, 183, 108030. [Google Scholar] [CrossRef]
- Engelen, J.E.V.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef]
- Odena, A. Semi-supervised learning with generative adversarial networks. arXiv 2016, arXiv:1606.01583. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. arXiv 2016, arXiv:1606.03498. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, PMLR, Sun, CA, USA, 12–18 July 2020; pp. 1597–1607. [Google Scholar]
- Zhai, X.; Oliver, A.; Kolesnikov, A.; Beyer, L. S4l: Self-supervised semi-supervised learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1476–1485. [Google Scholar]
- Rasmus, A.; Berglund, M.; Honkala, M.; Valpola, H.; Raiko, T. Semi-supervised learning with ladder networks. Adv. Neural Inf. Process. Syst. 2015, 28, 3532–3540. [Google Scholar]
- Kingma, D.P.; Mohamed, S.; Rezende, D.J.; Welling, M. Semi-supervised learning with deep generative models. Adv. Neural Inf. Process. Syst. 2014, 4, 3581–3589. [Google Scholar]
- Grandvalet, Y.; Bengio, Y. Semi-supervised learning by entropy minimization. Adv. Neural Inf. Process. Syst. 2005, 17, 529–536. [Google Scholar]
- Lee, D.-H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Proceedings of the ICML 2013 Workshop: Challenges in Representation Learning (WREPL), Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Gao, F.; Ma, F.; Wang, J.; Sun, J.; Yang, E.; Zhou, H. Semi-supervised generative adversarial nets with multiple generators for SAR image recognition. Sensors 2018, 18, 2706. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zhang, L.; Sun, J.; Yin, G.; Dong, Y. Consistency regularization teacher–student semi-supervised learning method for target recognition in SAR images. Vis. Comput. 2021, 38, 4179–4192. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, J.; Qi, P.; Yin, G.; Zhang, L. Multi-block mixed sample semi-supervised learning for sar target recognition. Remote Sens. 2021, 13, 361. [Google Scholar] [CrossRef]
- Gao, F.; Shi, W.; Wang, J.; Hussain, A.; Zhou, H. A semi-supervised synthetic aperture radar (SAR) image recognition algorithm based on an attention mechanism and bias-variance decomposition. IEEE Access 2019, 7, 108617–108632. [Google Scholar] [CrossRef]
- Vinyals, O.; Blundell, C.; Lillicrap, T.P.; Kavukcuoglu, K.; Wierstra, D. Matching networks for one shot learning. Neural Inf. Process. Syst. 2016, 29, 3637–3645. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical networks for few-shot learning. Neural Inf. Process. Syst. 2017, 30, 4077–4087. [Google Scholar]
- Li, W.; Wang, L.; Xu, J.; Huo, J.; Luo, J. Revisiting local descriptor based image-to-class measure for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15 June–20 June 2019; pp. 7260–7268. [Google Scholar]
- Ravi, S.; Larochelle, H. Optimization as a model for few-shot learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Shi, D.; Orouskhani, M.; Orouskhani, Y. A conditional triplet loss for few-shot learning and its application to image co-segmentation. Neural Netw. 2021, 137, 54–62. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, L.; Cheng, Z.; Luo, J. Transmatch: A transfer-learning scheme for semi-supervised few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 12856–12864. [Google Scholar]
- Ren, M.; Triantafillou, E.; Ravi, S.; Snell, J.; Swersky, K.; Tenenbaum, J.B.; Larochelle, H.; Zemel, R.S. Meta-learning for semi-supervised few-shot classification. arXiv 2018, arXiv:1803.00676. [Google Scholar]
- Liu, Y.; Lee, J.; Park, M.; Kim, S.; Yang, E.; Hwang, S.J.; Yang, Y. Learning to propagate labels: Transductive propagation network for few-shot learning. arXiv 2018, arXiv:1805.10002. [Google Scholar]
- Li, X.; Sun, Q.; Liu, Y.; Zhou, Q.; Zheng, S.; Chua, T.-S.; Schiele, B. Learning to self-train for semi-supervised few-shot classification. Adv. Neural Inf. Process. Syst. 2019, 32, 10276–10286. [Google Scholar]
- Phoo, C.P.; Hariharan, B. Self-training for few-shot transfer across extreme task differences. arXiv 2020, arXiv:2010.07734. [Google Scholar]
- Wang, L.; Bai, X.; Zhou, F. Few-shot SAR ATR based on conv-BiLSTM prototypical networks. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019. [Google Scholar]
- Fu, K.; Zhang, T.; Zhang, Y.; Wang, Z.; Sun, X. Few-shot SAR target classification via metalearning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Che, J.; Wang, L.; Bai, X.; Liu, C.; Zhou, F. Spatial-Temporal Hybrid Feature Extraction Network for Few-shot Automatic Modulation Classification. IEEE Trans. Veh. Technol. 2022, 71, 13387–13392. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, G.; Lin, Y.; Wu, H.; Yu, C.; Adachi, F. Few-Shot Specific Emitter Identification via Deep Metric Ensemble Learning. IEEE Internet Things J. 2022, 9, 24980–24994. [Google Scholar] [CrossRef]
- Yang, R.; Xu, X.; Li, X.; Wang, L.; Pu, F. Learning relation by graph neural network for SAR image few-shot learning. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1743–1746. [Google Scholar]
- Wang, L.; Bai, X.; Gong, C.; Zhou, F. Hybrid inference network for few-shot SAR automatic target recognition. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9257–9269. [Google Scholar] [CrossRef]
- Rostami, M.; Kolouri, S.; Eaton, E.; Kim, K. SAR image classification using few-shot cross-domain transfer learning. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Tang, J.; Zhang, F.; Zhou, Y.; Yin, Q.; Hu, W. A fast inference networks for SAR target few-shot learning based on improved siamese networks. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Lu, D.; Cao, L.; Liu, H. Few-shot learning neural network for sar target recognition. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019. [Google Scholar]
- Zhai, Y.; Deng, W.; Lan, T.; Sun, B.; Ying, Z.; Gan, J.; Mai, C.; Li, J.; Labati, R.D.; Piuri, V. MFFA-SARNET: Deep transferred multi-level feature fusion attention network with dual optimized loss for small-sample SAR ATR. Remote Sens. 2020, 12, 1385. [Google Scholar] [CrossRef]
- Tai, Y.; Tan, Y.; Xiong, S.; Sun, Z.; Tian, J. Few-shot transfer learning for SAR image classification without extra SAR samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2240–2253. [Google Scholar] [CrossRef]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 6–11 July 2015; Volume 2. [Google Scholar]
- Ding, B.; Wen, G. Exploiting multi-view SAR images for robust target recognition. Remote Sens. 2017, 9, 1150. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Zhang, Z.; Xiang, Y.; Li, J.; Nehorai, A. Sar automatic target recognition using joint low-rank and sparse multiview denoising. IEEE Geosci. Remote. Sens. Lett. 2018, 15, 1570–1574. [Google Scholar] [CrossRef]
- Zhang, F.; Fu, Z.; Zhou, Y.; Hu, W.; Hong, W. Multi-aspect SAR target recognition based on space-fixed and space-varying scattering feature joint learning. Remote Sens. Lett. 2019, 10, 998–1007. [Google Scholar] [CrossRef]
- Xue, R.; Bai, X.; Zhou, F. Spatial–temporal ensemble convolution for sequence SAR target classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1250–1262. [Google Scholar] [CrossRef]
- Pei, J.; Huang, Y.; Huo, W.; Zhang, Y.; Yang, J.; Yeo, T.-S. Sar automatic target recognition based on multiview deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2196–2210. [Google Scholar] [CrossRef]
- Ren, H.; Yu, X.; Zou, L.; Zhou, Y.; Wang, X. Joint supervised dictionary and classifier learning for multi-view sar image classification. IEEE Access 2019, 7, 165127–165142. [Google Scholar] [CrossRef]
- Lake, B.M.; Salakhutdinov, R.; Gross, J.; Tenenbaum, J.B. One shot learning of simple visual concepts. Cogn. Sci. 2011, 33, 2568–2573. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 39, 640–651. [Google Scholar]
- Scarnati, T.; Lewis, B. A deep learning approach to the synthetic and measured paired and labeled experiment (sample) challenge problem. In Algorithms for Synthetic Aperture Radar Imagery XXVI; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10987, p. 109870G. [Google Scholar]
- Lewis, B.; Scarnati, T.; Sudkamp, E.; Nehrbass, J.; Rosencrantz, S.; Zelnio, E. A SAR dataset for ATR development: The synthetic and measured paired labeled experiment (sample). In Algorithms for Synthetic Aperture Radar Imagery XXVI; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10987, p. 109870H. [Google Scholar]
- Allison, P.D. Logistic Regression Using the Sas System: Theory and Application; SAS Publishing: Cary, NC, USA, 1999. [Google Scholar]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man, Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Saunders, C.; Stitson, M.O.; Weston, J.; Holloway, R.; Bottou, L.; Scholkopf, B.; Smola, A. Support vector machine. Comput. EnCE 2002, 1, 1–28. [Google Scholar]
- Burez, J.; Poel, D. Handling class imbalance in customer churn prediction. Expert Syst. Appl. 2008, 36, 4626–4636. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Zhang, C.; Cai, Y.; Lin, G.; Shen, C.S. Deepemd: Few-shot image classification with differentiable earth mover’s distance and structured classifiers. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Zhang, C.; Cai, Y.; Lin, G.; Shen, C. Deepemd: Differentiable earth mover’s distance for few-shot learning. arXiv 2020, arXiv:2003.06777v3. [Google Scholar] [CrossRef] [PubMed]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1199–1208. [Google Scholar]
- Wang, Y.; Zhang, L.; Yao, Y.; Fu, Y. How to trust unlabeled data instance credibility inference for few-shot learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 6240–6253. [Google Scholar] [CrossRef]
- Rodríguez, P.; Laradji, I.; Drouin, A.; Lacoste, A. Embedding propagation: Smoother manifold for few-shot classification. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 121–138. [Google Scholar]
- Zhu, P.; Gu, M.; Li, W.; Zhang, C.; Hu, Q. Progressive point to set metric learning for semi-supervised few-shot classification. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 196–200. [Google Scholar]
- Wang, C.; Huang, Y.; Liu, X.; Pei, J.; Zhang, Y.; Yang, J. Global in local: A convolutional transformer for SAR ATR FSL. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).