Hyperspectral Image Super-Resolution via Adaptive Factor Group Sparsity Regularization-Based Subspace Representation
Abstract
:1. Introduction
- We propose an FGSSR-based HSI super-resolution method that overcomes the sensibility of the subspace dimension determination of earlier subspace representation-based methods. Specifically, by incorporating factor group sparsity regularization into subspace representation, FGSSR becomes rank-revealing, enabling it to adaptively and accurately approximate the subspace dimension to the rank of the latent HR-HSI.
- The FGSSR-based method utilizes the FGSSR model to explore spectral correlation and employs TNN regularization to capture spatial self-similarity in the latent HR-HSI. FGSSR can adaptively and effectively capture the high spectral correlation by fully leveraging the advantages of subspace representation and the Schatten-p norm while mitigating their limitations. TNN regularization on the low-dimensional coefficients can effectively capture the spatial self-similarity and facilitate efficient computations through dimensionality reduction.
- An effective PAM-based algorithm is developed with the aim of addressing the FGSSR-based model. Extensive studies carried out with simulated and real-world datasets reveal that our FGSSR-based method outperforms the state-of-the-art (SOTA) HSI super-resolution methods in both quantitative and visual judgements.
2. Related Work
2.1. Notations
2.2. Problem Formulation
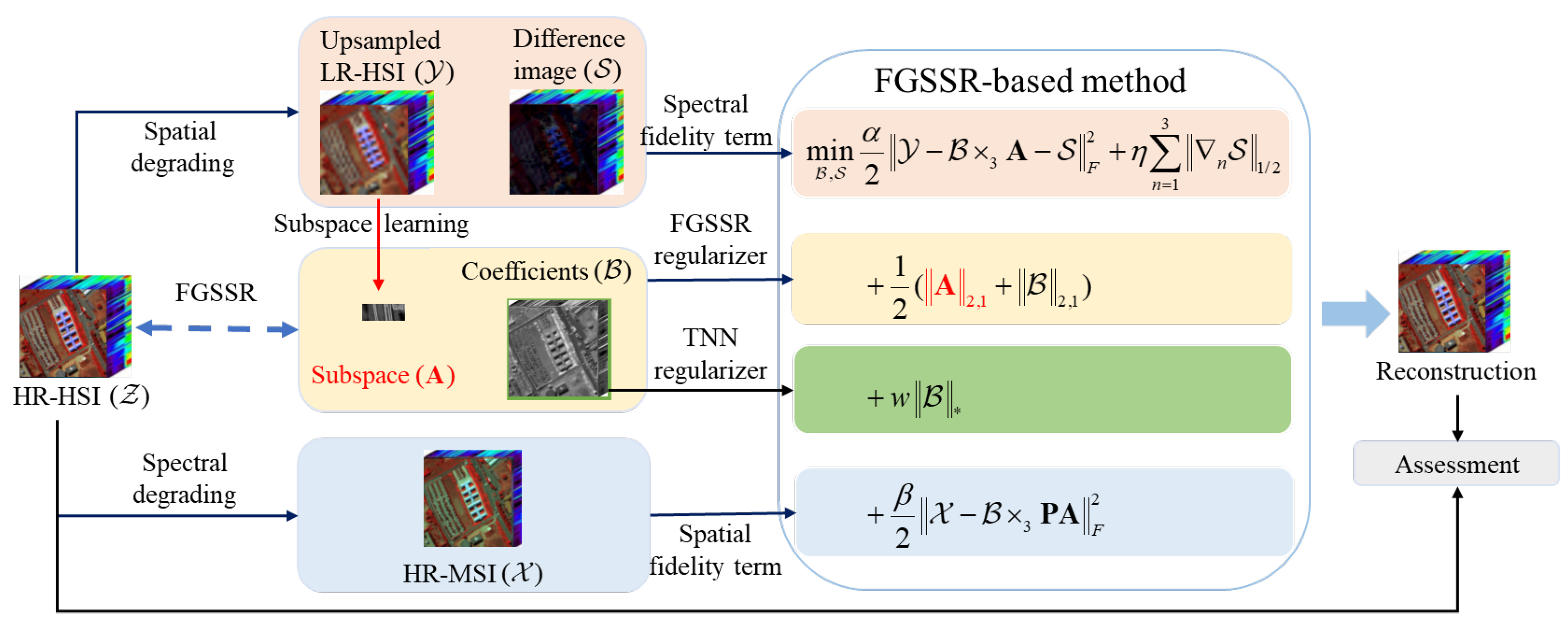
3. Proposed FGSSR-Based Method
3.1. Subspace Learning
- Enhanced Rank Minimization: The FGSSR model corresponds to the Schatten-p norm, which enables it to provide a more precise approximation to rank minimization compared to the nuclear norm.
- Reduced Computational Complexity: Unlike other rank minimization problems that require SVD calculation at each iteration, the FGSSR model can be effectively solved through the soft-threshold shrinkage operator or tiny linear equations, resulting in enhanced computational efficiency. In addition, the FGSSR model employs the subspace learning strategy to learn the spectral subspace , which can also reduce the computational complexity.
- Automatic Subspace Dimension Selection: Compared to the direct subspace representation model (12), the FGSSR model (13) imposes the group sparsity regularization on the coefficients . This leads to the rapid elimination of specific frontal slices in during the iterative optimization process, automatically reducing the number of non-zero frontal slices (i.e., subspace dimension d), and dynamically approximating the rank r of .
3.2. Adaptive FGSSR-Based HSI Super-Resolution Model
3.3. Optimization Algorithm
| Algorithm 1: ADMM Algorithm for Subproblem |
| Input: , , , , , , , , , , and |
| Initialization: Let , , . |
| 1: while not converged and do |
| 2: |
| 3: Update via (28). |
| 4: Update via (30). |
| 5: Update via (32). |
| 6: Update and via (25) and (26), respectively. |
| 7: Check the convergence condition: . |
| 8: end while |
| Output: Low-dimensional coefficient tensor |
| Algorithm 2: ADMM Algorithm for Subproblem |
| Input: , , , , , , , , and |
| Initialization: Let , ,, . |
| 1: while not converged and do |
| 2: . |
| 3: Update via (39). |
| 4: Update , , via solving (41) with the GST operator. |
| 5: Update , , via (37). |
| 6: Check the convergence condition: . |
| 7: end while |
| Output: Difference image |
| Algorithm 3: PAM Algorithm for FGSSR-based Model |
| Input: , , , , , , w, , , , and |
| Initialize: , , ,
, where , , and come from the SVD of . |
| 1: while not converged and do |
| 2: . |
| 3: Update via solving (20) with Algorithm 1. |
| 4: Update via solving (33) with Algorithm 2. |
| 5: Update , where is the number of the nonzero frontal slices of |
| 6: Remove the zero frontal slices of . |
| 7: Update via (16). |
| 8: Check the convergence condition: . |
| 9: end while |
| Output: Target HR-HSI: |
3.4. Computational Complexity
4. Experiments
4.1. Datasets
4.1.1. Datasets for Simulated Experiments
4.1.2. Dataset for Real Experiment
4.2. Evaluation Index
4.3. Experimental Results on Simulated Datasets
4.3.1. Results on Uniform Blur Simulated Datasets
4.3.2. Results on Gaussian Blur Simulated Datasets
4.3.3. Results on Noisy Simulated Datasets
4.4. Experimental Results on Real Dataset
5. Discussion
5.1. The Effectiveness of the Proposed FGSSR Model
5.2. Analysis of Model Parameters
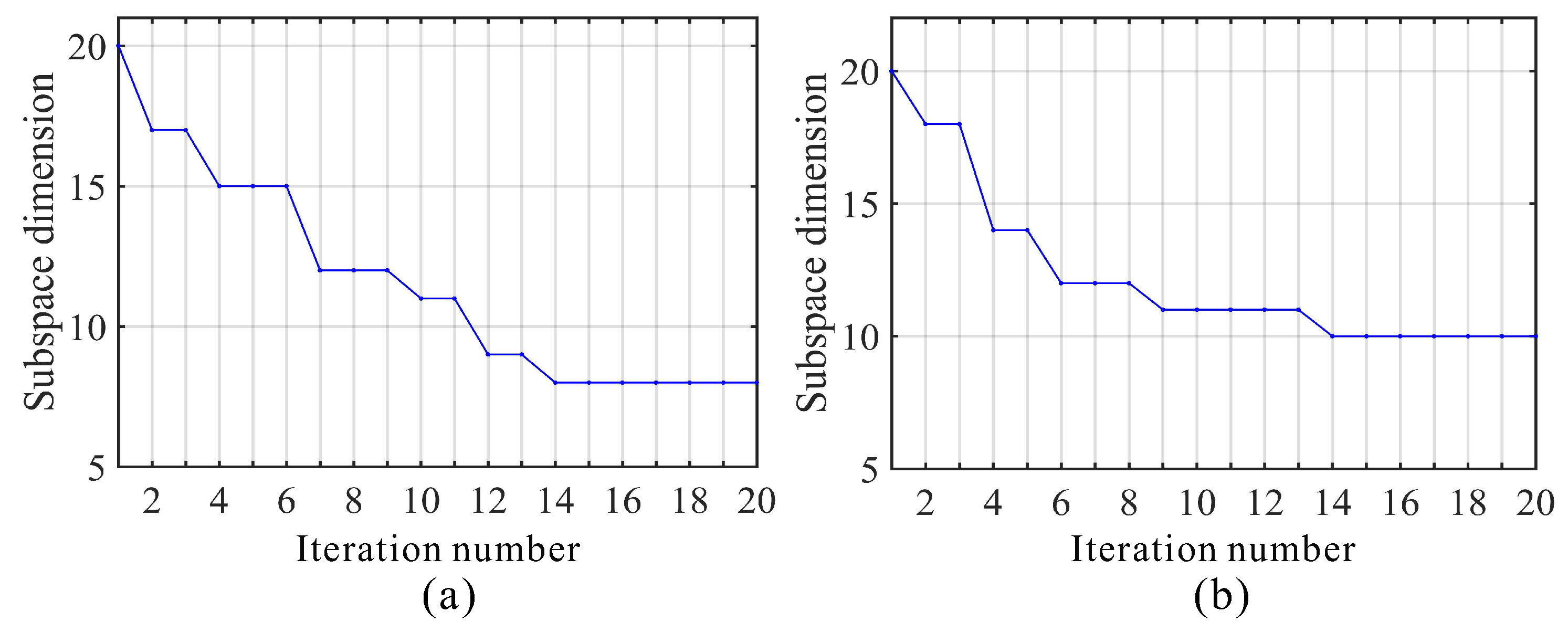
5.3. Automatic Adjustment of Subspace Dimension
5.4. Computation Efficiency
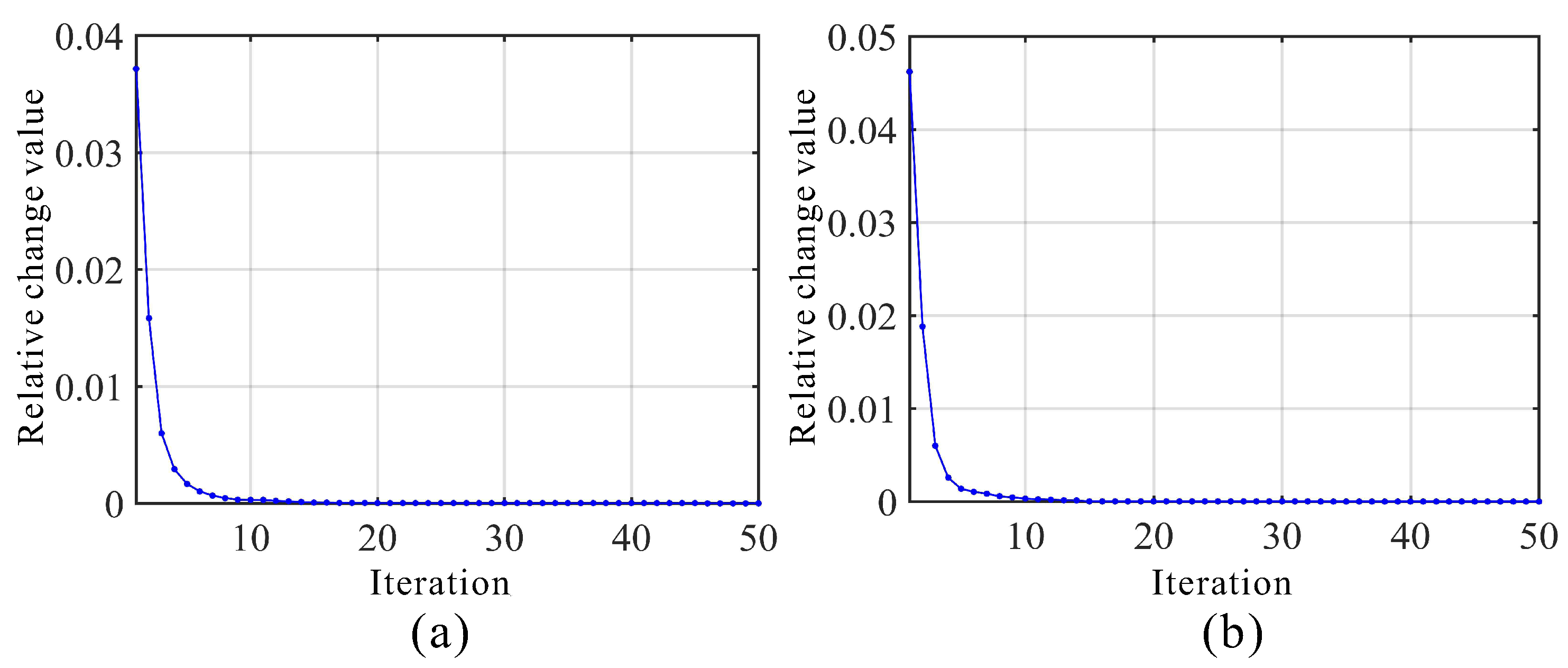
5.5. Numerical Convergence
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Ding, Y.; Zhao, X.; Siye, L.; Yang, N.; Cai, Y.; Zhan, Y. Multireceptive field: An adaptive path aggregation graph neural framework for hyperspectral image classification. Expert Syst. Appl. 2023, 217, 119508. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, X.; Deng, L.; Liu, Y. Monitor water quality through retrieving water quality parameters from hyperspectral images using graph convolution network with superposition of multi-point effect: A case study in Maozhou River. J. Environ. Manag. 2023, 342, 118283. [Google Scholar] [CrossRef]
- Wang, L.; Wang, L.; Wang, Q.; Atkinson, P.M. SSA-SiamNet: Spectral–spatial-wise attention-based Siamese network for hyperspectral image change detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Liu, C.; Fan, Z.; Zhang, G. GJTD-LR: A Trainable Grouped Joint Tensor Dictionary With Low-Rank Prior for Single Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Xu, T.; Huang, T.Z.; Deng, L.J.; Yokoya, N. An iterative regularization method based on tensor subspace representation for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar]
- Ding, M.; Fu, X.; Huang, T.Z.; Wang, J.; Zhao, X.L. Hyperspectral super-resolution via interpretable block-term tensor modeling. IEEE J. Sel. Top. Signal Process. 2020, 15, 641–656. [Google Scholar] [CrossRef]
- Peng, Y.; Li, W.; Luo, X.; Du, J.; Gan, Y.; Gao, X. Integrated fusion framework based on semicoupled sparse tensor factorization for spatio-temporal–spectral fusion of remote sensing images. Inf. Fusion 2021, 65, 21–36. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Fang, L. Learning a low tensor-train rank representation for hyperspectral image super-resolution. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2672–2683. [Google Scholar] [CrossRef]
- Li, Y.; Du, Z.; Wu, S.; Wang, Y.; Wang, Z.; Zhao, X.; Zhang, F. Progressive split-merge super resolution for hyperspectral imagery with group attention and gradient guidance. ISPRS J. Photogramm. Remote Sens. 2021, 182, 14–36. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Wang, Q. Hyperspectral and multispectral image fusion via nonlocal low-rank tensor approximation and sparse representation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 550–562. [Google Scholar] [CrossRef]
- Wu, X.; Huang, T.Z.; Deng, L.J.; Zhang, T.J. Dynamic cross feature fusion for remote sensing pansharpening. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 14687–14696. [Google Scholar]
- Cao, X.; Fu, X.; Hong, D.; Xu, Z.; Meng, D. PanCSC-Net: A model-driven deep unfolding method for pansharpening. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Hu, J.F.; Huang, T.Z.; Deng, L.J.; Jiang, T.X.; Vivone, G.; Chanussot, J. Hyperspectral image super-resolution via deep spatiospectral attention convolutional neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7251–7265. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wu, Z.; Xiao, L.; Wu, X.J. Model inspired autoencoder for unsupervised hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Fu, X.; Jia, S.; Xu, M.; Zhou, J.; Li, Q. Fusion of hyperspectral and multispectral images accounting for localized inter-image changes. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Xu, T.; Huang, T.Z.; Deng, L.J.; Zhao, X.L.; Huang, J. Hyperspectral image superresolution using unidirectional total variation with tucker decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4381–4398. [Google Scholar] [CrossRef]
- He, W.; Chen, Y.; Yokoya, N.; Li, C.; Zhao, Q. Hyperspectral super-resolution via coupled tensor ring factorization. Pattern Recognit. 2022, 122, 108280. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, J.; He, W.; Zhao, X.L.; Huang, T.Z. Hyperspectral and Multispectral Image Fusion Using Factor Smoothed Tensor Ring Decomposition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Li, K.; Zhang, W.; Yu, D.; Tian, X. HyperNet: A deep network for hyperspectral, multispectral, and panchromatic image fusion. ISPRS J. Photogramm. Remote Sens. 2022, 188, 30–44. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Guo, A.; Fang, L. Deep hyperspectral image sharpening. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5345–5355. [Google Scholar] [CrossRef]
- Qu, Y.; Qi, H.; Kwan, C. Unsupervised sparse dirichlet-net for hyperspectral image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2511–2520. [Google Scholar]
- Zhang, L.; Nie, J.; Wei, W.; Zhang, Y.; Liao, S.; Shao, L. Unsupervised adaptation learning for hyperspectral imagery super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 3073–3082. [Google Scholar]
- Wycoff, E.; Chan, T.H.; Jia, K.; Ma, W.K.; Ma, Y. A non-negative sparse promoting algorithm for high resolution hyperspectral imaging. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 1409–1413. [Google Scholar]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral super-resolution by coupled spectral unmixing. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3586–3594. [Google Scholar]
- Xue, J.; Zhao, Y.Q.; Bu, Y.; Liao, W.; Chan, J.C.W.; Philips, W. Spatial-spectral structured sparse low-rank representation for hyperspectral image super-resolution. IEEE Trans. Image Process. 2021, 30, 3084–3097. [Google Scholar] [CrossRef] [PubMed]
- Simoes, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A convex formulation for hyperspectral image superresolution via subspace-based regularization. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3373–3388. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral image super-resolution via non-negative structured sparse representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Spatial–spectral-graph-regularized low-rank tensor decomposition for multispectral and hyperspectral image fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1030–1040. [Google Scholar] [CrossRef]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing hyperspectral and multispectral images via coupled sparse tensor factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z. Hyperspectral images super-resolution via learning high-order coupled tensor ring representation. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4747–4760. [Google Scholar] [CrossRef]
- Kanatsoulis, C.I.; Fu, X.; Sidiropoulos, N.D.; Ma, W.K. Hyperspectral super-resolution: A coupled tensor factorization approach. IEEE Trans. Signal Process. 2018, 66, 6503–6517. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z. Nonlocal patch tensor sparse representation for hyperspectral image super-resolution. IEEE Trans. Image Process. 2019, 28, 3034–3047. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Huang, S.; Liao, W.; Chan, J.C.W.; Kong, S.G. Multilayer sparsity-based tensor decomposition for low-rank tensor completion. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6916–6930. [Google Scholar] [CrossRef]
- Dian, R.; Fang, L.; Li, S. Hyperspectral image super-resolution via non-local sparse tensor factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Dhaka, Bangladesh, 13–14 February 2017; pp. 5344–5353. [Google Scholar]
- Borsoi, R.A.; Prévost, C.; Usevich, K.; Brie, D.; Bermudez, J.C.; Richard, C. Coupled tensor decomposition for hyperspectral and multispectral image fusion with inter-image variability. IEEE J. Sel. Top. Signal Process. 2021, 15, 702–717. [Google Scholar] [CrossRef]
- Han, H.; Liu, H. Hyperspectral image super-resolution based on transform domain low rank tensor regularization. In Proceedings of the 2022 International Conference on Image Processing and Media Computing (ICIPMC), Xi’an, China, 27–29 May 2022; pp. 80–84. [Google Scholar]
- Dian, R.; Li, S. Hyperspectral Image Super-Resolution via Subspace-Based Low Tensor Multi-Rank Regularization. IEEE Trans. Image Process. 2019, 28, 5135–5146. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.; Zhang, Y.; Yang, S.; Zhang, Y. Hyperspectral and multispectral image fusion via variational tensor subspace decomposition. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Xu, H.; Qin, M.; Chen, S.; Zheng, Y.; Zheng, J. Hyperspectral-multispectral image fusion via tensor ring and subspace decompositions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8823–8837. [Google Scholar] [CrossRef]
- Xue, S.; Qiu, W.; Liu, F.; Jin, X. Low-rank tensor completion by truncated nuclear norm regularization. In Proceedings of the 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2600–2605. [Google Scholar]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 925–938. [Google Scholar] [CrossRef] [PubMed]
- Nie, F.; Huang, H.; Ding, C. Low-rank matrix recovery via efficient schatten p-norm minimization. In Proceedings of the AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012; Volume 26, pp. 655–661. [Google Scholar]
- Fan, J.; Ding, L.; Chen, Y.; Udell, M. Factor group-sparse regularization for efficient low-rank matrix recovery. Adv. Neural Inf. Process. Syst. 2019, 32, 5105–5115. [Google Scholar]
- Fang, L.; Zhuo, H.; Li, S. Super-resolution of hyperspectral image via superpixel-based sparse representation. Neurocomputing 2018, 273, 171–177. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, X.; Emery, W.J.; Wang, Y.; Li, J. An Integrated Spatio-Spectral–Temporal Sparse Representation Method for Fusing Remote-Sensing Images With Different Resolutions. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3358–3370. [Google Scholar] [CrossRef]
- Peng, Y.; Li, W.; Luo, X.; Du, J. Hyperspectral image superresolution using global gradient sparse and nonlocal low-rank tensor decomposition with hyper-laplacian prior. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5453–5469. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Deng, L.J.; Huang, T.Z. Bilateral filter based total variation regularization for sparse hyperspectral image unmixing. Inf. Sci. 2019, 504, 334–353. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.Z.; He, W.; Zhao, X.L.; Zhang, H.; Zeng, J. Hyperspectral image denoising using factor group sparsity-regularized nonconvex low-rank approximation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Attouch, H.; Bolte, J.; Svaiter, B.F. Convergence of descent methods for semi-algebraic and tame problems: Proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 2013, 137, 91–129. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Zuo, W.; Meng, D.; Zhang, L.; Feng, X.; Zhang, D. A generalized iterated shrinkage algorithm for non-convex sparse coding. In Proceedings of the IEEE International Conference on Computer Vision, Manchester, UK, 13–16 October 2013; pp. 217–224. [Google Scholar]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Trans. Geosci. Remote Sens. 2011, 50, 528–537. [Google Scholar] [CrossRef]
- Guo, H.; Bao, W.; Feng, W.; Sun, S.; Mo, C.; Qu, K. Multispectral and Hyperspectral Image Fusion Based on Joint-Structured Sparse Block-Term Tensor Decomposition. Remote Sens. 2023, 15, 4610. [Google Scholar] [CrossRef]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? In Proceedings of the Third Conference “Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images”, Sophia Antipolis, France, 26–28 January 2000; pp. 99–103. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the Summaries 4th JPL Airborne Earth Sci. Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and multispectral data fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Singh, D.; Kaur, M.; Jabarulla, M.Y.; Kumar, V.; Lee, H.N. Evolving fusion-based visibility restoration model for hazy remote sensing images using dynamic differential evolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]

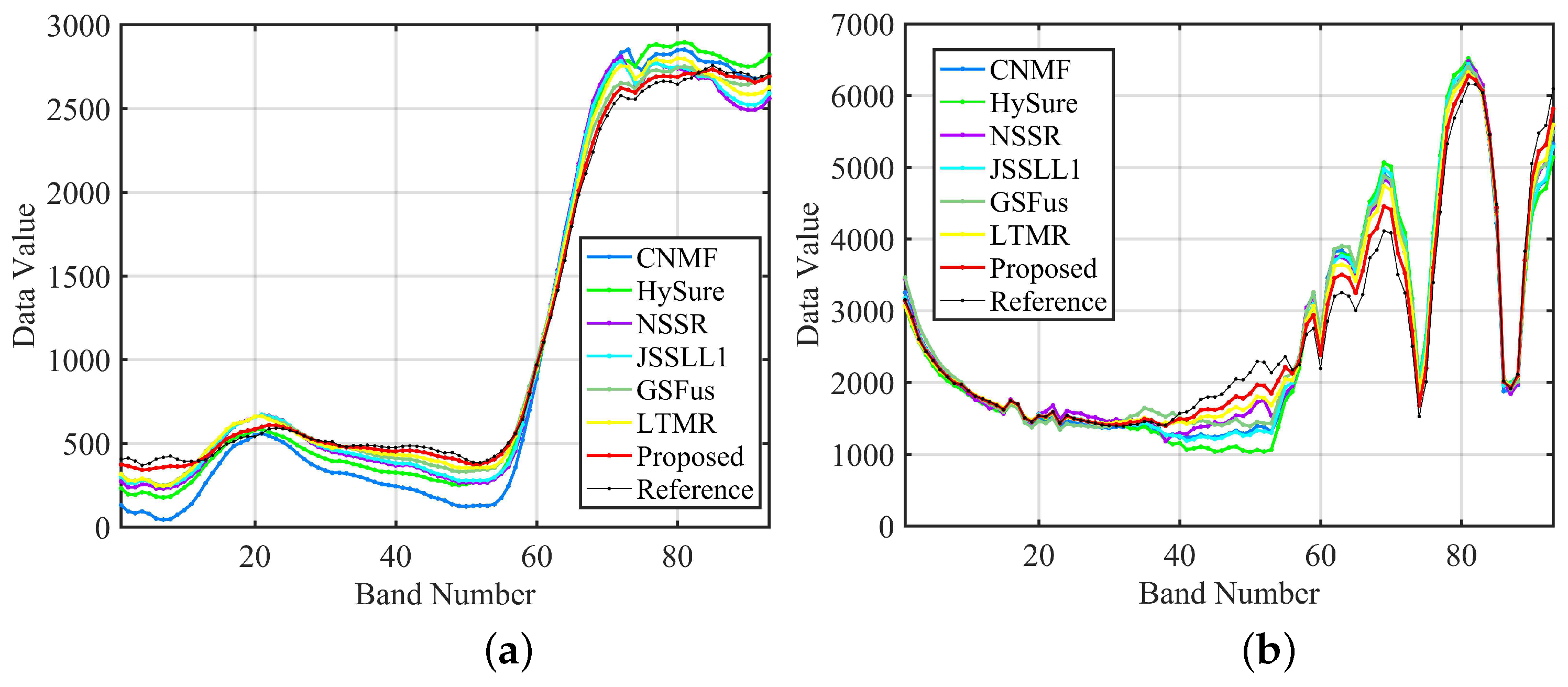

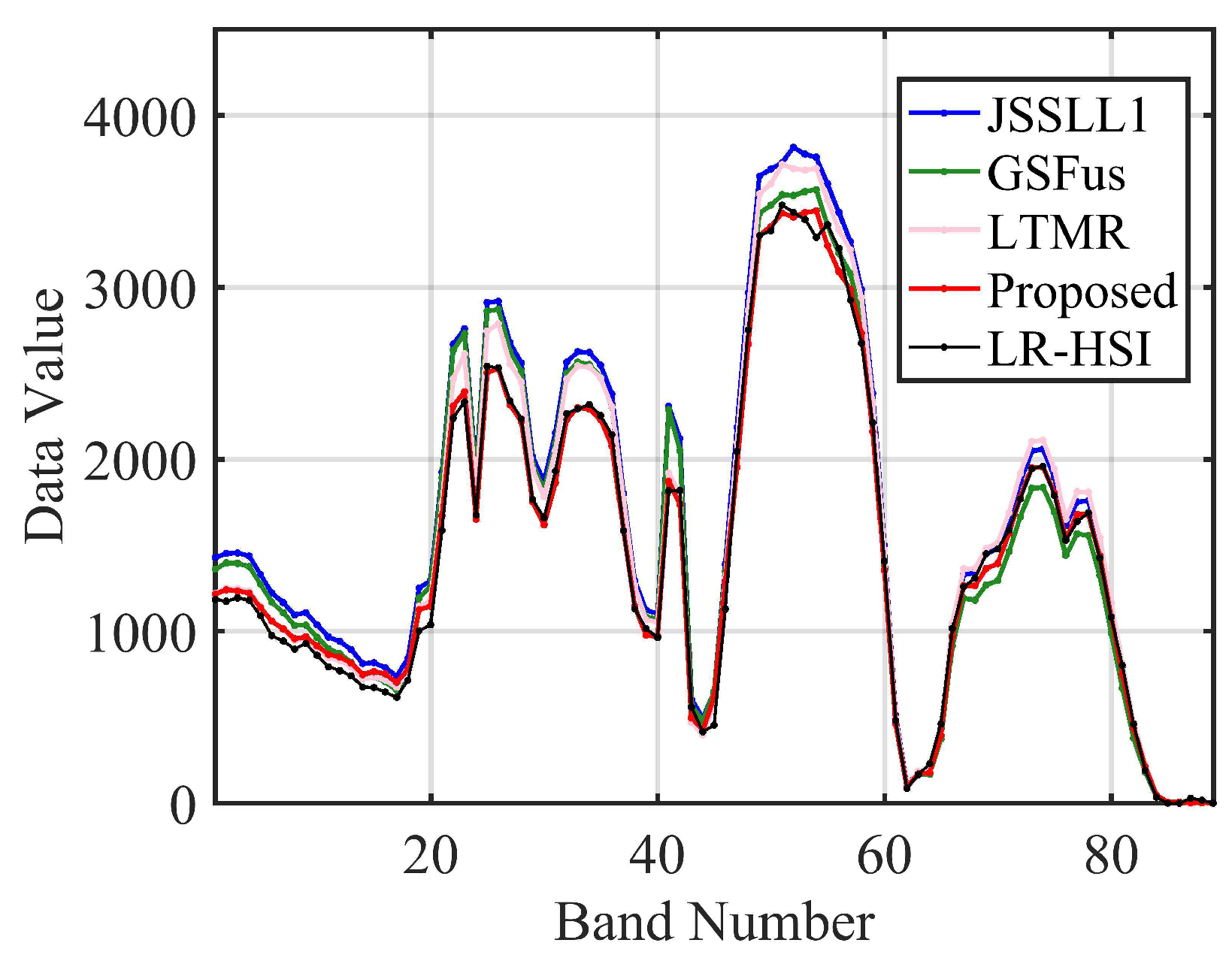

| Evaluation Index | PSNR | SAM | ERGAS | UIQI | SSIM |
|---|---|---|---|---|---|
| Best Value | 0 | 0 | 1 | 1 | |
| CNMF [54] | 42.107 | 1.9039 | 1.1855 | 0.9945 | 0.9896 |
| HySure [27] | 41.635 | 2.0066 | 1.2248 | 0.9940 | 0.9888 |
| NSSR [28] | 43.131 | 2.2042 | 1.1417 | 0.9921 | 0.9825 |
| JSSLL1 [55] | 44.022 | 1.8815 | 1.0145 | 0.9938 | 0.9896 |
| GSFus [16] | 43.697 | 2.0110 | 1.0409 | 0.9937 | 0.9891 |
| LTMR [38] | 44.953 | 1.6761 | 0.8867 | 0.9955 | 0.9912 |
| Proposed | 45.910 | 1.5669 | 0.7898 | 0.9963 | 0.9923 |
| CNMF [54] | 39.692 | 2.3796 | 0.7644 | 0.9907 | 0.9848 |
| HySure [27] | 39.087 | 2.5558 | 0.8246 | 0.9909 | 0.9841 |
| NSSR [28] | 42.757 | 2.3663 | 0.5939 | 0.9915 | 0.9820 |
| JSSLL1 [55] | 43.381 | 1.9963 | 0.5114 | 0.9935 | 0.9863 |
| GSFus [16] | 43.357 | 2.0910 | 0.5396 | 0.9933 | 0.9883 |
| LTMR [38] | 44.342 | 2.0232 | 0.5004 | 0.9946 | 0.9895 |
| Proposed | 45.101 | 1.7139 | 0.4357 | 0.9956 | 0.9913 |
| CNMF [54] | 39.161 | 2.4714 | 0.4103 | 0.9904 | 0.9844 |
| HySure [27] | 38.909 | 2.8017 | 0.4162 | 0.9893 | 0.9814 |
| NSSR [28] | 42.507 | 2.4716 | 0.3109 | 0.9911 | 0.9813 |
| JSSLL1 [55] | 42.737 | 2.2773 | 0.2920 | 0.9927 | 0.9862 |
| GSFus [16] | 43.253 | 2.1154 | 0.2732 | 0.9932 | 0.9880 |
| LTMR [38] | 43.979 | 2.1211 | 0.2522 | 0.9937 | 0.9889 |
| Proposed | 44.555 | 1.8265 | 0.2334 | 0.9950 | 0.9907 |
| Evaluation Index | PSNR | SAM | ERGAS | UIQI | SSIM |
|---|---|---|---|---|---|
| Best Value | 0 | 0 | 1 | 1 | |
| CNMF [54] | 40.486 | 2.0643 | 1.2656 | 0.9927 | 0.9890 |
| HySure [27] | 40.731 | 2.2544 | 1.2953 | 0.9925 | 0.9865 |
| NSSR [28] | 41.151 | 2.3756 | 1.3732 | 0.9929 | 0.9821 |
| JSSLL1 [55] | 41.886 | 2.2584 | 1.2521 | 0.9933 | 0.9858 |
| GSFus [16] | 41.815 | 2.3285 | 1.3101 | 0.9923 | 0.9867 |
| LTMR [38] | 43.110 | 2.0396 | 1.1182 | 0.9949 | 0.9884 |
| Proposed | 43.752 | 1.6558 | 1.0408 | 0.9959 | 0.9914 |
| CNMF [54] | 39.452 | 2.4361 | 0.7205 | 0.9903 | 0.9863 |
| HySure [27] | 38.929 | 2.8177 | 0.8370 | 0.9887 | 0.9828 |
| NSSR [28] | 40.777 | 2.6519 | 0.7233 | 0.9903 | 0.9817 |
| JSSLL1 [55] | 41.068 | 2.594 | 0.7187 | 0.9918 | 0.9842 |
| GSFus [16] | 40.644 | 2.8770 | 0.7554 | 0.9899 | 0.9860 |
| LTMR [38] | 41.919 | 2.5506 | 0.7215 | 0.9924 | 0.9837 |
| Proposed | 42.452 | 2.0956 | 0.6218 | 0.9938 | 0.9886 |
| CNMF [54] | 37.418 | 3.1868 | 0.4567 | 0.9850 | 0.9823 |
| HySure [27] | 36.335 | 3.4996 | 0.5335 | 0.9816 | 0.9760 |
| NSSR [28] | 39.522 | 3.2146 | 0.4298 | 0.9869 | 0.9779 |
| JSSLL1 [55] | 39.809 | 2.8308 | 0.4135 | 0.9870 | 0.9789 |
| GSFus [16] | 38.449 | 3.3989 | 0.5049 | 0.9818 | 0.9799 |
| LTMR [38] | 40.335 | 2.8135 | 0.4611 | 0.9881 | 0.9793 |
| Proposed | 41.499 | 2.4277 | 0.3539 | 0.9917 | 0.9870 |
| Evaluation Index | PSNR | SAM | ERGAS | UIQI | SSIM |
|---|---|---|---|---|---|
| Best Value | 0 | 0 | 1 | 1 | |
| PU dataset | |||||
| CNMF [54] | 39.144 | 2.3847 | 0.8216 | 0.9906 | 0.9847 |
| HySure [27] | 38.679 | 2.6830 | 0.8640 | 0.9901 | 0.9827 |
| NSSR [28] | 42.079 | 2.2543 | 0.6734 | 0.9914 | 0.9852 |
| JSSLL1 [55] | 42.851 | 2.1845 | 0.5923 | 0.9921 | 0.9863 |
| GSFus [16] | 43.195 | 2.1028 | 0.5467 | 0.9934 | 0.9884 |
| LTMR [38] | 44.125 | 1.9953 | 0.4924 | 0.9942 | 0.9893 |
| Proposed | 44.727 | 1.8090 | 0.4567 | 0.9953 | 0.9910 |
| WDCM dataset | |||||
| CNMF [54] | 38.932 | 2.5809 | 0.7642 | 0.9892 | 0.9848 |
| HySure [27] | 38.845 | 2.8448 | 0.8451 | 0.9885 | 0.9825 |
| NSSR [28] | 40.426 | 2.6366 | 0.7965 | 0.9899 | 0.9818 |
| JSSLL1 [55] | 40.543 | 2.5385 | 0.7145 | 0.9912 | 0.9834 |
| GSFus [16] | 40.804 | 2.5341 | 0.7234 | 0.9905 | 0.9864 |
| LTMR [38] | 41.225 | 2.6241 | 0.7939 | 0.9912 | 0.9809 |
| Proposed | 42.052 | 2.2358 | 0.6584 | 0.9931 | 0.9879 |
| Evaluation Index | PSNR | SAM | ERGAS | UIQI | SSIM |
|---|---|---|---|---|---|
| Best Value | 0 | 0 | 1 | 1 | |
| Noisy case 1 | |||||
| CNMF [54] | 41.192 | 1.4237 | 1.6872 | 0.9692 | 0.9855 |
| HySure [27] | 40.635 | 1.7182 | 1.8944 | 0.9631 | 0.9796 |
| NSSR [28] | 42.736 | 1.6560 | 1.5704 | 0.9644 | 0.9815 |
| JSSLL1 [55] | 43.365 | 1.4429 | 1.7172 | 0.9665 | 0.9828 |
| GSFus [16] | 43.723 | 1.4587 | 1.5946 | 0.9668 | 0.9861 |
| LTMR [38] | 44.517 | 1.3465 | 1.5730 | 0.9736 | 0.9867 |
| Proposed | 45.489 | 1.1652 | 1.4243 | 0.9742 | 0.9883 |
| Noisy case 2 | |||||
| CNMF [54] | 39.414 | 1.6403 | 1.7888 | 0.9623 | 0.9787 |
| HySure [27] | 39.596 | 2.0064 | 2.1211 | 0.9509 | 0.9678 |
| NSSR [28] | 39.450 | 2.4438 | 1.9339 | 0.9401 | 0.9624 |
| JSSLL1 [55] | 41.176 | 1.6936 | 1.9087 | 0.9584 | 0.9734 |
| GSFus [16] | 41.947 | 1.8207 | 1.6702 | 0.9581 | 0.9775 |
| LTMR [38] | 42.294 | 1.6918 | 1.7407 | 0.9610 | 0.9756 |
| Proposed | 43.295 | 1.4812 | 1.6072 | 0.9635 | 0.9794 |
| Methods | PU Dataset | WDCM Dataset | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SAM | ERGAS | UIQI | SSIM | PSNR | SAM | ERGAS | UIQI | SSIM | |
| Best Value | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | ||
| DSR-based | 42.380 | 2.2899 | 0.5761 | 0.9923 | 0.9833 | 38.677 | 3.2126 | 0.8330 | 0.9821 | 0.9692 |
| FGSSR-based | 43.764 | 1.9899 | 0.4991 | 0.9942 | 0.9884 | 41.001 | 2.5193 | 0.7023 | 0.9911 | 0.9848 |
| Dataset | CNMF | HySure | NSSR | JSSLL1 | GSFus | LTMR | Proposed |
|---|---|---|---|---|---|---|---|
| PU | 28.87 | 88.87 | 142.29 | 174.68 | 236.47 | 155.87 | 24.35 |
| WDCM | 37.14 | 94.40 | 145.68 | 211.45 | 243.33 | 160.92 | 25.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Li, W.; Luo, X.; Du, J. Hyperspectral Image Super-Resolution via Adaptive Factor Group Sparsity Regularization-Based Subspace Representation. Remote Sens. 2023, 15, 4847. https://doi.org/10.3390/rs15194847
Peng Y, Li W, Luo X, Du J. Hyperspectral Image Super-Resolution via Adaptive Factor Group Sparsity Regularization-Based Subspace Representation. Remote Sensing. 2023; 15(19):4847. https://doi.org/10.3390/rs15194847
Chicago/Turabian StylePeng, Yidong, Weisheng Li, Xiaobo Luo, and Jiao Du. 2023. "Hyperspectral Image Super-Resolution via Adaptive Factor Group Sparsity Regularization-Based Subspace Representation" Remote Sensing 15, no. 19: 4847. https://doi.org/10.3390/rs15194847
APA StylePeng, Y., Li, W., Luo, X., & Du, J. (2023). Hyperspectral Image Super-Resolution via Adaptive Factor Group Sparsity Regularization-Based Subspace Representation. Remote Sensing, 15(19), 4847. https://doi.org/10.3390/rs15194847






