River Discharge Inversion Algorithm Based on the Surface Velocity of Microwave Doppler Radar
Abstract
:1. Introduction
2. Inverting Surface Velocity Measurements to Estimate Mean Velocity in the Cross-Section and Discharge
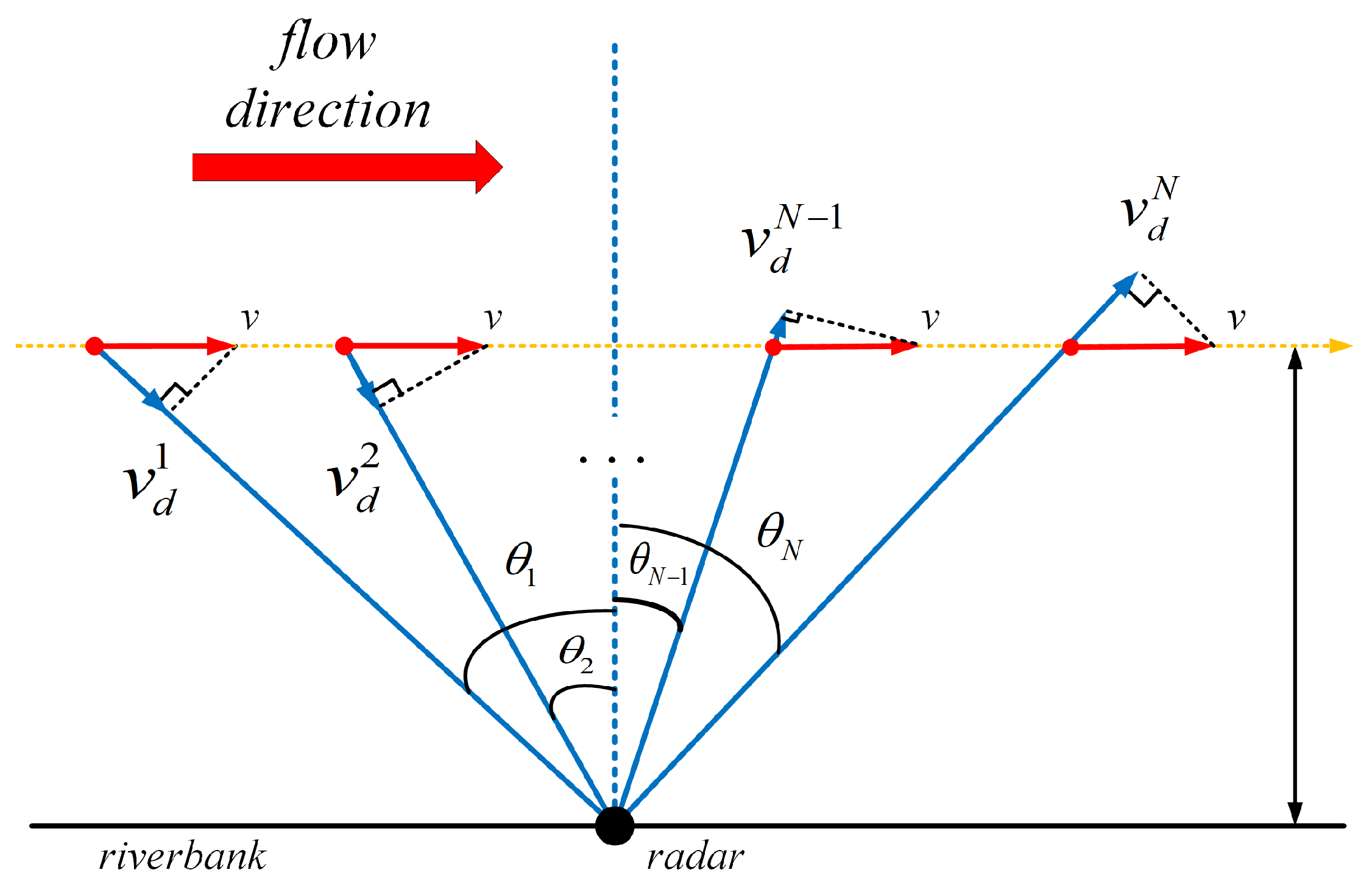
2.1. Measuring River Surface Velocities with Microwave Doppler Radar
2.2. Calculation of River Discharge
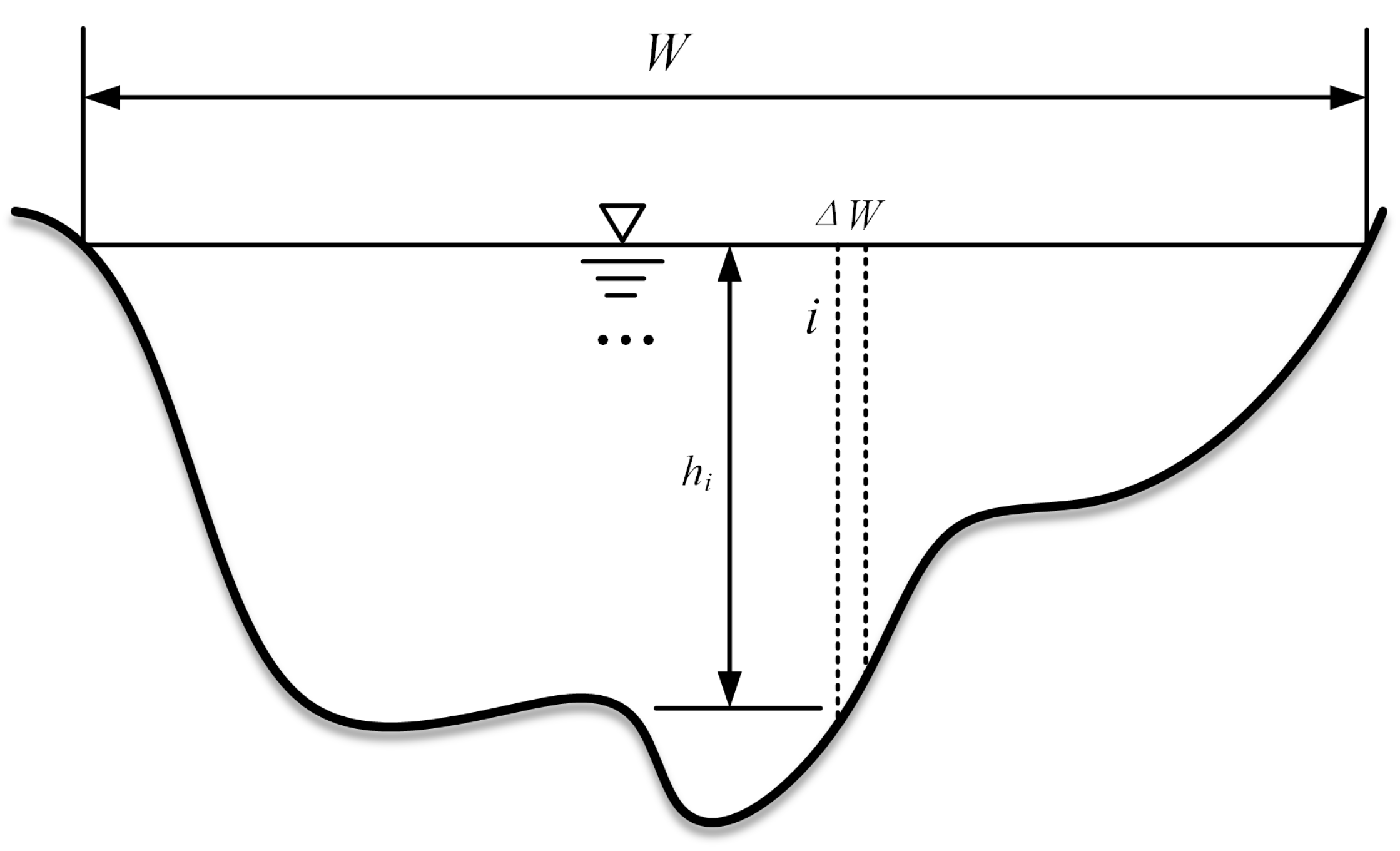
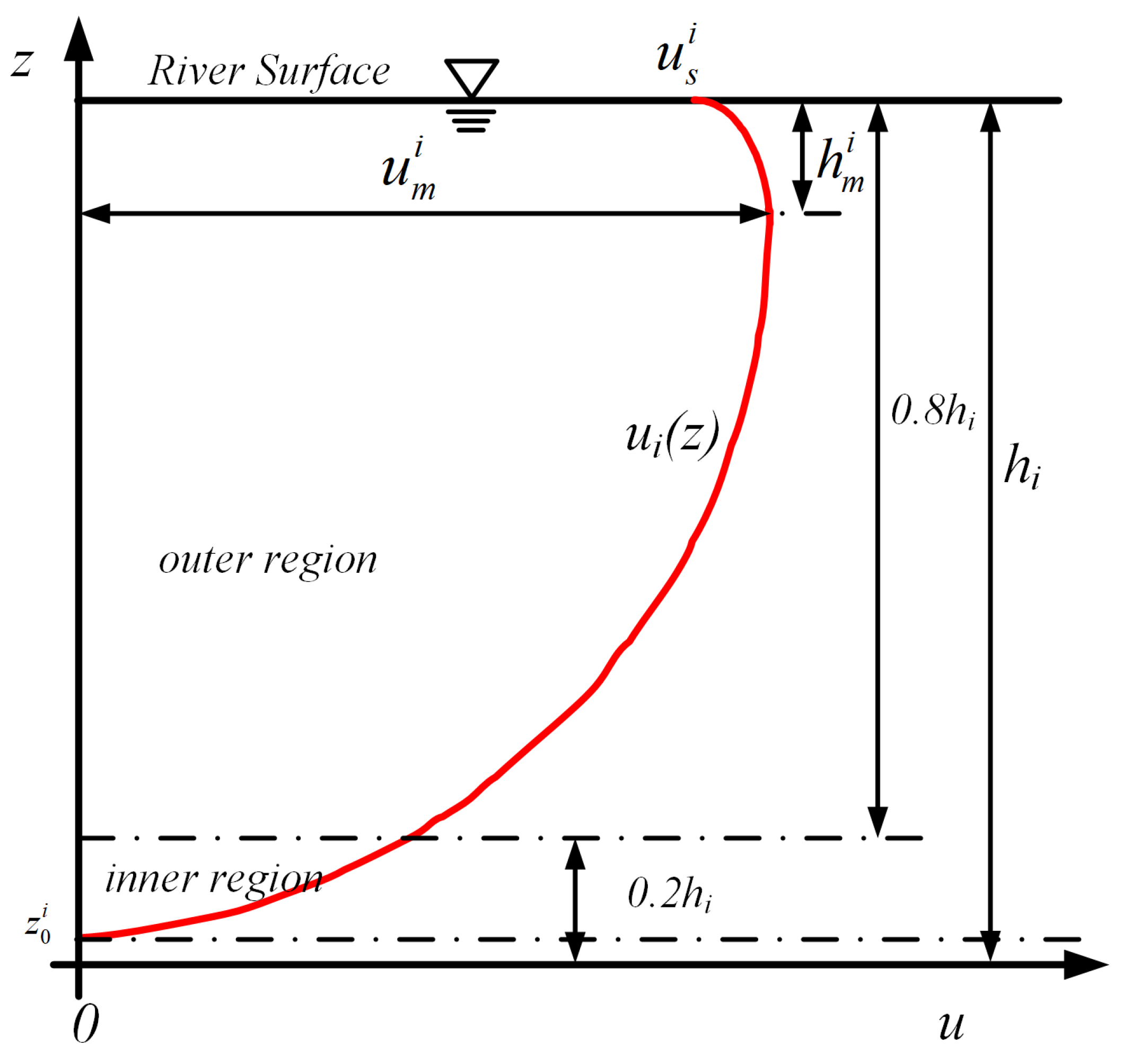
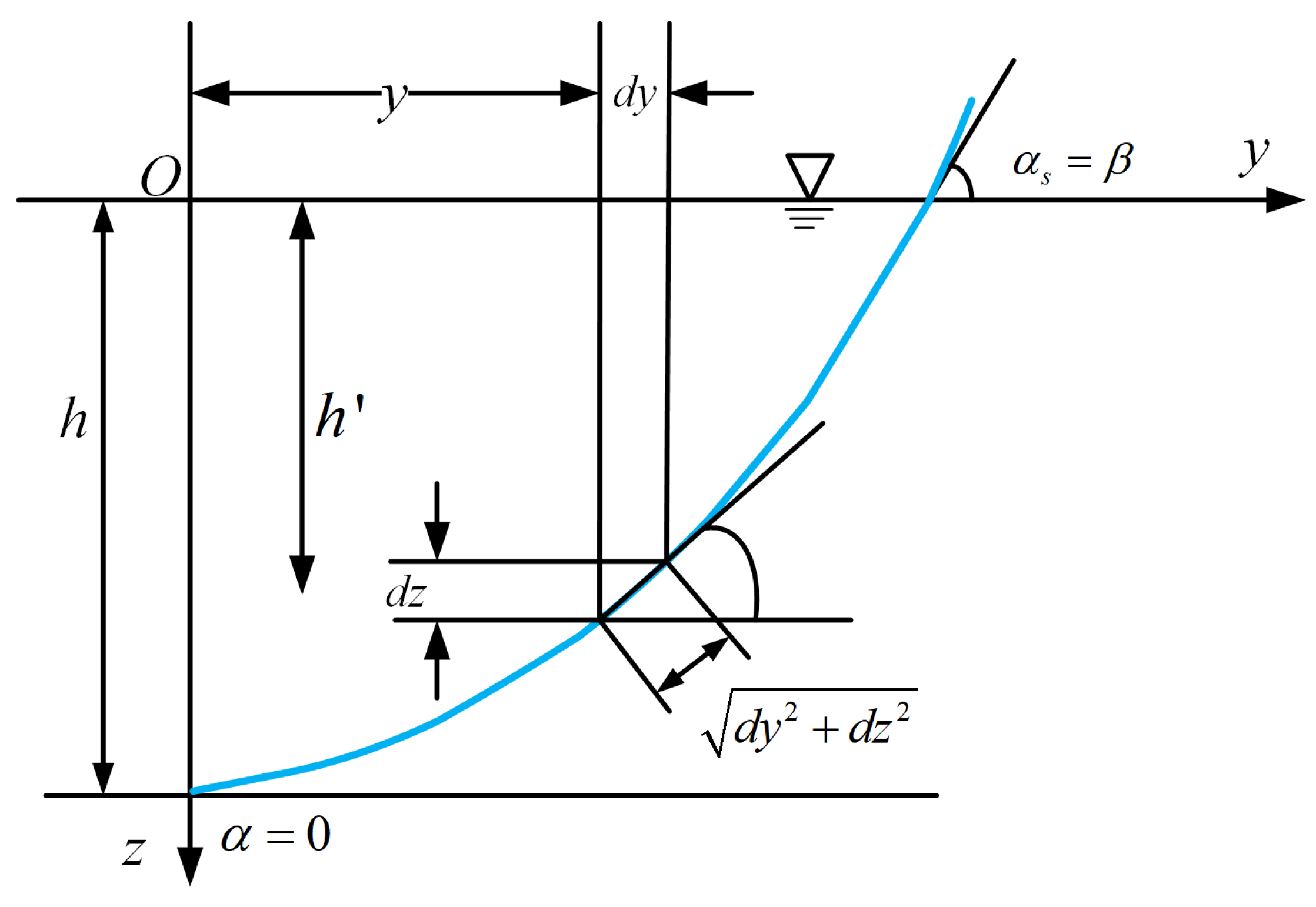
2.3. Estimation of Water Depth
2.4. Runoff Accuracy Assessment: Error Index
3. Radar
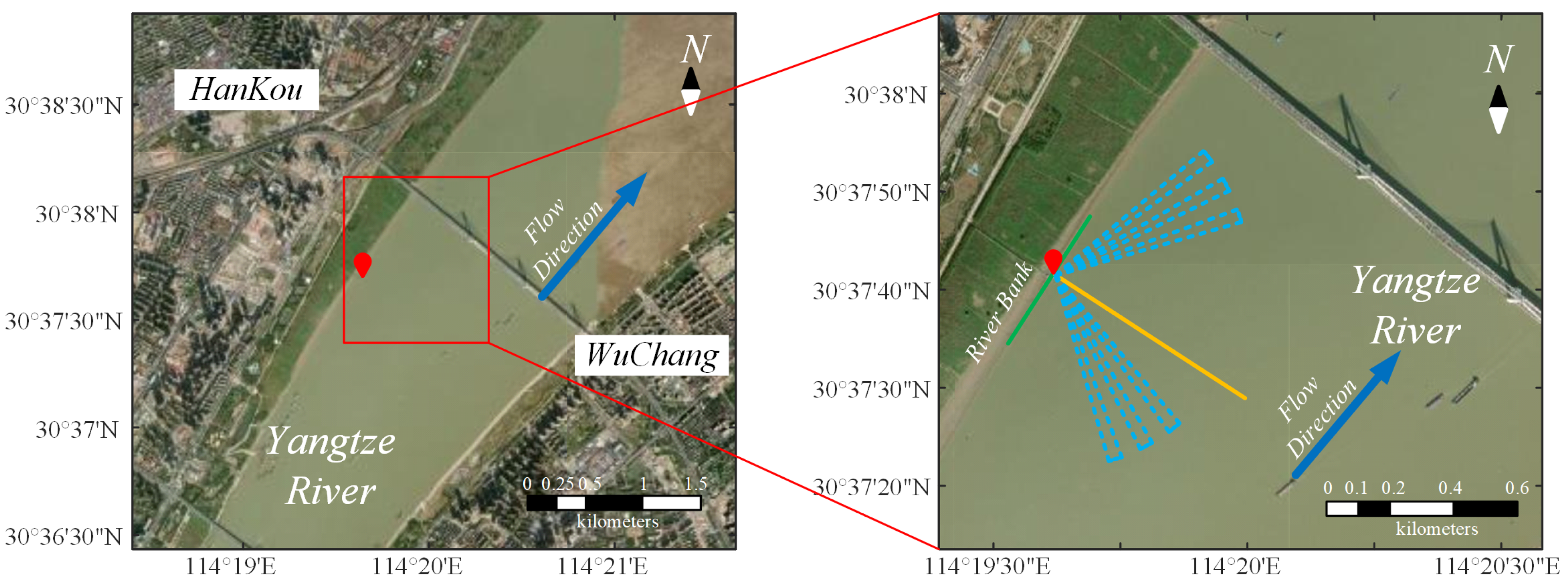
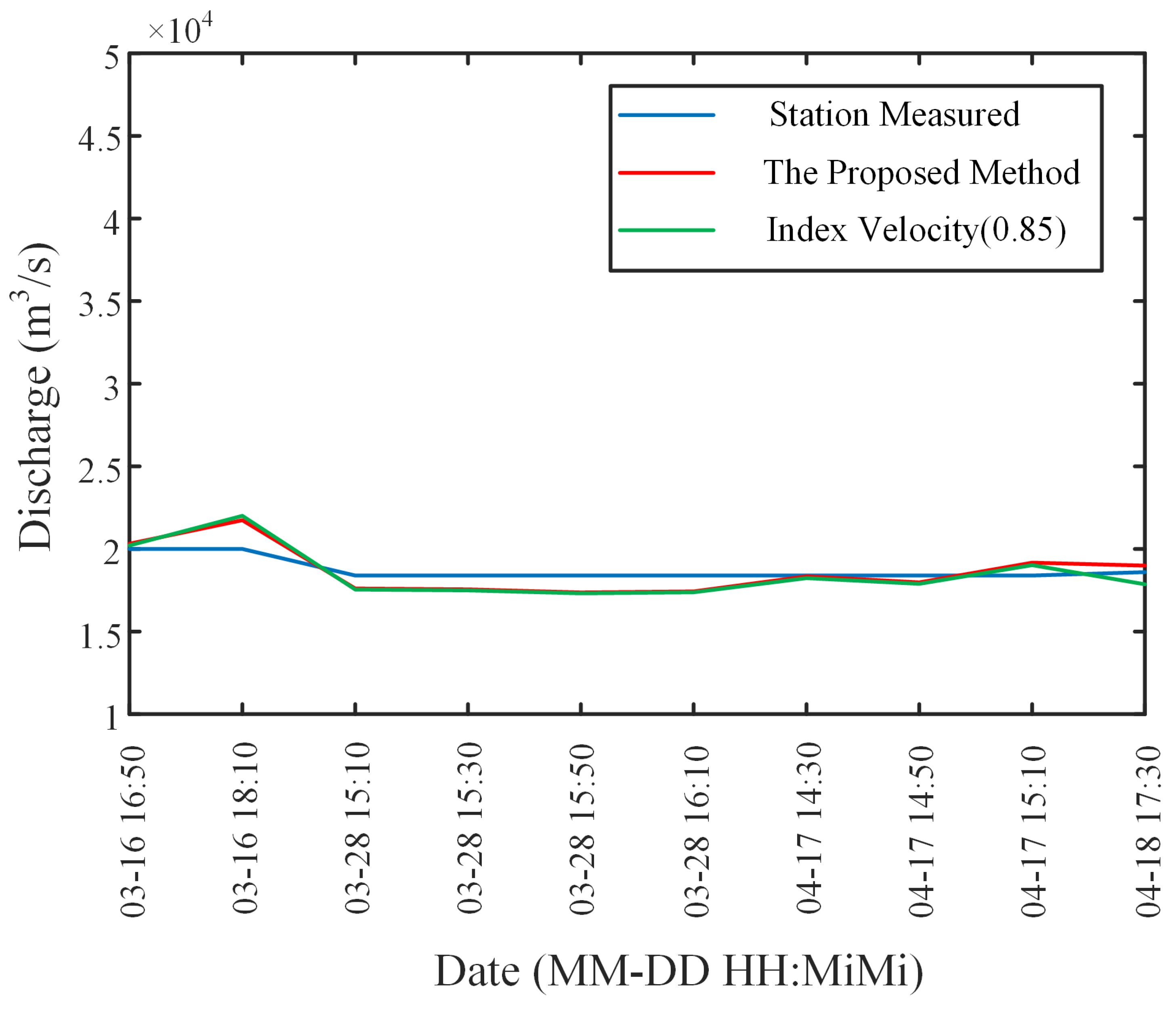
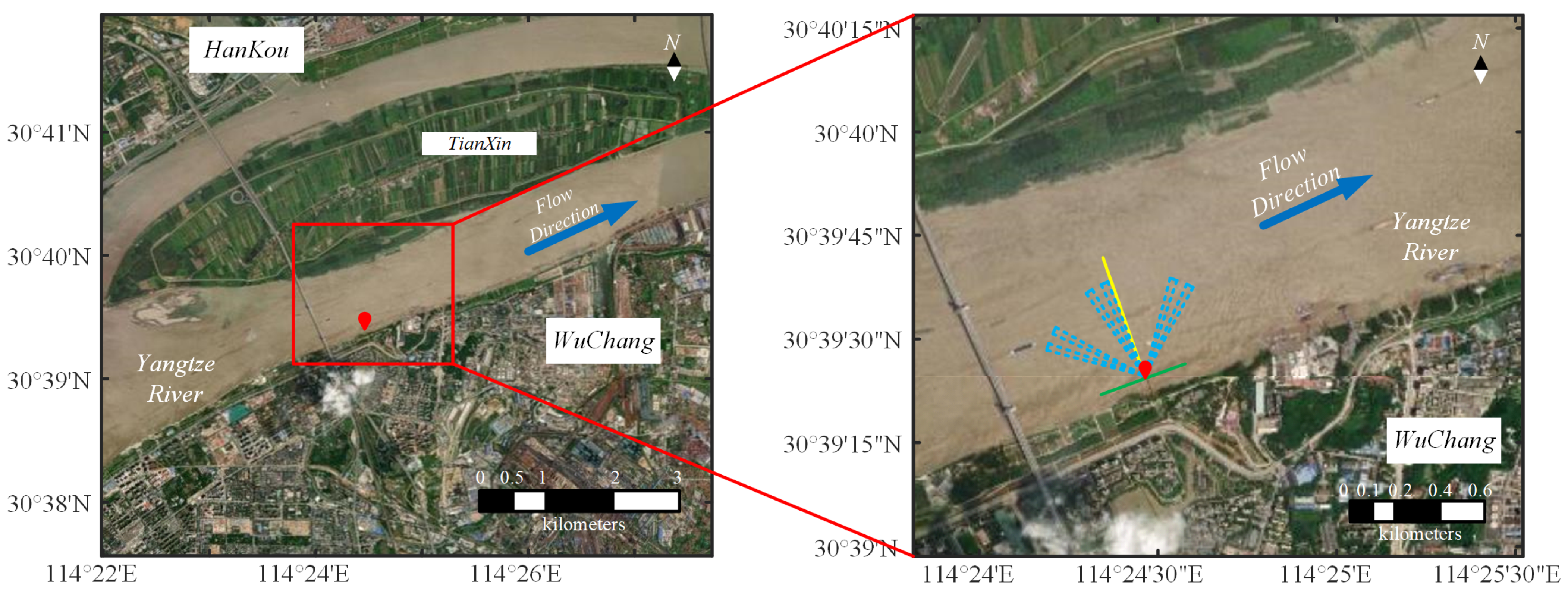
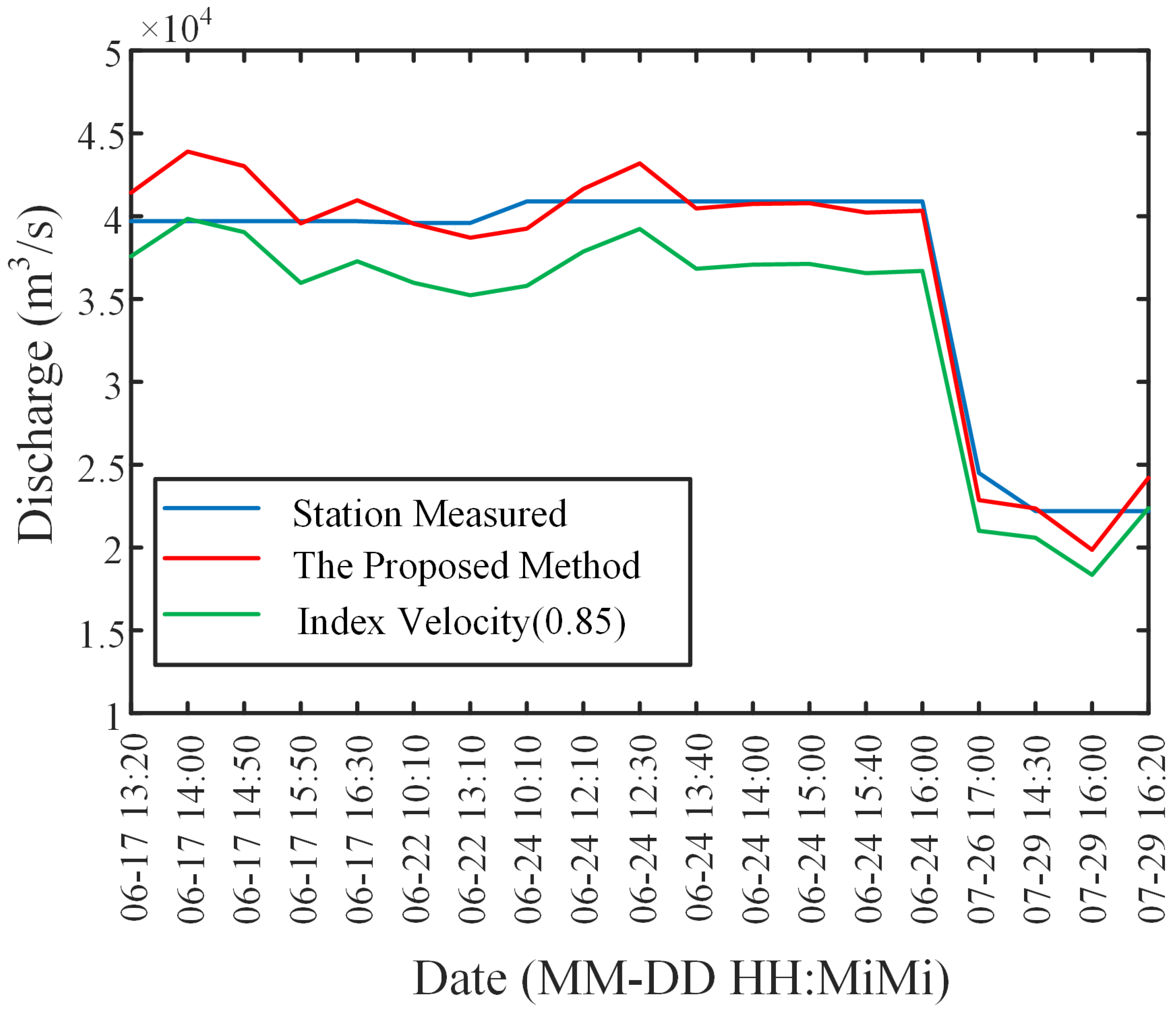
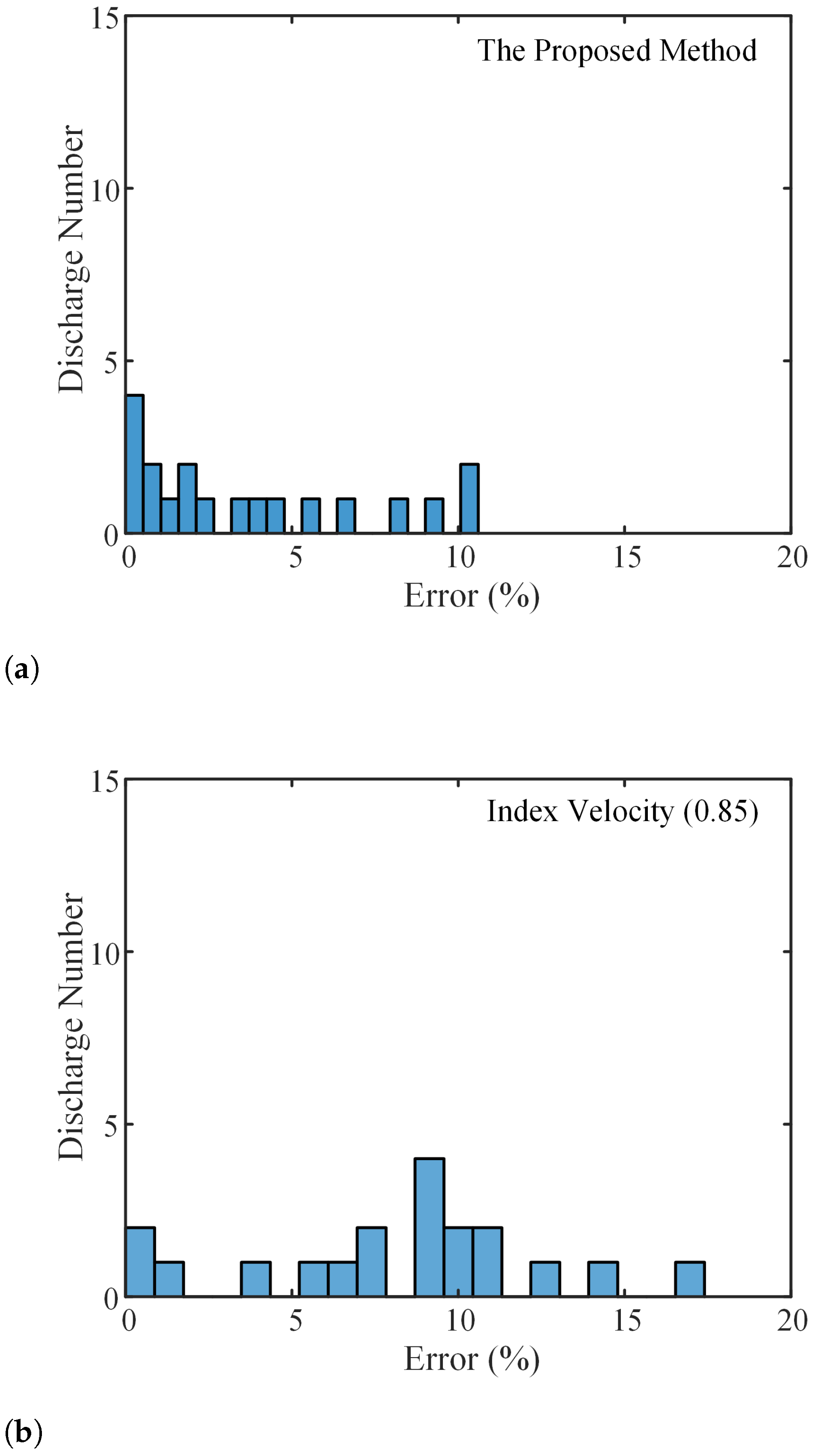
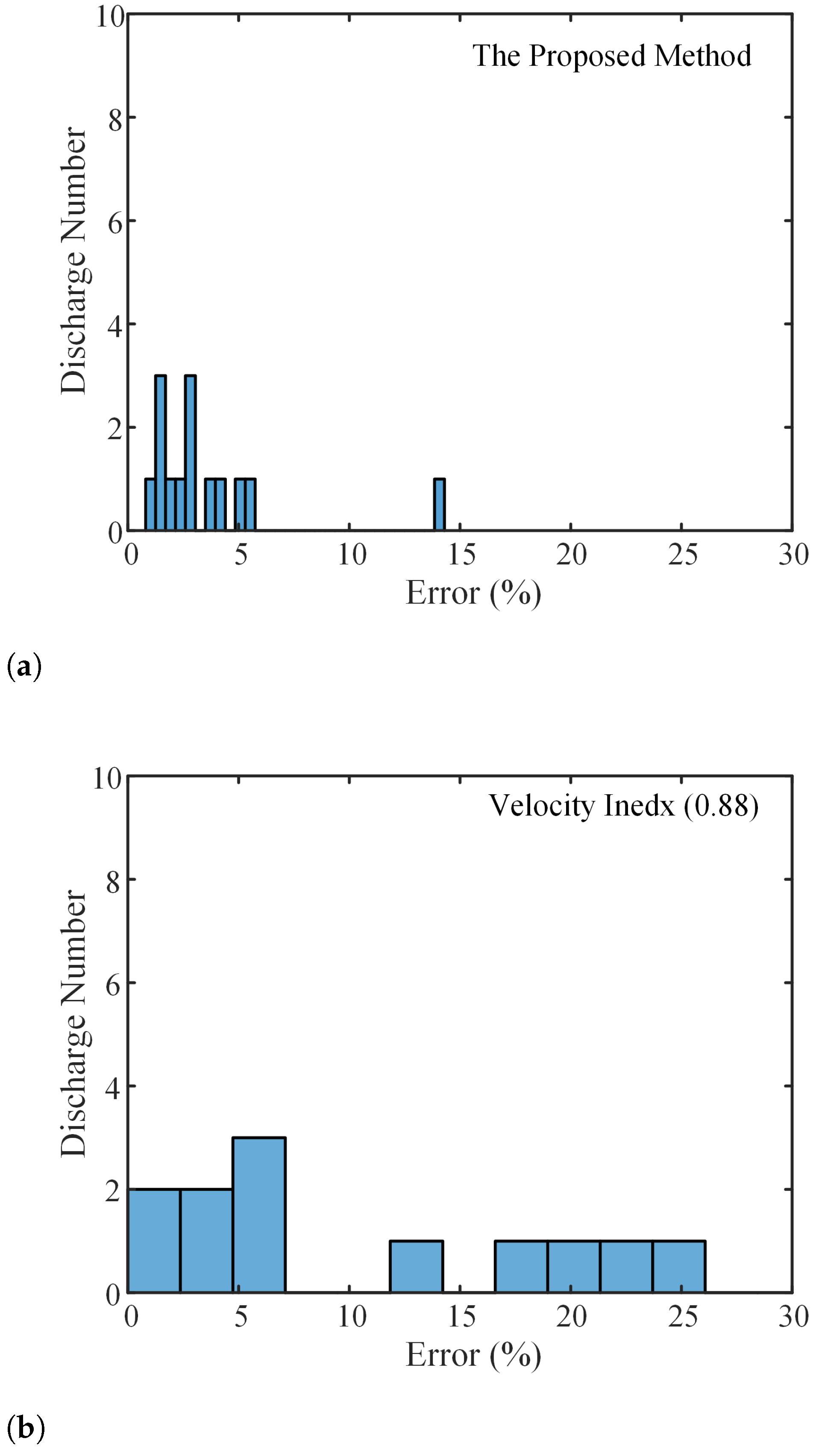
4. Field Experiment and Data Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Herschy, R. The Velocity-area Method. Flow Meas. Instrum. 1993, 4, 7–10. [Google Scholar] [CrossRef]
- Yorke, T.H.; Oberg, K.A. Measuring River Velocity and Discharge with Acoustic Doppler Profilers. Flow Meas. Instrum. 2002, 13, 191–195. [Google Scholar] [CrossRef]
- Coz, J.L.; Pierrefeu, G.; Paquier, A. Evaluation of River Discharges Monitored by a Fixed Side-Looking Doppler Profiler. Water Resour. Res. 2008, 44, 1–13. [Google Scholar]
- Costa, J.E.; Cheng, R.T.; Haeni, F.P.; Melcher, N.; Spicer, K.R.; Hayes, E.; Plant, W.; Hayes, K.; Teague, C.; Barrick, D. Use of Radars to Monitor Stream Discharge by Noncontact Methods. Water Resour. Res. 2006, 42, 1–14. [Google Scholar] [CrossRef]
- Hong, J.H.; Guo, W.D.; Wang, H.W.; Yeh, P.H. Estimating Discharge in Gravel-Bed River Using Non-Contact Ground-Penetrating and Surface-Velocity Radars. River Res. Appl. 2017, 33, 1177–1190. [Google Scholar] [CrossRef]
- Fulton, J.W.; Mason, C.A.; Eggleston, J.R.; Nicotra, M.J.; Chiu, C.L.; Henneberg, M.F.; Best, H.R.; Cederberg, J.R.; Holnbeck, S.R.; Lotspeich, R.R.; et al. Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages. Remote Sens. 2020, 12, 1296. [Google Scholar] [CrossRef]
- Yang, Y.H.; Wen, B.Y.; Wang, C.J.; Hou, Y. Real-Time and Automatic River Discharge Measurement with UHF Radar. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1851–1855. [Google Scholar] [CrossRef]
- Chen, Z.Z.; He, Z.Y.; Zhao, C.; Wang, T. Velocity Distribution Inversion Method Based on the RANS Equations Using Microwave Doppler Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5117609. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating Discharge in Rivers Using Remotely Sensed Hydraulic Information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Durand, M.; Rodriguez, E.; Alsdorf, D.E.; Trigg, M. Estimating River Depth from Remote Sensing Swath Interferometry Measurements of River Height, Slope, and Width. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 20–31. [Google Scholar] [CrossRef]
- Bogning, S.; Frappart, F.; Blarel, F.; Niño, F.; Mahé, G.; Bricquet, J.P.; Seyler, F.; Onguéné, R.; Etamé, J.; Paiz, M.C.; et al. Monitoring Water Levels and Discharges Using Radar Altimetry in an Ungauged River Basin: The Case of the Ogooué. Remote Sens. 2018, 10, 350. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.A.; Fulton, J.W.; Garambois, P.A. Satellite Remote Sensing Estimation of River Discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Bjerklie, D.M.; Fulton, J.W.; Tarpanelli, A. River Bathymetry Estimate and Discharge Assessment from Remote Sensing. Water Resour. Res. 2019, 55, 6692–6711. [Google Scholar] [CrossRef]
- Lou, H.; Zhang, Y.; Yang, S.; Wang, X.; Pan, Z.; Luo, Y. A New Method for Long-Term River Discharge Estimation of Small- and Medium-Scale Rivers by Using Multisource Remote Sensing and RSHS: Application and Validation. Remote Sens. 2022, 14, 1798. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C.; Hayes, K.; Contreras, R. Measurement of River Surface Currents Using Rough Surface Scattering. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA, 3–8 July 2005. [Google Scholar]
- Plant, W.J.; Keller, W.C.; Hayes, K. Measurement of River Surface Currents with Coherent Microwave Systems. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1242–1257. [Google Scholar] [CrossRef]
- Mutschler, M.A.; Scharf, P.A.; Rippl, P.; Gessler, T.; Walter, T.; Waldschmidt, C. River Surface Analysis and Characterization Using FMCW Radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2493–2502. [Google Scholar] [CrossRef]
- Costa, J.E.; Spicer, K.R.; Cheng, R.T.; Haeni, F.P.; Melcher, N.B.; Thurman, E.M.; Plant, W.J.; Keller, W.C. Measuring Stream Discharge by Non-Contact Methods: A Proof-of-Concept Experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Alimenti, F.; Bonafoni, S.; Gallo, E.; Palazzi, V.; Gatti, R.V.; Mezzanotte, P.; Roselli, L.; Zito, D.; Barbetta, S.; Corradini, C.; et al. Non-contact Measurement of River Surface Velocity and Discharge Estimation with a Low-Cost Doppler Radar Sensor. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5195–5207. [Google Scholar] [CrossRef]
- Fulton, J.W.; Anderson, I.E.; Chiu, C.L.; Sommer, W.; Adams, J.D.; Moramarco, T.; Bjerklie, D.M.; Fulford, J.M.; Sloan, J.L.; Best, H.R.; et al. QCam: sUAS-based Doppler Radar for Measuring River Discharge. Remote Sens. 2020, 12, 3317. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kinzel, P.J.; Nelson, J.M. Remote Measurement of River Discharge Using Thermal Particle Image Velocimetry (PIV) and Various Sources of Bathymetric Information. J. Hydrol. 2017, 554, 490–506. [Google Scholar] [CrossRef]
- Dolcetti, G.; Hortobágyi, B.; Perks, M.; Tait, S.J.; Dervilis, N. Using Noncontact Measurement of Water Surface Dynamics to Estimate River Discharge. Water Resour. Res. 2022, 58, e2022WR032829. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Dingman, S.L.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the Potential for Measuring River Discharge from Space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Simeonov, J.A.; Holland, K.T.; Anderson, S.P. River Discharge and Bathymetry Estimation from Inversion of Surface Currents and Water Surface Elevation Observations. J. Atmos. Ocean. Technol. 2019, 36, 69–86. [Google Scholar] [CrossRef]
- Chen, C.L. Unified Theory on Power Laws for Flow Resistance. J. Hydraul. Eng. 1991, 117, 371–389. [Google Scholar] [CrossRef]
- Absi, R. An Ordinary Differential Equation for Velocity Distribution and Dip-Phenomenon in Open Channel Flows. Int. J. Fluid Mech. Res. 2011, 39, 82–89. [Google Scholar] [CrossRef]
- Snehasis, K.; Koeli, G. An Analytical Model for Velocity Distribution and Dip-Phenomenon in Uniform Open Channel Flows. Int. J. Fluid Mech. Res. 2012, 39, 381–395. [Google Scholar]
- Sarma, K.V.N.; Lakshminarayana, P.; Rao, N.S.L. Velocity Distribution in Smooth Rectangular Open Channels. J. Hydraul. Eng. 1983, 109, 270–289. [Google Scholar] [CrossRef]
- Sun, D.P.; Wang, E.P.; Dong, Z.H.; Li, G.Q. Discussion and Application of Velocity Profile in Open Channel with Rectangular Cross-Section. J. Hydrodyn. 2004, 19, 144–151. [Google Scholar]
- Chiu, C.L.; Chiou, J.D. Structure of 3-D Flow in Rectangular Open Channels. J. Hydraul. Eng. 1986, 112, 1050–1067. [Google Scholar] [CrossRef]
- Lee, M.C.; Lai, C.J.; Leu, J.M.; Plant, W.J.; Keller, W.C.; Hayes, K. Non-contact Flood Discharge Measurements Using an X-Band Pulse Radar (I) Theory. Flow Meas. Instrum. 2002, 13, 256–270. [Google Scholar] [CrossRef]
- Lee, M.C.; Leu, J.M.; Lai, C.J.; Plant, W.J.; Keller, W.C.; Hayes, K. Non-Contact Flood Discharge Measurements Using an X-Band Pulse Radar (II) Improvements and Applications. Flow Meas. Instrum. 2002, 13, 271–276. [Google Scholar] [CrossRef]
- Li, Z.L.; Wang, C.J.; Li, Y.H. Study on the Measurement of the Yangtze River Flow Algorithm Based on UHF Radar. J. Wuhan Univ. (Nat. Sci. Ed.) 2013, 59, 242–244. [Google Scholar]
- Jin, T.; Liao, Q. Application of Large Scale PIV in River Surface Turbulence Measurements and Water Depth Estimation. Flow Meas. Instrum. 2019, 67, 142–152. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C. Evidence of Bragg Scattering in Microwave Doppler Spectra of Sea Return. J. Geophys. Res. Ocean. 1990, 95, 16299–16310. [Google Scholar] [CrossRef]
- Trizna, D. A Model for Doppler Peak Spectral Shift for Low Grazing Angle Sea Scatter. IEEE J. Ocean. Eng. 1985, 10, 368–375. [Google Scholar] [CrossRef]
- Polnikov, V.G. Semi-Phenomenological Model for a Wind-Drift Current. Bound.-Layer Meteorol. 2019, 172, 417–433. [Google Scholar] [CrossRef]
- Yang, Y.H.; Wen, B.C.; Wang, C.J.; Hou, Y. Two-dimensional Velocity Distribution Modeling for Natural River Based on UHF Radar Surface Current. J. Hydrol. 2019, 577, 123930. [Google Scholar] [CrossRef]
- Lang, S.; Ladson, T.; Anderson, B. A Review of Empirical Equations for Estimating Stream Roughness and Their Application to Four Streams in Victoria. Aust. J. Water Resour. 2004, 8, 69–82. [Google Scholar] [CrossRef]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Floodplains; US Government Printing Office: Washington, DC, USA, 1989.
- Powell, D.M. Flow Resistance in Gravel-Bed Rivers: Progress in Research. Earth-Sci. Rev. 2014, 136, 301–338. [Google Scholar] [CrossRef]
- Fujita, M.M.I.; Hauet, A. Large-scale Particle Image Velocimetry for Measurements in Riverine Environments. J. Hydraul. Eng. 2008, 44, 1–14. [Google Scholar]
- Graf, W.H.; Altinakar, M.S. Fluvial Hydraulics—Flow and Transport Processes in Channels of Simple Geometry; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Coleman, N. Velocity profiles with Suspended Sediment. J. Hydraul. Res. 1981, 19, 211–229. [Google Scholar] [CrossRef]
- Guo, J.K. Modified Log-wake-law for Smooth Rectangular Open Channel Flow. J. Hydraul. Res. 2014, 52, 121–128. [Google Scholar] [CrossRef]
- Camenen, B.; Bayram, A.; Larson, M. Equivalent Roughness Height for Plane Bed Under Steady Flow. J. Hydraul. Eng. 2006, 132, 1146–1158. [Google Scholar] [CrossRef]
- Camenen, B.; Larson, M.; Bayram, A. Equivalent Roughness Height for Plane Bed Under Oscillatory Flow. Estuar. Coast. Shelf Sci. 2009, 81, 409–422. [Google Scholar] [CrossRef]
- Sarma, K.V.N.; Prasad, B.V.R.; Sarma, A.K. Detailed Study of Binary Law for Open Channels. J. Hydraul. Eng. 2000, 126, 210–214. [Google Scholar] [CrossRef]
- Cheng, R.T.; Gartner, J.W.; Mason, R.R.; Costa, J.E.; Plant, W.J.; Spicer, K.R.; Haeni, F.P.; Melcher, N.B.; Keller, W.C.; Hayes, K. Evaluating a Radar-Based, Non-Contact Streamflow Measurement System in the San Joaquin River at Vernalis, California; USGS Open-File Report; USGS: Menlo Park, CA, USA, 2004.
- Wang, X.K.; Wang, Z.Y.; Li, M.Y. Velocity Profile of Sediment Suspensions and Comparison of Log-Law and Wake-Law. J. Hydraul. Res. 2001, 39, 211–217. [Google Scholar] [CrossRef]
- Yang, S.Q.; Tan, S.K.; Lim, S.Y. Velocity Distribution and Dip-Phenomenon in Smooth Uniform Open Channel Flows. J. Hydraul. Eng. 2004, 130, 1179–1186. [Google Scholar] [CrossRef]
- Chen, Z.Z.; Wang, Z.H.; Chen, X.; Zhao, C.; Xie, F.; He, C. S-Band Doppler Wave Radar System. Remote Sens. 2017, 9, 1302. [Google Scholar] [CrossRef]
- Gao, J. On the Formation of Shoal in River. J. Hydraul. Eng. 1999, 6, 66–70. [Google Scholar]


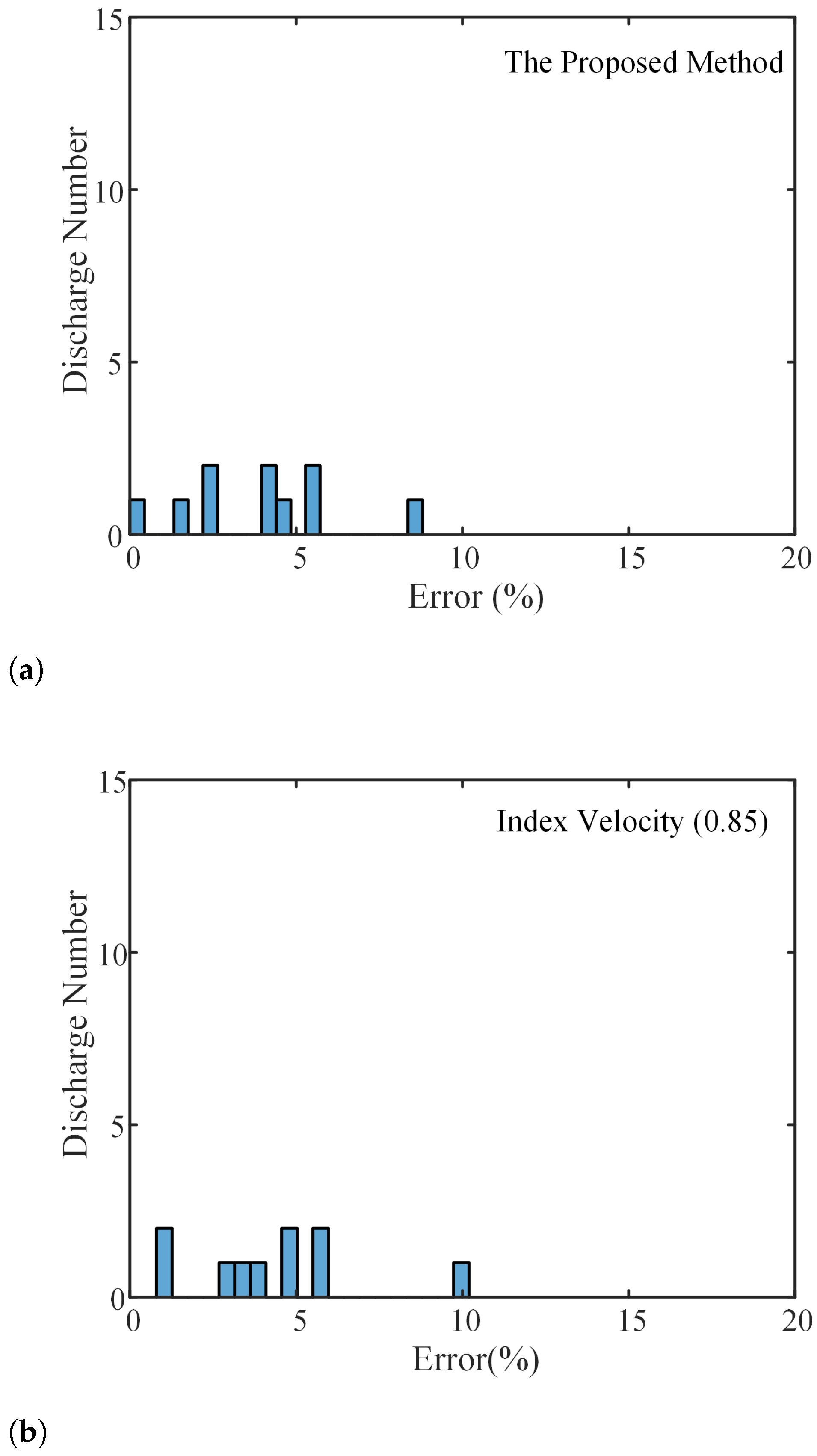

| Depth | Method | MPE (%) | RMSE (%) | MaPE (%) |
|---|---|---|---|---|
| 10 m | The proposed | 3.91 | 4.53 | 8.7 |
| velocity index (0.85) | 4.32 | 4.99 | 10.1 | |
| 20–25 m | The proposed | 3.82 | 5.19 | 10.6 |
| velocity index (0.85) | 8.2 | 9.27 | 17.3 |
| Method | MPE (%) | RMSE (%) | MaPE (%) |
|---|---|---|---|
| The proposed | 3.6 | 4.81 | 14.03 |
| Velocity index (0.88) | 16.73 | 24.91 | 70.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wang, T.; Zhao, C.; He, Z. River Discharge Inversion Algorithm Based on the Surface Velocity of Microwave Doppler Radar. Remote Sens. 2023, 15, 4727. https://doi.org/10.3390/rs15194727
Chen Z, Wang T, Zhao C, He Z. River Discharge Inversion Algorithm Based on the Surface Velocity of Microwave Doppler Radar. Remote Sensing. 2023; 15(19):4727. https://doi.org/10.3390/rs15194727
Chicago/Turabian StyleChen, Zezong, Tao Wang, Chen Zhao, and Zheyuan He. 2023. "River Discharge Inversion Algorithm Based on the Surface Velocity of Microwave Doppler Radar" Remote Sensing 15, no. 19: 4727. https://doi.org/10.3390/rs15194727
APA StyleChen, Z., Wang, T., Zhao, C., & He, Z. (2023). River Discharge Inversion Algorithm Based on the Surface Velocity of Microwave Doppler Radar. Remote Sensing, 15(19), 4727. https://doi.org/10.3390/rs15194727






