Improving Reliability in Reconstruction of Landsat EVI Seasonal Trajectory over Cloud-Prone, Fragmented, and Mosaic Agricultural Landscapes
Abstract
:1. Introduction
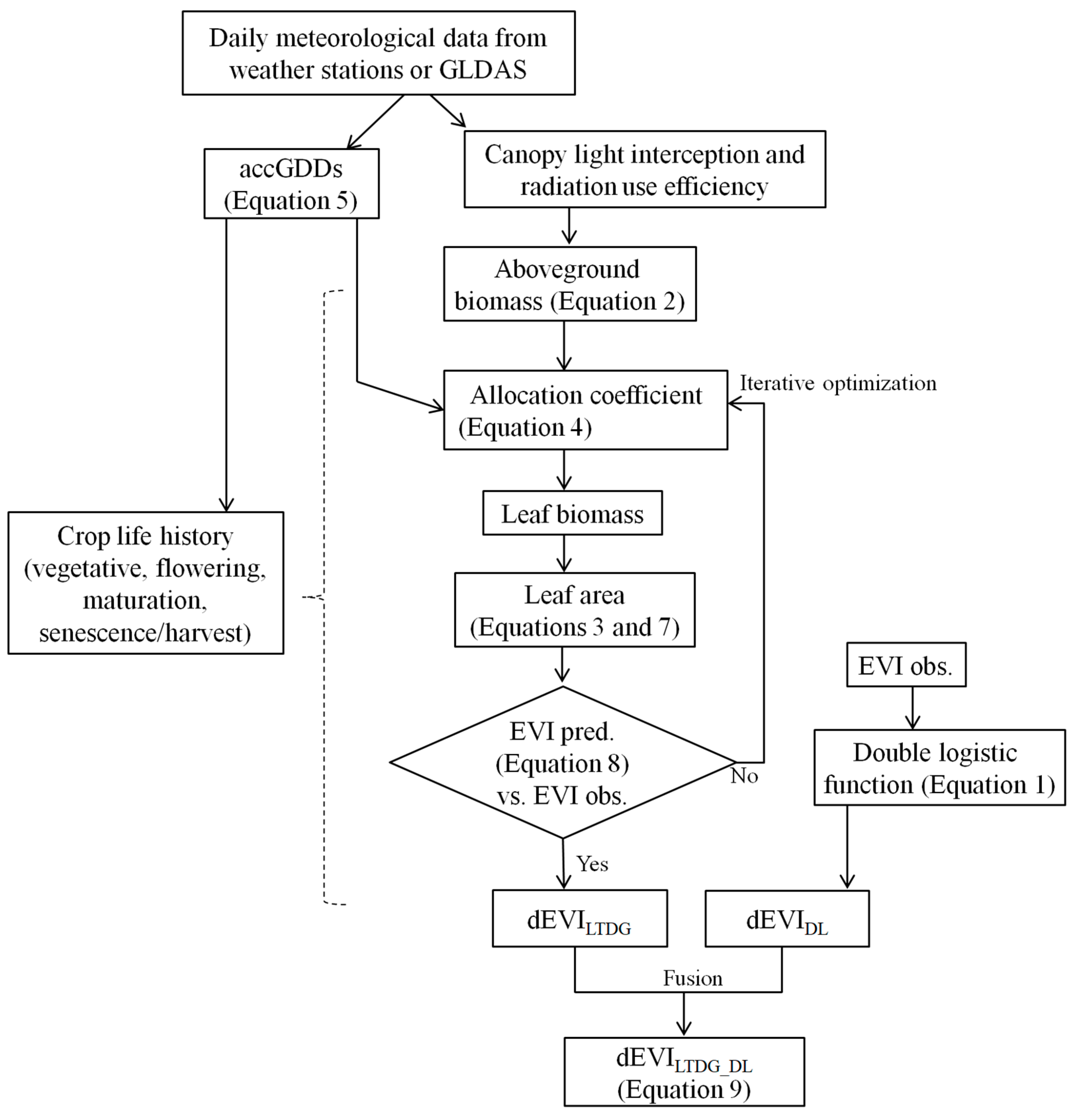
2. Development of the LTDG_DL Algorithm
2.1. Algorithm Principles
2.1.1. The DL Function
2.1.2. The LTDG Model
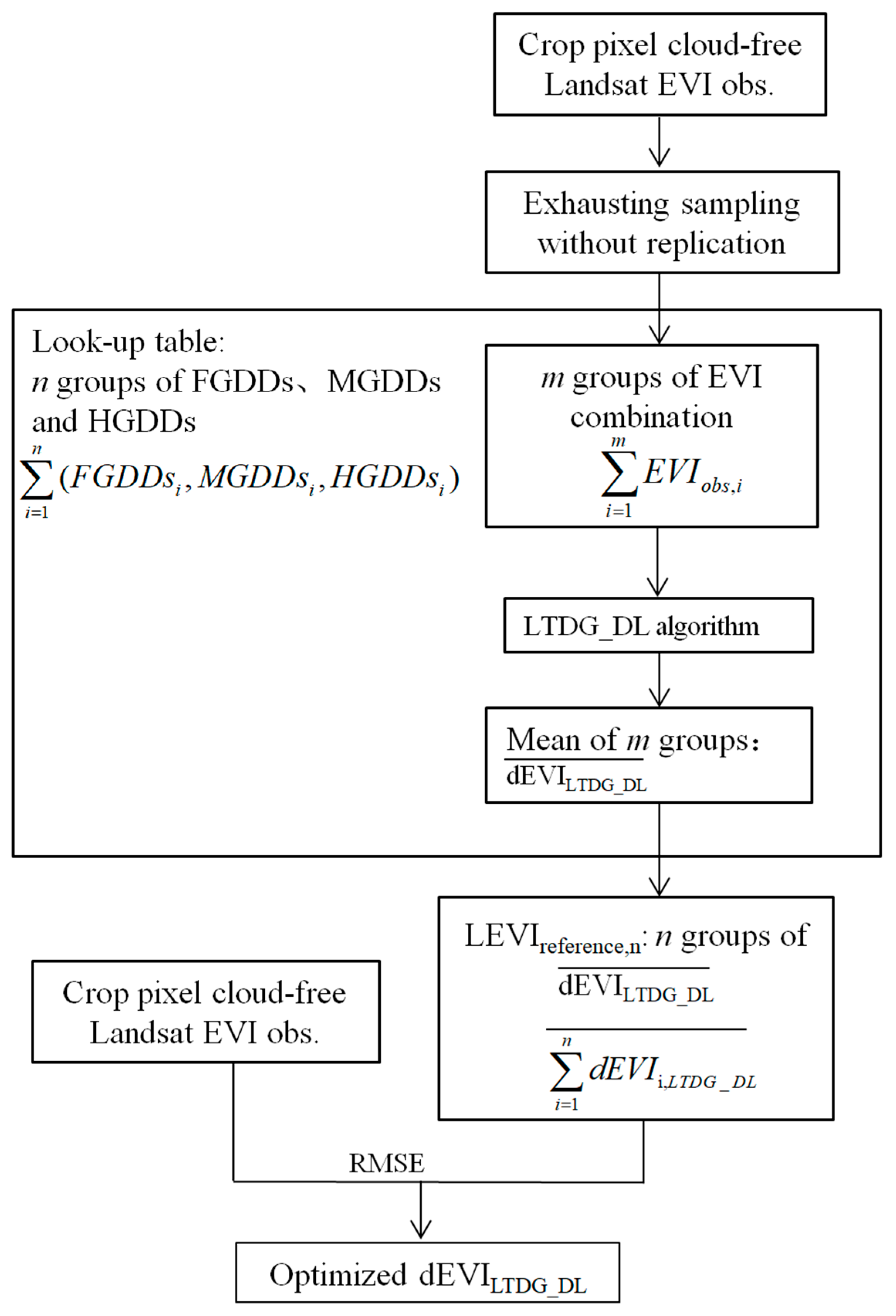
2.2. Bivariable-Constrained Optimization Solutions
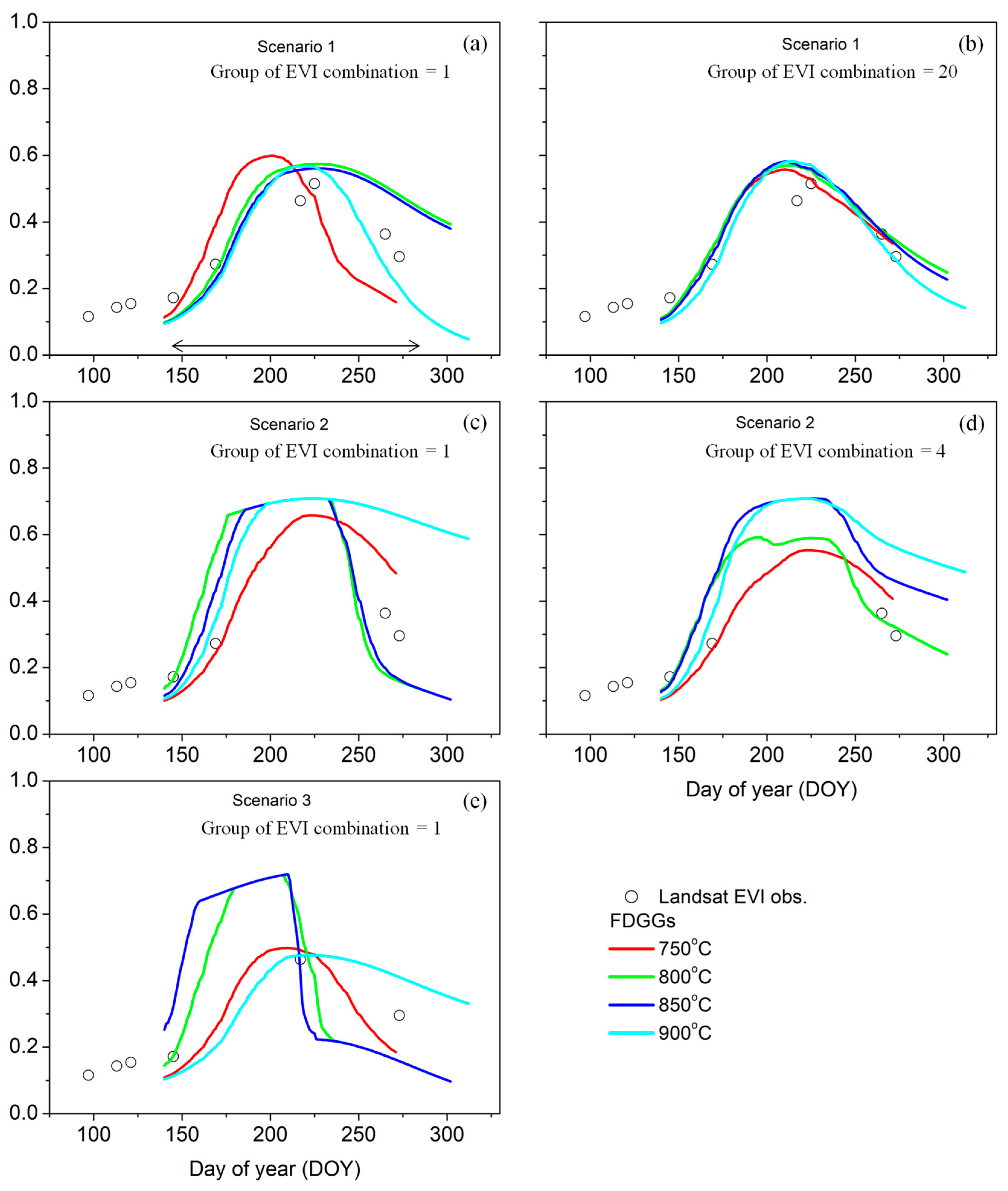
2.2.1. Constrained Configurations of DOYini
2.2.2. Constrained Configurations of the FGDDs
3. Algorithm Validations
3.1. Introduction of the Three Experimental Fields and Parameter Settings of the LTDG_DL
3.2. Introduction of Agricultural Landscapes in Haean Basin and Parameter Settings of LTDG_DL
3.3. Introduction of Regional Agricultural Landscapes in Shandong Province and Parameter Settings of LTDG_DL
4. Results
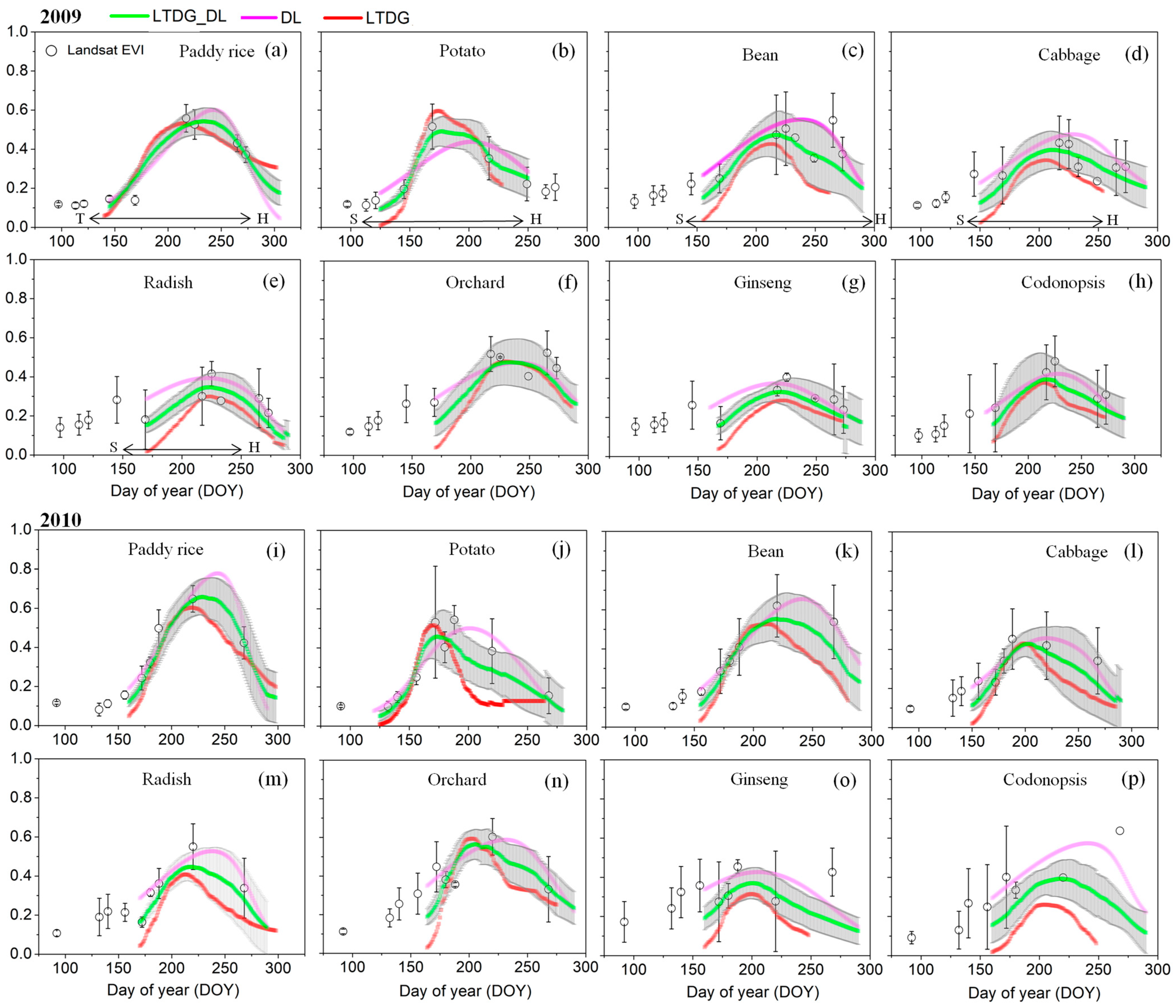
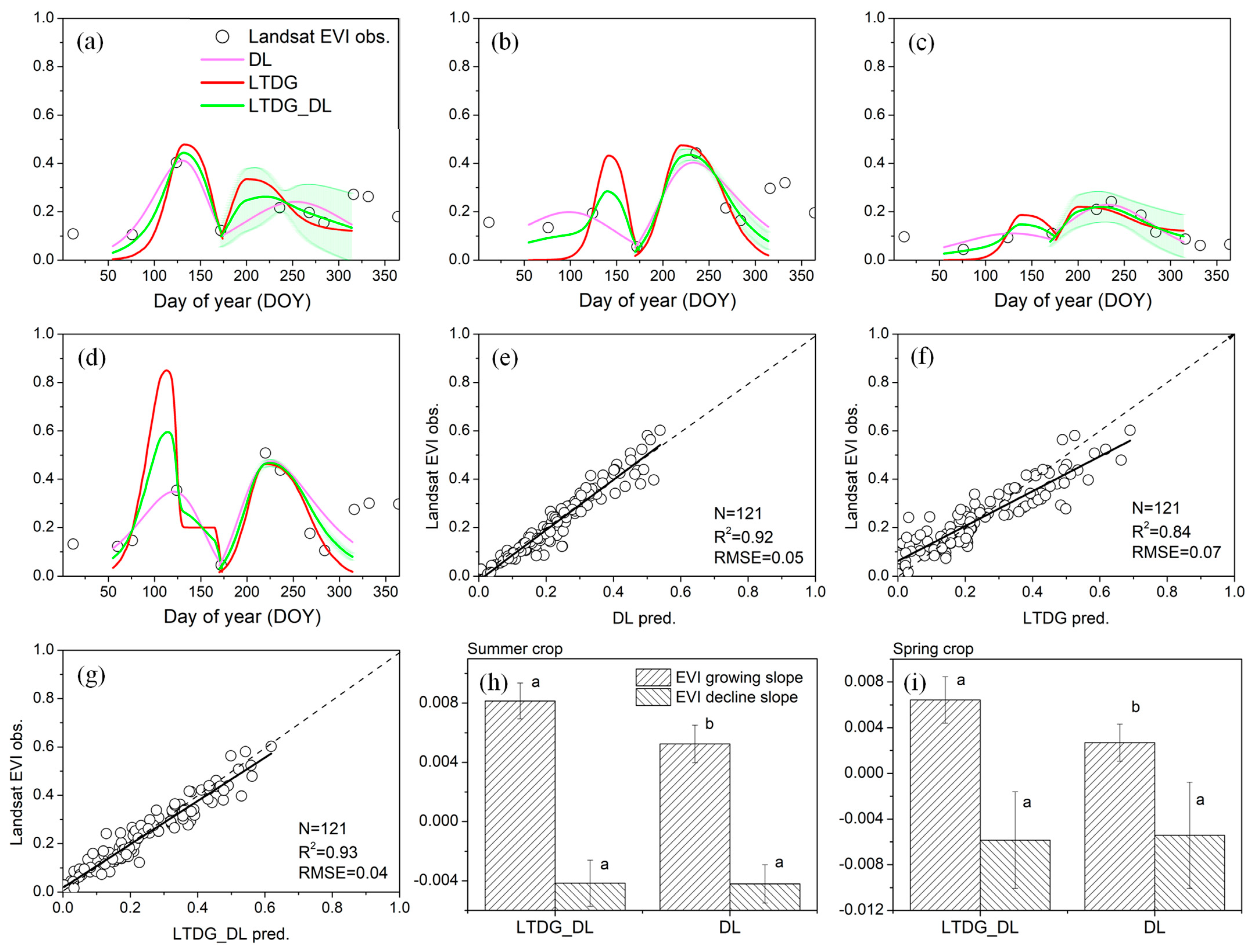
4.1. Performance of the LTDG_DL Algorithm in Experimental Fields
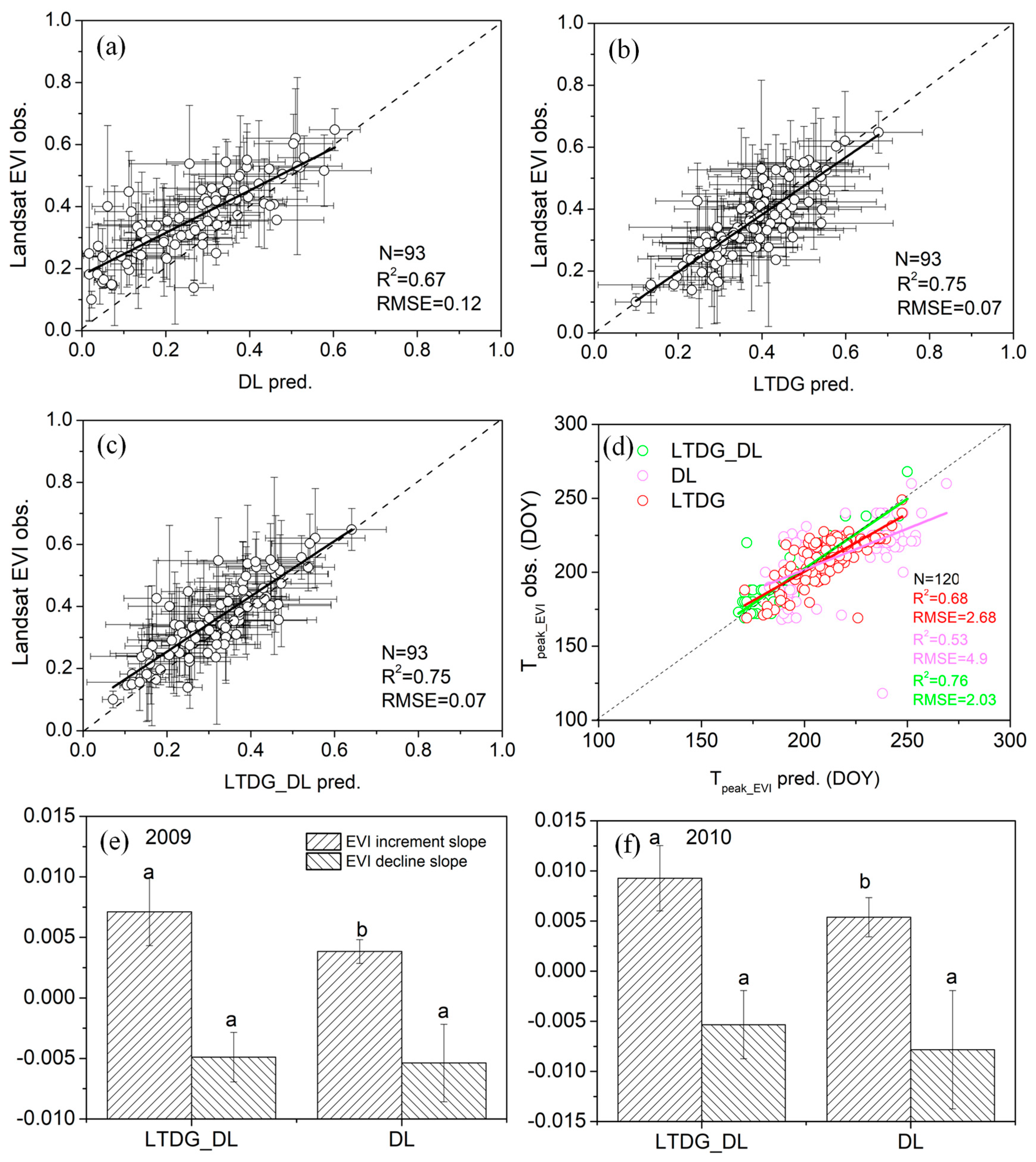
4.2. Performance of the LTDG_DL Algorithm in Agricultural Landscapes of Haean Basin
4.3. Performance of the LTDG_DL Algorithm in Regional Agricultural Landscapes of Shandong Province
5. Discussion
5.1. Superiority of the LTDG_DL Algorithm
5.2. Limitations of the LTDG_DL Algorithm
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, M.-L.; Shiu, Y.-S.; Chu, T.-H.; Huang, C.-H. Mapping paddy rice agriculture in a highly fragmented area using a geographic information system object-based post classification process. J. Appl. Remote Sens. 2012, 6, 063526. [Google Scholar] [CrossRef]
- Statistics Korea. 2017. Available online: http://kostat.go.kr/portal/eng/index.action (accessed on 25 January 2022).
- Lindner, S.; Otieno, D.; Lee, B.; Xue, W.; Arnhold, S.; Kwon, H.; Huwe, B.; Tenhunen, J. Carbon dioxide exchange and its regulation in the main agro-ecosystems of Haean catchment in South Korea. Agric. Ecosyst. Environ. 2015, 199, 132–145. [Google Scholar] [CrossRef]
- Lowder, S.K.; Skoet, J.; Raney, T. The number, size, and distribution of farms, smallholder farms, and family farms worldwide. World Dev. 2016, 87, 16–29. [Google Scholar] [CrossRef]
- Sun, L.; Gao, F.; Xie, D.; Anderson, M.; Chen, R.; Yang, Y.; Yang, Y.; Chen, Z. Reconstructing daily 30 m NDVI over complex agricultural landscapes using a crop reference curve approach. Remote Sens. Environ. 2021, 253, 112156. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D. Conterminous United States crop field size quantification from multi-temporal Landsat data. Remote Sens. Environ. 2016, 172, 67–86. [Google Scholar] [CrossRef]
- Seo, B.; Bogner, C.; Poppenborg, P.; Martin, E.; Hoffmeister, M.; Jun, M.; Koellner, T.; Reineking, B.; Shope, C.L.; Tenhunen, J. Deriving a per-field land use and land cover map in an agricultural mosaic catchment. Earth Syst. Sci. Data 2014, 6, 339–352. [Google Scholar] [CrossRef]
- You, N.; Dong, J.; Huang, J.; Du, G.; Zhang, G.; He, Y.; Yang, T.; Di, Y.; Xiao, X. The 10-m crop type maps in Northeast China during 2017–2019. Sci. Data 2021, 8, 41. [Google Scholar] [CrossRef]
- Kwon, H.; Kim, J.; Hong, J.; Lim, J.-H. Influence of the Asian monsoon on net ecosystem carbon exchange in two major ecosystems in Korea. Biogeosciences 2010, 7, 1493–1504. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Raza, M.; Kwon, K.D. Land use and land cover changes in the Haean Basin of Korea: Impacts on soil erosion. Episodes 2019, 42, 17–32. [Google Scholar] [CrossRef]
- Loveland, T.R.; Irons, J.R. Landsat 8: The plans, the reality, and the legacy. Remote Sens. Environ. 2016, 185, 1–6. [Google Scholar] [CrossRef]
- Lenney, M.P.; Woodcock, C.E.; Collins, J.B.; Hamdi, H. The status of agricultural lands in Egypt: The use of multitemporal NDVI features derived from landsat TM. Remote Sens. Environ. 1996, 56, 8–20. [Google Scholar] [CrossRef]
- Graesser, J.; Ramankutty, N. Detection of cropland field parcels from Landsat imagery. Remote Sens. Environ. 2017, 201, 165–180. [Google Scholar] [CrossRef]
- Song, X.-P.; Potapov, P.V.; Krylov, A.; King, L.; Di Bella, C.M.; Hudson, A.; Khan, A.; Adusei, B.; Stehman, S.V.; Hansen, M.C. National-scale soybean mapping and area estimation in the United States using medium resolution satellite imagery and field survey. Remote Sens. Environ. 2017, 190, 383–395. [Google Scholar] [CrossRef]
- Ju, J.; Roy, D.P. The availability of cloud-free Landsat ETM+ data over the conterminous United States and globally. Remote Sens. Environ. 2008, 112, 1196–1211. [Google Scholar] [CrossRef]
- Kovalskyy, V.; Roy, D. The global availability of Landsat 5 TM and Landsat 7 ETM+ land surface observations and implications for global 30m Landsat data product generation. Remote Sens. Environ. 2013, 130, 280–293. [Google Scholar] [CrossRef]
- Egorov, A.V.; Roy, D.P.; Zhang, H.K.; Li, Z.; Yan, L.; Huang, H. Landsat 4, 5 and 7 (1982 to 2017) analysis ready data (ARD) observation coverage over the conterminous United States and implications for terrestrial monitoring. Remote Sens. 2019, 11, 447. [Google Scholar] [CrossRef]
- Chen, B.; Huang, B.; Chen, L.; Xu, B. Spatially and temporally weighted regression: A novel method to produce continuous cloud-free Landsat imagery. IEEE Trans. Geosci. Remote Sens. 2017, 55, 27–37. [Google Scholar] [CrossRef]
- Moreno-Martínez, Á; Izquierdo-Verdiguier, E.; Maneta, M.P.; Camps-Valls, G.; Robinson, N.; Muñoz-Marí, J.; Sedano, F.; Clinton, N.; Running, S.W. Multispectral high resolution sensor fusion for smoothing and gap-filling in the cloud. Remote Sens. Environ. 2020, 247, 111901. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.; Jing, Y.; Yin, H.; Li, X.; Guan, X. High-quality vegetation index product generation: A review of NDVI time series reconstruction techniques. Int. J. Appl. Earth Obs. Geoinform. 2021, 105, 102640. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Wu, C.; Gonsamo, A.; Gough, C.M.; Chen, J.M.; Xu, S. Modeling growing season phenology in North American forests using seasonal mean vegetation indices from MODIS. Remote Sens. Environ. 2014, 147, 79–88. [Google Scholar] [CrossRef]
- Xue, W.; Jeong, S.; Ko, J.; Yeom, J.-M. Contribution of biophysical factors to regional variations of evapotranspiration and seasonal cooling effects in paddy rice in South Korea. Remote Sens. 2021, 13, 3992. [Google Scholar] [CrossRef]
- Melaas, E.K.; Friedl, M.A.; Zhu, Z. Detecting interannual variation in deciduous broadleaf forest phenology using Landsat TM/ETM+ data. Remote Sens. Environ. 2013, 132, 176–185. [Google Scholar] [CrossRef]
- Roy, D.; Yan, L. Robust Landsat-based crop time series modelling. Remote Sens. Environ. 2020, 238, 110810. [Google Scholar] [CrossRef]
- Pouliot, D.; Latifovic, R. Reconstruction of Landsat time series in the presence of irregular and sparse observations: Development and assessment in north-eastern Alberta, Canada. Remote Sens. Environ. 2018, 204, 979–996. [Google Scholar] [CrossRef]
- Liu, R.; Shang, R.; Liu, Y.; Lu, X. Global evaluation of gap-filling approaches for seasonal NDVI with considering vegetation growth trajectory, protection of key point, noise resistance and curve stability. Remote Sens. Environ. 2017, 189, 164–179. [Google Scholar] [CrossRef]
- Cao, R.; Chen, Y.; Shen, M.; Chen, J.; Zhou, J.; Wang, C.; Yang, W. A simple method to improve the quality of NDVI time-series data by integrating spatiotemporal information with the Savitzky-Golay filter. Remote Sens. Environ. 2018, 217, 244–257. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, R.Y.; Chen, J.; Zhu, X.L.; Zhou, J.; Wang, G.P.; Shen, M.G.; Chen, X.H.; Yang, W. A new cross-fusion method to automatically determine the optimal input image pairs for NDVI spatiotemporal data fusion. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5179–5194. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, Y.; Tong, X.; Atkinson, P.M. Virtual image pair-based spatio-temporal fusion. Remote Sens. Environ. 2020, 249, 112009. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, R.; Chen, J.; Liu, L.; Matsushita, B. A practical approach to reconstruct high-quality Landsat NDVI time-series data by gap filling and the Savitzky–Golay filter. ISPRS J. Photogramm. Remote Sens. 2021, 180, 174–190. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Luo, Y.; Guan, K.; Peng, J. STAIR: A generic and fully-automated method to fuse multiple sources of optical satellite data to generate a high-resolution, daily and cloud-/gap-free surface reflectance product. Remote Sens. Environ. 2018, 214, 87–99. [Google Scholar] [CrossRef]
- Liu, M.; Yang, W.; Zhu, X.L.; Chen, J.; Chen, X.H.; Yang, L.Q.; Helmer, E.H. An Improved Flexible Spatiotemporal DAta Fusion (IFSDAF) method for producing high spatiotemporal resolution normalized difference vegetation index time series. Remote Sens. Environ. 2019, 227, 74–89. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Bouman, B.A.M.; van Keulen, H.; van Laar, H.H.; Rabbinge, R. The ‘School of de Wit’ crop growth simulation models: A pedigree and historical overview. Agric. Syst. 1996, 52, 171–198. [Google Scholar] [CrossRef]
- Xue, W.; Ko, J. Radiation estimation and crop growth trajectory reconstruction by novel algorithms improve MOD16 evapotranspiration predictability for global multi-site paddy rice ecosystems. J. Hydrol. 2022, 612, 128204. [Google Scholar] [CrossRef]
- Connor, D.J.; Loomis, R.S.; Cassman, K.G. Development. In Crop Ecology: Productivity and Management in Agricultural Systems; Cambridge University Press: Cambridge, UK, 2011; pp. 96–122. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global Data sets of vegetation leaf area index (LAI)3g and fraction of photosynthetically active radiation (FPAR)3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G. Integration of MODIS LAI and vegetation index products with the CSM–CERES–Maize model for corn yield estimation. Int. J. Remote Sens. 2011, 32, 1039–1065. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Philos. Trans. R. Soc. Lond. Ser. B 1977, 281, 277–294. [Google Scholar]
- Russell, G.; Jarvis, P.; Monteith, J. Absorption of radiation by canopies and stand growth. In Plant Canopies: Their Growth, Form and Function; Cambridge University Press: Cambridge, UK, 1989; pp. 21–39. [Google Scholar] [CrossRef]
- Conte, S.D.; de Boor, C. Elementary Numerical Analysis: An Algorithmic Approach; McGraw-Hill: New York, NY, USA, 1965; p. 32. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992; p. 283. [Google Scholar]
- Yoshida, S. Rice Crop Science; The International Rice Research Institute: Manila, Philippines, 1981; p. 279. [Google Scholar]
- Guo, C.; Tang, Y.; Lu, J.; Zhu, Y.; Cao, W.; Cheng, T.; Zhang, L.; Tian, Y. Predicting wheat productivity: Integrating time series of vegetation indices into crop modeling via sequential assimilation. Agric. For. Meteorol. 2019, 272–273, 69–80. [Google Scholar] [CrossRef]
- Swain, S.; Wardlow, B.D.; Narumalani, S.; Rundquist, D.C.; Hayes, M.J. Relationships between vegetation indices and root zone soil moisture under maize and soybean canopies in the US Corn Belt: A comparative study using a close-range sensing approach. Int. J. Remote Sens. 2013, 34, 2814–2828. [Google Scholar] [CrossRef]
- Jeong, S.; Ko, J.; Choi, J.; Xue, W.; Yeom, J.-M. Application of an unmanned aerial system for monitoring paddy productivity using the GRAMI-rice model. Int. J. Remote Sens. 2018, 39, 2441–2462. [Google Scholar] [CrossRef]
- Goslee, S. Analyzing remote sensing data in R: The landsat package. J. Stat. Softw. 2011, 43, 4. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Franch, B.; Masek, J.G. Evaluation of the Landsat-5 TM and Landsat-7 ETM+ surface reflectance products. Remote Sens. Environ. 2015, 169, 390–403. [Google Scholar] [CrossRef]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef]
- Chen, B.; Huang, B.; Xu, B. Comparison of spatiotemporal fusion models: A review. Remote Sens. 2015, 7, 1798–1835. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, L.; Yao, F. Improved maize cultivated area estimation over a large scale combining MODIS–EVI time series data and crop phenological information. ISPRS J. Photogramm. Remote Sens. 2014, 94, 102–113. [Google Scholar] [CrossRef]
- Sakamoto, T.; Wardlow, B.D.; Gitelson, A.A.; Verma, S.B.; Suyker, A.E.; Arkebauer, T.J. A Two-Step Filtering approach for detecting maize and soybean phenology with time-series MODIS data. Remote Sens. Environ. 2010, 114, 2146–2159. [Google Scholar] [CrossRef]
- Boschetti, M.; Busetto, L.; Manfron, G.; Laborte, A.; Asilo, S.; Pazhanivelan, S.; Nelson, A. PhenoRice: A method for automatic extraction of spatio-temporal information on rice crops using satellite data time series. Remote Sens. Environ. 2017, 194, 347–365. [Google Scholar] [CrossRef]
- Huang, X.; Liu, J.; Zhu, W.; Atzberger, C.; Liu, Q. The optimal threshold and vegetation index time series for retrieving crop phenology based on a modified dynamic threshold method. Remote Sens. 2019, 11, 2725. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Chen, X.; Gao, Y.; Xie, S.; Mi, J. GLC_FCS30: Global land-cover product with fine classification system at 30 m using time-series Landsat imagery. Earth Syst. Sci. Data 2021, 13, 2753–2776. [Google Scholar] [CrossRef]
- Ramirez-Villegas, J.; Koehler, A.-K.; Challinor, A.J. Assessing uncertainty and complexity in regional-scale crop model simulations. Eur. J. Agron. 2017, 88, 84–95. [Google Scholar] [CrossRef]
- Melandri, G.; Thorp, K.R.; Broeckling, C.; Thompson, A.L.; Hinze, L.; Pauli, D. Assessing drought and heat stress-induced changes in the cotton leaf metabolome and their relationship with hyperspectral reflectance. Front. Plant Sci. 2021, 12, 751868. [Google Scholar] [CrossRef]
- Xue, W.; Ko, J.; Werner, C.; Tenhunen, J. A spatially hierarchical integration of close-range remote sensing, leaf structure and physiology assists in diagnosing spatiotemporal dimensions of field-scale ecosystem photosynthetic productivity. Agric. For. Meteorol. 2017, 247, 503–519. [Google Scholar] [CrossRef]
- Araya, S.; Ostendorf, B.; Lyle, G.; Lewis, M. CropPhenology: An R package for extracting crop phenology from time series remotely sensed vegetation index imagery. Ecol. Inform. 2018, 46, 45–56. [Google Scholar] [CrossRef]
- van Wart, J.; van Bussel, L.G.J.; Wolf, J.; Licker, R.; Grassini, P.; Nelson, A.; Boogaard, H.; Gerber, J.; Mueller, N.D.; Claessens, L.; et al. Use of agro-climatic zones to upscale simulated crop yield potential. Field Crop. Res. 2013, 143, 44–55. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, L.; Zhang, Z.; Chen, Y. Climate warming outweighed agricultural managements in affecting wheat phenology across China during 1981–2018. Agric. For. Meteorol. 2022, 316, 108865. [Google Scholar] [CrossRef]
- Zeng, N.; Zhao, F.; Collatz, G.J.; Kalnay, E.; Salawitch, R.J.; West, T.O.; Guanter, L. Agricultural Green Revolution as a driver of increasing atmospheric CO2 seasonal amplitude. Nature 2014, 515, 394–397. [Google Scholar] [CrossRef] [PubMed]



| Site | Crop Types | Life Cycle Classification | Edaphic Classification | Years | DOYini |
|---|---|---|---|---|---|
| Shandong Province | Paddy or upland crops (unknown crop types) | Unknown | Paddy/upland field | 1995 | 55 for spring crops; 170 for summer crops |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, W.; Ko, J.; Cao, R.; Yu, Z. Improving Reliability in Reconstruction of Landsat EVI Seasonal Trajectory over Cloud-Prone, Fragmented, and Mosaic Agricultural Landscapes. Remote Sens. 2023, 15, 4673. https://doi.org/10.3390/rs15194673
Xue W, Ko J, Cao R, Yu Z. Improving Reliability in Reconstruction of Landsat EVI Seasonal Trajectory over Cloud-Prone, Fragmented, and Mosaic Agricultural Landscapes. Remote Sensing. 2023; 15(19):4673. https://doi.org/10.3390/rs15194673
Chicago/Turabian StyleXue, Wei, Jonghan Ko, Ruyin Cao, and Zhiguo Yu. 2023. "Improving Reliability in Reconstruction of Landsat EVI Seasonal Trajectory over Cloud-Prone, Fragmented, and Mosaic Agricultural Landscapes" Remote Sensing 15, no. 19: 4673. https://doi.org/10.3390/rs15194673
APA StyleXue, W., Ko, J., Cao, R., & Yu, Z. (2023). Improving Reliability in Reconstruction of Landsat EVI Seasonal Trajectory over Cloud-Prone, Fragmented, and Mosaic Agricultural Landscapes. Remote Sensing, 15(19), 4673. https://doi.org/10.3390/rs15194673









