Abstract
This paper presents a novel version control system for point clouds, which allows the complete editing history of a dataset to be stored. For each intermediate version, this system stores only the information that changes with respect to the previous one, which is compressed using a new strategy based on several algorithms. It allows undo/redo functionality in memory, which serves to optimize the operation of the version control system. It can also manage changes produced from third-party applications, which makes it ideal to be integrated into typical Computer-Aided Design workflows. In addition to automated management of incremental versions of point cloud datasets, the proposed system has a much lower storage footprint than the manual backup approach for most common point cloud workflows, which is essential when working with LiDAR (Light Detection and Ranging) data in the context of spatial big data.
1. Introduction
A version control system (VCS) organizes and manages digital assets using incremental change logs. It is usually implemented as a type of software that manages changes to documents, typically textual information, among which software source code stands out. The main functionality of a VCS is to revert a document or dataset to a previous version (or revision), which is very useful in any complex information processing. It is also useful for storing a history of changes for later reference and comparison. In addition, it usually allows the forking of paths of versions (branches) for processing in parallel with different editing processes and/or development teams, which can later merge versions. It is usually implemented as an autonomous system that manages files independently, but it can also be integrated into other systems, such as text editors and document-oriented tools, as well as any type of data editor of any nature. The most advanced systems allow a document or dataset to be shared by several users who make changes concurrently and remotely, in addition to providing locking and protection mechanisms based on user privileges. In any discipline where digital assets are created and edited, having intermediate versions is essential to reverse operations carried out and keep a history of changes for analysis, as well as to recover and merge old data with the latest version.
Software development and office data processing environments are the most common for the use of VCSs. In most cases, they work with files and directories on disk, and are optimized to work with text, being format agnostic. The other disciplines use much more complex data than textual information, and managing different versions often involves manual full copies of datasets, using different identifying labels. Some VCSs can automatically handle binary data with no known semantics for the calculation of differences (delta), such as Git [1], and Kart [2] for point clouds. Therefore, as in the previous case, they store complete intermediate versions without any information about the changes made. This applies to all binary data that cannot be identified as text, such as multimedia data, Computer-Aided Design (CAD) models or point clouds (binary format). Non-textual data-oriented systems are also known as Data Version Control, and are especially used in data analytics and research in disciplines such as engineering, physics, geology, biology, medicine and social sciences, among others. Many of the datasets used change over time, either with the addition of new data or through different editing processes. Data Version Control allows operation on a specific state of data at a given time.
Point cloud models are a type of resource widely used in a multitude of decision-making processes [3]. Nowadays, the capture of spatial information of the real environment allows data to be obtained at different scales, from specific objects to large areas of terrain [4]. Due to its volume, this massive digital information from the real environment requires geospatial big data technologies for its treatment [5,6,7,8]. The applications of point clouds are diverse, such as CAD and Building Information Modeling (BIM), obtaining digital twins, topographic surveys, infrastructure surveying, the inspection and control of industrial facilities, interference detection, documentation for preservation, the restoration of cultural assets, land management, precision agriculture, etc.
Our VCS proposal is valid for all types of point clouds. However, it is the LiDAR (Light Detection and Ranging) data that benefit the most from it. LiDAR is the technology that allows the greatest amount of 3D data to be obtained from the real environment. For this reason, it is widely used in fields such as topography, civil engineering, environmental engineering and archaeology. The processing of large volumes of 3D point information implies a series of inconveniences related to its storage and transmission, as well as its editing, visualization and analysis. Boehler et al. [9] identify some tasks and uses that need accelerated processing. This includes topics such as modeling and simulation, feature extraction from point clouds, topography change detection and environmental engineering, among others. Therefore, in addition to efficient data storage, other processes such as efficient editing, visualization [10,11] and segmentation [12,13,14,15] are also necessary. Managing such a volume of data is challenging.
Having a version control system for point clouds allows large datasets to be worked with safely since the entire history of changes is preserved (see Figure 1), and branches can be generated for alternative workflows on the data. Based on what has been published so far, there is no specific VCS proposed for point clouds stored in a compressed binary format for minimal storage space that benefit from point semantics for calculating differences (delta). This work presents a version control system for point clouds that allows the editing history on a dataset to be stored with a minimal storage footprint. This system calculates each intermediate version of the dataset and stores only the information that changes with respect to the previous version. It allows keeping track of each of the operations performed and allows the quick restoration of previous versions. It also allows undo/redo functionality in memory, as well as incremental versions stored on a disk/server (many interactive point cloud editing applications do not allow undo/redo actions). With this approach, version control is possible in an automated and optimized way, whereby expensive operations such as denoising, filtering, colorizing, segmentation, etc., can be easily reversed without having to manually replicate the entire dataset between editing operations.
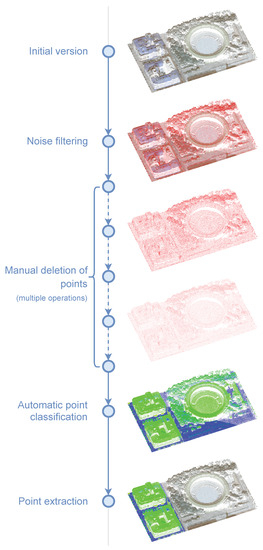
Figure 1.
Example workflow with a point cloud dataset.
The rest of this document is structured as follows: Section 2 reviews the relevant previous work related to VCSs and point clouds. Section 3 introduces some foundations of VCSs related to our system. Section 4 presents the details of the proposed system. Section 5 shows the results of the experiments carried out, as well as provides a discussion of the results. Finally, Section 6 presents the conclusions and describes future work.
2. Previous Works
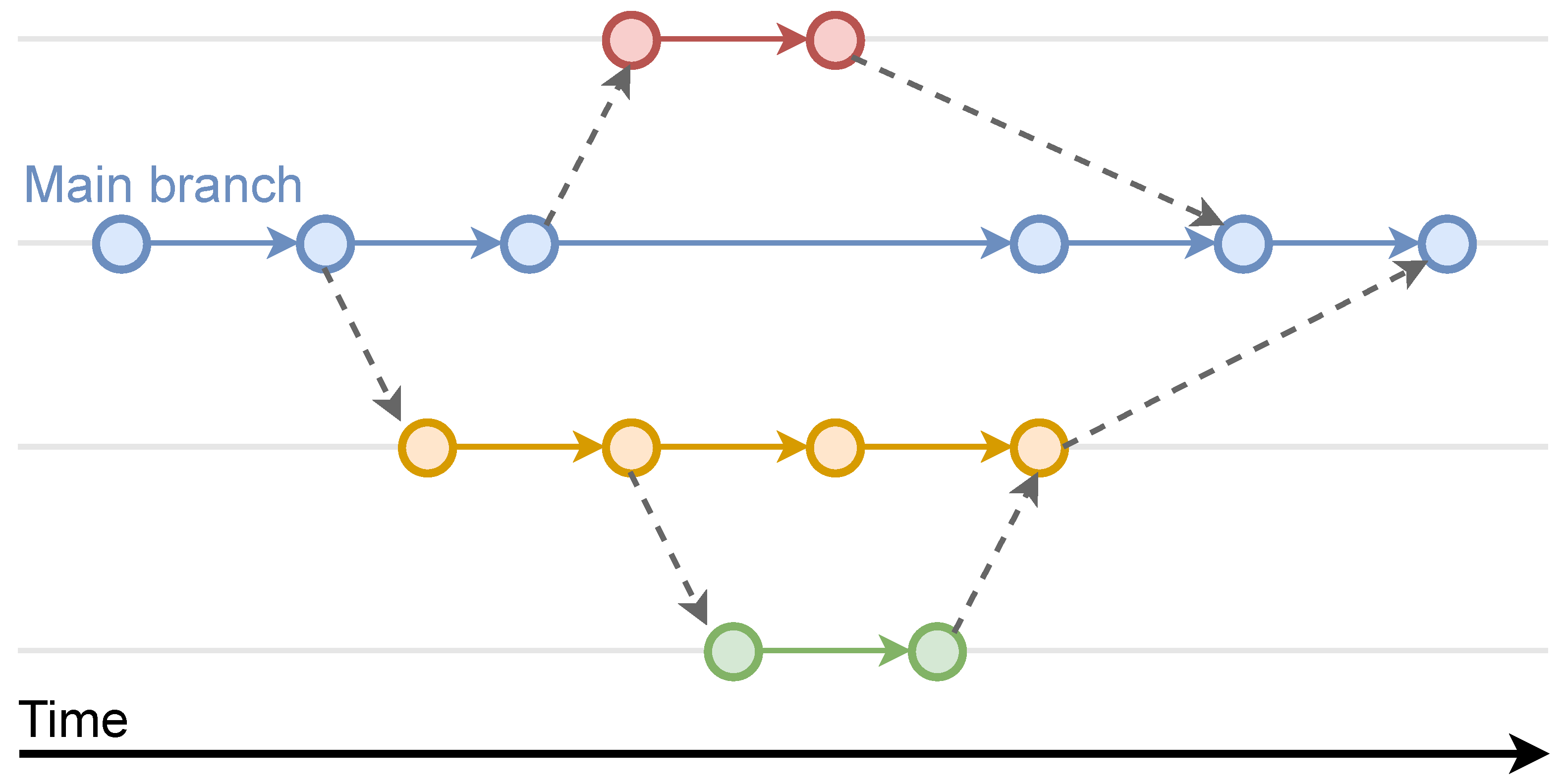
Typical text document-oriented VCSs allow management of the version history of source code [16], documents and other assets [17]. The main goal is to allow the recovery of old versions, which are usually labeled with metadata that indicate the type of change made at each moment and its author [18]. Everything is usually stored in repositories, which in some cases can be distributed [19]. Within each repository, there can be several branches or parallel lines of edition or development. Each branch is usually assigned to a work team or dedicated to a specific development or functionality, so that, in this way, a team can work in parallel on various parts of a project or an information system. There is always a main branch from which other ones are derived (see Figure 2). Sometimes a derived branch is used as an isolated compartment to experiment with a copy of the resources without altering the main dataset. This is called sandboxing [20]. In addition to the basic operation of restoring a previous version, a VCS normally allows the merging of different versions belonging to different branches, as well as the merging of data from an old version with the current version. General VCSs are the most widespread, with different free software options, such as RCS [21], Git [1] or Subversion [22].
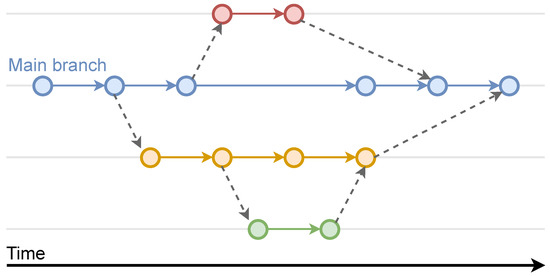
Figure 2.
The branch structure in a VCS. There is always a main branch from which the rest are created. A secondary branch can also be the origin of another branch.
When working with non-text assets, VCSs can still be effective. In fact, in development environments and office documents, there are usually resources of all kinds that cannot be edited as text. The main problem is that these types of files cannot be easily treated incrementally for the management of intermediate versions, so the solution is to store full assets. This has two drawbacks: (a) the nature of the changes made is not known, and (b) a complete copy has to be stored for each delta, which for very large datasets is normally unfeasible. In order to solve this, it is necessary to consider the internal structure of the assets. This leads to the creation of VCSs tailored for specific types of data. The most important aspects are the operations for calculating the differences between two states of an asset, recovering a previous version using registered deltas (rollback), and the merging of two versions into one.
In this sense, there are VCS proposals for specific data with semantics different from textual information. Therefore, there are systems adapted to topics such as Model-Driven Software Development [23], 3D modeling [24], CAD modeling [25], Building Information Modeling [26] or image editing [27]. As for point clouds, there are no specific systems that allow the storing of intermediate versions efficiently, so the only alternative is to use systems such as Git, which store the data completely in each version. Moreover, many of the point cloud editing programs do not even have any undo/redo functionality, so it is not possible to reverse the changes made at any time. This forces users to continuously store backup copies of datasets so that they can revert to a previous version when using long workflows such as that depicted in Figure 1.
The storage of point clouds on disk is important in the design of a specific VCS. Currently, there are several file formats that can be used for this purpose, both for storing genetic point clouds and for specific LiDAR data. The most common options are various ASCII formats (non-standards), the LAS format of the ASPRS (American Society for Photogrammetry and Remote Sensing), its compressed variant LAZ [28], SPD [29], Autodesk Recap RCP-RCS, Leica PTX, Faro FLS-FWS, PCD, HDF5, E57 and POD, and other 3D data formats such as STL, OBJ or PLY. Formats that allow data compression are more suitable, especially when large datasets must be stored [28,30,31]. In this work, we used the LAZ format for storing point clouds [28]. It achieves a very efficient compression, is one of the best lossless formats for LiDAR data from a storage-oriented perspective and above all allows the integration of the proposed VCS into existing systems that already use this format to store the datasets. As well as file storage, the other most popular option is to use databases [7,32,33,34]. Other works dealing with mass storage in secondary memory, on the network or in the cloud are [35,36,37,38,39]. In general, most point cloud users do not tend to organize their datasets in the most automated and efficient way possible.
3. Version Control Foundations
This section presents the most relevant concepts of a VCS related to our proposal. First, the data structure used to relate the different versions of a dataset is a directed acyclic graph (DAG). From the user’s perspective, it can be perceived as a directed tree with a bifurcation or branch for each data editing path, but since merging of multiple branches is allowed, it is usually loosely defined as a tree with merged nodes (see Figure 2). Revisions occur in order using identifying numbers or timestamps. A version is always based on a previous one, with the exception of the first one (the root). In the simplest case, there is only one branch or path, although more branches can be defined by cloning any version. As mentioned above, this is used so as to have alternate copies of the data for parallel editing processes that do not alter a given branch.
At any given time, two versions can be merged into one. This operation is performed with the most recent versions of two branches. They are merged into a single one, where that remaining is usually the main one. However, this depends on the nature of the editing process of the dataset (see Figure 2). This is the most complex operation of the VCS since it is necessary to have some semantics or a method for choosing which data will remain in the case of duplicates. Typically these semantics are application-dependent, and thus, multiple variants of the merge operation may be required.
All VCS data must be available to users. There are several ways to organize information, whether in a file system or database, and in a local, centralized or distributed way. Each dataset is managed through a repository or depot, which stores all the versions and the associated metadata, including the graph structure. Users usually have a local version called the working copy. This version can be uploaded as new to the VCS using the commit (push) operation, which generates a new version in the VCS. Moreover, the latest version can be downloaded to the client using the update (pull) operation, which overwrites the local data. In addition, it is possible to go back to a previous version available in the VCS by means of a rollback (revert), overwriting local data. In this case, a complete revert of the working copy will throw out all pending changes on the client.
Modifications that are uploaded to a repository in a VCS are typically not processed immediately, especially on server-hosted systems. In addition, the operations that are performed on a working copy of the dataset do not affect the VCS until the commit function is performed since they are two separate operations. This is for efficiency reasons, and commit operations are usually performed from time to time. Therefore a commit can include many modifications in the local copy of the dataset. During updates, the repository is locked so that other users cannot interfere with the operation. If there are several simultaneous commits, they are serialized and conflicts that may occur are resolved with mechanisms that depend on the VCS and the type of assets. Some VCSs also allow per-user asset locking, although this is uncommon. The commit and update operations are considered atomic since they must leave the repository in a consistent state if the operation is interrupted, analogous to database transactions.
4. Our Approach to Point Cloud Version Control
Our proposal for VCS consists of a system that allows the storage of versions of point cloud datasets in an optimized way. The VCS architecture may vary, and for the developed prototype, a local file-based system is chosen, using LAZ for point data storage. The data structure for version management is the directed acyclic graph described before, and the actions that can be performed are the usual ones in common VCSs, with some exceptions related to the limiting semantics of point cloud data. As mentioned in Section 2, the most important operations to adapt a VCS to a specific type of asset are calculating deltas or differences between two point clouds, performing a rollback using previous version deltas and the merging of two versions into one. To carry out the design and implementation of the proposed system, some aspects are taken into account that impose some limitations.
- Modifications to point clouds can be made from the same software that uses the VCS (managed modifications) or from external third-party tools (unmanaged modifications). The difference is that with an integrated tool, the nature of the changes that occur at each point are always known, while with third-party tools, it is necessary to use a difference calculation algorithm for inferring change information (Section 4.1). This is especially important for the coordinates of the points. If there is any unmanaged modification in them from a third-party tool, it is impossible to know if a point has moved in space. The consequence in the VCS is that a point deletion is recorded, followed by the creation of a new one (when actually they are the same point). The only drawback is the loss of metadata associated with the change operation for documentation purposes. Moreover, version delta data tend to compress a bit less. This is explained in Section 4.3.
- Given a point with multiple attributes, it is considered to have changed when any of its attributes or its position have also changed. As explained above, the 3D coordinates of the point cannot be considered when performing unmanaged operations; that is, when third-party software has been used.
- There are two options for working with deleted points: (a) mark the points as deleted and keep them, and (b) actually delete the points. The LAZ format used in the prototype allows points to be marked as deleted, so our system offers both options. It should be noted that with the proposed VCS, deleted points can be selectively recovered from previous versions and merged with the latest version. This is a special operation that is not available in conventional VCSs since it uses point-cloud-specific semantics. It is always more efficient to effectively delete the points (this is the option used in the tests) since otherwise, in successive versions, they must be processed and stored.
- To calculate the differences (delta) between two point clouds, the file format used must preserve the order of the points since it is necessary to reference them by their indices in external metadata files.
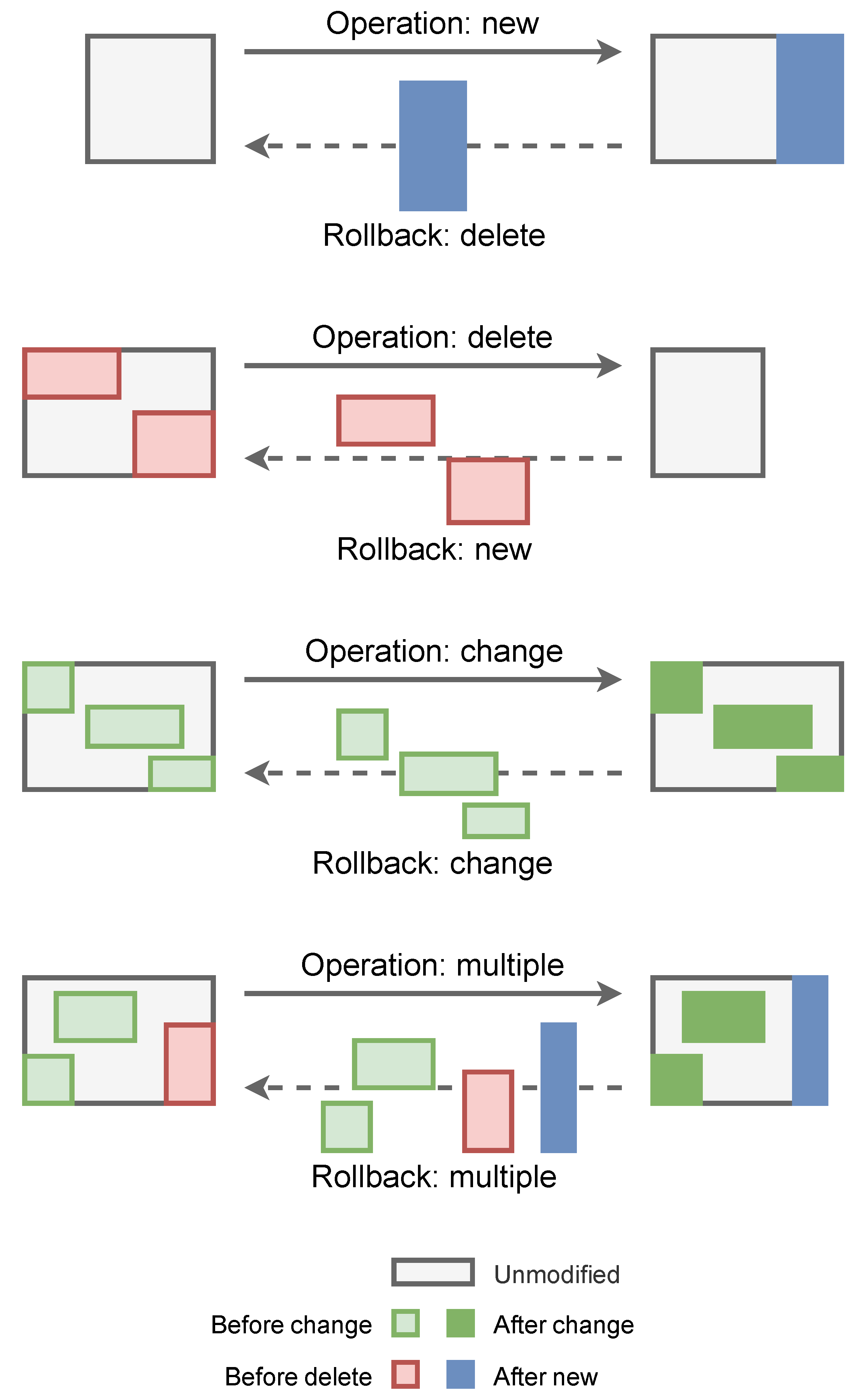
- The latest version of each dataset should be ready for direct use. This implies that changes must be stored not as increments over the previous version but as decrements over the next version. This affects the data that are stored for the description of each delta, as well as the rollback algorithm (see Figure 3).
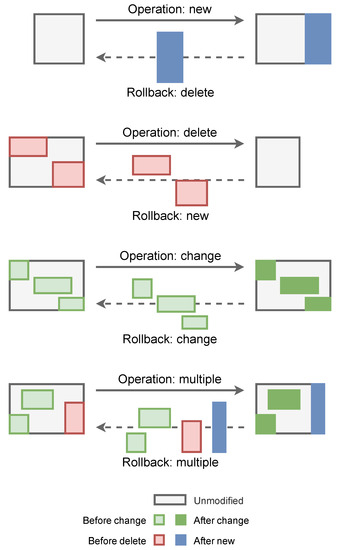 Figure 3. Sets of points involved in basic editing operations.
Figure 3. Sets of points involved in basic editing operations.
The following sections present the details of the operations developed for the calculation of point cloud differences, and the storage of the delta data of each version, which allow rollbacks and point cloud merges to be carried out. These are the operations adapted to the semantics of point clouds that allow having a VCS optimized for these types of data.
4.1. Calculation of Point-Level Cloud Differences
Calculating point cloud differences is the process used to infer the resulting changes from editing operations that have been carried out. It can be used for standalone point clouds and also for more complex datasets distributed in several point clouds stored in different files. In any case, given two point clouds or datasets, A and B, where A is the previous state of the data, and B is the current state of the data, the algorithm determines the following sets of points:
- Points in A that are not in B. This implies that those points have been removed.
- Points in B that are not in A. This implies that those points have been created or loaded.
- Points in A that are also in B, but with some attributes with a different value. This implies that the properties of those points have been modified.
- Points in A that are also in B, with all their attributes unchanged. This implies that those points have not been edited and are exactly the same as before.
In order to calculate the differences between A and B at a point level, it is necessary to obtain different sets of points that meet the conditions described above. That is, the set of points from A that are not included in B, the set of points from B that are not included in A and the points that are included in both clouds. It is also necessary to determine if the attributes of those points are the same in A and B, or if there are differences.
When the version control system is integrated into the same software that makes the changes, tracking them is relatively easy to do, since what changes and the result are known. These managed operations are discussed in Section 4.4. Here we present the case in which it is unknown what operations and changes have occurred between two stages of a point cloud editing process. These unmanaged operations can be performed in some circumstances, the most relevant being the use of third-party software (e.g., LAStools). This is very important since heterogeneous workflows in disciplines such as Remote Sensing involve the use of multiple unrelated programs and tools.
The most important part of the algorithm consists of finding the points of one cloud in the other. We assume that both clouds do not always have the same number of points, nor do their points have the same position in their respective memory arrays. Therefore, to determine that a point from one cloud is in the other, it must be found using its spatial coordinates. This generally implies that a point in A is also in B if there are two points in A and B that have the same spatial coordinates. These points are considered to be linked during the difference calculation algorithm, and are considered as different states of the same point. In this regard, the following issues should be noted. The numerical precision used to represent the 3D coordinates of the points is decisive to verify if points of different clouds occupy the same position in space. Whether using 32-bit or 64-bit precision, two points can be infinitesimally close and thus be considered two states or versions of the same point. It has been observed that many programs slightly alter the coordinates of the points after performing some operations, or after a file saving process that implies some transformation or change of the 3D coordinates to a local coordinate system. It is very common to use a global coordinate origin with 64-bit precision, and relative coordinates of points to that origin as 32-bit numbers. This situation can produce a situation where two points that are semantically the same cannot be linked. In this case, the algorithm will record a deletion of the point from A and the creation of the point from B. Although no information is lost, and version control still works correctly, the chance to mark a point as unchanged is lost. Unmodified points are not stored in the delta data, being the main reason for the decrease in the size of the stored files. To solve this problem of uncontrolled deviation of the point coordinates, a threshold value (epsilon) is used for the point coordinate comparison operator. This value must conform to the numerical precision used to store the data. In many programs, this can be easily controlled.
With the above considerations, it is not possible for two different points to share the same 3D coordinates. This situation is unlikely to arise due to the typical numerical precision used to represent point coordinates and the nature of 3D scanning processes. As explained above, it is more common for the opposite to occur. However, if it does, one of the two points must be displaced in space by a minimum distance above the precision threshold (epsilon) used to differentiate the coordinates of the points. Otherwise, only one of the coincident points in space can prevail. Usually, points do not move in the space between two states of a point cloud, which is common in disciplines such as Remote Sensing. If this occurs with modifications made with third-party programs, the registered operations will be the deletion of one point and the creation of another, in the same way that occurs when numerical precision problems arise. However, with managed editing operations, the link between the previous and current point states is implicit, and it is not necessary to use the algorithm for calculating the differences between point clouds because they are already known.
Taking all of the above into account, the algorithm for calculating the differences between two point clouds is as follows. For each point in cloud B, a point with the same coordinates is searched in cloud A. If this point is found, it is linked to the point in B and they are considered the same. Then, it is checked if their properties are the same or different. Each of the possible cases determines whether each point in B is new (was not in A), modified (was in A but with different properties) or unmodified (was in A with the same properties). Initially, all points from A are considered as deleted because they are not expected to be in B. This state is changed every time a point from B is found in A, so points from A that are not in B are simply not processed and their deletion state does not change because the algorithm only iterates over the set of points from B.
The main performance bottleneck of the algorithm is the method of finding a point in a cloud using its coordinates. This is well known in the literature, and spatial data structures are used to index the data and speed up the process [3,38,40,41,42,43]. The kd-tree is one of the most widely used spatial data structures for searching points, both in 2D and 3D. This approach is more suitable for finding the k-nearest neighbors of a point (kNN), and is used for our method. We use kNN with to find only the nearest point. As previously stated, there may be precision issues that cause the coordinates of the points to vary slightly when going from the state specified by cloud A to that specified by cloud B. To correctly link these points, the epsilon threshold value below which two points are considered equal is used. Subsequently, it is verified as to whether the attributes are also the same, and in such a case, it is concluded that the point has not been modified. The correct epsilon value depends on the precision used to store the dataset.
4.2. Rollback Data Storage
The naive approach for storing changes to a dataset would consist of storing the data of a specific version that varies from the previous one. In this way, to obtain the final result, it would be enough to accumulate the modifications stored in the VCS in order. This approach works in the same way as a program (a sequence of commands) that produces a final result. However, although the modification sequence is very easy to build, it has a major drawback. To obtain the latest version, which is the most used for access and editing, all stored modifications must be accumulated. This means that the longer the change history, the more computationally expensive it is to obtain the latest version. One of the objectives of any version control system is to have the latest version available at all times for direct access. To achieve this, the data describing the modifications must be expressed not as increments over the previous version but as decrements over the next version. This approach is followed in most version control systems, including our proposal.
Therefore, for each intermediate version of a point cloud dataset, it is necessary to store the changes that must be made to that version in order to obtain the previous one. This information is divided into two data files: a file with the points that must be used, and a rollback command file that contains information about the origin of the data that must be used in each rollback operation. Additionally, for the latest version available, there is a file that includes some information about version control management, such as some statistics and the number of the current version, to locate the files of the previous version without having to thoroughly scan the file system.
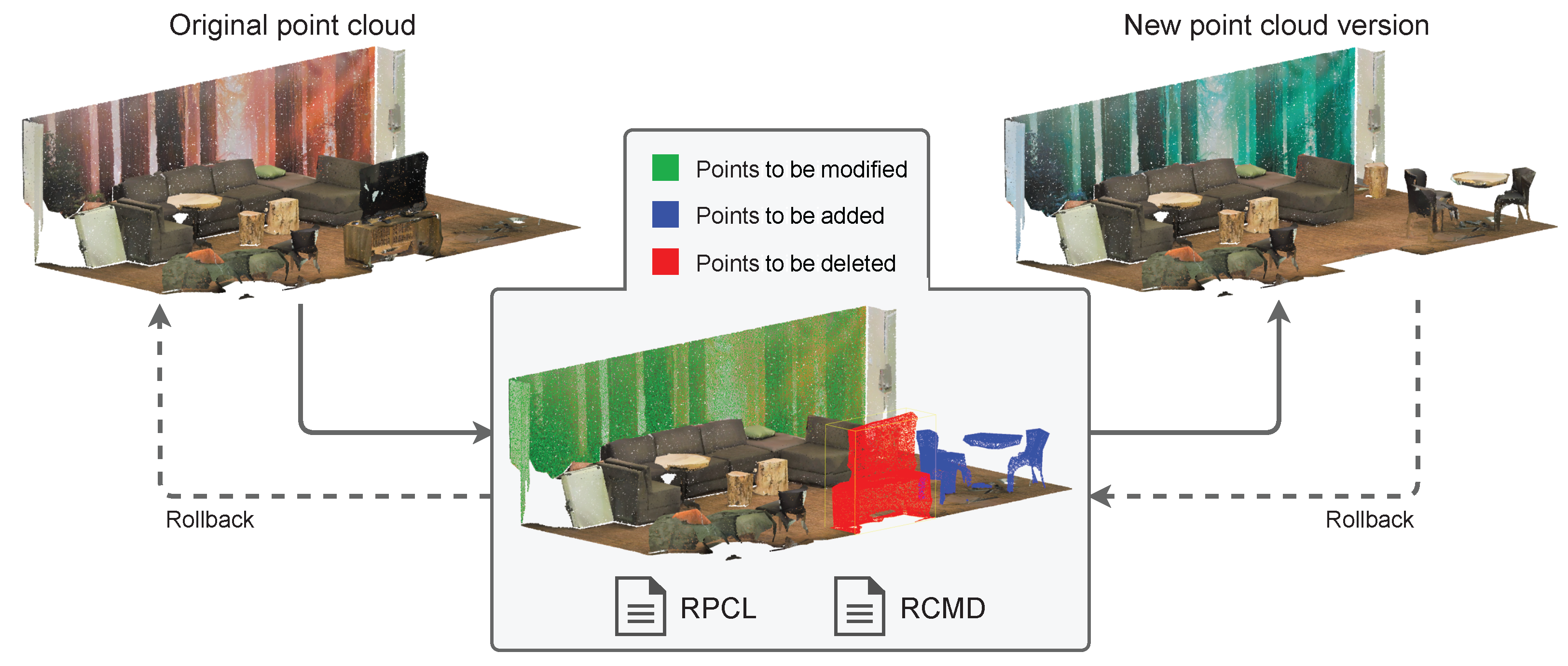
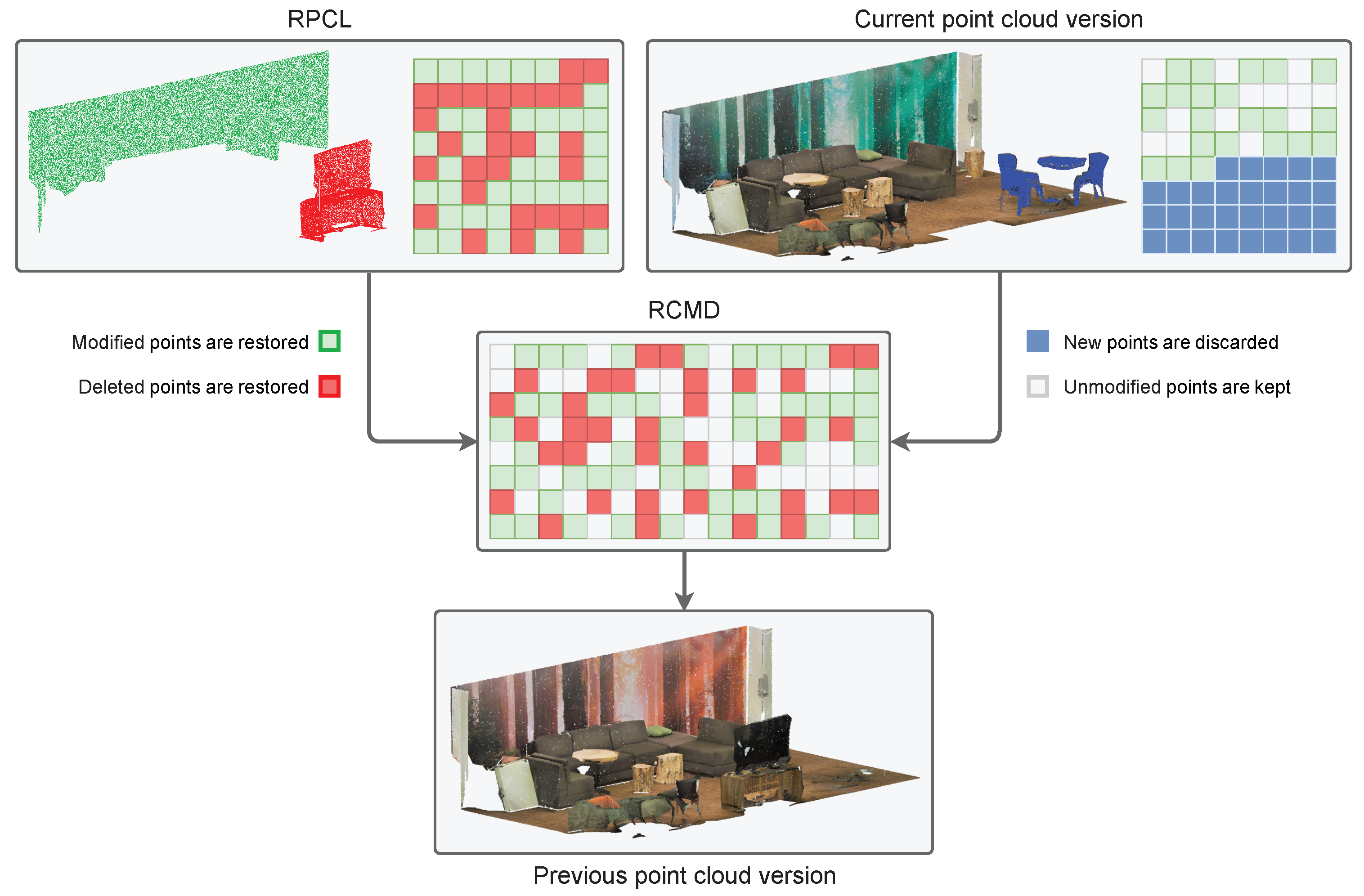
As shown in Figure 4, each of the operations that can be performed on a version of a point cloud dataset implies a series of sets of points to be created, deleted or modified. For each version, there is a rollback point cloud file (RPCL) to perform the transition to the previous version (if any). This file is stored in a standard format for point clouds. In the developed prototype, we use the LAZ format since it provides advanced data compression, which is ideal for storing the historical data in version control. This is because it takes advantage of spatial coherence to perform a coordinates delta compression, so it produces files with the smallest possible storage footprint. Therefore, this file stores a point cloud with all the necessary attributes, including custom fields supported by the LAZ format. In fact, it can be loaded and rendered at any time to check it. These points are used to perform a rollback, and it is the command file that saves the information on how to carry out the process, which is explained next.
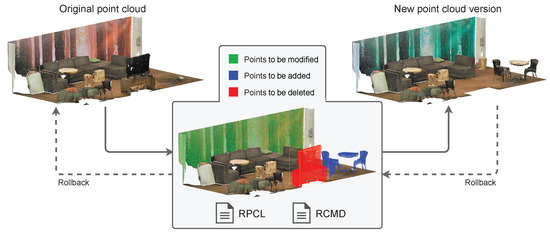
Figure 4.
Sets of points to be added, deleted or modified for an operation stored in RPCL and RCMD files in the VCS.
The rollback command data (RCMD) are a vector of numbers encoding information about which points should be used to restore a previous version of a point cloud and the origin of those points (see Figure 5). For each version, the VCS stores only the points that change from the previous version. Therefore, to complete the rollback operation, the algorithm uses points from the current version cloud, and points from the RPCL. The RCMD has information to perform a copy command for each point to be restored (see Figure 5). Each command indicates whether the origin of the point to be restored is in the cloud of the current version or in the rollback one. Point cloud editing operations that resulted in point deletion or modification will produce restore commands from the RPCL, while created or unmodified points between versions will produce copy commands from the current point cloud. In addition, the command includes the point index in the point cloud array specified as the source, in order to make the copy. This method is very fast, but it is not optimal in terms of storage. In the next section, an algorithm for optimizing the space used by this data file is presented.
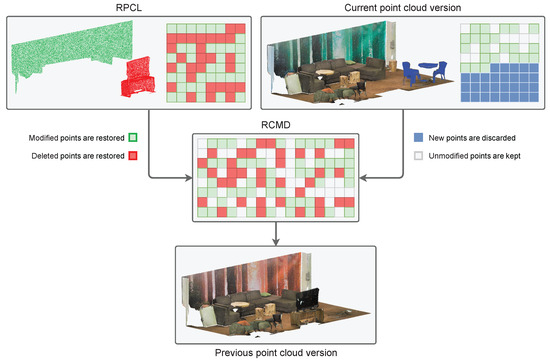
Figure 5.
An RCMD file stores references to points that are stored in an RPCL file and in the current point cloud version file. A rollback operation reads the data from the RCMD and takes the referenced points from the RPCL and the current version file to generate the previous version of the point cloud.
4.3. Rollback Command Data Compression Algorithm
RCMD data can be compressed using a combination of several strategies. One of the most notable aspects when generating a vector of point restore commands is that many of them form groups of referenced indices that are consecutive, either references to points in the RPCL or in the current version cloud. This can be used to perform compact encoding based on a Run Length Encoding algorithm (RLE) [44]. RLE produces compact representations of elements that are often repeated. An example can be seen in Figure 6. This algorithm works very well when there are a large number of sequences of equal values, which usually occurs with data that have low entropy [44]. The main problem with classic RLE is that in the worst case, when the longest sequence of equal values is 1, the encoded data become twice the size of the original, which defeats the purpose of data compression (see Figure 6). To avoid this, we use an adapted RLE algorithm (A-RLE from now on) that is based on a compact coding oriented both to isolated points and to sequences of consecutive points (point strips).

Figure 6.
Basic RLE example.
Table 1 shows the bit codes used for RCMD data encoding. Each point restore command can consist of one or two codes. The first code always includes a bit indicating the source of the data to be restored, 0 for RPCL and 1 for the current version point cloud. The rest of the bits in the first code as well as the entire second code depend on whether a restore command is coded for a single point or for a point strip:

Table 1.
32-bit codes used for A-RLE rollback command data encoding.
- Point strip restore command. Bits 27 to 30 (4 bits) of the first 32-bit code are set to the value 1111, leaving the first 27 bits available to indicate an index sequence length code; that is, the length of a point strip. A second 32-bit code stores the index of the first point of the strip to be restored. The maximum length of a point strip is approximately 134 million points. If a larger strip is detected, it will be divided into several consecutive ones with their respective restore commands.
- Single point restore command. The first 31 bits of the first and only 32-bit code directly specify the index of the point to restore. Bits 27 to 30 (4 bits) cannot contain the value 1111, as this would be indicative of a point strip restore command. The highest value allowed for these bits is 1110, which together with the rest of the bits of the 31-bit code, allows an indexing range of up to approximately 2 billion points, which, logically, will be the maximum number of points for each point cloud that the VCS can manage.
It should be noted that with this A-RLE coding scheme, in the worst case (all point indices are non-consecutive), the number of codes to produce is the same as the number of points to restore, while basic RLE produces twice as many codes. Thirty-two-bit and 64-bit precision can be used for codes in the prototype implementation. Sixty-four-bit codes greatly increase the maximum number of points in a single point cloud. However, 32-bit limits are more than sufficient for working with typical datasets because data partitioning is a common strategy for handling big data. It is more efficient to split larger clouds into smaller ones and use 32-bit codes than to use such large clouds with 64-bit codes. It is important to note that the partitions of the datasets into smaller point clouds must be non-overlapping, which is what our system does.
After the A-RLE encoding approach is used on rollback data, RCMD is further compressed using the Deflate algorithm, which is a lossless data compression method that uses a combination of LZ77 and Huffman coding [44,45]. LZ77 is a coding method based on dictionary, while Huffman coding uses variable-length codes based on entropy. This combination of three lossless compression algorithms makes it possible to achieve optimal compression ratios. Section 5 includes a comparison of the results with various combinations of compression algorithms for RCMD files.
4.4. Managed Editing Operations
In Section 4.1, a method is presented to obtain the changes between two states of a point cloud. This algorithm can be used by the version control system for all stages in a dataset editing process. However, when the operations are performed in the same software that performs version control, additional information can be used to optimize the process and make it much more efficient, both in performance and in the compression of the resulting data. We call these operations managed editing operations since their result is fully controlled, unlike those carried out with third-party software.
In our proposal, optimizations are made for version control related to several types of common operations in the workflow with point clouds. In these cases, it is always known what changes have been made to each point, and its status is tracked. These cases allow bypassing the point cloud differences algorithm, replacing it with a simpler process. It also allows grouping points in memory to increase RCMD data compression with some operations (using longer point strips):
- Add points. New points are added to a cloud or dataset. In this case, the new points will have consecutive indices following the indices of the pre-existing points. This produces a single strip of unmodified points and a single strip of new points, so the rollback command data will be a few bytes in size.
- Delete points. A selection of points is removed from the current version of the point cloud or dataset. In this case, the main advantage is that the point cloud comparison algorithm is not needed to locate the deleted points. For the resulting cloud version, the points will be compacted into the new array and the indices will change. However, the new index for each point in the resulting cloud is known.
- Change points’ attributes. The attributes of a selection of points are changed. In this case, it is not necessary to use the point cloud comparison algorithm either. In addition, it is known in advance that there are no changes in the indices of the points.
- Sort points. Points are reordered in the array in memory without altering their coordinates or their attributes. However, the indices change and must be recorded in an RCMD. The reordering of points can be performed by various criteria. The most relevant is ordering points in 3D to increase compression with formats such as LAZ, which take advantage of spatial coherence to perform a coordinates delta compression. The relative coordinates of a given point with respect to the previous one (in 3D space) will have smaller magnitudes and therefore a lower entropy, which increases the efficiency of the compressor. Sorting 3D points is usually conducted using Hilbert or Morton space filling curves using a spatial data structure, such as quadtree or octree. Logically, reordering with 3D spatial criteria entails a change in the indices of the points in the array where they are stored, which must be recorded in the RCMD.
4.5. Unmanaged Editing Operations
Section 4.4 shows the case in which the modifications to the point clouds are carried out by the same software. This allows having the necessary information about the status of each of the points after each editing operation. When the modifications are made using third-party software, this information is not available since the changes that have been carried out on the points are unknown. In this case, points from different versions on the VCS that have different spatial coordinates cannot be considered as the same point (that has been moved). The consequence is that a point deletion is recorded, followed by the creation of a new one. Metadata associated with the change operation cannot be stored for documentation purposes. Moreover, delta version data tend to occupy slightly more memory. With unmanaged operations, the algorithm presented in Section 4.1 must be used to obtain the changes between two states of a point cloud.
4.6. The Undo/Redo Stack
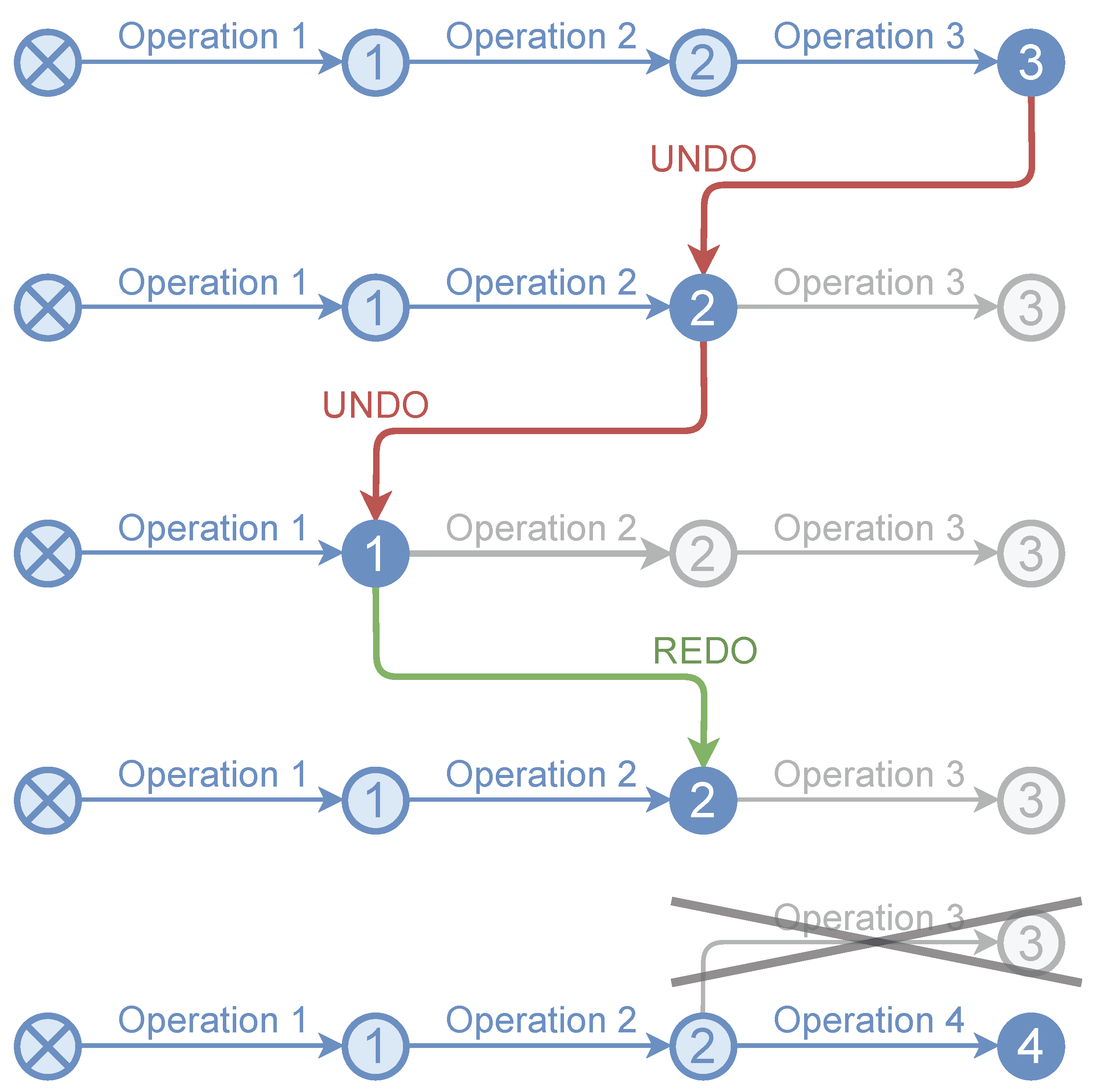
The undo and redo operations are very common in any type of editing software, from word processors to 3D modelers or video editors. The undo option allows us to return to the situation prior to performing the last editing operation, while the redo option involves redoing an operation reversed by an undo. Figure 7 shows an example. This functionality is closely related to the VCS. In fact, it can be considered a specific type of it, with only one branch and whose data are not usually stored in secondary memory. The usual data structure to implement the undo/redo functionality is a stack. In our proposal, the undo/redo stack becomes relevant for two reasons. First of all, some point cloud editing applications (especially LiDAR-based) do not have this type of functionality. Second, having the undo/redo option indirectly optimizes operating version control in interactive applications. Moreover, performing a rollback with information stored in memory is very fast.
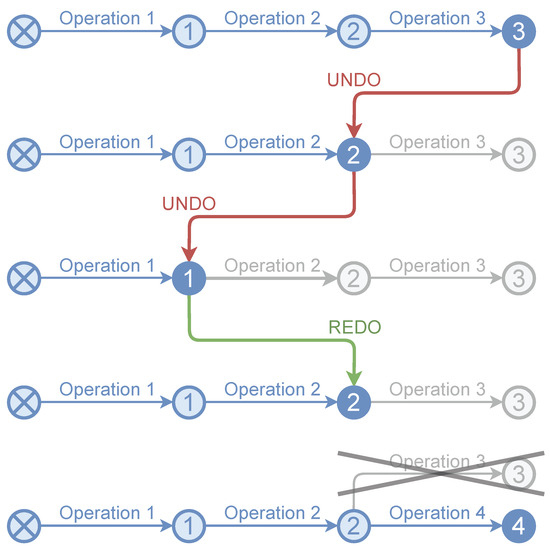
Figure 7.
Undo/redo example. When the result of a new operation is pushed to an intermediate node, all nodes above it in the stack are removed (in this case, node 3 when performing operation 4 from state 2).
The VCS is optimized by using the undo/redo functionality as an in-memory cache of operations not stored on disk (see Figure 8). When an operation is performed, it is logged into the undo/redo stack, and while the user continues working, a background CPU process compresses and stores the data on disk for version control. In this way, the system remains interactive as long as possible. This is important since saving the different versions of the edited point clouds to disk can be very slow. However, to perform an undo operation, the process would have to be completed before allowing other actions, thus blocking the user interface.

Figure 8.
The undo/redo functionality as an in-memory cache of operations not stored on disk by the VCS. This allows having a version history per editing session, and storage of only the relevant versions in the VCS.
5. Results and Discussion
This section presents the results of several experiments showing the performance of the proposed VCS in general, as well as the RCMD file compression algorithm in particular. The tests were carried out on a Intel i7-8700 3.2 GHz PC (12 logical processors) with 32 GB RAM. The prototype was implemented in C++17. Cloud Compare [46] was used for rendering some figures and as an external tool for generating versions of the datasets for testing.
We used two datasets for the experiments (see Figure 9). The goal was to have data from airborne lidar and terrestrial lidar, with different point densities and spatial distributions. Both the complete versions and specific subsets were used for the tests. The first dataset is a part of the Manhattan Island from NY City [47] (2017, WGS84 Zone center −74.002447E, 40.708918N, 4.42 km × 2.27 km, 325 M points in a single LAZ file). The second dataset is the Stanford 3D Indoor Scene Dataset (S3DIS) [48], which is divided into 6 areas with 271 rooms. A single LAZ file version of area-1 (44M points) was used.

Figure 9.
Datasets used in the experiments. Top: Manhattan dataset (325 M points); bottom: S3DIS dataset area-1 (44 M points).
To compare the new system with the classical approach, each dataset was merged into a single file for stress testing. Splitting into files and tracking changes on a per-file basis is a strategy that can also be applied to the manual backup approach, recording only the files that have changed and leaving the rest of the dataset intact.
5.1. A-RLE Algorithm
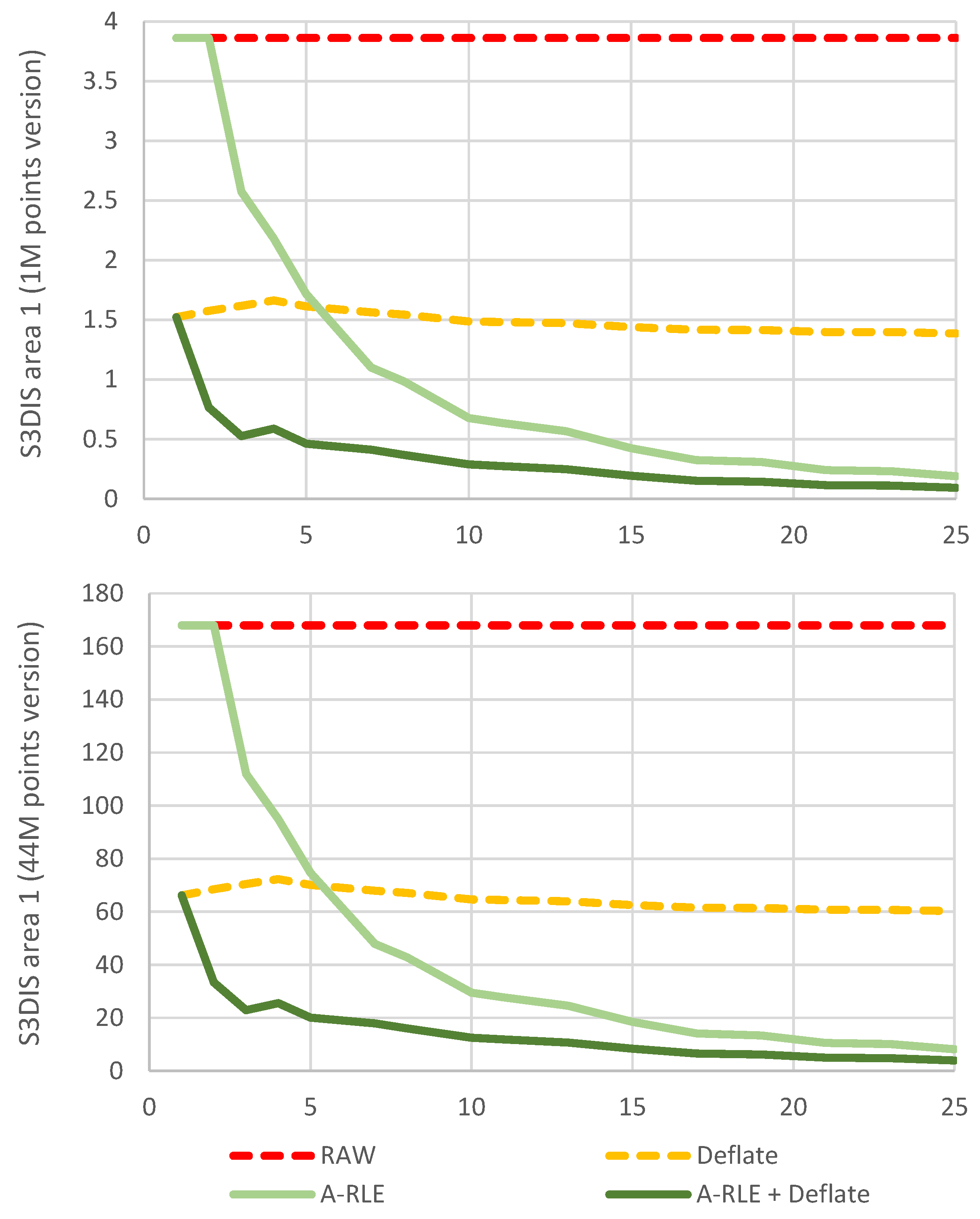
Before presenting the results of the VCS in general, this section shows the results of the performance tests carried out with the different compression algorithms considered for RCMD files: RAW (without compression), Deflate (RCMD is compressed without encoding with A-RLE), A-RLE and A-RLE+Deflate (see Figure 10). For these tests, point change simulation operations were carried out in the S3DIS dataset (area 1) with the aim of verifying the influence on the storage footprint of each compression algorithm regarding: (a) the total number of points processed, and (b) the average length of the strips of points in RCMD restore commands.
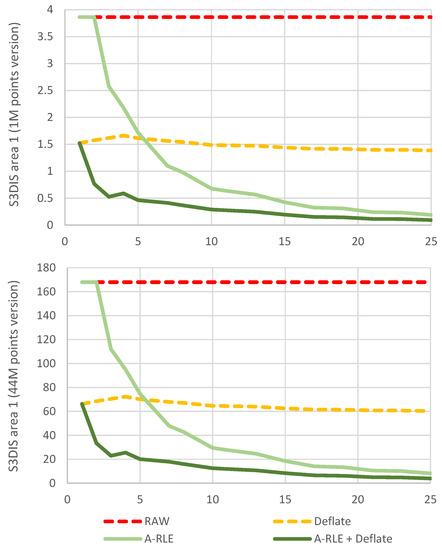
Figure 10.
Efficiency of compression algorithms used to encode RCMD files. The y-axis shows values of storage space used in MB. The x-axis shows the average point strip length for each experiment.
Multiple versions with different numbers of points were used. However, only two are shown in Figure 10, as the rest produce nearly identical results. As can be seen when comparing both graphs, the number of points does not affect the scalability of the compression algorithms. On the other hand, the length of the point strips does have an effect on our A-RLE as expected. To simulate the generation of point strips in each test, a normal distribution was used with the mean centered on the target average strip length (represented on the x-axis of Figure 10), with a standard deviation of 30% of that target value. The alternation between groups of modified and unmodified points was forced. The average of the total modified points is always around 50%.
As can be seen, larger point strips produce more compact commands that are much more compressed with the A-RLE algorithm. Although this simulation presents unrealistic conditions, the influence of the length of the point strips on the RCMD restore commands can be seen. In real cases, this depends on the type of editing that is performed on the point datasets. For example, a noise filtering operation tends to produce short strips (2–4 points), while erasing by large polygonal areas tends to generate larger strips. It should be noted that unmodified points also generate strips of points for the RCMD. When modifications affect only a few points in the cloud edited, few large strips are generated, resulting in an RCMD that is compressed to a few bytes. For all the above, it is shown that the approach proposed for the compression of RCMD data (A-RLE + Deflate) is the most efficient.
5.2. Overall VCS Performance
To test the overall efficiency of the VCS, several tests were performed. First of all, specific tests were carried out to determine the difference between manual storage of complete intermediate versions (RAW) and the use of the VCS. To do this, the impact on the storage footprint of each operation is analyzed separately. From the point of view of calculating intermediate versions (deltas), the operations that can be performed on a point cloud dataset can be grouped into two: the creation and alteration of points. Within the alteration of points are included the modification of attributes and the elimination of points. That is, it is necessary to take into account only the points that will be stored in the RPCL of a version in the VCS. As introduced in Section 4.2, unaltered points and new points are stored in the current point cloud version, which is always ready to be used directly.
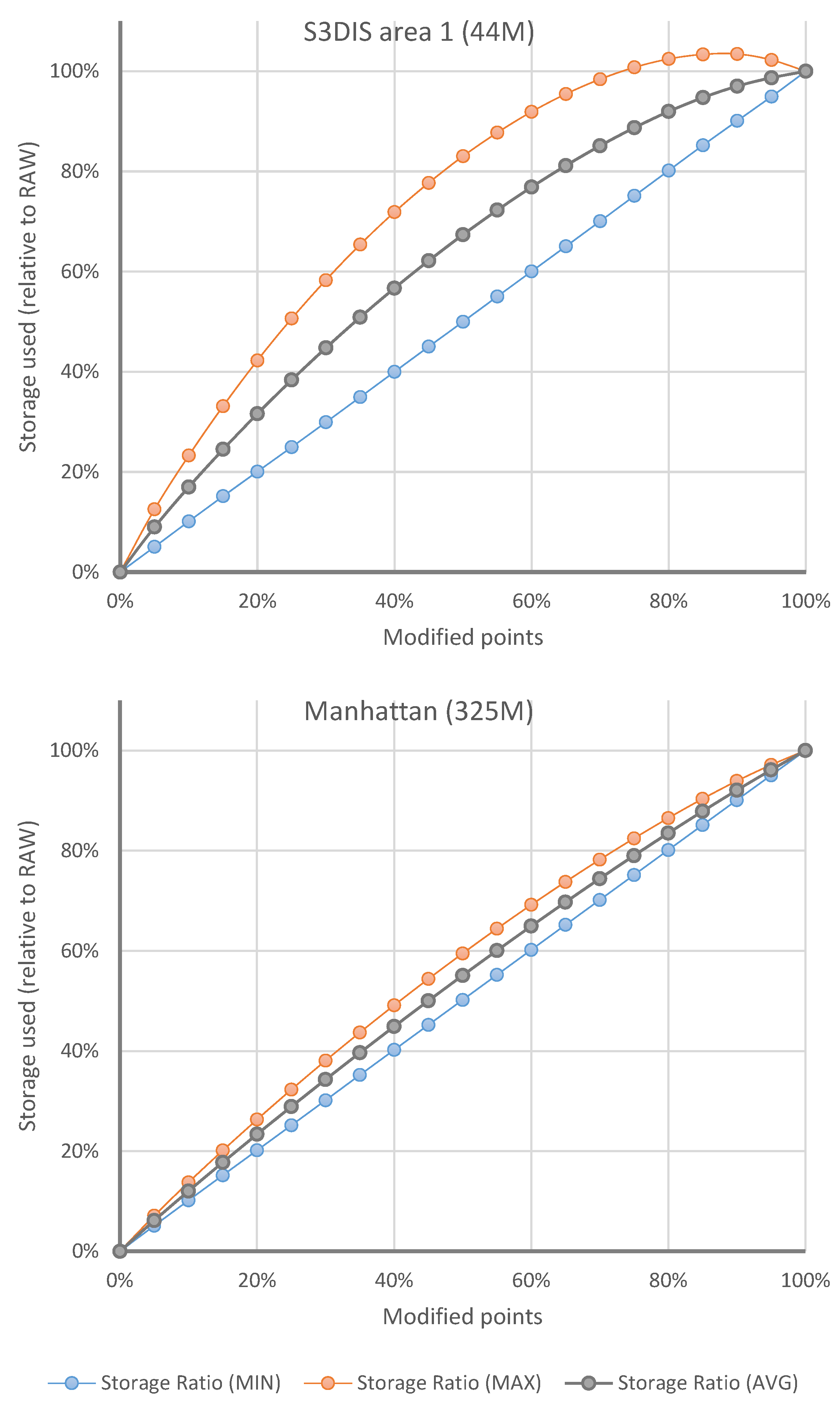
Figure 11 shows the results of delta files storage tests for point modification operations, which are the ones that produce the point clouds for the intermediate versions. The point adding operation does not produce any point storage in VCS delta files, only references on the RCMD file, which for this type of operation is negligible in size. Consequently, the most interesting results are those associated with point alteration operations. Figure 11 shows the influence of the number of points modified in each test on the size of the generated delta files. This number of points is displayed as a percentage of the total points in the dataset. The storage used as a result of each test is expressed as a percentage of the storage used by the full versions of the point clouds (RAW). In addition, the minimum, maximum and average values resulting from testing various configurations of consecutive point strips are shown. The graphs show the results for two datasets stored in a single file. As can be seen, the number of points is related to the amount of memory used in the delta files, as expected. It can also be seen that for smaller datasets, there is more variation depending on the presence of more or less point strips. This affects the compression of the RCMD files, which with smaller datasets have a greater relative weight over the total storage. The main conclusion is that the VCS has the same storage cost as the manual backup approach (RAW) when all the points are modified, which is logical since it must store all data that change between versions. However, with less modified points, the storage footprint is reduced substantially. Furthermore, it must be remembered that the operation of adding points has almost zero cost over delta files since only minimal information is stored in the RCMD but nothing in the RPCL.
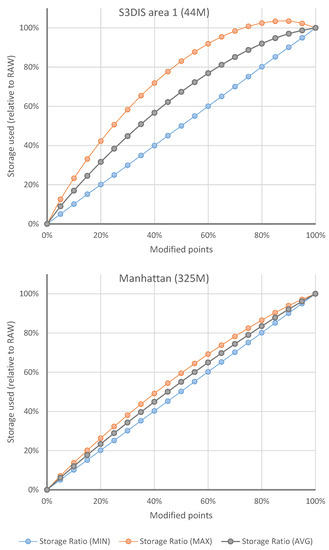
Figure 11.
Influence of the number of points modified on the size of the generated delta files. The x-axis shows the percentage of modified points out of the total points in the dataset. The y-axis shows values of storage space used as the percentage of the full versions of the dataset (RAW).
In addition to the above, tests were carried out with more realistic scenarios using third-party applications for verifying the efficiency of the VCS in real-world conditions. However, it must be said that the results are indicative since it greatly depends on the type of processing that is carried out on the data, the number of points to be edited, the number of versions registered in the VCS, etc. Figure 12 and Table 2 present the results of a test where several modification operations are carried out. First, an operation is performed to load new points into the dataset. Then, a filtering is performed, which is a global denoising operation based on the Statistical Outlier Removal method. Four manual point removal sessions are carried out to delete extraneous points, echoes and scan deviations. A global automatic classification is then performed, followed by four manual classification sessions to correct errors of the automatic classification. Finally, a branch is created using a point extraction based on point classification values. Then, a final subsampling operation is applied. Table 2 shows the number of points involved in each operation, as well as the percentage with respect to the total points of the latest version of the dataset at each moment. Table 3 shows the execution times for storing delta versions into the VCS. As expected, the proposed VCS consumes more computing time to calculate the delta versions since it performs operations that are not carried out with the RAW approach. The Unmanaged diff column refers to the calculation time for differences between point clouds, which only applies to unmanaged operations.
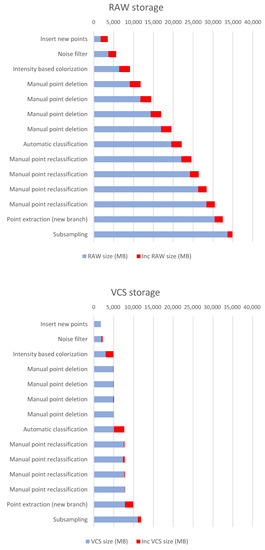
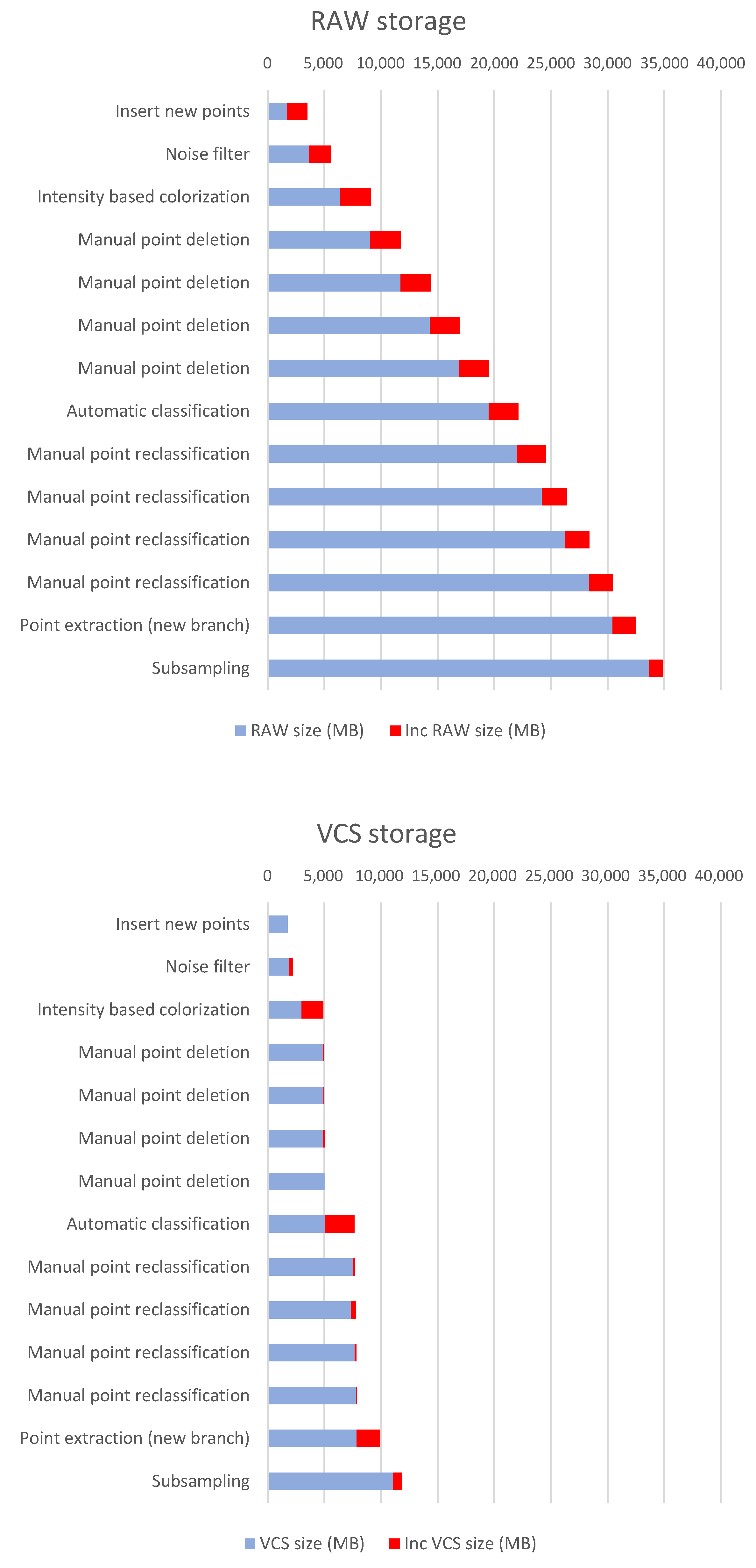
Figure 12.
Storage used for a workflow of the Manhattan dataset (325M points). The increase in the storage footprint in each operation (delta size) is indicated in red. The details of the operations are described in Table 2.

Table 2.
Storage used for a workflow of the Manhattan dataset (325M points).

Table 3.
Execution time for delta operations for a workflow of the Manhattan dataset (325M points).
As can be seen in Figure 12, the storage footprint is much smaller in the VCS than with the RAW approach. It can be argued that some of the editing operations need not generate a complete new version of the dataset. For example, manual point removal sessions could be compacted into one. However, it must be taken into account that many of the operations, especially those carried out interactively, have a very high working time, so not having previous versions can mean a high cost in case of errors. In addition, the proposed system allows for undo/redo stack management, as presented in Section 4.6. This means that fast operations can generate intermediate versions in the memory of the computer, allowing data to be restored in the event of an error, without using VCS storage. It should also be mentioned that it is possible at any time to compact several VCS incremental versions into a single delta increment, in order to reduce the storage footprint on consolidated versions.
6. Conclusions and Future Work
This paper presents a VCS for point clouds that allows the complete editing history of a dataset to be stored with a minimal storage footprint. This allows changes to be controlled during the life cycle of the point cloud dataset. For each version, this system stores only the information that changes with respect to the previous one. The data required for the incremental (delta) data are compressed using a strategy based on the Deflate algorithm and the proposed A-RLE. It also allows undo/redo functionality in memory, which serves to optimize the operation of the VCS. In addition to automated management of incremental versions of point cloud datasets, the system has a much lower storage footprint than the manual backup approach for most common point cloud workflows.
For future work, we plan to incorporate various improvements in our proposal. Intermediate version management could be optimized by making it possible to store partial point data; that is, only the attributes that change, instead of the entire points. Other point cloud formats for storage should be tested that allow partial descriptions of points (in addition to LAZ). Specific protocols for concurrent multi-user editing could also be incorporated to allow the blocking of editing by zone of the datasets, as well as resolving conflicts with simultaneous editing of the same points.
Author Contributions
Conceptualization, C.J.O.-A.; methodology, C.J.O.-A., A.L.-R., R.J.S.-S. and A.J.R.-R.; software, C.J.O.-A. and A.L.-R.; validation, C.J.O.-A. and A.L.-R.; writing—original draft preparation, C.J.O.-A.; writing—review and editing, A.L.-R., R.J.S.-S. and A.J.R.-R.; project administration, R.J.S.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This result is part of the research project RTI2018-099638-B-I00 funded by MCIN/ AEI/ 10.13039/ 501100011033/ and ERDF funds ’A way of doing Europe’. In addition, the work has been funded by the Spanish Ministry of Science, Innovation and Universities via a doctoral grant to the second author (FPU19/00100), and the University of Jaén (via ERDF funds) through the research project 1265116/2020.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spinellis, D. Git. IEEE Softw. 2012, 29, 100–101. [Google Scholar] [CrossRef]
- Kart—Distributed Version-Control for Geospatial and Tabular Data. Available online: https://kartproject.org/ (accessed on 2 September 2023).
- Poux, F. The Smart Point Cloud: Structuring 3D Intelligent Point Data. Ph.D. Thesis, Université de Liège, Liège, Belgique, 2019. [Google Scholar] [CrossRef]
- Bräunl, T. Lidar Sensors. In Robot Adventures in Python and C; Springer International Publishing: Cham, Switzerland, 2020; pp. 47–51. [Google Scholar]
- Deng, X.; Liu, P.; Liu, X.; Wang, R.; Zhang, Y.; He, J.; Yao, Y. Geospatial Big Data: New Paradigm of Remote Sensing Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3841–3851. [Google Scholar] [CrossRef]
- Evans, M.R.; Oliver, D.; Zhou, X.; Shekhar, S. Spatial Big Data. Case studies on volume, velocity, and varitety. In Big Data: Techniques and Technologies in Geoinformatics; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Lee, J.G.; Kang, M. Geospatial Big Data: Challenges and Opportunities. Big Data Res. 2015, 2, 74–81. [Google Scholar] [CrossRef]
- Pääkkönen, P.; Pakkala, D. Reference Architecture and Classification of Technologies, Products and Services for Big Data Systems. Big Data Res. 2015, 2, 166–186. [Google Scholar] [CrossRef]
- Boehler, W.; Marbs, A.; Bordas, V. OGC Testbed-14: Point Cloud Data Handling Engineering Report; Technical Report, I3mainz; Institute for Spatial Information and Surveying Technology: Mainz, Germany, 2018. [Google Scholar]
- Schutz, M.; Krosl, K.; Wimmer, M. Real-Time Continuous Level of Detail Rendering of Point Clouds. In Proceedings of the IEEE VR 2019, Osaka, Japan, 23–27 March 2019; pp. 103–110. [Google Scholar]
- Bohak, C.; Slemenik, M.; Kordež, J.; Marolt, M. Aerial LiDAR Data Augmentation for Direct Point-Cloud Visualisation. Sensors 2020, 20, 2089. [Google Scholar] [CrossRef] [PubMed]
- Guiotte, F.; Pham, M.T.; Dambreville, R.; Corpetti, T.; Lefèvre, S. Semantic Segmentation of LiDAR Points Clouds: Rasterization Beyond Digital Elevation Models. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2016–2019. [Google Scholar] [CrossRef]
- Xie, Y.; Tian, J.; Zhu, X.X. Linking Points With Labels in 3D: A Review of Point Cloud Semantic Segmentation. IEEE Geosci. Remote Sens. Mag. 2020, 8, 38–59. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm. Remote Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Cen, J.; Yun, P.; Zhang, S.; Cai, J.; Luan, D.; Wang, M.Y.; Liu, M.; Tang, M. Open-world Semantic Segmentation for LIDAR Point Clouds. arXiv 2022, arXiv:2207.01452. [Google Scholar]
- Zolkifli, N.N.; Ngah, A.; Deraman, A. Version control system: A review. Procedia Comput. Sci. 2018, 135, 408–415. [Google Scholar] [CrossRef]
- Ruparelia, N.B. The history of version control. ACM Sigsoft Softw. Eng. Notes 2010, 35, 5–9. [Google Scholar] [CrossRef]
- Swierstra, W.; Löh, A. The semantics of version control. In Proceedings of the 2014 ACM International Symposium on New Ideas, New Paradigms, and Reflections on Programming & Software, Portland, OR, USA, 20–24 October 2014; pp. 43–54. [Google Scholar] [CrossRef]
- Nizamuddin, N.; Salah, K.; Azad, M.A.; Arshad, J.; Rehman, M. Decentralized document version control using ethereum blockchain and IPFS. Comput. Electr. Eng. 2019, 76, 183–197. [Google Scholar] [CrossRef]
- Firmenich, B.; Koch, C.; Richter, T.; Beer, D.G. Versioning structured object sets using text based Version Control Systems. In Proceedings of the 22nd CIB-W78, Melbourne, Australia, 27–30 June 2022. [Google Scholar]
- Tichy, W.F. RCS—A system for version control. Softw. Pract. Exp. 1985, 15, 637–654. [Google Scholar] [CrossRef]
- Collins-Sussman, B.; Fitzpatrick, B.W.; Pilato, C.M. Version Control with Subversion; O’Reilly, California: St. Mountain View, CA, USA, 2007. [Google Scholar]
- Kuryazov, D.; Winter, A.; Reussner, R. Collaborative Modeling Enabled By Version Control. In Proceedings of the Modellierung 2018; Schaefer, I., Karagiannis, D., Vogelsang, A., Méndez, D., Seidl, C., Eds.; Gesellschaft für Informatik e.V.: Bonn, Germany, 2018; pp. 183–198. [Google Scholar]
- Doboš, J.; Mitra, N.J.; Steed, A. 3D Timeline: Reverse engineering of a part-based provenance from consecutive 3D models: 3D Timeline: Reverse engineering of a part-based provenance from consecutive 3D models. Comput. Graph. Forum 2014, 33, 135–144. [Google Scholar] [CrossRef]
- Khudyakov, P.Y.; Kisel’nikov, A.Y.; Startcev, I.; Kovalev, A. Version control system of CAD documents and PLC projects. J. Phys. Conf. Ser. 2018, 1015, 042020. [Google Scholar] [CrossRef]
- Esser, S.; Vilgertshofer, S.; Borrmann, A. Graph-based version control for asynchronous BIM collaboration. Adv. Eng. Inform. 2022, 53, 101664. [Google Scholar] [CrossRef]
- da Silva Junior, J.R.; Clua, E.; Murta, L. Efficient image-aware version control systems using GPU. Softw. Pract. Exp. 2016, 46, 1011–1033. [Google Scholar] [CrossRef]
- Isenburg, M. LASzip: Lossless compression of LiDAR data. Photogramm. Eng. Remote Sens. 2013, 79, 209–217. [Google Scholar] [CrossRef]
- Bunting, P.; Armston, J.; Lucas, R.M.; Clewley, D. Sorted pulse data (SPD) library. Part I: A generic file format for LiDAR data from pulsed laser systems in terrestrial environments. Comput. Geosci. 2013, 56, 197–206. [Google Scholar] [CrossRef]
- Cao, C.; Preda, M.; Zaharia, T. 3D Point Cloud Compression: A Survey. In Proceedings of the 24th International Conference on 3D Web Technology, Los Angeles, CA, USA, 26–28 July 2019; pp. 1–9. [Google Scholar] [CrossRef]
- Sugimoto, K.; Cohen, R.A.; Tian, D.; Vetro, A. Trends in efficient representation of 3D point clouds. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 364–369. [Google Scholar] [CrossRef]
- Boehm, J. File-centric Organization of large LiDAR Point Clouds in a Big Data context. In Proceedings of the Workshop on Processing Large Geospatial Data, Cardiff, UK, 8 July 2014. [Google Scholar]
- Hongchao, M.; Wang, Z. Distributed data organization and parallel data retrieval methods for huge laser scanner point clouds. Comput. Geosci. 2011, 37, 193–201. [Google Scholar] [CrossRef]
- Schön, B.; Mosa, A.S.M.; Laefer, D.F.; Bertolotto, M. Octree-based indexing for 3D pointclouds within an Oracle Spatial DBMS. Comput. Geosci. 2013, 51, 430–438. [Google Scholar] [CrossRef]
- Baert, J.; Lagae, A.; Dutré, P. Out-of-Core Construction of Sparse Voxel Octrees. Comput. Graph. Forum 2014, 33, 220–227. [Google Scholar] [CrossRef]
- Richter, R.; Discher, S.; Döllner, J. Out-of-Core Visualization of Classified 3D Point Clouds. In 3D Geoinformation Science; Breunig, M., Al-Doori, M., Butwilowski, E., Kuper, P.V., Benner, J., Haefele, K.H., Eds.; Springer: Cham, Switzerland, 2015; pp. 227–242. [Google Scholar] [CrossRef]
- van Oosterom, P.; Martinez-Rubi, O.; Ivanova, M.; Horhammer, M.; Geringer, D.; Ravada, S.; Tijssen, T.; Kodde, M.; Gonçalves, R. Massive point cloud data management: Design, implementation and execution of a point cloud benchmark. Comput. Graph. 2015, 49, 92–125. [Google Scholar] [CrossRef]
- Schütz, M.; Ohrhallinger, S.; Wimmer, M. Fast Out-of-Core Octree Generation for Massive Point Clouds. Comput. Graph. Forum 2020, 39, 155–167. [Google Scholar] [CrossRef]
- Lokugam Hewage, C.N.; Laefer, D.F.; Vo, A.V.; Le-Khac, N.A.; Bertolotto, M. Scalability and Performance of LiDAR Point Cloud Data Management Systems: A State-of-the-Art Review. Remote Sens. 2022, 14, 5277. [Google Scholar] [CrossRef]
- Huang, L.; Wang, S.; Wong, K.; Liu, J.; Urtasun, R. OctSqueeze: Octree-Structured Entropy Model for LiDAR Compression. arXiv 2020, arXiv:2005.0717. [Google Scholar] [CrossRef]
- Lu, B.; Wang, Q.; Li, A. Massive Point Cloud Space Management Method Based on Octree-Like Encoding. Arab. J. Sci. Eng. 2019, 44, 9397–9411. [Google Scholar] [CrossRef]
- Schuetz, M. Potree: Rendering Large Point Clouds in Web Browsers. Ph.D. Thesis, TU Wien, Vienna, Austria, 2016. [Google Scholar]
- Ströter, D.; Mueller-Roemer, J.S.; Stork, A.; Fellner, D.W. OLBVH: Octree linear bounding volume hierarchy for volumetric meshes. Vis. Comput. 2020, 36, 2327–2340. [Google Scholar] [CrossRef]
- Salomon, D. Data Compression: The Complete Reference; With Contributions by Giovanni Motta and David Bryant; Springer: New York, NY, USA, 2007. [Google Scholar]
- Deutsch, P. Rfc1951: Deflate Compressed Data Format Specification Version 1.3. 1996. Available online: https://www.rfc-editor.org/rfc/rfc1951 (accessed on 9 July 2023).
- Girardeau-Montaut, D. CloudCompare. Available online: https://www.danielgm.net/cc/ (accessed on 9 July 2023).
- City of New York. Topobathymetric LiDAR Data. 2017. Available online: https://data.cityofnewyork.us/City-Government/Topobathymetric-LiDAR-Data-2017-/7sc8-jtbz/data (accessed on 9 July 2023).
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).