A Sound Velocity Prediction Model for Seafloor Sediments Based on Deep Neural Networks
Abstract
:1. Introduction
2. Data Acquisition and Conditioning
2.1. Acoustic Data and Input Parameters
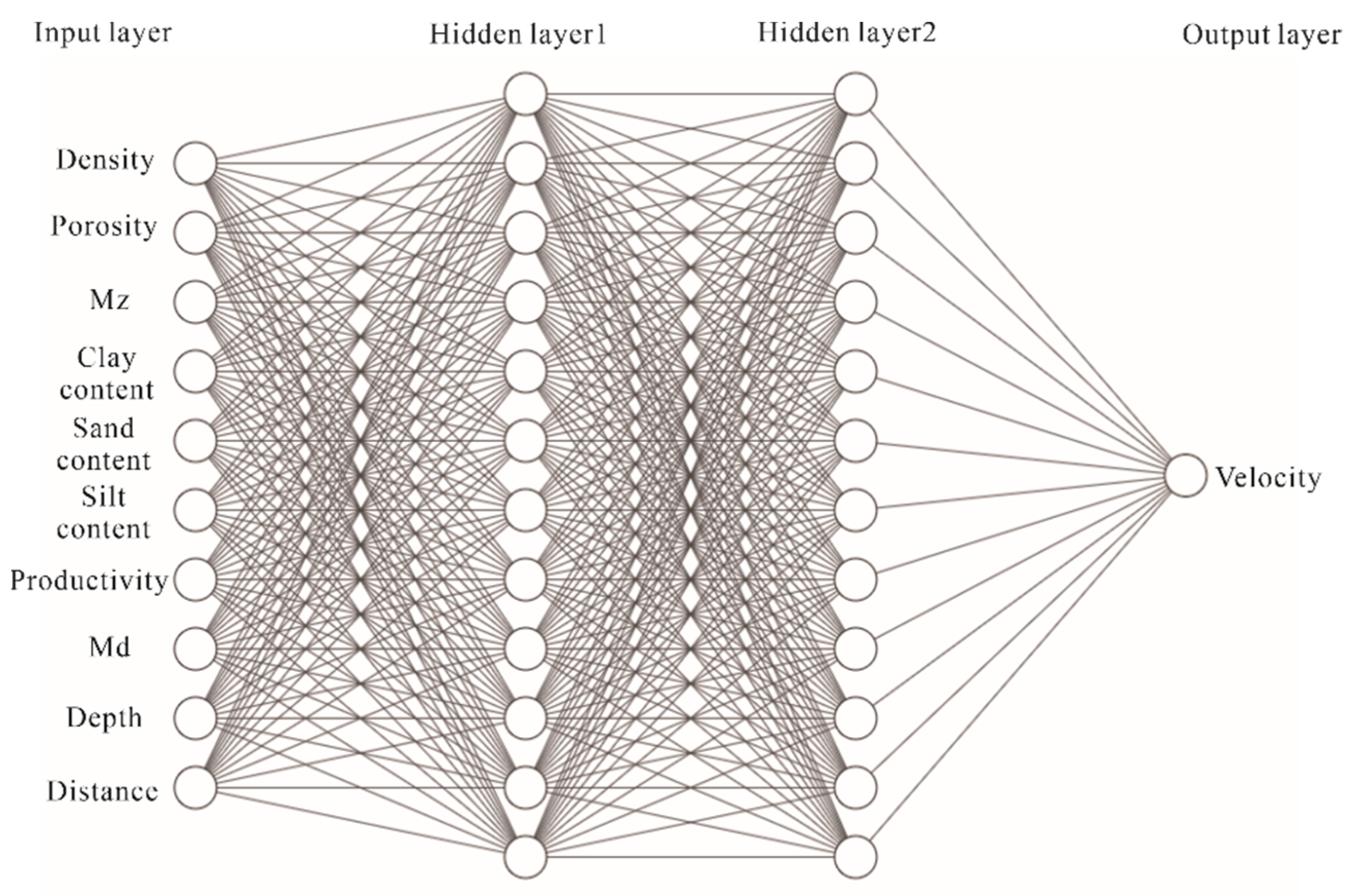
2.2. Machine Learning Method: Deep Neural Networks
- (1)
- Initialize the linear relationship between each hidden layer and output layer. The values of W and b are random values.
- (2)
- For iteration to 1 to max:
- (2-1)
- for I = 1 to m:
- (a)
- Set a1 to xi;
- (b)
- For l = 2 to L, use forward propagation calculation
- (c)
- Calculate the δi,l of output layer by the cost function;
- (d)
- For l = L to 2, backpropagation calculation is performed
- (2-2)
- For l = 2 to L, update Wl and bl at layer L
- (2-3)
- If all the change values of W and B are less than the threshold of stopping iteration, the iteration cycle will be skipped.
2.3. Feature Input
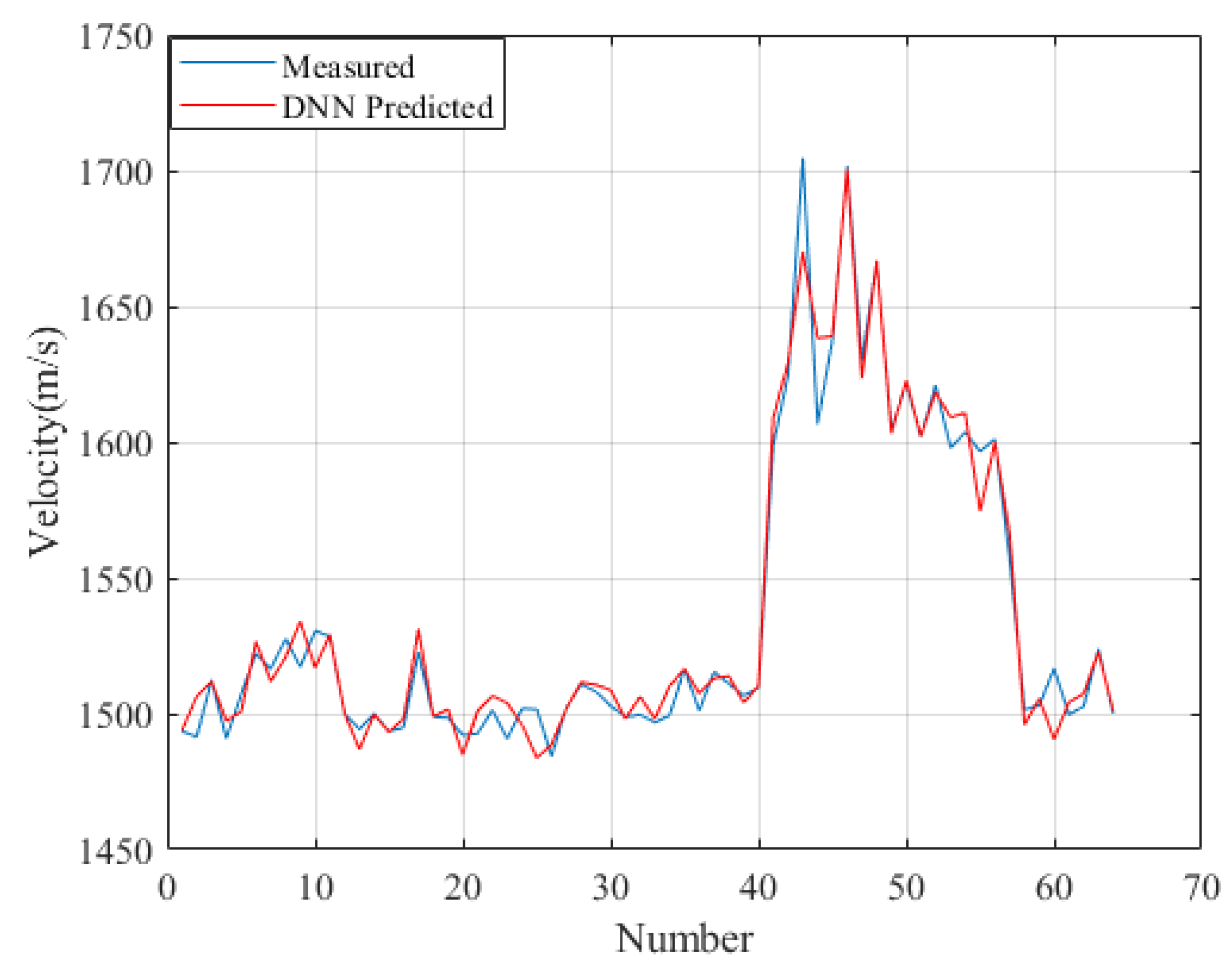
3. Results
- n_hidden_1 = 64; number of neurons in Hidden Layer 1;
- n_hidden_2 = 64; number of neurons in Hidden Layer 2;
- n_input = 10; number of input parameters;
- n_prediction = 1; since the output is the velocity of sound, the number of outputs was 1;
- training_epochs = 300; number of training cycles;
- batch_size = 10; the amount of data to be taken per batch.
4. Discussion
5. Conclusions
- (1)
- Compared with theoretical models and regression equations, not only can our new model easily take advantage of accessible data, such as remote sensing data, but it can also easily be applied in practice.
- (2)
- Due to the advantages of machine learning for processing multidimensional data, the DNN model can comprehensively consider various factors affecting the velocity of sound, such as the source of the sediment, the sedimentary environment and the physical properties, compared with traditional methods (regression equations), and thus the DNN model has improved predictive accuracy.
- (3)
- For the first time, this study shows the possibility of using remote sensing data in geo-acoustics, and it provides a new method for the rapid acquisition of the velocity of sound of sediment.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hamilton, E.L.; Bachman, R.T. Sound velocity and related properties of marine sediments. J. Acoust. Soc. Am. 1982, 72, 1891–1904. [Google Scholar]
- Endler, M.; Endler, R.; Wunderlich, J.; Bobertz, B.; Leipe, T.; Moros, M.; Jensen, J.B.; Arz, H. Geo-acoustic modelling of late and postglacial sedimentary units in the Baltic Sea and their acoustic visibility. Mar. Geol. 2016, 376, 86–101. [Google Scholar]
- Kan, G.; Zou, D.; Liu, B.; Wang, J.; Meng, X.; Li, G.; Pei, Y. Correction for effects of temperature and pressure on sound speed in shallow seafloor sediments. Mar. Georesources Geotechnol. 2019, 37, 1217–1226. [Google Scholar]
- Kim, S.R.; Lee, G.S.; Kim, D.C.; Bae, S.H.; Kim, S.P. Physical properties and geoacoustic provinces of surficial sediments in the southwestern part of the Ulleung Basin in the East Sea. Quat. Int. 2017, 459, 35–44. [Google Scholar]
- Chotiros, N.P.; Isakson, M.J. A broadband model of sandy ocean sediments: Biot–Stoll with contact squirt flow and shear drag. J. Acoust. Soc. Am. 2004, 116, 2011–2022. [Google Scholar]
- Rajan, S.D.; Lin, Y.T. Broadband Geoacoustic Inversions for Seabed Characterization of the New England Mud Patch. IEEE J. Ocean. Eng. 2022, 48, 264–276. [Google Scholar]
- Lee, K.M.; Ballard, M.S.; McNeese, A.R.; Wilson, P.S. Sound speed and attenuation measurements within a seagrass meadow from the water column into the seabed. J. Acoust. Soc. Am. 2017, 141, EL402–EL406. [Google Scholar]
- Potty, G.R.; Miller, J.H.; Michalopoulou, Z.H.; Bonnel, J. Estimation of geoacoustic parameters using machine learning techniques. J. Acoust. Soc. Am. 2019, 146, 2987. [Google Scholar]
- Hamilton, E.L. Geoacoustic modeling of the sea floor. J. Acoust. Soc. Am. 1980, 68, 1313–1340. [Google Scholar]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid. II. Higher Frequency Range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar]
- Stoll, R.D. Acoustic waves in ocean sediments. Geophysics 1977, 42, 715–725. [Google Scholar]
- Stoll, R.D.; Bautista, E.O. Using the Biot theory to establish a baseline geoacoustic model for seafloor sediments. Cont. Shelf Res. 1998, 18, 1839–1857. [Google Scholar] [CrossRef]
- Buckingham, M.J. Wave propagation, stress relaxation, and grain-to-grain shearing in saturated, unconsolidated marine sediments. J. Acoust. Soc. Am. 2000, 108, 2796–2815. [Google Scholar]
- Buckingham, M.J. Analysis of shear-wave attenuation in unconsolidated sands and glass beads. J. Acoust. Soc. Am. 2014, 136, 2478–2488. [Google Scholar]
- Williams, K.L. Adding thermal and granularity effects to the effective density fluid model. J. Acoust. Soc. Am. 2013, 133, EL431–EL437. [Google Scholar]
- Hou, Z.Y.; Wang, J.Q.; Chen, Z.; Yan, W.; Tian, Y.H. Sound velocity predictive model based on physical properties. Earth Space Sci. 2019, 6, 1561–1568. [Google Scholar] [CrossRef]
- Wang, J.; Hou, Z.; Li, G.; Kan, G.; Meng, X.; Liu, B. A new compressional wave speed inversion method based on granularity parameters. IEEE Access 2019, 7, 185849–185856. [Google Scholar]
- Chen, M.; Meng, X.; Kan, G.; Wang, J.; Li, G.; Liu, B.; Liu, C.; Liu, Y.; Liu, Y.; Lu, J. Predicting the Sound Speed of Seafloor Sediments in the East China Sea Based on an XGBoost Algorithm. J. Mar. Sci. Eng. 2022, 10, 1366. [Google Scholar]
- Hou, Z.; Guo, C.; Wang, J.; Chen, W.; Fu, Y.; Li, T. Seafloor sediment study from South China Sea: Acoustic & physical property relationship. Remote Sens. 2015, 7, 570–585. [Google Scholar]
- Witten, I.H.; Frank, E. Data mining: Practical machine learning tools and techniques with Java implementations. ACM Sigmod Rec. 2002, 31, 76–77. [Google Scholar] [CrossRef]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Shepard, F.P. Nomenclature based on sand-silt-clay ratios. J. Sediment. Res. 1954, 24, 151–158. [Google Scholar]
- Wessel, P.; Smith, W.H.F. A global, self-consistent, hierarchical, high-resolution shoreline. J. Geophys. Res. 1996, 101, 8741–8743. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Global sea floor topography from satellite altimetry and ship depth soundings. Science 1997, 277, 1956–1962. [Google Scholar] [CrossRef]
- Tang, S.; Chen, C. Novel maximum carbon fixation rate algorithms for remote sensing of oceanic primary productivity. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5202–5208. [Google Scholar] [CrossRef]

| Parameters | Feature Numbers | Abbreviation | Data Source | Label |
|---|---|---|---|---|
| Velocity of sound | Label | Vp | Laboratory measurement | Output |
| Wet bulk density | Feature 0 | ρ | Laboratory measurement | Input |
| Porosity | Feature 1 | n | Laboratory measurement | Input |
| Sand content | Feature 2 | sand | Laboratory measurement | Input |
| Silt content | Feature 3 | silt | Laboratory measurement | Input |
| Clay content | Feature 4 | clay | Laboratory measurement | Input |
| Mean grain size | Feature 5 | Mz | Laboratory measurement | Input |
| Median size | Feature 6 | Md | Laboratory measurement | Input |
| Distance to the nearest coast | Feature 7 | dis | Global Self-consistent, Hierarchical, High-resolution Geography Database from NOAA’s National Centers for Environmental Information [24] | Input |
| Water depth | Feature 8 | depth | SRTM15+ [25] | Input |
| Average primary productivity | Feature 9 | pro | Remote Sensing of Oceanic Primary Productivity [26] | Input |
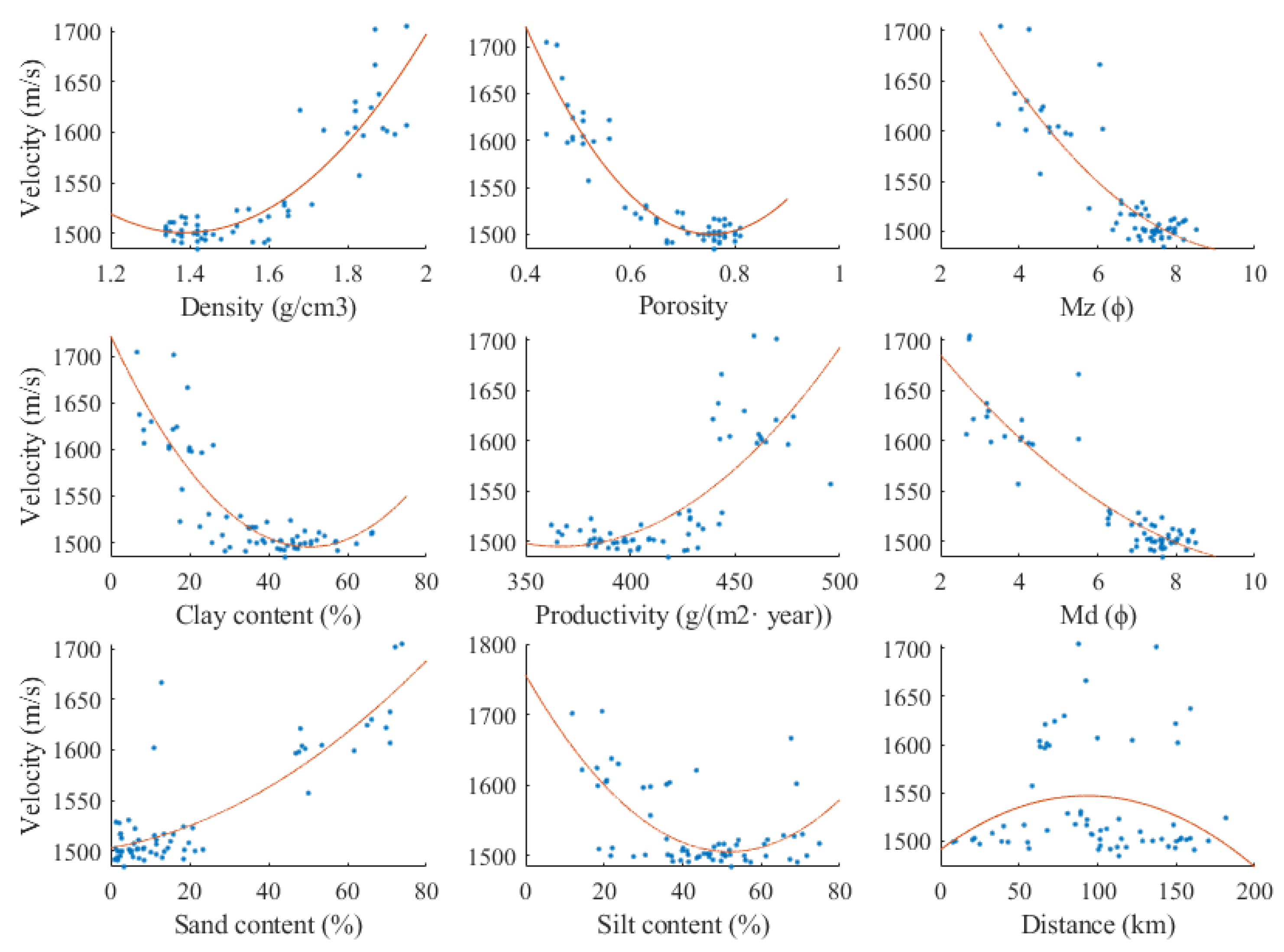
| Equations | Regression Equations | R2 |
|---|---|---|
| Vp = f(ρ) | Vp = 524.8ρ2 − 1457ρ + 2512 | 0.82 |
| Vp = f(n) | Vp = 1765n2 − 2662n + 2504 | 0.89 |
| Vp = f(sand) | Vp = 0.02036sand2 + 0.685sand + 1503 | 0.74 |
| Vp = f(silt) | Vp = 0.09307silt2 − 9.651silt + 1756 | 0.43 |
| Vp = f(clay) | Vp = 0.08951clay2 − 9.006clay + 1722 | 0.76 |
| Vp = f(Mz) | Vp = 4.57mz2 − 91.02mz + 1931 | 0.78 |
| Vp = f(md) | Vp = 2.498md2 − 56.15md + 1788 | 0.83 |
| Vp = f(dis) | Vp = −0.006457dis2 + 1.202dis + 1491 | 0.05 |
| Vp = f(depth) | Vp = 3.166 × 10−5 depth2 − 0.1391depth + 1617 | 0.65 |
| Vp = f(pro) | Vp = 0.01114pro2 − 8.17pro + 2993 | 0.58 |
| Equations | STDEV | RMSE |
|---|---|---|
| Vp = f(ρ) | 22.50 | 49.90 |
| Vp = f(n) | 22.66 | 38.54 |
| Vp = f(sand) | 24.45 | 37.53 |
| Vp = f(silt) | 24.45 | 37.53 |
| Vp = f(clay) | 36.68 | 64.75 |
| Vp = f(Mz) | 22.80 | 51.35 |
| Vp = f(md) | 27.24 | 53.03 |
| Vp = f(dis) | 48.09 | 75.15 |
| Vp = f(depth) | 43.12 | 81.80 |
| Vp = f(pro) | 388.27 | 439.52 |
| Vp = DNN model | 17.67 | 33.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Z.; Wang, J.; Li, G. A Sound Velocity Prediction Model for Seafloor Sediments Based on Deep Neural Networks. Remote Sens. 2023, 15, 4483. https://doi.org/10.3390/rs15184483
Hou Z, Wang J, Li G. A Sound Velocity Prediction Model for Seafloor Sediments Based on Deep Neural Networks. Remote Sensing. 2023; 15(18):4483. https://doi.org/10.3390/rs15184483
Chicago/Turabian StyleHou, Zhengyu, Jingqiang Wang, and Guanbao Li. 2023. "A Sound Velocity Prediction Model for Seafloor Sediments Based on Deep Neural Networks" Remote Sensing 15, no. 18: 4483. https://doi.org/10.3390/rs15184483
APA StyleHou, Z., Wang, J., & Li, G. (2023). A Sound Velocity Prediction Model for Seafloor Sediments Based on Deep Neural Networks. Remote Sensing, 15(18), 4483. https://doi.org/10.3390/rs15184483







