Multi-Granularity Modeling Method for Effectiveness Evaluation of Remote Sensing Satellites
Abstract
:1. Introduction
2. A Mathematical Description of Remote Sensing Satellite Effectiveness Evaluation Problem
2.1. Typical Satellite Effectiveness Evaluation Indicator
2.1.1. Millisecond-Level Time Resolution Indicator
2.1.2. Second-Level Time Resolution Indicator
2.1.3. Day-Level Time Resolution Indicator
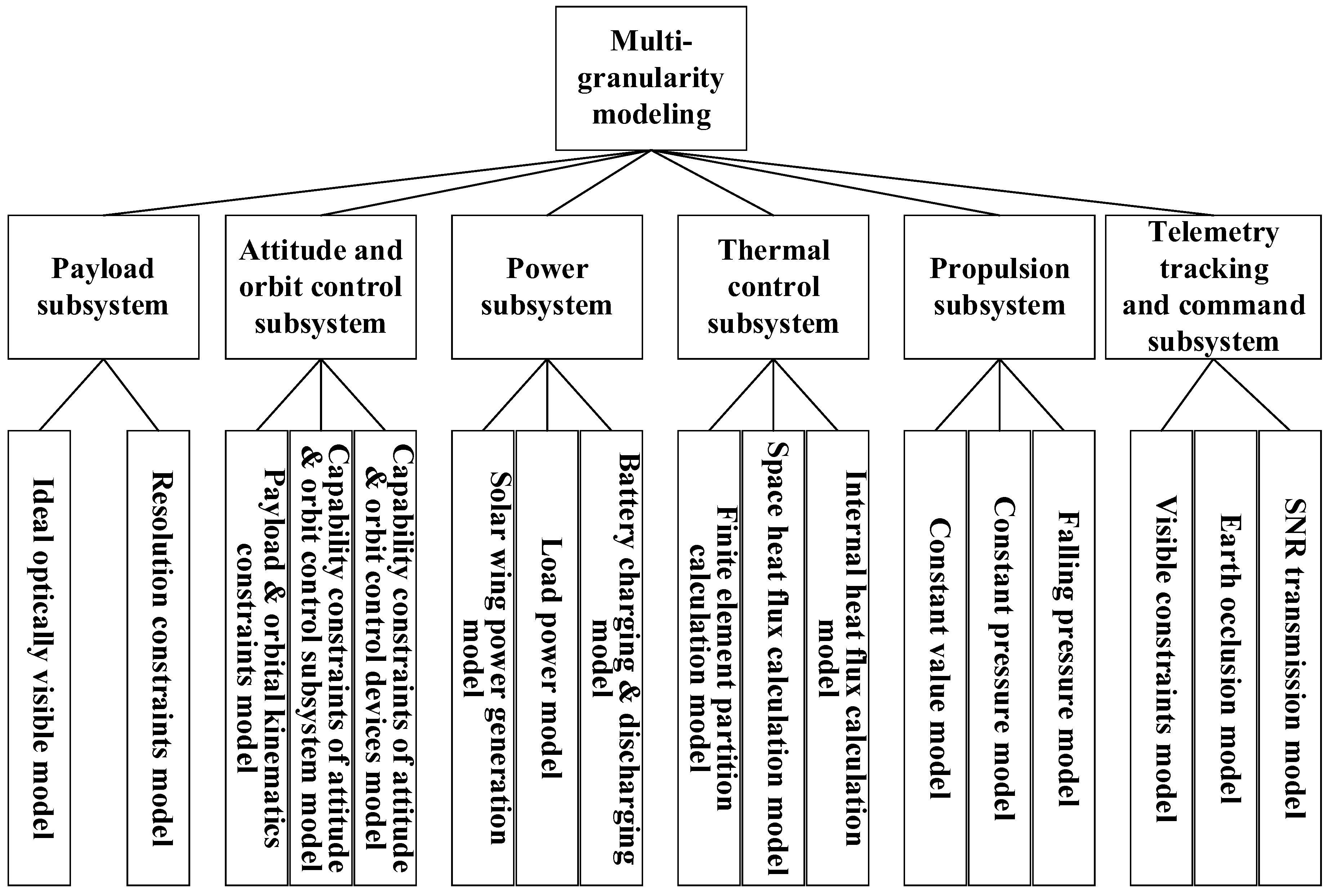
2.2. Multi-Granularity Modeling
2.2.1. Payload Subsystem
2.2.2. Attitude and Orbit Control Subsystem
2.2.3. Power Subsystem
2.2.4. Thermal Control Subsystem
2.2.5. Propulsion Subsystem
2.2.6. TTC Subsystem
3. Selection of Effectiveness Evaluation Indicator Models for Remote Sensing Satellites
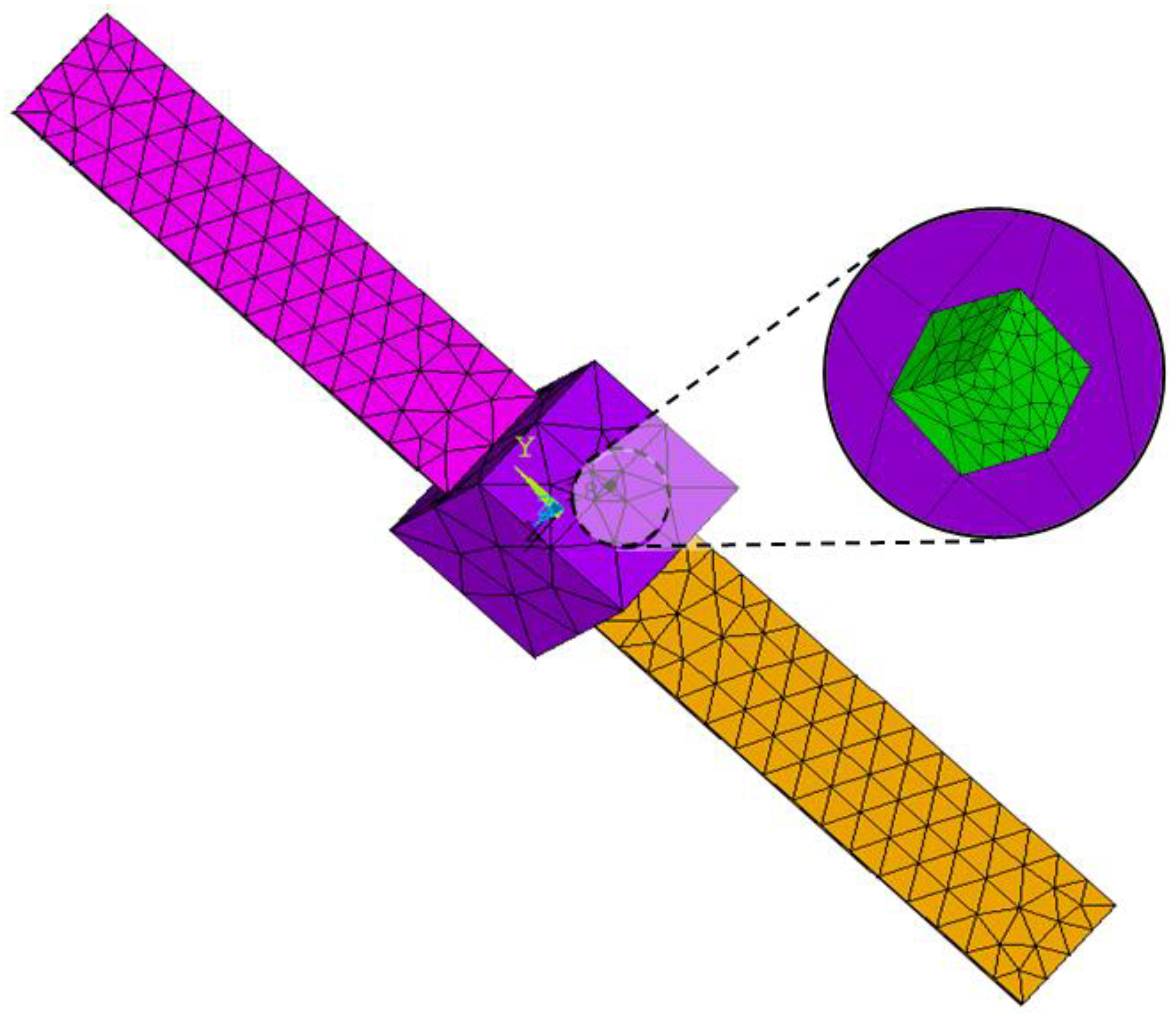
4. Simulation Case
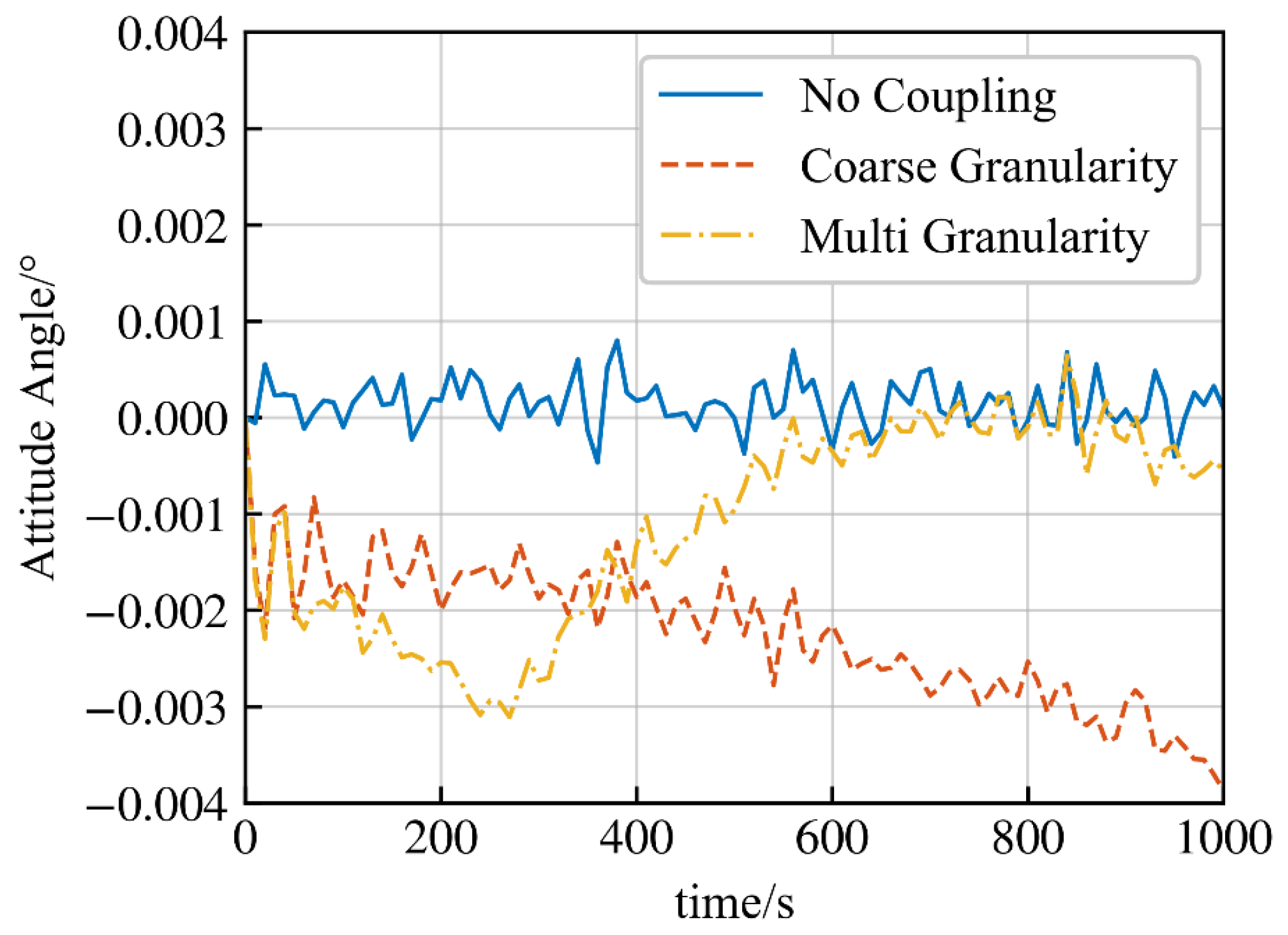
4.1. Millisecond-Level Time Resolution Indicator Calculation
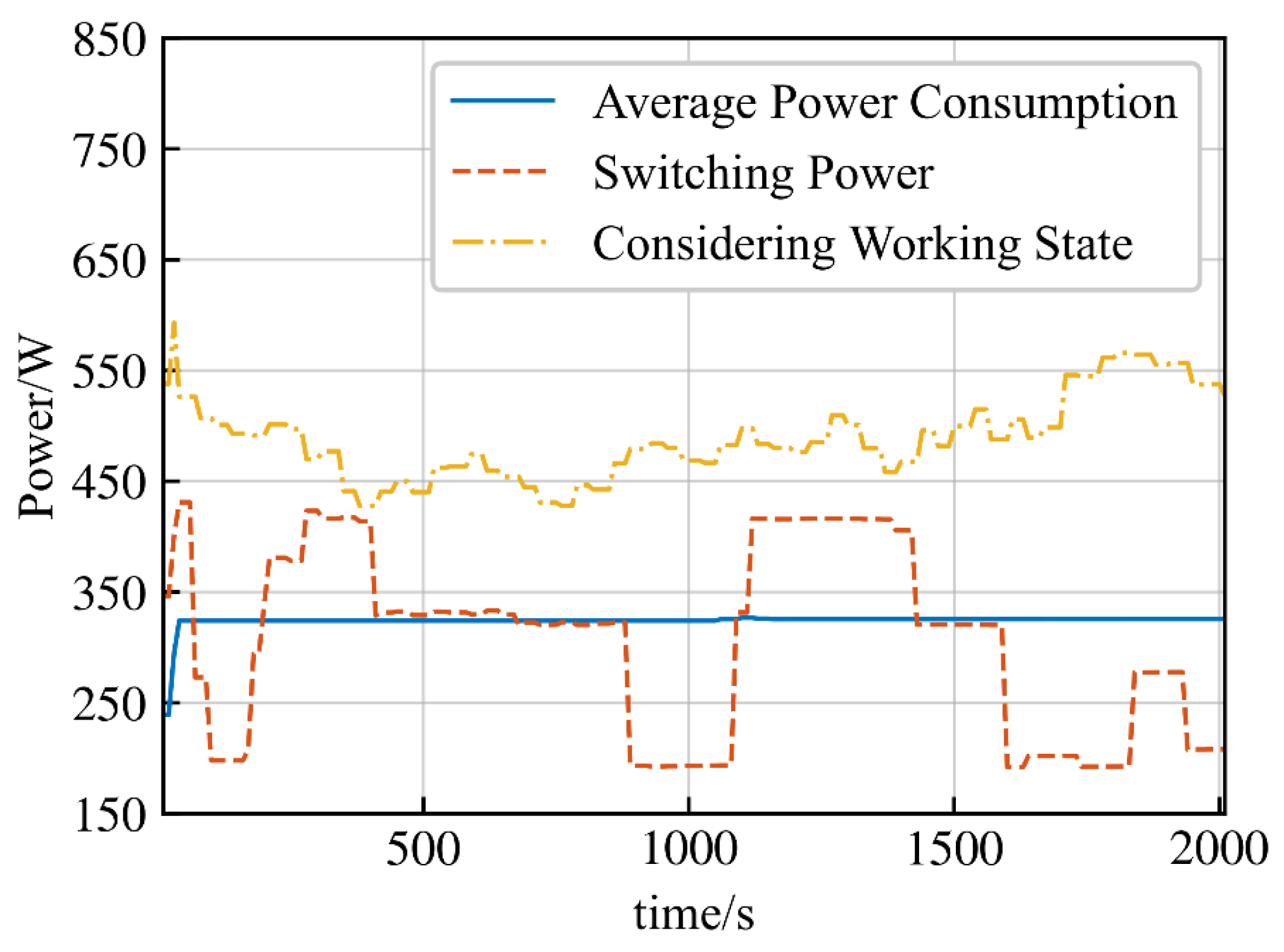
4.2. Second-Level Time Resolution Indicator Calculation
4.3. Day-Level Time Resolution Indicator Calculation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weiss, M.; Jacob, F.; Duveiller, G. Remote Sensing for Agricultural Applications: A Meta-Review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Farhadi, H.; Mokhtarzade, M.; Ebadi, H.; Beirami, B.A. Rapid and Automatic Burned Area Detection Using Sentinel-2 Time-Series Images in Google Earth Engine Cloud Platform: A Case Study over the Andika and Behbahan Regions, Iran. Environ. Monit. Assess. 2022, 194, 369. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Chen, Y.; Wang, J.; Bai, H.; Wu, B.; Li, W.; Li, S.; Zheng, T. The Assessment of More Suitable Image Spatial Resolutions for Offshore Aquaculture Areas Automatic Monitoring Based on Coupled NDWI and Mask R-CNN. Remote Sens. 2022, 14, 3079. [Google Scholar] [CrossRef]
- Dhanaraj, K.; Angadi, D.P. Land Use Land Cover Mapping and Monitoring Urban Growth Using Remote Sensing and GIS Techniques in Mangaluru, India. GeoJournal 2022, 87, 1133–1159. [Google Scholar] [CrossRef]
- Farhadi, H.; Esmaeily, A.; Najafzadeh, M. Flood Monitoring by Integration of Remote Sensing Technique and Multi-Criteria Decision Making Method. Comput. Geosci. 2022, 160, 105045. [Google Scholar] [CrossRef]
- Chen, Y.; Tao, F. Potential of Remote Sensing Data-Crop Model Assimilation and Seasonal Weather Forecasts for Early-Season Crop Yield Forecasting over a Large Area. Field Crops Res. 2022, 276, 108398. [Google Scholar] [CrossRef]
- Cui, Z.; Li, Q.; Cao, Z.; Liu, N. Dense Attention Pyramid Networks for Multi-Scale Ship Detection in SAR Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8983–8997. [Google Scholar] [CrossRef]
- Wang, J.; Song, G.; Liang, Z.; Demeulemeester, E.; Hu, X.; Liu, J. Unrelated Parallel Machine Scheduling with Multiple Time Windows: An Application to Earth Observation Satellite Scheduling. Comput. Oper. Res. 2023, 149, 106010. [Google Scholar] [CrossRef]
- Peng, G. Index System Construction of Information Support Capability Evaluation of Remote Sensing Satellite Task-Oriented. Command Control Simul. 2019, 41, 5–19. [Google Scholar] [CrossRef]
- Liu, F.; Li, L.; Meng, X. Research on Construction Model of the Capacity Index System for Remote Sensing Satellite System. Spacecr. Recovery Remote Sens. 2017, 38, 40. [Google Scholar] [CrossRef]
- Zhigeng, F.; Shuang, W.; Xiaoli, Z.; Yunke, S. ADC-GERT Network Parameter Estimation Model for Mission Effectiveness of Joint Operation System. J. Syst. Eng. Electron. 2021, 32, 1394–1406. [Google Scholar] [CrossRef]
- Liu, X.; Yang, X.; Zhang, T.; Wang, Z.; Zhang, J.; Liu, Y.; Liu, B. Remote Sensing Based Conservation Effectiveness Evaluation of Mangrove Reserves in China. Remote Sens. 2022, 14, 1386. [Google Scholar] [CrossRef]
- Li, H.; Li, D.; Li, Y. A Multi-Index Assessment Method for Evaluating Coverage Effectiveness of Remote Sensing Satellite. Chin. J. Aeronaut. 2018, 31, 2023–2033. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, Q.; Fu, K. Evaluation Model of Remote Sensing Satellites Cooperative Observation Capability. Remote Sens. 2021, 13, 1717. [Google Scholar] [CrossRef]
- Li, J.; Dong, Y.; Xu, M.; Li, H. Genetic Programming Method for Satellite System Topology and Parameter Optimization. Int. J. Aerosp. Eng. 2020, 2020, 6673848. [Google Scholar] [CrossRef]
- Shen, Q.; Yue, C.; Goh, C.H.; Wang, D. Active Fault-Tolerant Control System Design for Spacecraft Attitude Maneuvers with Actuator Saturation and Faults. IEEE Trans. Ind. Electron. 2019, 66, 3763–3772. [Google Scholar] [CrossRef]
- Wu, X.; Dong, Y. Hierarchical Model Updating Method for Vector Electric-Propulsion Satellites. Appl. Sci. 2023, 13, 4980. [Google Scholar] [CrossRef]
- Zammit, S.; Zammit, S. Control and Dynamics Simulation Facility at Hughes Space and Communications. In Proceedings of the Modeling and Simulation Technologies Conference; American Institute of Aeronautics and Astronautics, New Orleans, LA, USA, 11 August 1997. [Google Scholar]
- Schaaf, J.C.; Thompson, F.L. System concept development with virtual protlotyping. In Proceedings of the 1997 Winter Simulation Conference, Atlanta, GA, USA, 7–10 December 1997. [Google Scholar]
- Grieves, M.W. Product Lifecycle Management: The New Paradigm for Enterprises. IJPD 2005, 2, 71. [Google Scholar] [CrossRef]
- Martínez-Olvera, C. Towards the Development of a Digital Twin for a Sustainable Mass Customization 4.0 Environment: A Literature Review of Relevant Concepts. Automation 2022, 3, 197–222. [Google Scholar] [CrossRef]
- Li, J.; Dong, Y. Multi-Granularity Genetic Programming Optimization Method for Satellite System Topology and Parameter. IEEE Access 2021, 9, 89958–89971. [Google Scholar] [CrossRef]
- Wang, X.; Li, D.; Zhang, Y. Satellite Design; China Astronautic Publishing House: Beijing, China, 2014; ISBN 978-7-5159-0827-4. [Google Scholar]
- Qu, D.; Lu, Y.; Tao, Y.; Wang, M.; Zhao, X.; Lei, X. Study of Laser Gyro Temperature Compensation Technique on LINS. In Proceedings of the 2019 26th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, Russia, 27–29 May 2019; IEEE: Saint Petersburg, Russia; pp. 1–6. [Google Scholar]
- Huang, H.-Z.; Yu, K.; Huang, T.; Li, H.; Qian, H.-M. Reliability Estimation for Momentum Wheel Bearings Considering Frictional Heat. Eksploat. I Niezawodn. Maint. Reliab. 2020, 22, 6–14. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Z.; Lei, M. Research on Concept of Digital Satellite. Aerosp. Shanghai 2021, 38, 1–12. [Google Scholar] [CrossRef]
- Tang, Z.; Xu, Y.; Jiang, B.; Liao, H.; Zhao, Y. Integrated Structure and Precision Control of Flat Voice Coil Actuator for Non-contact Satellite. J. Eng. 2019, 2019, 566–570. [Google Scholar] [CrossRef]
- Zhong, X.; He, Y.; Liu, Q.; Wei, X. Power Control Approach in Distributed Satellite Cluster Network Based on Presetting and Prediction. In Proceedings of the 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chongqing, China, 20–22 May 2016; IEEE: Chongqing, China; pp. 265–269. [Google Scholar]
- Feng, T.; Chen, X.; Zhang, J.; Guo, J. Passive Satellite Solar Panel Thermal Control with Long-Wave Cut-Off Filter-Coated Solar Cells. Aerospace 2023, 10, 108. [Google Scholar] [CrossRef]
- Li, Z.; Dong, Y.; Li, P.; Li, H.; Liew, Y. A Real-Time Effectiveness Evaluation Method for Remote Sensing Satellite Clusters on Moving Targets. Sensors 2022, 22, 2993. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y. Study on the Theory and Application of Multidisciplinary Design Optimization for the Satellite System; Graduate School of National University of Defense Technology: Changsha, China, 2006. [Google Scholar]
- Dong, Y.; Chen, S.; Su, J.; Hu, D. Dynamic Simulation Technology of Satellite Attitude Control; Science Press: Beijing, China, 2010; ISBN 978-7-03-028248-4. [Google Scholar]
- Li, Z. Satellite Thermal Control Technology; China Astronautic Publishing House: Beijing, China, 2007; ISBN 978-7-80034-439-8. [Google Scholar]


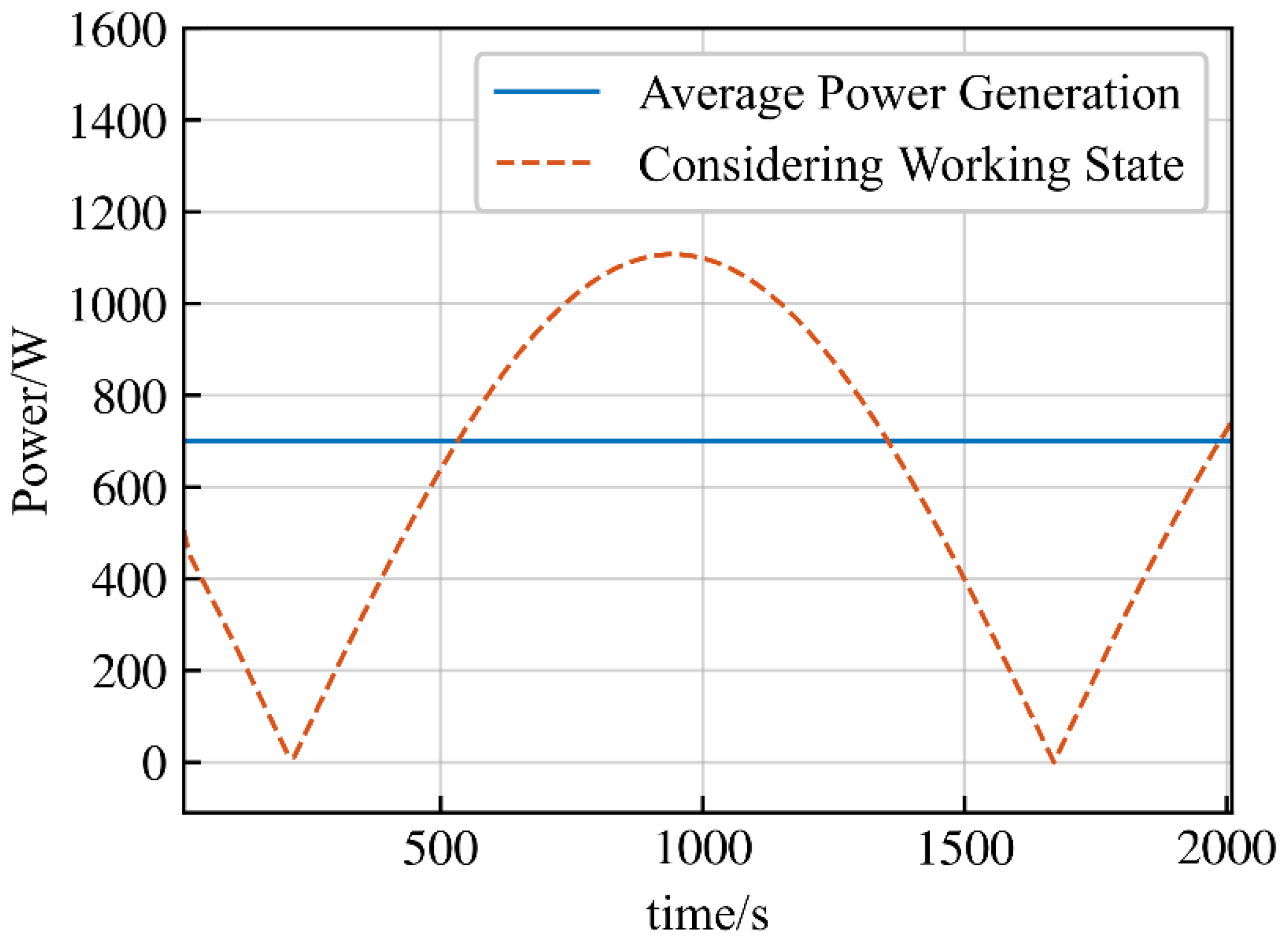



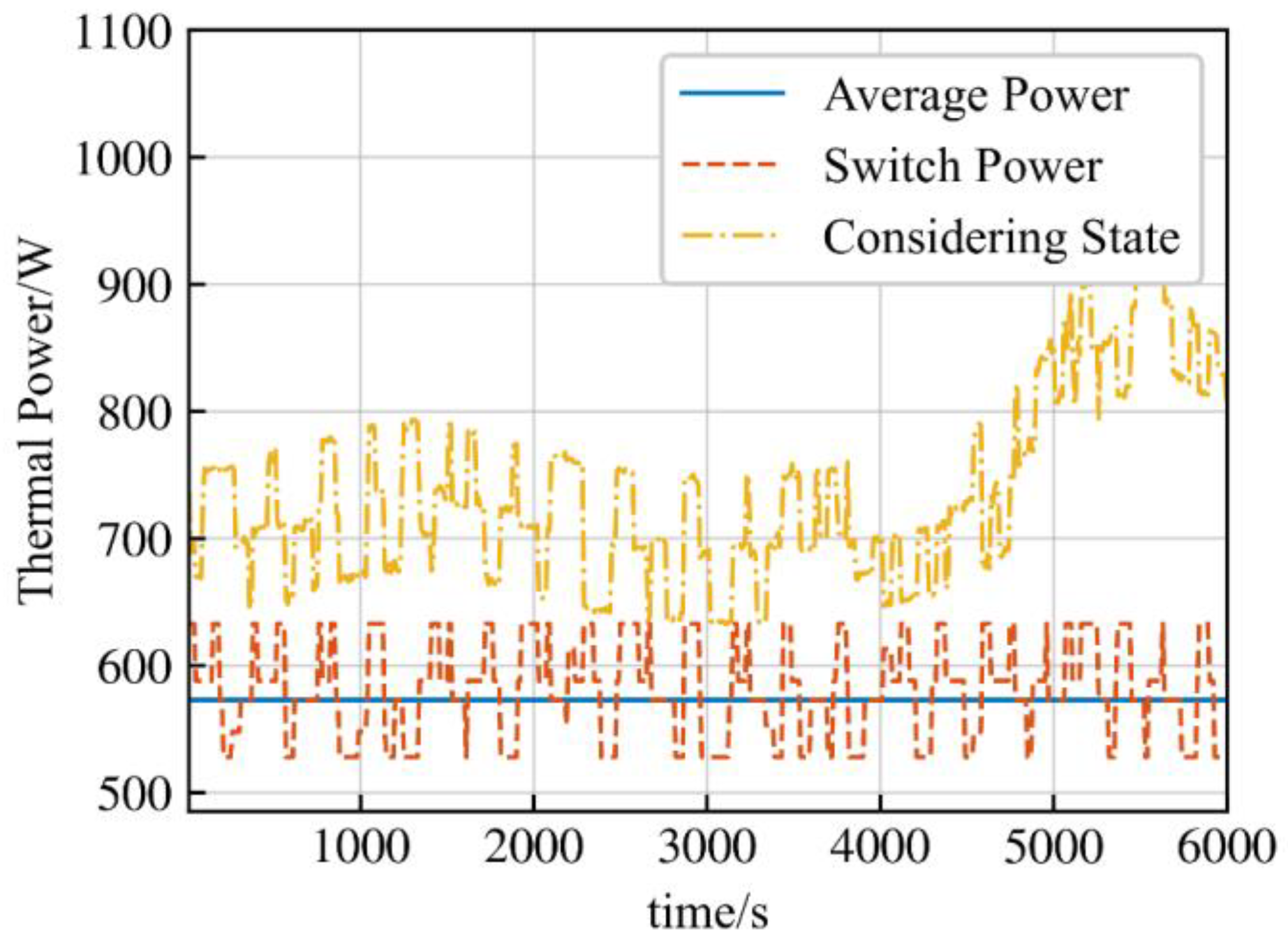



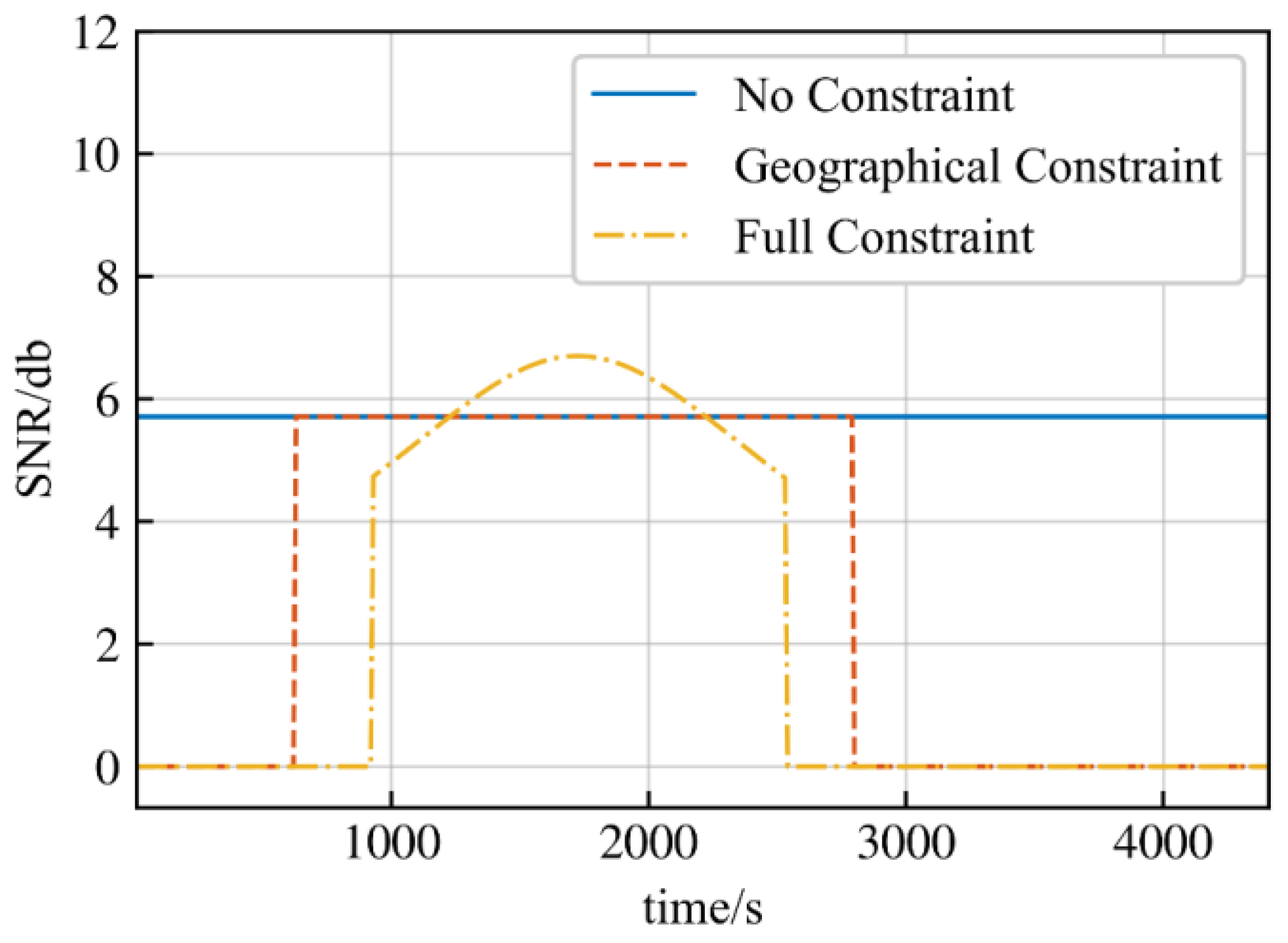
| Condition | Indicator | Coarse Granularity Model | Multi-Granularity Model | Finest Granularity Model |
|---|---|---|---|---|
| Summer shadow area | Attitude measurement accuracy, ° | {0.007221, 0.012858, 0.004928} | {0.000937, 0.003591, 0.002475} | {0.001569, 0.005330, 0.005320} |
| Attitude pointing accuracy, ° | {0.00081109, 0.00073728, 0.00087788} | {5.9431 × 10−5, 5.7519 × 10−5, 1.9169 × 10−5} | {4.5744 × 10−5, 7.9321 × 10−5, 1.9912 × 10−5} | |
| Attitude stable accuracy, °/s | {1.7563 × 10−5, 0.061789, 2.6152 × 10−5} | {3.6824 × 10−6, 0.0010768, 1.2905 × 10−6} | {0.000259, 0.022711, 9.5401 × 10−5} | |
| Summer light area | Attitude measurement accuracy, ° | {0.001023, 0.006607, 0.001043} | {0.000617, 0.002891, 0.002348} | {0.0013569, 0.0033304, 0.0015784} |
| Attitude pointing accuracy, ° | {0.00070272, 0.00021307, 0.00042044} | {4.6534 × 10−5, 5.8420 × 10−5, 2.9331 × 10−5} | {0.00001477, 0.00003382, 0.00012180} | |
| Attitude stable accuracy, °/s | {1.4804 × 10−5, 0.061776, 2.0781 × 10−5} | {3.6824 × 10−6, 0.001077, 1.2905 × 10−6} | {0.00025907, 0.061711, 9.5401 × 10−5} | |
| Winter shadow area | Attitude measurement accuracy, ° | {0.006816, 0.005794, 0.006563} | {0.000855, 0.002739, 0.001000} | {0.0001711, 0.0002992, 0.000143} |
| Attitude pointing accuracy, ° | {0.00065985, 0.00075851, 0.00054515} | {5.97 × 10−5, 5.9081 × 10−5, 1.9995 × 10−5} | {0.0033213, 0.0033195, 0.0011095} | |
| Attitude stable accuracy, °/s | {1.906 × 10−5, 0.061826, 2.2578 × 10−5} | {3.9381 × 10−6, 0.0010763, 1.4968 × 10−6} | {0.00020918, 0.061692, 6.9702 × 10−5} | |
| Winter light area | Attitude measurement accuracy, ° | {0.001309, 0.007855, 0.000871} | {0.000117, 0.001419, 0.004534} | {0.000175, 0.000647, 0.005868} |
| Attitude pointing accuracy, ° | {0.00056375, 0.00024599, 0.00098029} | {6.2353 × 10−5, 3.4354 × 10−5, 2.4509 × 10−5} | {0.00358970, 0.00338150, 0.00096535} | |
| Attitude stable accuracy, °/s | {1.357 × 10−5, 0.061808, 2.3135 × 10−5} | {2.3445 × 10−6, 0.001668, 4.9828 × 10−6} | {0.00025907, 0.061711, 1.4388 × 10−5} |
| Indicator | Coarse Granularity Model | Multi-Granularity Model | Finest Granularity Model |
|---|---|---|---|
| Maximum output power of the solar array, W | 1000 | 1189.5991 | 1189.603 |
| Maximum discharge depth of the battery, % | 2.5763 | 2.8437 | 2.8433 |
| Propellant extrusion efficiency, % | 0.03018 | 0.023637 | 0.023789 |
| Propellant specific impulse, m/s | 440.68875 | 440.68875 | 440.68875 |
| Condition | Indicator | Coarse Granularity Model | Multi-Granularity Model | Finest Granularity Model |
|---|---|---|---|---|
| Begin of lifespan | Average temperature of the satellite, °C | −10.07 | −20.5 | incalculable |
| Maximum temperature of the satellite, °C | 5.45 | −11.9 | incalculable | |
| Minimum temperature of the satellite, °C | −46.76 | −72.24 | incalculable | |
| Maximum temperature of the device, °C | 5.45 | 3.52 | incalculable | |
| Minimum temperature of the device, °C | −46.76 | −30.24 | incalculable | |
| End of lifespan | Average temperature of the satellite, °C | 2.45 | −15.42 | incalculable |
| Maximum temperature of the satellite, °C | 18.57 | 7.28 | incalculable | |
| Minimum temperature of the satellite, °C | −25.06 | −53.64 | incalculable | |
| Maximum temperature of the device, °C | 18.57 | 17.34 | incalculable | |
| Minimum temperature of the device, °C | −25.06 | −13.09 | incalculable |
| Indicator | Ideal Visible Model | Earth Occlusion Model | Finest Granularity Model |
|---|---|---|---|
| Discovery probability, % | 100 | 98 | 94 |
| Discovery response time, s | 0 | 71.5 | 88.8 |
| Payload data rate, kbps | 1.5 | 1.5 | 1.4 |
| Track telemetry and control coverage, % | 100 | 41.7 | 28.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, M.; Dong, Y. Multi-Granularity Modeling Method for Effectiveness Evaluation of Remote Sensing Satellites. Remote Sens. 2023, 15, 4335. https://doi.org/10.3390/rs15174335
Lei M, Dong Y. Multi-Granularity Modeling Method for Effectiveness Evaluation of Remote Sensing Satellites. Remote Sensing. 2023; 15(17):4335. https://doi.org/10.3390/rs15174335
Chicago/Turabian StyleLei, Ming, and Yunfeng Dong. 2023. "Multi-Granularity Modeling Method for Effectiveness Evaluation of Remote Sensing Satellites" Remote Sensing 15, no. 17: 4335. https://doi.org/10.3390/rs15174335
APA StyleLei, M., & Dong, Y. (2023). Multi-Granularity Modeling Method for Effectiveness Evaluation of Remote Sensing Satellites. Remote Sensing, 15(17), 4335. https://doi.org/10.3390/rs15174335






