A Novel Heterogeneous Ensemble Framework Based on Machine Learning Models for Shallow Landslide Susceptibility Mapping
Abstract
:1. Introduction
2. Study Area and Dataset
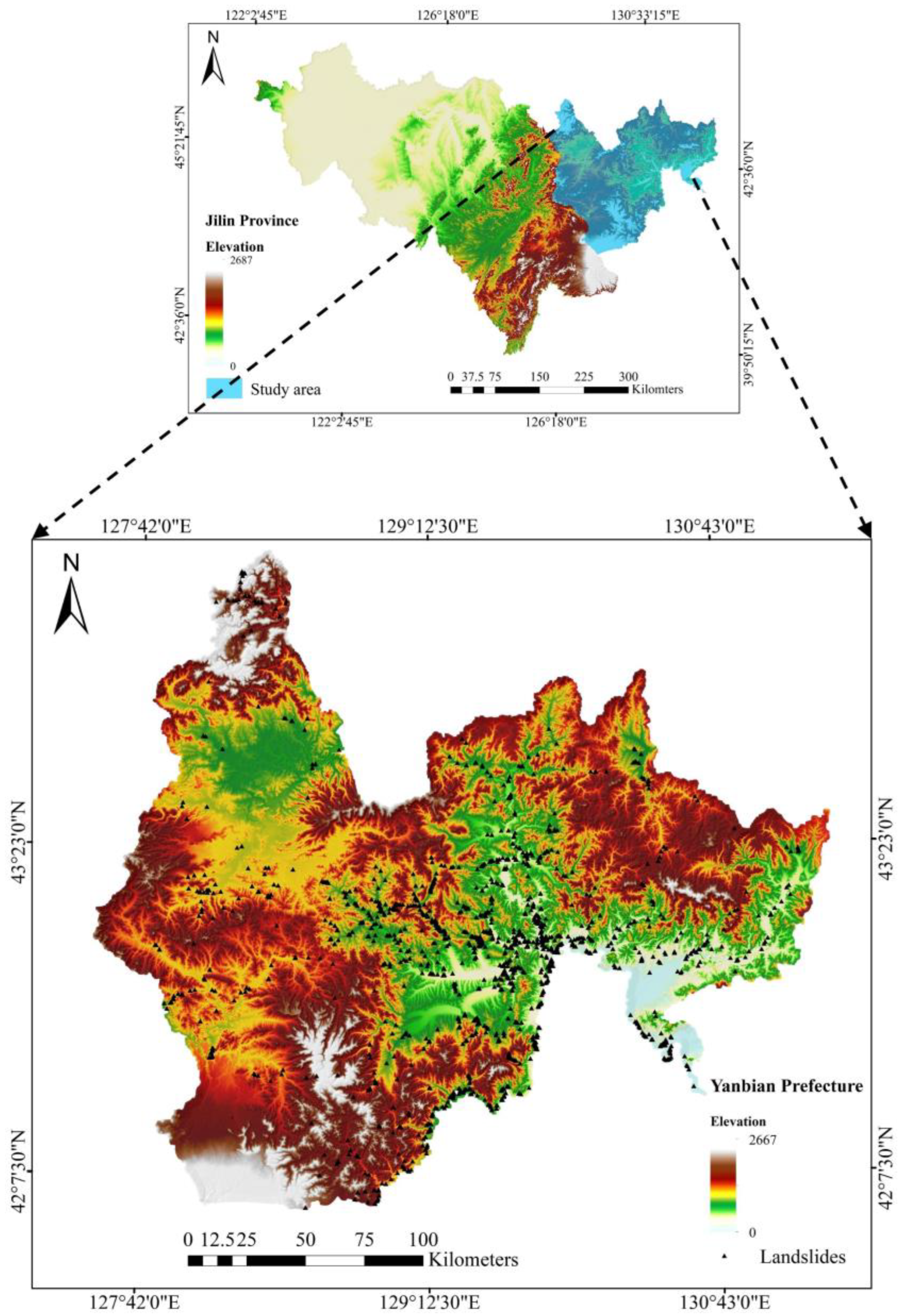
2.1. Description of the Area
2.2. Landslide Inventory
2.3. Data Preparation
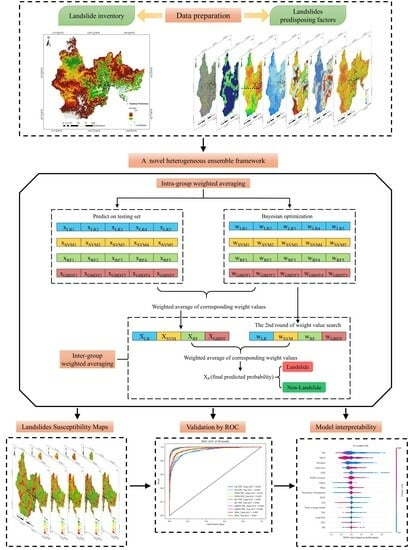
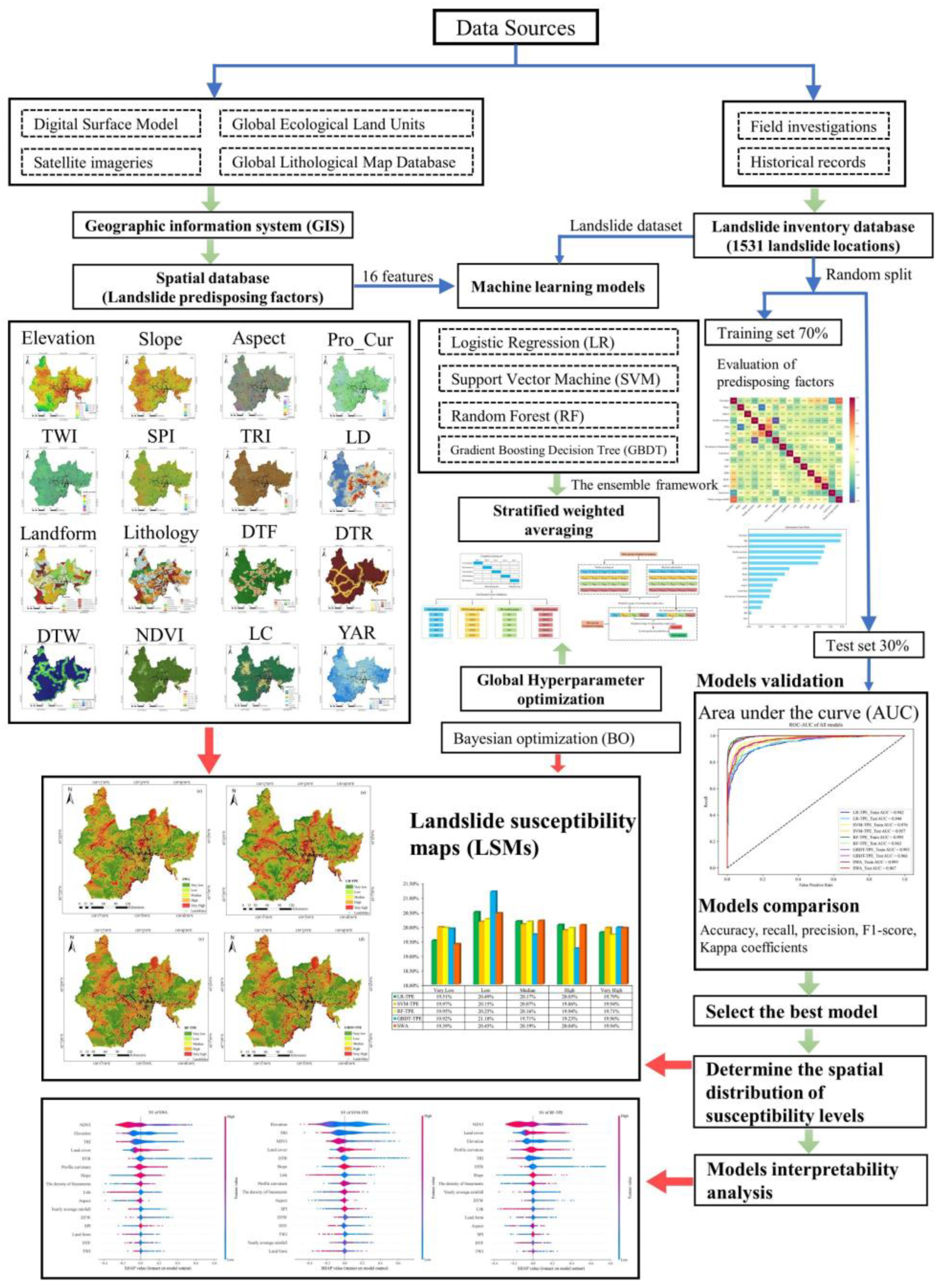
3. Methodology
3.1. Evaluation of Predisposing Factors
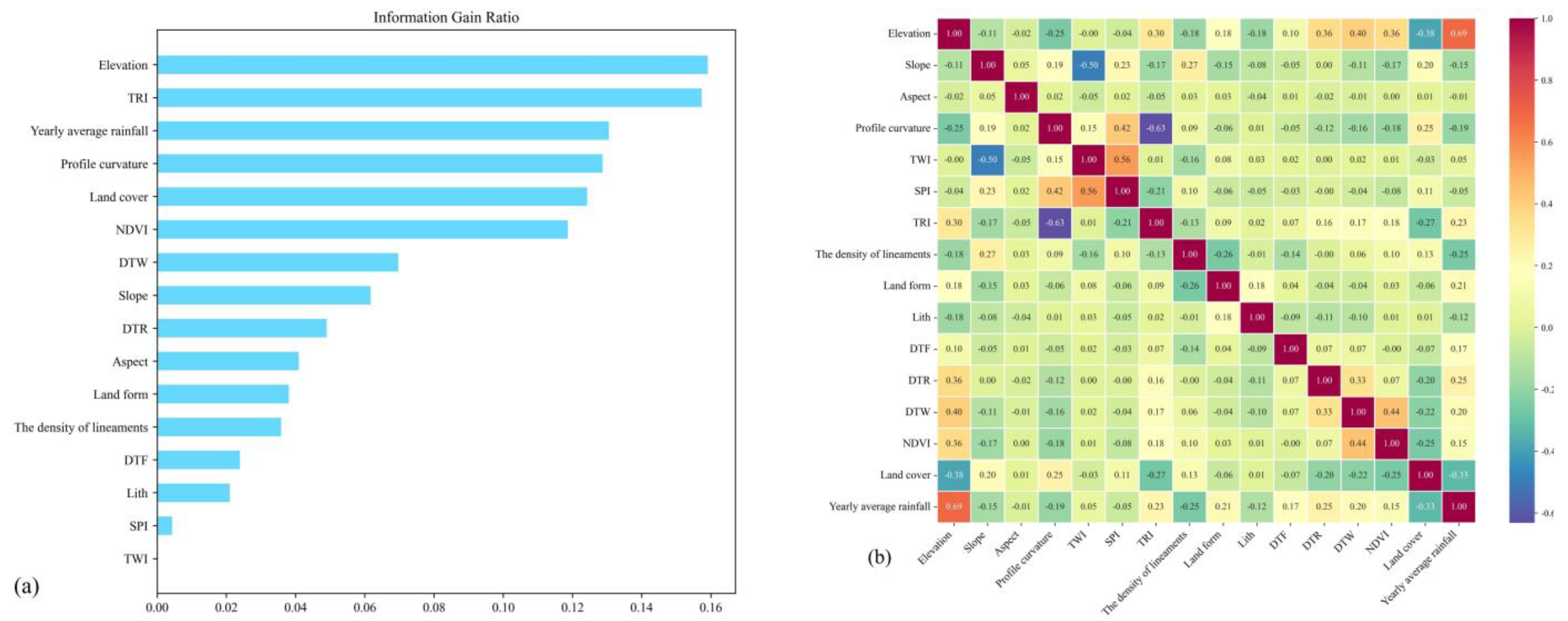
3.1.1. Information Gain Ratio
3.1.2. Multicollinearity Analysis
3.2. Machine Learning Models
3.2.1. Logistic Regression
3.2.2. Support Vector Machine
3.2.3. Random Forest
3.2.4. Gradient Boosting Decision Tree
3.3. Bayesian Optimization
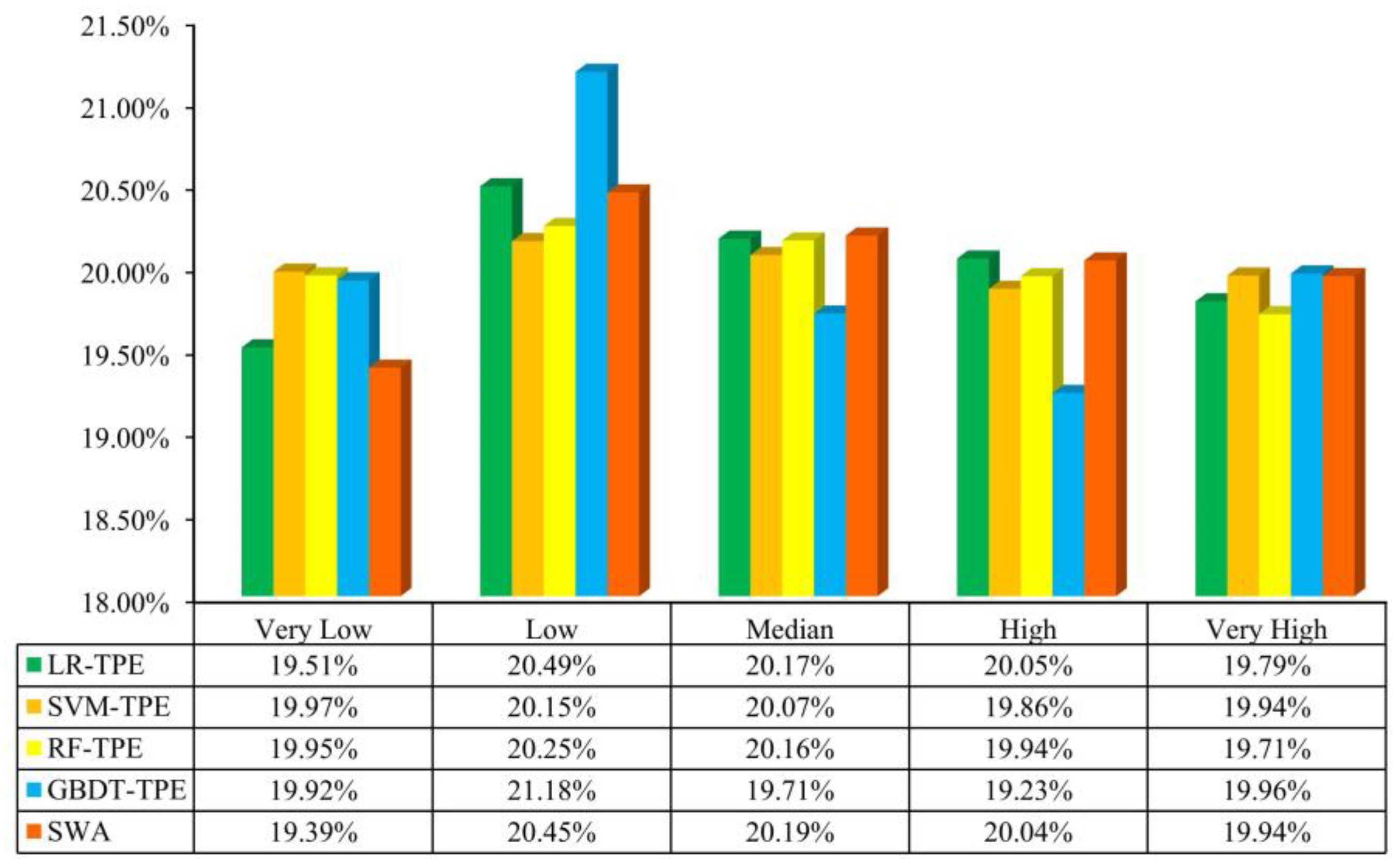
3.4. Stratified Weighted Averaging
3.5. Model Evaluation Metrics
4. Result
4.1. Factor Assessment Results
4.2. Landslide Susceptibility Maps
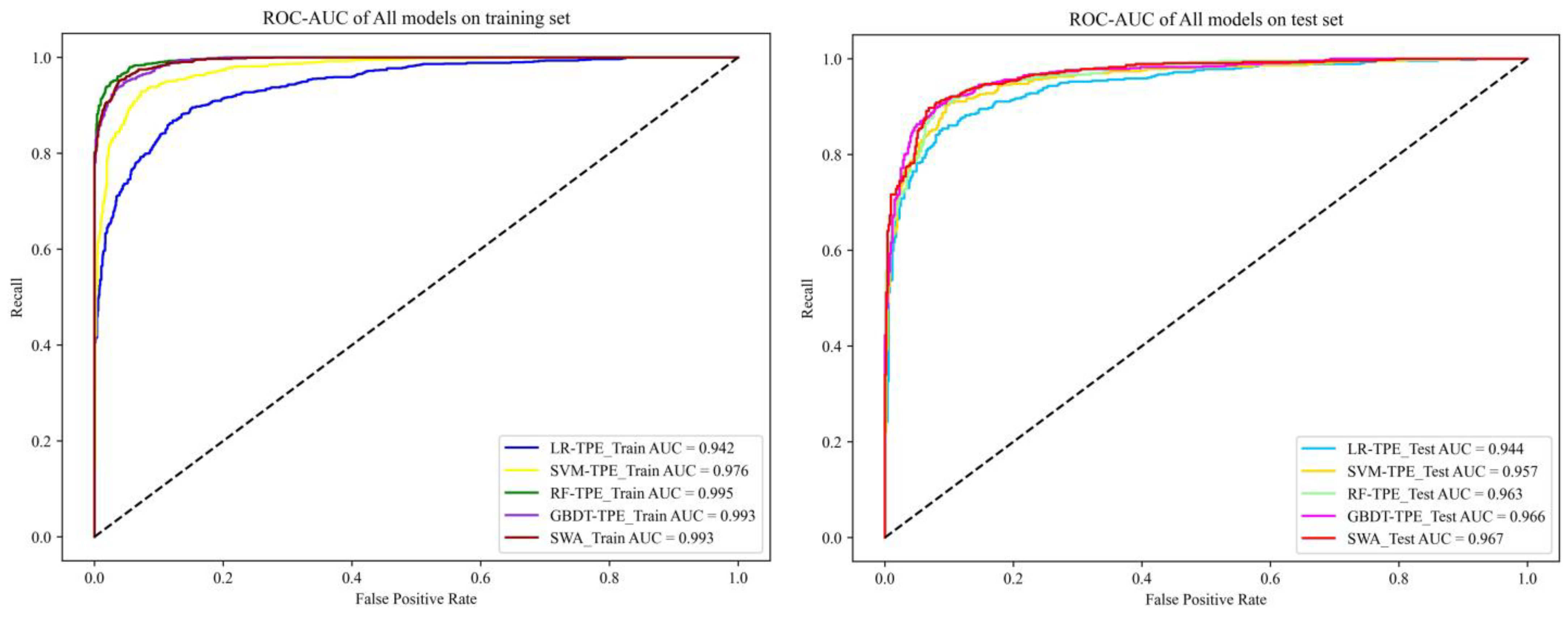
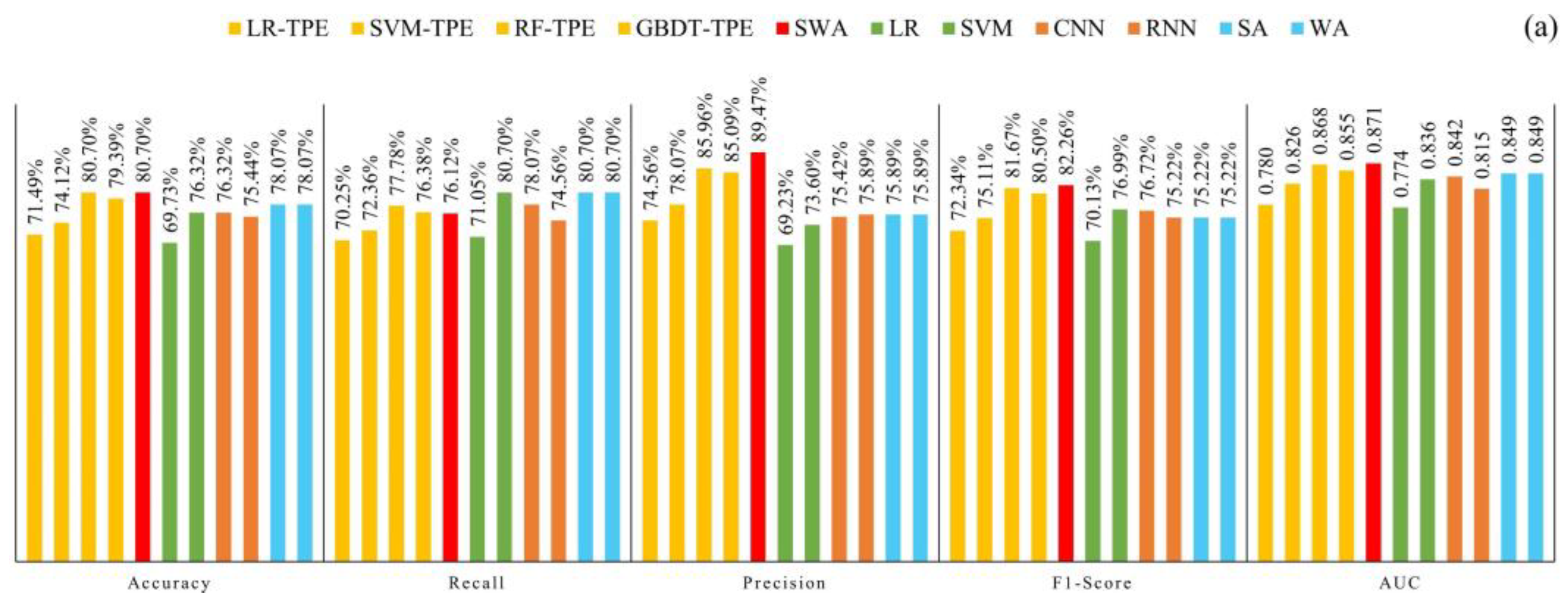
4.3. Model Validation and Comparison
5. Discussion
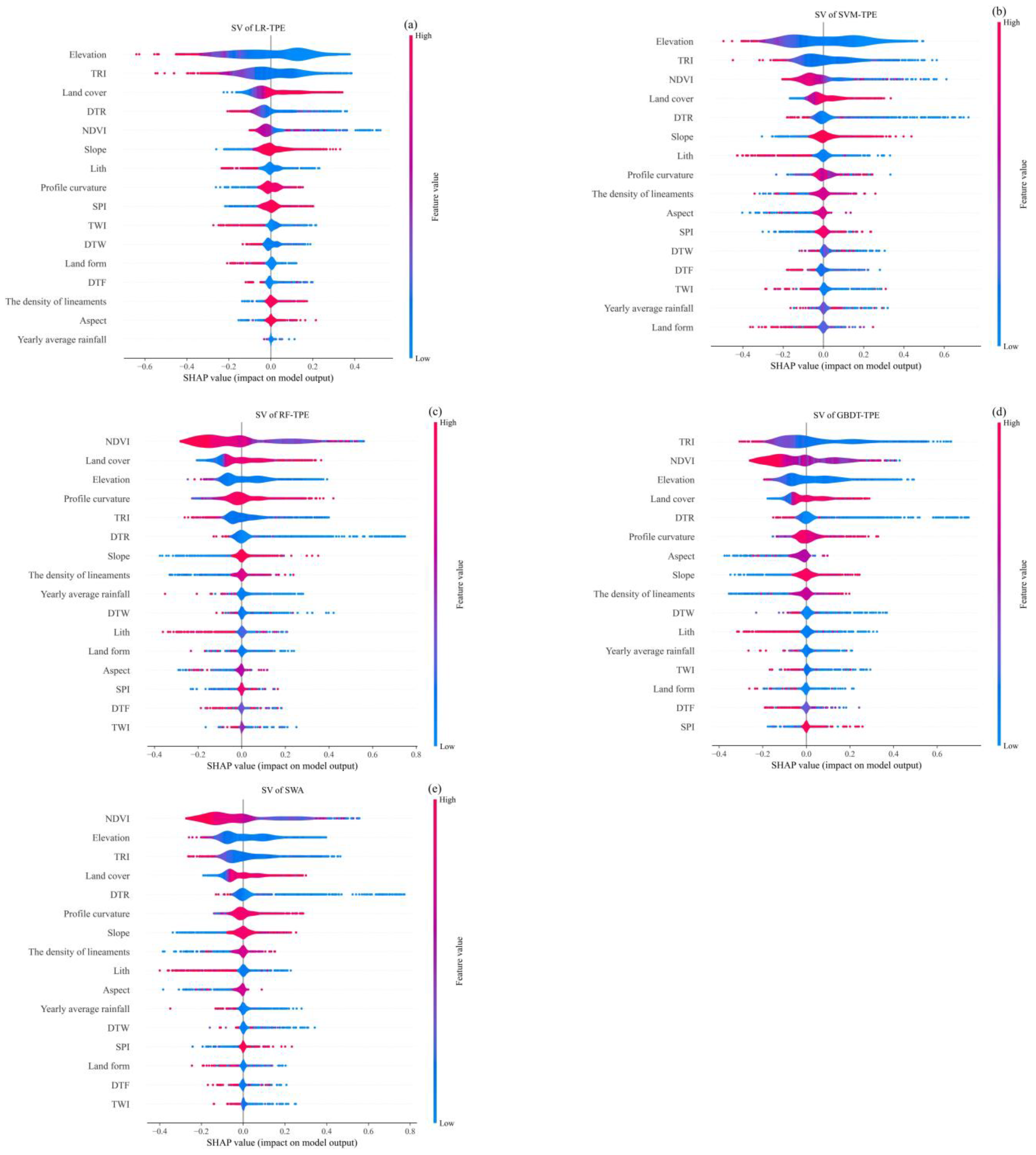
5.1. Analysis of Model Interpretability
5.2. Model Optimization
5.3. Exploration of Model Generalization Ability
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote. Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Chang, Z.; Catani, F.; Huang, F.; Liu, G.; Meena, S.R.; Huang, J.; Zhou, C. Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotech. Eng. 2023, 15, 1127–1143. [Google Scholar] [CrossRef]
- De Graff, J.V.; Romesburg, H.C.; Ahmad, R.; McCalpin, J.P. Producing landslide-susceptibility maps for regional planning in data-scarce regions. Nat. Hazards 2012, 64, 729–749. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Kumaravel, P.; Rajamanickam, G.V. Assessing landslide susceptibility using Bayesian probability-based weight of evidence model. Bull. Eng. Geol. Environ. 2014, 73, 147–161. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Tran, T.-T.-T.; Bui, D.T. Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Advanced hyperparameter optimization for improved spatial prediction of shallow landslides using extreme gradient boosting (XGBoost). Bull. Eng. Geol. Environ. 2022, 81, 201. [Google Scholar] [CrossRef]
- Rehman, A.; Song, J.; Haq, F.; Mahmood, S.; Ahamad, M.I.; Basharat, M.; Sajid, M.; Mehmood, M.S. Multi-Hazard Susceptibility Assessment Using the Analytical Hierarchy Process and Frequency Ratio Techniques in the Northwest Himalayas, Pakistan. Remote. Sens. 2022, 14, 554. [Google Scholar] [CrossRef]
- Lin, J.; Chen, W.; Qi, X.; Hou, H. Risk assessment and its influencing factors analysis of geological hazards in typical mountain environment. J. Clean. Prod. 2021, 309, 127077. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total. Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. CATENA 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Lv, L.; Chen, T.; Dou, J.; Plaza, A. A hybrid ensemble-based deep-learning framework for landslide susceptibility mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102713. [Google Scholar] [CrossRef]
- Zeng, T.; Wu, L.; Peduto, D.; Glade, T.; Hayakawa, Y.S.; Yin, K. Ensemble learning framework for landslide susceptibility mapping: Different basic classifier and ensemble strategy. Geosci. Front. 2023, 14, 101645. [Google Scholar] [CrossRef]
- Yao, J.; Qin, S.; Qiao, S.; Liu, X.; Zhang, L.; Chen, J. Application of a two-step sampling strategy based on deep neural network for landslide susceptibility mapping. Bull. Eng. Geol. Environ. 2022, 81, 148. [Google Scholar] [CrossRef]
- Godt, J.; Baum, R.; Savage, W.; Salciarini, D.; Schulz, W.; Harp, E. Transient deterministic shallow landslide modeling: Requirements for susceptibility and hazard assessments in a GIS framework. Eng. Geol. 2008, 102, 214–226. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.; Pradhan, B. Spatial landslide susceptibility assessment using machine learning techniques assisted by additional data created with generative adversarial networks. Geosci. Front. 2021, 12, 625–637. [Google Scholar] [CrossRef]
- Guo, Z.; Ferrer, J.V.; Hürlimann, M.; Medina, V.; Puig-Polo, C.; Yin, K.; Huang, D. Shallow landslide susceptibility assessment under future climate and land cover changes: A case study from southwest China. Geosci. Front. 2023, 14, 101542. [Google Scholar] [CrossRef]
- Yang, C.; Liu, L.-L.; Huang, F.; Huang, L.; Wang, X.-M. Machine learning-based landslide susceptibility assessment with optimized ratio of landslide to non-landslide samples. Gondwana Res. 2022, in press. [CrossRef]
- Ngo, P.T.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Kaur, H.; Gupta, S.; Parkash, S.; Thapa, R.; Gupta, A.; Khanal, G.C. Evaluation of landslide susceptibility in a hill city of Sikkim Himalaya with the perspective of hybrid modelling techniques. Ann. GIS 2019, 25, 113–132. [Google Scholar] [CrossRef]
- Sayre, R.; Dangermond, J.; Frye, C.; Vaughan, R.; Aniello, P.; Breyer, S.P.; Cribbs, D.; Hopkins, D.; Nauman, R.; Derrenbacher, W.; et al. A New Map of Global Ecological Land Units—An Ecophysiographic Stratification Approach; USGS Publications Warehouse: Washington, DC, USA, 2014.
- Hartmann, J.; Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochem. Geophys. Geosyst. 2012, 13, 5–6. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Panahi, M.; Gayen, A.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of landslide susceptibility using hybrid support vector regression (SVR) and the adaptive neuro-fuzzy inference system (ANFIS) with various metaheuristic algorithms. Sci. Total. Environ. 2020, 741, 139937. [Google Scholar] [CrossRef]
- Tao, Z.; Geng, Q.; Zhu, C.; He, M.; Cai, H.; Pang, S.; Meng, X. The mechanical mechanisms of large-scale toppling failure for counter-inclined rock slopes. J. Geophys. Eng. 2019, 16, 541–558. [Google Scholar] [CrossRef]
- Saha, S.; Arabameri, A.; Saha, A.; Blaschke, T.; Ngo, P.T.T.; Nhu, V.H.; Band, S.S. Prediction of landslide susceptibility in Rudraprayag, India using novel ensemble of conditional probability and boosted regression tree-based on cross-validation method. Sci. Total. Environ. 2021, 764, 142928. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Hoang, N.-D.; Nguyen, H.; Ngo, P.T.T.; Bui, T.T.; Hoa, P.V.; Samui, P.; Bui, D.T. Effectiveness assessment of Keras based deep learning with different robust optimization algorithms for shallow landslide susceptibility mapping at tropical area. Catena 2020, 188, 104458. [Google Scholar] [CrossRef]
- Sahin, E.K.; Colkesen, I.; Acmali, S.S.; Akgun, A.; Aydinoglu, A.C. Developing comprehensive geocomputation tools for landslide susceptibility mapping: LSM tool pack. Comput. Geosci. 2020, 144, 104592. [Google Scholar] [CrossRef]
- Singh, P.; Sharma, A.; Sur, U.; Rai, P.K. Comparative landslide susceptibility assessment using statistical information value and index of entropy model in Bhanupali-Beri region, Himachal Pradesh, India. Environ. Dev. Sustain. 2021, 23, 5233–5250. [Google Scholar] [CrossRef]
- Van Dao, D.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Van Phong, T.; Ly, H.-B.; Le, T.-T.; Trinh, P.T.; et al. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. catena 2020, 188, 104451. [Google Scholar] [CrossRef]
- Dong, M.; Zhang, F.; Yu, C.; Lv, J.; Zhou, H.; Li, Y.; Zhong, Y. Influence of a Dominant Fault on the Deformation and Failure Mode of Anti-dip Layered Rock Slopes. KSCE J. Civ. Eng. 2022, 26, 3430–3439. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. catena 2012, 96, 28–40. [Google Scholar] [CrossRef]
- Fan, J.; Guo, Z.; Tao, Z.; Wang, F. Method of equivalent core diameter of actual fracture section for the determination of point load strength index of rocks. Bull. Eng. Geol. Environ. 2021, 80, 4575–4585. [Google Scholar] [CrossRef]
- Desalegn, H.; Mulu, A.; Damtew, B. Landslide susceptibility evaluation in the Chemoga watershed, upper Blue Nile, Ethiopia. Nat. Hazards 2022, 113, 1391–1417. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Grabowski, D.; Laskowicz, I.; Małka, A.; Rubinkiewicz, J. Geoenvironmental conditioning of landsliding in river valleys of lowland regions and its significance in landslide susceptibility assessment: A case study in the Lower Vistula Valley, Northern Poland. Geomorphology 2022, 419, 108490. [Google Scholar] [CrossRef]
- Medina, V.; Hürlimann, M.; Guo, Z.; Lloret, A.; Vaunat, J. Fast physically-based model for rainfall-induced landslide susceptibility assessment at regional scale. catena 2021, 201, 105213. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Benardos, A. Estimating landslide susceptibility through a artificial neural network classifier. Nat. Hazards 2014, 74, 1489–1516. [Google Scholar] [CrossRef]
- Yao, J.; Qin, S.; Qiao, S.; Che, W.; Chen, Y.; Su, G.; Miao, Q. Assessment of Landslide Susceptibility Combining Deep Learning with Semi-Supervised Learning in Jiaohe County, Jilin Province, China. Appl. Sci. 2020, 10, 5640. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kornejady, A.; Kerle, N.; Shabani, F. Investigating the effects of different landslide positioning techniques, landslide partitioning approaches, and presence-absence balances on landslide susceptibility mapping. catena 2020, 187, 104364. [Google Scholar] [CrossRef]
- Huqqani, I.A.; Tay, L.T.; Mohamad-Saleh, J. Spatial landslide susceptibility modelling using metaheuristic-based machine learning algorithms. Eng. Comput. 2023, 39, 867–891. [Google Scholar] [CrossRef]
- Mandal, K.; Saha, S.; Mandal, S. Applying deep learning and benchmark machine learning algorithms for landslide susceptibility modelling in Rorachu river basin of Sikkim Himalaya, India. Geosci. Front. 2021, 12, 101203. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.-X. Modeling landslide susceptibility using LogitBoost alternating decision trees and forest by penalizing attributes with the bagging ensemble. Sci. Total. Environ. 2020, 718, 137231. [Google Scholar] [CrossRef] [PubMed]
- Kadavi, P.R.; Lee, C.-W.; Lee, S. Landslide-susceptibility mapping in Gangwon-do, South Korea, using logistic regression and decision tree models. Environ. Earth Sci. 2019, 78, 116. [Google Scholar] [CrossRef]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide susceptibility mapping & prediction using Support Vector Machine for Mandakini River Basin, Garhwal Himalaya, India. Geomorphology 2017, 295, 115–125. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Erratum to: Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 1315–1318. [Google Scholar] [CrossRef]
- Sachdeva, S.; Bhatia, T.; Verma, A.K. A novel voting ensemble model for spatial prediction of landslides using GIS. Int. J. Remote. Sens. 2020, 41, 929–952. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In International Conference on Neural Information Processing Systems; Curran Associates Inc.: Dutchess, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Liu, R.; Yang, X.; Xu, C.; Wei, L.; Zeng, X. Comparative Study of Convolutional Neural Network and Conventional Machine Learning Methods for Landslide Susceptibility Mapping. Remote. Sens. 2022, 14, 321. [Google Scholar] [CrossRef]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Bui, D.T.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Pradhan, B.; Sameen, M.I.; Al-Najjar, H.A.H.; Sheng, D.; Alamri, A.M.; Park, H.-J. A Meta-Learning Approach of Optimisation for Spatial Prediction of Landslides. Remote. Sens. 2021, 13, 4521. [Google Scholar] [CrossRef]
- Ozaki, Y.; Tanigaki, Y.; Watanabe, S.; Onishi, M. Multiobjective tree-structured parzen estimator for computationally expensive optimization problems. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancun, Mexico, 8–12 July 2020. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T.; Nazmfar, H. GIS-based ordered weighted averaging and Dempster–Shafer methods for landslide susceptibility mapping in the Urmia Lake Basin, Iran. Int. J. Digit. Earth 2014, 7, 688–708. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen-Thoi, T.; Qi, C.; Van Phong, T.; Dou, J.; Ho, L.S.; Van Le, H.; Prakash, I. Coupling RBF neural network with ensemble learning techniques for landslide susceptibility mapping. Catena 2020, 195, 104805. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.-T.; Van Liem, N.; Trinh, P.T. Comparing the prediction performance of a Deep Learning Neural Network model with conventional machine learning models in landslide susceptibility assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A Comprehensive Assessment of XGBoost Algorithm for Landslide Susceptibility Mapping in the Upper Basin of Ataturk Dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical landslide early warning systems. Earth-Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Petschko, H.; Glade, T. Exploring discrepancies between quantitative validation results and the geomorphic plausibility of statistical landslide susceptibility maps. Geomorphology 2016, 262, 8–23. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:abs/1705.0787. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A.; Yilmaz, E.O. Shared Blocks-Based Ensemble Deep Learning for Shallow Landslide Susceptibility Mapping. Remote. Sens. 2021, 13, 4776. [Google Scholar] [CrossRef]
- Martinez, A.d.l.I.; Labib, S. Demystifying normalized difference vegetation index (NDVI) for greenness exposure assessments and policy interventions in urban greening. Environ. Res. 2023, 220, 115155. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.P.; Jiang, B.; Kinzig, A.P.; Lee, K.N.; Ouyang, Z. Linking ecosystem characteristics to final ecosystem services for public policy. Ecol. Lett. 2015, 18, 108–118. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Xiao, L.; Guo, Q.; Liu, Y.; Mao, Q.; Kareiva, P. Evidence of causality between economic growth and vegetation dynamics and implications for sustainability policy in Chinese cities. J. Clean. Prod. 2020, 251, 119550. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, C.; He, M.; Dong, M.; Zhang, G.; Zhang, F. Failure Mechanism and Long Short-Term Memory Neural Network Model for Landslide Risk Prediction. Remote. Sens. 2022, 14, 166. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. A comparative study of heterogeneous ensemble-learning techniques for landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2021, 35, 321–347. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Steger, S.; Mair, V.; Kofler, C.; Pittore, M.; Zebisch, M.; Schneiderbauer, S. Correlation does not imply geomorphic causation in data-driven landslide susceptibility modelling—Benefits of exploring landslide data collection effects. Sci. Total. Environ. 2021, 776, 145935. [Google Scholar] [CrossRef]
- Lima, P.; Steger, S.; Glade, T. Counteracting flawed landslide data in statistically based landslide susceptibility modelling for very large areas: A national-scale assessment for Austria. Landslides 2021, 18, 3531–3546. [Google Scholar] [CrossRef]
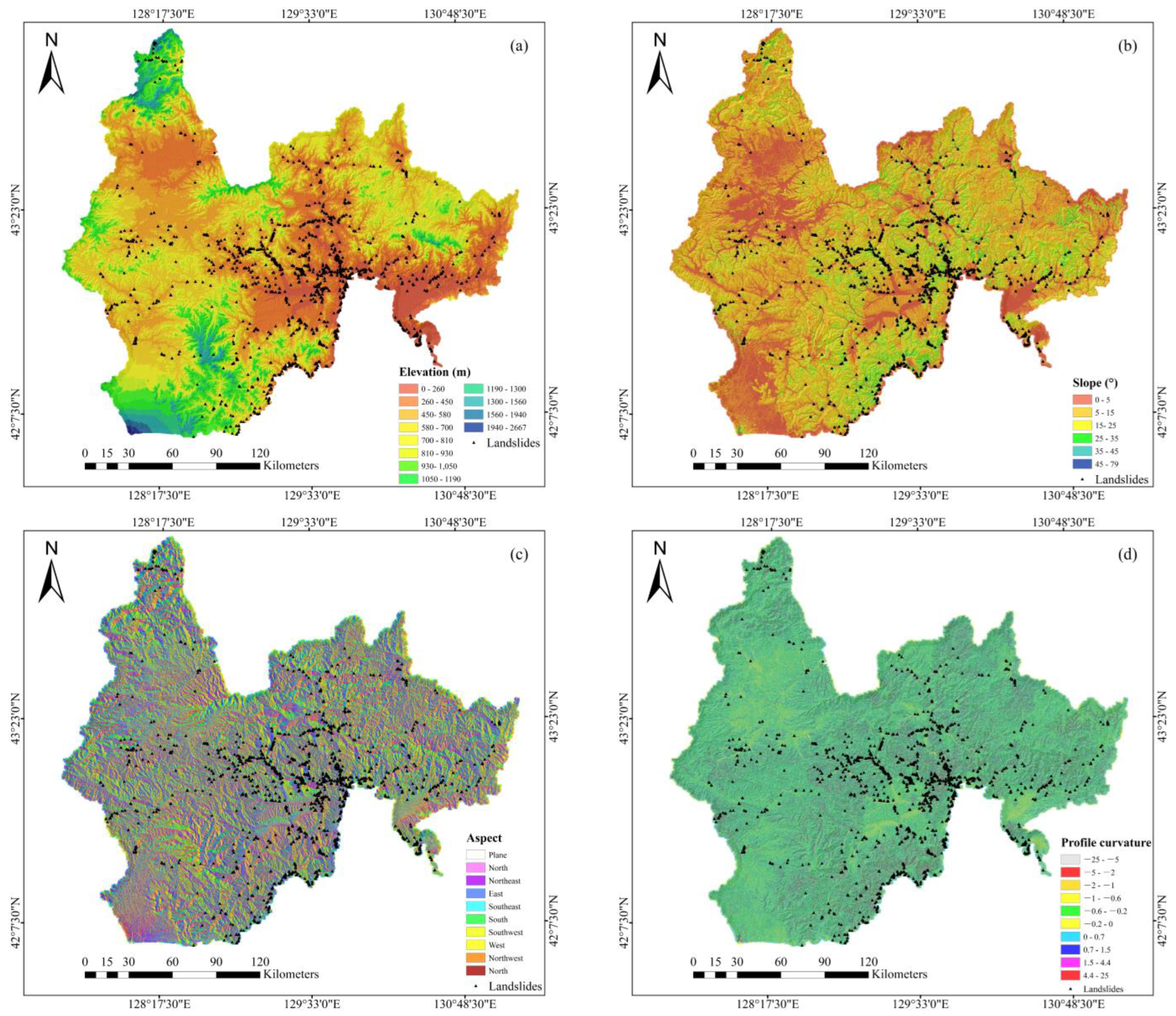







| Predisposing Factors | Data Type | Source | Scale/Resolution |
|---|---|---|---|
| Elevation | Raster | Derived from ALOS Global Surface Model ‘ALOS World 3D-30 m’ (http://www.eorc.jaxa.jp/ALOS/en/aw3d30/data/index.htm, accessed on 1 November 2022) | 30 m × 30 m |
| Slope | |||
| Aspect | |||
| Profile curvature | |||
| TWI | |||
| SPI | |||
| TRI | |||
| The density of lineaments | |||
| Landform | Raster | Derived from A New Map of Global Ecological Land Units | 250 m × 250 m |
| Lithology | Derived from A New Global Lithological Map Database | ||
| NDVI | Raster | Derived from Resource and Environment Science and Data Center (https://www.resdc.cn/, accessed on 8 October 2022) | 30 m × 30 m |
| Yearly average rainfall | Derived from Fine Resolution Mapping of Mountain Environment (http://digitalmountain.imde.ac.cn/home, accessed on 18 September 2022) | ||
| Land cover | Derived from ESRI (https://livingatlas.arcgis.com/landcover/, accessed on 15 October 2022) | 10 m × 10 m | |
| Distance to faults | Polygon | Derived from Seismic Fault Active Survey Data Center (https://www.activefault-datacenter.cn/, accessed on 20 September 2022) | 1:500,000 |
| Distance to roads | Derived from National Platform for Common Geospatial Information Services (https://www.tianditu.gov.cn/, accessed on 22 September 2022) | 1:500,000 | |
| Distance to the water system |
| Measures/Methods | LR-TPE | SVM-TPE | RF-TPE | GBDT-TPE | SWA |
|---|---|---|---|---|---|
| TP | 392 | 414 | 411 | 409 | 408 |
| FN | 50 | 50 | 42 | 40 | 34 |
| FP | 67 | 45 | 48 | 50 | 51 |
| TN | 478 | 478 | 486 | 488 | 494 |
| Accuracy | 88.15% | 90.37% | 90.37% | 90.88% | 91.39% |
| Recall | 88.69% | 89.22% | 90.63% | 91.09% | 92.31% |
| Precision | 85.40% | 90.20% | 88.45% | 89.11% | 88.91% |
| F1-Score | 0.870 | 0.897 | 0.895 | 0.901 | 0.906 |
| Kappa | 0.761 | 0.807 | 0.817 | 0.817 | 0.827 |
| Parameters | ‘penalty’ | ‘C’ | ‘tol’ | ‘max_iter’ | ‘solver’ |
|---|---|---|---|---|---|
| Selected range | [‘l1’, ’l2’] | [0.5, 3] | [0.0001, 0.1] | [100, 10,000] | [‘liblinear’, ’saga’] |
| Parameters | ‘kernal’ | ‘degree’ | ‘gamma’ | ‘class_weight’ | ‘C’ | ‘coef0’ |
|---|---|---|---|---|---|---|
| Selected range | [‘poly’, ’rbf’] | [0, 5] | [‘auto’, ‘scale’, [0.0001, 3]] | [None, ‘balanced’] | [0.001, 2] | [2, 7] |
| Parameters | ‘n_estimators’ | ‘criterion’ | ‘max_depth’ | ‘max_features’ | ‘min_samples_split’ |
|---|---|---|---|---|---|
| Selected range | [25, 50] | [‘gini’, ‘entropy’] | [4, 26] | [1, 10] | [4, 20] |
| Parameters | ‘n_estimators’ | ‘learning_rate’ | ‘criterion’ | ‘loss’ |
|---|---|---|---|---|
| Selected range | [130, 160] | [0.05, 2.05] | [‘friedman_mse’, ‘squared_error’] | [‘deviance’, ‘log_loss’, ‘exponential’] |
| Parameters | ‘max_depth’ | ‘subsample’ | ‘max_features’ | ‘min_impurity_decrease’ |
| Selected range | [5, 13] | [0.4, 0.8] | [‘log2’,’sqrt’,4,8,’auto’] | [0.4, 3.0] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Wang, C.; An, S.; Wang, Q.; Jiang, C. A Novel Heterogeneous Ensemble Framework Based on Machine Learning Models for Shallow Landslide Susceptibility Mapping. Remote Sens. 2023, 15, 4159. https://doi.org/10.3390/rs15174159
Tang H, Wang C, An S, Wang Q, Jiang C. A Novel Heterogeneous Ensemble Framework Based on Machine Learning Models for Shallow Landslide Susceptibility Mapping. Remote Sensing. 2023; 15(17):4159. https://doi.org/10.3390/rs15174159
Chicago/Turabian StyleTang, Haozhe, Changming Wang, Silong An, Qingyu Wang, and Chenglin Jiang. 2023. "A Novel Heterogeneous Ensemble Framework Based on Machine Learning Models for Shallow Landslide Susceptibility Mapping" Remote Sensing 15, no. 17: 4159. https://doi.org/10.3390/rs15174159
APA StyleTang, H., Wang, C., An, S., Wang, Q., & Jiang, C. (2023). A Novel Heterogeneous Ensemble Framework Based on Machine Learning Models for Shallow Landslide Susceptibility Mapping. Remote Sensing, 15(17), 4159. https://doi.org/10.3390/rs15174159