An Open Image Resizing Framework for Remote Sensing Applications and Beyond

Occorsio, Donatella; Ramella, Giuliana; Themistoclakis, Woula

doi:10.3390/rs15164039

Open AccessArticle

An Open Image Resizing Framework for Remote Sensing Applications and Beyond

by

Donatella Occorsio

^1,†

,

Giuliana Ramella

^2,*,†

and

Woula Themistoclakis

^2,†

¹

Department of Mathematics and Computer Science, University of Basilicata, Viale dell’Ateneo Lucano 10, 85100 Potenza, Italy

²

National Research Council (C.N.R.), Institute for Applied Computing “Mauro Picone”, Via P. Castellino, 111, 80131 Naples, Italy

^*

Author to whom correspondence should be addressed.

^†

These authors contributed equally to this work.

Remote Sens. 2023, 15(16), 4039; https://doi.org/10.3390/rs15164039

Submission received: 2 August 2023 / Revised: 8 August 2023 / Accepted: 8 August 2023 / Published: 15 August 2023

Download

Browse Figures

Versions Notes

Abstract

:

Image resizing (IR) has a crucial role in remote sensing (RS), since an image’s level of detail depends on the spatial resolution of the acquisition sensor; its design limitations; and other factors such as (a) the weather conditions, (b) the lighting, and (c) the distance between the satellite platform and the ground targets. In this paper, we assessed some recent IR methods for RS applications (RSAs) by proposing a useful open framework to study, develop, and compare them. The proposed framework could manage any kind of color image and was instantiated as a Matlab package made freely available on Github. Here, we employed it to perform extensive experiments across multiple public RS image datasets and two new datasets included in the framework to evaluate, qualitatively and quantitatively, the performance of each method in terms of image quality and statistical measures.

Keywords:

image resizing; image downscaling; remote sensing; image upscaling; remote sensing applications

1. Introduction

Remote sensing (RS) technology plays a crucial role in many fields, since it provides an efficient way to access a wide variety of information in real time for acquiring, detecting, analyzing, and monitoring the physical characteristics of an object or area without having any physical contact with it. Specifically, geoscience is one of the major fields in which RS technology is used to quantitatively and qualitatively study weather, forestry, agriculture, surface changes, biodiversity, and so on. The applications of geoscience extend far beyond mere data collection, as it aims to inform international policies through, for instance, environment monitoring, catastrophe prediction, and resource investigation.

The source of RS data is the electromagnetic radiation reflected/emitted by an object. The electromagnetic radiation is received by a sensor on an RS platform (towers/cranes at the ground level, helicopters/aircraft at the aerial level, and space shuttles/satellites at the space-borne level) and is converted into a signal that can be recorded and displayed in different formats: optical, infrared, radar, microwave, acoustic, and visual, according to the elaborative purpose. Different RS systems have been proposed, corresponding to each data source type [1,2,3,4].

In this paper, as a data source, we considered the RS visual images employed in RS applications (RSAs), referred to in the following simply as RS images. Specifically, we were interested in processing visual information in the same way as the human visual system (HVS), i.e., elaborating the information vector of visible light, a part of the electromagnetic spectrum, according to human perceptual laws and capabilities. In this framework, we were concerned with the notion of the scale representing, as reported in [5,6,7,8,9], “the window of visual perception and the observation capability reflecting knowledge limitation through which a visible phenomenon can be viewed and analyzed”. Indeed, since the objects in RS images usually have different scales, one of the most critical tasks is effectively resizing remotely sensed images by preserving the visual information. This task, usually termed image resizing (IR) for RSAs, has attracted huge interest and become a hot research topic, since IR can imply a scale effect such as constraining the accuracy and efficiency of RSAs.

Over the past few decades, the IR problem has been extensively studied [10,11,12,13]. It is still a popular research field distinguished by many applications in various domains, including RSAs [14,15,16,17,18]. IR can be carried out in an up or down direction, respectively denoted as upscaling and downscaling. Upscaling is a refinement process in which the size of the low-resolution (LR) input image is increased to regain the high-resolution (HR) target image. Conversely, downscaling is a compression process by which the size of the HR input image is reduced to recover the LR target image. In the literature, downscaling and upscaling are often considered separately, so most existing methods specialize in only one direction, sometimes for a limited range of scaling factors. IR methods can be evaluated in supervised or unsupervised mode, depending on whether a target image is available.

Traditionally, IR methods are classified into two categories: non-adaptive and adaptive [19,20,21]. In the first category, including well-known interpolation methods, all image pixels are processed equally. In the second category, including machine learning (ML) methods, suitable pixel changes are selectively arranged to optimize the resized image quality. Usually, non-adaptive methods [22,23] present blurring or artifacts, while adaptive methods [24,25] are more expensive, provide superior visual quality, and keep high-frequency components. In particular, ML methods ensure high-quality results and require widespread learning based on many labeled training images and parameters.

From a methodological point of view, the above considerations also hold for IR methods specifically designed for RSAs [26,27,28,29,30,31,32,33,34,35]. However, most of these methods concern either upscaling [26,27,28,29,30,31] or, to a lesser extent, downscaling [32,33,34,35], despite both being necessary and having equal levels of applicability (see Section 2.1). In addition, the number of IR methods for RSAs that can perform both upscaling and downscaling is very low.

Overall, researchers have developed a significant number of IR methods over the years, although a fair comparison of competing methods promoting reproducible research is missing. To fill this gap and promote the development of new IR methods and their experimental analysis, we proposed a useful framework for studying, developing, and comparing such methods. The framework was conceived to apply this analysis to multiple datasets and to evaluate quantitatively and qualitatively the performance of each method in terms of image quality and statistical measures. In its current form, the framework was designed to consider some IR methods not specifically proposed for RSAs (see Section 2.1), with the intent of evaluating them for this specific application area. However, the framework was made open-access, so that all authors who wish to make their code available can see their methods included and evaluated. Beyond being useful in ranking the considered benchmark methods, the framework is a valuable tool for making design choices and comparing the performance of IR methods. We are confident that this framework holds the potential to bring significant benefits to research endeavors in IR/RSAs.

The framework was instantiated as a Matlab package made freely available on GitHub to support experimental work within the field. A peculiarity of the proposed framework is that it can be used for any type of color image and can be generalized by including IR methods for 3D images. For more rationale and technical background details, see Section 2.2.

To our knowledge, the proposed framework represents a novelty within IR methods for RSAs. Precisely, the main contributions of this paper can be summarized as follows:

A platform for testing and evaluating IR methods for RSAs applied to multiple RS image datasets was made publicly available. It provided a framework where the performance of each method could be evaluated in terms of image quality and statistical measures.
Two RS image datasets with suitable features for testing are provided (see below and Section 2.2.2).
The ranking of the benchmark methods and the evaluation of their performance for RSAs were carried out.
Openness and robustness were guaranteed, since it was possible to include other IR methods and evaluate their performance qualitatively and quantitatively.

Using the framework, we analyzed six IR methods, briefly denoted as BIC [36], DPID [37], L₀ [38], LCI [20], VPI [21], and SCN [39] (see refMethods, Section 2.1). These methods were selected to provide a set of methodologically representative methods. According to the above remarks, an extensive review of all IR methods was outside of this paper’s scope.

Experiments were carried out on six datasets in total (see Section 2.2.2). Four datasets are extensively employed in RSAs, namely AID_cat [40], NWPU VHR-10 [41], UCAS_AOD [42], and UCMerced_LandUse [43]. The remaining two datasets, available on Github, comprised images that we extracted employing Google Earth, namely GE100-DVD and GE100-HDTV (see Section 2.2.2). We quantitatively evaluated the performance of each method in terms of the full-reference quality assessment (FRQA) and no-reference quality assessment (NRQA) measures, respectively, in supervised and unsupervised mode (see Section 2.2.1).

The proposed open framework provided the possibility of tuning and evaluating IR methods to obtain relevant results in terms of image quality and statistical measures. The experimental results confirmed the performance trends already highlighted in [21] for RSAs, showing significant statistical differences among the various IR benchmark methods, as well as the visual quality they could attain in RS image processing. The deep analysis of the results led to the conclusion that for RSAs, the quality measure and CPU time findings confirmed that, on average, VPI and LCI presented adequate and competitive performances, with experimental values generally better and/or more stable than those of the benchmark methods. Moreover, VPI and LCI, besides being much faster than the methods performing only downscaling or upscaling, had no implementation limitations and could be run in an acceptable CPU time on high image sizes and for large scale factors (see Section 4).

The paper is organized as follows: Section 2 describes the benchmark methods (see Section 2.1), the rationale and technical background (see Section 2.2), and the proposed framework (see Section 2.3). Section 3 reports a comprehensive comparison in quantitative and qualitative terms over multiple datasets. Section 4 provides a discussion and draws some conclusions.

2. Materials and Methods

This section is organized into several subsections, as follows: First, a short review of several methods available in the literature, performing the function of benchmark methods, is briefly presented (see Section 2.1). This subsection will help the reader to fully understand the main guidelines followed in the literature and the benchmark methods’ main features. Following this, the rationale and technical background necessary to realize the proposed framework are provided; see Section 2.2. This section also contains a description of the quality measures (see Section 2.2.1) and benchmark datasets (see Section 2.2.2) employed herein. Finally, the proposed framework is described, outlining its peculiarities, in Section 2.3. All materials, including the new benchmark datasets and the framework, are publicly available to the reader (refer to the GitHub link in the section named Data Availability Statement).

2.1. Benchmark Methods

In this subsection, we outline the benchmark methods considered in the validation phase (see Section 3), denoted as BIC [36], DPID [37], L₀ [38], LCI [20], VPI [21], and SCN [39]. Except for BIC, LCI, and VPI, these methods were developed and tested by considering the IR problem in one scaling mode, i.e., the downscaling (DPID and L₀) or upscaling mode (SCN). In the following, when necessary (for LCI and VPI), we distinguish the upscaling and downscaling modes using the notations u-LCI/u-VPI and d-LCI/d-VPI, respectively.

BIC (downscaling/upscaling)
Bicubic interpolation (BIC), the most popular IR method, employs piecewise bicubic interpolation. The value of each final pixel is a weighted average of the pixel values in the nearest $4 \times 4$ neighborhood. BIC produces sharper images than other non-adaptive classical methods, such as bilinear and nearest neighbors, offering a comparatively favorable image quality and processing time ratio. BIC was designed to perform scaling by selecting the size of the resized image or the scale factor.
DPID (downscaling)
The detail-preserving image downscaling (DPID) method employs adaptive low-pass filtering and a Laplacian edge detector to approximate the HVS behavior. The idea is to preserve details in the downscaling process by assigning larger filter weights to pixels that differ more from their local neighborhood. DPID was designed to perform scaling by selecting the size of the resized image.
$L_{0}$ (downscaling)
The L₀-regularized image downscaling method (L₀) is an optimization framework for image downscaling. It focuses on two critical issues: salient feature preservation and downscaled image construction. For this purpose, it introduces two L₀-regularized priors. The first, based on the gradient ratio, allows for preserving the most salient edges and the visual perceptual properties of the original image. The second optimizes the downscaled image with the guidance of the original image, avoiding undesirable artifacts. The two L₀-regularized priors are applied iteratively until the objective function is verified. L₀ was designed to perform scaling by selecting the scale factor.
LCI (downscaling/upscaling)
The Lagrange–Chebychev interpolation (LCI) method falls into the class of interpolation methods. Usually, interpolation methods are based on the piecewise interpolation of the initial pixels, and they traditionally use uniform grids of nodes. On the contrary, in LCI, the input image is globally approximated by employing the bivariate Lagrange interpolating polynomial at a suitable grid of first-kind Chebyshev zeros. LCI was designed to perform scaling by selecting the size of the resized image or the scale factor.
VPI (downscaling/upscaling)
The VPI method generalized to some extent the previous LCI method. It employs an interpolation polynomial [44] based on an adjustable de la Vallée–Poussin (VP)-type filter. The resized image is suitably selected by modulating a free parameter and fixing the number of interpolation nodes. VPI was designed to perform scaling by selecting the size of the resized image or the scale factor.
SCN (upscaling)
The sparse-coding-based network (SCN) method adopts a neural network based on sparse coding, trained in a cascaded structure from end to end. It introduces some improvements in terms of both recovery accuracy and human perception by employing a CNN (convolutional neural network) model. SCNs were designed to perform scaling by selecting the scale factor.

In Table 1, the main features of the benchmark methods are reported. Note that various other datasets, often employed in other image analysis tasks (e.g., color quantization [45,46,47,48,49,50,51] and image segmentation [52,53,54,55]) were employed in [21] to evaluate the performance of the benchmark methods. Moreover, some of the benchmark methods had limitations that were either overcome without altering the method itself too much or resulted in their inability to be used in some experiments (see Section 2.3 and Section 3).

2.2. Rationale and Technical Background

This section aims to present the rationale and the technical background on which the study was based, highlighting the evaluation process’s main constraints, challenges, and open problems. Further, we introduce the mandatory problem of the method’s effectiveness for RSAs. These aspects are listed below.

An adequate benchmark dataset suitable for testing IR methods is lacking in general. Indeed, experiments have generally been conducted on public datasets not designed for IR assessment, since the employed datasets, although freely available, do not contain both input and target images. This has significantly limited the quantitative evaluation process in supervised mode and prevented a fair comparison. To our knowledge, DIV2k (DIVerse 2k) is the only dataset containing both kinds of images [56]. For a performance evaluation of the benchmark methods on DIV2k, see [21]. This research gap is even more prominent for RS images, due to the nature of their application.
Since the performance of a method on a single dataset reflects its bias in relation to that dataset, running the same method on different datasets usually produces remarkably different experimental results. Thus, an adequate evaluation process should be based on multiple datasets.
Performance assessments performed on an empirical basis do not provide a fair comparison. In addition, a correct experimental analysis should be statistically sound and reliable. Thus, an in-depth statistical and numerical evaluation is essential.
A benchmark framework for the IR assessment of real-world and RS images is missing in the literature. In particular, as mentioned in Section 1, this research gap has a greater impact in the case of RSAs due to the crucial role of IR in relation to the acquisition sensor and factors connected to weather conditions, lighting, and the distance between the satellite platform and the ground targets.

As mentioned in Section 1, due to the importance of a fair method comparison and promoting reproducible research, we proposed a useful open framework for studying, developing, and comparing benchmark methods. This framework allowed us to address issues 1–3, considering the IR problem in relation to RSAs and extending the analysis performed in [21]. To assess the specific case of RS, in the validation process, we used some of the RS image datasets that are commonly employed in the literature, and we also generated a specific RS image dataset with features more suitable to quantitative analysis (see Section 2.2.2). The framework was employed here to assess IR methods for RS images, but it could be used for any type of color image [57] and generalized for 3D images [58].

2.2.1. Quality Metrics

Supervised quality measures
As usual, when a target image was available, we quantitatively evaluated the performance of each method in terms of the following full-reference quality assessment (FRQA) measures that provided a “dissimilarity rate” between the target resized image and the output resized image: the peak signal-to-noise ratio (PSNR) and the structural similarity index measure (SSIM). The definition of PSNR is based on the definition of the mean squared error (MSE) between two images and extended to color digital images [59] following two different methods [20,21,60]. The first method is based on the properties of the human eye, which is very sensitive to luma information. Consequently, the PSNR for color images is computed by converting the image to the color space YCbCr; separating the intensity Y (luma) channel, which represents a weighted average of the components R, G, and B; and considering the PSNR only for the luma component according to its definition for a single component. In the second method, the PSNR is the average PSNR computed for each image channel. In our experiments, the PSNR was calculated using both of these methods. However, since the use of the first or the second method did not produce a significant difference, for brevity, we report only the values obtained by the first method in this paper. A greater PSNR value (in decibels) indicates better image quality.
For an RGB color image, the SSIM is computed by converting it to the color space YCbCr and applying its definition to the intensity Y channel [61]. The resultant SSIM index is a decimal value between $- 1$ and 1, where 0 indicates no similarity, 1 indicates perfect similarity, and $- 1$ indicates perfect anti-correlation. More details can be found in [20,21,60].
Unsupervised quality measures
When the target image was not available, we quantitatively evaluated the performance of each method in terms of the following no-reference quality assessment (NRQA) measures: the Natural Image Quality Evaluator (NIQE) [62], Blind/Referenceless Image Spatial QUality Evaluator (BRISQUE) [63,64], and Perception-based Image Quality Evaluator (PIQE) [65,66], using a default model computed from images of natural scenes.
The NIQE involves constructing a quality-aware collection of statistical features based on a simple and successful space-domain natural scene statistic (NSS) model. These features are derived from a corpus of natural and undistorted images and are modeled as multidimensional Gaussian distributions. The NIQE measures the distance between the NSS-based features calculated from the image under consideration to the features obtained from an image database used to train the model.
The BRISQUE does not calculate the distortion-specific features (e.g., ringing, blur, or blocking). It uses the scene statistics of locally normalized luminance coefficients to quantify possible losses of “naturalness” in the image due to distortions.
The PIQE assesses distortion for blocks and determines the local variance of perceptibly distorted blocks to compute the image quality.
The output results of the three functions are all within the range of [0, 100], where the lower the score, the higher the perceptual quality.

2.2.2. Benchmark Datasets

The multidataset analysis included four datasets widely utilized in RSAs and possessing different features, namely AID [40], NWPU VHR-10 [41], UCAS_AOD [42], and UCMerced_LandUse [43]. Moreover, we employed two datasets comprising images we extracted from Google Earth, namely GDVD and GHDTV. All datasets, representing 6850 color images in total, are briefly described in the following list.

AID
The Aerial Image Dataset (AID), proposed in [67] and available at [40], was designed for method performance evaluation using aerial scene images. It contains 30 different scene classes, or categories (“airport”, “bare land”, “baseball field”, “beach”, “bridge”,“center”, “church”, “commercial”, “dense residential”, “desert”, “farmland”, “forest”, “industrial”, “meadow”, “medium residential”, “mountain, park”, “‘parking”, “playground”, “pond”, “port”, “railway station”, “resort”,“river”, “school”, “sparse residential”, “square”, “stadium”, “storage tanks”, and “viaduct”) and about 200/400 samples with sizes of 600 × 600 in each class. The images were collected from Google Earth and post-processed as RGB renderings from the original aerial images. They images are multisource, since, in Google Earth, they were acquired from different remote imaging sensors. Moreover, each class’s sample images were carefully chosen from several countries and regions worldwide, mainly in the United States, China, England, France, Italy, Japan, and Germany. These images were captured at different times and seasons under disparate imaging conditions, with the aim of increasing the data’s intra-class diversity. The images of the categories “‘beach”, “forest”, “parking”, and “sparse residential“ were considered altogether and are denoted as AID_cat in this paper. Note that these images and the images belonging to the same categories in UCAS_AOD were also considered altogether in Section 3.2.3.
GEDVD and GHDTV
Google Earth 100 Images—DVD (GDVD) and Google Earth 100 Images—HDTV (GHDTV) are datasets included with the proposed framework and publicly available for method performance evaluation using Google Earth aerial scene images. The GDVD and GHDTV datasets each contain 100 images generated by collecting the same scene in the two formats: 852 × 480 (DVD) and 1920 × 1080 (HDTV). These two size formats were chosen based on the following considerations: Firstly, these are standard formats that are widely used in practice, and, in particular, the HDTV format was large enough to allow scaling operations to be performed at high scaling factors. Secondly, each image dimension was a multiple of 2, 3, or 4, so resizing operations could be performed with all benchmark methods. Thirdly, since the corresponding images of the two datasets were acquired from the same scene with different resolutions for a specific, non-integer scale factor, these datasets could be considered interchangeably as containing the target and input images. Each image in the two datasets presents a diversity of objects and reliable quality.
NWPU VHR-10
The image dataset NWPU VHR-10 (NWV) proposed in [68,69,70] is publicly available at [41] for research purposes only. It contains images with geospatial objects belonging to the following ten classes: airplanes, ships, storage tanks, baseball diamonds, tennis courts, basketball courts, ground track fields, harbors, bridges, and vehicles. This dataset contains in total 800 very-high-resolution (VHR) remote sensing color images, with 715 color images acquired from Google Earth and 85 pan-sharpened color infrared images from Vaihingen data. The images of this dataset were originally divided into four different sets: a “positive image set” containing 150 images, a “negative image set” containing 150 images, a “testing set” containing 350 images, and an “optimizing set” containing 150 images. The images of this dataset were considered altogether in this paper.
UCAS_AOD
The image dataset UCAS_AOD (UCA) proposed in [71] (available at [42]) contains RS aerial color images collected from Google Earth, including two kinds of targets, automobile and aircraft, and negative background samples. The images of this dataset were considered both altogether and divided into certain categories (see Section 3.2.3) in this paper.
UCMerced_LandUse
The image dataset UCMerced_LandUse (UCML) proposed in [72] (available at [43]) for research purposes, contains 21 classes of land use images. Each class contains 100 images with a size of 256 × 256 manually extracted from larger images of the USGS National Map Urban Area Imagery collection, framing various urban areas around the country. The images of this dataset were considered altogether in this paper.

In Table 2, the main features of all datasets are reported. Each stand-alone dataset contained images that could be considered the target image starting from a given input image.

In order to test the benchmark methods in supervised mode, we needed to generate the input image to apply the chosen resizing method. To this end, we followed a practice established in the literature and often adopted by other authors, i.e., we rescaled the target image by BIC and used it as an input image in most cases in the framework validation (see Section 3.1). However, in Section 3.1.3, we also used the benchmark methods to generate the input image with the aim of studying the input image dependency. To discriminate how the input images were generated, we include the acronym of the resizing method used for their generation when referring to the images. For instance, “BIC input image” indicates the input image generated by BIC.

In unsupervised mode, besides the above datasets, we also tested the benchmark methods according to four categories: beach, forest, parking, and sparse residential. To this end, we fused the corresponding category images of AID and UCA to generate the subsets, indicated in the following as AU_Beach (500 images), AU_Forest (350 images), AU_Parking (390 images), and AU_SparseRes (400 images) (see Section 3.2.3).

2.3. Proposed Framework

As stated above, the proposed framework allowed us to test each benchmark method on any set of input images in two modes: “supervised” and “unsupervised”, depending on the availability of a target image. Three image folders were used: the folder of input images (mandatory), named “input_image”; the folder of output IR images (optional), named “output_image”; and the folder of ground-truth images (mandatory in supervised mode but not required in unsupervised mode), named “GT_image”. Note that the images in each folder should have the same graphic format. Moreover, in supervised mode, the GT_image folder should include ground-truth images whose file names are the same as those of the input images in the input_image folder.

Preliminarily, the user has to set the scale factor (Scale) to a real value not equal to 1. Then, the user has to complete an initialization step consisting of the following settings:

Supervised ‖ unsupervised;
Upscaling ‖ downscaling;
Input image format (.png ‖ .tif ‖ .jpg ‖ .bmp);
Benchmark method (BIC ‖ SCN ‖ LCI ‖ VPI for upscaling; BIC ‖ DPID ‖ L₀‖ LCI ‖ VPI for downscaling);
Ground-truth image format (.png ‖ .tif ‖ .jpg ‖ .bmp);
Image saving option (Y ‖ N);
Image showing option (Y ‖ N).

Note that if the downscaling option is selected, Scale is automatically updated to 1/Scale. The initialization step is managed through dialog boxes, as shown in Figure 1.

The dialog box for selecting the graphic format of the input and the GT image remains on hold until the user selects the correct file extension for the files included in their respective folders. A comprehensive table is generated at the end of the initialization step, according to the selected mode (supervised or unsupervised). The selected benchmark method is applied to each image in the folder input_image during a run using the default parameter values. Successively, the computed quality measures and CPU time are stored in the table. If the image saving option is selected (i.e., ‘Y’ is chosen), the corresponding resized image is stored in the output_image folder with the same file name. Similarly, if the image showing option is selected (i.e., ‘Y’ is chosen), the corresponding resized image is shown on the screen. In the end, the average CPU time and image quality measures are also computed and stored in the table. Then, the table is saved as an .xls file in the directory “output_image”. For more details, see the description reported as pseudo-code in Algorithm 1.

In unsupervised mode, each benchmark method, DPID excluded, was implemented by selecting the scale factor, and the resulting resized image was consequently computed. Since DPID was designed to perform scaling by selecting the size of the resized image, based on the selected scale factor, we computed the size of the resized image, which was used as a parameter for DPID.

In supervised mode, almost all benchmark methods were implemented by selecting the size of the resized image equal to the size of the ground-truth image taken from the folder GT_image. Indeed, in supervised mode this was possible for BIC, DPID, LCI, and VPI, since they were designed with the possibility of performing scaling by selecting the size of the resized image or the scale factor.

Since this did not apply to the SCN method and L₀, we had to introduce some minor variations to make them compliant with our framework. Specifically, for the SCN method, to perform the supervised resizing by indicating the size, we introduced minor algorithmic changes to the original code and modified the type of input parameters without significantly affecting the nature and the core of the SCN. The changes consisted in computing the scale factor corresponding to the size of the ground-truth image and then implementing the SCN with this scale factor as a parameter. However, these minor changes were not sufficient to remove three computational limitations of the SCN, which remained impractical, since a complete rewriting of the SCN method (outside our study’s scope) would be necessary. The first limitation involved the size of the resized image being incorrectly computed for some or all of the input images; for example, for the UCA dataset, if the desired resized image was equal to 1280 × 659, starting from an input image generated by BIC with a size of 640 × 330 and considering a scale factor equal to 2, the computed size of the resized image would be 1280 × 660. This computational limitation is indicated in the following as “not computable” using the notation “–”. The second SCN computational limitation was related to the resizing percentage, which could not correspond to a non-integer scale factor—for instance, in the case of supervised upscaling with input images from GDVD for the ground truths of GHDTV corresponding to a scale factor equal to about 2.253. This is indicated in the following as “not available” using the abbreviation “n.a.”. The third SCN computational limitation pertained to scale factors greater than or equal to 3 for larger or more numerous input images, as the available demo code of the SCN caused Matlab to run out of memory. This occurrence is indicated in the following as “out of memory” using the notation “OOM”.

Algorithm 1 Framework

$I n s e r t i o n S c a l e v a l u e$
if $S c a l e \neq 1$ then
$I n i t i a l i z e :$
$S u p e r v i s e d$ ‖ $U n s u p e r v i s e d$
$U p s c a l i n g$ ‖ $D o w n s c a l i n g$
$I n p u t I m a g e F o r m a t$
$I m a g e s a v i n g o p t i o n$
$I m a g e s h o w i n g o p t i o n$
if $S u p e r v i s e d$ then
$G T_f o r m a t \leftarrow S e l e c t G r o u n d T r u t h I m a g e F o r m a t$
end if
$G e n e r a t e a n a p p r o p r i a t e T a b l e$
$M E T H O D \leftarrow S e l e c t U p s c a l i n g$ ‖ $D o w n s c a l i n g R e s i z i n g M e t h o d$
$N \leftarrow C o m p u t e t h e n u m b e r o f i n p u t i m a g e s$
for i = 1 to N do
$R e a d I n p u t i m a g e (I_{i})$
$[T_{i}, R_{i}] \leftarrow M E T H O D (I_{i})$ { $w h e r e R_{i} \leftarrow r e s i z e d i m a g e, T_{i} \leftarrow C P U t i m e$ }
if $S u p e r v i s e d$ then
$R e a d t h e c o r r e s p o n d i n g G T i m a g e (G T_{i}) w i t h G T_f o r m a t$
end if
$C o m p u t e q u a l i t y m e a s u r e s f o r R_{i} . T h e n s t o r e t h e m a n d T_{i} i n t h e T a b l e$
if $I m a g e s a v i n g o p t i o n =^{'} Y^{'}$ then
$S a v e (R_{i})$
end if
if $I m a g e s h o w i n g o p t i o n =^{'} Y^{'}$ then
$S h o w (R_{i})$
end if
end for
$C o m p u t e a v e r a g e q u a l i t y m e a s u r e s a n d C P U t i m e . T h e n s t o r e t h e m i n t h e T a b l e$
$S a v e T a b l e a s . x l s f i l e$
else
$W a r n i n g : N o S c a l i n g m e t h o d h a s b e e n a p p l i e d!$
end if

It was not possible to implement L₀ because it is only available as a Matlab p-code. Using L₀ to perform resizing by selecting the size of the resized image, we computed the scale factor corresponding to the size of the ground-truth image, which was passed on as a parameter for L₀. However, in this way, it was not possible to avoid an error in the size calculation when each size dimension of the resized image was not equal to the product of the scaling factor and the corresponding size dimension of the input image or when different scale factors had to be considered for each dimension. In these cases, in the framework, the user is simply notified that the calculation is impossible. Note that this L₀ computational limitation did not affect the experimental results presented herein (see Section 3), since L₀ was used only for downscaling with an equal scale factor for each size dimension on images prior to zooming using the same scale as other benchmark methods, so that we did not have any problem in performing resizing.

The framework was made open-access so that other benchmark methods can be added. Thus, we invite other authors to make their method code available to expand the framework’s capabilities for a fair comparison. The proposed framework was instantiated as a Matlab package that is freely available on GitHub. It was run on a computer with an Intel Core i7 3770K CPU configuration @350 GHz and Matlab version 2022b.

3. Experimental Results and Discussion

This section reports the comprehensive performance assessment of the benchmark methods outlined in Table 1 over multiple datasets. We considered BIC, d-LCI, L₀, DPID, and d-VPI as downscaling benchmark methods, while BIC, SCN, u-LCI, and u-VPI were considered as upscaling benchmark methods. Indeed, although DPID and L₀ (SCN) could also be applied in upscaling (downscaling) mode, we did not focus on this unplanned comparison to avoid an incorrect experimental evaluation. Note that BIC was implemented using the built-in Matlab function imresize with the bicubic option. For the remaining methods, we employed the publicly available source codes in a common language (Matlab). These codes were run with the default parameter settings.

We tested the benchmark methods for scale factors varying from 2 to large values in both supervised and unsupervised mode for upscaling/downscaling. However, for brevity, in this paper, we limit ourselves to showing the results for the scale factors of 2, 3, and 4.

In the following, Section 3.1 and Section 3.2 are devoted to evaluating the quantitative results for the supervised and unsupervised modes, respectively. Moreover, for each type of quantitative evaluation, we distinguish the upscaling and downscaling cases. In addition, in Section 3.3, the trend of CPU time is investigated. Section 3.4 concerns the qualitative results for both the supervised/unsupervised modes and upscaling/downscaling cases. In particular, performance examples are given for different scale factors and modes. Finally, in Section 3.5, conclusive global assessments are presented.

3.1. Supervised Quantitative Evaluation

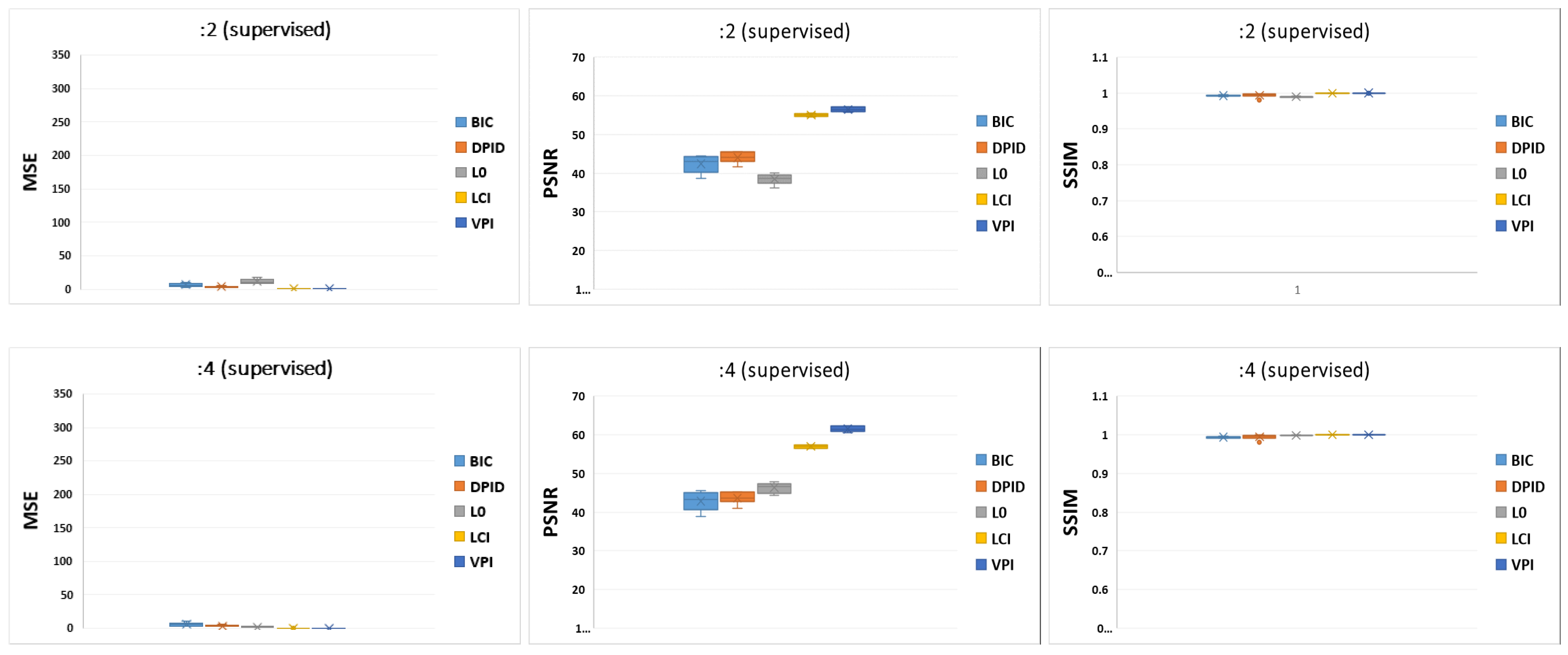
In supervised mode, for the quantitative evaluation of both upscaling and downscaling methods, we show the full-reference visual quality measures PSNR and SSIM (see Section 2.2.1) for all benchmark methods where the ground-truth image had a size corresponding to the scale factors s = 2, 3, 4.

Since the target image was necessary to estimate these quality measures, we employed the benchmark methods for both upscaling and downscaling by mainly modifying their input parameters so that the output image’s size was automatically computed after the ground-truth image was considered and its dimensions computed. For LCI, VPI, and BIC, we used the version of the method where the input parameters were the image dimensions of the resized image.

As mentioned above, we took the target images from the datasets and applied BIC in upscaling (or downscaling) mode to them in order to generate the input images for the downscaling (or upscaling) benchmark method. We refer to these images as “BIC input images”. This was performed for all datasets.

In Section 3.1.1 and Section 3.1.2 we interpret the results respectively for supervised downscaling and upscaling. In addition, as presented in Section 3.1.3, we studied the impact of how the input images were generated. For this purpose, we repeated the quantitative analysis and computed the average PSNR and SSIM values for the supervised benchmark methods while varying the unsupervised scaling method used to generate the input images from the target images in the dataset.

3.1.1. Supervised Downscaling

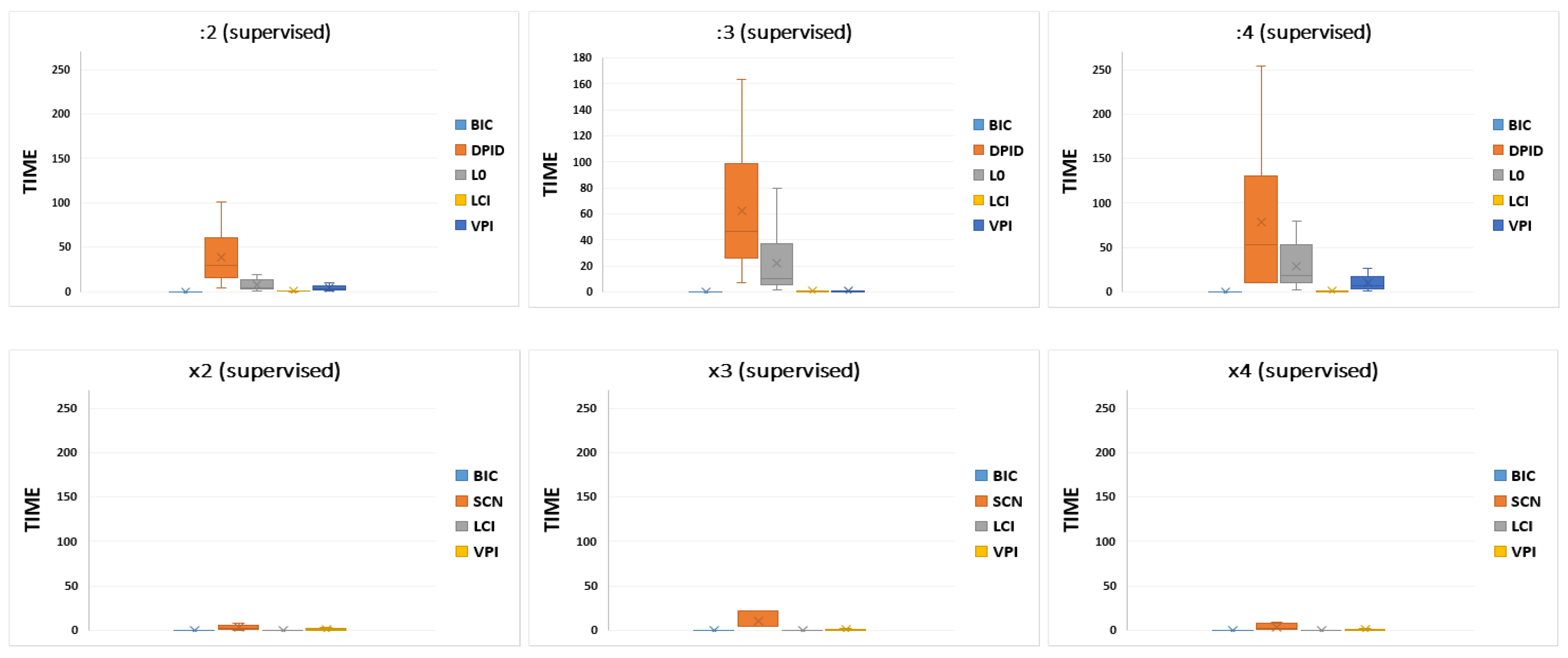
Table 3 and Figure 2 show the average performance of supervised downscaling methods with BIC input images for a ground-truth image with a size corresponding to the scale factors s = 2, 3, 4. The results confirmed the trend already observed in [21]. Specifically, for even scale factors (

s = 2, 4

), d-VPI always supplied much higher performance values than DPID and

L_{0}

, which always presented the lowest quality measures. For odd scale factors, d-VPI performed similarly to d-LCI, reaching the optimal quality measures for input images generated by BIC [21]. This trend was also detectable from the boxplots in Figure 2. The trend could also be observed for higher scale factors. To provide further insights, the results obtained for scale factors s = 6, 8, 10 on the GHDTV dataset with BIC input images are reported in Table 4.

Table 3. Average performance of supervised downscaling methods with BIC input images.

	:2				:3				:4
	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
AID_cat
BIC	4.012	44.844	0.994	0.011	3.680	45.669	0.995	0.018	3.743	45.530	0.994	0.033
DPID	2.760	45.602	0.997	22. 952	2.685	45.684	0.997	35.686	3.082	45.175	0.996	56.004
L₀	9.585	39.458	0.989	3.402	10.894	39.093	0.987	6.955	1.515	47.158	0.998	12.930
d-LCI	0.205	55.121	0.999	0.112	0.00	Inf	1.000	0.163	0.141	56.903	1.000	0.276
d-VPI	0.152	56.676	1.000	1.904	0.00	Inf	1.000	0.163	0.053	61.787	1.000	5.017
GDVD
BIC	10.416	38.636	0.989	0.012	9.711	38.955	0.990	0.018	9.843	38.895	0.990	0.036
DPID	5.055	41.591	0.996	20.071	5.105	41.565	0.996	32.671	5.913	40.935	0.995	49.898
L₀	17.573	36.169	0.988	3.552	170.353	26.453	0.882	7.945	2.625	44.346	0.998	14.063
d-LCI	0.212	54.903	0.999	0.107	0.00	Inf	1.000	0.177	0.149	56.513	1.000	0.277
d-VPI	0.164	56.065	1.000	1.959	0.00	Inf	1.000	0.177	0.059	60.544	1.000	4.912
GHDTV
BIC	3.167	44.322	0.996	0.034	2.900	44.829	0.997	0.044	2.945	44.746	0.996	0.067
DPID	2.681	44.449	0.997	101.297	2.697	44.411	0.997	163.577	3.107	43.806	0.997	253.606
L₀	10.956	38.351	0.992	19.607	1.482	46.854	0.999	79.947	1.482	46.854	0.999	79.640
d-LCI	0.185	55.489	0.999	0.481	0.00	Inf	1.000	0.863	0.124	57.361	1.000	1.323
d-VPI	0.127	57.160	1.000	9.808	0.00	Inf	1.000	0.863	0.041	62.262	1.000	26.009
NWV
BIC	5.015	43.218	0.992	0.018	4.641	43.695	0.993	0.031	4.709	43.618	0.993	0.050
DPID	2.463	45.576	0.996	35.596	2.359	45.763	0.997	57.479	2.694	45.214	0.996	89.015
L₀	7.989	40.058	0.990	5.255	64.247	21.445	0.641	12.826	1.304	47.870	0.998	22.503
d-LCI	0.189	55.452	0.999	0.308	0.00	Inf	1.000	0.302	0.125	57.387	1.000	0.443
d-VPI	0.134	57.065	1.000	3.423	0.00	Inf	1.000	0.302	0.043	62.225	1.000	7.852
UCA
BIC	7.394	40.912	0.993	0.019	6.825	41.330	0.994	0.026	6.943	41.246	0.994	0.042
DPID	3.559	43.488	0.996	47.762	3.257	43.887	0.997	77.220	3.452	43.366	1.000	10.966
L₀	9.547	39.055	0.990	10.743	12.595	37.911	0.987	22.979	1.694	46.435	0.998	43.939
d-LCI	0.234	54.548	0.999	0.244	0.00	Inf	1.000	0.451	0.133	57.019	1.000	0.729
d-VPI	0.180	55.796	0.999	5.307	0.00	Inf	1.000	0.025	0.057	60.936	1.000	14.452
UCML
BIC	6.977	42.931	0.992	0.003	6.430	43.422	0.993	0.003	6.552	43.339	0.992	0.006
DPID	3.481	43.685	0.980	4.293	3.317	43.807	0.980	6.672	3.865	43.235	0.980	10.553
L₀	13.755	37.832	0.987	0.565	49.057	32.747	0.958	1.245	2.606	45.108	0.997	2.194
d-LCI	0.251	54.838	0.999	0.014	0.00	Inf	1.000	0.024	0.159	56.384	1.000	0.035
d-VPI	0.201	56.148	1.000	0.258	0.00	Inf	1.000	0.024	0.068	61.027	1.000	0.612

Figure 2. Boxplots derived from Table 3.

Table 4. Average performance of supervised downscaling methods on the GHDTV dataset with BIC input images for other scale factors (OOM indicates “out of memory”).

	:6				:8				:10
	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
BIC	2.932	44.777	0.996	0.268	2.928	44.791	0.996	0.454	2.925	44.802	0.997	0.662
DPID	3.665	43.094	0.997	675.213	3.979	42.740	0.997	1057.820	4.180	42.527	0.996	1617.292
L₀	2.008	45.737	0.998	172.889	2.536	44.881	0.997	359.239	OOM	OOM	OOM	OOM
d-LCI	0.084	59.137	1.000	3.746	0.058	60.892	1.000	6.382	0.039	62.620	1.000	10.062
d-VPI	0.018	66.018	1.000	71.330	0.009	69.115	1.000	118.630	0.005	72.098	1.000	172.154

3.1.2. Supervised Upscaling

Table 5 and Figure 3 show the average performance of supervised upscaling methods with BIC input images for a ground-truth image with a size corresponding to the scale factors s = 2, 3, and 4. The results confirmed the trend already observed in [21]. Specifically, SCN produced the highest quality values in the case of BIC input images, followed by u-VPI, u-LCI, and BIC. This trend was also detectable from the boxplots in Figure 3. The trend could also be observed for higher scale factors. To provide further insights, the results obtained for scale factors s = 6, 8, and 10 on the GHDTV dataset with BIC input images are reported in Table 6.

3.1.3. Supervised Input Image Dependency

We conducted the following two experiments on GEHDTV and GDVD to test the supervised input image dependency. We selected these datasets due to their features and size.

Supervised Input Image Dependency–Experiment 1

We changed the input image for both downscaling and upscaling, generating it using the other methods in unsupervised mode. Indeed, for supervised downscaling, the input HR images were generated by the unsupervised upscaling methods BIC, SCN, u-LCI, and u-VPI. In contrast, for supervised upscaling, the input LR images were created using the unsupervised BIC, L₀, DPID, d-LCI, and d-VPI methods. The input-free parameter of unsupervised u-VPI and d-VPI, employed to generate the input image, was set to a prefixed value equal to 0.5.

In Table 7 and Table 8 (Table 9 and Table 10), the average performance of supervised downscaling (upscaling) methods with different input images is shown for scale factors s = 2, 3, and 4.

Table 5. Average performance of supervised upscaling methods with BIC input images (– indicates “not computable”).

	×2				×3				×4
	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
AID_cat
BIC	52.421	33.730	0.920	0.004	125.176	29.533	0.823	0.004	173.186	28.091	0.759	0.004
SCN	34.781	35.403	0.943	1.995	104.941	30.235	0.851	4.210	141.371	28.988	0.794	2.415
u-LCI	42.336	34.866	0.932	0.021	115.093	29.965	0.833	0.014	162.040	28.462	0.766	0.013
u-VPI	41.791	34.918	0.934	0.046	113.838	30.007	0.836	0.349	160.206	28.507	0.770	0.348
GDVD
BIC	110.341	28.323	0.885	0.005	226.175	25.149	0.779	0.005	287.487	24.110	0.718	0.005
SCN	70.700	30.327	0.922	2.001	188.604	25.959	0.818	4.160	230.674	25.086	0.765	2.457
u-LCI	94.945	29.028	0.897	0.027	213.260	25.414	0.787	0.019	273.375	24.335	0.724	0.015
u-VPI	93.865	29.075	0.900	0.545	211.541	25.449	0.791	0.438	271.386	24.364	0.728	0.375
GHDTV
BIC	49.487	32.310	0.941	0.016	198.067	25.855	0.821	0.014	186.544	26.191	0.800	0.014
SCN	28.120	34.671	0.963	7.654	205.939	25.713	0.832	22.342	136.649	27.624	0.842	9.415
u-LCI	38.194	33.629	0.951	0.146	194.723	25.942	0.824	0.121	171.400	26.631	0.806	0.109
u-VPI	37.690	33.682	0.953	3.211	192.858	25.981	0.828	2.342	169.586	26.676	0.810	2.541
NWV
BIC	66.156	31.461	0.895	0.006	121.121	28.665	0.816	0.006	161.265	27.290	0.764	0.006
SCN	–	–		–	–	–	–	–	–	–	–	–
u-LCI	62.809	31.767	0.901	0.040	118.937	28.799	0.819	0.028	159.109	27.382	0.765	0.021
u-VPI	62.220	31.807	0.903	0.795	117.727	28.842	0.822	0.613	157.707	27.420	0.768	0.532
UCA
BIC	96.844	29.229	0.897	0.007	210.907	25.608	0.779	0.006	213.253	25.703	0.755	0.007
SCN	–	–	–	–	–	–	–	–	–	–	–	–
u-LCI	92.463	29.437	0.903	0.074	212.377	25.582	0.779	0.061	208.064	25.844	0.757	0.051
u-VPI	91.758	29.468	0.905	1.731	209.280	25.644	0.782	1.377	206.237	25.882	0.762	1.288
UCML
BIC	75.233	31.873	0.910	0.001	319.719	24.854	0.729	0.002	222.251	26.625	0.754	0.001
SCN	44.938	33.598	0.922	0.422	–	–	–	–	170.748	27.314	0.777	0.480
u-LCI	63.395	32.881	0.921	0.003	327.294	24.766	0.727	0.003	207.548	27.001	0.761	0.002
u-VPI	62.573	32.934	0.923	0.088	319.763	24.865	0.728	0.084	205.230	27.044	0.765	0.074

Table 6. Average performance of supervised upscaling methods on the GHDTV dataset with BIC input images for other scale factors.

	×6				×8				×10
	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
BIC	299.353	24.037	0.717	0.021	383.714	22.924	0.674	0.021	448.808	22.229	0.651	0.020
SCN	240.168	25.044	0.754	21.233	323.354	23.694	0.702	12.154	389.037	22.867	0.672	30.237
d-LCI	284.941	24.274	0.719	0.083	369.640	23.096	0.675	0.074	435.666	22.365	0.651	0.069
d-VPI	282.678	24.309	0.722	1.829	367.357	23.124	0.678	1.673	433.169	22.390	0.653	1.597

Analyzing these tables, it follows that:

(a): For supervised downscaling (see Table 7 and Table 8) starting from HR input images created by the upscaling methods other than BIC, for even scale factors ( $s = 2, 4$ ), d-VPI always produced much higher quality values than DPID and $L_{0},$ , which always presented the lowest performance in qualitative terms. The d-VPI method, followed by d-LCI, obtained the best performance, apart from the case of SCN input images, where BIC showed the better performance, in agreement with the limitations reported in Section 2.3, followed by d-VPI, DPID, d-LCI, and $L_{0}$ . For odd scale factors, since d-VPI coincided with d-LCI, these methods attained better quality values in the case of input images created by BIC, u-LCI, or u-VPI. However, for SCN input images, the rating of the methods for even scale factors $s = 2, 4$ was as expected, i.e., the best performance was attributed to BIC, followed by d-LCI = d-VPI, DPID, and $L_{0}$ , respectively.
(b): For supervised upscaling (see Table 9 and Table 10), starting from LR input images created by downscaling methods other than BIC, SCN always produced the lowest quality values. The best performance was accomplished by u-VPI, apart from in the upscaling ×2 case with L₀ input images, where BIC had slightly higher performance values than u-VPI. Analogously to BIC, u-VPI had a more stable trend with regard to the variations in the input image. The quality values obtained by u-VPI were always higher than those obtained by u-LCI, which preformed better than BIC only for BIC input images.

Figure 3. Boxplots derived from Table 5.

Table 7. Average performance results of supervised downscaling methods on GHDTV dataset with input images generated by the BIC and SCN methods.

		BIC Input				SCN Input
		MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
GHDTV
:2
	BIC	3.167	44.322	0.996	0.034	0.844	49.440	0.999	0.036
	DPID	2.681	44.449	0.997	101.297	7.546	40.316	0.993	105.20
	L₀	10.956	38.351	0.992	19.607	23.228	35.423	0.981	19.150
	d-LCI	0.185	55.489	0.999	0.481	6.275	41.512	0.993	0.499
	d-VPI	0.127	57.160	1.000	9.808	0.936	49.277	0.999	10.591
:3
	BIC	2.900	44.829	0.997	0.018	0.942	48.946	0.999	0.046
	DPID	2.697	44.411	0.997	32.671	6.091	41.164	0.994	165.18
	L₀	1.482	46.854	0.999	7.945	19.016	36.190	0.983	44.421
	d-LCI	0.00	Inf	1.000	0.177	6.759	41.278	0.993	1.274
	d-VPI	0.00	Inf	1.000	0.177	6.659	41.278	0.993	1.274
:4
	BIC	2.945	44.746	0.996	0.067	0.964	48.951	0.999	0.065
	DPID	3.107	43.806	0.997	253.606	6.315	40.969	0.994	263.86
	L₀	1.482	46.854	0.999	79.640	4.343	42.529	0.996	68.453
	d-LCI	0.124	57.361	1.000	1.323	8.055	40.507	0.992	1.457
	d-VPI	0.041	62.262	1.000	26.009	3.263	44.208	0.997	27.397

Table 8. Average performance results of supervised downscaling methods on GHDTV dataset with input images generated by u-LCI and u-VPI.

		u-LCI Input				u-VPI Input
		MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
GHDTV
:2
	BIC	1.562	47.262	0.998	0.038	2.658	45.092	0.996	0.038
	DPID	3.782	43.079	0.997	100.833	3.110	43.873	0.997	105.12
	L₀	12.004	37.985	0.991	19.777	11.545	38.145	0.991	19.326
	d-LCI	0.073	59.615	1.000	0.510	0.070	59.712	1.000	0.517
	d-VPI	0.012	68.774	1.000	10.613	0.024	64.575	1.000	10.625
:3
	BIC	1.412	47.948	0.998	0.048	2.502	45.529	0.997	0.048
	DPID	3.637	43.195	0.997	168.89	3.110	43.840	0.997	207.796
	L₀	12.278	37.895	0.990	44.82	11.744	38.079	0.990	45.137
	d-LCI	0.00	Inf	1.000	0.863	0.000	Inf	1.000	0.865
	d-VPI	0.00	Inf	1.000	0.863	0.000	Inf	1.000	0.865
:4
	BIC	1.448	47.742	0.998	0.069	2.534	45.416	0.997	0.065
	DPID	4.073	42.697	0.996	258.79	3.524	43.295	0.997	316.138
	L₀	1.325	47.380	0.999	79.695	1.423	47.058	0.999	86.846
	d-LCI	0.053	60.977	1.000	1.33	0.053	60.974	1.000	1.342
	d-VPI	0.002	80.119	1.000	26.220	0.001	78.820	1.000	26.022

Table 9. Average performance results of supervised upscaling methods on GHDTV dataset with input images generated by BIC, L₀, DPID.

		BIC Input				L₀ Input				DPID Input
		MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
	GHDTV
×2
	BIC	49.487	32.310	0.941	0.016	53.119	31.699	0.949	0.016	46.659	32.514	0.950	0.016
	SCN	28.120	34.671	0.963	7.654	132.387	27.781	0.906	7.347	74.599	30.282	0.934	7.316
	u-LCI	38.194	33.629	0.951	0.146	79.672	30.029	0.917	0.143	53.518	31.986	0.936	0.145
	u-VPI	37.690	33.682	0.953	3.211	55.568	31.496	0.947	3.134	45.190	32.684	0.952	0.952
×3
	BIC	198.067	25.855	0.821	0.014	321.797	23.672	0.772	0.015	117.956	28.302	0.879	0.014
	SCN	205.939	25.713	0.832	22.342	476.268	22.003	0.716	16.311	163.018	26.840	0.864	16.358
	u-LCI	194.723	25.942	0.824	0.121	375.026	23.022	0.736	0.117	133.960	27.817	0.854	0.120
	u-VPI	192.858	25.981	0.828	2.342	312.075	23.805	0.766	2.634	116.398	28.403	0.880	2.638
×4
	BIC	186.544	26.191	0.800	0.014	175.799	26.481	0.819	0.014	175.799	26.481	0.819	0.014
	SCN	136.649	27.624	0.842	9.415	226.220	25.366	0.807	9.570	226.220	25.366	0.807	9.593
	u-LCI	171.400	26.631	0.806	0.109	197.676	26.033	0.788	0.112	197.676	26.033	0.788	0.108
	u-VPI	169.586	26.676	0.810	2.541	173.450	26.587	0.820	2.342	173.450	26.587	0.820	2.315

Table 10. Average performance results of supervised upscaling methods on GHDTV dataset with input images generated by d-LCI and d-VPI (– indicates “not computable”).

		d-LCI Input				d-VPI Input
		MSE	PSNR	SSIM	TIME	MSE	PSNR	SSIM	TIME
	GHDTV
×2
	BIC	45.604	32.782	0.948	0.016	39.019	33.438	0.954	0.016
	SCN	80.349	30.309	0.926	7.406	62.009	31.367	0.940	7.356
	u-LCI	55.250	32.206	0.929	0.138	43.203	33.275	0.941	0.141
	u-VPI	43.587	33.155	0.949	3.092	34.944	34.142	0.957	3.166
×3
	BIC	242.474	25.006	0.811	0.014	129.583	28.045	0.874	0.015
	SCN	–	–	–	–	239.088	25.348	0.826	16.157
	u-LCI	290.641	24.253	0.768	0.121	167.492	27.032	0.828	0.116
	u-VPI	239.576	25.051	0.808	2.713	127.752	28.156	0.874	2.629
×4
	BIC	226.910	25.445	0.806	0.013	219.069	25.597	0.810	0.014
	SCN	420.078	22.727	0.742	9.484	397.439	22.972	0.751	9.523
	u-LCI	292.124	24.389	0.748	0.105	280.268	24.569	0.753	0.105
	u-VPI	220.180	25.575	0.807	2.363	213.686	25.708	0.811	2.345

Supervised Input Image Dependency–Experiment 2

Since both GDVD and GHDTV were generated by collecting images of the same scene in two different formats with a scale ratio equal to about 2.253 (see Section 2.2.2), we used the images of the GHDTV dataset as the input for all supervised downscaling processes by considering as ground truth the images of the GDVD dataset. Correspondingly, we used the images of the GDVD dataset as the input for all supervised upscaling processes by considering the images of the GHDTV dataset as the ground truth. In Table 11 (Table 12), the average quality values of supervised downscaling (upscaling) methods with input images from GDVD (GHDTV) and ground-truth images from GHDTV (GDVD) are shown.

Analyzing these tables, it follows that:

(a): For supervised downscaling starting from the HR input image from GDVD with a scale factor of about s = 2.253, BIC produced moderately better quality values than d-VPI, followed by d-LCI, DPID, and $L_{0}$ .
(b): For supervised upscaling starting from the HR input image from GHDTV with a scale factor of s = 2.253, d-VPI produced better quality values than u-LCI and BIC. At the same time, the SCN method was not able to provide results, since it did not work in supervised mode with a non-integer scale factor.

3.2. Unsupervised Quantitative Evaluation

In unsupervised mode, for the quantitative evaluation, we report the no-reference visual quality measures NIQE, BRISQUE, and PIQE (see Section 2.2.1) for all benchmark methods; the scale factors s = 2, 3, and 4; and both downscaling and upscaling. The framework employed the unsupervised benchmark methods for both upscaling and downscaling, simply using the specified scale factor, since the target image was not necessary to compute these quality measures. In Section 3.2.1 and Section 3.2.2 we interpret the results respectively for unsupervised downscaling and upscaling. In addition, as presented in Section 3.2.3, to study the impact of the image category, we performed the same quantitative analysis and computed the average NIQE, BRISQUE, and PIQE values for the unsupervised benchmark methods on the image sub-datasets selected by category.

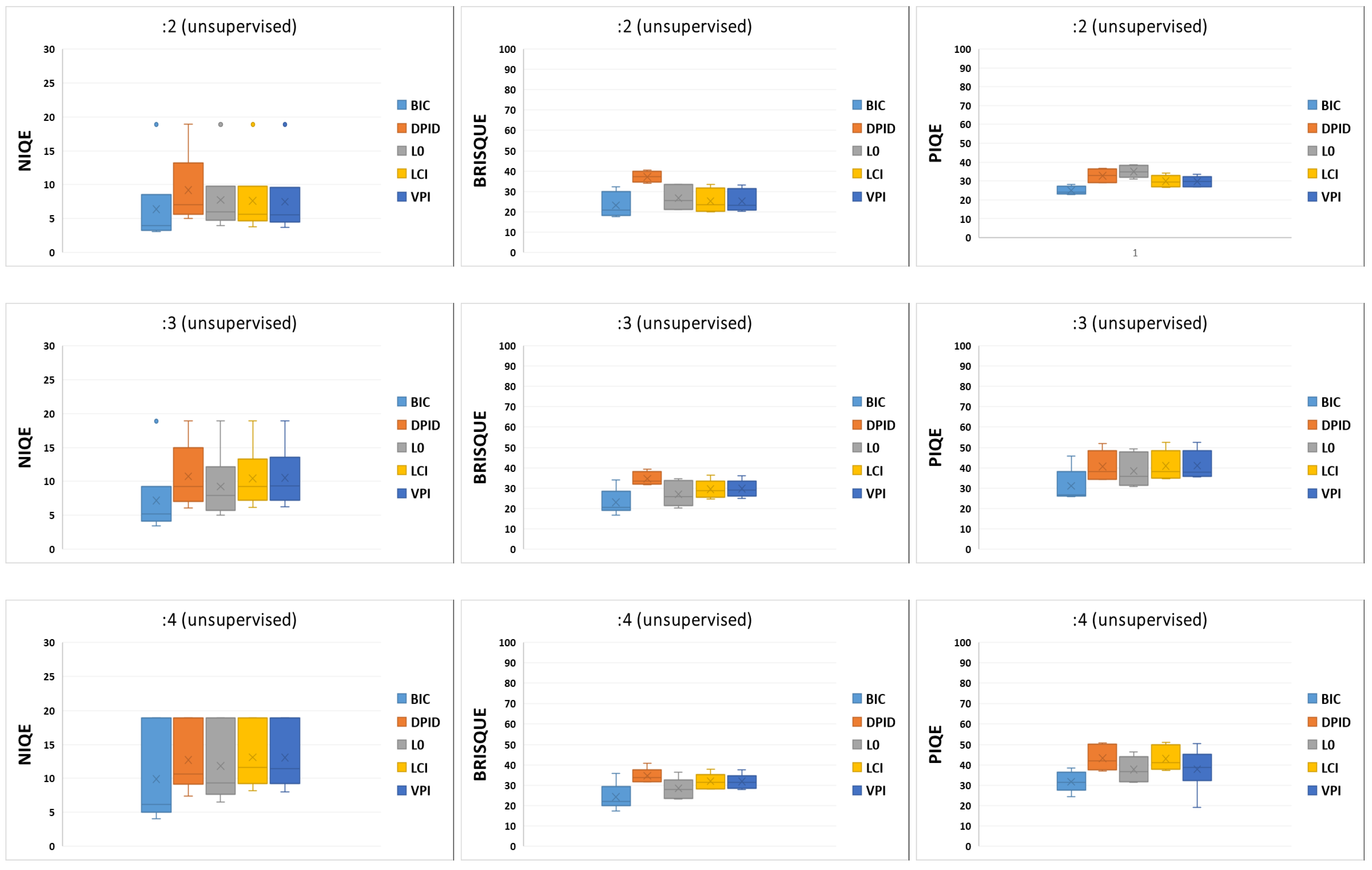
3.2.1. Unsupervised Downscaling

Table 13 and Figure 4 show the average performance of unsupervised downscaling methods for the scale factors s = 2, 3, and 4 on all datasets.

The results indicated that the best performance was attributable to BIC, followed by d-VPI, d-LCI,

L_{0},

and DPID, respectively. The same trend could be observed for higher scale factors as well. To provide further insights, the results obtained for scale factors s = 6, 8, and 10 on the GHDTV dataset are reported in Table 14.

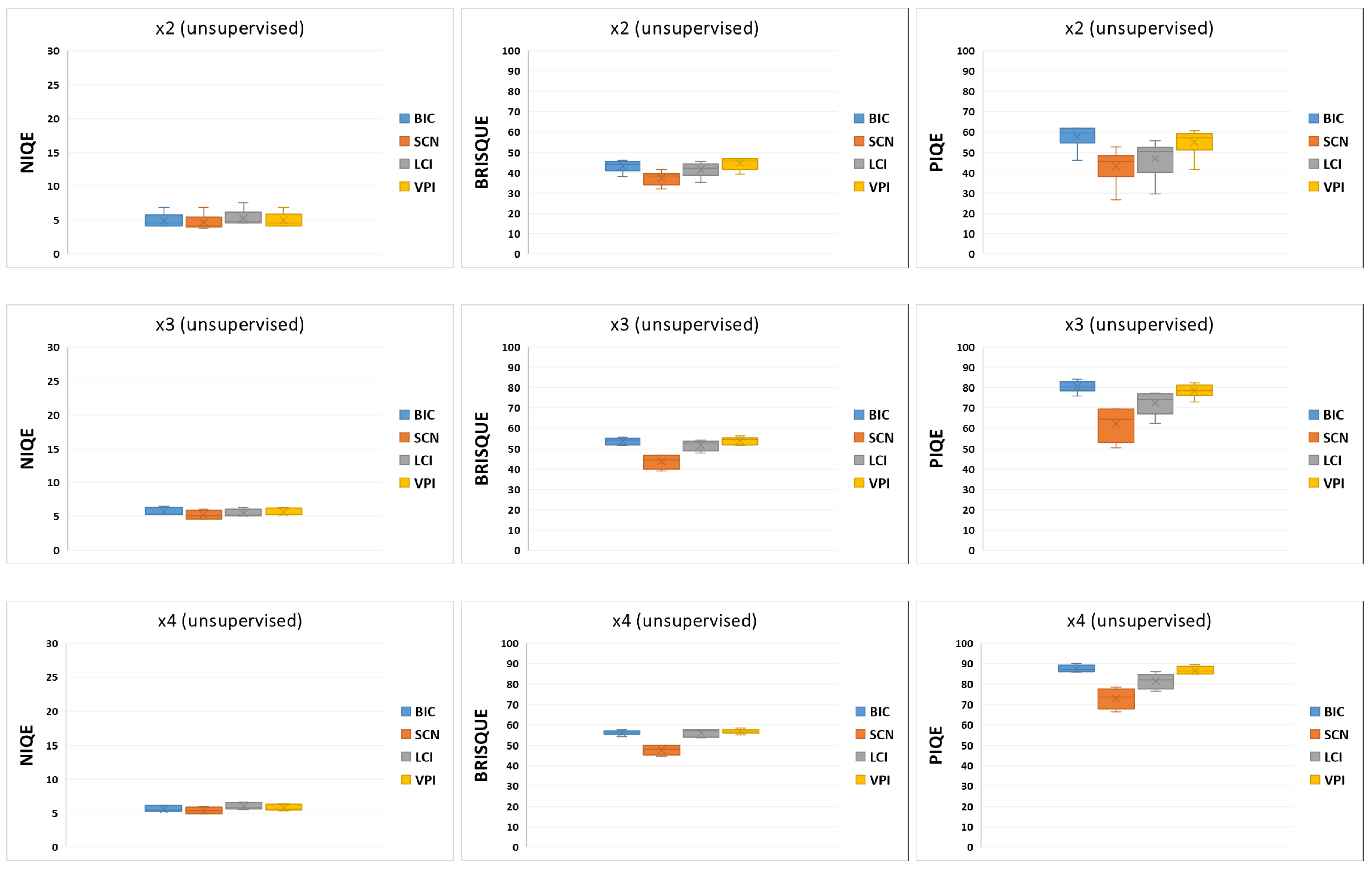
3.2.2. Unsupervised Upscaling

Table 15 and Figure 5 show the average performance of unsupervised upscaling methods for the scale factor s = 2, 3, 4 on all datasets.

The results indicated that the best performance was attributable to SCN, followed by u-VPI, u-LCI, BIC, and L₀, respectively. The same trend could be observed for higher scale factors as well. To provide further insights, the results obtained for scale factors s = 6, 8, and 10 on the GHDTV dataset are reported in Table 16.

Table 13. Average performance of unsupervised downscaling methods.

	:2				:3				:4
	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME
AID_cat
BIC	5.147	29.242	27.054	0.004	6.023	26.741	35.621	0.003	18.880	27.089	38.532	0.003
DPID	11.251	39.527	36.759	5.657	13.692	37.558	47.219	4.202	18.878	36.649	50.782	3.556
L₀	6.739	33.353	38.500	0.823	9.485	33.882	47.561	0.824	18.881	31.308	46.302	0.835
d-LCI	6.339	31.009	34.049	0.024	10.483	32.484	47.235	0.014	18.882	34.162	51.061	0.013
d-VPI	6.184	30.609	33.500	0.030	10.483	32.484	47.235	0.014	18.882	33.789	50.467	0.015
GDVD
BIC	3.910	17.698	24.632	0.004	5.886	19.987	26.148	0.004	6.275	22.486	35.670	0.004
DPID	7.554	34.082	36.059	6.595	10.937	32.194	39.806	4.796	11.643	33.413	49.788	4.047
L₀	6.765	24.805	38.179	0.921	9.919	27.361	37.694	0.920	10.286	28.892	43.381	0.976
d-LCI	6.714	22.966	32.659	0.025	11.409	29.972	39.986	0.018	12.950	33.464	49.578	0.015
d-VPI	6.502	22.573	31.809	0.031	11.802	30.639	39.791	0.021	12.449	32.844	48.988	0.017
GHDTV
BIC	3.091	18.196	22.834	0.023	3.472	16.618	25.837	0.019	4.011	17.297	24.477	0.015
DPID	4.983	34.709	30.127	34.047	6.089	31.589	36.280	24.283	7.367	31.571	36.985	20.761
L₀	3.944	21.288	30.967	4.083	4.983	21.645	34.016	4.116	6.537	23.584	31.895	4.123
d-LCI	3.826	19.861	26.933	0.146	6.173	24.547	35.094	0.106	8.188	28.211	37.146	0.087
d-VPI	3.710	20.221	26.938	0.178	6.230	24.827	35.520	0.125	8.036	27.805	36.884	0.100
NWV
BIC	3.370	19.481	23.754	0.006	4.334	19.833	26.575	0.005	6.068	20.752	28.709	0.004
DPID	5.860	35.350	29.366	11.687	7.516	31.966	34.362	8.684	9.718	31.611	37.862	7.437
L₀	5.039	21.079	32.706	1.384	6.282	20.344	31.589	1.378	8.323	23.322	31.434	1.363
d-LCI	5.002	20.541	26.981	0.045	8.072	25.941	34.744	0.028	10.248	28.346	38.033	0.023
d-VPI	4.850	21.239	27.702	0.053	8.208	26.582	35.698	0.034	10.434	28.724	38.422	0.026
UCA
BIC	3.940	22.410	23.350	0.010	4.506	21.335	27.062	0.08	5.350	21.571	29.022	0.007
DPID	6.550	38.872	28.987	18.459	7.366	34.679	34.369	16.083	9.694	34.131	39.354	11.182
L₀	5.172	26.068	32.346	2.121	6.016	24.507	30.767	2.086	8.033	26.928	33.403	2.085
d-LCI	4.938	23.953	26.694	0.071	7.523	27.478	36.059	0.049	9.581	29.600	38.526	0.038
d-VPI	4.787	23.669	26.846	0.085	7.574	27.742	36.081	0.057	9.696	30.164	38.754	0.045
UCML
BIC	18.878	32.331	28.198	0.001	18.878	33.958	45.817	0.001	18.878	35.676	33.524	0.001
DPID	18.875	40.497	35.564	1.066	18.876	39.356	52.020	1.145	18.876	40.651	44.790	0.672
L₀	18.880	33.306	36.646	0.147	18.879	34.637	49.134	0.143	18.878	36.518	39.791	0.143
d-LCI	18.879	33.339	32.174	0.003	18.879	36.283	52.429	0.003	18.879	37.808	43.669	0.003
d-VPI	18.878	33.163	31.917	0.004	18.879	36.136	52.350	0.003	18.879	37.579	43.343	0.003

Table 14. Average performance of unsupervised downscaling methods on GHDTV dataset for other scale factors (OOM indicates “out of memory”).

	:6				:8				:10
	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME
BIC	3.833	30.542	25.055	0.264	3.836	30.543	25.022	0.447	3.833	30.569	24.960	0.666
DPID	4.456	36.624	24.248	618.400	4.443	36.614	24.330	1.099.824	4.493	36.717	24.350	1.571.694
L₀	3.490	28.952	24.340	173.938	3.570	29.502	24.938	349.645	OOM	OOM	OOM	OOM
d-LCI	3.213	27.227	22.817	3.989	3.224	27.173	22.832	6.358	3.230	27.156	22.851	9.302
d-VPI	3.230	27.206	22.874	4.265	3.231	27.184	22.883	7.031	3.232	27.175	22.866	9.769

Figure 4. Boxplots derived from Table 13.

Figure 5. Boxplots derived from Table 15.

Table 15. Average performance of unsupervised upscaling methods (OOM indicates “out of memory”).

	×2				×3				×4
	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME
AID_cat
BIC	5.511	46.137	60.961	0.019	6.300	54.606	84.114	0.034	6.089	56.880	90.072	0.044
SCN	4.954	41.759	44.649	6.810	5.580	46.534	68.778	32.226	5.737	49.338	78.464	36.273
u-LCI	5.640	45.602	49.749	0.112	6.033	53.292	77.299	0.170	6.590	57.121	85.928	0.264
u-VPI	5.558	47.069	58.454	0.151	6.245	54.782	82.513	0.247	6.354	57.548	89.619	0.406
GDVD
BIC	4.159	38.024	45.976	0.023	5.464	51.620	75.954	0.039	5.232	55.886	85.886	0.058
SCN	4.050	32.100	26.690	7.435	4.614	38.881	50.570	37.611	4.875	44.598	66.384	36.491
u-LCI	4.840	35.244	29.687	0.138	5.123	47.808	62.489	0.233	5.560	54.041	76.456	0.353
u-VPI	4.149	39.341	41.727	0.174	5.260	51.702	72.957	0.309	5.363	56.302	84.908	0.496
GHDTV
BIC	4.600	45.243	61.791	0.075	5.285	55.751	82.571	0.125	5.412	57.725	87.739	0.204
SCN	4.130	38.827	46.202	41.271	OOM	OOM	OOM	OOM	OOM	OOM	OOM	OOM
u-LCI	4.641	43.782	51.363	0.817	5.147	54.291	77.137	1.299	5.734	57.865	83.961	2.179
u-VPI	4.627	46.866	58.726	1.053	5.340	56.306	80.972	1.659	5.667	58.639	86.632	2.954
NWV
BIC	4.104	42.862	57.460	0.029	5.275	54.023	80.634	0.051	5.285	56.122	86.505	0.069
SCN	3.829	34.834	46.900	10.639	OOM	OOM	OOM	OOM	OOM	OOM	OOM	OOM
u-LCI	4.538	39.783	51.150	0.178	5.133	52.152	74.552	0.302	5.752	57.133	82.417	0.485
u-VPI	4.181	44.918	56.006	0.228	5.204	54.480	79.037	0.402	5.467	56.351	85.867	0.645
UCA
BIC	4.478	45.141	61.809	0.041	5.354	54.948	80.193	0.063	5.387	56.798	85.772	0.097
SCN	4.080	38.435	52.804	17.223	4.643	46.539	69.608	132.644	4.905	49.747	74.276	133.794
u-LCI	4.573	42.633	55.653	0.298	5.166	53.189	73.964	0.545	5.627	57.647	78.101	0.883
u-VPI	4.590	46.975	60.633	0.486	5.311	55.090	78.395	0.788	5.592	57.010	84.680	1.165
UCML
BIC	6.871	42.085	57.862	0.005	6.538	51.958	79.503	0.007	6.097	54.232	88.876	0.011
SCN	6.862	38.411	41.871	1.349	6.052	42.871	60.530	5.731	5.947	46.992	72.435	5.825
u-LCI	7.580	41.832	43.705	0.018	6.307	49.469	68.655	0.030	6.665	53.715	81.340	0.046
u-VPI	6.856	42.413	54.593	0.024	6.337	51.922	77.516	0.038	6.301	55.224	88.085	0.068

Table 16. Average performance of unsupervised upscaling methods on GHDTV dataset for other scale factors.

	×6				×8				×10
	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME
BIC	6.891	59.236	89.523	0.025	6.992	59.282	97.206	0.022	6.858	61.451	100.00	0.021
SCN	5.402	48.950	78.023	21.135	5.481	51.565	85.429	12.174	5.386	53.224	87.700	30.241
d-LCI	7.107	57.226	82.019	0.088	7.281	58.435	95.896	0.080	7.265	60.402	100.000	0.073
d-VPI	6.836	58.686	89.908	0.135	7.163	59.282	97.390	0.127	7.177	62.215	100.000	0.118

3.2.3. Unsupervised Category Dependency

For unsupervised upscaling (downscaling), we also tested the benchmark methods according to the four categories: “beach”, “forest”, “parking”, and “sparse residential” defined in Section 2.2.2 on the corresponding sub-datasets in AID_cat and UCA. In Table 17 and Table 18, we report the average performance of unsupervised downscaling and upscaling methods, respectively, for the scale factors s = 2, 3, and 4 for each category. The resulting quality measures, shown in these tables, confirmed the same trends detected for unsupervised downscaling and upscaling. On this basis, we could confirm that the methods’ performances did not seem to be dependent on the image category.

3.3. CPU Time Assessment

Since an evaluation in terms of computation time is a crucial element to consider for a quantitative performance assessment, in all Tables, we report the CPU time taken by each benchmark method to produce the resized images for each dataset and scale factor. In Figure 6 and Figure 7, we also show boxplots representing the CPU time derived from Table 3 and Table 5 and from Table 3 and Table 15, respectively. Upon analyzing the results, we found no significant variations with respect to the trend detected in [20,21]. In particular, the results confirmed that BIC required the least CPU time, with u-LCI and u-VPI producing similar values to those of BIC. Much more CPU time was required by SCN for upscaling and DPID and L₀ for downscaling, principally on datasets with larger images. Specifically, DPID exhibited the slowest performance, often resulting in impractical and unsustainable processing times. Of course, for each benchmark method, the greater the increase in time, the higher the image resolution.

3.4. Supervised and Unsupervised Qualitative Evaluation for Upscaling and Downscaling

In this subsection, some visual results of the many tests performed herein are presented for scale factors equal to 2, 3, and 4. For simplicity, we show only the results obtained in the supervised mode for downscaling (see Figure 8 and Figure 9) and upscaling (see Figure 10 and Figure 11) using BIC input images, since no appreciable visual difference was present in the corresponding images obtained in the unsupervised mode. All images are shown at the same printing size to provide accurate evidence regarding the visual details. Figure 12 and Figure 13 are examples related to the image dependency, displaying the results in supervised mode at the scale factor of 4 with u-LCI and L₀ input images for downscaling and upscaling, respectively.

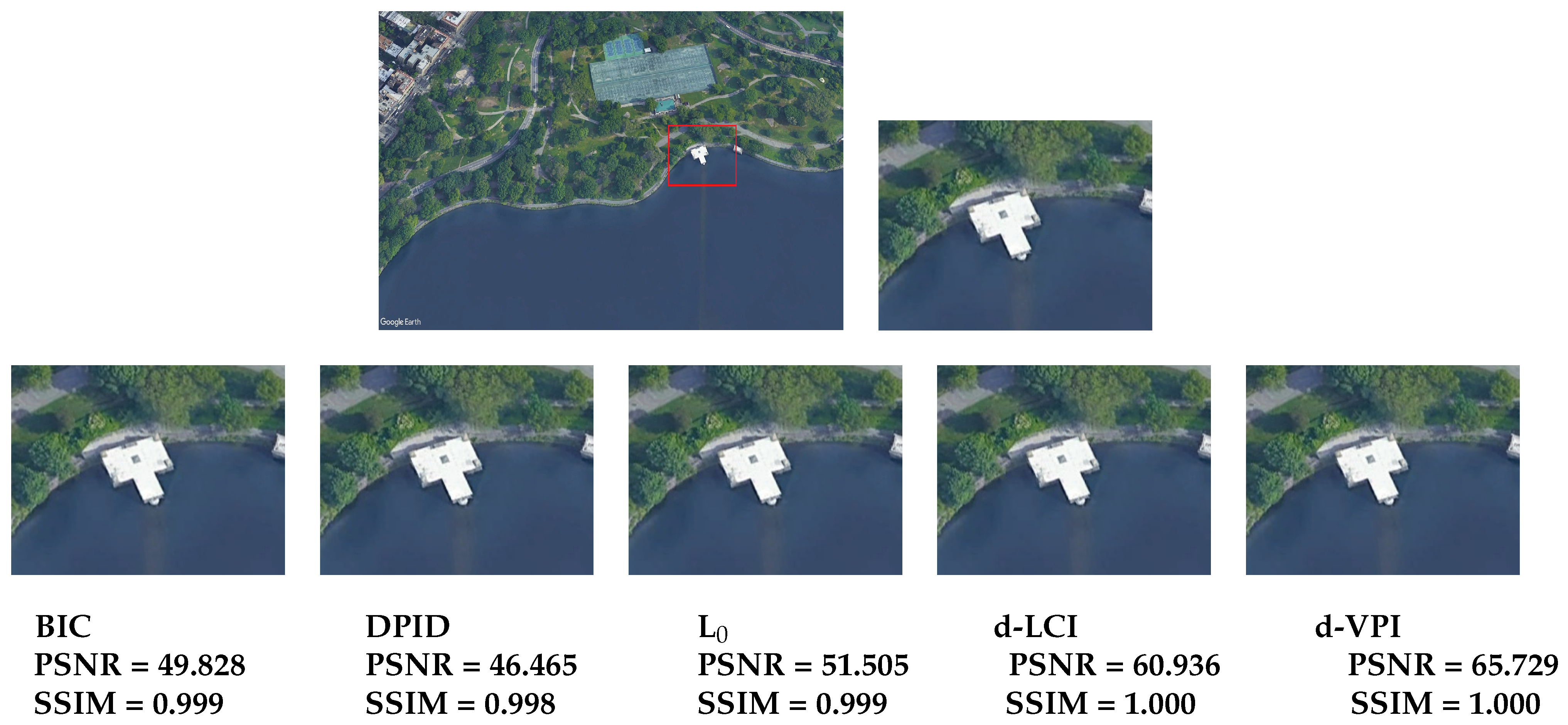
The visual inspection of these results validated the quantitative evaluation in terms of the quality measures presented in Section 3.1 and Section 3.2. Indeed, the results obtained by VPI and LCI, on average, appeared visually to be more attractive, since (a) the detectable object structure was captured; (b) the input image local contrast and luminance were retained; (c) most of the salient borders and the small details were preserved; and (d) the presence of over-smoothing artifacts and ringing was minimal. Unfortunately, some aliasing effects in downscaling are visible for any benchmark methods, especially when the HR image had high-frequency details. The extent and type of aliasing visual effects depends on many factors and vary according to the local context. Thus, aliasing in downscaling remains an open problem.

Figure 9. Examples of supervised downscaling performance results using BIC input images at the scale factors of 2 (left), 3 (middle), and 4 (right).

Figure 10. Examples of supervised upscaling performance results using BIC input images at the scale factors of 2 (left), 3 (middle), and 4 (right).

Figure 11. Examplesof supervised upscaling performance results using BIC input images at the scale factors of 2 (left), 3 (middle), and 4 (right).

Figure 12. Target image im30 (top left) with size 1080 × 1920 from GE100-HDTV; tile (top right) with size 200 × 280; qualitative comparison of :4 supervised downscaling performance results with u-LCI image input (bottom).

Figure 13. Target image im40 (top left) with size 1080 × 1920 from GE100-HDTV; tile (top right) with size 272 × 326; qualitative comparison of × 4 supervised upscaling performance results with L₀ image input (bottom).

3.5. Final Remarks

Overall, the experimental results from the current working hypotheses confirmed the trend already outlined in [20,21]. Indeed, for RSAs, the quality measures and CPU time results demonstrated that, on average, VPI and LCI showed suitable and competitive performances, since their experimental quality values were more stable and generally better than those of the benchmark methods. Furthermore, VPI and LCI had no implementation limitations, were much faster than the methods specializing in only downscaling or upscaling, and demonstrated adequate CPU times for large images and scale factors.

4. Conclusions

The primary aim of this paper was twofold: firstly, to ascertain the notable performance disparities among some IR benchmark methods, and secondly, to assess the visual quality they could achieve in RS image processing. To reach this objective, we realized and utilized an open framework designed to evaluate and compare the performance of the benchmark methods across a suite of six datasets.

The proposed framework was intended to encourage the adoption of the best practices in designing, analyzing, and conducting comprehensive assessments of IR methods. Implemented in a widely popular and user-friendly scientific language, Matlab, it already incorporates a selection of representative IR methods. Furthermore, a distinctive aspect introduced was the framework’s utilization of diverse FR and NR quality assessment measures tailored to whether the evaluation was supervised or unsupervised. In particular, we highlight the novelty of using NRQA measures, which are not typically employed for evaluating IR methods.

The publicly available framework for tuning and evaluating IR methods is a flexible and extensible tool, since other IR methods could be added in the future. This leaves open the possibility of contributing by introducing new benchmark methods. Furthermore, although the framework was primarily conceived for evaluating IR methods in RSAs, it can be used for any type of color image and a large number of different applications.

In this study, the framework yielded a good amount of results, encompassing CPU time, statistical analysis, and visual quality measures for RSAs. This facilitated the establishment of a standardized evaluation methodology, overcoming the limitations associated with conventional approaches commonly used to assess IR methods, often leading to uncorrected and untested valuations. Adhering to this research direction, the statistical and quality evaluations, conducted through multiple comparisons across numerous RS datasets, played a crucial role, since, in this way, the variance stemmed from the dissimilarities among the independent datasets at different image scales.

The performance evaluation was conducted using four datasets selected from the most representative within the RSA field and two new datasets generated to highlight and test several experimental aspects of RS. These additional datasets were made publicly available, serving as a valuable resource for the research community.

Overall, the study successfully achieved its primary objective by providing valuable assistance to researchers in selecting and comparing diverse image scaling methods. We are optimistic that our efforts will have a positive impact on future research, fostering advancements in image scaling and its applications. We hope that our efforts will prove beneficial for future research endeavors, driving advancements in the field of image scaling and its applications. Moving forward, our focus for future research will be on extending the proposed framework to 3D images and validating its applicability for biomedical applications.

Author Contributions

Conceptualization; methodology; software; validation; formal analysis; investigation; resources; data curation; writing (original draft preparation, review, and editing); visualization; supervision: D.O., G.R. and W.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding. The research was accomplished within the Research ITalian network on Approximation (RITA) and Approximation Theory research group of Unione Matematica Italiana (TA–UMI). It was partially supported by GNCS–INdAM and the University of Basilicata (local funds).

Data Availability Statement

The code and the supplementary data are openly available at https://github.com/ImgScaling/IR_framework (accessed on 15 June 2023).

Acknowledgments

The authors would like to thank Luciano De Leo for the IT support.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

AID	Aerial Image Dataset
BIC	Bicubic interpolation
BRISQUE	Blind/Referenceless Image Spatial Quality Evaluator
d-LCI	Downscaling Lagrange–Chebychev interpolation
DIV2k	DIVerse 2K resolution image dataset
DPID	Detail-preserving image downscaling
d-VPI	Downscaling de la Valleé–Poussin interpolation
IR	Image resizing
FRQA	Full-reference quality assessment
GDVD	Google Earth 100 Images—DVD
GHDTV	Google Earth 100 Images—HDTV
HVS	Human visual system
L₀	L₀-regularized image downscaling
LCI	Lagrange–Chebychev interpolation
ML	Machine learning
MSE	Mean squared error
NIQE	Natural Image Quality Evaluator
NRQA	No-reference quality assessment
NWV	NWPU VHR-10 dataset
PIQE	Perception-based Image Quality Evaluator
PSNR	Peak signal-to-noise ratio
RS	Remote sensing
RSA	Remote sensing application
SCN	Sparse-coding-based network
SSIM	Structural similarity index measure
UCA	UCAS_AOD dataset
u-LCI	Upscaling Lagrange–Chebychev interpolation
UCML	UCMerced_LandUse dataset
u-VPI	Upscaling de la Vallée–Poussin interpolation
VHR	Very high resolution
VPI	de la Vallée–Poussin interpolation

References

Richards, J.A. Sources and Characteristics of Remote Sensing Image Data. In Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
Bai, B.; Tan, Y.; Donchyts, G.; Haag, A.; Xu, B.; Chen, G.; Weerts, A.H. Naive Bayes classification-based surface water gap-filling from partially contaminated optical remote sensing image. J. Hydrol. 2023, 616, 128791. [Google Scholar] [CrossRef]
Massi, A.; Ortolani, M.; Vitulano, D.; Bruni, V.; Mazzanti, P. Enhancing the Thermal Images of the Upper Scarp of the Poggio Baldi Landslide (Italy) by Physical Modeling and Image Analysis. Remote Sens. 2023, 15, 907. [Google Scholar] [CrossRef]
Zhang, T.; Zeng, T.; Zhang, X. Synthetic Aperture Radar (SAR) Meets Deep Learning. Remote Sens. 2023, 15, 303. [Google Scholar] [CrossRef]
Goodchild, M.F.; Quattrochi, D.A. Introduction: Scale, Multiscaling, Remote Sensing, and GIS. In Scale in Remote Sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 1–12. [Google Scholar]
Marceau, D.J.; Hay, G.J. Remote sensing contributions to the scale issue. Can. J. Remote Sens. 1999, 25, 357–366. [Google Scholar] [CrossRef]
Cao, C.Y.; Lam, N. Understanding the scale and resolution effects in remote sensing and GIS. In Scale in Remote Sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 57–72. [Google Scholar]
Wu, H.; Li, Z.-L. Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling. Sensors 2009, 9, 1768–1793. [Google Scholar]
Chen, G.; Zhao, H.; Pang, C.K.; Li, T.; Pang, C. Image Scaling: How Hard Can It Be? IEEE Access 2019, 7, 129452–129465. [Google Scholar]
Arcelli, C.; Brancati, N.; Frucci, M.; Ramella, G.; di Baja, G.S. A fully automatic one-scan adaptive zooming algorithm for color images. Signal Process. 2011, 91, 61–71. [Google Scholar] [CrossRef]
Lin, X.; Ma, Y.-l.; Ma, L.-z.; Zhang, R.-l. A survey for image resizing. J. Zhejiang Univ. Sci. C 2014, 15, 697–716. [Google Scholar] [CrossRef]
Ghosh, S.; Garai, A. Image downscaling via co-occurrence learning. J. Vis. Commun. Image Represent. 2023, 91, 103766. [Google Scholar] [CrossRef]
Hach, T.; Knob, S. A Magnifier on Accurate Depth Jumps. In Proceedings of the IS&T Int’l. Symp. on Electronic Imaging: 3D Image Processing, Measurement (3DIPM), and Applications, Burlingame, CA, USA, 29 January–2 February 2017; pp. 15–26. [Google Scholar] [CrossRef]
Lee, C.-C.; So, E.C.; Saidy, L.; Wang, M.-J. Lung Field Segmentation in Chest X–ray Images Using Superpixel Resizing and Encoder–Decoder Segmentation Networks. Bioengineering 2022, 9, 351. [Google Scholar] [CrossRef]
Weissleder, R. Scaling down imaging: Molecular mapping of cancer in mice. Nat. Rev. Cancer 2002, 2, 11–18. [Google Scholar] [CrossRef] [PubMed]
Liu, H.; Xie, X.; Ma, W.Y.; Zhang, H.J. Automatic Browsing of Large Pictures on Mobile Devices. In Proceedings of the 11th ACM International Conference on Multimedia, Berkeley, CA, USA, 2–8 November 2003. [Google Scholar]
Zhang, M.; Zhang, L.; Sun, Y.; Feng, L.; Ma, W. Auto cropping for digital photographs. In Proceedings of the 2005 IEEE International Conference on Multimedia and Expo, Amsterdam, The Netherlands, 6–8 July 2005; p. 4. [Google Scholar]
Chen, H.; Lu, M.; Ma, Z.; Zhang, X.; Xu, Y.; Shen, Q.; Zhang, W. Learned Resolution Scaling Powered Gaming-as-a-Service at Scale. IEEE Trans. Multimed. 2021, 23, 584–596. [Google Scholar] [CrossRef]
Pratt, W.K. Digital Image Processing; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
Occorsio, D.; Ramella, G.; Themistoclakis, W. Lagrange-Chebyshev Interpolation for image resizing. Math. Comput. Simul. 2022, 197, 105–126. [Google Scholar] [CrossRef]
Occorsio, D.; Ramella, G.; Themistoclakis, W. Image Scaling by de la Vallée-Poussin Filtered Interpolation. J. Math. Imaging Vis. 2023, 65, 513–541. [Google Scholar] [CrossRef]
Han, D. Comparison of Commonly Used Image Interpolation Methods. In Proceedings of the 2nd International Conference on Computer Science and Electronics Engineering, Hong Kong, China, 17–18 June 2013; pp. 1556–1559. [Google Scholar]
Madhukar, B.N.; Narendra, R. Lanczos Resampling for the Digital Processing of Remotely Sensed Images. In Proceedings of International Conference on VLSI, Communication, Advanced Devices, Signals & Systems and Networking (VCASAN-2013); Chakravarthi, V., Shirur, Y., Prasad, R., Eds.; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2013; Volume 258, pp. 403–411. [Google Scholar]
Zhou, D.-X. Theory of deep convolutional neural networks: Downsampling. Neural Netw. 2020, 124, 319–327. [Google Scholar]
Hayat, K. Multimedia super-resolution via deep learning: A survey. Digit. Signalprocess. 2018, 81, 198–217. [Google Scholar]
Ran, Q.; Xu, X.; Zhao, S.; Li, W.; Du, Q. Remote sensing images super-resolution with deep convolution networks. Multimed. Tools Appl. 2020, 79, 8985–9001. [Google Scholar] [CrossRef]
Chen, L.; Liu, H.; Yang, M.; Qian, Y.; Xiao, Z.; Zhong, X. Remote Sensing Image Super-Resolution via Residual Aggregation and Split Attentional Fusion Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9546–9556. [Google Scholar] [CrossRef]
Dong, X.; Sun, X.; Jia, X.; Xi, Z.; Gao, L.; Zhang, B. Remote Sensing Image Super-Resolution Using Novel Dense-Sampling Networks. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1618–1633. [Google Scholar] [CrossRef]
Liu, B.; Zhao, L.; Li, J.; Zhao, H.; Liu, W.; Li, Y.; Wang, Y.; Chen, H.; Cao, W. Saliency-Guided Remote Sensing Image Super-Resolution. Remote Sens. 2021, 13, 5144. [Google Scholar] [CrossRef]
Wang, X.; Yi, J.; Guo, J.; Song, Y.; Lyu, J.; Xu, J.; Yan, W.; Zhao, J.; Cai, Q.; Min, H. A Review of Image Super-Resolution Approaches Based on Deep Learning and Applications in Remote Sensing. Remote Sens. 2022, 14, 5423. [Google Scholar] [CrossRef]
Cheng, R.; Wang, H.; Luo, P. Remote sensing image super-resolution using multi-scale convolutional sparse coding network. PLoS ONE 2022, 17, e0276648. [Google Scholar] [CrossRef] [PubMed]
Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar]
Wonsook; Ha, W.; Gowda, P.H.; Howell, T.A. A review of downscaling methods for remote sensing-based irrigation management: Part I. Irrig. Sci. 2013, 31, 831–850. [Google Scholar]
Zhou, J.; Liu, S.; Li, M.; Zhan, W.; Xu, Z.; Xu, T. Quantification of the Scale Effect in Downscaling Remotely Sensed Land Surface Temperature. Remote Sens. 2016, 8, 975. [Google Scholar] [CrossRef] [Green Version]
Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef] [Green Version]
Keys, R.G. Cubic Convolution Interpolation for Digital Image Processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef] [Green Version]
Weber, N.; Waechter, M.; Amend, S.C.; Guthe, S.; Goesele, M. Rapid, Detail-Preserving Image Downscaling. ACM Trans. Graph. 2016, 35, 205. [Google Scholar] [CrossRef] [Green Version]
Liu, J.; He, S.; Lau, R.W.H. L₀ Regularized Image Downscaling. IEEE Trans. Image Process. 2018, 27, 1076–1085. [Google Scholar] [CrossRef]
Wang, Z.; Liu, D.; Yang, J.; Han, W.; Huang, T. Deep networks for image super-resolution with sparse prior. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
AID (Aerial Image Dataset). Available online: https://www.kaggle.com/datasets/jiayuanchengala/aid-scene-classification-datasetsandhttps://captain-whu.github.io/AID/ (accessed on 1 January 2023).
NWPU VHR-10 Dataset. Available online: https://gcheng-nwpu.github.io/ (accessed on 1 January 2023).
UCAS_AOD Dataset. Available online: https://opendatalab.com/102 (accessed on 1 January 2023).
UCMerced_LandUse Dataset. Available online: http://weegee.vision.ucmerced.edu/datasets/landuse.html (accessed on 1 January 2023).
Occorsio, D.; Themistoclakis, W. Uniform weighted approximation on the square by polynomial interpolation at Chebyshev nodes. Appl. Math. Comput. 2020, 385, 125457. [Google Scholar]
Ramella, G.; di Baja, G.S. Color quantization by multiresolution analysis. In Computer Analysis of Images and Patterns; Jiang, X., Petkov, N., Eds.; Lecture Notes in Computer Science 5702; Springer: Berlin/Heidelberg, Germany, 2009; pp. 525–532. [Google Scholar]
Ramella, G.; di Baja, G.S. Multiresolution histogram analysis for color reduction. In Progress in Pattern Recognition, Image Analysis, Computer Vision and Applications; Bloch, I., Cesar, R.M., Jr., Eds.; Lecture Notes in Computer Science 6419; Springer: Berlin/Heidelberg, Germany, 2010; pp. 22–29. [Google Scholar]
Ramella, G.; di Baja, G.S. A new technique for color quantization based on histogram analysis and clustering. Int. J. Patt. Recog. Artif. Intell. 2013, 27, 1–17. [Google Scholar]
Ramella, G.; di Baja, G.S. Color quantization via spatial resolution reduction. In VISAPP 2013; Battiato, S., Braz, J., Eds.; Scitepress Science and Technology Publications: Montreal, QC, Canada, 2013; pp. 78–83. ISBN 9789898565471. [Google Scholar]
Bruni, V.; Ramella, G.; Vitulano, D. Automatic Perceptual Color Quantization of Dermoscopic Images. In VISAPP 2015; Braz, J., Battiato, S., Imai, F., Eds.; Scitepress Science and Technology Publications: Montreal, QC, Canada, 2015; Volume 1, pp. 323–330. [Google Scholar]
Ramella, G.; di Baja, G.S. A new method for color quantization. In Proceedings of the 12th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Naples, Italy, 28 November–1 December 2016; pp. 1–6. [Google Scholar]
Bruni, V.; Ramella, G.; Vitulano, D. Perceptual-based Color Quantization. In Image Analysis and Processing—ICIAP 2017; Battiato, S., Gallo, G., Schettini, R., Stanco, F., Eds.; Lecture Notes in Computer Science 10484; Springer: Berlin/Heidelberg, Germany, 2017; pp. 671–681. [Google Scholar]
Ramella, G.; di Baja, G.S. Color histogram-based image segmentation. In Computer Analysis of Images and Patterns–CAIP 2011; Real, P., Diaz-Pernil, D., Molina-Abril, H., Berciano, A., Kropatsch, W., Eds.; Lecture Notes in Computer Science 6854; Springer: Berlin/Heidelberg, Germany, 2011; Volume I, pp. 76–83. [Google Scholar]
Ramella, G.; di Baja, G.S. Image segmentation based on representative colors and region merging. In Pattern Recognition; Carrasco-Ochoa, J.A., Martínez-Trinidad, J.F., Rodríguez, J.S., di Baja, G.S., Eds.; 611 Lecture Notes in Computer Science 7914; Springer: Berlin/Heidelberg, Germany, 2013; pp. 175–184. [Google Scholar]
Ramella, G.; di Baja, G.S. From color quantization to image segmentation. In Proceedings of the 12th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Naples, Italy, 28 November–1 December 2016; pp. 798–804. [Google Scholar]
Mittal, H.; Pandey, A.C.; Saraswat, M.; Kumar, S.; Pal, R.; Modvel, G. A comprehensive survey of image segmentation: Clustering methods, performance parameters, and benchmark datasets. Multimed. Tools Appl. 2022, 81, 35001–35026. [Google Scholar] [CrossRef]
DIV2K Dataset. Available online: https://data.vision.ee.ethz.ch/cvl/DIV2K/ (accessed on 1 January 2023).
Chaki, J.; Dey, N. Introduction to Image Color Feature. In Image Color Feature Extraction Techniques; Springer Briefs in Applied Sciences and Technology; Springer: Singapore, 2021. [Google Scholar]
Wohker, C. 3D Computer Vision: Efficient Methods and Applications; X.media.publising Series; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
PSNR Definition. Available online: https://it.mathworks.com/help/vision/ref/psnr.html (accessed on 1 January 2023).
Ramella, G. Evaluation of quality measures for color quantization. Multimed. Tools Appl. 2021, 80, 32975–33009. [Google Scholar] [CrossRef]
Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Imag. Proc. 2004, 13, 600–612. [Google Scholar]
Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a Completely Blind Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 22, 209–212. [Google Scholar] [CrossRef]
Mittal, A.; Moorthy, A.K.; Bovik, A.C. Referenceless Image Spatial Quality Evaluation Engine. In Proceedings of the 45th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2011. [Google Scholar]
Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-Reference Image Quality Assessment in the Spatial Domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef] [PubMed]
Sheikh, H.R.; Wang, Z.; Cormack, L.; Bovik, A.C. LIVE Image Quality Assessment Database Release 2. Image & Video Quality Assessment at LIVE. Available online: https://live.ece.utexas.edu/research/quality/ (accessed on 3 February 2023).
Venkatanath, N.; Praneeth, D.; Bh, M.C.; Channappayya, S.S.; Medasani, S.S. Blind Image Quality Evaluation Using Perception Based Features. In Proceedings of the 21st National Conference on Communications (NCC), Mumbai, India, 27 February–1 March 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
Xia, G.-S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L. AID: A Benchmark Dataset for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar]
Cheng, G.; Han, J.; Zhou, P.; Guo, L. Multi-class geospatial object detection and geographic image classification based on collection of part detectors. Isprs J. Photogramm. Remote Sens. 2014, 98, 119–132. [Google Scholar]
Cheng, G.; Han, J. A survey on object detection in optical remote sensing images. Isprs J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar]
Cheng, G.; Zhou, P.; Han, J. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
Haigang, Z.; Xiaogang, C.; Weiqun, D.; Kun, F.; Qixiang, Y.; Jianbin, J. Orientation robust object detection in aerial images using deep convolutional neural network. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec, QC, Canada, 27–30 September 2015; pp. 3735–3739. [Google Scholar]
Yang, Y.; Newsam, S. Bag-Of-Visual-Words and Spatial Extensions for Land-Use Classification. In Proceedings of the ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM GIS), San Jose, CA, USA, 2–5 November 2010. [Google Scholar]

Figure 1. Dialog boxes employed in the framework.

Figure 6. Boxplots derived from Table 3 and Table 5.

Figure 7. Boxplots derived from Table 13 and Table 15.

Figure 8. Examples of supervised downscaling performance results using BIC input images at the scale factors of 2 (left), 3 (middle), and 4 (right).

Table 1. Benchmark methods.

Method	Type	Selection	Features
BIC	Down/up	Scale/size	Bicubic interpolation
DPID	Down	Size	Higher convolutional filter weights assigned to pixels differing from their neighborhoods
L₀	Down	Scale	Optimization framework based on two priors iteratively applied
LCI	Down/up	Scale/size	Lagrange interpolation at Chebyshev zeros
VPI	Down/up	Scale/size	Filtered VP interpolation at Chebyshev zeros
SCN	Up	Scale	Cascade of SCNs trained for scaling factors

Table 2. Datasets (# is the short way to indicate ”number of”).

Dataset	# Total Images	# Categories	Image Format	Image Size
AID_cat	1340	30	jpg	600 × 600
GDVD	100	1	jpg	852 × 480
GHDTV	100	1	jpg	1920 × 1080
NWV	800	2	jpg	From 381 × 601 to 939 × 1356
UCA	2410	3	png	1280 × 659
UCML	2100	21	tif	256 × 256

Table 11. Average performance of supervised downscaling methods with input images from GDVD for the ground truth from GHDTV—scale factor :2.253.

	MSE	PSNR	SSIM	TIME
BIC	121.116	27.860	0.916	0.013
DPID	152.851	26.814	0.897	34.260
L₀	309.388	23.673	0.817	5.028
d-LCI	175.546	26.213	0.880	0.114
d-VPI	139.928	27.208	0.900	2.143

Table 12. Average performance of supervised upscaling methods with input images from GDVD for the ground truth from GHDTV—scale factor x2.253 (n.a. indicates “not available”).

	MSE	PSNR	SSIM	TIME
BIC	188.974	25.902	0.837	0.015
SCN	n.a.	n.a.	n.a.	n.a.
u-LCI	188.304	25.916	0.835	0.134
u-VPI	184.094	26.001	0.840	2.953

Table 17. Average performance of unsupervised downscaling methods for the five considered categories common to AID_cat and UCA.

	:2				:3				:4
	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME
Beach
BIC	7.165	22.791	23.223	0.003	7.825	21.478	31.644	0.003	18.876	23.488	31.295	0.003
DPID	8.754	30.702	26.399	4.866	9.859	27.447	36.761	3.496	18.877	27.910	36.480	2.971
L₀	8.236	24.361	28.389	0.628	9.654	24.563	36.433	0.612	18.876	25.256	36.427	0.630
d-LCI	8.146	23.624	24.406	0.017	10.226	25.154	36.922	0.011	18.878	27.189	36.608	0.010
d-VPI	8.076	23.982	24.665	0.020	10.233	25.282	37.213	0.012	18.877	26.702	36.097	0.011
Forest
BIC	10.438	39.922	27.845	0.004	11.022	39.673	44.932	3.286	18.885	39.142	45.881	0.003
DPID	22.078	43.421	44.107	4.513	25.509	43.508	60.804	3.286	18.874	43.600	64.024	2.763
L₀	11.782	41.848	47.852	0.558	14.187	41.723	59.867	0.562	18.886	41.738	59.111	0.562
d-LCI	11.280	40.366	41.576	0.016	15.736	42.467	61.499	0.010	18.885	43.435	64.493	0.009
d-VPI	11.195	40.200	40.009	0.018	15.932	42.417	61.442	0.012	18.885	43.318	63.981	0.011
Parking
BIC	8.273	30.648	26.590	0.003	9.204	26.935	37.071	0.003	18.880	27.683	37.196	0.003
DPID	11.314	42.514	32.252	4.629	12.343	39.276	44.849	3.313	18.880	38.192	47.311	2.788
L₀	8.756	33.340	32.606	0.628	11.015	34.615	45.077	0.627	18.881	31.670	41.820	0.628
d-LCI	8.371	30.631	28.288	0.018	10.912	31.041	43.501	0.011	18.881	33.255	45.201	0.010
d-VPI	8.279	29.719	28.421	0.021	10.909	30.672	43.815	0.013	18.881	33.204	45.060	0.011
Residential
BIC	7.898	26.817	26.910	0.003	8.349	26.001	36.619	0.003	18.882	27.130	33.055	0.003
DPID	12.446	43.424	45.196	4.398	14.982	42.627	54.725	3.241	18.880	42.069	53.418	2.792
L₀	10.125	35.465	48.627	0.596	12.709	34.975	54.446	0.595	18.883	33.179	45.921	0.596
d-LCI	9.811	32.386	43.013	0.017	13.870	36.625	56.065	0.011	18.885	38.163	55.738	0.009
d-VPI	9.564	31.359	40.780	0.020	13.905	36.266	55.972	0.012	18.884	37.487	54.161	0.011

Table 18. Average performance of unsupervised upscaling methods for the five considered categories common to AID_cat and UCA.

	×2				×3				×4
	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME	NIQE	BRISQUE	PIQE	TIME
Beach
BIC	4.944	43.392	56.662	0.018	5.771	51.797	83.463	0.031	5.917	52.859	92.155	0.045
SCN	4.447	38.711	42.088	5.184	5.166	46.363	65.894	25.654	5.591	50.049	77.292	25.360
u-LCI	4.905	42.972	46.546	0.086	5.654	51.583	74.759	0.148	6.380	54.211	86.545	0.205
u-VPI	4.904	45.265	54.925	0.112	5.776	52.959	81.551	0.204	6.168	54.332	91.873	0.327
Forest
BIC	6.696	46.770	58.747	0.016	7.353	54.820	83.616	0.029	6.804	57.638	91.129	0.041
SCN	6.552	44.614	40.786	4.903	6.859	46.748	67.210	24.335	6.600	48.840	77.886	23.469
u-LCI	7.215	46.952	48.107	0.082	7.131	53.587	76.966	0.135	7.550	57.417	87.054	0.203
u-VPI	6.795	46.942	55.603	0.108	7.257	54.578	81.899	0.187	7.133	57.932	90.819	0.303
Parking
BIC	5.091	47.562	69.904	0.018	5.788	56.718	85.280	0.031	5.694	58.787	89.570	0.045
SCN	4.562	42.321	55.489	5.297	5.067	47.164	73.586	25.390	5.250	50.129	79.852	25.339
u-LCI	5.207	45.659	58.065	0.089	5.507	54.320	78.966	0.142	6.020	58.245	85.803	0.211
u-VPI	5.165	48.185	67.438	0.116	5.742	56.578	84.145	0.208	5.946	59.338	88.924	0.327
Residential
BIC	5.663	43.232	50.595	0.017	6.875	52.807	79.537	0.029	6.242	56.833	87.626	0.042
SCN	5.360	39.832	30.213	5.062	6.049	42.414	58.062	24.474	6.041	45.919	72.643	24.785
u-LCI	6.218	44.091	35.170	0.087	6.422	50.430	70.130	0.142	6.895	56.181	81.822	0.212
u-VPI	5.701	43.682	46.537	0.113	6.628	52.439	77.450	0.197	6.463	57.226	87.141	0.332

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Occorsio, D.; Ramella, G.; Themistoclakis, W. An Open Image Resizing Framework for Remote Sensing Applications and Beyond. Remote Sens. 2023, 15, 4039. https://doi.org/10.3390/rs15164039

AMA Style

Occorsio D, Ramella G, Themistoclakis W. An Open Image Resizing Framework for Remote Sensing Applications and Beyond. Remote Sensing. 2023; 15(16):4039. https://doi.org/10.3390/rs15164039

Chicago/Turabian Style

Occorsio, Donatella, Giuliana Ramella, and Woula Themistoclakis. 2023. "An Open Image Resizing Framework for Remote Sensing Applications and Beyond" Remote Sensing 15, no. 16: 4039. https://doi.org/10.3390/rs15164039

APA Style

Occorsio, D., Ramella, G., & Themistoclakis, W. (2023). An Open Image Resizing Framework for Remote Sensing Applications and Beyond. Remote Sensing, 15(16), 4039. https://doi.org/10.3390/rs15164039

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

An Open Image Resizing Framework for Remote Sensing Applications and Beyond

Abstract

1. Introduction

2. Materials and Methods

2.1. Benchmark Methods

2.2. Rationale and Technical Background

2.2.1. Quality Metrics

2.2.2. Benchmark Datasets

2.3. Proposed Framework

3. Experimental Results and Discussion

3.1. Supervised Quantitative Evaluation

3.1.1. Supervised Downscaling

3.1.2. Supervised Upscaling

3.1.3. Supervised Input Image Dependency

3.2. Unsupervised Quantitative Evaluation

3.2.1. Unsupervised Downscaling

3.2.2. Unsupervised Upscaling

3.2.3. Unsupervised Category Dependency

3.3. CPU Time Assessment

3.4. Supervised and Unsupervised Qualitative Evaluation for Upscaling and Downscaling

3.5. Final Remarks

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI