Evaluation of the Horizontal Winds Simulated by IAP-HAGCM through Comparison with Beijing MST Radar Observations
Abstract
1. Introduction
2. Data and Methods
2.1. The IAP-HAGCM Simulations
2.2. Beijing MST Radar Observations
2.3. Tidal Extraction Method
3. Results
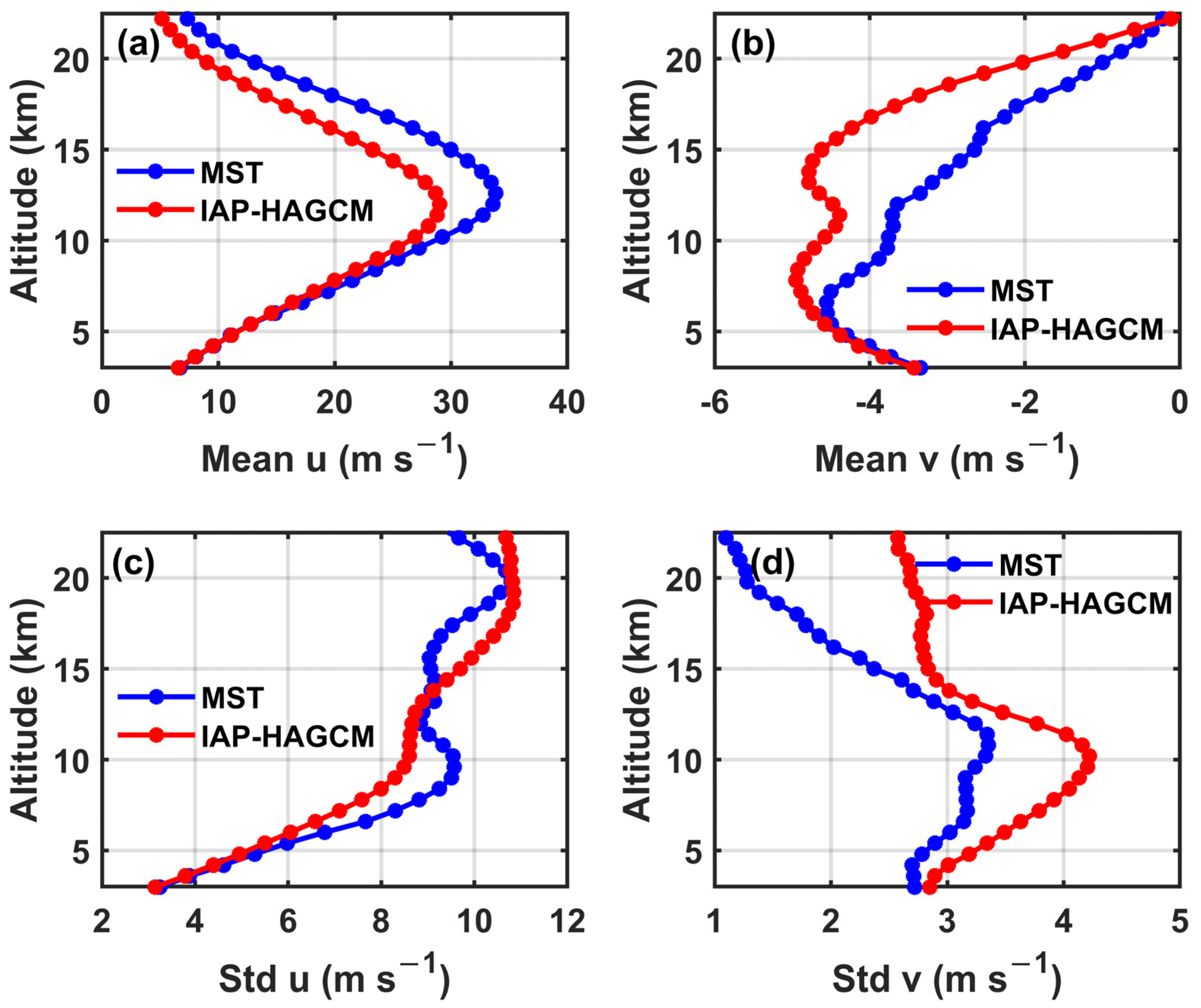
3.1. Comparison of the Distribution and Variation in the Horizontal Winds between the IAP-HAGCM Simulations and Beijing MST Radar Observations
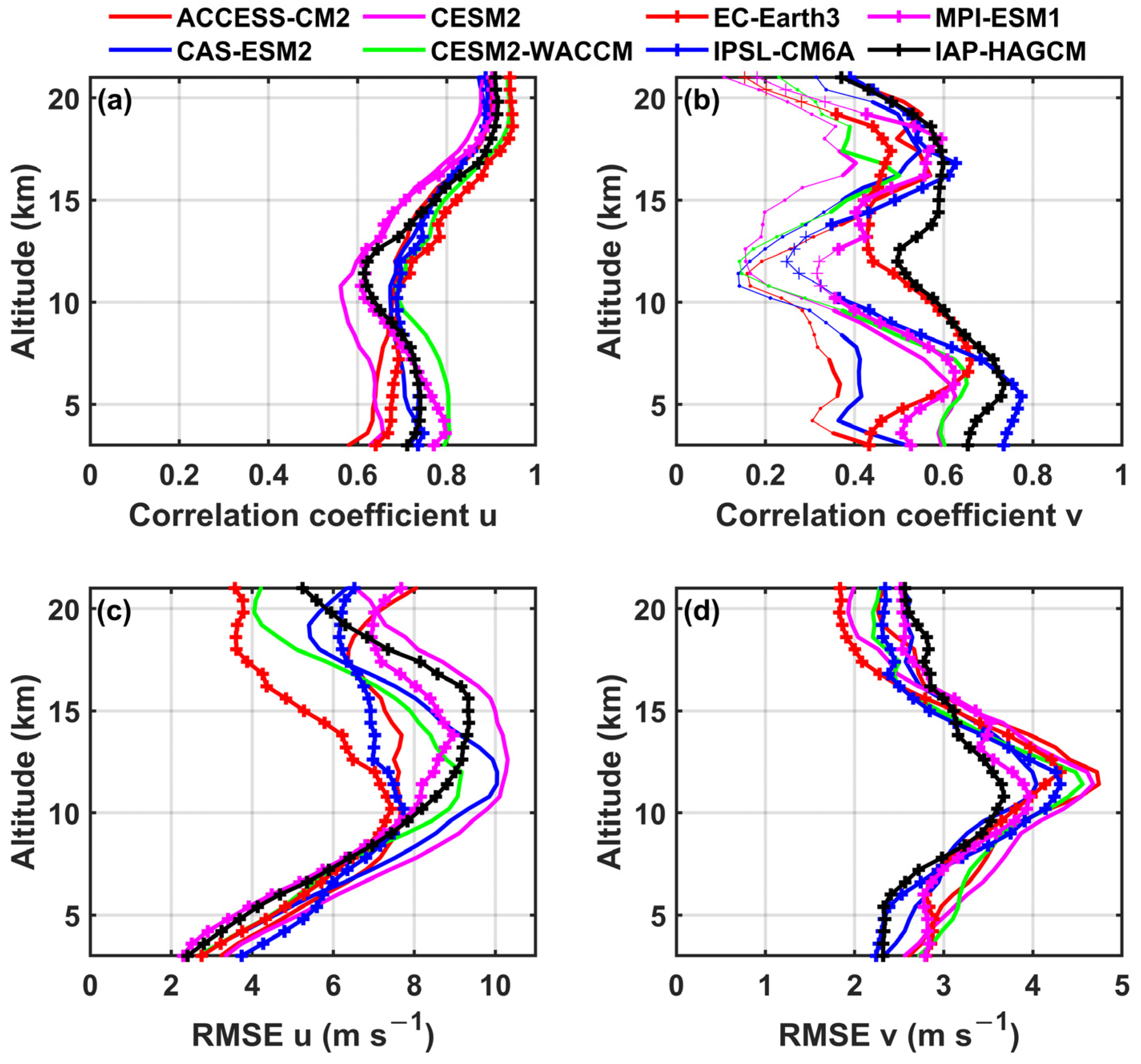
3.2. Statistical Analysis
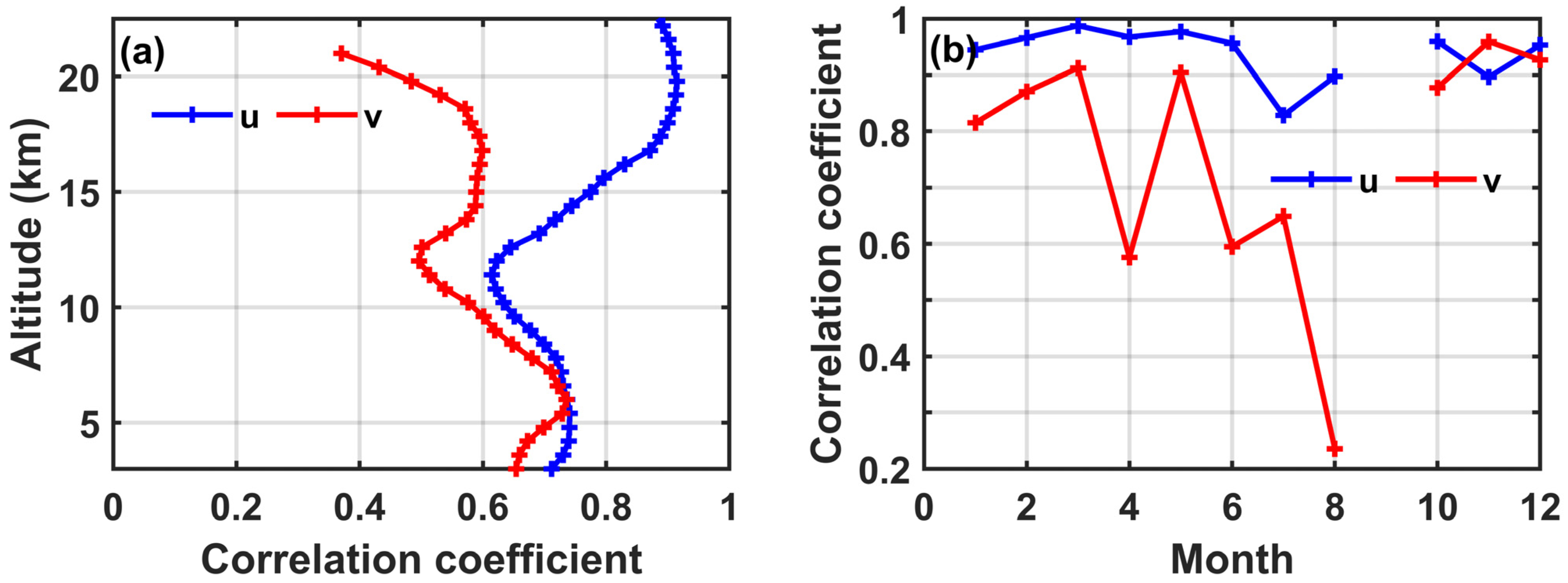
3.2.1. Correlation Coefficients
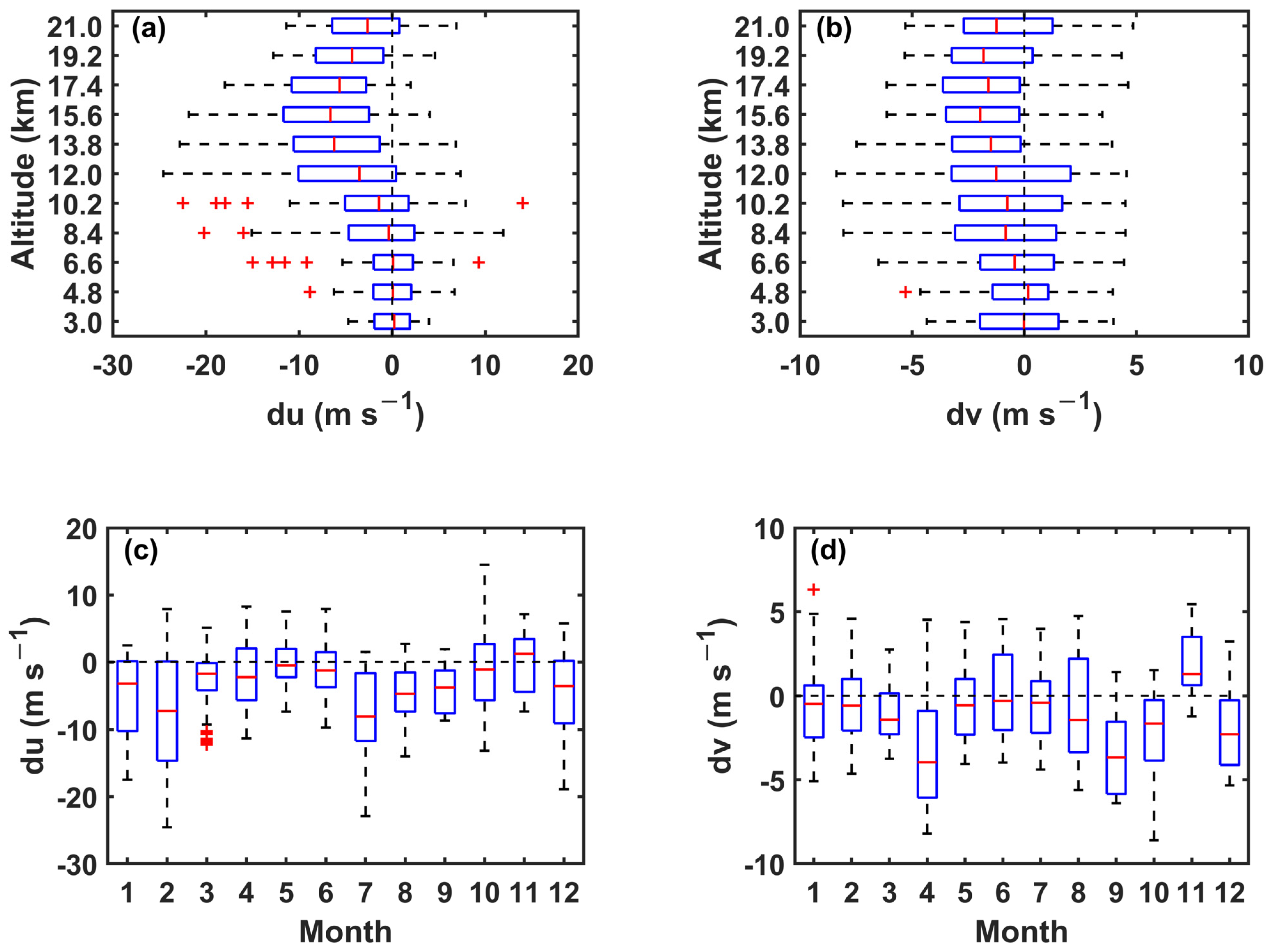
3.2.2. Differences
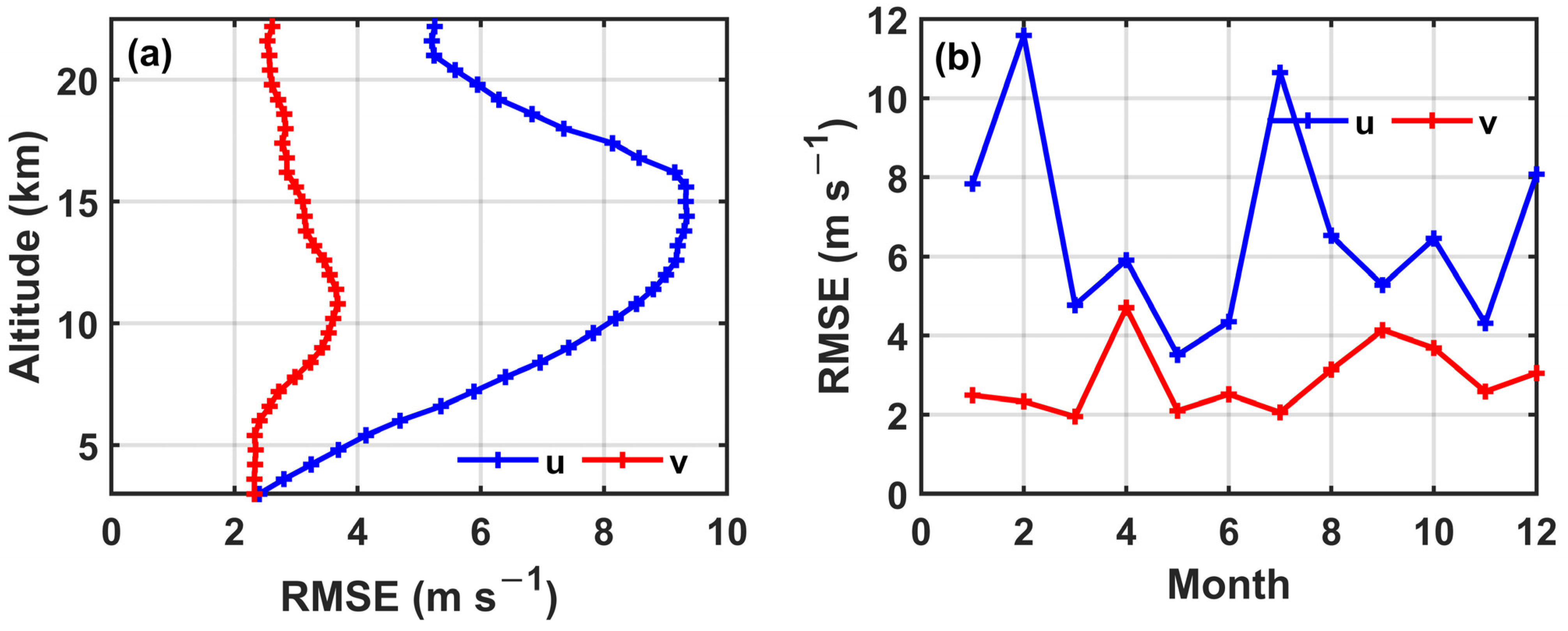
3.2.3. RMSE
3.3. Tides
3.3.1. Diurnal Tides
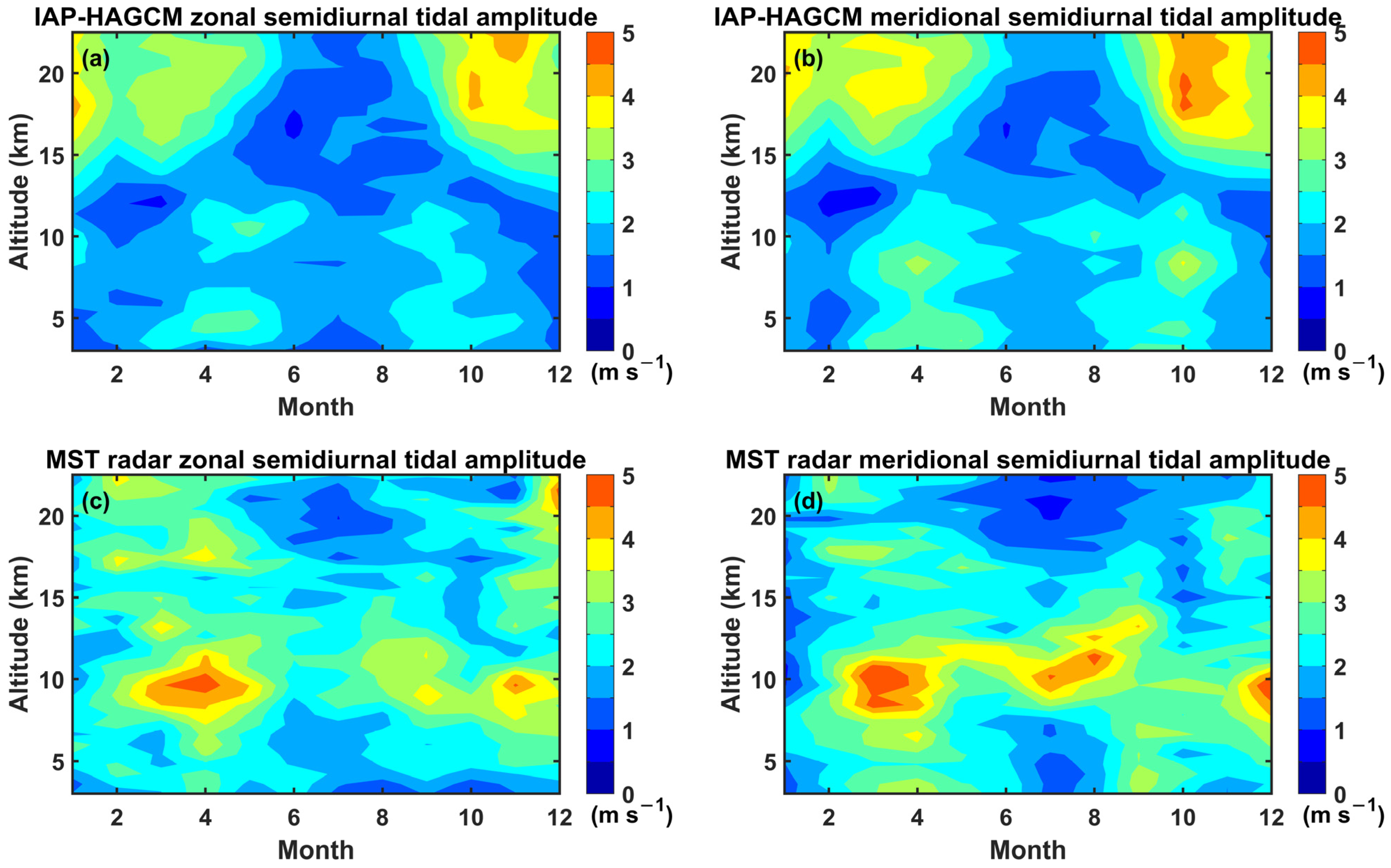
3.3.2. Semidiurnal Tides
4. Discussion
4.1. The Performance of the IAP-HAGCM in Simulating the Horizontal Wind Changes with Altitude, Season, and Month
- The IAP-HAGCM reproduces a relatively reasonable altitude–month distribution of the zonal wind compared with Beijing MST radar observations, albeit the westerly wind velocity is underestimated and the easterly wind velocity is overestimated with a larger time–altitude region.
- The consistency of the meridional wind between the IAP-HAGCM simulations and MST radar observations is not as good as it is for the zonal wind. This phenomenon has also been reported in previous studies, such as in a comparison of high-resolution regional model (WRF) wind outputs at Cochin from 315 m to 20 km with ST radar observations [65].
- The IAP-HAGCM reproduces a similar temporal variation in the zonal and meridional components as exhibited by the radar observations, suggesting that the IAP-HAGCM-simulated horizontal winds can be used for analysis of the temporal variation.
- In the lower troposphere, below 5 km, the horizontal winds obtained from the model and radar observations are in good agreement. However, larger discrepancies exist in the altitudinal range of the westerly jet’s location, as well as in the transition regions of the troposphere and stratosphere. The variation in the correlation coefficient, mean difference, and RMSE with altitude all show the above results.
- The IAP-HAGCM can also simulate seasonal variation in horizontal wind similar to that observed by the radar. A larger discrepancy between the model simulations and radar observations can be found in certain months such as February and July for the zonal component, and April and September for the meridional component.
4.2. Possible Reasons
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernando, H.J.S.; Mann, J.; Palma, J.M.L.M.; Lundquist, J.K.; Barthelmie, R.J.; Belo-Pereira, M.; Brown, W.O.J.; Chow, F.K.; Gerz, T.; Hocut, C.M.; et al. The Perdigao: Peering into Microscale Details of Mountain Winds. Bull. Am. Meteorol. Soc. 2019, 100, 799–820. [Google Scholar] [CrossRef]
- Simpson, C.C.; Sharples, J.J.; Evans, J.P. Sensitivity of atypical lateral fire spread to wind and slope. Geophys. Res. Lett. 2016, 43, 1744–1751. [Google Scholar] [CrossRef]
- Hoolohan, V.; Tomlin, A.S.; Cockerill, T. Improved near surface wind speed predictions using Gaussian process regression combined with numerical weather predictions and observed meteorological data. Renew. Energ. 2018, 126, 1043–1054. [Google Scholar] [CrossRef]
- Coccia, M. The effects of atmospheric stability with low wind speed and of air pollution on the accelerated transmission dynamics of COVID-19. Int. J. Environ. Stud. 2021, 78, 1–27. [Google Scholar] [CrossRef]
- Xing, W.; Sun, J.; Liu, H.; Xu, L. Numerical Simulation of the Local Circulation of Complex Topography on the Gaoligong Mountains. Chin. J. Atmos. Sci. 2021, 45, 746–758. [Google Scholar] [CrossRef]
- Su, Y.; Shi, C.; Mao, W.; Sun, S.; Xie, B.; Zhai, D. Hydrological Utility of CLDAS-Prcp Multi-source Fusion Precipitation Products in Qijiang River BasinTakingWRF-Hydro Model as an Example. Plateau Meteorol. 2022, 41, 617–629. [Google Scholar] [CrossRef]
- Zhang, C.; He, J.; Lai, X.; Liang, T.; Liu, Y.; Yang, W.; Che, H.; Gong, S. Impacts of High-Resolution Land Surface Data on Meteorological Field Simulation over Hainan. Plateau Meteorol. 2022, 41, 775–789. [Google Scholar] [CrossRef]
- Pan, L.L.; Liu, Y.B.; Roux, G.; Cheng, W.; Liu, Y.W.; Hu, J.; Jin, S.L.; Feng, S.L.; Du, J.; Peng, L.X. Seasonal variation of the surface wind forecast performance of the high-resolution WRF-RTFDDA system over China. Atmos. Res. 2021, 259, 105673. [Google Scholar] [CrossRef]
- Bao, J.W.; Michelson, S.A.; Persson, P.O.G.; Djalalova, I.V.; Wilczak, J.M. Observed and WRF-simulated low-level winds in a high-ozone episode during the Central California Ozone Study. J. Appl. Meterol. Clim. 2008, 47, 2372–2394. [Google Scholar] [CrossRef]
- Michelson, S.A.; Bao, J.W. Sensitivity of Low-Level Winds Simulated by the WRF Model in California’s Central Valley to Uncertainties in the Large-Scale Forcing and Soil Initialization. J. Appl. Meterol. Clim. 2008, 47, 3131–3149. [Google Scholar] [CrossRef]
- Fadnavis, S.; Deshpande, M.; Ghude, S.D.; Raj, P.E. Simulation of severe thunder storm event: A case study over Pune, India. Nat. Hazards 2014, 72, 927–943. [Google Scholar] [CrossRef]
- Boadh, R.; Satyanarayana, A.N.V.; Krishna, T.V.B.P.S.R.; Madala, S. Sensitivity of PBL schemes of the WRF-ARW model in simulating the boundary layer flow parameters for its application to air pollution dispersion modeling over a tropical station. Atmósfera 2016, 29, 61–81. [Google Scholar] [CrossRef]
- Kadaverugu, R.; Matli, C.; Biniwale, R. Suitability of WRF model for simulating meteorological variables in rural, semi-urban and urban environments of Central India. Meteorol. Atmos. Phys. 2021, 133, 1379–1393. [Google Scholar] [CrossRef]
- Xin, Y.F.; Rinke, A.; Bian, L.G.; Dethloff, K.; Xiao, C.D.; Mielke, M. Climate and Forecast Mode Simulations for Antarctica: Implications for Temperature and Wind. Adv. Atmos. Sci. 2010, 27, 1453–1472. [Google Scholar] [CrossRef]
- Bell, A. A Statistical Comparison of Radiosonde Observations to NCEP RCM3 Climate Model Atmospheric Wind Speed (Presentation). 2010. Available online: http://n2t.net/ark:/85065/d7n87cft (accessed on 16 July 2023).
- Weissmann, M.; Cardinali, C. Impact of airborne Doppler lidar observations on ECMWF forecasts. Q. J. Roy. Meteor. Soc. 2007, 133, 107–116. [Google Scholar] [CrossRef]
- Fritts, D.C.; Wang, D.-Y.; Blanchard, R.C. Gravity Wave and Tidal Structures between 60 and 140 km Inferred from Space Shuttle Reentry Data. J. Atmos. Sci. 1993, 50, 837–849. [Google Scholar] [CrossRef]
- Sun, L.; Lian, P.; Chang, X.; Yan, J. Near Space Atmosphere Modeling and its Effect on the Aircraft. Command. Control. Simul. 2016, 38, 107–111. [Google Scholar] [CrossRef]
- Cheng, X.; Xiao, C.; Hu, X. Research progress of the influence of atmospheric environment in near space on aerodynamic characteristics of hypersonic vehicles. Aerosp. Technol. 2018, 401, 22–28. [Google Scholar] [CrossRef]
- Wing, R.; Martic, M.; Triplett, C.; Hauchecorne, A.; Porteneuve, J.; Keckhut, P.; Courcoux, Y.; Yung, L.; Retailleau, P.; Cocuron, D. Gravity Wave Breaking Associated with Mesospheric Inversion Layers as Measured by the Ship-Borne BEM Monge Lidar and ICON-MIGHTI. Atmosphere 2021, 12, 1386. [Google Scholar] [CrossRef]
- Borchert, S.; Zhou, G.D.; Baldauf, M.; Schmidt, H.; Zangl, G.; Reinert, D. The upper-atmosphere extension of the ICON general circulation model (version: Ua-icon-1.0). Geosci. Model Dev. 2019, 12, 3541–3569. [Google Scholar] [CrossRef]
- Stober, G.; Kuchar, A.; Pokhotelov, D.; Liu, H.X.; Liu, H.L.; Schmidt, H.; Jacobi, C.; Baumgarten, K.; Brown, P.; Janches, D.; et al. Interhemispheric differences of mesosphere-lower thermosphere winds and tides investigated from three whole-atmosphere models and meteor radar observations. Atmos. Chem. Phys. 2021, 21, 13855–13902. [Google Scholar] [CrossRef]
- Wilks, D.S. Chapter 9—Forecast Verification. In Statistical Methods in the Atmospheric Sciences, 4th ed.; Wilks, D.S., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 369–483. [Google Scholar] [CrossRef]
- Gunwani, P.; Mohan, M. Sensitivity of WRF model estimates to various PBL parameterizations in different climatic zones over India. Atmos. Res. 2017, 194, 43–65. [Google Scholar] [CrossRef]
- Guo, J.P.; Liu, B.M.; Gong, W.; Shi, L.J.; Zhang, Y.; Ma, Y.Y.; Zhang, J.; Chen, T.M.; Bai, K.X.; Stoffelen, A.; et al. Technical note: First comparison of wind observations from ESA’s satellite mission Aeolus and ground-based radar wind profiler network of China. Atmos. Chem. Phys. 2021, 21, 2945–2958. [Google Scholar] [CrossRef]
- Munoz, L.E.; Campozano, L.V.; Guevara, D.C.; Parra, R.; Tonato, D.; Suntaxi, A.; Maisincho, L.; Paez, C.; Villacis, M.; Cordova, J.; et al. Comparison of Radiosonde Measurements of Meteorological Variables with Drone, Satellite Products, and WRF Simulations in the Tropical Andes: The Case of Quito, Ecuador. Atmosphere 2023, 14, 264. [Google Scholar] [CrossRef]
- Zhou, B.; Xue, X.; Yi, W.; Ye, H.; Zeng, J.; Chen, J.; Wu, J.; Chen, T.; Dou, X. A comparison of MLT wind between meteor radar chain data and SDWACCM results. Earth Planet. Phys. 2022, 6, 451–464. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wei, Z.G.; Chen, G.Y.; Liu, Y.J.; Zhu, X.; Zheng, Z.Y. Shift of the Arctic polar vortex in recent decades and its simulation by the NCEP CFSv2. Phys. Chem. Earth 2020, 115, 102823. [Google Scholar] [CrossRef]
- Richter, J.H.; Garcia, R.R. On the forcing of the Mesospheric Semi-Annual Oscillation in the whole atmosphere community climate model. Geophys. Res. Lett. 2006, 33, L01806. [Google Scholar] [CrossRef]
- Hamilton, K.; Hertzog, A.; Vial, F.; Stenchikov, G. Longitudinal variation of the stratospheric quasi-biennial oscillation. J. Atmos. Sci. 2004, 61, 383–402. [Google Scholar] [CrossRef]
- Butchart, N.; Anstey, J.A.; Hamilton, K.; Osprey, S.; McLandress, C.; Bushell, A.C.; Kawatani, Y.; Kim, Y.H.; Lott, F.; Scinocca, J.; et al. Overview of experiment design and comparison of models participating in phase 1 of the SPARC Quasi-Biennial Oscillation initiative (QBOi). Geosci. Model Dev. 2018, 11, 1009–1032. [Google Scholar] [CrossRef]
- Chai, Z.; Zhang, M.; Zeng, Q.; Xie, J.; You, T.; Zhang, H. Simulation of the QBO in IAP-AGCM: Analysis of momentum budget. Atmos. Oceanic Sci. Lett. 2021, 14, 100021. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, X.; Liang, X.; Yuan, C.; Chen, S. Documentation of IAP two-level atmospheric general circulation model. USDo Energy 1989, 383, 90143–90145. [Google Scholar]
- Zhang, X. Dynamical framework of IAP nine-level atmospheric general circulation model. Adv. Atmos. Sci. 1990, 7, 67–77. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.H.; Jin, J.B.; Fei, K.C.; Ji, D.Y.; Wu, C.L.; Zhu, J.W.; He, J.X.; Chai, Z.Y.; Xie, J.B.; et al. Description and Climate Simulation Performance of CAS-ESM Version 2. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002210. [Google Scholar] [CrossRef]
- Zuo, R.; Zeng, Q.; Zhang, M. A Numerical Simulation of Monsoon and the Correlation Between Monsoon and Westerlies. Chin. J. Atmos. Sci. 2004, 28, 7–22. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.H.; Zeng, Q.C. Sensitivity of Simulated Climate to Two Atmospheric Models: Interpretation of Differences between Dry Models and Moist Models. Mon. Weather Rev. 2013, 141, 1558–1576. [Google Scholar] [CrossRef]
- Bi, X. An Improved Nine-Level Atmospheric General Circulation Model and Its Application to Climate Simulation. Ph.D. Thesis, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China, 1993. [Google Scholar]
- Liang, X. Description of a nine-level grid point atmospheric general circulation model. Adv. Atmos. Sci. 1996, 13, 269–298. [Google Scholar] [CrossRef]
- Zuo, R. Development of New Generation Grid Point Atmospheric General Circulation Model with High Resolution. Ph.D. Thesis, China People’s Liberation Army University of Science and Technology, Changsha, China, 2003. [Google Scholar]
- Zhang, H.; Lin, Z.; Zeng, Q. The Computational Scheme and the Test for Dynamical Framework of IAP AGCM-4. Chin. J. Atmos. Sci. 2009, 33, 1267–1285. [Google Scholar] [CrossRef]
- Zhang, H. Development of IAP Atmospheric General Circulation Model Version 4.0 and Its Climate Simulations. Ph.D. Thesis, Institute of Atmospheric Physics, Chinese Academy of Sciences, Bejing, China, 2009. [Google Scholar]
- Chai, Z.; Zhang, M.; Zeng, Q.; Zhang, H.; Jin, J.; Xie, J.; You, T. A high-top version of IAP-AGCM: Preliminary assessment and sensitivity IAP-AGCM. Atmos. Oceanic Sci. Lett. 2021, 14, 100025. [Google Scholar] [CrossRef]
- Xue, F.; Bi, X.Q.; Lin, Y.H. Modelling the global monsoon system by IAP 9L AGCM. Adv. Atmos. Sci. 2001, 18, 404–412. [Google Scholar] [CrossRef]
- Zuo, R.; Zhang, M.; Zhang, D.; Wang, A.; Zeng, Q. Designing and Climatic Numerical Modeling of 21-Level AGCM (IAP AGCM-Ⅲ) Part Ⅰ. Dynamical Framework. Chin. J. Atmos. Sci. 2004, 28, 659–674. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, G.; Zeng, Q. Assessments of the Climate System Model (CAS-ESM-C) Using IAP AGCM4 as Its Atmospheric Component. Chin. J. Atmos. Sci. 2012, 36, 215–233. [Google Scholar] [CrossRef]
- Richter, J.H.; Sassi, F.; Garcia, R.R. Toward a Physically Based Gravity Wave Source Parameterization in a General Circulation Model. J. Atmos. Sci. 2010, 67, 136–156. [Google Scholar] [CrossRef]
- Lindzen, R.S. On the Development of the Theory of the Qbo. Bull. Am. Meteorol. Soc. 1987, 68, 329–337. [Google Scholar] [CrossRef]
- Mcfarlane, N.A. The Effect of Orographically Excited Gravity-Wave Drag on the General-Circulation of the Lower Stratosphere and Troposphere. J. Atmos. Sci. 1987, 44, 1775–1800. [Google Scholar] [CrossRef]
- Beres, J.H.; Alexander, M.J.; Holton, J.R. A method of specifying the gravity wave spectrum above convection based on latent heating properties and background wind. J. Atmos. Sci. 2004, 61, 324–337. [Google Scholar] [CrossRef]
- Beres, J.H.; Garcia, R.R.; Boville, B.A.; Sassi, F. Implementation of a gravity wave source spectrum parameterization dependent on the properties of convection in the Whole Atmosphere Community Climate Model (WACCM). J. Geophys. Res.-Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Zhang, G.J.; Mcfarlane, N.A. Sensitivity of Climate Simulations to the Parameterization of Cumulus Convection in the Canadian Climate Center General-Circulation Model. Atmos. Ocean 1995, 33, 407–446. [Google Scholar] [CrossRef]
- Richter, J.H.; Solomon, A.; Bacmeister, J.T. On the simulation of the quasi-biennial oscillation in the Community Atmosphere Model, version 5. J. Geophys. Res. Atmos. 2014, 119, 3045–3062. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of Cmip5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.; Lu, D.; Yue, X.; Xue, X.; Chen, G.; Yan, J.; Yan, Y.; Lan, A.; Wang, J.; et al. Construction Progress of Chinese Meridian Project Phase II. Chin. J. Atmos. Sci. 2022, 42, 539–545. [Google Scholar] [CrossRef]
- Tian, Y.F.; Lu, D.R. Preliminary analysis of Beijing MST radar observation results in the mesosphere-lower thermosphere. Chin. J. Geophys. 2016, 59, 440–452. [Google Scholar] [CrossRef]
- Tian, Y.F.; Lu, D.R. Comparison of Beijing MST radar and radiosonde horizontal wind measurements. Adv. Atmos. Sci. 2017, 34, 39–53. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, Z.; Lyu, D. A dataset of Beijing MST radar horizontal wind fields at Xianghe Station in 2012. China Sci. Data 2021, 6, 1. [Google Scholar] [CrossRef]
- Chen, F.L.; Chen, G.; Shi, C.H.; Tian, Y.F.; Zhang, S.D.; Huang, K.M. Strong downdrafts preceding rapid tropopause ascent and their potential to identify cross-tropopause stratospheric intrusions. Ann. Geophys. 2018, 36, 1403–1417. [Google Scholar] [CrossRef]
- Chen, F.L.; Chen, G.; Tian, Y.F.; Zhang, S.D.; Huang, K.M.; Wu, C.; Zhang, W.F. High-resolution Beijing mesosphere-stratosphere-troposphere (MST) radar detection of tropopause structure and variability over Xianghe (39.75 degrees N, 116.96 degrees E), China. Ann. Geophys. 2019, 37, 631–643. [Google Scholar] [CrossRef]
- Chen, Z.; Tian, Y.F.; Lue, D.R. Turbulence Parameters in the Troposphere-Lower Stratosphere Observed by Beijing MST Radar. Remote Sens. 2022, 14, 947. [Google Scholar] [CrossRef]
- Chen, Z.; Tian, Y.F.; Wang, Y.A.; Bi, Y.H.; Wu, X.; Huo, J.; Pan, L.J.; Wang, Y.; Lu, D.R. Turbulence parameters measured by the Beijing mesosphere-stratosphere-troposphere radar in the troposphere and lower stratosphere with three models: Comparison and analyses. Atmos. Meas. Tech. 2022, 15, 4785–4800. [Google Scholar] [CrossRef]
- Chen, Z.; Tian, Y.; Lu, D. Improving the Processing Algorithm of Beijing MST Radar Power Spectral Density Data. J. Appl. Meterol. Sci. 2020, 31, 694–705. [Google Scholar] [CrossRef]
- Jacobi, C. 6 year mean prevailing winds and tides measured by VHF meteor radar over Collm (51.3 degrees N, 13.0 degrees E). J. Atmos. Solar-Terr. Phys. 2012, 78–79, 8–18. [Google Scholar] [CrossRef]
- Sivan, C.; Rakesh, V.; Abhilash, S.; Mohanakumar, K. Evaluation of global reanalysis winds and high-resolution regional model outputs with the 205 MHz stratosphere-troposphere wind profiler radar observations. Q. J. Roy. Meteor. Soc. 2021, 147, 2562–2579. [Google Scholar] [CrossRef]
- Chun, H.Y.; Song, I.S.; Baik, J.J.; Kim, Y.J. Impact of a convectively forced gravity wave drag parameterization in NCAR CCM3. J. Clim. 2004, 17, 3530–3547. [Google Scholar] [CrossRef]
- Ribstein, B.; Millet, C.; Lott, F.; de la Camara, A. Can We Improve the Realism of Gravity Wave Parameterizations by Imposing Sources at All Altitudes in the Atmosphere? J. Adv. Model. Earth Syst. 2022, 14, e2021MS002563. [Google Scholar] [CrossRef]
- Danabasoglu, G.; Lamarque, J.-F.; Bacmeister, J.; Bailey, D.A.; DuVivier, A.K.; Edwards, J.; Emmons, L.K.; Fasullo, J.; Garcia, R.; Gettelman, A.; et al. The Community Earth System Model Version 2 (CESM2). J. Adv. Model. Earth Syst. 2020, 12, e2019MS001916. [Google Scholar] [CrossRef]
- Bi, D.; Dix, M.; Marsland, S.; O’Farrell, S.; Sullivan, A.; Bodman, R.; Law, R.; Harman, I.; Srbinovsky, J.; Rashid, H.A.; et al. Configuration and spin-up of ACCESS-CM2, the new generation Australian Community Climate and Earth System Simulator Coupled Model. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 225–251. [Google Scholar] [CrossRef]
- Döscher, R.; Acosta, M.; Alessandri, A.; Anthoni, P.; Arsouze, T.; Bergman, T.; Bernardello, R.; Boussetta, S.; Caron, L.P.; Carver, G.; et al. The EC-Earth3 Earth system model for the Coupled Model Intercomparison Project 6. Geosci. Model Dev. 2022, 15, 2973–3020. [Google Scholar] [CrossRef]
- Boucher, O.; Servonnat, J.; Albright, A.L.; Aumont, O.; Balkanski, Y.; Bastrikov, V.; Bekki, S.; Bonnet, R.; Bony, S.; Bopp, L.; et al. Presentation and Evaluation of the IPSL-CM6A-LR Climate Model. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002010. [Google Scholar] [CrossRef]
- Mauritsen, T.; Bader, J.; Becker, T.; Behrens, J.; Bittner, M.; Brokopf, R.; Brovkin, V.; Claussen, M.; Crueger, T.; Esch, M.; et al. Developments in the MPI-M Earth System Model version 1.2 (MPI-ESM1.2) and Its Response to Increasing CO2. J. Adv. Model. Earth Syst. 2019, 11, 998–1038. [Google Scholar] [CrossRef]
- Jun, S.-Y.; Choi, S.-J.; Kim, B.-M. Dynamical Core in Atmospheric Model Does Matter in the Simulation of Arctic Climate. Geophys. Res. Lett. 2018, 45, 2805–2814. [Google Scholar] [CrossRef]
- Hall, D.M.; Ullrich, P.A.; Reed, K.A.; Jablonowski, C.; Nair, R.D.; Tufo, H.M. Dynamical Core Model Intercomparison Project (DCMIP) tracer transport test results for CAM-SE. Q. J. Roy. Meteor. Soc. 2016, 142, 1672–1684. [Google Scholar] [CrossRef]



| Version | Vertical Levels | Model Top | Horizontal Resolution |
|---|---|---|---|
| IAP-AGCM1 [33] | 2 | 200 hPa | 4° × 5° |
| IAP-AGCM2 [34,38,39] | 9 | 10 hPa | 4° × 5° |
| IAP-AGCM3 [40] | 21 | 10 hPa | 2° × 2.5° |
| IAP-AGCM4 [41,42] | 26 | 2.3 hPa | 1.4° × 1.4° |
| IAP-AGCM5 [35] | 35 | 2.3 hPa | 1.4° × 1.4° |
| MAM | JJA | SON | DJF | ALL | |
|---|---|---|---|---|---|
| Ru | 0.98 | 0.89 | 0.93 | 0.95 | 0.94 |
| Rv | 0.80 | 0.52 | 0.78 | 0.84 | 0.73 |
| du | −1.20 | −4.77 | −0.68 | −4.87 | −3.00 |
| dv | −1.35 | −0.41 | −0.29 | −0.67 | −0.70 |
| RMSEu | 4.73 | 7.17 | 5.35 | 9.16 | 6.60 |
| RMSEv | 2.92 | 2.57 | 3.47 | 2.63 | 2.90 |
| Source_id | ATM | Model Top (Levels) | Horizontal Resolution | Dynamical Core | NGWD |
|---|---|---|---|---|---|
| ACCESS-CM2 | UM10.6 GA7.1 | 85 km (85) | 1.25° × 1.875° | ENDGame non-hydrostatic scheme | Yes |
| CAS-ESM2-0 | IAP-AGCM5.0 | 40 km (35) | 1.4° × 1.4° | IAP finite difference scheme | No |
| CESM2 | CAM6 | 40 km (32) | 0.9° × 1.25° | Finite volume scheme | No |
| CESM2-WACCM | WACCM6 | 130 km (70) | 0.9° × 1.25° | Finite volume scheme | Yes |
| EC-Earth3 | IFS cy36r4 | 80 km (91) | T255 (80 km) | Spectral transform method and finite element scheme | Yes |
| IPSL-CM6A-LR | LMDZ 6A-LR | 80 km (79) | 2.5° × 1.3° | Finite difference scheme | Yes |
| MPI-ESM1-2-LR | ECHAM6.3 | 80 km (47) | T63 (200 km) | Spectral transform method | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Chai, Z.; Yu, Z.; Chen, Z.; Jin, J. Evaluation of the Horizontal Winds Simulated by IAP-HAGCM through Comparison with Beijing MST Radar Observations. Remote Sens. 2023, 15, 3571. https://doi.org/10.3390/rs15143571
Tian Y, Chai Z, Yu Z, Chen Z, Jin J. Evaluation of the Horizontal Winds Simulated by IAP-HAGCM through Comparison with Beijing MST Radar Observations. Remote Sensing. 2023; 15(14):3571. https://doi.org/10.3390/rs15143571
Chicago/Turabian StyleTian, Yufang, Zhaoyang Chai, Zipeng Yu, Ze Chen, and Jiangbo Jin. 2023. "Evaluation of the Horizontal Winds Simulated by IAP-HAGCM through Comparison with Beijing MST Radar Observations" Remote Sensing 15, no. 14: 3571. https://doi.org/10.3390/rs15143571
APA StyleTian, Y., Chai, Z., Yu, Z., Chen, Z., & Jin, J. (2023). Evaluation of the Horizontal Winds Simulated by IAP-HAGCM through Comparison with Beijing MST Radar Observations. Remote Sensing, 15(14), 3571. https://doi.org/10.3390/rs15143571







