An Investigation of lp-Norm Minimization for the Artifact-Free Inversion of Gravity Data
Abstract
1. Introduction
2. Methods
2.1. Forward Problem
2.2. Depth Weighting
2.3. Model Objective Function
2.4. Inverse Problem
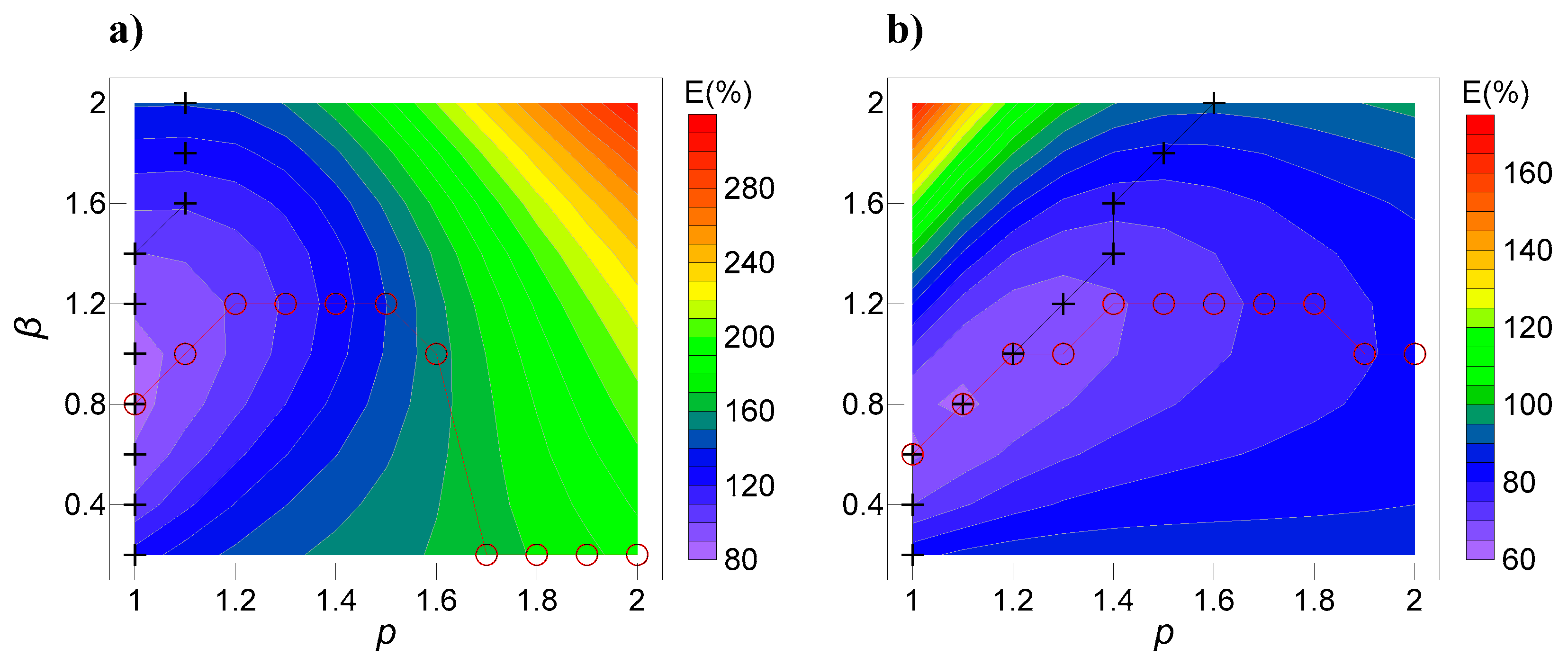
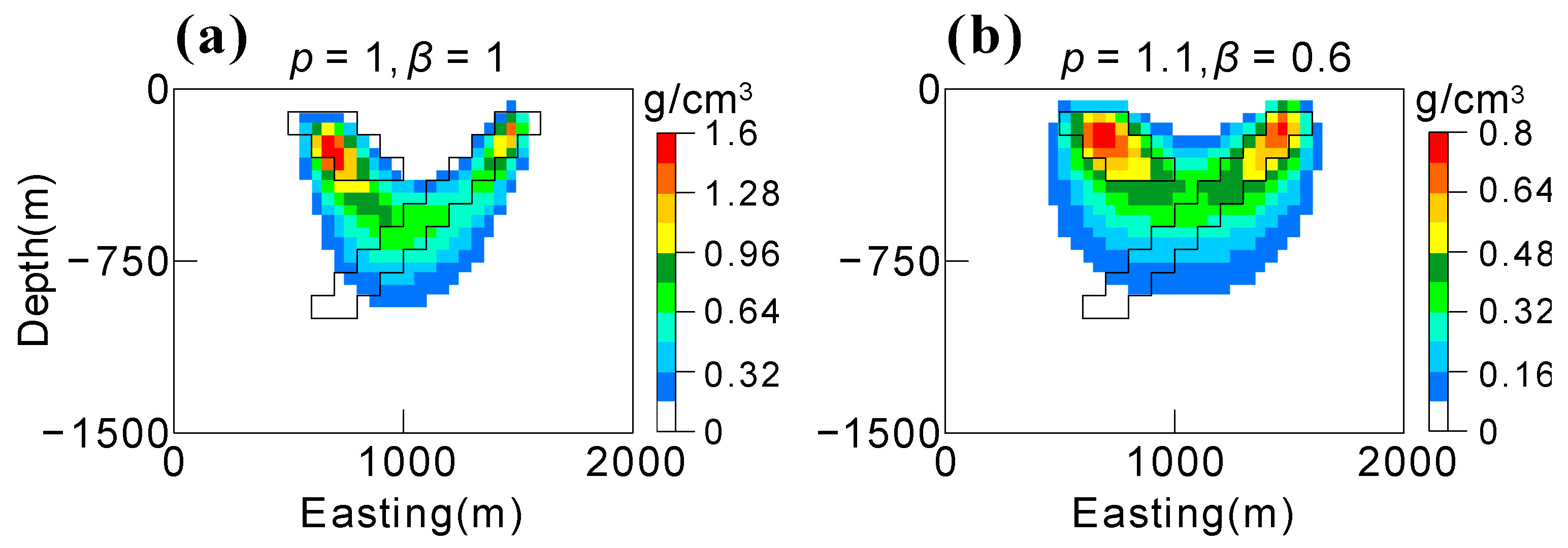
3. Choosing Proper β and p Values
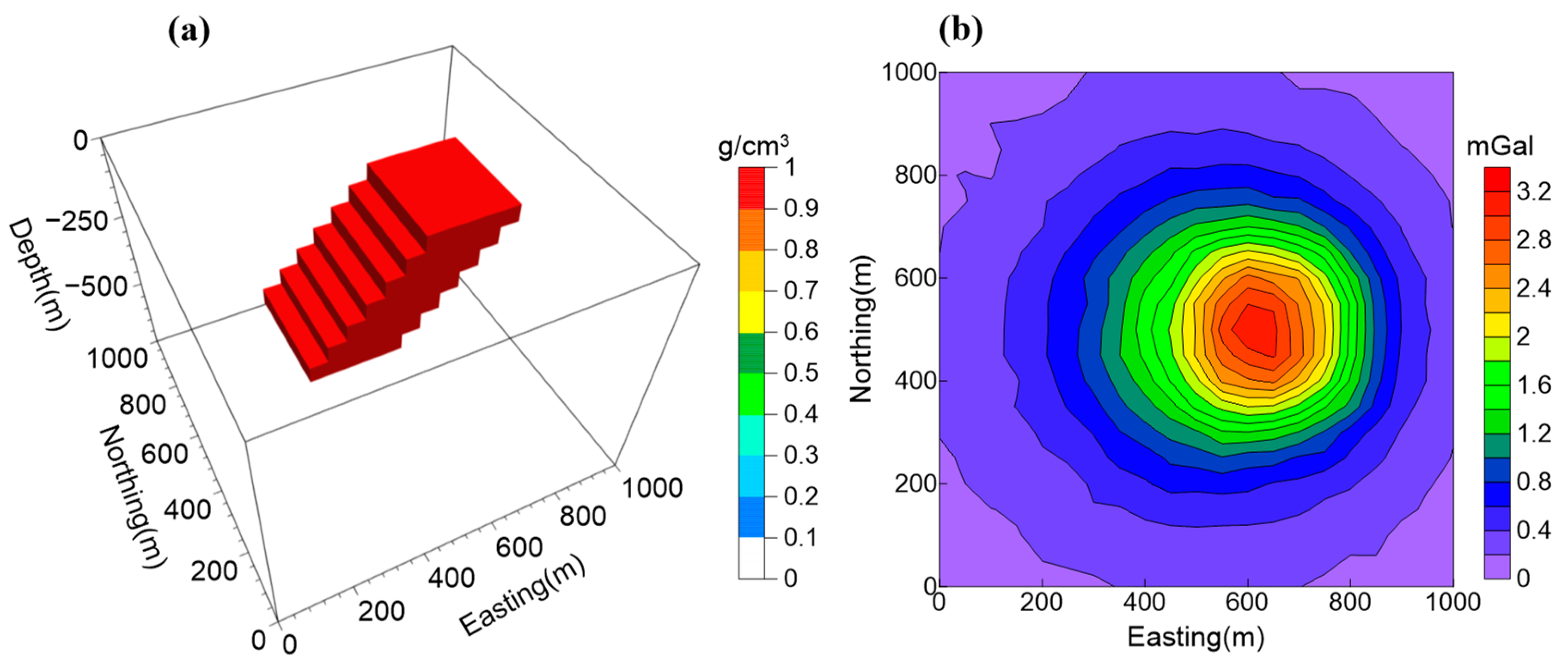
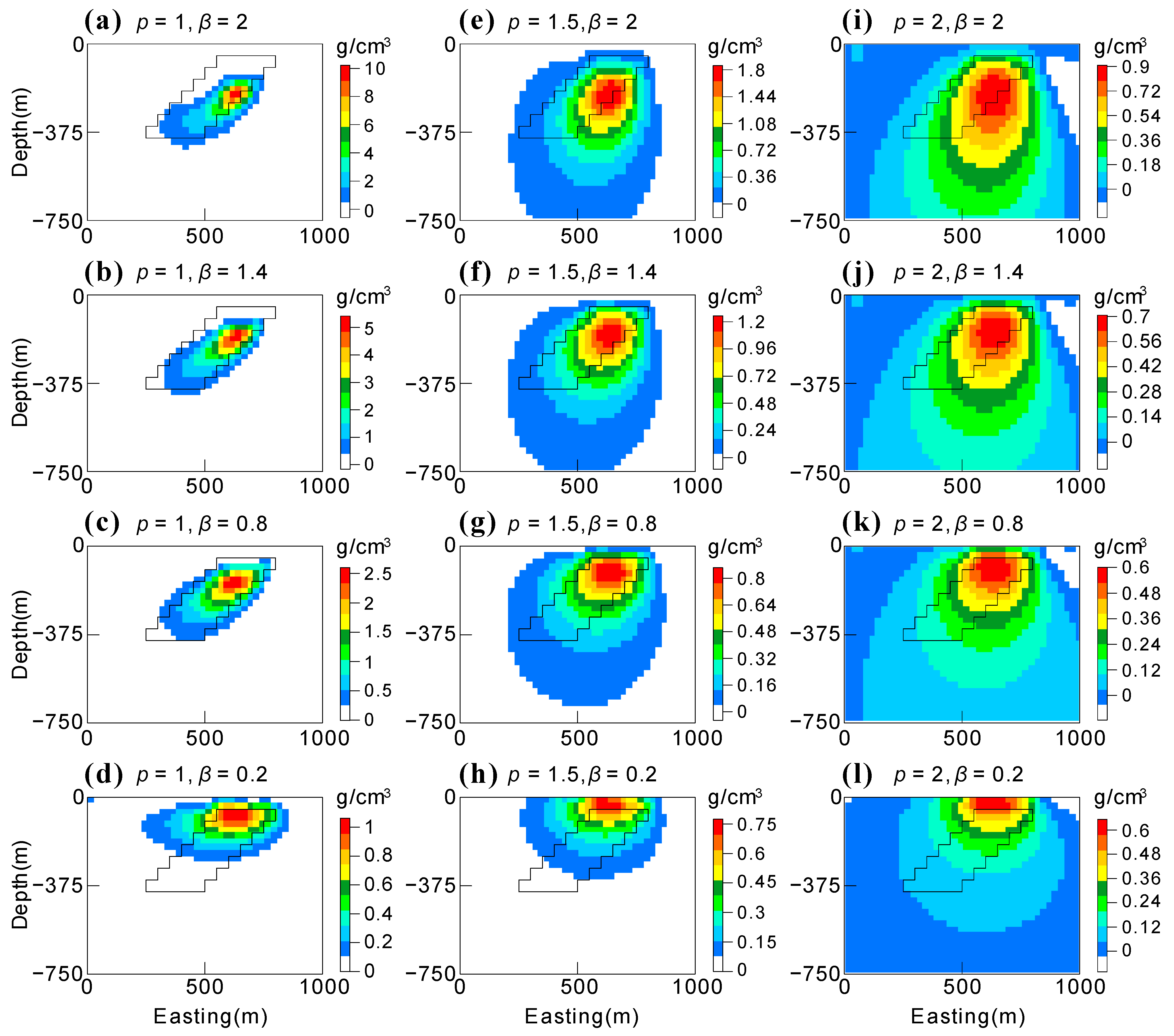
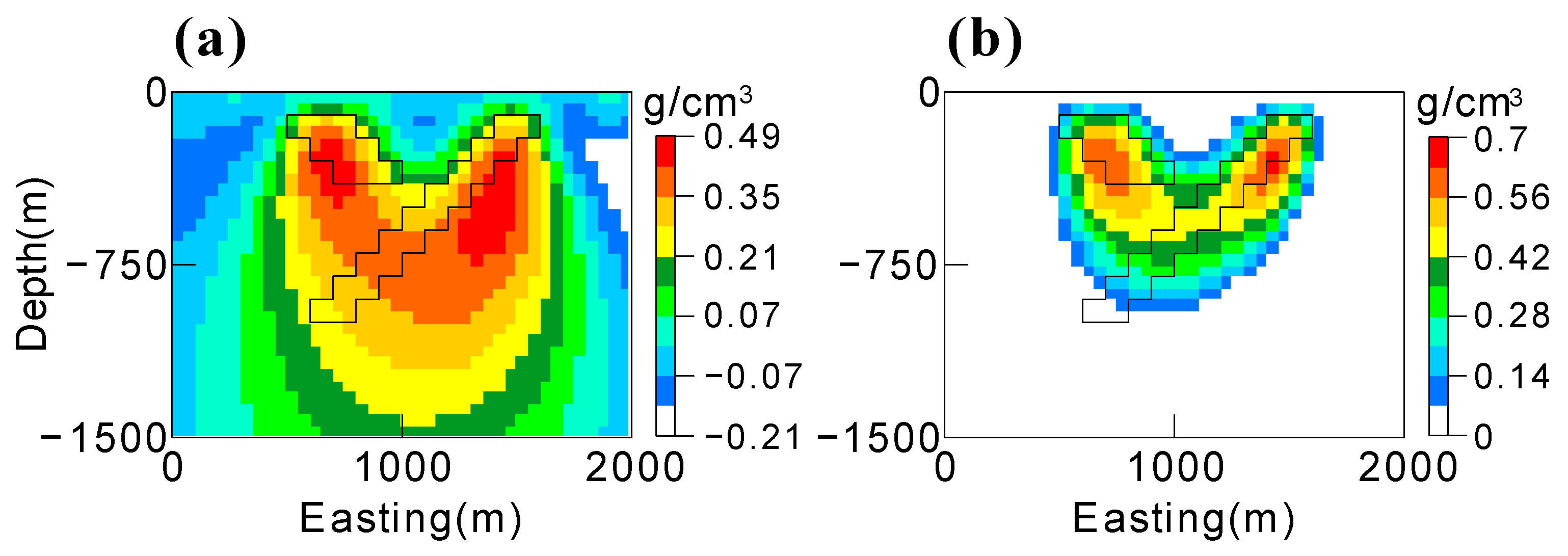
4. Synthetic Example
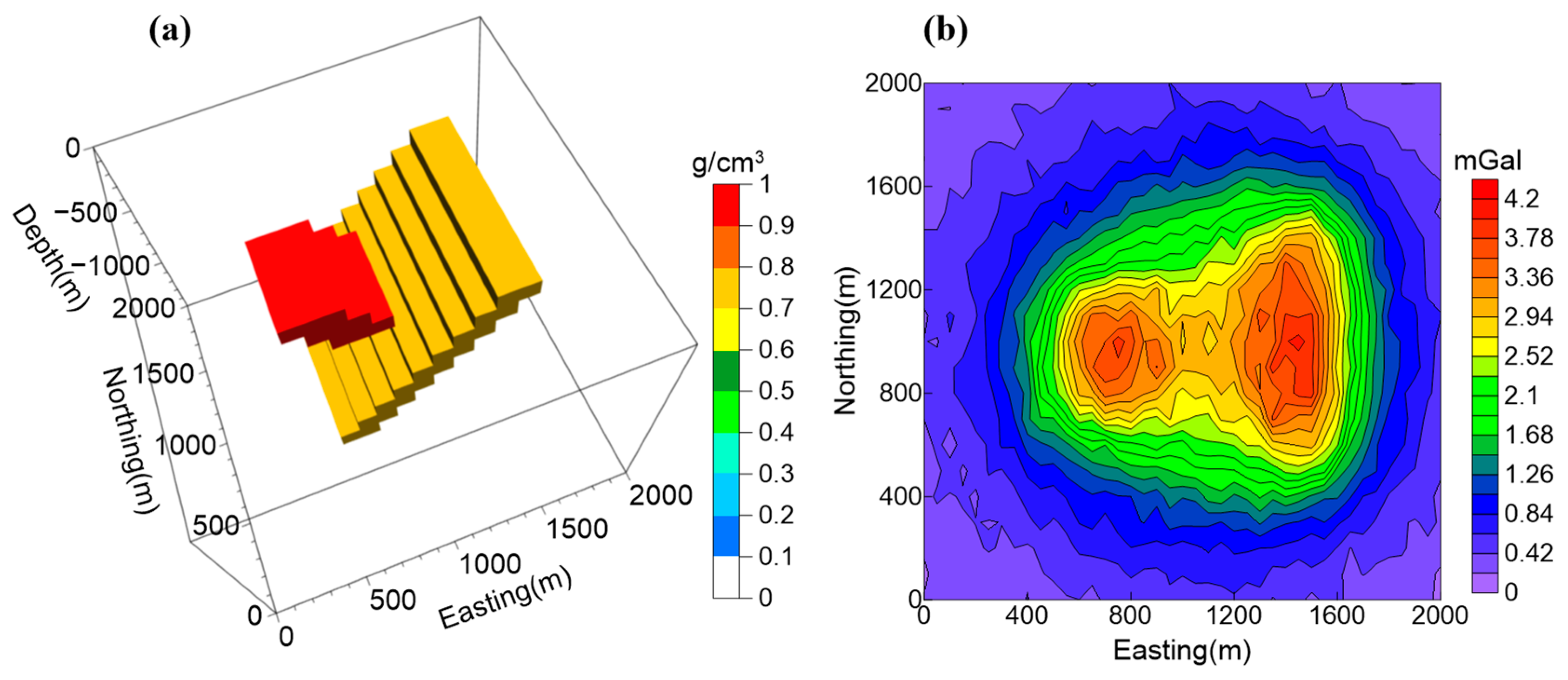
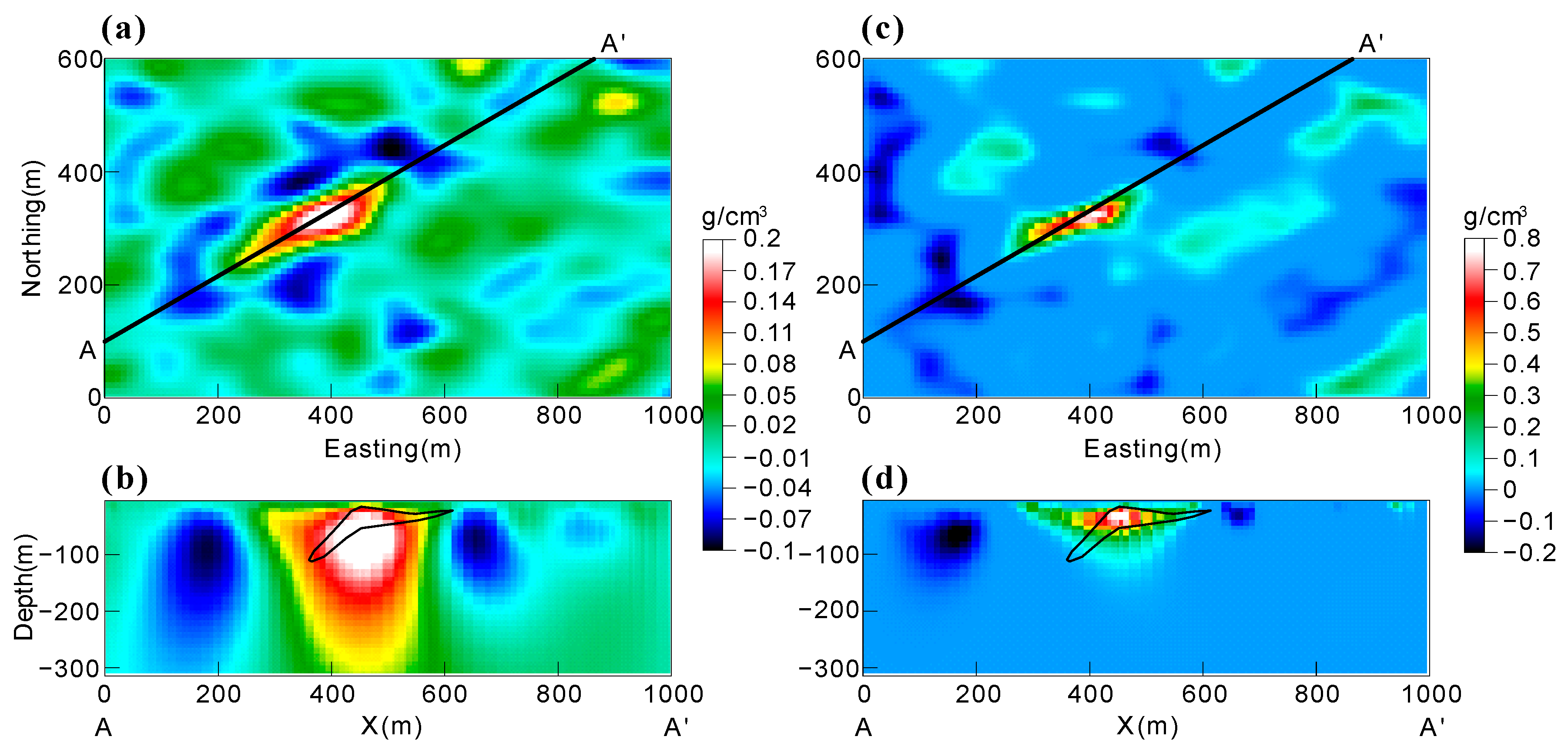
5. Field Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications, 1st ed.; Cambridge University Press: Cambridge, UK, 1995; pp. 59–61. [Google Scholar]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Last, B.J.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Camacho, A.G.; Montesinos, F.G.; Vieira, R. Gravity inversion by means of growing bodies. Geophysics 2000, 65, 95–101. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef]
- Krahenbuhl, R.A.; Li, Y. Inversion of gravity data using a binary formulation. Geophys. J. Int. 2006, 167, 543–556. [Google Scholar] [CrossRef]
- Uieda, L.; Barbosa, V.C.F. Robust 3D gravity gradient inversion by planting anomalous densities. Geophysics 2012, 77, G55–G66. [Google Scholar] [CrossRef]
- Lu, W.; Qian, J. A local level-set method for 3D inversion of gravity-gradient data. Geophysics 2015, 80, G35–G51. [Google Scholar] [CrossRef]
- Guillen, A.; Menichetti, V. Gravity and magnetic inversion with minimization of a specific functional. Geophysics 1984, 49, 1354–1360. [Google Scholar] [CrossRef]
- Barbosa, V.C.F.; Silva, J.B.C. Generalized compact gravity inversion. Geophysics 1994, 59, 57–68. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. Incorporating geological dip information into geophysical inversions. Geophysics 2000, 65, 148–157. [Google Scholar] [CrossRef]
- Lelievre, P.G.; Oldenburg, D.W. A comprehensive study of including structural orientation information in geophysical inversions. Geophys. J. Int. 2009, 178, 623–637. [Google Scholar] [CrossRef]
- Zhou, J.; Revil, A.; Karaoulis, M.; Hale, D.; Doetsch, J.; Cuttler, S. Image-guided inversion of electrical resistivity data. Geophys. J. Int. 2014, 197, 292–309. [Google Scholar] [CrossRef]
- Lines, L.R.; Schultz, A.K.; Treitel, S. Cooperative inversion of geophysical data. Geophysics 1988, 53, 8–20. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints. J. Geophys. Res. 2004, 109, B03311. [Google Scholar] [CrossRef]
- Lelièvre, P.G.; Farquharson, C.G.; Hurich, C.A. Joint inversion of seismic traveltimes and gravity data on unstructured grids with application to mineral exploration. Geophysics 2012, 77, K1–K15. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Pilkington, M. 3D magnetic data-space inversion with sparseness constraints. Geophysics 2009, 74, L7–L15. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Oldenburg, D.W. Non-linear inversion using general measures of data misfit and model structure. Geophys. J. Int. 1998, 134, 213–227. [Google Scholar] [CrossRef]
- Kirkendall, B.; Li, Y.; Oldenburg, D. Imaging cargo containers using gravity gradiometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1786–1797. [Google Scholar] [CrossRef]
- Farquharson, C.G. Constructing piecewise-constant models in multidimensional minimum-structure inversions. Geophysics 2008, 73, K1–K9. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering. Geophysics 2015, 80, ID1–ID18. [Google Scholar] [CrossRef]
- Fournier, D.; Oldenburg, D.W. Inversion using spatially variable mixed ℓp norms. Geophys. J. Int. 2019, 218, 268–282. [Google Scholar] [CrossRef]
- Utsugi, M. 3-D inversion of magnetic data based on the L1–L2 norm regularization. Earth Planets Space 2019, 71, 73. [Google Scholar] [CrossRef]
- Sun, J.; Wei, X. Research Note: Recovering sparse models in 3D potential-field inversion without bound dependence or staircasing problems using a mixed Lp norm regularization. Geophys. Prospect. 2021, 69, 901–910. [Google Scholar] [CrossRef]
- Nagy, D. The gravitational attraction of a right rectangular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Li, X.; Chouteau, M. Three-dimensional gravity modeling in all space. Surv. Geophys. 1998, 19, 339–368. [Google Scholar] [CrossRef]
- Boulanger, O.; Chouteau, M. Constraints in 3D gravity inversion. Geophys. Prospect. 2001, 49, 265–280. [Google Scholar] [CrossRef]
- Cella, F.; Fedi, M. Inversion of potential field data using the structural index as weighting function rate decay. Geophys. Prospect. 2012, 60, 313–336. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. Joint inversion of surface and three-component borehole magnetic data. Geophysics 2000, 65, 540–552. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y. Inversion for applied geophysics: A tutorial. In Near-Surface Geophysics; Society of Exploration Geophysicists: Houston, TX, USA, 2005; pp. 89–150. [Google Scholar]
- Barbosa, V.C.F.; Silva, J.B.C.; Medeiros, W.E. Practical applications of uniqueness theorems in gravimetry: Part II—Pragmatic incorporation of concrete geologic information. Geophysics 2002, 67, 795–800. [Google Scholar] [CrossRef]
- Pilkington, M. 3-D magnetic imaging using conjugate gradients. Geophysics 1997, 62, 1132–1142. [Google Scholar] [CrossRef]
- Lelievre, P.G.; Oldenburg, D.W. Magnetic forward modelling and inversion for high susceptibility. Geophys. J. Int. 2006, 166, 76–90. [Google Scholar] [CrossRef]
- Beaton, A.E.; Tukey, J.W. The fitting of power series, meaning polynomials, illustrated on band-spectroscopic data. Technometrics 1974, 16, 147–185. [Google Scholar] [CrossRef]
- Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat. Theory Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Rao, B.D.; Kreutz-Delgado, K. An affine scaling methodology for best basis selection. IEEE Trans. Signal Process. 1999, 47, 187–200. [Google Scholar] [CrossRef]
- Yan, J.Y.; Meng, G.X.; Yang, Y.Q.; Deng, Z.; Zhao, J.H.; Tang, H.J. Discovery and metallogenic characteristics of Layikeleke magmatic skarn type of rich copper-iron deposit, Eastern Junggar, Xinjiang. Geol. Rev. 2017, 63, 413–426. [Google Scholar]
- Cui, Y.; Guo, L. A wavenumber-domain iterative approach for rapid 3-D imaging of gravity anomalies and gradients. IEEE Access 2019, 7, 34179–34188. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yao, C. An Investigation of lp-Norm Minimization for the Artifact-Free Inversion of Gravity Data. Remote Sens. 2023, 15, 3465. https://doi.org/10.3390/rs15143465
Li Z, Yao C. An Investigation of lp-Norm Minimization for the Artifact-Free Inversion of Gravity Data. Remote Sensing. 2023; 15(14):3465. https://doi.org/10.3390/rs15143465
Chicago/Turabian StyleLi, Zelin, and Changli Yao. 2023. "An Investigation of lp-Norm Minimization for the Artifact-Free Inversion of Gravity Data" Remote Sensing 15, no. 14: 3465. https://doi.org/10.3390/rs15143465
APA StyleLi, Z., & Yao, C. (2023). An Investigation of lp-Norm Minimization for the Artifact-Free Inversion of Gravity Data. Remote Sensing, 15(14), 3465. https://doi.org/10.3390/rs15143465



