Land Use/Land Cover Optimized SAR Coherence Analysis for Rapid Coastal Disaster Monitoring: The Impact of the Emma Storm in Southern Spain
Abstract
1. Introduction
2. Materials and Methods
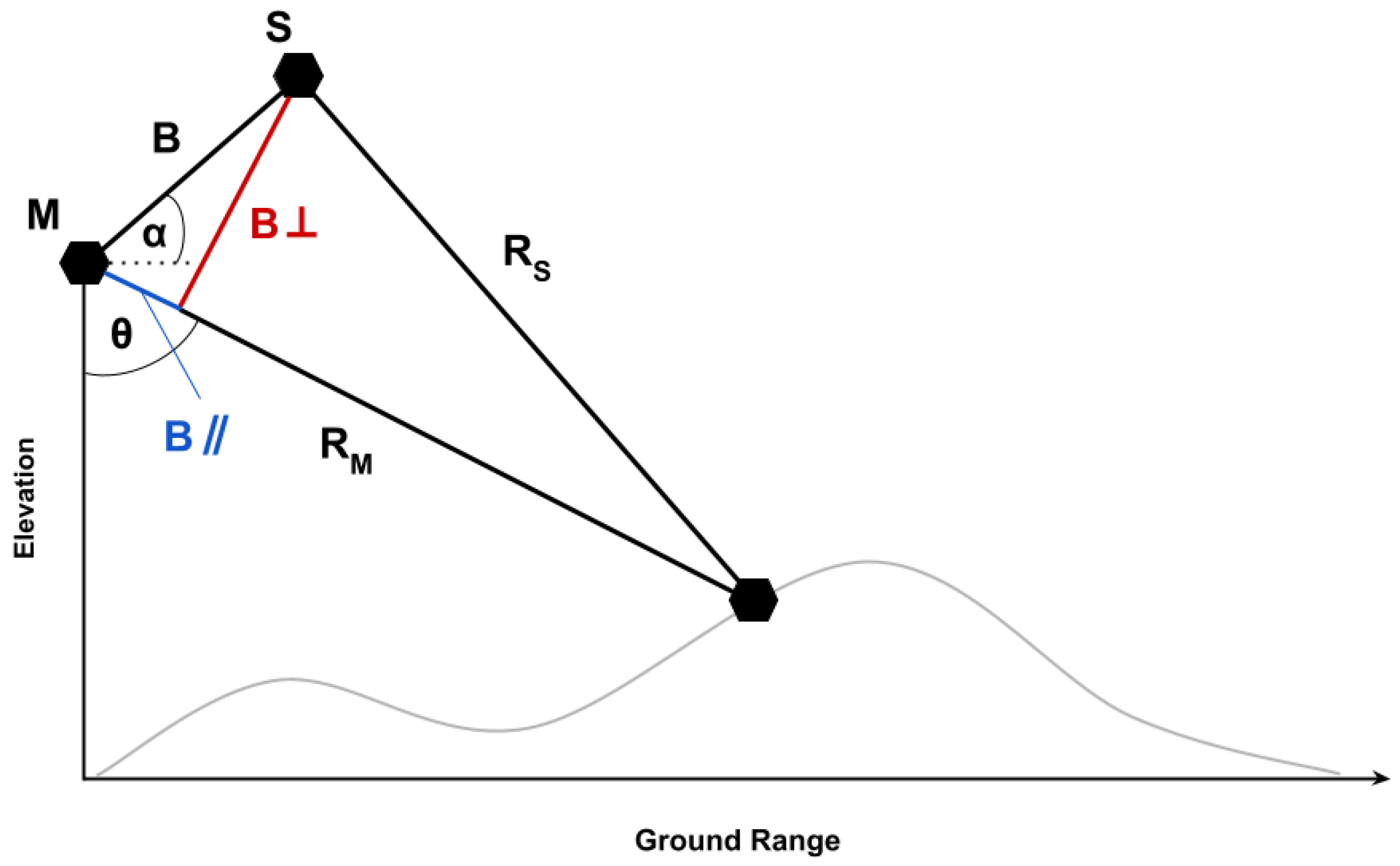
2.1. Fundamentals of InSAR Technique
2.2. Interferometric Coherence
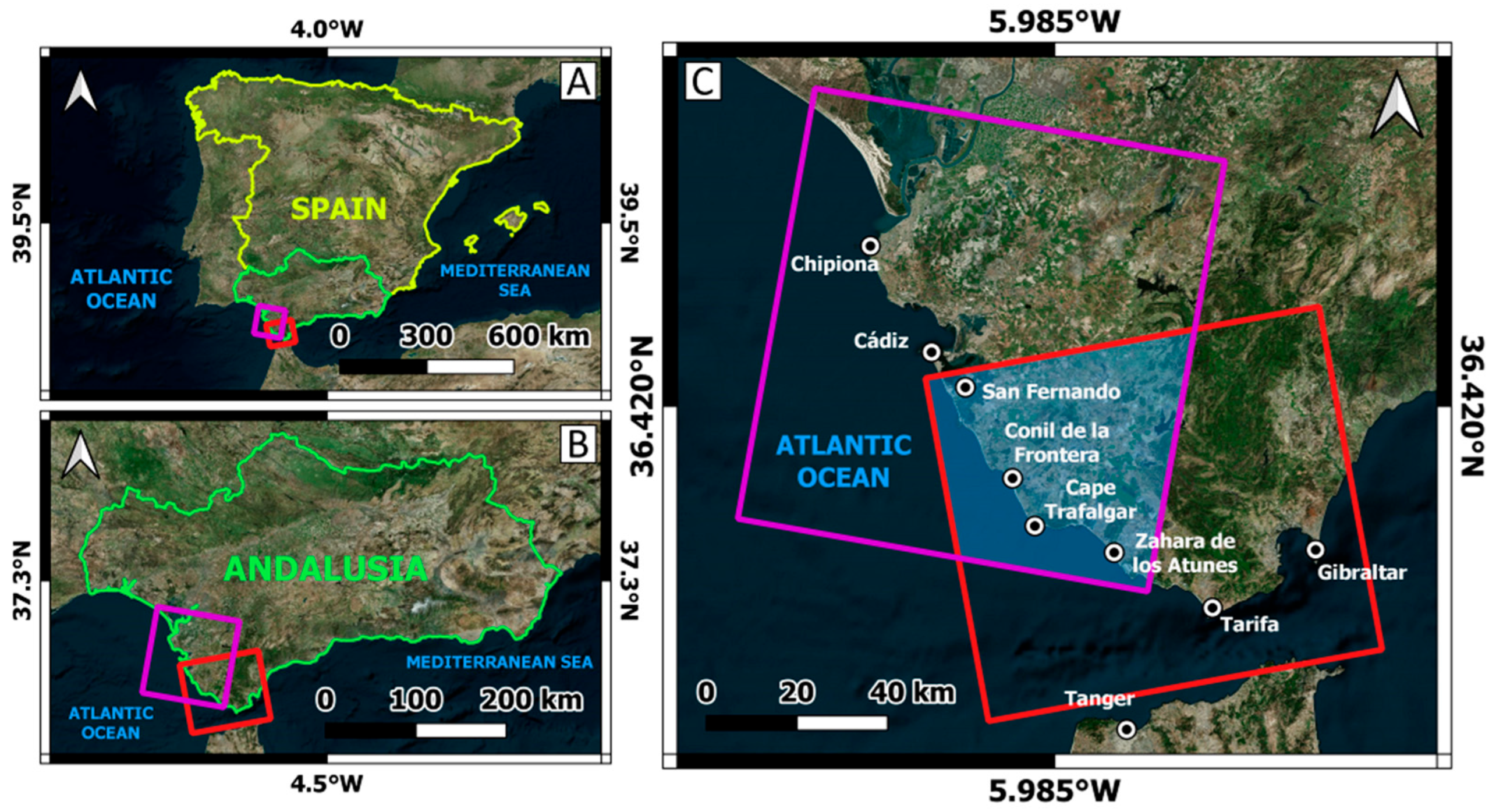
2.3. Study Area and the Emma Storm
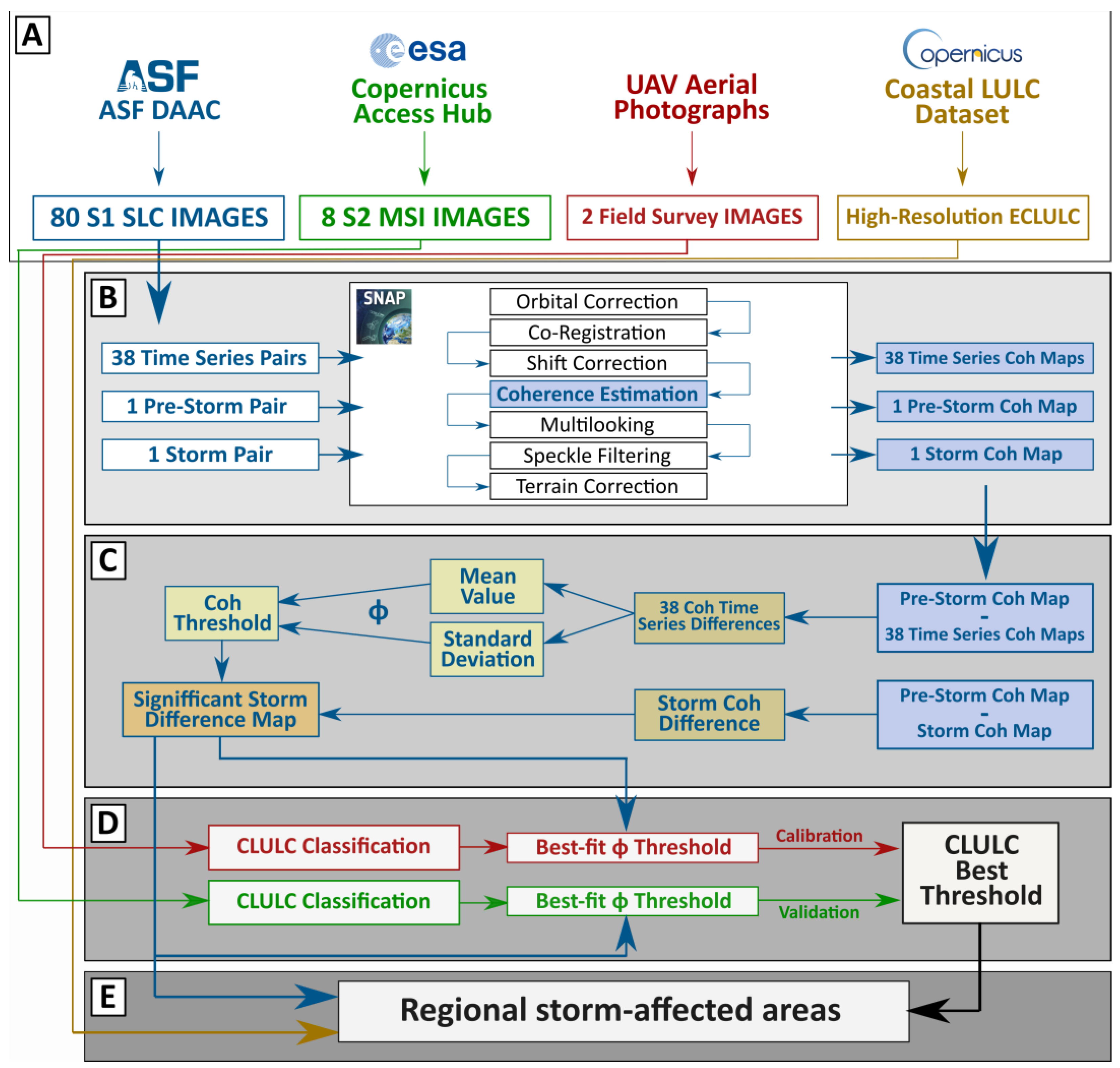
2.4. Method Workflow
2.5. Datasets
2.5.1. Satellite Data
2.5.2. UAV Aerial Photographs
2.5.3. Coastal Zones Land Use/Land Cover Dataset
2.6. InSAR Processing
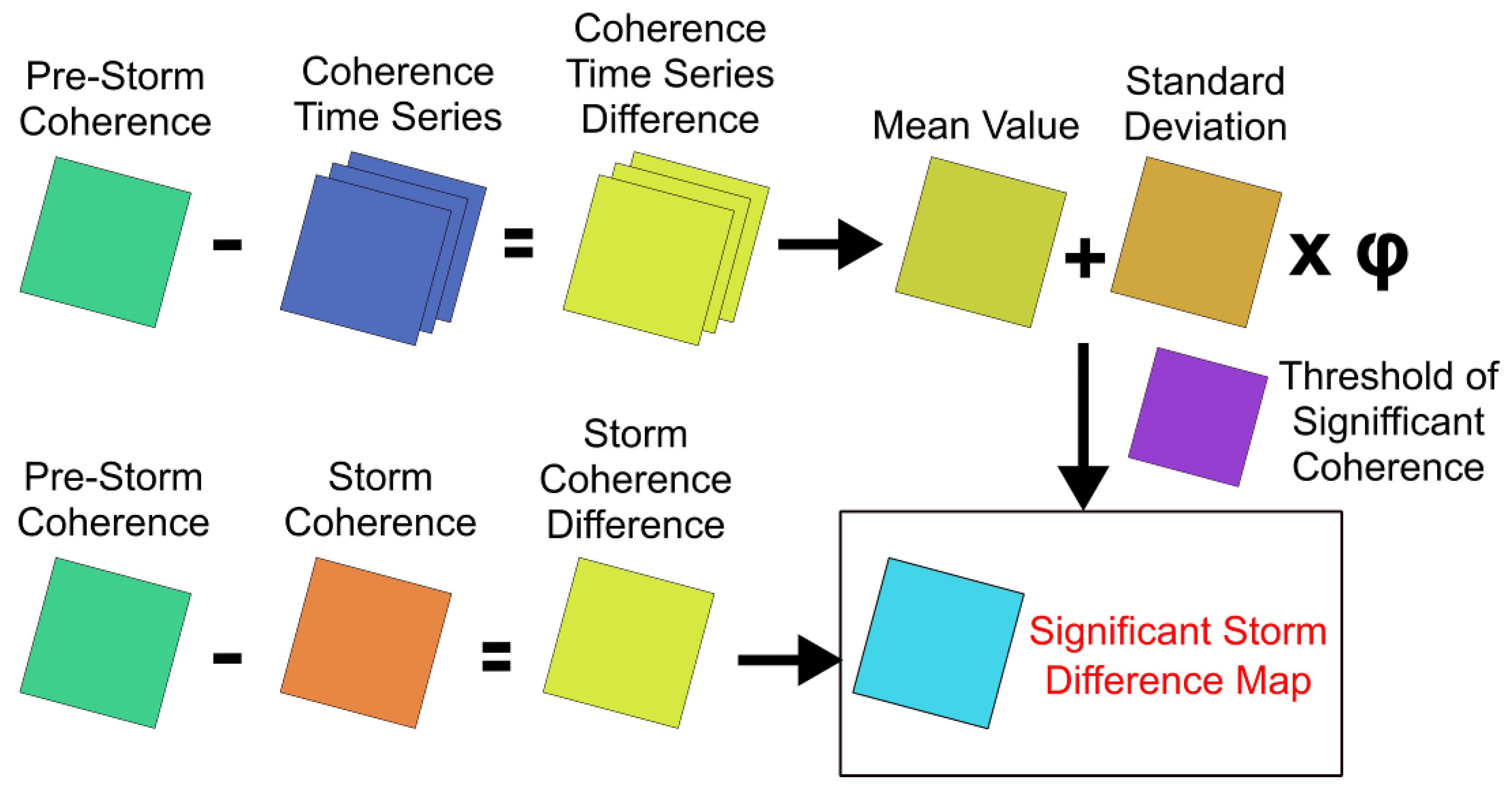
2.7. Coherence Difference Analysis
2.8. Method Calibration by CLULC-Optimized Thresholds
2.9. Validation of CLULC-Optimized Method
2.10. Regional Extraction and Identification of Storm-Affected Areas
3. Results
3.1. Coherence Difference Analysis
3.2. Calibration of Coastal Disaster-Affected Areas by CLULC-Optimized Thresholds
3.3. Validation of Coastal Disaster-Affected Area Detection Method
3.4. Regional Assessment
4. Discussion
4.1. Regional Assessment
4.2. Method Limitations and Advantages
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASC | Ascending Orbit Image |
| ASF DAAC | Alaska Satellite Facility Distributed Active Archive Center |
| CDA | Coherence Difference Analysis |
| CLULC | Coastal Land Use/Land Cover |
| DEM | Digital Elevation Model |
| DESC | Descending Orbit Image |
| ECLULC | Euroepan Coastal Land Use/Land Cover |
| ESA | European Space Agency |
| InSAR | SAR Interferometry |
| IW | Interferometric Wide Swath |
| RADAR | Radio Detecting and Ranging |
| RS | Remote Sensing |
| S1 | Sentinel-1 |
| S2 | Sentinel-2 |
| SAR | Synthetic Aperture Radar |
| SLC | Single Look Complex |
| SRTM | Shuttle Radar Topography Mission |
| UAV | Unmanned Aerial Vehicle |
| VH | Vertical-Horizontal Polarization |
| VV | Vertical-Vertical Polarization |
References
- Gogoberidze, G. Tools for comprehensive estimate of coastal region marine economy potential and its use for coastal planning. J. Coast. Conserv. 2012, 16, 251–260. [Google Scholar] [CrossRef]
- Busayo, E.T.; Kalumba, A.M. Recommendations for linking climate change adaptation and disaster risk reduction in urban coastal zones: Lessons from East London, South Africa. Ocean Coast. Manag. 2021, 203, 105454. [Google Scholar] [CrossRef]
- Zhao, Q.; Pan, J.; Devlin, A.T.; Tang, M.; Yao, C.; Zamparelli, V.; Falabella, F.; Pepe, A. On the Exploitation of Remote Sensing Technologies for the Monitoring of Coastal and River Delta Regions. Remote Sens. 2022, 14, 2384. [Google Scholar] [CrossRef]
- Enriquez-Acevedo, T.; Botero, C.M.; Cantero-Rodelo, R.; Pertuz, A.; Suarez, A. Willingness to pay for Beach Ecosystem Services: The case study of three Colombian beaches. Ocean Coast. Manag. 2018, 161, 96–104. [Google Scholar] [CrossRef]
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future coastal population growth and exposure to sea-level rise and coastal flooding-a global assessment. PLoS ONE 2015, 10, e0118571. [Google Scholar] [CrossRef] [PubMed]
- Vitousek, S.; Barnard, P.L.; Fletcher, C.H.; Frazer, N.; Erikson, L.; Storlazzi, C.D. Doubling of coastal flooding frequency within decades due to sea-level rise. Sci. Rep. 2017, 7, 1399. [Google Scholar] [CrossRef]
- Edmonds, D.A.; Caldwell, R.L.; Brondizio, E.S.; Siani, S.M. Coastal flooding will disproportionately impact people on river deltas. Nat. Commun. 2020, 11, 4741. [Google Scholar] [CrossRef]
- Dasgupta, S.; Laplante, B.; Meisner, C.; Wheeler, D.; Yan, J. The impact of sea level rise on developing countries: A comparative analysis. Clim. Chang. 2009, 93, 379–388. [Google Scholar] [CrossRef]
- Quesada-Román, A.; Pérez-Briceño, P.M. Geomorphology of the Caribbean coast of Costa Rica. J. Maps 2019, 15, 363–371. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Dolan, R.; Davis, R.E. Coastal storm hazards. J. Coast. Res. 1994, Special Issue No. 12, 103–114. [Google Scholar]
- Woodruff, J.D.; Irish, J.L.; Camargo, S.J. Coastal flooding by tropical cyclones and sea-level rise. Nature 2013, 504, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Kantamaneni, K. Coastal infrastructure vulnerability: An integrated assessment model. Nat. Hazards 2016, 84, 139–154. [Google Scholar] [CrossRef]
- Kelley, S.W.; Ramsey, J.S.; Byrnes, M.R. Evaluating Shoreline Response to Offshore Sand Mining for Beach Nourishment. J. Coast. Res. 2004, 201, 89–100. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Coastal erosion and control. Ocean Coast. Manag. 2011, 54, 867–887. [Google Scholar] [CrossRef]
- Kvočka, D.; Falconer, R.A.; Bray, M. Flood hazard assessment for extreme flood events. Nat. Hazards 2016, 84, 1569–1599. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction UNDRR. Sendai Framework for Disaster Risk Reduction 2015–2030; United Nations Office: Geneva, Switzerland, 2015; 37p. [Google Scholar]
- Coppola, D.P. Introduction to International Disaster Management; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- O’Brien, G.; O’Keefe, P.; Rose, J.; Wisner, B. Climate change and disaster management. Disasters 2006, 30, 64–80. [Google Scholar] [CrossRef]
- Yue, P.; Baumann, P.; Bugbee, K.; Jiang, L. Towards intelligent GIServices. Earth Sci. Inform. 2015, 8, 463–481. [Google Scholar] [CrossRef]
- Hu, L.; Fang, Z.; Zhang, M.; Jiang, L.; Yue, P. Facilitating Typhoon-Triggered Flood Disaster-Ready Information Delivery Using SDI Services Approach—A Case Study in Hainan. Remote Sens. 2022, 14, 1832. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Garzo, P.A.; Dadon, J.R.; Castro, L.N. Modelling environmental vulnerability of the Biosphere Reserve Parque Atlántico Mar Chiquito, Argentina, under agricultural and urban impacts. Ocean Coast. Manag. 2019, 170, 72–79. [Google Scholar] [CrossRef]
- Pereira, J.M.C. Remote sensing of burned areas in tropical savannas. Int. J. Wildland Fire 2003, 12, 259–270. [Google Scholar] [CrossRef]
- Virdis, S.G.; Oggiano, G.; Disperati, L. A Geomatics Approach to Multitemporal Shoreline Analysis in Western Mediterranean: The Case of Platamona-Maritza Beach (Northwest Sardinia, Italy). J. Coast. Res. 2012, 28, 624. [Google Scholar] [CrossRef]
- Yang, Y.; Wong, L.N.Y.; Chen, C.; Chen, T. Using multitemporal Landsat imagery to monitor and model the influences of landscape pattern on urban expansion in a metropolitan region. J. Appl. Remote Sens. 2014, 8, 083639. [Google Scholar] [CrossRef]
- Dong, C. Remote sensing, hydrological modeling and in situ observations in snow cover research: A review. J. Hydrol. 2018, 561, 573–583. [Google Scholar] [CrossRef]
- Pavlidou, E.; Van Der Meijde, M.; Van Der Werff, H.; Hecker, C. Time series analysis of land surface temperatures in 20 earthquake cases worldwide. Remote Sens. 2018, 11, 61. [Google Scholar] [CrossRef]
- Lechner, A.M.; Foody, G.M.; Boyd, D.S. Applications in Remote Sensing to Forest Ecology and Management. One Earth 2020, 2, 405–412. [Google Scholar] [CrossRef]
- Spinosa, A.; Ziemba, A.; Saponieri, A.; Damiani, L.; El Serafy, G. Remote Sensing-Based Automatic Detection of Shoreline Position: A Case Study in Apulia Region. J. Mar. Sci. Eng. 2021, 9, 575. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Cabezas-Rabadán, C.; Pardo-Pascual, J.; Almonacid-Caballer, J.; Rodilla, M. Detecting problematic beach widths for the recreational function along the Gulf of Valencia (Spain) from Landsat 8 subpixel shorelines. Appl. Geogr. 2019, 110, 102047. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Ruiz, L.A.; Palomar-Vázquez, J. Automatic extraction of shorelines from Landsat TM and ETM+ multi-temporal images with subpixel precision. Remote Sens. Environ. 2012, 123, 1–11. [Google Scholar] [CrossRef]
- Viaña-Borja, S.P.; Ortega-Sánchez, M. Automatic Methodology to Detect the Coastline from Landsat Images with a New Water Index Assessed on Three Different Spanish Mediterranean Deltas. Remote Sens. 2019, 11, 2186. [Google Scholar] [CrossRef]
- Lee, J.S.; Jurkevich, L.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Rev. 1994, 8, 313–340. [Google Scholar] [CrossRef]
- Orusa, T.; Cammareri, D.; Mondino, E.B. A Possible Land Cover EAGLE Approach to Overcome Remote Sensing Limitations in the Alps Based on Sentinel-1 and Sentinel-2: The Case of Aosta Valley (NW Italy). Remote Sens. 2022, 15, 178. [Google Scholar] [CrossRef]
- Orusa, T.; Cammareri, D.; Mondino, E.B. A Scalable Earth Observation Service to Map Land Cover in Geomorphological Complex Areas beyond the Dynamic World: An Application in Aosta Valley (NW Italy). Appl. Sci. 2022, 13, 390. [Google Scholar] [CrossRef]
- Samuele, D.P.; Filippo, S.; Orusa, T.; Enrico, B.-M. Mapping SAR geometric distortions and their stability along time: A new tool in Google Earth Engine based on Sentinel-1 image time series. Int. J. Remote Sens. 2021, 42, 9135–9154. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. Wetland mapping with LiDAR derivatives, SAR polarimetric decompositions, and LiDAR–SAR fusion using a random forest classifier. Can. J. Remote Sens. 2013, 39, 290–307. [Google Scholar] [CrossRef]
- Bamler, R. Principles of Synthetic Aperture Radar. Surv. Geophys. 2000, 21, 147–157. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A review of interferometric synthetic aperture RADAR (InSAR) multi-track approaches for the retrieval of Earth’s surface displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Shu, Y.; Li, J.; Gomes, G. Shoreline Extraction from RADARSAT-2 Intensity Imagery Using a Narrow Band Level Set Segmentation Approach. Mar. Geod. 2010, 33, 187–203. [Google Scholar] [CrossRef]
- Pradhan, B.; Rizeei, H.M.; Abdulle, A. Quantitative Assessment for Detection and Monitoring of Coastline Dynamics with Temporal RADARSAT Images. Remote Sens. 2018, 10, 1705. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Tu, C.; Wang, H.; Zhou, Z.; Feng, Z.; Shen, F.; Li, Z. Spatiotemporal Change Detection of Coastal Wetlands Using Multi-Band SAR Coherence and Synergetic Classification. Remote Sens. 2022, 14, 2610. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Z. Advances in InSAR Imaging and Data Processing. Remote Sens. 2022, 14, 4307. [Google Scholar] [CrossRef]
- Lu, Z.; Kwoun, O.; Rykhus, R. Interferometric synthetic aperture radar (InSAR): Its past, present and future. Photogramm. Eng. Remote Sens. 2007, 73, 217. [Google Scholar]
- ElGharbawi, T.; Tamura, M. Coseismic and postseismic deformation estimation of the 2011 Tohoku earthquake in Kanto Region, Japan, using InSAR time series analysis and GPS. Remote Sens. Environ. 2015, 168, 374–387. [Google Scholar] [CrossRef]
- Teshebaeva, K.; Roessner, S.; Echtler, H.; Motagh, M.; Wetzel, H.-U.; Molodbekov, B. ALOS/PALSAR InSAR Time-Series Analysis for Detecting Very Slow-Moving Landslides in Southern Kyrgyzstan. Remote Sens. 2015, 7, 8973–8994. [Google Scholar] [CrossRef]
- Zhou, C.; Lan, H.; Bürgmann, R.; Warner, T.A.; Clague, J.J.; Li, L.; Wu, Y.; Zhao, X.; Zhang, Y.; Yao, J. Application of an improved multi-temporal InSAR method and forward geophysical model to document subsidence and rebound of the Chinese Loess Plateau following land reclamation in the Yan’an New District. Remote Sens. Environ. 2022, 279, 113102. [Google Scholar] [CrossRef]
- Scardino, G.; Anzidei, M.; Petio, P.; Serpelloni, E.; De Santis, V.; Rizzo, A.; Liso, S.I.; Zingaro, M.; Capolongo, D.; Vecchio, A.; et al. The Impact of Future Sea-Level Rise on Low-Lying Subsiding Coasts: A Case Study of Tavoliere Delle Puglie (Southern Italy). Remote Sens. 2022, 14, 4936. [Google Scholar] [CrossRef]
- Seppi, S.A.; López-Martinez, C.; Joseau, M.J. Assessment of L-Band SAOCOM InSAR Coherence and Its Comparison with C-Band: A Case Study over Managed Forests in Argentina. Remote Sens. 2022, 14, 5652. [Google Scholar] [CrossRef]
- de Wit, K.; Lexmond, B.R.; Stouthamer, E.; Neussner, O.; Dörr, N.; Schenk, A.; Minderhoud, P.S.J. Identifying Causes of Urban Differential Subsidence in the Vietnamese Mekong Delta by Combining InSAR and Field Observations. Remote Sens. 2021, 13, 189. [Google Scholar] [CrossRef]
- Manavalan, R. SAR image analysis techniques for flood area mapping—Literature survey. Earth Sci. Inform. 2017, 10, 1–14. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea Volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res. Atmos. 1996, 101, 23109–23125. [Google Scholar] [CrossRef]
- Fielding, E.J.; Talebian, M.; Rosen, P.A.; Nazari, H.; Jackson, J.A.; Ghorashi, M.; Walker, R. Surface ruptures and building damage of the 2003 Bam, Iran, earthquake mapped by satellite synthetic aperture radar interferometric correlation. J. Geophys. Res. Atmos. 2005, 110, B03302. [Google Scholar] [CrossRef]
- Lu, C.-H.; Ni, C.-F.; Chang, C.-P.; Yen, J.-Y.; Chuang, R.Y. Coherence Difference Analysis of Sentinel-1 SAR Interferogram to Identify Earthquake-Induced Disasters in Urban Areas. Remote Sens. 2018, 10, 1318. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Kim, J.-R.; Lin, C.-W.; Lin, S.-Y. The Use of InSAR Phase Coherence Analyses for the Monitoring of Aeolian Erosion. Remote Sens. 2021, 13, 2240. [Google Scholar] [CrossRef]
- Manzoni, M.; Molinari, M.E.; Monti-Guarnieri, A. Multitemporal InSAR Coherence Analysis and Methods for Sand Mitigation. Remote Sens. 2021, 13, 1362. [Google Scholar] [CrossRef]
- Gaber, A.; Abdelkareem, M.; Abdelsadek, I.S.; Koch, M.; El-Baz, F. Using InSAR Coherence for Investigating the Interplay of Fluvial and Aeolian Features in Arid Lands: Implications for Groundwater Potential in Egypt. Remote Sens. 2018, 10, 832. [Google Scholar] [CrossRef]
- Wang, L.; Yang, L.; Wang, W.; Chen, B.; Sun, X. Monitoring Mining Activities Using Sentinel-1A InSAR Coherence in Open-Pit Coal Mines. Remote Sens. 2021, 13, 4485. [Google Scholar] [CrossRef]
- Moon, J.; Lee, H. Analysis of Activity in an Open-Pit Mine by Using InSAR Coherence-Based Normalized Difference Activity Index. Remote Sens. 2021, 13, 1861. [Google Scholar] [CrossRef]
- Chini, M.; Pelich, R.; Pulvirenti, L.; Pierdicca, N.; Hostache, R.; Matgen, P. Sentinel-1 InSAR Coherence to Detect Floodwater in Urban Areas: Houston and Hurricane Harvey as a Test Case. Remote Sens. 2019, 11, 107. [Google Scholar] [CrossRef]
- Chaabani, C.; Chini, M.; Abdelfattah, R.; Hostache, R.; Chokmani, K. Flood mapping in a complex environment using bistatic TanDEM-X/TerraSAR-X InSAR coherence. Remote Sens. 2018, 10, 1873. [Google Scholar] [CrossRef]
- Borlaf-Mena, I.; Badea, O.; Tanase, M.A. Assessing the Utility of Sentinel-1 Coherence Time Series for Temperate and Tropical Forest Mapping. Remote Sens. 2021, 13, 4814. [Google Scholar] [CrossRef]
- Ishitsuka, K.; Tsuji, T.; Matsuoka, T. Detection and mapping of soil liquefaction in the 2011 Tohoku earthquake using SAR interferometry. Earth Planets Space 2012, 64, 1267–1276. [Google Scholar] [CrossRef]
- Barra, A.; Solari, L.; Béjar-Pizarro, M.; Monserrat, O.; Bianchini, S.; Herrera, G.; Crosetto, M.; Sarro, R.; González-Alonso, E.; Mateos, R.M.; et al. A Methodology to Detect and Update Active Deformation Areas Based on Sentinel-1 SAR Images. Remote Sens. 2017, 9, 1002. [Google Scholar] [CrossRef]
- Tzouvaras, M.; Danezis, C.; Hadjimitsis, D.G. Small Scale Landslide Detection Using Sentinel-1 Interferometric SAR Coherence. Remote Sens. 2020, 12, 1560. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing; CRC Press: Boca Ratón, FL, USA, 2018. [Google Scholar]
- Goldstein, R. Atmospheric limitations to repeat-track radar interferometry. Geophys. Res. Lett. 1995, 22, 2517–2520. [Google Scholar] [CrossRef]
- Foucher, S.; Lopez-Martinez, C. Analysis, Evaluation, and Comparison of Polarimetric SAR Speckle Filtering Techniques. IEEE Trans. Image Process. 2014, 23, 1751–1764. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, 1–54. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.J.; Yun, S.H.; Lavalle, M. Damage mapping based on coherence model using multi-temporal polarimetric-interferometric UAVSAR data. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 189–192. [Google Scholar]
- Mastro, P.; Masiello, G.; Serio, C.; Pepe, A. Change Detection Techniques with Synthetic Aperture Radar Images: Experiments with Random Forests and Sentinel-1 Observations. Remote Sens. 2022, 14, 3323. [Google Scholar] [CrossRef]
- Del Río-Rodríguez, L.; Gracia, F.J.; Benavente, J. Shoreline change patterns in sandy coasts. A case study in SW Spain. Geomorphology 2013, 196, 252–266. [Google Scholar] [CrossRef]
- Instituto Hidrográfico De La Marina. Anuario de Mareas; Ministry of Defense: Madrid, Spain, 2009; 367p.
- Fernández-Montblanc, T.; Bethencourt, M.; Izquierdo, A. Underwater Cultural heritage risk assessment methodology for wave-induced hazards: The showcase of the Bay of Cadiz. Front. Mar. Sci. 2022, 9, 1005514. [Google Scholar] [CrossRef]
- Fernandez-Montblanc, T.; Benavente, J.; Plomaritis, T. Flood hazard characterization in the Guadalete Estuary: Combined effect of the tide and the river flow. Cuatern. Y Geomorfol. 2014, 28, 27–50. [Google Scholar]
- Talavera, L.; Del Río, L.; Benavente, J. UAS-based High-resolution Record of the Response of a Seminatural Sandy Spit to a Severe Storm. J. Coast. Res. 2020, 95, 679–683. [Google Scholar] [CrossRef]
- Gracia, J.; Río, L.D.; Alonso, C.; Benavente, J.; Anfuso, G. Historical evolution and present state of the coastal dune systems in the Atlantic coast of Cádiz (SW Spain): Palaeoclimatic and environmental implications. J. Coast. Res. 2006, 48, 55–63. [Google Scholar]
- Malvarez, G.; Ferreira, O.; Navas, F.; Cooper, J.; Gracia-Prieto, F.; Talavera, L. Storm impacts on a coupled human-natural coastal system: Resilience of developed coasts. Sci. Total Environ. 2021, 768, 144987. [Google Scholar] [CrossRef] [PubMed]
- Talavera, L.; del Río, L.; Benavente, J.; Barbero, L.; López-Ramírez, J.A. UAS as tools for rapid detection of storm-induced morphodynamic changes at Camposoto beach, SW Spain. Int. J. Remote Sens. 2018, 39, 5550–5567. [Google Scholar] [CrossRef]
- Innerbichler, F.; Kreisel, A.; Gruber, C. Coastal Zones Nomenclature Guideline. Technical Report. 2021. Available online: https://land.copernicus.eu/user-corner/technical-library/coastal-zones-nomenclature-and-mapping-guideline.pdf (accessed on 10 March 2023).
- Braun, A.; Veci, L. ESA SNAP Sentinel-1 Toolbox: S1 TOPS InSAR Tutorial; Skywatch Space Applications Inc., European Space Agency: New York, NY, USA, 2021; 25p. [Google Scholar]
- Lee, J.-S. Speckle analysis and smoothing of synthetic aperture radar images. Comput. Graph. Image Process. 1981, 17, 24–32. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2022. Available online: http://qgis.osgeo.org (accessed on 15 April 2023).
- Andalusian Government. Modelo Digital del Terreno de Andalucía. Relieve y Orografía; Junta de Andalucía: Sevilla, Spain, 2005.
- Alfieri, L.; Salamon, P.; Bianchi, A.; Neal, J.; Bates, P.; Feyen, L. Advances in pan-European flood hazard mapping. Hydrol. Process. 2014, 28, 4067–4077. [Google Scholar] [CrossRef]
- Braun, A. Retrieval of digital elevation models from Sentinel-1 radar data–open applications, techniques, and limitations. Open Geosci. 2021, 13, 532–569. [Google Scholar] [CrossRef]
- Gebremichael, E.; Molthan, A.L.; Bell, J.R.; Schultz, L.A.; Hain, C. Flood Hazard and Risk Assessment of Extreme Weather Events Using Synthetic Aperture Radar and Auxiliary Data: A Case Study. Remote Sens. 2020, 12, 3588. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Anfuso, G. Coastal storm characterization and morphological impacts on sandy coasts. Earth Surf. Process. Landf. 2011, 36, 1997–2010. [Google Scholar] [CrossRef]
- Silva, R.; Martínez, M.; Odériz, I.; Mendoza, E.; Feagin, R. Response of vegetated dune–beach systems to storm conditions. Coast. Eng. 2016, 109, 53–62. [Google Scholar] [CrossRef]
- De Sanjosé Blasco, J.J.; Gómez-Lende, M.; Sánchez-Fernández, M.; Serrano-Cañadas, E. Monitoring Retreat of Coastal Sandy Systems Using Geomatics Techniques: Somo Beach (Cantabrian Coast, Spain, 1875–2017). Remote Sens. 2018, 10, 1500. [Google Scholar] [CrossRef]
- Del Río Rodríguez, L.; González, J.B.; Prieto, F.J.G.; Ruiz, J.A.C. Riesgos de erosión en la costa de Cádiz: Gestión actual y perspectivas futuras. Geotemas 2015, 15, 149–152. [Google Scholar]
- Benavente, J.; Borja, F.; Gracia, F.J.; Rodríguez, A. Introduction to the Gulf of Cadiz coast. In Geomorphology of the South-Atlantic Spanish Coast, Proceedings of the Guide for Fieldtrip A4, 6th International Conference on Geomorphology, Zaragoza, Spain, 7–11 September 2005; Gracia, F.J., Ed.; Spanish Society of Geomorphology: Zaragoza, Spain, 2005; pp. 1–11. [Google Scholar]
- Dehghani, M.; Zoej, M.J.V.; Entezam, I.; Mansourian, A.; Saatchi, S. InSAR monitoring of progressive land subsidence in Neyshabour, northeast Iran. Geophys. J. Int. 2009, 178, 47–56. [Google Scholar] [CrossRef]
- Rahimi, R.; Tavakol-Davani, H.; Graves, C.; Gomez, A.; Valipour, M.F. Compound Inundation Impacts of Coastal Climate Change: Sea-Level Rise, Groundwater Rise, and Coastal Watershed Precipitation. Water 2020, 12, 2776. [Google Scholar] [CrossRef]
- Clark, J.R. Coastal zone management for the new century. Ocean Coast. Manag. 1997, 37, 191–216. [Google Scholar] [CrossRef]
- Liu, J.G.; Black, A.; Lee, H.; Hanaizumi, H.; Moore, J.M. Land surface change detection in a desert area in Algeria using multi-temporal ERS SAR coherence images. Int. J. Remote Sens. 2001, 22, 2463–2477. [Google Scholar] [CrossRef]
- Turner, I.L.; Harley, M.D.; Drummond, C.D. UAVs for coastal surveying. Coast. Eng. 2016, 114, 19–24. [Google Scholar] [CrossRef]
- Hu, L.; Yue, P.; Zhang, M.; Gong, J.; Jiang, L.; Zhang, X. Task-oriented Sensor Web data processing for environmental monitoring. Earth Sci. Inform. 2015, 8, 511–525. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Z.; Tian, B.; Zhou, J.; Zeng, J. A method for monitoring hydrological conditions beneath herbaceous wetlands using multi-temporal ALOS PALSAR coherence data. Remote Sens. Lett. 2015, 6, 618–627. [Google Scholar] [CrossRef]
- Spizzichino, D.; Margottini, C. Satellite monitoring of geo-hazards affecting cultural heritage. In A Research Agenda for Heritage Planning: Perspectives from Europe; Edward Elgar Publishing: Cheltenham, UK, 2021; p. 133. [Google Scholar]
- Elfadaly, A.; Abutaleb, K.; Naguib, D.M.; Lasaponara, R. Detecting the environmental risk on the archaeological sites using satellite imagery in Basilicata Region, Italy. Egypt. J. Remote Sens. Space Sci. 2022, 25, 181–193. [Google Scholar] [CrossRef]


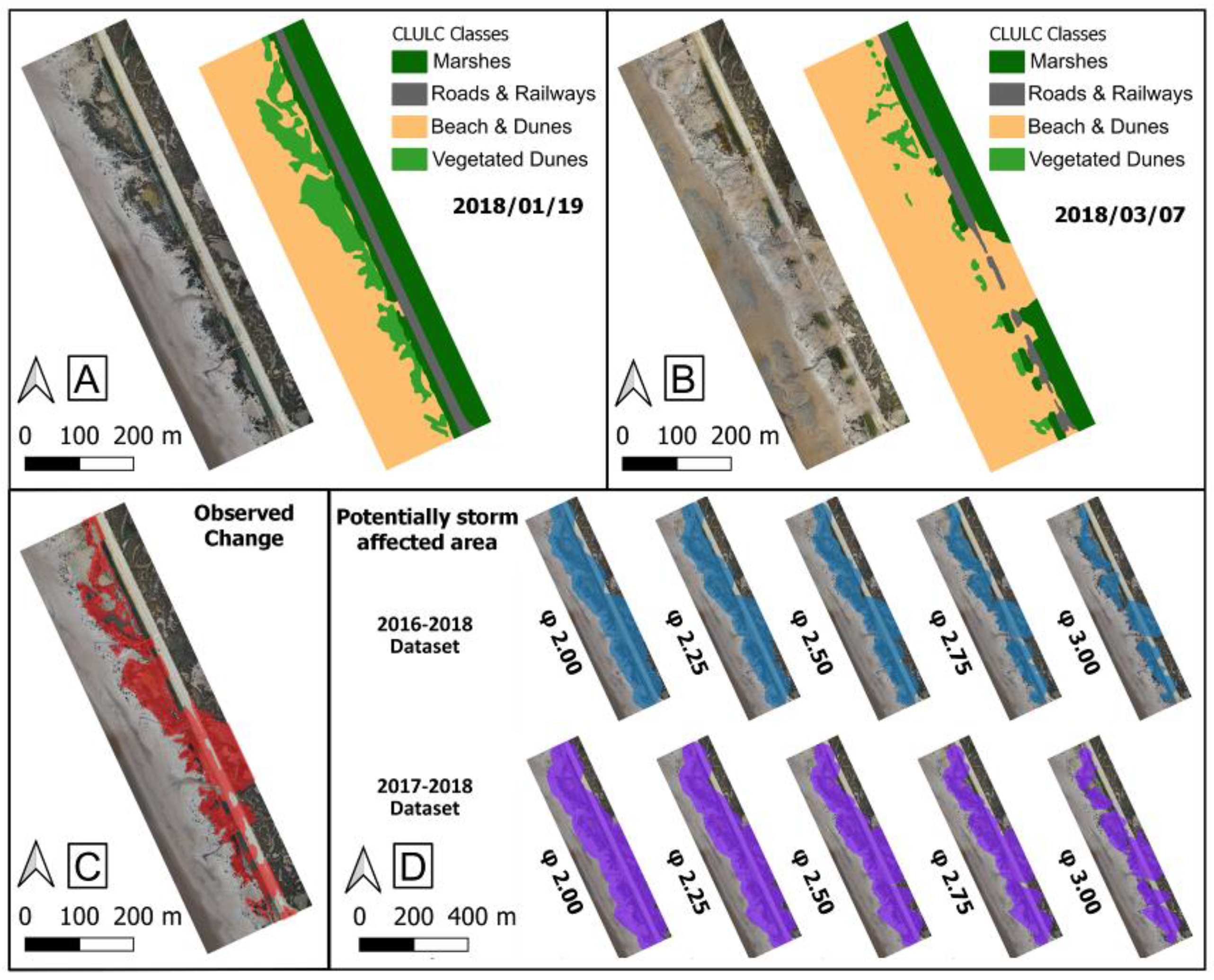
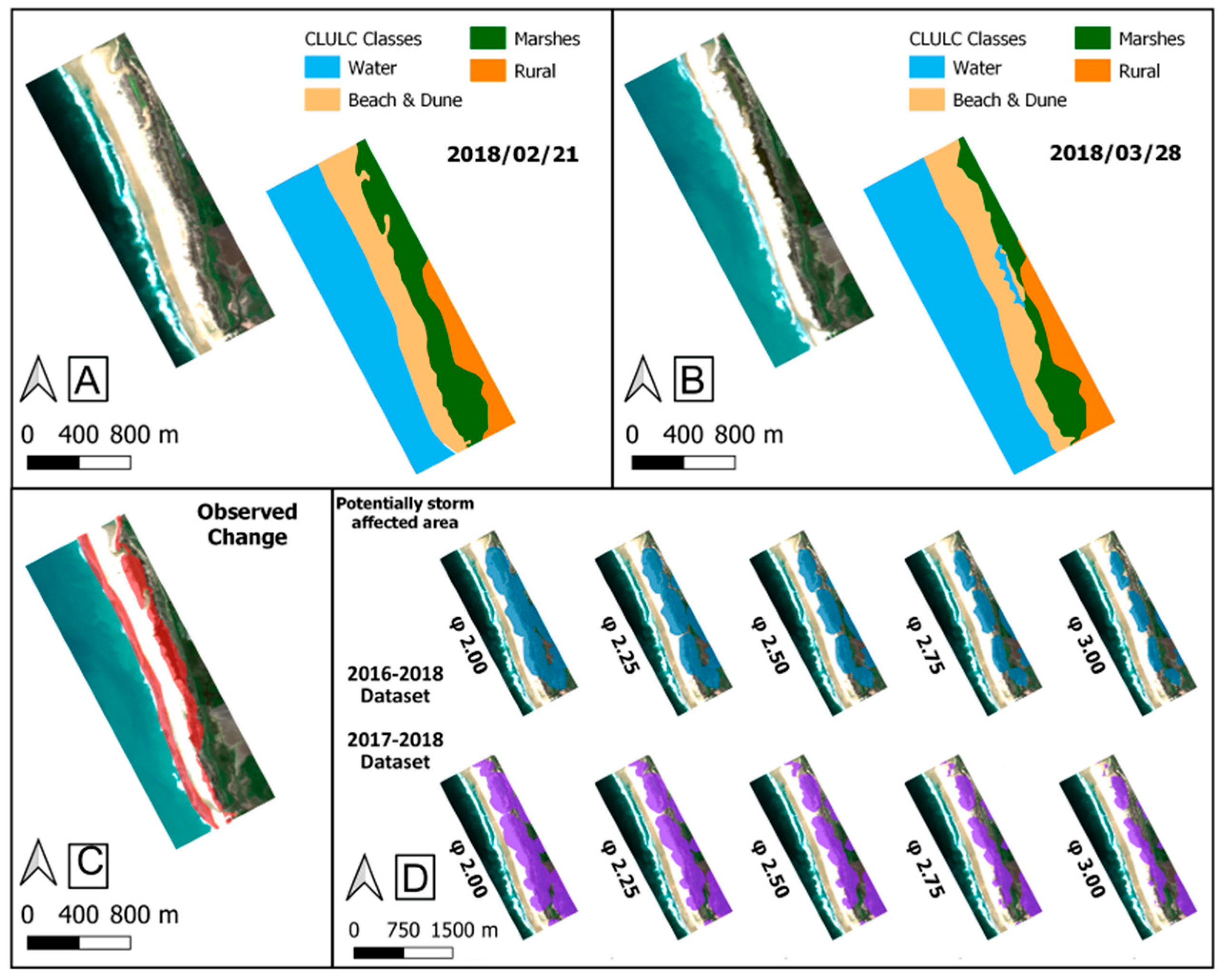

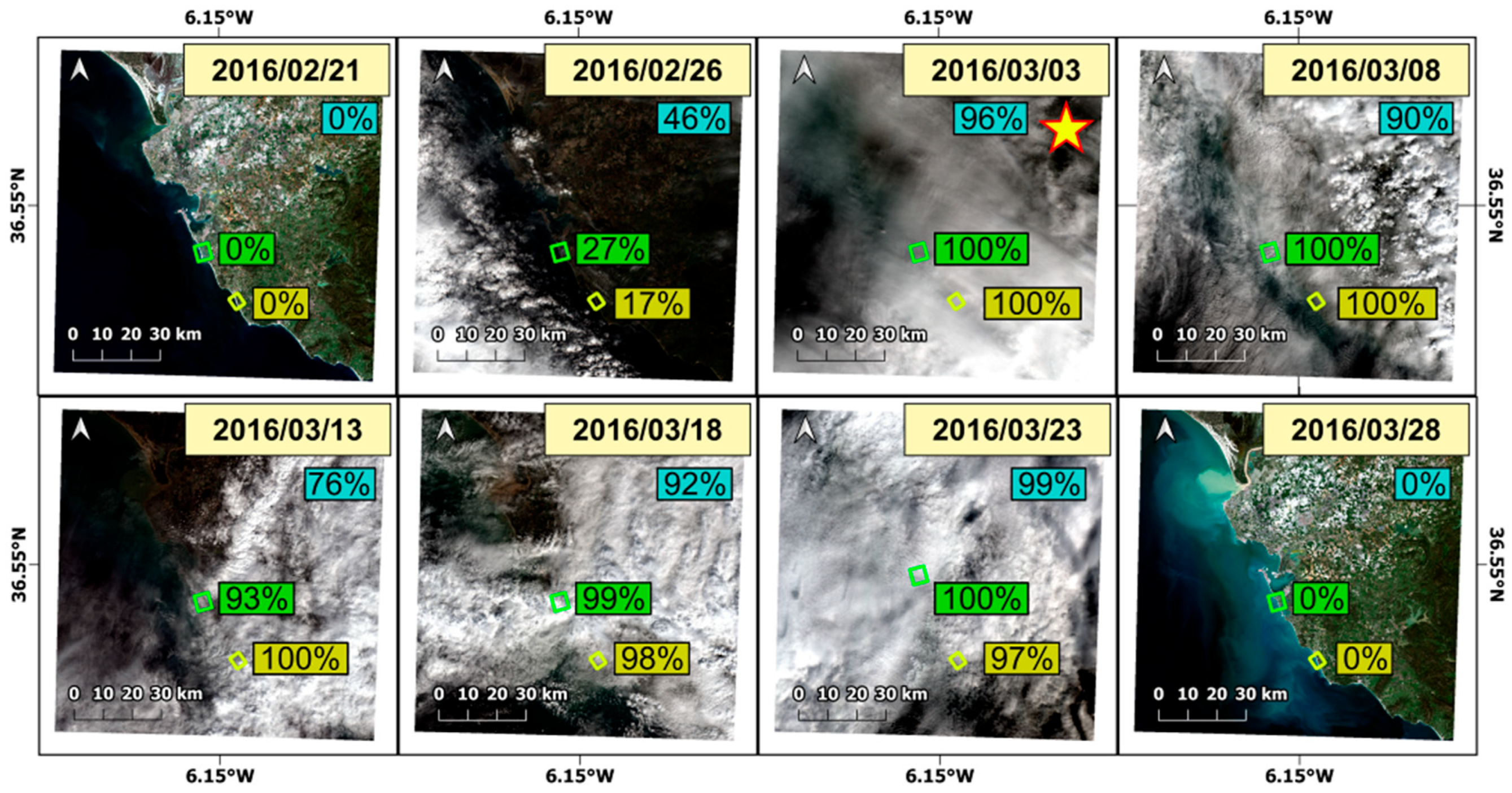
| 1 June 2016–9 February 2018 | |||||
|---|---|---|---|---|---|
| Test Site | φ | Beach and Dunes | Vegetated Dunes | Roads and Railways | Marshes |
| Camposoto | 3 | 0 | 49 | 81 | 65 |
| Camposoto | 2.75 | 0 | 50 | 79 | 64 |
| Camposoto | 2.5 | 8 | 51 | 78 | 60 |
| Camposoto | 2.25 | 13 | 49 | 75 | 56 |
| Camposoto | 2 | 17 | 46 | 72 | 52 |
| Conil de la Frontera | 3 | 0 | - | - | 77 |
| Conil de la Frontera | 2.75 | 0 | - | - | 60 |
| Conil de la Frontera | 2.5 | 1 | - | - | 44 |
| Conil de la Frontera | 2.25 | 4 | - | - | 36 |
| Conil de la Frontera | 2 | 7 | - | - | 36 |
| 1 June 2016–9 February 2018 | |||
|---|---|---|---|
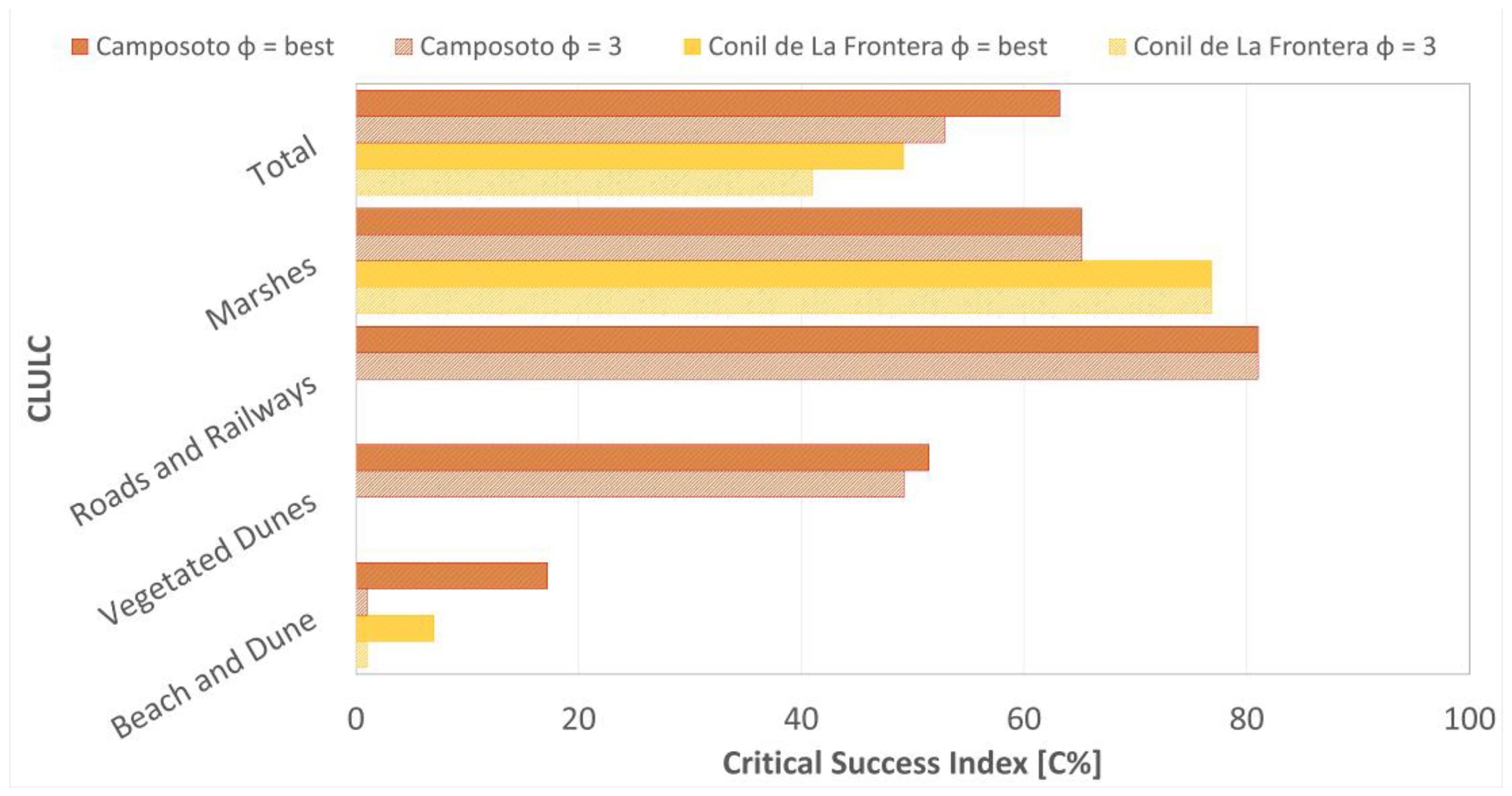
| Test Site | H [%] | F [%] | C [%] |
| Camposoto | 79 | 22 | 63 |
| Conil de la Frontera | 64 | 43 | 49 |
| 1 June 2016–9 February 2018 | 4 March 2017–9 February 2018 | |||||
|---|---|---|---|---|---|---|
| Test Site | H [%] | F [%] | C [%] | H [%] | F [%] | C [%] |
| Camposoto | 79 | 22 | 63 | 85 | 35 | 55 |
| Conil de la Frontera | 64 | 43 | 49 | 64 | 83 | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garzo, P.A.; Fernández-Montblanc, T. Land Use/Land Cover Optimized SAR Coherence Analysis for Rapid Coastal Disaster Monitoring: The Impact of the Emma Storm in Southern Spain. Remote Sens. 2023, 15, 3233. https://doi.org/10.3390/rs15133233
Garzo PA, Fernández-Montblanc T. Land Use/Land Cover Optimized SAR Coherence Analysis for Rapid Coastal Disaster Monitoring: The Impact of the Emma Storm in Southern Spain. Remote Sensing. 2023; 15(13):3233. https://doi.org/10.3390/rs15133233
Chicago/Turabian StyleGarzo, Pedro Andrés, and Tomás Fernández-Montblanc. 2023. "Land Use/Land Cover Optimized SAR Coherence Analysis for Rapid Coastal Disaster Monitoring: The Impact of the Emma Storm in Southern Spain" Remote Sensing 15, no. 13: 3233. https://doi.org/10.3390/rs15133233
APA StyleGarzo, P. A., & Fernández-Montblanc, T. (2023). Land Use/Land Cover Optimized SAR Coherence Analysis for Rapid Coastal Disaster Monitoring: The Impact of the Emma Storm in Southern Spain. Remote Sensing, 15(13), 3233. https://doi.org/10.3390/rs15133233






