Abstract
The eruption of the Hunga Tonga–Hunga Ha’apai volcano on 15 January 2022 was the first powerful explosive eruption in history to be recorded with high quality by a wide range of geophysical equipment. The atmospheric Lamb wave caused by the explosion repeatedly circled the Earth and served as one of the reasons for the formation of tsunami waves. In this paper, the Lamb wave manifestations are analyzed in the recordings of tsunamimeters, i.e., in data from DONET and DART pressure sensors located in the area of the Japanese Islands. The work is aimed at studying the physics of the formation of pressure variations at the ocean floor in order to develop a method for isolating free gravity waves in records obtained by bottom pressure sensors. Within the framework of shallow water theory, an analysis of the response of the water layer to the atmospheric Lamb wave was performed. This response combines a forced perturbation, the amplitude of which depends on the depth of the ocean, and free gravity waves arising as a result of the restructuring of the forced perturbation on the submarine slopes. Analytical formulas are given for the amplitude and energy of the forced perturbation and free waves arising at the depth jump. With the aid of numerical simulation, the finite length of a slope was revealed to significantly affect the parameters of free waves when exceeding 50 km. The analysis of in situ data (DONET, DART) confirms the validity of theoretical concepts presented in the work. In particular, it is shown that variations of bottom pressure in the deep ocean exceed the amplitude of atmospheric pressure fluctuations in the Lamb wave.
1. Introduction
The powerful explosive eruption of the Hunga Tonga–Hunga Ha’apai volcano, which occurred in the South Pacific Ocean on 15 January 2022, led to the formation of a Lamb wave in the atmosphere and tsunami waves in the ocean. The atmospheric wave was clearly observed from the GOES-17 geostationary satellite [1], its manifestations were in the Earth’s ionosphere [2], and it was recorded by numerous ground-based barographs [3,4,5,6,7]. Tsunami waves were observed throughout the Pacific Ocean; according to the Global Historical Tsunami Database/NOAA (doi:10.7289/V5PN93H7), the maximum water height reached in the near zone and in the far zone (Chile, Mexico, USA, Japan)—at a distance of thousand from the volcano.
In the 1960s and 1970s, S.L. Soloviev [8,9] proposed a reliable and convenient method for recording tsunami waves in the open ocean, which was based on precision measurements of bottom pressure variations. This method is currently widely used both for solving problems of operational forecasting and for studying the tsunami phenomenon [10,11,12]. In this work, we will use data from two systems well known to specialists to provide in situ data: DONET (Dense Ocean floor Network system for Earthquakes and Tsunamis) [13,14] and DART (Deep-ocean Assessment and Reporting of Tsunamis) [15,16]. The signals recorded by DART stations on 15 January 2022 were analyzed both directly during the event for the purposes of early tsunami warning, and later—as a unique scientific material—by many researchers, e.g. [3,17,18,19]. The records received by the DONET system on 15 January 2022 have also been analyzed in a number of papers [20,21,22,23]. Note that the data on bottom pressure variations obtained by the DONET observatories compare favorably with the DART data by a significantly higher sampling rate ().
In addition to DART and DONET, another system of ocean-bottom observatories S-net (Seafloor Observation Network for Earthquakes and Tsunamis) is deployed near the Japanese Islands, which includes 150 stations [24]. S-net stations also successfully recorded manifestations of the explosive eruption on 15 January 2022. S-net records have been analyzed, for example in [20,25]. In this work, we do not plan to consider S-net data.
One of the few disadvantages of deep-sea tsunami recorders is the noisiness of the signal due to manifestations of seismic and hydroacoustic waves. During strong tsunamigenic earthquakes, especially near the tsunami source, the level of these “noises” can exceed the tsunami signal level by several orders of magnitude [26,27], but when recording seismogenic tsunamis, the “useful” and “noise” components of bottom pressure variations pertain to different frequency ranges [11,28,29]. Therefore, it is advisable to use frequency filtering to isolate the tsunami signal. However, at large distances from the source, the manifestation of seismic and hydroacoustic waves is recorded much earlier than the tsunami; in such cases, the tsunami signal is clearly distinguishable, even without frequency filtering, e.g. [30,31].
Atmospheric pressure fluctuations in the Lamb wave are also capable of providing a kind of “noise” contribution to bottom pressure variations. How can direct manifestations of the Lamb wave and of free gravity waves (tsunami), generated by this atmospheric wave, be distinguished in the records of bottom pressure variations? In this case, frequency filtering cannot provide for signal separation, because the period of the Lamb wave observed on 15 January 2022 (tens of minutes) corresponds to typical periods of tsunami waves.
The problem of tsunami excitation by a Lamb wave in the atmosphere is similar to the problem of meteotsunami generation [32,33,34,35]. The main difference consists of the clearly defined cylindrically symmetrical structure of the traveling atmospheric perturbation and in its propagation velocity. In the case of a typical meteorological tsunami excitation, the Proudman resonance [36], i.e., the proximity of the propagation velocities of an atmospheric perturbation and of long waves in the ocean, is realized in shallow water. However, if the source is a Lamb wave traveling at a speed of approximately , then the Proudman resonance is achieved in the areas of deep-sea trenches.
Over the past year, many papers have been published on the numerical simulation of tsunami waves caused by the explosion of the volcano on 15 January 2022, e.g. [17,18,19,25,37]. In these works, in addition to the “traditional” mechanisms of generation of volcanogenic tsunamis, which are localized directly at the source (underwater explosion, flank failure, caldera subsidence, pyroclastic flow, etc. [38]), special attention was paid to the formation of tsunami waves in the ocean by the atmospheric Lamb wave. Note that the first interest in the process of wave generation in the ocean by an atmospheric wave from a volcano explosion did not arise in 2022, but much earlier.
The surge of interest was due to the explosive eruption of the Krakatoa volcano in 1883 [39]. An unusual feature of the tsunami waves resulting from this eruption was the early arrival of the tsunami waves in the far zone, which was ahead of the calculated times. On the whole, it was clear that perturbations outpacing gravity waves arising at the source can only be due to the Lamb wave, which, on average, propagates in the atmosphere faster than long waves in the ocean [40,41,42]. The eruption of the Krakatoa volcano occurred already in the instrumental epoch, but the amount and quality of data did not allow a full analysis of the phenomenon. The eruption of the Hunga Tonga–Hunga Ha’apai volcano was the first powerful explosive eruption in the history of science to be experimentally recorded with such high quality and detail.
At the end of the introductory part, let us dwell upon several results presented in our papers [6,7], which we will rely on in this work. Based on the data of the IRIS network ground-based barographs located in the Pacific region, it was found that the atmospheric Lamb wave propagated at a velocity of , and its arisal time at the source was 04:27 UTC ( confidence interval). Note that the estimates of speed and time in the source are consistent with data obtained by other authors, e.g. [3,4,5,18]. Moreover, in these articles, we carried out a theoretical analysis of the problem of the generation of waves in the ocean by an atmospheric Lamb wave within the framework of the potential theory of waves. In this case in particular, the possibility of using the theory of long waves was demonstrated. It was also shown that—due to the Proudman resonance [11,36]—amplitude of pressure variations at the bottom should exceed the amplitude of atmospheric pressure fluctuations in the Lamb wave by a factor of , where is the ocean depth at the location of the DART station and is the acceleration of gravity. Using signals recorded in the area of the Hawaiian Islands (POHA and KIP barographs of the IRIS network; DART51407), we compared the observed atmospheric pressure fluctuations with the observed bottom pressure variations. It was found that when the waveshapes coincided, the amplitude of pressure variations at the bottom exceeded the amplitude of atmospheric pressure fluctuations in the Lamb wave by a theoretically predicted factor of .
The first goal of this paper is a detailed presentation of the theory of the generation of long-wave perturbations in the water layer by an atmospheric Lamb wave, caused by explosion of the Hunga Tonga–Hunga Ha’apai volcano on 15 January 2022. The second goal is to analyze and to interpret in situ data: pressure variations recorded by ground-based barographs and deep-sea pressure gauges (DONET, DART) in the Japan Islands region during the passage of the Lamb wave.
2. Basic Properties of Waves Excited in a Water Layer by an Atmospheric Pressure Wave
In this section, we will theoretically analyze the main features of the process of generation of long-wave disturbances in a water layer by the atmospheric Lamb wave. The atmospheric wave formed by a volcanic explosion at a large distance from the “point” source will be considered to be cylindrically symmetric. The expediency of this approach not only follows from general physical considerations but is also confirmed by observational data [3,4,5]. At large distances from the source, the curvature of the wave front is obviously small, and the amplitude changes slowly with the distance, so to understand the physics of the impact of the atmospheric wave on the water layer, it is sufficient to consider a one-dimensional problem, directing the axis of the local rectangular coordinate system 0x in the radial direction (from the volcano). In this case, the atmospheric pressure fluctuations in the Lamb wave are represented by the following formula:
where is the dimensionless function of a dimensionless argument, which describes the form of the atmospheric disturbance, is the amplitude of atmospheric pressure fluctuations, is the wave number of the atmospheric wave, and is the velocity of the atmospheric wave propagation.
To determine the perturbations of a water layer initiated by running fluctuations of atmospheric pressure, we will resort to equations of the linear theory of shallow water:
where is the horizontal flow velocity, is the displacement of the free water surface from the equilibrium position, is the water density, and is the ocean depth.
We shall first consider a constant-depth ocean. Because significant areas of the Pacific ocean are abyssal plains, such a simplified formulation of the problem is not a meaningless abstraction. When , the systems (2) and (3) can be easily reduced to the classical inhomogeneous wave equations for the displacement of a free surface,
and for the horizontal flow velocity
For a running perturbation of the form (1), the solutions of Equations (4) and (5) are well known, e.g. [11], and have the form of forced waves, whose shape and propagation velocity are the same as those of an atmospheric wave:
Knowing the pressure at the water surface (1) and the displacement of the free surface (6), it is easy to find the pressure fluctuations at the ocean floor:
The value , that is a dynamic addition to the hydrostatic pressure at the ocean floor , will be needed later for the interpretation of data obtained by bottom pressure gauges (deep water sea level stations).
It can be seen from Formulas (6)–(8) that the amplitude of perturbations in the water layer can become quite significant when the propagation velocity of an atmospheric perturbation, , approaches the velocity of long waves, . This effect is known as the Proudman resonance [11,36]. In the case of a Lamb wave velocity of , which was observed during the propagation of an atmospheric perturbation over the Pacific ocean [6], the resonance should occur at the depth , which is close to the limit depths of the world ocean. Such depths are reached only in areas of deep-water depressions, which are clearly insufficiently extended for the development of significant resonance phenomena. Below we shall deal with the issue of how quickly a forced perturbation of the limiting amplitude develops.
It is noteworthy that, in accordance with Formula (8), atmospheric pressure fluctuations created by a Lamb wave always manifest themselves in variations of the bottom pressure with a certain increase, and at great depths with a significant increase [7]. Note that, naturally, only fully developed forced perturbation is intended.
Let us calculate the potential and kinetic energies of a forced perturbation in a water layer. Hereinafter we will refer to the energy per unit front length (). The potential energy of the wave perturbation is calculated from the displacement of the free surface of the water by the formula
and the kinetic energy is calculated from the horizontal flow velocity,
Substituting expressions (6) and (7) into Formulas (9) and (10) we obtain
where .
Comparing Formulas (11) and (12), we find the ratio of the kinetic and potential energies of the forced perturbation,
where is the Froude number, known in hydrodynamics. At a Lamb wave velocity , (or even ) for most regions of the world ocean; therefore, the kinetic energy of the forced disturbance should be expected to exceed the potential energy, and in some cases multiply.
The total energy of a forced perturbation is calculated by the formula
It is important to understand that in a boundless ocean of constant depth, a running atmospheric disturbance forms an exclusively forced perturbation of the water layer. Free gravity waves can only arise in an ocean of variable depth [6,43,44]. When the depth changes, the forced perturbation, which represents a response of the water layer to the atmospheric wave, must undergo reformation, and this process is accompanied by the generation of free gravity waves.
Consider the ocean depth to change abruptly at the point from to . To calculate the free waves arising at the jump in depth, it is necessary to write down Equations (4) and (5) separately for subregions and . At point , the solutions are made to “match”, taking into account the continuity of the displacement of the free surface () and of the flow of matter () [45]. The solutions sought include the forced perturbation propagating with the velocity , as well as a free gravity wave propagating with the same velocity as long waves:
at
at
where and are coefficients determining the amplitude of free waves propagating in the respective negative and positive directions of the 0x axis, and and are the wavenumbers in the regions of depths, and , respectively. The wavenumbers can be determined from the condition of frequency conservation in the linear system: , . In writing Formulas (16) and (18) for the flow velocities, we took into account the fact that the free surface displacement in the running (free) wave and the velocity are related by the formula .
Matching solutions (15)–(18) at point with account of the above indicated conditions, we obtain the following formulas for the coefficients:
Note that Formulas (19) and (20) also hold valid when the depths or turn to zero. This essentially expands the possibilities for application of these analytical expressions in testing numerical models, permitting one to calculate the amplitudes of free waves arising both at jumps in depth in the middle of a water basin and at boundaries between land and water. Formulas (15)–(20) are very close to the expressions that were obtained earlier in the original work [41] and reproduced with misprints in a recent article [37]. The coefficients in our formulas (, , etc.) and in Garrett’s expressions are completely equivalent. The difference actually lies in the fact that in our formulas the function f, which describes the shape of the wave disturbance, is introduced as a function of the dimensionless argument, which is traditional for wave physics, while in Garrett’s expressions it is a function of the dimensional argument.
From the free surface displacement and the flow velocity in free waves arising at a jump in depth, one can readily calculate the total energy of waves propagating in the positive and negative directions of the 0x axis:
The potential and kinetic energies in a propagating linear wave are known to be equal to each other, so there is no sense in calculating these quantities separately.
Expressions (21) and (22) permit one to calculate the ratio between the energies of free waves propagating in the positive and in the negative directions of the 0x axis:
In accordance with Formula (23), we obtain that for velocities and the energy of free gravity waves, arising at a jump in depth from to , will be mainly directed towards deep water, along the direction of propagation of the Lamb wave: . In the case of a jump in depth from to , the energy of free gravity waves, propagating in the direction of propagation of the Lamb wave, in this case towards shallow water, also prevails, although not so significantly: .
The formation process of free gravity waves at the jump point in depth is clearly shown in Figure 1. Calculation of waves was performed, applying the numerical model and analytical Formulas (15)–(18), which allowed mutual testing of the analytical formulas and of the numerical method.
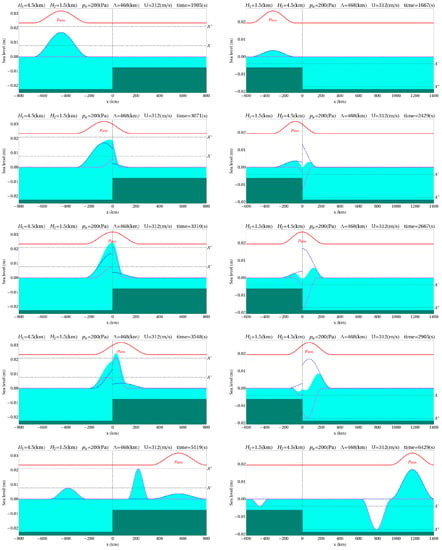
Figure 1.
Formation of free gravity waves when an atmospheric pressure wave crosses a depth jump. Snapshots are constructed at consecutive points in time, indicated in the figure. The left column of images corresponds to the case of jump in depth “from deep to shallow” (, ), while the right column corresponds to the case “from shallow to deep” (, ). The bottom relief is schematically (not to scale) shown by a dark fill. The atmospheric pressure wave is shown by the red curve. The celestial blue fill presents the results of numerical simulation and the dotted curves are calculated by analytic Formulas (15)–(18). The blue dotted line represents forced waves and the purple dotted line is for free waves. Calculations were performed for , , and .
The numerical model resolved the 1D Equations (2) and (3) for shallow water in a basin of variable depth by the explicit finite-difference method making use of the Arakawa C-grid [46]. A grid with a constant step in the space was used. The step in time was determined taking into account the Courant condition: /, where is the maximum ocean depth within the computational domain. The problem was resolved with zero initial conditions: . The propagating atmospheric pressure perturbation (1) was considered the source of waves. The shape of the model atmospheric perturbation was chosen to be the following:
At the initial moment of time the perturbation was situated outside the computational domain. The flow velocity (7), corresponding to forced perturbation of the water layer, was assumed as the boundary condition of “free passage”through the boundaries of the computational domain. Thus, both the entrance of the atmospheric perturbation to the computational domain and the exit of the perturbation outside its limits took place without the generation of free gravity waves at the boundaries of the computational domain.
The results of numerical calculations of the perturbation dynamics of a free surface are shown in Figure 1 in celestial blue fill, while the results of analytical calculations are indicated by dotted curves. The forced wave calculated by Formula (6) is represented by the blue dotted curve. Free gravity waves (see Formulas (15) and (17)) are shown by purple dotted curves. The red solid curve in the upper part of the figure indicates the position and shape of a propagating atmospheric perturbation. The length of the atmospheric perturbation adopted in the calculations was (), and its amplitude was . The grid step was set to . The perturbation length corresponds to the observed period of the positive Lamb wave phase: , where .
The left column of snap-shots in Figure 1 represents an example of the situation, when a Lamb wave crosses the region of a jump-like decrease of depths: , (which approximately corresponds to drops in depth within the region where DONET stations are established). In this case, the forced wave reduces its amplitude, so the polarities of both arising free waves turn out to be positive, or, to be more precise, they coincide with the polarity of the atmospheric perturbation. The right column of images in Figure 1 represents the opposite situation, when the atmospheric wave crosses the region of a jump-like increase of depths: , . In this case, the amplitude of the forced wave increases, while the polarity of free waves becomes negative.
From Figure 1 it can be seen how exactly the forced perturbation undergoes restructuring when the atmospheric wave crosses the depth jump. We note that in the region of the forced perturbation of maximum amplitude arises immediately after the atmospheric wave crosses the point of jump-like change in depths. But during a certain time, the forced perturbation interferes with the free gravity wave. Therefore, the amplitude of the total perturbation changes smoothly as the forced and free waves diverge in space. The time required for total divergence of these waves, i.e., for the forced perturbation to achieve its maximum energy, is
From Figure 1 and Videos S1 and S2, it is also seen that for the forced perturbation to achieve its maximum amplitude, a lesser time is required: (in the case of symmetric atmospheric perturbation). It is remarkable that the closer to the Proudman resonance conditions (), the longer is the time required for development of forced perturbation. For typical conditions of an open ocean () in the case of , we obtain from (25) that the time a forced perturbation of maximum energy will develop is . In this time, the forced perturbation will cover a distance of . Incidentally, the forced perturbation will reach its maximum amplitude two times faster, already after . If the perturbation turns out to be in the region of depth , the formation of a forced perturbation is essentially more rapid: , .
In actuality, variation of the ocean depth is not jump-like, but quite smooth. The maximum average bottom slopes reached, for instance on the continental slope, amount to 0.1. Data available in the GEBCO numerical atlas indicate that local bottom slopes are, as a rule, limited by the value of 0.3 [47]. The numerical model permits one to analyze how the submarine slope steepness influences the parameters of arising free waves. In Figure 2, examples are shown of free wave calculations for various slopes of the bottom. The minimum depth in the examples presented was , while the maximum amounted to . The length of the plane slope varied between 4 and , which corresponded to the range of bottom slopes from 0.00586 up to 0.75. As in Figure 1, the blue and purple dotted curves show the theoretical wave shapes, which correspond to jump-like depth variation. From Figure 2, it can be seen that the parameters of free waves arising on a gentle slope and at a jump in depth may differ significantly. A free wave propagating in a direction opposite to the propagation of atmospheric perturbation is subject to the largest variations: enhancement of the slope length reduces the amplitude of this wave and increases its length. A free wave propagating in the same direction as the atmospheric perturbation behaves in a totally different manner. Enhancement of the slope length starts to noticeably reduce the amplitude of this free wave only in the case of slope lengths exceeding .
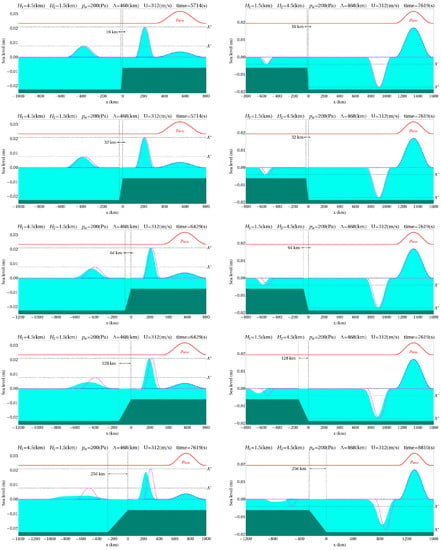
Figure 2.
Influence of the bottom slope on the formation of free gravity waves. Snapshots are made at consecutive moments of time, indicated in the figure. The bottom relief is schematically shown (not to scale) by the dark fill, and the slope length is in km. The left column of images corresponds to depth reduction from to , the right column corresponds to depth enhancement from to . The atmospheric pressure wave is shown by the red curve. The celestial blue fill represents the results of numerical simulation and the dotted lines are calculated by analytic Formulas (15)–(18), obtained for the depth jump case. The blue dotted line corresponds to forced waves and the purple one corresponds to free waves. Calculations were performed for , , and .
The influence of the bottom slope on the amplitude and energy of free gravity waves can be traced in detail in Figure 3. The amplitudes and energies, calculated numerically for a given slope length, , are normalized to the theoretical values, corresponding to the depth jump. Numerical calculations were performed for , , a minimal depth of , and a maximum depth of . In calculating energies, we made use of the precise value of the integral for the shape of the atmospheric perturbation (24):
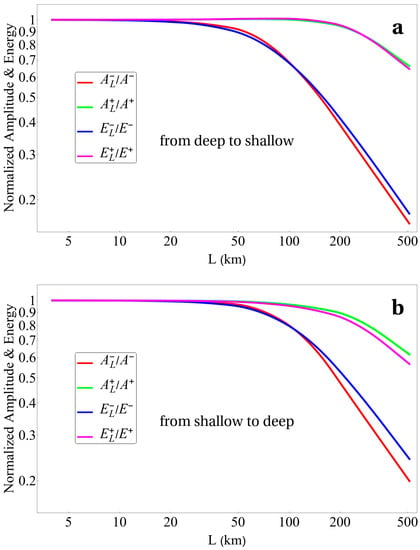
Figure 3.
Influence of the slope length, L, on the amplitude and energy of free gravity waves. The amplitude and energy are normalized to the theoretical values, determined by Formulas (19)–(22), which were obtained for the depth jump case. Calculations were performed for , , and . (a) depth reduction from to ; (b) depth enhancement from to .
From Figure 3, it can be seen that the amplitude and energy of waves propagating in the same direction as the Lamb wave remain close to the values corresponding to jump-like variation of depths, straight up to slope lengths of . In the case of waves propagating in the opposite direction, amplitude and energy reduction starts noticeably earlier, already at . In other words, if a submarine slope is shorter than , then for estimation of the amplitude and energy of free gravity waves it can be dealt with a jump-like change of depth. It is remarkable that the normalized curves for the “from deep to shallow” case and for the “from shallow to deep” case do not differ much from each other.
To conclude this section, we will consider manifestations of the atmospheric Lamb wave in variations of the bottom pressure. As noted above, in the framework of the hydrostatical approximation (or shallow water theory), pressure fluctuations at the ocean floor are a superposition of atmospheric pressure and pressure created by disturbances of the free surface of the ocean. In the case of a flat horizontal bottom, when the response of the water layer exists only as a forced wave, pressure fluctuations are described by analytical Formula (8). However, ocean-bottom pressure gauges (PGs) are often installed in areas with a complex bottom relief. In the region of variable depth, free gravity waves arising on underwater slopes begin to make a noticeable contribution to variations in bottom pressure. To estimate the amplitude of these waves, Formula (19) or Formula (20) can be used. Depths and should correspond to the typical depth difference in the area under consideration. If the assessment is carried out in a coastal area, the depth on the coast should be set to 0.
We will illustrate the basic features of bottom pressure variations arising under the influence of the atmospheric Lamb wave in an area with a complex bottom relief using the 1D numerical model described above. For numerical experiments, we will choose a model depth profile, which is typical for the location area of the DONET system (see Supporting information, Figure S1). This region is characterized by a transition from abyssal depths of across the continental slope to an underwater plateau with depths of and only then to the shelf zone.
The model depth profile is shown in the lower fragment of Figure 4. The shape of the Lamb model wave, as in the experiments described above, was determined by Formula (24); its velocity, length, and amplitude were set equal to , , and . At the left boundary of the computational domain, the non-reflective condition for the Lamb wave was first set, and after the atmospheric wave was completely inside the computational domain, the non reflective condition for long gravity waves was set: . At the right boundary on the isobath of , the reflection condition was set: .
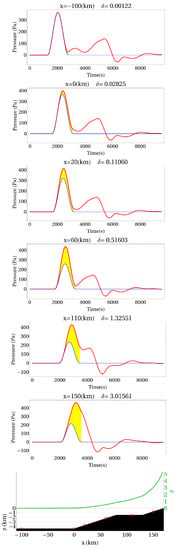
Figure 4.
Bottom pressure variations calculated as a function of time at six different points along the depth profile (the lower fragment of the figure). Coordinates of points and values of parameter are indicated in each of the upper six fragments of the figure. The red curve shows the total pressure and the blue curve shows the pressure in the forced wave, calculated by Formula (8). The yellow fill shows the difference between the red and blue curves during the passage of an atmospheric perturbation. The green curve in the lower fragment of the figure shows the behavior of parameter along the slope.
The results of numerical calculations are shown in Figure 4. The red curve shows the course of bottom pressure over time, calculated for six virtual PGs. The blue curve represents the forced wave calculated by Formula (8), taking into account the depth of the PG location. The yellow fill shows the difference between the red and blue curves during the passage of the Lamb wave. The following dimensionless parameter was calculated as a quantitative measure of the difference between the curves:
where represents variations of the bottom pressure, is the bottom pressure in the forced wave, and and are the entry and end times of the Lamb model wave. The value for each of the six examples is shown in the figure.
It can be seen from Figure 4 that the first entry of the signal always corresponds to the Lamb wave and the forced disturbance of the water layer; manifestations of free gravity waves enter somewhat later. At a distance of from the foot of the slope, the value is not zero; this indicates that a free wave generated by the underwater slope and running from the shore has already been added to the forced disturbance. For virtual PGs located higher up the slope, the manifestations of free waves increase, and the amplitude of the forced disturbance decreases. Thus, when approaching the shore, the forced disturbance is increasingly distorted by free waves, which manifests itself in the growth of parameter . The course of parameter along the slope is represented by the green curve above the depth profile in the lower fragment of the figure. To obtain this green curve, we calculated the value δ for virtual sensors located at intervals (step of the numerical grid was ).
Once again, we note that, at great depths, the leading role in bottom pressure fluctuations should belong precisely to the forced disturbance. This is due to the resonant nature of the response of the water layer, as a result of which pressure fluctuations in the forced wave at the bottom have a noticeably greater amplitude than the forcing effect in the atmosphere. With a decrease in the depth of the ocean, the role of the resonance effect decreases, and the amplitude of variations of the bottom pressure tends toward the amplitude of atmospheric pressure fluctuations. At the same time, the manifestations of free (long) gravity waves in the variations of bottom pressure do not depend on the depth (). In this regard, the fluctuations of near-bottom pressure in shallow water should be dominated by free wave manifestations, masking the direct manifestation of the atmospheric wave.
3. Observational Data and Their Preliminary Handling
Manifestations of the explosive eruption of the Hunga Tonga–Hunga Ha’apai volcano, which took place on 15 January 2022, were registered by numerous different geophysical sensors all over the world. In the present work, we concentrate on the variations of pressure that were registered in the atmosphere and at the ocean bottom in the vicinity of the Japanese islands within the region indicated in Figure 5 (, ).
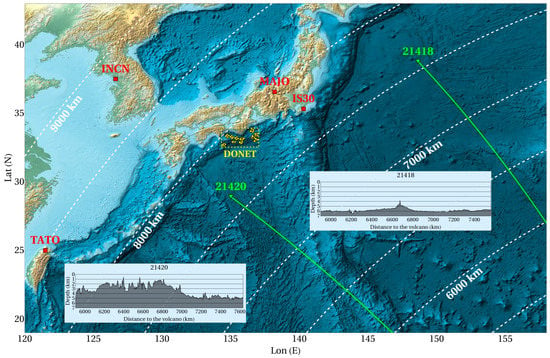
Figure 5.
Relative position of land-based barographs (red squares), deep-water tsunami detectors DART (green triangles), and deep-sea observatories DONET (yellow diamonds). The white dotted lines showing distances from the volcano Hunga Tonga–Hunga Ha’apai are drawn with an interval of . The insets show the depth profiles constructed along arcs of the large circle connecting the volcano and the DART stations (green lines).
In the above-mentioned region, the atmospheric Lamb wave, caused by the explosive eruption, was recorded by four land-based barographs, three of which (MAJO, TATO, INCN) belong to the IRIS network (http://ds.iris.edu/ds/ (accessed on 25 January 2022)) and are characterized by a data sampling rate of . The fourth barograph of IS30 refers to The International Monitoring System Infrasound Network/CTBTO; data sampling rate is . The location of the barographs is shown in Figure 5 with red squares.
Atmospheric pressure fluctuations caused by the passage of the Lamb wave are presented in Figure 6. A low-frequency component approximated by a polynomial was previously removed from the original signals. The signal registered by the IS30 barograph was subjected to additional processing: smoothing by a Gaussian filter with a kernel of radius 20 sampling intervals (=1 s) with further downsampling to . Figure 6 shows that the amplitude and shape of the head wave remain virtually unchanged from station to station; only the times of arrival differ, which is related to the distances of the barographs from the volcano being different. Taking into account that the distances between the four barographs dealt with are quite significant ( and more), one can conclude that the parameters of the Lamb wave within the region considered are characterized by quite a high spatial uniformity. This fact essentially simplifies the analysis of the Lamb wave manifestations in variations of the bottom pressure. Data on atmospheric pressure fluctuations at any point of interest to us within the region considered can be obtained by shifting in time the signal registered by one of the barographs. To this end, one can, in principle, take advantage of the data registered by any one of the four barographs, but the one most suitable for the role of a “reference” gauge is the barograph IS30, because its location is the closest to where the deep-sea observatories for DONET and deep-water tsunami detectors for DART (21418, 21420) are established.
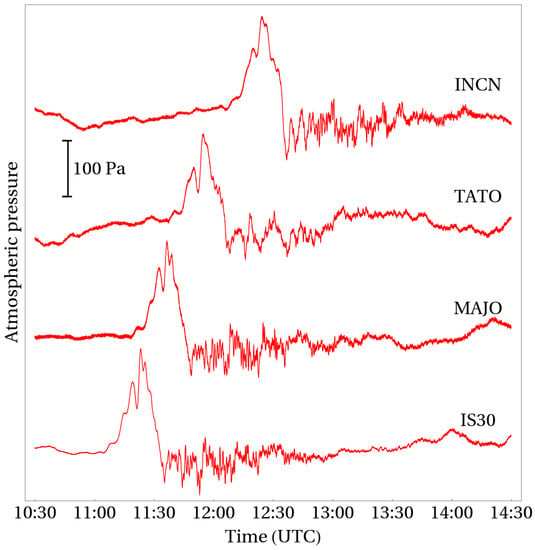
Figure 6.
Oscillations of the atmospheric pressure registered by barographs in the vicinity of the Japanese islands on 15.01.2022 during passage of the Lamb wave.
As we noted in [6], of the 33 deep-water tsunami detectors, DART, that were functioning on 15 January 2022, only 9 stations registered the event, including its initial phase, with a sampling rate not worse than . The resolution of the remaining stations amounted to , or the data included significant gaps, which rendered interpretation of the signals impossible. Only two DART stations (21418, 21420), located in the vicinity of the Japanese islands, recorded a signal with a reasonable sampling rate—their locations are indicated in Figure 5 by green triangles. These stations were established at depths of (21418) and (21420). The official site of the DART system (https://www.ndbc.noaa.gov/ (accessed on 1 February 2022)) presents the bottom pressure in meters of the water column. We recalculated the pressure in Pascals, making use of the constant indicated at this site. The signals were de-tided by subtraction of the trend represented by a polynomial. The sampling interval of bottom pressure variations recorded by DART stations was . The signals registered are presented in Figure 7.
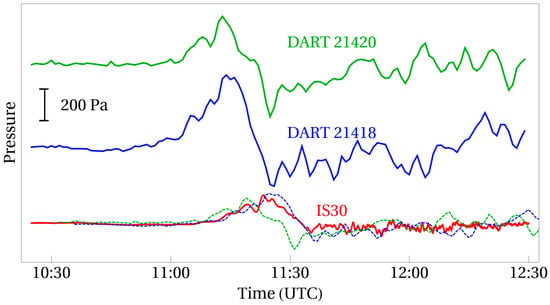
Figure 7.
Variations of pressure registered by DART stations at the ocean bottom (blue and green solid lines) and by barograph IS30 in the atmosphere (red solid line). The blue and green dotted lines show variations of the bottom pressure multiplied by the correcting coefficient and shifted in time by , where is the difference in distance (geo-distance) from the Hunga Tonga–Hunga Ha’apai volcano to the barograph IS30 and from the Hunga Tonga–Hunga Haʻapai volcano to the DART station.
The location of the DONET system is shown in Figure 5 by yellow diamonds. Manifestations of the volcanic explosion were successfully registered by 44 pressure gauges (PGs) of the DONET system, which were located at depths between 1077 and . Variations of the bottom pressure were registered with a sampling frequency of . The original signals were processed applying a Gaussian filter with a kernel of radius 10 sampling intervals (=1 s) and downsampled to . Then, the signals were de-tided by subtraction of the trend represented by a polynomial. Ten examples of PGs/DONET records are presented in Figure 8. The complete set of records from all 44 PGs can be found in the Supporting Information (Figures S2–S45).
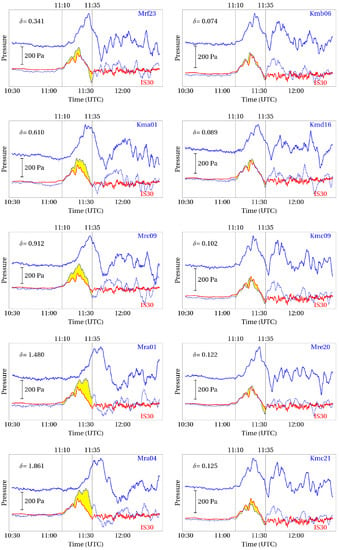
Figure 8.
Variations of pressure, registered by PG/DONET (blue solid line) at the ocean bottom and by the barograph IS30 in the atmosphere (red solid line). The blue dotted line shows variations of the bottom pressure multiplied by the correcting coefficient and shifted in time by , where is the difference in distance (geo-distance) from the Hunga Tonga–Hunga Ha’apai volcano to the barograph IS30 and from the Hunga Tonga–Hunga Ha’apai volcano to the DONET station. The yellow fill shows the difference between the red and blue dotted lines during passage of the positive phase of the Lamb wave. The values of parameter are indicated in each of the fragments of the figure.
4. Analysis and Interpretation of Observational Data
The blue and green solid curves in Figure 7 represent the variations of bottom pressure recorded by DART21418 and DART21420 stations, respectively. Atmospheric pressure fluctuations recorded by the IS30 ground barograph are shown by the red curve. Despite the fact that the pressure variations at the ocean floor were recorded with a sampling rate, which was significantly less than for atmospheric pressure, it is clearly seen from the figure that the first positive inputs of signals at the ocean floor repeat in shape the first positive phase of the Lamb atmospheric wave, including the details of the wave profile. It is important to note that the amplitude of pressure variations at the ocean floor is approximately two times higher than the amplitude of atmospheric pressure fluctuations. In other words, manifestation of the atmospheric Lamb wave at the bottom of the ocean is amplified.
From the map showing the relief of the ocean floor (Figure 5), it can be concluded that the stations DART21418 and DART21420 are located on more or less flat sections of the bottom at a considerable distance from the mainland slope. In Section 2, it was theoretically shown (see Figure 4) that a forced disturbance recorded by pressure fluctuations at the ocean floor is distorted by free gravity waves that arise when a Lamb wave passes over an underwater slope, only if the slope is located close enough, i.e., no farther than from the pressure recorder (forward in the direction of propagation of the atmospheric wave). It can be seen from Figure 5 that the two DART stations under consideration are located at significantly longer distances from the mainland slope, namely, at several hundred . Consequently, the influence of the continental slope on the forced wave in this case is certainly excluded.
The insets in Figure 5 show the depth profiles along the atmospheric wave propagation “tracks” (green lines on the map). By “track” we mean the arc of the great circle passing through the volcano Hunga Tonga–Hunga Haʻapai and the registering station. From the depth profile for the DART21418 station, it can be seen that for at least the ocean depth along the track is approximately and the ocean floor is practically flat, even if individual relief inhomogeneities are encountered. With the use of Formula (25), it is possible to estimate the time, , and distance, , required for complete establishment of a forced perturbation in the ocean at a depth (the depth at which the DART21418 station is located). In the case of the propagation velocity and wavelength of the Lamb wave, equal, respectively, to and , we obtain . We can assume formation of the forced perturbation to be actually fully completed when approaching DART21418.
For the DART21420 station, the situation is not as ideal. The depth profile shows that the track crosses an underwater ridge, from the foot of which to the station there is only approximately of a more or less even bottom, with an average ocean depth of approximately . For the ocean depth corresponding to the setting depth of DART21420 (), the distance of complete establishment of the forced perturbation is estimated by the value . However, taking into account that the amplitude of the forced wave is established twice as fast (see Section 2), we can expect that in this case the influence of free waves on the forced disturbance will not be fundamental.
As for small inhomogeneities of the bottom, free gravity waves of significant amplitude cannot form on them during the passage of the Lamb wave. There are at least three reasons for this. First, as the depth difference decreases, the amplitude of free waves tends to zero, which directly follows from Formulas (19) and (20). Secondly, if the horizontal size of the bottom inhomogeneity (for instance, a narrow underwater ridge) is significantly less than the Lamb wavelength, then the free waves formed on the left and right slopes will have different signs and will compensate each other during interference. Thirdly, in a real spatial problem, free waves that have arisen on a localized bottom inhomogeneity (for instance, a local underwater hill) will attenuate with distance from the inhomogeneity due to geometric divergence.
In Section 2, it was shown that, in the idealized case, when the Lamb wave passes over a flat horizontal bottom, the relationship between atmospheric and bottom pressure fluctuations is described by Formula (8). It follows from this formula that the waveshapes in the atmosphere and at the ocean floor are identical, while their amplitudes differ by the factor .
The blue and green dotted lines in Figure 7 show the bottom pressure variations multiplied by the correction factor , where is the ocean depth at the location of the DART station. The values of the correction coefficients at are and . The signals registered by DART were also shifted in time based on the difference in distances between the Hunga Tonga–Hunga Ha’apai volcano and the pressure recording points. Compared to the IS30 barograph, the DART21418 station is located closer to the volcano, and the DART21420 station is closer. When calculating the time shift, the propagation velocity of the Lamb wave, , was used. The time shift for the DART21418 signal was , and for the DART21420 it was . As a result of the amplitude transformation and the signal shift in time, we restore the course of atmospheric pressure at the location of the IS30 barograph. Signals reconstructed from DART21418 and DART21420 data are shown by dotted blue and green lines, respectively. It can be concluded from the figure that the blue dotted line (DART21418), as could be expected from the theoretical concepts, happens to be very close to the red curve showing the evolution of atmospheric pressure.
For the green dotted line (DART21420), the match is not so good. At a first glance, one could assume an error in the positioning of the recording stations and additionally shift the green dotted curve in time, thereby achieving better agreement, but the required shift is approximately . During this time, the Lamb wave travels over . Such an error in determining the position of the recording stations seems quite unlikely. Most likely, in this case, the forced disturbance interferes with free waves formed on the slopes of an underwater ridge, the distance to the foot of which amounts to approximately (). When entering deep water, free waves have a negative polarity; therefore, they should reduce the amplitude of the recorded signal (see Supporting Information, Videos S2 and S4). Because the distance between the foot of the underwater ridge and the location of the DART21420 station is still quite significant, the forced disturbance interferes with free waves mainly in the tail part of its signal—after 11:20 UTC.
Figure 8 shows 10 examples of signals recorded by DONET deep-sea observatories. A complete set of illustrations for all 44 observatories is presented in the Supporting Information (Figures S2–S45). Despite the fact that, unlike DART stations, the DONET system is located in an area of variable depth (Figure 9), the waveshapes recorded at the ocean floor and in the atmosphere are also close in many cases.
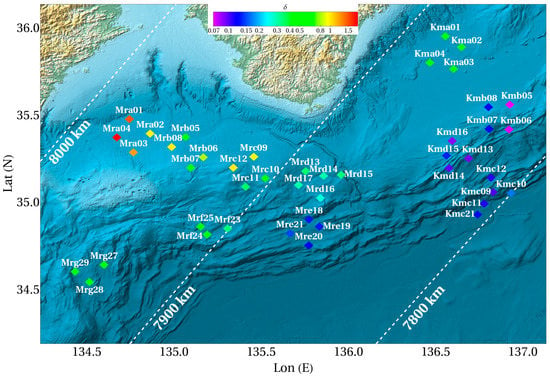
Figure 9.
Bottom relief in the area of the location of the deep-sea observatories DONET (colored diamonds). The color of the diamond corresponds to the value of the quantity, , that characterizes the difference between the observed signal and the theoretically calculated forced perturbation. The color scale is shown at the top of the picture. The white dotted lines showing the distance from the Hunga Tonga–Hunga Ha’apai volcano are constructed at intervals of .
The signals registered by PGs/DONET were processed in the same way as was done for DART stations (multiplication by a correction factor, , calculated by the depth of the ocean at the DONET observatory location, and the signal time shift depending on the distance between the recorders and the volcano). It can be seen from Figure 8 that the blue dotted curves obtained as a result of processing in some cases correspond very well to the red curves showing the behavior of the atmospheric pressure. During passage of the positive phase of the Lamb wave (from 11:10 to 11:35 UTC), the difference between the curves is highlighted with a yellow fill. As a quantitative measure of the difference between the waveshapes, the value was calculated according to Formula (27). The values of the quantity, , for each observatory are shown in the figure.
Figure 9 shows a map with the location of all 44 DONET observatories that successfully recorded variations in bottom pressure during the passage of the Lamb wave. Stations are shown with diamonds, the color of which varies depending on the value of the quantity, . The color scale is shown at the top of the picture. It can be seen that the color distribution of the stations is not random, but quite natural. Minimum values of are observed in the lower part of the slope (Mre and Kmc) and in the eastern part of the region, including the deep-water plateau (Kmb, Kmd). In these cases, the free wave formed over the underwater slope either has not yet managed to distort the forced disturbance, or this distortion is insignificant due to a relatively small depth difference (from to ). For observatories located higher up the slope (Mrg, Mrf, Mrd, Kma), the value of increases up to , which indicates a noticeable contribution of free waves to variations in the bottom pressure. Finally, for the shallowest observatories (Mrc, Mrb, Mra), the value of reaches 1 or more, which indicates the predominant contribution of free gravity waves to variations in the bottom pressure.
If we compare the full-scale data presented in Figure 8 and the results of a numerical experiment shown in Figure 4, then synthetic and measured in situ variations of the bottom pressure can have common features. On the abyssal plain far from the mainland slope, the first performance, which is recorded by the bottom pressure sensor, belongs to a forced disturbance. This perturbation, due to its proximity to the conditions of the Proudman resonance, gives a predominant contribution to the observed signal. At the foot of the continental slope and in its lower part—still at sufficiently great depths—the forced disturbance continues to play a leading role, but it is already distorted by free waves, which somewhat increase the amplitude of the observed signal. However, the main free waves formed near the shore appear on the record much later, and they are comparable in amplitude to a forced perturbation. At shallow depths—near the shore—the forced perturbation makes a negligible contribution to variations in the bottom pressure; in this area, the main contribution is due to free gravity waves, and the forced perturbation is actually lost against the background of free waves.
5. Discussion
The paper analyzes the long-wavelength response of the water layer to the atmospheric Lamb wave caused by the explosion of a volcano. It is shown that the response of the water layer is a superposition of forced perturbation and free gravity waves. The shape of the forced perturbation repeats the shape of the atmospheric wave. The amplitude of the forced perturbation essentially depends on the ratio of the propagation velocity of an atmospheric wave and the velocity of long waves, which is determined by the depth of the ocean. Free waves arise as a result of the restructuring of a forced perturbation when the ocean depth changes. For an abrupt change in depth, explicit analytical formulas are presented that describe the amplitude and energy of free gravity waves. The formulas can be used to verify numerical models. It is shown that the time required for the forced perturbation to be settled is proportional to the ratio of the atmospheric wavelength to the difference between the velocities of the atmospheric wave and long waves in the ocean.
With the aid of numerical simulation, it has been established that the amplitude and energy of free gravity waves arising on an underwater slope of finite length, , and traveling in the direction of propagation of an atmospheric perturbation depend weakly on the length of the slope up to . With a further increase in the length of the slope, the amplitude and energy of free waves both begin to decrease. For free waves traveling in the opposite direction (against the atmospheric wave), the finite length of the underwater slope begins to weaken their amplitude and energy, starting from . For short slopes (), the amplitude and energy of free waves can be estimated using the analytical formulas obtained for an abrupt change in depth.
Manifestations of the atmospheric Lamb wave caused by the explosion of the Hunga Tonga–Hunga Ha’apai volcano on 15 January 2022 were analyzed on the basis of data from atmospheric and bottom pressure recorders located in the region of the Japanese Islands (4 ground-based barographs, 2 DART stations, and 44 DONET observatories). The bottom pressure gauges located on the vast abyssal plain (DART21418) and in the deep part of the continental slope (DONET: Mre, Kmc, Kmd, Kmb) were found to record pressure variations similar in shape to the Lamb wave in the atmosphere. The amplitude of bottom pressure variations has always noticeably exceeded the amplitude of atmospheric pressure fluctuations. It is shown that in these cases the ratio of the amplitudes corresponds to the theoretical value, which is true for the following forced perturbation: , where is the propagation velocity of the Lamb wave and is the ocean depth at the pressure gauge location.
For bottom pressure gauges located at a short distance from large ocean floor landforms along the propagation of the Lamb wave (DART21420), in the upper part of the continental slope (DONET: Mrg, Mrf, Mrd) or in a relatively shallow area closer to the coast (DONET: Mra, Mrb, Mrc, Kma), the free gravity waves formed during the passage of the Lamb wave over underwater slopes are superimposed on the forced wave. In these cases, no equivalence of the signal shapes recorded at the bottom and in the atmosphere is observed.
It should be noted that, according to Formula (15), the amplitude of the forced perturbation tends to zero near the shore (when the ocean depth tends to zero), while the amplitude of the free gravity waves remains significant or even increases near the shore. Due to this fact, to assess the tsunami hazard from signals recorded by bottom pressure sensors it is important to have an easy-to-use method for isolating free gravity waves. The theoretical concepts presented in this paper and the analysis of in situ data allow us to propose the following method. From the initial series of bottom pressure variations, one should subtract the record of atmospheric pressure fluctuations in the Lamb wave, multiplied by . Thus, the component corresponding to the forced perturbation is excluded from the bottom pressure variations, and the signal that remains corresponds to free gravity waves. It should be noted that the described method is easily algorithmized, which makes it possible, in principle, to use it in the tsunami early warning mode. The only necessary condition for the application of this method is the presence of a Lamb wave record made by a barograph in the region under consideration.
We see further development of the issue under consideration in spatial numerical modeling of the response of the water layer to the atmospheric Lamb wave. The main goals of such modeling are assumed to be reproduction of bottom pressure variations at the locations of bottom PGs, comparison of simulation results with recorded signals, and development of the proposed method for extracting free gravity waves from signals recorded by bottom pressure sensors.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15123071/s1, Figure S1: Position of deep-sea observatories DONET (yellow diamonds). The white dotted lines showing distances from the volcano Hunga Tonga–Hunga Ha’apai are drawn with an interval of 500 km. The insets show the depth profiles constructed along arcs of the large circle drawn by green lines; Figures S2–S45: Variations of pressure, registered by PG/DONET (blue solid line) at the ocean bottom and by the barograph IS30 in the atmosphere (red solid line). The blue dotted line shows variations of the bottom pressure multiplied by the correcting coefficient and shifted in time by , where is the difference in distance (geo-distance) from the Hunga Tonga–Hunga Ha’apai volcano to the barograph IS30 and from the Hunga Tonga–Hunga Ha’apai volcano to the DONET station. The yellow fill shows the difference between the red and blue dotted lines during the passage of the positive phase of the Lamb wave. Values of parameter are indicated in each of the fragments of the figure; Table S1: Locations of the DONET stations and the value δ for each station, calculated using Formula (27); Video S1: Formation of free gravity waves when an atmospheric pressure wave crosses a depth jump for the case of “from deep to shallow” (, ). The bottom relief is schematically (not to scale) shown by a dark fill. The atmospheric pressure wave is shown by the red curve. The celestial blue fill presents the results of numerical simulation and the dotted curves are calculated by analytic Formulas (15)–(18). The blue dotted line represents forced waves and the purple dotted line is for free waves. Calculations were performed for , and ; Video S2: Formation of free gravity waves when an atmospheric pressure wave crosses a depth jump for the case of “from shallow to deep” (, ). The bottom relief is schematically (not to scale) shown by a dark fill. The atmospheric pressure wave is shown by the red curve. The celestial blue fill presents the results of numerical simulation and the dotted curves are calculated by analytic Formulas (15)–(18). The blue dotted line represents forced waves, the purple dotted line is for free waves. Calculations were performed for , and ; Video S3: Influence of the bottom slope on the formation of free gravity waves when an atmospheric pressure wave crosses a depth reduction from to . The bottom relief is schematically shown (not to scale) by the dark fill, the slope length is in km. The atmospheric pressure wave is shown by the red curve. The celestial blue fill represents the results of numerical simulation, the dotted lines are calculated by analytic Formulas (15)–(18) obtained for the depth jump case. The blue dotted line corresponds to forced waves and the purple one corresponds to free waves. Calculations were performed for , and ; Video S4: Influence of the bottom slope on the formation of free gravity waves when an atmospheric pressure wave crosses a depth enhancement from to . The bottom relief is schematically shown (not to scale) by the dark fill, the slope length is in km. The atmospheric pressure wave is shown by the red curve. The celestial blue fill represents the results of numerical simulation, and the dotted lines are calculated by analytic Formulas (15)–(18) obtained for the depth jump case. The blue dotted line corresponds to forced waves and the purple one corresponds to free waves. Calculations were performed for , and .
Author Contributions
Conceptualization, M.A.N.; methodology, M.A.N.; software, M.A.N. and S.V.K.; validation, M.A.N. and S.V.K.; formal analysis, M.A.N. and K.A.S.; investigation, M.A.N.; resources, M.A.N. and K.A.S.; data curation, K.A.S. and S.V.K.; writing—original draft preparation, M.A.N.; writing—review and editing, M.A.N., S.V.K. and S.V.K.; visualization, M.A.N. and S.V.K.; supervision, M.A.N.; project administration, M.A.N.; funding acquisition, K.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 22-27-00415, https://rscf.ru/en/project/22-27-00415/ (accessed on 13 May 2023).
Data Availability Statement
In this study, we used the bottom pressure records of the Dense Ocean floor Network system for Earthquakes and Tsunamis (DONET), which can be downloaded from the web-site of the National Research Institute for Earth Science and Disaster Resilience (https://doi.org/10.17598/nied.0008, accessed on 31 January 2022); the bottom pressure records of the Deep ocean Assessment and Reporting of Tsunami system (DART), which can be downloaded from the from National Data Buoy Center web-site (https://www.ndbc.noaa.gov/ (accessed on 1 February 2022)); and also we used the observation data of four land-based barographs, three of which (MAJO, TATO, INCN) belong to the IRIS network (http://ds.iris.edu/ds/ (accessed on 25 January 2022)) and the fourth one (IS30) to The International Monitoring System Infrasound Network/CTBTO.
Acknowledgments
We are grateful to NIED, NOAA, IRIS, CTBTO, and S.N. Kulichkov for the provided observation data.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Amores, A.; Monserrat, S.; Marcos, M.; Argüeso, D.; Villalonga, J.; Jordà, G.; Gomis, D. Numerical simulation of atmospheric Lamb waves generated by the 2022 Hunga-Tonga volcanic eruption. Geophys. Res. Lett. 2022, 49, e2022GL098240. [Google Scholar] [CrossRef]
- Solovieva, M.S.; Padokhin, A.M.; Shalimov, S.L. Mega-Eruption of the Hunga Volcano on January 15, 2022: Detection of Ionospheric Perturbations by VLF and GNSS Radio Sounding. JETP Lett. 2022, 116, 846–851. [Google Scholar] [CrossRef]
- Kubota, T.; Saito, T.; Nishida, K. Global fast-traveling tsunamis driven by atmospheric Lamb waves on the 2022 Tonga eruption. Science 2022, 377, 91–94. [Google Scholar] [CrossRef]
- Matoza, R.S.; Fee, D.; Assink, J.D.; Iezzi, A.M.; Green, D.N.; Kim, K.; Toney, L.; Lecocq, T.; Krishnamoorthy, S.; Lalande, J.-M.; et al. Atmospheric waves and global seismoacoustic observations of the January 2022 Hunga eruption, Tonga. Science 2022, 377, 95–100. [Google Scholar] [CrossRef]
- Kulichkov, S.N.; Chunchuzov, I.P.; Popov, O.E.; Gorchakov, G.I.; Mishenin, A.A.; Perepelkin, V.G.; Bush, G.A.; Skorokhod, A.I.; Vinogradov, Y.A.; Semutnikova, E.G.; et al. Acoustic-Gravity Lamb Waves from the Eruption of the Hunga-Tonga-Hunga-Hapai Volcano, Its Energy Release and Impact on Aerosol Concentrations and Tsunami. Pure Appl. Geophys. 2022, 179, 1533–1548. [Google Scholar] [CrossRef]
- Nosov, M.A.; Sementsov, K.A.; Kolesov, S.V.; Pryadun, V.V. The Volcanogenic Tsunami on January 15, 2022, Based on the Records of Deep-Ocean DART Stations. Dokl. Earth Sci. 2022, 507, 904–908. [Google Scholar] [CrossRef]
- Nosov, M.A.; Sementsov, K.A.; Kolesov, S.V.; Pryadun, V.V. Atmospheric Lamb Wave Manifestations in Bottom Pressure Variations. Mosc. Univ. Phys. Bull. 2022, 77, 896–904. [Google Scholar] [CrossRef]
- Soloviev, S.L. The tsunami problem and its significance for Kamchatka and the Kuril Islands. In The Tsunami Problem; Nauka: Moscow, Russia, 1968; pp. 7–50. (In Russian) [Google Scholar]
- Jaque, V.M.; Soloviev, S.L. Remote registration of tsunami type weak waves on the shelf of the Kuril Islands. Dokl. Akad. Nauk USSR 1971, 198, 816–817. (In Russian) [Google Scholar]
- Rabinovich, A.B.; Eblé, M.C. Deep-ocean measurements of tsunami waves. Pure Appl. Geophys. 2015, 172, 3281–3312. [Google Scholar] [CrossRef]
- Levin, B.W.; Nosov, M.A. Physics of Tsunamis, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Mulia, I.E.; Satake, K. Developments of Tsunami observing systems in Japan. Front. Earth Sci. 2020, 8145. [Google Scholar] [CrossRef]
- Kaneda, Y. The advanced ocean floor real time monitoring system for mega thrust earthquakes and tsunamis-application of DONET and DONET2 data to seismological research and disaster mitigation. In OCEANS 2010; MTS/IEEE SEATTLE: Seattle, WA, USA, 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Kaneda, Y.; Kawaguchi, K.; Araki, E.; Matsumoto, H.; Nakamura, T.; Kamiya, S.; Ariyoshi, K.; Hori, T.; Baba, T.; Takahashi, N. Development and application of an advanced ocean floor network system for megathrust earthquakes and tsunamis. In Seafloor Observatories; Springer: Berlin/Heidelberg, Germany, 2015; pp. 643–662. [Google Scholar]
- Mofjeld, H.O. Tsunami measurements. In The Sea; Robinson, A., Bernard, E., Eds.; Harvard University Press: Cambridge, MA, USA, 2009; Volume 15, pp. 201–235. [Google Scholar]
- Mungov, G.; Eblé, M.; Bouchard, R. DART tsunameter retrospective and real-time data: A reflection on 10 years of processing in support of tsunami research and operations. Pure Appl. Geophys. 2013, 170, 1369–1384. [Google Scholar] [CrossRef]
- Lynett, P.; McCann, M.; Zhou, Z.; Renteria, W.; Borrero, J.; Greer, D.; Fa’anunu, O.; Bosserelle, C.; Jaffe, B.; La Selle, S.; et al. Diverse tsunamigenesis triggered by the Hunga Tonga-Hunga Ha’apai eruption. Nature 2022, 609, 728–733. [Google Scholar] [CrossRef]
- Gusman, A.R.; Roger, J.; Noble, C.; Wang, X.; Power, W.; Burbidge, D. The 2022 Hunga Tonga-Hunga Ha’apai Volcano Air-Wave Generated Tsunami. Pure Appl. Geophys. 2022, 179, 3511–3525. [Google Scholar] [CrossRef]
- Pakoksung, K.; Suppasri, A.; Imamura, F. The near-field tsunami generated by the 15 January 2022 eruption of the Hunga Tonga-Hunga Ha’apai volcano and its impact on Tongatapu, Tonga. Sci. Rep. 2022, 12, 15187. [Google Scholar] [CrossRef]
- Kubo, H.; Kubota, T.; Suzuki, W.; Aoi, S.; Sandanbata, O.; Chikasada, N.; Ueda, H. Ocean-wave phenomenon around Japan due to the 2022 Tonga eruption observed by the wide and dense ocean-bottom pressure gauge networks. Earth Planets Space 2022, 74, 104. [Google Scholar] [CrossRef]
- Mizutani, A.; Yomogida, K. Source estimation of the tsunami later phases associated with the 2022 Hunga Tonga volcanic eruption. Geophys. J. Int. 2023, 234, 1885–1902. [Google Scholar] [CrossRef]
- Chikasada, N.Y. Consideration of meteotsunami real-time forecasting method using high quality atmospheric and ocean bottom pressure records. In Proceedings of the 2023 IEEE Underwater Technology (UT), Tokyo, Japan, 6–9 March 2023; IEEE: Tokyo, Japan, 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, Y.; Imai, K.; Kusumoto, S.; Takahashi, N. Tsunami early warning of the Hunga volcanic eruption using an ocean floor observation network off the Japanese Islands. Seism. Res. Lett. 2023, 94, 567–577. [Google Scholar] [CrossRef]
- Kanazawa, T. Japan Trench earthquake and tsunami monitoring network of cable-linked 150 ocean bottom observatories and its impact to earth disaster science. In Proceedings of the 2013 IEEE International Underwater Technology Symposium (UT), Tokyo, Japan, 5–8 March 2013; IEEE: Tokyo, Japan, 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Tanioka, Y.; Yamanaka, Y.; Nakagaki, T. Characteristics of the deep sea tsunami excited offshore Japan due to the air wave from the 2022 Tonga eruption. Earth Planets Space 2022, 74, 61. [Google Scholar] [CrossRef]
- Watanabe, O.; Matsumoto, H.; Sugioka, H.; Mikada, H.; Suyehiro, K.; Otsuka, R. Offshore monitoring system records recent earthquake off Japan’s northernmost island. Eos Trans. Am. Geophys. Union 2004, 85, 14. [Google Scholar] [CrossRef]
- Nosov, M.A.; Kolesov, S.V. Elastic oscillations of water column in the 2003 Tokachi-oki tsunami source: In-situ measurements and 3-D numerical modelling. Hazards Earth Syst. Sci. 2007, 7, 243–249. [Google Scholar] [CrossRef]
- Nosov, M.A.; Karpov, V.A.; Kolesov, S.V.; Sementsov, K.A.; Matsumoto, H.; Kaneda, Y. Relationship between pressure variations at the ocean bottom and the acceleration of its motion during a submarine earthquake. Earth Planets Space 2018, 70, 100. [Google Scholar] [CrossRef]
- Saito, T.; Kubota, T. Tsunami modeling for the deep sea and inside focal areas. Ann. Rev. Earth Planet. Sci. 2020, 48, 121–145. [Google Scholar] [CrossRef]
- Nosov, M.A.; Moshenceva, A.V.; Kolesov, S.V. Horizontal motions of water in the vicinity of a tsunami source. Pure Appl. Geophys. 2013, 170, 1647–1660. [Google Scholar] [CrossRef]
- Bernard, E.; Wei, Y.; Tang, L.; Titov, V. Impact of near-field, deep-ocean tsunami observations on forecasting the 7 December 2012 Japanese tsunami. Pure Appl. Geophys. 2014, 171, 3483–3491. [Google Scholar] [CrossRef]
- Monserrat, S.; Vilibić, I.; Rabinovich, A.B. Meteotsunamis: Atmospherically induced destructive ocean waves in the tsunami frequency band. Nat. Hazards Earth Syst. Sci. 2006, 6, 1035–1051. [Google Scholar] [CrossRef]
- Vilibić, I.; Šepić, J.; Rabinovich, A.B.; Monserrat, S. Modern approaches in meteotsunami research and early warning. Front. Mar. Sci. 2016, 3, 57. [Google Scholar] [CrossRef]
- Rabinovich, A.B. Twenty-seven years of progress in the science of meteorological tsunamis following the 1992 Daytona Beach event. Pure Appl. Geophys. 2020, 177, 1193–1230. [Google Scholar] [CrossRef]
- Dogan, G.G.; Pelinovsky, E.; Zaytsev, A.; Metin, A.D.; Ozyurt Tarakcioglu, G.; Yalciner, A.C.; Yalciner, B.; Didenkulova, I. Long wave generation and coastal amplification due to propagating atmospheric pressure disturbances. Nat. Hazards 2021, 106, 1195–1221. [Google Scholar] [CrossRef]
- Proudman, J. The Effects on the Sea of Changes in Atmospheric Pressure. Geophys. Suppl. Mon. Notices R. Astr. Soc. 1929, 2, 197–209. [Google Scholar] [CrossRef]
- Suzuki, T.; Nakano, M.; Watanabe, S.; Tatebe, H.; Takano, Y. Mechanism of a meteorological tsunami reaching the Japanese coast caused by Lamb and Pekeris waves generated by the 2022 Tonga eruption. Ocean Modell. 2023, 181, 102153. [Google Scholar] [CrossRef]
- Paris, R. Source mechanisms of volcanic tsunamis. Philosoph. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140380. [Google Scholar] [CrossRef] [PubMed]
- Symons, G.J. The eruption of Krakatoa and subsequent phenomena. Q. J. R. Meteorol. Soc. 1888, 14, 301–307. [Google Scholar] [CrossRef]
- Press, F.; Harkrider, D. Air-sea waves from the explosion of Krakatoa. Science 1966, 154, 1325–1327. [Google Scholar] [CrossRef]
- Garrett, C.J.R. A theory of the Krakatoa tide gauge disturbances. Tellus 1970, 22, 43–52. [Google Scholar] [CrossRef]
- Choi, B.H.; Pelinovsky, E.N.; Kim, K.O.; Lee, J.S. Simulation of the trans-oceanic tsunami propagation due to the 1883 Krakatau volcanic eruption. Nat. Hazards Earth Syst. Sci. 2003, 3, 321–332. [Google Scholar] [CrossRef]
- Nosov, M.A.; Sementsov, K.A.; Kolesov, S.V.; Matsumoto, H.; Levin, B.W. Recording of gravity waves formed in the ocean by surface seismic waves during the earthquake of March 11, 2011, off the coast of Japan. Dokl. Earth Sci. 2015, 461, 408–413. [Google Scholar] [CrossRef]
- Sementsov, K.A.; Nosov, M.A.; Kolesov, S.V.; Karpov, V.A.; Matsumoto, H.; Kaneda, Y. Free gravity waves in the ocean excited by seismic surface waves: Observations and numerical simulations. J. Geophys. Res. Oceans 2019, 124, 8468–8484. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Kämpf, J. Ocean Modelling for Beginners: Using Open-Source Software; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nosov, M.A.; Sementsov, K.A. Calculation of the initial elevation at the tsunami source using analytical solutions. Izv. Atmos. Ocean. Phys. 2014, 50, 539–546. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).