Estimating Three-Dimensional Distribution of Leaf Area Using Airborne LiDAR in Deciduous Broad-Leaved Forest
Abstract
1. Introduction
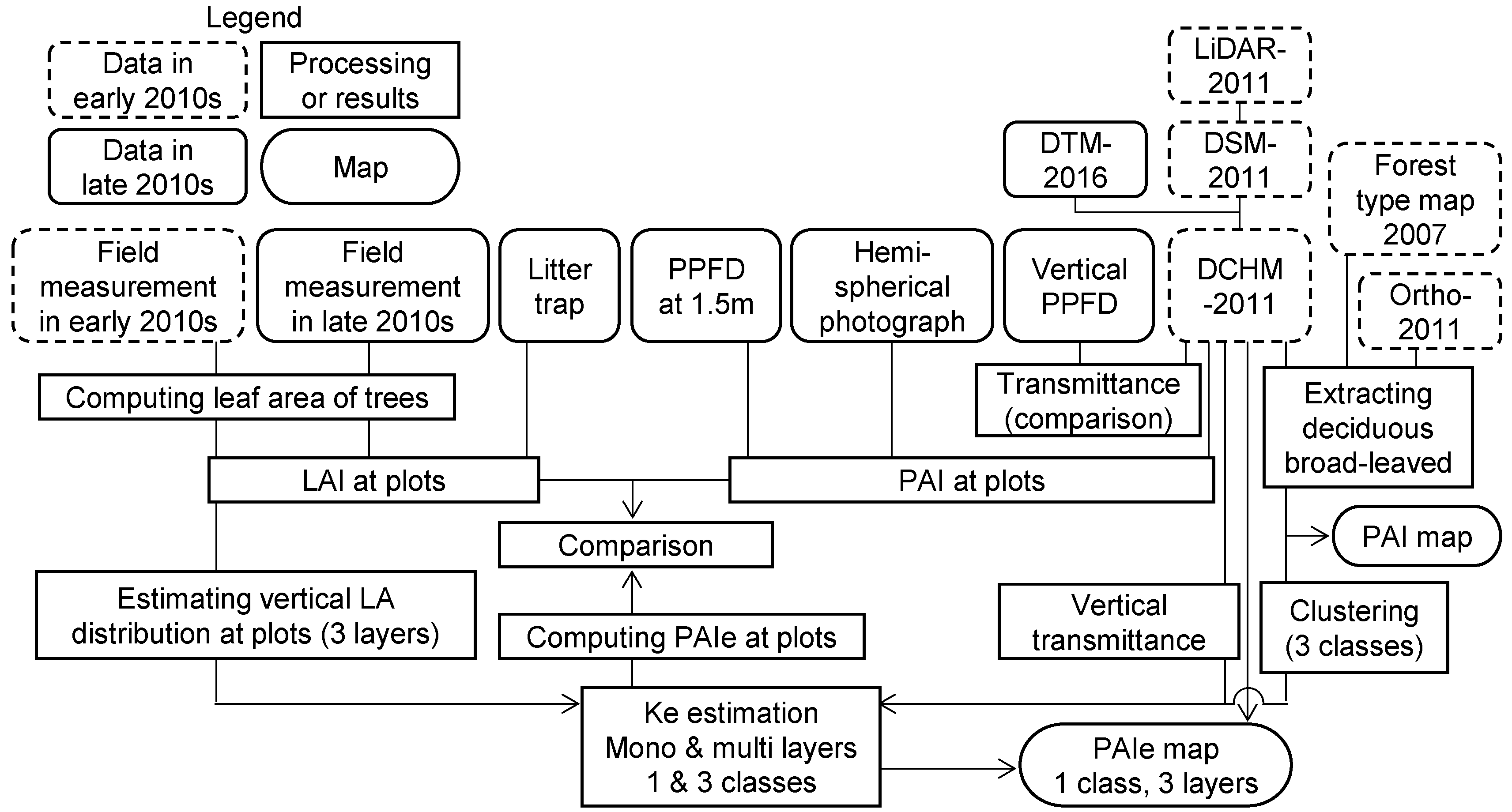
2. Materials and Methods
2.1. Study Site
2.2. Forest Plot Survey
2.3. Airbone LiDAR Data
2.4. Forest Type Map and Aerial Photography
2.5. Analysis
2.5.1. Estimation of Leaf Area Using Allometric Equations
2.5.2. Estimation of Vertical Leaf Area Distribution
2.5.3. LAI Measurement by Litter Trap
2.5.4. Effective PAI and Vertical Effective PAD Distribution Estimation
PPFD Measurement
Estimation of ePAI and Vertical Transmittance of PPFD
2.5.5. PAI Estimation Using Hemispherical Photographs
Taking Hemispherical Photos
Computing PAI
2.5.6. Estimation of ePAI and Vertical ePAD Distributions Using LiDAR Data
Pre-Processing
Summarizing the Number of Pulses in Cubes
ePAD Estimation Using the Beer–Lambert Law
Estimation of PAI and Vertical PAD Distribution Using LiDAR Data with an Empirically Estimated Ke
3. Results
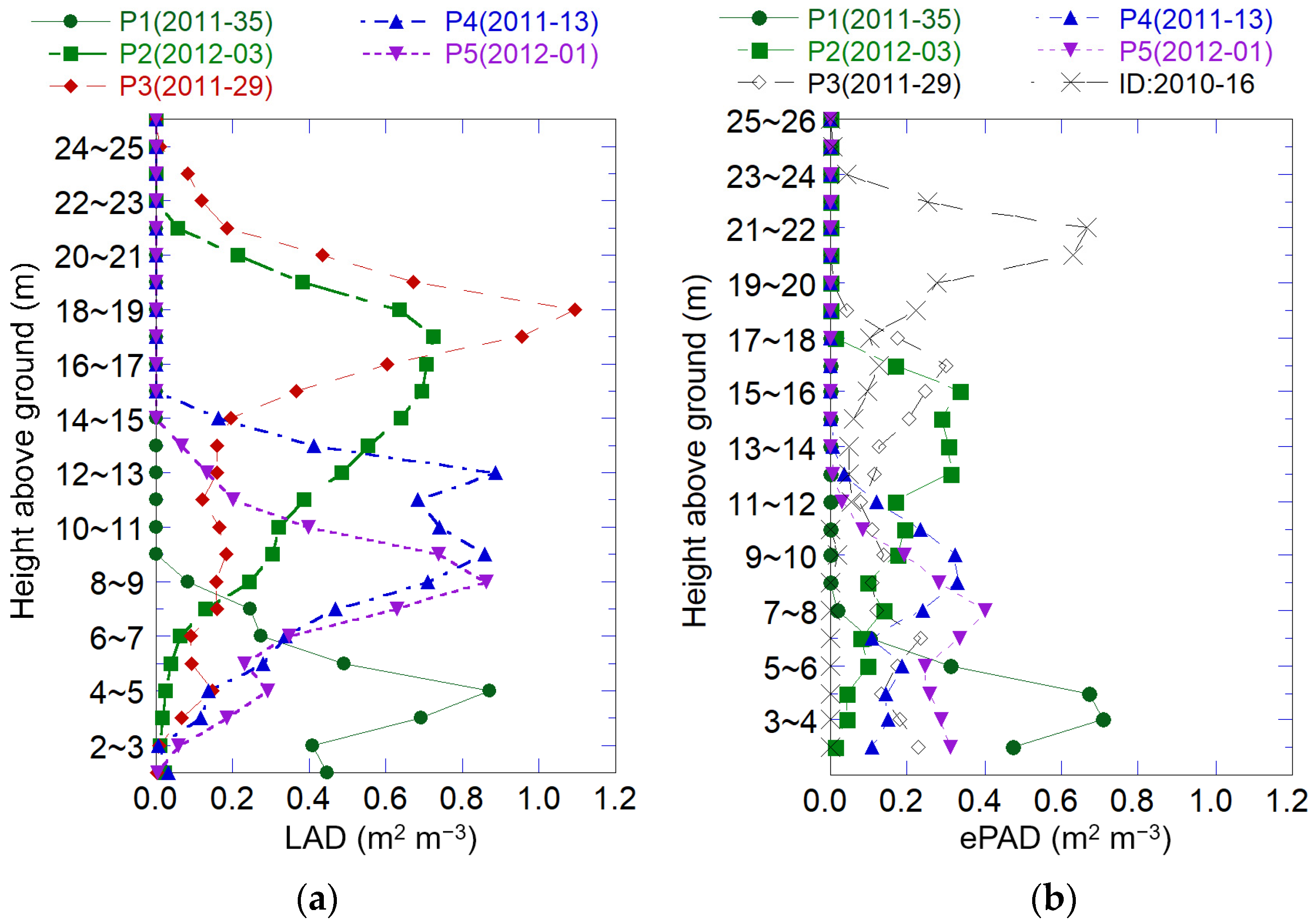
3.1. Vertical Leaf Area Distribution by Allometric and the Weibull Distribution Equation
3.2. LAI Estimation Using Collected Litter
3.3. ePAI Estimation by PPFD and PPFD Vertical Transmittance
3.4. PAI Estimated by Hemispherical Photography
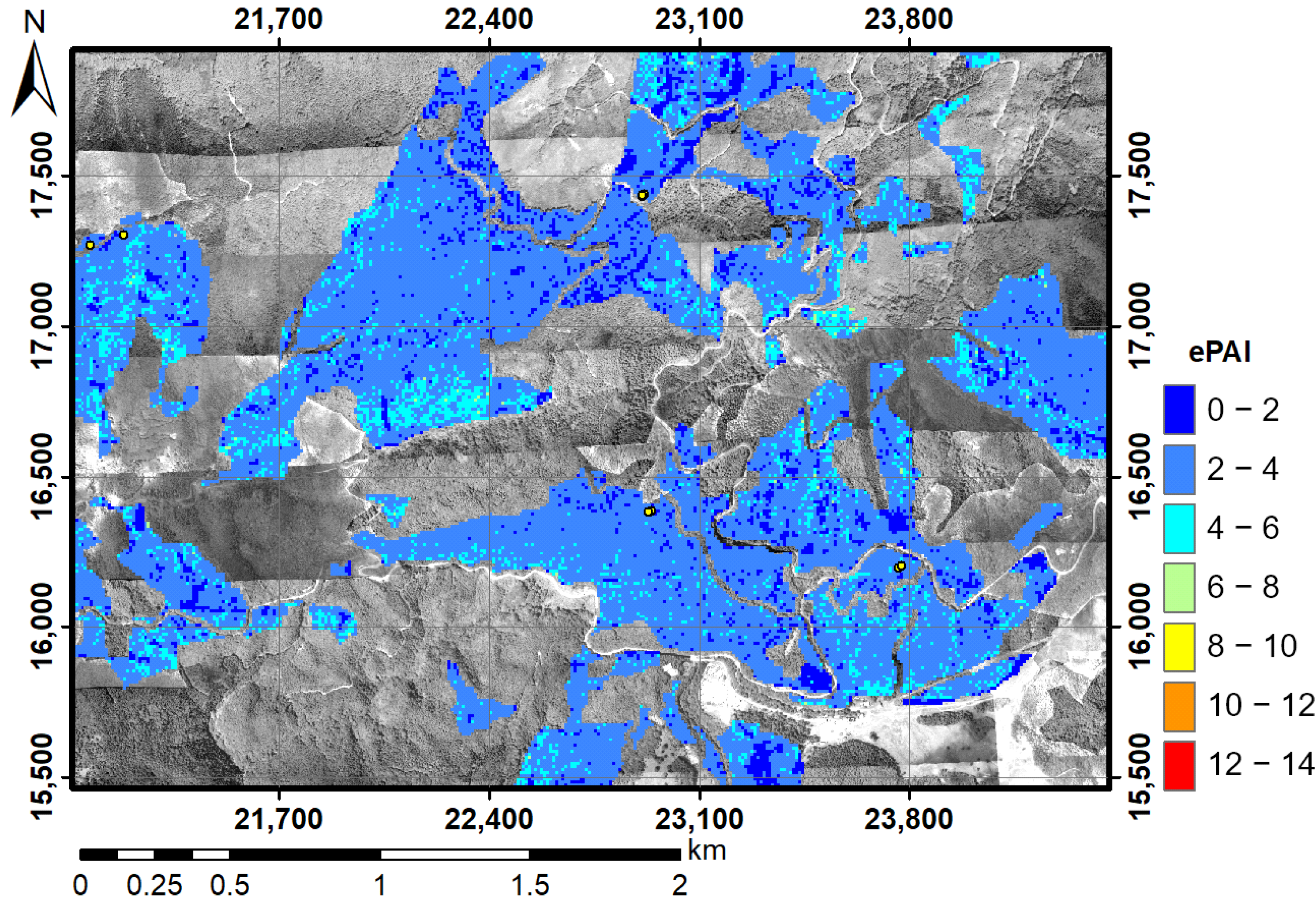
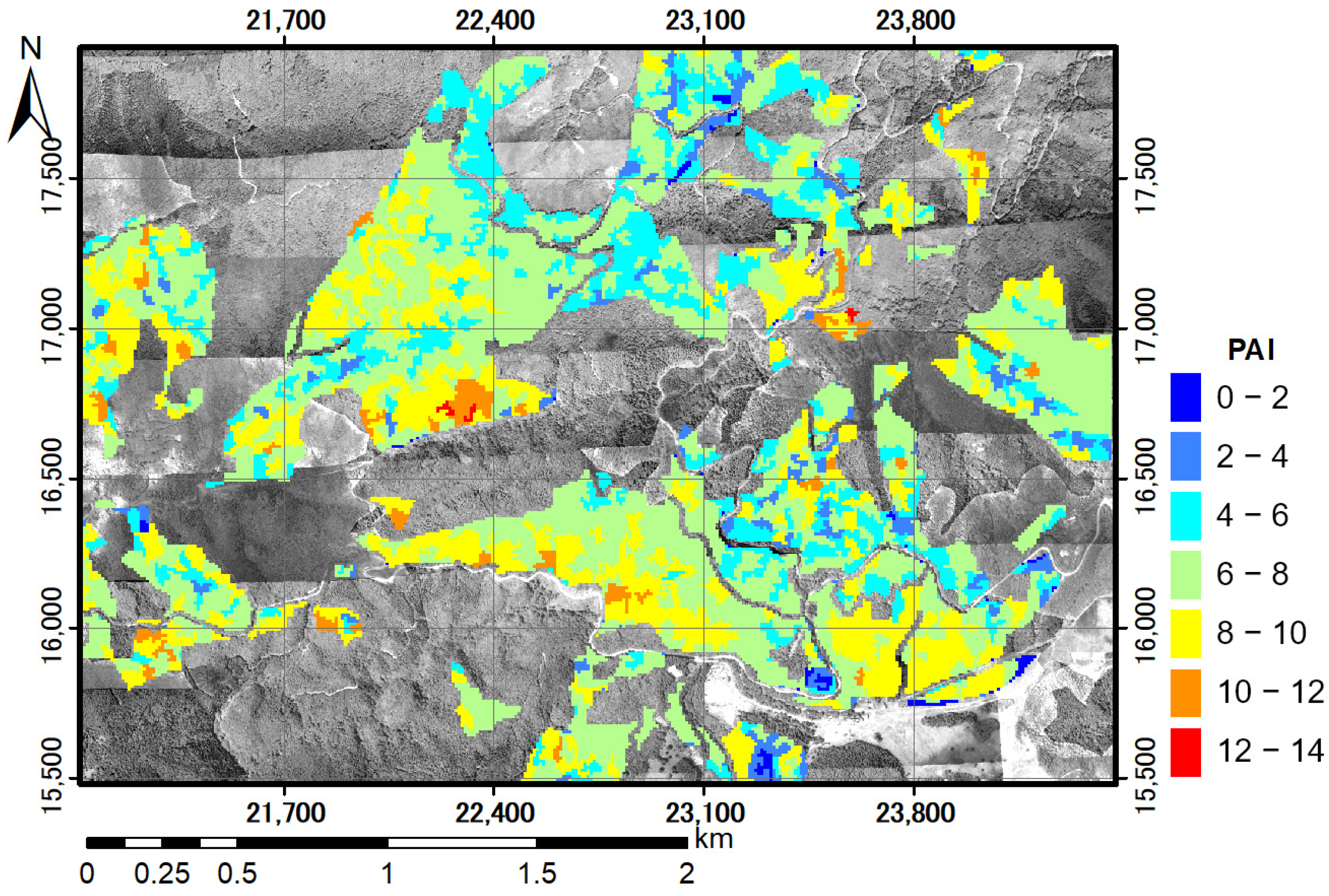
3.5. ePAI and Vertical ePAD Distribution Estimated by LiDAR Data
3.6. PAI Estimation Using LiDAR Data and Empirically Estimated Ke
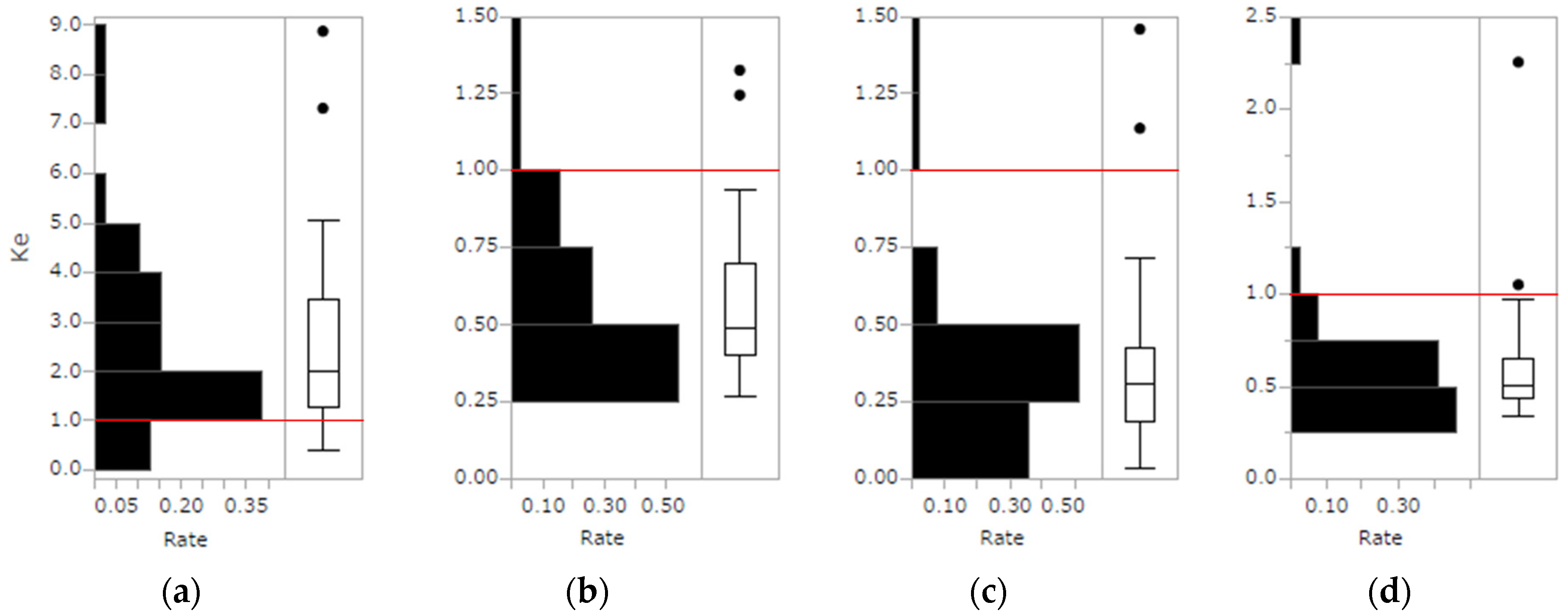
3.6.1. Estimating Ke
3.6.2. Forest Type Classification Map
3.6.3. Estimating Ke, PAI, and Vertical PAD Distribution
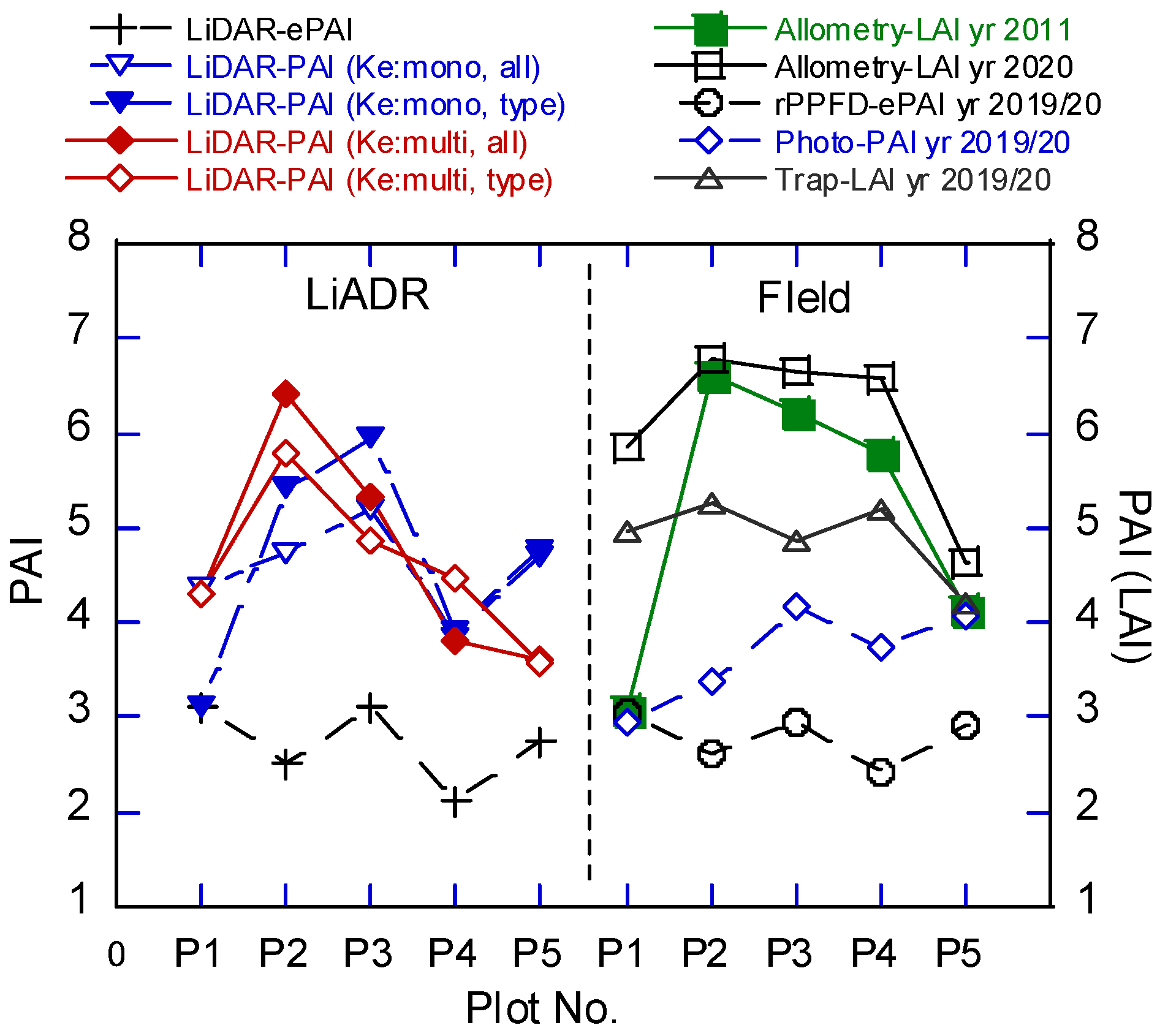
3.7. Comparison of Estimated LAI, Vertical LAD Estimation, PAI, and Vertical PAD Distribution
3.7.1. Comparison of Estimates Using Litter Traps and Plot Survey Data
3.7.2. Comparison of Estimates Using LiDAR and Forest Plot Data
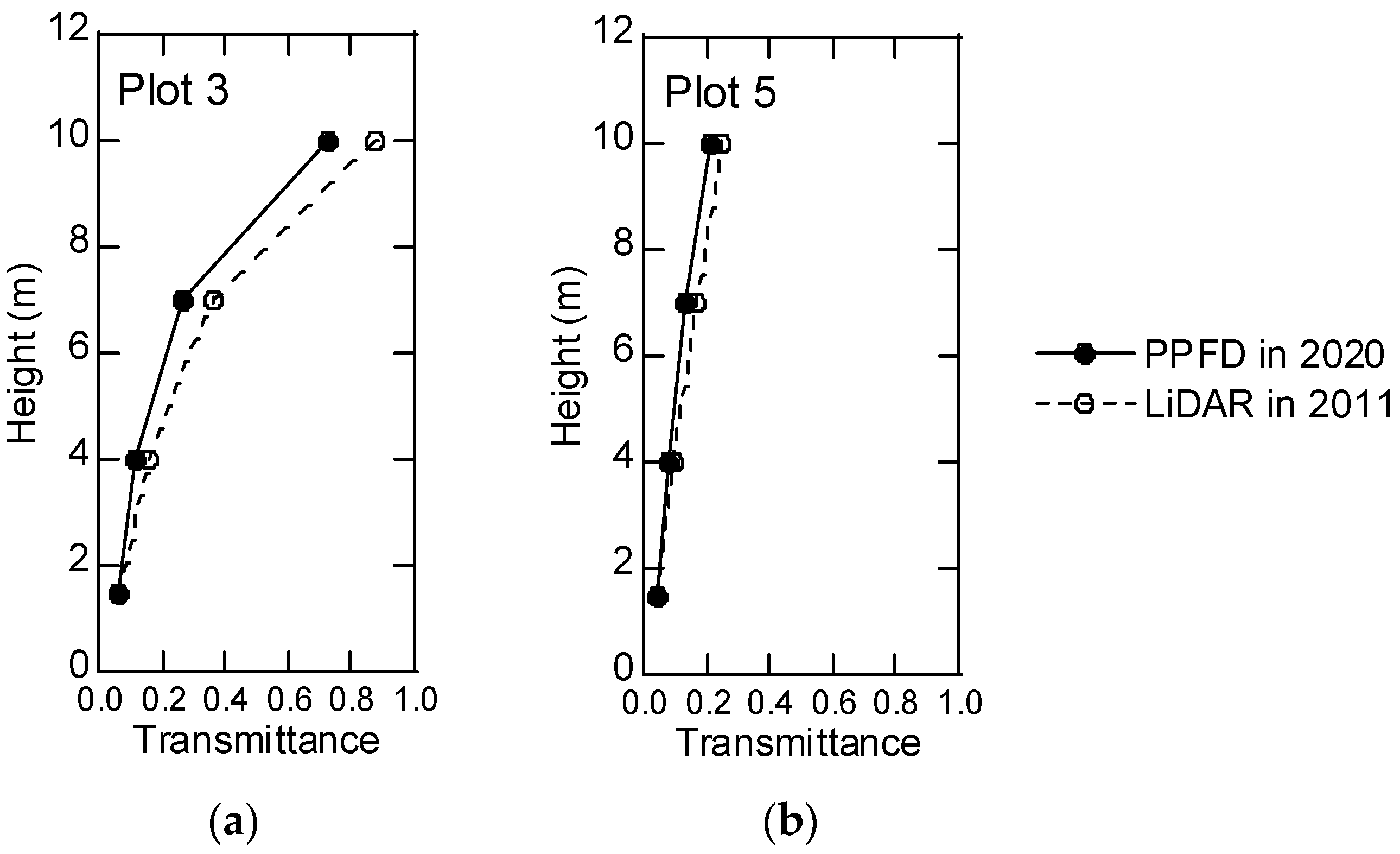
3.7.3. Comparison of Transmittance between LiDAR Pulse and PPFD
3.7.4. Comparison of All LiDAR and Field Estimations
4. Discussion
4.1. Appropriateness of Field Measurements
4.2. Validation of Empirically Estimated Extinction Coefficient Ke
4.3. Importance of Applying Vertically Distinct Ke
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jones, H.G. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology, 3rd ed.; Cambridge University Press: Cambrige, UK, 2014; p. 407. [Google Scholar]
- Chapin, F.S., III; Matson, P.A.; Mooney, H.A. Principles of Terrestrial Ecosystem Ecology; Sringer-Verlag: New York, NY, USA, 2002; p. 436. [Google Scholar]
- Kato, A.; Tamura, T.; Ichihashi, A.; Kobayashi, T.; Takahashi, T. An automatic method to estimate forest coverage and strata from terrestrial laser data. J. Jpn. Soc. Reveget. Tech. 2019, 45, 121–126, (In Japanese with English Summary). [Google Scholar]
- Murai, H.; Higuchi, H. Factors affecting bird Species diversity in Japanese forests. Strix 1998, 7, 83–100, (In Japanese with an English Summary). [Google Scholar]
- Clawges, R.; Vierling, K.; Vierling, L.; Rowell, E. The use of airborne lidar to assess avian species diversity, density, and occurrence in a pine/aspen forest. Remote Sens Environ. 2008, 112–115, 2064–2073. [Google Scholar] [CrossRef]
- Melin, M.; Matala, J.; Mehtätalo, L.; Pusenius, J.; Packalen, P. Ecological dimensions of airborne laser scanning—Analyzing the role of forest structure in moose habitat use within a year. Remote Sens. Environ. 2016, 173, 238–247. [Google Scholar] [CrossRef]
- Martinuzzi, S.; Vierling, L.A.; Gould, W.A.; Falkowski, M.J.; Evans, J.S.; Hudak, A.T.; Vierling, K.T. Mapping snags and understory shrubs for a LiDAR-based assessment of wildlife habitat suitability. Remote Sens. Environ. 2009, 113, 2533–2546. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T.; Schortemeyer, M. On the factor light in plant communities and its importance for matter production. Ann. Bot. 2005, 95, 549–567. [Google Scholar] [CrossRef]
- Asner, G.P.; Scurlock, J.M.O.; Hicke, J.A. Global synthesis of leaf area index observations: Implications for ecological and remote sensing studies. Glob. Ecol. Biogeogr. 2003, 12–13, 191–205. [Google Scholar] [CrossRef]
- Goodwin, N.R.; Coops, N.C.; Culvenor, D.S. Assessment of forest structure with airborne LiDAR and the effects of platform altitude. Remote Sens. Environ. 2006, 113, 2317–2327. [Google Scholar] [CrossRef]
- Richardson, J.J.; Moskal, L.M.; Kim, S.H. Modeling approaches to estimate effective leaf area index from aerial discrete-return LIDAR. Agric. For. Meteorol. 2009, 149, 1152–1160. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with lidar data: An evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113–115, 946–956. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S. Lidar-based mapping of leaf area index and its use for validating GLOBCARBON satellite LAI product in a temperate forest of the southern USA. Remote Sens. Environ. 2009, 113, 1628–1645. [Google Scholar] [CrossRef]
- Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. Forest Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ. 2011, 115, 1065–1080. [Google Scholar] [CrossRef]
- Peduzzi, A.; Wynne, R.H.; Fox, T.R.; Nelson, R.F.; Thomas, V.A. Estimating leaf area index in intensively managed pine plantations using airborne laser scanner data. For. Ecol. Manag. 2012, 270, 54–65. [Google Scholar] [CrossRef]
- Stark, S.C.; Leitold, V.; Wu, J.L.; Hunter, M.O.; de Castilho, C.V.; Costa, F.R.C.; Mcmahon, S.M.; Parker, G.G.; Shimabukuro, M.T.; Lefsky, M.A.; et al. Amazon forest carbon dynamics predicted by profiles of canopy leaf area and light environment. Ecol. Lett. 2012, 15, 1406–1414. [Google Scholar] [CrossRef]
- Hopkinson, C.; Lovell, J.; Chasmer, L.; Jupp, D.; Kljun, N.; van Gorsel, E. Integrating terrestrial and airborne lidar to calibrate a 3D canopy model of effective leaf area index. Remote Sens. Environ. 2013, 136, 301–314. [Google Scholar] [CrossRef]
- Sabol, J.; PatoČka, Z.; Mikita, T. Usage of LiDAR data for leaf area index estimation. GeoScience Eng. 2014, 60–63, 10–18. [Google Scholar] [CrossRef]
- Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return lidar data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef]
- Sumnall, M.J.; Peduzzi, A.; Fox, T.R.; Wynne, R.H.; Thomas, V.A.; Cook, B. Assessing the transferability of statistical predictive models for leaf area index between two airborne discrete return LiDAR sensor designs within multiple intensely managed Loblolly pine forest locations in the south-eastern USA. Remote Sens. Environ. 2016, 176, 308–319. [Google Scholar] [CrossRef]
- Sumnall, M.J.; Trlica, A.; Carter, D.R.; Cook, R.L.; Schulte, M.L.; Campoe, O.C.; Rubilar, R.A.; Wynne, R.H.; Thomas, V.A. Estimating the overstory and understory vertical extents and their leaf area index in intensively managed loblolly pine (Pinus taeda L.) plantations using airborne laser scanning. Remote Sens. Environ. 2021, 254, 112250. [Google Scholar] [CrossRef]
- Tseng, Y.; Lin, L.; Wang, C. Mapping CHM and LAI for heterogeneous forests using airborne full-waveform LiDAR data. Terr. Atmos. Ocean. Sci. 2016, 27, 537–548. [Google Scholar] [CrossRef]
- Muraoka, H.; Maruya, Y.; Nagai, S. Long-term and multidisciplinary research on carbon cycling and forest ecosystem functions in a mountainous landscape: Development and perspectives. J. Geogr. 2019, 128, 129–146, (In Japanese with an English Summary). [Google Scholar] [CrossRef]
- Almeida, D.R.A.; Stark, S.C.; Shao, G.; Schietti, J.; Nelson, B.W.; Silva, C.A.; Gorgens, E.B.; Valbuena, R.; Papa, D.A.; Brancalion, P.H.S. Optimizing the remote detection of tropical rainforest structure with airborne lidar: Leaf area profile sensitivity to pulse density and spatial sampling. Remote Sens. 2019, 11, 92. [Google Scholar] [CrossRef]
- Kamoske, A.G.; Dahlin, K.M.; Stark, S.C.; Shawn, P.; Serbind, S.P. Leaf area density from airborne LiDAR: Comparing sensors and resolutions in a temperate broadleaf forest ecosystem. For. Ecol. Manag. 2019, 433, 364–375. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, J.; Skidmore, A.K.; Premiere, J.; Heuriche, M. A voxel matching method for effective leaf area index estimation in temperate deciduous forests from leaf-on and leaf-off airborne LiDAR data. Remote Sens. Environ. 2020, 240, 111696. [Google Scholar] [CrossRef]
- Pascual, C.; García-Abril, A.; García-Montero, L.G.; Martín-Fernández, S.; Cohen, W.B. Object-based semi-automatic approach for forest structure characterization using lidar data in heterogeneous Pinus sylvestris stands. For. Ecol. Manag. 2008, 255, 3677–3685. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Noland, T.L. Classification of tree species based on structural features derived from high density LiDAR data. Agric. For. Meteorol. 2013, 171–172, 104–114. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface lidar remote sensing of basal area and biomass in deciduous forests of eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Ohmasa, K.; Hosoi, F.; Nakai, Y. Observation of forest structural parameters by three-dimensional remote sensing. Heredity 2009, 63–66, 44–50, (In Japanese. The title is author’s tentative translation). [Google Scholar]
- Maltamo, M.; Eerikäinenn, K.; Pitkänen, J.; Hyyppä, J.; Vehmas, M. Estimation of timber volume and stem density based on scanning laser altimetry and expected tree size distribution functions. Remote Sens. Environ. 2004, 90, 319–330. [Google Scholar] [CrossRef]
- Utsugi, G. Influences of Forest Leaf Structure on Photosythetic Production of Canopies—Focusing Effects by Leaf Inclination. Ph.D. Thesis, No 24728. University of Tokyo, Tokyo, Japan, 2009; p. 191. [Google Scholar]
- Parker, G.G. Tamm review: Leaf Area Index (LAI) is both a determinant and a consequence of important processes in vegetation canopies. For. Ecol. Manag. 2020, 477, 118496. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. 3-D remote sensing for measurement and analysis of forest structure. Jpn. J. Ecol. 2014, 64, 223–231. [Google Scholar]
- Li, S.; Dai, L.; Wang, H.; Wang, Y.; He, Z.; Lin, S. Estimating Leaf Area Density of Individual Trees Using the Point Cloud Segmentation of Terrestrial LiDAR Data and a Voxel-Based Model. Remote Sens. 2017, 9, 1202. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Pan, F.; Xi, X.; Li, G.; Nie, S.; Shaobo Xia, S. Estimation of wetland vegetation height and leaf area index using Airborne laser scanning data. Ecol. Indic. 2015, 48, 550–559. [Google Scholar] [CrossRef]
- Spanner, M.A.; Pierce, L.L.; Peterson, D.L.; Running, S.W. Remote-sensing ofntemperate coniferous forest leaf-area index—The influence of canopy closure, understory vegetation and background reflectance. Int. J. Remote Sens. 1990, 11, 95–111. [Google Scholar] [CrossRef]
- Melnikova, I.; Awaya, Y.; Saitoh, T.M.; Muraoka, H.; Sasai, T. Estimation of Leaf Area Index in a Mountain Forest of Central Japan with a 30-m Spatial Resolution Based on Landsat Operational Land Imager Imagery: An Application of a Simple Model for Seasonal Monitoring. Remote Sens. 2018, 10, 179. [Google Scholar] [CrossRef]
- Bréda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Nasahara, K.N.; Muraoka, H.; Nagai, S.; Mikami, H. Vertical integration of leaf area index in a Japanese deciduous broad-leaved forest. Agric. For. Meteorol. 2008, 148, 1136–1146. [Google Scholar] [CrossRef]
- Beraldin, J.; Blais, F.; Lohr, U. Laser Scanning Technology. In Airborne and Terrestrial Laser Scanning; Vosselman, G., Mass, H., Eds.; Whittles Publishing: Scotland, UK, 2010; pp. 19–30. [Google Scholar]
- Vosselman, G.; Mass, H. (Eds.) Airborne and Terrestrial Laser Scanning; Whittles Publishing: Scotland UK, 2010; p. 318. [Google Scholar]
- Næsset, E.; Bjerknes, K.O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner data. Remote Sens. Environ. 2001, 78, 328–340. [Google Scholar] [CrossRef]
- Hirata, Y. Relationship between Tree Height and Topography in a Chamaecyparis obtusa Stand Derived from Airborne Laser Scanner Data. J. Jpn. For. Soc. 2005, 87, 497–503, (In Japanese with English Summary). [Google Scholar] [CrossRef]
- Nelson, R.; Krabil, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ. 1988, 24, 247–267. [Google Scholar] [CrossRef]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.C.; Spies, T.A.; Harding, D. Lidar Remote Sensing of the Canopy Structure and Biophysical Properities of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Matsue, K.; Itoh, T.; Naito, K. Estimating forest resources using airbone LiDAR-Estimating stand parameters of Sugi (Cryptomeria japonica D. Don) and Hinoki (Chamaecyparis obtusa Endl.) stands with differing densities. J. Jpn. Soc. Photogramm. 2006, 45, 4–13, (In Japanese with English Summary). [Google Scholar]
- Takahashi, T.; Awaya, Y.; Hirata, Y.; Furuya, N.; Sakai, T.; Sakai, A. Stand volume estimation by combining low laser-sampling density LiDAR data with QuickBird panchromatic imagery in closed-canopy Japanese cedar (Cryptomeria japonica) plantations. Int. J. Remote Sens. 2010, 31–35, 1281–1301. [Google Scholar] [CrossRef]
- Awaya, Y.; Takahashi, T. Evaluating the differences in modeling biophysical attributes between deciduous broadleaved and evergreen conifer forests using low-density small-footprint LiDAR data. Remote Sens. 2017, 9, 572. [Google Scholar] [CrossRef]
- Ko, C.; Sohn, G.; Remmel, T.K.; Miller, J. Hybrid Ensemble Classification of Tree Genera Using Airborne LiDAR Data. Remote Sens. 2014, 6, 11225–11243. [Google Scholar] [CrossRef]
- Hovi, A.; Korhonen, L.; Vauhkonen, J.; Korpela, I. LiDAR waveform features for tree species classification and their sensitivity to tree- and acquisition related parameters. Remote Sens. Environ. 2016, 173, 224–237. [Google Scholar] [CrossRef]
- Awaya, Y.; Kameta, C.; Gotoh, S.; Miyasaka, S.; Unome, S. Cassification of Sugi and Hinoki using high density airborne LiDAR data and two canopy shape parameters. Jpn. J. For. Plann. 2017, 51, 9–18, (In Japanese with English Summary). [Google Scholar] [CrossRef]
- Nakatake, S.; Yamamoto, K.; Yoshida, N.; Yamaguchi, A.; Unome, S. Development of a Single Tree Classification Method Using Airborne LiDAR. J. Jpn. For. Soc. 2018, 100, 149–157, (In Japanese with an English Summary). [Google Scholar] [CrossRef]
- Zhang, K. Identification of gaps in mangrove forests with airborne LIDAR. Remote Sens. Environ. 2008, 112, 2309–2325. [Google Scholar] [CrossRef]
- Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Spatially explicit characterization of boreal forest gap dynamics using multi-temporal lidar data. Remote Sens. Environ. 2008, 112–115, 2326–2340. [Google Scholar] [CrossRef]
- Choi, H.; Song, Y.; Jang, Y. Urban Forest Growth and Gap Dynamics Detected by Yearly Repeated Airborne Light Detection and Ranging (LiDAR): A Case Study of Cheonan, South Korea. Remote Sens. 2019, 11, 1551. [Google Scholar] [CrossRef]
- Araki, K.; Awaya, Y. Analysis and prediction of gap dynamics in a secondary deciduous broadleaf forest of central Japan using airborne multi-LiDAR observations. Remote Sens. 2021, 13, 100. [Google Scholar] [CrossRef]
- Pearse, G.D.; Morgenroth, J.; Watt, M.S.; Dash, J.P. Optimising prediction of forest leaf area index from discrete airborne lidar. Remote Sens. Environ. 2017, 200, 220–239. [Google Scholar] [CrossRef]
- Qu, Y.; Shaker, A.; Silva, C.A.; Klauberg, C.; Pinagé, E.R. Remote sensing of leaf area index from LiDAR height percentile metrics and comparison with MODIS product in a selectively logged tropical forest area in Eastern Amazonia. Remote Sens. 2018, 10, 970. [Google Scholar] [CrossRef]
- Shao, G.; Stark, S.C.; de Almeida, M.D.R.A.; Smith, M.N. Towards high throughput assessment of canopy dynamics: The estimation of leaf area structure in Amazonian forests with multitemporal multi-sensor airborne lidar. Remote Sens. Environ. 2019, 221, 1–13. [Google Scholar] [CrossRef]
- Li, Q.; Wong, F.K.K.; Fung, T.; Brown, L.A.; Dash, J. Assessment of Active LiDAR Data and Passive Optical Imagery for Double-Layered Mangrove Leaf Area Index Estimation: A Case Study in Mai Po, Hong Kong. Remote Sens. 2023, 15, 2551. [Google Scholar] [CrossRef]
- Hyer, E.J.; Goetz, S.J. Comparison and sensitivity analysis of instruments and radiometric methods for LAI estimation: Assessments from a boreal forest site. Agric. For. Meteorol. 2004, 122, 157–174. [Google Scholar] [CrossRef]
- Sumida, A.; Nakai, T.; Yamada, M.; Ono, K.; Uemura, S.; Sumida, T.H.; Nakai, A.; Yamada, T.; Ono, M.; Uemura, K. Ground-based estimation of leaf area index and vertical distribution of leaf area density in a Betula ermanii forest. Silva Fenn. 2009, 43–45, 799–816. [Google Scholar] [CrossRef]
- Sumida, A. Background (Behind) of Vertical Leaf Distribution Estimation Using MacArthur-Horn Method. 2012. Available online: https://www2.kpu.ac.jp/for_ecol/Erman/Hosoku1.pdf (accessed on 6 April 2022).
- Majasalmia, T.; Korhonenb, L.; Korpelaa, I.; Vauhkonenca, J. Application of 3D triangulations of airborne laser scanning data toestimate boreal forest leaf area index. Int. J. Appl. Earth Obs. Geoinf. 2017, 59, 53–62. [Google Scholar]
- Tian, L.; Qu, Y.; Qi, J. Estimation of Forest LAI Using Discrete Airborne LiDAR: A Review. Remote Sens. 2021, 13, 2408. [Google Scholar] [CrossRef]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Fuchs, M.; Asrar, G.; Kanemasu, E.T. Leaf area esimates from measurements of photosynthetically active radiation in wheat canopies. Agrc. For. Meteorol. 1984, 32, 13–22. [Google Scholar] [CrossRef]
- Wang, W.M.; Li, Z.L.; Su, H.B. Comparison of leaf angle distribution functions: Effects on extinction coefficient and fraction of sunlit foliage. Agric. For. Meteorol. 2007, 143, 106–122. [Google Scholar] [CrossRef]
- Morsdorf, F.; Kötz, B.; Meier, E.; Itten, K.I.; Allgöwer, B. Estimation of LAI and fractional cover from small footprint airborne laser scanning data based on gap fraction. Remote Sens. Environ. 2006, 104, 50–61. [Google Scholar] [CrossRef]
- Lovell, J.L.; Jupp, D.L.B.; Culvenor, D.S.; Coops, N.C. Using airborne and ground-based ranging lidar to measure canopy structure in Australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Muraoka, H.; Saigusa, N.; Nasahara, K.N.; Noda, H.; Yoshino, J.; Saitoh, T.M.; Nagai, S.; Murayama, S.; Koizumi, H. Effects of seasonal and interannual variations in leaf photosynthesis and canopy leaf area index on gross primary production of a cool-temperate deciduous broadleaf forest in Takayama, Japan. J. Plant Res. 2010, 123, 563–576. [Google Scholar] [CrossRef]
- Masaharu, H. Map Projections-Technique on Geospatial Information; Asakura Publishing Co. Ltd.: Tokyo, Japan, 2011; pp. 19–26. (In Japanese) [Google Scholar]
- Fukuda, N.; Awaya, Y.; Kojima, T. Classification of forest vegetation types using LiDAR data and Quickbird images—Case study of the Daihachiga River Basin in Takayama city. J. JASS 2012, 28, 115–122, (In Japanese with English Summary). [Google Scholar]
- Komiyama, A.; Kato, S.; Ninomiya, I. Allometric Relationships for Deciduous Broad-leaved Forests in Hida District, Gifu Prefecture, Japan. J. Jpn. For. Soc. 2002, 84, 130–134, (In Japanese with English Summary). [Google Scholar]
- Yamamoto, K. LIA for Win32 (LIA32) ver.0.376β1 Users Manual (Revised Version). 2003. Available online: https://www.agr.nagoya-u.ac.jp/~shinkan/LIA32/ (accessed on 6 April 2022). (In Japanese).
- Welles, J.M.; Norman, J.M. Instrument for indirect measurement of canopy architecture. Agron. J. 1991, 83, 818–825. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Muraoka, H.; Koizumi, H. Photosynthetic and structural characteristics of canopy and shrub trees in a cool-temperate deciduous broadleaved forest: Implication to the ecosystem carbon gain. Agric. For. Meteorol. 2005, 134, 39–59. [Google Scholar] [CrossRef]





| Abbreviation | Unit | Term or Explanation | Abbreviation | Unit | Term or Explanation | Abbreviation | Unit | Term or Explanation |
|---|---|---|---|---|---|---|---|---|
| LAI | m2 m−2 | Leaf Area Index | LAD | m2 m−3 | Leaf Area Density | |||
| LAT | m2/tree | Leaf Area per Tree | LAP | m2/plot | Leaf Area per Tree | Leaf Area per Tree | ||
| PAI | m2 m−2 | Plant Area Index | PAD | m2 m−3 | Plant Area Density | SAI | m2 m−2 | Stem Area Index |
| ePAI | m2 m−2 | Effective PAI when K is 1. | ePAD | m2 m−3 | Effective PAD when K is 1. | ePADh-top | m2 m−3 | ePAD between h (m) above ground and the canopy top. |
| LAD(0–33) | m2 m−3 | LAD in the normalized height layer, e.g., between 0% and 33%. | ePAD(0–33) | m2 m−3 | ePAD in the normalized height layer, e.g., between 0% and 33%. | |||
| K | Extinction coefficient. K = 1, 0.5 or 0.46 [11,25,71,74]. | Ke: multi | Ke for three layers (relative H: 0–33%, 34–66%, 67–100%). | Ke: mono | Ke for all layers (relative H: 0–100%). | |||
| Ke | K which is estimated using field measurement data. | Ke: type | Ke for the three forest types by the Ward classification. | Ke: all | Ke for all forest types. | |||
| CL | m | Canopy Length | CLA | m2 | Cumulative Leaf Area | |||
| I | Light intensity either PPFD or No. of pulses. | I0 | Downward I at the top of canopy. | Ih | Downward I at h (m) above the ground. | |||
| Iini | Number of pulses entering to layer i from the above. | Iouti | Number of pulses passing through layer i. | TRh | Transmittance of PPFD at h meter layer. | |||
| LA | Multi-layer data of DCHM points; used to compare with results of allometric equations. | LAn | pulses/cube or cylinder | LA at layer n (m) (1 m interval) | DBH | cm | Stem diameter at breast height (1.2 m) | |
| LP | Multi-layer data of DCHM points; used to compare with estimates by rPPFD. | LPn | pulses/cube or cylinde | LP at layer by photon sensor positions. 1.5–4 m, 4–7.5 m, 7.5–10 m. | H | m | Tree height | |
| Plot-1 | Plot-2 | Plot-3 | Plot-4 | Plot-5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID (Year-No) | 2011-35 | 2012-03 | 2011-29 | 2011-13 | 2012-01 | |||||
| Measurement (year) | 2011 | 2019 | 2012 | 2019 | 2011 | 2019 | 2011 | 2020 | 2012 | 2020 |
| Density (trees ha−1) | 18,589 1 | 10,313 1 | 1103 | 962 | 1945 | 1724 | 4327 2 | 3084 2 | 57202 | 4277 2 |
| Max DBH (cm) | 9.6 | 14.8 | 45.5 | 51.6 | 36.0 | 39.7 | 21.4 | 25.5 | 15.0 | 20.1 |
| Mean DBH (cm) | 2.7 | 4.7 | 20.0 | 21.9 | 12.8 | 13.5 | 8.5 | 10.6 | 6.0 | 7.2 |
| Max H (m) | 9.1 | 14.0 | 21.5 | 24.6 | 24.3 | 25.3 | 14.7 | 19.7 | 13.3 | 15.8 |
| Mean H (m) | 4.0 | 6.2 | 16.2 | 17.0 | 12.8 | 12.9 | 9.2 | 11.4 | 7.1 | 8.2 |
| Species in the upper layer | Japanese bird cherry, Birch spp., Japanese umbrella tree | Mongolian oak | Birch spp. | Birch spp., Japanese umbrella tree, Japanese lime tree, Japanese chestnut (Castanea crenata) | Birch spp., Mongolian oak, Cherry spp. | |||||
| Observation Date | Contractor | Scanner, Manufacturer | Pulse Diver-Gence (Mrad) | Wave-Length (nm) | Flight Altitude Above Ground (m) | Foot-Print Size (m) | Field of View (°) | Average Pulse Density (Pulse m−2) |
|---|---|---|---|---|---|---|---|---|
| 28 August 2011 | Nakanihon Air Co., Nagoya, Aichi, Japan | LMS-Q560 RIEGL, Horn, Horn, Austria | 0.50 | 1550 | 600 | 0.30 | ±30 | 4.83 |
| Parameter | Method | Year | Date | Plot-1 ID:2011-35 | Plot-2 ID:2012-03 | Plot-3 ID:2011-29 | Plot-4 ID:2011-13 | Plot-5 ID:2012-01 |
|---|---|---|---|---|---|---|---|---|
| LAI | Litter trap | 2019 2020 | - - | 3.53 | 3.91 5.27 | 4.62 4.88 | 5.20 | 4.21 |
| ePAI | PPFD | 2019 2020 | August 6 September 1, 9, 10 | 3.05 | 2.20 2.62 | 3.22 2.97 | 2.41 | 2.93 |
| PAI | Hemispherical photograph | 2019 2020 | September 9 August 28 | 2.82 | 2.87 3.38 | 3.06 4.18 | 3.74 | 4.06 |
| Relative Height | 0–33 (%) | 34–66 (%) | 67–100 (%) | 0–100 (%) |
|---|---|---|---|---|
| No. of plots | 35 | 35 | 35 | 35 |
| Maximum | 4.82 | 0.94 | 0.72 | 0.97 |
| Minimum | 0.40 | 0.27 | 0.05 | 0.34 |
| Average | 2.15 | 0.52 | 0.30 | 0.52 |
| Standard deviation | 1.21 | 0.18 | 0.15 | 0.15 |
| Forest Type 1 (Plot-2, Plot-3) | ||||
|---|---|---|---|---|
| Relative Height | 0–33 (%) | 34–66 (%) | 67–100 (%) | 0–100 (%) |
| No of plots | 21 | 21 | 21 | 21 |
| Maximum | 4.82 | 0.84 | 0.55 | 0.64 |
| Minimum | 0.40 | 0.28 | 0.20 | 0.34 |
| Average | 2.02 | 0.48 | 0.36 | 0.45 |
| Standard deviation | 1.24 | 0.17 | 0.09 | 0.07 |
| Forest type 2 (Plot-4, Plot-5) | ||||
| No. of plots | 7 | 7 | 7 | 7 |
| Maximum | 4.45 | 0.77 | 0.44 | 0.67 |
| Minimum | 1.16 | 0.45 | 0.08 | 0.34 |
| Average | 2.62 | 0.57 | 0.18 | 0.51 |
| Standard deviation | 1.44 | 0.13 | 0.13 | 0.11 |
| Forest type 3 (Plot-1) | ||||
| No. of plots | 7 | 7 | 7 | 7 |
| Maximum | 3.36 | 0.94 | 0.72 | 0.97 |
| Minimum | 1.08 | 0.27 | 0.05 | 0.49 |
| Average | 2.09 | 0.59 | 0.25 | 0.73 |
| Standard deviation | 0.86 | 0.26 | 0.23 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awaya, Y.; Araki, K. Estimating Three-Dimensional Distribution of Leaf Area Using Airborne LiDAR in Deciduous Broad-Leaved Forest. Remote Sens. 2023, 15, 3043. https://doi.org/10.3390/rs15123043
Awaya Y, Araki K. Estimating Three-Dimensional Distribution of Leaf Area Using Airborne LiDAR in Deciduous Broad-Leaved Forest. Remote Sensing. 2023; 15(12):3043. https://doi.org/10.3390/rs15123043
Chicago/Turabian StyleAwaya, Yoshio, and Kazuho Araki. 2023. "Estimating Three-Dimensional Distribution of Leaf Area Using Airborne LiDAR in Deciduous Broad-Leaved Forest" Remote Sensing 15, no. 12: 3043. https://doi.org/10.3390/rs15123043
APA StyleAwaya, Y., & Araki, K. (2023). Estimating Three-Dimensional Distribution of Leaf Area Using Airborne LiDAR in Deciduous Broad-Leaved Forest. Remote Sensing, 15(12), 3043. https://doi.org/10.3390/rs15123043










