Assimilation and Inversion of Ionospheric Electron Density Data Using Lightning Whistlers
Abstract
1. Introduction
1.1. Ionospheric Data Assimilation
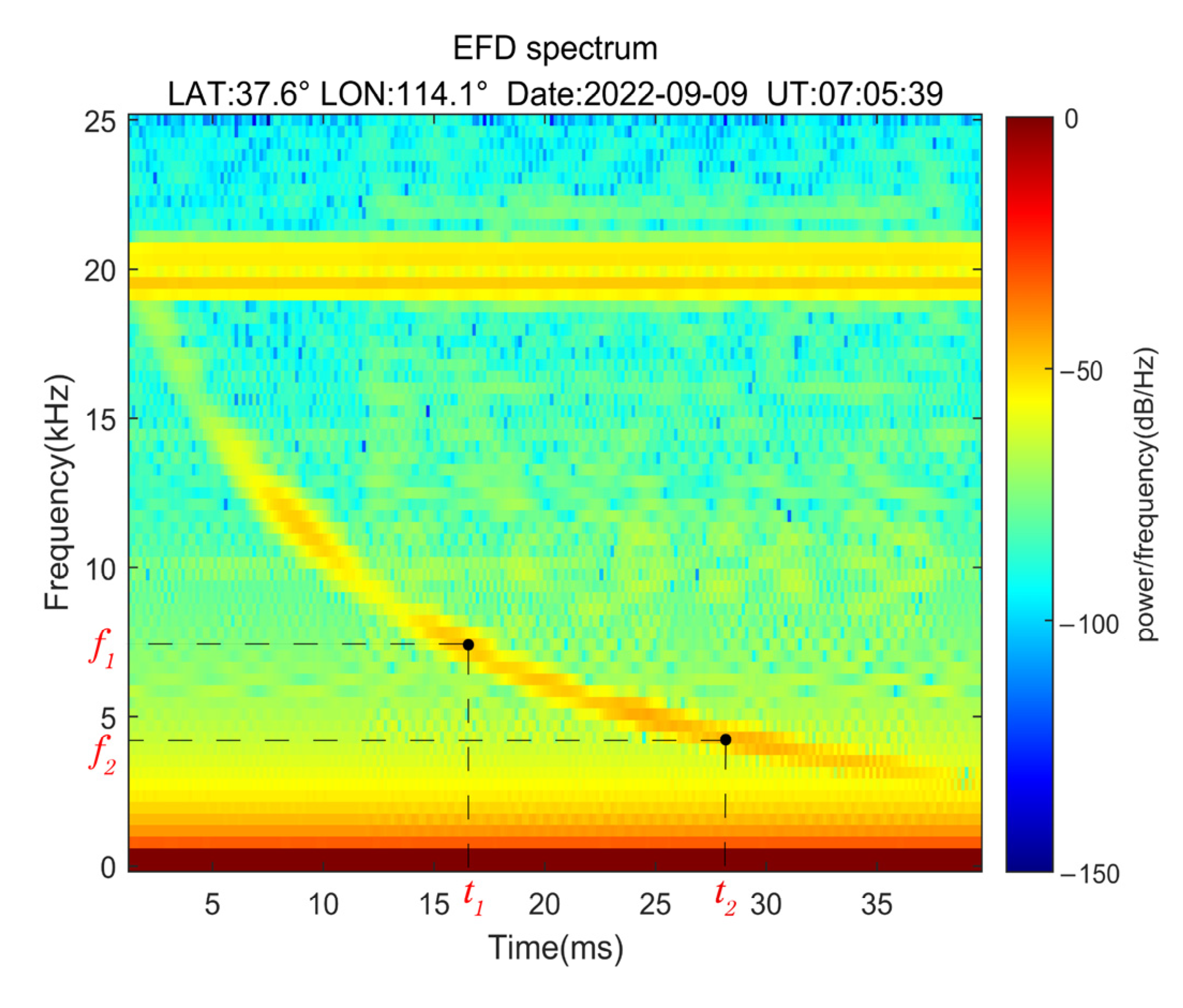
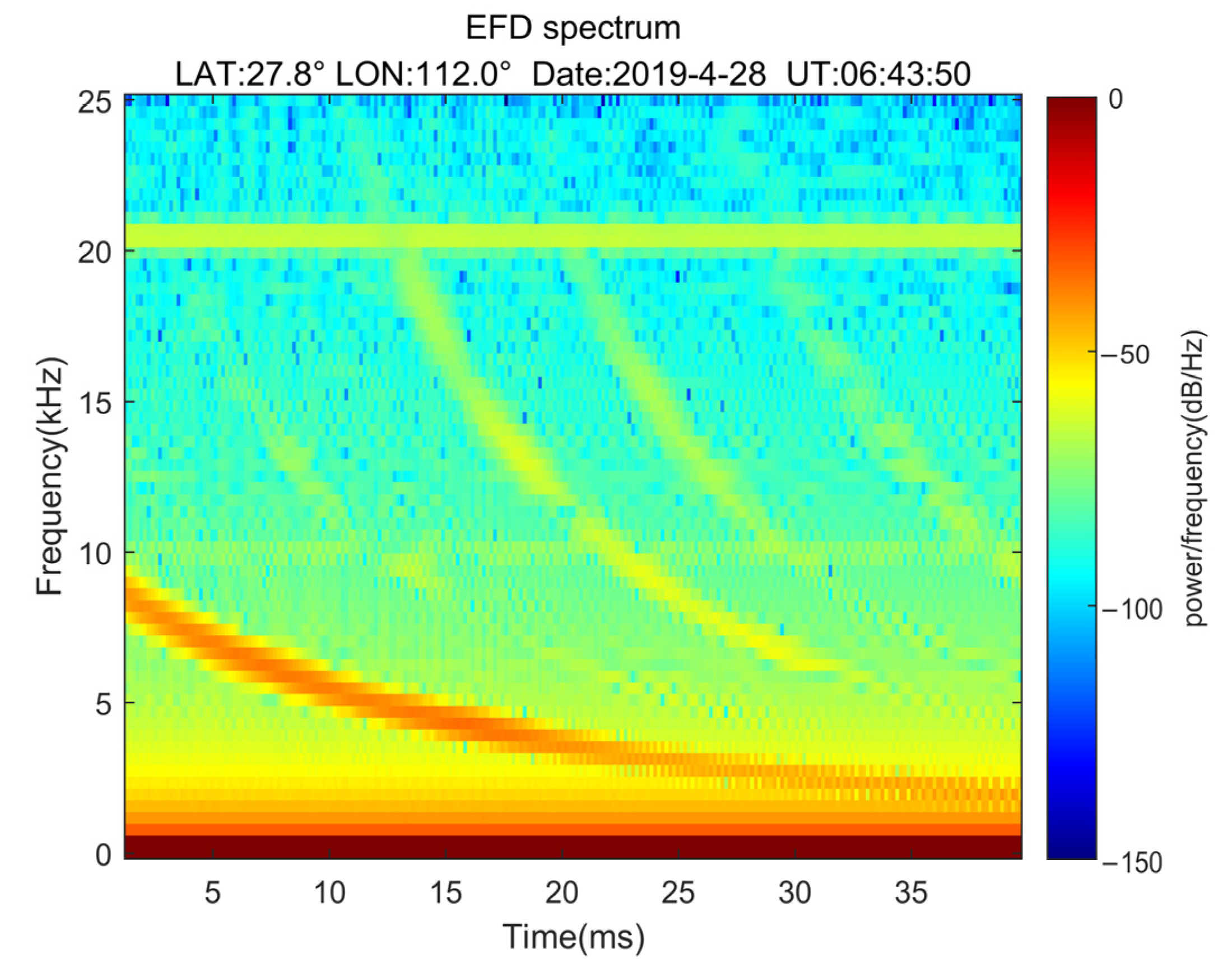
1.2. Lightning Whistlers
1.3. Innovation
2. Values
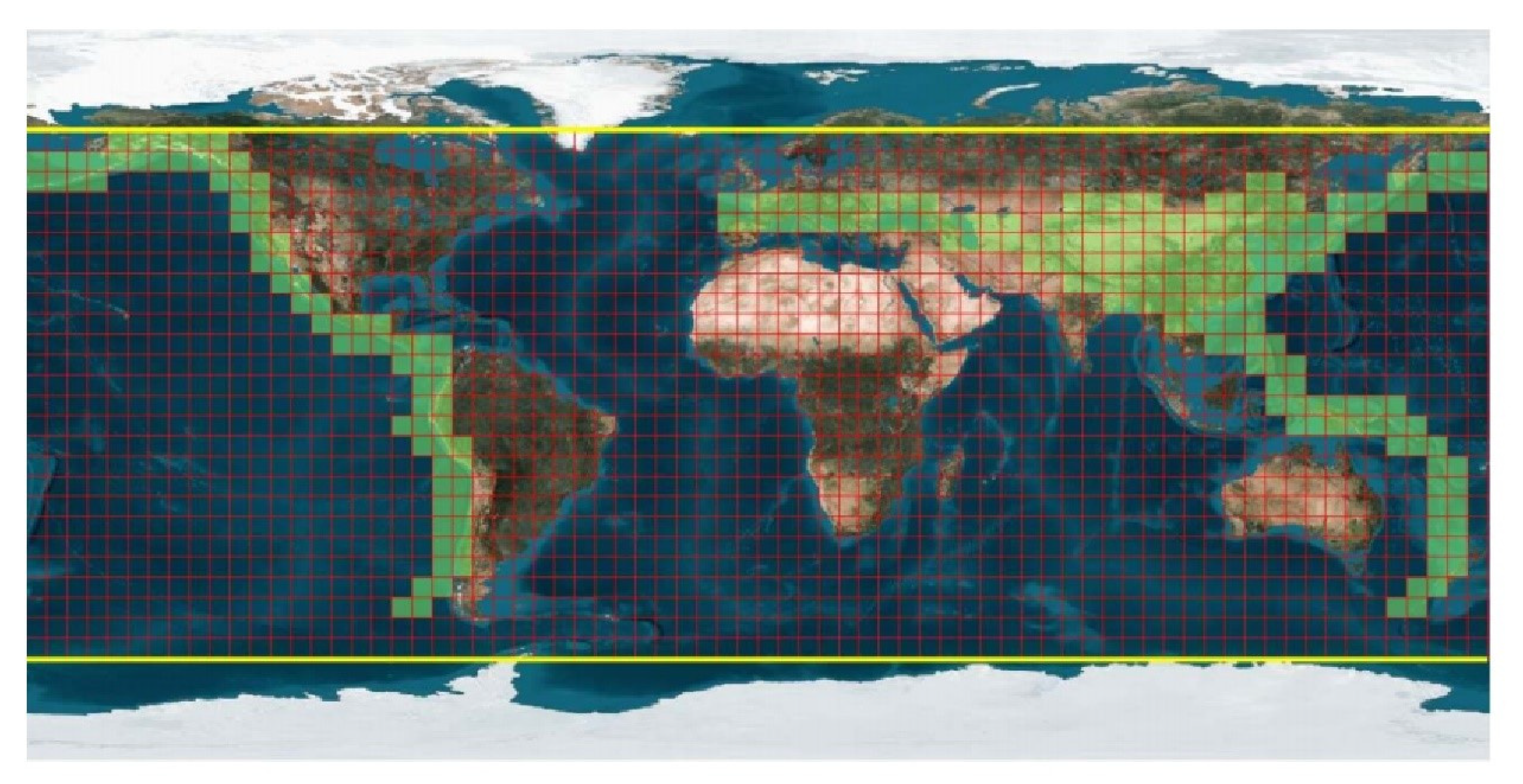
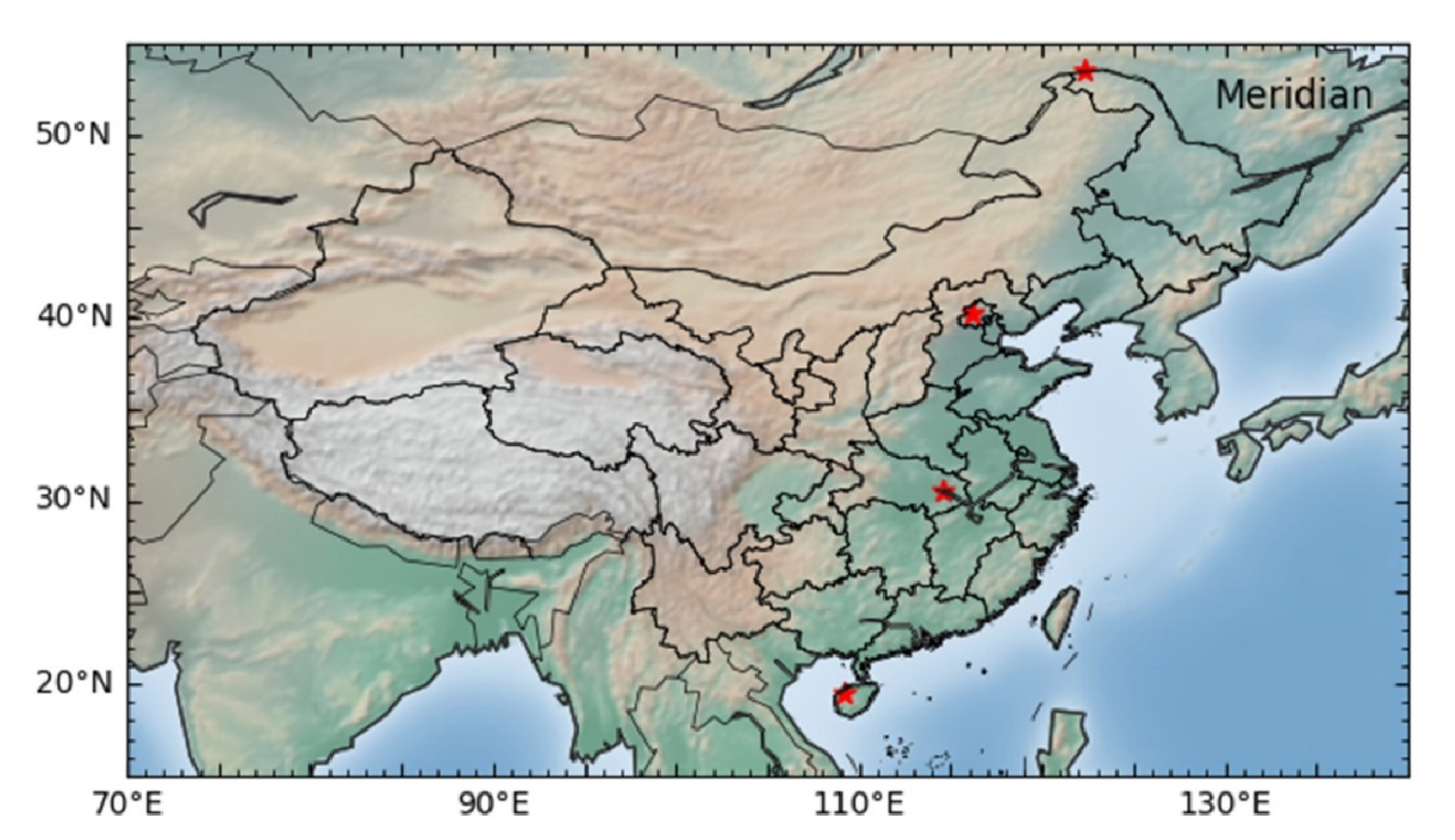
2.1. Observation
2.2. Background Model
2.3. Verification Data
3. Materials and Methods
3.1. Meshing Method
3.2. Assimilation Algorithm
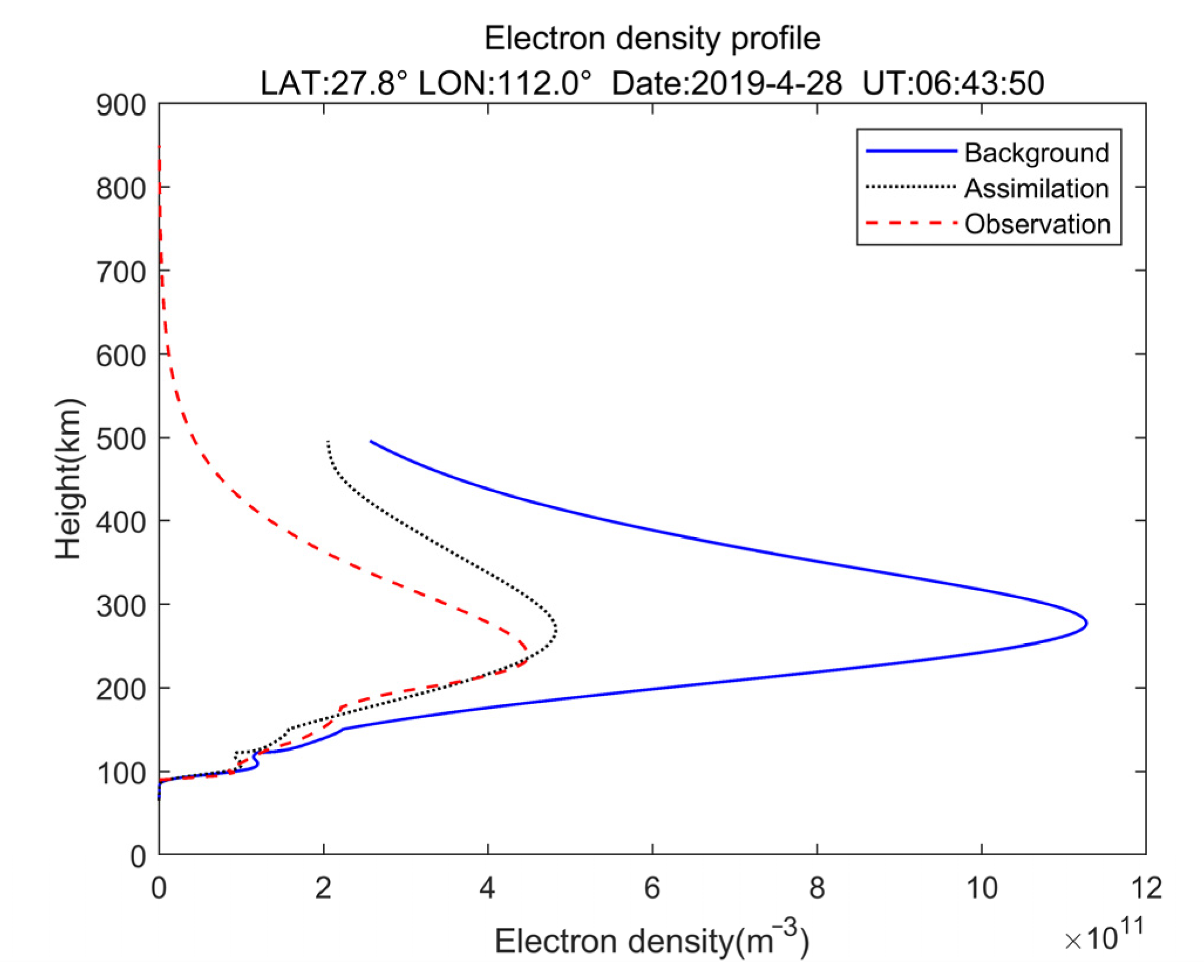
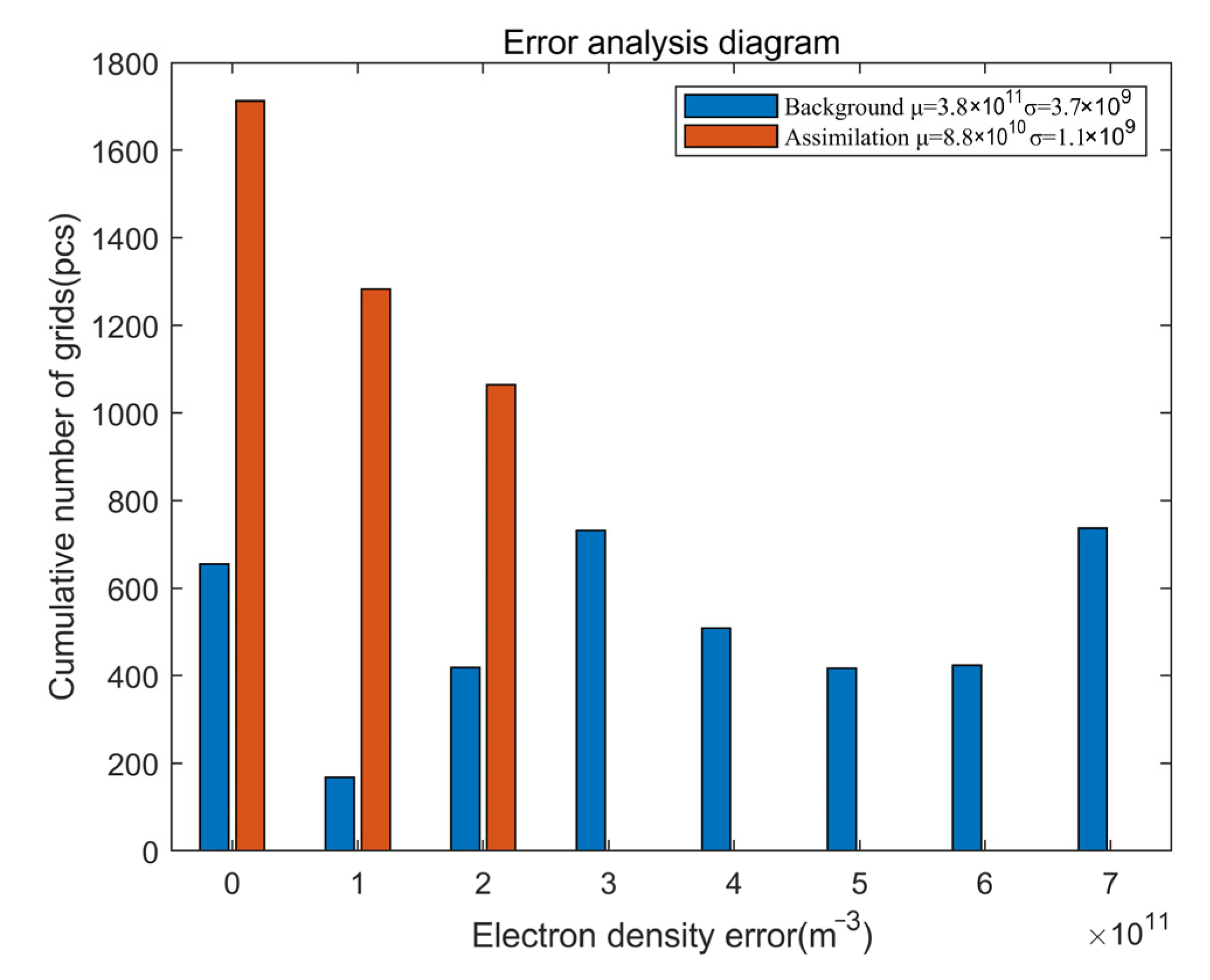
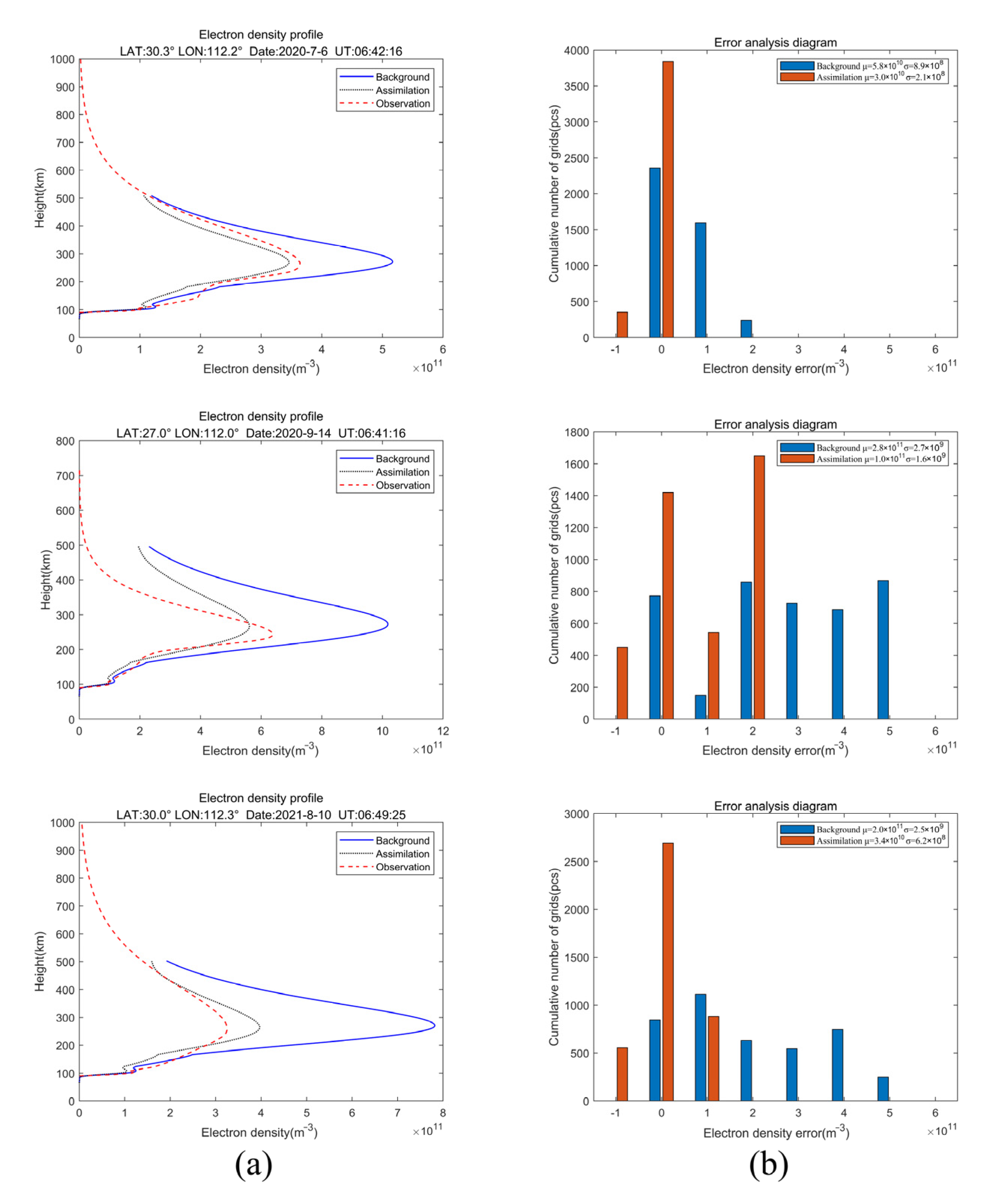
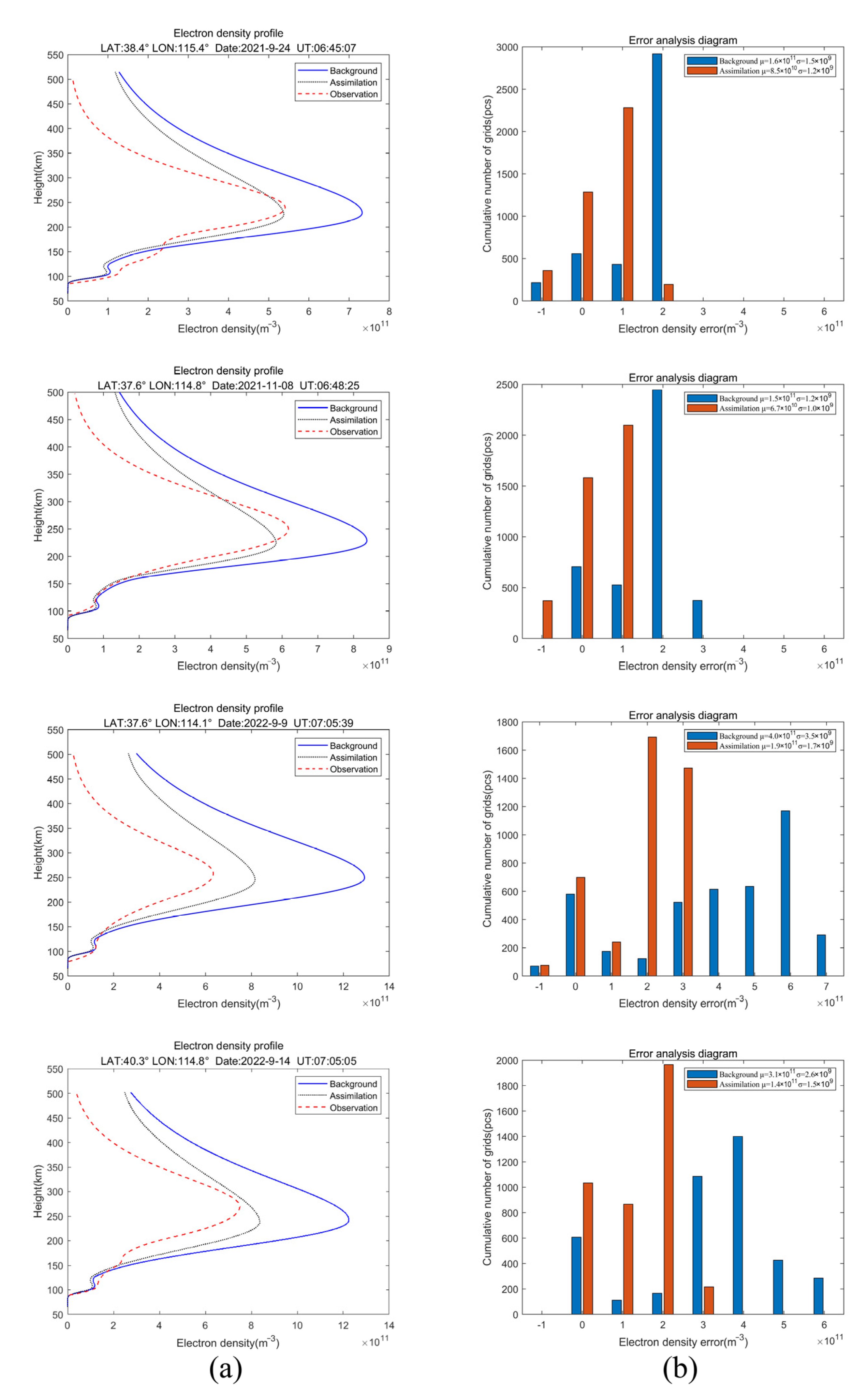
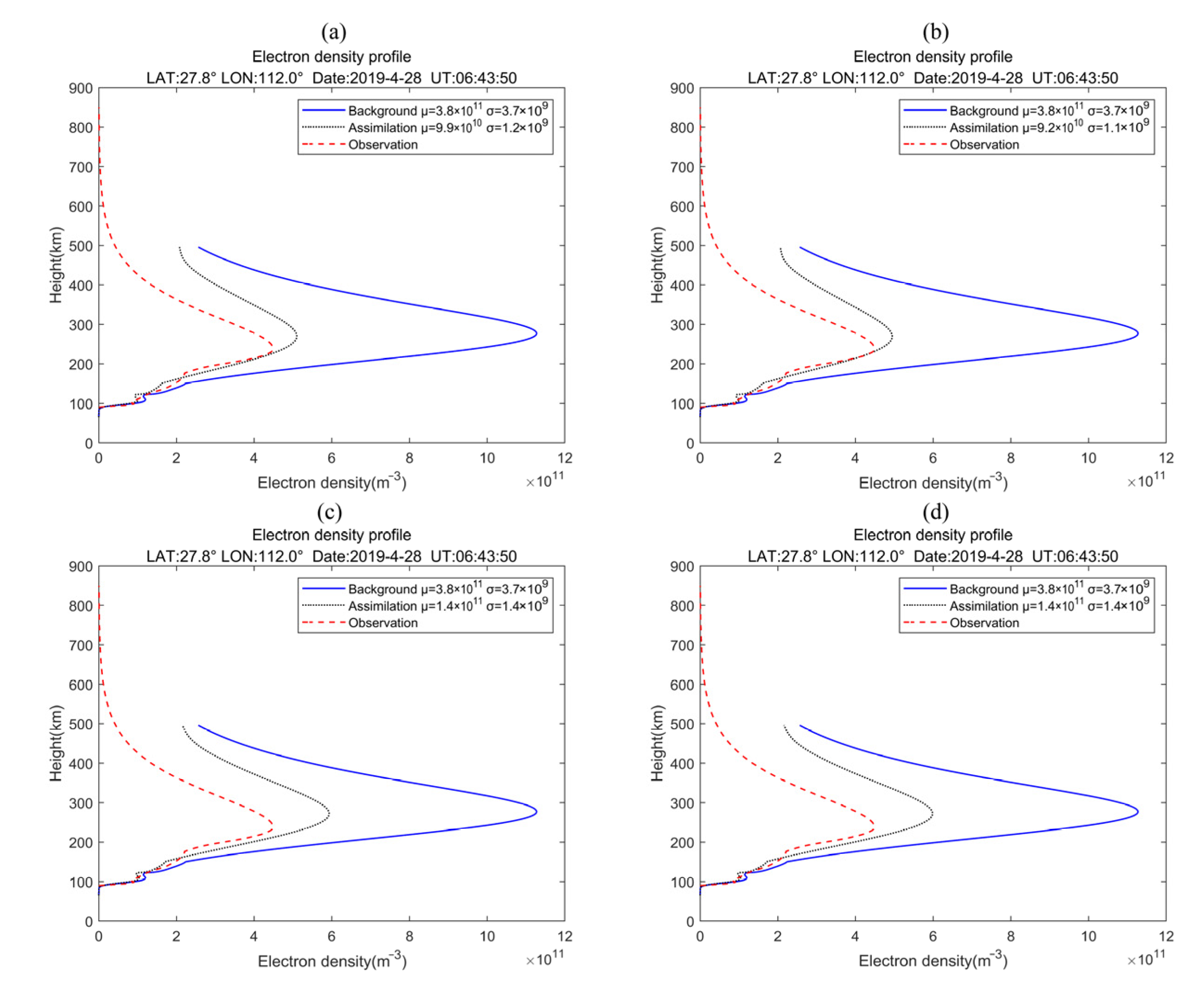
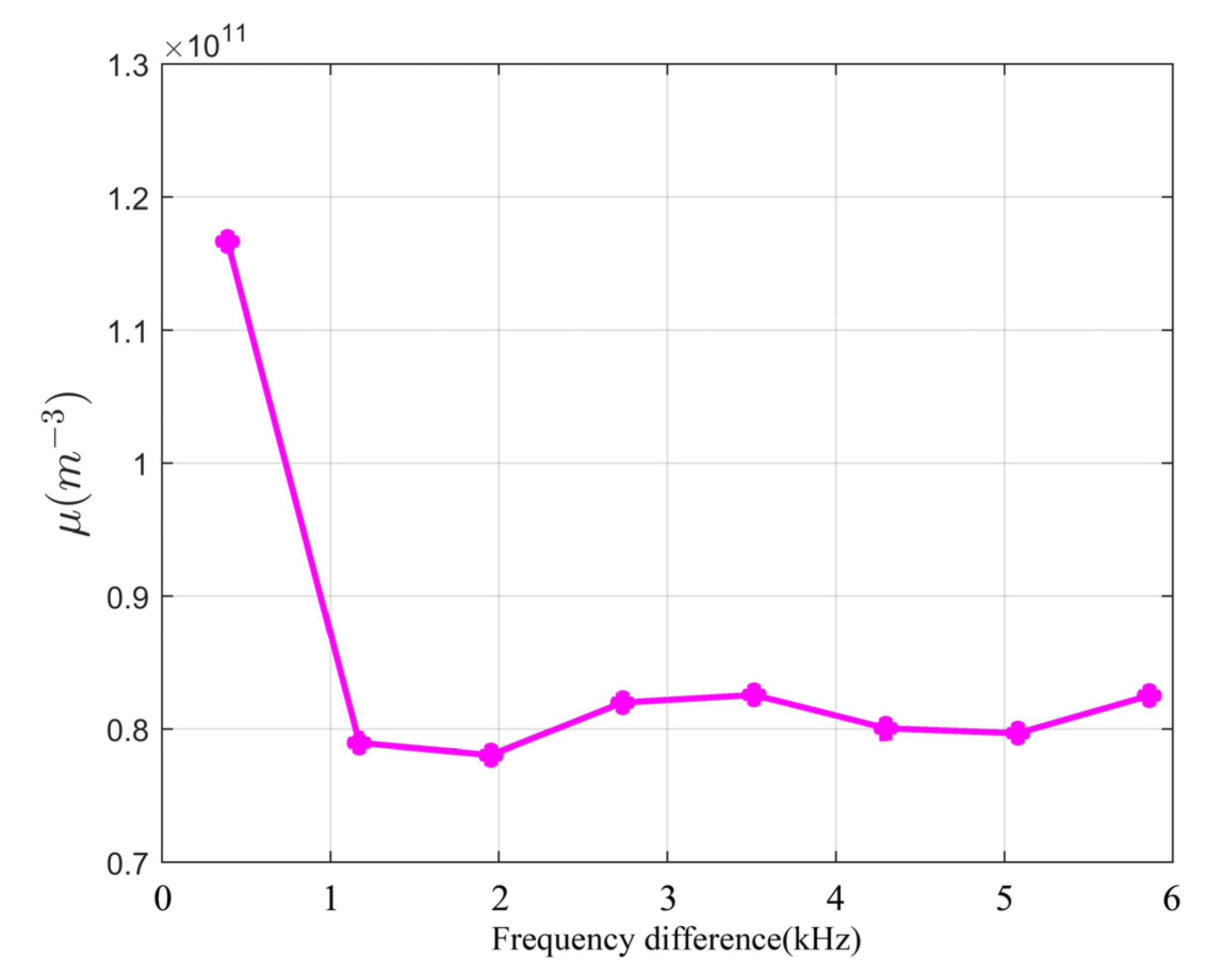
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stanislawska, I.; Lastovicka, J.; Bourdillon, A.; Zolesi, B.; Cander, L.R. Monitoring and modeling of ionospheric characteristics in the framework of European COST 296 Action MIERS. Space Weather 2010, 8, S02001. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Lin, Y.C.; Rocken, C.; Kuo, Y.H.; Zhao, B. Data assimilation retrieval of electron density profiles from radio occultation measurements. J. Geophys. Res. 2011, 116, A03317. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Kuo, Y.-H.; Hunt, D.C.; Wang, W.; Solomon, S.C.; Burns, A.G.; Bilitza, D.; Liu, J.Y.; Wan, W.; et al. Global 3-D ionospheric electron density reanalysis based on multisource data assimilation. J. Geophys. Res. 2012, 117, A09325. [Google Scholar] [CrossRef]
- Qiao, J.; Zhou, C.; Liu, Y.; Zhao, J.; Zhao, Z. Ionospheric Kalman Filter Assimilation Based on Covariance Localization Technique. Remote Sens. 2022, 14, 4003. [Google Scholar] [CrossRef]
- Richmond, A.D.; Kamide, Y. Mapping electrodynamic features of the high-latitude ionosphere from localized observations—Technique. J. Geophys. Res. Space Phys. 1988, 93, 5741–5759. [Google Scholar] [CrossRef]
- Angling, M.J.; Cannon, P.S. Assimilation of radio occultation measurements into background ionospheric models. Radio Sci. 2004, 39, RS1S08. [Google Scholar] [CrossRef]
- Angling, M.J. First assimilations of COSMIC radio occultation data into the Electron Density Assimilative Model (EDAM). Ann. Geophys. 2008, 26, 353–359. [Google Scholar] [CrossRef]
- Bust, G.S.; Garner, T.W.; Gaussiran, T.L., II. Ionospheric Data Assimilation Three-Dimensional (IDA3D): A global, multisensor, electron density specification algorithm. J. Geophys. Res. 2004, 109, A11312. [Google Scholar] [CrossRef]
- Bust, G.S.; Crowley, G. Tracking of polar cap ionospheric patches using data assimilation. J. Geophys. Res. 2007, 112, A05307. [Google Scholar] [CrossRef]
- Bust, G.S.; Immel, T.J. IDA4D: Ionospheric Data Assimilation for the ICON Mission. Space Sci. Rev. 2020, 216, 33. [Google Scholar] [CrossRef]
- Aa, E.; Zhang, S.R.; Erickson, P.J.; Wang, W.; Coster, A.J.; Rideout, W. 3-D regional ionosphere imaging and SED reconstruction with a new TEC-based ionospheric data assimilation system (TIDAS). Space Weather 2022, 20, e2022SW00305. [Google Scholar] [CrossRef]
- Wang, C.; Hajj, G.; Pi, X.; Rosen, I.G.; Wilson, B. Development of the Global Assimilative Ionospheric Model. Radio Sci. 2004, 39, RS1S06. [Google Scholar] [CrossRef]
- Schunk, R.W.; Scherliess, L.; Sojka, J.J.; Thompson, D.C.; Anderson, D.N.; Codrescu, M.; Minter, C.; Fuller-Rowell, T.J.; Heelis, R.; Hairston, M.; et al. Global Assimilation of Ionospheric Measurements (GAIM). Radio Sci. 2004, 39, RS1S02. [Google Scholar] [CrossRef]
- Scherliess, L.; Schunk, R.W.; Sojka, J.J.; Thompson, D.C.; Zhu, L. Utah State University Global Assimilation of Ionospheric Measurements Gauss-Markov Kalman filter model of the ionosphere: Model description and validation. J. Geophys. Res. 2006, 111, A11315. [Google Scholar] [CrossRef]
- Helliwell, B. Whistlers and related ionospheric phenomena. Am. J. Phys. 1966, 34, 81. [Google Scholar] [CrossRef]
- Bernstein, S.; Burrows, M.; Evans, J.; Griffiths, A.; McNeill, D.; Niessen, C.; Richer, I.; White, D.; Willim, D. Long-Range Communications at Extremely Low Frequencies. Proc. IEEE 1974, 62, 292–312. [Google Scholar] [CrossRef]
- Crouchley, J. A Study of Whistling Atmospherics. V. Dispersion. Aust. J. Phys. 1964, 17, 88. [Google Scholar] [CrossRef]
- Carpenter, D.L. Remote sensing of the magnetospheric plasma by means of whistler mode signals. Rev. Geophys. 1988, 26, 535–549. [Google Scholar] [CrossRef]
- Menietti, J.D.; Gurnett, D.A. Whistler propagation in jovian magnetoshere. Geophys. Res. Lett. 1980, 7, 49–52. [Google Scholar] [CrossRef]
- Daniell, G.J. Approximate dispersion formulae for whistlers. J. Atmos. Terr. Phys. 1986, 48, 267–270. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, G.; Ni, B.; Zhao, Z.; Gu, X.; Zhou, C.; Wang, F. Development of ground-based ELF/VLF receiver system in Wuhan and its first results. Adv. Space Res. 2016, 57, 1871–1880. [Google Scholar] [CrossRef]
- Cohen, M.B.; Inan, U.S.; Paschal, E.W. Sensitive Broadband ELF/VLF Radio Reception with the AWESOME Instrument. IEEE Trans. Geosci. Remote Sens. 2009, 48, 3–17. [Google Scholar] [CrossRef]
- Farges, T.; Blanc, E. Lightning and TLE electric fields and their impact on the ionosphere. Comptes Rendus Phys. 2011, 12, 171–179. [Google Scholar] [CrossRef]
- Dharma, K.S.; Bayupati, I.; Buana, P.W. Automatic lightning whistler detection using connected component labeling method. J. Theor. Appl. Inf. Technol. 2014, 66, 638–645. Available online: http://www.jatit.org/volumes/Vol66No2/34Vol66No2.pdf (accessed on 1 October 2022).
- Ali Ahmad, U.; Kasahara, Y.; Matsuda, S.; Ozaki, M.; Goto, Y. Automatic Detection of Lightning Whistlers Observed by the Plasma Wave Experiment Onboard the Arase Satellite Using the OpenCV Library. Remote Sens. 2019, 11, 1785. [Google Scholar] [CrossRef]
- Konan, O.; Mishra, A.K.; Lotz, S. Machine Learning Techniques to Detect and Characterise Whistler Radio Waves. arXiv 2020, arXiv:2002.01244. [Google Scholar]
- Bayupati, I.P.A.; Kasahara, Y.; Goto, Y. Study of Dispersion of Lightning Whistlers Observed by Akebono Satellite in the Earth’s Plasmasphere. IEICE Trans. Commun. 2012, 95, 3472–3479. [Google Scholar] [CrossRef]
- Oike, Y.; Kasahara, Y.; Goto, Y. Spatial distribution and temporal variations of occurrence frequency of lightning whistlers observed by VLF/WBA onboard Akebono. Radio Sci. 2014, 49, 753–764. [Google Scholar] [CrossRef]
- Záhlava, J.; Němec, F.; Santolík, O.; Kolmašova, I.; Hospodarskyy, G.B.; Parrot, M.; Kurth, W.S.; Bortnik, J.; Kletzing, C. Longitudinal dependence of whistler mode electromagnetic waves in the Earth’s inner magnetosphere. J. Geophys. Res. Space Phys. 2018, 123, 6562–6575. [Google Scholar] [CrossRef]
- Santolik, O.; Parrot, M.; Inan, U.S.; Buresova, D.; Gurnett, D.A.; Chum, J. Propagation of unducted whistlersfrom their source lightning: A case study. J. Geophys. Res. 2009, 114, A03212. [Google Scholar] [CrossRef]
- Putri, D.P.S.; Kasahara, Y.; Ota, M.; Matsuda, S.; Tsuchiya, F.; Kumamoto, A.; Matsuoka, A.; Miyoshi, Y. A Proposal for Modification of Plasmaspheric Electron Density Profiles Using Characteristics of Lightning Whistlers. Remote Sens. 2023, 15, 1306. [Google Scholar] [CrossRef]
- Coïsson, P.; Hulot, G.; Vigneron, P.; Deram, P.; Léger, J.M.; Jager, T. 0+ whistlers in the ELF band recorded by Swarm satellites used to reconstruct the ionosphere below the satellite height. In Geophysical Research Abstracts; EGU General Assembly: Vienna, Austria, 2019; Volume 21. [Google Scholar]
- Huang, J.; Shen, X.; Zhang, X.; Lu, H.; Tan, Q.; Wang, Q.; Yan, R.; Chu, W.; Yang, Y.; Liu, D.; et al. Application system and data description of the China Seismo-Electromagnetic Satellite. Earth Planet. Phys. 2018, 2, 444–454. [Google Scholar] [CrossRef]
- Huang, J.; Lei, J.; Li, S.; Zeren, Z.; Li, C.; Zhu, X.; Yu, W. The Electric Field Detector (EFD) onboard the ZH-1 satellite and first observational results. Earth Planet. Phys. 2018, 2, 469–478. [Google Scholar] [CrossRef]
- Zhima, Z.; Huang, J.; Shen, X.; Xia, Z.; Chen, L.; Piersanti, M.; Yang, Y.; Wang, Q.; Zeng, L.; Lei, J.; et al. Simultaneous observations of ELF/VLF rising-tone quasiperiodic waves and energetic electron precipitations in the high-latitude upper ionosphere. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027574. [Google Scholar] [CrossRef]
- Bilitza, D. International Reference Ionosphere 2000. Radio Sci. 2016, 36, 261–275. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82D, 35–45. [Google Scholar] [CrossRef]
- Lefeuvre, F.; Marshall, R.; Pinc, J.L.; Inan, U.S.; Lagoutte, D.; Parrot, M.; Berthelier, J.J. On remote sensing oftransient luminous events’ parent lightning discharges by ELF/VLF wave measurements on board a satellite. J. Geophys. Res. 2009, 114, A09303. [Google Scholar] [CrossRef]
- Kang, N.; Bortnik, J. Structure of energy precipitation induced by superbolt-lightning generated whistler waves. Geophys. Res. Lett. 2022, 49, e2022GL097770. [Google Scholar] [CrossRef]
- Booker, H.G. The magneto-ionic theory and its application to the ionosphere: J. A. RATCLIFFE: Cambridge University Press, 1959. x + 206pp., 40s. J. Atmos. Terr. Phys. 1959, 16, 398. [Google Scholar] [CrossRef]
- Belrose, J.S.; Burke, M.J. Study of the Lower Ionosphere using Partial Reflection: 1. Experimental Technique and Method of Analysis. J. Geophys. Res. 1964, 69, 2799–2818. [Google Scholar] [CrossRef]
- Kane, J. Re-evaluation of ionospheric electron densities and collision frequencies derived from rocket measurements of refractive index and attenuation. J. Atmos. Terr. Phy. 1961, 23, 338–347. [Google Scholar] [CrossRef]
- Fišer, J.; Chum, J.; Diendorfer, G.; Parrot, M.; Santolik, O. Whistler intensities above thunderstorms. Ann. Geophys. 2010, 28, 37–46. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, T.; Liu, M.; He, S.; Zhou, C. Assimilation and Inversion of Ionospheric Electron Density Data Using Lightning Whistlers. Remote Sens. 2023, 15, 3037. https://doi.org/10.3390/rs15123037
Xiang T, Liu M, He S, Zhou C. Assimilation and Inversion of Ionospheric Electron Density Data Using Lightning Whistlers. Remote Sensing. 2023; 15(12):3037. https://doi.org/10.3390/rs15123037
Chicago/Turabian StyleXiang, Tian, Moran Liu, Shimin He, and Chen Zhou. 2023. "Assimilation and Inversion of Ionospheric Electron Density Data Using Lightning Whistlers" Remote Sensing 15, no. 12: 3037. https://doi.org/10.3390/rs15123037
APA StyleXiang, T., Liu, M., He, S., & Zhou, C. (2023). Assimilation and Inversion of Ionospheric Electron Density Data Using Lightning Whistlers. Remote Sensing, 15(12), 3037. https://doi.org/10.3390/rs15123037






