High-Accuracy Positioning in GNSS-Blocked Areas by Using the MSCKF-Based SF-RTK/IMU/Camera Tight Integration
Abstract
1. Introduction
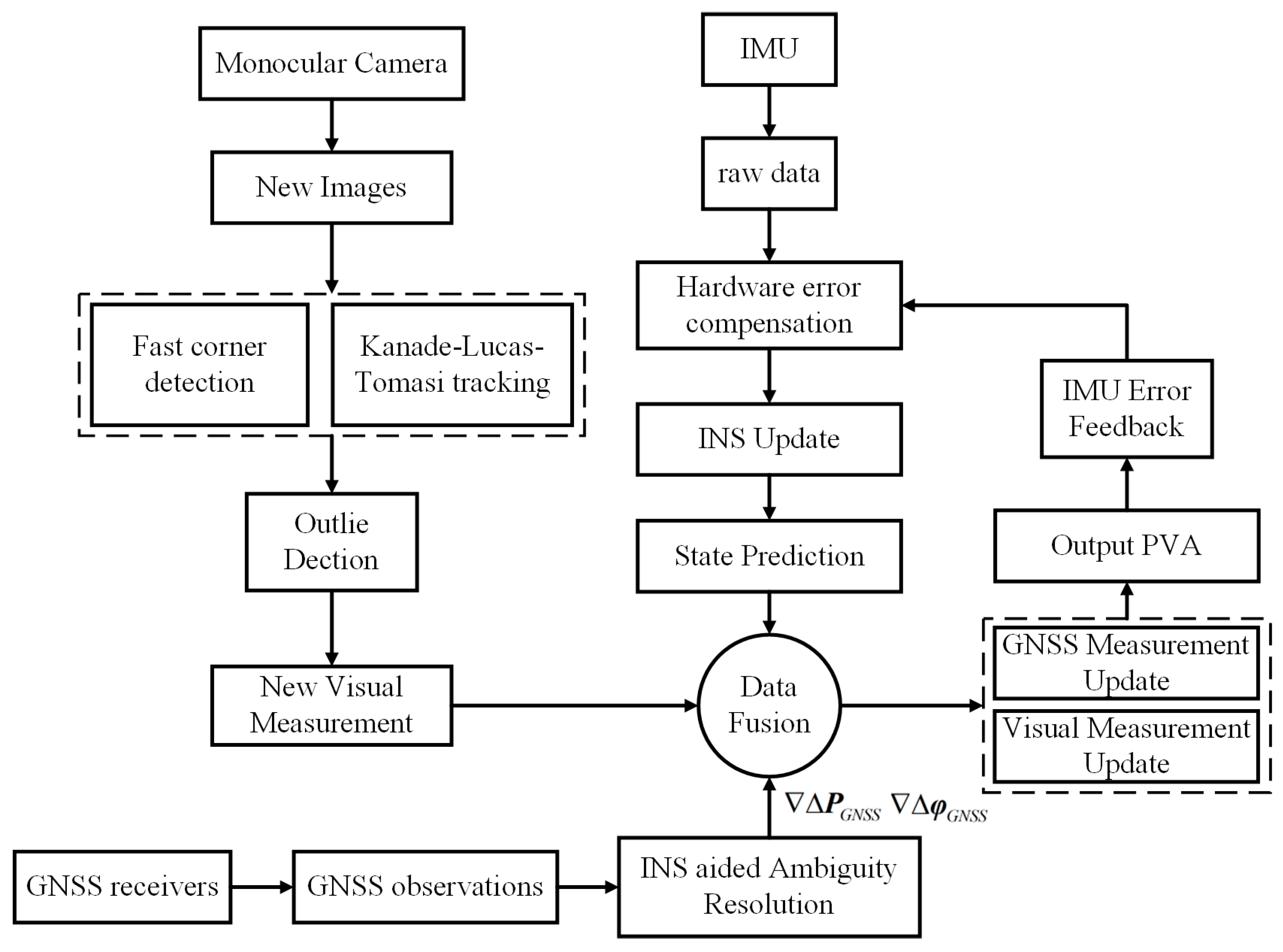
2. Methods
2.1. State Model
2.2. GNSS Measurement Model
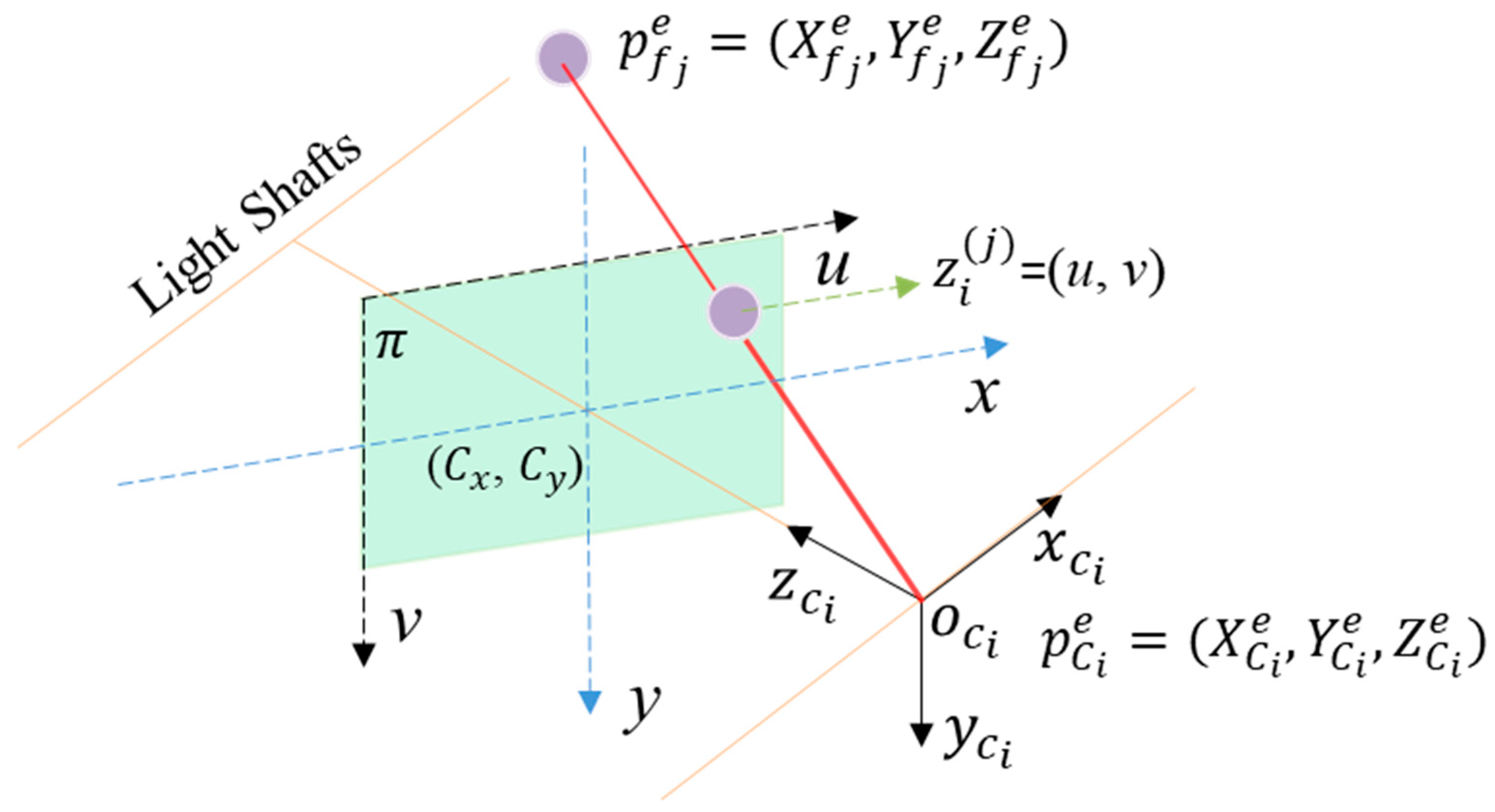
2.3. Visual Measurement Model
2.4. Robust MSCKF
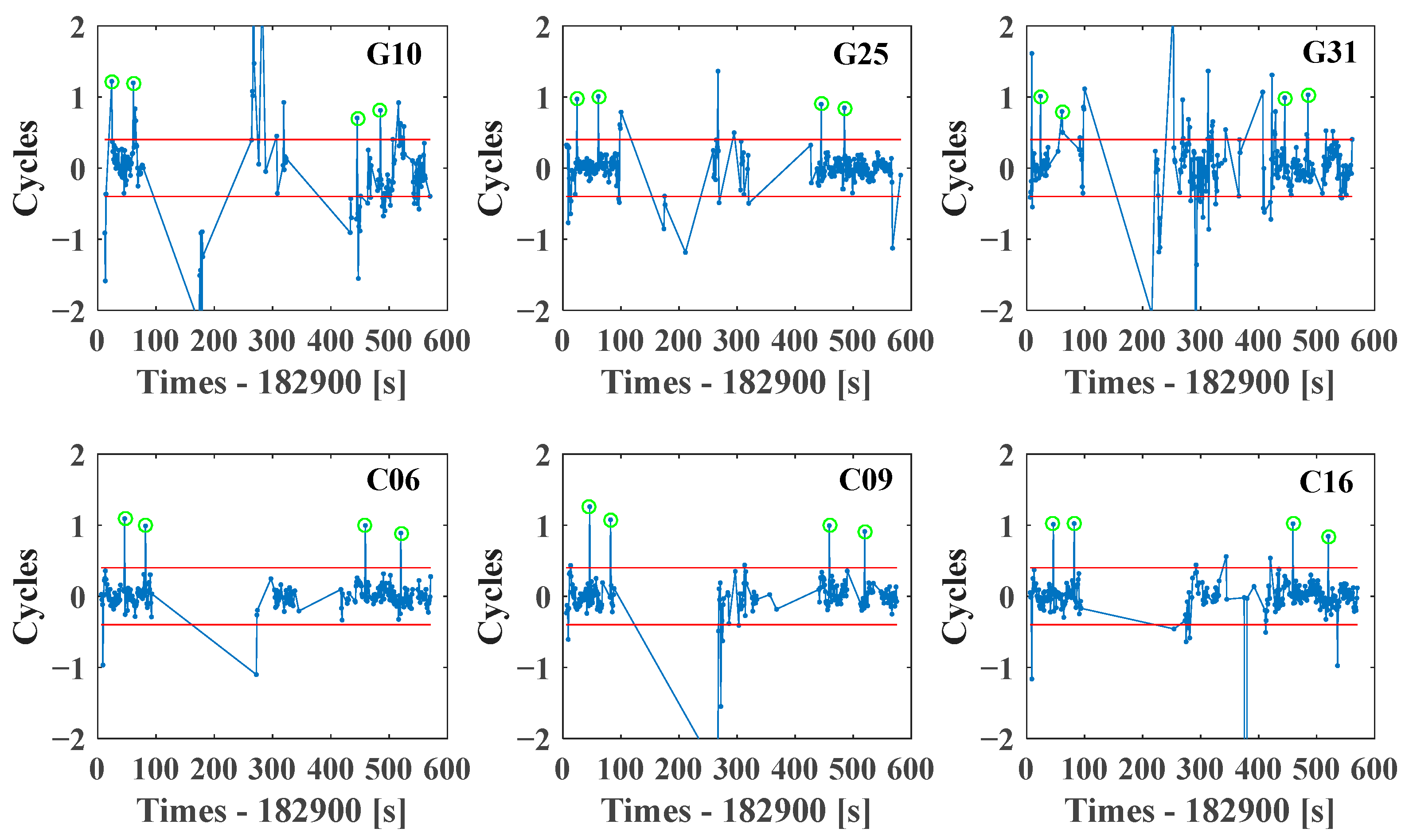
2.5. Sensors-Aided Cycle Slip Detection
2.6. Algorithm Summary
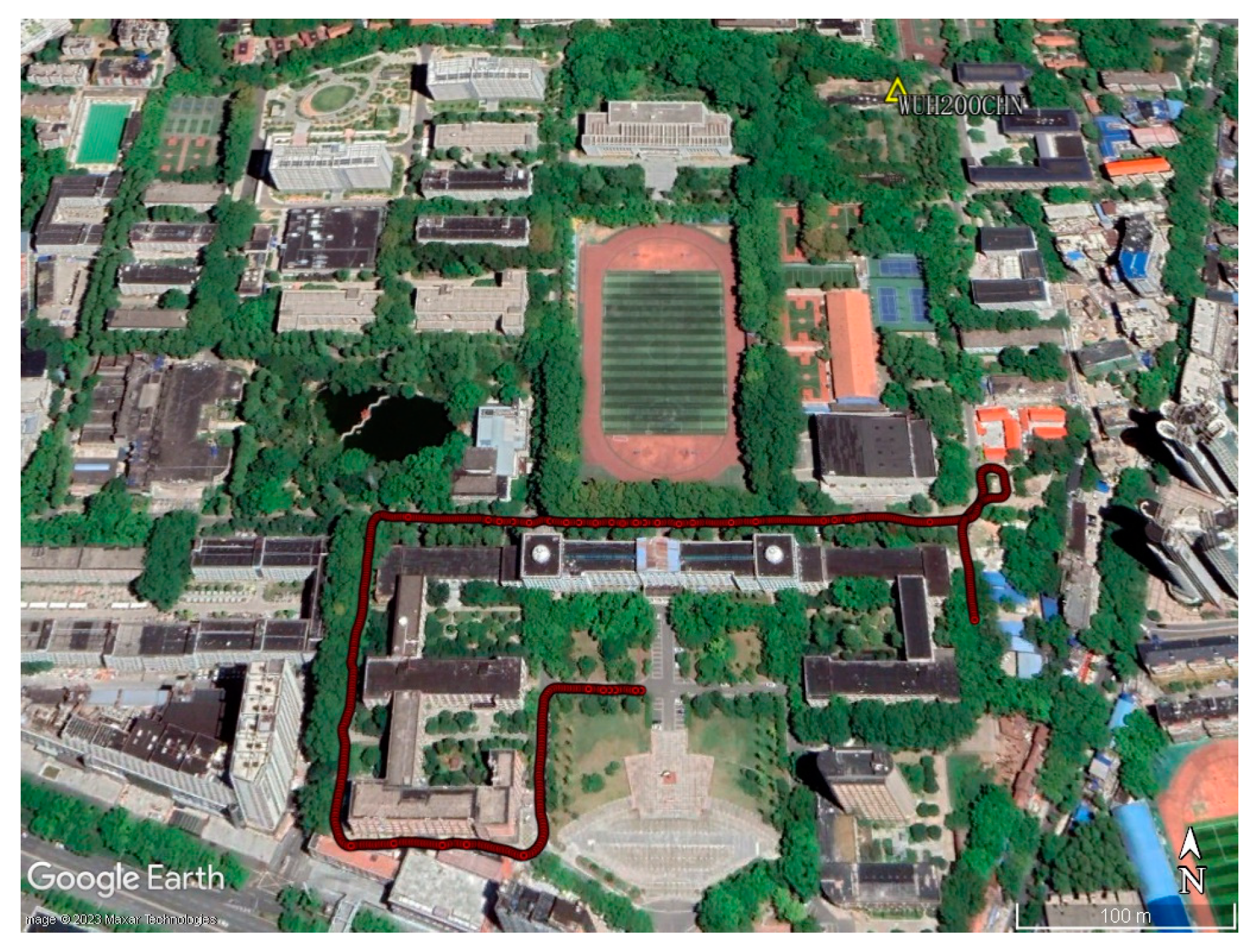
3. Experiments and Data Processing Schemes
4. Discussions
4.1. Sensors-Aided Cycle Slip Detection
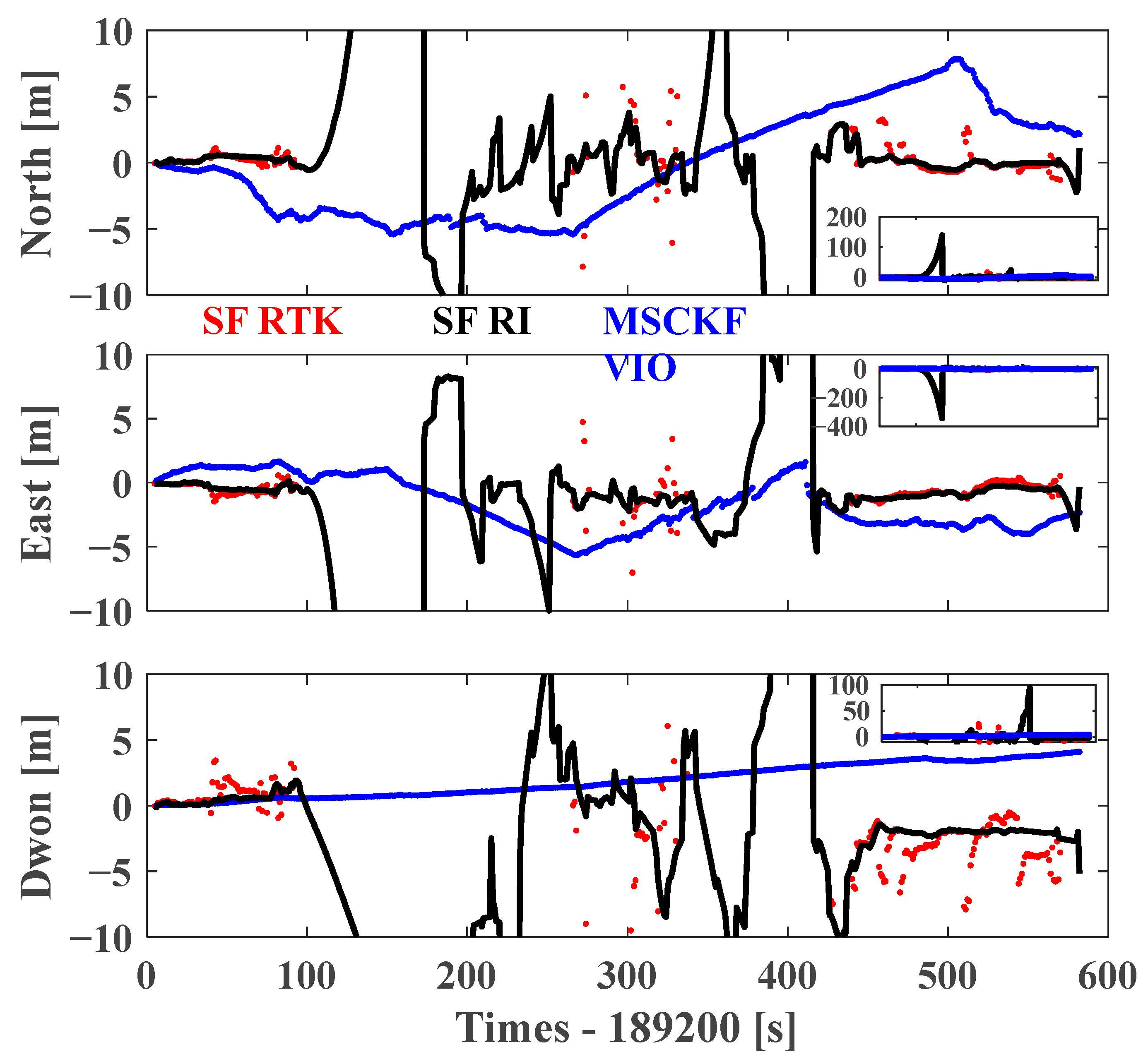
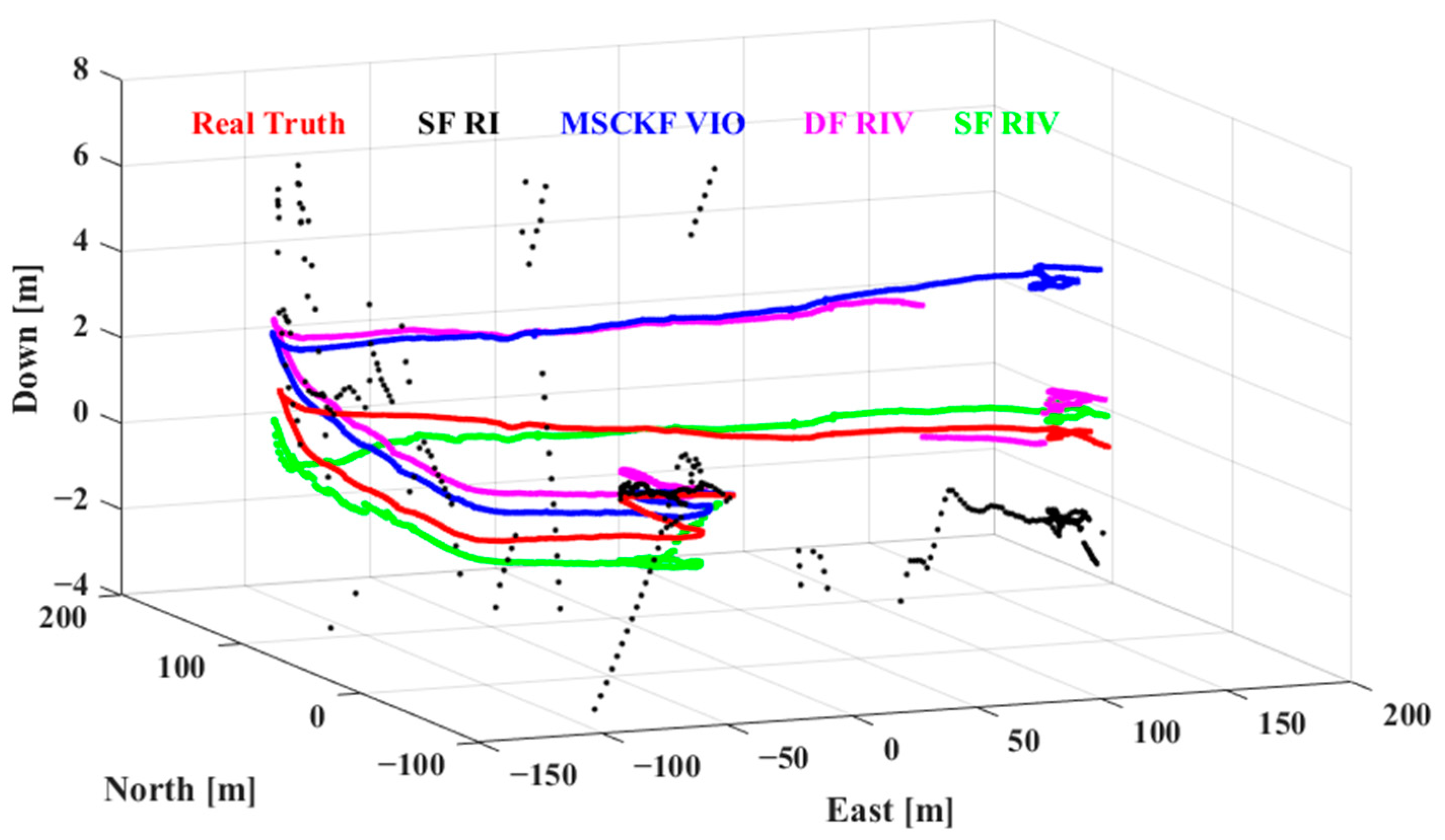
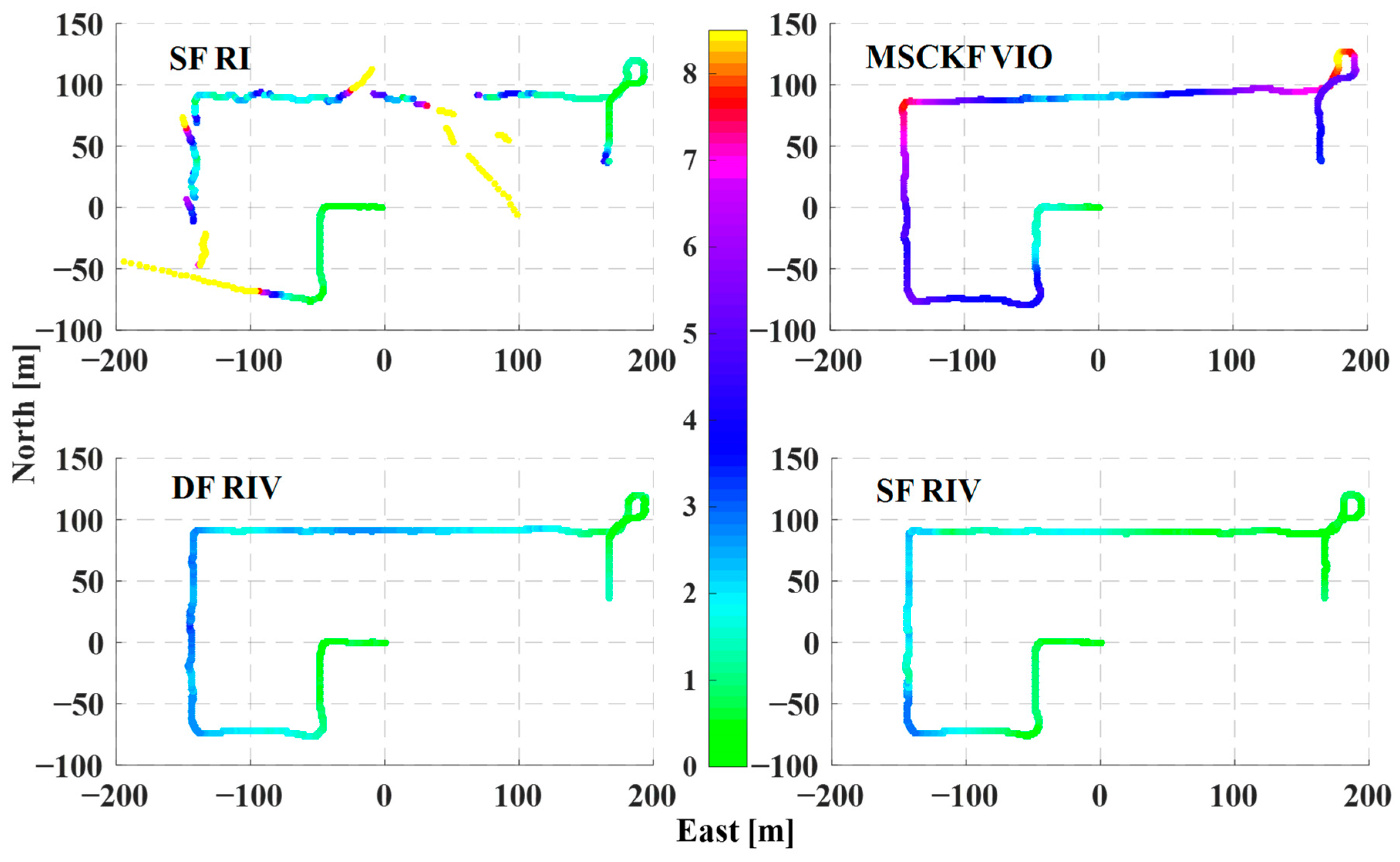
4.2. Enhancements in Positioning Accuracy
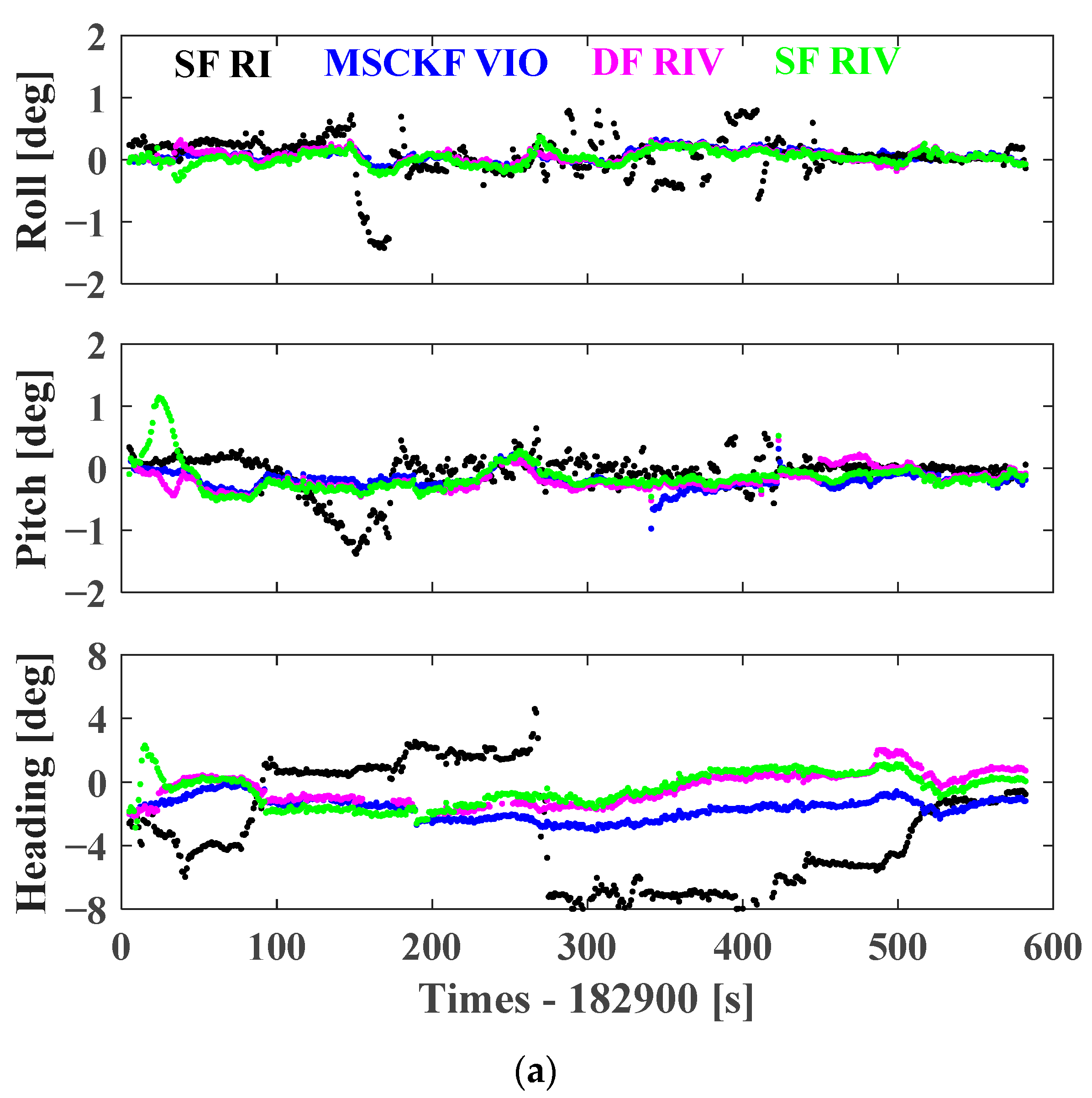
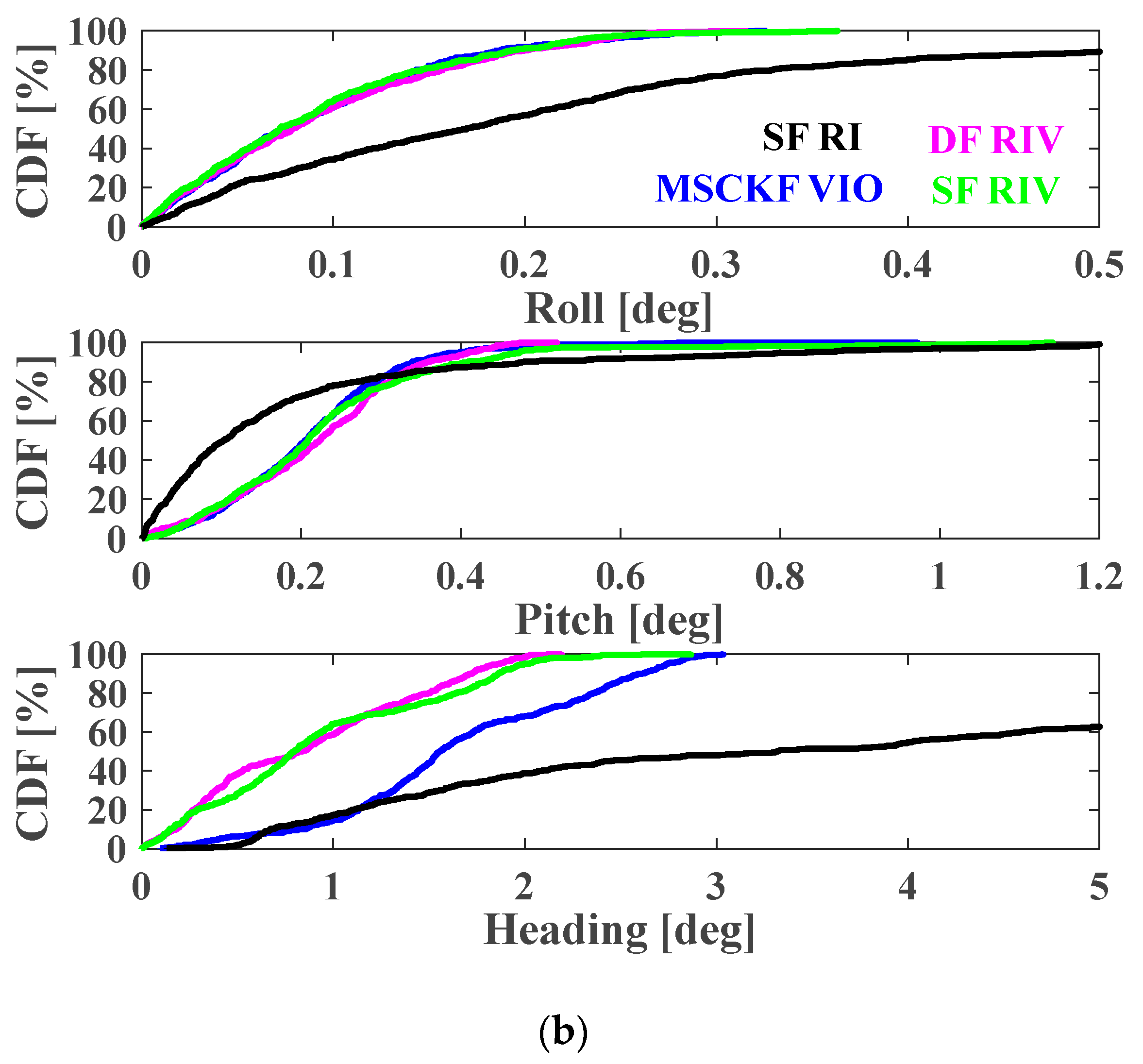
4.3. Contributions to Attitude Determination
4.4. Analysis of Running Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhuang, Y.; Sun, X.; Li, Y.; Huai, J.; Hua, L.; Yang, X.; Cao, X.; Zhang, P.; Cao, Y.; Qi, L.; et al. Multi-sensor integrated navigation/positioning systems using data fusion: From analytics-based to learning-based approaches. Inf. Fusion 2023, 95, 62–90. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Z.; Xu, Q.; Li, Y.; Chen, L. Assessing partial ambiguity resolution and WZTD-constraint multi-frequency RTK in an urban environment using new BDS signals. GPS Solut. 2022, 8, 88. [Google Scholar] [CrossRef]
- Yuan, Y.; Mi, X.; Zhang, B. Initial assessment of single-and dual-frequency BDS-3 RTK positioning. Satell. Navig. 2020, 1, 31. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China-Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Z.; He, X.; Wen, Y.; Zeng, J. An Extended robust estimation method considering the multipath effects in GNSS real-time kinematic positioning. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Li, Z.; Xu, G.; Guo, J.; Zhao, Q. A sequential ambiguity selection strategy for partial ambiguity resolution during RTK positioning in urban areas. GPS Solut. 2022, 26, 92. [Google Scholar] [CrossRef]
- Li, B.; Liu, T.; Nie, L.; Qin, Y. Single-frequency GNSS cycle slip estimation with positional polynomial constraint. J. Geod. 2019, 93, 1781–1803. [Google Scholar] [CrossRef]
- Niu, X.; Zhang, Q.; Gong, L.; Liu, C.; Zhang, H.; Shi, C. Development and evaluation of GNSS/INS data processing software for position and orientation systems. Surv. Rev. 2015, 47, 87–98. [Google Scholar] [CrossRef]
- Hu, G.; Gao, B.; Zhong, Y.; Gu, C. Unscented Kalman Filter with Process Noise Covariance Estimation for Vehicular INS/GPS Integration System. Inf. Fusion 2020, 64, 194–204. [Google Scholar] [CrossRef]
- Petovello, M.G.; Cannon, M.E.; Lachapelle, G. Benefits of Using a Tactical-Grade IMU for High-Accuracy Positioning. Navigation 2004, 51, 1–12. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Gao, Z.; Chen, Q.; Niu, X. High-Accuracy Positioning in Urban Environments Using Single-Frequency Multi-GNSS RTK/MEMS-IMU Integration. Remote Sens. 2018, 10, 205. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhong, Y.; Zhu, X. Cubature Kalman Filter With Both Adaptability and Robustness for Tightly-Coupled GNSS/INS Integration. Inf. Fusion 2021, 21, 14997–15011. [Google Scholar] [CrossRef]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual-inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2015, 34, 314–334. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar]
- Usenko, V.; Demmel, N.; Schubert, D.; Stückler, J.; Cremers, D. Visual-Inertial Mapping with Non-Linear Factor Recovery. IEEE Robot. Autom. Lett. 2019, 5, 422–429. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tard´os, J.D. Visual-inertial monocular SLAM with map reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Mourikis, A.I.; Roumeliotis, S.I. A multi-state constraint Kalman fifilter for vision-aided inertial navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar]
- Huang, G.P.; Mourikis, A.I.; Roumeliotis, S.I. Analysis and improvement of the consistency of extended Kalman filter based SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 473–479. [Google Scholar]
- Li, M.; Mourikis, A.I. Improving the Accuracy of EKF-Based Visual-Inertial Odometry. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 828–835. [Google Scholar]
- Sibley, G.; Matthies, L.; Sukhatme, G. Sliding window filter with application to planetary landing. J. Field Robot. 2010, 27, 587–608. [Google Scholar] [CrossRef]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Li, M.; Mourikis, A.I. High-precision, consistent EKF-based visual-inertial odometry. Int. J. Robot. Res. 2013, 32, 690–711. [Google Scholar] [CrossRef]
- Lynen, S.; Achtelik, M.W.; Weiss, S.; Chli, M.; Siegwart, R. A robust and modular multi-sensor fusion approach applied to mav navigation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3923–3929. [Google Scholar]
- Niu, X.; Tang, H.; Zhang, T.; Fan, J.; Liu, J. IC-GVINS: A Robust, Real-time, INS-Centric GNSS-Visual-Inertial Navigation System for Wheeled Robot. IEEE Robot. Autom. Lett. 2022, 5, 216–223. [Google Scholar] [CrossRef]
- Liao, J.; Li, X.; Wang, X.; Li, S.; Wang, H. Enhancing navigation performance through visual-inertial odometry in GNSS-degraded environment. GPS Solut. 2021, 25, 50. [Google Scholar] [CrossRef]
- Cao, S.; Lu, X.; Shen, S. GVINS: Tightly Coupled GNSS-Visual-Inertial for Smooth and Consistent State Estimation. IEEE Trans. Robot. 2022, 38, 2004–2021. [Google Scholar] [CrossRef]
- Won, D.H.; Lee, E.; Heo, M.; Sung, S.; Lee, J.; Lee, Y. GNSS integration with vision-based navigation for low GNSS visibility conditions. GPS Solut. 2014, 18, 177–187. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, S.; Zhou, Y.; Sun, M.; Xu, Q.; Xu, Z. Centimeter-accurate vehicle navigation in urban environments with a tightly integrated PPP-RTK/MEMS/vision system. GPS Solut. 2022, 26, 124. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Gao, Z.; Niu, X.; EI-sheimy, N. Tight Fusion of a Monocular Camera, MEMS-IMU, and Single-Frequency Multi-GNSS RTK for Precise Navigation in GNSS-Challenged Environments. Remote Sens. 2019, 11, 610. [Google Scholar] [CrossRef]
- Shin, E.H. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Dissertation, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Gao, Z.; Ge, M.; Shen, W.; Zhang, H.; Niu, X. Ionospheric and receiver DCB-constrained multi-GNSS single-frequency PPP integrated with MEMS inertial measurements. J. Geod. 2017, 91, 1351–1366. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Shen, W.; You, L.; Chen, Q.; Zhang, H.; Niu, X. Evaluation on the impact of IMU grades on BDS+GPS PPP/INS tightly coupled integration. Adv. Space Res. 2017, 60, 1283–1299. [Google Scholar] [CrossRef]
- Xu, Q.; Gao, Z.; Lv, J.; Yang, C. Tightly Coupled Integration of BDS-3 B2b RTK, IMU, Odometer, and Dual-Antenna Attitude. IEEE Internet Things J. 2022, 10, 6415–6427. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Li, T. Research on the Tightly Coupled Single-Frequency Multi-GNSS/INS/Vision Integration for Precise Position and Orientation Estimation. Ph.D. Dissertation, University of Wuhan, Wuhan, China, 2019. [Google Scholar]
- Jin, R.; Liu, J.; Zhang, H.; Niu, X. Fast and accurate initialization for monocular vision/INS/GNSS integrated system on land vehicle. IEEE Sens. J. 2021, 21, 26074–26085. [Google Scholar] [CrossRef]
- Teunnissen, P.J.G. The least-square ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Du, Z.; Chai, H.; Xiao, G.; Yin, X.; Wang, M.; Xiang, M. Analyzing the contributions of multi-GNSS and INS to the PPP-AR outage re-fixing. GPS Solut. 2021, 25, 81. [Google Scholar] [CrossRef]
- Trajkovic, M.; Hedley, M. Fast corner detection. Image Vis. Comput. 1998, 16, 75–87. [Google Scholar] [CrossRef]
- Lucas, B.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the International Joint Conference on Artifcial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; pp. 24–28. [Google Scholar]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust stereo visual inertial odometry for fast autonomous fight. IEEE Robot. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef]
- Zuo, X.; Geneva, P.; Lee, W.; Liu, Y.; Huang, G. LIC-fusion: Lidar-inertial-camera odometry. In Proceedings of the IEEE/RSJ IROS 2019, Macau, China, 4–8 November 2019; pp. 5848–5854. [Google Scholar]
- Chen, G.; Li, B.; Zhang, Z.; Liu, T. Integer ambiguity resolution and precise positioning for tight integration of BDS-3, GPS, GALILEO, and QZSS overlapping frequencies signals. GPS Solut. 2022, 26, 26. [Google Scholar]
- Ge, Y.; Cao, X.; Lyu, D.; He, Z.; Ye, F.; Xiao, G.; Shen, F. An investigation of PPP time transfer via BDS-3 PPP-B2b service. GPS Solut. 2023, 27, 61. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, Q.; Gao, W.; Li, J.; Xu, Y.; Sun, B. Principle and performance of BDSBAS and PPP-B2b of BDS-3. Satell. Navig. 2022, 3, 5. [Google Scholar] [CrossRef]
- Nezhadshahbodaghi, M.; Mosavi, M.R.; Hajialinajar, M.T. Fusing denoised stereo visual odometry, INS and GPS measurements for autonomous navigation in a tightly coupled approach. GPS Solut. 2021, 25, 47. [Google Scholar] [CrossRef]







| Bias | Random Walk | ||
|---|---|---|---|
| Acce. (mGal) | |||
| 36 | 3000 | 3.17 | 2.7 |
| Mode | Visual Data | IMU Data | Dual Frequency GNSS Data | Single Frequency GNSS Data |
|---|---|---|---|---|
| MSCKF VIO | Δ | Δ | ||
| SF-RI | Δ | Δ | ||
| DF-RIV | Δ | Δ | Δ | |
| SF-RIV | Δ | Δ | Δ |
| Modes | SF RTK | SF RI | MSCKF VIO | DF RIV | SF RIV |
|---|---|---|---|---|---|
| North (m) | 1.84 | 22.72 | 4.01 | 1.33 | 0.88 |
| East (m) | 1.33 | 49.91 | 2.67 | 0.99 | 0.88 |
| Down (m) | 5.09 | 15.08 | 2.26 | 1.60 | 0.65 |
| Modes | SF RI | MSCKF VIO | DF RIV | SF RIV |
|---|---|---|---|---|
| Roll (°) | 0.35 | 0.11 | 0.12 | 0.11 |
| Pitch (°) | 0.36 | 0.24 | 0.24 | 0.28 |
| Heading (°) | 4.57 | 1.79 | 1.04 | 1.04 |
| Types | Time (ms) |
|---|---|
| Feature detecting and tracking | 26.42 |
| Visual measurement update | 59.24 |
| GNSS measurement processing | 1.36 |
| Total | 87.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Gao, Z.; Yang, C.; Lv, J. High-Accuracy Positioning in GNSS-Blocked Areas by Using the MSCKF-Based SF-RTK/IMU/Camera Tight Integration. Remote Sens. 2023, 15, 3005. https://doi.org/10.3390/rs15123005
Xu Q, Gao Z, Yang C, Lv J. High-Accuracy Positioning in GNSS-Blocked Areas by Using the MSCKF-Based SF-RTK/IMU/Camera Tight Integration. Remote Sensing. 2023; 15(12):3005. https://doi.org/10.3390/rs15123005
Chicago/Turabian StyleXu, Qiaozhuang, Zhouzheng Gao, Cheng Yang, and Jie Lv. 2023. "High-Accuracy Positioning in GNSS-Blocked Areas by Using the MSCKF-Based SF-RTK/IMU/Camera Tight Integration" Remote Sensing 15, no. 12: 3005. https://doi.org/10.3390/rs15123005
APA StyleXu, Q., Gao, Z., Yang, C., & Lv, J. (2023). High-Accuracy Positioning in GNSS-Blocked Areas by Using the MSCKF-Based SF-RTK/IMU/Camera Tight Integration. Remote Sensing, 15(12), 3005. https://doi.org/10.3390/rs15123005






