MCPT: Mixed Convolutional Parallel Transformer for Polarimetric SAR Image Classification
Abstract
1. Introduction
- (1)
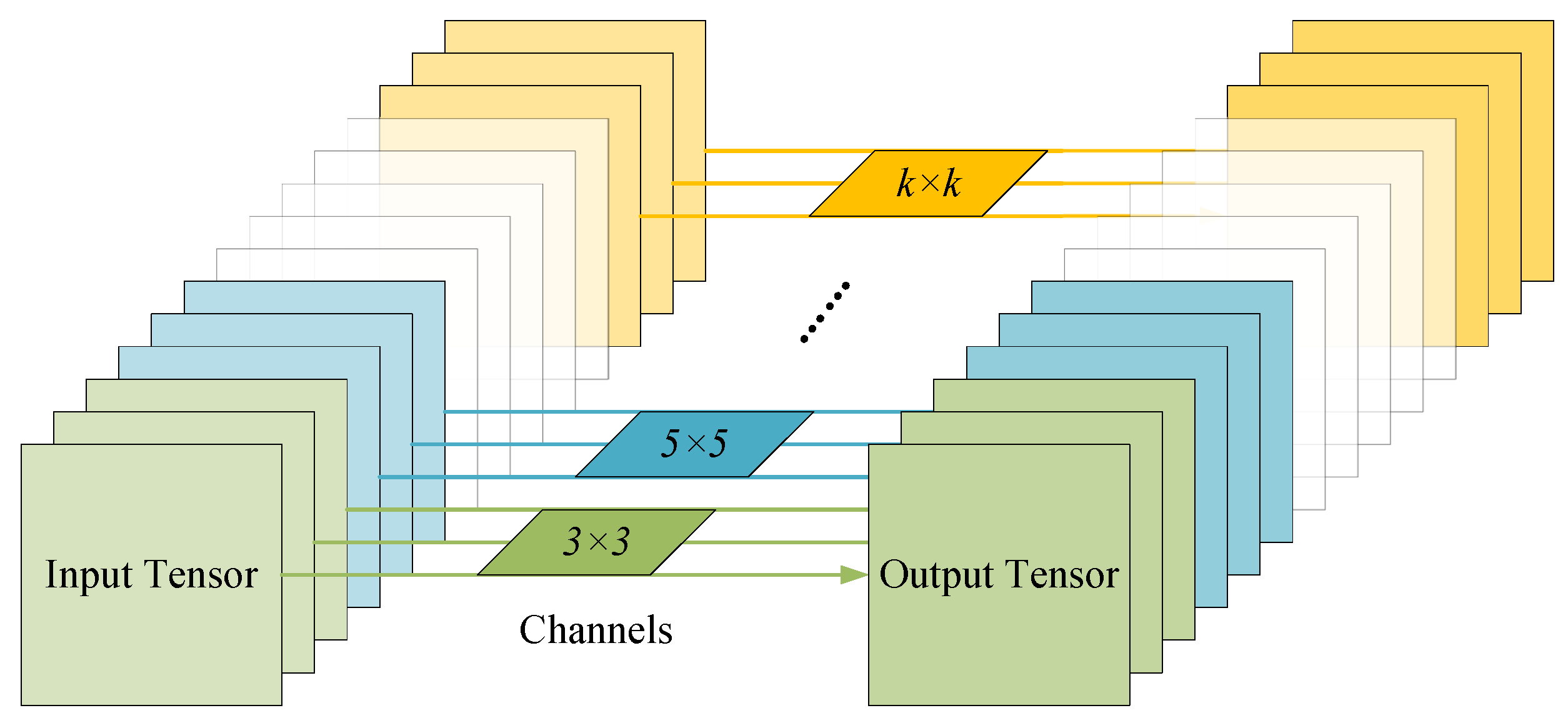
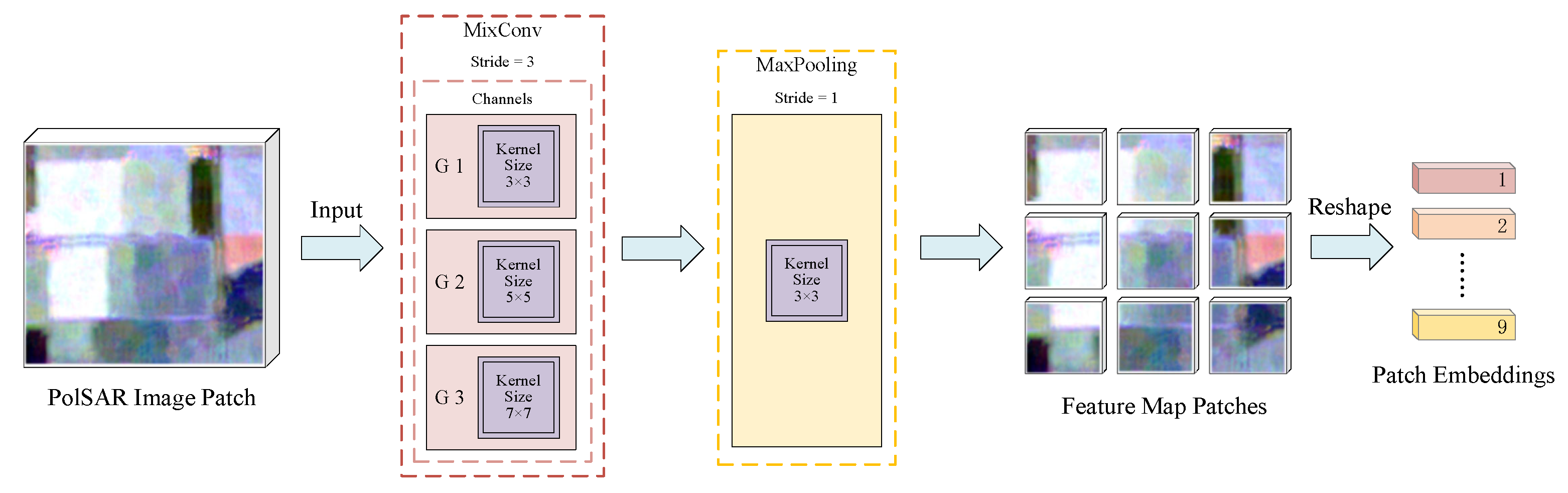
- Mixed depthwise convolution tokenization. A mixed depthwise convolution (MixConv) is introduced in the data pre-processing part of the model for the tokenization of the input data, which replaces the linear projection used in the original ViT. MixConv naturally mixes multiple kernel sizes in a single convolution and can extract feature maps with different receptive fields at the same time. This tokenization process makes the proposed method more flexible than the original ViT. It is no longer limited by the input resolution, which must be strictly divisible by a pre-defined patch size. It also facilitates the removal of position embedding and enriches training data information. Additionally, the class and position embeddings in ViT are removed, further reducing the number of parameters and computation cost.
- (2)
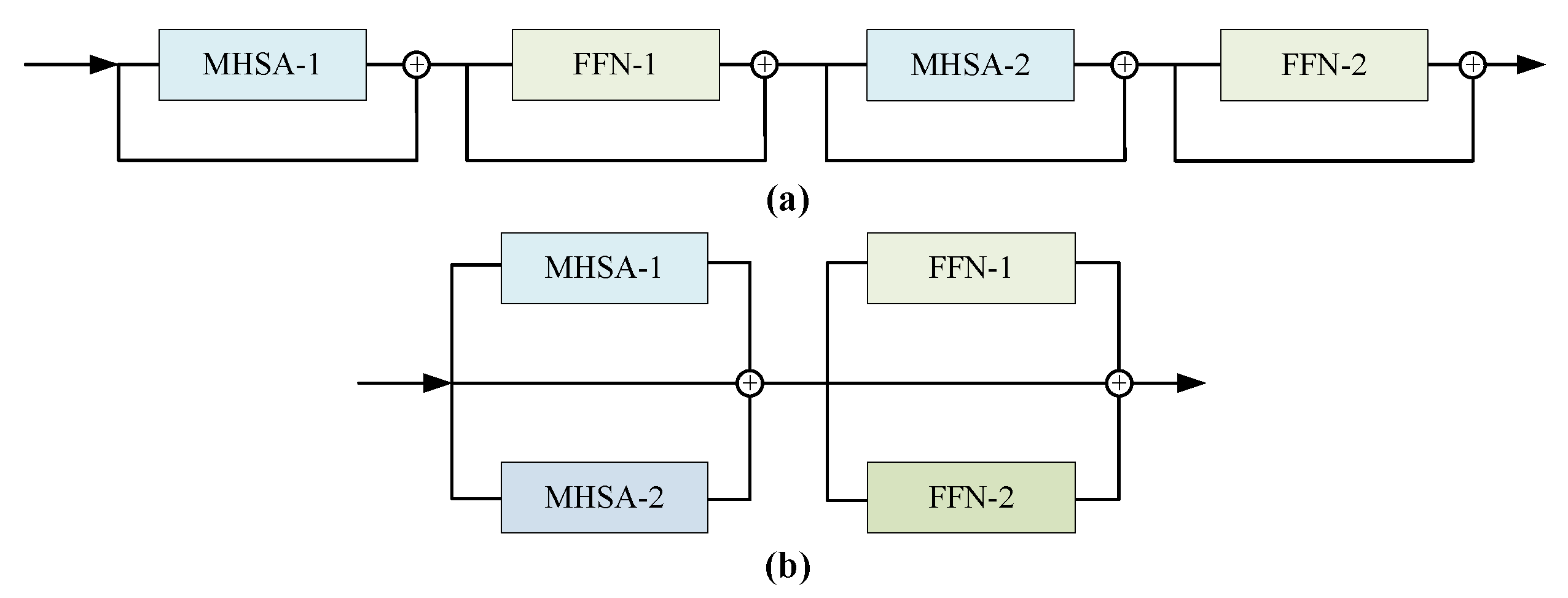
- Parallel encoder. The idea of parallel structure is introduced to implement an parallel encoder. It can still have a relatively low depth when superimposed with multiple encoders during training, thus achieving a lower latency and making it easier to optimize. Consequently, the speed of training and prediction is accelerated and good training results can be achieved even on less powerful personal platforms.
- (3)
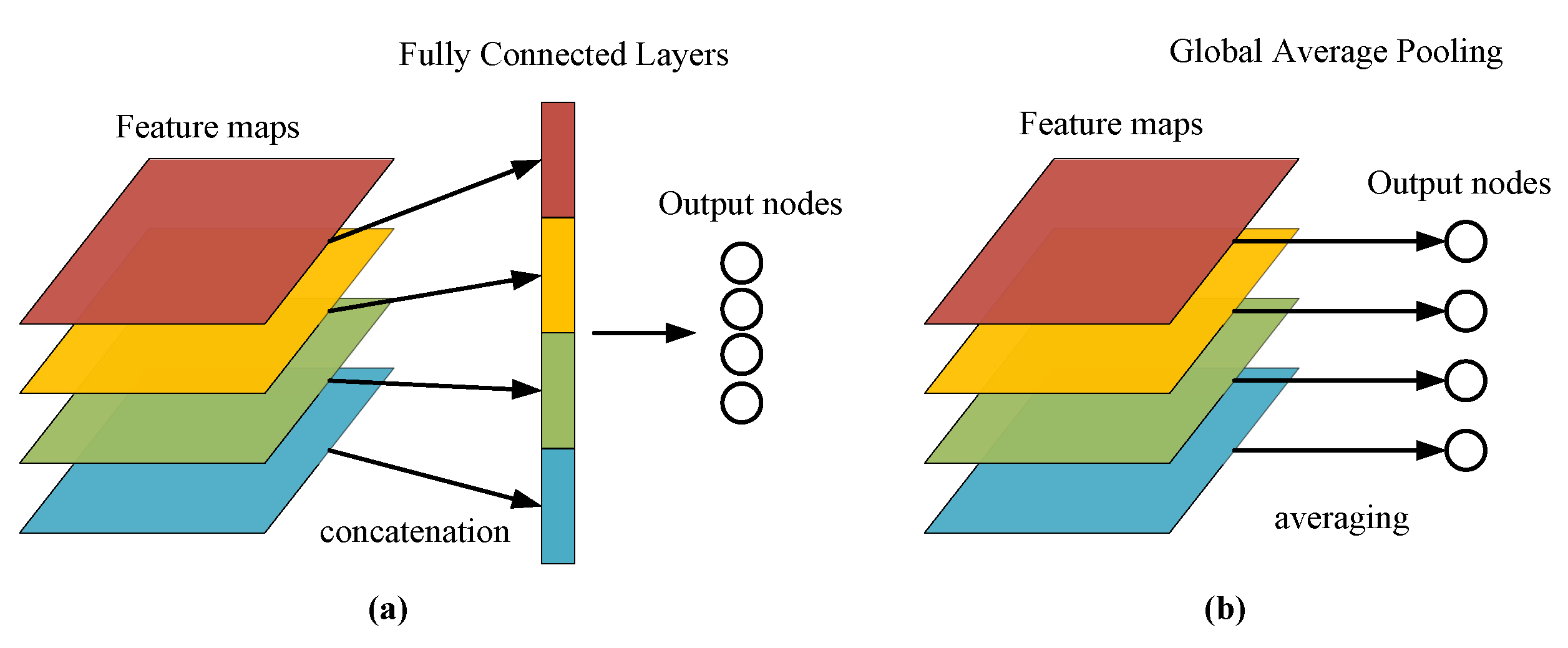
- Global average pooling. The global average pooling (GAP) method is used as a substitute for class embedding. A GAP layer is added after the encoder and the average of all the pixels in the feature maps of each channel is taken to give an output. This operation is simple and effective, does not increase additional parameters, and avoids over-fitting. It summarizes spatial information and is more stable to spatial transformations of the input.
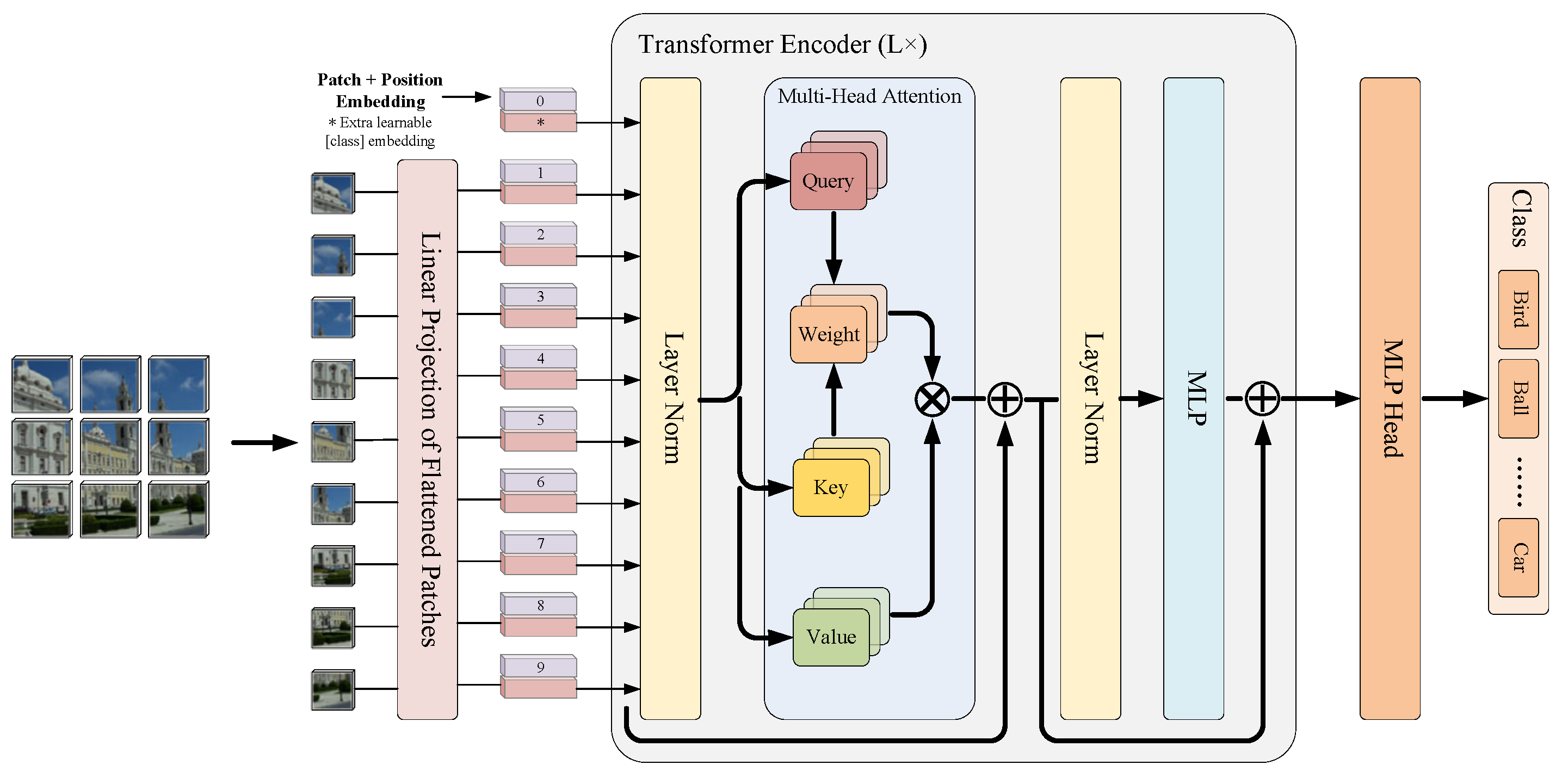
2. The Proposed Method
2.1. Mixed Depthwise Convolution Tokenization
2.2. Parallel Encoder
2.3. Global Average Pooling
3. Experimental Analysis and Results
3.1. Datasets Description
- (1)
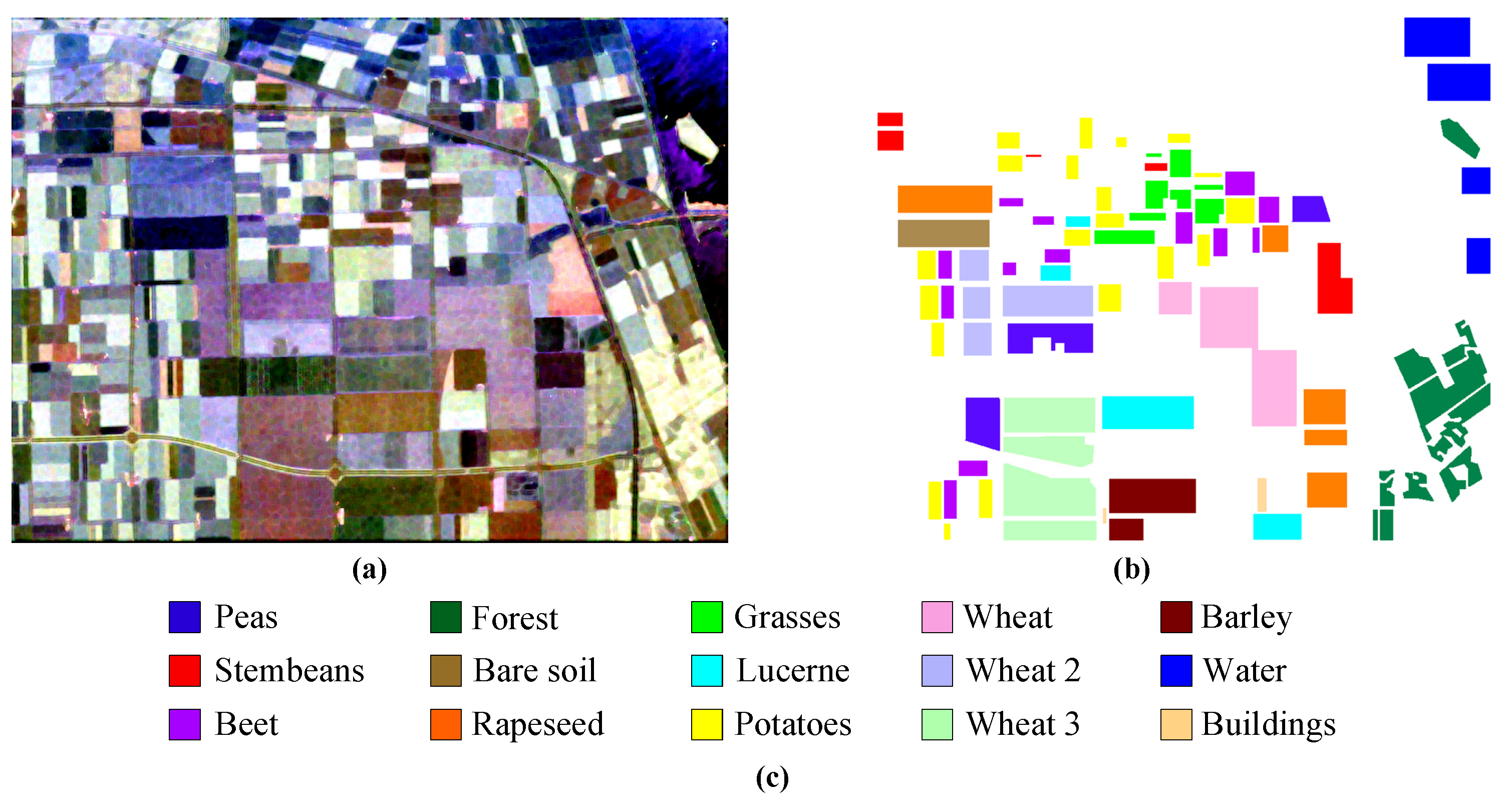
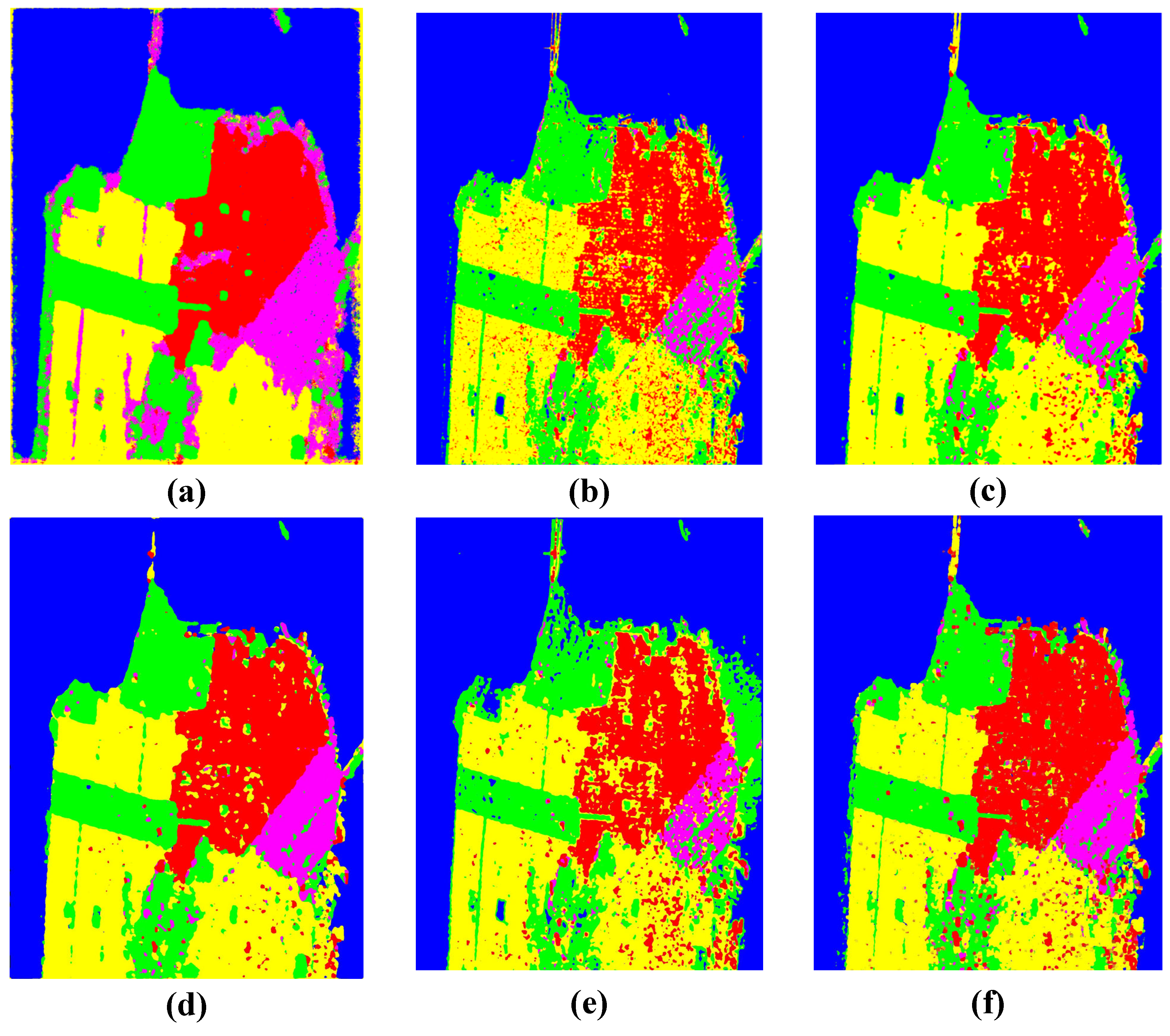
- AIRSAR Flevoland: The Flevoland image is a 750 × 1024 subimage of the L-band multi-view PolSAR dataset acquired by the AIRSAR platform on 16 August 1989. The ground resolution of the image is 6.6 m × 12.1 m, and it includes 15 kinds of ground objects, each represented by a unique color. Figure 7a illustrates the Pauli map and Figure 7b shows the ground truth map of the dataset. Figure 7c shows the corresponding ground truth map and legend of the dataset, which consists of 167,712 labeled pixels [64].
- (2)
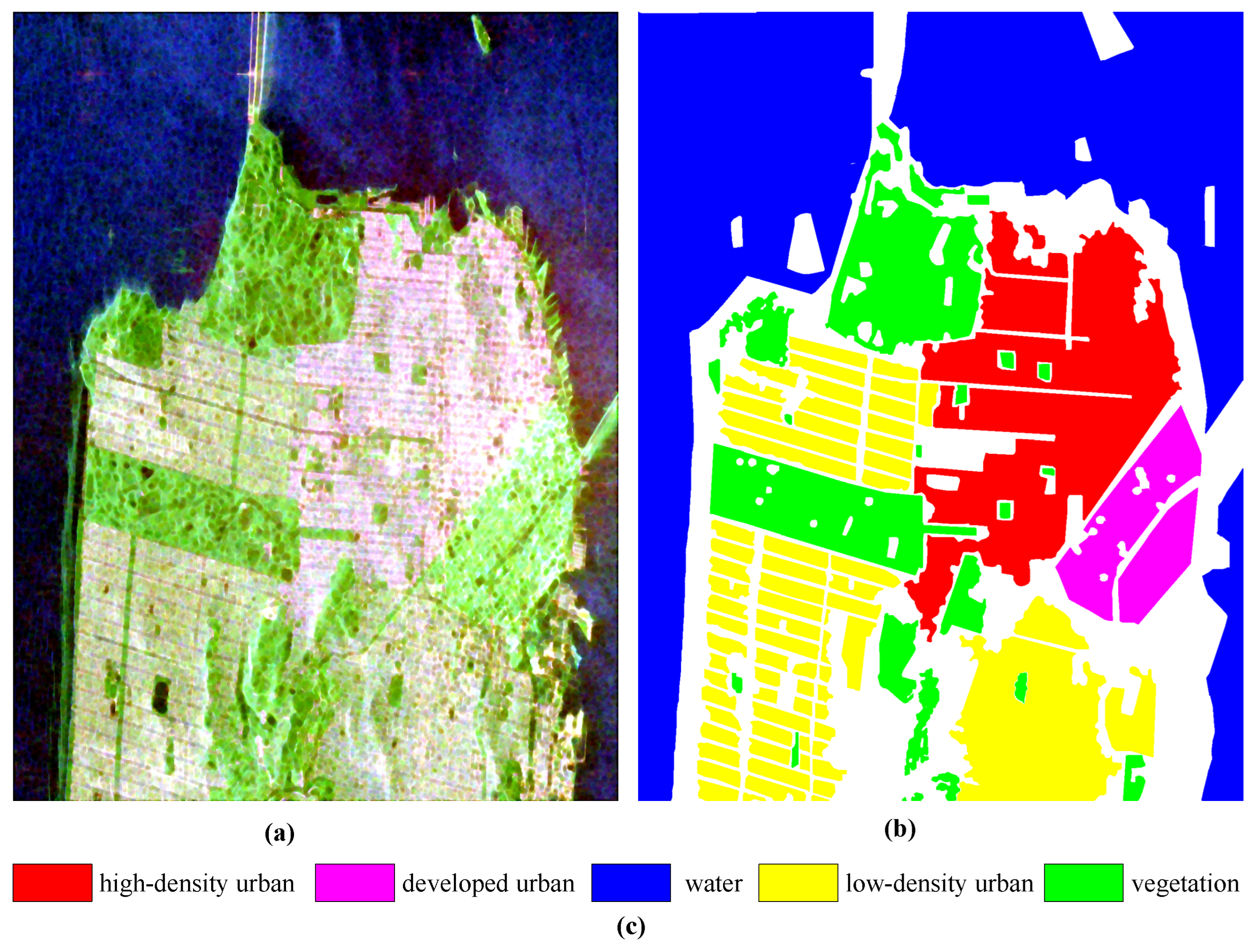
- RADARSAT-2 San Francisco: The second dataset is a San Francisco Bay Area image with C-band acquired by the RADARSAT-2 satellite. Figure 8a displays the PauliRGB image of the selected scene with a size of 1380 × 1800, which primarily contains five land cover types: high-density urban areas, water, vegetation, developed urban areas, and low-density urban areas. Figure 8b shows the ground truth map consisting of 1804087 pixels with known label information. Figure 8c respectively show the corresponding ground truth map and the legend explaining the land cover types [65].
3.2. Experimental Setup
3.3. Classification Results
3.3.1. Experimental Results on The AIRSAR Flevoland Dataset
3.3.2. Experiment Results on The RADARSAT-2 San Francisco Dataset
4. Discussion
4.1. Ablation Experiments
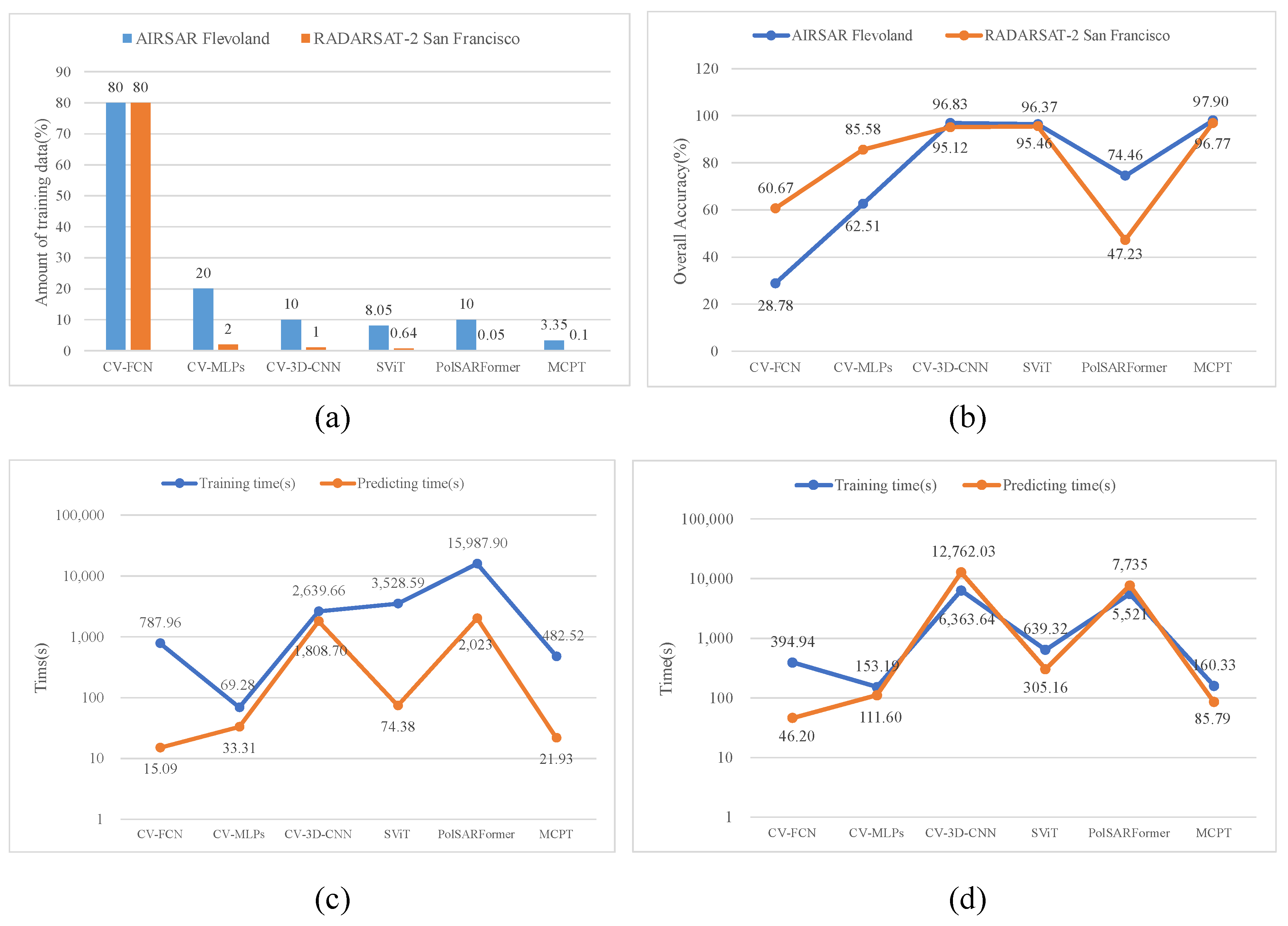
4.2. Impact of Training Data Amount
4.3. About PolSAR Image Classification Metrics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ViT | Vision transformer |
| MCPT | Mixed convolutional parallel transformer |
| SAR | Synthetic aperture radar |
| PolSAR | Polarimetric synthetic aperture image |
| CNN | Convolutional neural network |
| NLP | Natural language processing |
| SA | Self-attention |
| MixConv | Mixed depthwise convolution |
| GAP | Global average pooling |
| MHSA | Multi-head self-attention |
| MLP | Multi-layer perceptron |
| LN | Layer normalization |
| GELU | Gaussian error linear unit |
| FFN | Feed-forward network |
| FC | Fully connected |
| OA | Overall accuracy |
| AA | Average accuracy |
References
- Chan, Y.K.; Koo, V.C. An introduction to synthetic aperture radar (SAR). Prog. Electromagn. Res. B 2008, 2, 27–60. [Google Scholar] [CrossRef]
- Bamler, R. Principles of Synthetic Aperture Radar. Surv. Geophys. 2000, 21, 147–157. [Google Scholar] [CrossRef]
- Pasmurov, A.; Zinoviev, J. Radar Imaging Application. In Radar Imaging and Holography; IET Digital Library: London, UK, 2005; pp. 191–230. [Google Scholar] [CrossRef]
- Ulander, L.; Barmettler, A.; Flood, B.; Frölind, P.O.; Gustavsson, A.; Jonsson, T.; Meier, E.; Rasmusson, J.; Stenström, G. Signal-to-Clutter Ratio Enhancement in Bistatic Very High Frequency (VHF)-Band SAR Images of Truck Vehicles in Forested and Urban Terrain. IET Radar Sonar Navig. 2010, 4, 438. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, L.; Liu, F.; Bo, L.; Gong, M. Spectral Clustering Ensemble Applied to SAR Image Segmentation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2126–2136. [Google Scholar] [CrossRef]
- Chai, H.; Yan, C.; Zou, Y.; Chen, Z. Land Cover Classification of Remote Sensing Image of Hubei Province by Using PSP Net. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1224–1232. [Google Scholar] [CrossRef]
- Zhang, L.; Duan, B.; Zou, B. Research Development on Target Decomposition Method of Polarimetric SAR Image. J. Electron. Inf. Technol. 2016, 38, 3289–3297. [Google Scholar] [CrossRef]
- West, R.D.; Riley, R.M. Polarimetric Interferometric SAR Change Detection Discrimination. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3091–3104. [Google Scholar] [CrossRef]
- Holm, W.; Barnes, R. On Radar Polarization Mixed Target State Decomposition Techniques. In Proceedings of the 1988 IEEE National Radar Conference, Ann Arbor, MI, USA, 20–21 April 1988; pp. 249–254. [Google Scholar] [CrossRef]
- Cameron, W.; Leung, L. Feature Motivated Polarization Scattering Matrix Decomposition. In Proceedings of the IEEE International Conference on Radar, Arlington, VA, USA, 7–10 May 1990; pp. 549–557. [Google Scholar] [CrossRef]
- Cloude, S. Target Decomposition Theorems in Radar Scattering. Electron. Lett. 1985, 21, 22–24. [Google Scholar] [CrossRef]
- Cloude, S.; Pottier, E. An Entropy Based Classification Scheme for Land Applications of Polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Krogager, E. New Decomposition of the Radar Target Scattering Matrix. Electron. Lett. 1990, 26, 1525. [Google Scholar] [CrossRef]
- Parikh, H.; Patel, S.; Patel, V. Classification of SAR and PolSAR Images Using Deep Learning: A Review. Int. J. Image Data Fusion 2020, 11, 1–32. [Google Scholar] [CrossRef]
- Wang, H.; Xu, F.; Jin, Y.Q. A Review of Polsar Image Classification: From Polarimetry to Deep Learning. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3189–3192. [Google Scholar] [CrossRef]
- Chua, L.; Roska, T. The CNN Paradigm. IEEE Trans. Circuits Syst. I 1993, 40, 147–156. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y. Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Chen, S.; Tao, C. PolSAR Image Classification Using Polarimetric-Feature-Driven Deep Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 627–631. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper With Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Li, Y.; Wang, X.; Xiao, S.; Sato, M. Modeling and Interpretation of Scattering Mechanisms in Polarimetric Synthetic Aperture Radar: Advances and Perspectives. IEEE Signal Process. Mag. 2014, 31, 79–89. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Sato, M. Uniform Polarimetric Matrix Rotation Theory and Its Applications. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4756–4770. [Google Scholar] [CrossRef]
- Yang, C.; Hou, B.; Ren, B.; Hu, Y.; Jiao, L. CNN-Based Polarimetric Decomposition Feature Selection for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8796–8812. [Google Scholar] [CrossRef]
- Shang, R.; He, J.; Wang, J.; Xu, K.; Jiao, L.; Stolkin, R. Dense Connection and Depthwise Separable Convolution Based CNN for Polarimetric SAR Image Classification. Knowl.-Based Syst. 2020, 194, 105542. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A Survey on Vision Transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 87–110. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, L.; Zou, B. Exploring Vision Transformers for Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Xing, C.; Yin, J.; Yang, J. Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer. Remote Sens. 2022, 14, 4656. [Google Scholar] [CrossRef]
- Jamali, A.; Roy, S.K.; Bhattacharya, A.; Ghamisi, P. Local Window Attention Transformer for Polarimetric SAR Image Classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Li, Q.; Cai, W.; Wang, X.; Zhou, Y.; Feng, D.D.; Chen, M. Medical Image Classification with Convolutional Neural Network. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; pp. 844–848. [Google Scholar] [CrossRef]
- Qin, J.; Pan, W.; Xiang, X.; Tan, Y.; Hou, G. A Biological Image Classification Method Based on Improved CNN. Ecol. Inform. 2020, 58, 101093. [Google Scholar] [CrossRef]
- Sultana, F.; Sufian, A.; Dutta, P. Advancements in Image Classification Using Convolutional Neural Network. In Proceedings of the 2018 Fourth International Conference on Research in Computational Intelligence and Communication Networks (ICRCICN), Kolkata, India, 22–23 November 2018; pp. 122–129. [Google Scholar] [CrossRef]
- Dolz, J.; Gopinath, K.; Yuan, J.; Lombaert, H.; Desrosiers, C.; Ben Ayed, I. HyperDense-Net: A Hyper-Densely Connected CNN for Multi-Modal Image Segmentation. IEEE Trans. Med. Imaging 2019, 38, 1116–1126. [Google Scholar] [CrossRef]
- Liu, F.; Lin, G.; Shen, C. CRF Learning with CNN Features for Image Segmentation. Pattern Recognit. 2015, 48, 2983–2992. [Google Scholar] [CrossRef]
- Mortazi, A.; Bagci, U. Automatically Designing CNN Architectures for Medical Image Segmentation. In Proceedings of the Machine Learning in Medical Imaging, Granada, Spain, 16 September 2018; Shi, Y., Suk, H.I., Liu, M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; pp. 98–106. [Google Scholar] [CrossRef]
- Chandrasegaran, K.; Tran, N.T.; Cheung, N.M. A Closer Look at Fourier Spectrum Discrepancies for CNN-generated Images Detection. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 7196–7205. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Maitra, M. MRI-based Brain Tumour Image Detection Using CNN Based Deep Learning Method. Neurosci. Inform. 2022, 2, 100060. [Google Scholar] [CrossRef]
- Chauhan, R.; Ghanshala, K.K.; Joshi, R. Convolutional Neural Network (CNN) for Image Detection and Recognition. In Proceedings of the 2018 First International Conference on Secure Cyber Computing and Communication (ICSCCC), Jalandhar, India, 15–17 December 2018; pp. 278–282. [Google Scholar] [CrossRef]
- Zhou, Z.; Wu, Q.M.J.; Wan, S.; Sun, W.; Sun, X. Integrating SIFT and CNN Feature Matching for Partial-Duplicate Image Detection. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 593–604. [Google Scholar] [CrossRef]
- Bhatt, D.; Patel, C.; Talsania, H.; Patel, J.; Vaghela, R.; Pandya, S.; Modi, K.; Ghayvat, H. CNN Variants for Computer Vision: History, Architecture, Application, Challenges and Future Scope. Electronics 2021, 10, 2470. [Google Scholar] [CrossRef]
- Jia, W.; Tian, Y.; Luo, R.; Zhang, Z.; Lian, J.; Zheng, Y. Detection and Segmentation of Overlapped Fruits Based on Optimized Mask R-CNN Application in Apple Harvesting Robot. Comput. Electron. Agric. 2020, 172, 105380. [Google Scholar] [CrossRef]
- Ravanbakhsh, M.; Nabi, M.; Mousavi, H.; Sangineto, E.; Sebe, N. Plug-and-Play CNN for Crowd Motion Analysis: An Application in Abnormal Event Detection. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1689–1698. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, C.; Zhang, Y.; Hu, C.; Jiang, H.; Wang, Z. An Energy-Efficient FPGA-Based Embedded System for CNN Application. In Proceedings of the 2018 IEEE International Conference on Electron Devices and Solid State Circuits (EDSSC), Shenzhen, China, 6–8 June 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the Computer Vision—ECCV, Munich, Germany, 8–14 September 2018; Springer: Cham, Switzerland, 2018; pp. 122–138. [Google Scholar] [CrossRef]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning Transferable Architectures for Scalable Image Recognition. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8697–8710. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. MixConv: Mixed Depthwise Convolutional Kernels. arXiv 2019, arXiv:1907.09595. [Google Scholar]
- Hassani, A.; Walton, S.; Shah, N.; Abuduweili, A.; Li, J.; Shi, H. Escaping the Big Data Paradigm with Compact Transformers. arXiv 2022, arXiv:2104.05704. [Google Scholar]
- Chen, X.; Xie, S.; He, K. An Empirical Study of Training Self-Supervised Vision Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 9620–9629. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2020, arXiv:1606.08415. [Google Scholar]
- Chen, C.F.R.; Fan, Q.; Panda, R. CrossViT: Cross-Attention Multi-Scale Vision Transformer for Image Classification. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 347–356. [Google Scholar] [CrossRef]
- Chu, X.; Tian, Z.; Wang, Y.; Zhang, B.; Ren, H.; Wei, X.; Xia, H.; Shen, C. Twins: Revisiting the Design of Spatial Attention in Vision Transformers. In Proceedings of the Advances in Neural Information Processing Systems 34, Online, 7 December 2021; Curran Associates, Inc.: New York City, NY, USA, 2021; pp. 9355–9366. [Google Scholar]
- Heo, B.; Yun, S.; Han, D.; Chun, S.; Choe, J.; Oh, S.J. Rethinking Spatial Dimensions of Vision Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 11916–11925. [Google Scholar] [CrossRef]
- Tu, Z.; Talebi, H.; Zhang, H.; Yang, F.; Milanfar, P.; Bovik, A.; Li, Y. MaxViT: Multi-axis Vision Transformer. In Computer Vision—ECCV 2022. ECCV 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; pp. 459–479. [Google Scholar] [CrossRef]
- Yang, R.; Ma, H.; Wu, J.; Tang, Y.; Xiao, X.; Zheng, M.; Li, X. ScalableViT: Rethinking the Context-Oriented Generalization of Vision Transformer. In Computer Vision—ECCV 2022. ECCV 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; pp. 480–496. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, Nevada, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Goyal, A.; Bochkovskiy, A.; Deng, J.; Koltun, V. Non-Deep Networks. In Proceedings of the Advances in Neural Information Processing Systems 35, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Zhou, J.; Wei, C.; Wang, H.; Shen, W.; Xie, C.; Yuille, A.; Kong, T. Image BERT Pre-training with Online Tokenizer. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Touvron, H.; Cord, M.; El-Nouby, A.; Verbeek, J.; Jégou, H. Three Things Everyone Should Know About Vision Transformers. In Proceedings of the 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2022; pp. 497–515. [Google Scholar] [CrossRef]
- Goodfellow, I.; Warde-Farley, D.; Mirza, M.; Courville, A.; Bengio, Y. Maxout Networks. In Proceedings of the 30th International Conference on Machine Learning (PMLR), Atlanta, GA, USA, 17–19 June 2013; pp. 1319–1327. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Liu, F. PolSAR Image Classification and Change Detection Based on Deep Learning. Ph.D. Thesis, Xidian University, Xi’an, China, 2017. [Google Scholar]
- Liu, X.; Jiao, L.; Liu, F.; Zhang, D.; Tang, X. PolSF: PolSAR Image Datasets on San Francisco. In Proceedings of the IFIP Advances in Information and Communication Technology, Xi’an, China, 28–31 October 2022; Shi, Z., Jin, Y., Zhang, X., Eds.; Springer: Cham, Switzerland, 2022; pp. 214–219. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Y.; Zhang, P.; Liang, W.; Li, M. Pixel-Wise PolSAR Image Classification via a Novel Complex-Valued Deep Fully Convolutional Network. Remote Sens. 2019, 11, 2653. [Google Scholar] [CrossRef]
- Ronny, H. Complex-Valued Multi-Layer Perceptrons—An Application to Polarimetric SAR Data. Photogramm. Eng. Remote Sens. 2010, 76, 1081–1088. [Google Scholar] [CrossRef]
- Tan, X.; Li, M.; Zhang, P.; Wu, Y.; Song, W. Complex-Valued 3-D Convolutional Neural Network for PolSAR Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1022–1026. [Google Scholar] [CrossRef]

| Method | CV-FCN | CV-MLPs | CV-3D-CNN | SViT | PolSARFormer | MCPT |
|---|---|---|---|---|---|---|
| Water | 96.49 | 49.96 | 99.83 | 100.00 | 99.87 | 99.16 |
| Forest | 99.59 | 60.98 | 99.87 | 97.76 | 96.33 | 99.05 |
| Lucerne | 99.77 | 73.37 | 97.90 | 99.87 | 81.21 | 99.92 |
| Grass | 99.10 | 0.00 | 99.69 | 98.24 | 62.75 | 96.36 |
| Peas | 99.79 | 90.59 | 99.95 | 99.36 | 92.14 | 99.80 |
| Barley | 97.79 | 0.00 | 97.03 | 99.88 | 97.57 | 98.55 |
| Bare Soil | 99.53 | 0.00 | 98.90 | 99.61 | 93.80 | 100.00 |
| Beet | 98.80 | 81.47 | 98.84 | 97.74 | 91.20 | 98.65 |
| Wheat 2 | 99.34 | 56.37 | 95.54 | 97.28 | 69.65 | 95.95 |
| Wheat 3 | 99.70 | 36.66 | 99.80 | 99.95 | 97.88 | 98.91 |
| Steambeans | 95.93 | 89.70 | 99.10 | 99.81 | 95.98 | 97.35 |
| Rapeseed | 99.86 | 80.46 | 98.74 | 98.88 | 75.98 | 92.85 |
| Wheat | 99.94 | 66.19 | 98.92 | 95.47 | 91.28 | 97.37 |
| Buildings | 99.42 | 0.00 | 100.00 | 93.74 | 83.35 | 98.23 |
| Potatoes | 99.72 | 87.63 | 99.99 | 98.89 | 89.04 | 97.47 |
| AA | 98.98 | 51.56 | 98.94 | 98.49 | 87.87 | 97.97 |
| Kappa | 99.33 | 51.67 | 98.92 | 98.43 | 88.22 | 97.71 |
| OA | 99.39 | 56.62 | 99.01 | 98.62 | 89.19 | 97.90 |
| Training time(s) | 9034.43 | 65.79 | 2180.03 | 4294.07 | 93,703.70 | 482.52 |
| Predicting time(s) | 15.85 | 38.46 | 1856.65 | 85.97 | 1697.50 | 21.93 |
| Method | CV-FCN | CV-MLPs | CV-3D-CNN | SViT | PolSARFormer | MCPT |
|---|---|---|---|---|---|---|
| Water | 99.86 | 99.60 | 99.90 | 99.97 | 98.12 | 99.99 |
| Vagetation | 97.48 | 87.89 | 95.42 | 94.79 | 77.31 | 91.00 |
| High-Density Urban | 99.70 | 88.97 | 95.14 | 95.57 | 87.24 | 96.17 |
| Developed | 97.49 | 93.39 | 93.94 | 95.68 | 84.72 | 92.79 |
| Low-Density Urban | 99.49 | 84.82 | 92.57 | 97.83 | 83.14 | 94.29 |
| AA | 98.80 | 90.93 | 95.39 | 96.76 | 86.11 | 94.84 |
| Kappa | 99.02 | 90.16 | 95.47 | 97.10 | 85.83 | 95.35 |
| OA | 99.28 | 93.17 | 96.85 | 97.98 | 90.16 | 96.77 |
| Training time(s) | 8227.01 | 153.35 | 4865.09 | 1506.58 | 77,593.12 | 160.33 |
| Predicting time(s) | 103.31 | 114.66 | 12,210.48 | 338.28 | 6038.70 | 85.79 |
| Method | OA | Training Time (s) | Prediction Time (s) | FLOPs (M) | Params (M) |
|---|---|---|---|---|---|
| (1) ViT | 97.96 | 4615.73 | 284.09 | 1703.363 | 85.241 |
| (2) ViT + Mixed Depthwise Convolution Tokenization | 97.48 | 465.93 | 24.42 | 74.919 | 4.103 |
| (3) ViT + Parallel Encoder | 95.45 | 436.99 | 22.08 | 74.014 | 4.118 |
| (4) ViT + Mixed Depthwise Convolution Tokenization + Parallel Encoder | 97.84 | 458.14 | 23.24 | 74.919 | 4.103 |
| (5) MCPT | 97.82 | 457.53 | 23.09 | 74.919 | 4.103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, J.; Lu, B.; Liu, B.; Zhang, Y.; Wang, C. MCPT: Mixed Convolutional Parallel Transformer for Polarimetric SAR Image Classification. Remote Sens. 2023, 15, 2936. https://doi.org/10.3390/rs15112936
Wang W, Wang J, Lu B, Liu B, Zhang Y, Wang C. MCPT: Mixed Convolutional Parallel Transformer for Polarimetric SAR Image Classification. Remote Sensing. 2023; 15(11):2936. https://doi.org/10.3390/rs15112936
Chicago/Turabian StyleWang, Wenke, Jianlong Wang, Bibo Lu, Boyuan Liu, Yake Zhang, and Chunyang Wang. 2023. "MCPT: Mixed Convolutional Parallel Transformer for Polarimetric SAR Image Classification" Remote Sensing 15, no. 11: 2936. https://doi.org/10.3390/rs15112936
APA StyleWang, W., Wang, J., Lu, B., Liu, B., Zhang, Y., & Wang, C. (2023). MCPT: Mixed Convolutional Parallel Transformer for Polarimetric SAR Image Classification. Remote Sensing, 15(11), 2936. https://doi.org/10.3390/rs15112936







