A Multi-Variable Sentinel-2 Random Forest Machine Learning Model Approach to Predicting Perennial Ryegrass Biomass in Commercial Dairy Farms in Southeast Australia
Abstract
1. Introduction
- Combine S2 and ML modelling approaches to predict perennial ryegrass biomass across a range of regions and seasons with an accuracy of +/−500 kg DM/ha.
- Provide technical evidence that utilising SWIR bands can improve the ability to predict pasture yields above 3000 kg DM/ha and, therefore, enable measurements of high-yielding pastures at any stage in the growth cycle in irrigated and dryland farm management systems.
- Examine the pasture biomass prediction model quality through a fusion of S2 sensor-derived datasets and broad management and seasonal datasets.
- Show that it is possible to predict pasture biomass across large regions and growing seasons on commercial dairy farms with one ‘global’ model with an extensive ground sampling campaign and the use of numerous bands and SI of the S2 sensor and the ML modelling framework.
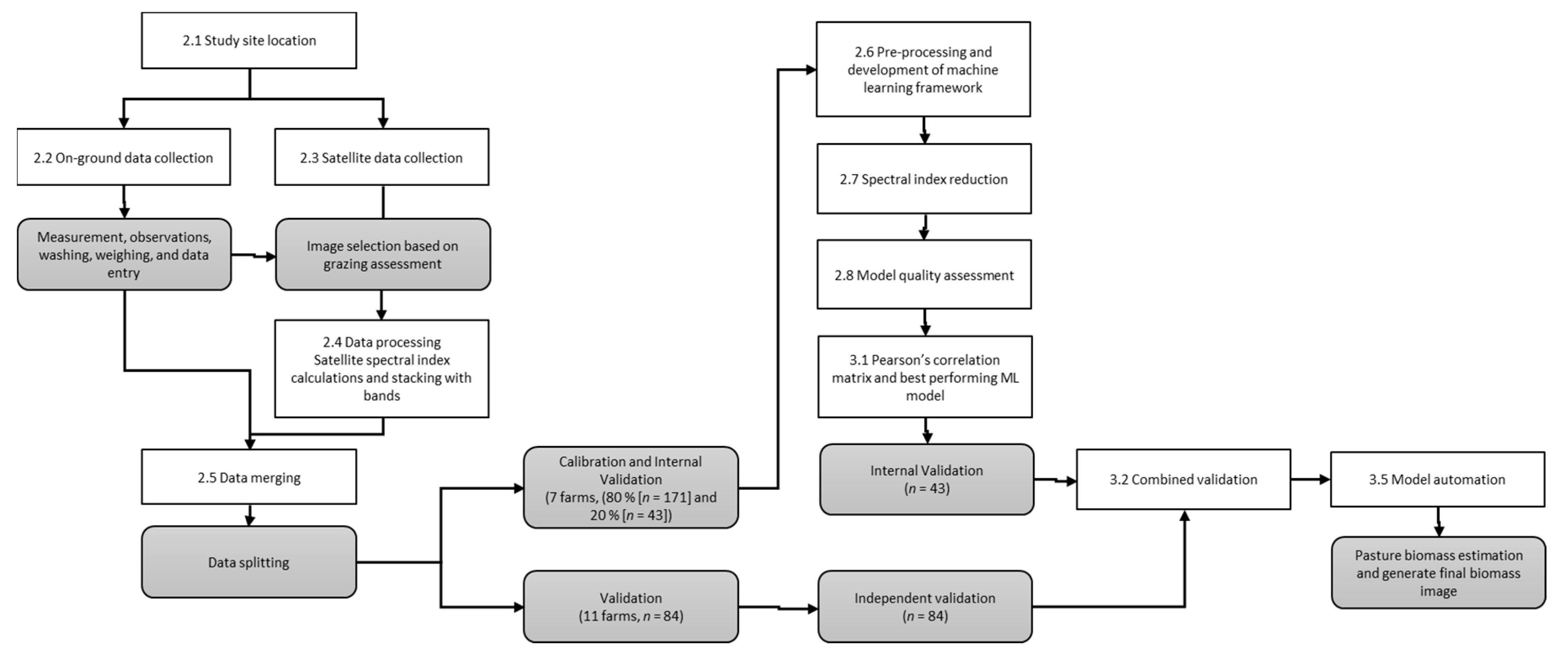
2. Materials and Methods
2.1. Study Site Location, Soil, and Climate and Sampling Design
2.2. Ground Data Collection
2.3. Satellite Data Collection
2.4. Data Processing—Satellite Spectral Index Calculations and Stacking with Bands
2.5. Data Merging
2.6. Pre-Processing and Development of Machine Learning Framework
2.6.1. Shapiro–Wilk Test
2.6.2. Conditional Latin Hypercube Sampling
2.6.3. Variable Importance Section through Boruta Algorithm
2.6.4. Random Forest Modelling
- Ntree: The parameter Ntree refers to the number of decision trees generated. As per the literature, the standard requirement to analyse remote sensing data, i.e., a default value of Ntree = 500 was used [44].
- mtry: The parameter mtry denotes the number of variables to be selected and tested for the best split while growing trees. Lower mtry values have been attributed to stability enhancement, as it reduces the number of correlated trees [110]. Several tests were included before selecting mtry values, as advised by Probst et al. [110]. In the present model, mtry = 6 was found to be the best with reduced computational time.
2.7. Spectral Index Reduction
2.8. Model Quality Assessment
3. Results
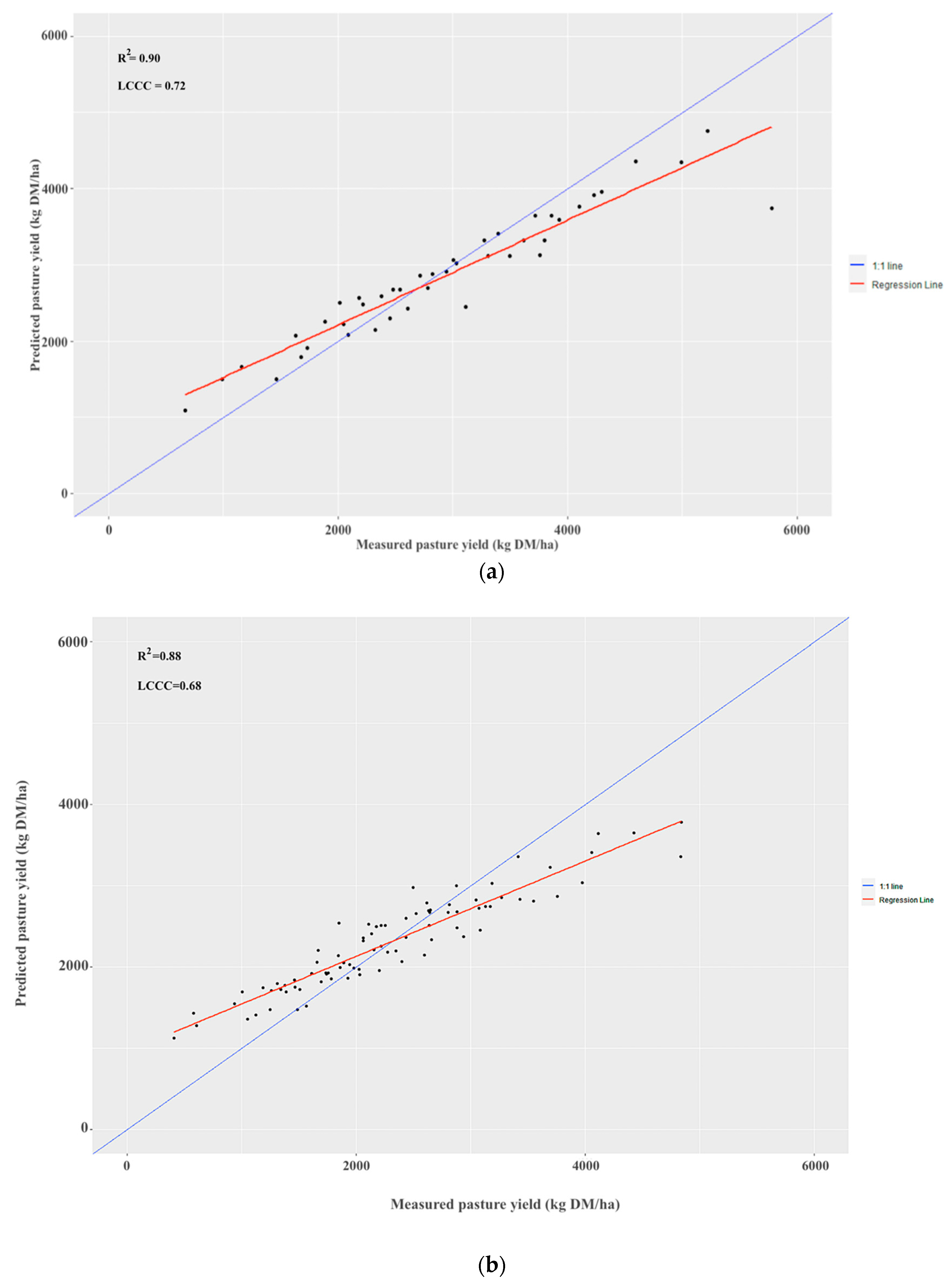
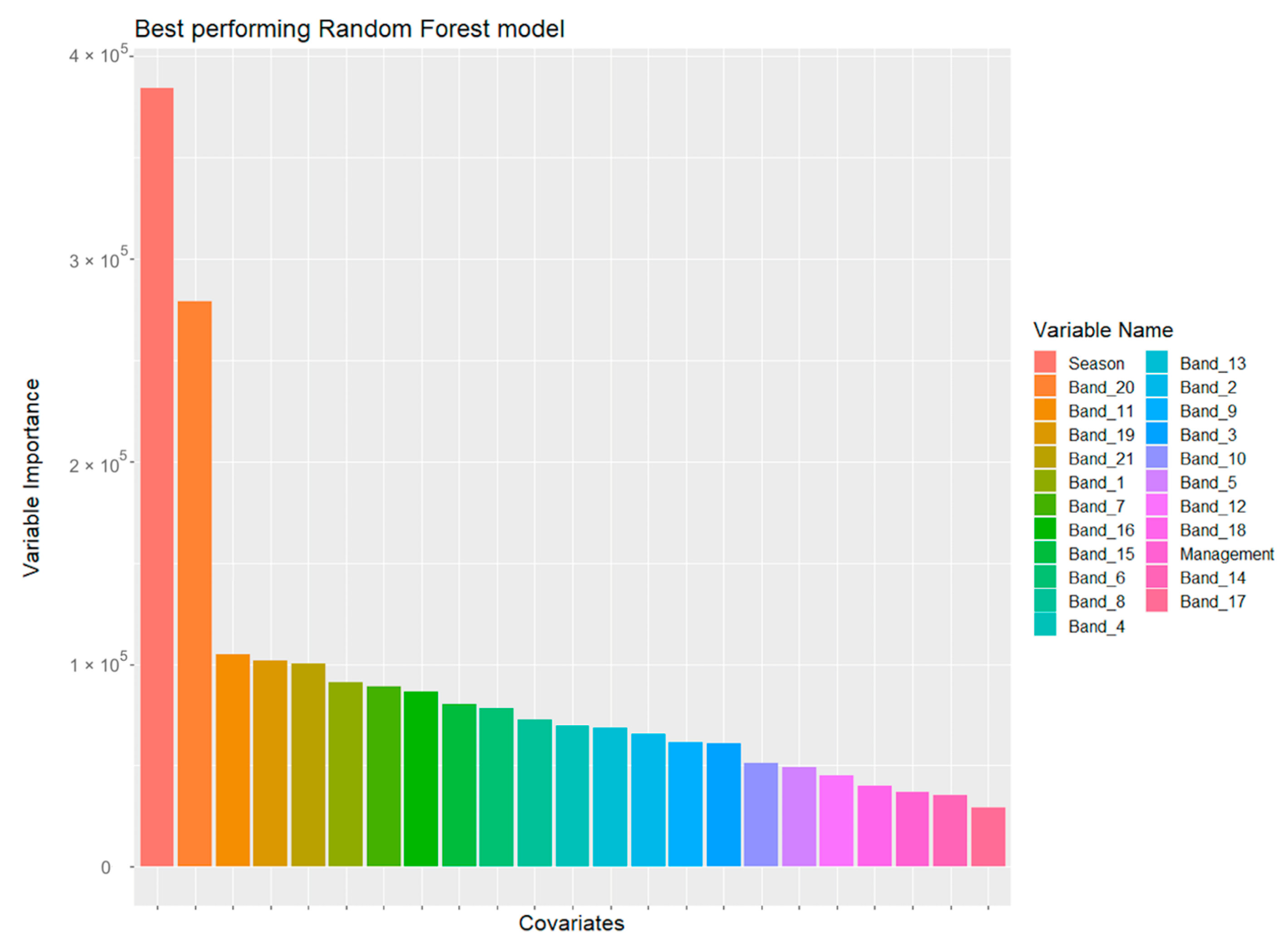
3.1. Pearson Correlation Matrix and Best-Performing ML Model
3.2. Combined Validation
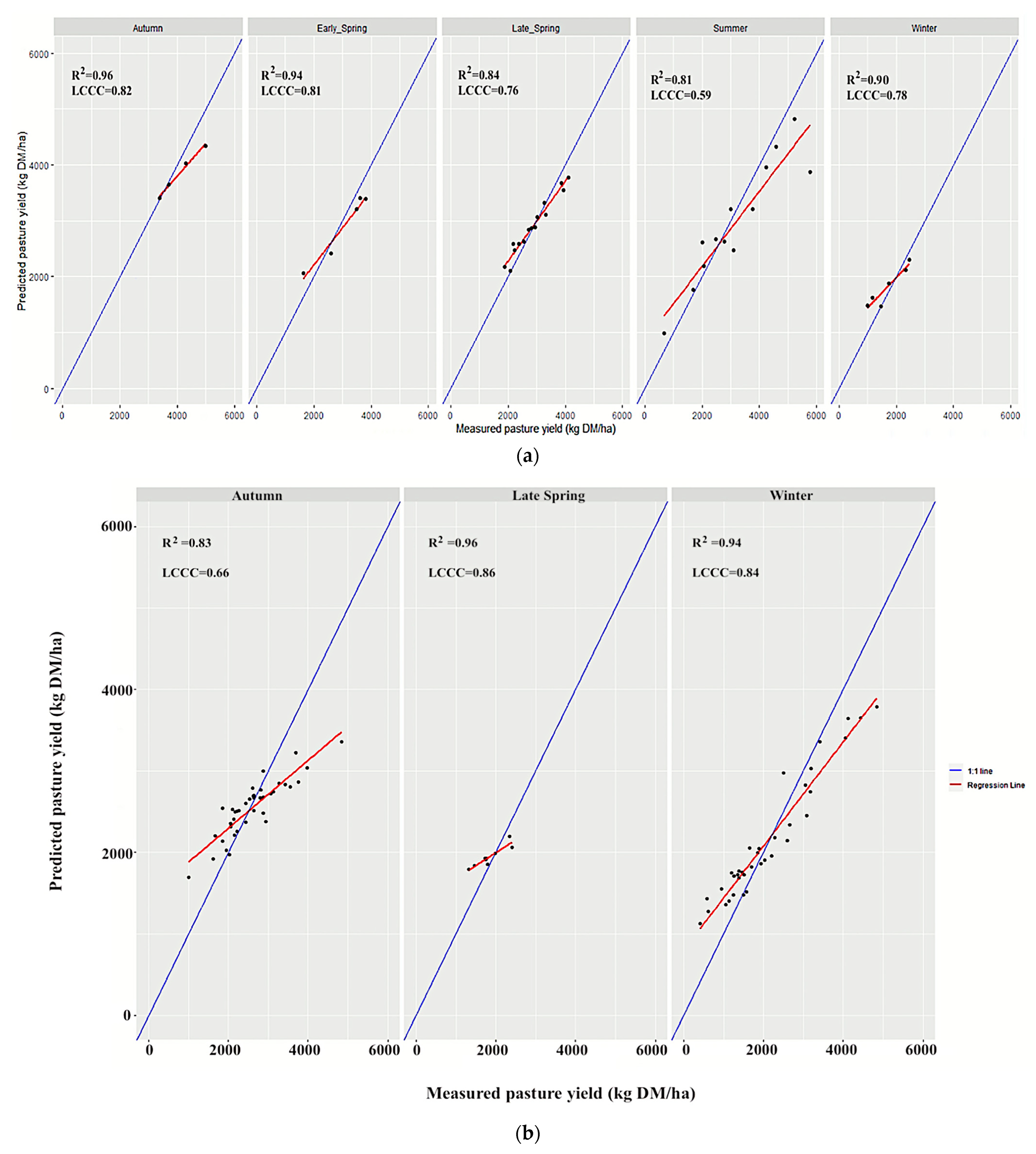
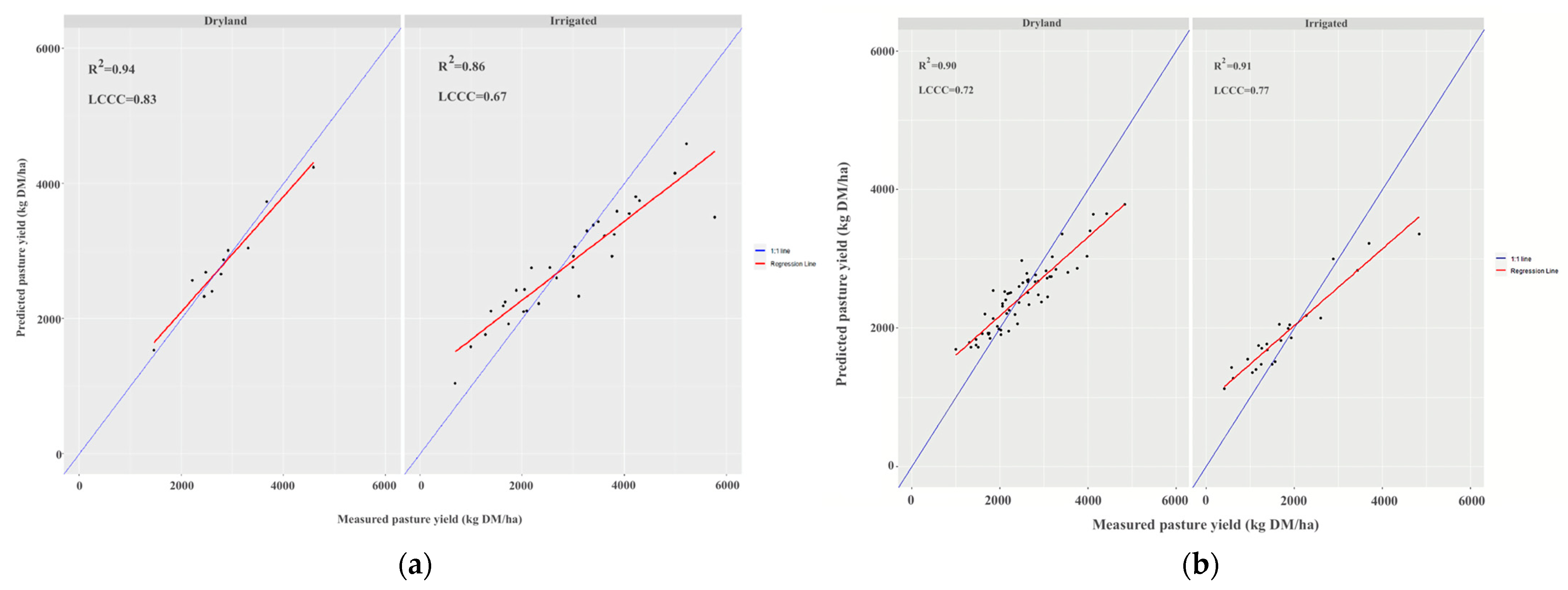
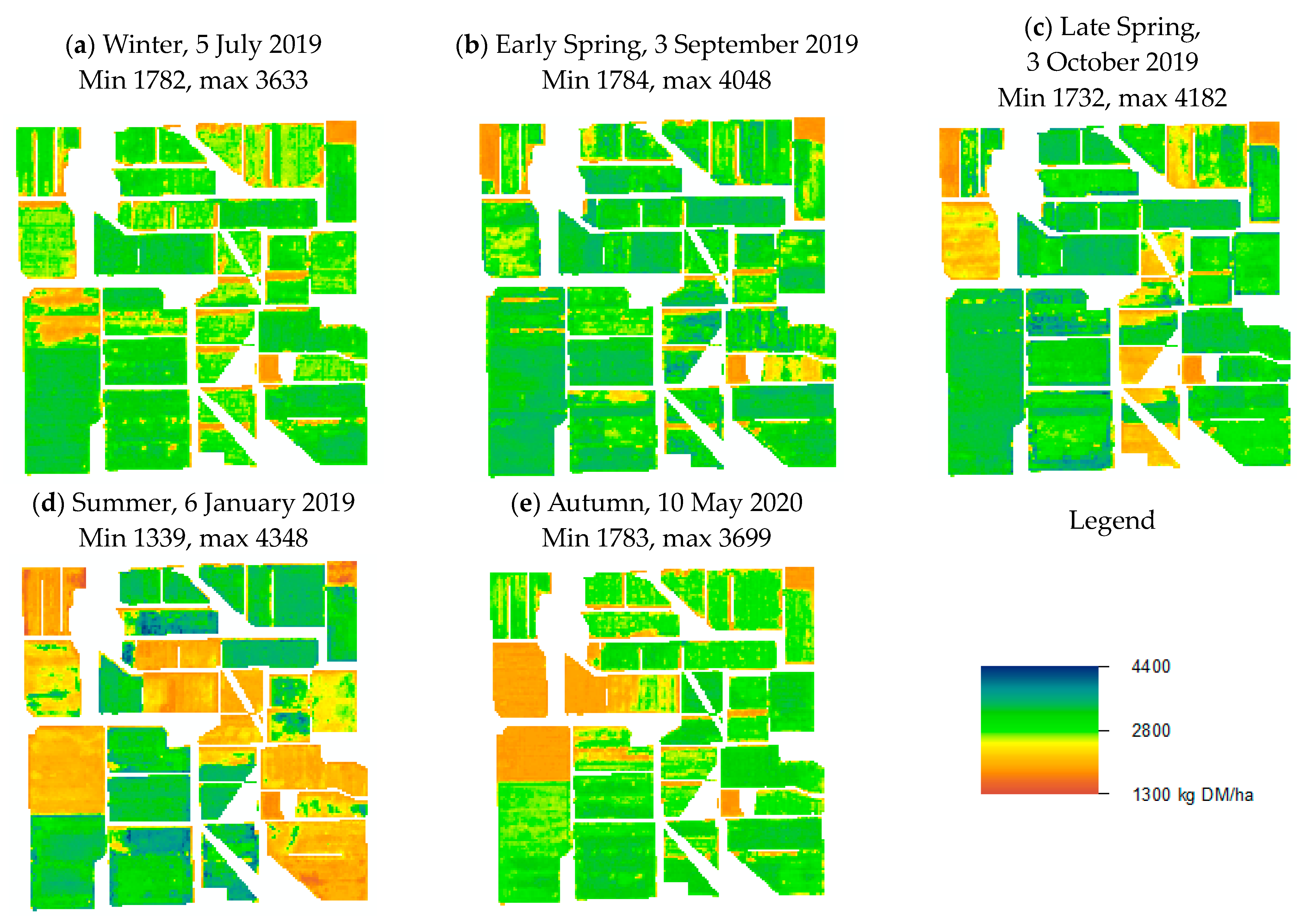
3.3. Validations Based on Season and Management
3.4. SWIR Band Validation
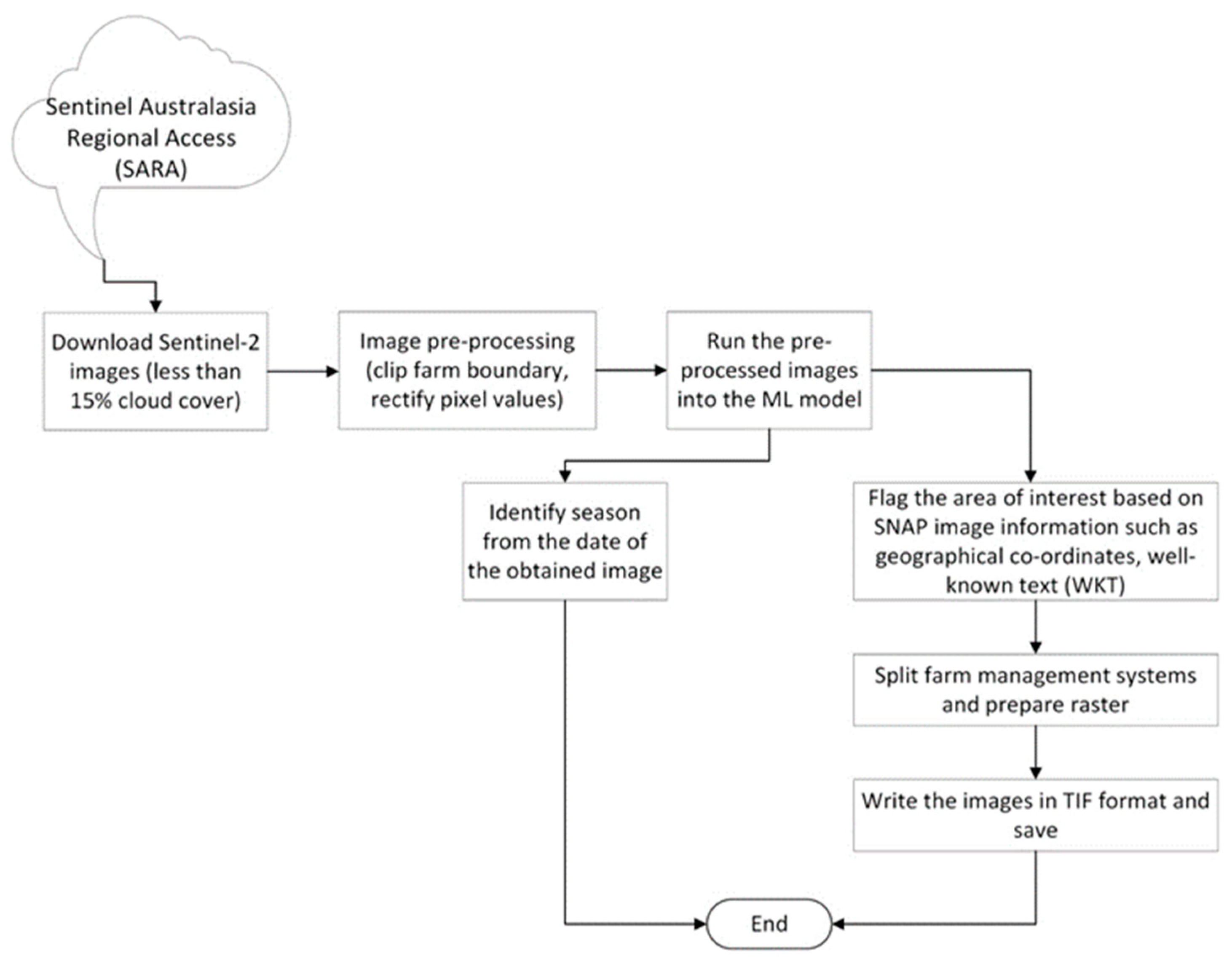
3.5. Model Automation
4. Discussion
4.1. Overview of the Prediction Model Accuracy
4.2. Significance of S2 SWIR Bands in Improving Prediction Accuracy
4.3. Consideration of ML for Data Analysis and Model Development
4.4. Impact of Soils, Climate, and Farm Activities on Satellite Images and Biomass Estimation
4.5. Limitations of the Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang-Fung-Martel, J.; Harrison, M.T.; Rawnsley, R.; Smith, A.P.; Meinke, H. The impact of extreme climatic events on pasture-based dairy systems: A review. Crop Pasture Sci. 2017, 68, 1158–1169. [Google Scholar] [CrossRef]
- Dairy Feeding Update Briefing Notes 2015. Dairy Australia. Available online: https://www.dairyaustralia.com.au/resource-repository/2020/07/09/dairy-feeding-update-briefing-notes-2015 (accessed on 15 June 2022).
- Fulkerson, W.J.; McKean, K.; Nandra, K.S.; Barchia, I.M. Benefits of accurately allocating feed on a daily basis to dairy cows grazing pasture. Aust. J. Experiment. Agri. 2005, 45, 331–336. [Google Scholar] [CrossRef]
- Rogers, M.J.; Lawson, A.; Ho, C.; Kelly, K.; Wales, W.; Jacobs, J. The changing role of perennial ryegrass in dairy pastures in northern Victoria, Australia. Grass Forag. Sci. 2022, 77, 131–140. [Google Scholar] [CrossRef]
- Beukes, P.C.; McCarthy, S.; Wims, C.M.; Gregorini, P.; Romera, A.J. Regular estimates of herbage mass can improve profitability of pasture-based dairy systems. Anim. Prod. Sci. 2019, 59, 359–367. [Google Scholar] [CrossRef]
- De Rosa, D.; Basso, B.; Fasiolo, M.; Friedl, J.; Fulkerson, B.; Grace, P.R.; Rowlings, D.W. Predicting pasture biomass using a statistical model and machine learning algorithm implemented with remotely sensed imagery. Comput. Electron. Agric. 2021, 180, 105880. [Google Scholar] [CrossRef]
- Earle, D.F.; McGowan, A.A. Evaluation and calibration of an automated rising plate meter for estimating dry-matter yield of pasture. Aust. J. Exp. Agric. 1979, 19, 337–343. [Google Scholar] [CrossRef]
- Ehlert, D.; Hammen, V.; Adamek, R. Online sensor pendulum-meter for determination of plant mass. Precis. Agric. 2003, 4, 139–148. [Google Scholar] [CrossRef]
- Serrano, J.M.; Shahidian, S.; Marques da Silva, J.R. Monitoring pasture variability: Optical OptRx® crop sensor versus Grassmaster II capacitance probe. Environ. Mon. Assess. 2016, 188, 117. [Google Scholar] [CrossRef]
- Legg, M.; Bradley, S. Ultrasonic arrays for remote sensing of pasture biomass. Remote Sens. 2019, 12, 111. [Google Scholar] [CrossRef]
- Alckmin, G.T.; Lucieer, A.; Rawnsley, R.; Kooistra, L. Perennial ryegrass biomass retrieval through multispectral UAV data. Comput. Electron. Agric. 2022, 193, 106574. [Google Scholar] [CrossRef]
- Sinde-González, I.; Gil-Docampo, M.; Arza-García, M.; Grefa-Sánchez, J.; Yánez-Simba, D.; Pérez-Guerrero, P.; Abril-Porras, V. Biomass estimation of pasture plots with multitemporal UAV-based photogrammetric surveys. Int. J. Appl. Earth Obs. Geoinfo. 2021, 101, 102355. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation, Type II Report for the Period April 1973–September 1973; Texas A&M University, Remote Sensing Center: College Station, Texas, USA, 1973. [Google Scholar]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using Landsat TM images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Gara, T.W.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Heurich, M. Accurate modelling of canopy traits from seasonal Sentinel-2 imagery based on the vertical distribution of leaf traits. ISPRS J. Photogramm. Remote Sens. 2019, 157, 108–123. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in Northeast China using SAR Sentinel-1B, multispectral Sentinel-2A, and DEM imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Chen, D.; Huang, J.; Jackson, T.J. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near-and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Meza, C.M.; Rivera, J.P.; Alonso, L.; Moreno, J. A red-edge spectral index for remote sensing estimation of green LAI over agroecosystems. Euro. J. Agron. 2013, 46, 42–52. [Google Scholar] [CrossRef]
- Hunt, M.L.; Blackburn, G.A.; Carrasco, L.; Redhead, J.W.; Rowland, C.S. High resolution wheat yield mapping using Sentinel-2. Remote Sens. Environ. 2019, 233, 111410. [Google Scholar] [CrossRef]
- Hill, M.J.; Vickery, P.J.; Furnival, E.P.; Donald, G.E. Pasture Land Cover in Eastern Australia from NOAA-AVHRR NDVI and Classified Landsat TM. Remote Sens. Environ. 1999, 67, 32–50. [Google Scholar] [CrossRef]
- Crabbe, R.A.; Lamb, D.; Edwards, C. Discrimination of species composition types of a grazed pasture landscape using Sentinel-1 and Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101978. [Google Scholar] [CrossRef]
- Yeganeh, H.; Khajedein, S.; Jamale Amiri, F.; Shariff, A.R.B.M. Monitoring rangeland ground cover vegetation using multitemporal MODIS data. Arab. J. Geosci. 2014, 7, 287–298. [Google Scholar] [CrossRef]
- Cicore, P.; Serrano, J.; Shahidian, S.; Sousa, A.; Costa, J.L.; da Silva, J.R.M. Assessment of the spatial variability in tall wheatgrass forage using LANDSAT 8 satellite imagery to delineate potential management zones. Environ. Monit. Assess. 2016, 188, 513. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Barrett, B.; Cawkwell, F.; Green, S.; Dwyer, E.; Neumann, M. Application of repeat-pass TerraSAR-X staring spotlight interferometric coherence to monitor pasture biophysical parameters: Limitations and sensitivity analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3225–3231. [Google Scholar] [CrossRef]
- Chen, Y.; Guerschman, J.; Shendryk, Y.; Henry, D.; Harrison, M.T. Estimating pasture biomass using Sentinel-2 imagery and machine learning. Remote Sens. 2021, 13, 603. [Google Scholar] [CrossRef]
- Porter, T.F.; Chen, C.; Long, J.A.; Lawrence, R.L.; Sowell, B.F. Estimating biomass on CRP pastureland: A comparison of remote sensing techniques. Biomass Bioenerg. 2014, 66, 268–274. [Google Scholar] [CrossRef]
- Reinermann, S.; Asam, S.; Kuenzer, C. Remote sensing of grassland production and management—A review. Remote Sens. 2020, 12, 1949. [Google Scholar] [CrossRef]
- Vickery, P.J.; Hedges, D.A.; Duggin, M.J. Assessment of the fertiliser requirement of improved pasture from remote sensing information. Remote Sens. Environ. 1980, 9, 131–148. [Google Scholar] [CrossRef]
- Taylor, B.F.; Dini, P.W.; Kidson, J.W. Determination of seasonal and interannual variation in New Zealand pasture growth from NOAA-7 data. Remote Sens. Environ. 1985, 18, 177–192. [Google Scholar] [CrossRef]
- Edirisinghe, A.; Clark, D.; Waugh, D. Spatio-temporal modelling of biomass of intensively grazed perennial dairy pastures using multispectral remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2012, 16, 5–16. [Google Scholar] [CrossRef]
- Edirisinghe, A.; Hill, M.J.; Donald, G.E.; Hyder, M. Quantitative mapping of pasture biomass using satellite imagery. Int. J. Remote Sens. 2011, 32, 2699–2724. [Google Scholar] [CrossRef]
- Guerini Filho, M.; Kuplich, T.M.; Quadros, F.L.D. Estimating natural grassland biomass by vegetation indices using Sentinel 2 remote sensing data. Int. J. Remote Sens. 2020, 41, 2861–2876. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal combination of predictors and algorithms for forest above-ground biomass mapping from Sentinel and SRTM data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the potential of Sentinel-2 MSI spectral resolution in quantifying above ground biomass across different fertilizer treatments. ISPRS J. Photogramm. Remote Sens. 2015, 110, 55–65. [Google Scholar] [CrossRef]
- Maynard, C.L.; Lawrence, R.L.; Nielsen, G.A.; Decker, G. Modeling vegetation amount using bandwise regression and ecological site descriptions as an alternative to vegetation indices. GISci. Remote Sens. 2007, 44, 68–81. [Google Scholar] [CrossRef]
- Numata, I.; Roberts, D.A.; Chadwick, O.A.; Schimel, J.; Sampaio, F.R.; Leonidas, F.C.; Soares, J.V. Characterization of pasture biophysical properties and the impact of grazing intensity using remotely sensed data. Remote Sens. Environ. 2007, 109, 314–327. [Google Scholar] [CrossRef]
- Grigera, G.; Oesterheld, M.; Pacín, F. Monitoring forage production for farmers’ decision making. Agric. Syst. 2007, 94, 637–648. [Google Scholar] [CrossRef]
- Punalekar, S.M.; Verhoef, A.; Quaife, T.L.; Humphries, D.; Bermingham, L.; Reynolds, C.K. Application of Sentinel-2A data for pasture biomass monitoring using a physically based radiative transfer model. Remote Sens. Environ. 2018, 218, 207–220. [Google Scholar] [CrossRef]
- Boschetti, M.; Bocchi, S.; Brivio, P.A. Assessment of pasture production in the Italian Alps using spectrometric and remote sensing information. Agric. Ecosyst. Environ. 2007, 118, 267–272. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens. 1985, 6, 1335–1372. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Gargiulo, J.; Clark, C.; Lyons, N.; de Veyrac, G.; Beale, P.; Garcia, S. Spatial and temporal pasture biomass estimation integrating electronic plate meter, planet cubesats and sentinel-2 satellite data. Remote Sens. 2020, 12, 3222. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Deb, D.; Deb, S.; Chakraborty, D.; Singh, J.P.; Singh, A.K.; Dutta, P.; Choudhury, A. Aboveground biomass estimation of an agro-pastoral ecology in semi-arid Bundelkhand region of India from Landsat data: A comparison of support vector machine and traditional regression models. Geocarto Int. 2022, 37, 1043–1058. [Google Scholar] [CrossRef]
- Xu, K.; Su, Y.; Liu, J.; Hu, T.; Jin, S.; Ma, Q.; Zhai, Q.; Wang, R.; Zhang, J.; Li, Y.; et al. Estimation of degraded grassland aboveground biomass using machine learning methods from terrestrial laser scanning data. Ecol. Indicat. 2020, 108, 105747. [Google Scholar] [CrossRef]
- Yang, S.; Feng, Q.; Liang, T.; Liu, B.; Zhang, W.; Xie, H. Modeling grassland above-ground biomass based on artificial neural network and remote sensing in the Three-River Headwaters Region. Remote Sens. Environ. 2018, 204, 448–455. [Google Scholar] [CrossRef]
- Aguirre-Salado, C.A.; Treviño-Garza, E.J.; Aguirre-Calderón, O.A.; Jiménez-Pérez, J.; González-Tagle, M.A.; Valdéz-Lazalde, J.R.; Sánchez-Díaz, G.; Haapanen, R.; Aguirre-Salado, A.I.; Miranda-Aragón, L. Mapping aboveground biomass by integrating geospatial and forest inventory data through a k-nearest neighbor strategy in North Central Mexico. J. Arid Land 2014, 6, 80–96. [Google Scholar] [CrossRef]
- Habyarimana, E.; Piccard, I.; Catellani, M.; De Franceschi, P.; Dall’Agata, M. Towards predictive modeling of sorghum biomass yields using fraction of absorbed photosynthetically active radiation derived from sentinel-2 satellite imagery and supervised machine learning techniques. Agronomy 2019, 9, 203. [Google Scholar] [CrossRef]
- Bretas, I.L.; Valente, D.S.; Silva, F.F.; Chizzotti, M.L.; Paulino, M.F.; D’Áurea, A.P.; Paciullo, D.S.; Pedreira, B.C.; Chizzotti, F.H. Prediction of aboveground biomass and dry-matter content in Brachiaria pastures by combining meteorological data and satellite imagery. Grass Forage Sci. 2021, 76, 340–352. [Google Scholar] [CrossRef]
- Victorian Resources Online, 2022. Available online: https://vro.agriculture.vic.gov.au/dpi/vro/vrosite.nsf/pages/soil-home (accessed on 1 October 2022).
- Searle, R. Australian Soil Classification Map, Version 1.0.0; Terrestrial Ecosystem Research Network. (Dataset); TERN: Indooroopilly, QLD, Australia, 2021. [CrossRef]
- Esri, 2022a. Esri, Collector for ArcGIS Overview. Available online: https://www.esri.com/en-us/arcgis/products/collector-for-arcgis/overview (accessed on 19 May 2022).
- Karunaratne, S.; Thomson, A.; Morse-McNabb, E.; Wijesingha, J.; Stayches, D.; Copland, A.; Jacobs, J. The fusion of spectral and structural datasets derived from an airborne multispectral sensor for estimation of pasture dry matter yield at paddock scale with time. Remote Sens. 2020, 12, 2017. [Google Scholar] [CrossRef]
- Lawson, A.R.; Giri, K.; Thomson, A.L.; Karunaratne, S.B.; Smith, K.F.; Jacobs, J.L.; Morse-McNabb, E.M. Multi-site calibration and validation of a wide-angle ultrasonic sensor and precise GPS to estimate pasture mass at the paddock scale. Comput. Electron. Agric. 2022, 195, 106786. [Google Scholar] [CrossRef]
- Thomson, A.L.; Karunaratne, S.B.; Copland, A.; Stayches, D.; McNabb, E.M.; Jacobs, J. Use of traditional, modern, and hybrid modelling approaches for in situ prediction of dry matter yield and nutritive characteristics of pasture using hyperspectral datasets. Anim. Feed Sci. Technol. 2020, 269, 114670. [Google Scholar] [CrossRef]
- Esri, 2022b. Esri, ArcGIS Online. Available online: https://www.arcgis.com/home/ (accessed on 19 May 2022).
- Doyle, P.T.; Stockdale, C.R.; Lawson, A.R.; Cohen, D.C. Pastures for Dairy Production in Victoria; Agriculture Victoria, Department of Natural Resources and Environment: Tatura, VIC, Australia, 2001. [Google Scholar]
- L3Harris Technologies, Inc., 2022. ENVI®. Available online: https://www.l3harris.com/all-capabilities/envi (accessed on 20 August 2022).
- SENTINEL-2 User Handbook, 2015. European Space Agency. Available online: https://sentinel.esa.int/documents/247904/685211/sentinel-2_user_handbook (accessed on 10 June 2022).
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical properties and nondestructive estimation of anthocyanin content in plant leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Pinty, B.; Verstraete, M.M. GEMI: A non-linear index to monitor global vegetation from satellites. Vegetation 1992, 101, 15–20. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Phys. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Sripada, R.P. Determining In-Season Nitrogen Requirements of Corn Using Aerial Color-Intrared Photography. Ph.D. Dissertation, North Carolina State University, Raleigh, NC, USA, 2005. [Google Scholar]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially located platform and aerial photography for documentation of grazing impacts on wheat. Geocarto Int. 2001, 16, 65–70. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Broge, N.; Hasager, C.B.; Jensen, N.O.; Schelde, K.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey, J.E., III. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Datt, B. A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using Eucalyptus leaves. J. Plant Phys. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Chen, J. Evaluation of Vegetation Indices and Modified Simple Ratio for Boreal Applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Goel, N.S.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and LAI and FPAR: A computer simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Phys. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosyn 1995, 31, 221–230. [Google Scholar]
- Bannari, A.; Asalhi, H.; Teillet, P.M. Transformed difference vegetation index (TDVI) for vegetation cover mapping. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 5, pp. 3053–3055. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Daughtry, C.S.T.; Eitel, J.U.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Phys. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Henebry, G.M.; Viña, A.; Gitelson, A.A. The Wide Dynamic Range Vegetation Index and Its Potential Utility for Gap Analysis; University of Nebraska Lincoln: Lincoln, NE, USA, 2004. [Google Scholar]
- Gamon, J.A.; Surfus, J.S. Assessing leaf pigment content and activity with a reflectometer. New Phyt. 1999, 143, 105–117. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.; Leavitt, B. Remote estimation of leaf area index and green leaf biomass in maize canopies. Geophys. Res. Lett. 2003, 30, 1248. [Google Scholar] [CrossRef]
- Esri, 2022c. Esri, ArcMap. Available online: https://desktop.arcgis.com/en/arcmap/ (accessed on 19 May 2022).
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Leddin, C.M.; Jacobs, J.L.; Smith, K.F.; Giri, K.; Malcolm, B.; Ho, C.K.M. Development of a system to rank perennial ryegrass cultivars according to their economic value to dairy farm businesses in south-eastern Australia. Anim. Prod. Sci. 2018, 58, 1552–1558. [Google Scholar] [CrossRef]
- Mu, Y.; Biggs, T.; Stow, D.; Numata, I. Mapping heterogeneous forest-pasture mosaics in the Brazilian Amazon using a spectral vegetation variability index, band transformations and random forest classification. Int. J. Remote Sens. 2020, 41, 8682–8692. [Google Scholar] [CrossRef]
- Phan, T.N.; Kuch, V.; Lehnert, L.W. Land cover classification using Google Earth Engine and random forest classifier—The role of image composition. Remote Sens. 2020, 12, 2411. [Google Scholar] [CrossRef]
- Torre-Tojal, L.; Bastarrika, A.; Boyano, A.; Lopez-Guede, J.M.; Graña, M. Above-ground biomass estimation from LiDAR data using random forest algorithms. J. Comput. Sci. 2022, 58, 101517. [Google Scholar] [CrossRef]
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Analys. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Loecher, M. Unbiased variable importance for random forests. Comm. Stat. Theor. Meth. 2022, 51, 1413–1425. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinfo. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Otgonbayar, M.; Atzberger, C.; Chambers, J.; Damdinsuren, A. Mapping pasture biomass in Mongolia using partial least squares, random forest regression and Landsat 8 imagery. Int. J. Remote Sens. 2019, 40, 3204–3226. [Google Scholar] [CrossRef]
- Ramoelo, A.; Cho, M.; Mathieu, R.; Skidmore, A.K. Potential of Sentinel-2 spectral configuration to assess rangeland quality. J. Appl. Remote Sens. 2015, 9, 094096. [Google Scholar] [CrossRef]
- Hanusz, Z.; Tarasinska, J.; Zielinski, W. Shapiro-Wilk test with known mean. REVSTAT-Stat. J. 2016, 14, 89–100. [Google Scholar] [CrossRef]
- Bernabucci, U.; Basiricò, L.; Morera, P.; Dipasquale, D.; Vitali, A.; Cappelli, F.P.; Calamari, L. Effect of summer season on milk protein fractions in Holstein cows. J. Dairy Sci. 2015, 98, 1815–1827. [Google Scholar] [CrossRef]
- Gao, B.; Pan, Y.; Chen, Z.; Wu, F.; Ren, X.; Hu, M. A spatial conditioned Latin hypercube sampling method for mapping using ancillary data. Trans. GIS 2016, 20, 735–754. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. A conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput. Geosci. 2006, 32, 1378–1388. [Google Scholar] [CrossRef]
- Rad, M.R.P.; Toomanian, N.; Khormali, F.; Brungard, C.W.; Komaki, C.B.; Bogaert, P. Updating soil survey maps using random forest and conditioned Latin hypercube sampling in the loess derived soils of northern Iran. Geoderma 2014, 232, 97–106. [Google Scholar] [CrossRef]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 2019, 340, 55–69. [Google Scholar] [CrossRef]
- Xu, Y.; Smith, S.E.; Grunwald, S.; Abd-Elrahman, A.; Wani, S.P. Incorporation of satellite remote sensing pan-sharpened imagery into digital soil prediction and mapping models to characterize soil property variability in small agricultural fields. ISPRS J. Photogramm. Remote Sens. 2017, 123, 1–19. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Soft. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. ranger: A fast implementation of random forests for high dimensional data in C++ and R. arXiv 2015, arXiv:1508.04409. [Google Scholar] [CrossRef]
- Kuhn, M. Caret: Classification and Regression Training; Astrophysics Source Code Library: Houghton, MI, USA, 2015; p. ascl-1505. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomised trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Patt. Recog. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Lawrence, I.; Lin, K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 255–268. [Google Scholar] [CrossRef]
- Rowlingson, B.S.; Diggle, P.J. Splancs: Spatial point pattern analysis code in S-Plus. Comput. Geosci. 1993, 19, 627–655. [Google Scholar] [CrossRef]
- Insua, J.R.; Utsumi, S.A.; Basso, B. Estimation of spatial and temporal variability of pasture growth and digestibility in grazing rotations coupling unmanned aerial vehicle (UAV) with crop simulation models. PLoS ONE 2019, 14, e0212773. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Chen, Z.; Ren, J.; Li, H.; Wu, S. Modeling winter wheat leaf area index and canopy water content with three different approaches using Sentinel-2 multispectral instrument data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 482–492. [Google Scholar] [CrossRef]
- Everitt, J.H.; Escobar, D.E.; Richardson, A.J. Estimating grassland phytomass production with near-infrared and mid-infrared spectral variables. Remote Sens. Environ. 1989, 30, 257–261. [Google Scholar] [CrossRef]
- Dang, A.T.N.; Nandy, S.; Srinet, R.; Luong, N.V.; Ghosh, S.; Kumar, A.S. Forest aboveground biomass estimation using machine learning regression algorithm in Yok Don National Park, Vietnam. Ecol. Inform. 2019, 50, 24–32. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Estimating above-ground biomass in sub-tropical buffer zone community forests, Nepal, using Sentinel 2 data. Remote Sens. 2018, 10, 601. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Nandy, S.; Singh, R.; Ghosh, S.; Watham, T.; Kushwaha, S.P.S.; Kumar, A.S.; Dadhwal, V.K. Neural network-based modelling for forest biomass assessment. Carbon Manag. 2017, 8, 305–317. [Google Scholar] [CrossRef]
- Yadav, B.K.; Nandy, S. Mapping aboveground woody biomass using forest inventory, remote sensing and geostatistical techniques. Environ. Monit. Assess. 2015, 187, 308. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sen. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Fourty, T.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: Direct and inverse problems. Remote Sens. Environ. 1996, 56, 104–117. [Google Scholar] [CrossRef]
- Salisbury, F.B.; Ross, C.W. Plant Physiology, 4th ed.; Wadsworth: Belmont, CA, USA, 1991. [Google Scholar]
- The European Space Agency, 2022, Sentinel Online User Guides Level-2. Available online: https://sentinels.copernicus.eu/web/sentinel/user-guides/sentinel-2-msi/processing-levels/level-2 (accessed on 24 November 2022).
- Ali, I.; Cawkwell, F.; Green, S.; Dwyer, N. Application of statistical and machine learning models for grassland yield estimation based on a hypertemporal satellite remote sensing time series. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 5060–5063. [Google Scholar] [CrossRef]
- Tang, R.; Zhao, Y.; Lin, H. Spatio-Temporal Variation Characteristics of Aboveground Biomass in the Headwater of the Yellow River Based on Machine Learning. Remote Sens. 2021, 13, 3404. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef]
- Lee, J.S.; Jurkevich, L.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Rev. 1994, 8, 313–340. [Google Scholar] [CrossRef]
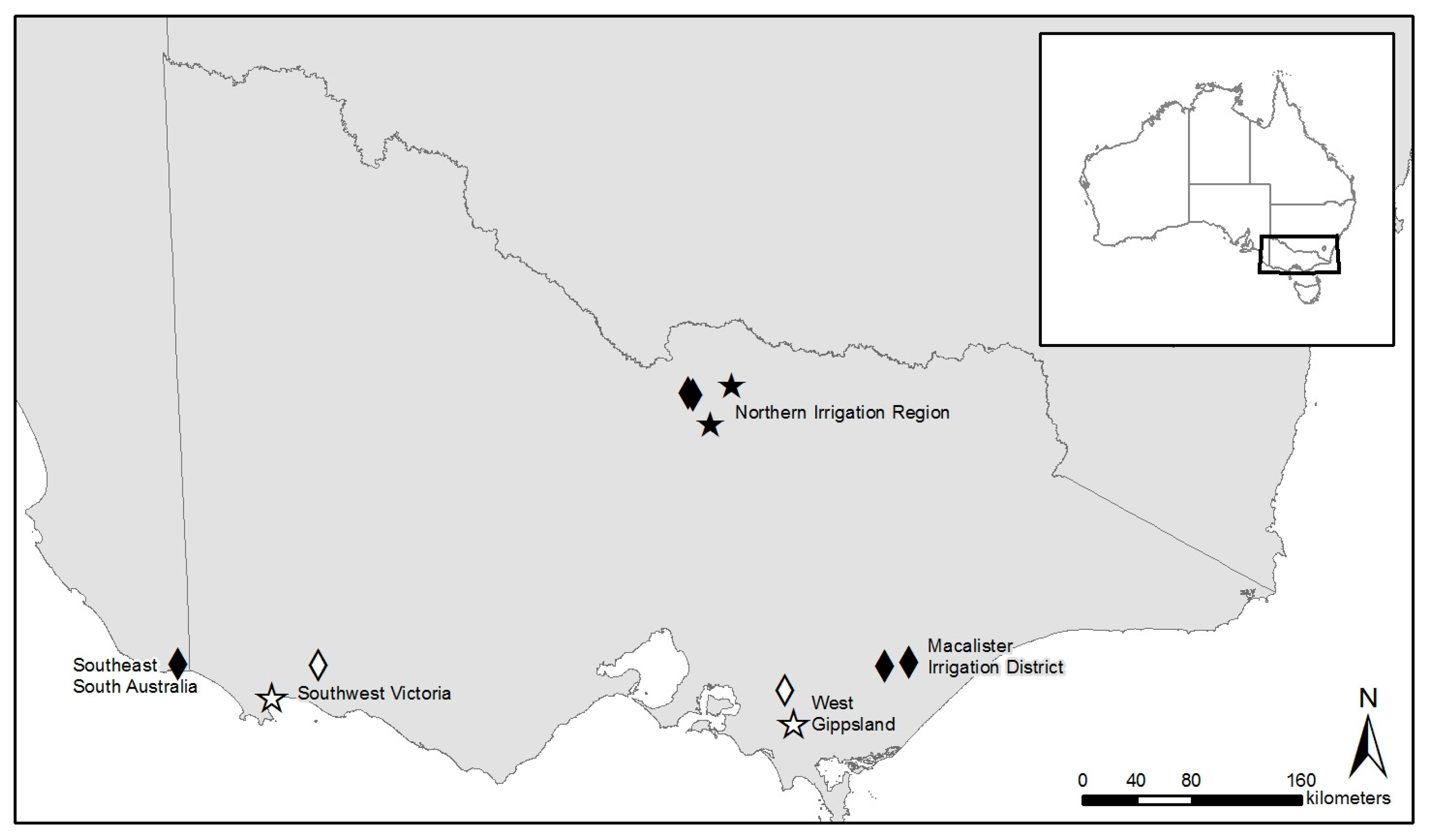
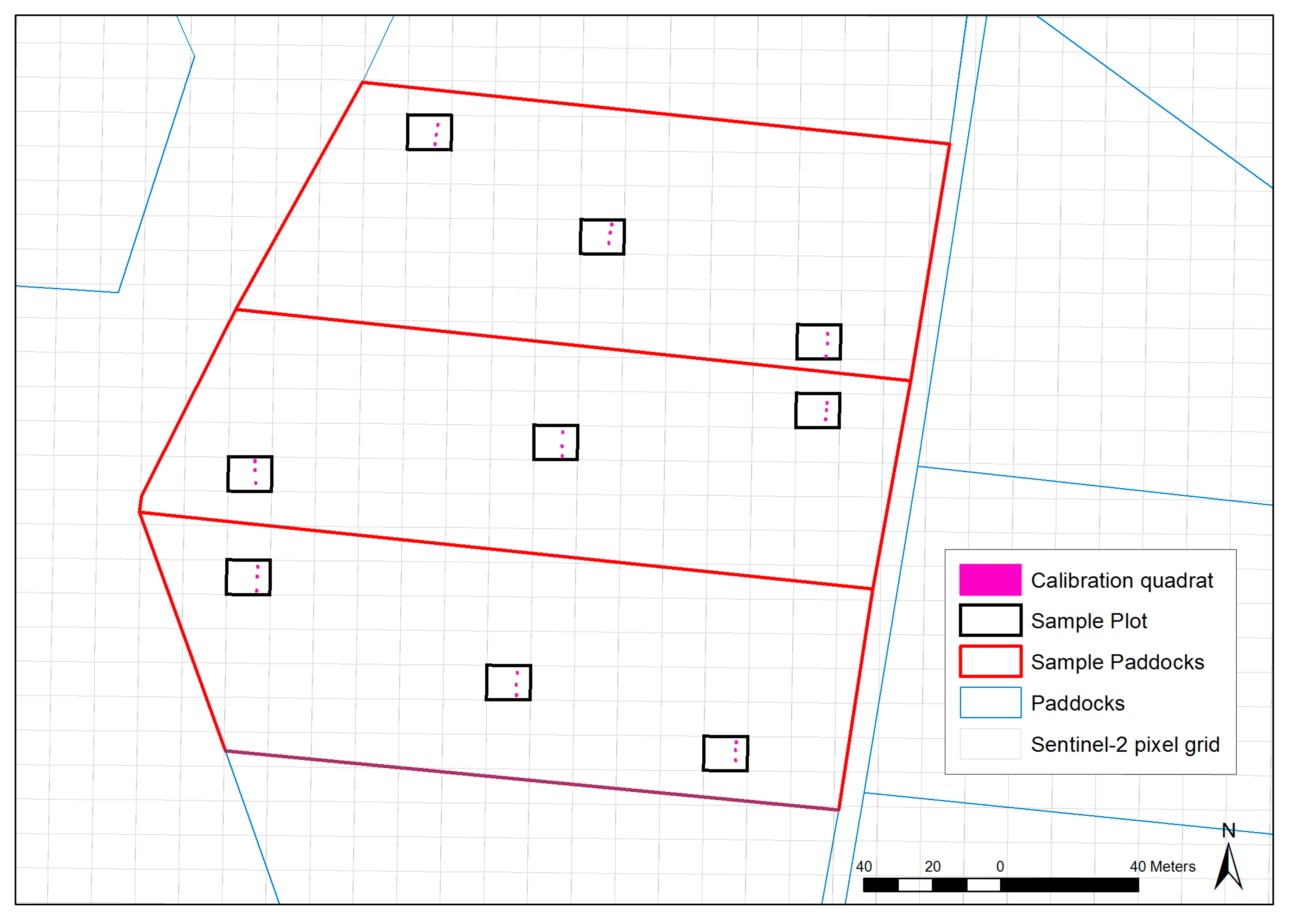




| Farm | Region | Annual Median Rainfall (mm) | Annual Median Temperature Range (°C) | Predominant Australian Soil Order | Irrigated/Dryland | Farm Size (ha) | Average Paddock Size (ha) |
|---|---|---|---|---|---|---|---|
| PS01 | Macalister Irrigation District | 594 | 8.2–19.7 | Chromosol (brown) [52] | Irrigated | 348 | 5.4 |
| PS02 | Macalister Irrigation District | 594 | 8.2–19.7 | Sodosol (brown) [52] | Irrigated | 410 | 6.4 |
| PS03 | Northern Irrigation Region | 437 | 8.7–21.8 | Sodosol (red) [52] | Irrigated | 72 | 2.3 |
| PS04 | Northern Irrigation Region | 437 | 8.7–21.8 | Sodosol (red) [52] | Irrigated | 196 | 1.2 |
| PS05 | Southeast South Australia | 767 | 8.3–19.1 | Tenosol [53] | Irrigated | 471 | 15.7 |
| PS06 | Southwest Victoria | 750 | 7.8–19.2 | Dermosol (brown) [52] | Dryland | 358 | 5.3 |
| PS07 | West Gippsland | 1001 | 9.0–19.7 | Hydrosol (redoxic), Ferrosol (red) [52] | Dryland | 231 | 1.6 |
| PS11 | Southwest Victoria | 779 | 9.4–18.0 | Chromosol (brown) [52] | Dryland | 380 | 4.5 |
| PS19 | West Gippsland | 975 | 8.5–18.7 | Ferrosol (red) [52] | Dryland | 115 | 2.2 |
| PS28 | Northern Irrigation Region | 486 | 9.4–21.9 | Sodosol (brown) [52] | Irrigated | 338 | 1.7 |
| PS31 | Northern Irrigation Region | 527 | 8.7–21.2 | Sodosol (red) [52] | Irrigated | 970 | 1.9 |
| Row No. | Image Index | Name/Description | SI Formulae or Original Band Information | Source (If Applicable) |
|---|---|---|---|---|
| 1 | Anthocyanin Ref 1 | (1/B3 G) − (1/B5 RE) | [62] | |
| 2 | Anthocyanin Ref 2 | B8 NIR × (1/B3 G) − (1/B5 RE) | [62] | |
| 3 | Atmospherically Resistant Veg | B8A RE − (B4 R − 1 × (B2 Bl − B4 R))/B8A RE − (B4 R − 1 × (B2 BL − B4 R)) | [63] | |
| 4 | B11 SWIR/B12 SWIR | B11 SWIR/B12 SWIR | E | |
| 5 | B12 SWIR/B11 SWIR | B12 SWIR/B11 SWIR | E | |
| 6 | Band_1 | Difference Vegetation Index (DVI) | B8 NIR−B4 R | [40] |
| 7 | Enhanced Vegetation Index (EVI) | 2.5 × ((B8A RE − B4 R)/(B8A RE + 6 × B4 R − 7.5 × B2 BL + 1)) | [64] | |
| 8 | Band_2 | EVI 2 | 2.5 × (B8 NIR − B4 R)/(B8 NIR + 2.4) × (B4 R + 1) | [65] |
| 9 | B11 SWIR/B8 NIR | B11 SWIR/B8 NIR | E | |
| 10 | B11 SWIR/B8A NIR | B11 SWIR/B8A NIR | E | |
| 11 | B12 SWIR/B8 NIR | B12 SWIR/B8 NIR | E | |
| 12 | Band_3 | B12 SWIR/B8A NIR | B12 SWIR/B8A NIR | E |
| 13 | Band_4 | Global Environmental Monitoring Index | (2 × ((B8 NIR × B8 NIR) − (B4 R × B4 R)) + (1.5 × B8 NIR + 0.5 × B4 R)/(B8 NIR + B4 R + 0.5)) × (1 − 0.25 × (2 × ((B8 NIR × B8 NIR) − (B4 R × B4 R)) + (1.5 × B8 NIR + 0.5 × B4 R)/(B8 NIR + B4 R + 0.5))) − (B4 R − 0.125)/(1 − B4 R) | [66] |
| 14 | Green Atmospherically Resistant Index | (B8 NIR − (B3 G − 1.7 × (B2 BL − B4 R)))/(B8 NIR + (B3 G − 1.7 × (B2 BL − B4 R))) | [67] | |
| 15 | Green Chlorophyll Index (B8) | B8 NIR | [68] | |
| 16 | Green Chlorophyll Index (B8A) | B8A NIR | [68] | |
| 17 | Band_5 | Green Difference Vegetation Index (B8) | B8 NIR − B3 G | [69] |
| 18 | Green Difference Index (B8A) | B8A NIR − B3 G | V | |
| 19 | Band_6 | Green Leaf index (GLI) | ((B3 G − B4 R) + (B3 G − B2 BL))/(B3 G + B4 R + B3 G + B2 BL) | [70] |
| 20 | Green NDVI | (B8 NIR − B3 G)/(B8 NIR + B3 G) | [71] | |
| 21 | B8 NIR/B3 Green | B8 NIR/B3 G | E | |
| 22 | B8A NIR/B3 Green | B8A NIR/B3 G | E | |
| 23 | Band_7 | Leaf Area Index (LAI) from EVI | 3.618 × (2.5 × (B8 NIR − B4 R)/1 + B8 NIR + (6 × B4 R) − (7.5 × B2 BL)) − 0.118 | [72] |
| 24 | Modified Chlorophyll Absorption Ratio | ((B5 RE − B4 R) − 0.2 × (B5 RE − B3 G)) × (B5 RE/B4 R) | [73] | |
| 25 | Modified Chlorophyll Abs Ratio IMPROVED | (1.5 × (2.5 × (B7 RE-B4 R)) − 1.3 × (B7 RE − B3 G))/sqrt((2 × B7 RE + 1) × (2 × B7 RE + 1)) − (6 × B7 RE − 5 × sqrt(B4 R) − 0.5) | [74] | |
| 26 | Modified Red Edge NDVI | (B6 RE − B5 RE)/(B6 RE + B5 RE − 2 × B2 BL) | [75] | |
| 27 | Modified Red Edge Simple Ratio | (B6 RE − B2 BL)/(B5 RE − B2 BL) | [75,76] | |
| 28 | Modified simple ratio | ((B8 NIR/B4 R) − 1)/((sqrt((B8 NIR/B4 R))) + 1) | [77] | |
| 29 | M SAVI 2 | (2 × B8 NIR + 1 − sqrt((2 × B8 NIR + 1) × (2 × B8 NIR + 1) − 8 × (B8 NIR − B4 R)))/2 | [78] | |
| 30 | Modified Triangular Veg Index | 1.2 × (1.2 × (B7 RE − B3 G) − 2.5 × (B4 R − B3 G)) | [74] | |
| 31 | Modified Triangular VI IMPROVED | (1.5 × (2.5 × (B7 RE − B4 R)) − 1.3 × (B7 RE − B3 G))/sqrt((2 × B7 RE + 1) × (2 × B7 RE + 1)) − (6 × B7 RE − 5 × sqrt(B4 R) − 0.5) | [74] | |
| 32 | Non-linear Index | ((B8 NIR × B8 NIR) − B4 R)/((B8 NIR × B8 NIR) + B4 R) | [79] | |
| 33 | Normalised Difference Vegetation Index (NDVI) | (B8 NIR − B4 R)/(B8 NIR + B4 R) | [13] | |
| 34 | Optimised Soil Adjusted Vegetation Index (OSAVI) | (B8A RE − B4 R)/(B8A RE + B4 R + 0.16) | [80] | |
| 35 | Plant Senescence Reflectance index | (B4 R − B2 BL)/B6 RE | [81] | |
| 36 | Band_8 | Red Edge NDVI | (B6 RE − B5 RE)/(B6 RE + B5 RE) | [76] |
| 37 | Renormalised Difference Vegetation Index | (B8 NIR − B4 R)/sqrt(B8 NIR + B4 R) | [82] | |
| 38 | B8 NIR/B4 Red | B8 NIR/B4 R | E | |
| 39 | B8A NIR/B4 Red | B8A NIR/B4 R | E | |
| 40 | Soil Adjusted Vegetation Index (SAVI) | ((B8 NIR − B4 R)/(B8 NIR + B4 R + 0.5)) × 1.5 | [83] | |
| 41 | Structure Insensitive Pigment Index | B7 RE − B2 BL/B7 RE − B4 R | [84] | |
| 42 | Transformed Difference Veg Index | 1.5 × ((B8 NIR − B4 R)/(sqrt(B8 NIR × B8 NIR) + B4 R + 0.5)) | [85] | |
| 43 | Triangular Greenness Index | (−0.5 × ((665 − 492) × (B4 R − B3 G) − (665 − 492) × (B4 R − B2 BL)) | [86] | |
| 44 | Triangular Vegetation Index | (120 × (B6 RE − B3 G) − 200 × (B4 R − B3 G))/2 | [42] | |
| 45 | Visible Atmospherically Resistant Index | (B3 G − B4 R)/(B3 G + B4 R − B2 BL) | [62] | |
| 46 | Wide Dynamic Range Veg Index | (0.2 × B8 NIR − B4 R)/(0.2 × B8 NIR + B4 R) | [87,88] | |
| 47 | Red Edge(B5) Simple Ratio Index | B8 NIR/B5 RE | [89] | |
| 48 | Band_9 | Red Edge(B6) Simple Ratio Index | B8 NIR/B6 RE | V |
| 49 | Red Edge(B7) Simple Ratio Index | B8 NIR/B7 RE | V | |
| 50 | Red Edge(8A) Simple Ratio Index | B8 NIR/B8A NIR | V | |
| 51 | Red Edge(B5) Chlorophyll Index | (B8 NIR/B5 RE) − 1 | [90] | |
| 52 | Red Edge(B6) Chlorophyll Index | (B8 NIR/B6 RE) − 1 | V | |
| 53 | Red Edge(B7) Chlorophyll Index | (B8 NIR/B7 RE) − 1 | V | |
| 54 | Red Edge(B8A) Chlorophyll Index | (B8 NIR/B8A NIR) − 1 | V | |
| Original S2 Bands | S2A, S2B band centre/S2A, S2B band width/resolution | |||
| 55 | Band_10 | B1 Aerosols | 442.7, 442.2/21, 21/60 | |
| 56 | Band_11 | B2 Blue | 492.4, 492.1/66, 66/10 | |
| 57 | Band_12 | B3 Green | 559.8, 559.0/36, 36/10 | |
| 58 | Band_13 | B4 Red | 664.6, 664.9/31, 31/10 | |
| 59 | Band_14 | B5 Red Edge | 704.1, 703.8/15, 16/20 | |
| 60 | Band_15 | B6 Red Edge | 740.5, 739.1/15, 15/20 | |
| 61 | Band_16 | B7 Red Edge | 782.8, 779.7/20, 20/20 | |
| 62 | Band_17 | B8 NIR | 832.8, 832.9/106, 106/10 | |
| 63 | Band_18 | B8A NIR | 864.7, 864.0/21, 22/20 | |
| 64 | Band_19 | B9 Water Vapour | 945.1, 943.2/20, 21/60 | |
| 65 | Band_20 | B11 SWIR 1 | 1613.7, 1610.4/91, 94/20 | |
| 66 | Band_21 | B12 SWIR 2 | 2202.4, 2185.7/175, 185/20 |
| Model Accuracy Indicators | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type | Field Data (kg DM/ha) | Model Development Data | Shapiro-Wilk Test | Random Forest Model | ||||||
| Min | Max | Calibration | Validation | w-Value | p-Value | R2 | LCCC | RMSE (kg DM/ha) | NRMSE | |
| Internal validation | 668 | 5777 | 171 | 43 | 0.9596 | <0.05 | 0.90 | 0.72 | 439.49 | 15.08 |
| Independent validation | 411 | 4838 | 84 | 0.9571 | <0.05 | 0.88 | 0.68 | 457.05 | 19.83 | |
| Accuracy and Efficiency Indicators | R2 | LCCC | RMSE (kg DM/ha) | NRMSE | Maximum Biomass Predicted (kg DM/ha) |
|---|---|---|---|---|---|
| With SWIR bands | 0.90 | 0.72 | 439.49 | 15.08 | 4348.25 |
| Without SWIR bands | 0.79 | 0.57 | 635.46 | 21.80 | 3379.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morse-McNabb, E.M.; Hasan, M.F.; Karunaratne, S. A Multi-Variable Sentinel-2 Random Forest Machine Learning Model Approach to Predicting Perennial Ryegrass Biomass in Commercial Dairy Farms in Southeast Australia. Remote Sens. 2023, 15, 2915. https://doi.org/10.3390/rs15112915
Morse-McNabb EM, Hasan MF, Karunaratne S. A Multi-Variable Sentinel-2 Random Forest Machine Learning Model Approach to Predicting Perennial Ryegrass Biomass in Commercial Dairy Farms in Southeast Australia. Remote Sensing. 2023; 15(11):2915. https://doi.org/10.3390/rs15112915
Chicago/Turabian StyleMorse-McNabb, Elizabeth M., Md Farhad Hasan, and Senani Karunaratne. 2023. "A Multi-Variable Sentinel-2 Random Forest Machine Learning Model Approach to Predicting Perennial Ryegrass Biomass in Commercial Dairy Farms in Southeast Australia" Remote Sensing 15, no. 11: 2915. https://doi.org/10.3390/rs15112915
APA StyleMorse-McNabb, E. M., Hasan, M. F., & Karunaratne, S. (2023). A Multi-Variable Sentinel-2 Random Forest Machine Learning Model Approach to Predicting Perennial Ryegrass Biomass in Commercial Dairy Farms in Southeast Australia. Remote Sensing, 15(11), 2915. https://doi.org/10.3390/rs15112915






