Weakly Supervised Perennial Weed Detection in a Barley Field

Abstract

In the field of precision agriculture, weed detection models combined with selective spraying by ground or aerial robotics are seen as promising approaches for increasing yield harvests while simultaneously minimizing herbicide use. The available labeled training data are a major bottleneck for developing and applying supervised deep learning models, and more automated methods for labeled data generation are therefore needed. Our research aims to address this need by introducing a rule-based method for label data generation for perennial weeds. For this research, a dataset of a barley field was collected using an unmanned aerial vehicle (UAV) with a flight altitude of 10 m. A multispectral and a thermal camera were used for the data collection. The preprocessed dataset consists of multispectral and thermal orthomosaic images along with a canopy height model. The methodological part of this article introduces a proposed rule-based method for labeled data generation for perennial weeds based on the Normalized Difference Vegetation Index (NDVI), and this approach is further used to generate labels for the measured data. The preprocessed data combined with the generated labels was used to train U-net models. Three data combinations are used for the training and testing: multispectral, multispectral–thermal and multispectral–thermal–canopy–height–model. This approach was used to evaluate whether additional data improve model performance. To evaluate the models on ground truth labels, they are tested on a manually annotated test dataset, which consists of 10% of the whole dataset. The tested models achieved an F1 score of 0.82–0.83 on the test dataset. This finding demonstrates that the rule-based labeling method generates valid labels for the perennial weed detection task. Furthermore, our study shows that data fusion improved the model slightly. The data combination of multispectral–thermal–canopy–height–model as input resulted in the best-performing model, with an F1 score of 0.835.

1. Introduction

Application and research in precision agriculture experienced a sudden increase in recent years due to the rapid performance improvement of state-of-the-art deep learning models and the growing availability of data collection platforms and more financially affordable sensors. The goal of precision agriculture lies in reducing the environmental impact of agriculture by curtailing the quantities of fertilizers, herbicides, and pesticides [1]. This goal is aimed to be achieved by implementing aerial vehicles and ground robotics, which can apply the desired chemicals selectively to the necessary parts of agricultural fields [2,3].

The urgent reduction of pesticides and herbicides to decrease environmental impacts is shown by the need for more environmentally friendly farming strategies to minimize the negative impact of agriculture on the environment [2]. To employ selective spraying by robotics in an agricultural environment, the machinery must differentiate between weeds and non-weeds in a recorded image. Several studies have focused on developing accurate detection models to enable this robotic vision. Recently, these models have mainly been driven by deep learning models. Most of these models follow a supervised strategy. This means they rely on manually labeled ground truth training data [4,5,6]. Annotating vegetation images into weeds and non-weeds or into crops or soil is a very time-consuming task. This task can be complicated by factors that depend on image resolution, background complexity, and required data levels. As deep learning models perform better with larger amounts of data, it is necessary to annotate hundreds to thousands of plant images to be able to train one model. To address this issue, automatic weed-labeling functions or approaches are needed to generate labels for collected data. Recent strategies developed to address this, by taking the line-based structure of a field into account, rely on active learning or on generating labels in combination with a designed field experiment or a greenhouse [7,8,9].

This paper contributes to the field by proposing a semi-automatic label-generation approach for perennial weed detection, with an approach that exploits the Normalized Difference Vegetation Index (NDVI) and spatial structure, without relying on line detection algorithms. We hypothesize that the rule-based classifier produces labels that resemble real-world data, and a deep learning model can learn to successfully detect perennial weeds in real-world data from these labels.

Further, this article contributes to the research field by evaluating the benefits of a multisource dataset for perennial weed detection, particularly the combination of a multispectral and thermal sensor with a canopy height model (CHM). Our hypothesis, which is evaluated in this context, is that combining thermal and multispectral inputs leads to higher model performance for perennial weed detection. Another hypothesis is that additional data sources in the form of a canopy height model will improve model performance.

For this research, a dataset of a barley field was collected with an unmanned aerial vehicle (UAV) and a flight height of 10 m using a multispectral and a thermal camera. The data were preprocessed and georeferenced for an accurate overlap. Additionally, a CHM was computed. As the first methodological step we introduced our newly developed rule-based classifier. This method uses near-infrared information along with spatial structure to divide the image pixels into class labels: perennial weeds and background. This method is further used to generate labels for the collected data. The generated labels are then used with three data combinations—multispectral, multispectral–thermal and multispectral–thermal–canopy–height–model—to generate three training and validation datasets. Further, three test datasets consisting of 10% of the data are created with the same data combinations. For these test datasets, the labels are not generated by the rule-based classifier but are manually annotated so that the test labels are ground truth labels. This is done to evaluate the model on ground truth data, and it is performed independently from the label-generation approach. Further, a deep learning model is introduced in the methodological part of this study, specifically, a U-net with an expanded pretrained Resnet101v2 backbone. A variation of this model is trained on each data combination to evaluate the benefits of additional input data. In the last step, these models are tested on manually labeled weed images that contain 10% of the dataset to evaluate the model independently from the label-generation method. In the results, the F1 score, precision, recall, along with intersection over union (IoU) for the perennial weeds and background and their averages are displayed. Additionally, we performed an experiment to evaluate the labels of the rule-based classifier to assess the quality of the labels individually. These results are then contextualized in the discussion, and limitations are outlined before concluding the study.

2. Related Work

Precision agriculture has become a widely researched field over the last decades. This development has predominantly been driven by new sensor development and more available platforms. As it is a fast-developing research field, several surveys and reviews of the field have been conducted to provide an overview of recent developments [10,11,12].

Data collection for weed detection research is performed in person or, more commonly, by using various platforms, for example, field robots, ground vehicles, UAVs, and satellites [4]. RGB, multispectral, and sometimes hyperspectral or thermal cameras are typical camera sensors used in weed detection [4,13].

As an additional source in some studies, 3D data are used as lidar-point clouds or a rasterized point cloud in the form of a CHM [14,15]. However, particularly UAV-based studies using canopy models are very limited and are not mentioned in reviews concerning weed detection [4,5].

Before deep learning methods became popular in computer vision, most weed detection research was based on machine learning algorithms. In contrast to deep learning methods, these algorithms require task-specific feature extraction as a data preprocessing step. Task-specific shapes, textures, and spectral or color features were commonly computed in weed detection [4,16]. Nowadays, most weed detection approaches rely on deep learning models [4]. These models do not require specifically designed feature extraction by experts but rather perform this automatically [4].

Machine and deep learning models can be supervised, semi-supervised, or unsupervised. Models employed in weed detection are most commonly supervised [4]. While supervised deep learning models achieve incredible accuracy performances, they rely on a high amount of training data, which also creates several obstacles [4]. As our study evaluates supervised deep learning models, this topic and related studies are outlined in more detail in the following.

2.1. Supervised Deep Learning for Weed Detection

Most supervised deep learning models applied for weed detection are based on convolutional neural networks (CNNs) [17]. Further, transfer learning is a commonly applied practice of applying pretrained models to a customized dataset. The benefit of this approach is that pretrained networks do not have random weights, but rather, they have weights in the CNN layers that are specialized for image feature extraction tasks, e.g., edge detection [18]. Using pretrained models also allows training a model without using millions of images but instead enables retraining and fine-tuning it only using hundreds to thousands of images. In weed detection, mostly RGB sensors are used for data collection, and therefore, applying transfer learning using pretrained weights is seamless [4]. For higher channel images, for instance, in the case of multispectral images, transfer learning can also be used. However, this requires random weight initialization for the extra channels or other weight-initialization techniques.

Common pretrained architectures for weed detection are: VGG-16,VGG-19, ResNet-18, ResNet-50, ResNet-100, AlexNet, GoogLeNet, Inception-v3, Yolo-v3, Mask-RCNN, Faster-RCNN, Deeplab, Deeplab-v3, Darknet-53, SegNet, U-net, and EfficientNet [4,19]. A new model type based on vision transformers is also worth mentioning, as these models have recently achieved high performances in various fields of computer vision. They are also already applied for weed detection and are expected to become more popular for this research topic [19].

In weed detection, the mentioned models are applied in different ways, either for classification, object detection, semantic segmentation, or instance segmentation tasks. In many research studies, weeds are defined as a common group, and a specific crop is identified as the other target [3]. This is due to weeds on a single-crop field potentially showing a high level of class variability and consisting of tens of plant species. A study by Salonen et al. [20] concerning the composition of weed flora in cereal spring crop fields in Finland concluded that conventionally farmed spring cereal fields in Finland average 12 weed species per field, while organically farmed fields of the same crop average 32 weed species per field.

Semantic segmentation research commonly divides the segmentation task into three classes: weeds, crops, and background [21,22]. Common architectures used for semantic segmentation are U-net and SegNet, which are used with various pretrained backbone models [8,22].

2.2. Supervised Weed Detection Using Sensors and Input Data

Several data sources are used in weed detection. The use of multispectral and thermal images along with CHMs are outlined in the following related studies.

In the case of multispectral images, Sa, Chen, et al. [8] trained several models based on the SegNet architecture on data, which they collected using a micro-aerial vehicle, a flight altitude of 2 m, and a Sequoia multispectral sensor. They achieved a model performance of ~0.8 F1 score for weed class detection and a 0.78 ROC area.

Sa, Popović, et al. [21] collected multispectral images of eight field areas using a RedEdge-M and a Sequioa Sensor and a flight altitude of 10 m. Further, they computed additional channels, e.g., NDVI and a color-infrared for their data. Their best-performing model had a SegNet architecture that achieved area under curve (AUC) scores of 0.839 for the background 0.863 for the crop, and 0.782 for the weeds. AUC scores measure the areas under a precision and recall curve, and they are used to optimize the balance between recall and precision using specific thresholds [23].

Moreover, Ramirez et al. further applied a SegNet, a U-net, and a DeepLabv3 on the data collected by Sa, Popović, et al. [21]. Their best-performing model was a DeepLabv3 that achieved an AUC of 0.89 and a 0.81 F1 score for weeds [22].

Osorio, Puerto, et al. [24] also used multispectral images collected at an altitude of 2 m using a UAV in their research for weed estimation. They did not use the semantic segmentation approach but rather object detection models—namely, Mask-RCNN and YOLOV3. They achieved an F1 score of 0.94 for crop detection. After running their models, they removed the detected crop classes from the images by postprocessing and used the remaining plant pixels to estimate the weed coverage of the images [24].

Using thermal sensors for weed detection is not a common practice. No studies using thermal sensors were listed in several reviews on weed detection [5,6]. Further, Tsouros et al. [11] state that thermal sensors are mostly applied for irrigation management in the context of agriculture.

Using thermal imaging for weed detection is rare. However, Zamani and Baleghi [13] explored the benefits of visual and thermal imaging for weed classification. They applied several models, specifically, a multilayer perceptron neural network (MLP) and two neural network models based on extreme learning machines. Their best-performing model was an extreme learning machine model that achieved an accuracy of 98.08% in a late fusion approach [13]. Further, they showed that thermal imaging improved the model by 0.75% to 1.28%, while the late fusion approach improved the model by 0.27% [13]. In another study, Eide and Koparan et al. [25] used thermal and multispectral imaging to distinguish between different weed biotypes to evaluate their glyphosate resistance. This study concluded, however, that multispectral imaging provided better results [25].

Using a CHM or 3D data for weed detection is also uncommon. In their review, Wu et al. [5] states that height measurements are rarely incorporated, as they may experience a great deal of noise from the UAV vibration. However, a few UAV-related weed detection approaches use CHM as an input. Commonly, a CHM is computed by subtracting a digital terrain model from a digital surface model [26,27]. Kawamura et al. [28] used a CHM in combination with spectral and textural features derived from RGB images to train a superpixel-based random forest. The best model achieved an accuracy of 0.915 using hue, saturation, intensity (HSV), and texture features. Their model used a CHM and HSV features as inputs and did not achieve the best performances, yet their model showed improvement over models which used HSV features or not well-fitting spectral indices as input [28].

Zisi et al. [27] explored the benefits of using a CHM as a model input to differentiate between weed patches and crops. They showed that using texture and height as features improved the model performances from 70% to 87% and from 82% to 95%, respectively.

Torres-Sánchez et al. [15] studied the effect of using a CHM as additional features in an artificial neural network (ANN), which they applied to UAV-collected RGB images of a cotton and sunflower field. In the case of the sunflower crop, they showed that the CHM was the eighth most important feature for model performance out of ten important features. For the cotton crop field, the CHM was not one of the ten most important features. They concluded that a CHM can be an important input feature for a model, but the importance depends on the field structure or the types of weeds and crops involved [15].

2.3. Automatic Label Generation for Weed Detection

As stated, most deep learning methods are based on supervised learning approaches, which require a large amount of manually labeled data. Some studies try to tackle this issue by proposing methods for automated label data generation.

Bah et al. [7] developed an approach that is used to generate automatic labels for weed detection. This approach first detects crop lines with a Hough transform and then applies a superpixel segmentation for arranging all interrow pixels into groups, thereby developing a small weeds-only dataset. For this weeds-only dataset, they further compute texture and spatial and spectral features and use a machine learning model to detect not only interrow weeds, but also weeds within the crop rows. They applied this strategy on two fields to generate a training dataset with automatically generated labels. Further, they compare models using fully supervised labels with models that only used automatically generated labels. While the fully supervised models in this comparison achieved AUCs of 94.84% and 95.70%, the models based on their automatic labeling strategy achieved AUCs of 88.73% and 94.34%, respectively [7].

Moreover, Sheikh et al. [9] proposed a weak supervision approach combined with an active learning strategy for weed label generations for a semantic segmentation task. This strategy relies on transfer learning of an already trained weed crop detection model, which is applied iteratively to a new dataset. For this approach, they used a model trained on a sugar beet dataset captured in Bonn and retrained it for a sugar beet dataset from Zurich and Stuttgart.

In between each model iteration, the model predicts pseudo-labels for the sample images. These were then ranked using various methods to determine which samples should be annotated next to gain the most weight improvements. These selected samples are then annotated by a human, and the model is trained with the additional samples. After training with additional annotated samples, the model is once again used to predict pseudo-labels and rank the additional samples for annotation, etc. This leads to an improved segmentation mask after each iteration and, consequently, to an improvement in model performance. With this approach, they achieved remarkable results on two datasets with only 10 additional annotated images. A fully supervised model run of the Stuttgart dataset achieved a mean IoU of 0.79. With this dataset, they achieved 90% of the fully supervised performance when only using 10 additional images for retraining the model. While on the Zurich dataset, where a fully supervised model achieved a mean IoU of 0.7, they achieved 70% of the fully supervised performance with 10 additional samples [9].

Despite computational approaches, artificial growing setups and field experiments can be used to support label generation. Sa et al. [8] used an artificial field setup that was divided into three plots. Only crops were planted on the first plot and a maximum level of a possible herbicide was applied. On the second plot, they planted crops and applied no herbicides. They planted no crops on the third plot, so only weeds grew on this plot. They used the crops-only and weeds-only plots to generate semantic labels by separating the plant from background pixels using an NDVI-Otsu threshold. With the generated labels, they trained several deep learning models and tested these models on the plot with weeds and crops and achieved an F1 score of 0.8–0.85 for weeds in a multiclassification semantic segmentation [8].

3. Materials and Methods

This chapter introduces the research data along with the data collection and preprocessing steps. Then, the proposed label data generation approach is introduced. This approach was used to generate labels and combine them with the input data to generate three data combinations for training, validation, and testing. A further three test datasets were created with the same data combinations, but with self-annotated ground truth labels.

The deep learning models that were applied to the data are introduced at the end of the chapter. In Figure 1, a visual overview is given of the research steps used in this study. Further, an additional experiment was performed to individually evaluate the quality of the produced labels of the rule-based classifier.

3.1. Study Area

The chosen field for our study is a barley crop field located in Helsinki, Finland. In Figure 2, the extent of the study area is visualized in yellow. At the time of data collection, the barley crops were in early growth stages—i.e., the fourth leaf stage. This was just 2–3 weeks after the field was sown. The barley field showed some weed infestation patches, e.g., larger patches of couch grass. Further, the field itself had multiple areas with higher crop density, resulting from double seeding. As our data collection took place in a field corner, the dataset also showed non-linear seeding directions along the field shapes. This is worth mentioning, as a chosen dataset for weed detection often shows a clear linear line structure of crop rows.

The field showed a large number of perennial weeds, which are the focus of our study. In contrast to annual weeds, perennial weeds have a specific root structure that enables the plants to store nutrients and survive for several years [29]. Examples of perennial weeds that were present in the barley field during the data collection include the creeping thistle (Sonchus arvensis), scentless may weed (Tripleurospermum inodorum), rumex (Rumex sp.), and couch grass (Agropyri repentis rhizome). We considered these perennial weeds to be one class group, and they are the focus of the weed detection task. An example region of the collected data is shown in Figure 3 to provide a visual representation of how the field and plants looked during data collection.

3.2. Data Collection

For this study, we collected a dataset of a barley field using a custom-built UAV, which was provided by the Agrotechnology research group of the University of Helsinki. The barley field is located in Helsinki, Finland. The data collection took place on 18 July 2021 from 1 pm to 2 pm under blue-sky conditions.

For the data collection, we used a multispectral camera, namely, MicaSense RedEdge 3, and a thermal camera, namely, FLIR Duo Pro R (FDPR), with a 640 resolution and 13 mm lens. The flight missions were performed at an altitude of 10 m and a front and side overlap of 80% was used for the flight campaign.

Flying below 10 m with a commercial automatic flight planning software is not possible, but since we wanted to have as high resolution as possible for our data collection, we chose the minimum altitude of 10 m.

A calibration image for the multispectral camera was taken directly after flight collection. The geolocations of six ground control points (GCPs) were measured during the data collection in the fields with a precision global navigation satellite system (GNSS, Reach RS2+). The ground control points were self-built white check boards, which used white and aluminum squares instead of white and black squares and had a size of 40 cm². These self-built GCPs were used because the material is identifiable in multispectral and thermal images. This is essential for georeferencing the data. Using aluminum for georeferencing thermal images is a common practice [30].

The FDPR camera can be adjusted to target emissivity, ambient air temperature, and relative humidity [31]. The humidity value is a categorical range. For this study, we used a medium setting, as the relative humidity measured by the closest weather station was 39% [32]. The ambient temperature was adjusted to the temperature measured by the closest weather station—Helsinki Malmi Airfield [32]. A summary of the flight campaign used for data collection is given in

Table 1. Summary of data collection.

Description	Flight Campaign Details
Crop	Barley (fourth leave stage)
Weeds	Perennial weeds
Location	Helsinki, Finland
Time and date	1–2 p.m., 18 June 2021
Sky conditions	Mostly blue-sky conditions
Humidity	39%
Air temperature	26.5 °C
Aerial platform	Custom-built unmanned aerial vehicle
Cameras	MicaSense RedEdge 3 and FLIR Duo Pro R (640, 13 mm)
Altitude	10 m
Front and side overlap	80%
Ground control points	Six self-built white and aluminum check boards
Global navigation satellite system (GNSS) receiver	Reach RS2+
Ground sample distance: MicaSense RedEdge 3	0.00663 m
Ground sample distance: FLIR Duo Pro R	0.012810 m

.

3.3. Data Preprocessing

The collected image data were preprocessed into orthomosaic maps, which are geometrically corrected aerial images. The preprocessing of the image data for the two sensors was performed individually using the software PIX4D mapper. Both sensor data were preprocessed into orthomosaics in the same manner—described below—and only the spectral correction method differed for each sensor.

To generate the orthomosaics, the software PIX4D mapper was used to first identify key points in the collected images and match them accordingly across overlapping images. Further, we used a global bundle adjustment method to correct the camera parameters and to generate a sparse 3D triangulation point cloud from the key points [21]. In the next step, the midpoints of the six GCPs were marked in eight pictures per GCP. This information was then used to georeference all images accordingly with the software. In a continuous step, the software densified and corrected the 3D point cloud and then used these to create a 2D orthomosaic [21].

The multispectral orthomosaics, which consist of the five spectral bands of the MicaSense RedEdge 3 sensor (blue, green, red, red-edge, near-infrared (NIR)), were further spectral calibrated into reflectance maps. For the spectral calibration, an image of a reflectance panel was taken directly after the flight. The applied radiometrical correction uses the reference targets and the recommended procedures of the sensor companies to correct the orthomosaics accordingly. A detailed procedure of the math behind this radiometric correction for the reflectance map creation is shown in a study by Sa et al. [21]. It is worth mentioning that the MicaSense RedEdge 3 camera also uses a sensor to correct the effect of sun orientation and irradiance, which is also used by the manufacturer’s algorithm to further correct the reflectance maps [21].

In addition to the regular spectral bands of the MicaSense RedEdge 3 sensor, we calculated an NDVI as an additional orthomosaic using the following formula by Rouse et al. [33]:

$$NDVI=\frac{NIR-R}{NIR+R}$$

As previously stated, the procedure of generating an orthomosaic map is performed by matching key points across various images and creating and filtering a 3D point cloud. This 3D point cloud can be processed to a digital surface and digital terrain model [26].

The digital surface model was created with the same resolution as the multispectral orthomosaics. The digital terrain model had a lower resolution and was further upsampled to the same resolution, using a nearest-neighbor resampling approach [34]. To create the CHM, which consists solely of plant height, the digital terrain model was subtracted from the digital surface model [15].

The thermal images collected by the FDPR camera were also preprocessed onto an orthomosaic. The information of the camera setting, which was stated in the data collection settings, was used with the default algorithm of the manufacturer to form the calibrated reflectance map of the longwave infrared spectra [31]. The manufacturer states that these values are corrected radiometrically to absolute temperatures and do not need further calibration [31]. The corrected reflectance map was used without additional ground target calibration, as no correct absolute values were needed.

However, the ground sample distance (GSD) of the thermal camera was larger than that of the multispectral camera. The thermal dataset was therefore upsampled to the same GSD as the multispectral dataset, using the nearest neighbor resampling technique [34].

Moreover, all channel layers were scaled to 0–255 and were further zero-centered using mean and standard deviation to fit the pretrained weights of the chosen deep learning model backbone, which is introduced later.

3.4. Label Generation and Data Split

Labels are required to generate training data for a supervised deep learning model. This chapter is divided into two parts. The first part covers label generation for the data and the second part explains how they are used in combination with the collected data to split the orthomosaics into image tiles and to further generate training data, validation data, and test datasets.

3.4.1. Proposed Method for Label Data Generation

Annotating orthomosaics or images into a fully semantic segmentation mask is a complex and laborious task. For this reason, a rule-based classifier was developed and is proposed here, to automatically label all image pixels as perennial weeds or as background. This classifier will be introduced in detail below. For testing, we randomly selected and manually annotated 10% of the images. This was done to allow for model testing and for real ground truth data.

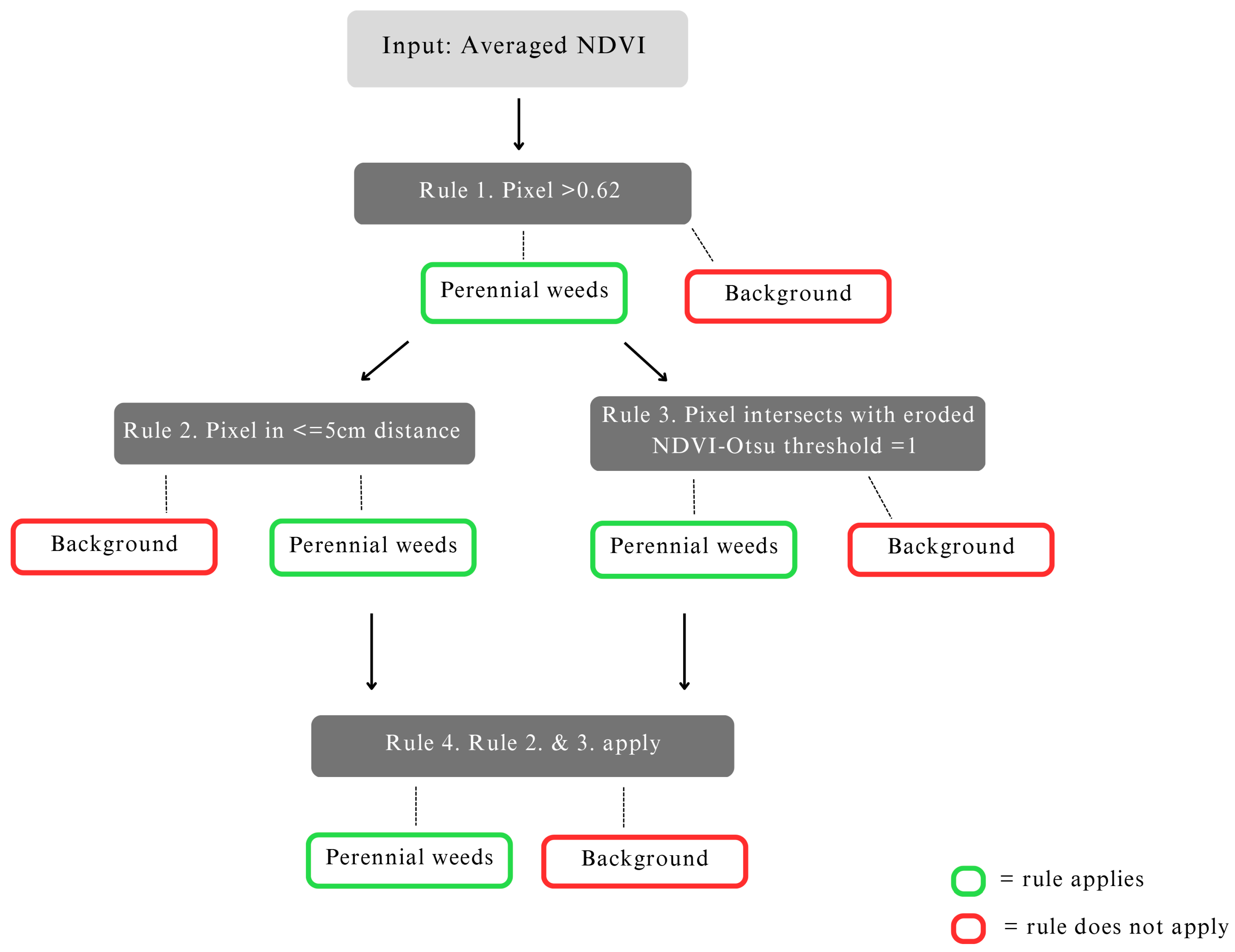
The rule-based classification is primarily based on various spatial thresholds that are applied to the NDVI orthomosaic. Further, the classification also accounts for the spatial structure of NDVI values. By this approach, higher NDVI values, which appear in clusters, are identified as perennial weeds. The logic behind this classifier lies in using the biological characteristics of perennial weeds. As they have a specific root structure and have already stored nutritive elements, they have a growth advantage compared with crops, meaning that perennial weeds are larger in size at the time of data collection and show a higher chlorophyll content. Therefore, the perennial weeds and crops should be distinguishable from each other by a spatial thresholding scheme, which we expressed in the form of a rule-based classifier. A schematic overview of the rule-based classifier is given in Figure 4.

The rule-based classifier introduced here is based on four rules. As an input, the rule-based classifier uses an NDVI that was averaged with a 16 × 16 kernel. This averaging of the input is done to emphasize larger spatial patterns and to suppress small outliers of single high NDVI values.

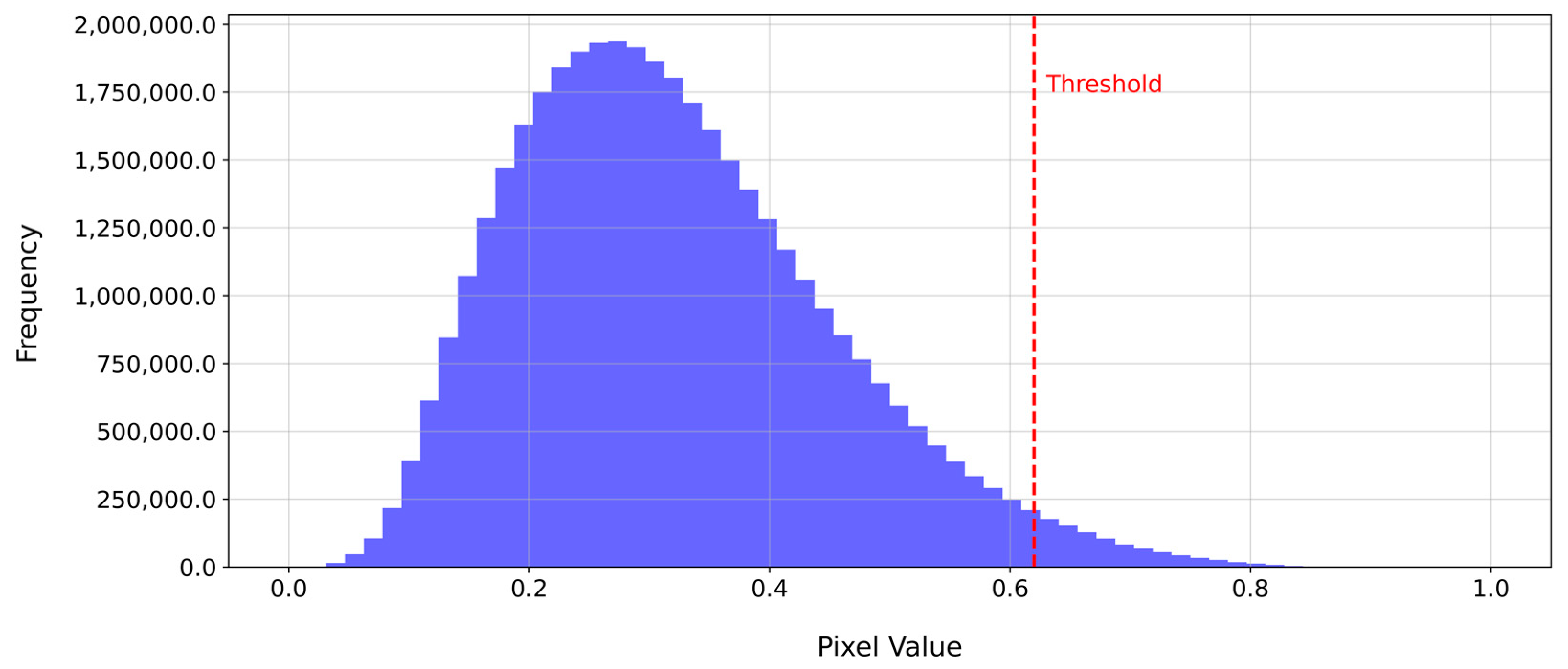
The first rule that is applied focuses on recognizing perennial weed plant cores. According to the first rule, a pixel that is >0.62 is considered a potential perennial weed pixel, while a pixel that is <0.62 is not considered a potential perennial weed pixel. This threshold was estimated with trial and error experiments. Previous research by Kim et al. [35] showed that a threshold on an averaged NDVI can be suitable to separate weed patches from the crop buckwheat and background. The distribution of the averaged NDVI values with our applied threshold is visualized in Figure 5.

According to the second rule, if a pixel is within a 5 cm buffer distance from pixels that were identified as potential perennial weeds by the first rule, then this pixel is still considered a potential perennial weed pixel. However, if the pixels are further away, they are not considered potential weed pixels.

The third rule uses an NDVI-Otsu threshold that was eroded by a 5 × 5 kernel to separate pixels belonging to other plants and non-plant pixels from the buffered distance. Separating plant and non-plant pixels or obtaining the extent of plants is commonly performed with an NDVI-Otsu threshold. We used an eroded version to minimize overlaps between plants. The third rule applies if a pixel that was identified by the first rule intersects with a plant pixel, meaning the pixel intersects with a pixel that has an NDVI-Otsu threshold value equal to one. If this is true then the pixel is considered a perennial weed pixel, if it intersects with a threshold value of zero it is considered a background pixel.

The fourth rule exists to evaluate whether the second and the third rule apply simultaneously. If both the second and third apply simultaneously, the pixels are considered perennial weeds, and if not, the pixels are considered background. Therefore, if at least one rule does not apply, they are considered background pixels. The background class consists of soil, crops, and non-perennial weeds (annual weeds).

This rule-based classifier was applied on an averaged NDVI orthomosaic to generate a perennial weed and background label mask for the entire orthomosaic. This perennial weed and background label mask was then further upsampled to the same resolution of the collected multispectral dataset. Figure 6 shows an example region of the collected data and the corresponding rule-based generated labels.

3.4.2. Training, Validating, and Test Data Generation

All preprocess data layers—multispectral, thermal, and CHM orthomosaics—were merged into one dataset with eight channels and combined with the generated perennial weed and background label mask orthomosaic. This orthomosaic was then split into 256 × 256 × 8 images, using a defined area of interest that only included the actual field area. This resulted in 544 images.

From this, we used 80% of the data, i.e., 435 image tiles, for training and 10% for validation (54 image tiles) and testing (55 image tiles), as shown in

Table 2. Overview of the training, validation, and test datasets.

Data	Images	Labels
Training data	435 images (80%)	Weak labels generated by rule-based classifier
Validation data	54 images (10%)	Weak labels generated by the rule-based classifier
Test data	55 images (10%)	Self-annotated ground truth labels

. The generated labels are used for the training and validation data, whereas these labels were not considered for the testing data. Instead, all test images were manually annotated to create ground truth label masks of perennial weeds and background, which are independent from the label-generation approach.

To evaluate the deep learning models for various data combinations, we created three spatially identical sets for training, validation, and test datasets. The only difference between these datasets is the varying number of channels in the image tiles. Therefore, the last two channels were removed from each image tile for the multispectral dataset the last channel was removed for the multispectral–thermal dataset, and no channel was removed for the multispectral–thermal–canopy–height–model data. An overview of the created data combinations is shown in

Table 3. Overview of data combinations for the training, validation, and test datasets.

Type	Data Combination a	Channel Number
Multispectral	B, G, R, RE, NIR, NDVI	6
Multispectral–thermal	B, G, R, RE, NIR, NDVI, LWIR	7
Multispectral–thermal–CHM	B, G, R, RE, NIR, NDVI, LWIR, CHM	8

^a R, G, B, RE, NIR, NDVI, LWIR, CHM indicate red, green, blue, red edge, near-infrared, normalized difference vegetation index, long-wave infrared, and canopy height model channel, respectively.

.

Further, it is worth mentioning that the data distribution for the generated labels for the training and validation data is 91% background and 9% perennial weeds. This distribution may not reflect the actual data distribution, as it is estimated using the generated labels by our proposed approach. The actual data distribution would require field annotation and is thus unavailable.

For the test set, which uses ground truth labels, the data distribution is 86.4% background to 13.6% perennial weeds. Comparing the computed distribution using the generated labels with the ground truth labels shows that they differ by 4.6%. However, both show the main trend of a high class imbalance for perennial weeds. In Figure 7, test images and their ground truth masks are shown.

It is worth mentioning that the annotation time for the ground truth mask of the test dataset took one researcher two weeks. To compare, it would take one researcher up to 4–5 months to manually label the entire data set of 544 images.

3.5. Deep Learning Model

The chosen deep learning model that we applied to the datasets has a U-net architecture. This model was developed by Ronneberger et al. [36] and is particularly good for semantic segmentation tasks.

We chose a Resnet101V2 for the backbone of the U-net model. Resnet backbones are well performing and widely applied [4]. To use the backbone network, we used the pretrained weights, which stemmed from training on the imageNet dataset. As the dataset has more channels than the imageNet dataset, which has three channels, the remaining weights for each additional channel for the first convolutional layer of the backbone cannot be directly initialized with pretrained weights. They were therefore initialized differently. To account for the pretrained weights of the first three channels, we averaged the first three channel weights, and the average of these weights was used for the weight initialization of each additional channel [37]. This was done to incorporate some of benefits of the pretrained weights for the additional channels. As the different numbers of input channels require slight modification of the deep learning model in the first convolutional layer of the backbone, in the following, these variations are considered different deep learning models with the same base architecture. An overview of the U-net models is given in

Table 4. Overview of U-net models and their data combinations.

Model Name	Data Combination a	Channel Number
Multispectral U-net (M-Unet)	B, G, R, RE, NIR, NDVI	6
Multispectral–Thermal U-net (MT-Unet)	B, G, R, RE, NIR, NDVI, LWIR	7
Multispectral–Thermal–CHM U-net (MTCHM-Unet)	B, G, R, RE, NIR, NDVI, LWIR, CHM	8

^a R, G, B, RE, NIR, NDVI, LWIR, CHM indicate red, green, blue, red edge, near-infrared, normalized difference vegetation index, long-wave infrared, and canopy height model channel, respectively.

.

3.6. Class Imbalance and Training Weights

In an imbalanced dataset, class weights are commonly used to penalize the loss of the minority class, to emphasize the learning of the minority class. These weights can be computed as follows:

$$wj=\frac{n_{samples\_t}}{\begin{array}{c}{n}_{classes}\times n_{samples\_j}\end{array}}$$

• wj = class weight
• n_{samples_t} = total number of pixels
• n_classes = number of classes
• n_{samples_j} = total number of pixels of class for which weight is computed

The class weights wj per class are calculated using the total number of pixels divided by the total number of classes multiplied by the number of pixels of the class for which the weights are computed, based on King and Zeng [38].

These weights consider the generated distribution by the rule-based classifier for the entire dataset. The generated data distribution training set is background 86.4% and 13.6% perennial weeds.

The calculated class weights are 0.5785 for background and 3.6841 for perennial weeds. As the distribution of each class per image may change, these weights have to be mapped on a pixel basis in an additional label weight mask for each image and given to the model to enable the model to use the class weights in the training for the semantic segmentation task [8].

3.7. Experimental Setup for Deep learning models

All models were initialized with the modified pretrained weights in the Resnet backbone.

Each model is trained under the same conditions, with the used input data being the only variation between the models. The input channels therefore vary from six to eight. The training data with the generated weak labels is used for the training, and the validation data were used solely for monitoring over or underfitting of the models during the training process.

Each model is trained in two phases, which is a common practice in the domain of transfer learning. In the first training phase, the backbone weights are frozen, except for the last layers. In this phase, the model is trained for 150 epochs using a batch of 32 images with a channel size of 256 × 256 ×. Further, an early stopping with a patience value of 20 is implemented, which monitors the validation loss to prevent overfitting during the training phase. This means that the training stops early if the validation loss does not improve in a continuous sequence of 20 epochs. Further, this training takes place with a balanced dataset because the weights for each pixel class were computed, as explained before.

Moreover, augmentation is implemented to help the model learn how to generalize data. For data augmentation, a random vertical and horizontal flip and a random rotation of 30 degrees was chosen. Both data augmentations have an occurrence probability of 50%. The learning rate for this training phase is 0.0001, and the used optimizer is Adam. Adam is a common optimizer method in deep learning, and it is a computationally efficient optimization method of stochastic gradient descent [39].

After this phase, the best-performing model per data combination is chosen depending on the F1 score, recall, and precision, and it is further trained during the second training phase. In this training phase, the model weights are unfrozen, meaning the model can learn new weights. For this training phase, we applied the same batch size, the same class balance, and the same data augmentation, along with the same number of epochs and the same early stopping scheme. The only difference in the training parameter was that the model used a learning rate of 0.00001, which is smaller than before.

After the second training phase, the best-performing model based on F1 score, recall, and precision is chosen and then used to test the manually annotated test data. A summary of the used training parameters is shown in

Table 5. Overview of training parameters.

Training Parameter	Training Phase 1: Retrain	Training Phase 2: Fine Tuning
Image tile size	256 × 256 × channel	256 × 256 × channel
Batch	32	32
Class balance	yes	yes
Data augmentation	yes	yes
Optimizer	Adam	Adam
Learning rate	0.0001	0.00001
Epochs	150	150
Weights	Frozen backbone weights	Unfrozen backbone weights
Early stopping	yes (patience = 20)	yes (patience = 20)

.

3.8. Experimental Setup for Rule-Based Classifier

Further, an additional experiment was performed to visually and quantifiably assess the overlap between generated labels with our rule-based classifier and the test ground truth annotations. For this experiment we generated labels for the test dataset using the rule-based classifier. The generated masks were then visually compared to ground truth masks. Further, the overlap of the generated and ground truth masks were calculated using Intersection over Union metrics. We calculated the Intersection over Union by class and their mean. In this experiment the calculated Intersection over Union measures the ratio of correctly generated pixels per class divided by the actual ground truth number of pixels per class [40].

4. Results

The results section is subdivided into three sections. The first section introduces the performance metrics used. The second section shows the results of the experimental test of the rule-based classifier. In the third section, the performances of the deep learning models are displayed.

4.1. Performance Metrics

To evaluate deep learning model performances, we used several metrics that are common for evaluating supervised deep learning models [4]. The first one is the F1 score, which is the harmonic mean of precision and recall. Precision is the number of true positives (TP) divided by the sum of true positives and false positives (FP). Recall is the number of true positives divided by the sum of TPs and false negatives (FN) [4]. In a binary classification task, an F1 score is only calculated for the whole model and not per class. In a binary classification, positives are the target class one, which, in our case, is perennial weeds, and negatives are class zero, which, in our case, is background.

$$F1=2\times \frac{precision\times recall}{precision+recall}$$

$$precision=\frac{TP}{TP+FP}$$

$$recall=\frac{TP}{TP+FN}$$

Further, we also used IoU as a metric to analyze the deep learning model performances and the rule-based classifier. Intersection over Union measures the ratio of correctly classified pixels, i.e., the ratio of predicted pixels per class divided by the actual ground truth number of pixels per class. We used three IoU measures. One for measuring IoU for the perennial weeds class, the second for the background class, and the third measure was a mean IoU for the whole model, calculated by taking the average of the IoUs of the individual classes. The IoU per class is calculated using the formula:

$$Io{U}_c=\frac{TP}{TP+FP+FN}$$

(1)

Weed pixels are positives for the IoU calculation of the class perennial weeds and background pixels are negatives. For the IoU calculation of the background class, background pixels are positives and weed pixels are negatives. Further, an average of both IoUs is computed to obtain a mean IoU score for model performance [40].

4.2. Results of the Experimental Test for Rule-Based Classifier

To analyze the quality of generated labels, we performed a visual comparison of generated labels for the test dataset to compare them with ground truth labels. This visual comparison is shown in Figure 8.

By comparing the generated labels with the ground truth labels, we can state that the generated labels do not have as detailed boundaries as the ground truth labels. Further, the rule-based classifier is not able to generate labels for all perennial weeds. As shown in Figure 8, the first two test images show no generated labels for smaller perennial weeds. Additionally, we computed the generated mask for the test dataset. This step was performed to assess the overlap of the generated mask with the ground truth masks. The Intersection over Union values for the class background, weeds, and their mean are 0.95, 0.54, and 0.75, respectively.

4.3. Results of Deep Learning Models

All models that were trained with generated weak labels achieved F1 scores around 0.8 in the ground truth test dataset. A summary of the performance evaluation of the models on the test dataset is shown in

Table 6. Performance evaluation of the models on the test dataset.

Model	F1 Score	Precision	Recall	IoU Mean a	IoU Background a	IoU Weeds a
Multispectral–Thermal U-net (M-Unet)	0.8302	0.7449	0.9375	0.8358	0.9620	0.7097
Multispectral–Thermal U-net (MT-Unet)	0.8272	0.7428	0.9333	0.8333	0.9614	0.7053
Multispectral–Thermal-CHM U-net (MTCHM-Unet)	0.8358	0.7850	0.8937	0.8417	0.9654	0.7180

^a IoU = Intersection over Union.

.

In terms of recall and precision, the model that achieved the highest precision is the MTCHM-Unet model, with a score of 0.7850 and a lowest recall score of 0.8937. M-Unet achieved the second highest precision and the highest recall score, with scores of 0.7449 and 0.9375, respectively. The model with the lowest precision and second highest recall is MT-Unet, with scores of 0.7428 and 0.9333, respectively.

In terms of IoU scores, the MTCHM-Unet model achieved the best mean IoU score of 0.8417 and the best performance on background and perennial weeds with values 0.9654 and 0.7180. The second highest IoU scores were achieved by the M-Unet model, with an average IoU score of 0.8358 and background and perennial weed IoU scores of 0.9620 and 0.7097, respectively. The MT-Unet model had the lowest IoU score (mean IoU score of 0.8333) and background and perennial weed scores of 0.9614 and 0.7053, respectively.

In addition to the test dataset performances, summary tables are available for the achieved performance metrics on the training and validation datasets (see

Table A1. Performance evaluation of the models on the training dataset.

Model	F1 Score	Precision	Recall	IoU Average	IoU Background	IoU Weeds
M-Unet	0.9366	0.9374	0.9382	0.9320	0.9811	0.8829
MT-Unet	0.9338	0.9396	0.9316	0.9274	0.9789	0.8759
MTCHM-Unet	0.9744	0.9696	0.9803	0.9716	0.9920	0.9511

and

Table A2. Performance evaluation of the models on the validation dataset.

Model	F1 Score	Precision	Recall	IoU Average	IoU Background	IoU Weeds
M-Unet	0.9455	0.9474	0.9436	0.9415	0.9864	0.8966
MT-Unet	0.9219	0.9205	0.9233	0.9178	0.9805	0.8552
MTCHM-Unet	0.8917	0.9331	0.8538	0.8895	0.9743	0.8538

in Appendix A).

As a qualitative result, the semantic segmentation prediction for images in the test dataset of the MTCHM-Unet is presented in Figure 9. This Figure shows two test images with their ground truth labels and the masks predicted by the model. Figure 9 shows that the model is able to predict a detailed object boundary. However, both the results and the performance metrics show that the model is not able to detect all perennial weeds in the test dataset.

5. Discussion

One of our hypotheses was that the rule-based classifier produces labels that resemble real-world data. To evaluate if the generated labels resemble real-world data, we visually compared them to the ground truth test labels found in Figure 7. This visual comparison showed that the generated labels resemble the ground truth annotations. Furthermore, the calculated overlap between the test dataset annotation and generated labels was high with a mean IoU of 0.74, indicating that the generated labels resemble the ground truth labels well. However, the IoU of the weeds class, with a value of 0.54, was lower than expected. The low value likely stems from not matching the boundary pixels, which is due to the eroded NDVI mask used in the rule-based classifier.

Another hypothesis was that a deep learning model can learn to successfully detect perennial weeds in real-world data from the generated labels. We can state that the models trained on generated labels achieved high performances on the test dataset. All models achieved F1 scores of ~0.8 and generalize well on the test set. Therefore, the model was able to learn useful weights for perennial weed detection from the generated labels and performed successfully when detecting perennial weeds from the real data. Though there is a difference between the performance metrics of the validation dataset score and test dataset scores (see Appendix A), we can state that the model learns well to generalize from real-world data.

In comparison to other studies using automatic or semi-automatic label-generation approaches for weed detection, our method produces comparably good performance. However, the reported differences in performance metrics may not only stem from the different applied methods, but also from the use of different models and datasets. Therefore, this comparison to other studies should serve only as an approximation.

Bah, Hafiane, et al. [7] generated labels in their research using an unsupervised approach based on line detection and inter-crop row weeds. They achieved high AUC scores of 94.84% and 95.70% with full supervision and 88.73% and 94.34% with an automatic labeling strategy. These values are not fully comparable to our findings, since AUC scores become highly distorted with class imbalance. Moreover, a high detection rate of true negatives (background) leads to large AUC scores, even if true positives (weeds) are the sole interest. However, their study states that their models achieve a false positive rate of 20% and a true positive rate of 80%. This can be compared with our findings, since our best-performing model on the test dataset achieved an F1 score of 0.8 and a precision of 0.785, meaning a false positive rate of 21.5% and a true positive rate of 78.5%.

In contrast to Bah, Hafiane, et al. [7], our label-generation approach seems to be limited, as it is not fully automatic nor semi-automatic. However, their approach requires the field to have a line-based structure, while our approach is not based on line structures. Since a coherent line structure did not exist in the field chosen for our data collection due to double seeding along with non-linear and crossing seeding lines, this approach was essential for our method design.

Moreover, Sheikh et al. [9] propose a weak supervision approach combined with an active learning strategy for weed label generations for a semantic segmentation task. With retraining using 10 additional annotated image samples of two datasets, they were able to obtain a mean IoU of 0.79 and 0.7 for the datasets. Further, they achieved 0.4–0.59 precision for weeds and 0.7–0.83 for crops in a semantic segmentation task in their Stuttgart sugar beet dataset, along with a recall of 0.48–0.68 for weeds and 0.58–0.84 for crops [9]. We achieved comparable model performances in our research. We obtained a mean IoU of 0.83–0.84 with our models. Our total model performances precision ranked from 0.74 to 0.78 and the recall range was 0.89–0.93. As our study uses a binary classification, the target class in the model metrics is equivalent to the weeds class. Therefore, our models can be said to have achieved greater results in average IoU along with precision and recall for weeds.

A study by Sa et al. [8] that used an artificial growing setting for crops and weeds to produce their training data achieved model performances with F1 scores of 0.8–0.85 for weeds in a fully supervised multiclassification segmentation. This F1 score comes from a multi-class classification, but can be nevertheless considered similar to our model score. True negatives in a multi-class classification are counted as one class, which is equal to our background class. That said, compared to our approach, the performance of our models was only slightly worse than their models’.

Another study by Ramirez et al. [22] obtained an F1 score by using several supervised models for weeds, ranging from 0.56 to 0.78, with 0.78 being the best-performing one. Our weakly supervised models achieved a similarly high F1 score—even a slightly better one with a score of 0.8—as the fully supervised models in their research.

Another hypothesis of ours was that combining thermal and multispectral inputs leads to higher model performance for the perennial weed detection task. In our findings, the model based on multispectral data performed similarly to the models based on additional data. The M-Unet, which only used multispectral data, and the MT-Unet, which used both multispectral and thermal data, performed so similarly that it is difficult to draw clear conclusions. However, in our experiment the M-Unet performed slightly better. The addition of thermal data leads to similar or worse results and did not improve the model for perennial weed detection. Our results pair with findings in previous studies. In 2022, Zamani and Baleghi [13] concluded that additional thermal images improved the model only slightly—by 0.27%, to 1.28%. In a study by Eide, Koparan, et al. [25], which aimed for differentiation between various weed biotypes using thermal images and multispectral imaging, the authors concluded that only multispectral imaging resulted in better results. All of these studies indicate that thermal imaging as the sole method improved weed detection either slightly or not at all, and ours supports that.

Our last hypothesis suggested that additional data sources in the form of a CHM improve the model performance. Adding the CHM generated from the multispectral images as input data improved the model performance. Our MTCHM-Unet model achieved the highest performance, with an F1 score of 0.835, and further, had a better balance between recall and precision values. Therefore, the additional data sources in the form of a CHM improved the model performance in our research.

Previous research has shown varying results in the context of adding a CHM as input. Adding a CHM to the input data in Kawamura et al. [28] led to a model improvement when compared with solely using HSV features. However, they concluded that a CHM was not the most important input data and other input variables led to even better results [28]. In a study by Zisi et al. [27], the addition of a CHM also led to improvements in model performance. Torres-Sánchez et al. (2021) found that a CHM can improve model performance, but its added value depends on the crop type. In their estimation, a CHM was the eighth most important input variable in a sunflower crop field, whereas in a cotton field, it was not among the ten most important input variables [15]. In most cases, including ours, it seems that a CHM as an input improves model performances, yet its impact depends on the given input data and crop type.

6. Limitations and Challenges

Our weak label generation using the proposed rule-based classifier worked successfully on our dataset and the crop barley. However, to test the robustness and transportability of this method for other crop fields, more research is needed. It is seen likely that for future studies, the specific values of thresholds and distances along with the averaging and erosion kernel sizes will need to be adjusted, since they are specially customized for our research data. It can be assumed that these values depend on the growth state of the given crop, crop type, and field density. Therefore, in order to transfer our approach to a different dataset for future research, these values and parameters must be found in an explorative manner and studied more in depth. In terms of data fusion and evaluation of the data combinations from the multispectral and thermal cameras, despite the data being georeferenced using high-precision GNSS and six GCPs measurements, we cannot fully exclude the possibility of errors in the dataset as a result of the georeferencing. This is because no additional GCP measures were made to evaluate the accuracy of the georeferencing procedure. Further, another limitation that should be considered regarding the sensor combination is that the thermal data required upsampling to fit the multispectral resolution, and the nearest neighbor technique was chosen for this upsampling. Although this a common upsampling technique, it may have led to distortions. The CHM data quality may have suffered from noise values, since the digital terrain model needed upsampling to the multispectral resolution to compute the CHM. This was done using the nearest neighbor technique, which may have led to distortions in the data.

7. Conclusions

We have shown that our rule-based classifier produces labels that resemble ground truth data. Further, the IoU comparison of generated labels and ground truth test labels showed that our rule-based classifier produces labels with a mean IoU of 0.74 and a IoU of 0.54 for perennial weeds. Moreover, we have demonstrated that the chosen deep learning models, which were trained with generated labels with our rule-based classifier, performed well on ground truth test data, with F1 scores of 0.82–0.83. This indicates that the proposed rule-based classifier generates valid weak labels that are useful for perennial weed detection. Further, the models are able to successfully detect perennial weeds in real-world data and achieve results that are competitive with models using weak or automatically generated labels, or even achieve results similar to those from fully supervised models.

We also conclude that the combination of thermal and multispectral data did not improve the model performance in our findings. However, an additional data source, in the form of a CHM, improved model performance. The best-performing model was MTCHM-Unet, which used all the given data sources, i.e., multispectral and thermal data and CHM. This model achieved an F1 score of 0.8335 and a precision and recall of 0.78 and 0.89, respectively.

Our research only addressed a data-fusion approach of a multispectral and thermal sensor. Whether sensor fusion would improve the performance of a model for perennial weed detection still requires further research, including different sensor types. Furthermore, more studies are needed for the specific combination of multispectral and thermal sensors, to draw more generalizable conclusions. This article addresses the issue of lacking label data. Even though the proposed approach addresses this need by being able to produce labels in a semi-automatic manner, the need for more versatile and easily transferable label-generation approaches still exists, to make weed-detection models faster and applicable for various types of crops and fields. In future research, this aim will be addressed continuously but from a different starting point by not generating labels automatically, rather, by using only very limited available labels.