Ocean Clutter Characterization Based on PolSAR Data and Second-Order Statistics of Elementary Scatterers
Abstract
1. Introduction
2. Cameron Decomposition
3. Sea PolSAR Data
3.1. Data Properties
3.2. SLC Fully Polarimetric Data Preprocessing Stage
- -
- Radiometric Calibration
- -
- Polarimetric Matrix Generation
- -
- Polarimetric Speckle Filtering
- -
- Polarimetric Decomposition
- -
- Geometric Correction utilizing Range Doppler Terrain Correction
3.3. Statistical Feature Extraction
4. Statistical Analysis of PolSAR Data and Experimental Results
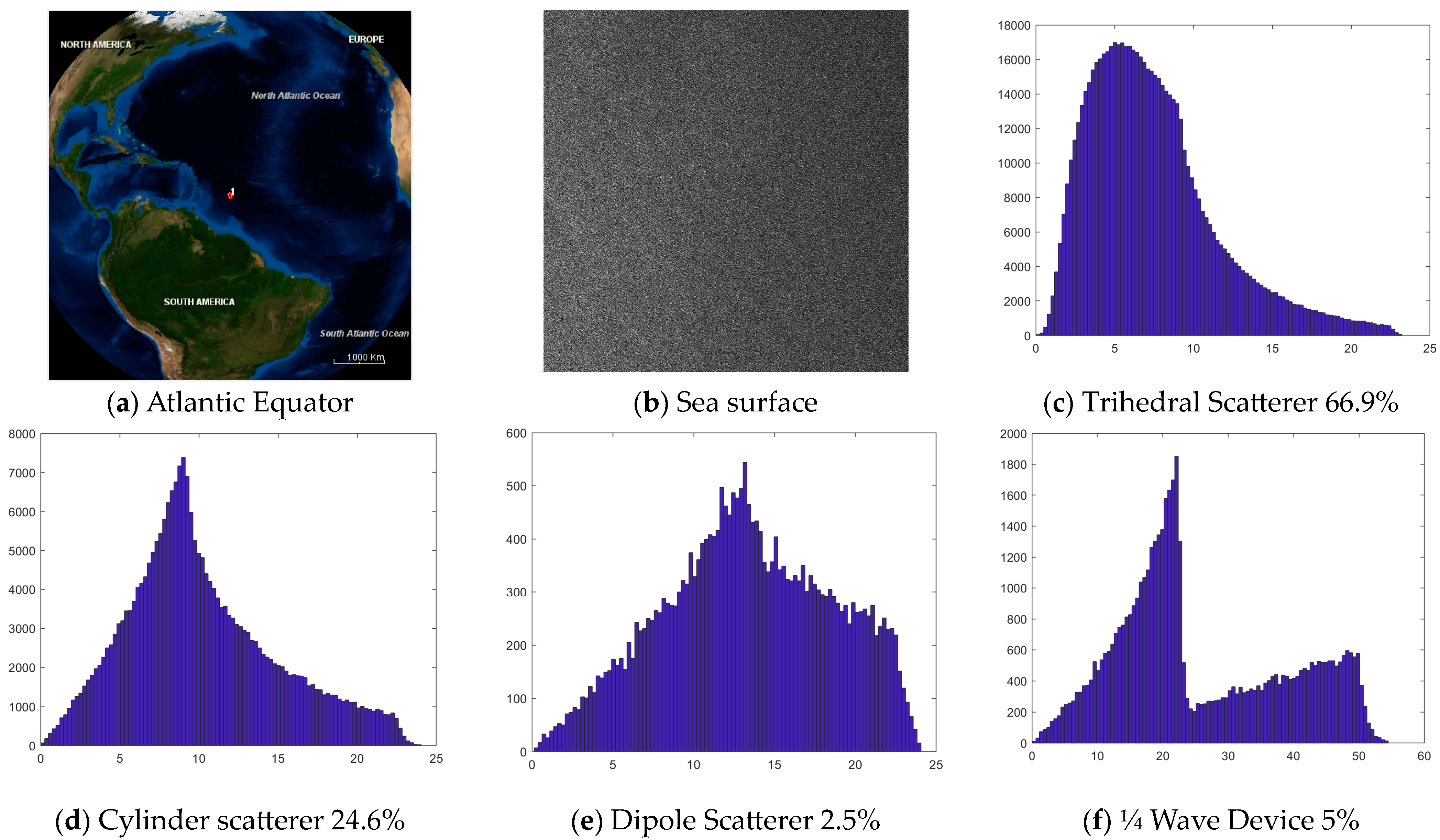
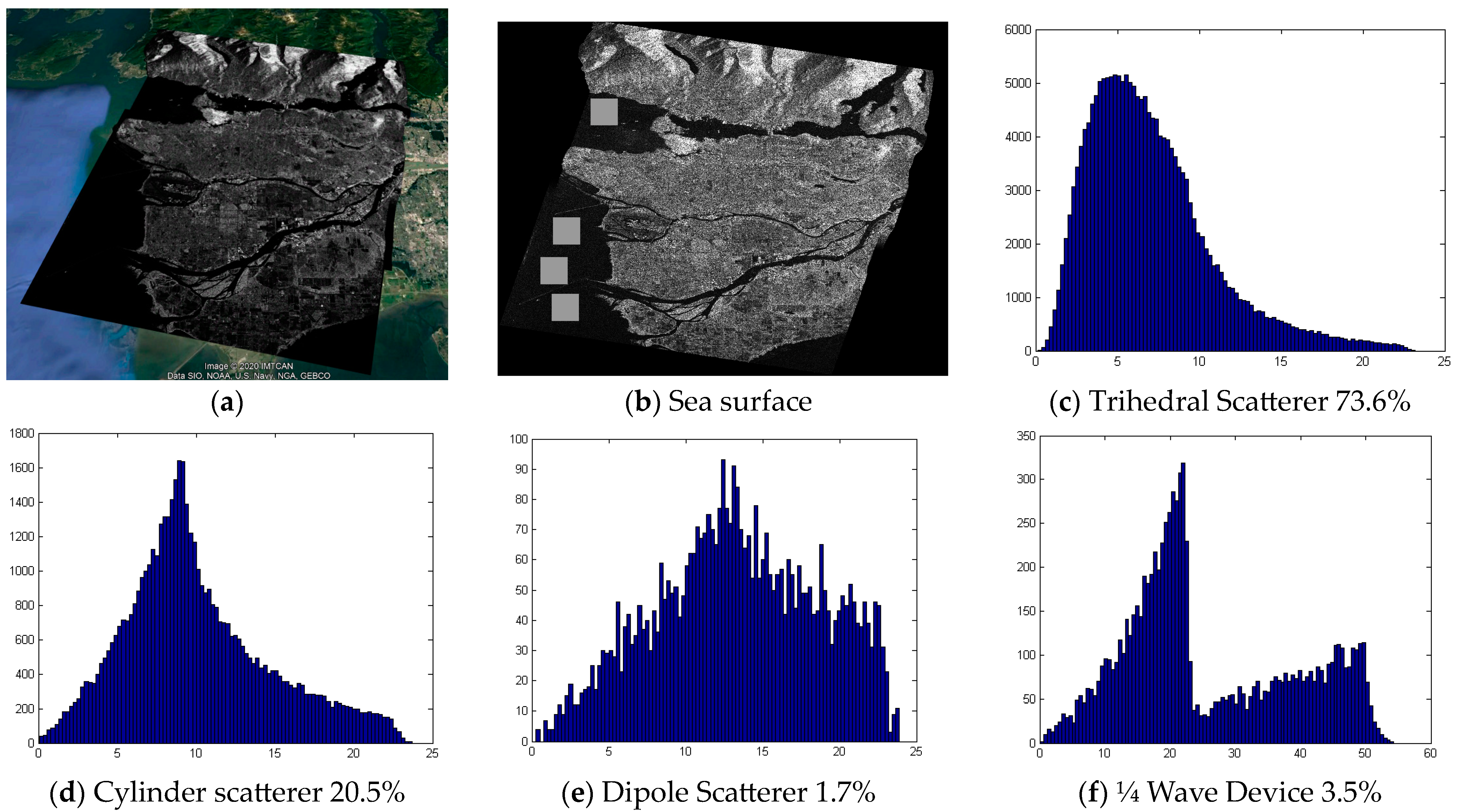
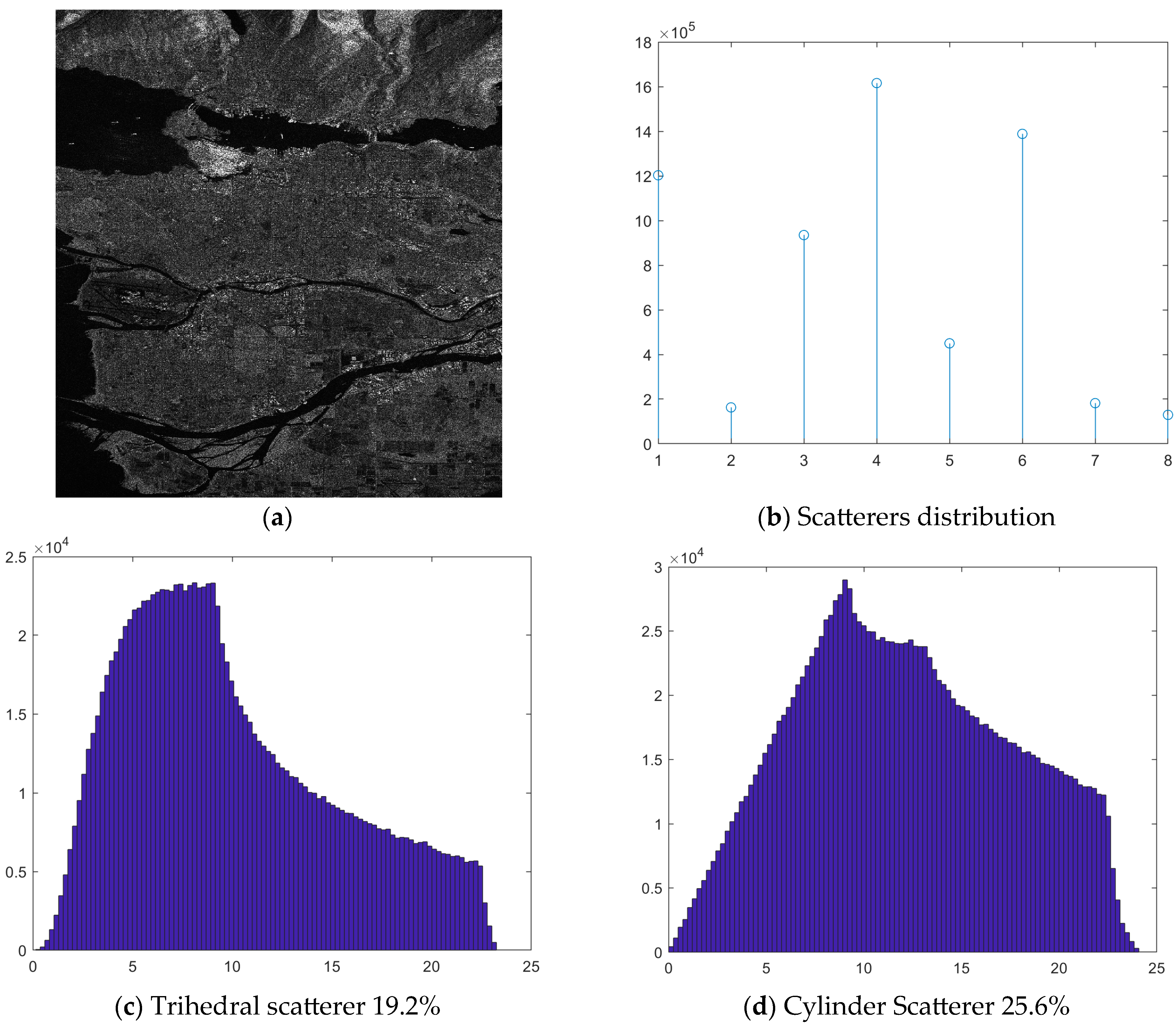
- The percentage of the appearance of each dominating elementary scatterer in the specific sea region.
- The statistical distribution of the closeness of the estimated dominating elementary scatterer on each separate pixel to the ideal (reference) elementary scatterers. The closeness is evaluated by means of the distance given in Equation (4) and analyzed in Section 2. Accordingly, in a specific region of the ocean, all pixels characterized by the same elementary scatterer contribute to the same distribution describing their distance from this ideal elementary scatterer.
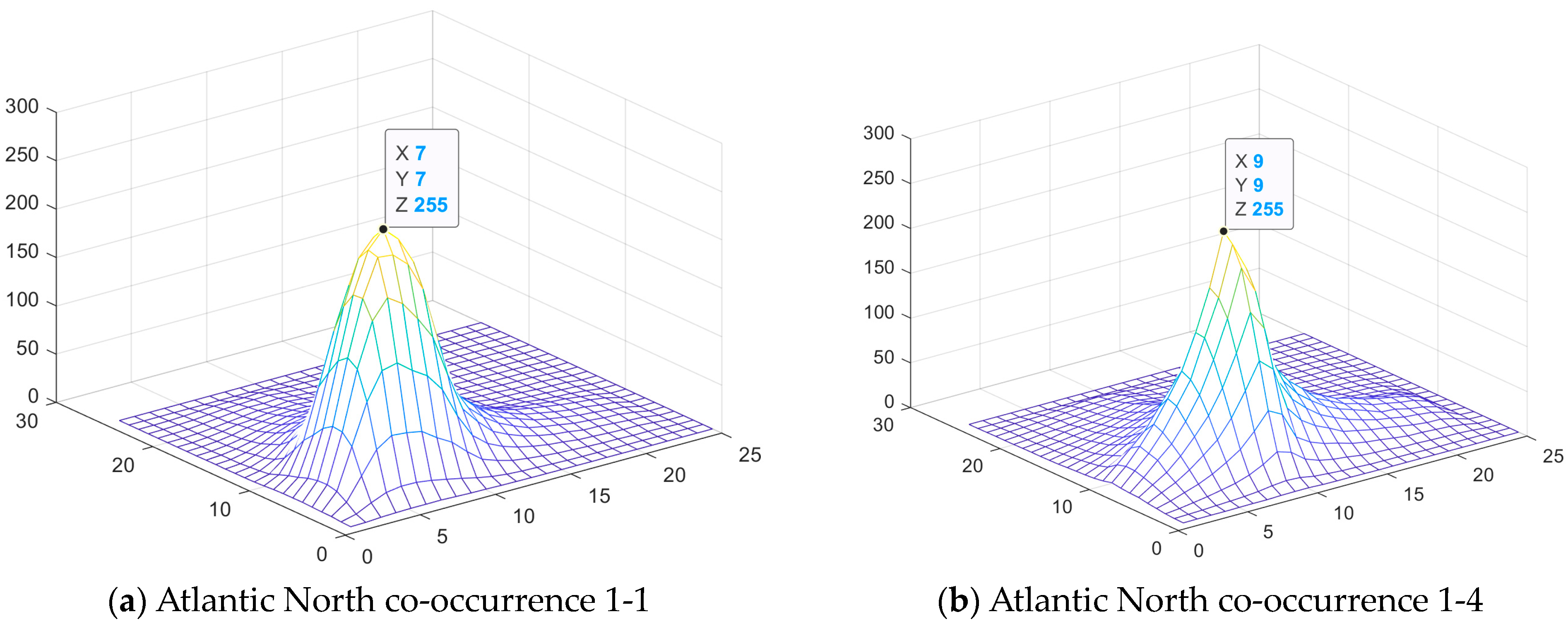
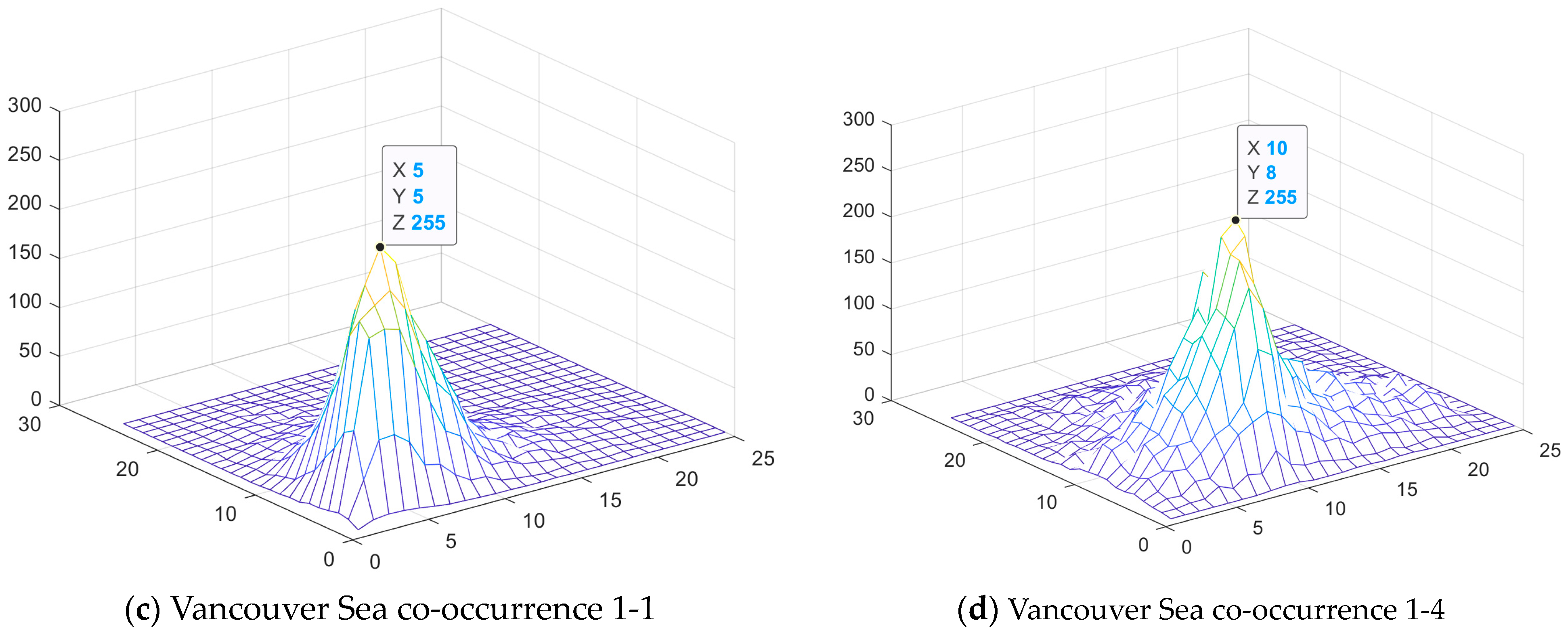
- The co-occurrence matrix for encountering the neighboring SAR pixels which correspond to the same elementary scatterer; the matrix axes reveal the closeness to this ideal common elementary scatterer.
- The co-occurrence matrix for encountering the neighboring SAR pixels which correspond to different elementary scatterers; the matrix axes reveal the closeness to the corresponding ideal elementary scatterers.
- PolSAR pixels at sea are mainly represented by the trihedral elementary scatterer followed by the cylinder. The ¼-wave device is usually not negligible to around 5%.
- For land cover, the percentage of trihedral scatterer is small (<20%) compared to that found on the sea surface (>50%). The percentages of the cylinder, the dipole, the narrow diplane, and the ¼-wave device are large compared to the percentages of the corresponding elementary scatterers on the sea surface.
- In the case of calm sea state conditions, the percentage of the trihedral elementary scatterer becomes quite large (over 70%).
- In the open sea, for moderate sea waves height, the percentage of cylinder elementary scatterers increases.
- The closeness of each elementary scatterer to the corresponding ideal scatterer, evaluated for each separate PolSAR pixel, does not change significantly with the sea state conditions.
- Co-occurrences for the same most frequent elementary scatterer, the trihedral, happens in the calm sea (Vancouver), most frequently between scatterers which are close to the ideal counterparts. Co-occurrences between the most frequent different elementary scatterers (trihedral and cylinder) show no significant difference between calm and rough sea (Figure 9).
- The mean for each of the four elementary scatterers does not change significantly from one sea region to another sea region, even if the sea state conditions change.
- The variance for the trihedral is large mainly for rough sea state. The variance for the rest of the three elementary scatterers remains unchanged for various sea conditions.
- The skewness and the kurtosis slightly increase for the trihedral in calm sea. For the dipole, both the third and fourth moments remain almost unchanged. The same happens for the cylinder and the ¼-wave device as well.
- In general, skewness is of small values (near zero), so the distributions, especially for the dipole, are expected to be symmetric around the mean.
- For small wave heights, the skewness and kurtosis for 1-1 co-occurrence is relatively large.
- For low wind speed, large values for skewness and kurtosis of the 2D co-occurrences are noted.
- The 2D skewness and the kurtosis for the co-occurrence matrices in case of transitions from cylinder to trihedral and vice versa are relatively smaller for low wind speed and wave height.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anastassopoulos, V.; Lampropoulos, G.A. A generalized compound model for radar clutter. In Proceedings of the IEEE National Radar Conference, Atlanta, GA, USA, 29–31 March 1994. [Google Scholar]
- Anastassopoulos, V.; Lampropoulos, G.A. High resolution radar clutter classification. In Proceedings of the IEEE International Radar Conference, Washington, DC, USA, 8–11 May 1995. [Google Scholar]
- Anastassopoulos, V.; Lampropoulos, G.A.; Drosopoulos, A.; Rey, M. High Resolution Radar Clutter Statistics. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 43–60. [Google Scholar] [CrossRef]
- Nohara, T.J.; Haykin, S. Canadian East Coast radar trials and the K-distribution. IEEE Process. Part F 1991, 138, 80–81. [Google Scholar] [CrossRef]
- Watts, S. Radar detection prediction in K-distributed sea clutter and thermal noise. IEEE Trans. Aerosp. Electron. Syst. 1987, 1, 40–45. [Google Scholar] [CrossRef]
- Trunk, G.V. Radar properties of Non-Rayleigh Sea clutter. IEEE Trans. Aerosp. Electron. Syst. 1972, 8, 196–204. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Nascimento, A.D.C.; Frery, A.C. PolSAR Models with Multimodal Intensities. Remote Sens. 2022, 14, 5083. [Google Scholar] [CrossRef]
- Schuler, D.L.; Leea, J.S.; Kasilingamb, D.; Pottier, E. Measurement of ocean surface slopes and wave spectra using polarimetric SAR image data. Remote Sens. Environ. 2004, 91, 198–211. [Google Scholar] [CrossRef]
- He, Y.; Shen, H.; Perrie, W. Remote Sensing of Ocean Waves by Polarimetric SAR. J. Atmos. Ocean. Technol. 2006, 23, 1768–1773. [Google Scholar] [CrossRef]
- Salberg, A.B.; Larsen, S.O. Classification of Ocean Surface Slicks in Simulated Hybrid-Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7062–7073. [Google Scholar] [CrossRef]
- Yeremy, M.; Campbell, J.W.M.; Mattar, K.; Potter, T. Ocean Surveillance with Polarimetric SAR. Can. J. Remote Sens. 2001, 27, 328–344. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Vachon, P.W.; Li, X.; Pichel, W.G.; Guo, J.; He, Y. Ocean Vector Winds Retrieval From C-Band Fully Polarimetric SAR Measurements. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4252–4261. [Google Scholar] [CrossRef]
- Ibrahim, Z.; Bahnacy, A.I.; Hussein, K.F.A.; Farahat, A.E. PolSAR Target Decomposition Technique to Estimate Ocean Surface temperature and Salinity. In Proceedings of the 39th National Radio Science Conference (NRSC 2022), Cairo, Egypt, 29 November–1 December 2022. [Google Scholar]
- Viana, R.D.; Lorenzzetti, J.A.; Carvalho, J.T.; Nunziata, F. Estimating Energy Dissipation Rate from Breaking Waves Using Polarimetric SAR Images. Sensors 2020, 20, 6540. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Fan, C.; Meng, J.; Yang, J.; Zhang, J. Shallow sea topography detection using fully polarimetric Gaofen-3 SAR data based on swell patterns. Acta Oceanol. Sin. 2022, 41, 150–162. [Google Scholar] [CrossRef]
- Xie, T.; Ouyang, R.; Perrie, W.; Zhao, L.; Zhang, X. Proof and Application of Discriminating Ocean Oil Spills and Seawater Based on Polarization Ratio Using Quad-Polarization Synthetic Aperture Radar. Remote Sens. 2023, 15, 1855. [Google Scholar] [CrossRef]
- Kumar, A.; Mishra, V.; Panigrahi, R.K.; Martorella, M. Application of Hybrid-Pol SAR in Oil-Spill Detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Li, H.; Perrie, W.; Wu, J. Retrieval of Oil–Water Mixture Ratio at Ocean Surface Using Compact Polarimetry Synthetic Aperture Radar. Remote Sens. 2019, 11, 816. [Google Scholar] [CrossRef]
- Kreithen, D.E.; Halversen, S.S.; Owirka, G.J. Discriminating targets from clutter. Linc. Lab. J. 1993, 6, 25–52. [Google Scholar]
- Chaney, R.D.; Burl, M.C.; Novak, L.M. On the performance of polarimetric target detection algorithms. In Proceedings of the IEEE 1990 International Radar Conference, Arlington, VA, USA, 7–10 May 1990; pp. 520–525. [Google Scholar]
- Pottier, E.; Saillard, J. Optimal polarimetric detection of radar target in a slowly fluctuating environment of clutter. In Proceedings of the IEEE 1990 International Radar Conference, Arlington, VA, USA, 7–10 May 1990; pp. 211–216. [Google Scholar]
- Novak, L.M.; Burl, M.C.; Chaney, R.D.; Owirka, G.J. Optimal processing of polarimetric synthetic-aperture radar imagery. Linc. Lab. J. 1990, 3, 273–290. [Google Scholar]
- Gu, D.; Xu, X. Multi-Feature Extraction of Ships from SAR Images. Image and Signal Processing (CISP). In Proceedings of the 6th International Congress, Hangzhou, China, 16–18 December 2013; Volume 1, pp. 454–458. [Google Scholar]
- Anastassopoulos, V.; Lampropoulos, G.A. Optimal CFAR Detection in Weibull Clutter. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 52–64. [Google Scholar] [CrossRef]
- Fei, C.; Liu, T.; Lampropoulos, G.A.; Anastassopoulos, V. Markov Chain CFAR Detection for Polarimetric Data Using Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 397–408. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Radar Imaging, 1st ed.; CRC Press: New York, NY, USA, 2009. [Google Scholar]
- Nunziata, F.; Migliaccio, M.; Brown, C.E. Reflection Symmetry for Polarimetric Observation of Man-Made Metallic Targets at Sea. IEEE J. Ocean. Eng. 2012, 37, 384–394. [Google Scholar] [CrossRef]
- Addabbo, P.; Biondi, F.; Clemente, C.; Orlando, D.; Pallotta, L. Classification of covariance matrix eigenvalues in polarimetric SAR for environmental monitoring applications. IEEE Trans. Aerosp. Electron. Syst. Mag. 2019, 34, 28–43. [Google Scholar] [CrossRef]
- Pallotta, L.; Clemente, C.; De Maio, A.; Soraghan, J.J. Detecting Covariance Symmetries in Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 80–95. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3452–3459. [Google Scholar] [CrossRef]
- Touzi, R.; Charbonneau, F.; Hawkins, R.; Murnaghan, K.; Kavoun, X. Ship–sea contrast optimization when using polarimetric SARs. In Proceedings of the Geoscience and Remote Sensing Symposium, IGARSS ‘01, Sydney, NSW, Australia, 9–13 July 2001; Volume 1, pp. 426–428. [Google Scholar]
- Touzi, R.; Charbonneau, F.; Hawkins, R.; Vachon, P. Ship detection and characterization using polarimetric SAR. Can. J. Remote Sens. 2004, 30, 552–559. [Google Scholar] [CrossRef]
- Ringrose, R.; Harris, N. Ship detection using polarimetric SAR data. In Proceedings of the SAR Workshop: CEOS Committee on Earth Observation Satellites, Toulouse, France, 26–29 October 1999; pp. 687–691. [Google Scholar]
- Cameron, W.L.; Youssef, N.N.; Leung, L.K. Simulated polarimetric signatures of primitive geometrical shapes. IEEE Trans. Geosci. Remote Sens. 1996, 34, 793–803. [Google Scholar] [CrossRef]
- Kouroupis, G.; Anastassopoulos, V. Scatterer Characterization Based on the Condiagonalization of the Sinclair Backscattering Matrix. Prog. Electromagn. Res. M 2019, 85, 59–69. [Google Scholar] [CrossRef]
- Kouroupis, G.; Anastassopoulos, V. A polarimetric CFAR ship detector based on the joint probability function of simulated first-order Markov chains. Int. J. Remote Sens. 2019, 40, 5121–5140. [Google Scholar] [CrossRef]
- Therrien, C.W. Random Processes; Prentice Hall Signal Processing Series; Prentice-Hall: Hoboken, NJ, USA, 1992. [Google Scholar]
- Kouroupis, G.; Anastassopoulos, V. A Markov Chain Model Based on Cameron’s CTD Ship Detection Scheme. In Proceedings of the IEEE Imaging Systems and Techniques, Chania, Greece, 4–6 October 2016; pp. 100–105. [Google Scholar]
- SNAP Toolboxes. Science Toolbox Exploitation Platform. Available online: https://step.esa.int/main/doc/ (accessed on 1 December 2022).
- Cameron, W.L.; Rais, H. Conservative polarimetric scatterers and their role in incorrect extensions of the Cameron decomposition. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3506–3516. [Google Scholar] [CrossRef]
- Sarker, S.; Veremyev, A.; Boginski, V.; Arvind Singh, A. Critical nodes in river networks. Sci. Rep. Nat. Res. 2019, 9, 11178. [Google Scholar] [CrossRef]
- MDA, RADARSAT-2 Product Description, RN-SP-52-1238 Issue 1/14. Available online: https://earth.esa.int/eogateway/documents/20142/0/Radarsat-2-Product-description.pdf/f2783c7b-6a22-cbe4-f4c1-6992f9926dca (accessed on 1 December 2022).
- Copernicus Climate Data Store. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 1 January 2023).
- Kaushik, P.; Jabin, S. A Comparative study of Pre-processing Techniques of SAR Images. In Proceedings of the 4th International Conference on Computing Communication and Automation (ICCCA), Greater Noida, India, 14–15 December 2018; pp. 1–4. [Google Scholar]
- Veci, L.; Lu, J.; Prats-Iraola, P.; Scheiber, R.; Collard, F.; Norman, F.; Engdahl, M. The Sentinel-1 Toolbox. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, QC, Canada, 13–18 July 2014; pp. 1–3. [Google Scholar]
- Lee, J.S.; Jurkevich, L.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Lett. 2009, 8, 313–340. [Google Scholar] [CrossRef]
- Joanes, D.N.; Gill, C.A. Comparing measures of sample skewness and kurtosis. J. R. Stat. Soc. 1998, 47, 183–189. [Google Scholar] [CrossRef]
- Westfall, P.H. Kurtosis as Peakedness, 1905–2014. R.I.P. Am. Stat. 2014, 68, 191–195. [Google Scholar] [CrossRef] [PubMed]




| Complex Parameter z | Scattering Mechanism | |
|---|---|---|
| 1 | Trihedral | |
| −1 | Diplane | |
| 0 | Dipole | |
| +1/2 | Cylinder | |
| −1/2 | Narrow diplane | |
| ¼-wave device |
| Symmetric Elementary Scatterer | Class | Cameron Color Representation |
|---|---|---|
| Trihedral | 1 |  |
| Diplane | 2 | |
| Dipole | 3 | |
| Cylinder | 4 | |
| Narrow Diplane | 5 | |
| 1/4 Wave Device | 6 | |
| Left Helix | 7 | |
| Right Helix | 8 |
| Region | Trihedral | Diplane | Dipole | Cylinder | Narrow Diplane | 1/4 Wave Device | Left Helix | Right Helix | swh | ws |
|---|---|---|---|---|---|---|---|---|---|---|
| Atlantic center | 51.2 | 0.2 | 2.9 | 39 | 0.6 | 5.3 | 0.3 | 0.3 | 1.73 | 5 |
| Atlantic Equator | 66.9 | 0.2 | 2.5 | 24.6 | 0.7 | 5 | 0.01 | 0.01 | 2.34 | 6.6 |
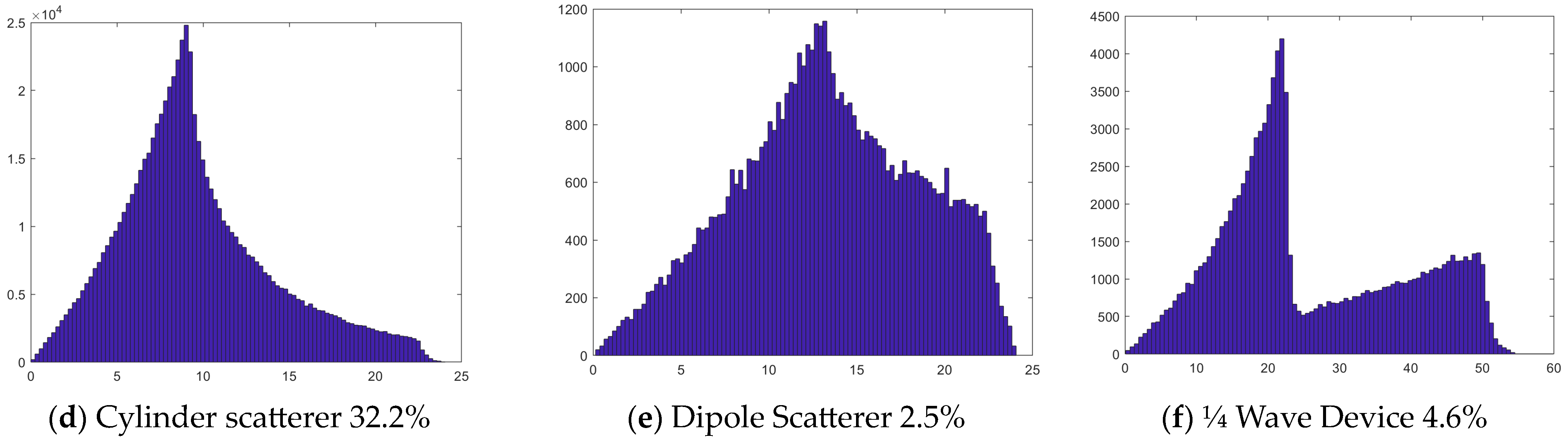
| Atlantic North | 59.5 | 0.2 | 2.5 | 32.2 | 0.6 | 4.6 | 0.2 | 0.2 | 2.93 | 6.51 |
| Vancouver Sea | 73.6 | 0.1 | 1.7 | 20.5 | 0.4 | 3.5 | 0.1 | 0.1 | 0.19 | 3.7 |
| Vancouver Sea + Land | 19.2 | 3 | 15.2 | 25.6 | 8 | 23 | 3 | 2.5 | 0.19 | 3.7 |
| Region | Moment | Trihedral | Dipole | Cylinder | 1/4 Wave Device | swh | ws |
|---|---|---|---|---|---|---|---|
| Atlantic center | Mean | 8.89 | 13.26 | 9.49 | 25.93 | 1.73 | 5 |
| Variance | 15.22 | 26.90 | 20.12 | 169.7 | |||
| Skewness | 1.02 | −0.08 | 0.72 | 0.43 | |||
| Kurtosis | 4.10 | 2.33 | 3.30 | 2.0 | |||
| Atlantic Equator | Mean | 7.47 | 13.32 | 10.23 | 25.76 | 2.34 | 6.6 |
| Variance | 17.11 | 27.33 | 22.47 | 169.02 | |||
| Skewness | 1.05 | −0.08 | 0.57 | 0.44 | |||
| Kurtosis | 4.07 | 2.3 | 2.86 | 2.03 | |||
| Atlantic North | Mean | 8.26 | 13.3 | 9.66 | 25.85 | 2.93 | 6.51 |
| Variance | 14.8 | 26.71 | 20.18 | 168.22 | |||
| Skewness | 1.08 | −0.09 | 0.7 | 0.44 | |||
| Kurtosis | 4.36 | 2.34 | 3.25 | 2.03 | |||
| Vancouver Sea | Mean | 7.05 | 13.35 | 10.1 | 25.84 | 0.19 | 3.7 |
| Variance | 14.83 | 27.99 | 21.35 | 170.09 | |||
| Skewness | 1.16 | −0.1 | 0.62 | 0.44 | |||
| Kurtosis | 4.58 | 2.26 | 3.02 | 2.01 |
| Region | Co-Occurrence 1-1 Skewness | Co-Occurrence 1-1 Kurtosis | Co-Occurrence 4-4 Skewness | Co-Occurrence 4-4 Kurtosis | Co-Occurrence 1-4 Skewness | Co-Occurrence 1-4 Kurtosis | swh | ws |
|---|---|---|---|---|---|---|---|---|
| Atlantic center | 3.023 | 17.756 | 2.733 | 11.89 | 2.862 | 12.227 | 1.73 | 5 |
| Atlantic Equator | 2.245 | 7.238 | 2.283 | 9.428 | 2.239 | 8.071 | 2.34 | 6.6 |
| Atlantic North | 3.019 | 11.927 | 2.879 | 13.056 | 3.152 | 14.611 | 2.93 | 6.51 |
| Vancouver Sea | 3.055 | 12.317 | 2.71 | 12.356 | 2.829 | 12.273 | 0.19 | 3.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koukiou, G.; Anastassopoulos, V. Ocean Clutter Characterization Based on PolSAR Data and Second-Order Statistics of Elementary Scatterers. Remote Sens. 2023, 15, 2837. https://doi.org/10.3390/rs15112837
Koukiou G, Anastassopoulos V. Ocean Clutter Characterization Based on PolSAR Data and Second-Order Statistics of Elementary Scatterers. Remote Sensing. 2023; 15(11):2837. https://doi.org/10.3390/rs15112837
Chicago/Turabian StyleKoukiou, Georgia, and Vassilis Anastassopoulos. 2023. "Ocean Clutter Characterization Based on PolSAR Data and Second-Order Statistics of Elementary Scatterers" Remote Sensing 15, no. 11: 2837. https://doi.org/10.3390/rs15112837
APA StyleKoukiou, G., & Anastassopoulos, V. (2023). Ocean Clutter Characterization Based on PolSAR Data and Second-Order Statistics of Elementary Scatterers. Remote Sensing, 15(11), 2837. https://doi.org/10.3390/rs15112837






