Abstract
As a cutting-edge research direction in the field of radar imaging, video SAR has the capability of high-resolution and persistent imaging at any time and under any weather. Video SAR requires high computational efficiency of the imaging algorithm, and PFA has become the preferred imaging algorithm because of its applicability to the spotlight mode and relatively high computational efficiency. However, traditional PFA also has problems, such as low efficiency and limited scene size. To address the above problems, a generalized persistent polar format algorithm, called GPPFA, is proposed for airborne video SAR imaging that is applicable to the persistent imaging requirements of airborne video SAR under multitasking conditions. Firstly, the wavenumber domain resampling characteristics of video SAR PFA are analyzed, and a generalized resampling method is proposed to obtain higher efficiency. Secondly, for the problem of scene size limitation caused by wavefront curvature error, an efficient compensation method applicable to different scene sizes is proposed. GPPFA is capable of video SAR imaging at different wavebands, different slant ranges, and arbitrary scene sizes. Point target and extended target experiments verify the effectiveness and efficiency of the proposed method.
1. Introduction
Video synthetic aperture radar (SAR) combines SAR with high frame rate video display technology, which allows for continuous observation of targets at night and in harsh conditions such as rain, fog, sand, and dust [1,2]. As an inheritance and expansion of traditional SAR, video SAR can display information on ground motion targets in all directions [3,4]. Sandia National Laboratories (SNL) and Defense Advanced Research Projects Agency (DARPA) first proposed the concept of video SAR [5], and then video SAR has been listed as a key research project by many countries and institutes. Currently, many institutions have published their video SAR systems and results, such as SNL [6,7], DARPA [8], General Atomics Aeronautical Systems Incorporated (GA-ASI) [9], Fraunhofer Institute for High-Frequency Physics and Radar Techniques (FHR) [10], Jet Propulsion Laboratory (JPL) [11], and ICEYE [12,13], which proves the importance and broad application value of video SAR.
SAR image formation can be treated as a class of ill-posed linear inverse problems [14,15], so the imaging algorithm is the core part of video SAR systems. The persistent imaging characteristics of video SAR require it to work in spotlight mode [16]; therefore, the traditional strip SAR imaging algorithms, such as range Doppler algorithm (RDA) [17], chirp scaling algorithm (CSA) [18], and frequency scaling algorithm (FSA) [19], are no longer applicable to video SAR. The current mainstream imaging algorithms for spotlight mode mainly include the back-projection algorithm (BPA) [20,21] and the polar format algorithm (PFA) [22,23,24]. BPA requires point-by-point processing of echo signals, which makes its computational load too high to be applied in video SAR. The modified version, such as the fast back-projection algorithm (FBP) [25] and the fast factorized back-projection algorithm (FFBP) [26], has improved the efficiency of BPA, but this comes at the cost of losing imaging accuracy and is still less efficient than frequency-domain algorithms. PFA is the preferred imaging algorithm for video SAR due to its relatively high computational efficiency and ease of incorporating motion compensation algorithms [27].
However, traditional PFA also has some problems. Firstly, the two-dimensional (2D) wavenumber domain interpolation is inefficient, which affects the efficiency of PFA. Secondly, due to the use of the planar wavefront approximation, the wavefront curvature error of PFA makes its effective scene size and image fidelity limited under the conditions of short slant range or large scene size [28,29,30]. Thirdly, the video SAR frames should be oriented in a fixed direction on the ground output coordinate system (GOCS); otherwise, the image will rotate with the azimuth angle of video SAR [31]. In [32], by changing the sampling rate and sampling time of the radar system in real-time, the wavenumber domain signal with azimuth-uniform distribution can be obtained directly, while the azimuth chirp-z transform (CZT) is used to avoid the wavenumber domain interpolation and has higher efficiency. In [33], a parameter adjusting autoregistration PFA (PAAR-PFA) for linear spotlight mode video SAR is proposed; PAAR-PFA calculates the relevant parameters based on a parameter adjustment strategy to avoid range interpolation and geometric correction, but as in [32], the system architecture has higher hardware cost, and the scene size limitation problem is still not solved. In [34], a unified coordinate system algorithm (UCSA) is proposed for terahertz (THz) video SAR imaging; UCSA exploits the small-angle assumption property of THz video SAR, then a 2D CZT is used to achieve wavenumber domain resampling and ignores the effect of residual quadratic phase error, showing the great advantages of THz technology [35,36] in video SAR. However, the UCSA cannot be applied well to low-band video SAR, which limits its application. In [37], an efficient video SAR imaging algorithm based on type-3 non-uniform fast Fourier transform (NuFFT-3) is proposed by R. Hu; the method combines Fourier imaging and image correction to directly obtain distortion-free images. Then R. Hu extends the method to solve the defocusing problem, called refocusing and zoom-in PFA (RZPFA) [28]. In [38], the orthorectified polar format algorithm (OPFA) incorporates RZPFA with the digital elevation model (DEM); OPFA can obtain the orthorectified image efficiently without postprocessing, even with the residual distortion and defocus caused by rugged terrain.
To address the scene size limitation of PFA, some methods, such as spatially variant post filtering (SVPF) [39,40], are proposed to solve the defocus of imaging results. In [41], an extended polar format algorithm (EPFA) is proposed to solve the wavenumber domain resampling and wavefront curvature error of squint SAR, but EPFA does not consider the geometric correction, which leads to the constant and primary terms of wavefront curvature error still exist and thus causes geometric distortion of the image. In [42], a quadtree beam segmentation-based PFA is proposed to solve the image defocus problem of wide-angle staring SAR (WAS-SAR), but the computational load of this method increases significantly with the number of sub-beams. In [43], an extended PFA is proposed to reduce the number of segmentations by combining sub-block imaging with spatially variant post-filtering. However, the extensive operation of image interpolation and alignment makes its computational complexity too high and, therefore, not suitable for application in video SAR.
In this paper, a generalized persistent polar format algorithm (GPPFA) is proposed to address the above problem. First, the imaging model of airborne video SAR is established, and the principles of high resolution and high frame rate of video SAR are analyzed. Then, the critical conditions of azimuth uniform and non-uniform resampling are analyzed, and the most suitable methods are used to achieve wavenumber domain resampling for THz video SAR and X-band video SAR, respectively. In addition, for the scene size limitation problem, the geometric distortion mapping (GDM) of video SAR PFA is established, and a residual phase error compensation method is proposed, which selects different processing procedures for different scene sizes to achieve higher operational efficiency. The main contributions of this paper are:
- (1)
- The principle of wavenumber domain resampling in video SAR PFA is analyzed, and a resampling criterion applicable to different wavebands of video SAR is proposed;
- (2)
- The effect of wavefront curvature error in video SAR PFA is analyzed, and an efficient compensation method applicable to different scene sizes is proposed;
- (3)
- The proposed method is capable of video SAR fast imaging with high image fidelity in different wavebands, as well as arbitrary slant range and scene size.
The construction of the paper is organized as follows: Section 2 establishes the airborne video SAR imaging model, analyzes the high-resolution and high-frame-rate imaging characteristics of video SAR, and briefly introduces the PFA in video SAR. Section 3 analyzes the wavefront curvature error of PFA and discusses the proposed GPPFA in detail. Section 4 validates the proposed method by point target and extended target experiments and compares it with other methods to verify the generality, effectiveness, and efficiency of the proposed method. Finally, Section 5 summarizes the findings of the study.
2. Materials
2.1. Video SAR Geometric Definition
The imaging model of the airborne video SAR is shown in Figure 1, where is the flight radius, is the altitude, is the flight speed, denotes the central degree of the kth frame sub-aperture, is the rotation angle of the video SAR, and the ground scene center coincides with the coordinate center O of the Cartesian coordinate system X-Y-Z. During the flight, the radar beam always illuminates the region of interest (ROI) and receives echoes. For simplicity, the position of the antenna phase center (APC) in the spherical coordinate system can be defined as:
where represents the slant range between APC and scene center O, indicates the carrier azimuth angle, represents the elevation angle of the radar platform.
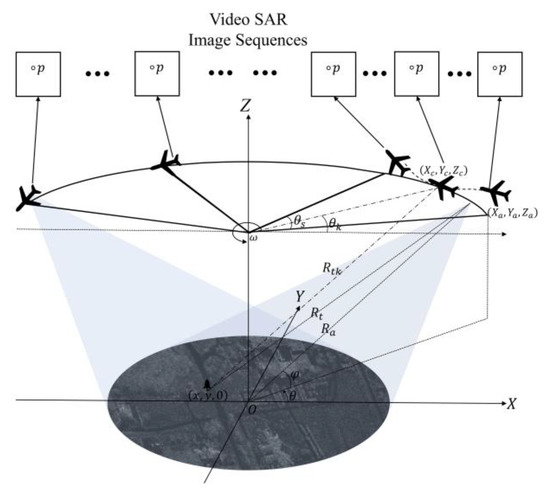
Figure 1.
Imaging model for airborne video SAR.
The slant range between APC and ground target can be expressed as:
Let represents the position of the APC at the center of the aperture , and then the instantaneous slant range can be expressed as:
The circular spotlight mode ensures the continuous acquisition of ground targets, and in order to form a real-time updated video, the following two points must be met: (1) Efficient processing of the echo signals to quickly obtain a single frame video SAR image. (2) The consistency between different frame images should be ensured; that is, the position of stationary ground targets in the image should be at the same pixel point . This requires the final image to be located in a unified ground output coordinate system (GOCS), where the X-Y-Z axis of the Cartesian coordinate system always points towards the range, azimuth, and altitude directions, respectively.
2.2. The Resolution and Frame Rate of Video SAR
High frame rate imaging is the most significant feature that distinguishes video SAR from traditional SAR. In order to achieve continuous tracking of ground-moving targets, the system frame rate of video SAR must reach at least 5 Hz, and the imaging resolution of video SAR must reach at least 0.2 m to accurately identify the observed targets [16].
According to the theory of SAR imaging [44], the range resolution and azimuth resolution are described as:
where is the bandwidth, denotes the speed of light, and denotes the wavelength.
Assuming that , in order to achieve a range resolution of 0.2 m, the system bandwidth must reach at least 1.06 GHz. Usually, in order to achieve consistency between different frame images, the range resolution and azimuth resolution should match, i.e., . According to (4), the synthetic aperture angle should be . The azimuth resolution is inversely proportional to the frequency and synthetic aperture angle, which means that for high-frequency video SAR, only a small synthetic aperture angle is required to achieve the required azimuth resolution. Under the condition of constant speed, its corresponding synthetic aperture time is relatively shorter. When the system parameters and azimuth resolution are constant, the imaging frame rate of video SAR is related to the system carrier frequency and sub-aperture overlap ratio ω:
where is the aperture overlap rate.
Assuming the average slant range of video SAR is and average speed . To achieve a 5 Hz frame rate without considering aperture overlap, the carrier frequency of video SAR needs to exceed 207 GHz. Therefore, video SAR usually works at a high-frequency band to meet the system frame rate requirements. In addition, it is also necessary to consider the impact of atmospheric attenuation on the signal [45]. As the frequency of 220 GHz is near the atmospheric window, the relatively small attenuation makes it a reasonable choice. Table 1 show the video SAR parameters at different frequencis, it can be seen that to achieve an imaging rate of 5 Hz, X-band video SAR requires a minimum aperture overlap of 94%, while THz video SAR does not require aperture overlap at all, and X-band video SAR requires longer synthetic aperture time. When the hardware cannot meet the high frequency, increasing the aperture overlap ratio ω can also improve the image frame rate, but the synthetic aperture time of the system remains unchanged; that is, the delay between the video SAR and the actual scene remains unchanged [10,46].

Table 1.
Video SAR parameters at different carrier frequencies.
2.3. Signal Model and Polar Format Algorithm
Assuming the transmission signal of video SAR is linear frequency modulation (LFM), the echo signal of any ground target has the following form:
where is the fast time, is the slow time, is the pulse width, is the center frequency, is the chirp rate, is the rectangular window function, and the delay of radar echo is .
Assuming that the actual position of the platform is accurately measured by the difference global positioning system and inertial measurement unit (DGPS AND IMU). Then, the DGPS AND IMU-based motion compensation (MOCO) is applied by multiplying the scene center echo as a reference. After that, the dechirped signal prepared for polar format storage can be described as:
where is the differential distance between the scene center and the ground target :
During the dechirp processing, additional residual video phase (RVP) and skew terms are generated, which may cause image distortion and defocus. An effective compensation method is to multiply the following compensation function in the range-Doppler domain [47]:
Then perform the range inverse fast Fourier transform (IFFT) to obtain the intermediate frequency signal after removing the RVP term and envelope skew term:
PFA uses the plane wavefront assumption; that is, only the first-order Taylor approximation of at the slow time is retained:
Let , , and denote the spatial wavenumber, range wavenumber, and azimuth wavenumber, respectively:
Then, the signal can be represented in the wavenumber domain as:
where the amplitude is ignored as it hardly affects the process of the imaging algorithm.
is uniformly distributed in domain, yet it is non-uniform in . In order to use an efficient 2D fast Fourier transform (2D-FFT), it is necessary to perform 2D resampling on the wavenumber domain signal to distribute it in a uniform rectangular format. This process can be achieved through a two-dimensional wavenumber domain interpolation, or it can be decomposed into cascaded range and azimuth interpolation. After completing the 2D resampling of the signal, the PFA image can be obtained by using 2D-FFT once on the wavenumber domain signal distributed in a rectangular format:
As shown in Figure 2a, (14) is based on line-of-sight polar interpolation (LOSPI). With the movement of video SAR, will rotate accordingly. As shown in Figure 2b, stabilized scene polar interpolation (SSPI) can also be applied to the wavenumber domain signal and then obtain the PFA image under GOCS:
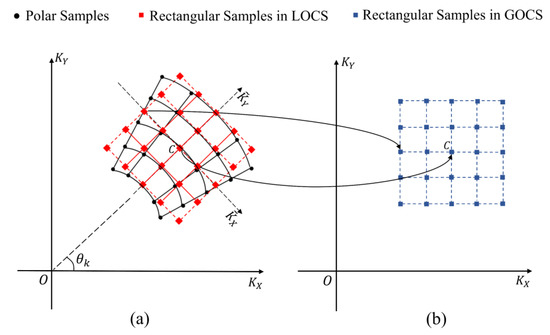
Figure 2.
2D resampling of wavenumber domain signals. (a) LOSPI. (b) SSPI.
The relationship between and is related to the azimuth angle of video SAR:
3. Methods
There are still some problems when using PFA to process video SAR data. First, the 2D interpolation in the polar format transformation affects the computational efficiency of PFA. In addition, the wavefront curvature error leads to the limitation of the scene size of PFA. Considering the target localization tasks of video SAR, this wavefront curvature error must be corrected. To address the above issues, a generalized persistent polar format algorithm (GPPFA) is proposed to achieve a more efficient video SAR imaging that can be applied to different scenes.
3.1. Polar Format Transformation of GPPFA
The discrete form of range and azimuth wavenumber before PFA resampling can be expressed as:
where is the range sample index such as , is the number of range sampling, n is the azimuth sample index such as , is the number of pulses.
There is a coupling between m and n in and , therefore, a polar-to-rectangular transformation should be carried out to remove the coupling [48]. The range and azimuth wavenumber after resampling can be rewritten as:
To improve the efficiency, a 2D resampling is usually decomposed into range and azimuth resampling. The range wavenumber is always uniformly distributed, which is consistent with the sampling properties of CZT [49,50]. For the azimuth resampling, it is not always uniformly distributed because the azimuth wavenumber is related to the azimuth angle. Therefore, more efficient CZT can be used for range resampling, while for azimuth resampling, it can only be used within certain constraints.
CZT can actively set the start frequency and frequency interval, and it can calculate the Fourier transform of the signal on any arc on the unit circle. The z-transform of a sequence is defined as:
where and are parameters of CZT:
where represents the start digital frequency, is the digital frequency interval between adjacent two points.
The purpose of range resampling is to remove the coupling between range wavenumber and pulse number . Select the reference value as the range wavenumber at the azimuth index center . Then, let , the index before and after range resampling can be calculated as:
According to (21), the digital frequency after the range CZT can be calculated as:
Therefore, the initial digital frequency and the frequency interval can be expressed as:
Then, the parameters of range CZT are:
As shown in Figure 3a, after the range CZT, the wavenumber domain signal distribution is converted from a polar format to a keystone format, where the azimuth wavenumber changes to the following form:
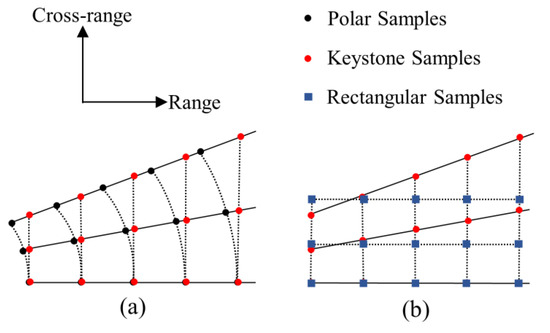
Figure 3.
Resampling in the wavenumber domain. (a) Range resampling. (b) Azimuth resampling.
As shown in Figure 3b, the purpose of azimuth resampling is to remove the coupling between azimuth wavenumber and range index m. Select the reference value as the azimuth wavenumber at the range index center . Then, let :
Make the following approximation for (26):
The index before and after azimuth resampling can be calculated as:
According to (28), the digital frequency after the azimuth CZT can be calculated as:
Therefore, the initial digital frequency and the frequency interval can be expressed as:
Then, the parameters of azimuth CZT are:
The process of azimuth CZT can be expressed as:
where represents the azimuth CZT, is the range FFT.
The CZT-based azimuth resampling is based on a small-angle approximation of (27), which means that the azimuth wavenumbers are uniformly distributed; otherwise, it will lead to errors. Therefore, for the process of azimuth resampling, it is necessary to choose different processing methods according to different scenarios. For X-band video SAR (), the synthetic accumulation angle , while for THz video SAR () . Therefore, for THz video SAR, the azimuth CZT is sufficiently accurate, while X-band video SAR is not. To obtain an explicit criterion, it is necessary to derive the threshold for azimuth resampling.
Assume that the azimuth wavenumber is uniformly distributed in a two-dimensional wavenumber domain, then the azimuth phase error can be written as:
where can be approximated as by Taylor series expansion, and the Taylor expansion of can be expressed as:
A practical guideline is that the cubic error between two edges can be ignored if it does not exceed π/4 [51]. Therefore, the phase error needs to satisfy:
The synthetic aperture angle , then can be expressed in the form of the carrier frequency:
Equation (36) reveals the information that the azimuth uniform resampling can be considered sufficiently accurate when is kept within the threshold.
Figure 4 shows the relationship between the frequency and scene size when the azimuth uniform resampling is satisfied. When , , and , the frequency should satisfy . Therefore, under this condition, X-band video SAR needs to use non-uniform azimuth resampling, such as interpolation, while THz video SAR can use a more efficient azimuth CZT to complete the process of azimuth resampling. After the azimuth resampling is completed, a range IFFT is used to obtain the preliminary PFA image.
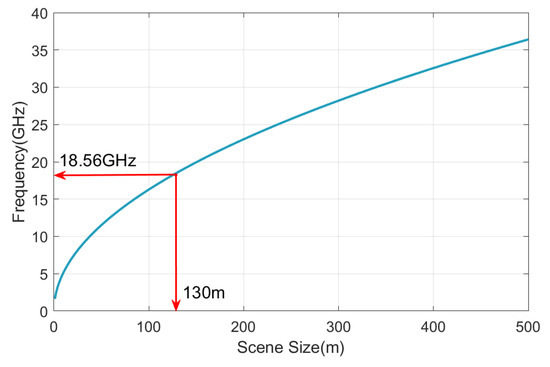
Figure 4.
The relationship between frequency and scene size when azimuth uniform resampling is satisfied.
3.2. Wavefront Curvature Error Analysis and Compensation
The phase of the target can be expressed as:
Constant and linear phase errors lead to target offset, quadratic phase errors lead to image defocus, while higher-order phase errors have little impact on the image quality [47]. Therefore, only constant terms, linear terms, and quadratic phase errors need to be considered, which decomposes wavefront curvature error compensation into geometric distortion correction and image defocus compensation.
From (37), it can be seen that the only term related to t in phase is the differential distance . Implementing the second order of Taylor series expansion to and the approximate difference distance at the aperture center moment :
The constant terms are:
where is the distortion position of the target .
The linear terms are:
Associate the following relationships:
Then the following relationship can be obtained:
According to (42), the relationship between distortion position and is obtained, which is called GOCS geometric distortion mapping (GDM):
According to (16) and (43), the LOCS-GDM is obtained as:
Let denotes the offset distance, and then the offset distance of the kth frame image is:
The effect of geometric distortion can be ignored only if it is within the distortion negligible region (DiR), which is defined as:
Geometric distortion correction can be accomplished by image domain interpolation, the key of which is to find the image coordinate positions of resampling points, and the GDM shown in (43) and (44) gives this relationship. The schematic diagram of geometric distortion correction is shown in Figure 5. Since image rotation and distortion correction can be accomplished by one image domain, 2D interpolation, distortion correction, and coordinate system unification can be achieved simultaneously.
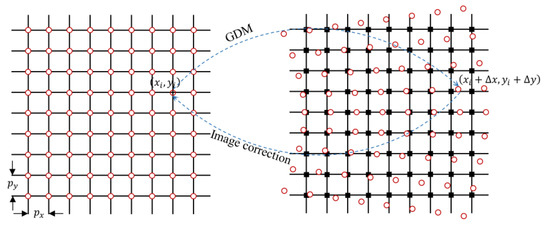
Figure 5.
Distortion correction and coordinate system unification.
The quadratic terms of the difference distance are:
Additionally, the quadratic phase error is expressed in the form of the difference of the second-order derivatives of the difference distance:
The residual quadratic phase error is a two-dimensional spatial variable, so it is impossible to construct a filter to accurately compensate for the phase error at all points, which is the difficulty of compensating for the residual phase error. However, it is not necessary to compensate for it in all scenarios. In fact, it can be ignored if the phase error is less than a certain threshold during time-to-frequency conversion, and an approximate judgment formula is given in [20]. Based on the threshold, the effective scene size is:
where and are the effective scene radius at thresholds of and , respectively, and is the radar wavelength.
Similarly, the effect of image defocus can be ignored only within the defocus negligible region (DeR), which is defined as:
According to (46) and (50), the DiR and DeR at different frequencies can be calculated as shown in Table 2, where the DiR is independent of the frequency and only related to the distance of the point target from the center point, both of which are 23.8 m.

Table 2.
DiR and DeR at different carrier frequencies.
In addition, Figure 6 shows the residual quadratic phase error and the effective scene size at different wavebands, where the scene size is set to 200 m × 200 m. As shown in Figure 6a,b, THz video SAR has a larger DeR of 171.3 m, while the X-band video SAR only has a DeR of 35.7 m. Generally, the scene size of video SAR is between 50 m and 150 m, so the effect of residual quadratic phase error can be ignored for THz video SAR, while the error must be corrected for X-band video SAR. This indicates that THz video SAR can ignore the effect of defocus in many cases, while it must be corrected for X-band video SAR.
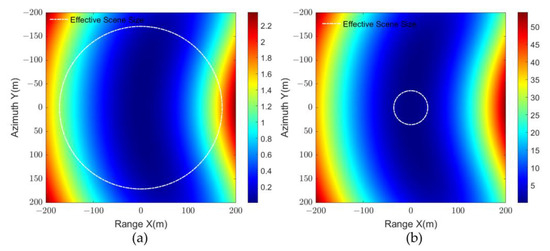
Figure 6.
Residual quadratic phase error and effective scene range at different wavebands. (a) THz PFA (). (b) X-band PFA ().
Figure 7 depicts the residual quadratic phase error in different coordinate systems under X-band video SAR with a scene size of 65 m, where Figure 7a is shown in the actual coordinates , and Figure 7b is shown in the distorted coordinates . It can be seen that the residual quadratic phase error is mainly a function of distance to the distorted coordinates . Therefore, a correction for each range bin in the distorted coordinates can complete the compensation of the residual quadratic phase error.
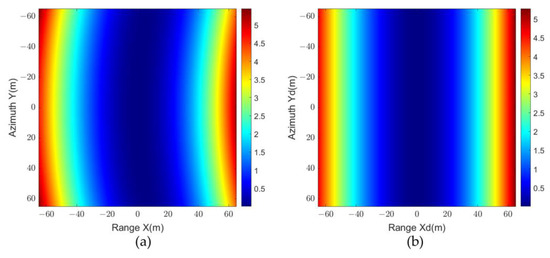
Figure 7.
Residual quadratic phase error in different coordinate systems in X-band. (a) Actual coordinates. (b) Distorted coordinates.
Perform an azimuth FFT on the PFA image and perform a residual phase error compensation. The compensation function is:
The process of the compensation is:
where and denotes the azimuth FFT and azimuth IFFT, respectively. Then, a distortion-free video SAR image is obtained by applying geometric distortion correction to .
3.3. Imaging Approach of GPPFA
Based on the criteria obtained from the previous calculations, the flowchart of the proposed GPPFA can be described in Figure 8.
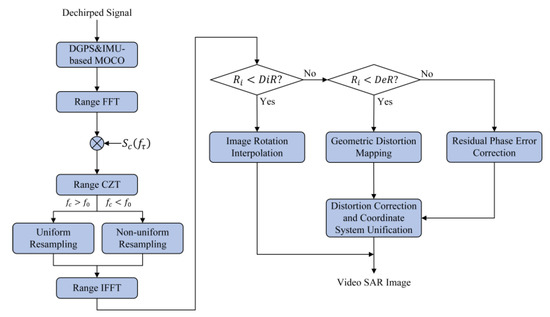
Figure 8.
Flow chart of the proposed GPPFA.
Considering the possible trajectory deviation or platform vibration during the video SAR flight, which usually adversely affects the received SAR signal, a DGPS and IMU-based MOCO is applied before processing. After that, most of the motion errors are compensated, and the Map-drift algorithm (MD) [52] or phase gradient autofocus algorithm (PGA) [53] can be applied if the residual motion errors exist and affect the image.
Then, the range processing is based on range FFT, RVP compensation, and range CZT. For the possible wavefront curvature errors in the preliminary PFA image, the two criteria in (46) and (50) are chosen as the criteria to ensure the optimal processing flow in different scenarios.
For the case , only an image rotation is implemented. For the case , the distortion coordinate positions are calculated using the GDM, and the distortion correction and coordinate system unification are completed using an image domain 2D interpolation. For the case , the residual phase error compensation is required. The proposed GPPFA is capable of adapting to airborne video SAR imaging at any waveband, any slant range, and any scene size.
4. Results
4.1. Point Target Results
To validate the proposed method, point target and extended target experiments of THz and X-band video SAR are performed. The system parameters are listed in Table 3. According to the analysis in Section 3.2, the shorter the slant range is, the more serious the distortion is, so a shorter slant range is used to highlight the effect of distortion.

Table 3.
Video SAR System Parameter.
As shown in Figure 9a, the scene size is 130 m × 130 m, and the point targets are distributed in a rectangle of 100 m × 100 m at an interval of 10 m. Figure 9b shows the GDM of the first frame video SAR image (), whose shape changes from rectangle to sector, and Figure 9c shows the GDM of the second frame video SAR image (), whose shape exhibits a distorted and rotated sector.
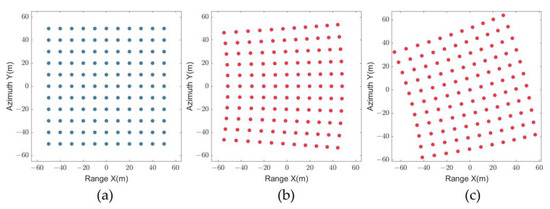
Figure 9.
(a) Point targets distribution. (b) GDM of frame 1. (c) GDM of frame 2.
First, the proposed method is validated in THz video SAR mode, and the traditional PFA and UCSA [34] are chosen as comparison methods. The imaging results are shown in Figure 10, where the first and second rows correspond to the first frame () and second frame () frames of the video SAR, respectively. It can be seen that the plane wave assumption is no longer accurate enough at a short slant range, which makes the PFA image distorted. Additionally, with the motion of the video SAR, the distorted image is subsequently rotated, but the point target position always coincides with the theoretical position of the labeled GDM. For UCSA and GPPFA, the point targets are located at the real position in different video SAR frame images due to distortion correction and coordinate system unification, and the effect of residual phase error is ignored with the advantage of the THz band.
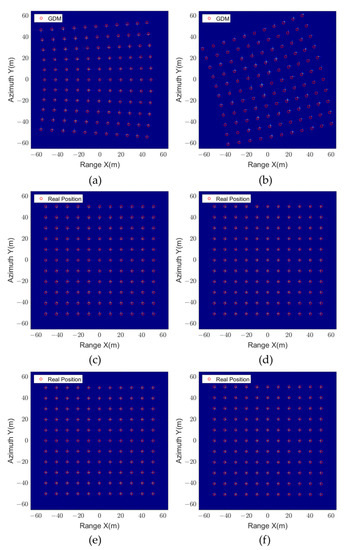
Figure 10.
Imaging results of THz video SAR. (a,b) Imaging result obtained by PFA. (c,d) Imaging results obtained by UCSA [34]. (e,f) Imaging result obtained by GPPFA.
The imaging results of X-band video SAR are shown in Figure 11. Compared with THz video SAR, X-band video SAR requires a larger synthetic aperture angle. From the GDM, it is known that the distortion position is independent of the frequency, so the target position is the same as in Figure 10. The effective scene size of PFA is marked in Figure 11a,b, and the target is well-focused within the range and defocused outside the range. For UCSA, since the synthetic aperture angle no longer satisfies the small angle assumption, the resulting azimuth phase error increases and affects the range wavenumber signal, so the images of UCSA are significantly defocused. For GPPFA, it is first processed with azimuth interpolation by the criterion (49), and then the residual quadratic phase error compensation is implemented because the scene size satisfies the criterion , and it can be seen that the images of GPPFA are well-focused and free of distortion.
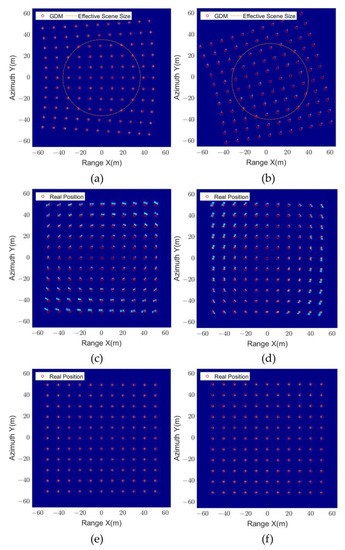
Figure 11.
Imaging results of X-band video SAR. (a,d) Imaging results obtained by PFA. (b,e) Imaging results obtained by UCSA [34]. (c,f) Imaging results obtained by GPPFA.
To compare the effect of geometric distortion, the position of three targets in the first frame of THz video SAR image: , and with different distances from the center point are measured. The geometry position of three point targets are listed in Table 4, it can be seen that in the first frame video SAR image, the point target has a large offset from the actual position, and the offset reaches tens of meters in the second frame image, which makes the target localization and tracking of video SAR difficult. For UCSA and GPPFA, the point target position basically overlaps with the actual position and can be considered accurate enough.

Table 4.
Geometry position of point targets.
To quantitatively analyze the imaging performance of the point target, the range and azimuth profiles of the point target in the first frame of THz video SAR and X-band video SAR are shown in Figure 12, respectively. Additionally, the measured parameters, including impulse response width (IRW), peak side lobe ratio (PSLR), and integral side lobe ratio (ISLR), are shown in Table 5. For THz video SAR, the point target resolutions of several methods are close to the theoretical resolution , and the PSLR and ISLR meet the requirements of SAR imaging (PSLR = −13 dB, ISLR = −20 dB) [54]. Then, for X-band video SAR, the point is defocused due to being outside the effective scene range, and the defocus is due to wavefront curvature error. Since the X-band video SAR does not satisfy the small azimuthal accumulation angle assumption, the defocus also occurs for the UCSA based on 2D CZT, which leads to its IRW and PSLR deterioration. For GPPFA, geometric distortion and image defocus are basically absent in GPPFA images due to the use of the wavefront curvature error compensation method.
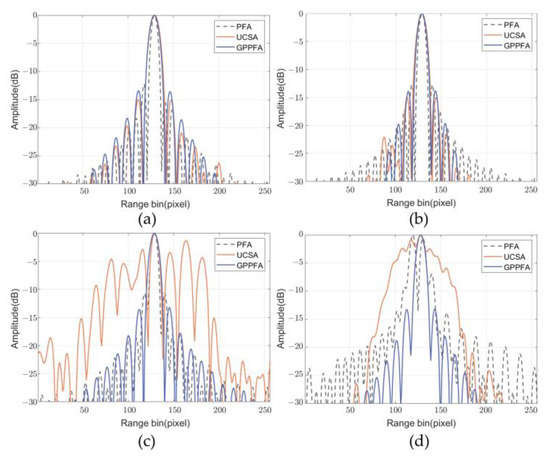
Figure 12.
Image profiles of point target . (a) Range profiles of THz video SAR. (b) Azimuth profiles of THz video SAR. (c) Range profiles of X-band video SAR. (d) Azimuth profiles of X-band video SAR.

Table 5.
Imaging quality analysis of point target .
4.2. Extended Target Results
To further validate the performance of the proposed method, the extended target experiments are performed. The open source original image is obtained from the website of the Air Force Research Laboratory (AFRL) [55], which is shown in Figure 13a. The scene size is 130 m × 130 m, and the same system parameters are used as in the previous point target experiments. The echo data are obtained by the time domain simulation method [56], and the pre-processed range compressed image is shown in Figure 13b.

Figure 13.
(a) Original SAR image. (b) Range compressed image.
The imaging results of THz video SAR are shown in Figure 14. Figure 14a,c,e shows the imaging results of PFA, UCSA, and GPPFA at the first frame of video SAR (), and Figure 14b,d,f shows the imaging results of PFA, UCSA, and GPPFA at the second frame of video SAR (). It can be seen that the images of PFA are distorted and rotated, while UCSA and GPPFA enable high-quality and distortion-free imaging at different video SAR frames.

Figure 14.
THz video SAR imaging results of extended targets. (a,b) Imaging result obtained by PFA. (c,d) Imaging result obtained by UCSA [34]. (e,f) Imaging result obtained by GPPFA.
In order to more intuitively illustrate the compensation effect of the proposed method on wavefront curvature error, a strong scattering point target set in the opposite target edge region is tested in X-band video SAR. Figure 15a shows the original image, with the strongly scattering points divided into three rows and three columns, with a square shape. Figure 15b shows the imaging result of PFA. It can be seen that the distortion and defocus of the targets are so severe that they obscure the nearby “rivers”. Figure 15c shows the imaging result of UCSA, the UCSA image is severely defocused in X-band. Figure 15d shows the imaging result of GPPFA, and it can be seen that the image is distortion-free and well-focused, and the river near the target is not covered by the side flaps of the target, which proves the capability of the proposed method under X-band video SAR.

Figure 15.
X-band video SAR imaging results of extended targets with strong scattering points. (a) Original input SAR image with strong scattering points. (b) Imaging result obtained by PFA. (c) Imaging result obtained by UCSA [34]. (d) Imaging result obtained by GPPFA.
The quantitative results of the expanded target imaging results are shown in Table 6, including image entropy, root mean square error (RMSE), peak signal-to-noise ratio (PSNR), and structural similarity index measure (SSIM) [57], and the best value of each metric is the value of the original image. It can be seen that GPPFA has better image metrics than PFA and UCSA, which indicates that the proposed method meets the image quality requirements.

Table 6.
Quantitative analysis of extended target imaging results.
To compare the actual computing efficiency of several methods, the average running times of PFA, UCSA, GPPFA, and BPA are listed in Table 7. The system environment of the PC is Microsoft Windows 11 (64-bit OS and 16 GB memory size), the processor is AMD Ryzen 5 5600H, the simulation environment is MATLAB 2021a, and the image interpolation is based on the Cubic interpolation of MATLAB. Performing 10 processes for each method and calculating the average time, it can be seen that PFA takes the shortest time, which is due to the fact that it does not use any additional processing, as a cost PFA image may be distorted, rotated, and defocused. UCSA and the proposed GPPFA have corrected the distortion and unified the coordinate system. The average elapsed time increased slightly, while the imaging time of BPA reached 45.02 s. However, PFA is only applicable to conditions that long slant range and small scene size are satisfied together, UCSA is only applicable to tasks with THz video SAR with scene radius less than DeR, while the proposed GPPFA is applicable to airborne video SAR imaging in any scene.

Table 7.
Evaluation of average elapsed time.
4.3. Large Observation Scenarios Experiments
To verify the performance of the GPPFA in different scenarios, a larger observation scenario, with a scene size of 500 m × 500 m, is validated to demonstrate the real applicability of the proposed method. The system parameters are listed in Table 8. The imaging scene is shown in Figure 16, and the interval of each point target is 100 m. It can be calculated that the DiR is 27 m, and the DeR is 382 m for THz-band video SAR, while it is 80 m for X-band video SAR. Moreover, motion errors have been added to validate the effectiveness of the MOCO method. The platform vibration is modeled as follows:
where M is the number of platform vibration components, , and represents the amplitude, frequency, and initial phase of the i-th vibration component, respectively. In this article, , the value of is two times the corresponding wavelength, and .

Table 8.
System parameters for large observation scenario experiments.
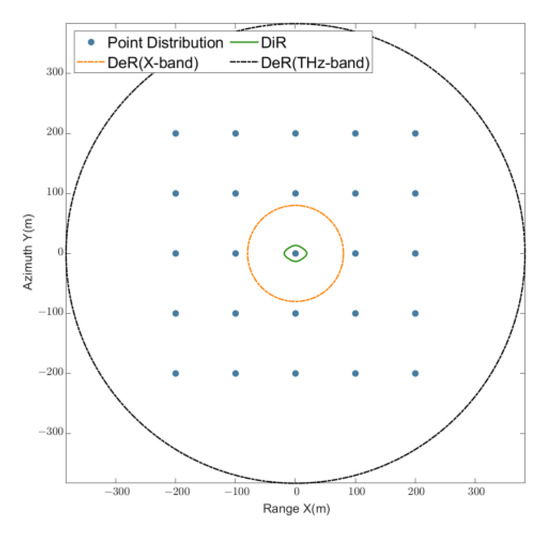
Figure 16.
Image scene of large observation scene experiments.
The large observation scenarios imaging results are shown in Figure 17, where Figure 17a,b show the imaging results of the proposed method in THz-band without using MOCO and using MOCO, respectively, and Figure 17c,d show the corresponding imaging results of the proposed method in X-band, respectively. It can be seen that for the method that does not use MOCO, motion errors cause severe defocusing in its imaging results, while for a method with MOCO, the distortion or defocusing does not exist, and each target is accurately focused. Therefore, the proposed GPPFA is applicable to any slant range, scene size, and flight trajectory.
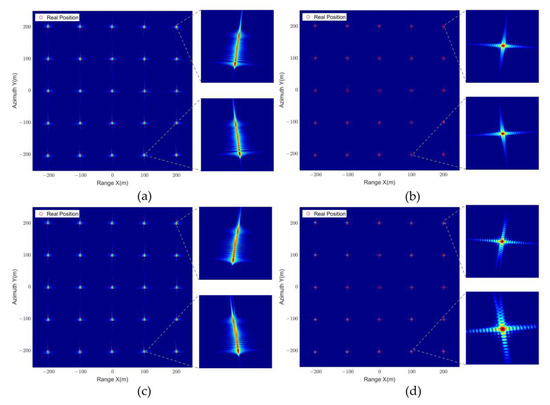
Figure 17.
Imaging results of the proposed method in large observation scenarios with motion errors. (a,b) Imaging results without MOCO and using MOCO in THz-band. (c,d) Imaging results without MOCO and using MOCO in X-band.
5. Conclusions
In this paper, a generalized persistent polar format algorithm (GPPFA) is proposed, which can meet the fast imaging of airborne video SAR in arbitrary waveband, arbitrary slant range, and scene size. Firstly, an airborne video SAR imaging model is established, and the high-resolution and high-frame rate characteristics and requirements of video SAR are analyzed. Then, the principle of CZT is introduced, and range resampling is completed based on CZT. For azimuth resampling, the critical of azimuth uniform resampling is analyzed, and the azimuth resampling of different waveband video SAR systems is completed based on azimuth CZT or interpolation, respectively. For the wavefront curvature error of PFA, the geometric distortion mapping of airborne video SAR in circular spotlight mode is derived, and a geometric distortion and image defocus correction method is proposed. GPPFA is capable of video SAR imaging at different wavebands, arbitrary scene sizes, and arbitrary flight trajectories. Point target and extended target experiments verify the accuracy, generality, and imaging efficiency of the proposed method. Although the proposed method is derived in circular spotlight mode, it can be applied to various working modes, such as linear spotlight mode and curve flight trajectories, as long as the platform position is accurately measured.
There are still some improvements to the proposed method. In reality, the THz video SAR platform is small and cannot carry high-precision DGPS AND IMU devices, and it is more sensitive to motion errors which may be introduced by airflow disturbance and attitude control. Therefore, the more accurate and efficient motion error compensation algorithm and its combination with the proposed method will be studied in the future to further improve the performance and generality of the algorithm.
Author Contributions
Conceptualization, J.J.; methodology, J.J.; validation, J.J. and Y.L.; formal analysis, J.J. and Y.L.; writing—original draft preparation, J.J.; writing—review and editing, J.J., Y.L. and Y.Y.; visualization, J.J.; supervision, Y.L., Y.Y. and Y.Z.; funding acquisition, Y.L. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Shanghai under Grant 21ZR1444300, in part by the National Nature Science Foundation of China under Grants 12105177, 61988102, and 21731020, in part by the National Key R&D Project of China under Grant 2018YFF01013003, the Opened Foundation of Hongque Innovation Center (HQ202204002), and the Shanghai Social Development Science and Technology Research Project (Grant No. 22dz1200302).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, P.; Wu, F.; Tang, S.; Jiang, C.; Liu, C. Implementation Method of Automotive Video SAR (ViSAR) Based on Sub-Aperture Spectrum Fusion. Remote Sens. 2023, 15, 476. [Google Scholar] [CrossRef]
- Chen, J.; An, D.; Wang, W.; Chen, L.; Feng, D.; Zhou, Z. A Novel Generation Method of High Quality Video Image for High Resolution Airborne ViSAR. Remote Sens. 2021, 13, 3706. [Google Scholar] [CrossRef]
- Yang, C.; Chen, Z.; Deng, Y.; Wang, W.; Wang, P.; Zhao, F. Generation of Multiple Frames for High Resolution Video SAR Based on Time Frequency Sub-Aperture Technique. Remote Sens. 2023, 15, 264. [Google Scholar] [CrossRef]
- Kim, S.; Yu, J.; Jeon, S.-Y.; Dewantari, A.; Ka, M.-H. Signal Processing for a Multiple-Input, Multiple-Output (MIMO) Video Synthetic Aperture Radar (SAR) with Beat Frequency Division Frequency-Modulated Continuous Wave (FMCW). Remote Sens. 2017, 9, 491. [Google Scholar] [CrossRef]
- Wells, L.; Sorensen, K.; Doerry, A.; Remund, B. Developments in Sar and Ifsar Systems and Technologies at Sandia National Laboratories. In Proceedings of the 2003 IEEE Aerospace Conference Proceedings (Cat. No.03TH8652), Big Sky, MT, USA, 8–15 March 2003; Volume 2. [Google Scholar]
- Yocky, D.A.; West, R.D.; Riley, R.M.; Calloway, T.M. Monitoring Surface Phenomena Created by an Underground Chemical Explosion Using Fully Polarimetric VideoSAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2481–2493. [Google Scholar] [CrossRef]
- Yocky, D.A.; Calloway, T.M.; Wahl, D.E. VideoSAR Collections to Image Underground Chemical Explosion Surface Phenomena. In Proceedings of the Radar Sensor Technology XXI, Anaheim, CA, USA, 1 May 2017; Volume 10188, pp. 222–234. [Google Scholar]
- Kim, S.-H.; Fan, R.; Dominski, F. ViSAR: A 235 GHz Radar for Airborne Applications. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 1549–1554. [Google Scholar]
- Miller, J.; Bishop, E.; Doerry, A. An Application of Backprojection for Video SAR Image Formation Exploiting a Subaperature Circular Shift Register. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XX, Baltimore, MA, USA, 23 May 2013; Volume 8746, pp. 66–79. [Google Scholar]
- Johannes, W.; Stanko, S.; Wahlen, A.; Sommer, R.; Pohl, N.; Wellig, P.; Sennhauser, C.; Meier, E.; Kallfass, I. Implementation of a 35 GHz SAR Sensor and a High Resolution Camera to Enable Real-Time Observation. In Proceedings of the EUSAR 2014; 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Ogut, M.; Cooke, C.; Deal, W.; Kangaslahti, P.; Tanner, A.; Reising, S. A Novel 1/f Noise Mitigation Technique Applied to a 670 GHz Receiver. IEEE Trans. Terahertz Sci. Technol. 2020, 11, 109–112. [Google Scholar] [CrossRef]
- Ignatenko, V.; Nottingham, M.; Radius, A.; Lamentowski, L.; Muff, D. ICEYE Microsatellite SAR Constellation Status Update: Long Dwell Spotlight and Wide Swath Imaging Modes. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 1493–1496. [Google Scholar]
- Muff, D.; Ignatenko, V.; Dogan, O.; Lamentowski, L.; Leprovost, P.; Nottingham, M.; Radius, A.; Seilonen, T.; Tolpekin, V. The ICEYE Constellation—Some New Achievements. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York City, NY, USA, 21–25 March 2022; pp. 1–4. [Google Scholar]
- Wang, J.; Liang, X.-D.; Chen, L.-Y.; Wang, L.-N.; Li, K. First Demonstration of Joint Wireless Communication and High-Resolution SAR Imaging Using Airborne MIMO Radar System. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6619–6632. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Yu, H.; Chen, J.; Hong, W. Sparse Synthetic Aperture Radar Imaging From Compressed Sensing and Machine Learning: Theories, Applications, and Trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–69. [Google Scholar] [CrossRef]
- Yan, H.; Mao, X.; Zhang, J.; Zhu, D. Frame Rate Analysis of Video Synthetic Aperture Radar (ViSAR). In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24–28 October 2016; pp. 446–447. [Google Scholar]
- Mehrdad, S. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR Processing Using Chirp Scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Mittermayer, J.; Moreira, A.; Loffeld, O. Spotlight SAR Data Processing Using the Frequency Scaling Algorithm. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2198–2214. [Google Scholar] [CrossRef]
- Desai, M.D.; Jenkins, W.K. Convolution Backprojection Image Reconstruction for Spotlight Mode Synthetic Aperture Radar. IEEE Trans. Image Process. 1992, 1, 505–517. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Xu, G.; Zhou, R.; Zhang, H.; Hong, W. Multi-Channel Back-Projection Algorithm for Mmwave Automotive MIMO SAR Imaging with Doppler-Division Multiplexing. IEEE J. Sel. Top. Signal Process. 2022, 1–13. [Google Scholar] [CrossRef]
- Walker, J.L. Range-Doppler Imaging of Rotating Objects. IEEE Trans. Aerosp. Electron. Syst. 1980, AES-16, 23–52. [Google Scholar] [CrossRef]
- Rigling, B.D.; Moses, R.L. Polar Format Algorithm for Bistatic SAR. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1147–1159. [Google Scholar] [CrossRef]
- Jiang, J.; Li, Y.; Zheng, Q. A THz Video SAR Imaging Algorithm Based on Chirp Scaling. In Proceedings of the 2021 CIE International Conference on Radar (Radar 2021), Haikou, China, 15–19 December 2021; pp. 656–660. [Google Scholar]
- Song, X.; Yu, W. Processing Video-SAR Data with the Fast Backprojection Method. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2838–2848. [Google Scholar] [CrossRef]
- Xie, H.; Shi, S.; An, D.; Wang, G.; Wang, G.; Xiao, H.; Huang, X.; Zhou, Z.; Xie, C.; Wang, F.; et al. Fast Factorized Backprojection Algorithm for One-Stationary Bistatic Spotlight Circular SAR Image Formation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1494–1510. [Google Scholar] [CrossRef]
- Jakowatz, C.V., Jr.; Doren, N. Comparison of Polar Formatting and Back-Projection Algorithms for Spotlight-Mode SAR Image Formation. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XIII, Orlando, FL, USA, 17 May 2006; Volume 6237, pp. 137–143. [Google Scholar]
- Hu, R.; Li, X.; Yeo, T.S.; Yang, Y.; Chi, C.; Zuo, F.; Hu, X.; Pi, Y. Refocusing and Zoom-in Polar Format Algorithm for Curvilinear Spotlight SAR Imaging on Arbitrary Region of Interest. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7995–8010. [Google Scholar] [CrossRef]
- Gorham, L.A.; Rigling, B.D. Scene Size Limits for Polar Format Algorithm. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 73–84. [Google Scholar] [CrossRef]
- Gorham, L.; Rigling, B. Fast Corrections for Polar Format Algorithm with a Curved Flight Path. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2815–2824. [Google Scholar] [CrossRef]
- Zuo, F.; Li, J. A Persistent Imaging Method for Video-SAR in Terahertz Band. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium (ACES), Suzhou, China, 1–4 August 2017; pp. 1–2. [Google Scholar]
- Doerry, A.W. Forming Rotated SAR Images by Real-Time Motion Compensation; Sandia National Lab: Albuquerque, NM, USA, 2012. [Google Scholar]
- Gao, A.; Sun, B.; Li, J.; Li, C. A Parameter-Adjusting Autoregistration Imaging Algorithm for Video Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zuo, F.; Li, J.; Hu, R.; Pi, Y. Unified Coordinate System Algorithm for Terahertz Video-SAR Image Formation. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 725–735. [Google Scholar] [CrossRef]
- Yinwei, L.; Ding, L.; Zheng, Q.; Zhu, Y.; Sheng, J. A Novel High-Frequency Vibration Error Estimation and Compensation Algorithm for THz-SAR Imaging Based on Local FrFT. Sensors 2020, 20, 2669. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Q.; Wu, J.; Li, P.; Zheng, Q.; Ding, L. Estimation of High-Frequency Vibration Parameters for Terahertz SAR Imaging Based on FrFT with Combination of QML and RANSAC. IEEE Access 2021, 9, 5485–5496. [Google Scholar] [CrossRef]
- Hu, R.; Zuo, F.; Li, X.; Hu, X.; Soon, Y.T.; Ma, C. Curvilinear Video-SAR Persistent Imaging with Distortion Correction Based on Nufft-3. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July 2–August 2019; pp. 684–687. [Google Scholar]
- Hu, R.; Rao, B.S.M.R.; Alaee-Kerahroodi, M.; Ottersten, B. Orthorectified Polar Format Algorithm for Generalized Spotlight SAR Imaging with DEM. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3999–4007. [Google Scholar] [CrossRef]
- Garber, W.L.; Hawley, R.W. Extensions to Polar Formatting with Spatially Variant Post-Filtering. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XVIII, Orlando, FL, USA, 4 May 2011; Volume 8051, pp. 30–41. [Google Scholar]
- Doren, N.E.; Jakowatz, C.V.; Wahl, D.E.; Thompson, P.A. General Formulation for Wavefront Curvature Correction in Polar-Formatted Spotlight-Mode SAR Images Using Space-Variant Post-Filtering. In Proceedings of the Proceedings of International Conference on Image Processing; Santa Barbara, CA, USA, 26–29 October 1997, Volume 1, pp. 861–864.
- Guo, P.; Wu, F.; Wang, A. Extended Polar Format Algorithm (EPFA) for High-Resolution Highly Squinted SAR. Remote Sens. 2023, 15, 456. [Google Scholar] [CrossRef]
- Nie, X.; Zhuang, L.; Shen, S. A Quadtree Beam-Segmenting Based Wide-Swath SAR Polar Format Algorithm. IEEE Access 2020, 8, 147682–147691. [Google Scholar] [CrossRef]
- Chen, J.; An, D.; Wang, W.; Luo, Y.; Chen, L.; Zhou, Z. Extended Polar Format Algorithm for Large-Scene High-Resolution WAS-SAR Imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5326–5338. [Google Scholar] [CrossRef]
- John, C.; Robert, M. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: Hoboken, NJ, USA, 1992; ISBN 978-0-471-85770-9. [Google Scholar]
- Rosker, M.J.; Wallace, H.B. Imaging through the Atmosphere at Terahertz Frequencies. In Proceedings of the 2007 IEEE/MTT-S International Microwave Symposium, Honolulu, HI, USA, 3–8 June 2007; pp. 773–776. [Google Scholar]
- Palm, S.; Wahlen, A.; Stanko, S.; Pohl, N.; Wellig, P.; Stilla, U. Real-Time Onboard Processing and Ground Based Monitoring of FMCW-SAR Videos. In Proceedings of the EUSAR 2014; 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Carrara, W.G.; Goodman, R.S.; Majewski, R.M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House Remote Sensing Library; Artech House: Boston, MA, USA, 1995; ISBN 978-0-89006-728-4. [Google Scholar]
- Zhu, D.; Zhu, Z. Range Resampling in the Polar Format Algorithm for Spotlight SAR Image Formation Using the Chirp Z-Transform. IEEE Trans. Signal Process. 2007, 55, 1011–1023. [Google Scholar] [CrossRef]
- Rabiner, L.; Schafer, R.; Rader, C. The Chirp Z-Transform Algorithm. IEEE Trans. Audio Electroacoust. 1969, 17, 86–92. [Google Scholar] [CrossRef]
- Lawton, W. A New Polar Fourier Transform for Computer-Aided Tomography and Spotlight Synthetic Aperture Radar. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 931–933. [Google Scholar] [CrossRef]
- Zuo, F.; Min, R.; Pi, Y.; Li, J.; Hu, R. Improved Method of Video Synthetic Aperture Radar Imaging Algorithm. IEEE Geosci. Remote Sens. Lett. 2019, 16, 897–901. [Google Scholar] [CrossRef]
- Samczynski, P.; Kulpa, K.S. Coherent MapDrift Technique. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1505–1517. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase Gradient Autofocus-a Robust Tool for High Resolution SAR Phase Correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House Remote Sensing Library; Artech House: Boston, MA, USA, 2005; ISBN 978-1-58053-058-3. [Google Scholar]
- Air Force Research Laboratory. Available online: https://www.sdms.afrl.af.mil/ (accessed on 3 March 2023).
- Mori, A.; Vita, F. A Time-Domain Raw Signal Simulator for Interferometric SAR. Geosci. Remote Sens. IEEE Trans. 2004, 42, 1811–1817. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).