Image Texture as Quality Indicator for Optical DEM Generation: Geomorphic Applications in the Arid Central Andes
Abstract
1. Introduction
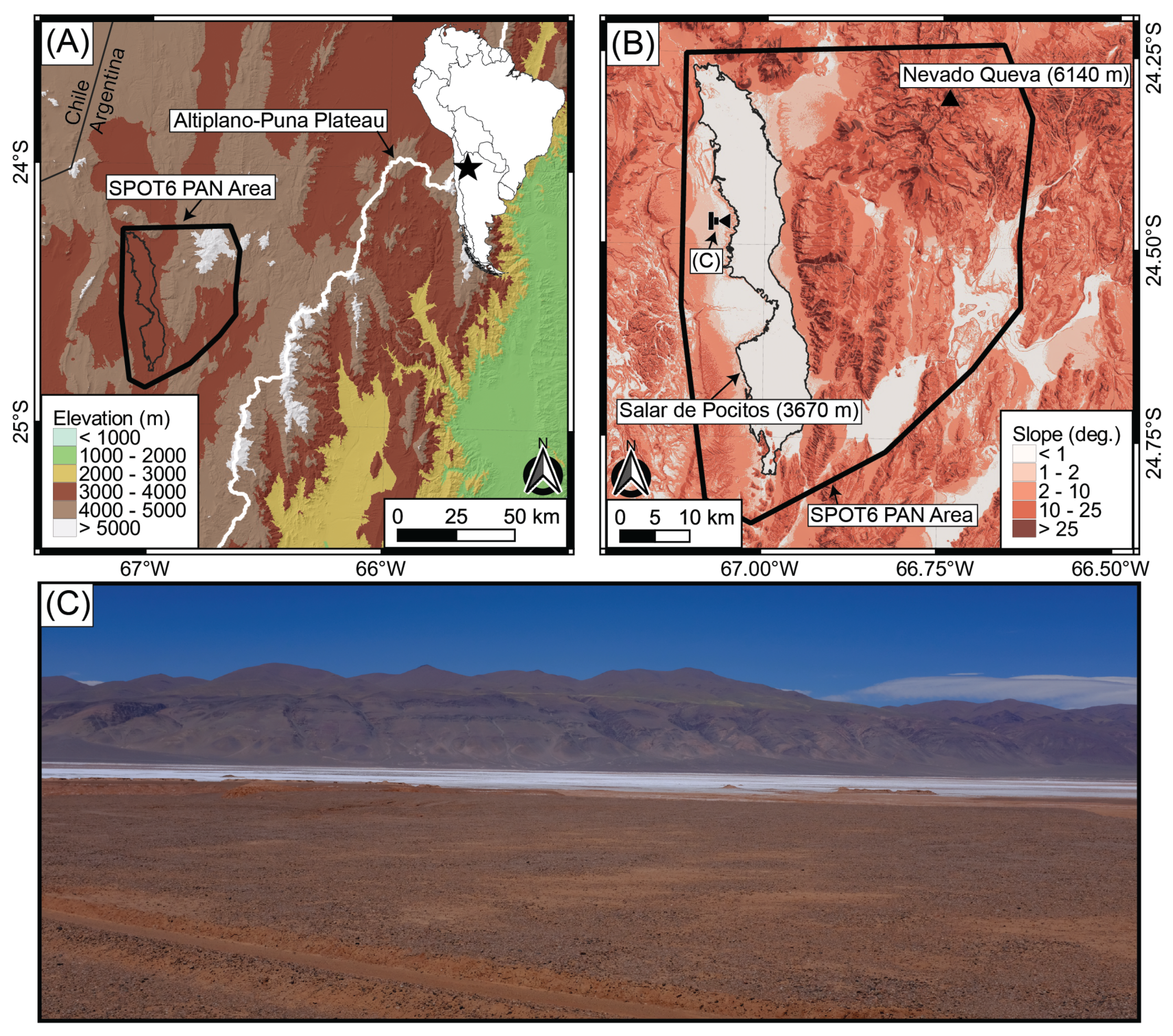
2. Study Area
3. Data and Methods
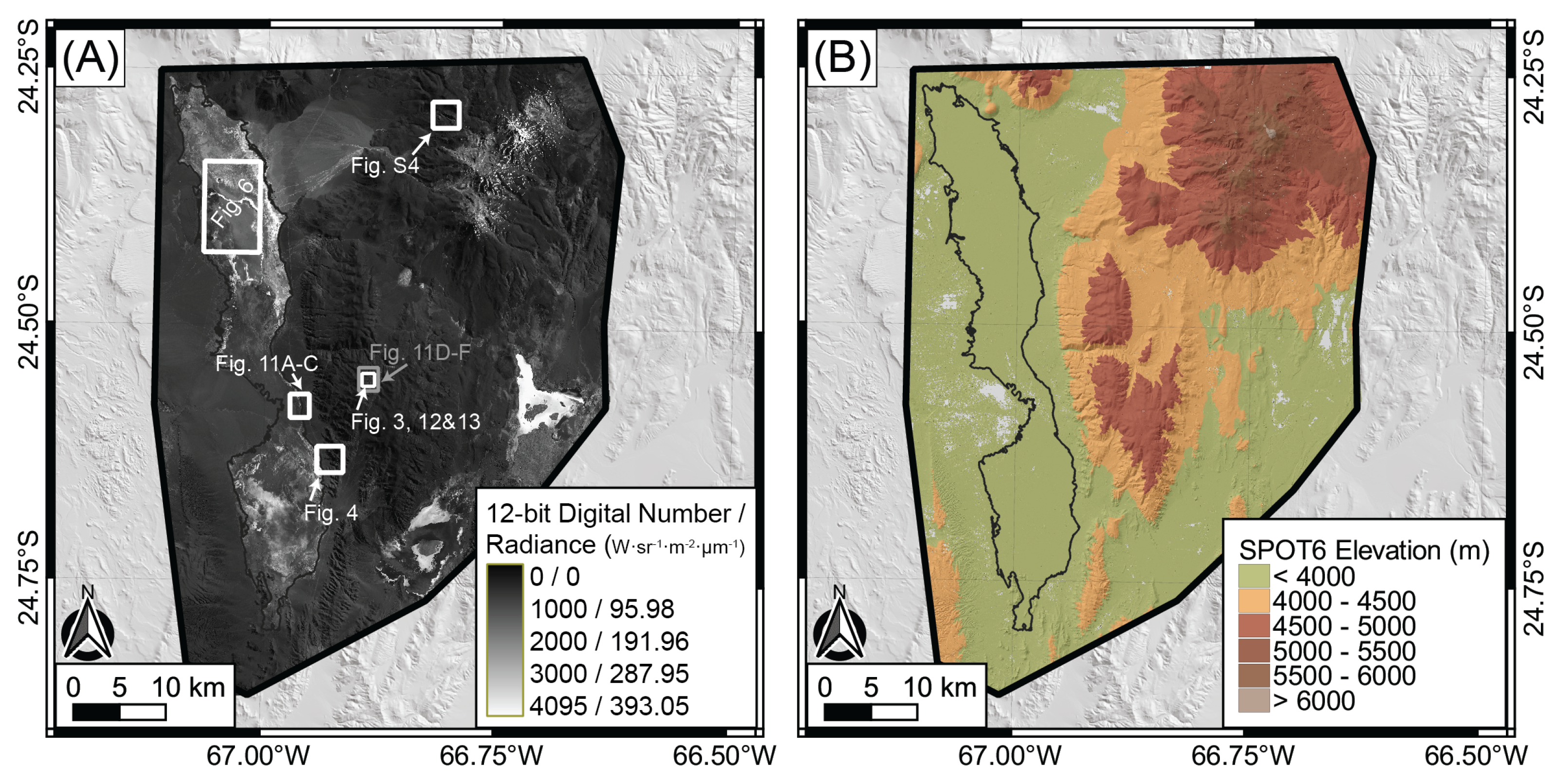
3.1. SPOT6/7 Satellite Data
3.2. DEM Generation with the Ames Stereo Pipeline
3.2.1. Bundle Adjustment and Map-Projection
3.2.2. Stereo-Correlation Algorithms and Parameters
3.2.3. Example of ASP Processing and Outputs
- SPOT6 Level 1A images in their native, tiled format are converted to GeoTiffs with RPC information contained in the file header, using the external GDAL command gdal_translate.
- An initial bundle adjustment is carried out on all three (A, B, and C) images using the bundle_adjust tool. In this way, satellite positions and orientations are adjusted relative to each other to improve the self-consistency of observations in all three images.
- Stereo correlation is performed on the AC image pair with the parallel_stereo tool and default BM parameters. Since the images are not yet map-projected, the initial rectification is done using the default affine epipolar approach. This step results in a low-quality preliminary matching.
- A low-quality 3 m DEM is generated from the preliminary matching using the point2dem tool.
- The low-quality preliminary AC BM-ck25 DEM is aligned to a reference 30 m DEM using the pc_align tool. We use the Copernicus 30 m global DEM, as it is of highest available quality for the study area [10]. This results in improved alignment of the preliminary DEM with the smoothed topography. Alternatively, the low-resolution point cloud of matches obtained during bundle adjustment could be coarsely gridded and aligned to a reference DEM to avoid the initial stereo correlation and reduce processing time.
- Another run of bundle_adjust is performed on the original SPOT6 images, now passing the results of the first bundle adjustment and the results of the 30 m DEM alignment in the previous step as initial conditions for camera positioning. This results in additional improvements in camera positioning with respect to tie-points observed in each image and with the smoothed topography from the Copernicus DEM.
- Using the final bundle adjustment parameters from the previous step, each SPOT6 image (A, B, and C) is independently map-projected onto the reference 30 m DEM (Copernicus) using the mapproject tool. This results in orthorectified SPOT6 images in a WGS84 decimal degree projection with pixel resolutions of 1.5 m, equivalent to SPOT6 Level 2A data.
- The map-projected scenes are run pairwise (AC, AB, BC) through parallel_stereo using all tested algorithms and parameters. Each parallel_stereo output is converted to a 3 m DEM (or 6, 12, and 24 m for the BM-ck25 output) with point2dem.
3.3. Comparison of DEM Quality with Image Texture
3.4. Curvature Dependence on Matching Algorithms
4. Results
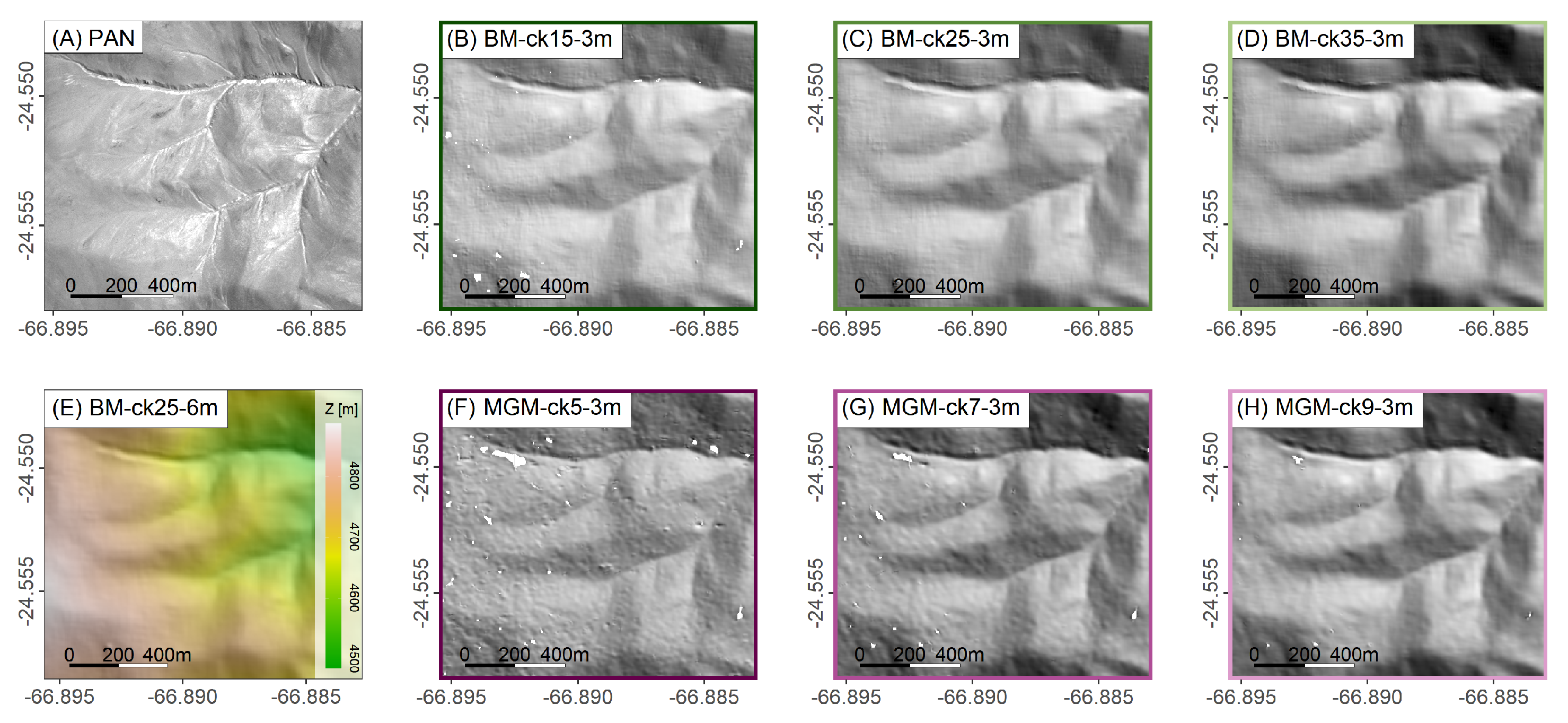
4.1. Visual Assessment of DEM Quality
4.2. Comparison of DEM Heights to dGNSS Measurements
4.3. Image Texture as a Proxy for DEM Quality
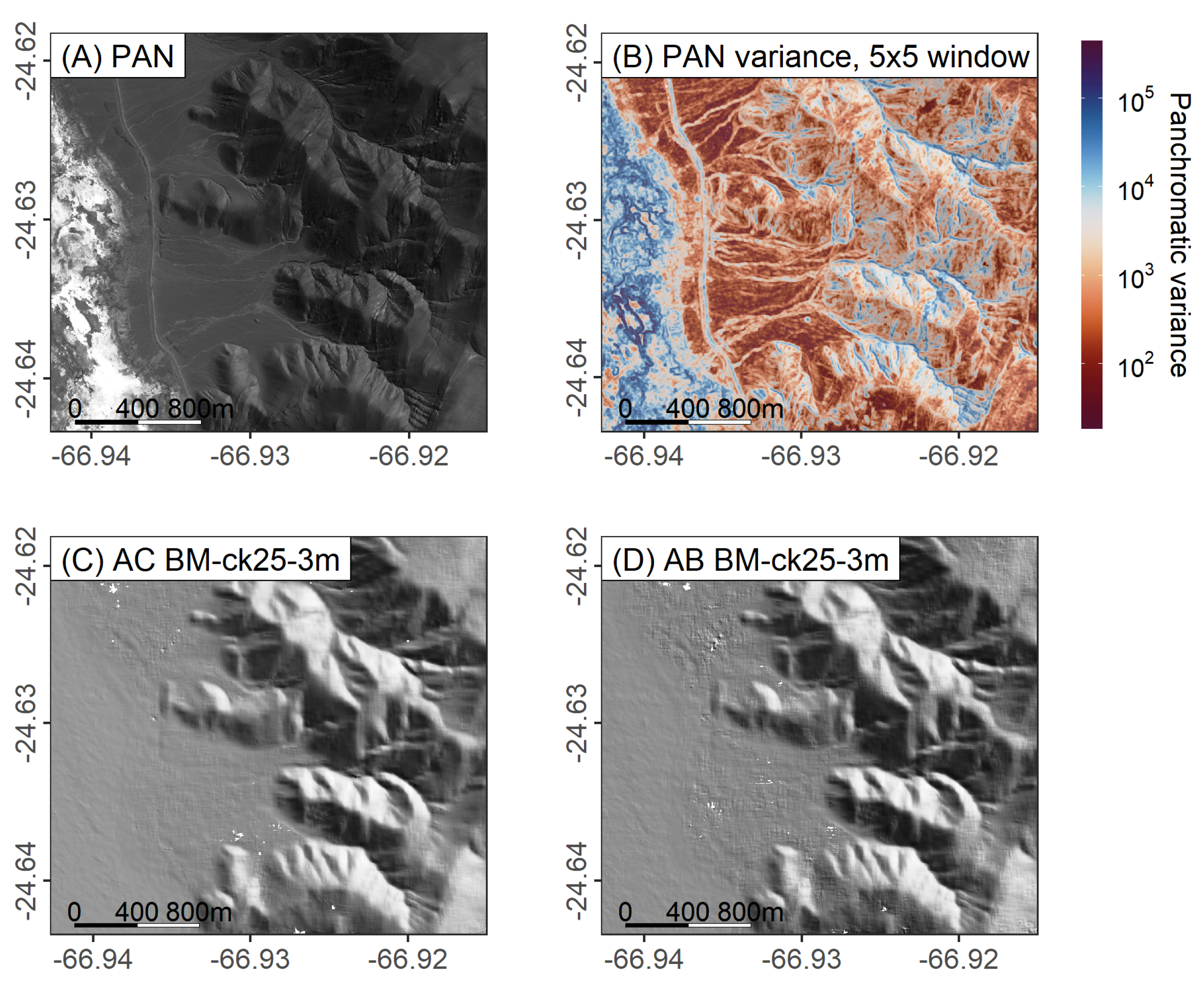
4.3.1. AC versus Neighboring Pairs
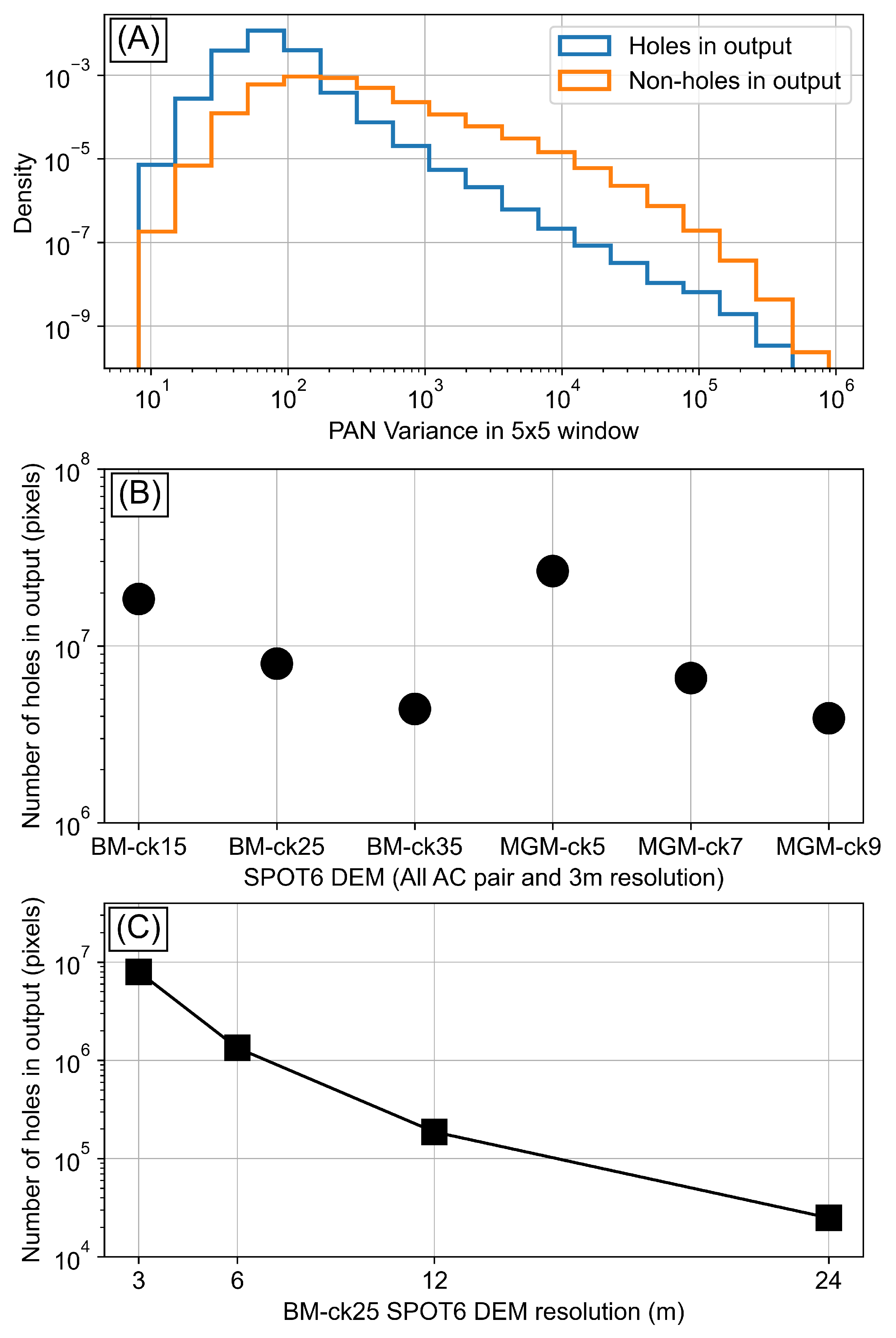
4.3.2. Where Image Correlation Fails
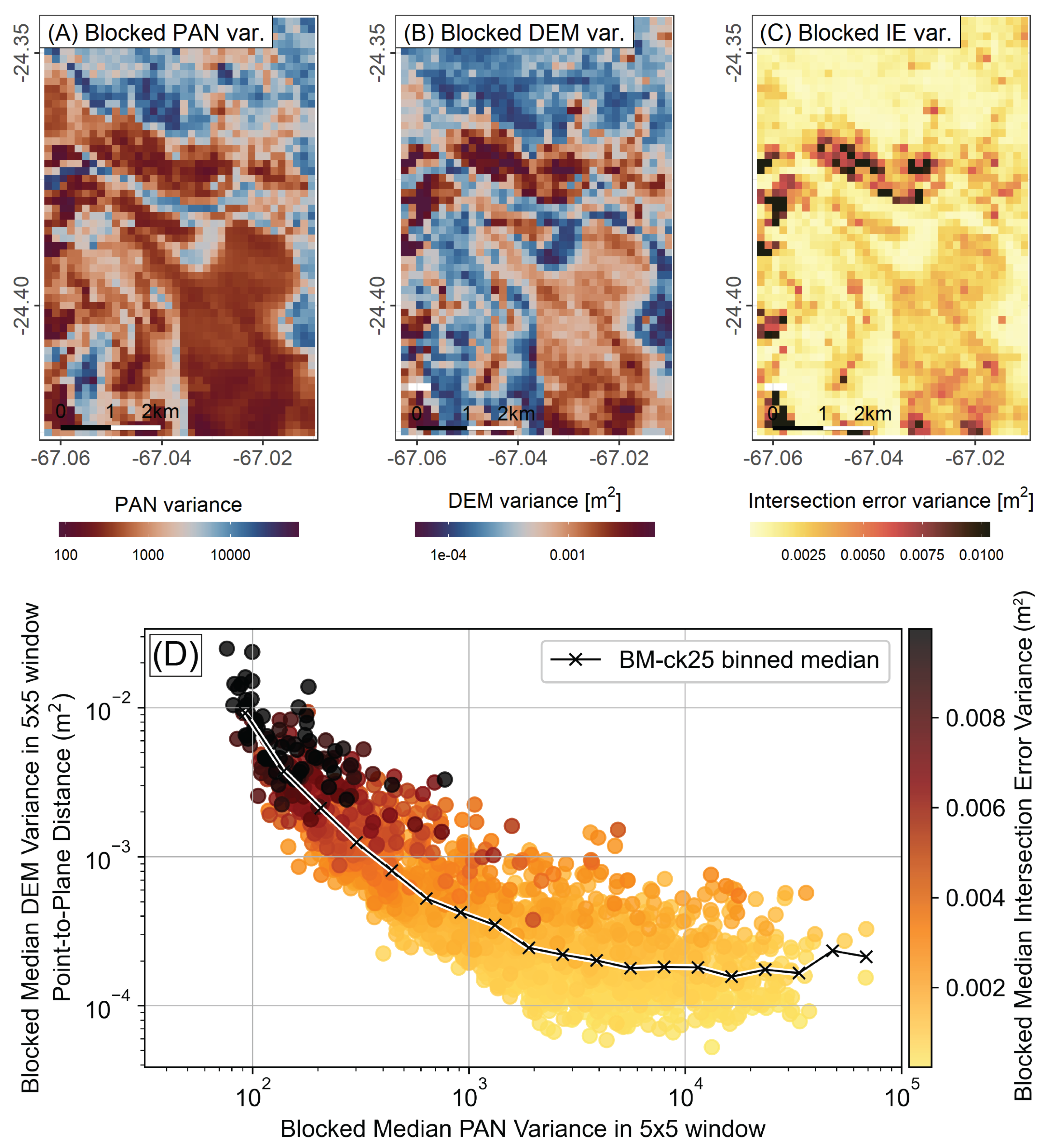
4.3.3. Flat-Area DEM Variance versus Image Texture
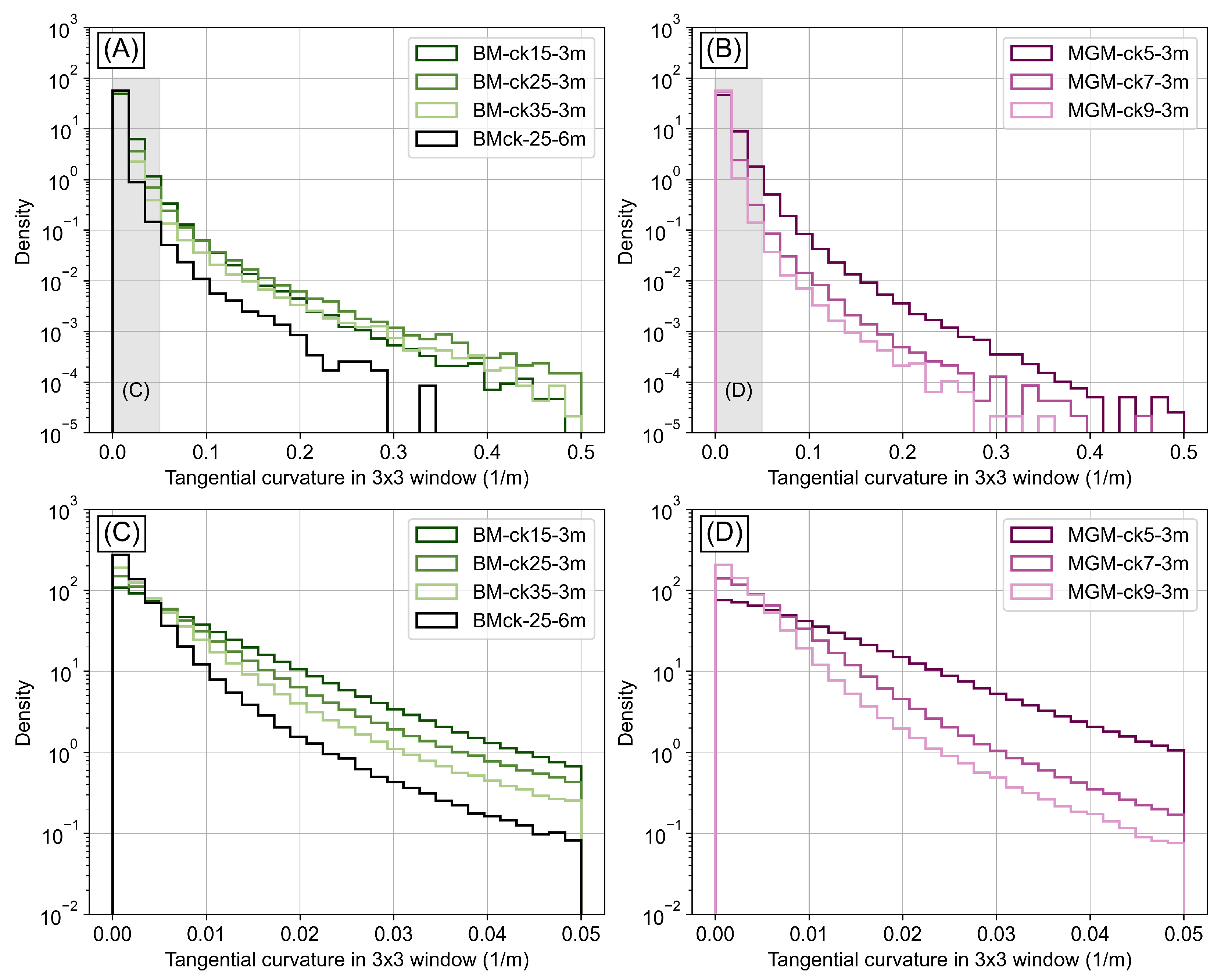
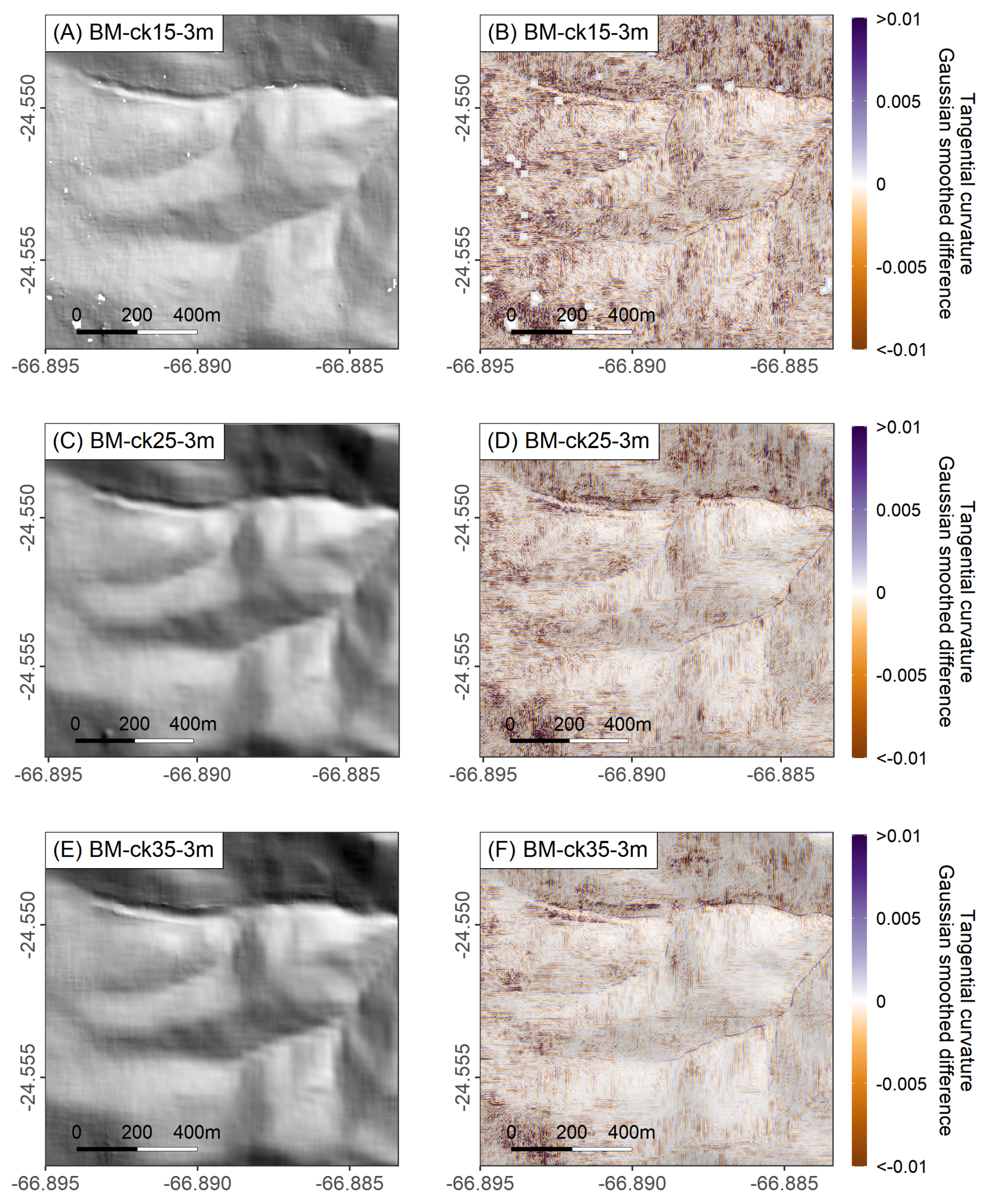
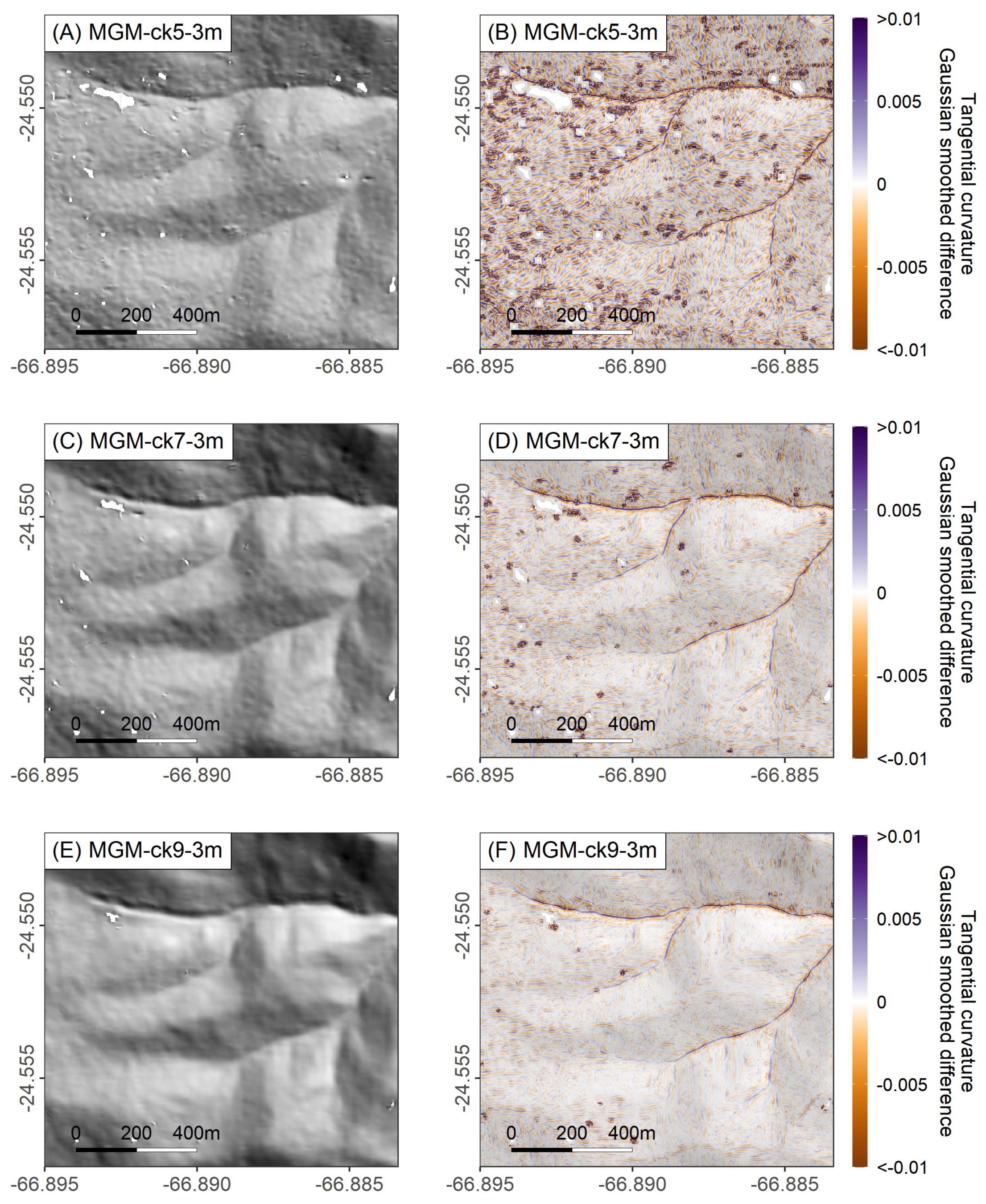
4.4. Curvature Distributions
5. Discussion
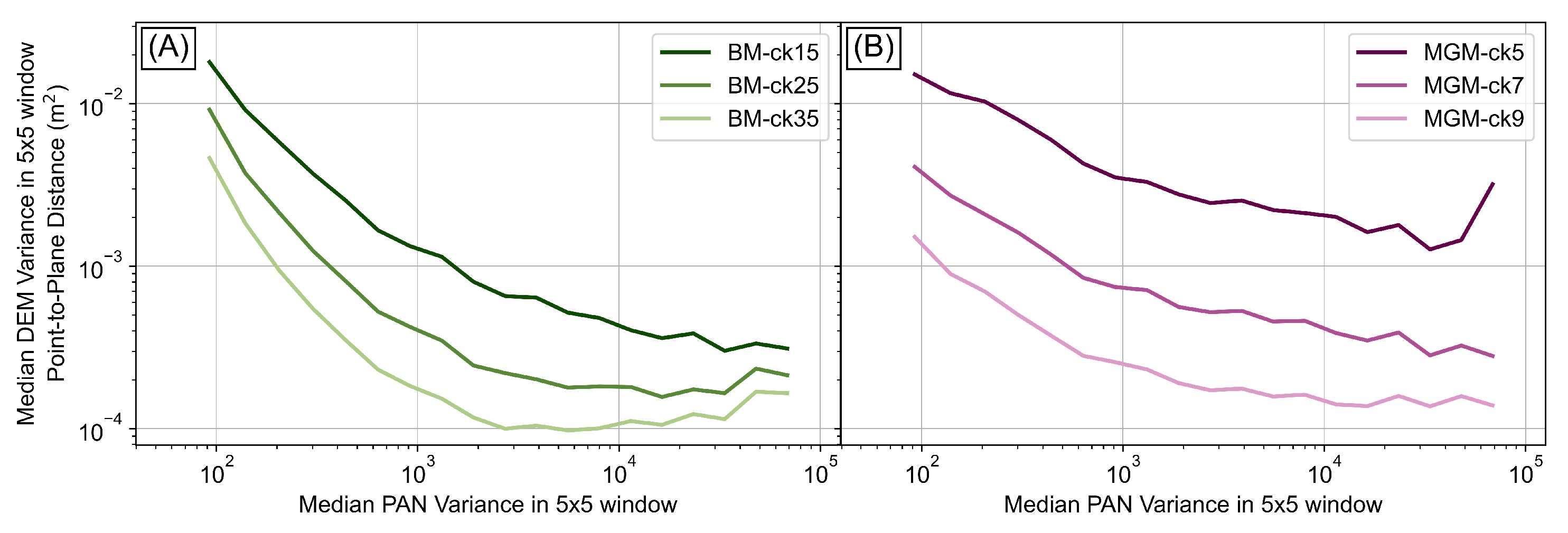
5.1. Predicting DEM Quality from Image Texture
5.2. Implications for Geomorphic Analysis
5.3. Best Practices for Generating DEMs in Ames for SPOT6/7
6. Conclusions
- The unique salar (salt flat) in our study area allowed us to explore the relationship between image texture and DEM uncertainty. Higher image texture (measured by local panchromatic variance) improved DEM quality due to better stereo matching up to a certain point (∼10 panchromatic variance), beyond which other factors such as satellite view geometry and sensor biases may dominate.
- Compared to the Block Matching stereo-correlation algorithm, the More-Global Matching algorithm (with the ternary census cost function) preserved smaller scale features using smaller correlation kernels and had improved matching in low-texture areas.
- Larger correlation kernels improved matching (less holes) at the cost of smoothing the landscape. Increasing the kernel size will lead to more reliable matches and the ability to output a DEM at 2× the input image resolution and should be preferred in geomorphic applications to a naive smoothing by downsampling the final DEM to 4× the input image resolution.
- Using only the AC image pair (widest view-angle difference) for stereo-DEM generation produced higher-quality results than using the neighboring (AB, BC) pairs with the nadir scene (B). Mixing them (e.g., by median blending) likely degrades overall quality. However, the neighboring pairs with the nadir image are useful for filling holes (e.g., in steep canyons with occluded views). Images with optimal, wide viewing angles (even if they are from different dates) are therefore recommended for high-quality DEM generation.
- The higher curvature that we found using a smaller correlation kernel available in the More-Global Matching algorithm (9 × 9 pixels) likely demonstrates the preservation of landscape sharpness. Smaller kernels may also preserve even finer features, but this comes at the expense of more noise on hillslopes and other low-texture areas.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taud, H.; Parrot, J.F.; Alvarez, R. DEM generation by contour line dilation. Comput. Geosci. 1999, 25, 775–783. [Google Scholar] [CrossRef]
- Polidori, L.; El Hage, M. Digital Elevation Model Quality Assessment Methods: A Critical Review. Remote Sens. 2020, 12, 3522. [Google Scholar] [CrossRef]
- Hugonnet, R.; Brun, F.; Berthier, E.; Dehecq, A.; Mannerfelt, E.S.; Eckert, N.; Farinotti, D. Uncertainty Analysis of Digital Elevation Models by Spatial Inference From Stable Terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6456–6472. [Google Scholar] [CrossRef]
- Bagnardi, M.; González, P.J.; Hooper, A. High-resolution digital elevation model from tri-stereo Pleiades-1 satellite imagery for lava flow volume estimates at Fogo Volcano. Geophys. Res. Lett. 2016, 43, 6267–6275. [Google Scholar] [CrossRef]
- Bessette-Kirton, E.K.; Coe, J.A.; Zhou, W. Using Stereo Satellite Imagery to Account for Ablation, Entrainment, and Compaction in Volume Calculations for Rock Avalanches on Glaciers: Application to the 2016 Lamplugh Rock Avalanche in Glacier Bay National Park, Alaska. J. Geophys. Res. Earth Surf. 2018, 123, 622–641. [Google Scholar] [CrossRef]
- Wang, S.; Ren, Z.; Wu, C.; Lei, Q.; Gong, W.; Ou, Q.; Zhang, H.; Ren, G.; Li, C. DEM generation from Worldview-2 stereo imagery and vertical accuracy assessment for its application in active tectonics. Geomorphology 2019, 336, 107–118. [Google Scholar] [CrossRef]
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A Systematic, Regional Assessment of High Mountain Asia Glacier Mass Balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar] [CrossRef]
- Brasington, J.; Vericat, D.; Rychkov, I. Modeling river bed morphology, roughness, and surface sedimentology using high resolution terrestrial laser scanning. Water Resour. Res. 2012, 48, W11519. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-based surface reconstruction in geomorphometry—Merits, limits and developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Purinton, B.; Bookhagen, B. Validation of digital elevation models (DEMs) and comparison of geomorphic metrics on the southern Central Andean Plateau. Earth Surf. Dyn. 2017, 5, 211–237. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Bates, P.D. The Need for a High-Accuracy, Open-Access Global DEM. Front. Earth Sci. 2018, 6, 225. [Google Scholar] [CrossRef]
- Smith, T.; Rheinwalt, A.; Bookhagen, B. Determining the optimal grid resolution for topographic analysis on an airborne lidar dataset. Earth Surf. Dyn. 2019, 7, 475–489. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. The Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Girod, L.; Nuth, C.; Kääb, A.; McNabb, R.; Galland, O. MMASTER: Improved ASTER DEMs for Elevation Change Monitoring. Remote Sens. 2017, 9, 704. [Google Scholar] [CrossRef]
- Purinton, B.; Bookhagen, B. Beyond Vertical Point Accuracy: Assessing Inter-pixel Consistency in 30 m Global DEMs for the Arid Central Andes. Front. Earth Sci. 2021, 9, 758606. [Google Scholar] [CrossRef]
- Ouimet, W.B.; Whipple, K.X.; Granger, D.E. Beyond threshold hillslopes: Channel adjustment to base-level fall in tectonically active mountain ranges. Geology 2009, 37, 579–582. [Google Scholar] [CrossRef]
- Bookhagen, B.; Strecker, M.R. Spatiotemporal trends in erosion rates across a pronounced rainfall gradient: Examples from the southern Central Andes. Earth Planet. Sci. Lett. 2012, 327–328, 97–110. [Google Scholar] [CrossRef]
- Schwanghart, W.; Scherler, D. Bumps in river profiles: Uncertainty assessment and smoothing using quantile regression techniques. Earth Surf. Dyn. 2017, 5, 821–839. [Google Scholar] [CrossRef]
- Hawker, L.; Bates, P.; Neal, J.; Rougier, J. Perspectives on Digital Elevation Model (DEM) Simulation for Flood Modeling in the Absence of a High-Accuracy Open Access Global DEM. Front. Earth Sci. 2018, 6, 233. [Google Scholar] [CrossRef]
- Gailleton, B.; Mudd, S.M.; Clubb, F.J.; Peifer, D.; Hurst, M.D. A segmentation approach for the reproducible extraction and quantification of knickpoints from river long profiles. Earth Surf. Dyn. 2019, 7, 211–230. [Google Scholar] [CrossRef]
- Mueting, A.; Bookhagen, B.; Strecker, M.R. Identification of Debris-Flow Channels Using High-Resolution Topographic Data: A Case Study in the Quebrada del Toro, NW Argentina. J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006330. [Google Scholar] [CrossRef]
- Zhang, K.; Sun, J.; Snavely, N. Leveraging Vision Reconstruction Pipelines for Satellite Imagery. arXiv 2019, arXiv:1910.02989. [Google Scholar] [CrossRef]
- Shean, D.E.; Alexandrov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.R.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high-resolution commercial stereo satellite imagery. ISPRS J. Photogramm. Remote Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef]
- Beyer, R.A.; Alexandrov, O.; McMichael, S. The Ames Stereo Pipeline: NASA’s Open Source Software for Deriving and Processing Terrain Data. Earth Space Sci. 2018, 5, 537–548. [Google Scholar] [CrossRef]
- Beyer, R.; Alexandrov, O.; McMichael, S.; Broxton, M.; Lundy, M.; Husmann, K.; Edwards, L.; Nefian, A.; Smith, B.; Shean, D.; et al. NeoGeographyToolkit/StereoPipeline 3.0.0. 2021. Available online: https://zenodo.org/record/5140581#.Y6FiCBVBy70 (accessed on 28 September 2022).
- Crespi, M.; De Vendictis, L. A Procedure for High Resolution Satellite Imagery Quality Assessment. Sensors 2009, 9, 3289–3313. [Google Scholar] [CrossRef]
- Poli, D.; Remondino, F.; Angiuli, E.; Agugiaro, G. Radiometric and geometric evaluation of GeoEye-1, WorldView-2 and Pléiades-1A stereo images for 3D information extraction. ISPRS J. Photogramm. Remote Sens. 2015, 100, 35–47. [Google Scholar] [CrossRef]
- Allmendinger, R.W.; Jordan, T.E.; Kay, S.M.; Isacks, B.L. The evolution of the altiplano-puna plateau of the central andes. Annu. Rev. Earth Planet. Sci. 1997, 25, 139–174. [Google Scholar] [CrossRef]
- Strecker, M.; Alonso, R.; Bookhagen, B.; Carrapa, B.; Hilley, G.; Sobel, E.; Trauth, M. Tectonics and Climate of the Southern Central Andes. Annu. Rev. Earth Planet. Sci. 2007, 35, 747–787. [Google Scholar] [CrossRef]
- Bookhagen, B.; Strecker, M.R. Orographic barriers, high-resolution TRMM rainfall, and relief variations along the eastern Andes. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Luna, L.V.; Bookhagen, B.; Niedermann, S.; Rugel, G.; Scharf, A.; Merchel, S. Glacial chronology and production rate cross-calibration of five cosmogenic nuclide and mineral systems from the southern Central Andean Plateau. Earth Planet. Sci. Lett. 2018, 500, 242–253. [Google Scholar] [CrossRef]
- Leister-Taylor, V.; Jacob, P.; Schrader, H.; Kahabka, H. Copernicus Digital Elevation Model Product Handbook; Technical Report GEO.2018-1988-2; AIRBUS: Potsdam, Germany, 2020. [Google Scholar]
- AIRBUS. SPOT Imagery User Guide; Technical Report; AIRBUS and ESA: 2022. Available online: https://earth.esa.int/eogateway/documents/20142/37627/SPOT-6-7-imagery-user-guide.pdf (accessed on 28 September 2022).
- Dehecq, A.; Gardner, A.S.; Alexandrov, O.; McMichael, S.; Hugonnet, R.; Shean, D.; Marty, M. Automated Processing of Declassified KH-9 Hexagon Satellite Images for Global Elevation Change Analysis Since the 1970s. Front. Earth Sci. 2020, 8, 566802. [Google Scholar] [CrossRef]
- Bhushan, S.; Shean, D.; Alexandrov, O.; Henderson, S. Automated digital elevation model (DEM) generation from very-high-resolution Planet SkySat triplet stereo and video imagery. ISPRS J. Photogramm. Remote Sens. 2021, 173, 151–165. [Google Scholar] [CrossRef]
- Huang, Y.W.; Chen, C.Y.; Tsai, C.H.; Shen, C.F.; Chen, L.G. Survey on block matching motion estimation algorithms and architectures with new results. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2006, 42, 297–320. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef]
- Broxton, M.J.; Nefian, A.V.; Moratto, Z.; Kim, T.; Lundy, M.; Segal, A.V. 3D Lunar Terrain Reconstruction from Apollo Images. In International Symposium on Visual Computing; Bebis, G., Boyle, R., Parvin, B., Koracin, D., Kuno, Y., Wang, J., Wang, J.X., Wang, J., Pajarola, R., Lindstrom, P., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 710–719. [Google Scholar]
- Nefian, A.V.; Husmann, K.; Broxton, M.; To, V.; Lundy, M.; Hancher, M.D. A bayesian formulation for sub-pixel refinement in stereo orbital imagery. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 2361–2364. [Google Scholar] [CrossRef]
- Facciolo, G.; Franchis, C.D.; Meinhardt, E. MGM: A Significantly More Global Matching for Stereovision. In British Machine Vision Conference 2015 (BMVC 2015); BMVA Press: Swansea, UK, 2015. [Google Scholar] [CrossRef]
- Hu, H.; Chen, C.; Wu, B.; Yang, X.; Zhu, Q.; Ding, Y. Texture-aware dense image matching using ternary census transform. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-3, 59–66. [Google Scholar] [CrossRef]
- Grieve, S.W.D.; Mudd, S.M.; Milodowski, D.T.; Clubb, F.J.; Furbish, D.J. How does grid-resolution modulate the topographic expression of geomorphic processes? Earth Surf. Dyn. 2016, 4, 627–653. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Trevisani, S.; Rocca, M. MAD: Robust image texture analysis for applications in high resolution geomorphometry. Comput. Geosci. 2015, 81, 78–92. [Google Scholar] [CrossRef]
- Becek, K. Assessing global digital elevation models using the runway method: The advanced spaceborne thermal emission and reflection radiometer versus the shuttle radar topography mission case. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4823–4831. [Google Scholar] [CrossRef]
- Mudd, S.M.; Clubb, F.J.; Grieve, S.W.D.; Milodowski, D.T.; Hurst, M.D.; Gailleton, B.; Valters, D.A. LSDTopoTools2. 2019. Available online: https://zenodo.org/record/3245041#.Y6FeVhVBy70 (accessed on 28 September 2022).
- Minár, J.; Evans, I.S.; Jenčo, M. A comprehensive system of definitions of land surface (topographic) curvatures, with implications for their application in geoscience modelling and prediction. Earth-Sci. Rev. 2020, 211, 103414. [Google Scholar] [CrossRef]
- Hurst, M.D.; Mudd, S.M.; Walcott, R.; Attal, M.; Yoo, K. Using hilltop curvature to derive the spatial distribution of erosion rates. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Grieve, S.W.; Mudd, S.M.; Hurst, M.D. How long is a hillslope? Earth Surf. Process. Landf. 2016, 41, 1039–1054. [Google Scholar] [CrossRef]
- Grieve, S.W.D.; Mudd, S.M.; Hurst, M.D.; Milodowski, D.T. A nondimensional framework for exploring the relief structure of landscapes. Earth Surf. Dyn. 2016, 4, 309–325. [Google Scholar] [CrossRef]
- Clubb, F.J.; Mudd, S.M.; Milodowski, D.T.; Hurst, M.D.; Slater, L.J. Objective extraction of channel heads from high-resolution topographic data. Water Resour. Res. 2014, 50, 4283–4304. [Google Scholar] [CrossRef]
- Clubb, F.J.; Mudd, S.M.; Attal, M.; Milodowski, D.T.; Grieve, S.W. The relationship between drainage density, erosion rate, and hilltop curvature: Implications for sediment transport processes. J. Geophys. Res. Earth Surf. 2016, 121, 1724–1745. [Google Scholar] [CrossRef]
- Clubb, F.J.; Bookhagen, B.; Rheinwalt, A. Clustering River Profiles to Classify Geomorphic Domains. J. Geophys. Res. Earth Surf. 2019, 124, 1417–1439. [Google Scholar] [CrossRef]
- Rheinwalt, A.; Goswami, B.; Bookhagen, B. A Network-Based Flow Accumulation Algorithm for Point Clouds: Facet-Flow Networks (FFNs). J. Geophys. Res. Earth Surf. 2019, 124, 2013–2033. [Google Scholar] [CrossRef]
- Atwood, A.; West, A.J. Evaluation of high-resolution DEMs from satellite imagery for geomorphic applications: A case study using the SETSM algorithm. Earth Surf. Process. Landf. 2022, 47, 706–722. [Google Scholar] [CrossRef]
- Noh, M.J.; Howat, I.M. Automated stereo-photogrammetric DEM generation at high latitudes: Surface Extraction with TIN-based Search-space Minimization (SETSM) validation and demonstration over glaciated regions. GISci. Remote Sens. 2015, 52, 198–217. [Google Scholar] [CrossRef]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Facciolo, G.; De Franchis, C.; Meinhardt-Llopis, E. Automatic 3D Reconstruction from Multi-date Satellite Images. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1542–1551. [Google Scholar] [CrossRef]
- Aati, S.; Avouac, J.P. Optimization of Optical Image Geometric Modeling, Application to Topography Extraction and Topographic Change Measurements Using PlanetScope and SkySat Imagery. Remote Sens. 2020, 12, 3418. [Google Scholar] [CrossRef]
- Lastilla, L.; Belloni, V.; Ravanelli, R.; Crespi, M. DSM Generation from Single and Cross-Sensor Multi-View Satellite Images Using the New Agisoft Metashape: The Case Studies of Trento and Matera (Italy). Remote Sens. 2021, 13, 593. [Google Scholar] [CrossRef]
- Agisoft. Agisoft Metashape Professional. 2022. Available online: https://www.geoscan.aero/en/software/agisoft/metashape_pro (accessed on 28 September 2022).




| SPOT6 DEM Name | Correlation Algorithm | Cost Function | CK/SK Sizes |
|---|---|---|---|
| BM-ck15 | BM | NCC | 15 × 15/25 × 25 |
| BM-ck25 | BM | NCC | 25 × 25/35 × 35 |
| BM-ck35 | BM | NCC | 35 × 35/45 × 45 |
| MGM-ck5 | MGM | Ternary Census | 5 × 5/9 × 9 |
| MGM-ck7 | MGM | Ternary Census | 7 × 7/15 × 15 |
| MGM-ck9 | MGM | Ternary Census | 9 × 9/21 × 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Purinton, B.; Mueting, A.; Bookhagen, B. Image Texture as Quality Indicator for Optical DEM Generation: Geomorphic Applications in the Arid Central Andes. Remote Sens. 2023, 15, 85. https://doi.org/10.3390/rs15010085
Purinton B, Mueting A, Bookhagen B. Image Texture as Quality Indicator for Optical DEM Generation: Geomorphic Applications in the Arid Central Andes. Remote Sensing. 2023; 15(1):85. https://doi.org/10.3390/rs15010085
Chicago/Turabian StylePurinton, Benjamin, Ariane Mueting, and Bodo Bookhagen. 2023. "Image Texture as Quality Indicator for Optical DEM Generation: Geomorphic Applications in the Arid Central Andes" Remote Sensing 15, no. 1: 85. https://doi.org/10.3390/rs15010085
APA StylePurinton, B., Mueting, A., & Bookhagen, B. (2023). Image Texture as Quality Indicator for Optical DEM Generation: Geomorphic Applications in the Arid Central Andes. Remote Sensing, 15(1), 85. https://doi.org/10.3390/rs15010085






