A Parallel Principal Skewness Analysis and Its Application in Radar Target Detection
Abstract
1. Introduction
2. Background
2.1. Preliminaries
2.2. PSA Algorithm
3. Parallel PSA Algorithm
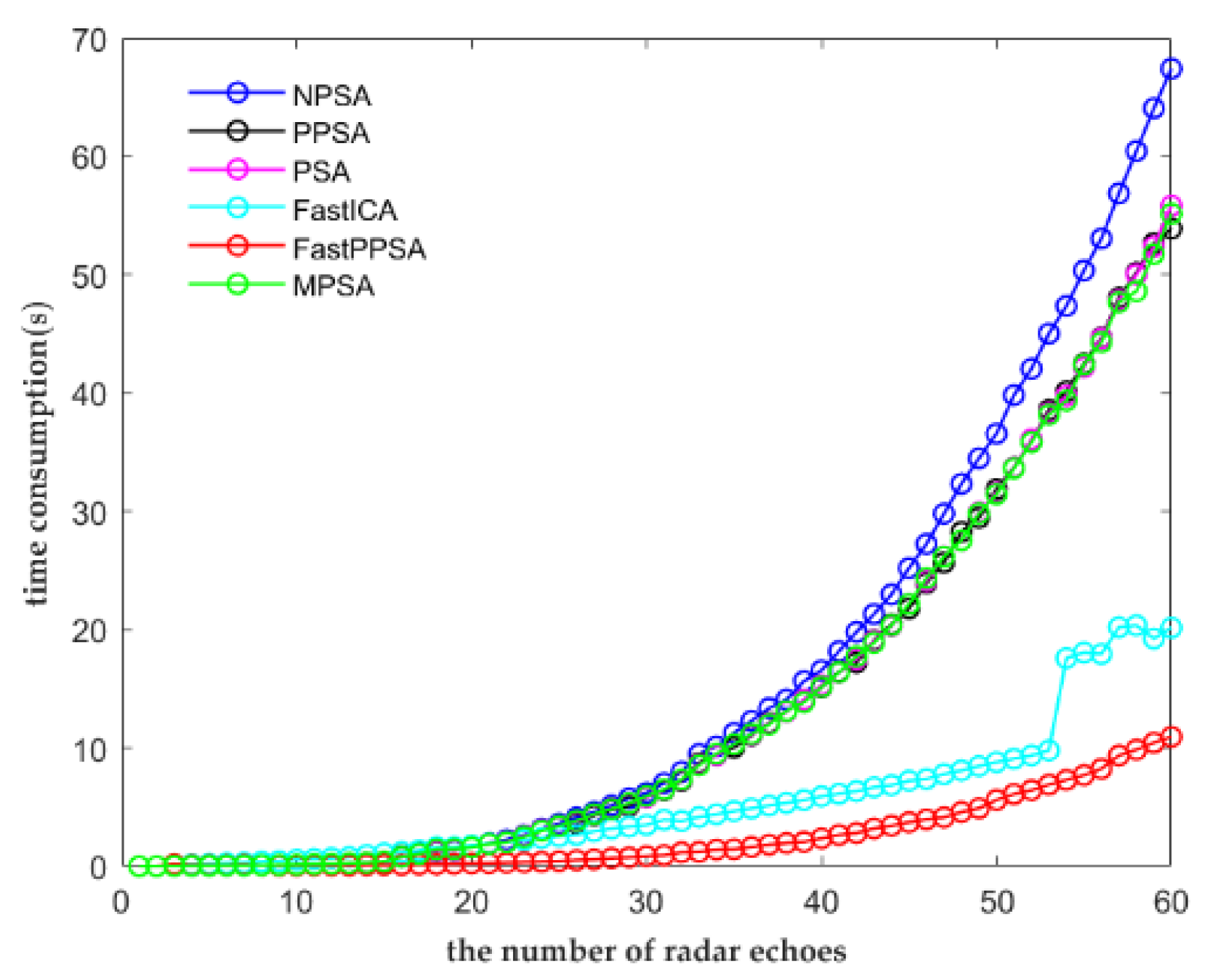
3.1. Limitations of Existing PSA Algorithms
3.2. PPSA
| Algorithm 1 PPSA |
| Input: Input data . |
| Output: output transformation matrix , . |
| 1: whiten the data to obtain . |
| 2: calculate the co-skewness tensor according to (1). |
| 3: calculate all eigenvectors of slices of tensor (), denoted as |
| % main loop: % |
| 4: |
| 5: k = 0 |
| 6: |
| 7: while stop conditions are not meet do |
| 8: |
| 9: |
| 10: end while |
| 11: |
| 12: end for |
| % output % |
| 13: ;// is the final principal skewness transformation matrix, and is the transformed image. |
3.3. Complexity Analysis
4. Experiment
4.1. Experiment 1: Blind Image Separation
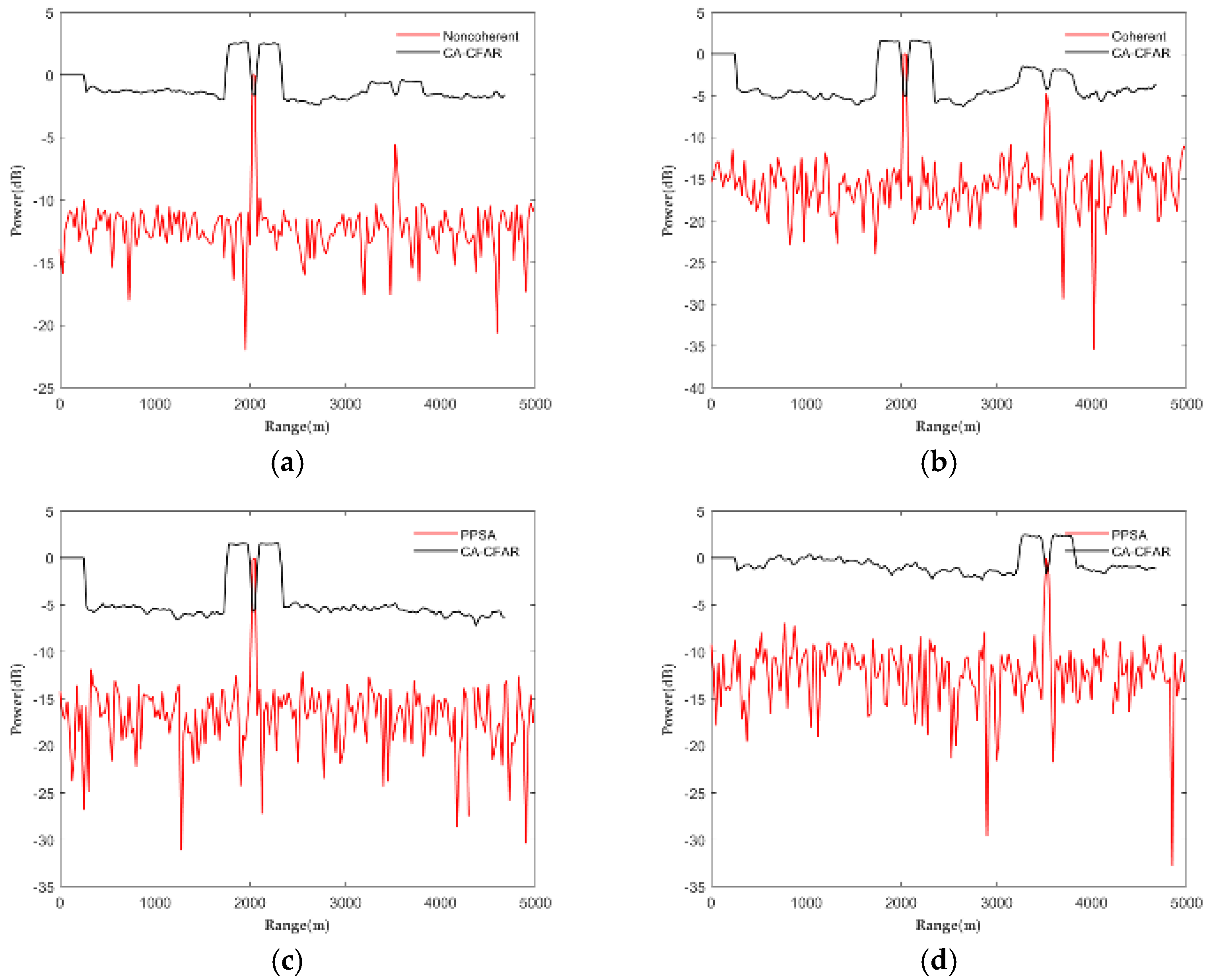
4.2. Experiment 2: Moving Target Detection under Low SNR
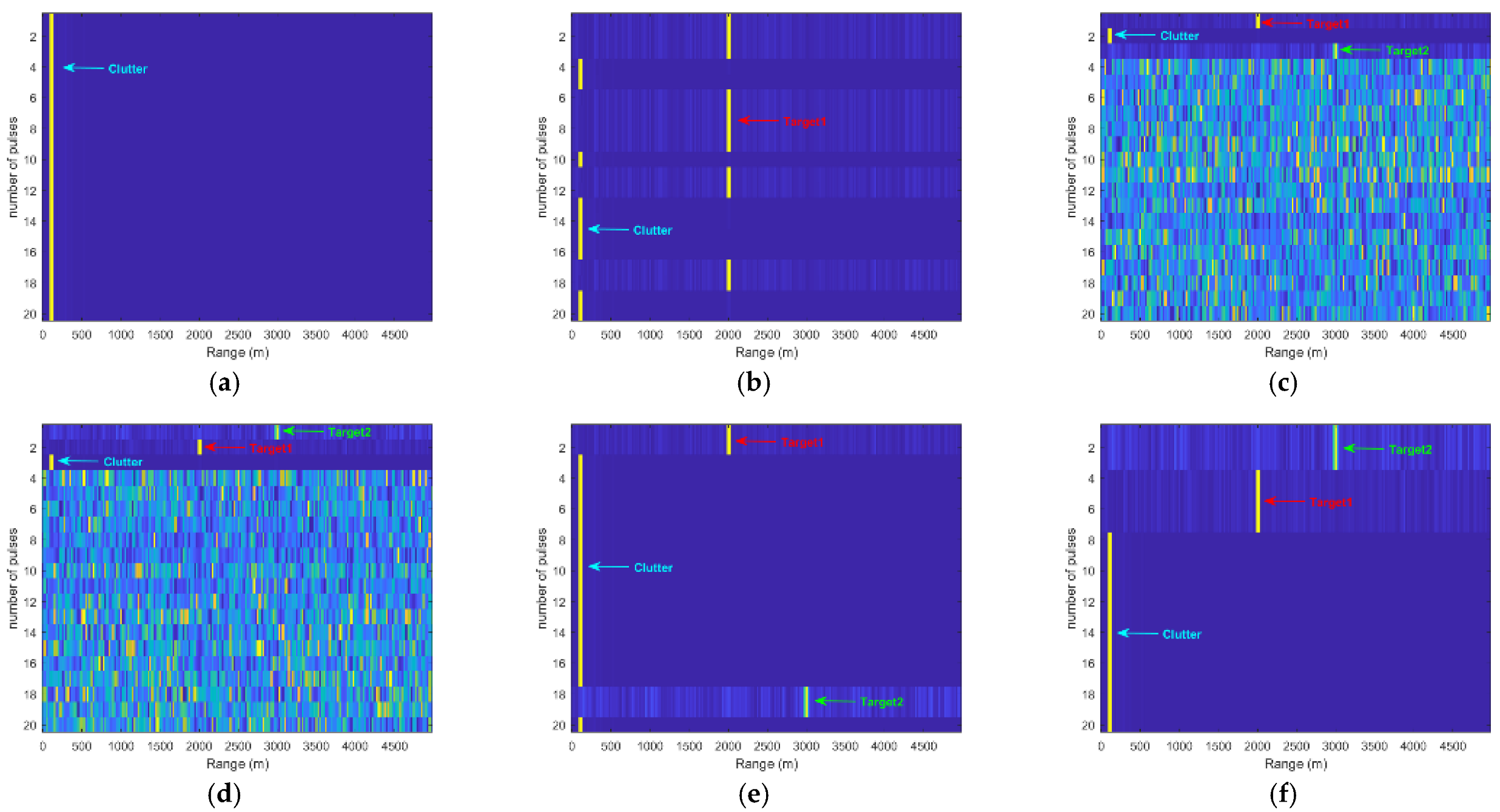
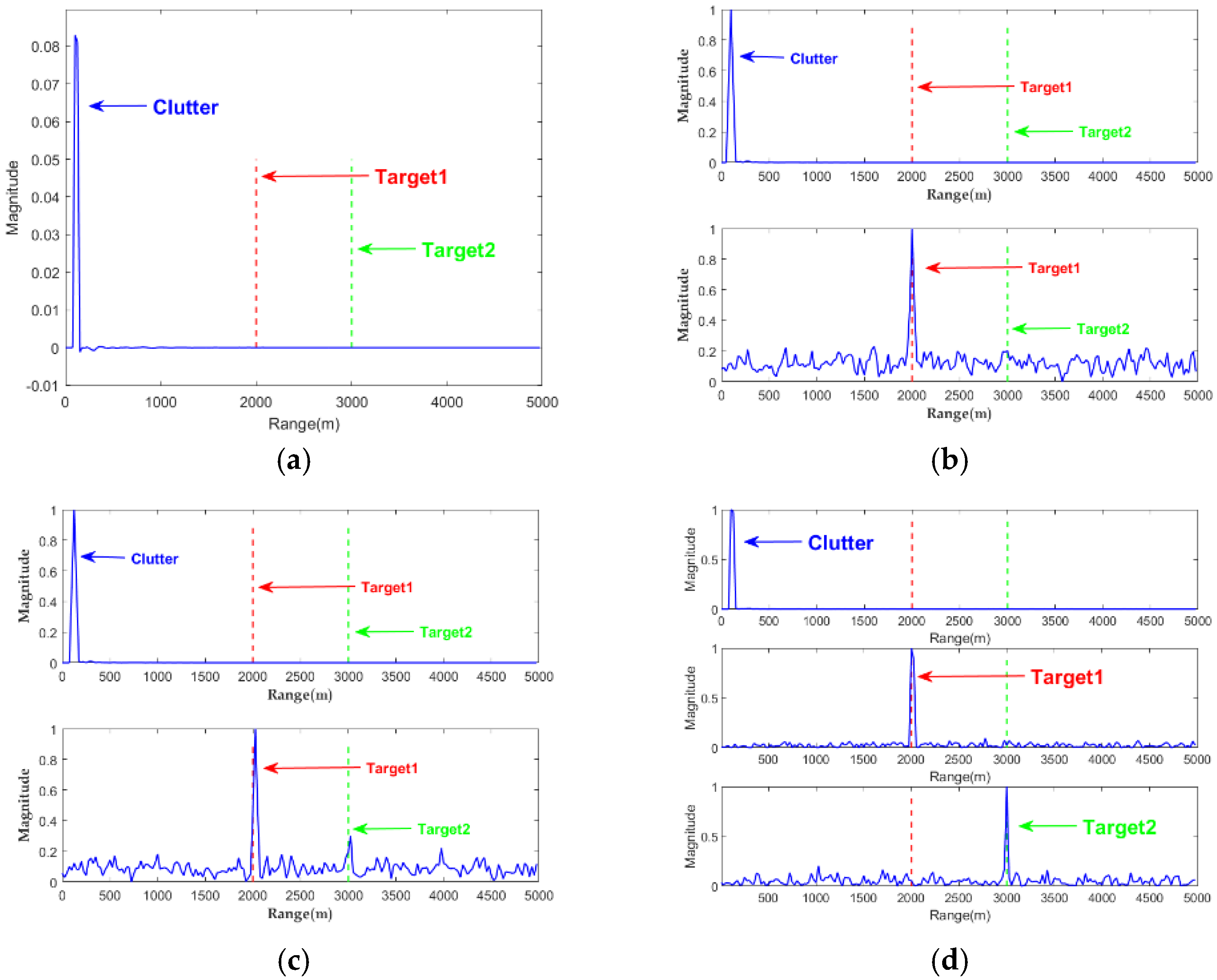
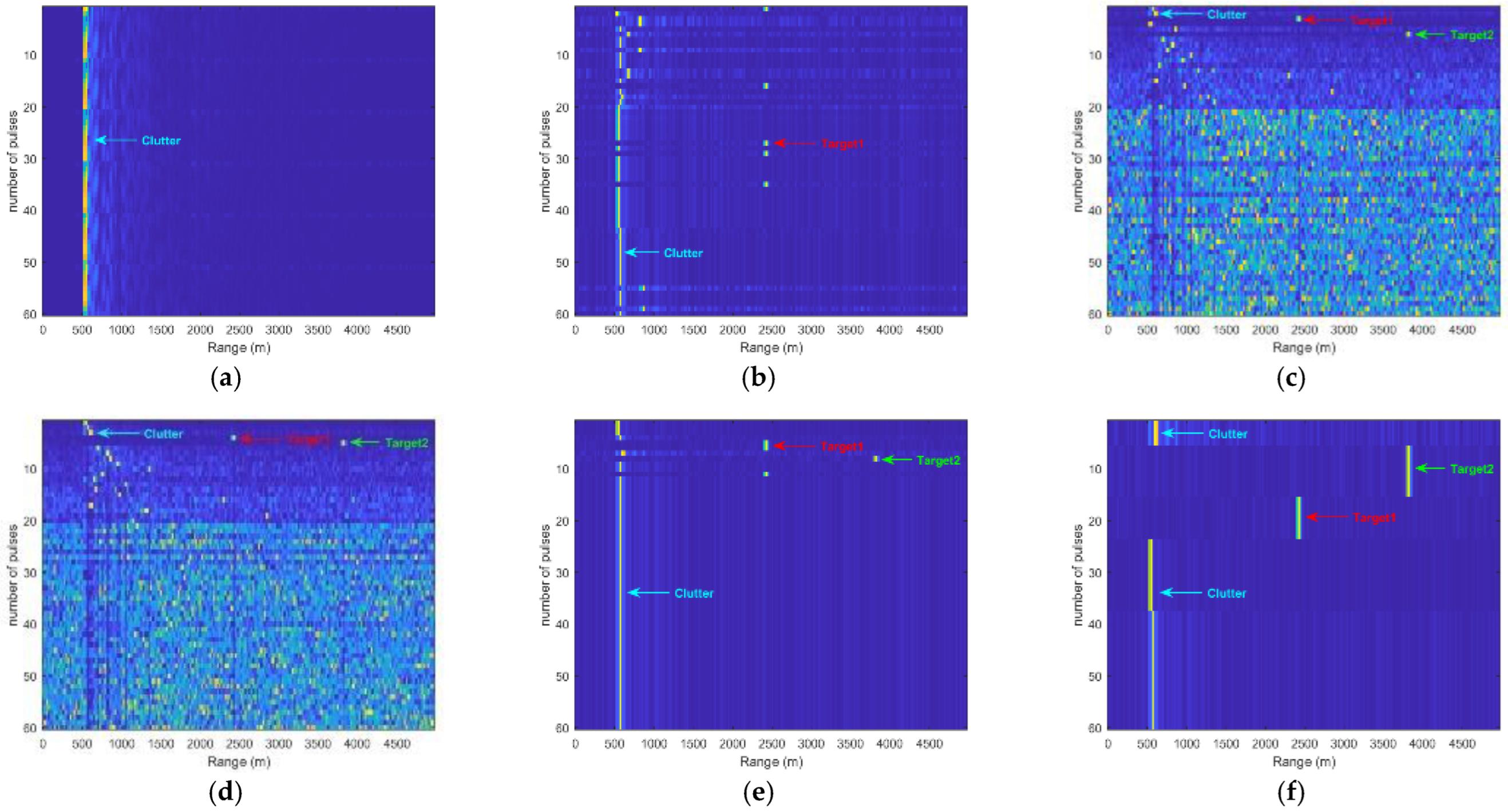
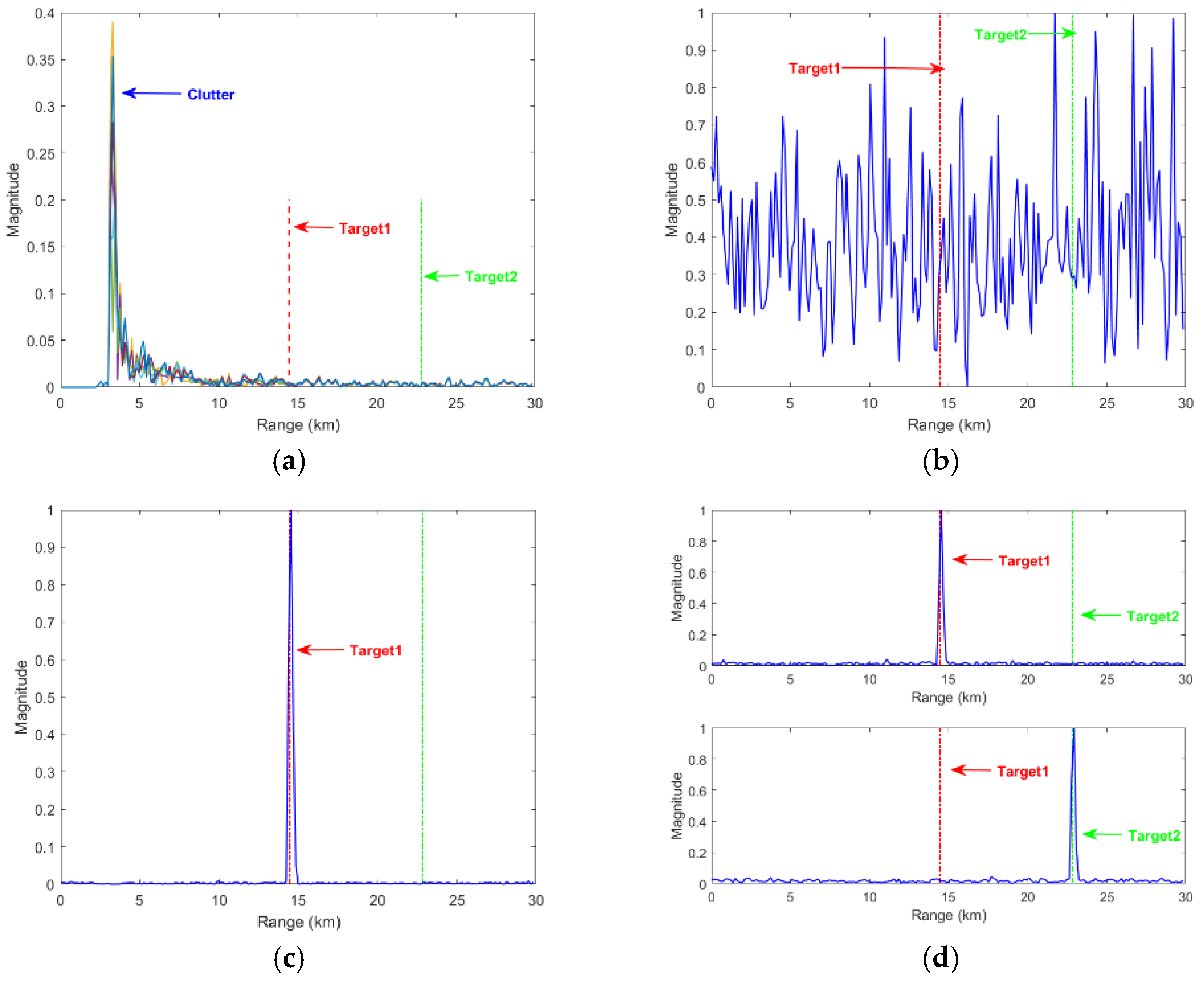
4.3. Experiment 2: Single-Channel Complex Background Micro-Moving Target Detection
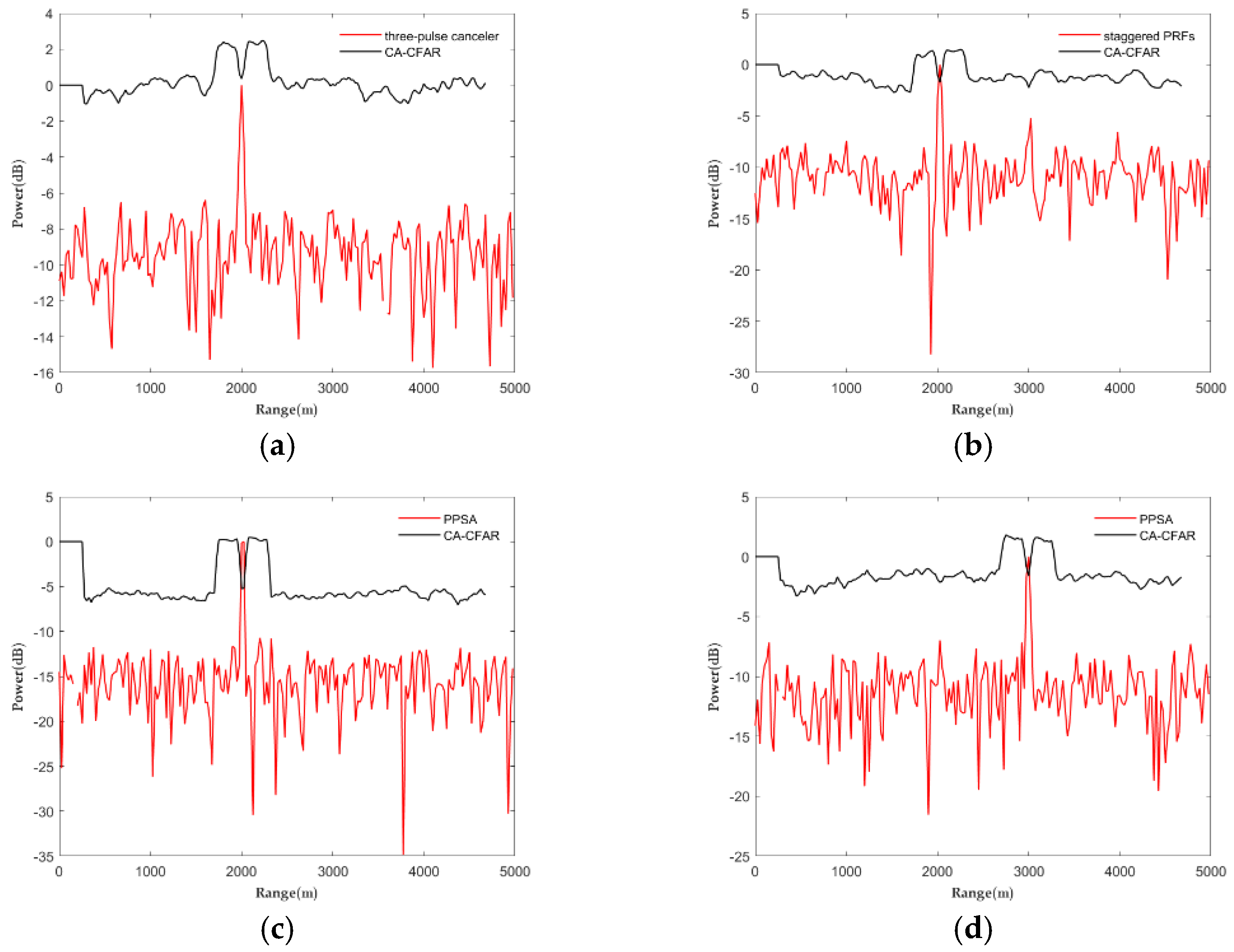
4.4. Experiment 3: Detection of Small Targets in Multi-Channel Complex Background
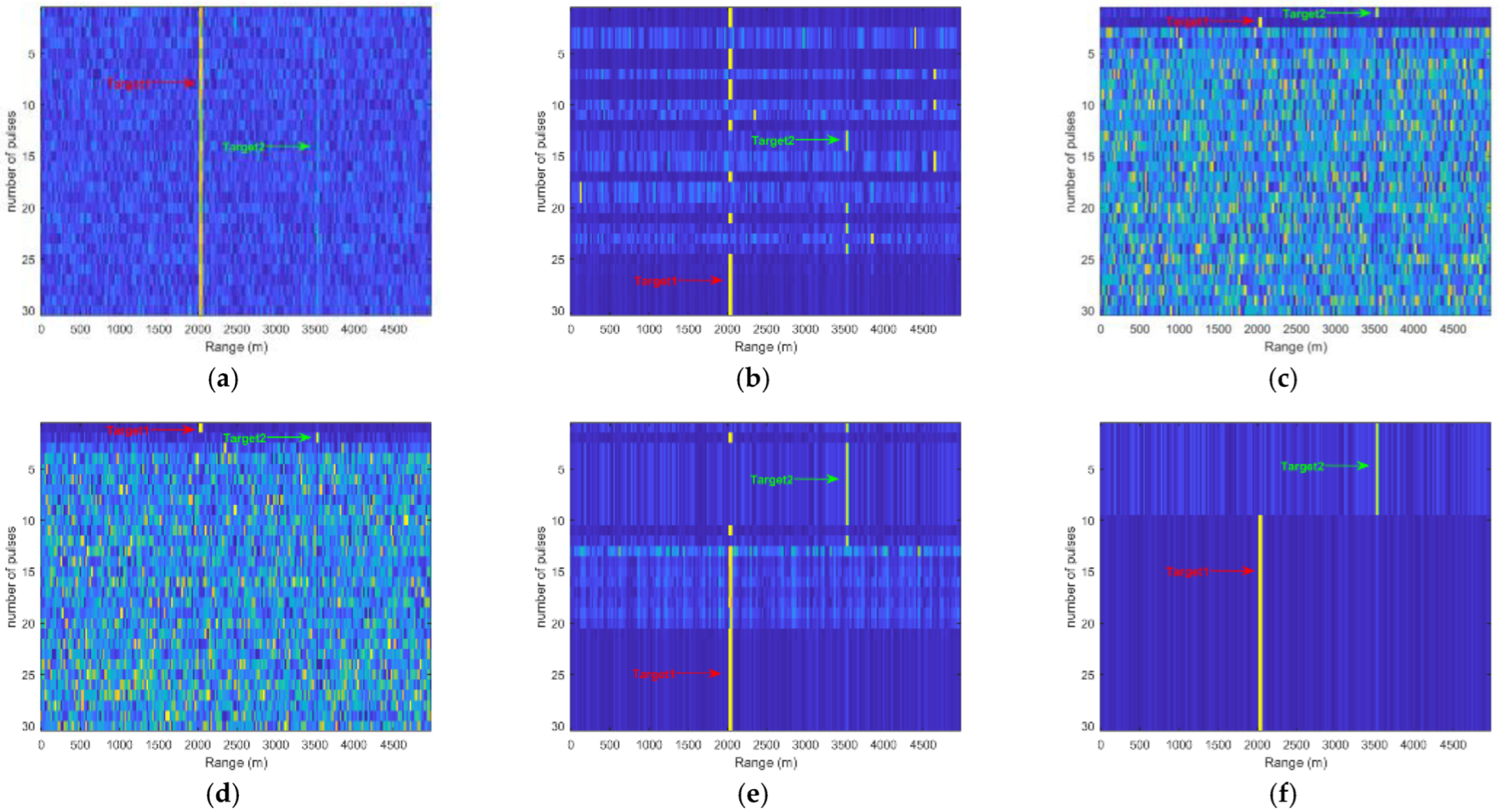
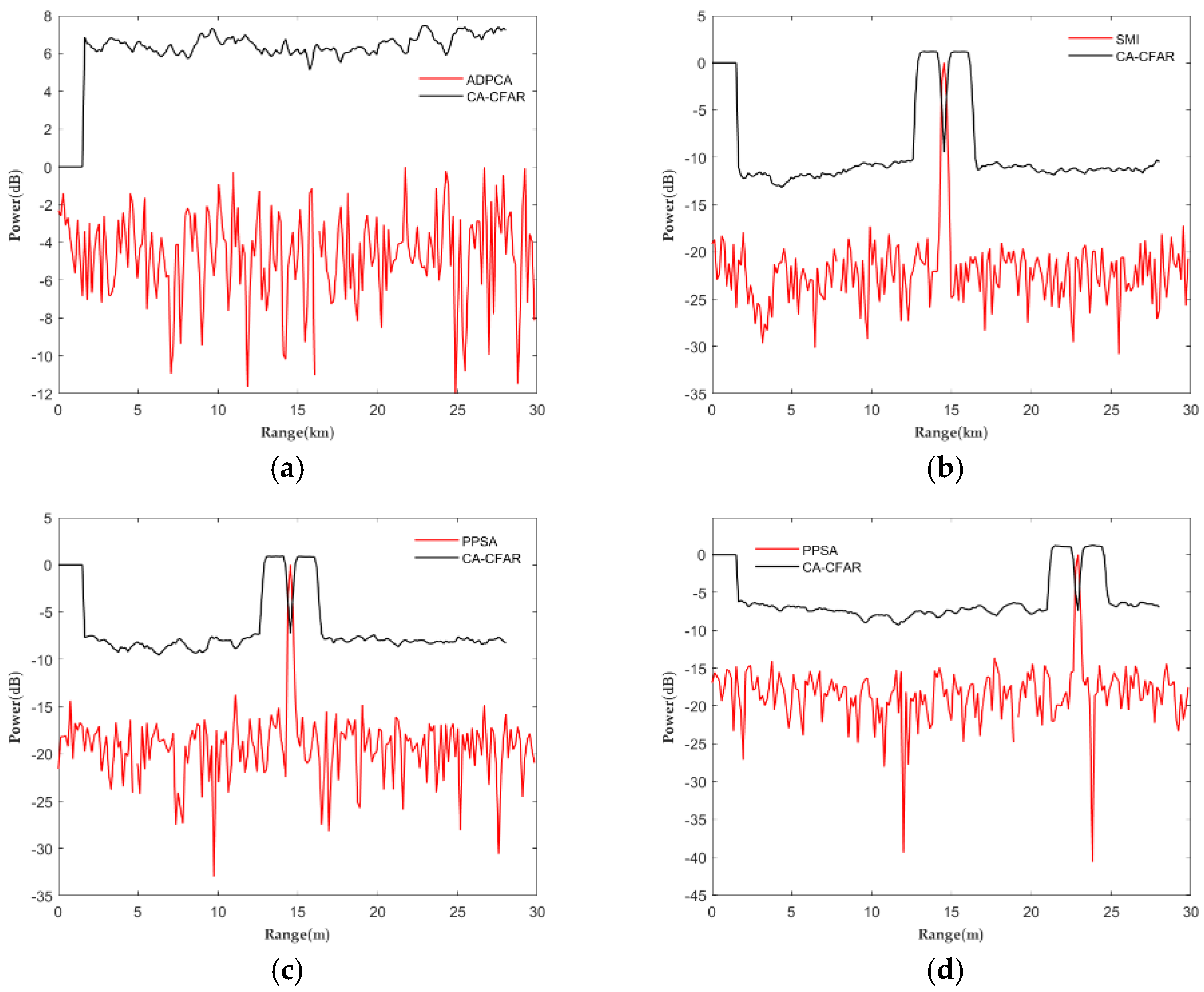
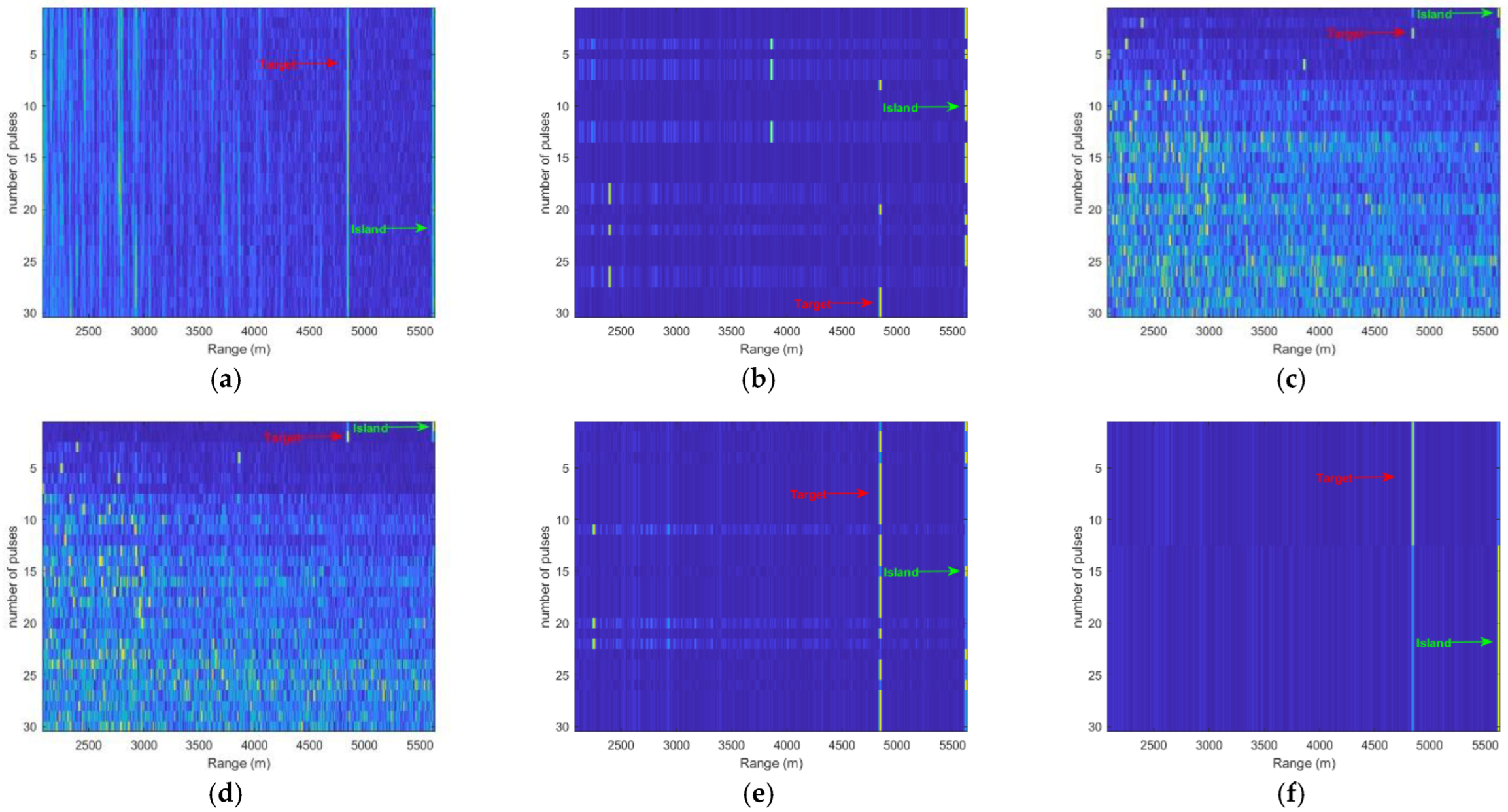
4.5. Experiment 4: Real Radar Echo Data Target Detection Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bakr, O.; Johnson, M.; Mudumbai, R.; Ramchandran, K. Multi-antenna interference cancellation techniques for cognitive radio applications. In Proceedings of the 2009 IEEE Wireless Communications and Networking Conference, Budapest, Hungary, 5–8 April 2009; pp. 1–6. [Google Scholar]
- Muehe, C.E.; Labitt, M. Displaced-phase-center antenna technique. Linc. Lab. J. 2000, 12, 281–296. [Google Scholar]
- Pour, Z.A.; Shafai, L. Adaptive aperture antennas with adjustable phase centre locations. In Proceedings of the 2012 IEEE International Workshop on Antenna Technology (iWAT), Tucson, AZ, USA, 5–7 March 2012; pp. 355–357. [Google Scholar]
- Brennan, L.E.; Reed, L. Theory of adaptive radar. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 237–252. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, W.; Zhang, T.; Xing, M.; Wang, Y. Improved Dimension-Reduced Structures of 3D-STAP on Nonstationary Clutter Suppression for Space-Based Early Warning Radar. Remote Sens. 2022, 14, 4011. [Google Scholar] [CrossRef]
- Knudsen, K.S.; Bruton, L.T. Mixed domain filtering of multidimensional signals. IEEE Trans. Circuits Syst. Video Technol. 1991, 1, 260–268. [Google Scholar] [CrossRef]
- Klemm, R. Antenna design for adaptive airborne MTI. In Proceedings of the 92 International Conference on Radar, Brighton, UK, 12–13 October 1992; pp. 296–299. [Google Scholar]
- Gui, R.; Wang, W.Q.; Farina, A.; So, H.C. FDA radar with doppler-spreading consideration: Mainlobe clutter suppression for blind-doppler target detection. Signal Process. 2021, 179, 107773. [Google Scholar] [CrossRef]
- Weinberg, G.V. Constant false alarm rate detectors for Pareto clutter models. IET Radar Sonar Navig. 2013, 7, 153–163. [Google Scholar] [CrossRef]
- Jia, F.; Sun, G.; He, Z.; Li, J. Grating-lobe clutter suppression in uniform subarray for airborne radar STAP. IEEE Sens. J. 2019, 19, 6956–6965. [Google Scholar] [CrossRef]
- Qian, L. Radar clutter suppression solution based on ICA. In Proceedings of the 2013 Fourth International Conference on 189Intelligent Systems Design and Engineering Applications, Zhangjiajie, China, 6–7 November 2013; pp. 429–432. [Google Scholar]
- Karlsen, B.; Larsen, J.; Sorensen, H.B.; Jakobsen, K.B. Comparison of PCA and ICA based clutter reduction in GPR systems for anti-personal landmine detection. In Proceedings of the Proceedings of the 11th IEEE Signal Processing Workshop on Statistical Signal Processing (Cat. No. 01TH8563), Singapore, 8 August 2001; pp. 146–149. [Google Scholar]
- Tannous, O.; Kasilingam, D. Independent component analysis of polarimetric SAR data for separating ground and vegetation components. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. IV-93–IV-96. [Google Scholar]
- Comon, P. Independent component analysis, a new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Oja, E.; Yuan, Z. The FastICA algorithm revisited: Convergence analysis. IEEE Trans. Neural Netw. 2006, 17, 1370–1381. [Google Scholar] [CrossRef] [PubMed]
- Geng, X.; Ji, L.; Sun, K. Principal skewness analysis: Algorithm and its application for multispectral/hyperspectral images indexing. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1821–1825. [Google Scholar] [CrossRef]
- Geng, X.; Meng, L.; Li, L.; Ji, L.; Sun, K. Momentum principal skewness analysis. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2262–2266. [Google Scholar] [CrossRef][Green Version]
- Meng, L.; Geng, X.; Ji, L. Principal kurtosis analysis and its application for remote-sensing imagery. Int. J. Remote Sens. 2016, 37, 2280–2293. [Google Scholar] [CrossRef]
- Anandkumar, A.; Ge, R.; Hsu, D.; Kakade, S.M.; Telgarsky, M. Tensor decompositions for learning latent variable models. J. Mach. Learn. Res. 2014, 15, 2773–2832. [Google Scholar]
- Geng, X.; Wang, L. NPSA: Nonorthogonal principal skewness analysis. IEEE Trans. Image Process. 2020, 29, 6396–6408. [Google Scholar] [CrossRef] [PubMed]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Lim, L.H. Singular values and eigenvalues of tensors: A variational approach. In Proceedings of the 1st IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Puerto Vallarta, Mexico, 13–15 December 2005; p. 129. [Google Scholar]
- Qi, L. Eigenvalues of a real supersymmetric tensor. J. Symb. Comput. 2005, 40, 1302–1324. [Google Scholar] [CrossRef]
- Wang, L.; Geng, X. The real eigenpairs of symmetric tensors and its application to independent component analysis. IEEE Trans. Cybern. 2021, 52, 10137–10150. [Google Scholar] [CrossRef] [PubMed]
- Guerci, J.R. Space-Time Adaptive Processing for Radar; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Ningbo, L.; Hao, D.; Yong, H.; Yunlong, D.; Guoqing, W.; Kai, D. Annual progress of the sea-detecting X-band radar and data acquisition program. J. Radars 2021, 10, 173–182. [Google Scholar]

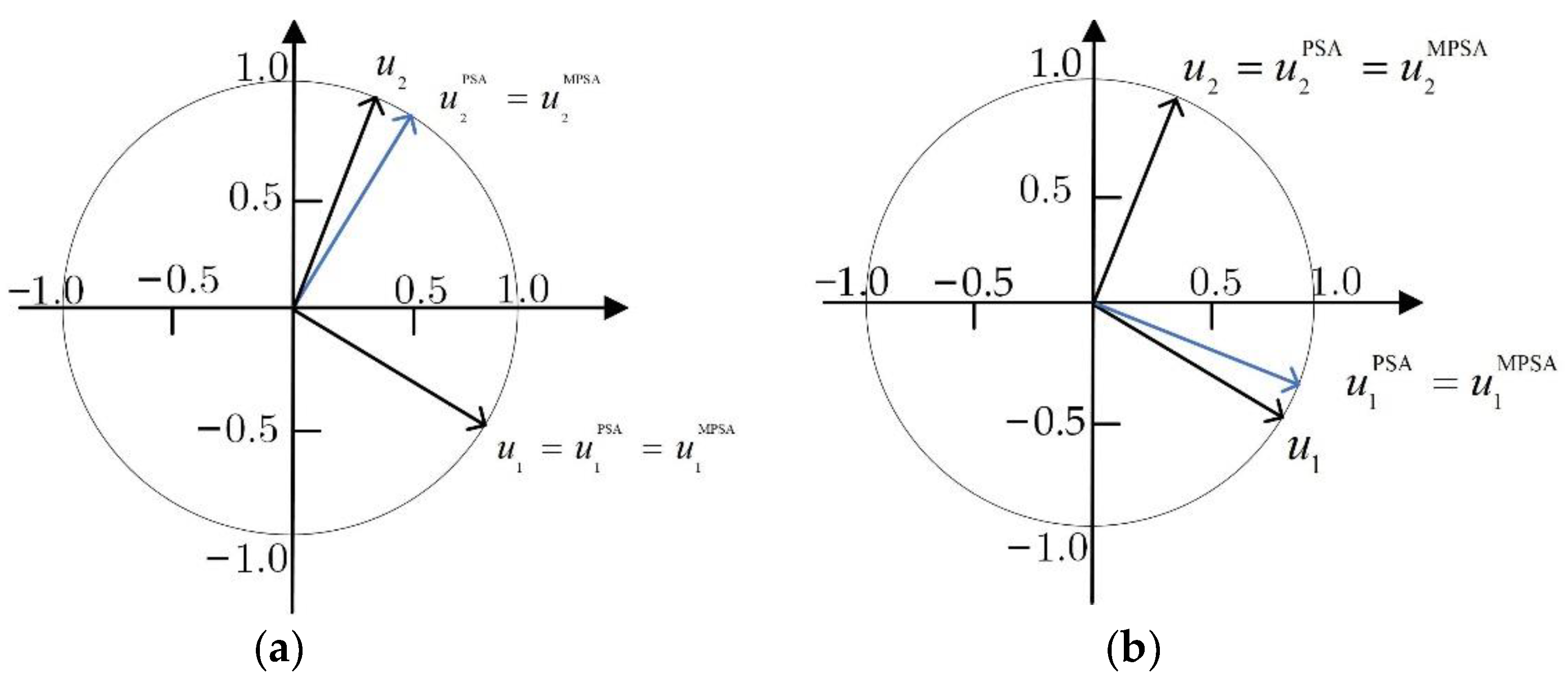
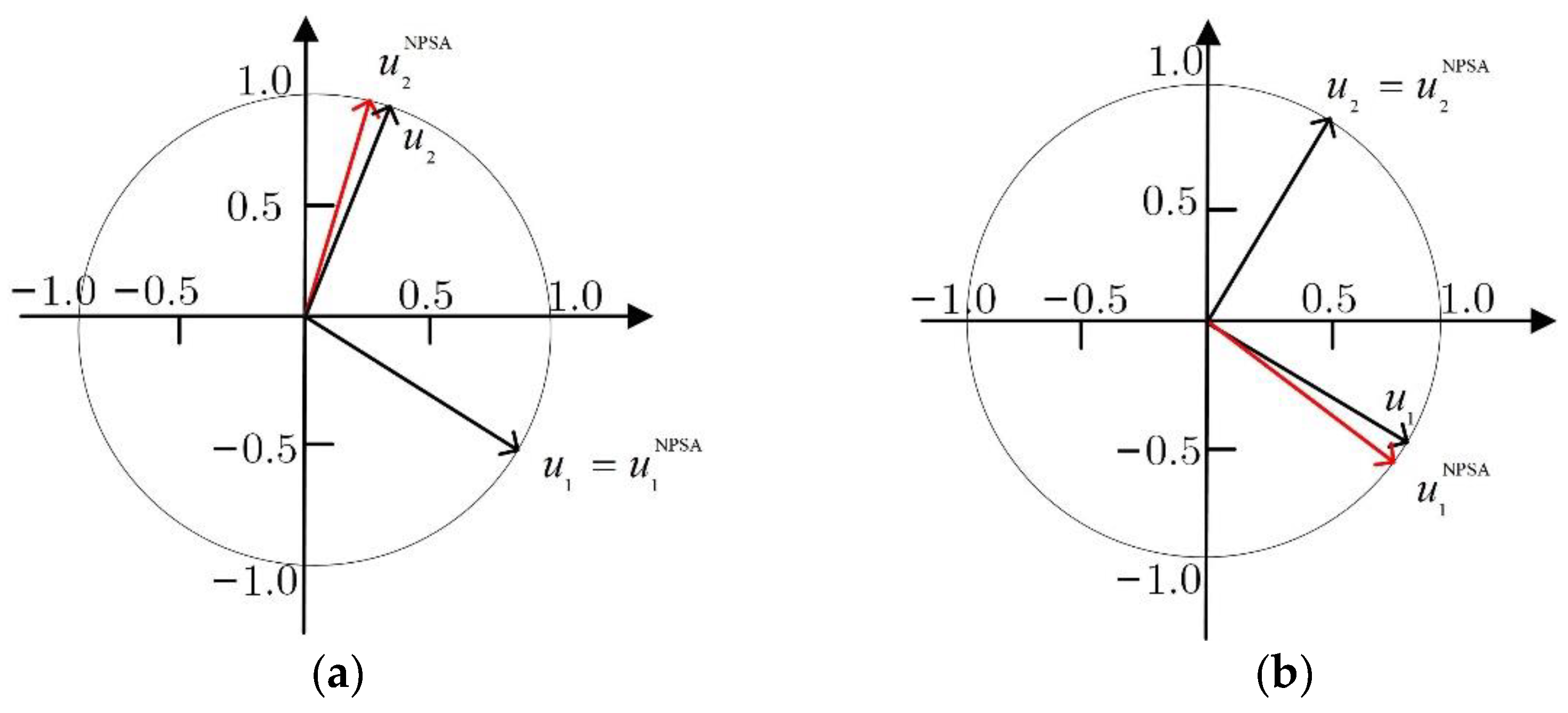
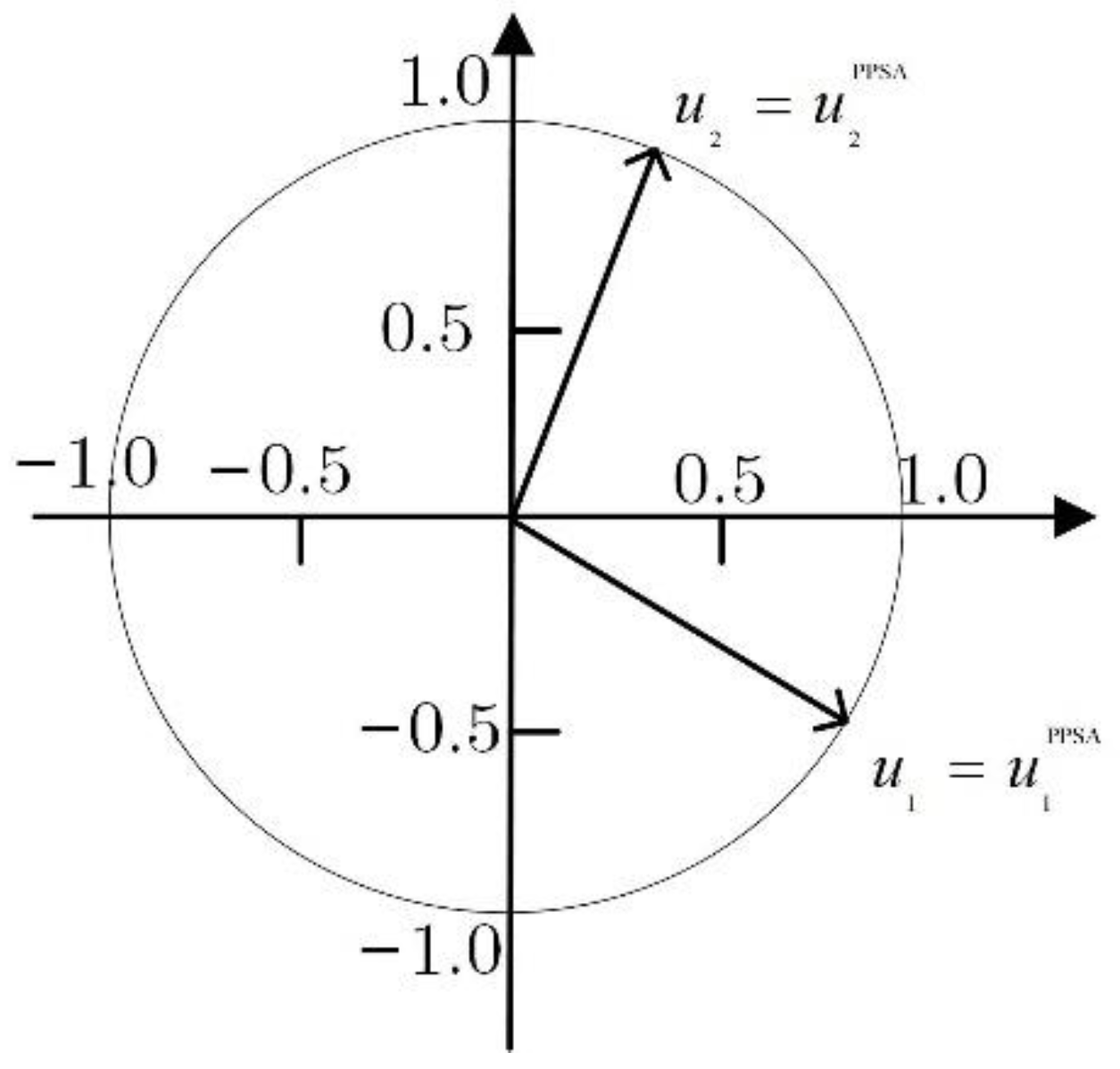


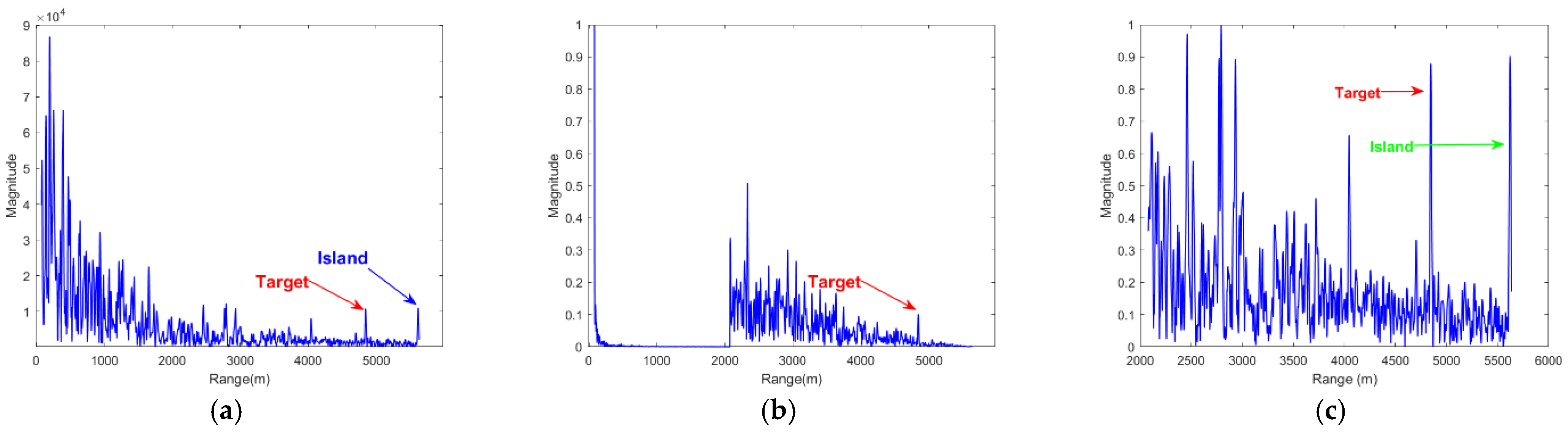
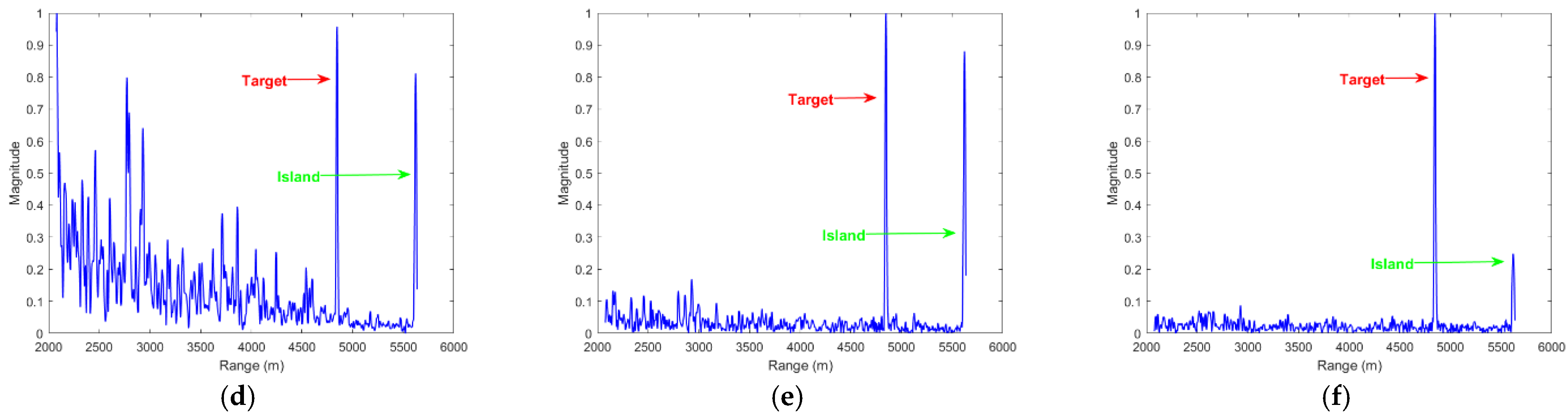
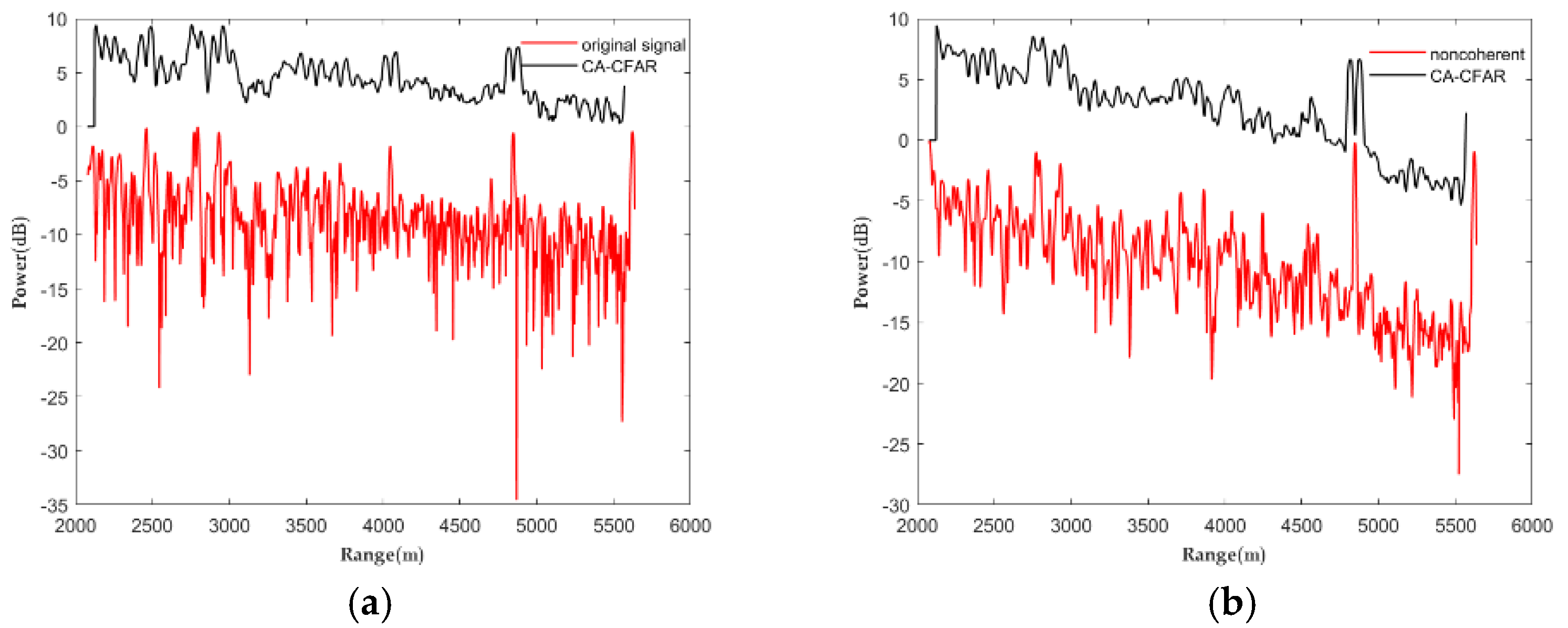
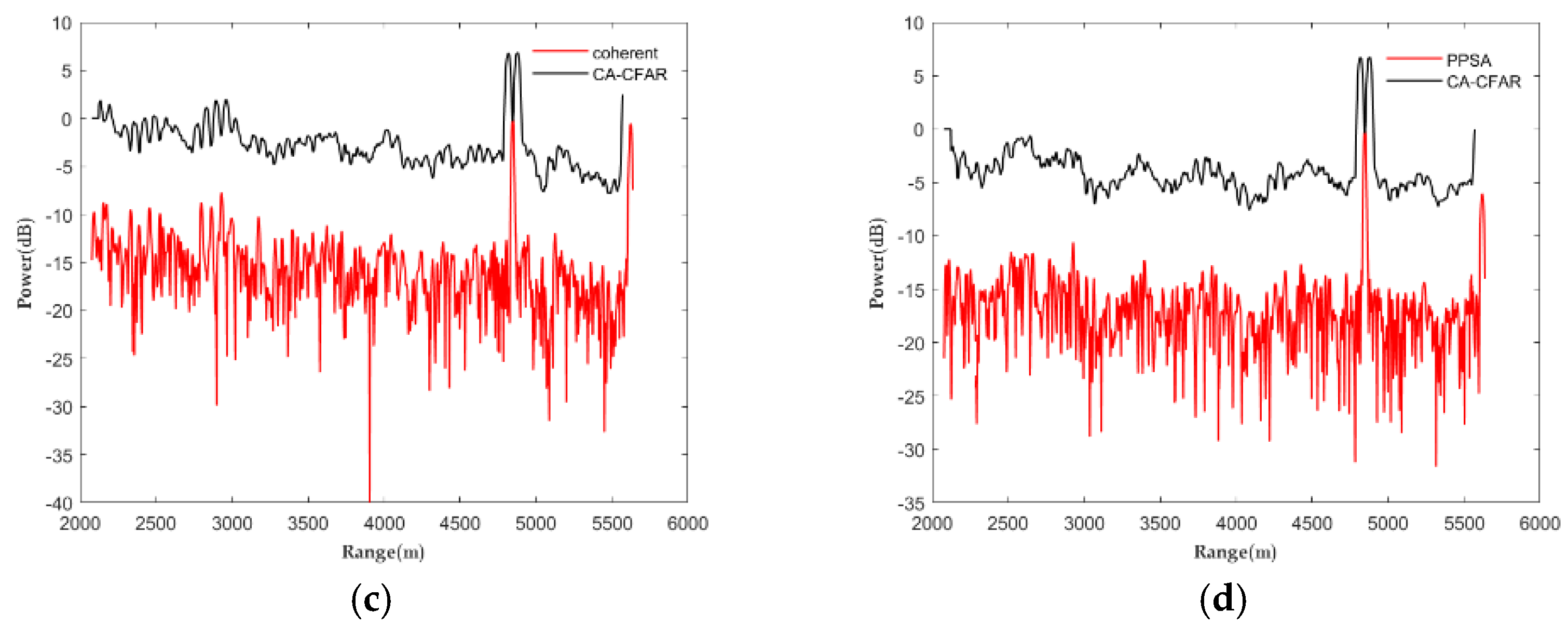
| Index | FastICA | PSA | MPSA | NPSA | MSDP | PPSA | |
|---|---|---|---|---|---|---|---|
| 1 | ISI | 0.6757 | 0.0681 | 0.0551 | 0.0253 | 0.0203 | 0.0203 |
| TMSE | 3.2856 × 10−11 | 2.5547 × 10−11 | 2.5548 × 10−11 | 3.8168 × 10−11 | 1.8645 × 10−11 | 1.8645 × 10−11 | |
| 0.9544 0.9889 0.9968 | 0.9954 0.9992 1.0000 | 0.9954 0.9988 1.0000 | 0.9992 0.99997 1.0000 | 0.9998 0.9992 1.0000 | 0.9998 0.9992 1.0000 | ||
| PSNR/dB | 66.1696 70.0325 79.2579 | 76.6105 72.6448 90.9901 | 77.7449 73.7954 90.4324 | 83.6350 74.4358 91.1667 | 85.9129 74.4870 91.3285 | 85.9129 74.4870 91.3285 | |
| T/s | 0.0042 | 0.0011 | 0.0010 | 0.0043 | 2.8594 | 0.0009 | |
| 2 | ISI | 0.4844 | 0.1442 | 0.1524 | 0.0787 | 0.0745 | 0.0745 |
| TMSE | 3.2241 × 10−11 | 2.6798 × 10−11 | 2.6337 × 10−11 | 2.5154 × 10−11 | 1.9555 × 10−14 | 1.9555 × 10−14 | |
| 0.9749 0.9900 0.9970 | 0.9967 0.9905 0.9999 | 0.9967 0.9907 0.9998 | 0.9995 0.9920 1.0000 | 0.9997 0.9921 1.0000 | 0.9997 0.9921 1.0000 | ||
| PSNR/dB | 69.1886 73.7143 76.9175 | 74.9389 73.1186 89.0466 | 75.6708 74.3531 90.4683 | 83.4588 70.1218 94.0776 | 83.7674 70.6017 94.7823 | 83.7674 70.6017 94.7823 | |
| T/s | 0.0052 | 0.0011 | 0.0010 | 0.0042 | 3.1046 | 0.0008 | |
| 3 | ISI | 0.2965 | 0.0405 | 0.0452 | 0.0041 | 0.0006 | 0.0006 |
| TMSE | 2.6603 × 10−10 | 2.6628 × 10−10 | 1.9986 × 10−10 | 3.4050 × 10−10 | 1.7480 × 10−10 | 1.7480 × 10−10 | |
| 0.9756 0.9950 0.9969 | 0.9966 0.9994 0.9998 | 0.9962 0.9995 0.9999 | 0.9997 1.0000 1.0000 | 1.0000 1.0000 1.0000 | 1.0000 1.0000 1.0000 | ||
| PSNR/dB | 69.9228 61.8123 82.3327 | 83.2559 61.1492 87.5416 | 78.8206 58.8872 90.4749 | 91.4669 61.2297 94.0424 | 96.6388 64.0212 95.1910 | 96.6388 64.0212 95.1910 | |
| T/s | 0.0048 | 0.0012 | 0.0009 | 0.0033 | 2.9786 | 0.0007 |
| Parameter | Numerical Value |
|---|---|
| pulse repetition frequency/Hz | 30,000 |
| radar wavelength/m | 0.03 |
| Pulse train length | 200 |
| Radar operating frequency range/GHz | 5~15 |
| Antenna height/m | 100 |
| bandwidth | 3 M |
| Sampling Rate | 6 M |
| Receiver gain/dB | 20 |
| Noise figure/dB | 0 |
| Parameter | Target 1 | Target 2 |
|---|---|---|
| distance/m | 2024.66 | 3518.63 |
| radar cross section/m2 | 1.00 | 1.00 |
| radial velocity/m/s | 30 | 60 |
| Method | FastICA | PSA | MPSA | NPSA | PPSA | FastPPSA |
|---|---|---|---|---|---|---|
| Time (s) | 1.5076 | 5.9706 | 5.8058 | 7.9262 | 5.7963 | 0.8143 |
| Method | Target 1 Echo Amplitude | Mean Noise Amplitude | SNR/dB |
|---|---|---|---|
| original signal | 1.0000 | 0.1238 | 18.1456 |
| noncoherent | 1.0000 | 0.0601 | 24.4225 |
| coherent | 1.0000 | 0.0291 | 30.7221 |
| PPSA | 1.0000 | 0.0237 | 32.5050 |
| Method | Target 2 Echo Amplitude | Mean Noise Amplitude | SNR/dB |
|---|---|---|---|
| original signal | 0.3040 | 0.1238 | 7.8031 |
| noncoherent | 0.2801 | 0.0601 | 13.3688 |
| coherent | 0.3351 | 0.0291 | 21.2256 |
| PPSA | 1.0000 | 0.0687 | 23.2609 |
| Parameter | Sports Goal 1 | Sports Goal 2 |
|---|---|---|
| distance/m | 2000 | 3000 |
| radar cross section/m2 | 1 | 1 |
| radial velocity/m/s | −80 | blind speed |
| Method | FastICA | PSA | MPSA | NPSA | PPSA | FastPPSA |
|---|---|---|---|---|---|---|
| Time (s) | 0.7189 | 1.6342 | 1.5340 | 1.7045 | 1.5023 | 0.2196 |
| Method | Target 1 Echo Amplitude | Clutter Amplitude Value | SCNR/dB |
|---|---|---|---|
| original signal | 1.4316 × 10−4 | 1.0000 | −76.8836 |
| TPC | 1.0000 | 0.1176 | 18.5919 |
| SPC | 1.0000 | 0.0842 | 21.4938 |
| PPSA | 1.0000 | 0.0309 | 30.2008 |
| Method | Target 2 Echo Amplitude | Clutter Amplitude Value | SCNR/dB |
|---|---|---|---|
| original signal | 2.2708 × 10−5 | 1.0000 | −92.8764 |
| TPC | 0.2022 | 0.1176 | 4.7075 |
| SPC | 0.3003 | 0.0842 | 11.0449 |
| PPSA | 1.0000 | 0.0799 | 21.9491 |
| Parameter | Numerical Value |
|---|---|
| pulse repetition frequency/Hz | 50000 |
| radar wavelength/m | 0.0749 |
| Pulse train length | 200 |
| Radar operating frequency range/GHz | 4 |
| Antenna height/m | 3000 |
| aircraft speed (m/s) | 100 |
| Sampling Rate | 1 M |
| Parameter | Sports Goal 1 | Sports Goal 2 |
|---|---|---|
| distance/m | 14,457 | 22,825 |
| radar cross section/m2 | 1 | 0.6 |
| radial velocity/m/s | 30 | 60 |
| Method | FastICA | PSA | MPSA | NPSA | PPSA | FastPPSA |
|---|---|---|---|---|---|---|
| Time (s) | 5.5095 | 61.3586 | 60.9625 | 74.6430 | 60.3657 | 10.7760 |
| Method | Target 1 Echo Amplitude | Clutter Amplitude Value | SCNR/dB |
|---|---|---|---|
| original signal | 0.0103 | 1.0000 | −39.7433 |
| ADPCA | 0.4363 | 0.3821 | 1.1522 |
| SMI | 1.0000 | 0.0123 | 38.2019 |
| PPSA | 1.0000 | 0.0135 | 37.3933 |
| Method | Target 2 Echo Amplitude | Clutter Amplitude Value | SCNR/dB |
|---|---|---|---|
| original signal | 0.0080 | 1.0000 | −41.9382 |
| ADPCA | 0.3148 | 0.3821 | −1.6828 |
| SMI | 0.2876 | 0.0123 | 6.5317 |
| PPSA | 1.0000 | 0.0165 | 35.6503 |
| Method | Target 1 Echo Amplitude | Clutter Amplitude Value | SCNR/dB |
|---|---|---|---|
| original signal | 0.8767 | 0.1798 | 13.7612 |
| noncoherent | 0.9425 | 0.1384 | 16.6639 |
| coherent | 1.0000 | 0.0342 | 29.3310 |
| PPSA | 1.0000 | 0.0242 | 32.3237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Liu, C.; Wang, C. A Parallel Principal Skewness Analysis and Its Application in Radar Target Detection. Remote Sens. 2023, 15, 288. https://doi.org/10.3390/rs15010288
Wang D, Liu C, Wang C. A Parallel Principal Skewness Analysis and Its Application in Radar Target Detection. Remote Sensing. 2023; 15(1):288. https://doi.org/10.3390/rs15010288
Chicago/Turabian StyleWang, Dahu, Chang Liu, and Chao Wang. 2023. "A Parallel Principal Skewness Analysis and Its Application in Radar Target Detection" Remote Sensing 15, no. 1: 288. https://doi.org/10.3390/rs15010288
APA StyleWang, D., Liu, C., & Wang, C. (2023). A Parallel Principal Skewness Analysis and Its Application in Radar Target Detection. Remote Sensing, 15(1), 288. https://doi.org/10.3390/rs15010288






