Dropsonde-Based Heat Fluxes and Mixed Layer Height over the Sea Surface near the Korean Peninsula
Abstract
1. Introduction
2. Materials and Method
2.1. Dropsonde
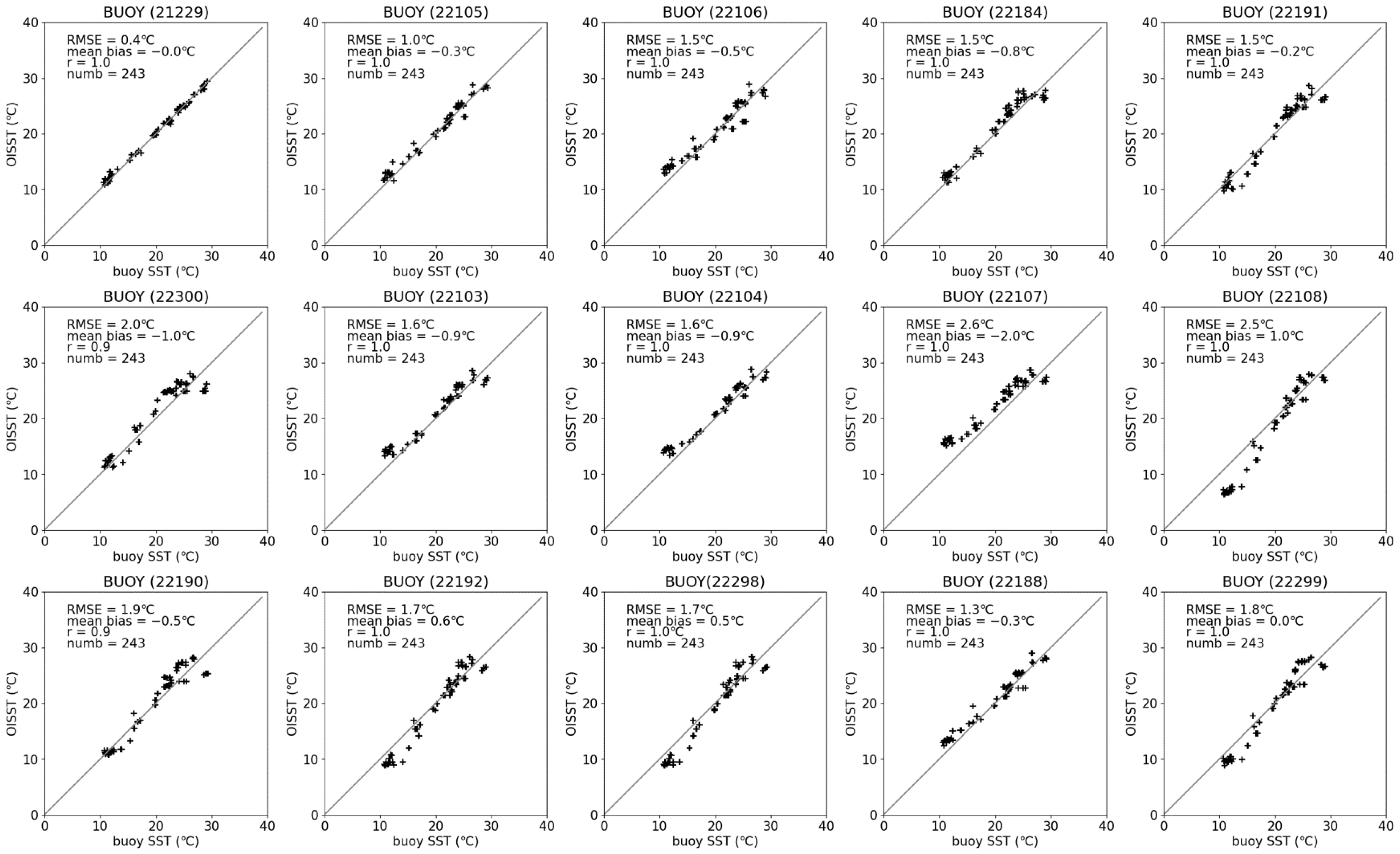
2.2. Sea Surface Temperature
2.3. Model-Based Heat Fluxes
2.4. Bulk Transfer Method
3. Results
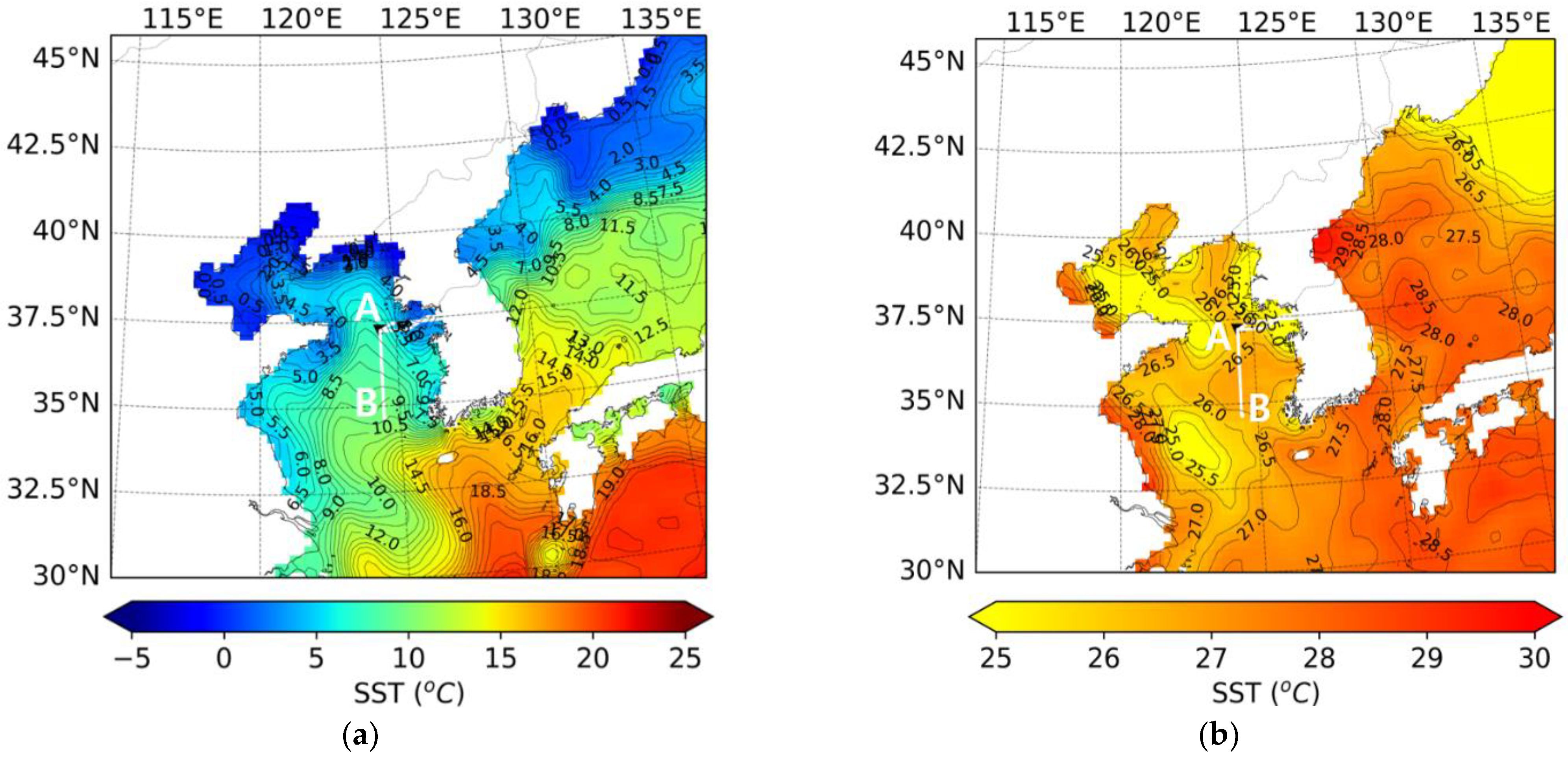
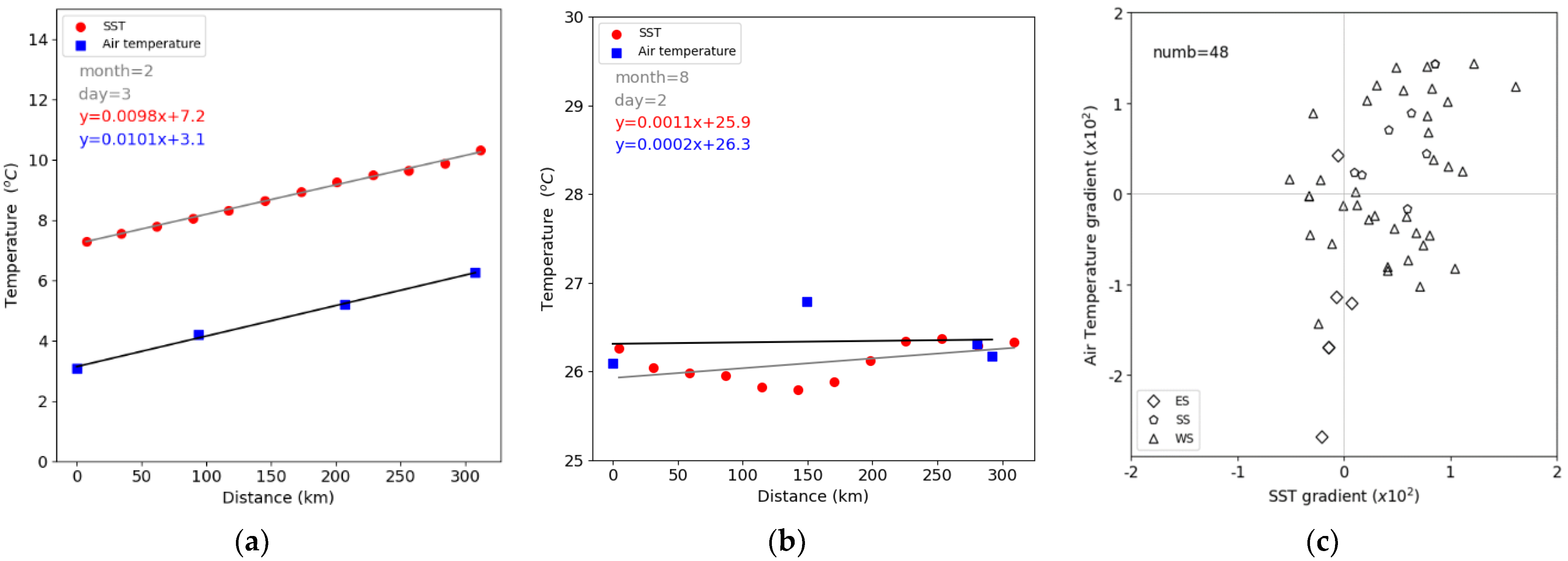
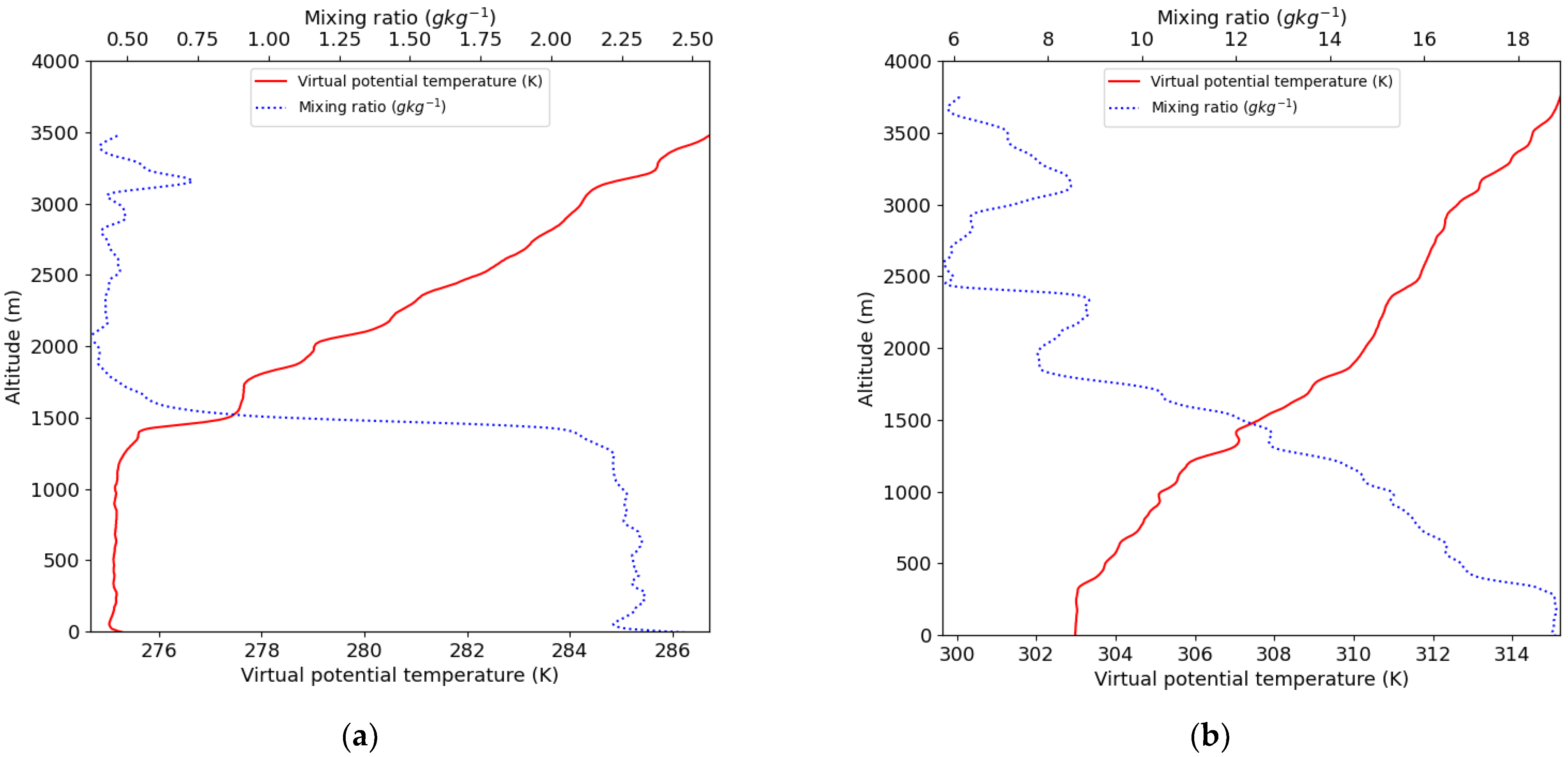
3.1. Sea Surface Temperature Field
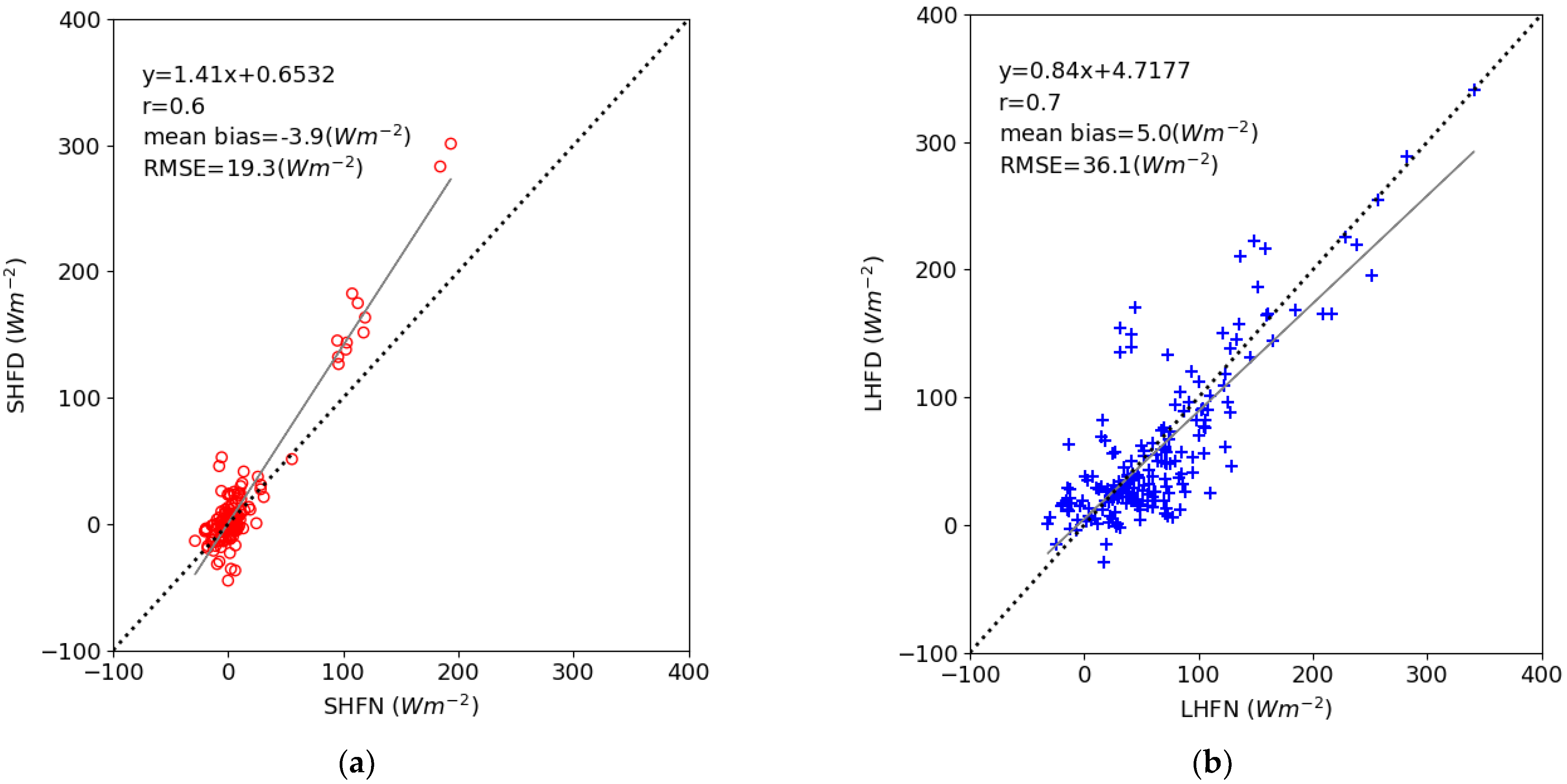
3.2. Sensible and Latent Heat Fluxes
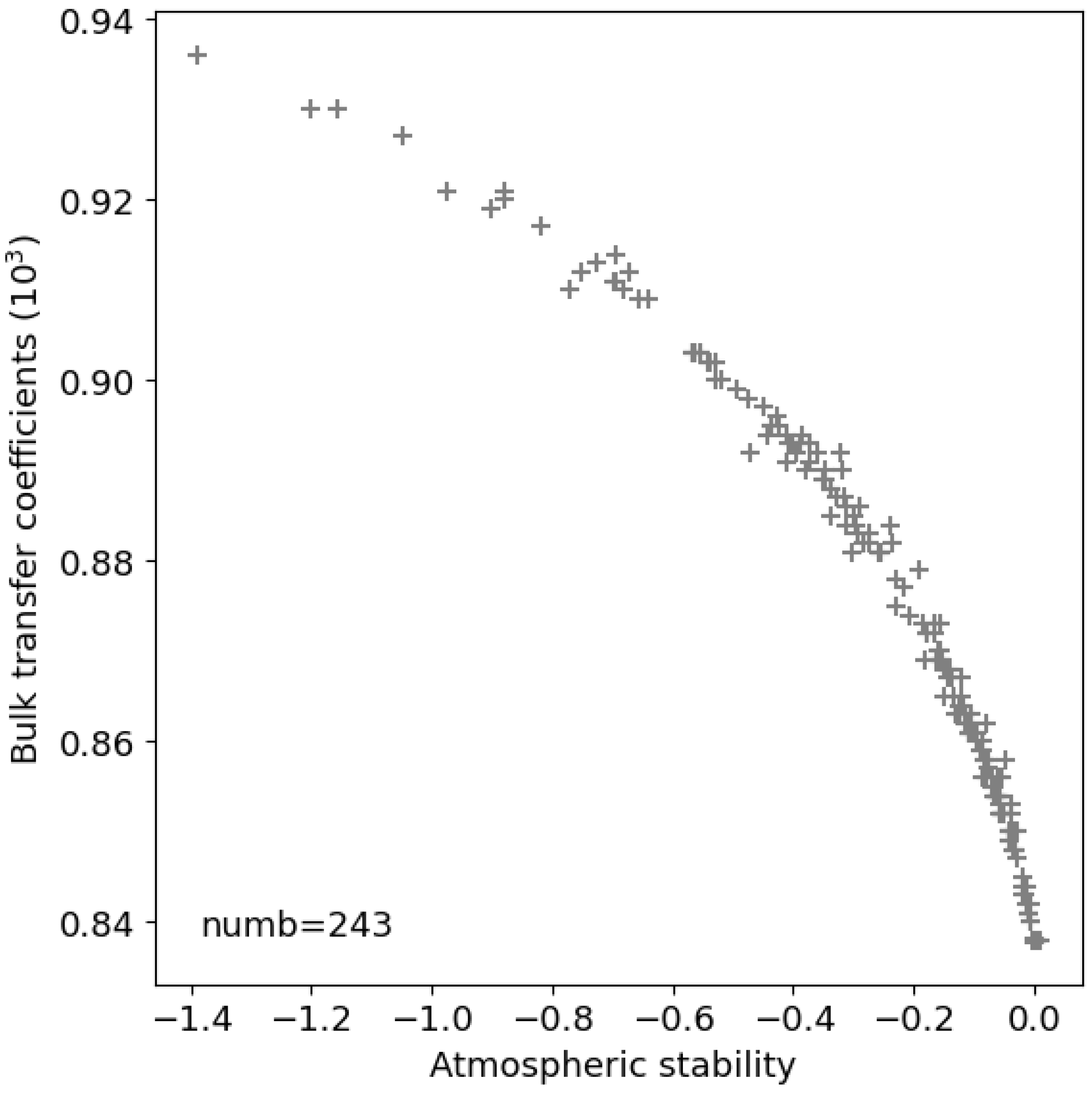
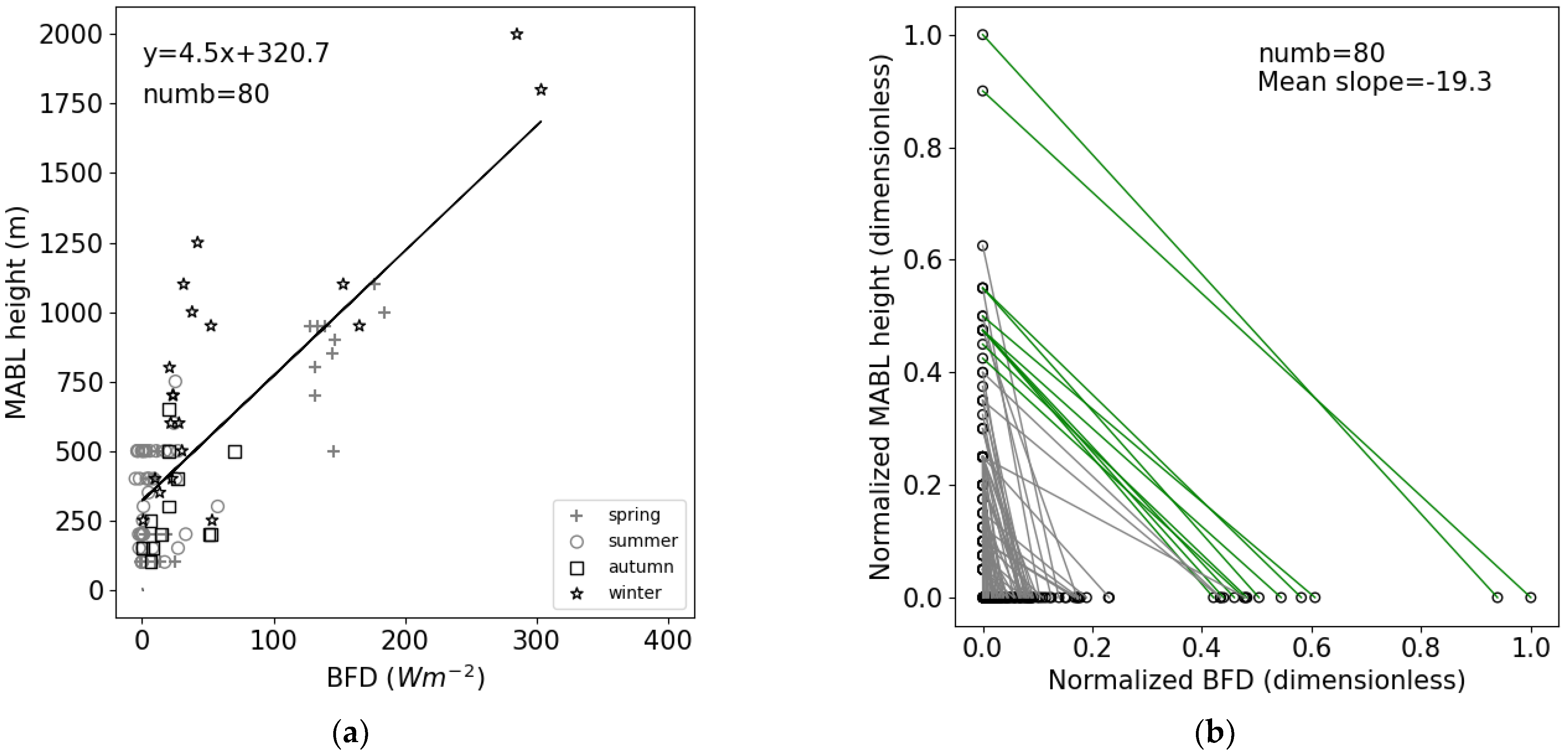
3.3. Marine Atmospheric Boundary Layer
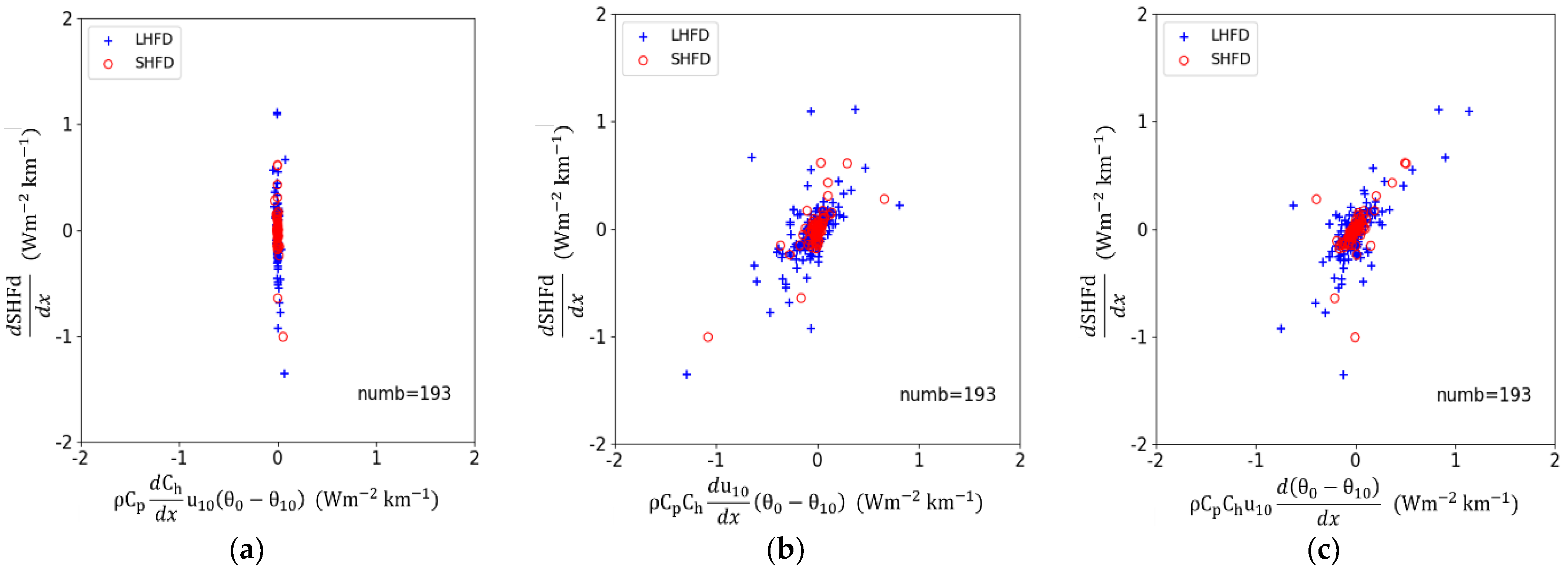
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khim, J.S.; Lee, C.; Song, S.J.; Bae, H.; Noh, J.; Lee, J.; Kim, H.G.; Choi, J.W.; Seong Khim, J.; Lee, C.; et al. Marine biodiversity in Korea: A review of macrozoobenthic assemblages, their distributions, and long-term community changes from human impacts. In Oceanography and Marine Biology: An Annual Review; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Farach-Espinoza, E.B.; López-Martínez, J.; García-Morales, R.; Otilio Nevárez-Martínez, M.; Lluch-Cota, D.B.; Ortega-García, S. Temporal variability of oceanic mesoscale events in the Gulf of California. Remote Sens. 2021, 13, 1774. [Google Scholar] [CrossRef]
- Park, J.E.; Park, K.A.; Kang, C.K.; Park, Y.J. Short-Term Response of Chlorophyll-a Concentration to Change in Sea Surface Wind Field over Mesoscale Eddy. Estuaries Coasts 2020, 43, 646–660. [Google Scholar] [CrossRef]
- Curry, J.A.; Bentamy, A.; Bourassa, M.A.; Bourras, D.; Bradley, E.F.; Brunke, M.; Castro, S.; Chou, S.H.; Clayson, C.A.; Emery, W.J.; et al. SEAFLUX. Bull. Am. Meteorol. Soc. 2004, 85, 409–424. [Google Scholar] [CrossRef]
- Praveen Kumar, B.; Cronin, M.F.; Joseph, S.; Ravichandran, M.; Sureshkumar, N. Latent Heat Flux Sensitivity to Sea Surface Temperature: Regional Perspectives. J. Clim. 2017, 30, 129–143. [Google Scholar] [CrossRef]
- Ming, J.; Zhang, J.A. Effects of surface flux parameterization on the numerically simulated intensity and structure of Typhoon Morakot (2009). Adv. Atmos. Sci. 2015, 33, 58–72. [Google Scholar] [CrossRef]
- Zhang, J.A.; Cione, J.J.; Kalina, E.A.; Uhlhorn, E.W.; Hock, T.; Smith, J.A. Observations of Infrared Sea Surface Temperature and Air–Sea Interaction in Hurricane Edouard (2014) Using GPS Dropsondes. J. Atmos. Ocean. Technol. 2017, 34, 1333–1349. [Google Scholar] [CrossRef]
- Wu, L.; Wang, B.; Braun, S.A. Impacts of Air–Sea Interaction on Tropical Cyclone Track and Intensity. Mon. Weather Rev. 2005, 133, 3299–3314. [Google Scholar] [CrossRef]
- Yun, K.S.; Chan, J.C.L.; Ha, K.J. Effects of SST magnitude and gradient on typhoon tracks around East Asia: Acase study for Typhoon Maemi (2003). Atmos. Res. 2012, 109–110, 36–51. [Google Scholar] [CrossRef]
- Song, Q.; Cornillon, P.; Hara, T. Surface wind response to oceanic fronts. J. Geophys. Res. Ocean. 2006, 111, 12006. [Google Scholar] [CrossRef]
- Liu, W.T.; Xie, X.; Niiler, P.P. Ocean–Atmosphere Interaction over Agulhas Extension Meanders. J. Clim. 2007, 20, 5784–5797. [Google Scholar] [CrossRef]
- Businger, J.A. Evaluation of the Accuracy with Which Dry Deposition Can Be Measured with Current Micrometeorological Techniques. J. Appl. Meteorol. Climatol. 1986, 25, 1100–1124. [Google Scholar] [CrossRef]
- Cronin, M.F.; Gentemann, C.L.; Edson, J.B.; Ueki, I.; Bourassa, M.; Brown, S.; Clayson, C.A.; Fairall, C.; T. Farrar, J.; Gille, S.T.; et al. Air-sea fluxes with a focus on heat and momentum. Front. Mar. Sci. 2019, 6, 430. [Google Scholar] [CrossRef]
- Kubota, M.; Iwasaka, N.; Kizu, S.; Konda, M.; Kutsuwada, K. Japanese Ocean Flux Data Sets with Use of Remote Sensing Observations (J-OFURO). J. Oceanogr. 2002, 58, 213–225. [Google Scholar] [CrossRef]
- Shie, C.L.; Chiu, L.S.; Adler, R.; Nelkin, E.; Lin, I.I.; Xie, P.; Wang, F.C.; Chokngamwong, R.; Olson, W.; Chu, D.A. A note on reviving the Goddard Satellite-based Surface Turbulent Fluxes (GSSTF) dataset. Adv. Atmos. Sci. 2009, 26, 1071–1080. [Google Scholar] [CrossRef]
- Andersson, A.; Fennig, K.; Klepp, C.; Bakan, S.; Graßl, H.; Schulz, J. The Hamburg ocean atmosphere parameters and fluxes from satellite data-HOAPS-3. Earth Syst. Sci. Data 2010, 2, 215–234. [Google Scholar] [CrossRef]
- Bentamy, A.; Desbiolles, F.; Grodsky, S.A.; Katsaros, K.; Mestas-Nuñez, A.M.; Blanke, B.; Desbiolles, F. Improvement in air–sea flux estimates derived from satellite observations. Int. J. Remote Sens. 2013, 34, 5243–5261. [Google Scholar] [CrossRef]
- Renfrew, I.A.; Petersen, G.N.; Sproson, D.A.J.; Moore, G.W.K.; Adiwidjaja, H.; Zhang, S.; North, R. A comparison of aircraft-based surface-layer observations over Denmark Strait and the Irminger Sea with meteorological analyses and QuikSCAT winds. Q. J. R. Meteorol. Soc. 2009, 135, 2046–2066. [Google Scholar] [CrossRef]
- Bharti, V.; Schulz, E.; Fairall, C.W.; Blomquist, B.W.; Huang, Y.I.; Protat, A.; Siems, S.T.; Manton, M.J. Assessing Surface Heat Flux Products with In Situ Observations over the Australian Sector of the Southern Ocean. J. Atmos. Ocean. Technol. 2019, 36, 1849–1861. [Google Scholar] [CrossRef]
- Petersen, G.N.; Renfrew, I.A. Aircraft-based observations of air–sea fluxes over Denmark Strait and the Irminger Sea during high wind speed conditions. Q. J. R. Meteorol. Soc. 2009, 135, 2030–2045. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Kim, J.-H.; Goo, T.-Y.; Jung, S.-P.; Kim, M.-S.; Lee, K.; Kang, M.; Lee, C.; Yang, J.; Hong, S.; Ko, H.; et al. Overview of the KMA/NIMS Atmospheric Research Aircraft (NARA) and its data archive: Annual airborne observations over the Korean peninsula. Geosci. Data J. 2022, in press. [Google Scholar] [CrossRef]
- Li, S.; Kim, Y.; Kim, J.; Takele, S.; Goo, T.Y.; Labzovskii, L.D.; Byun, Y.H. In Situ Aircraft Measurements of CO2 and CH4: Mapping Spatio-Temporal Variations over Western Korea in High-Resolutions. Remote Sens. 2020, 12, 3093. [Google Scholar] [CrossRef]
- Yeh, S.W.; Kim, C.H. Recent warming in the Yellow/East China Sea during winter and the associated atmospheric circulation. Cont. Shelf Res. 2010, 30, 1428–1434. [Google Scholar] [CrossRef]
- Kim, K.; Kim, K.R.; Kim, Y.G.; Cho, Y.K.; Kang, D.J.; Takematsu, M.; Volkov, Y. Water masses and decadal variability in the East Sea (Sea of Japan). Prog. Oceanogr. 2004, 61, 157–174. [Google Scholar] [CrossRef]
- George, G.; Stevens, B.; Bony, S.; Klingebiel, M.; Vogel, R. Observed Impact of Mesoscale Vertical Motion on Cloudiness. J. Atmos. Sci. 2021, 78, 2413–2427. [Google Scholar]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily High-Resolution-Blended Analyses for Sea Surface Temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Banzon, V.; Smith, T.M.; Mike Chin, T.; Liu, C.; Hankins, W. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling and environmental studies. Earth Syst. Sci. Data 2016, 8, 165–176. [Google Scholar] [CrossRef]
- Jang, J.C.; Park, K.A. High-Resolution Sea Surface Temperature Retrieval from Landsat 8 OLI/TIRS Data at Coastal Regions. Remote Sens. 2019, 11, 2687. [Google Scholar] [CrossRef]
- Stolzenberger, S.; Rietbroek, R.; Wekerle, C.; Uebbing, B.; Kusche, J. Simulated signatures of Greenland melting in the North Atlantic: A model comparison with Argo floats, satellite observations, and ocean reanalysis. J. Geophys. Res. Ocean. 2022, 127, e2022JC018528. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Freeman, E.; Graham, G.; Smith, T.; Zhang, H.M. Assessment and Intercomparison of NOAA Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 7421–7441. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.M. Improvements of the Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Lee, E.Y.; Park, K.A. Validation of Satellite Sea Surface Temperatures and Long-Term Trends in Korean Coastal Regions over Past Decades (1982–2018). Remote Sens. 2020, 12, 3742. [Google Scholar] [CrossRef]
- Yang, W.; John, V.O.; Zhao, X.; Lu, H.; Knapp, K.R. Satellite climate data records: Development, applications, and societal benefits. Remote Sens. 2016, 8, 331. [Google Scholar] [CrossRef]
- Rodell, M.; Beaudoing, H.K.; L’Ecuyer, T.S.; Olson, W.S.; Famiglietti, J.S.; Houser, P.R.; Adler, R.; Bosilovich, M.G.; Clayson, C.A.; Chambers, D.; et al. The Observed State of the Water Cycle in the Early Twenty-First Century. J. Clim. 2015, 28, 8289–8318. [Google Scholar] [CrossRef]
- Cuijpers, J.W.M.; Bechtold, P. A simple parameterization of cloud water related variables for use in boundary layer models. J. Atmos. Sci. 1995, 52, 2486–2490. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F.; Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile Relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Abbasi, A.; Annor, F.O.; van de Giesen, N. Effects of atmospheric stability conditions on heat fluxes from small water surfaces in (semi-)arid regions. Hydrol. Sci. J. 2017, 62, 1422–1439. [Google Scholar] [CrossRef]
- Arya, S.P. Introduction to Micrometeorology; Academic Press: Cambridge, MA, USA, 1988; ISBN 9788578110796. [Google Scholar]
- Deardorff, J.W. Parameterization of the Planetary Boundary layer for Use in General Circulation Models 1. Mon. Weather Rev. 1972, 100, 93–106. [Google Scholar] [CrossRef]
- Katz, J.; Zhu, P. Evaluation of surface layer flux parameterizations using in-situ observations. Atmos. Res. 2017, 194, 150–163. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Tr. Akad. Nauk SSSR Geophiz. Inst. 1954, 151, e187. [Google Scholar]
- Geernaert, G.L.; Larsen, S.E.; Hansen, F. Measurements of the wind stress, heat flux, and turbulence intensity during storm conditions over the North Sea. J. Geophys. Res. Ocean. 1987, 92, 13127–13139. [Google Scholar] [CrossRef]
- Hussein, M.M.A. Impact of atmospheric stability conditions on heat fluxes from Alexandria Eastern Harbor, Egypt. Egypt. J. Aquat. Res. 2019, 45, 313–319. [Google Scholar] [CrossRef]
- Verburg, P.; Antenucci, J.P. Persistent unstable atmospheric boundary layer enhances sensible and latent heat loss in a tropical great lake: Lake Tanganyika. J. Geophys. Res. Atmos. 2010, 115, 11109. [Google Scholar] [CrossRef]
- Launiainen, J.; Vihma, T. Derivation of turbulent surface fluxes—An iterative flux-profile method allowing arbitrary observing heights. Environ. Softw. 1990, 5, 113–124. [Google Scholar] [CrossRef]
- Kim, M.-S.; Kwon, B.H. Estimation of sensible heat flux and atmospheric boundary layer height using an unmanned aerial vehicle. Atmosphere 2019, 10, 363. [Google Scholar] [CrossRef]
- Kwon, B.H.; Bénech, B.; Lambert, D.; Durand, P.; Druilhet, A.; Giordani, H.; Planton, S. Structure of the marine atmospheric boundary layer over an oceanic thermal front: SEMAPHORE experiment. J. Geophys. Res. Ocean. 1998, 103, 25159–25180. [Google Scholar] [CrossRef]
- Foussard, A.; Lapeyre, G.; Plougonven, R. Response of Surface Wind Divergence to Mesoscale SST Anomalies under Different Wind Conditions. J. Atmos. Sci. 2019, 76, 2065–2082. [Google Scholar] [CrossRef]
- Zhang, J.A.; Black, P.G.; French, J.R.; Drennan, W.M. First direct measurements of enthalpy flux in the hurricane boundary layer: The CBLAST results. Geophys. Res. Lett. 2008, 35, L14813. [Google Scholar] [CrossRef]
- Haus, B.K.; Jeong, D.; Donelan, M.A.; Zhang, J.A.; Savelyev, I. Relative rates of sea-air heat transfer and frictional drag in very high winds. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Bell, M.M.; Montgomery, M.T.; Emanuel, K.A. Air–Sea Enthalpy and Momentum Exchange at Major Hurricane Wind Speeds Observed during CBLAST. J. Atmos. Sci. 2012, 69, 3197–3222. [Google Scholar] [CrossRef]
- Bae, H.J.; Yang, S.; Jeong, T.B.; Yang, A.R.; Cha, D.H.; Lee, G.; Lee, H.Y.; Byun, D.S.; Kim, B.M. An Estimation of Ocean Surface Heat Fluxes during the Passage of Typhoon at the Ieodo Ocean Research Station: Typhoon Lingling Case Study 2019. Asia-Pac. J. Atmos. Sci. 2022, 58, 305–314. [Google Scholar] [CrossRef]
- Richter, D.H.; Bohac, R.; Stern, D.P. An assessment of the flux profile method for determining air–sea momentum and enthalpy fluxes from dropsonde data in tropical cyclones. J. Atmos. Sci. 2016, 73, 2665–2682. [Google Scholar] [CrossRef]
- Sobel, A.H. On the Coexistence of an Evaporation Minimum and Precipitation Maximum in the Warm Pool. J. Clim. 2003, 16, 1003–1009. [Google Scholar] [CrossRef]
- DiNezio, P.N.; Clement, A.C.; Vecchi, G.A.; Soden, B.J.; Kirtman, B.P.; Lee, S.K. Climate Response of the Equatorial Pacific to Global Warming. J. Clim. 2009, 22, 4873–4892. [Google Scholar] [CrossRef]
- Kim, M.S.; Kwon, B.H.; Goo, T.Y. Comparisons between Mean and Turbulent Parameters of Aircraft-Based and Ship-Based Measurements in the Marine Atmospheric Boundary Layer. Atmosphere 2021, 12, 1088. [Google Scholar] [CrossRef]
- Nieuwstadt, F. The computation of the friction velocity u * and the temperature scale T * from temperature and wind velocity profiles by least-square methods. Boundary-Layer Meteorol. 1978, 14, 235–246. [Google Scholar] [CrossRef]


| Date | Time (KST) | Site | Available Profile | Date | Time (LST) | Site | Available Profile | Date | Time (LST) | Site | Available Profile |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 21 January | 15 | WS | 1 | 27 May | 13–14 | WS | 5 | 2 August | 13–14 | WS | 4 |
| 22 January | 13–14 | ES | 4 | 8 June | 13–14 | WS | 6 | 7 August | 13–14 | WS | 3 |
| 27 January | 13–14 | WS | 2 | 10 June | 13–14 | WS | 6 | 9 August | 13–14 | WS | 3 |
| 29 January | 13 | ES | 2 | 18 June | 14–15 | SS | 7 | 12 August | 13–14 | WS | 6 |
| 1 February | 14 | WS | 2 | 22 June | 13–14 | WS | 6 | 20 August | 09–10 | WS | 6 |
| 3 February | 14 | WS | 4 | 23 June | 13–14 | WS | 6 | 21 August | 08–09 | WS | 4 |
| 4 February | 13 | ES | 2 | 25 June | 13–14 | WS | 6 | 23 August | 08–09 | WS | 6 |
| 25 February | 13–14 | WS | 4 | 28 June | 13–14 | WS | 6 | 24 August | 08–09 | WS | 5 |
| 2 March | 14 | ES | 4 | 29 June | 13–14 | WS | 6 | 31 August | 08–10 | WS | 6 |
| 6 March | 13–14 | ES | 6 | 1 July | 13–15 | SS | 8 | 1 September | 08–09 | WS | 6 |
| 9 March | 13 | WS | 2 | 3 July | 13–14 | SS | 4 | 6 September | 09–10 | WS | 6 |
| 17 March | 13–14 | WS | 4 | 5 July | 13–15 | SS | 7 | 12 September | 09–10 | SS | 10 |
| 26 March | 13–14 | WS | 4 | 7 July | 13–14 | SS | 8 | 13 September | 09–10 | WS | 6 |
| 30 March | 13–14 | WS | 3 | 9 July | 13–14 | SS | 8 | 14 September | 09–10 | WS | 6 |
| 23 April | 13–14 | WS | 6 | 27 July | 13–14 | WS | 6 | 18 November | 15 | WS | 2 |
| 11 May | 13–14 | WS | 5 | 29 July | 13–14 | WS | 5 | ||||
| 20 May | 13–14 | WS | 6 | 30 July | 13–14 | WS | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-S.; Kwon, B.H.; Goo, T.-Y.; Jung, S.-P. Dropsonde-Based Heat Fluxes and Mixed Layer Height over the Sea Surface near the Korean Peninsula. Remote Sens. 2023, 15, 25. https://doi.org/10.3390/rs15010025
Kim M-S, Kwon BH, Goo T-Y, Jung S-P. Dropsonde-Based Heat Fluxes and Mixed Layer Height over the Sea Surface near the Korean Peninsula. Remote Sensing. 2023; 15(1):25. https://doi.org/10.3390/rs15010025
Chicago/Turabian StyleKim, Min-Seong, Byung Hyuk Kwon, Tae-Young Goo, and Sueng-Pil Jung. 2023. "Dropsonde-Based Heat Fluxes and Mixed Layer Height over the Sea Surface near the Korean Peninsula" Remote Sensing 15, no. 1: 25. https://doi.org/10.3390/rs15010025
APA StyleKim, M.-S., Kwon, B. H., Goo, T.-Y., & Jung, S.-P. (2023). Dropsonde-Based Heat Fluxes and Mixed Layer Height over the Sea Surface near the Korean Peninsula. Remote Sensing, 15(1), 25. https://doi.org/10.3390/rs15010025






