Response of Industrial Warm Drainage to Tide Revealed by Airborne and Sea Surface Observations
Abstract
1. Introduction
2. Materials and Methods
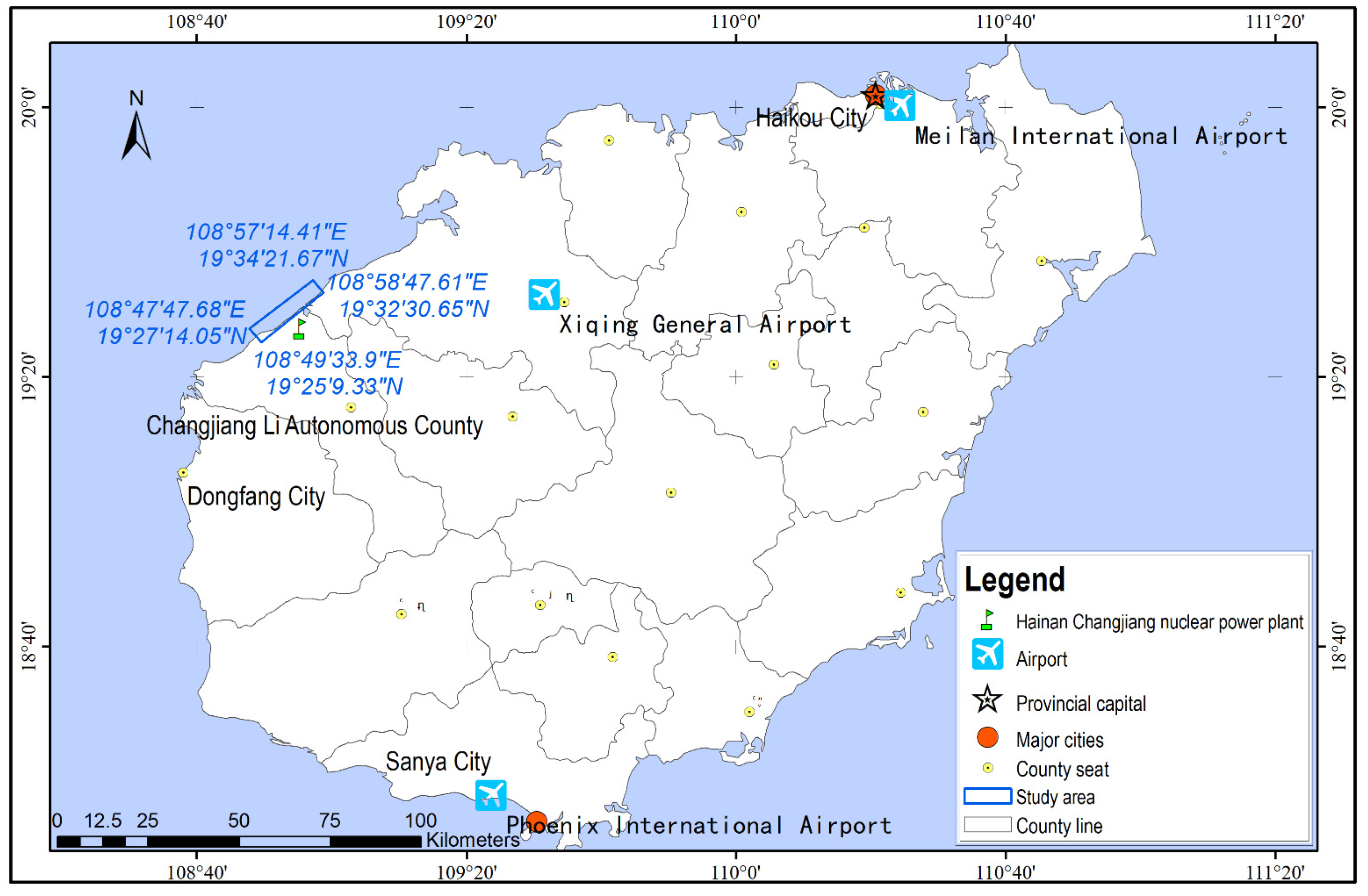
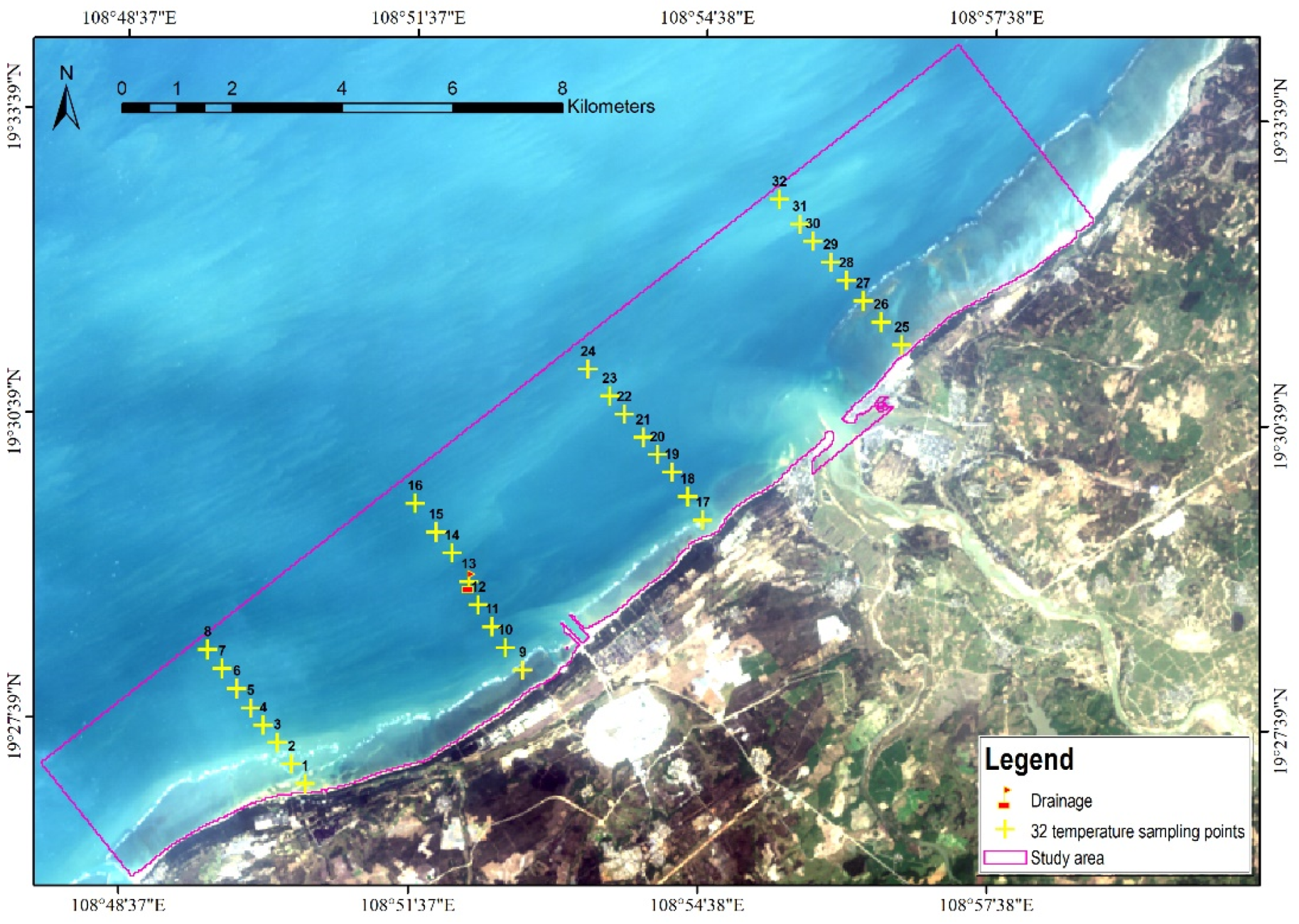
2.1. Study Area
2.1.1. Background
2.1.2. Coastal Environment
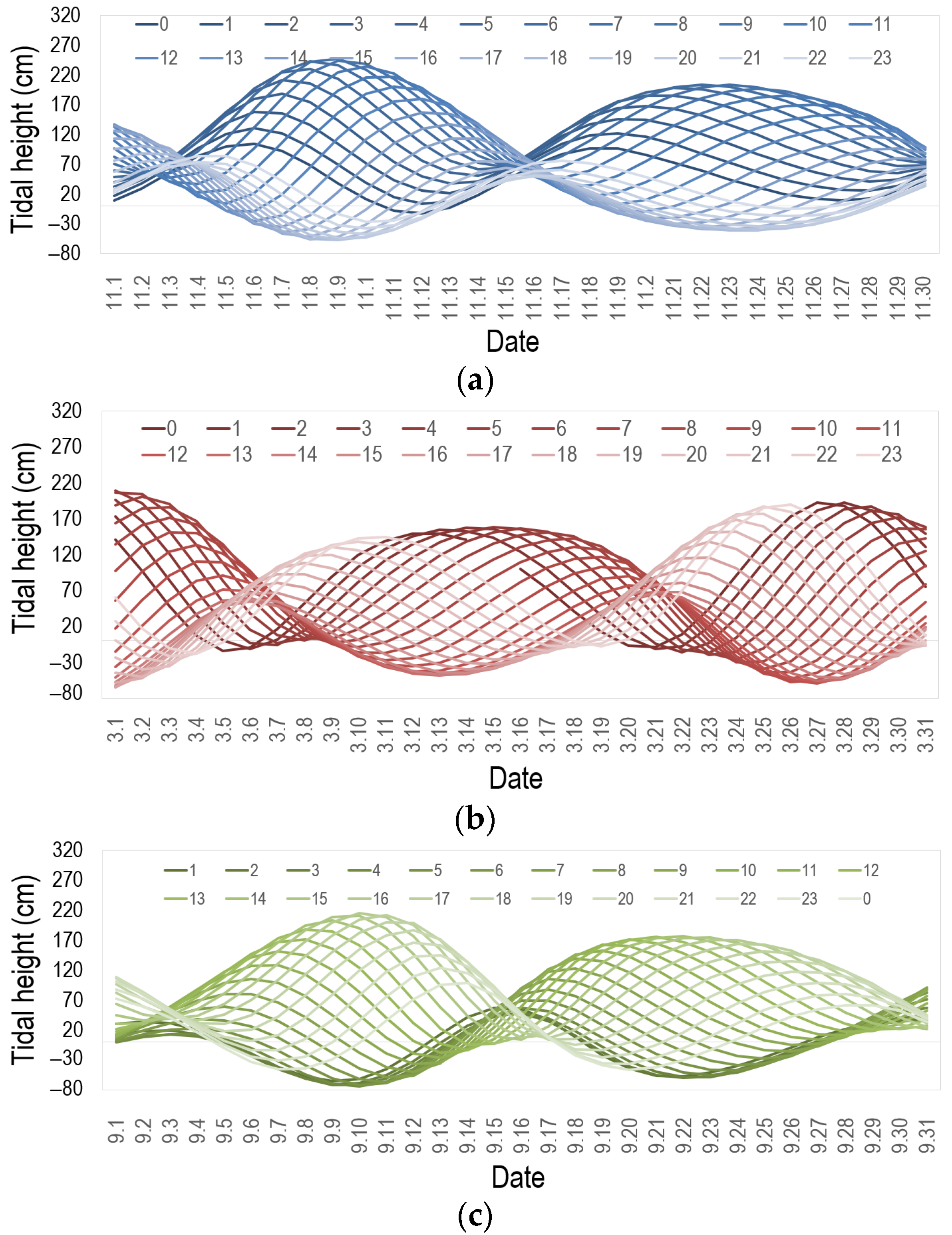
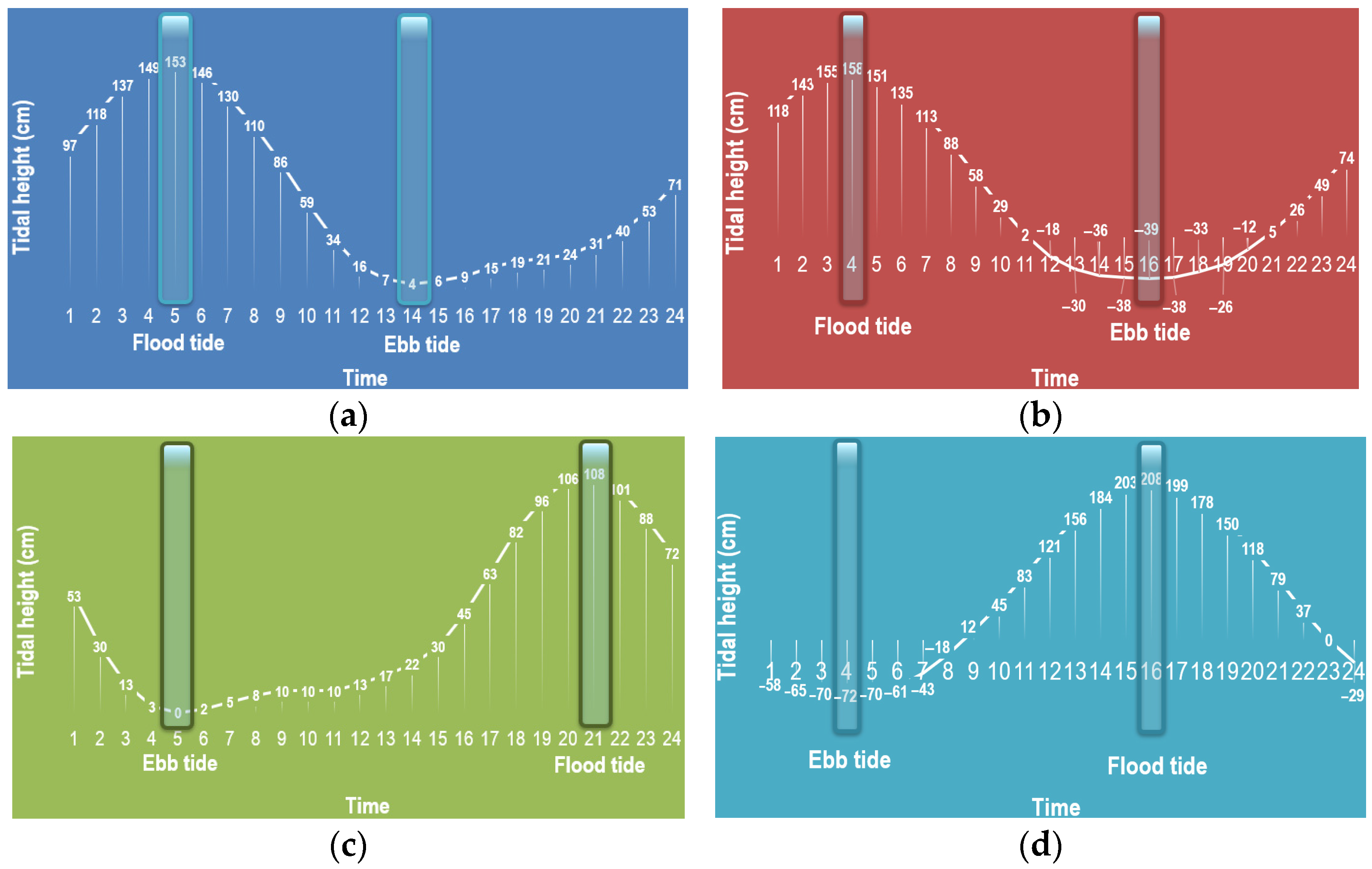
2.1.3. Tide Activity
2.2. Instruments
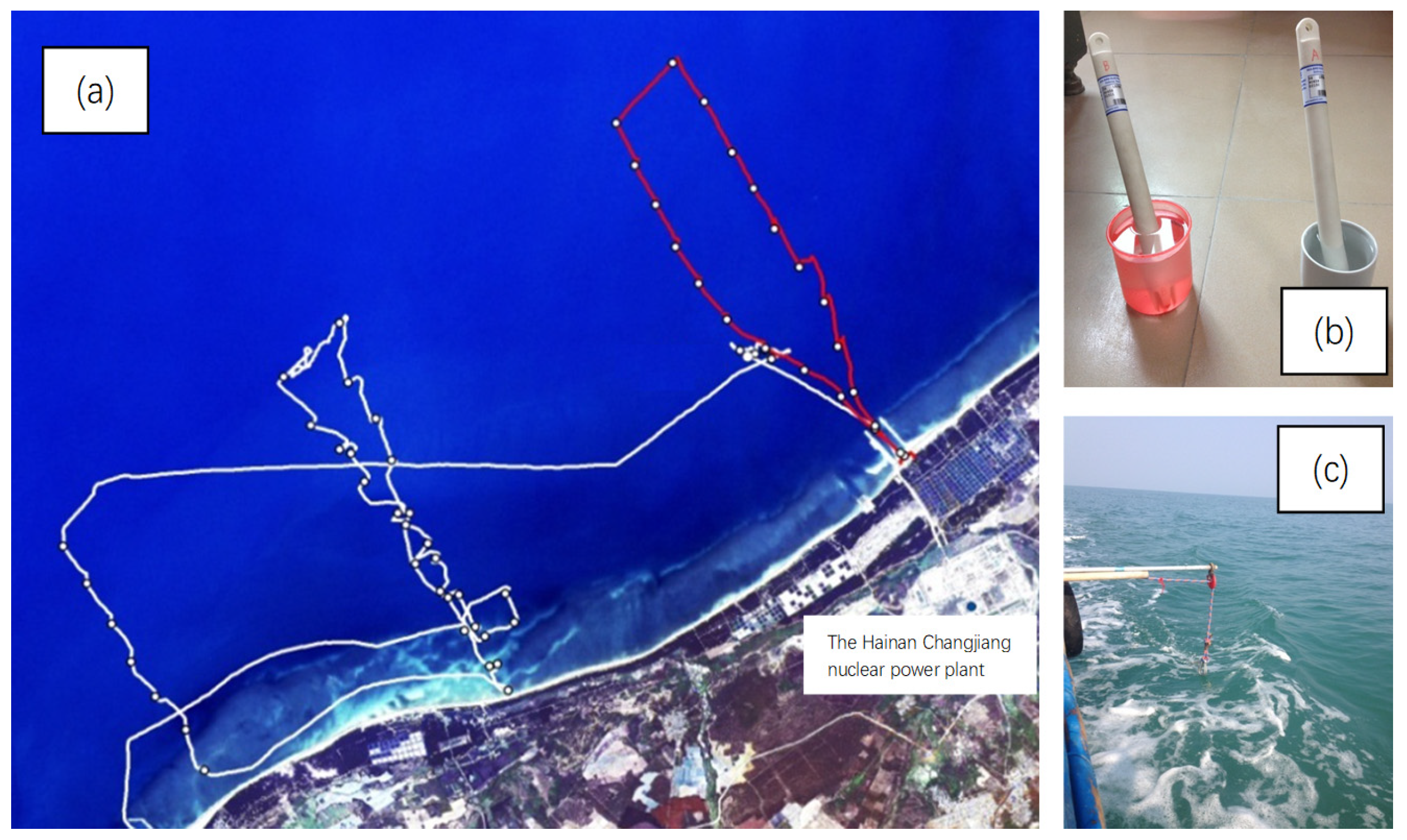
2.3. Airborne Hyperspectral Thermal Infrared Data
2.4. Sea Surface Temperature Data
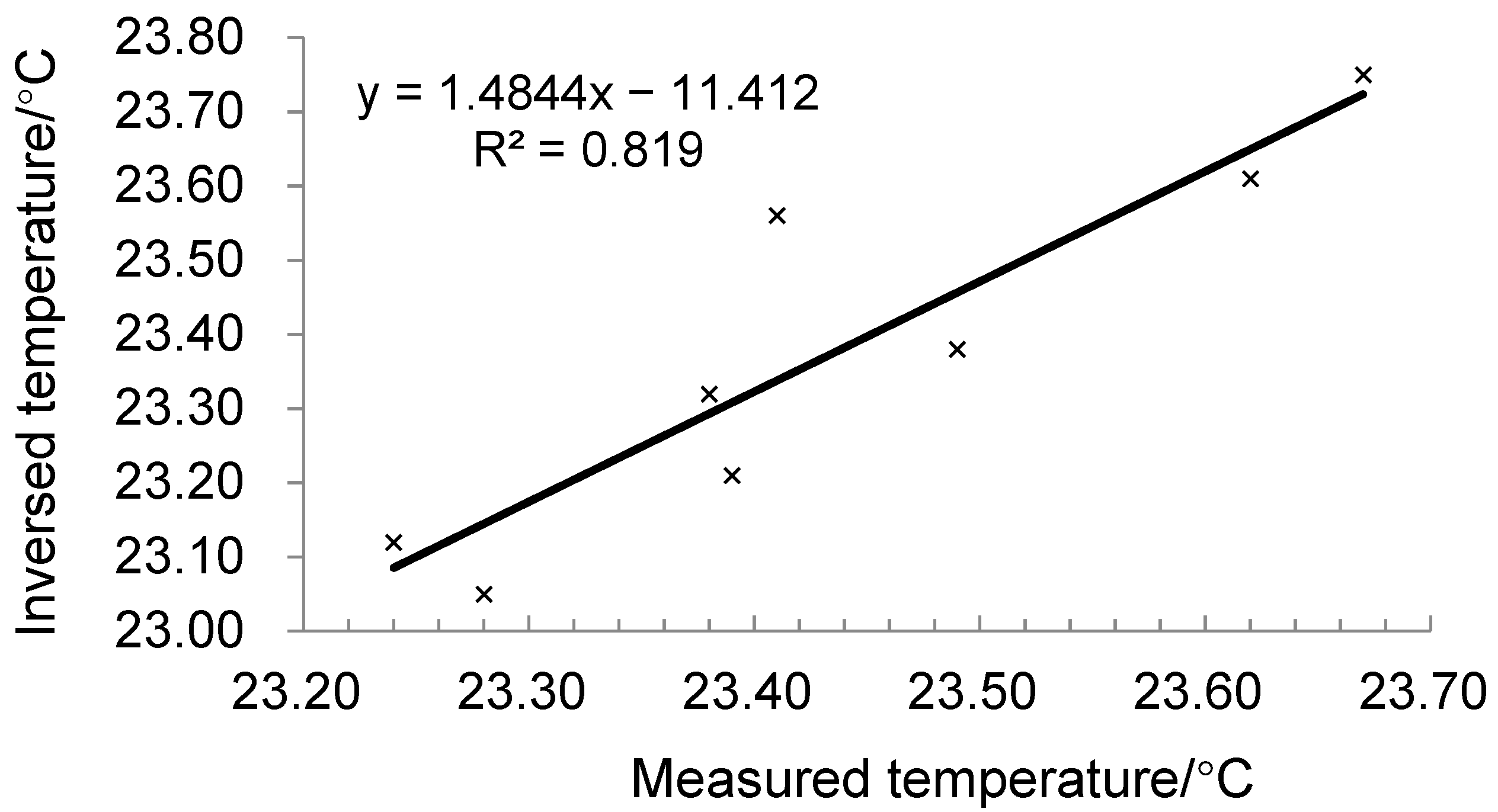
2.5. Algorithm Development
3. Results
- (1)
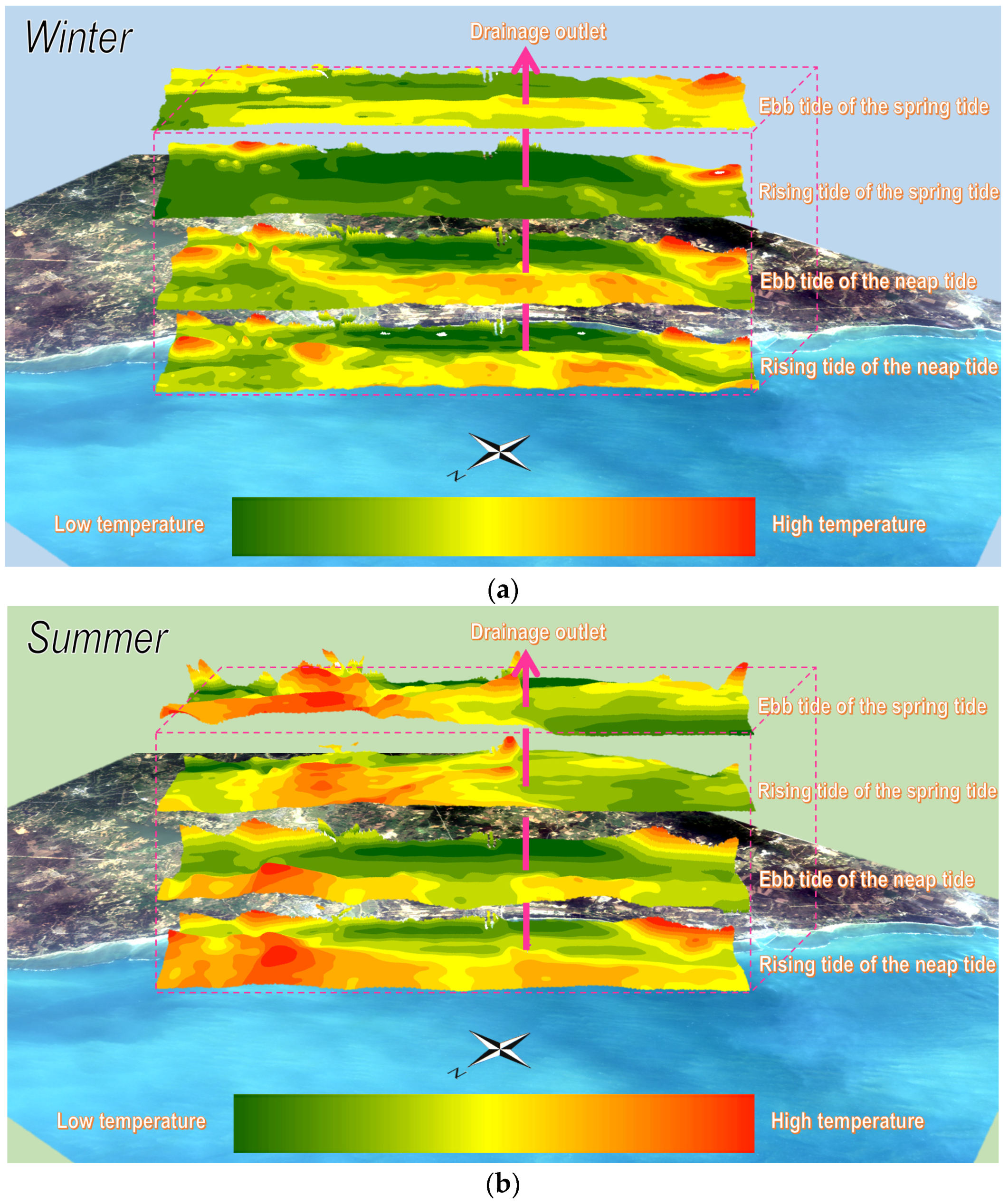
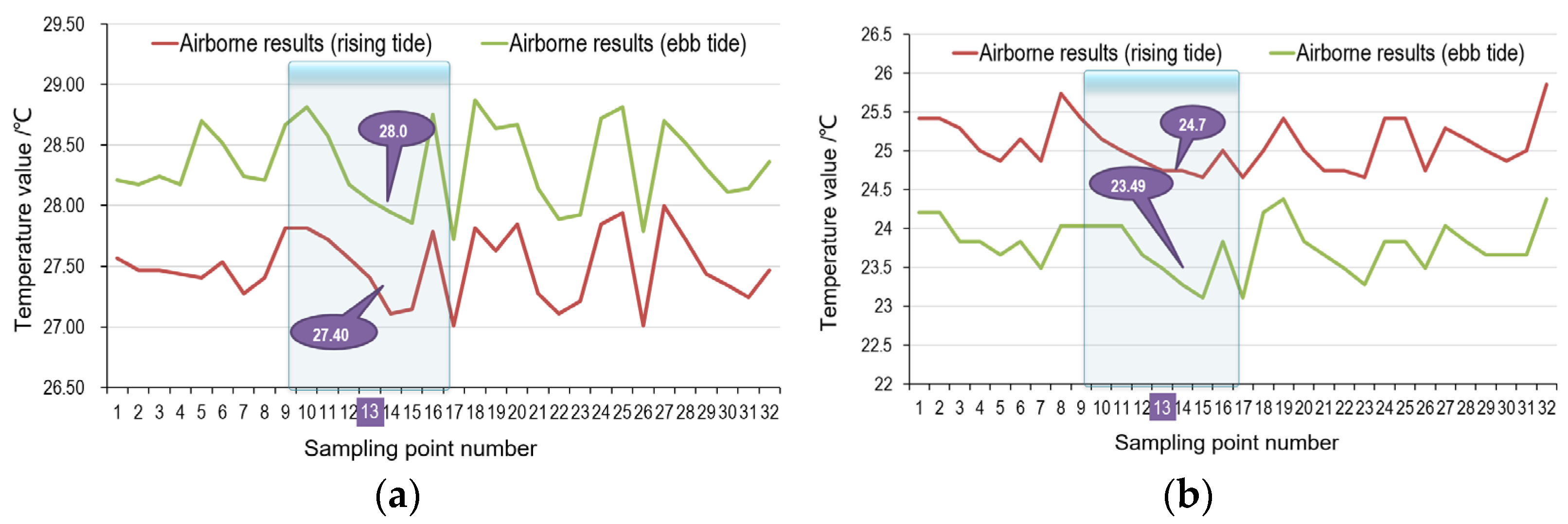
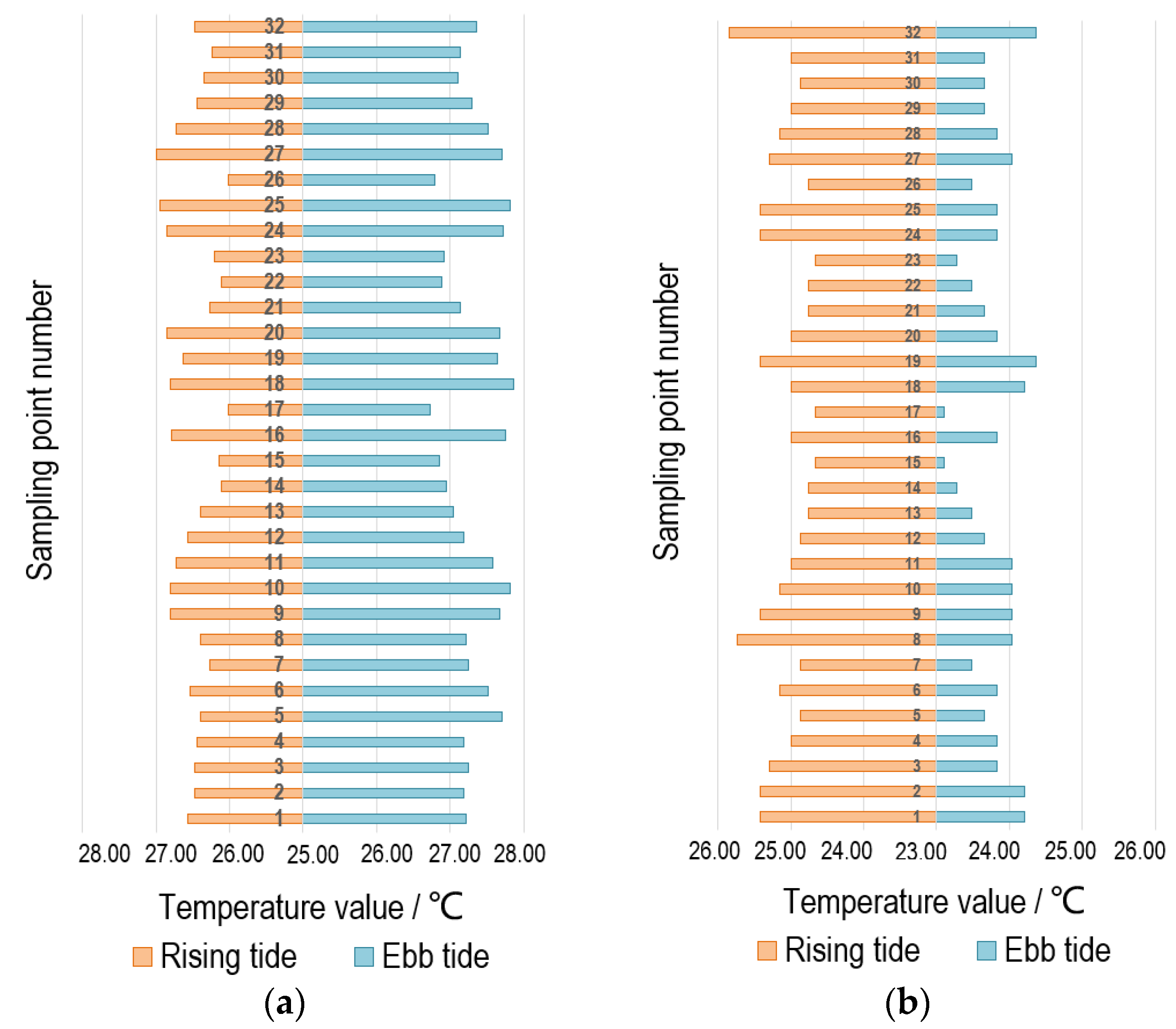
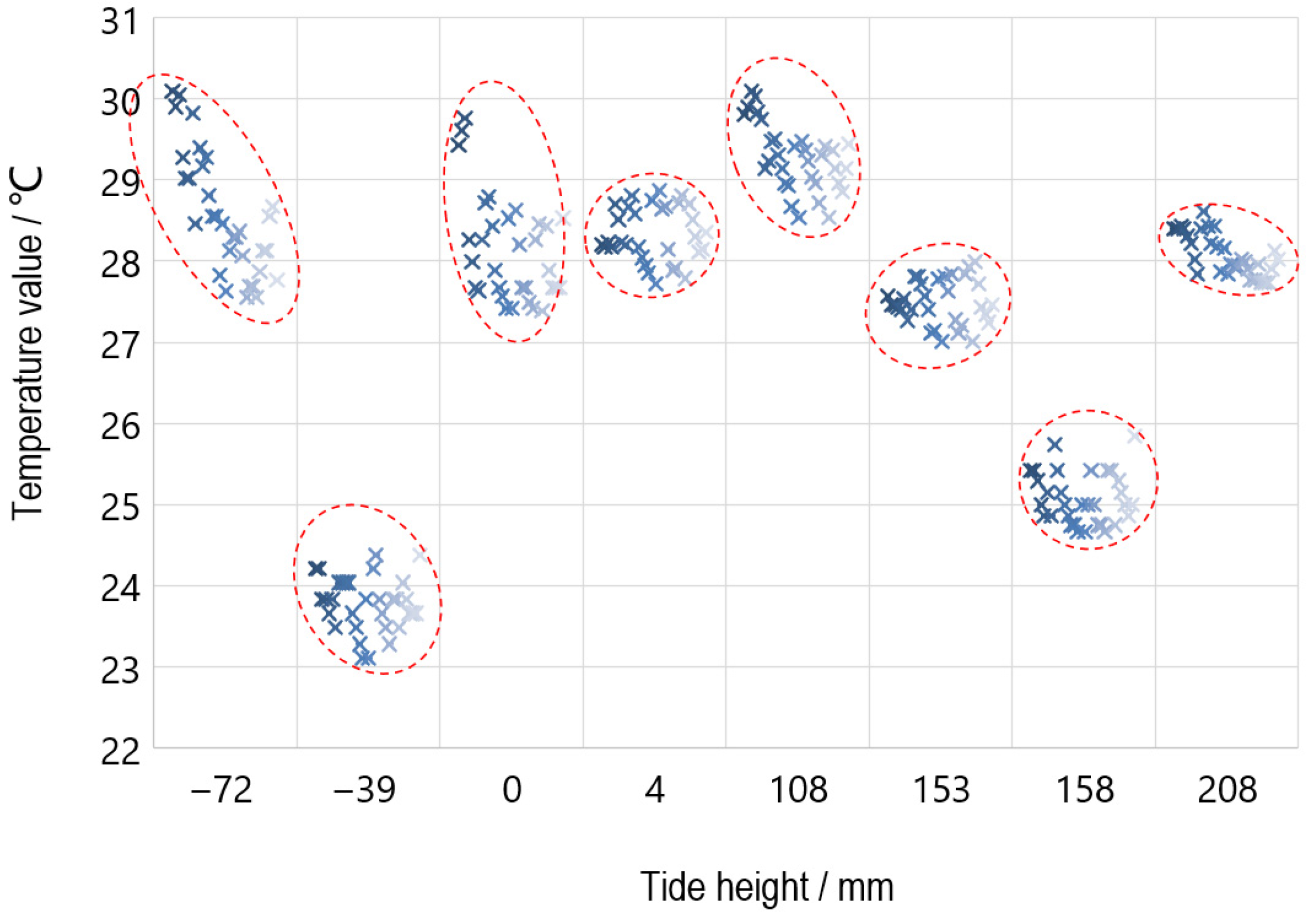
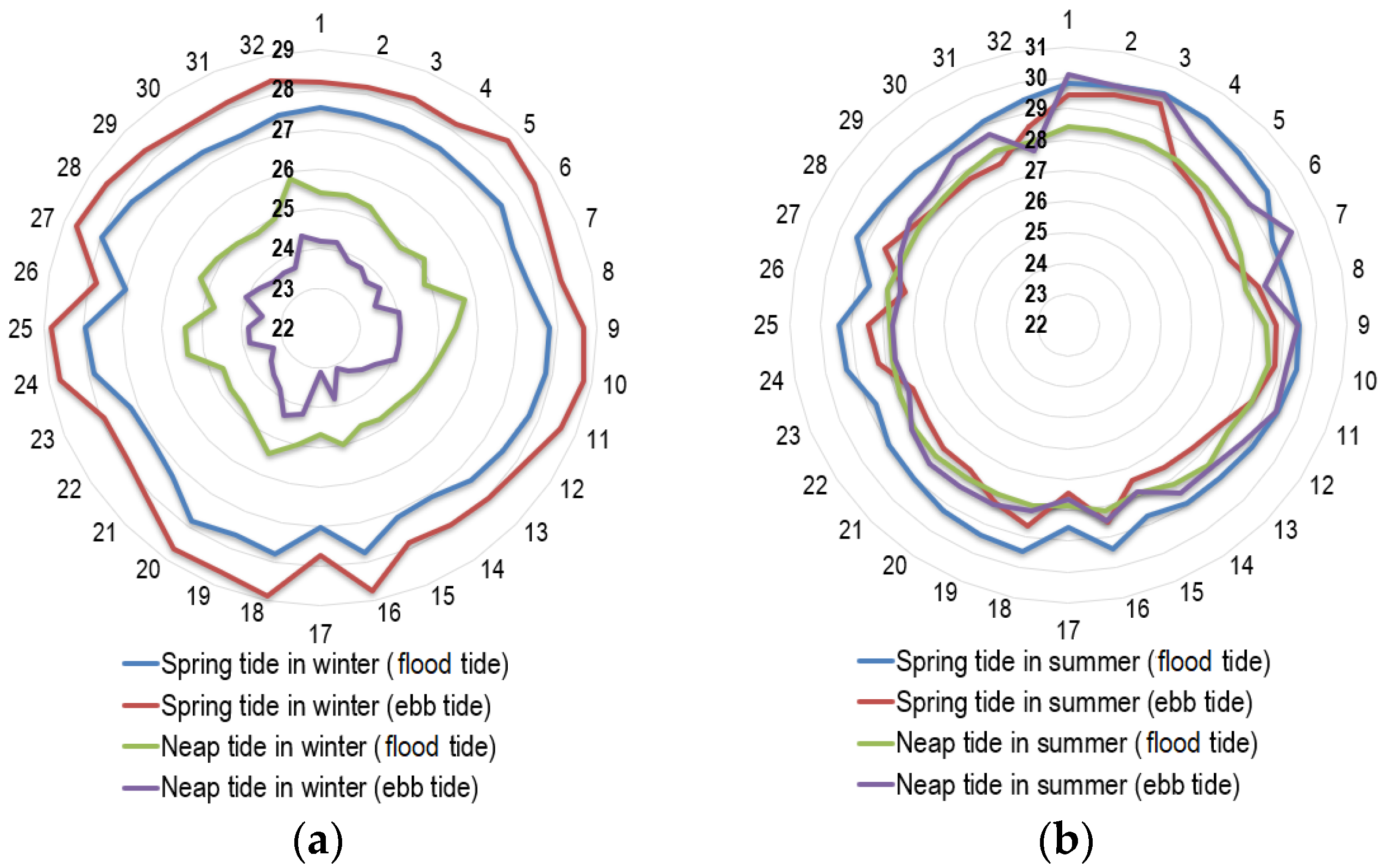
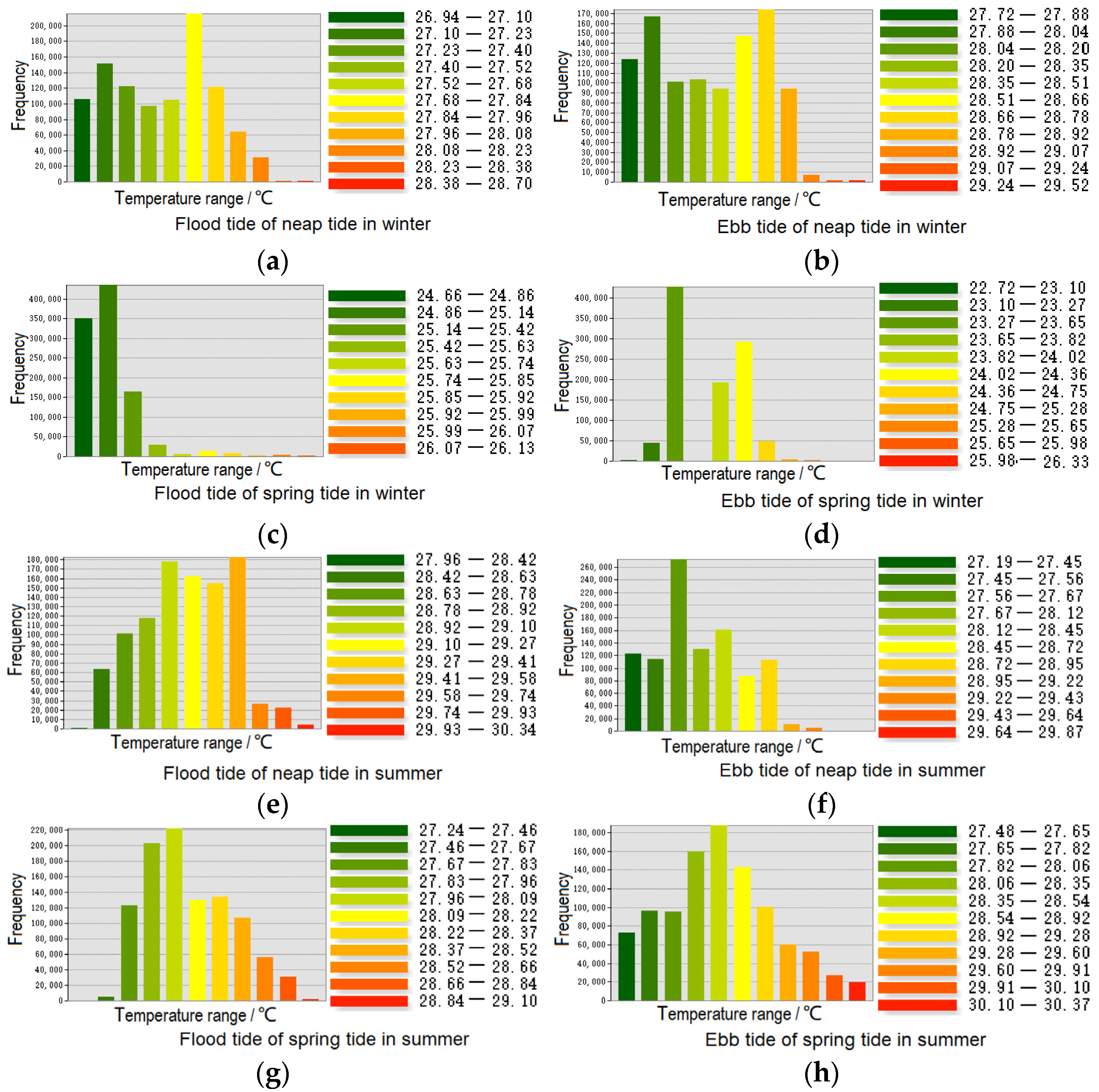
- The seawater temperature monitored on neap tides in winter suggested that the water temperature increases gradually with the distance from the coast, which was consistent with those observed in both the flooding-type tide and ebb tide periods. Obvious temperature diffusion lines can be seen near the outlet, and the seawater temperature is nearly 1 °C higher than that of the sea area along the coastline. The water temperature in the ebb tide period is higher than that in the flooding tide period, which is 28.75 °C and 27.78 °C, respectively. In the northeast of the study area, due to the ebb of the sea during the neap tide, some shallow beaches and reefs at the base were exposed or were close to emerging over the sea, and the temperature rising effect was also obvious. The abnormally high temperature in this area was not caused by the warm drainage of the nuclear power plant only but also by the bare foreshore on the northeast and southwest coastline where the seawater temperature was high.
- (2)
- The heating effect of the warm drainage of the nuclear power plant on the whole study area was gradually weakened with the rise of the seawater level in spring tides in winter. During rising and ebb tides, the seawater temperature near the drainage was about 24.87 °C and 23.83 °C, respectively. The flooding-type tide inundated the reefs in the northeast of the study area, making the overall temperature tended to increase gradually from the coastline to the sea. The increase in water volume in the spring tide period and the stirring effect of deep seawater exacerbated the heat dissipation effect of the warm drainage of the nuclear power plant dramatically.
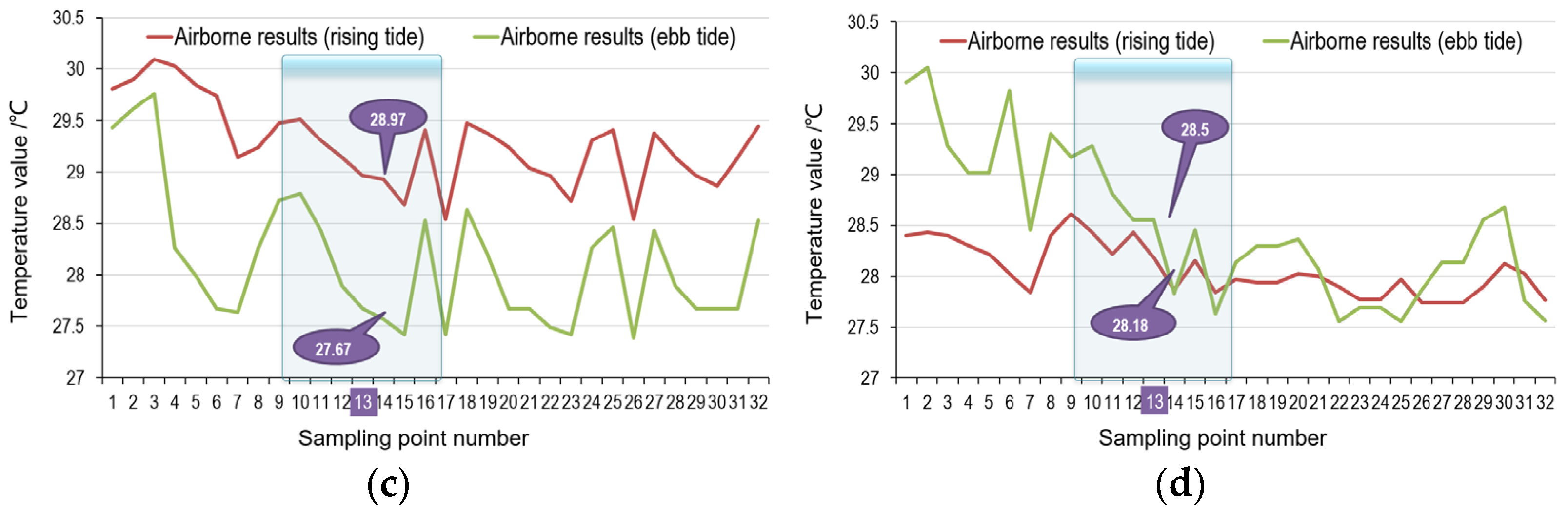
- (3)
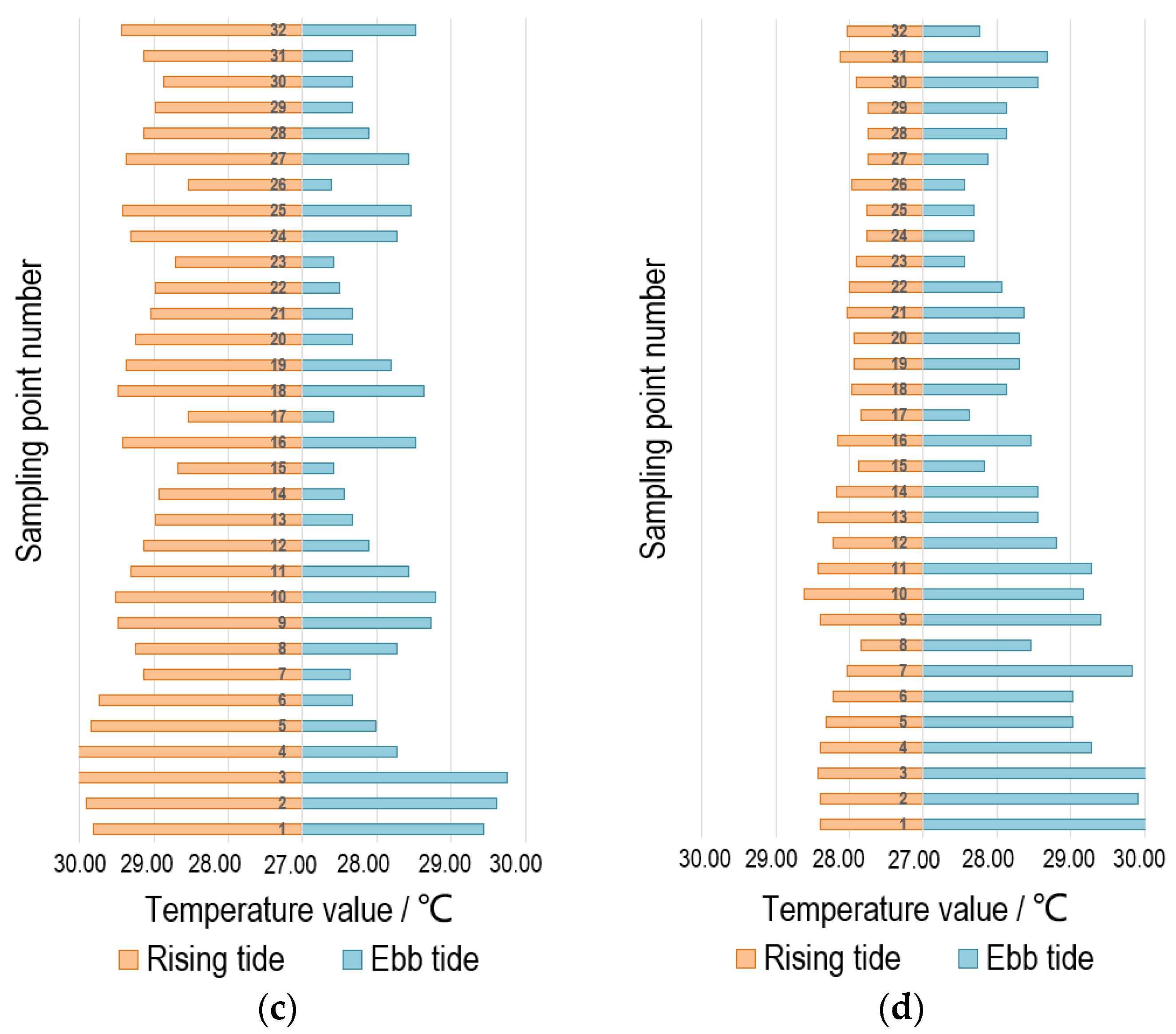
- The monitored seawater temperature in neap tides in summer exhibited that the nuclear power plant drainage mainly affected the water temperature of the northwest sea area, so did those in the rising and the ebb tide period, and the central water temperature was approximately 29.18 °C and 27.67 °C, respectively. It was worth noting that the reef temperature in the northeast and the beach temperature in the southwest of the study area was higher than that near the drainage, but the value is lower than that in the ebb tide in winter. The reason was that the overall seawater temperature was high, owing to the high ambient temperature in summer. The water temperature tended to increase from the coastline to the drainage, and the seawater temperature near the nuclear power plant was relatively low, which was consistent with those monitored in spring and neap tide in winter.
- (4)
- The temperature at the drainage diffused to the northeast sea area according to monitored results of spring tides in summer, which occurred in both rising and ebb tides, and the water temperature in the center of the drainage was 28.73 °C and 30.19 °C, respectively. Due to the high tide level, the temperature interference of the reef and foreshore was not obvious. An interesting phenomenon was observed, namely that an obvious temperature-rising area in the coastal area perpendicular to the discharge drainage and the coast with a relatively high range and degree of temperature rising existed, which was probably caused by a new engineering project carried out on the bank resulting in the shallower seawater and higher temperature rising after on-site investigation.
4. Discussion
4.1. Multi-Scale Seawater Temperature Analysis
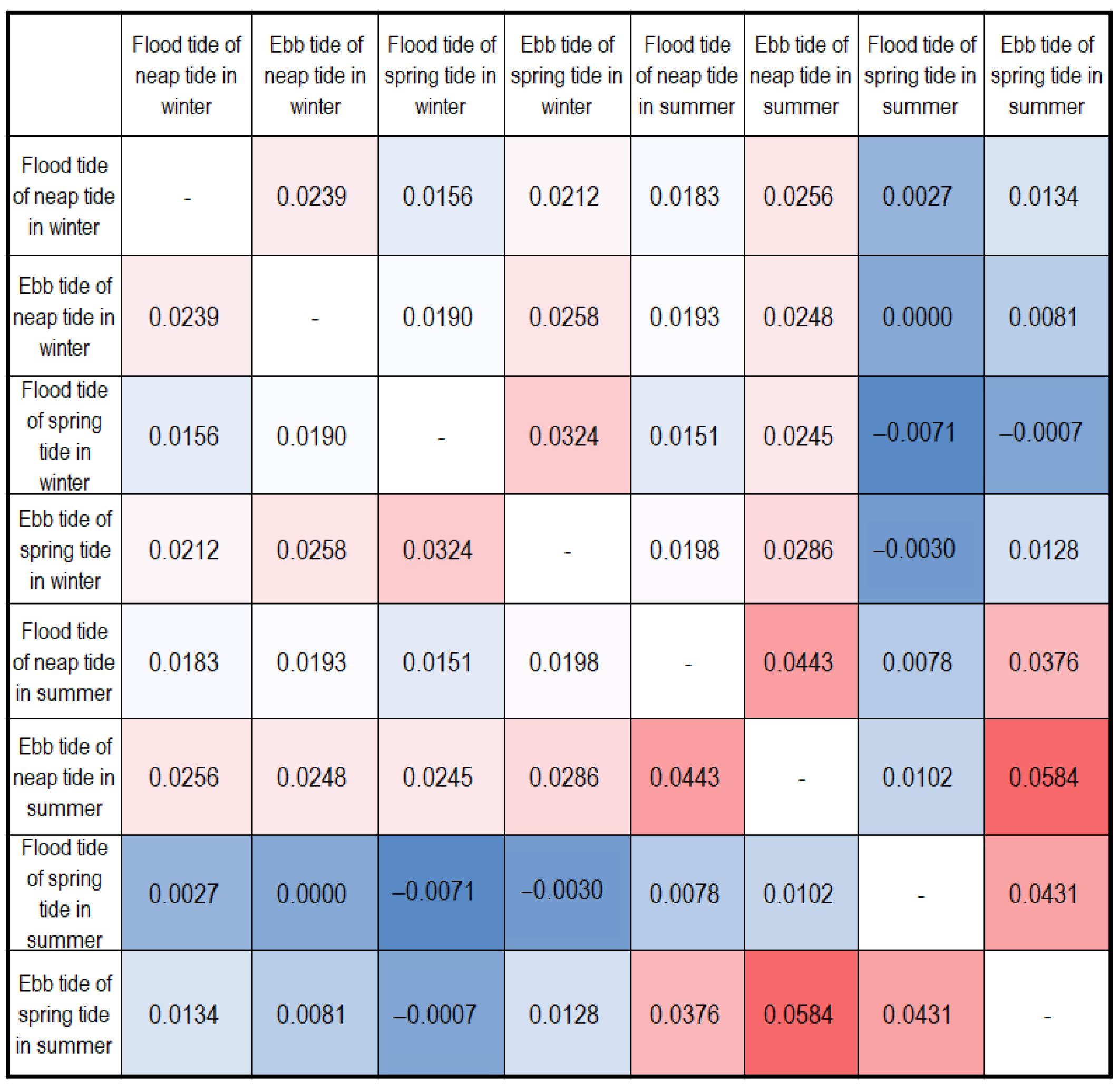
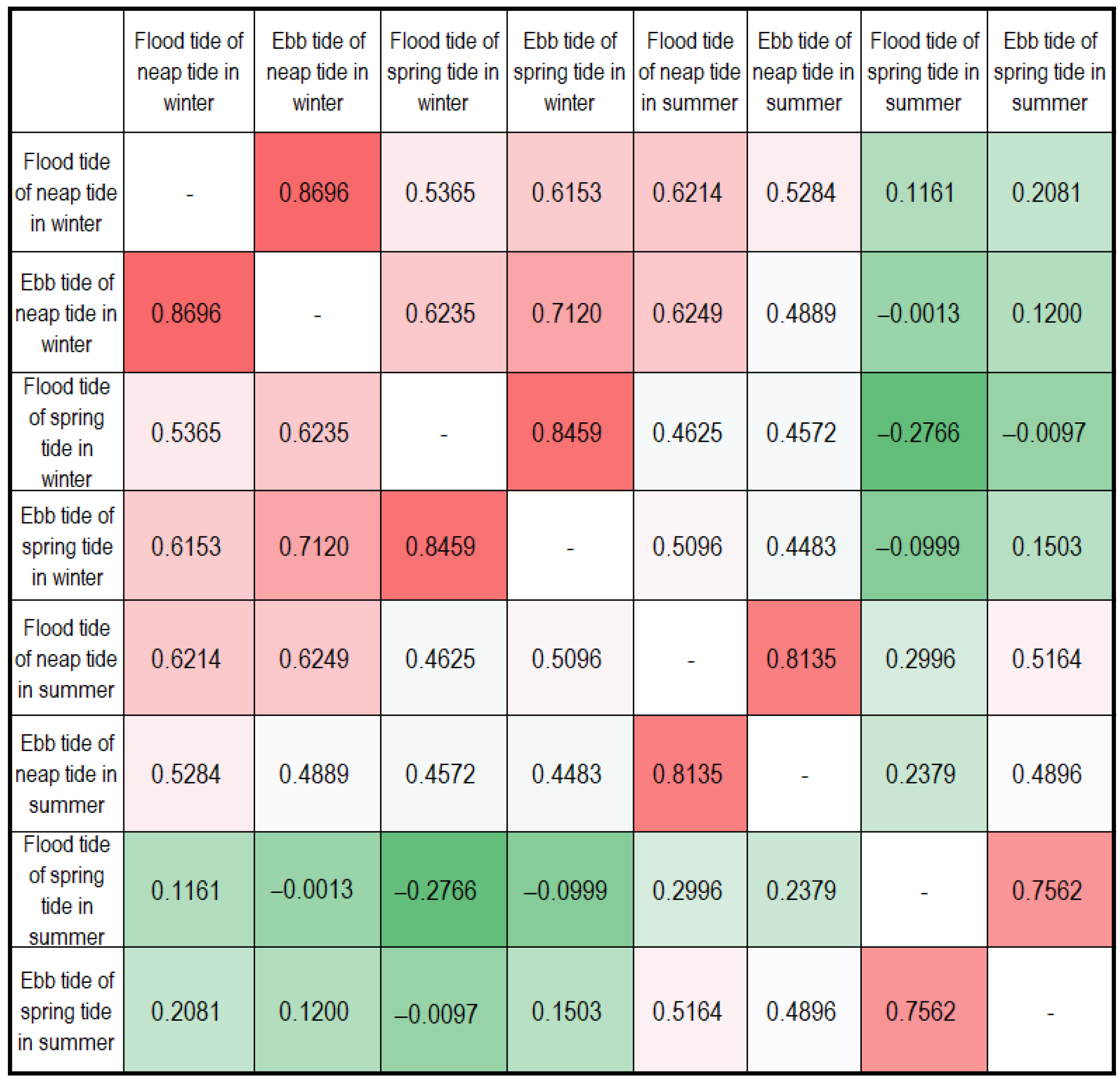
4.2. Temperature and Tide Response
4.3. Seasonal Variation Characteristics of Seawater Temperatures
4.4. Seawater Temperature Distribution Characteristics under Different Tides
4.5. Exploration on the Determinants of Temperature
5. Conclusions
- (1)
- The monitoring results show that the surrounding 120 km2 of sea area has a warming effect due to the role of thermal drainage. The effect is most obvious in the 1 km buffer zone centered on the drainage. The seawater temperature is increased by 1.5 °C to 4.0 °C at various tide levels. Remote sensing technology provides an effective investigation means for the temperature measurement caused by drainage in industrial sea areas with its macro, fast and dynamic characteristics [12]. However, the current time resolution of aerospace remote sensing data cannot meet the measurement requirements due to the precise time required for the measurement of typical tidal conditions, such as floods, ebb periods of spring and neap tides, etc. (about 60 min). The research indicates that airborne remote sensing has the advantages of controllable measurement time and high measurement accuracy compared with aerospace remote sensing technology [35]. The implementation of airborne thermal infrared remote sensing measurement and data processing technology in this paper has important enlightening significance for the research in this field.
- (2)
- Combined with the observation data of sea surface fixed-point water temperature according to the inversion of airborne remote sensing data of water temperature in the nearshore sea area of the plant site, the distribution map of water temperature rise area under 8 tides in winter and summer is obtained, which provided important information for the environmental impact assessment of warm drainage. The results have significant application value for mastering the response relationship between industrial warm drainage and different seasons, different tidal levels, and tidal periods, as well as the flow direction, area and distribution range of warm drainage.
- (3)
- This study suggested that the advantages of satellite data are low cost and large-scale monitoring, but the disadvantages are that the temporal and spatial resolution is not high enough, and its application in monitoring industrial temperature and drainage is very limited. However, these shortcomings will be overcome, and the application prospect will be broad with the deployment of the constellation plan. Airborne data is flexible and can obtain multiple tidal thermal infrared data in one day. So, it is a relatively scientific data acquisition method at present.
- (4)
- Warm drainage will cause the coastal waters to warm up, and the original phytoplankton will be wiped out massively, then bringing new species [2,3]. Consequently, a chain of ecological disasters will be triggered in the absence of natural enemies. It was concluded that the decisive factor dominating the diffusion of warm drainage was season by calculating the controlling factor of water temperature under various combinations. This conclusion has important enlightening significance for industrial drainage site selection, diffusion condition simulation and environmental impact assessment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Song, Y.; Sun, X.; Xia, P.; Cui, Z.; Zhao, X. Research on the spatiotemporal evolution and influencing factors of green economic efficiency in the Yangtze River economic belt. Environ. Sci. Pollut. Res. 2022, 29, 68257–68268. [Google Scholar] [CrossRef]
- Anthony, E.J.; Marriner, N.; Morhange, C. Human influence and the changing geomorphology of Mediterranean deltas and coasts over the last 6000years: From progradation to destruction phase? Earth–Sci. Rev. 2014, 139, 336–361. [Google Scholar] [CrossRef]
- Walden, G.; Noirot, C.; Nagelkerken, I. A future 1.2 °C increase in ocean temperature alters the quality of mangrove habitats for marine plants and animals Georgia. Sci. Total Environ. 2019, 690, 596–603. [Google Scholar] [CrossRef]
- Joseph, J.T.; Rogers, A.D.; Henry, J.B.; Cochran, J.K.; Caitlin, R.Y. Identification and quantification of diffuse fresh submarine groundwater discharge via airborne thermal infrared remote sensing. Remote Sens. Environ. 2015, 171, 202–217. [Google Scholar] [CrossRef]
- Zhang, M.; Townend, I.; Cai, H. The influence of seasonal climate on the morphology of the mouth–bar in the Yangtze estuary, China. Cont. Shelf Res. A Companion J. Deep–Sea Res. Prog. Oceanogr. 2018, 153, 30–49. [Google Scholar] [CrossRef]
- Lou, Y.; Dai, Z.; He, Y.; Mei, X.; Wei, W. Morphodynamic couplings between the Biandan Shoal and Xinqiao Channel; Changjiang (Yangtze) Estuary. Ocean. Coast. Manag. 2020, 183, 105036.1–105036.13. [Google Scholar] [CrossRef]
- Ashikur, M.R.; Rupom, R.S.; Sazzad, M.H. A remote sensing approach to ascertain spatial and temporal variations of seawater quality parameters in the coastal area of bay of Bengal, Bangladesh. Remote Sens. Appl. Soc. Environ. 2021, 23, 100593. [Google Scholar] [CrossRef]
- Chan, H.P.; Konstantinou, K.I. Multiscale and multitemporal surface temperature monitoring by satellite thermal infrared imagery at mayon volcano; philippines. J. Volcanol. Geotherm. Res. 2020, 401, 106976. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The new VIIRS 375m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1–km all–weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Storto, A.; Oddo, P. Optimal Assimilation of daytime SST retrievals from SEVIRI in a regional ocean prediction system. Remote Sens. 2019, 11, 2776. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Smith, G.B. Thermal remote sensing of estuarine spatial dynamics: Effects of bottom–generated vertical mixing. Estuarine. Coast. Shelf Sci. 2008, 78, 587–591. [Google Scholar] [CrossRef]
- Calderon, R.; Navas–Cortes, J.A.; Lucena, C. High–resolution airborne hyperspectral and thermal imagery for early; detection of Verticillium wilt of olive using fluorescence; temperature and narrow–band spectral indices. Remote Sens. Environ. 2013, 139, 231–245. [Google Scholar] [CrossRef]
- Wu, Y.; Shan, Y.; Lai, Y.; Zhou, S. Method of Calculating Land Surface Temperatures Based on the Low–altitude UAV Thermal Infrared Remote Sensing Data and the Near–ground Meteorological Data. Sustain. Cities Soc. 2021, 78, 103615. [Google Scholar] [CrossRef]
- Longfei, C.; Wanchang, Z.; Yaning, Y.; Zhijie, Z.; Shijun, C. Long Time–Series Glacier Outlines in the Three–Rivers Headwater Region from 1986 to 2021 Based on Deep Learning. IEEE J.–STARS 2022, 15, 5734–5752. [Google Scholar] [CrossRef]
- Lou, Y.; Dai, Z.; Long, C.; Dong, H.; Ge, Z. Image–based machine learning for monitoring the dynamics of the largest salt marsh in the Yangtze River delta. J. Hydrol. 2022, 608, 127681. [Google Scholar] [CrossRef]
- Htk, A.; Wkla, B. Remote sensing of coastal hydro–environment with portable unmanned aerial vehicles (pUAVs) a state–of–the–art review—ScienceDirect. J. Hydro–Environ. Res. 2021, 37, 32–45. [Google Scholar] [CrossRef]
- Rossini, M.; Fava, F.; Cogliati, S. Assessing canopy PRI from airborne imagery to map water stress in maize. Isprs J. Photogramm. Remote Sens. 2013, 86, 168–177. [Google Scholar] [CrossRef]
- Sheng, L.Y.; Azhari, A.W.; Ibrahim, A.H. Unmanned aerial vehicle for eutrophication process monitoring in Timah Tasoh Dam, Perlis, Malaysia. IOP Conf. Ser. Earth Environ. Sci. 2021, 646, 012057. [Google Scholar] [CrossRef]
- Yu, X. Retrieval of Water Quality from UAV–Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms. Remote Sens. 2021, 13, 3928. [Google Scholar] [CrossRef]
- Acharya, B.S.; Bhandari, M.; Bandini, F.; Pizarro, A.; Perks, M.; Joshi, D.R.; Wang, S.; Dogwiler, T.; Ray, R.L.; Kharel, G.; et al. Unmanned Aerial Vehicles in Hydrology and Water Management: Applications, Challenges, and Perspectives. Water Resour. Res. 2021, 57, e2021WR029925. [Google Scholar] [CrossRef]
- Ma, B.; Pang, W.; Lou, Y.; Mei, X.; Dai, Z. Impacts of river engineering on multi–decadal water discharge of the mega–Changjiang river. Sustainability 2020, 12, 8060. [Google Scholar] [CrossRef]
- Pang, W.; Zhou, X.; Dai, Z.; Li, S.; Huang, H.; Lei, Y. ADV–Based Investigation on Bed Level Changes Over a Meso–Macro Tidal Beach. Front. Mar. Sci. 2021, 8, 733923. [Google Scholar] [CrossRef]
- Jie, W.; Zhijun, D.; Sergio, F.; Xiaohe, Z.; Xiaoqiang, L. Hydro–morphodynamics triggered by extreme riverine floods in a mega fluvial–tidal delta. Sci. Total Environ. 2021, 809, 152076. [Google Scholar] [CrossRef]
- Chuqi, L.; Zhijun, D.; Xiaoyan, Z.; Xuefei, M.; Cong, M. Mapping mangrove forests in the red river delta, Vietnam. For. Ecol. Manag. 2021, 483, 118910. [Google Scholar] [CrossRef]
- Leonardi, N.; Mei, X.; Carnacina, I.; Dai, Z. Marine sediment sustains the accretion of a mixed fluvial–tidal delta. Mar. Geol. 2021, 438, 106520. [Google Scholar] [CrossRef]
- Pang, W.; Dai, Z.; Ma, B.; Wang, J.; Li, S. Linkage between turbulent kinetic energy; waves and suspended sediment concentrations in the nearshore zone. Mar. Geol. 2020, 425, 106190. [Google Scholar] [CrossRef]
- Zhang, M.; Townend, I.; Zhou, Y.; Cai, H. Seasonal variation of river and tide energy in the Yangtze estuary, China. Earth Surf. Process. Landforms. 2015, 41, 98–116. [Google Scholar] [CrossRef]
- Xm, A.; Zda, B.; Sed, C.; Min, Z.; Hc, E.; Jie, W.A. Landward shifts of the maximum accretion zone in the tidal reach of the Changjiang estuary following construction of the three gorges dam. J. Hydrol. 2020, 592, 125789. [Google Scholar] [CrossRef]
- Zhang, M.; Townend, I.; Zhou, Y.; Wang, L.; Dai, Z. An examination of estuary stability in response to human interventions in the south branch of the Yangtze (Changjiang) estuary, China. Estuar. Coast. Shelf Sci. 2019, 228, 106383.1–106383.14. [Google Scholar] [CrossRef]
- Richardson, L.L.; Ledrew, E.F. Remote sensing and the science, monitoring, and management of aquatic coastal ecosystems. In Remote Sensing of Aquatic Coastal Ecosystem Processes; Springer: Dordrecht, The Netherlands, 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, J.; Dai, Z.J.; Mei, X.; Fagherazzi, S. Tropical cyclones significantly alleviate mega–deltaic erosion induced by high riverine flow. Geophys. Res. Lett. 2020, 47, e2020GL089065. [Google Scholar] [CrossRef]
- Zhang, M.; Dai, Z.; Bouma, T.J.; Bricker, J.; Cai, H. Tidal–flat reclamation aggravates potential risk from storm impacts. Coast. Eng. 2021, 166, 103868. [Google Scholar] [CrossRef]
- Zhou, X.; Dai, Z.; Mei, X. The multi–decadal morphodynamic changes of the mouth bar in a mixed fluvial–tidal estuarine channel. Mar. Geol. 2020, 429, 106311. [Google Scholar] [CrossRef]
- Klose, A.D.; Ntziachristos, V.; Hielscher, A.H. The inverse source problem based on the radiative transfer equation in optical molecular imaging. J. Comput. Phys. 2005, 202, 323–345. [Google Scholar] [CrossRef]
- Guo, J.; Shi, J.; Qi, W. Inversion land surface temperature by using TM data. Proc. SPIE Int. Soc. Opt. Eng. 2012, 8513, 85130D-9. [Google Scholar] [CrossRef]
- Jimenez–Munoz, J.C.; Cristobal, J.; Sobrino, J.A.; Soria, G.; Pons, X. Revision of the single–channel algorithm for land surface temperature retrieval from Landsat thermal–infrared data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Luo, B.K.; Minnett, P.J.; Gentemann, C.; Szczodrak, G. Improving satellite retrieved night–time infrared sea surface temperatures in aerosol contaminated regions. Remote Sens. Environ. 2019, 223, 8–20. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Katsuaki, K. Comparison of hyperspectral transformation accuracies of multispectral Landsat TM.; ETM+; OLI and EO–1 ALI images for detecting minerals in a geothermal prospect area. ISPRS J. Photogramm. Remote Sens. 2018, 137, 15–28. [Google Scholar] [CrossRef]

| No. | Type | Imaging Time | Spatial Resolution | Tidal Condition |
|---|---|---|---|---|
| 1 | TASI | 18 November 2017 | 1.0 m | Neap tide in winter |
| 2 | TASI | 15 March 2018 | 1.0 m | Spring tide in winter |
| 3 | TASI | 1 September 2018 | 1.0 m | Neap tide in summer |
| 4 | TASI | 9 September 2018 | 1.0 m | Spring tide in summer |
| No. | Date | Minimum Value (°C) | Maximum Value (°C) | Mean Value (°C) | Range (°C) | Standard Deviation (°C) | Tidal Condition |
|---|---|---|---|---|---|---|---|
| 1 | 18 November 2017 | 25.43 | 29.21 | 27.52 | 3.78 | 0.41 | Neap tide in winter |
| 26.35 | 30.01 | 28.31 | 3.66 | 0.42 | |||
| 2 | 15 March 2018 | 24.33 | 27.02 | 26.03 | 2.69 | 0.38 | Spring tide in winter |
| 22.54 | 26.53 | 24.03 | 3.99 | 0.45 | |||
| 3 | 1 September 2018 | 28.51 | 30.52 | 29.21 | 2.01 | 0.38 | Neap tide in summer |
| 26.39 | 30.41 | 28.24 | 4.02 | 0.63 | |||
| 4 | 9 September 2018 | 26.85 | 29.63 | 28.11 | 2.78 | 0.35 | Spring tide in summer |
| 26.89 | 30.85 | 28.58 | 3.96 | 0.82 |
| Point Number | C-01 | C-02 | C-03 | C-04 | C-05 | C-06 | C-07 | C-08 |
|---|---|---|---|---|---|---|---|---|
| Measured temperature | 23.39 °C | 23.38 °C | 23.41 °C | 23.67 °C | 23.62 °C | 23.49 °C | 23.28 °C | 23.24 °C |
| Inversed temperature | 23.21 °C | 23.32 °C | 23.56 °C | 23.75 °C | 23.61 °C | 23.38 °C | 23.05 °C | 23.12 °C |
| Relative error | −0.18 °C | −0.06 °C | 0.15 °C | 0.08 °C | −0.01 °C | −0.11 °C | −0.23 °C | −0.12 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhu, Z.; Zhang, L.; Sun, X.; Zhang, Z.; Zhang, W.; Li, X.; Zhu, Q. Response of Industrial Warm Drainage to Tide Revealed by Airborne and Sea Surface Observations. Remote Sens. 2023, 15, 205. https://doi.org/10.3390/rs15010205
Zhang D, Zhu Z, Zhang L, Sun X, Zhang Z, Zhang W, Li X, Zhu Q. Response of Industrial Warm Drainage to Tide Revealed by Airborne and Sea Surface Observations. Remote Sensing. 2023; 15(1):205. https://doi.org/10.3390/rs15010205
Chicago/Turabian StyleZhang, Donghui, Zhenchang Zhu, Lifu Zhang, Xuejian Sun, Zhijie Zhang, Wanchang Zhang, Xusheng Li, and Qin Zhu. 2023. "Response of Industrial Warm Drainage to Tide Revealed by Airborne and Sea Surface Observations" Remote Sensing 15, no. 1: 205. https://doi.org/10.3390/rs15010205
APA StyleZhang, D., Zhu, Z., Zhang, L., Sun, X., Zhang, Z., Zhang, W., Li, X., & Zhu, Q. (2023). Response of Industrial Warm Drainage to Tide Revealed by Airborne and Sea Surface Observations. Remote Sensing, 15(1), 205. https://doi.org/10.3390/rs15010205







