Plot Quality Aided Plot-to-Track Association in Dense Clutter for Compact High-Frequency Surface Wave Radar
Abstract
1. Introduction
2. Preliminaries
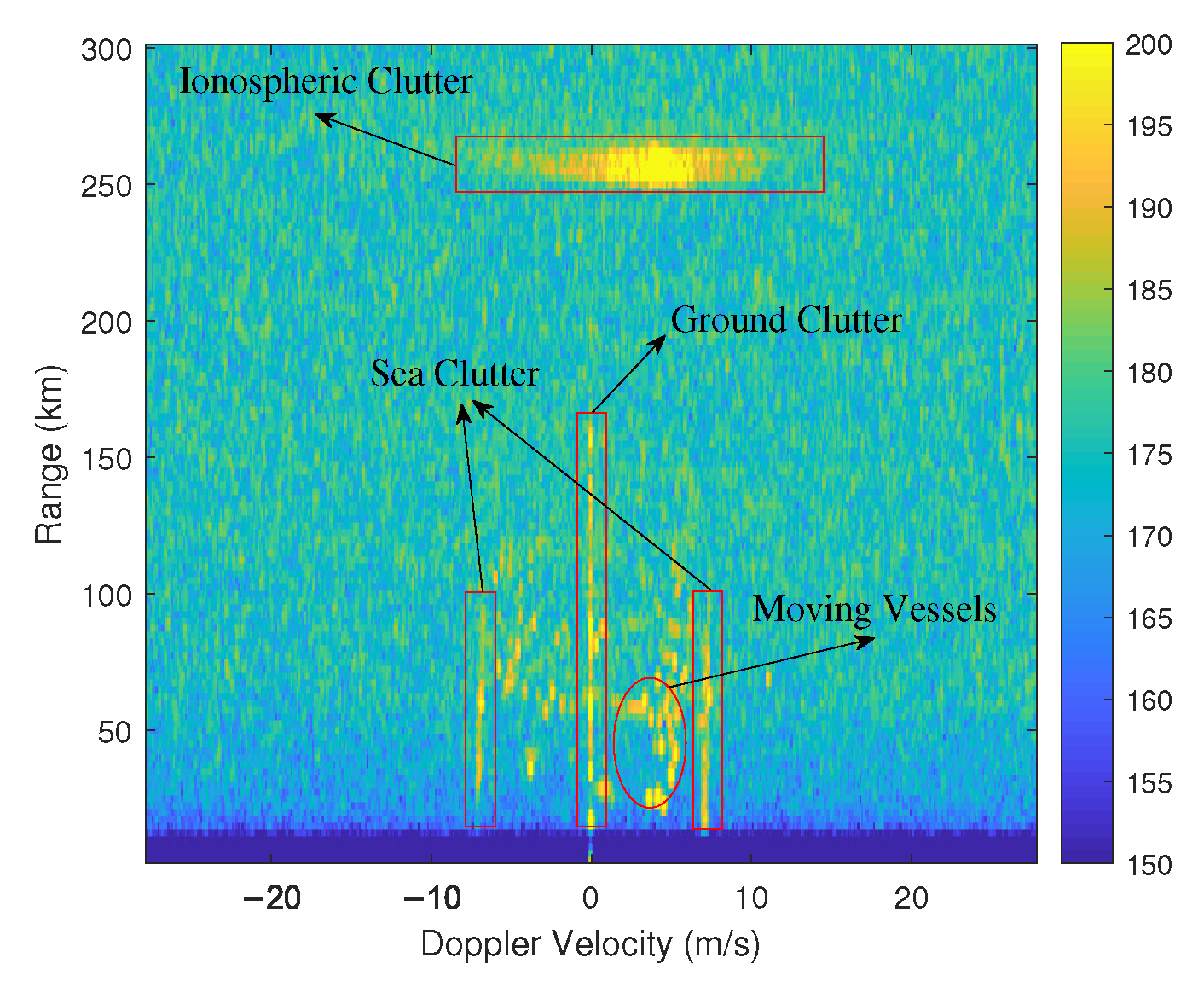
2.1. Moving Vessel Detection
2.2. Feature Analysis of Moving Vessels, Clutters, and Noise
2.3. Moving Vessel Tracking
- (1)
- The motion and measurement models
- (2)
- State prediction
- (3)
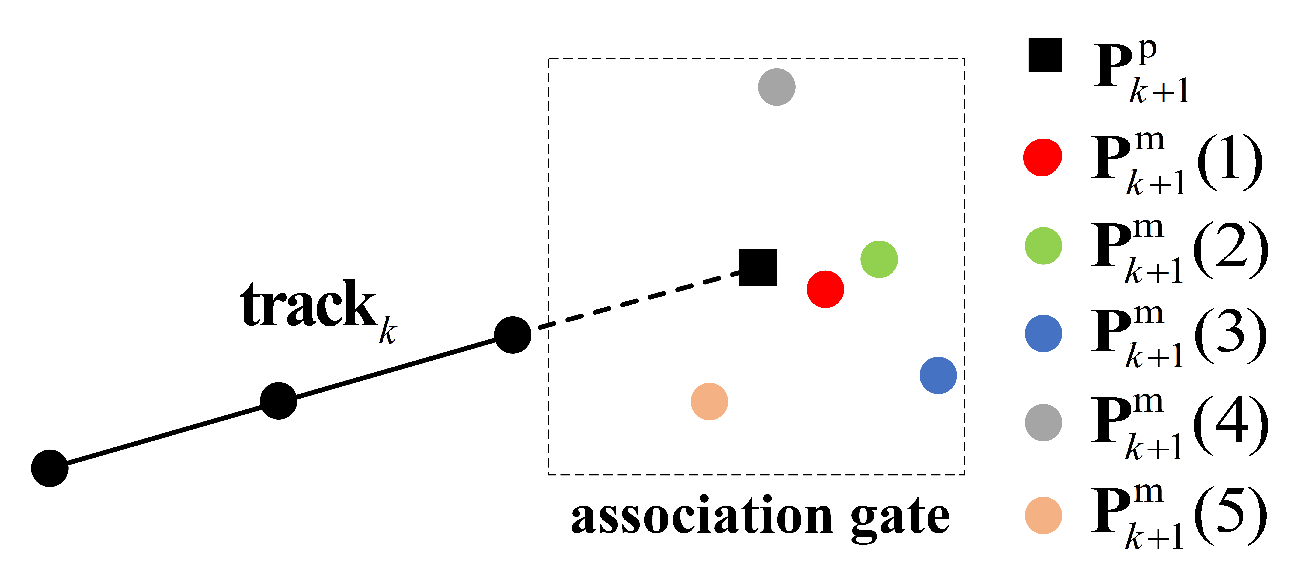
- Plot-to-track association
- (4)
- State estimation
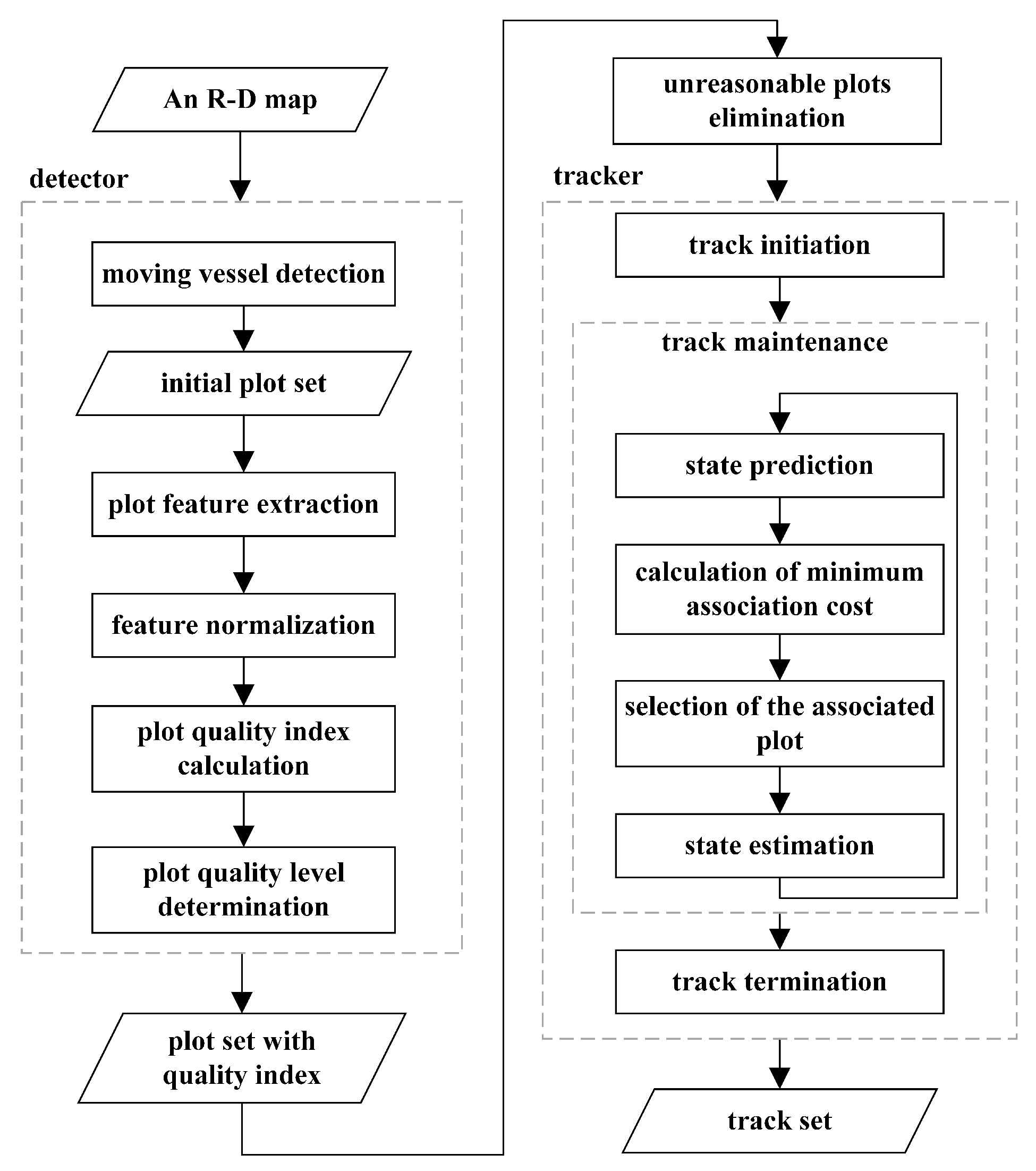
3. Methodology
3.1. Plot Quality Evaluation
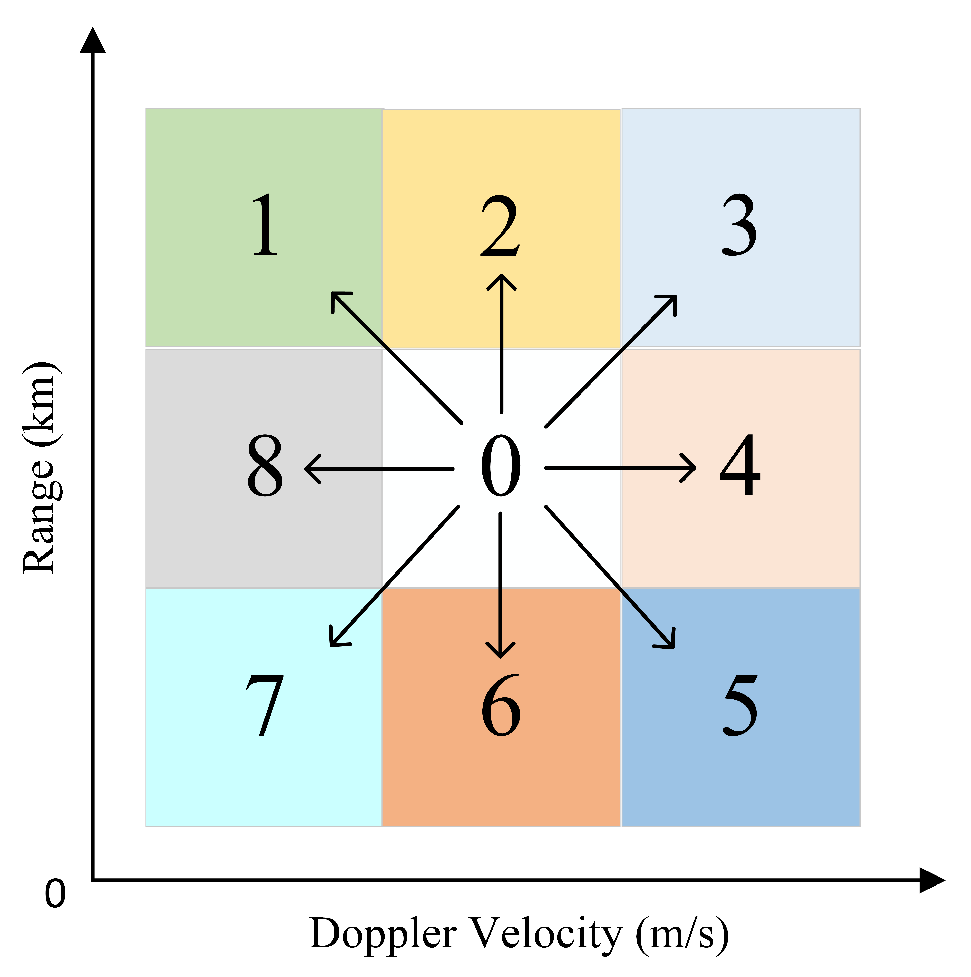
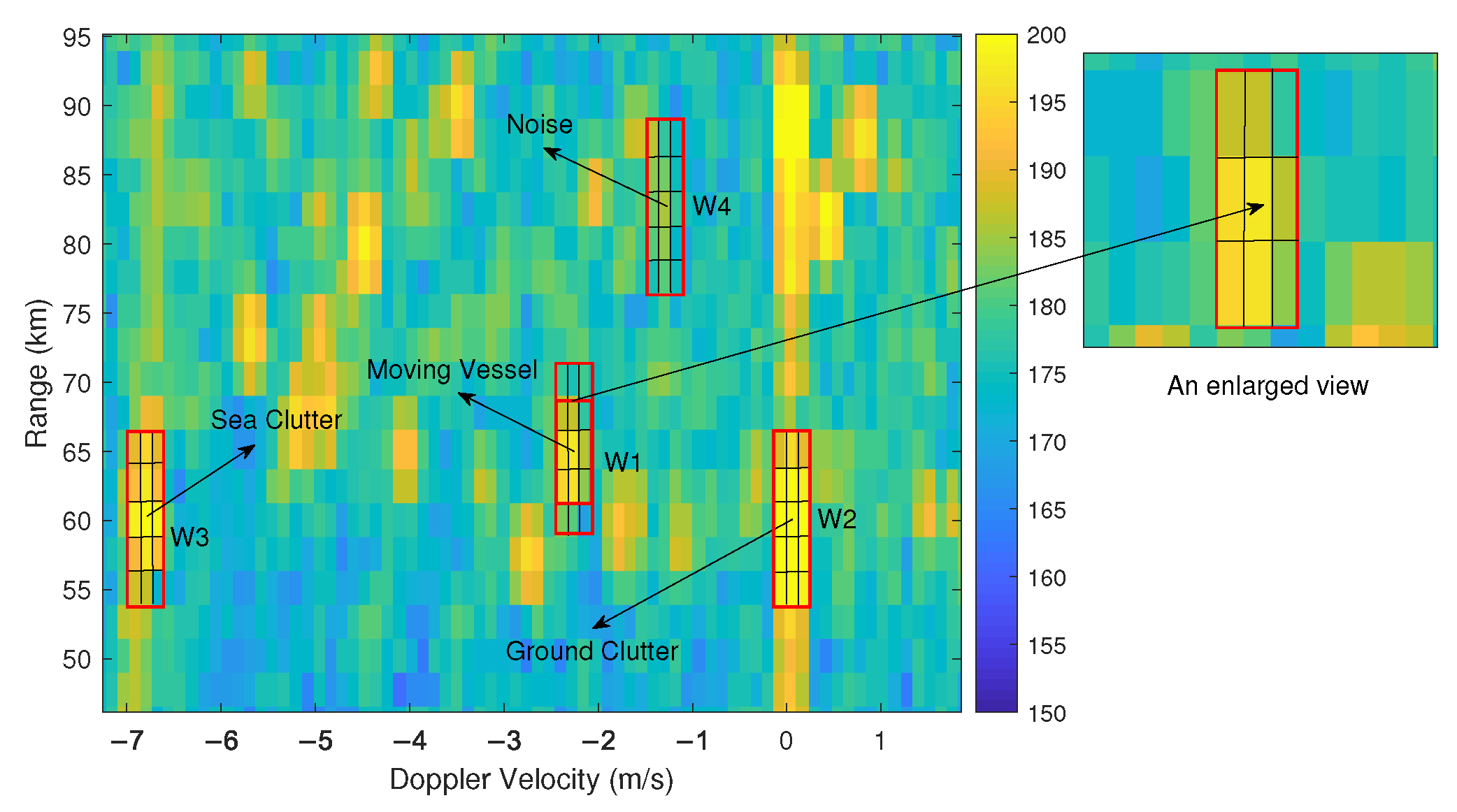
3.1.1. Plot Feature Extraction
- Multi-directional gradient
- Local variance
- Plot position probability
3.1.2. Feature Normalization
3.1.3. Plot Quality Index Calculation
3.1.4. Plot Quality Level Determination
3.2. Plot Quality Aided Plot-to-Track Association in Dense Clutter
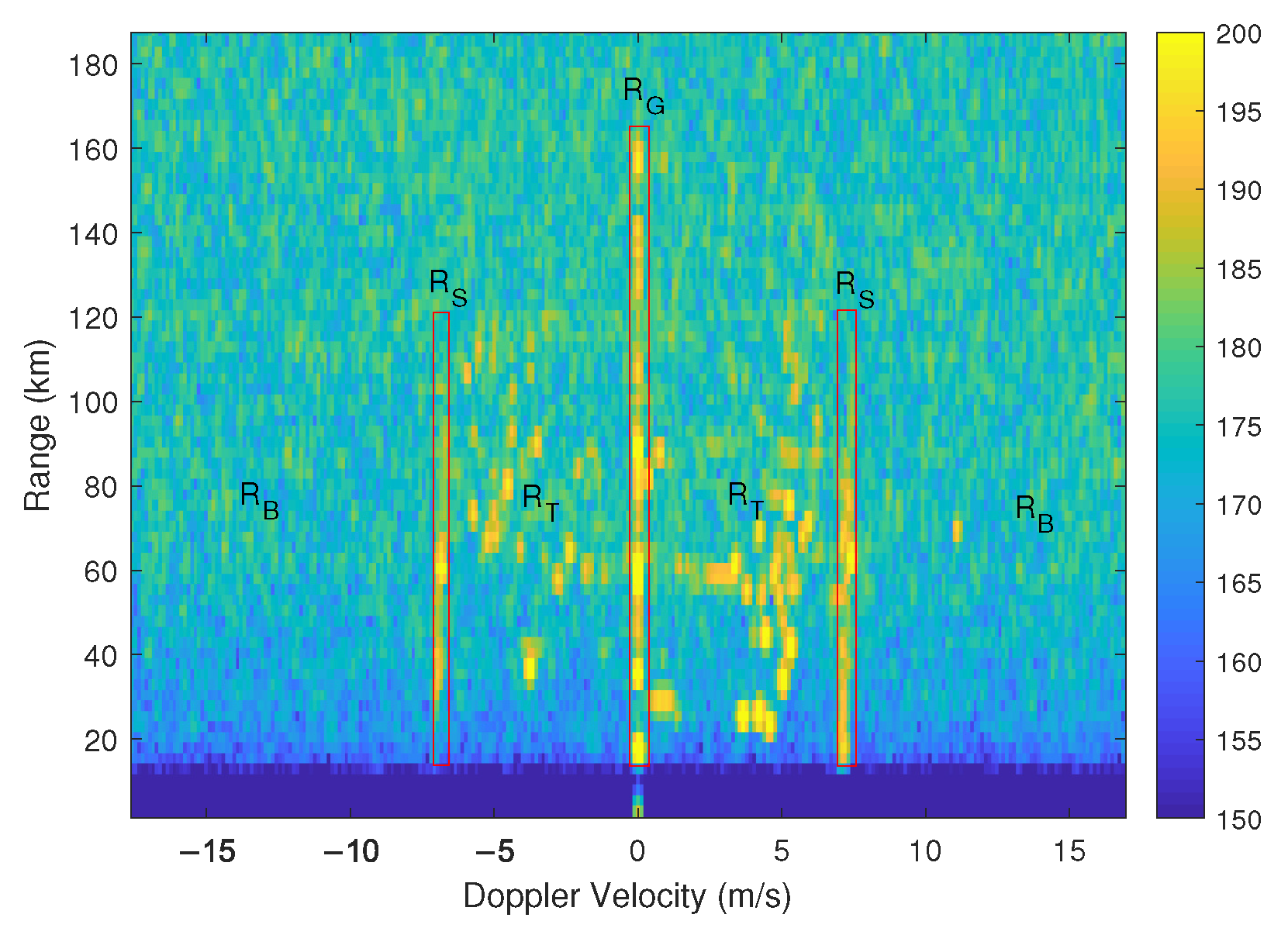
3.2.1. Unreasonable Plots Elimination
3.2.2. Calculation of Minimum Association Cost
3.2.3. Selection of the Associated Plot
4. Results of Experiments
- (1)
- Determination of U and V.
- (2)
- Determination of .
- (3)
- Determination of .
- (4)
- Determination of and .
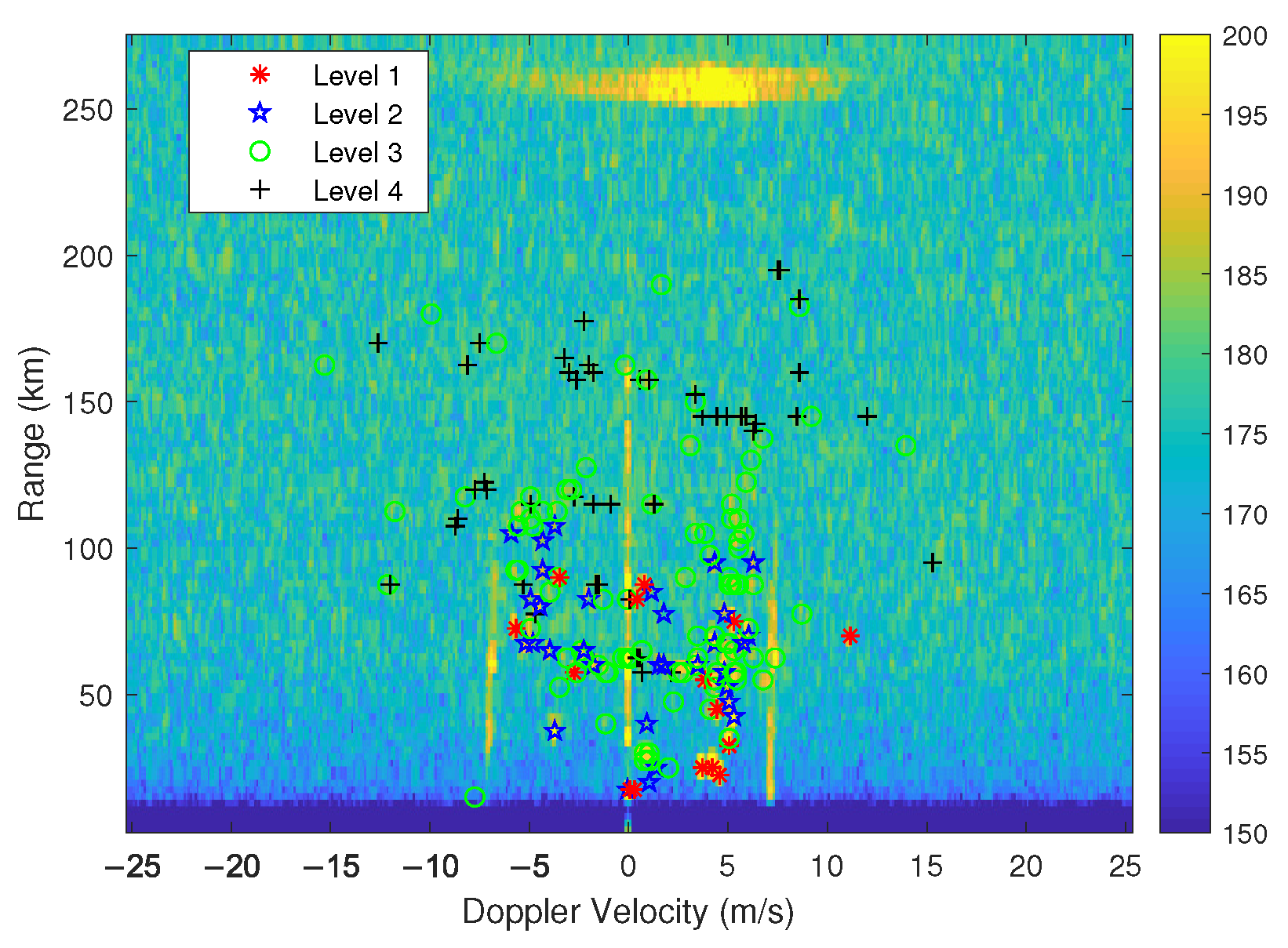
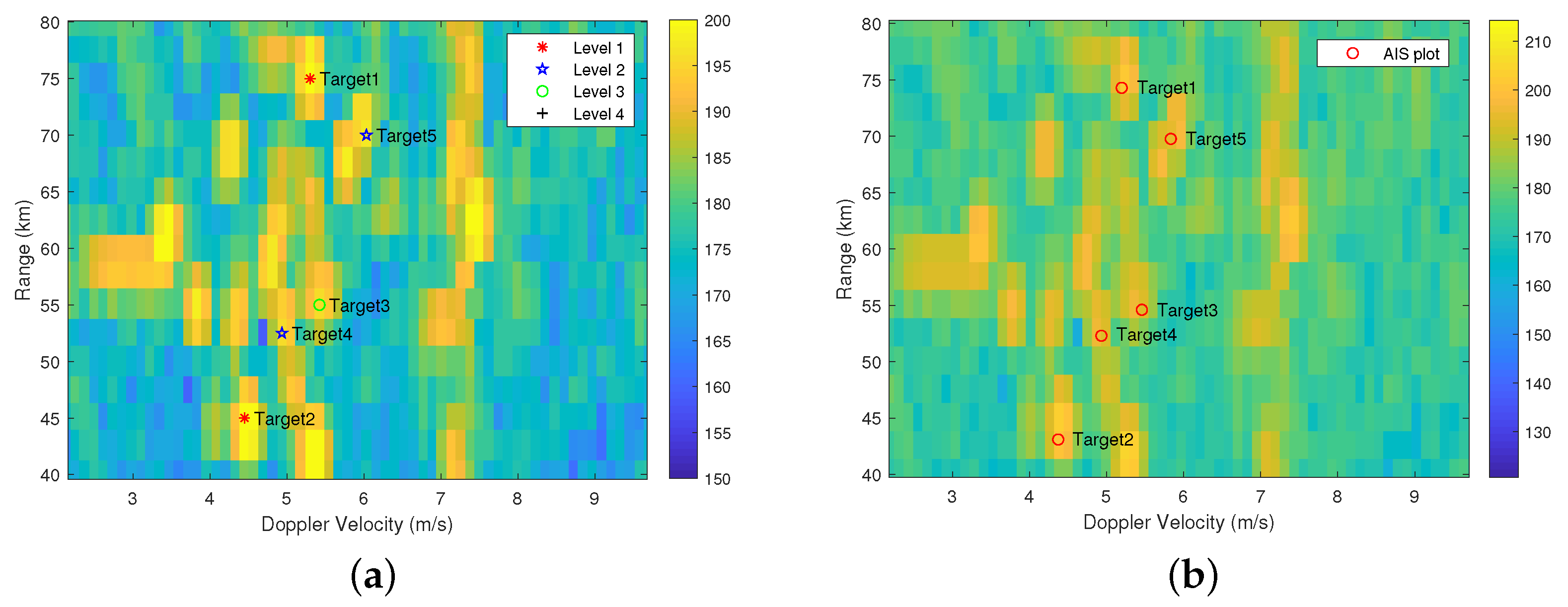
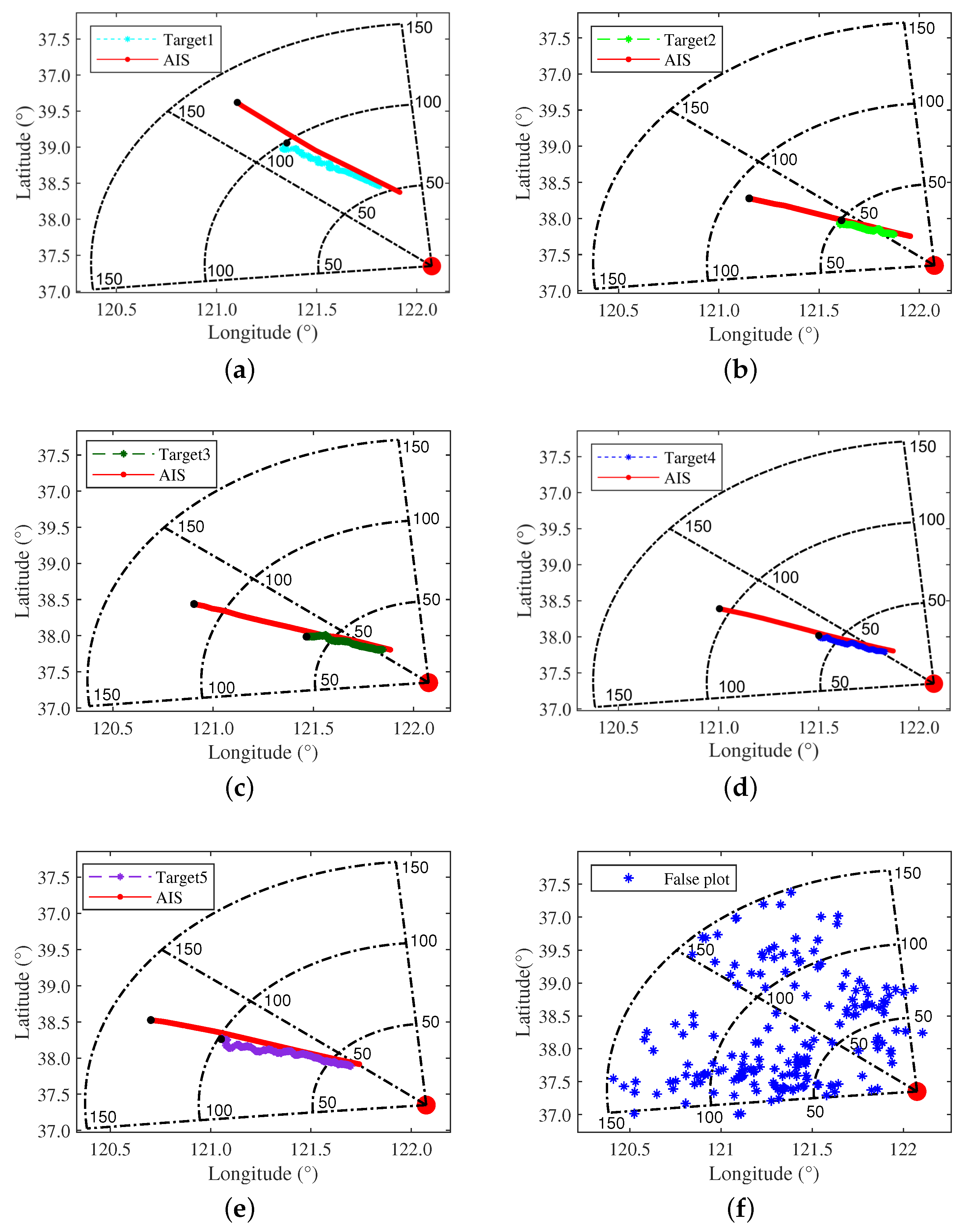
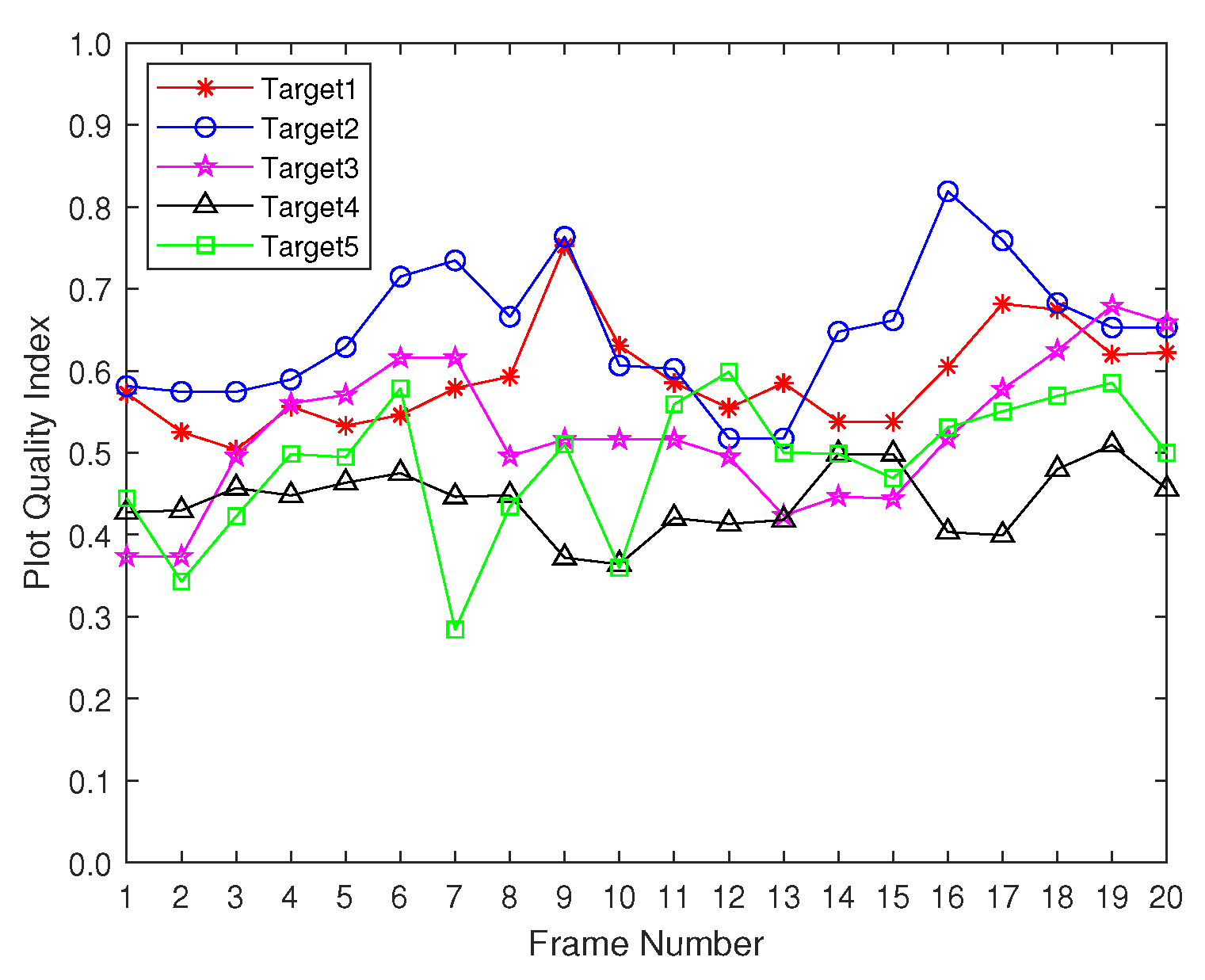
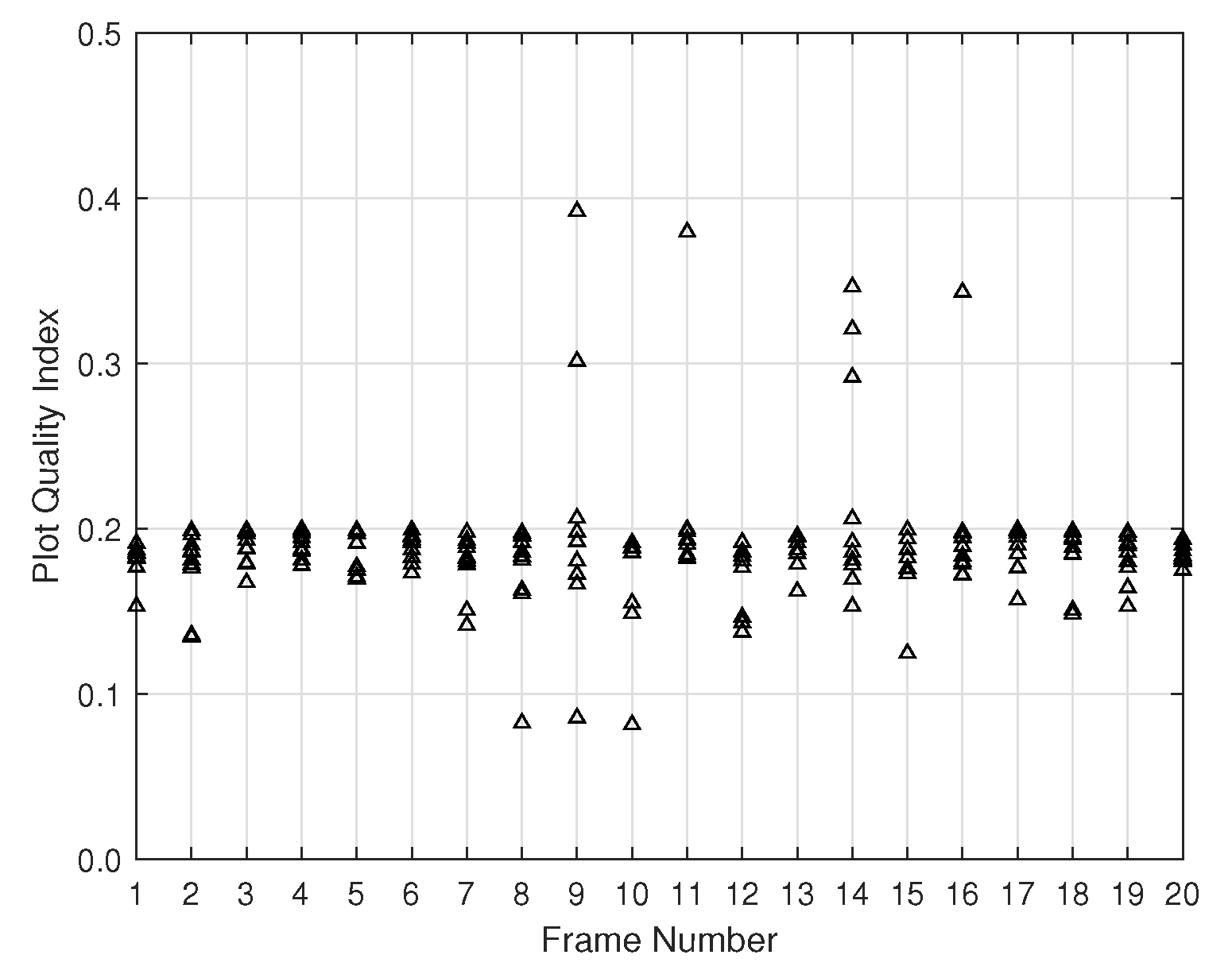
4.1. Plot Quality Evaluation and Results Analysis
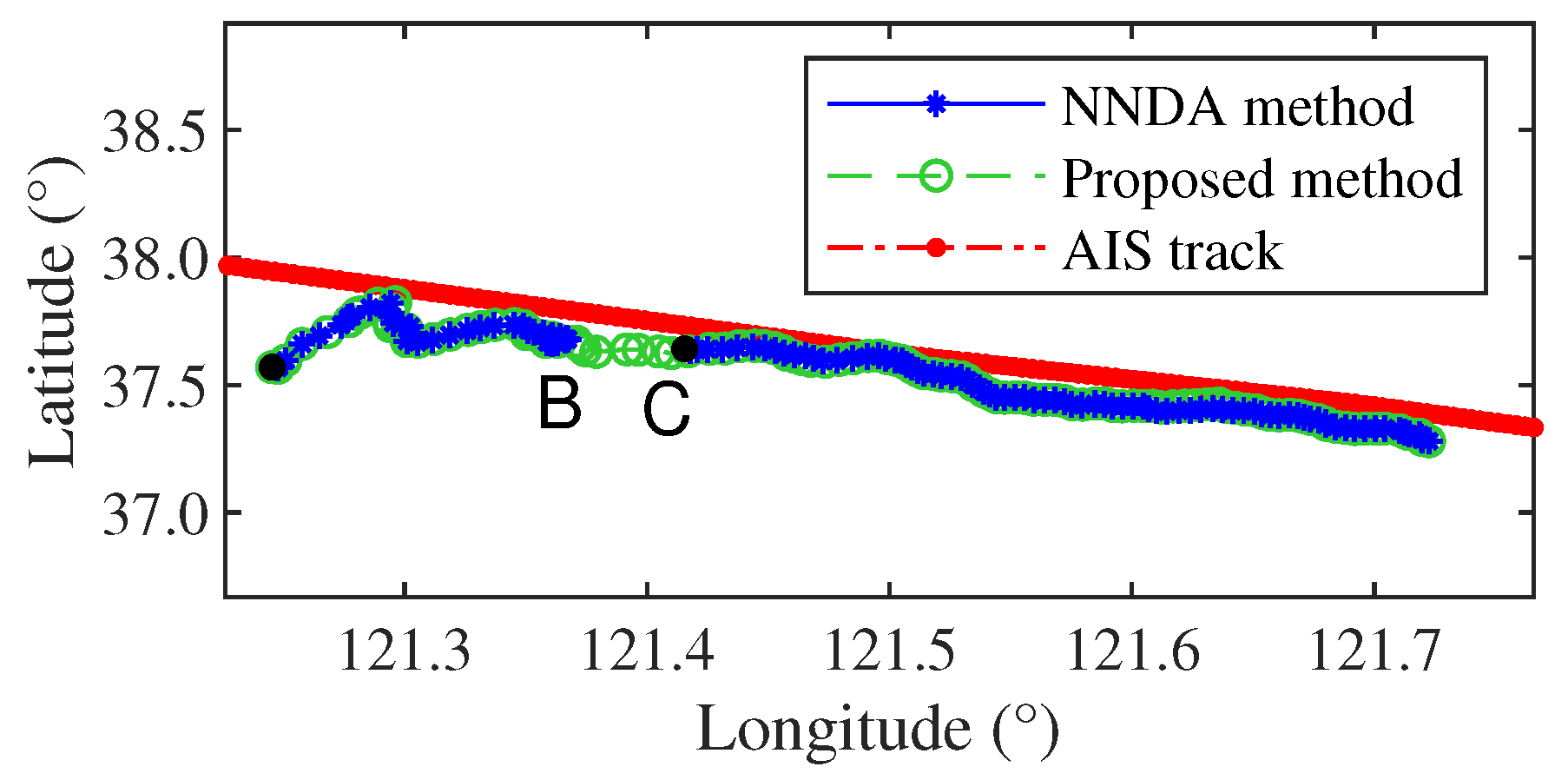
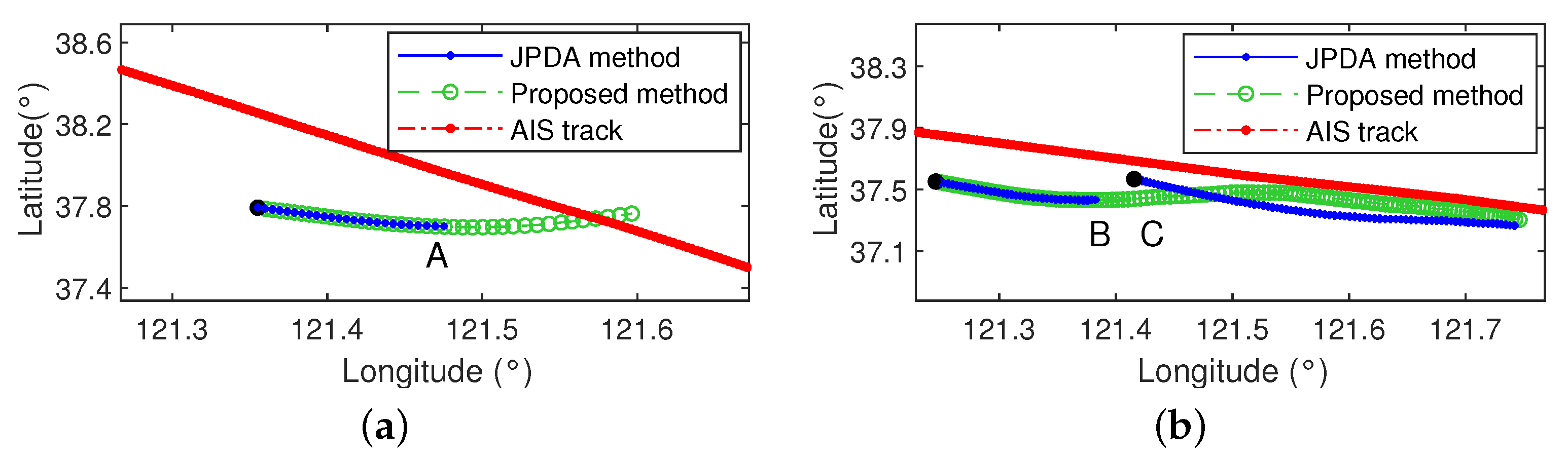
4.2. Analysis of Tracking Performance
- (1)
- Tracking results analysis of T1
- (2)
- Tracking results analysis of T2
4.3. Analysis of Computational Complexity
4.4. Analysis of Parameter Sensitivity
5. Discussion
- (i)
- The working environment of compact HFSWR is extremely complex and a great number of false plots may be produced, which will cause plot-to-track association errors for moving vessel tracking. The proposed plot quality evaluation method can effectively evaluate the quality of plots according to their quality indexes, which can be used to filter out some false plots and provide assistant information for resolving the plot-to-track association ambiguity.
- (ii)
- The plot quality evaluation method based on spatial correlation of echo spectrum amplitudes and plot position probability may not accurately classify moving vessel plots and false plots. However, the proposed plot quality index can indicate the possibility that a plot derives from a real moving vessel. The higher the plot quality index is, the more likely the plot comes from a real moving vessel.
- (iii)
- Experimental results show that the proposed plot quality evaluation method can reasonably calculate the quality indexes of most plots. However, it is worth noting that the extracted features of false plots may be similar to those of moving vessel plots since some clutter appears in the form of blocks, so the evaluation results of these plots may be inaccurate.
- (iv)
- The NNDA method only uses kinematic parameters to calculate the similarities between measured plots and moving vessel tracks. In dense clutter scenarios, it often causes false tracking and track fragmentation due to plot-to-track association errors. The proposed plot-to-track association method introduces the plot quality index as auxiliary information to collaboratively determine the associated plot. Experimental results show that this method can effectively increase tracking time on moving vessels and improve tracking continuity.
- (v)
- During the moving vessel tracking experiments, the authors found that the proposed plot-to-track association method has better tracking performance in dense clutter scenarios, but false tracking caused by the interference of adjacent moving vessels may occur in multi-target tracking scenarios. Because the plot quality indexes of different moving vessel plots may be similar, as shown in Figure 10, it is difficult to accurately distinguish the source of moving vessel plots by their quality indexes and kinematic parameters when multiple moving vessels are close to each other. Therefore, the optimal assignment of plot-track pairs in multi-target tracking scenarios needs to be further investigated.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HFSWR | high-frequency surface wave radar |
| CFAR | constant false alarm rate |
| NNDA | nearest neighbor data association |
| SNR | signal-to-noise ratio |
| RCS | radar cross section |
| PDA | probabilistic data association |
| JPDA | joint probabilistic data association |
| R-D | range-Doppler |
| MUSIC | multiple signal classification |
| DBF | digital beam-forming |
| CMKF | converted measurement Kalman filter |
| AIS | automatic identification system |
| CORMS | compact over-the-horizon radar for maritime surveillance |
References
- Ji, Y.; Zhang, J.; Wang, Y.; Sun, W.; Li, M. Target Monitoring Using Small-aperture Compact High-frequency Surface Wave Radar. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 22–31. [Google Scholar] [CrossRef]
- Sun, W.; Pang, Z.; Huang, W.; Ma, P.; Ji, Y.; Dai, Y.; Li, X. A Multi-Stage Vessel Tracklet Association Method for Compact High-Frequency Surface Wave Radar. Remote Sens. 2022, 14, 1601. [Google Scholar] [CrossRef]
- Huang, W.; Gill, E.W. (Eds.) Ocean Remote Sensing Technologies—High-Frequency, Marine and GNSS-Based Radar; SciTech Publishing: Luxembourg, 2021. [Google Scholar]
- Sun, W.; Ji, M.; Huang, W.; Ji, Y.; Dai, Y. Vessel Tracking Using Bistatic Compact HFSWR. Remote Sens. 2020, 12, 1266. [Google Scholar] [CrossRef]
- Sun, W.; Huang, W.; Ji, Y.; Dai, Y.; Ren, P.; Zhou, P.; Hao, X. A Vessel Azimuth and Course Joint Re-Estimation Method for Compact HFSWR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1041–1051. [Google Scholar] [CrossRef]
- Sun, W.; Pang, Z.; Huang, W.; Ji, Y.; Dai, Y. Vessel Velocity Estimation and Tracking from Doppler Echoes of T/R-R Composite Compact HFSWR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4427–4440. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, H.; Tian, Y.; Zhao, J. Improved CFAR Detection and Direction Finding on Time–Frequency Plane with High-Frequency Radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3505005. [Google Scholar] [CrossRef]
- Barrick, D.E.; Lipa, B.J. A Compact Transportable HF Radar System for Directional Coastal Wave Field Measurements. In Ocean Wave Climate. Marine Science; Earle, M.D., Malahoff, A., Eds.; Springer: Boston, MA, USA, 1979; Volume 8. [Google Scholar]
- Su, R.; Tang, J.; Yuan, J.; Bi, Y. Nearest Neighbor Data Association Algorithm Based on Robust Kalman Filtering. In Proceedings of the 2021 2nd International Symposium on Computer Engineering and Intelligent Communications (ISCEIC), Nanjing, China, 6–8 August 2021; pp. 177–181. [Google Scholar]
- Clark, D.; Ristic, B.; Vo, B.N.; Vo, B.T. Bayesian Multi-Object Filtering with Amplitude Feature Likelihood for Unknown Object SNR. IEEE T. Signal. Proces. 2010, 58, 26–37. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, J.; Lei, P.; Bi, Y.; Sun, Z. Multi-Target Tracking Based on Multi-Bernoulli Filter with Amplitude for Unknown Clutter Rate. Sensors 2015, 15, 30385–30402. [Google Scholar] [CrossRef]
- Liu, C.; Sun, J.; Lei, P.; Qi, Y. δ-Generalized Labeled Multi-Bernoulli Filter Using Amplitude Information of Neighboring Cells. Sensors 2018, 18, 1153. [Google Scholar] [CrossRef]
- Zhang, L.; You, W.; Wu, Q.M.J.; Qi, S.; Ji, Y. Deep Learning-Based Automatic Clutter/Interference Detection for HFSWR. Remote Sens. 2018, 10, 1517. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Wang, S.; Zhao, T.; Wang, Y.; Li, Y. Radar HRRP Target Recognition Using Scattering Centers Fuzzy Matching. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–5. [Google Scholar]
- Zhang, W.; Wu, Q.M.J.; Wang, Y.; Akilan, T.; Zhao, W.G.W.; Li, Q.; Niu, J. Fast Ship Detection with Spatial-Frequency Analysis and ANOVA-Based Feature Fusion. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3506305. [Google Scholar] [CrossRef]
- Huang, Y.; Song, T.L.; Kim, D.S. Linear Multitarget Integrated Probabilistic Data Association for Multiple Detection Target Tracking. IET Radar. Sonar. Nav. 2018, 12, 945–953. [Google Scholar] [CrossRef]
- Ainsleigh, P.L.; Luginbuhl, T.E.; Willett, P.K. A Sequential Target Existence Statistic for Joint Probabilistic Data Association. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 371–381. [Google Scholar] [CrossRef]
- Uner, M.K.; Varshney, P.K. Distributed CFAR Detection in Homogeneous and Nonhomogeneous Backgrounds. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 84–97. [Google Scholar] [CrossRef]
- Meng, X. Rank Sum Nonparametric CFAR Detector in Nonhomogeneous Background. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 397–403. [Google Scholar] [CrossRef]
- Wang, R.; Wen, B.; Huang, W. A Support Vector Regression-Based Method for Target Direction of Arrival Estimation From HF Radar Data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 674–678. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Zhang, X.; Ji, X.; Xiao, D. Space-Time Adaptive Processing Clutter-Suppression Algorithm Based on Beam Reshaping for High-Frequency Surface Wave Radar. Remote Sens. 2022, 14, 2935. [Google Scholar] [CrossRef]
- Park, S.; Cho, C.J.; Ku, B.; Lee, S.; Ko, H. Compact HF Surface Wave Radar Data Generating Simulator for Ship Detection and Tracking. IEEE Geosci. Remote Sens. Lett. 2017, 14, 969–973. [Google Scholar] [CrossRef]
- Lyu, Z.; Yu, C.; Liu, A.; Quan, T. Comparative Study on Chaos Identification of Ionospheric Clutter From HFSWR. IEEE Access. 2019, 7, 157437–157448. [Google Scholar]
- Nazari, M.E.; Huang, W.; Zhao, C. Radio Frequency Interference Suppression for HF Surface Wave Radar Using CEMD and Temporal Windowing Methods. IEEE Geosci. Remote Sens. Lett. 2020, 17, 212–216. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, L.; Niu, J.; Wu, Q.M.J. Target Detection in Clutter/Interference Regions Based on Deep Feature Fusion for HFSWR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5581–5595. [Google Scholar] [CrossRef]
- Bordonaro, S.; Willett, P.; Bar-Shalom, Y. Decorrelated Unbiased Converted Measurement Kalman Filter. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1431–1444. [Google Scholar] [CrossRef]
- Tian, Z.; Tian, Y.; Wen, B. Quality Control of Compact High-Frequency Radar-Retrieved Wave Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 929–939. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, W.; Li, M.; Niu, J.; Wu, Q.M.J. Automatic Detection of Ship Targets Based on Wavelet Transform for HF Surface Wavelet Radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 714–718. [Google Scholar] [CrossRef]
- Chen, Y.R.; Chuang, L.Z.H.; Chung, Y.J. Automated Peak Detection in Doppler Spectra of HF Surface Wave Radar. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar]
- Cai, J.; Zhou, H.; Huang, W.; Wen, B. Ship Detection and Direction Finding Based on Time-Frequency Analysis for Compact HF Radar. IEEE Geosci. Remote Sens. Lett. 2021, 18, 72–76. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Zhang, N.; Cong, Y. An Automatic Target Detection Method Based on Multidirection Dictionary Learning for HFSWR. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3504105. [Google Scholar] [CrossRef]
- Sinaga, K.P.; Yang, M.S. Unsupervised K-Means Clustering Algorithm. IEEE Access. 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Shang, X.; Li, X.; Morales-Esteban, A.; Asencio-Cortés, G.; Wang, Z. Data Field-Based K-Means Clustering for Spatio-Temporal Seismicity Analysis and Hazard Assessment. Remote Sens. 2018, 10, 461. [Google Scholar] [CrossRef]
- Xiang, H.; Lei, B.; Li, Z.; Zhao, K.; Lv, Q.; Zhang, Q.; Geng, Y. Analysis of Parameter Sensitivity of Induction Coil Launcher Based on Orthogonal Experimental Method. IEEE Trans. Plasma Sci. 2015, 43, 1198–1202. [Google Scholar] [CrossRef]
- Nikolic, D.; Stojkovic, N.; Lekic, N. Maritime over the Horizon Sensor Integration: High Frequency Surface-wave-radar and Automatic Identification System Data Integration Algorithm. Sensors 2018, 18, 1147. [Google Scholar] [CrossRef]


| Specification | Value |
|---|---|
| Transmitting waveform | FMICW |
| Receiving antenna number | 8 |
| Working frequency (MHz) | 4.7 |
| Coherent integration time (s) | 262.144 |
| Data rate (frame/min) | 1 |
| Parameter | Value |
|---|---|
| U | 0.025 |
| V | 4 |
| 0.2 | |
| 0.15 | |
| (0.2, 0.4, 0.4) | |
| (0.7, 0.2, 0.1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Li, X.; Ji, Y.; Dai, Y.; Huang, W. Plot Quality Aided Plot-to-Track Association in Dense Clutter for Compact High-Frequency Surface Wave Radar. Remote Sens. 2023, 15, 138. https://doi.org/10.3390/rs15010138
Sun W, Li X, Ji Y, Dai Y, Huang W. Plot Quality Aided Plot-to-Track Association in Dense Clutter for Compact High-Frequency Surface Wave Radar. Remote Sensing. 2023; 15(1):138. https://doi.org/10.3390/rs15010138
Chicago/Turabian StyleSun, Weifeng, Xiaotong Li, Yonggang Ji, Yongshou Dai, and Weimin Huang. 2023. "Plot Quality Aided Plot-to-Track Association in Dense Clutter for Compact High-Frequency Surface Wave Radar" Remote Sensing 15, no. 1: 138. https://doi.org/10.3390/rs15010138
APA StyleSun, W., Li, X., Ji, Y., Dai, Y., & Huang, W. (2023). Plot Quality Aided Plot-to-Track Association in Dense Clutter for Compact High-Frequency Surface Wave Radar. Remote Sensing, 15(1), 138. https://doi.org/10.3390/rs15010138








