Abstract
Convolution-based recurrent neural networks and convolutional neural networks have been used extensively in spatiotemporal prediction. However, these methods tend to concentrate on fixed-scale spatiotemporal state transitions and disregard the complexity of spatiotemporal motion. Through statistical analysis, we found that the distribution of the spatiotemporal sequence and the variety of spatiotemporal motion state transitions exhibit some regularity. In light of these statistics and observations, we propose the Multi-scale Spatiotemporal Neural Network (MSSTNet), an end-to-end neural network based on 3D convolution. It can be separated into three major child modules: a distribution feature extraction module, a multi-scale motion state capture module, and a feature decoding module. Furthermore, the MSST unit is designed to model multi-scale spatial and temporal information in the multi-scale motion state capture module. We first conduct the experiments on the MovingMNIST dataset, which is the most commonly used dataset in the field of spatiotemporal prediction, MSSTNet can achieve state-of-the-art results for this dataset, and ablation experiments demonstrate that the MSST unit has positive significance for spatiotemporal prediction. In addition, this paper applies the model to valuable precipitation nowcasting, due to efficiently capturing the multi-scale information of distribution and motion, the new MSSTNet model can predict the real-world radar echo more accurately.
1. Introduction
For some complex dynamic spatiotemporal systems, we are unable to fully understand their intrinsic mechanisms, so it is difficult to construct accurate numerical prediction models for them. Researchers have been concentrating more on constructing suitable deep neural networks to forecast the future spatiotemporal state as big data and deep learning technologies continue to advance [1]. Numerous deep-learning-based spatiotemporal prediction efforts have been made in recent years. Typical applications include precipitation nowcasting [2,3,4], sea temperature prediction [5,6], and El Niño Southern Oscillation (ENSO) forecasting [7,8]. Convolution-based recurrent neural networks [9] occupy the prime position in spatiotemporal prediction, for instance, ConvLSTM [10], TrajGRU [11], and PredRNN++ [12]. These models construct convolution-based recurrent neural networks by combining convolutional structures with recurrent neural networks. However, these models access past spatiotemporal information using fixed-scale spatiotemporal memory units, which do not directly acquire connections between long-term and short-term spatiotemporal properties and may overlook the availability features of historical spatiotemporal information. Several researchers have designed convolution-only spatiotemporal prediction models, which typically only utilize 2D convolution [13,14], where the information of the time dimension is merged into the channel dimension to represent the time dimension’s spatiotemporal dependency. However, the effectiveness of modeling may be greatly diminished when the spatiotemporal states change quickly due to the lack of characterization of spatiotemporal connections at various scales.
In Figure 1, the horizontal axis denotes the radar echo intensity (dBZ) and the vertical axis denotes the proportion of a certain echo’s intensity value and the distribution changes in a collection of typical spatiotemporal moving radar echo images at the fourth hour of 0.5, 1, 1.5, and 2 are shown. The echo value corresponding to the gradient augmentation and gradient weakening of the echo value distribution curve is comparable, and it is discovered that, with time, the echo value distribution of the radar echo images exhibits some regularity. Future spatiotemporal prediction may benefit if the historical spatiotemporal distribution data can be completely exploited. In addition, the model is inspired by MotionRNN’s concept of breaking down motion into trend motion and instantaneous motion [15]. As shown in Figure 1, curve ➀ describes the state of clouds with a huge physical space span during Doppler weather radar scanning, which this paper describes as a relatively large-scale spatial motion state. Curve ➁ describes the motion state of clouds with a small physical space span during Doppler weather radar scanning, which is described in this paper as a relatively tiny spatial scale motion state. It has been noted that the direction of a large-scale cloud cluster’s movement in an echo image typically correlates to the long-term movement trend and that this shift is frequently gradual and continuous. The instantaneous motion is equivalent to the violent and unstable creation and dissipation of and changes in tiny-scale clouds. To take into account changes in spatiotemporal motion states at multiple time scales and spatial scales, the model should dynamically construct multi-scale spatiotemporal motion states.
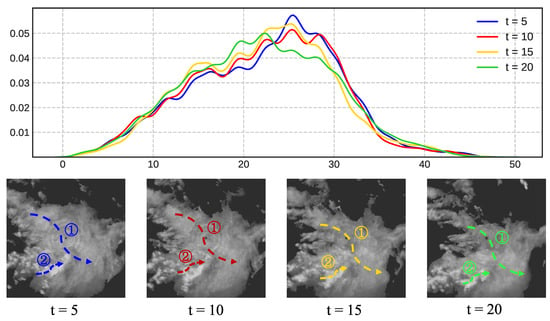
Figure 1.
The changes in distribution characteristics and motion state of radar echo images.
By investigating the distribution and motion of spatiotemporal sequences, we propose a 3D convolution-based end-to-end neural network termed the Multi-scale Spatiotemporal Neural Network (MSSTNet). The backbone of the neural network can be divided into three modules: the feature decoding module, the multi-scale motion state capture module, and the distribution feature extraction module. Specifically, motivated by the promising performance of U-net [16] in the field of medical segmentation, in order to more efficiently implement the spatiotemporal distribution information in future image production, the model integrates the distribution feature extraction network at the input and the feature decoding network at the output by skipping connections. The multi-scale motion state capture module’s core MSST unit dynamically extracts motion characteristics at multiple time scales and spatial scales using 3D separation convolution [17,18]. After combining distribution information features and motion features, the distribution feature extraction module completes the spatial and temporal prediction. In this paper, the spatiotemporal prediction performance of MSSTNet is verified on the artificial MovingMNIST dataset and the radar echo dataset. The results show that MSSTNet achieves the optimal effect in several evaluation indices. The contributions of this paper are summarized as follows:
- A novel multi-scale spatiotemporal prediction neural network is proposed. Spatiotemporal prediction in synthetic datasets, radar echoes, and visualization of radar echo prediction;
- A multi-scale spatiotemporal feature extraction unit is proposed. This unit completes the unified modeling of the multiple temporal and spatial scales in the neural network’s deep layers, which is necessary for capturing complicated spatiotemporal motion, particularly the state of clouds in motion. The ablation experiment further demonstrates the viability and efficiency of the neural network’s design;
- The quantitative and qualitative analyses are compared with the model proposed in this paper. Comparative experiments are expected to compare the earlier convolution-based recurrent neural networks and convolutional neural networks in order to judge the dependability of the model developed in this research. The results demonstrated that the proposed model performs competitively on the two datasets.
The remainder of this paper is organized as follows: Section 2 outlines previous benchmarking methods for this field. The model presented in this research is introduced in Section 3. The comparative findings and analyses for the two datasets are presented in Section 4. This paper’s general strategy and experimental findings are discussed in Section 5. The conclusion is provided in Section 6.
2. Related Works
Consider a dynamic system that generates T measurements at predetermined times. Each measurement can be correlated spatially to size grid data, denoted as . The purpose of spatiotemporal prediction is to generate sequence images of the most probable future time period from sequence images of the historical time period, as shown in Equation (1) [10]:
Currently, convolution-based recurrent neural networks and convolutional neural networks are the most widely used models for spatiotemporal prediction. The convolution-based recurrent neural network technique, as illustrated in the left part of Figure 2, typically uses LSTM as the core, with the input , the hidden unit , and the memory unit from the prior moment generating the output at the next moment. The efficiency of the overall model prediction process is determined by the input and output sequence length. Combining this fixed-order structure with convolution can effectively express spatiotemporal information since it has sufficient timing on its own. ConvLSTM [10], the first recurrent neural network based on convolutions, uses a convolution structure in place of LSTM’s fully connected structure to capture temporal and spatial information. Since the convolutional recursive structure in the model of ConvLSTM is position invariant, a trajectory GRU (TrajGRU) model was proposed [11], which can actively learn the position change structure of repeated connections. According to PredRNN [19], the memory state of spatiotemporal prediction learning should be remembered simultaneously in a single memory pool rather than being restricted to each LSTM unit as it currently is. As a result, a novel spatiotemporal LSTM (ST-LSTM) unit was developed, which can extract and recall both spatial and temporal information at the same time. Since then, a new phase of development for the convolution-based recurrent neural network has begun. To address the issue that gradient disappearance is likely to occur during the training of the PredRNN model, PredRNN++ [12] proposes to combine the Gradient Highway Unit (GHU) structure and the Causal LSTM structure connection. The spatiotemporal sequence information is made up of stationary and non-stationary information, according to MIM [20] analysis. Deep learning networks are excellent at predicting stationary data, but struggle to do so with non-stationary data due to their irregular nature. Afterward, MIM structures are stacked to mine high-order, non-stationary information. It is notable that deterministic terms, time-variable polynomials, and zero-mean random terms could all be used to deconstruct non-stationary information. E3D-LSTM [21] combines 3D convolution [22] and RNN to predict spatiotemporal sequences. SA-convlstm [23] was used to discover that the short-term local spatial information can only be effectively used by existing model methods, and the self-attention memory (SAM) was proposed based on the self-attention mechanism, which nested the current structure with SAM to obtain long-term global spatial information. CrevNet [24] uses reversible neural networks based on 3D convolution to encode and decode the input, with PredRNN serving as the prediction unit for spatiotemporal prediction. PredRNNv2 [25] asserts that a pair of memory units in PredRNN is redundant, proposes a memory decoupling loss function, and proposes a reverse sampling strategy to force the model to perform long-term spatiotemporal learning from the context framework. Movement in the real world may be separated into two types of movement: motion trends and transitory variations in space and time, which is something that MotionRNN takes into consideration [15]. On this basis, the modeling of motion trends and transient change using the MotionRNN model is presented. The aforementioned models, which are built on the convolution-based recurrent neural network, can only predict data once every time and cannot be trained and forecasted in parallel. As the duration of the prediction sequence increases, the total forecast impact will deviate due to the mistake in each individual prediction. However, past spatiotemporal information cannot be used to make predictions straight; rather, it can only be transformed into spatiotemporal properties that have a significant impact on future predictions by passing data between fixed-scale memory units at various times.
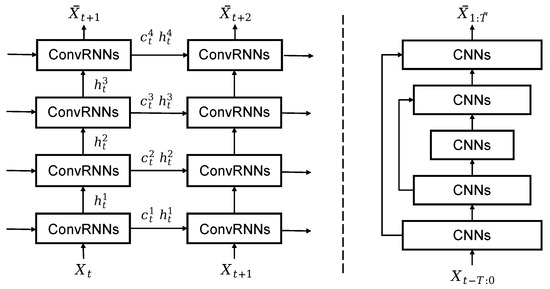
Figure 2.
Left: convolution-based recurrent neural networks. Right: convolutional neural networks.
Spatiotemporal sequence modeling is a method based on pure convolution with a U-net structure as a benchmark. The U-net structure is presented first in the field of medical image segmentation [16,26,27]. Due to its great extensibility, researchers in the field of spatiotemporal prediction have found several ways to improve the U-net structure’s capacity for extracting spatial information. Meanwhile, information about the time dimension is integrated into the channel dimension to determine the dependent relationship of the time dimension. As shown on the right of Figure 2, the input of the method is the historical spatiotemporal sequence , where T represents the length of the input sequence, and the output is the predicted spatiotemporal sequence , where represents the length of the output sequence. SE-ResUnet [28] develops a nowcasting model that is completely based on convolutional neural networks, outperforming the standard model’s performance at the time-convolution-based recurrent neural networks by combining the benefits of U-net, Squeeze-and-Excitation, and residual networks. Due to the use of separable convolution and the addition of an attention mechanism to the U-net, SmaAT-UNet [29] uses just a fourth of the trainable parameters and achieves prediction performance that is on par with other test models. SimVP [30] suggested a convolution-only neural network model that was both straightforward and effective. Spatiotemporal information could be adequately modeled using the Inception module and group convolution, and state-of-the-art (SOTA) results have been produced on several datasets. The end-to-end structure of a convolutional spatiotemporal prediction network, in contrast to the stacked structure of a convolution-based recurrent neural network, is better able to extract spatiotemporal distribution information and spatiotemporal motion information at all moments, preventing information loss throughout continuous transmission. However, at the moment, these models frequently disregard the precise modeling of the temporal dimension and instead concentrate on the feature modeling of the spatial dimension, potentially missing the spatiotemporal information at various time scales.
Inspired by the construction model of SimVP, this paper constructs an end-to-end spatiotemporal prediction network based on 3D convolution. In contrast to other predictive learning techniques, the proposed model utilizes 3D separated convolution to describe complicated spatiotemporal motion states at various time scales and spatial scales and dynamically develops the relationship between the spatial and temporal dimensions. The method proposed in this paper effectively enhances the capabilities of pure convolution-based spatiotemporal sequence modeling methods to represent temporal dimension information by absorbing their advantages.
3. Method
The model’s construction concepts and techniques will be thoroughly explained in this section. We will first go over the general organization of MSSTNet and the method used to transmit the model’s spatial-temporal series data. Following that, the MSST unit, an important module for multi-scale temporal and spatial information modeling, is presented.
As shown in Figure 3, the overall model architecture proposed in this paper is expanded on the basis of the U-net structure, taking advantage of its solid performance in the field of spatiotemporal prediction. The structure of MSSTNet consists of an encoder and a decoder, just like the U-net structure. The distribution feature extraction module (a) and the motion feature extraction module (b) make up the encoder. To create the target sequence picture after decoding, the feature decoding module (c) integrates the features retrieved from (a) and (b).
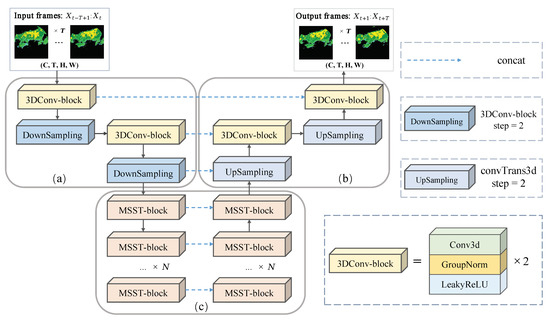
Figure 3.
MSSTNet network structure. The input sequence frames are sent into (a) shallow distribution feature extraction module for shallow feature extraction. After shallow feature extraction, the features will enter (b) deep motion feature extraction module for spatial-temporal motion feature extraction. Finally, deep motion feature and shallow distribution feature are sent to (c) decoding network module to generate predicted sequence frames.
Distribution feature extraction module (a): Each unit of the module is composed of two 3DConv-block layers and a downsampling layer, a wider receptive field, and enhanced nonlinearity through stacking the unit twice, allowing for more accurate modeling of the spatiotemporal distribution properties of sequence images. Specifically, to extract the input sequence features, each unit utilizes two 3D convolution kernels of size (3, 3, 3). Through skip connection, the extracted features are applied to the feature decoding module, and the step size of 3D convolution is set to 2 for the downsampling operation. The architecture of module (a) is described in Table 1.

Table 1.
Architecture of 3D convolution in module (a).
The dimensions of the input features are , and the hidden layer features’ dimensions following two feature extraction units are , where C and represent the input and output channel dimensions, which are determined by the number of input image channels and the number of manually set output channels, respectively. It should be made clear that when designing the model, the padding operation is used to guarantee that the sequence length T of the input and output is constant. The spatial resolution of the input is represented by H and W, whereas the spatial resolution of the output feature is represented by and . The feature extraction module’s formula is written in Equation (2) as follows:
Multi-scale motion state capture module (b): Multi-scale spatiotemporal (MSST) units are designed to capture multi-scale spatiotemporal motion states in this module. As illustrated in Figure 4, the MSST unit constructs spatial units of two scales and temporal units of three scales to dynamically establish the spatiotemporal dependency of the input sequence by varying the size and distribution of the convolution kernel of 3D convolution. In order to extract spatial feature information at various scales, the convolution kernel size is separated into (1, 3, 3) and (1, 11, 11). To extract temporal feature information at different scales, the convolution kernel size is divided into (3, 1, 1), (5, 1, 1), and (7, 1, 1). The architecture of module (b) is described in Table 2.
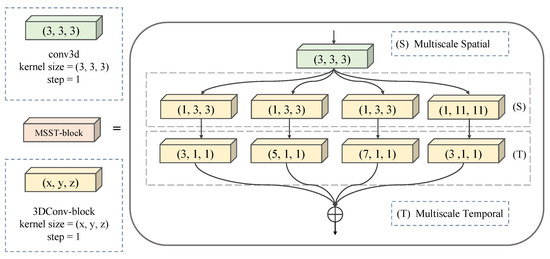
Figure 4.
The MSST unit’s internal structure.

Table 2.
Architecture of 3D convolution in module (b).
The structure of this unit can be described using the following Equation (3):
Furthermore, 2N MSST units make up the module for extracting motion features. The input and output feature dimensions of the left N units are , whereas the input and output dimensions of the right N units are and , respectively. This module’s formula is expressed as Equation (4):
Feature decoding module (c): For the purpose of generating future spatiotemporal sequence images, this module merges the output features of modules (a) and (b). An upsampling layer, two 3DConv-block layers, and a unit of the feature decoding module make up each unit. The architecture of module (a) is described in Table 3.

Table 3.
Architecture of 3D convolution in module (c).
When the unit is stacked twice, the associated module’s upsampling is performed twice (a). The dimensions of the input features are , while are the dimensions of the output features. The formula of this module is shown in Equation (5):
In general, through the structure of the encoder and decoder, MSSTNet unifies the three modules into a model, and the core MSST unit separates 3D convolution to describe the deep features of spatiotemporal sequences at multiple scales.
4. Experiments
In this section, the performance of MSSTNet is evaluated quantitatively and qualitatively using two datasets, MovingMNIST and Radar Echo. The statistical table of the two datasets is shown in Table 4, including the number of training samples , the number of test samples , the input dimensions , and the output dimensions , where C represents the number of channels of the input data, T and represent the sequence lengths of the input and predicted data, H represents the length of the input sequence, and W represents the width of the input sequence. At the same time, we performed an interpretable analysis on our model and ablation experiments using MovingMNIST, the most used dataset in spatiotemporal prediction.

Table 4.
Dataset statistics.
Implementation details: Our method is trained with the MSE loss, the batch size is set to 16, the ADAM optimizer [31] is used, and all data are normalized to [0, 1]. Moreover, when applied to the MovingMNIST dataset, the model had eight MSST unit layers, 0.01 was set as the starting learning rate, and training was stopped after 2000 epochs. The RadarEcho dataset had two MSST unit layers, and the initial learning rate was set at 0.001. The training was stopped after 20 epochs. All methods are executed on a single NVIDIA 3090 GPU using Pytorch.
4.1. Experiments on MovingMNIST
The MovingMNIST dataset is the most commonly used public dataset for spatiotemporal prediction. In this dataset, the initial positions and initial speeds of the handwritten digits sampled by static MNIST are random. After colliding, they will rebound off the edge of the image. The dataset requires the model to extrapolate from the digital movement trajectory of historical sequence frames to predict future frames. Two factors contribute to the difficulty of prediction: the potential movement trend of various numbers and the phenomenon of moving numbers overlapping. This experiment uses the SimVP [30] dataset configuration to provide a truly fair comparison, and all performance measurements for the earlier advanced approaches utilize the best metrics described in the original publications to prevent findings from being impacted by the reproduction process.
4.1.1. Evaluation Index
Two indices are used to evaluate the performance of different models: Mean Squared Error (MSE) and Structural Similarity Index Measure (SSIM) [32]. MSE can be calculated as:
where n represents the number of image pixels, represents the true value, and is the predicted value. Lower values of MSE indicate smaller differences between the predicted frames and the ground truth. The calculation of SSIM is as follows:
where x is the real value, y is the predicted value, is the average of x, is the average of y, is the variance of x, is the variance of y, and is the covariance of x and y. and are the constants used to maintain stability: , . L is the dynamic range of pixel values. The value of SSIM ranges from −1 to 1, and it can evaluate the brightness, contrast, and structural quality of the generated frames. It is equal to 1 when two images are perfectly duplicated. Meanwhile, the Mean Absolute Error (MAE) was also used as the evaluation index in the ablation experiment, and its formula was as follows:
where n represents the number of image pixels, represents the true value, and is the predicted value.
4.1.2. Experimental Results and Analysis
First, a quantitative analysis of MSSTNet was performed as shown in Table 5. The model presented in this paper outperformed CrevNet by in terms of the MSE index (MSE decreased from 22.3 to 21.4). The MSE was enhanced by almost as compared to the convolution-based recurrent neural network series model (MSE decreased from 48.4 to 21.4). The experimental results demonstrate that the proposed MSSTNet is able to predict future sequence images in the MovingMNIST dataset more accurately.

Table 5.
Comparison of evaluation indices of various methods in MovingMNIST. ↓ (or ↑) means lower (or higher) is better. The optimal results are marked by bold.
Figure 5 shows the three stages that digit 1 and digit 9 go through. Upon input, the two digits’ states overlap to separation, and their future motion states are separated to overlap and finally to separation. The future mobile digital state can also be clearly and precisely predicted by MSSTNet in this type of complicated motion. The visualization results demonstrate that MSSTNet is capable of simulating the spatiotemporal sequence picture distribution as well as the changing trend of both long-term and short-term motions.

Figure 5.
Visualization of the MovingMNIST dataset.
4.1.3. Ablation Experiments
An ablation experiment refers to understanding the effect of a component on the overall system by studying the performance of a component removed from the AI system. In this subsection, ablation experiments are performed for each module of MSSTNet in order to verify the rationality of the network structure. Each comparison method was trained uniformly for 50 epochs, and the performance of each method was evaluated by MSE, MAE, and SSIM indicators, as shown in Table 6.

Table 6.
The ablation experiment results of MSSTNet’s different modeling training for 50 epochs.
The comparison of Methods 1 and 2 demonstrates the significance of multi-scale spatial modeling, while Methods 3 and 4 demonstrate the advantages of multi-scale temporal modeling. The number of 3D convolutions performed before downsampling should be taken into account when designing a spatiotemporal distribution feature extraction network. While the typical U-net network performs two convolution operations, SimVP [30] performs just one. They are both 2D convolutions. The comparison of Methods 2 and 3 for 3D convolution demonstrates that 3D convolution performs better after two iterations. In Method 5, the 3D convolution of MSST units was replaced by a separate convolution, and the optimal result was obtained. Ablation experiments show that multi-scale temporal modeling and multi-scale geographical modeling greatly enhance the prediction outcomes as compared to fixed-scale motion state modeling, demonstrating the validity and effectiveness of the overall architecture of MSSTNet.
4.2. Experiments on Radar Echo
Nowcasting precipitation has historically been a crucial topic of study for meteorologists. The main aim of research in this area is to generate high-resolution rainfall intensity forecasts in local areas within a relatively short time frame (0–6 h) in the future. Nowcasting precipitation demands a higher temporal and geographical precision than traditional weather prediction techniques such as numerical weather prediction (NWP) [34]. Precipitation forecasting is therefore quite difficult [35,36]. The dynamics suggested in the space-time domain can be taught to predict the path of clouds in the near future based on past observations of weather radar echoes. Radar echo intensity and precipitation intensity may be converted using the Z–R relationship to estimate short-term precipitation in the future.
The data utilized in this experiment are the basic reflectance products of a dual-polarization Doppler weather radar and are recorded every 6 min. The radar echo image has a resolution of , which corresponds to a 1 km spatial resolution. It should be mentioned that throughout the experiment, the image’s resolution will be compressed to in order to lower the requirements for GPU Memory. The pixel value of radar echo image ranges from 0 to 70, representing the physical meaning of radar echo intensity from 0 dBZ to 70 dBZ. A single radar echo image was quality-controlled to form a total of 25,500 continuous image sequences, and 10 input images and 10 output images from the previous and following hours’ worth of weather are included in each image sequence. Finally, the constructed dataset is then split into a training set and a test set, each involving 23,000 and 2500 continuous radar echo sequences.
4.2.1. Evaluation Index
In this experiment, SSIM was used as the evaluation index for the generated image’s sharpness, while MSE was used to measure the overall prediction effect. If the radar echo strength is higher than 30 dBZ at the same time, precipitation or severe convective weather may develop. The CSI score and HSS score are used from a meteorological perspective in radar echo regions bigger than 30 dBZ, which are of positive relevance for precise rainfall forecasts. These two indices are defined as follows:
where the pixel values of real sequence images and forecasted sequence images over 30 dBZ were set to 1, while the pixel values of less than 30 dBZ were assigned to 0 in order to compute the CSI and HSS scores. False Positives () are the number of pixels with a forecast image of 1 and a real image of 0, respectively. True Positives () are the number of pixels where the forecast image is 1 and the real image is 1. False Negative () denotes the number of pixels where the actual picture is 1 and the forecasted image is 0. True Negative () denotes the number of pixels where the actual image is zero and the forecasted image is zero.
4.2.2. Experimental Results and Analysis
The proposed model is compared with four previous models that have achieved promising performance for radar echo prediction: PredRNN++ [12], MIM [20], PredRNNv2 [25], and MotionRNN [15]. SimVP [30] is also utilized in the experiment to forecast radar echo, owing to its excellent performance in other spatiotemporal prediction tasks. In order to fairly compare the performance of the model, the settings and training methods of the comparison experiment were set according to the parameters described in the paper. We provide the quantitative results of MSSTNet on the radar echo dataset in Table 7. The 4 evaluation indices indicate the average evaluation indices for forecasting the following 10 images.

Table 7.
Performance comparison results of the models in Radar Echo.
The results demonstrated that MSSTNet outperforms the other models’ average predictions for 10 radar echo images in terms of MSE, CSI, and HSS indices. The lower the value of MSE, the better the overall prediction effect of the model. Moreover, MSSTNet performs exceptionally well in CSI and HSS scores, which are more significant in precipitation forecasting, demonstrating that this model is more reliable in identifying the regions where future rainfall is likely to occur.
The performance of several models on the multiple indices during radar echo prediction is shown in Figure 6. The MSE value was determined using the actual radar echo map and the expected radar echo map at each moment. The chart shows that MSSTNet, when compared to other benchmark models, has had a superior prediction impact since the second time. It also offers several benefits over the most sophisticated benchmark models, MotionRNN and SimVP.
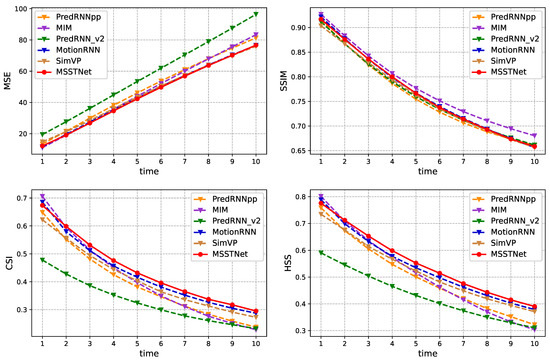
Figure 6.
Compare the index of each frame in the Radar Echo dataset.
Figure 6 also shows the results of several benchmark models using the SSIM index, which measures how closely each frame matches the actual radar echo picture in terms of image structure. Other models’ findings, with the exception of the MIM model, are quite close to each frame, and MSSTNet also produces good prediction results. Furthermore, CSI and HSS indices are also the two indices that precipitation nowcasting researchers are most focused on. It can be shown that MSSTNet performs better at 0.5 h and 1 h than other benchmark models, which suggests that as time goes on, MSSTNet becomes more accurate in predicting where rain will fall.
Figure 7 provides a quantitative comparison of the CSI index situations of radar echo intensity that are more likely to experience severe convective weather. The figure shows that the MSSTNet proposed in this paper has certain benefits over the previous state-of-the-art methods in forecasting the CSI score of the next 60 min, regardless of whether the radar echo intensity technique threshold is set at 35 dBZ and 40 dBZ. The MSSTNet model has much greater prediction accuracy than other models at 30 min, especially when the radar echo intensity threshold is 40 dBZ.
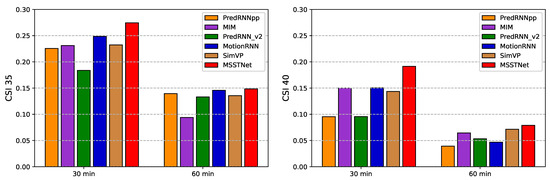
Figure 7.
Quantitative comparison of multiple CSI indicators.
Figure 8 presents the radar frames predicted by different methods. A sequence is taken from the test set, and the grayscale map is then translated into RGB space using different pixel values. The red areas correspond to regions with echo values of more than 40 dBZ, which may cause severe weather. It can be observed that although the advanced MotionRNN method and PredRNN++ method based on the convolution-based recurrent neural network can estimate the approximate position of the region with a high echo value, the image is fuzzy and inaccurate. Similarly, the high-value echo area cannot be accurately predicted using the MIM or PredRNNv2 methods. In comparison to such methods, MSSTNet forecasts the red high dBZ area with greater precision and accuracy and performs better when forecasting the general movement trend and distribution condition of radar echo.
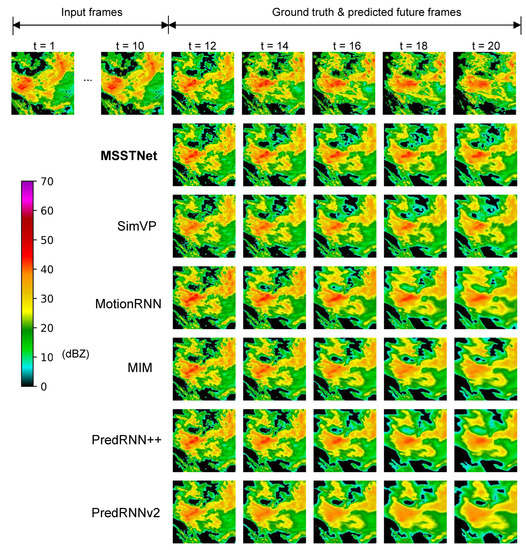
Figure 8.
Visualization of radar echo image prediction.
5. Discussion
In this study, we propose a novel spatiotemporal prediction model. On the one hand, from the perspective of statistics and observation, we find that the spatial pixel distribution of spatiotemporal movement has a certain regularity based on the statistics and analysis of typical spatiotemporal movement radar echo data. Therefore, the “Distribution feature extraction module” is constructed to extract shallow spatiotemporal features. In the meantime, it was thought that, according to MotionRNN’s [15] theory of spatiotemporal motion decomposition, spatiotemporal motion may be made up of trend motion and instantaneous motion at multiple scales. To simulate spatiotemporal motion at various temporal scales and spatial scales, a “Multi-scale motion state capture module” was created. On the other hand, from the perspective of the development of deep learning in the field of spatiotemporal prediction, the current methods may be broadly classified into convolution-based recurrent neural networks and convolutional neural networks. Both methods perform well when it comes to spatiotemporal prediction. In recent years, numerous works have examined the use of convolution-based recurrent neural networks to carry out spatiotemporal prediction, yielding numerous notable results. It is challenging to capture long-term dependency in spatiotemporal data because such deep neural networks are trapped by gradient disappearance and error accumulation, and past spatiotemporal state variables are transferred forward by memory units of fixed scale. We see the promise of pure convolutional networks in the field of spatiotemporal prediction in the most recent study, where SimVP, based on a pure convolutional structure, achieves SOTA results on numerous public datasets [30]. The pure convolution depth prediction model performs better in terms of preventing gradient disappearance and cumulative mistakes because of its end-to-end structure. However, the majority of the earlier spatiotemporal prediction models based on convolution are based on two-dimensional convolution, which often integrates the temporal dimension data into the channel dimension and does not specifically model the temporal dimension. The deep prediction network with a pure convolutional structure is the basis in this study. To make up for the absence of fine modeling of the temporal dimension in earlier structures, 3D convolution is applied, based on statistical analysis and observation of spatiotemporal data. Specifically, to extract shallow spatiotemporal features, the distribution feature extraction module of our proposed method makes use of 3D convolution. A number of convolutions of various sizes were employed in the multi-scale motion state capture module of the model to capture spatiotemporal motion at multiple temporal scales and spatial scales. It accomplishes independent precise modeling of time on the one hand and unified modeling of spatiotemporal motion at various scales on the other.
In the experiments using the MovingMNIST dataset, compared with the two-dimensional convolution structure of SimVP, the MSSTNet using 3D convolution achieves better performance in the exact same dataset, demonstrating the significance and usefulness of the more accurate representation of the temporal dimension. Despite using 3D convolution for feature extraction, the MSE of MSSTNet on the MovingMNIST dataset is improved by when compared to E3D-LSTM [21]. This suggests that for a dataset with relatively simple spatial and temporal distribution, a pure 3D convolution depth prediction network with a structure comparable to U-net [16] can outperform a recurrent neural network using 3D convolution. The multi-scale spatiotemporal motion modeling that has been suggested performs well in the MovingMNIST dataset ablation experiment, as shown in Table 6. Multi-scale spatial modeling is used in Method 2 to lower the MSE index from 57.1 to 47.2 in comparison to Method 1’s fixed convolution spatial modeling. In the meantime, Method 4’s MSE is lowered from 44.2 to 42.6 based on Method 3, demonstrating the value and necessity of multi-scale spatiotemporal modeling. Real weather radar echoes have more complicated spatiotemporal distribution variations and spatiotemporal motion states compared to artificial datasets because clouds are produced and evaporate. In the experiment using the radar echo dataset, MSSTNet performs better than other models because it gives greater weight to the CSI and HSS score in forecasting rainfall in the meteorological sector. According to Figure 6, which compare the performance for each frame, MSSTNet outperforms other models in terms of performance decay as the prediction time increases. This further demonstrates the need for a precise time-dimensional representation of the pure convolution structure.
However, there are still issues with the spatiotemporal prediction problem. First of all, the SSIM score in Table 7 and the frame-by-frame SSIM score in Figure 6 indicate that, with the exception of the MIM model, the current model is unable to significantly improve the results and that it is still challenging to make accurate predictions of structural similarity in complex spatiotemporal dynamic motion. The distinct forecast image can assist in weather prediction more accurately. The formulation of the forecast picture and other image characteristics can be specifically investigated from the standpoint of digital images in a future study. Second, none of the models are accurate enough to forecast high echo values (the red region) in the final radar echo visualization in Figure 8, which might cause errors in forecasting where rainfall would occur. Future model creation may employ a particular design to direct the model’s attention toward areas with high echo values. Finally, it is challenging to precisely identify the change rules by deep learning since image-based spatiotemporal prediction is too straightforward for sophisticated spatiotemporal dynamic systems. Radar echo images could not be the only observation used in the future to aid prediction. Currently, some studies have performed radar echo prediction from this perspective with several input variables and have generated superior prediction results [37].
6. Conclusions
This paper has proposed a multi-scale spatiotemporal prediction network (MSSTNet), which enhances the modeling capability of the spatiotemporal prediction model with a pure convolution structure in the temporal dimension, based on statistical and observed spatiotemporal distribution and spatiotemporal motion characteristics. Specifically, this paper divides the construction of MSSTNet into three modules: a spatiotemporal distribution feature extraction module that generates the future sequence images to fully use the historical sequence images information; a multi-scale motion capture module that captures the long- and short-range-dependent relationships of temporal and spatial input sequences to capture complex, time-varying, and spatiotemporal motion; and a module that combines spatiotemporal distribution features and movement features into a decoding module to generate future images. We have performed experiments on the MovingMNIST dataset, which outperforms previous state-of-the-art methods in terms of the MSE and SSIM indices. Ablation experiments on this dataset have also been performed to demonstrate the effectiveness of the MSST unit design. As an important application in the field of spatiotemporal prediction, experiments on the Radar Echo dataset have been performed, and the results have demonstrated that our method is superior to previous methods in terms of MSE, CSI, and HSS, and is more precise in predicting areas where severe convective weather is more likely to occur.
Author Contributions
Conceptualization, Y.Y., W.C. and C.L.; Data curation, Y.Y.; Formal analysis, Y.Y., F.G., W.C., C.L. and S.Z.; Funding acquisition, F.G. and C.L.; Investigation, Y.Y., F.G., W.C., C.L. and S.Z.; Methodology, Y.Y.; Resources, F.G., W.C. and C.L.; Software, Y.Y.; Supervision, F.G., W.C., C.L. and S.Z.; Validation, F.G., W.C., C.L. and S.Z.; Visualization, Y.Y.; Writing—original draft, Y.Y.; Writing—review and editing, F.G., W.C., C.L. and S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This researchwas supported by the National Key R&D Program of China (No. 2022YFE0106400), the Special funds of Shandong Province for Qingdao Marine Science and technology National Laboratory (No. 2022QNLM010203-3), the National Natural Science Foundation of China (Grant No. 41830964), and Shandong Province’s “Taishan” Scientist Program (ts201712017).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Beijing Institute of Applied Meteorology for providing the free data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, X.; Yeung, D.Y. Machine learning for spatiotemporal sequence forecasting: A survey. arXiv 2018, arXiv:1808.06865. [Google Scholar]
- Sun, N.; Zhou, Z.; Li, Q.; Jing, J. Three-Dimensional Gridded Radar Echo Extrapolation for Convective Storm Nowcasting Based on 3D-ConvLSTM Model. Remote Sens. 2022, 14, 4256. [Google Scholar] [CrossRef]
- Veillette, M.; Samsi, S.; Mattioli, C. Sevir: A storm event imagery dataset for deep learning applications in radar and satellite meteorology. Adv. Neural Inf. Process. Syst. 2020, 33, 22009–22019. [Google Scholar]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Sun, N.; Zhou, Z.; Li, Q.; Zhou, X. Spatiotemporal Prediction of Monthly Sea Subsurface Temperature Fields Using a 3D U-Net-Based Model. Remote Sens. 2022, 14, 4890. [Google Scholar] [CrossRef]
- Mao, K.; Gao, F.; Zhang, S.; Liu, C. An Information Spatial-Temporal Extension Algorithm for Shipborne Predictions Based on Deep Neural Networks with Remote Sensing Observations—Part I: Ocean Temperature. Remote Sens. 2022, 14, 1791. [Google Scholar] [CrossRef]
- Hou, S.; Li, W.; Liu, T.; Zhou, S.; Guan, J.; Qin, R.; Wang, Z. MIMO: A Unified Spatio-Temporal Model for Multi-Scale Sea Surface Temperature Prediction. Remote Sens. 2022, 14, 2371. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 1–12. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.k.; Woo, W.c. Deep learning for precipitation nowcasting: A benchmark and a new model. Adv. Neural Inf. Process. Syst. 2017, 30, 1–17. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Philip, S.Y. Predrnn++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5123–5132. [Google Scholar]
- Han, L.; Liang, H.; Chen, H.; Zhang, W.; Ge, Y. Convective precipitation nowcasting using U-Net Model. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–8. [Google Scholar] [CrossRef]
- Agrawal, S.; Barrington, L.; Bromberg, C.; Burge, J.; Gazen, C.; Hickey, J. Machine learning for precipitation nowcasting from radar images. arXiv 2019, arXiv:1912.12132. [Google Scholar]
- Wu, H.; Yao, Z.; Wang, J.; Long, M. MotionRNN: A flexible model for video prediction with spacetime-varying motions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 15435–15444. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Qiu, Z.; Yao, T.; Mei, T. Learning spatio-temporal representation with pseudo-3d residual networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5533–5541. [Google Scholar]
- Xie, S.; Sun, C.; Huang, J.; Tu, Z.; Murphy, K. Rethinking spatiotemporal feature learning: Speed-accuracy trade-offs in video classification. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 305–321. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H.; Long, M.; Wang, J.; Yu, P.S. Memory in memory: A predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 9154–9162. [Google Scholar]
- Wang, Y.; Jiang, L.; Yang, M.H.; Li, L.J.; Long, M.; Fei-Fei, L. Eidetic 3D LSTM: A model for video prediction and beyond. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning spatiotemporal features with 3d convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Lin, Z.; Li, M.; Zheng, Z.; Cheng, Y.; Yuan, C. Self-attention convlstm for spatiotemporal prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11531–11538. [Google Scholar]
- Yu, W.; Lu, Y.; Easterbrook, S.; Fidler, S. Efficient and Information-Preserving Future Frame Prediction and Beyond. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Wang, Y.; Wu, H.; Zhang, J.; Gao, Z.; Wang, J.; Yu, P.; Long, M. Predrnn: A recurrent neural network for spatiotemporal predictive learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2018; pp. 3–11. [Google Scholar]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.W.; Wu, J. Unet 3+: A full-scale connected unet for medical image segmentation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1055–1059. [Google Scholar]
- Song, K.; Yang, G.; Wang, Q.; Xu, C.; Liu, J.; Liu, W.; Shi, C.; Wang, Y.; Zhang, G.; Yu, X.; et al. Deep learning prediction of incoming rainfalls: An operational service for the city of Beijing China. In Proceedings of the 2019 International Conference on Data Mining Workshops (ICDMW), Beijing, China, 8–11 November 2019; pp. 180–185. [Google Scholar]
- Trebing, K.; Staǹczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. SimVP: Simpler Yet Better Video Prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2022; pp. 3170–3180. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Guen, V.L.; Thome, N. Disentangling physical dynamics from unknown factors for unsupervised video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11474–11484. [Google Scholar]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Chkeir, S.; Anesiadou, A.; Mascitelli, A.; Biondi, R. Nowcasting extreme rain and extreme wind speed with machine learning techniques applied to different input datasets. Atmos. Res. 2022, 282, 106548. [Google Scholar] [CrossRef]
- Caseri, A.N.; Santos, L.B.L.; Stephany, S. A convolutional recurrent neural network for strong convective rainfall nowcasting using weather radar data in Southeastern Brazil. Artif. Intell. Geosci. 2022, 3, 8–13. [Google Scholar] [CrossRef]
- Pan, X.; Lu, Y.; Zhao, K.; Huang, H.; Wang, M.; Chen, H. Improving Nowcasting of Convective Development by Incorporating Polarimetric Radar Variables Into a Deep-Learning Model. Geophys. Res. Lett. 2021, 48, e2021GL095302. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).