A Mesh Mapping-Based Cooperative Inversion Strategy for Airborne Transient Electromagnetic and Magnetic Methods
Abstract
1. Introduction
2. Methods
2.1. Inversion of the Quasi-2D ATEM with IP Effect
2.2. 2D Magnetic Method Inversion
2.3. Cooperative Inversion with Cross-Gradient and Mesh Mapping
2.3.1. Cross-Gradient Constraint
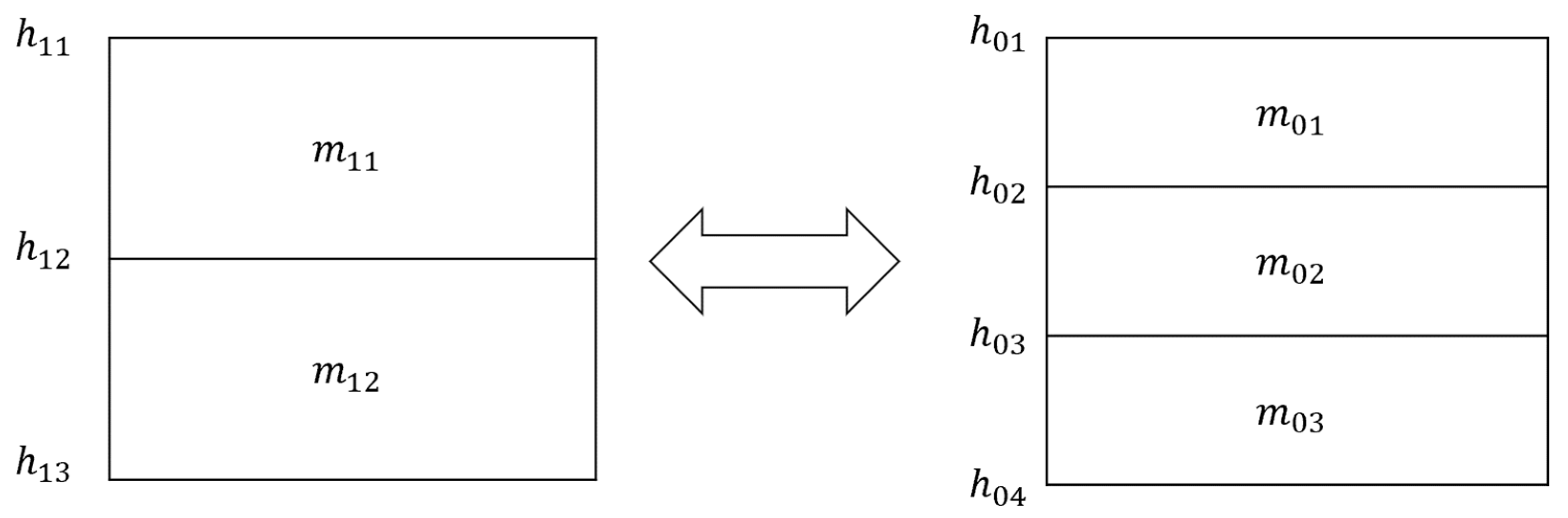
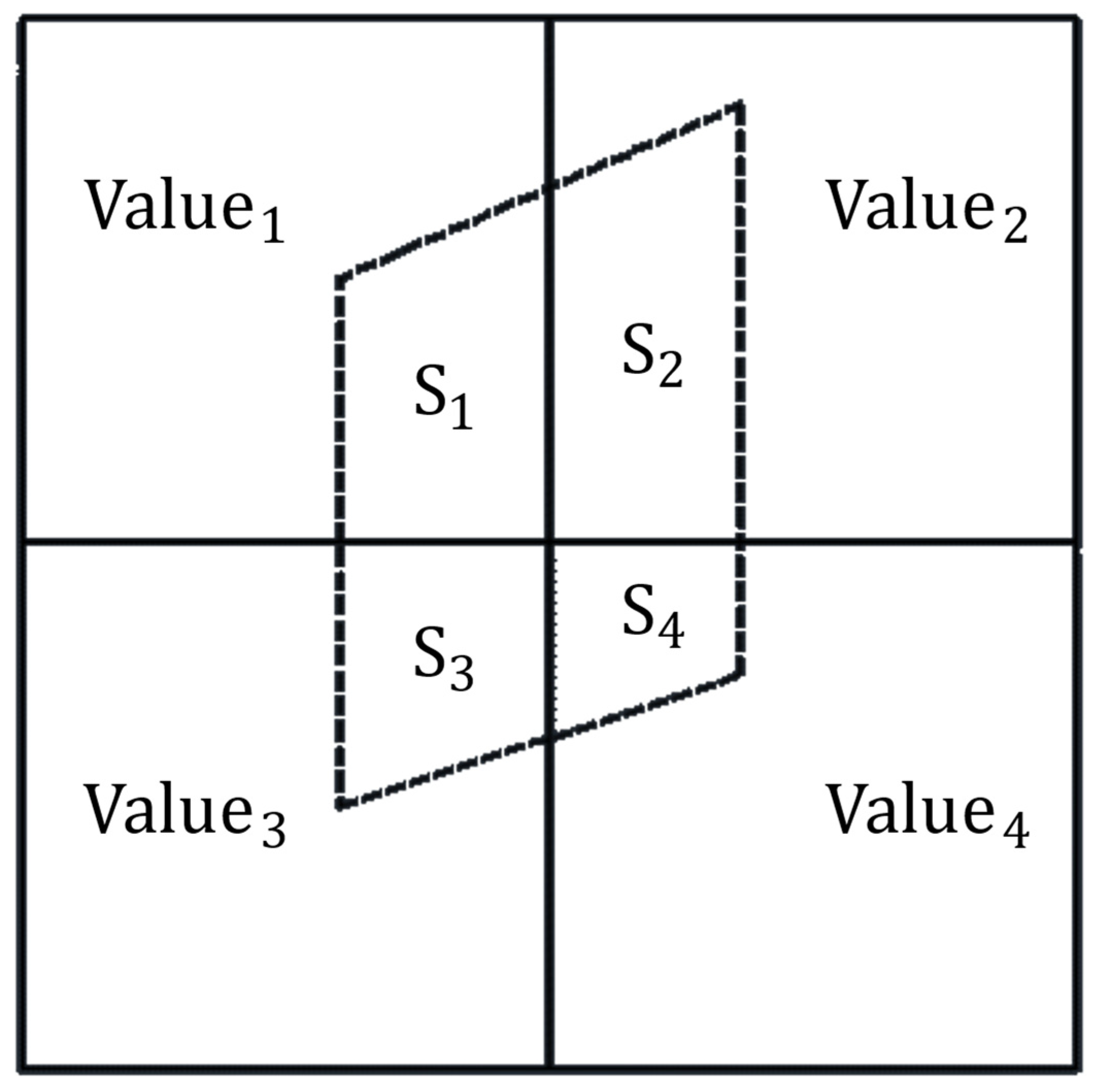
2.3.2. Mesh Mapping Method
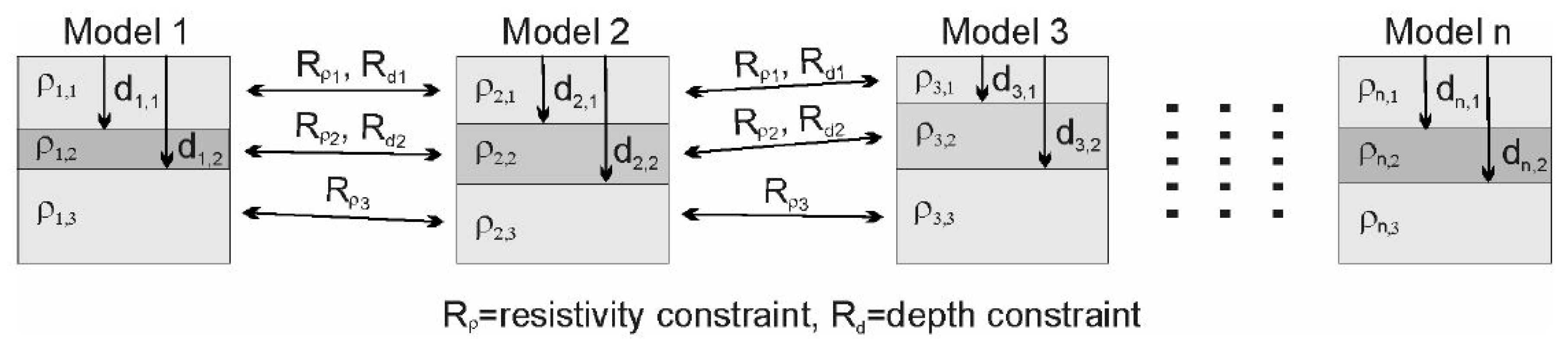
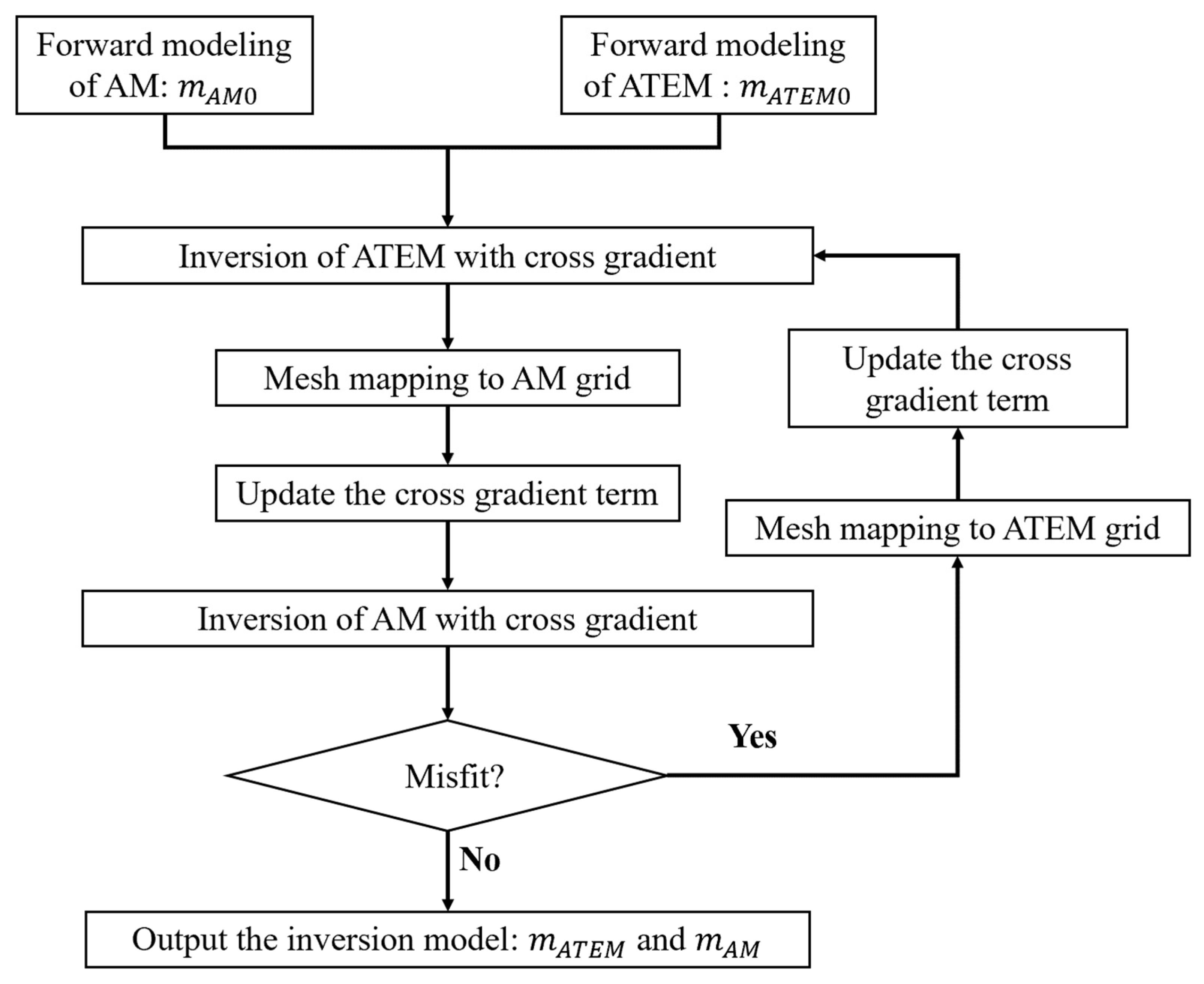
2.3.3. Cooperative Inversion Strategy
3. Results
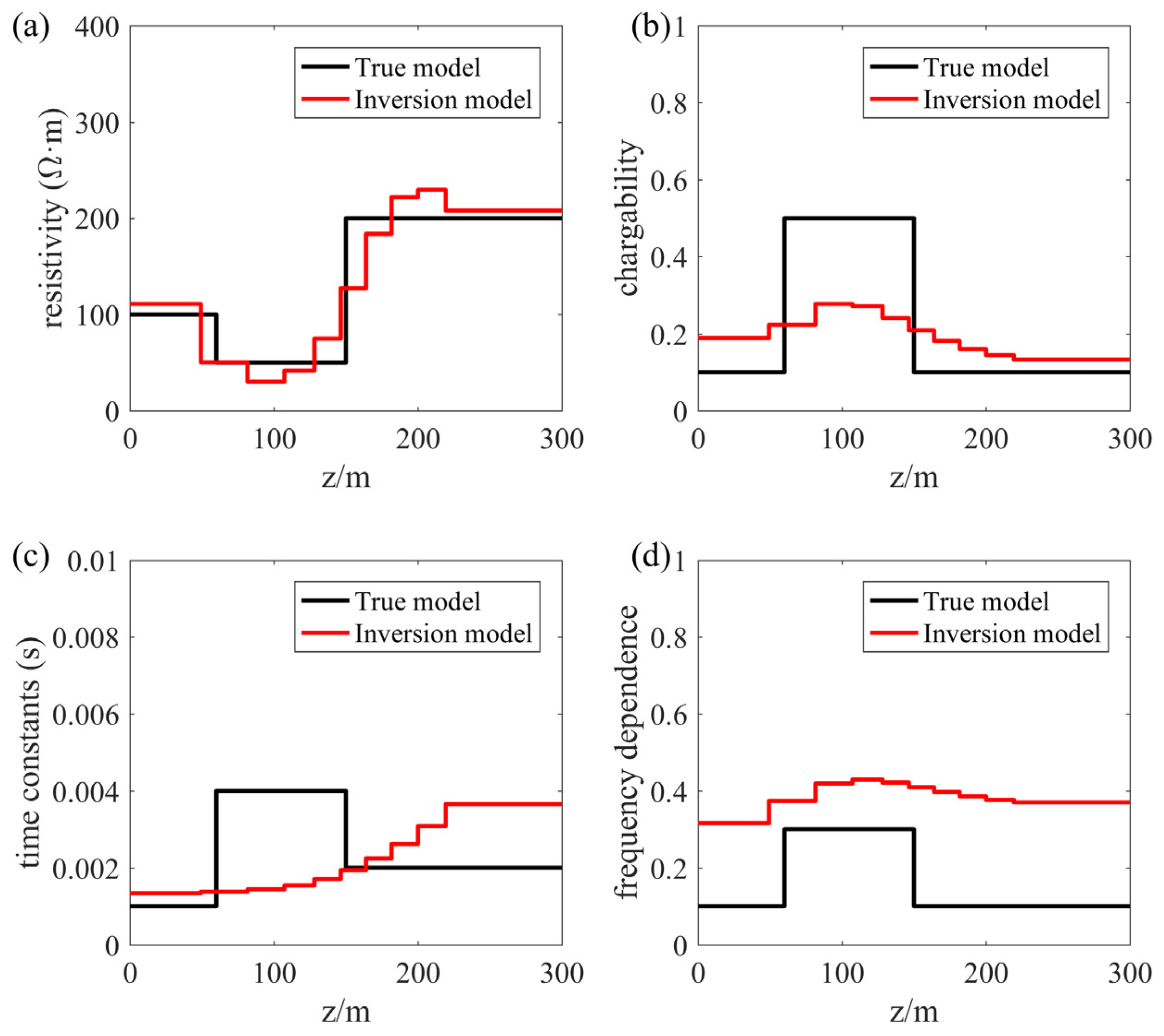
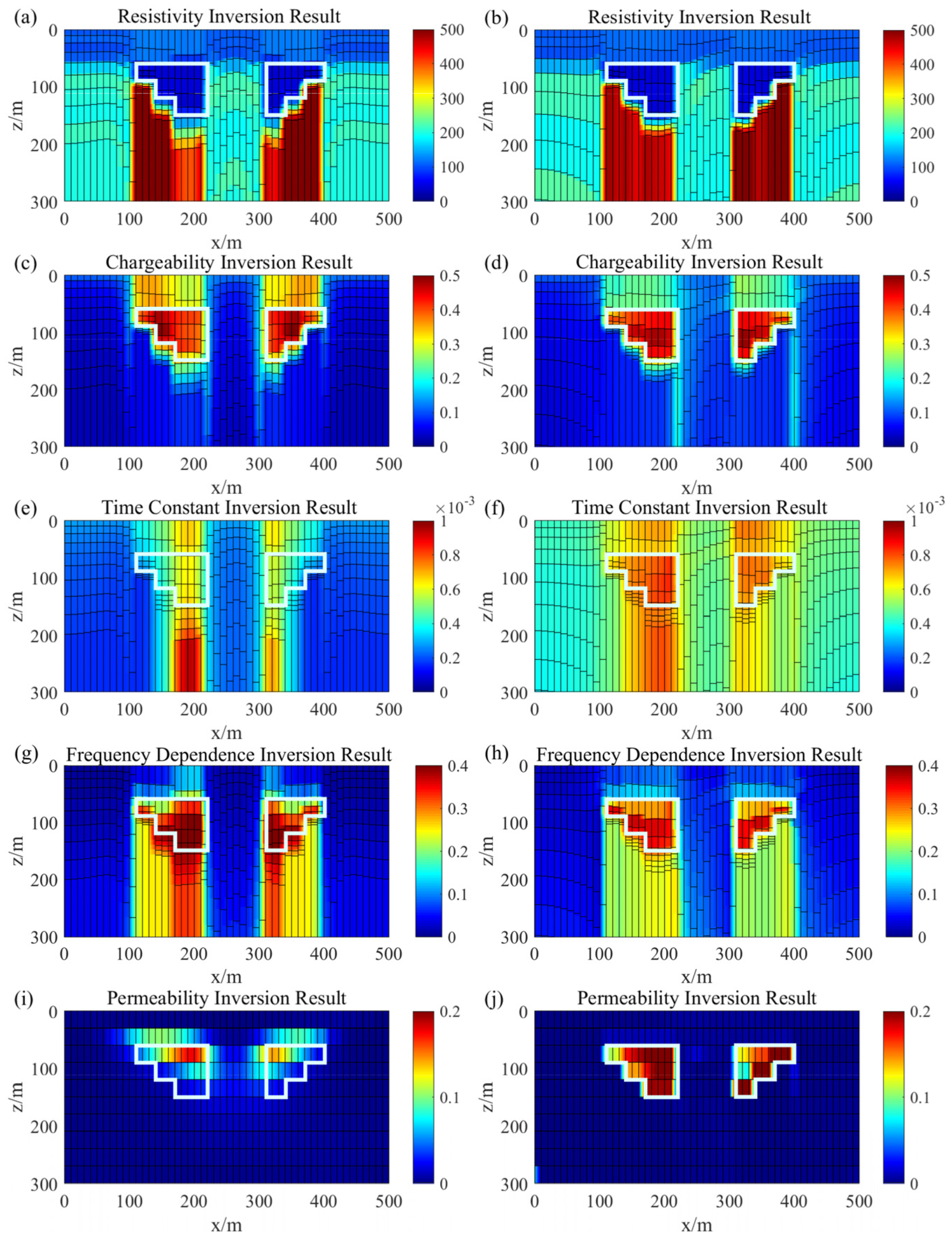
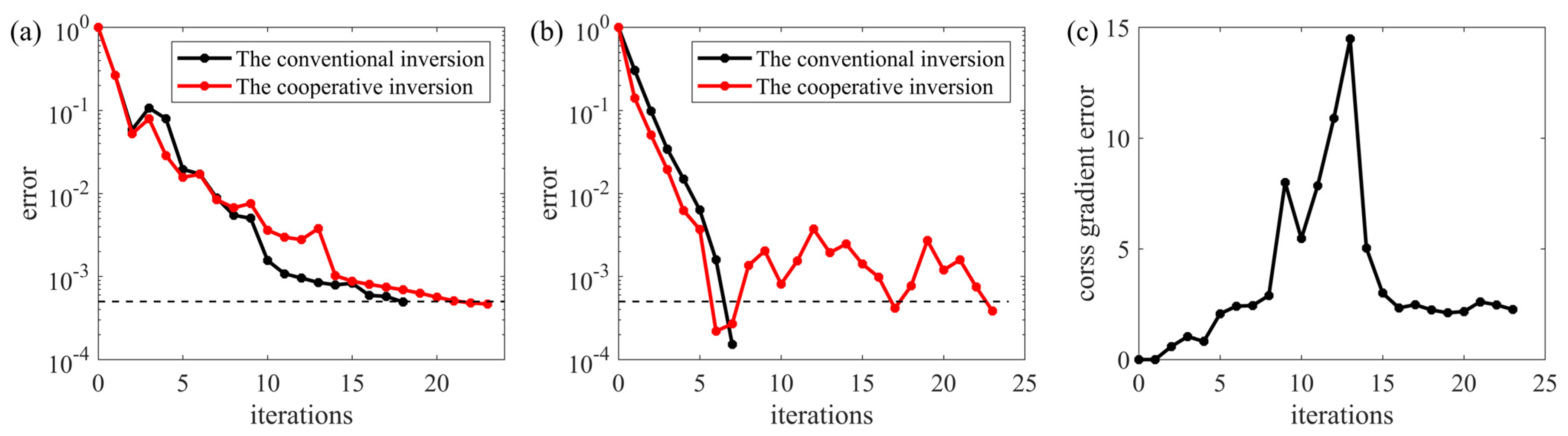
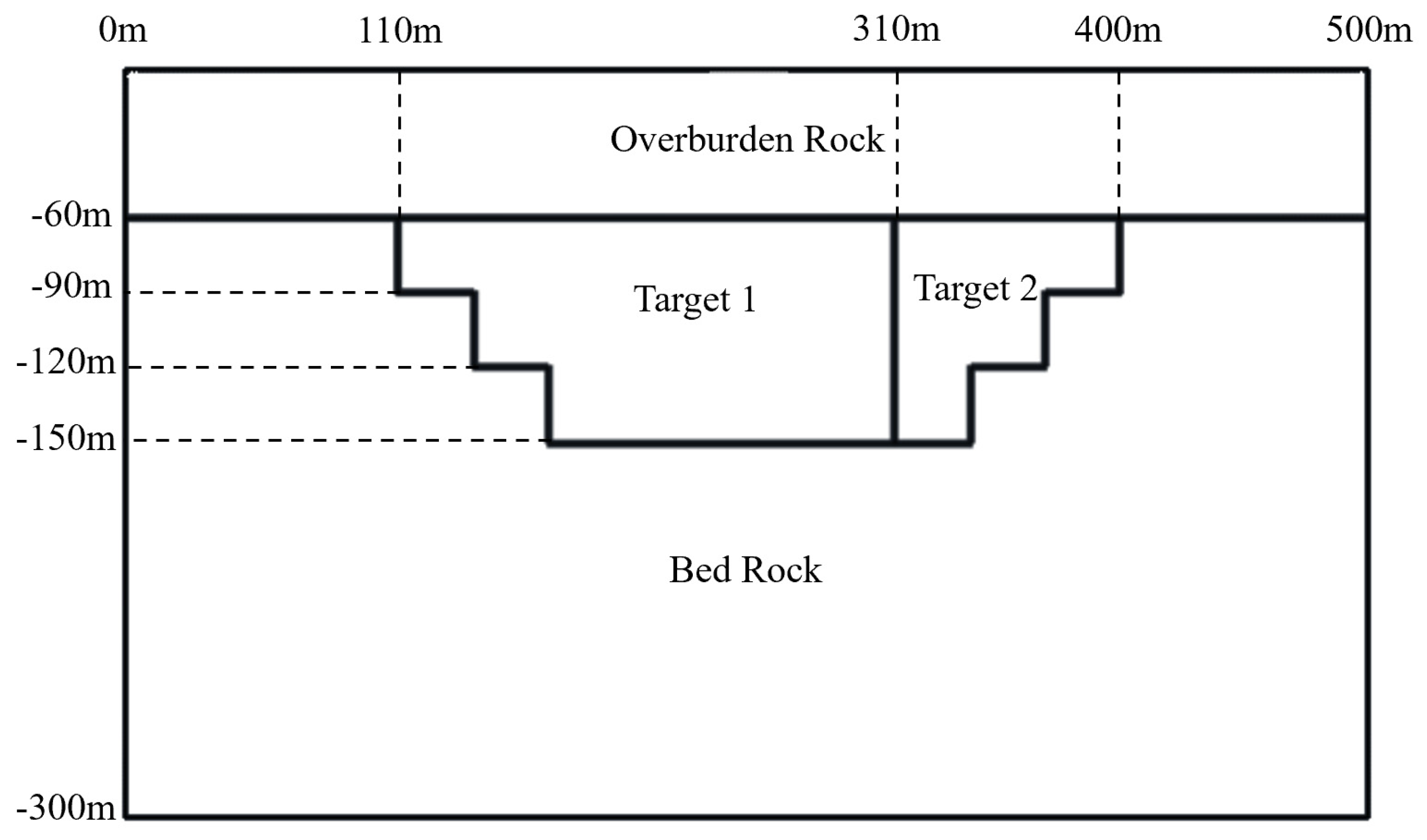
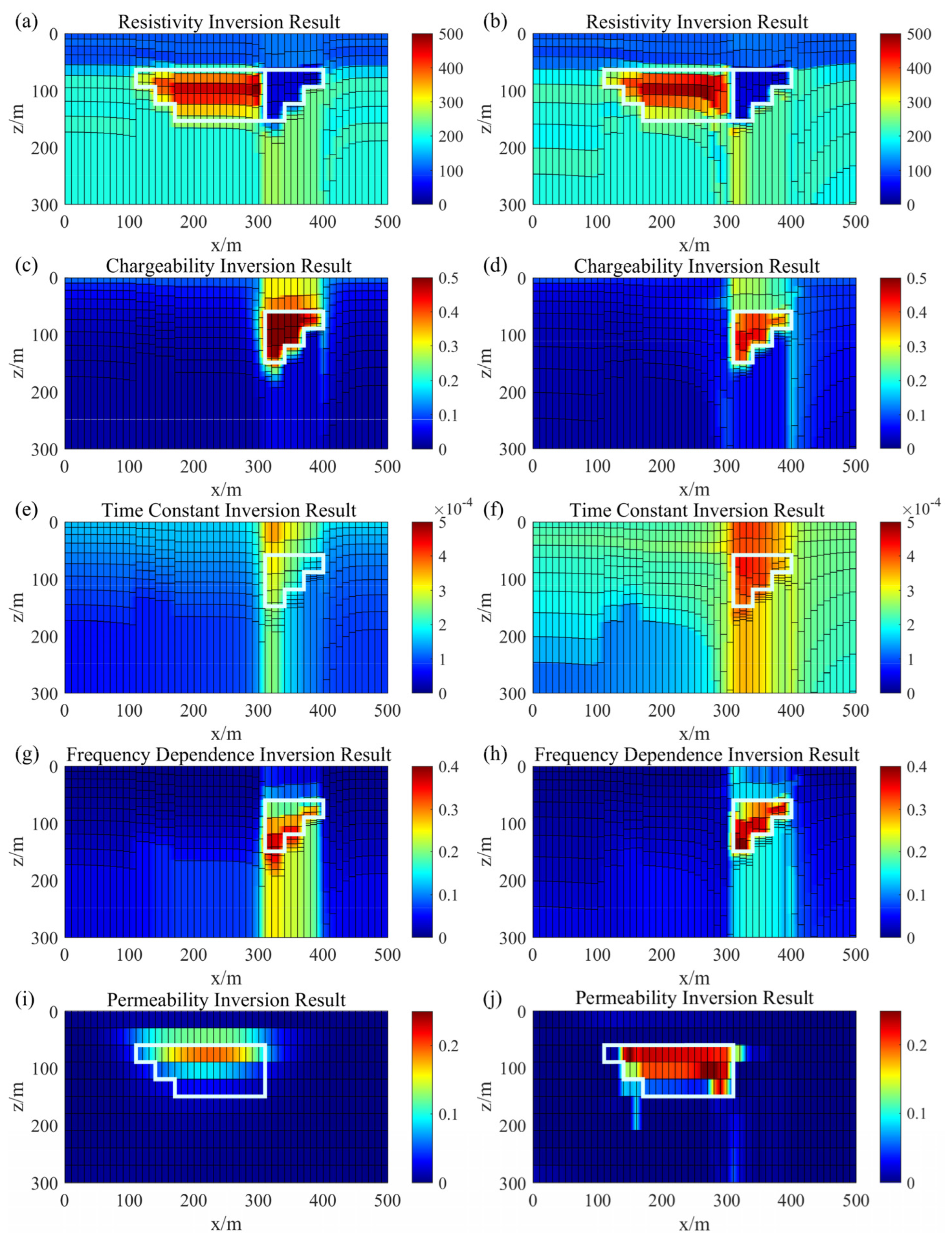
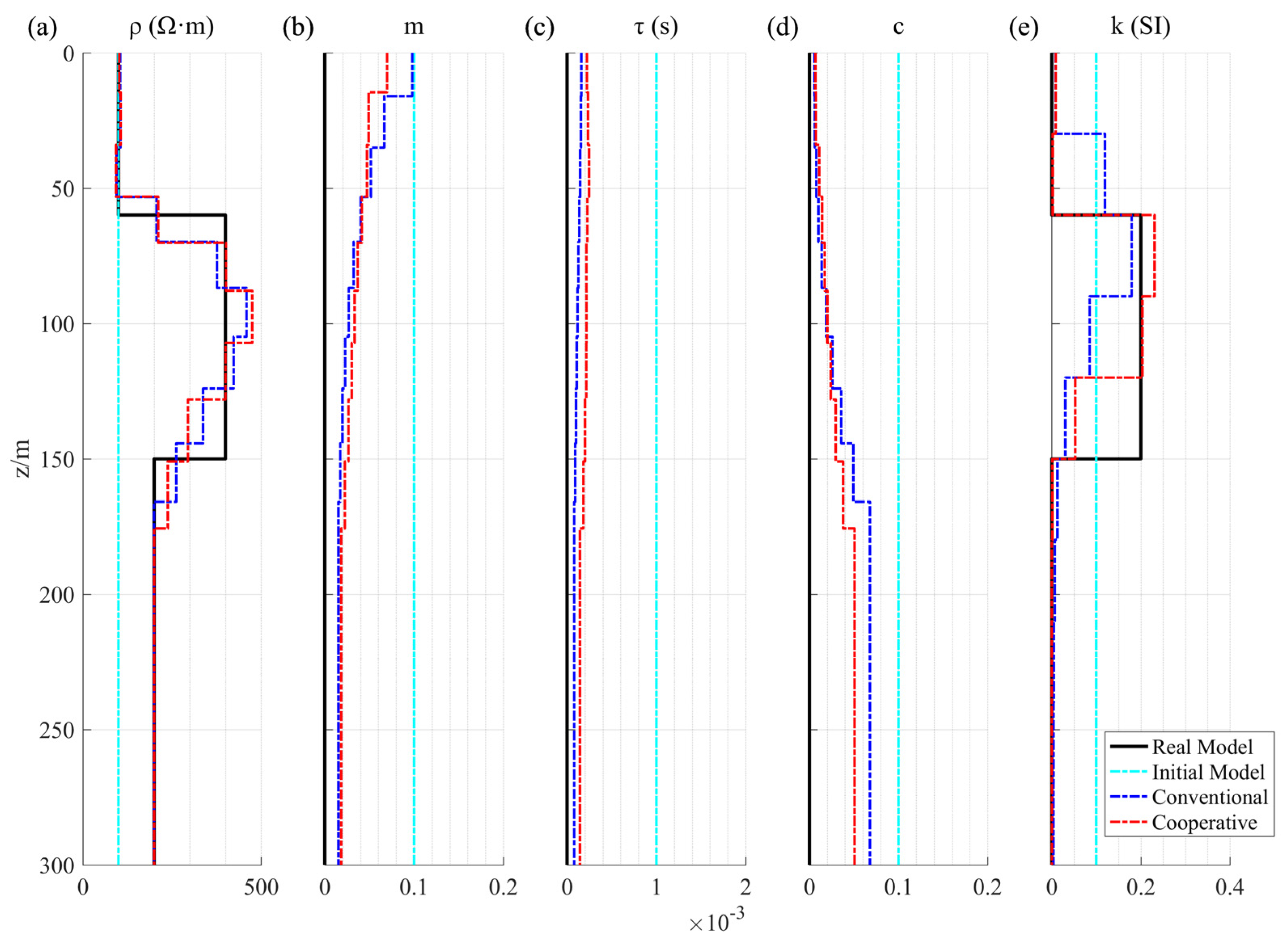
3.1. Model 1 Inversion Results of the Synthetic Data
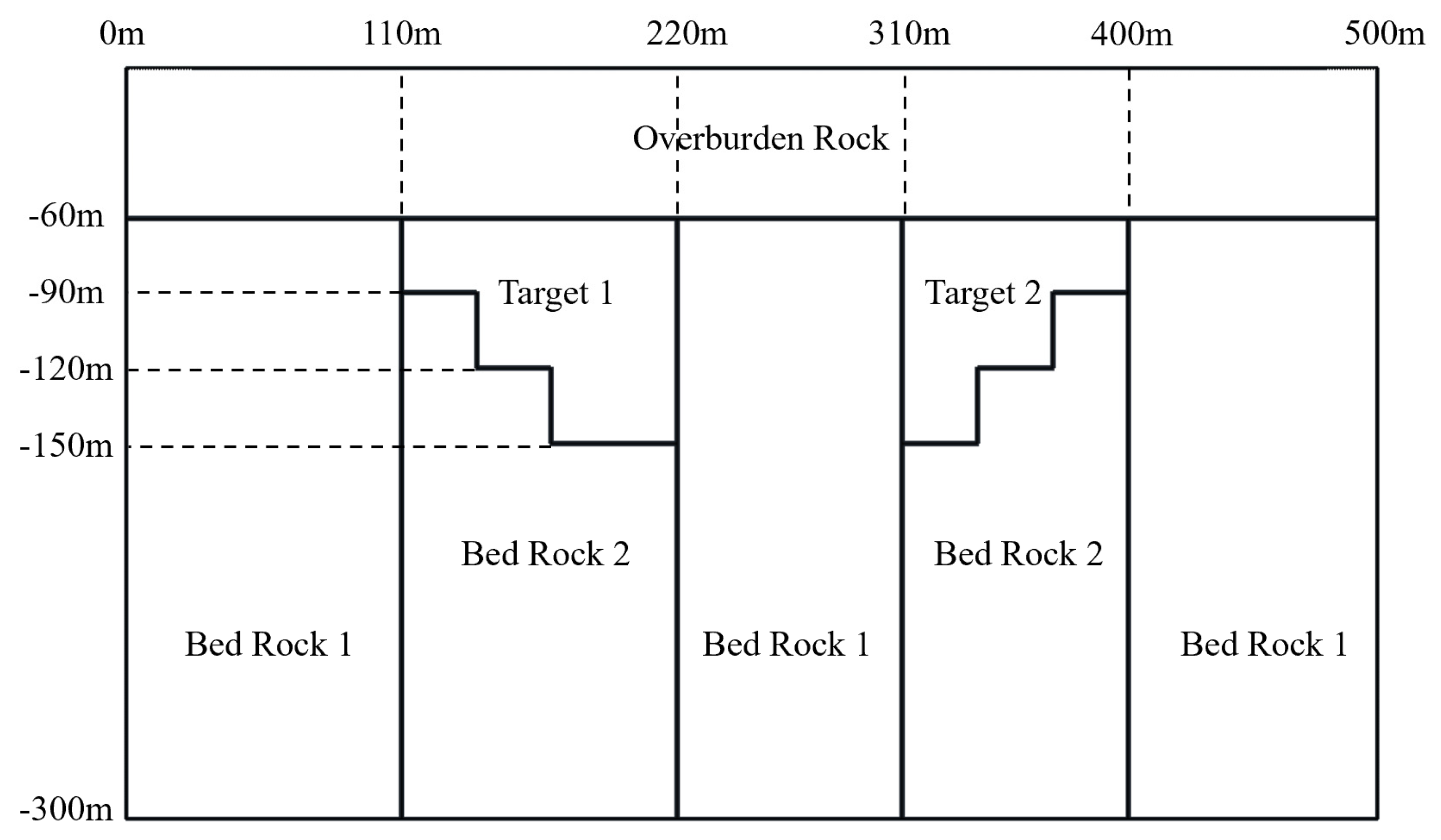
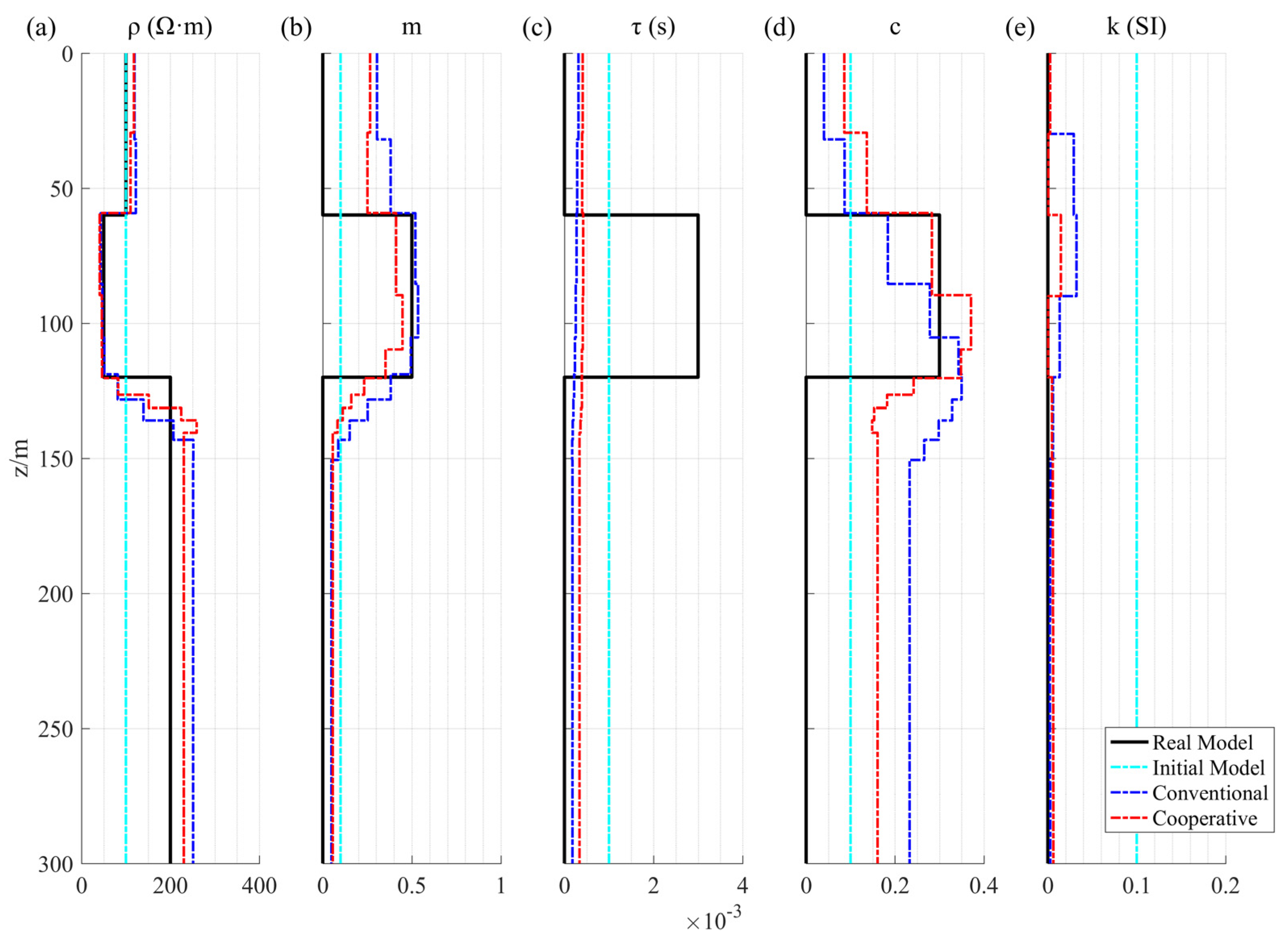
3.2. Model 2 Inversion Results of the Synthetic Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Moorkamp, M. Integrating Electromagnetic Data with Other Geophysical Observations for Enhanced Imaging of the Earth: A Tutorial and Review. Surv. Geophys. 2017, 38, 935–962. [Google Scholar] [CrossRef]
- Vozoff, K.; Jupp, D.L.B. Joint Inversion of Geophysical Data. Geophys. J. Int. 1975, 42, 977–991. [Google Scholar] [CrossRef]
- Sasaki, Y. Two-dimensional joint inversion of magnetotelluric and dipole data. In SEG Technical Program Expanded Abstracts 1986; SEG: Houston, TX, USA, 1986; pp. 55–57. [Google Scholar]
- Maxwell, A.; Meju. Joint inversion of TEM and distorted MT soundings: Some effective practical considerations. Geophysics 1996, 61, 56–65. [Google Scholar] [CrossRef]
- Hering, A.; Misiek, R.; Gyulai, A.; Ormos, T.; Dresen, L. A joint inversion algorithm to process geoelectric and sutface wave seismic data. Part I: Basic ideas1. Geophys. Prospect. 1995, 43, 135–156. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G.A. Three-dimensional controlled-source electromagnetic and magnetotelluric joint inversion. Geophys. J. Int. 2009, 178, 1305–1316. [Google Scholar] [CrossRef]
- Moorkamp, M.; Heincke, B.; Jegen, M.; Hobbs, R.W.; Roberts, A.W. Joint Inversion in Hydrocarbon Exploration; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 167–189. [Google Scholar]
- Lines, L.R.; Schultz, A.K.; Treitel, S. Cooperative inversion of geophysical data. Geophysics 1988, 53, 8–20. [Google Scholar] [CrossRef]
- Paasche, H.; Tronicke, J. Cooperative inversion of 2D geophysical data sets: A zonal approach based on fuzzy c-means cluster analysis. Geophysics 2007, 72, A35–A39. [Google Scholar] [CrossRef]
- Mcmillan, M.S.; Oldenburg, D.W. Cooperative constrained inversion of multiple electromagnetic data sets. Geophysics 2014, 79, B173–B185. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Jorgensen, M.; Cox, L. Advanced Methods of Joint Inversion of Multiphysics Data for Mineral Exploration. Geosciences 2021, 11, 262. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. Aime 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Faust, L.Y. A Velocity Function Incluing Lithologic Variation. Geophysics 1953, 18, 271–288. [Google Scholar] [CrossRef]
- Gao, G.; Abubakar, A.; Habashy, T.M. Joint petrophysical inversion of electromagnetic and full-waveform seismic data. Geophysics 2012, 77, WA3–WA18. [Google Scholar] [CrossRef]
- Jegen, M.D.; Hobbs, R.W.; Tarits, P.; Chave, A. Joint inversion of marine magnetotelluric and gravity data incorporating seismic constraints: Preliminary results of sub-basalt imaging off the Faroe Shelf. Earth Planet. Sci. Lett. 2009, 282, 47–55. [Google Scholar] [CrossRef]
- Haber, E.; Oldenburg, D.W. Joint inversion: A structural approach. Inverse Probl. 1997, 13, 63. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Characterization of heterogeneous near-surface materials by joint 2D inversion of dc resistivity and seismic data. Geophys. Res. Lett. 2003, 30, 1658. [Google Scholar] [CrossRef]
- Molodtsov, D.M.; Troyan, V.N.; Roslov, Y.V.; Zerilli, A. Joint inversion of seismic traveltimes and magnetotelluric data with a directed structural constraint. Geophys. Prospect. 2013, 61, 1218–1228. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Joint two-dimensional cross-gradient imaging of seismic traveltime data for structural and lithological classification. Geophys. J. Int. 2007, 169, 1261–1272. [Google Scholar] [CrossRef]
- Pak, Y.-C.; Li, T.; Kim, G.-S. 2D data-space cross-gradient joint inversion of MT, gravity and magnetic data. J. Appl. Geophys. 2017, 143, 212–222. [Google Scholar] [CrossRef]
- Varfinezhad, R.; Oskooi, B.; Fedi, M. Joint Inversion of DC Resistivity and Magnetic Data, Constrained by Cross Gradients, Compactness and Depth Weighting. Pure Appl. Geophys. 2020, 177, 4325–4343. [Google Scholar] [CrossRef]
- Sudha; Tezkan, B.; Siemon, B. Appraisal of a new 1D weighted joint inversion of ground based and helicopter-borne electromagnetic data. Geophys. Prospect. 2014, 62, 597–614. [Google Scholar] [CrossRef]
- Carter, S.; Xie, X.; Zhou, L.; Yan, L. Hybrid Monte Carlo 1-D joint inversion of LOTEM and MT. J. Appl. Geophys. 2021, 194, 104424. [Google Scholar] [CrossRef]
- Giraud, J.; Seillé, H.; Lindsay, M.D.; Visser, G.; Ogarko, V.; Jessell, M.W. Utilisation of probabilistic MT inversions to constrain magnetic data inversion: Proof-of-concept and field application. Solid Earth Discuss. 2021, 2021, 1–33. [Google Scholar] [CrossRef]
- He, H.; Li, T.; Zhang, R. Joint Inversion of 3D Gravity and Magnetic Data under Undulating Terrain Based on Combined Hexahedral Grid. Remote Sens. 2022, 14, 4651. [Google Scholar] [CrossRef]
- Spies, B.R. A Field Occurrence of Sign Reversals with the Transient Electromagnetic method. Geophys. Prospect. 1980, 28, 620–632. [Google Scholar] [CrossRef]
- Smith, R.S.; Klein, J. A special circumstance of airborne induced-polarization measurements. Geophysics 1996, 61, 66–73. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Pelton, W.H.; Ward, S.H.; Hallof, P.G.; Sill, W.R.; Nelson, P.H. Mineral Discrimination and Removal of Inductive Coupling with Multifrequency IP. Geophysics 1978, 43, 588–609. [Google Scholar] [CrossRef]
- Auken, E.; Christiansen, A.V. Layered and laterally constrained 2D inversion of resistivity data. Geophysics 2004, 69, 752–761. [Google Scholar] [CrossRef]
- Macnae, J. Quantifying Airborne Induced Polarization effects in helicopter time domain electromagnetics. J. Appl. Geophys. 2016, 135, 495–502. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Caratori Tontini, F.; Cocchi, L.; Carmisciano, C. Depth-to-the-bottom optimization for magnetic data inversion: Magnetic structure of the Latium volcanic region, Italy. J. Geophys. Res. Solid Earth 2006, 111, B11104. [Google Scholar] [CrossRef]
- Nabighian, M.; Corbett, J. Electromagnetic Methods in Applied Geophysics; SEG: Houston, TX, USA, 1988; pp. 203–221. [Google Scholar]
- Commer, M.; Newman, G.A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int. 2008, 172, 513–535. [Google Scholar] [CrossRef]
- Jupp, D.L.B.; Vozoff, K. Stable Iterative Methods for the Inversion of Geophysical Data. Geophys. J. R. Astron. Soc. 1975, 42, 957–976. [Google Scholar] [CrossRef]
- Viezzoli, A.; Kaminski, V.; Fiandaca, G. Modeling induced polarization effects in helicopter time domain electromagnetic data: Synthetic case studies. Geophysics 2017, 82, E31–E50. [Google Scholar] [CrossRef]
- Auken, E.; Christiansen, A.V.; Jacobsen, B.H.; Foged, N.; Sørensen, K.I. Piecewise 1D laterally constrained inversion of resistivity data. Geophys. Prospect. 2005, 53, 497–506. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Cohen, I., Huang, Y., Chen, J., Benesty, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- ChangChun, Y.I.N.; SiYuan, S.U.N.; XiuHe, G.A.O.; YunHe, L.I.U.; Hui, C. 3D joint inversion of magnetotelluric and gravity data based on local correlation constraints. Chinese J. Geophys. 2018, 61, 358–367. (In Chinese) [Google Scholar] [CrossRef]
- Korenius, T.; Laurikkala, J.; Juhola, M. On principal component analysis, cosine and Euclidean measures in information retrieval. Inf. Sci. 2007, 177, 4893–4905. [Google Scholar] [CrossRef]
- Chakrabarti, S. Data Mining for Hypertext: A Tutorial Survey. SIGKDD Explor. 2000, 1, 1–11. [Google Scholar] [CrossRef]
- Xia, P.; Zhang, L.; Li, F. Learning similarity with cosine similarity ensemble. Inf. Sci. 2015, 307, 39–52. [Google Scholar] [CrossRef]
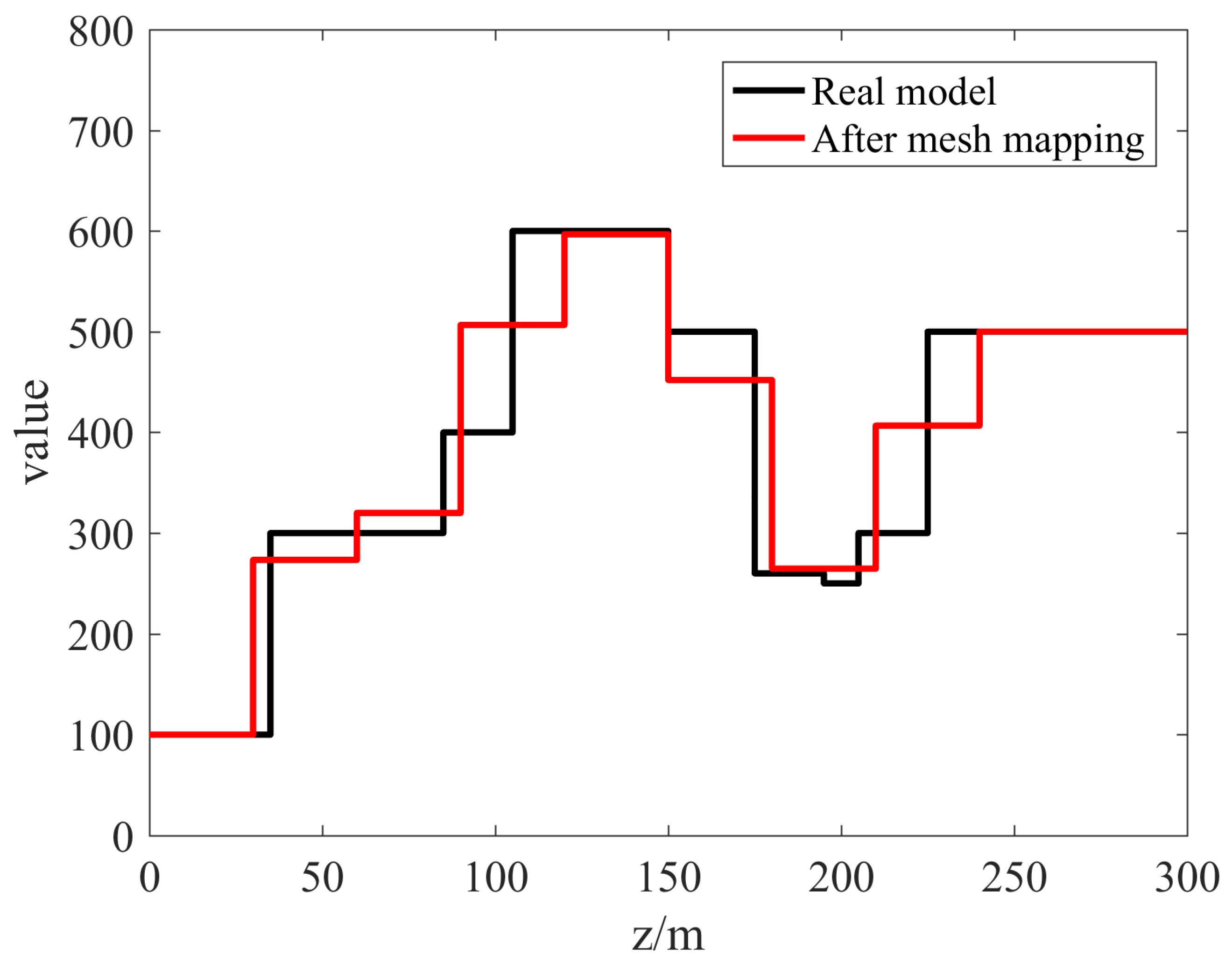

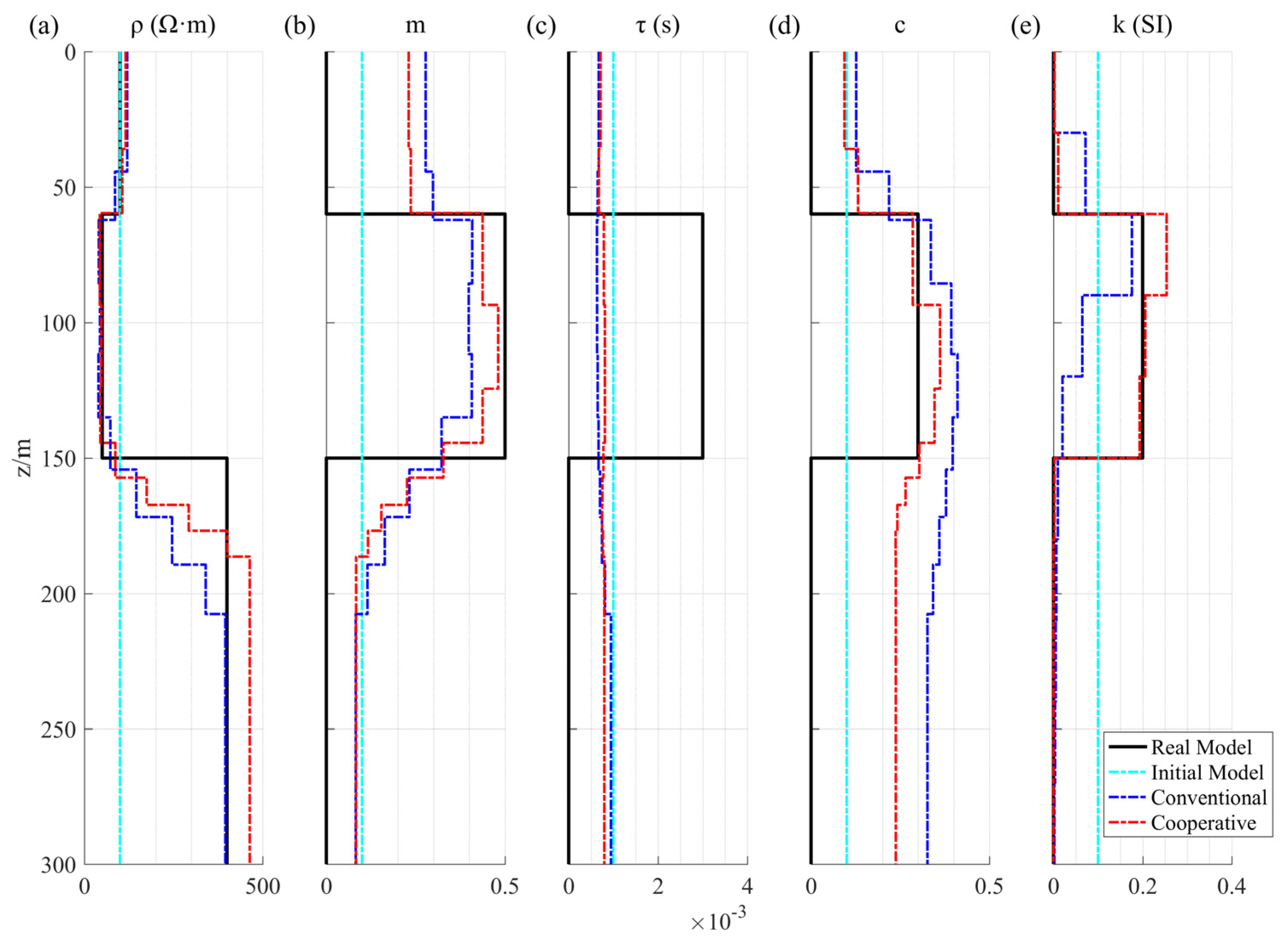
| Layer | Thickness (before) | Value (before) | Thickness (after) | Value (after) |
|---|---|---|---|---|
| 1 | 35 | 100 | 30 | 100 |
| 2 | 25 | 300 | 30 | 273.3 |
| 3 | 25 | 300 | 30 | 320 |
| 4 | 20 | 400 | 30 | 506.6 |
| 5 | 45 | 600 | 30 | 596.6 |
| 6 | 25 | 500 | 30 | 452 |
| 7 | 20 | 260 | 30 | 246.6 |
| 8 | 10 | 250 | 30 | 406.6 |
| 9 | 20 | 300 | 30 | 500 |
| 10 | - | 500 | - | 500 |
| Resistivity | Chargeability | Time Constant (s) | Frequency Dependence | Permeability (SI) | |
|---|---|---|---|---|---|
| Overburden Rock | 100 | 0 | 0 | 0 | 0 |
| Target 1 | 50 | 0.5 | 0.003 | 0.3 | 0.2 |
| Target 2 | 50 | 0.5 | 0.003 | 0.3 | 0.2 |
| Bed Rock 1 | 200 | 0 | 0 | 0 | 0 |
| Bed Rock 2 | 400 | 0 | 0 | 0 | 0 |
| Resistivity | Chargeability | Time Constant (s) | Frequency Dependence | Permeability (SI) | |
|---|---|---|---|---|---|
| Overburden Rock | 100 | 0 | 0 | 0 | 0 |
| Target 1 | 400 | 0 | 0 | 0 | 0.2 |
| Target 2 | 50 | 0.5 | 0.003 | 0.3 | 0 |
| Bed Rock | 200 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Lei, D.; Wang, Z.; Fu, C. A Mesh Mapping-Based Cooperative Inversion Strategy for Airborne Transient Electromagnetic and Magnetic Methods. Remote Sens. 2023, 15, 125. https://doi.org/10.3390/rs15010125
Ren H, Lei D, Wang Z, Fu C. A Mesh Mapping-Based Cooperative Inversion Strategy for Airborne Transient Electromagnetic and Magnetic Methods. Remote Sensing. 2023; 15(1):125. https://doi.org/10.3390/rs15010125
Chicago/Turabian StyleRen, Hao, Da Lei, Zhongxing Wang, and Changmin Fu. 2023. "A Mesh Mapping-Based Cooperative Inversion Strategy for Airborne Transient Electromagnetic and Magnetic Methods" Remote Sensing 15, no. 1: 125. https://doi.org/10.3390/rs15010125
APA StyleRen, H., Lei, D., Wang, Z., & Fu, C. (2023). A Mesh Mapping-Based Cooperative Inversion Strategy for Airborne Transient Electromagnetic and Magnetic Methods. Remote Sensing, 15(1), 125. https://doi.org/10.3390/rs15010125






