Estimates of Hyperspectral Surface and Underwater UV Planar and Scalar Irradiances from OMI Measurements and Radiative Transfer Computations
Abstract
:1. Introduction
2. Data and Methods
2.1. TSIS-1 Data
2.2. OMI Data
2.3. Atmospheric RT Model
2.4. Oceanic RT Model
2.5. Scalar Irradiance
3. Results
3.1. Surface Irradiance
3.2. In-Water Irradiance
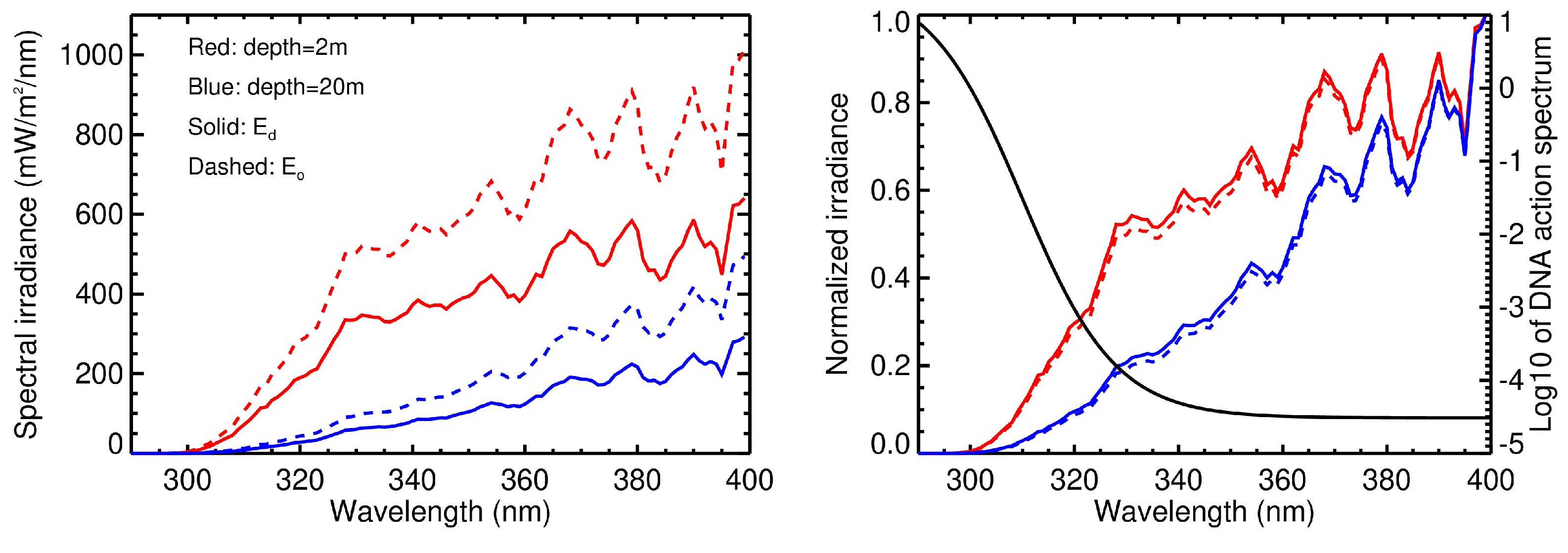
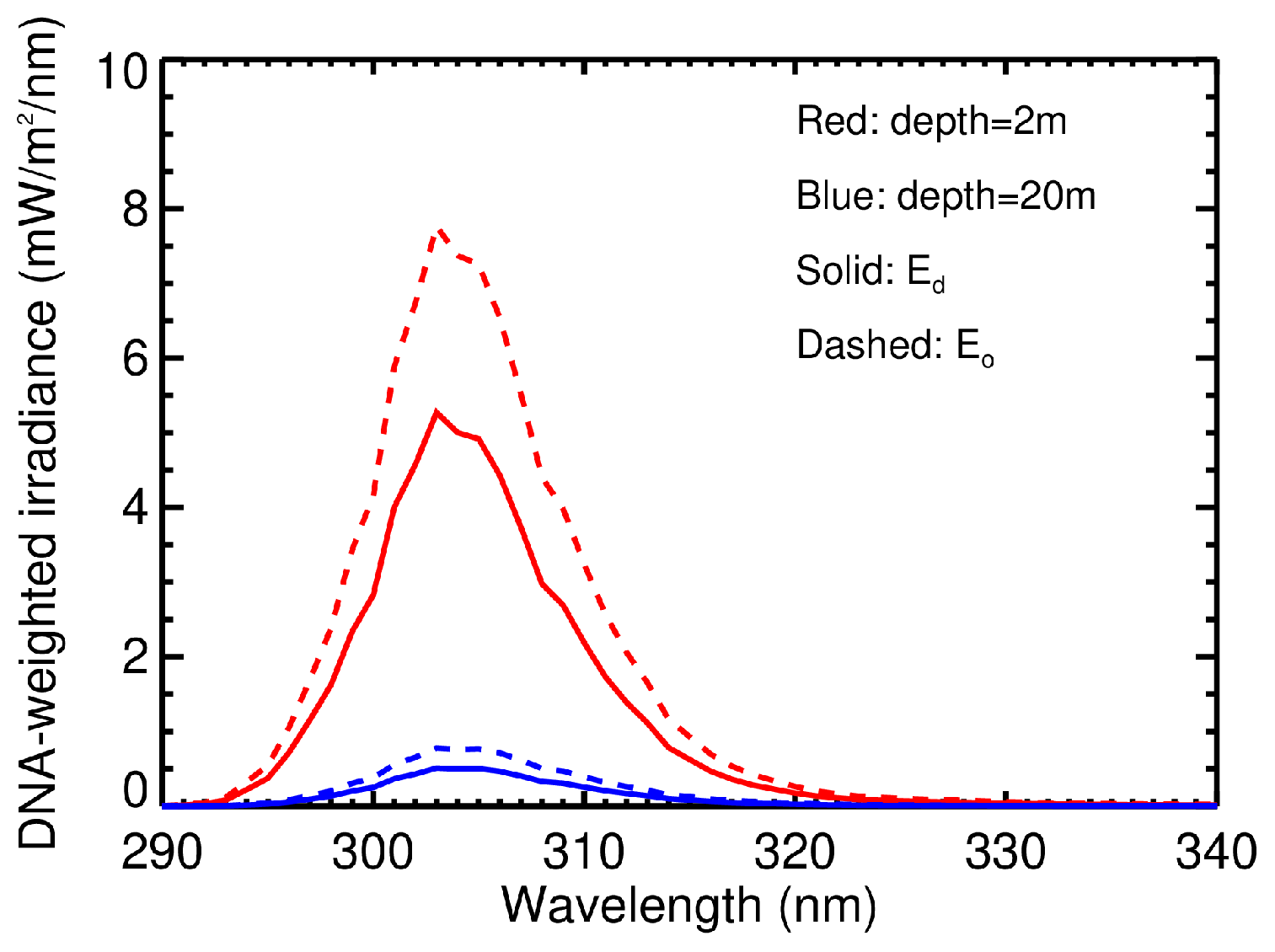
3.2.1. Spectral Irradiance
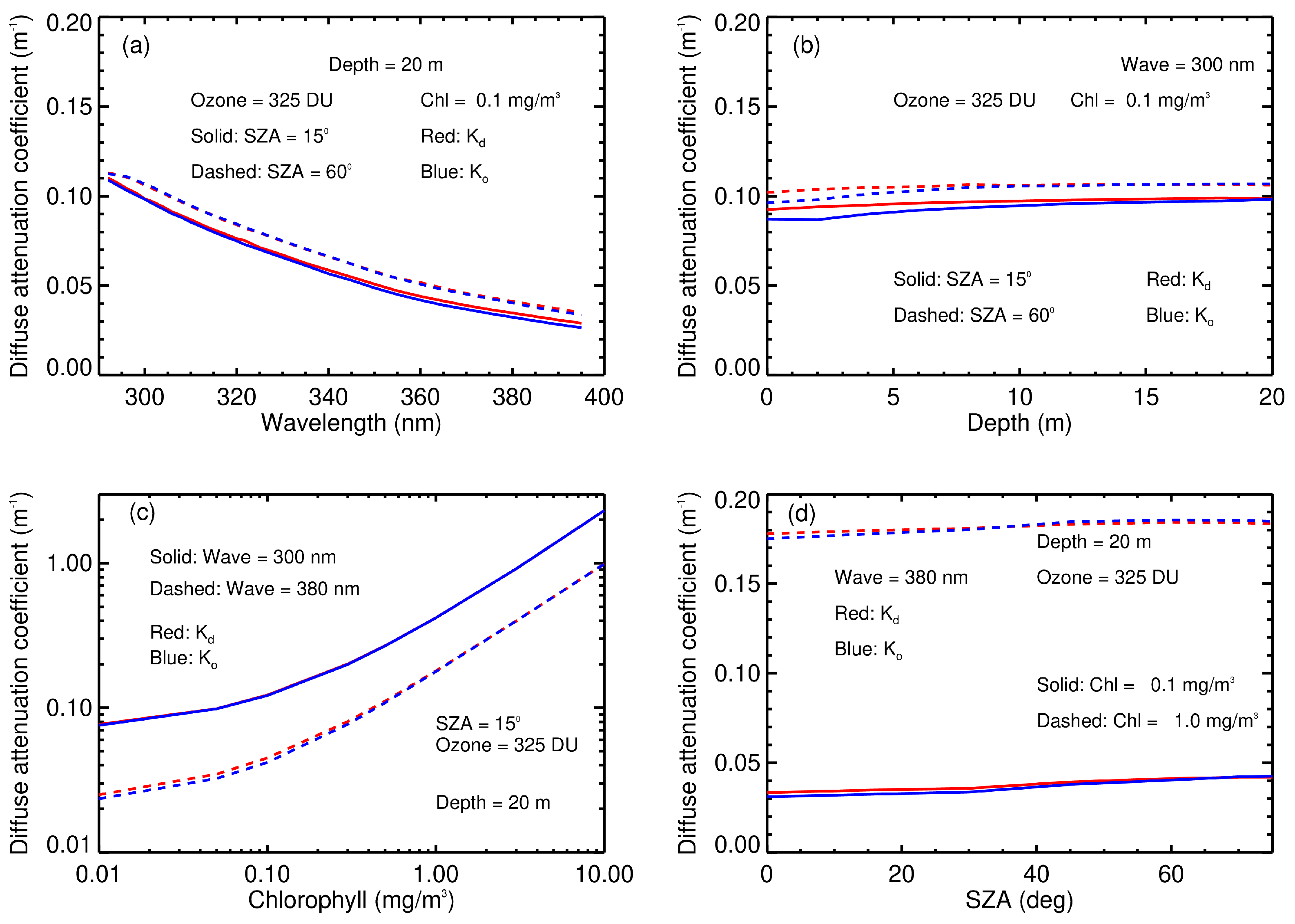
3.2.2. K-Functions in the UV
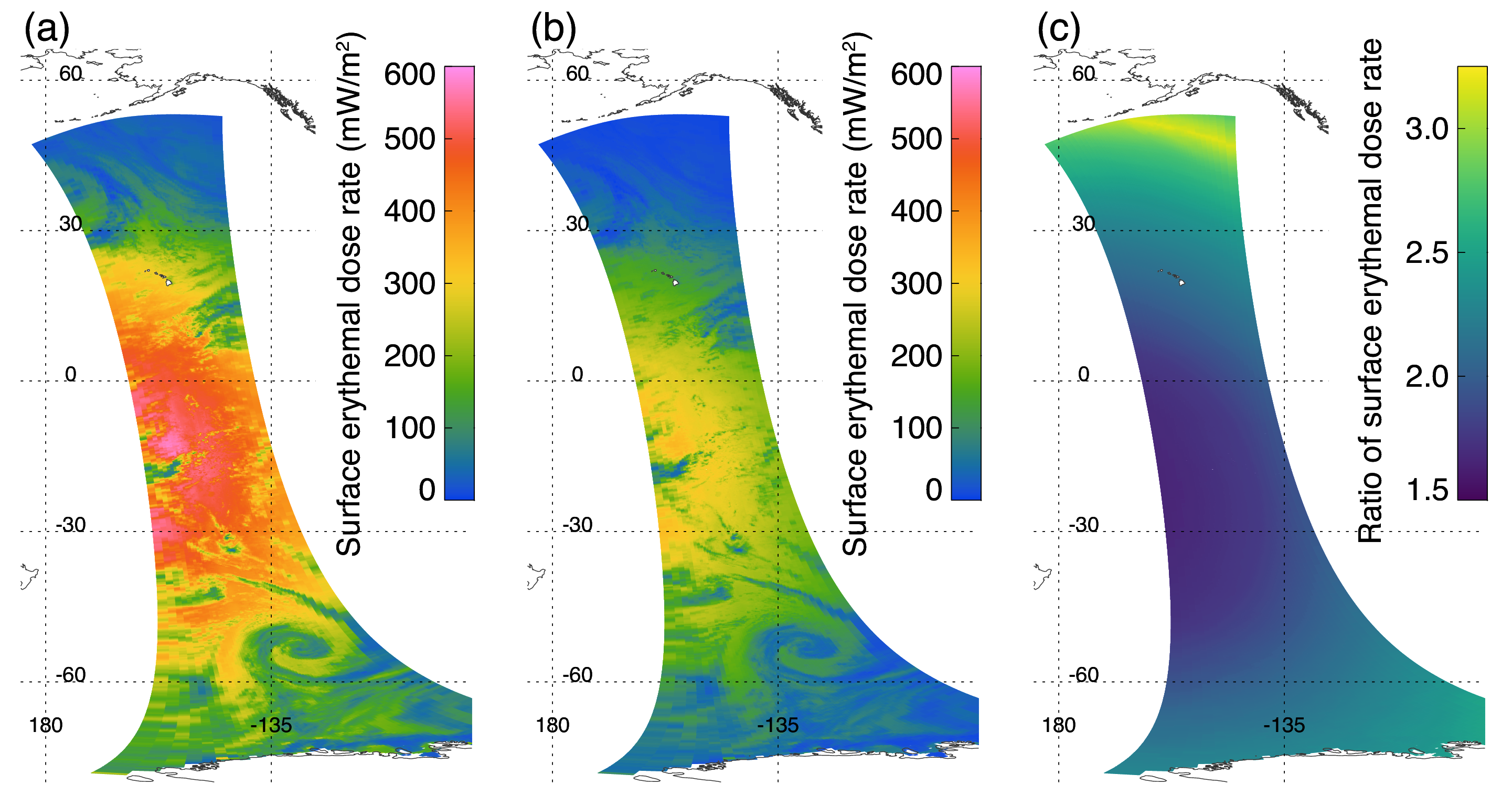
3.2.3. OMI Retrievals
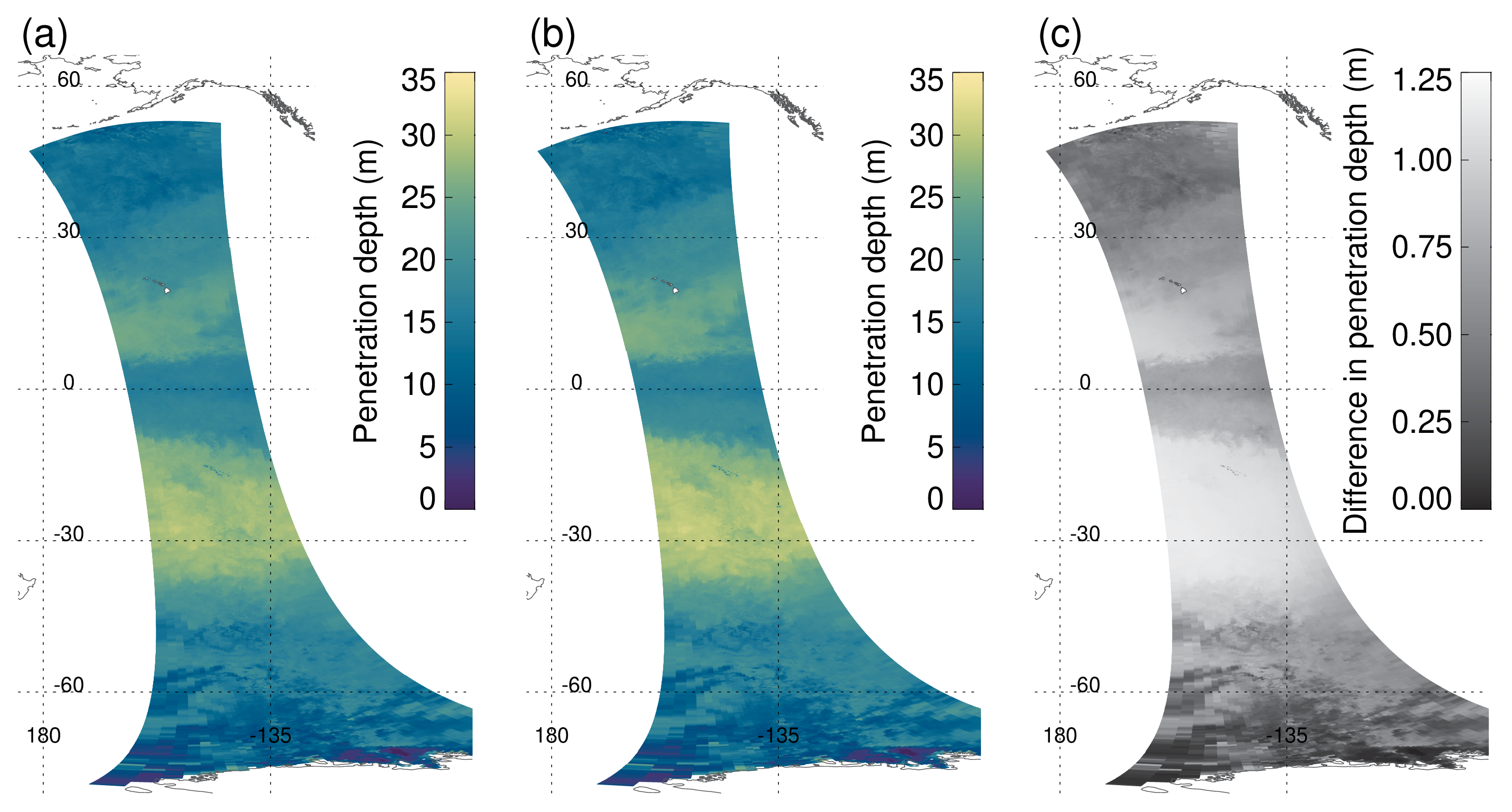
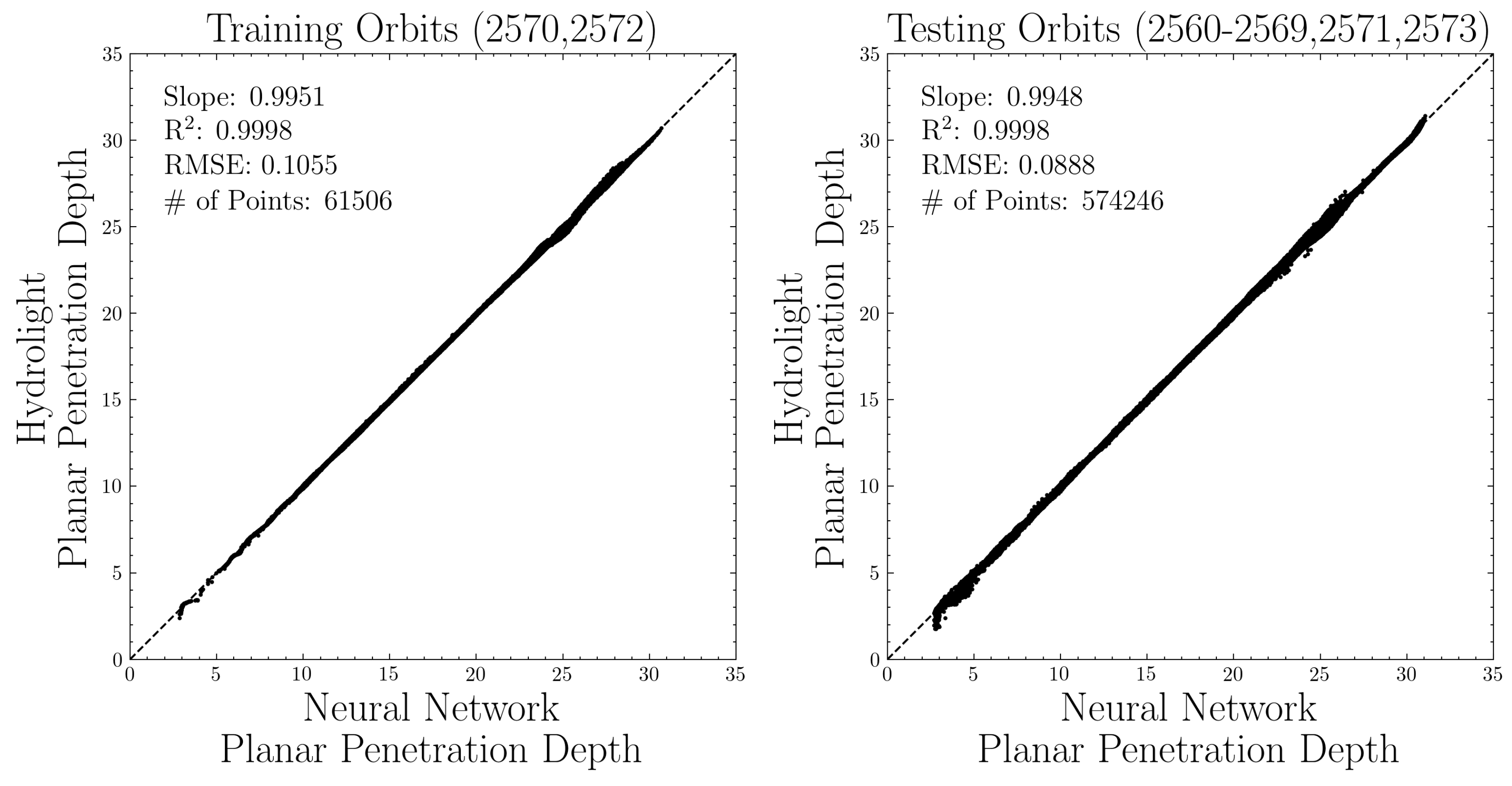
3.3. Machine Learning Results
4. Discussion
4.1. IOP Model Limitations
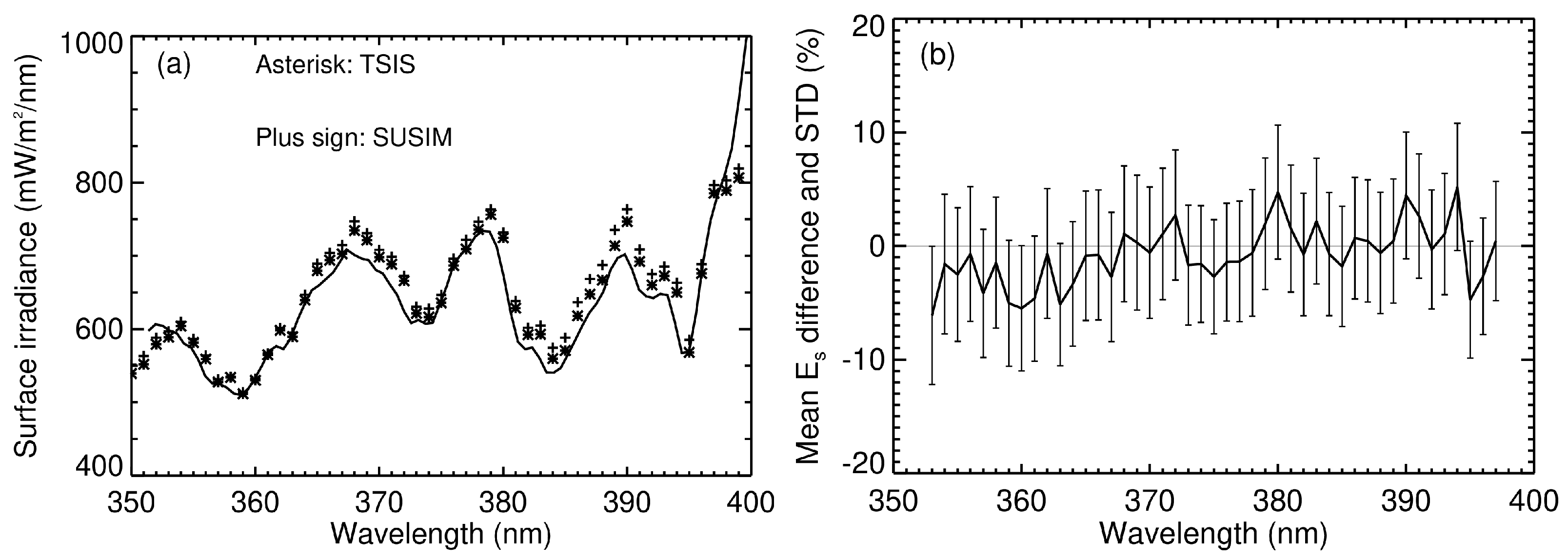
4.2. Verification of the IOP Model
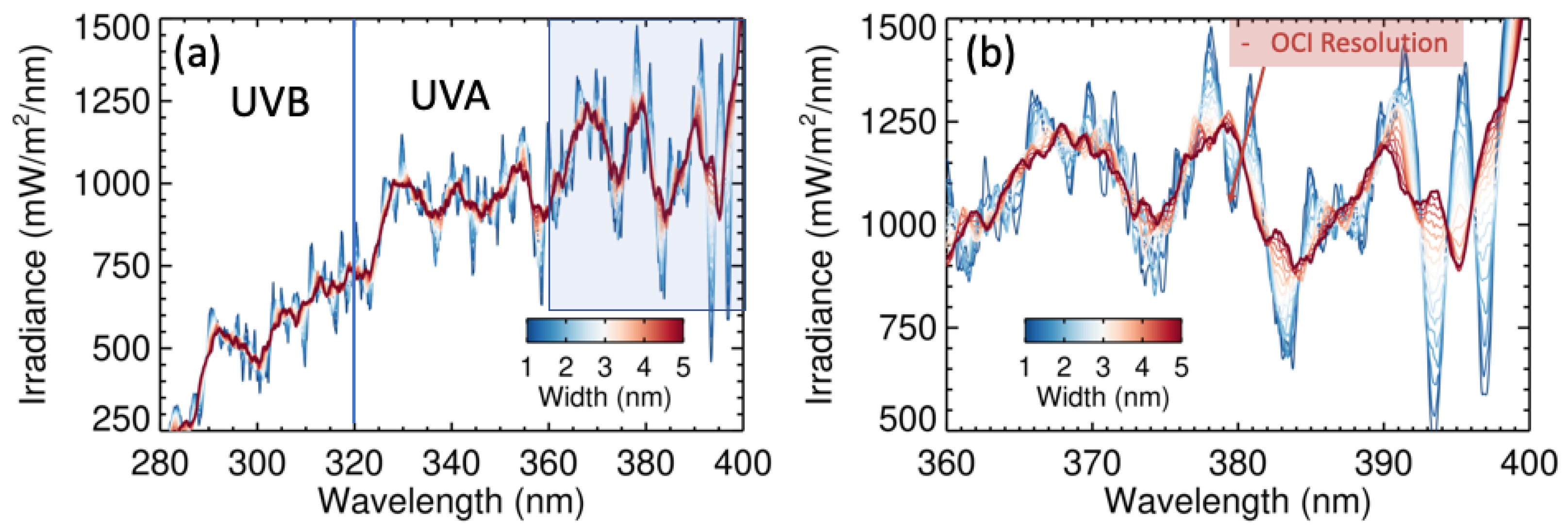
4.3. Ozone Availability for OCI
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AU | Astronomical Unit |
| BWF | Biological Weighting Function |
| CDOM | Colored Dissolved Organic Matter |
| DNA | Deoxyribonucleic Acid |
| DU | Dobson Unit |
| FOV | Field of View |
| IOP | Inherent Optical Property |
| MOBY | Marine Optical Buoy |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| OCI | Ocean Color Instrument |
| OMI | Ozone Monitoring Instrument |
| RMS | Root Mean Square |
| RT | Radiative Transfer |
| SZA | Solar Zenith Angle |
| TOA | Top of the Atmosphere |
| TSIS-1 HSRS | Total and Spectral Solar Irradiance Sensor Hybrid Solar Reference Spectrum |
| UV | Ultraviolet |
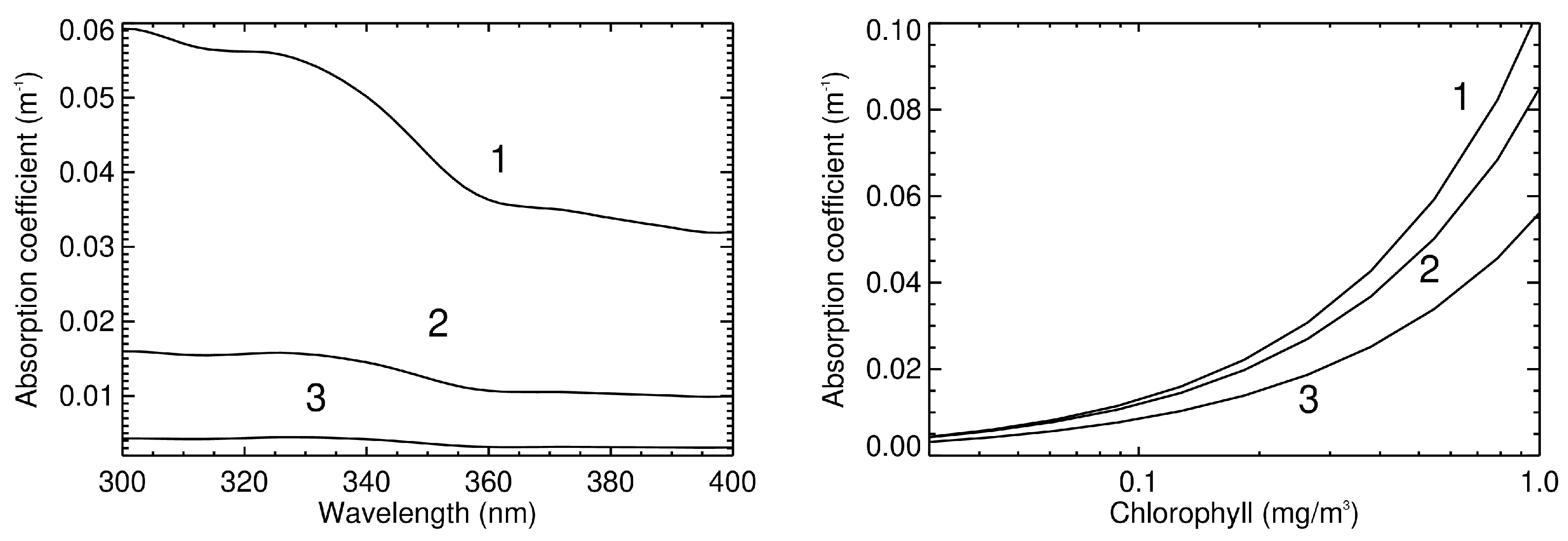
Appendix A. IOP Model
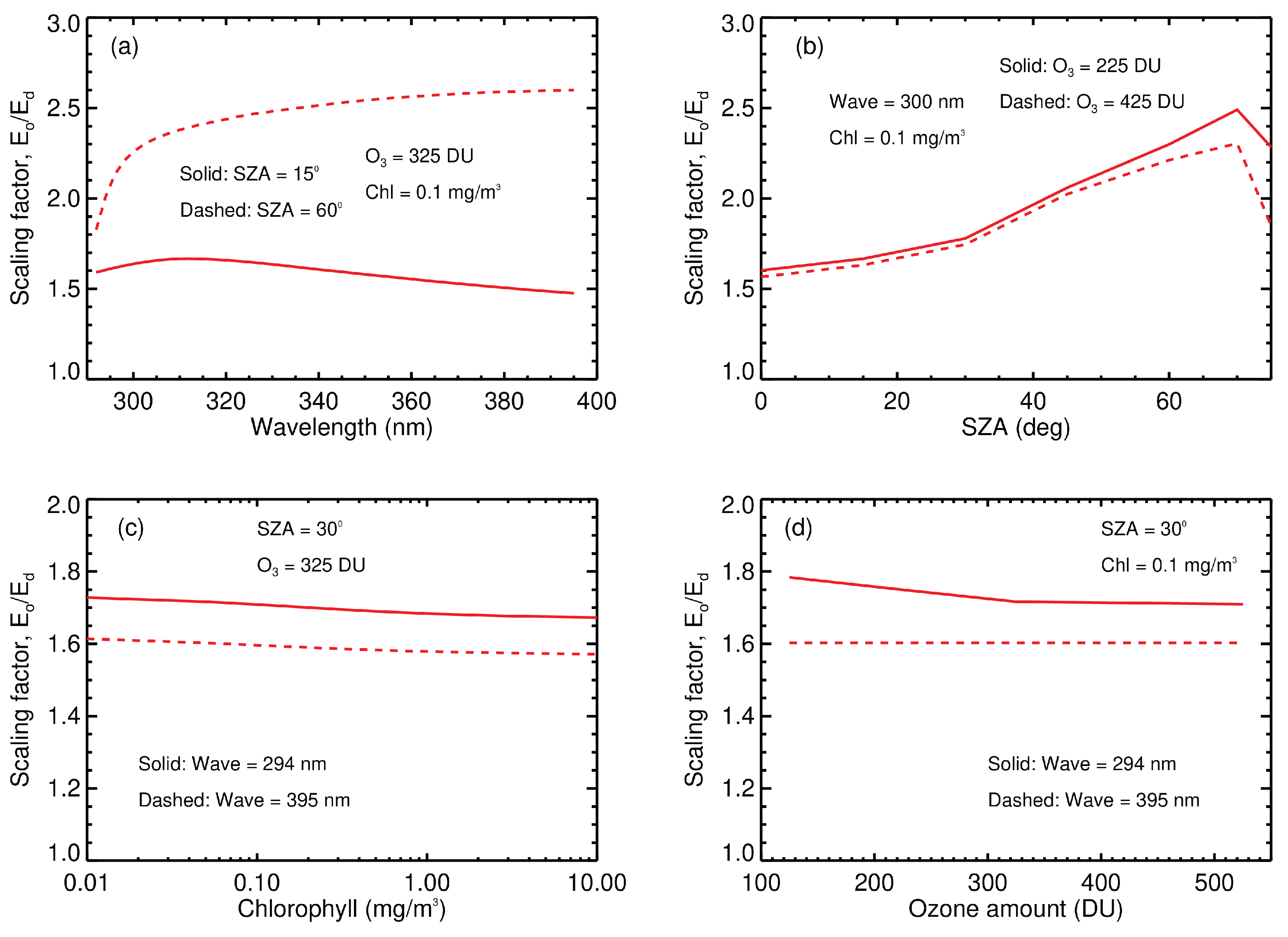
Appendix B. Scaling Factor
References
- Häder, D.-P.; Williamson, C.E.; Wängberg, S.-A.; Rautio, M.; Rose, K.C.; Gao, K.; Helbling, E.W.; Sinhahand, R.P.; Worrest, R. Effects of UV radiation on aquatic ecosystems and interactions with other environmental factors. Photochem. Photobiol. Sci. 2015, 14, 108–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Litchman, E.; Neale, P.J. UV effects on photosynthesis, growth and acclimation of an estuarine diatom and cryptomonad. Mar. Ecol. Prog. Ser. 2005, 100, 53–62. [Google Scholar] [CrossRef]
- Cullen, J.J.; Neale, P.J.; Lesser, M.P. Biological weighting function for the inhibition of phytoplankton photosynthesis by ultraviolet radiation. Science 1992, 258, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Boucher, N.P.; Prezelin, B.B. An in situ biological weighting function for UV inhibition of phytoplankton carbon fixation in the Southern Ocean. Mar. Ecol. Prog. Ser. 1996, 144, 223–236. [Google Scholar] [CrossRef]
- Neale, P.J.; Pritchard, A.L.; Ihnacik, R. UV effects on the primary productivity of picophytoplankton: Biological weighting functions and exposure response curves of Synechococcus. Biogeosciences 2014, 11, 2883–2895. [Google Scholar] [CrossRef] [Green Version]
- Bélanger, S.; Xie, H.; Krotkov, N.; Larouche, P.; Vincent, W.F.; Babin, M. Photomineralization of terrigenous dissolved organic matter in Arctic coastal waters from 1979 to 2003: Interannual variability and implications of climate change. Global Biogeochem. Cycles 2006, 20, GB4005. [Google Scholar] [CrossRef]
- Moran, M.A.; Zepp, E.G. Role of photoreactions in the formation of biologically labile compounds from dissolved organic matter. Limnol. Oceanogr. 1997, 42, 1307–1316. [Google Scholar] [CrossRef] [Green Version]
- Vasilkov, A.P.; Krotkov, N.A. Modeling the effect of seawater optical properties on the ultraviolet radiant fluxes in the ocean. Izv. Atmos. Ocean. Phys. 1997, 33, 349–357. [Google Scholar]
- Vasilkov, A.P.; Krotkov, N.; Herman, J.R.; McClain, C.; Arrigo, K.; Robinson, W. Global mapping of underwater UV irradiance and DNA-weighted exposures using TOMS and SeaWiFS data products. J. Geophys. Res. 2001, 106, 27205–27219. [Google Scholar] [CrossRef]
- Vasilkov, A.; Herman, J.; Ahmad, Z.; Kahru, M.; Mitchell, B.G. Assessment of the ultraviolet radiation field in ocean waters from space-based measurements and full radiative-transfer calculations. Appl. Opt. 2005, 44, 2863–2869. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994; 592p. [Google Scholar]
- Ahmad, Z.; Herman, J.R.; Vasilkov, A.; Tzortziou, M.; Mitchell, G.; Kahru, M. Seasonal variation of UV radiation in the ocean under clear and cloudy conditions. In Ultraviolet Ground-and Space-Based Measurements, Models, and Effects III; Slusser, J.R., Herman, J.R., Gao, W., Eds.; SPIE: Bellingham, WA, USA, 2003; pp. 63–73. [Google Scholar]
- Fichot, C.G.; Sathyendranath, S.; Miller, W.L. SeaUV and SeaUVC: Algorithms for the retrieval of UV/visible diffuse attenuation coefficients from ocean color. Remote Sens. Environ. 2008, 112, 1584–1602. [Google Scholar] [CrossRef]
- Smyth, T.J. Penetration of UV irradiance into the global ocean. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Lee, Z.; Hu, C.; Shang, A.; Du, K.; Lewis, M.; Arnone, R.; Brewin, R. Penetration of UV-visible solar radiation in the global oceans: Insights from ocean color remote sensing. J. Geophys. Res. Oceans 2013, 118, 4241–4255. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Lee, Z.; Ondrusek, M.; Li, X.; Zhang, S.; Wu, J. An evaluation of remote sensing algorithms for the estimation of diffuse attenuation coefficients in the ultraviolet bands. Opt. Express 2022, 30, 6640–6655. [Google Scholar] [CrossRef] [PubMed]
- Dinter, T.; Rozanov, V.V.; Burrows, J.P.; Bracher, A. Retrieving the availability of light in the ocean utilising spectral signatures of vibrational Raman scattering in hyper-spectral satellite measurements. Ocean Sci. 2015, 11, 373–389. [Google Scholar] [CrossRef] [Green Version]
- Oelker, J.; Richter, A.; Dinter, T.; Rozanov, V.V.; Burrows, J.P.; Bracher, A. Global diffuse attenuation derived from vibrational raman scattering detected in hyperspectral backscattered satellite spectra. Opt. Express 2019, 27, A829–A855. [Google Scholar] [CrossRef]
- Oelker, J.; Losa, S.N.; Richter, A.; Bracher, A. TROPOMI-Retrieved underwater light attenuation in three spectral regions in the ultraviolet and blue. Front. Mar. Sci. 2022, 9, 296. [Google Scholar] [CrossRef]
- Frouin, R.; Ramon, D.; Boss, E.; Jolivet, D.; Compiègne, M.; Tan, J.; Bouman, H.; Jackson, T.; Franz, B.; Platt, T.; et al. Satellite radiation products for ocean biology and biogeochemistry: Needs, State-of-the-Art, Gaps, Development Priorities, and Opportunities. Front. Mar. Sci. 2018, 5, 3. [Google Scholar] [CrossRef] [Green Version]
- Cetinić, I.; McClain, C.R.; Werdell, P.J. (Eds.) PreAerosol, Clouds, and ocean Ecosystem (PACE) Mission Science Definition Team Report; PACE Tech. Rep. NASA/TM2018-219027; NASA: Greenbelt, MD, USA, 2018; Volume 2, p. 316. [Google Scholar]
- Tanskanen, A.; Krotkov, N.; Herman, J.R.; Bhartia, P.K.; Arola, A. Surface UV irradiance from OMI. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1267–1271. [Google Scholar] [CrossRef]
- Coddington, O.M.; Richard, E.C.; Harber, D.; Pilewskie, P.; Woods, T.N.; Chance, K.; Liu, X.; Sun, K. The TSIS-1 Hybrid Solar Reference Spectrum. Geophys. Res. Lett. 2021, 48, e2020GL091709. [Google Scholar] [CrossRef]
- Richard, E.; Harber, D.; Coddington, O.; Drake, G.; Rutkowski, J.; Triplett, M.; Pilewskie, P.; Woods, T. SI-traceable spectral irradiance radiometric characterization and absolute calibration of the TSIS-1 Spectral Irradiance Monitor (SIM). Remote Sens. 2020, 12, 1818. [Google Scholar] [CrossRef]
- Levelt, P.F.; Joiner, J.; Tamminen, J.; Veefkind, J.P.; Bhartia, P.K.; Stein Zweers, D.C.; Duncan, B.N.; Streets, D.G.; Eskes, H.; van der, A.R.; et al. The Ozone Monitoring Instrument: Overview of 14 years in space. Atmos. Chem. Phys. 2018, 18, 5699–5745. [Google Scholar] [CrossRef] [Green Version]
- Levelt, P.F.; van den Oord, G.H.J.; Dobber, M.R.; Mälkki, A.; Visser, H.; de Vries, J.; Stammes, P.; Lundell, J.; Saari, H. The Ozone Monitoring Instrument. IEEE Trans. Geosci. Remote 2006, 44, 1093–1101. [Google Scholar] [CrossRef]
- Dobber, M.R. OMI/Aura Level 1B UV Global Geolocated Earthshine Radiances (V003) [Dataset], Goddard Earth Sciences Data and Information Services Center (GES DISC). 2007. Available online: https://disc.gsfc.nasa.gov/datasets/OML1BRUG_003/summary (accessed on 30 March 2022).
- Dobber, M.R. OMI/Aura Level 1B IRR Solar Irradiances (V003) [Dataset], Goddard Earth Sciences Data and Information Services Center (GES DISC). 2007. Available online: https://disc.gsfc.nasa.gov/datasets/OML1BIRR_003/summary (accessed on 30 March 2022).
- Schenkeveld, V.M.E.; Jaross, G.; Marchenko, S.; Haffner, D.; Kleipool, Q.L.; Rozemeijer, N.C.; Veefkind, J.P.; Levelt, P.F. In-flight performance of the Ozone Monitoring Instrument. Atmos. Meas. Tech. 2017, 10, 1957–1986. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balis, D.; Kroon, M.; Koukouli, M.E.; Brinksma, E.J.; Labow, G.; Veefkind, J.P.; McPeters, R.D. Validation of Ozone Monitoring Instrument total ozone column measurements using Brewer and Dobson spectrophotometer ground-based observations. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Bhartia, P.K. OMI/Aura Ozone (O3) Total Column 1-Orbit L2 Swath 13 × 24 km V003, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2005. Available online: https://disc.gsfc.nasa.gov/datasets/OMTO3_003/summary (accessed on 30 March 2022).
- Kleipool, Q.L.; Dobber, M.R.; de Haan, J.F.; Levelt, P.F. Earth surface reflectance climatology from 3 years of OMI data. J. Geophys. Res. 2008, 113, D18308. [Google Scholar] [CrossRef]
- Kleipool, Q.L. OMI/Aura Surface Reflectance Climatology L3 Global Gridded 0.5 degree x 0.5 degree V3, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). 2010. Available online: https://disc.gsfc.nasa.gov/datasets/OMLER_003/summary (accessed on 30 March 2022).
- Zhai, P.; Hu, Y.; Chowdhary, J.; Trepte, C.R.; Lucker, P.L.; Josset, D.B. A vector radiative transfer model for coupled atmosphere and ocean systems with a rough interface. J. Quant. Spectr. Radiat. Trans. 2010, 111, 1025–1040. [Google Scholar] [CrossRef]
- Krotkov, N.A.; Bhartia, P.K.; Herman, J.R.; Fioletov, V.; Kerr, J. Satellite estimation of spectral surface UV irradiance in the presence of tropospheric aerosols 1. Cloud-free case. J. Geophys. Res. 1998, 103, 8779–8794. [Google Scholar] [CrossRef] [Green Version]
- Krotkov, N.A.; Herman, J.R.; Bhartia, P.K.; Fioletov, V.; Ahmad, Z. Satellite estimation of spectral surface UV irradiance 2. Effects of homogeneous clouds and snow. J. Geophys. Res. 2001, 106, 11743–11760. [Google Scholar] [CrossRef]
- Deirmendjian, D. Electromagnetic Scattering on Spherical Polydispersions; Elsevier: New York, NY, USA, 1969; 290p. [Google Scholar]
- Joiner, J.; Vasilkov, A.P.; Flittner, D.E.; Gleason, J.F.; Bhartia, P.K. Retrieval of cloud pressure and oceanic chlorophyll content using Raman scattering in GOME ultraviolet spectra. J. Geophys. Res. 2004, 109, D01109. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Z.; Fraser, R. An iterative radiative transfer code for ocean-atmosphere systems. J. Atrnos. Sci. 1982, 39, 656–665. [Google Scholar] [CrossRef] [Green Version]
- Krotkov, N.A.; Herman, J.R.; Bhartia, P.K.; Seftor, C.; Arola, A.; Kaurola, J.; Taalas, P.; Vasilkov, A.P. OMI Surface UV Irradiance Algorithm. OMI Algorithm Theoretical Basis Document. Clouds, Aerosols, and Surface UV Irradiance. Available online: http://eospso.gsfc.nasa.gov/sites/default/files/atbd/ATBD-OMI-03.pdf (accessed on 30 March 2022).
- Frouin, R.; Tan, J.; Ramon, D.; Franz, B.; Murakami, H. Estimating photosynthetically available radiation at the ocean surface from EPIC/DSCOVR data. In Remote Sensing of the Open and Coastal Ocean and Inland Waters; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10778, p. 1077806. [Google Scholar]
- Morel, A. Optical modeling of the upper ocean in relation to its biogeneous matter content (Case I waters). J. Geophys. Res. 1988, 93, 10749–10768. [Google Scholar] [CrossRef] [Green Version]
- Vasilkov, A.; Lyapustin, A.; Mitchell, B.G.; Huang, D. UV Reflectance of the Ocean from DSCOVR/EPIC: Comparisons with a Theoretical Model and Aura/OMI Observations. J. Atmos. Oceanic Tech. 2019, 36, 2087–2099. [Google Scholar] [CrossRef]
- Vasilkov, A.P.; Joiner, J.; Gleason, J.; Bhartia, P.K. Ocean Raman scattering in satellite backscatter UV measurements. Geophys. Res. Lett. 2002, 29, 14–18. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.-C.; Carder, K.L.; Miller, R.L.; Ivey, J.E. Fast and accurate model of underwater scalar irradiance. Appl. Opt. 2002, 41, 4962–4974. [Google Scholar] [CrossRef]
- Clark, D.K.; Feinholz, M.E.; Yarbrough, M.A.; Johnson, B.C.; Brown, S.W.; Kim, Y.S.; Barnes, R.A. Overview of the radiometric calibration of MOBY. In Earth Observing Systems VI; International Society for Optics and Photonics: Bellingham, WA, USA, 2002; Volume 4483, pp. 64–76. [Google Scholar]
- Setlow, R.B. The wavelengths in sunlight effective in producing skin cancer: A theoretical analysis. Proc. Natl. Acad. Sci. USA 1974, 71, 3363–3366. [Google Scholar] [CrossRef] [Green Version]
- Tedetti, M.; Sempere, R.; Vasilkov, A.; Charriere, B.; Nerini, D.; Miller, W.L.; Kawamura, K.; Raimbault, P. High penetration of ultraviolet radiation in the south east Pacific waters. Geophys. Reas. Lett. 2007, 34, L12610. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Weidemann, A.; Kindle, J.; Arnone, R.; Carder, K.L.; Davis, C. Euphotic zone depth: Its derivation and implication to ocean-color remote sensing. J. Geophys. Res. 2007, 112, C03009. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.-P.; Du, K.-P.; Arnone, R. A model for the diffuse attenuation coefficient of downwelling irradiance. J. Geophys. Res. 2005, 110, C02016. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B.A. Chlorophyll-a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. 2012, 117, C01011. [Google Scholar] [CrossRef] [Green Version]
- NASA Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group. Moderate-Resolution Imaging Spectroradiometer (MODIS) Aqua Chlorophyll Data; 2018 Reprocessing; NASA OB.DAAC: Greenbelt, MD, USA, 2018. [Google Scholar] [CrossRef]
- McKinlay, A.; Diffey, B. A reference action spectrum for ultraviolet induced erythema in human skin. CIE J. 1987, 6, 17–22. [Google Scholar]
- Fan, Y.; Li, W.; Chen, N.; Ahn, J.-H.; Park, Y.-J.; Kratzer, S.; Schroeder, T.; Ishizaka, J.; Chang, R.; Stamnes, K. A machine learning based data analysis platform for satellite ocean color sensors. Remote Sens. Environ. 2021, 253, 112236. [Google Scholar] [CrossRef]
- Fasnacht, Z.; Joiner, J.; Haffner, D.; Qin, W.; Vasilkov, A.; Castellanos, P.; Krotkov, N. Using machine learning for timely estimates of ocean color information from hyperspectral satellite measurements in the presence of clouds, aerosols, and sunglint. Front. Remote Sens. 2022, 2, 34. [Google Scholar] [CrossRef]
- Westberry, T.K.; Boss, E.; Lee, Z. Influence of Raman scattering on ocean color inversion models. Appl. Opt. 2013, 52, 5552–5561. [Google Scholar] [CrossRef]
- Chowdhary, J.; Zhai, P.-W.; Boss, E.; Dierssen, H.; Frouin, R.; Ibrahim, A.; Lee, Z.; Remer, L.A.; Twardowski, M.; Xu, F.; et al. Modeling atmosphere-ocean radiative transfer: A PACE mission perspective. Front. Earth Sci. 2019, 7, 100. [Google Scholar] [CrossRef]
- Morrison, J.R.; Nelson, N.B. Seasonal cycle of phytoplankton UV absorption at the Bermuda Atlantic Time-series Study (BATS) site. Limnol. Oceanogr. 2004, 49, 215–224. [Google Scholar] [CrossRef]
- Hedley, J.D.; Mobley, C.D. HYDROLIGHT 6.0 ECOLIGHT 6.0 Technical Documentation; Numerical Optics Ltd.: Tiverton, UK, 2019. [Google Scholar]
- Vasilkov, A.; Herman, J.; Krotkov, N.A.; Kahru, M.; Mitchell, B.G.; Hsu, C. Problems in assessment of the ultraviolet penetration into natural waters from space-based measurements. Opt. Eng. 2002, 41, 3019–3027. [Google Scholar] [CrossRef]
- Lee, Z.; Wei, J.; Voss, K.; Lewis, M.; Bricaud, A.; Huot, Y. Hyperspectral absorption coefficient of ‘‘pure’’ seawater in the range of 350–550 nm inverted from remote sensing reflectance. Appl. Opt. 2015, 54, 546–558. [Google Scholar] [CrossRef]
- Mannino, A.; Haffner, D.; Robinson, W.; Ahmad, Z. Extended UV Capability on OCI for Ozone Retrieval, in PACE Technical Report Series: Ocean Color Instrument (OCI) Concept Design Studies (NASA/TM-2018-2018–219027-); Cetinić, I., McClain, C.R., Werdell, P.J., Eds.; NASA Goddard Space Flight Space Center Greenbelt: Prince George’s County, MD, USA, 2018; Volume 7. [Google Scholar]
- Fournier, G.; Forand, J.L. Analytic phase functions for ocean water. Proc. SPIE 1994, 2258, 194–201. [Google Scholar]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Quickenden, T.I.; Irvin, J.A. The ultraviolet absorption spectrum of liquid water. J. Chem. Phys. 1980, 72, 4416–4428. [Google Scholar] [CrossRef]
- Fry, E.S. Visible and near ultraviolet absorption spectrum of liquid water. Appl. Opt. 2000, 39, 2743–2744. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. 2001, 106, 7163–7180. [Google Scholar] [CrossRef] [Green Version]
- Kopelevich, O.V.; Lutsarev, S.V.; Rodionov, V.V. Light spectral absorption by yellow substance of ocean water. Oceanology 1989, 29, 409–414. [Google Scholar]
- Morel, A.; Gentili, B.; Claustre, H.; Babin, M.; Bricaud, A.; Ras, J.; Tieche, F. Optical properties of the ‘‘clearest’’ natural waters. Limnol. Oceanogr. 2007, 52, 217–229. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilkov, A.; Krotkov, N.; Haffner, D.; Fasnacht, Z.; Joiner, J. Estimates of Hyperspectral Surface and Underwater UV Planar and Scalar Irradiances from OMI Measurements and Radiative Transfer Computations. Remote Sens. 2022, 14, 2278. https://doi.org/10.3390/rs14092278
Vasilkov A, Krotkov N, Haffner D, Fasnacht Z, Joiner J. Estimates of Hyperspectral Surface and Underwater UV Planar and Scalar Irradiances from OMI Measurements and Radiative Transfer Computations. Remote Sensing. 2022; 14(9):2278. https://doi.org/10.3390/rs14092278
Chicago/Turabian StyleVasilkov, Alexander, Nickolay Krotkov, David Haffner, Zachary Fasnacht, and Joanna Joiner. 2022. "Estimates of Hyperspectral Surface and Underwater UV Planar and Scalar Irradiances from OMI Measurements and Radiative Transfer Computations" Remote Sensing 14, no. 9: 2278. https://doi.org/10.3390/rs14092278
APA StyleVasilkov, A., Krotkov, N., Haffner, D., Fasnacht, Z., & Joiner, J. (2022). Estimates of Hyperspectral Surface and Underwater UV Planar and Scalar Irradiances from OMI Measurements and Radiative Transfer Computations. Remote Sensing, 14(9), 2278. https://doi.org/10.3390/rs14092278






