Analysis of Different Weighting Functions of Observations for GPS and Galileo Precise Point Positioning Performance
Abstract
1. Introduction
2. Methodology and Data
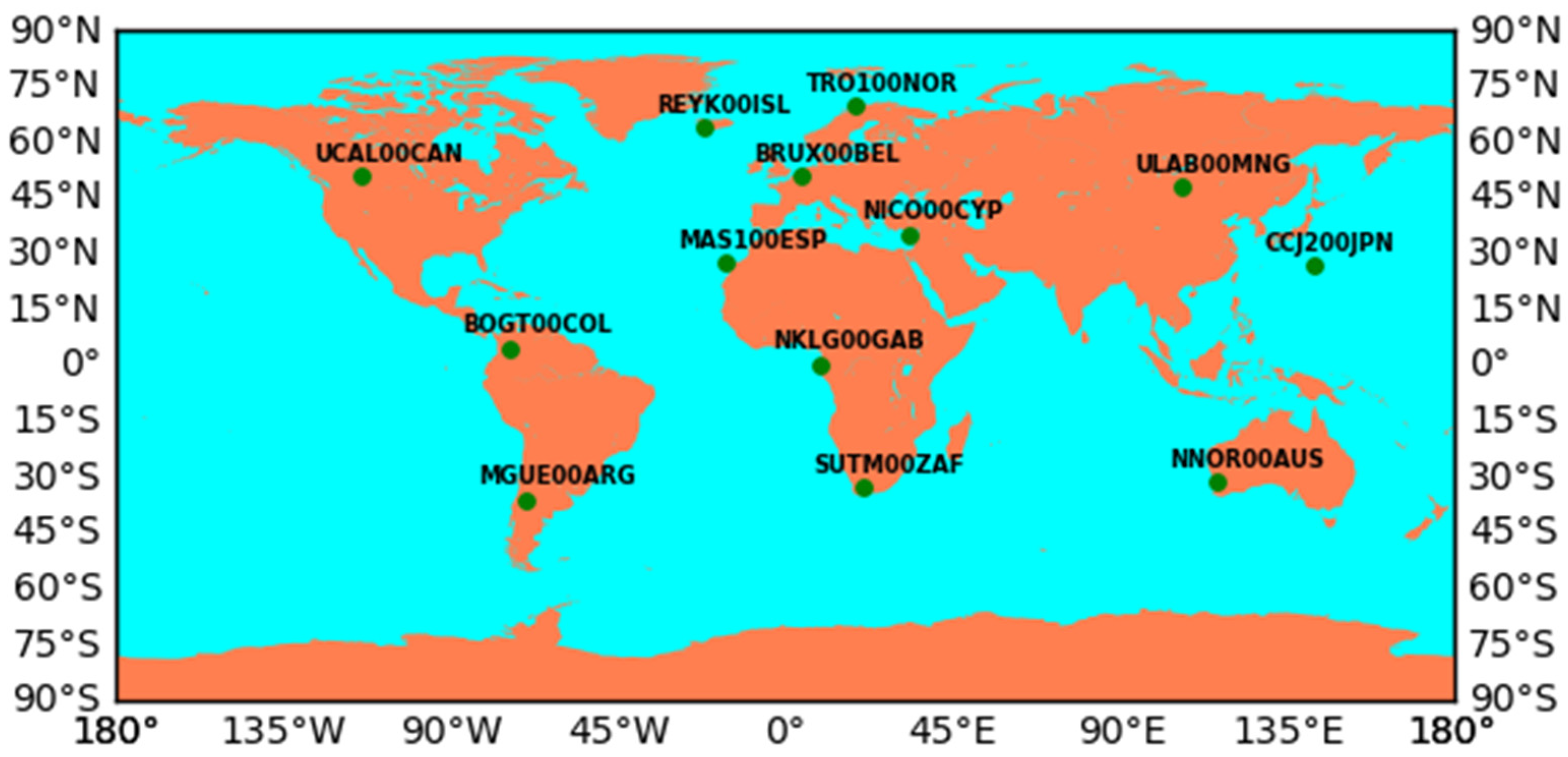
2.1. Data and Solutions
| Items | Models/Methods |
|---|---|
| PPP model | static mode, conventional PPP model using undifferenced dual-frequency code and phase ionosphere-free linear combination |
| Signals | L1 and L2 for GPS; E1 and E5a for Galileo |
| Stochastic modeling | different weighting functions shown in Table 2 |
| Constellation | GPS, Galileo, GPS+Galileo |
| Cut-off elevation angle | 7° |
| Interval estimation | 30-s |
| Periods | one week: from 38 DoY to 44 DoY of 2021 |
| Reference frame | IGS14 |
| Orbit | sp3 CODE MGEX with 5-min intervals |
| Clock | clk CODE MGEX with 30-s intervals |
| PCO and PCV for satellite antenna | igs14.atx |
| PCO and PCV for receiver antenna | igs14.atx; for Galileo used model from GPS |
| Ionospheric delay | ionosphere-free linear combination |
| Tropospheric delay | a priori value: Saastamoinen model with GPT2 estimated: wet component mapping function: GMF |
| Solid earth tide, relativistic effect, phase wind-up | IERS convention 2010 |
| Ambiguities | Estimated float value with remaining bias as constant for arc |
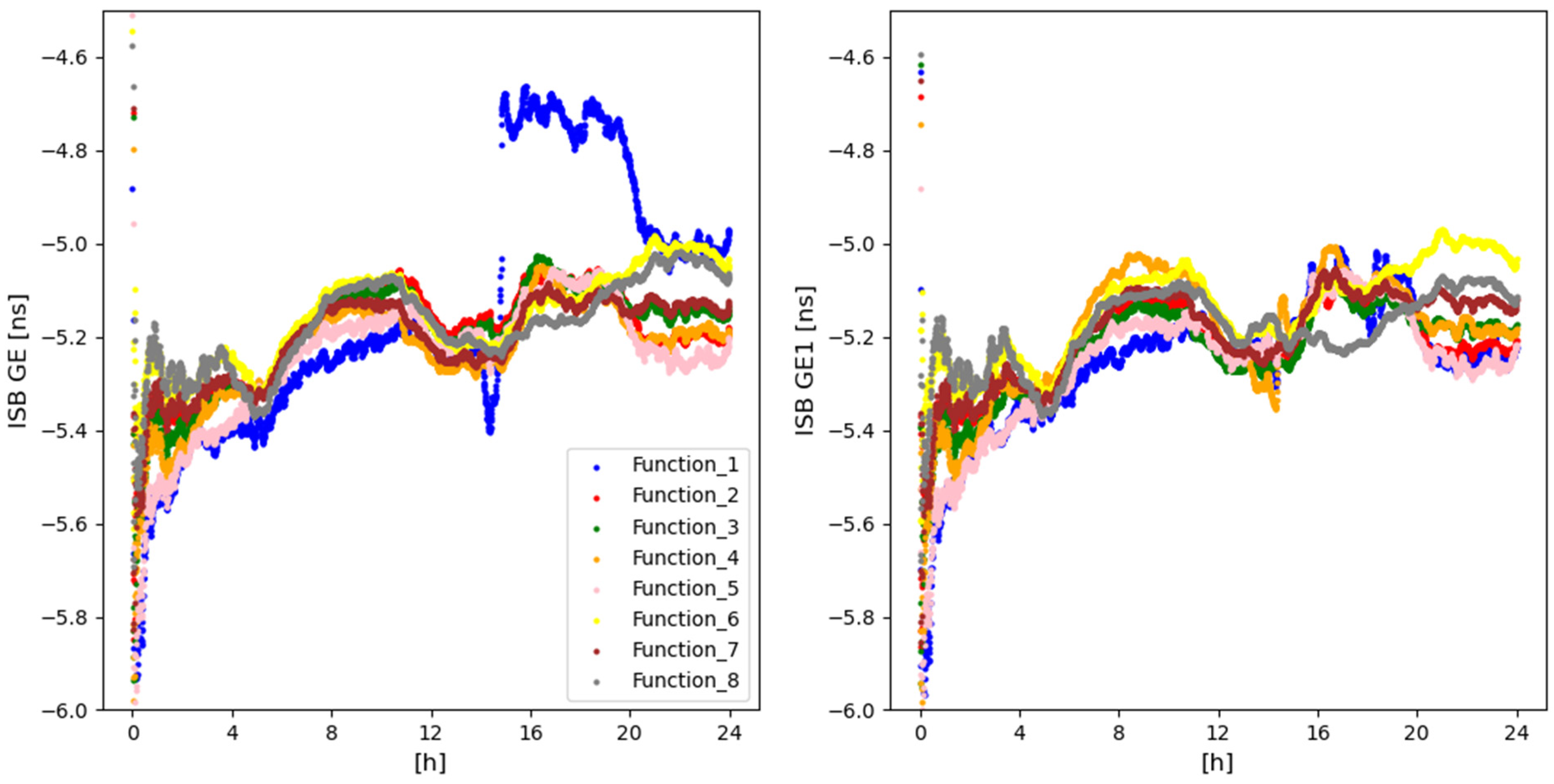
| ISB between GPS and Galileo | Estimated as random walk: 1.0 × 10−7 |
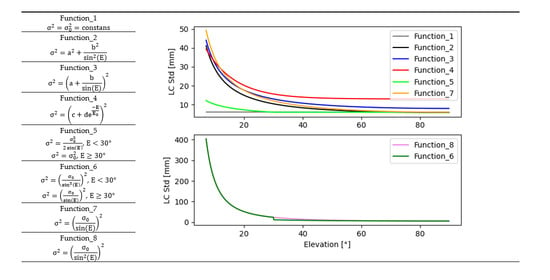
| Functions | Solutions | Precision of Pseudorange | Precision of Carrier-Phase |
|---|---|---|---|
| Function_1 | G, E, GE GE1 | ||
| Function_2 | G, E, GE GE1 | | |
| Function_3 | |||
| Function_4 | G, E, GE GE1 | | |
| Function_5 | G, E, GE GE1 | | |
| Function_6 | |||
| Function_7 | |||
| Function_8 |
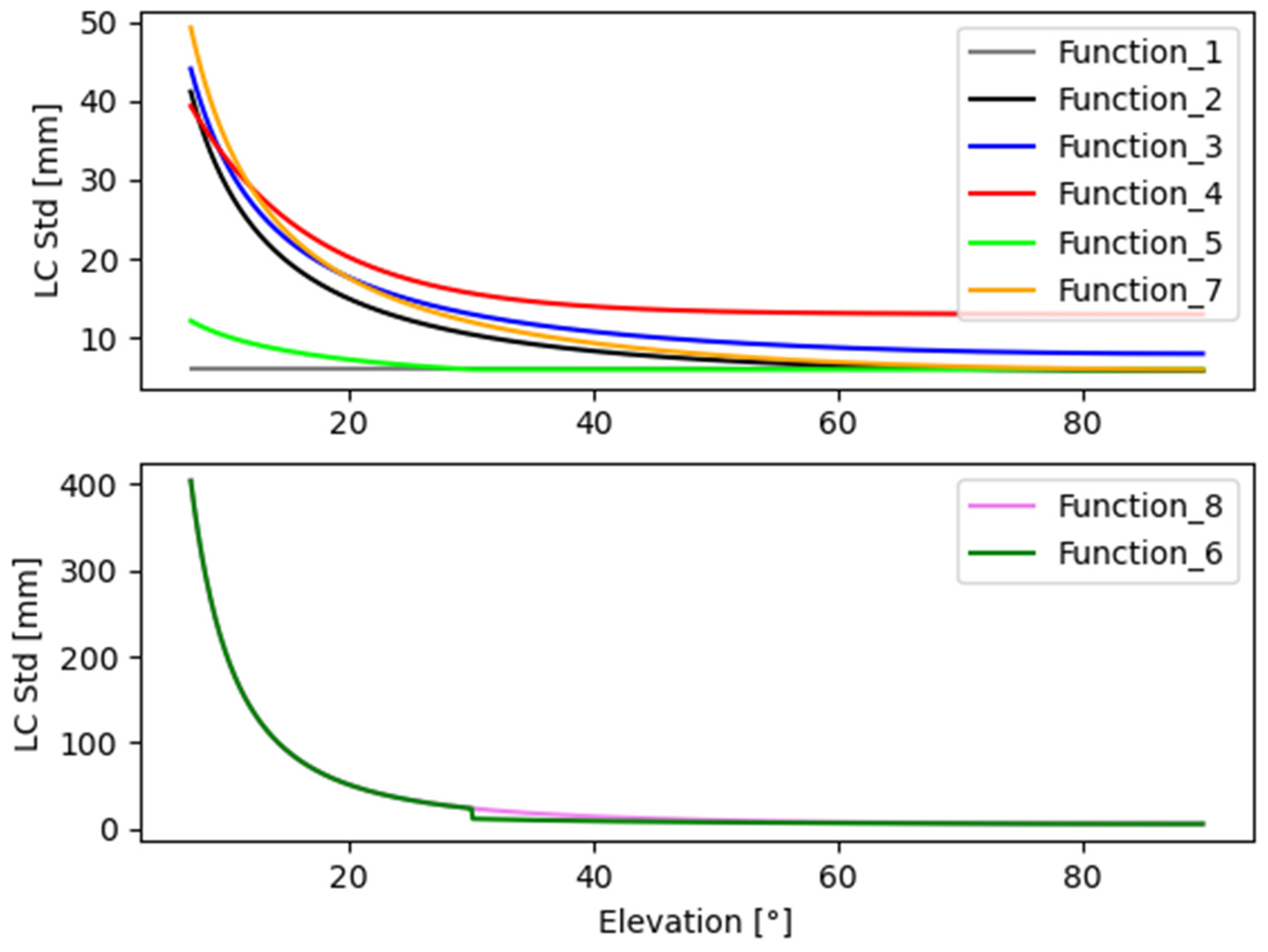
2.2. Weighting of Observation
2.3. Reference Coordinates
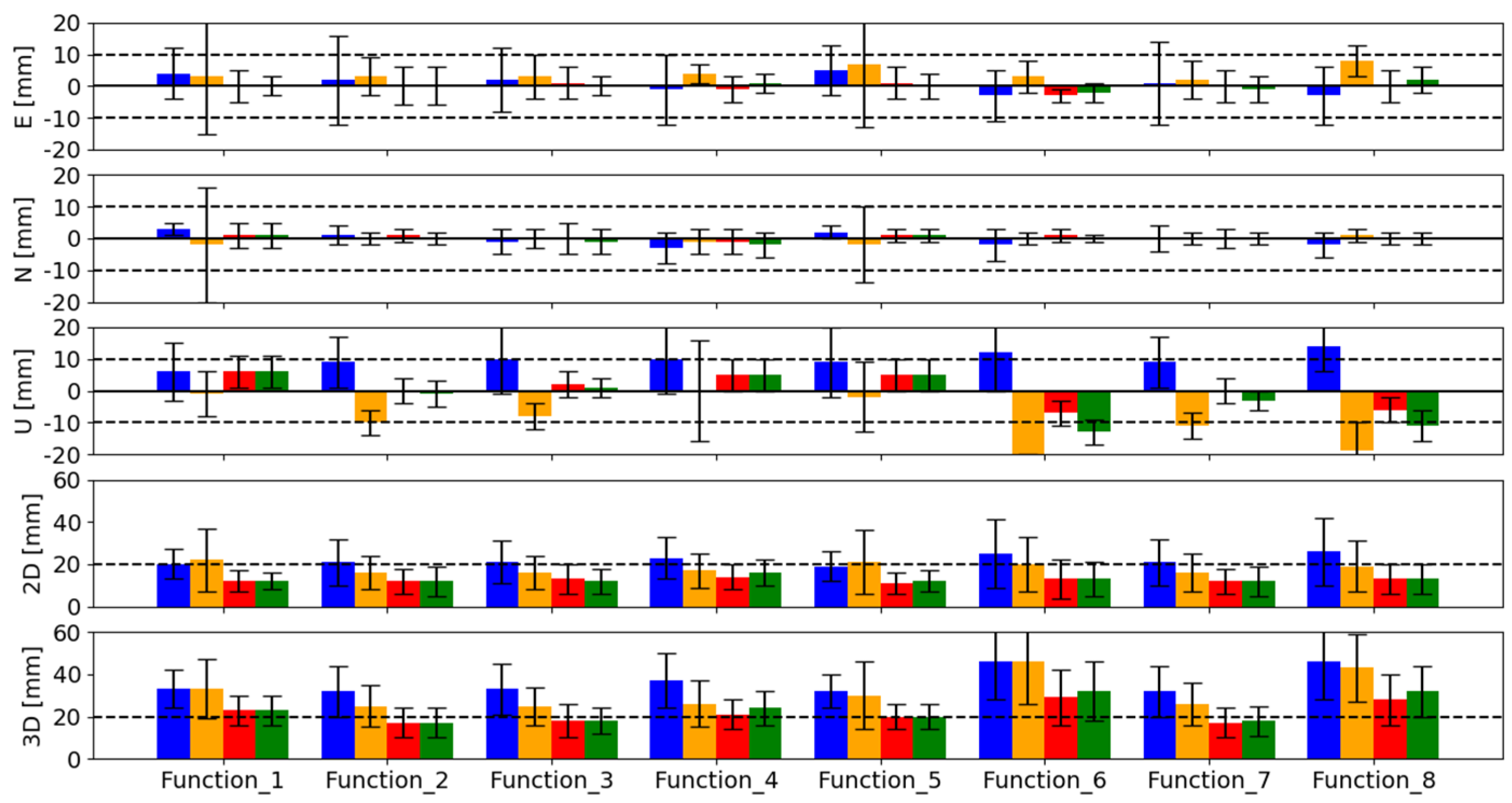
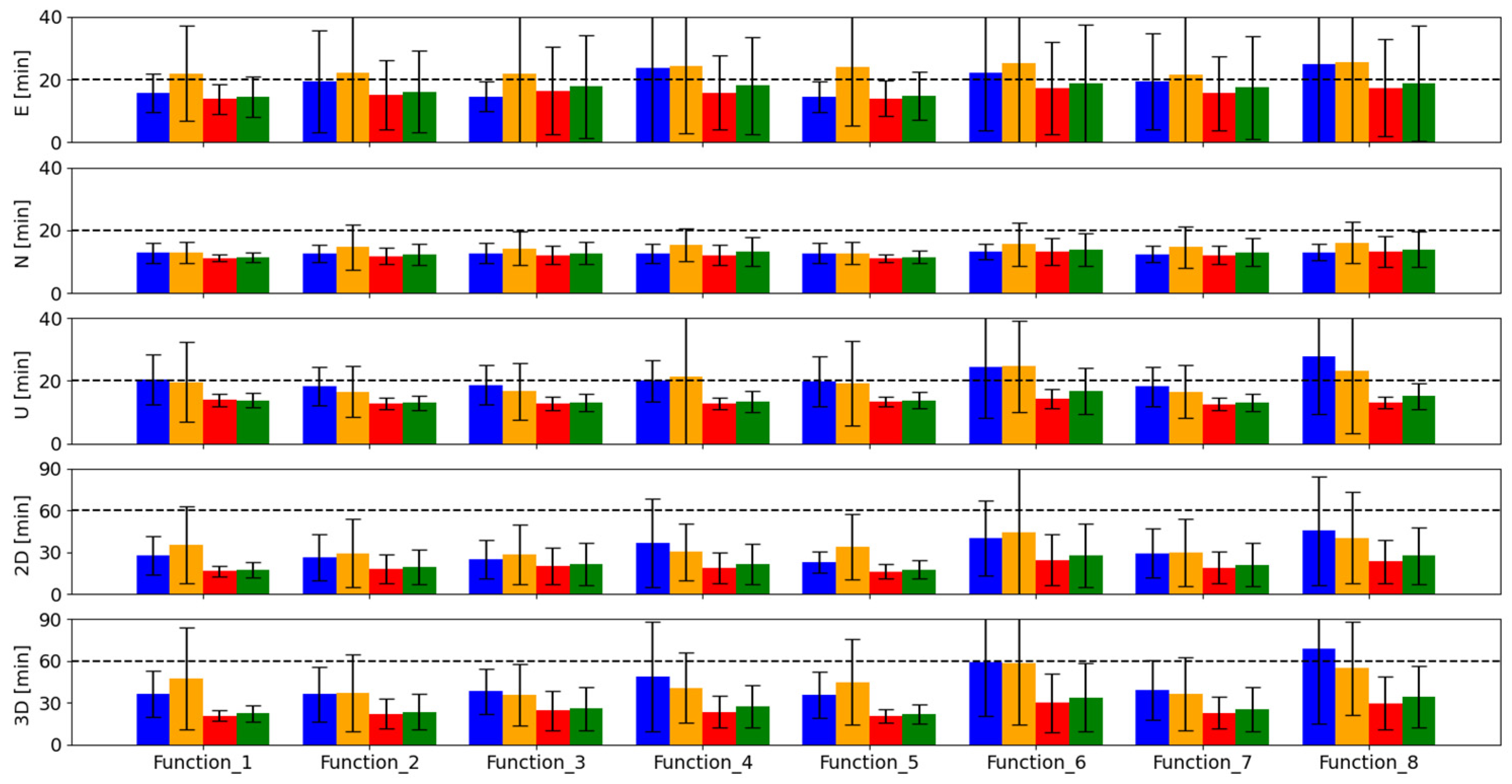
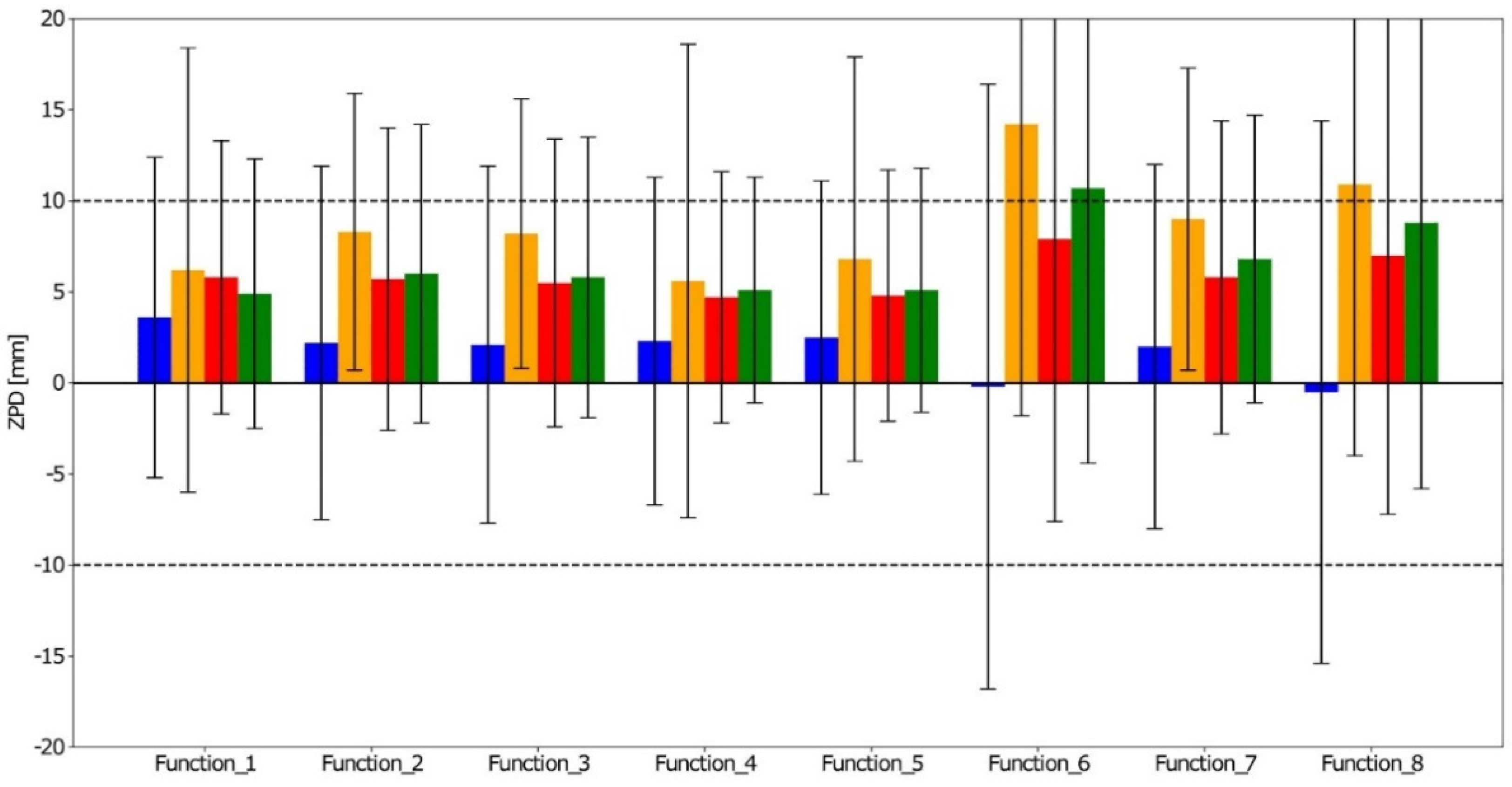
3. Results
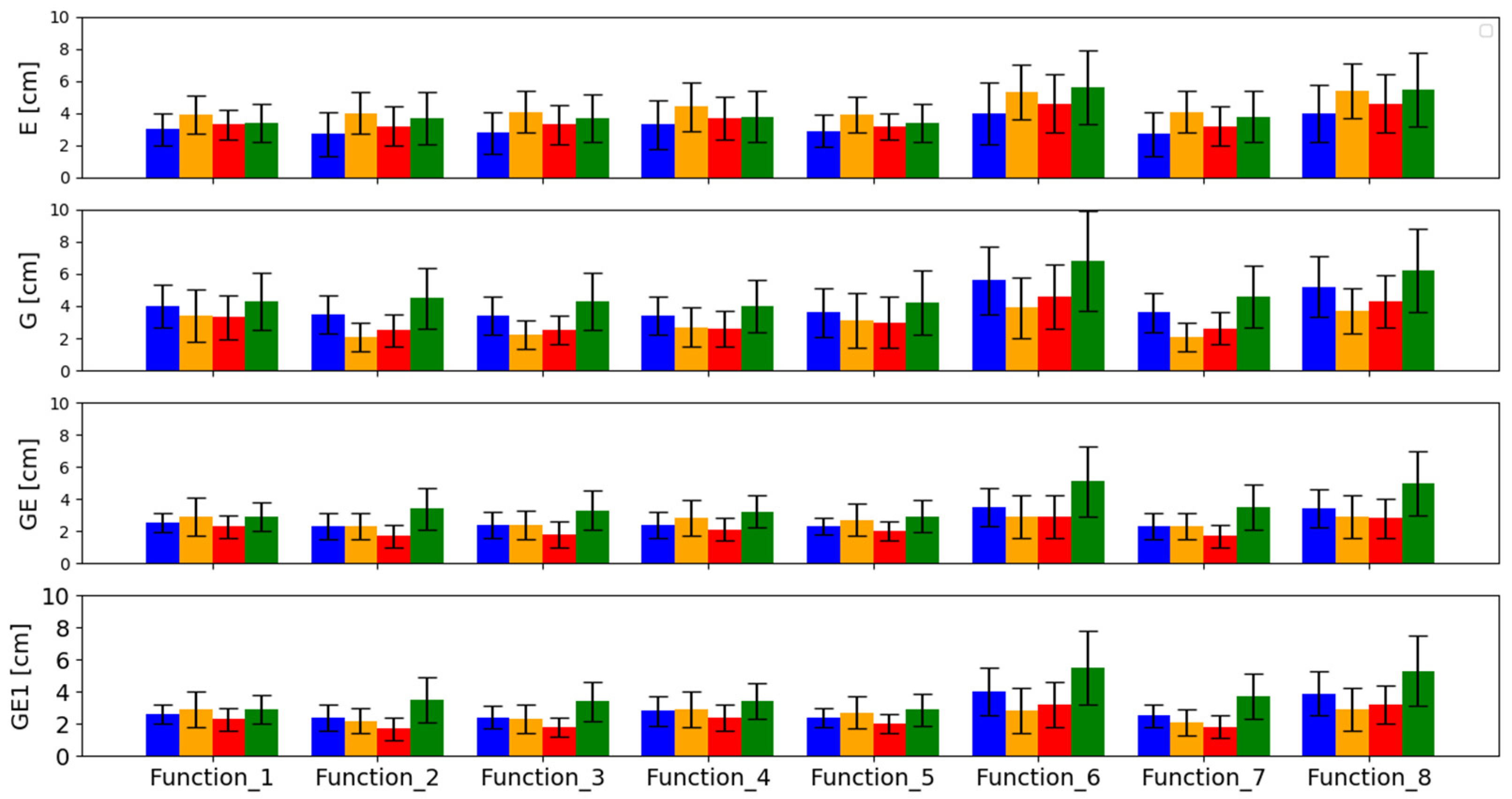
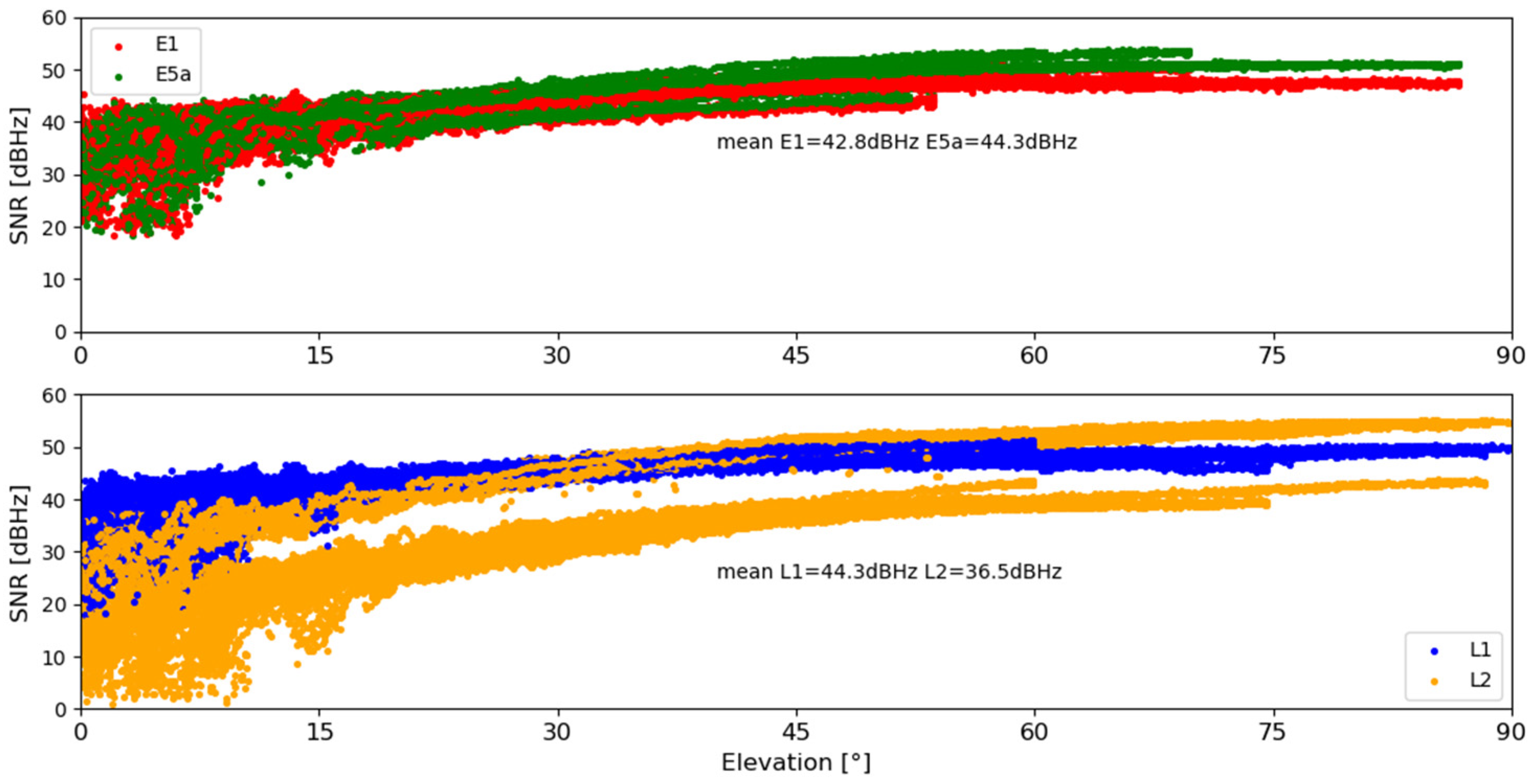
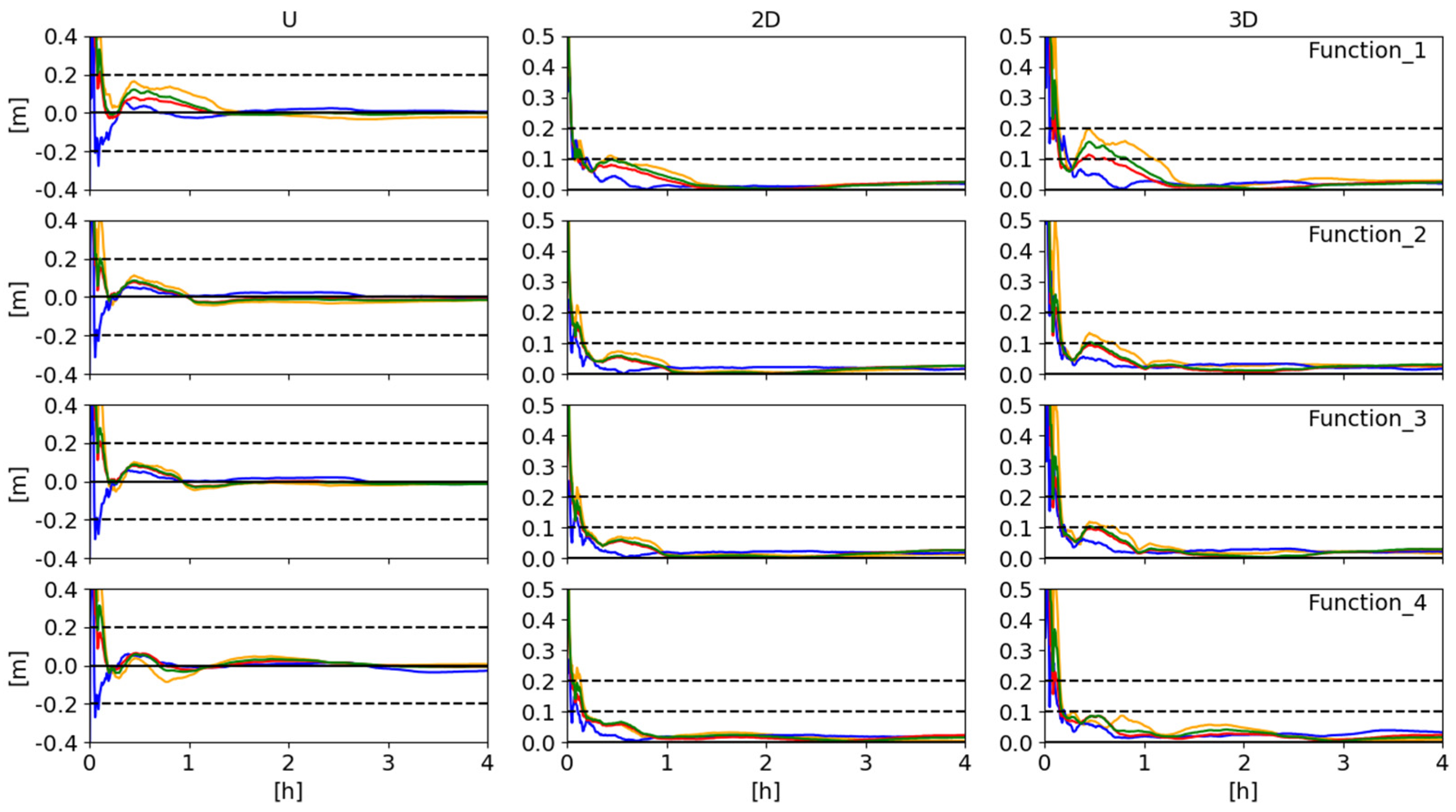
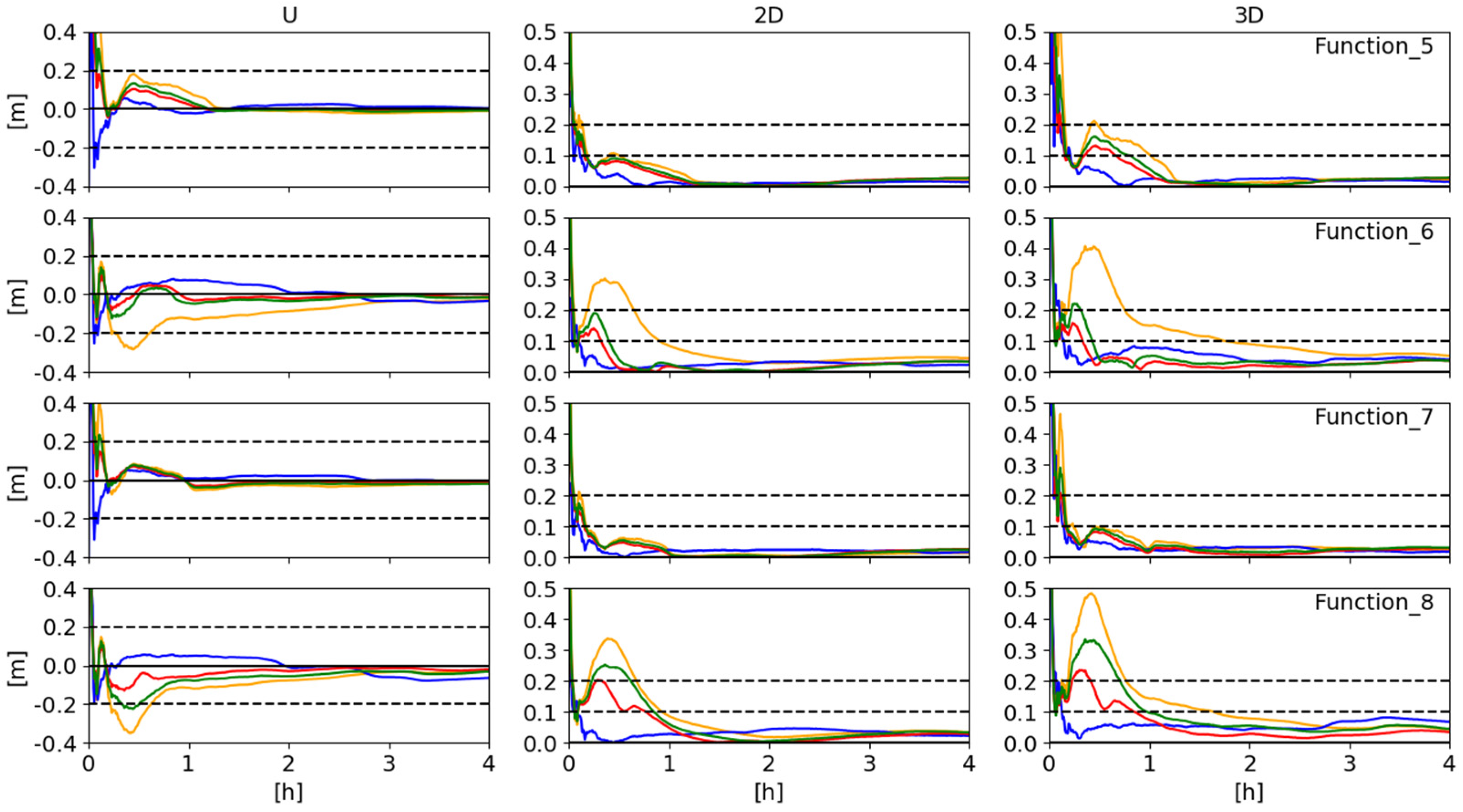
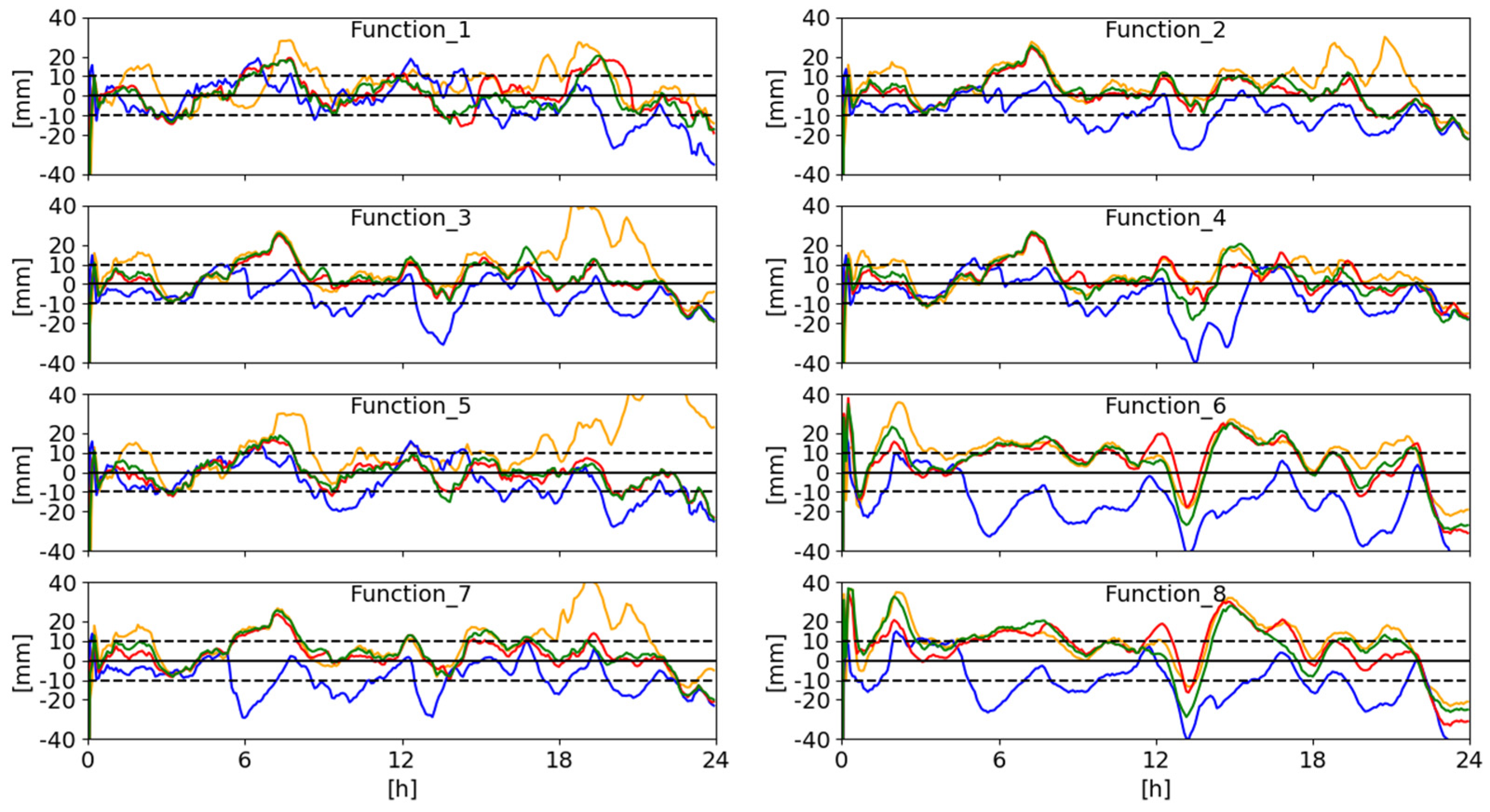
3.1. Detailed Analysis for MAS100ESP Station
3.2. Overall Analysis
4. Proposed Approach for GPS+Galileo Solution
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Station | Receiver | Clock | Date of the Latest Changed Receiver |
|---|---|---|---|
| SUTM00ZAF | JAVAD TRE_3 | INTERNAL | 10.05.2019 |
| ULAB00MNG | JAVAD TRE_3 | INTERNAL | 20.09.2018 |
| BOGT00COL | JAVAD TRE_3 DELTA | INTERNAL | 19.08.2015 |
| TRO100NOR | TRIMBLE NETR9 | EXTERNAL RUBIDIUM | 30.06.2017 |
| UCAL00CAN | TRIMBLE NETR9 | INTERNAL | 21.08.2013 |
| CCJ200JPN | TRIMBLE NETR9 | INTERNAL | 22.02.2012 |
| NKLG00GAB | SEPT POLARX5 | INTERNAL | 21.08.2019 |
| MAS100ESP | SEPT POLARX5 | EXTERNAL CESIUM | 15.10.2019 |
| MGUE00ARG | SEPT POLARX5TR | EXTERNAL H-MASER | 29.04.2019 |
| BRUX00BEL | SEPT POLARX5TR | EXTERNAL CH1-75A MASER | 25.02.2020 |
| NNOR00AUS | SEPT POLARX5TR | EXTERNAL SLAVED CRYSTAL | 25.10.2019 |
| NICO00CYP | LEICA GR50 | INTERNAL | 08.11.2019 |
| REYK00ISL | LEICA GR50 | INTERNAL | 14.05.2019 |
References
- Kouba, J.; Lahaye, F.; Tétreault, P. Precise Point Positioning. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; p. 723. [Google Scholar]
- Héroux, P.; Kouba, J. GPS Precise Point Positioning with a Difference; Natural Resources Canada, Geomatics Canada, Geodetic Survey Division: Ottawa, ON, Canada, 1995.
- Malys, S.; Jensen, P.A. Geodetic Point Positioning with GPS Carrier Beat Phase Data from the CASA UNO Experiment. In Geophysical Research Letters; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1990; Volume 17, pp. 651–654. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Héroux, P.; Kouba, J. GPS Precise Point Positioning Using IGS Orbit Products. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Kouba, J.; Springer, T. New IGS Station and Satellite Clock Combination. GPS Solut. 2001, 4, 31–36. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Precise Point Positioning Using Combined GPS and GLONASS Observations. J. Glob. Position. Syst. 2007, 6, 13–22. [Google Scholar] [CrossRef]
- Tegedor, J.; Øvstedal, O.; Vigen, E. Precise Orbit Determination and Point Positioning Using GPS, Glonass, Galileo and BeiDou. J. Geod. Sci. 2014, 4, 65–73. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Li, X.; Zhou, F.; Feng, G.; Yuan, Y.; Zhang, K. Galileo PPP Rapid Ambiguity Resolution with Five-Frequency Observations. GPS Solut. 2019, 24, 24. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Analytical Performance and Validations of the Galileo Five-Frequency Precise Point Positioning Models. Measurement 2021, 172, 108890. [Google Scholar] [CrossRef]
- Guo, J.; Geng, J.; Wang, C. Impact of the Third Frequency GNSS Pseudorange and Carrier Phase Observations on Rapid PPP Convergences. GPS Solut. 2021, 25, 30. [Google Scholar] [CrossRef]
- Geng, J.; Pan, Y.; Yang, S.; Li, P.; Geng, J.; Pan, Y.; Yang, S.; Li, P. Combining Multi-GNSS Phase Bias Products for Improved Undifferenced Ambiguity Resolution. In Proceedings of the EGU General Assembly Conference Abstracts, Online, 19–30 April 2021; p. EGU21-2531. [Google Scholar]
- Mansur, G.; Sakic, P.; Männel, B.; Schuh, H. Multi-Constellation GNSS Orbit Combination Based on MGEX Products. Adv. Geosci. 2020, 50, 57–64. [Google Scholar] [CrossRef][Green Version]
- Sośnica, K.; Zajdel, R.; Bury, G.; Bosy, J.; Moore, M.; Masoumi, S. Quality Assessment of Experimental IGS Multi-GNSS Combined Orbits. GPS Solut. 2020, 24, 54. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Consistency of MGEX Orbit and Clock Products. Engineering 2020, 6, 898–903. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Jiao, G. Assessment of Multi-Frequency Global Navigation Satellite System Precise Point Positioning Models Using GPS, BeiDou, GLONASS, Galileo and QZSS. Meas. Sci. Technol. 2020, 31, 064008. [Google Scholar] [CrossRef]
- Ogutcu, S. Assessing the Contribution of Galileo to GPS+GLONASS PPP: Towards Full Operational Capability. Measurement 2020, 151, 107143. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems. GPS, GLONASS, Galileo, and More; Springer: Vienna, Austria, 2008; ISBN 978-3-211-73012-6. [Google Scholar]
- Luo, X. GPS Stochastic Modelling: Signal Quality Measures and ARMA Processes; Springer Theses: Berlin, Germany; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-34835-8. [Google Scholar]
- Prochniewicz, D.; Wezka, K.; Kozuchowska, J. Empirical Stochastic Model of Multi-GNSS Measurements. Sensors 2021, 21, 4566. [Google Scholar] [CrossRef]
- Tiberius, C.C.J.M.; Kenselaar, F. Estimation of the Stochastic Model for GPS Code and Phase Observables. Surv. Rev. 2000, 35, 441–454. [Google Scholar] [CrossRef]
- Wang, J.-G.; Gopaul, N.; Scherzinger, B. Simplified Algorithms of Variance Component Estimation for Static and Kinematic GPS Single Point Positioning. J. Glob. Position. Syst. 2009, 8, 43–52. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Amiri-Simkooei, A.R. Least-Squares Variance Component Estimation. J. Geod. 2007, 82, 65–82. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Teunissen, P.J.G.; Tiberius, C.C.J.M. Application of Least-Squares Variance Component Estimation to GPS Observables. J. Surv. Eng. 2009, 135, 149–160. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Tu, R.; Lu, X.; Ge, M.; Schuh, H. Automatic Calibration of Process Noise Matrix and Measurement Noise Covariance for Multi-GNSS Precise Point Positioning. Mathematics 2020, 8, 502. [Google Scholar] [CrossRef]
- Mirmohammadian, F.; Asgari, J.; Verhagen, S.; Amiri-Simkooei, A. Improvement of Multi-GNSS Precision and Success Rate Using Realistic Stochastic Model of Observations. Remote Sens. 2021, 14, 60. [Google Scholar] [CrossRef]
- Hou, P.; Zha, J.; Liu, T.; Zhang, B. LS-VCE Applied to Stochastic Modeling of GNSS Observation Noise and Process Noise. Remote Sens. 2022, 14, 258. [Google Scholar] [CrossRef]
- [IGSMAIL-1569] IGS Workshop, GB Meeting 1997 in Pasadena. Available online: https://lists.igs.org/pipermail/igsmail/1997/002941.html (accessed on 8 April 2022).
- [IGSMAIL-1586] Elevation Cut-Off Angle. Available online: https://lists.igs.org/pipermail/igsmail/1997/002958.html (accessed on 8 April 2022).
- [IGSMAIL-1705] CODE Analysis Changes. Available online: https://lists.igs.org/pipermail/igsmail/1997/003077.html (accessed on 8 April 2022).
- Gao, C.; Wu, F.; Chen, W.; Wang, W. An Improved Weight Stochastic Model in GPS Precise Point Positioning. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering, TMEE, Changchun, China, 16–18 December 2011; pp. 629–632. [Google Scholar] [CrossRef]
- Yu, X.; Gao, J. Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations. ISPRS Int. J. Geo-Inf. 2017, 6, 6. [Google Scholar] [CrossRef]
- Kazmierski, K.; Hadas, T.; Sośnica, K. Weighting of Multi-GNSS Observations in Real-Time Precise Point Positioning. Remote Sens. 2018, 10, 84. [Google Scholar] [CrossRef]
- Liu, T.; Wang, J.; Yu, H.; Cao, X.; Ge, Y. A New Weighting Approach with Application to Ionospheric Delay Constraint for GPS/GALILEO Real-Time Precise Point Positioning. Appl. Sci. 2018, 8, 2537. [Google Scholar] [CrossRef]
- Kiliszek, D.; Szołucha, M.; Kroszczyński, K. Accuracy of Precise Point Positioning (PPP) with the Use of Different International GNSS Service (IGS) Products and Stochastic Modelling. Geod. Cartogr. 2018, 67, 207–238. [Google Scholar] [CrossRef]
- Jiang, N.; Xu, T.; Xu, Y.; Xu, G.; Schuh, H. Assessment of Different Stochastic Models for Inter-System Bias between GPS and BDS. Remote Sens. 2019, 11, 989. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, L.; Zhou, J. A Weighting Method for Code and Phase Observations in Precise Point Positioning. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference, CGNCC, Xiamen, China, 10–12 August 2018. [Google Scholar] [CrossRef]
- Pan, L.; Gao, X.; Hu, J.; Ma, F.; Zhang, Z.; Wu, W. Performance Assessment of Real-Time Multi-GNSS Integrated PPP with Uncombined and Ionospheric-Free Combined Observables. Adv. Space Res. 2021, 67, 234–252. [Google Scholar] [CrossRef]
- Constellation Information|European GNSS Service Centre. Available online: https://www.gsc-europa.eu/system-service-status/constellation-information (accessed on 8 April 2022).
- Hadas, T.; Kazmierski, K.; Sośnica, K. Performance of Galileo-Only Dual-Frequency Absolute Positioning Using the Fully Serviceable Galileo Constellation. GPS Solut. 2019, 23, 108. [Google Scholar] [CrossRef]
- Kiliszek, D.; Kroszczyński, K. Performance of the Precise Point Positioning Method along with the Development of GPS, GLONASS and Galileo Systems. Measurement 2020, 164, 108009. [Google Scholar] [CrossRef]
- Douša, J.; Václavovic, P.; Kala, M.; Bezděka, P.; Zhao, L. GOP Contribution to Independent Monitoring of Galileo OS Navigation Performance; VSB—Technical University of Ostrava: Ostrava, Czechia, 2021. [Google Scholar]
- Carlin, L.; Hauschild, A.; Montenbruck, O. Precise Point Positioning with GPS and Galileo Broadcast Ephemerides. GPS Solut. 2021, 25, 77. [Google Scholar] [CrossRef]
- Caporali, A.; Zurutuza, J.; Paziewski, J.; Li, X. Broadcast Ephemeris with Centimetric Accuracy: Test Results for GPS, Galileo, Beidou and Glonass. Remote Sens. 2021, 13, 4185. [Google Scholar] [CrossRef]
- Liu, T.; Chen, H.; Chen, Q.; Jiang, W.; Laurichesse, D.; An, X.; Geng, T. Characteristics of Phase Bias from CNES and Its Application in Multi-Frequency and Multi-GNSS Precise Point Positioning with Ambiguity Resolution. GPS Solut. 2021, 25, 58. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Meng, X.; Gao, K. Speeding up PPP Ambiguity Resolution Using Triple-Frequency GPS/BeiDou/Galileo/QZSS Data. J. Geod. 2020, 94, 6. [Google Scholar] [CrossRef]
- Glaner, M.; Weber, R. PPP with Integer Ambiguity Resolution for GPS and Galileo Using Satellite Products from Different Analysis Centers. GPS Solut. 2021, 25, 102. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Selmke, I.; Wang, N. Estimating Ambiguity Fixed Satellite Orbit, Integer Clock and Daily Bias Products for GPS L1/L2, L1/L5 and Galileo E1/E5a, E1/E5b Signals. J. Geod. 2021, 95, 44. [Google Scholar] [CrossRef]
- Schaer, S.; Villiger, A.; Arnold, D.; Dach, R.; Prange, L.; Jäggi, A. The CODE Ambiguity-Fixed Clock and Phase Bias Analysis Products: Generation, Properties, and Performance. J. Geod. 2021, 95, 81. [Google Scholar] [CrossRef]
- Zhao, L.; Blunt, P.; Yang, L. Performance Analysis of Zero-Difference GPS L1/L2/L5 and Galileo E1/E5a/E5b/E6 Point Positioning Using CNES Uncombined Bias Products. Remote Sens. 2022, 14, 650. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Q.; Li, G.; Zhang, K. Assessment of Multi-Frequency PPP Ambiguity Resolution Using Galileo and BeiDou-3 Signals. Remote Sens. 2021, 13, 4746. [Google Scholar] [CrossRef]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the Interoperability of IGS Products for Precise Point Positioning with Ambiguity Resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- MGEX Product Analysis—International GNSS Service. Available online: https://igs.org/mgex/analysis/ (accessed on 8 April 2022).
- Kp-Index. Available online: https://www.gfz-potsdam.de/kp-index/ (accessed on 8 April 2022).
- Bahadur, B.; Nohutcu, M. PPPH: A MATLAB-Based Software for Multi-GNSS Precise Point Positioning Analysis. GPS Solut. 2018, 22, 113. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products; Geodetic Survey Division Natural Resources Canada Ottawa: Ottawa, ON, Canada, 2015.
- Petit, G.; Brian, L. IERS Conventions; Bureau International des Poids et Mesures Sevres (France): Saint-Cloud, France, 2010. [Google Scholar]
- Ray, J.; Griffiths, J. Overview of IGS Products and Analysis Center Modeling. In Proceedings of the IGS Analysis Center Workshop, Miami Beach, FL, USA, 2–6 June 2008. [Google Scholar]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. Documentation for the GAMIT GPS Analysis Software 10.70; MIT: Cambridge, MA, USA, 2018. [Google Scholar]
- Jin, X.X.; de Jong, C.D. Relationship Between Satellite Elevation and Precision of GPS Code Observations. J. Navig. 1996, 49, 253–265. [Google Scholar] [CrossRef]
- Rothacher, M.; Springer, T.A.; Schaer, S.; Beutler, G. Processing Strategies for Regional GPS Networks. In Proceedings of the IAG General Assembly 1997, Rio de Janeiro, Brazil, 2–13 July 1997; Brunner, F.K., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1998; pp. 93–100. [Google Scholar]
- ÖZLÜDEMİR, M.T. The Stochastic Modeling of GPS Observations. Turk. J. Eng. Environ. Sci. 2004, 28, 223–231. [Google Scholar] [CrossRef]
- Tiberius, C.C.J.M.; Borre, K. Are GPS Data Normally Distributed. In Geodesy Beyond; Springer: Berlin/Heidelberg, Germany, 2000; pp. 243–248. [Google Scholar] [CrossRef]
- Luo, X.; Mayer, M.; Heck, B. On the Probability Distribution of GNSS Carrier Phase Observations. GPS Solut. 2010, 15, 369–379. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Wielgosz, P. On the Applicability of Galileo FOC Satellites with Incorrect Highly Eccentric Orbits: An Evaluation of Instantaneous Medium-Range Positioning. Remote Sens. 2018, 10, 208. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, Prospects and Challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Sakic, P.; Mansur, G.; Viegas, E.; Männel, B.; Schuh, H. Towards a Multi-Constellation Combination: Improving the IGS Orbit and Clock Combination Software for MGEX Products. In Proceedings of the IGS Workshop, Wuhan, China, 19–21 March 2018. [Google Scholar]
- Paziewski, J.; Wielgosz, P. Assessment of GPS+Galileo and Multi-Frequency Galileo Single-Epoch Precise Positioning with Network Corrections. GPS Solut. 2013, 18, 571–579. [Google Scholar] [CrossRef]
- Araszkiewicz, A.; Kiliszek, D. Impact of Using GPS L2 Receiver Antenna Corrections for the Galileo E5a Frequency on Position Estimates. Sensors 2020, 20, 5536. [Google Scholar] [CrossRef]
- Villiger, A.; Dach, R.; Schaer, S.; Prange, L.; Zimmermann, F.; Kuhlmann, H.; Wübbena, G.; Schmitz, M.; Beutler, G.; Jäggi, A. GNSS Scale Determination Using Calibrated Receiver and Galileo Satellite Antenna Patterns. J. Geod. 2020, 94, 93. [Google Scholar] [CrossRef]
- Xia, F.; Ye, S.; Xia, P.; Zhao, L.; Jiang, N.; Chen, D.; Hu, G. Assessing the Latest Performance of Galileo-Only PPP and the Contribution of Galileo to Multi-GNSS PPP. Adv. Space Res. 2019, 63, 2784–2795. [Google Scholar] [CrossRef]
- Tian, Y.; Sui, L.; Xiao, G.; Zhao, D.; Tian, Y. Analysis of Galileo/BDS/GPS Signals and RTK Performance. GPS Solut. 2019, 23, 37. [Google Scholar] [CrossRef]
- GPS.Gov: Space Segment. Available online: https://www.gps.gov/systems/gps/space/#generation (accessed on 8 April 2022).
- Hadas, T.; Hobiger, T. Benefits of Using Galileo for Real-Time GNSS Meteorology. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1756–1760. [Google Scholar] [CrossRef]
- Hong, J.; Tu, R.; Gao, Y.; Zhang, R.; Fan, L.; Zhang, P.; Liu, J. Characteristics of Inter-System Biases in Multi-GNSS with Precise Point Positioning. Adv. Space Res. 2019, 63, 3777–3794. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Wielgosz, P. Selected Properties of GPS and Galileo-IOV Receiver Intersystem Biases in Multi-GNSS Data Processing. Meas. Sci. Technol. 2015, 26, 095008. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations. J. Geod. 2007, 82, 389–399. [Google Scholar] [CrossRef]
- Satirapod, C.; Luansang, M. Comparing Stochastic Models Used in GPS Precise Point Positioning Technique. Surv. Rev. 2013, 40, 188–194. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, L. Current Performance of Open Position Service with Almost Fully Deployed Multi-GNSS Constellations: GPS, GLONASS, Galileo, BDS-2, and BDS-3. Adv. Space Res. 2022, 69, 1994–2019. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiliszek, D.; Kroszczyński, K.; Araszkiewicz, A. Analysis of Different Weighting Functions of Observations for GPS and Galileo Precise Point Positioning Performance. Remote Sens. 2022, 14, 2223. https://doi.org/10.3390/rs14092223
Kiliszek D, Kroszczyński K, Araszkiewicz A. Analysis of Different Weighting Functions of Observations for GPS and Galileo Precise Point Positioning Performance. Remote Sensing. 2022; 14(9):2223. https://doi.org/10.3390/rs14092223
Chicago/Turabian StyleKiliszek, Damian, Krzysztof Kroszczyński, and Andrzej Araszkiewicz. 2022. "Analysis of Different Weighting Functions of Observations for GPS and Galileo Precise Point Positioning Performance" Remote Sensing 14, no. 9: 2223. https://doi.org/10.3390/rs14092223
APA StyleKiliszek, D., Kroszczyński, K., & Araszkiewicz, A. (2022). Analysis of Different Weighting Functions of Observations for GPS and Galileo Precise Point Positioning Performance. Remote Sensing, 14(9), 2223. https://doi.org/10.3390/rs14092223