A Multi-Sensor Interacted Vehicle-Tracking Algorithm with Time-Varying Observation Error
Abstract
:1. Introduction
- (1)
- For complex tracking environments with changing noise, we establish a jointed and time-varying observation error model for each sensor to indicate the variation of observation noise, which improves the vehicle tracking performance with high tracking accuracy.
- (2)
- We propose a multi-sensor interacted vehicle-tracking algorithm which can predict the statistical information of time varying observation error and fuse the tracking result of each sensor to give a global estimation. The algorithm reduces the computational complexity and improve the tracking robustness with time varying observation error.
- (3)
- We verify the effectiveness of the proposed algorithm through simulation and experiments with real data. The experiments are performed by designing an unmanned mobile platform (UMP) positioning system with an inertial navigation system (INS) and ultra-wideband (UWB) platform. From the simulation and experiments result, we can improve the tracking performance significantly with time-varying observation noise.
2. Related Works
2.1. Adaptive Tracking Methods
2.2. Tracking Methods with Complex Noise
2.3. Real-Time Tracking Methods
2.4. Former Works
3. Models
3.1. Mobility Model
3.2. Jointed Observation Model
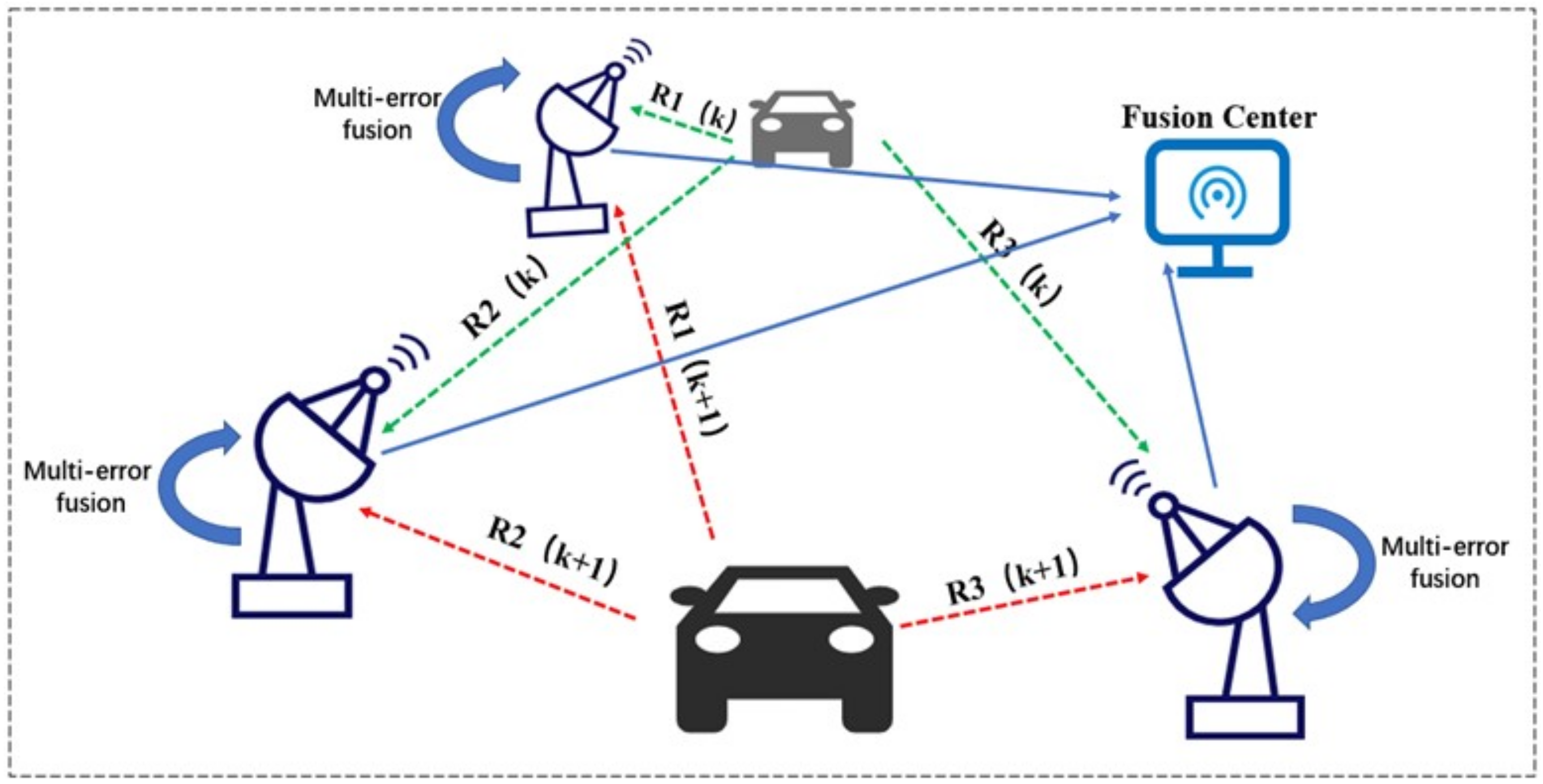
4. Vehicle-Tracking Algorithm
4.1. Jointed and Time Varying Observation Error Model
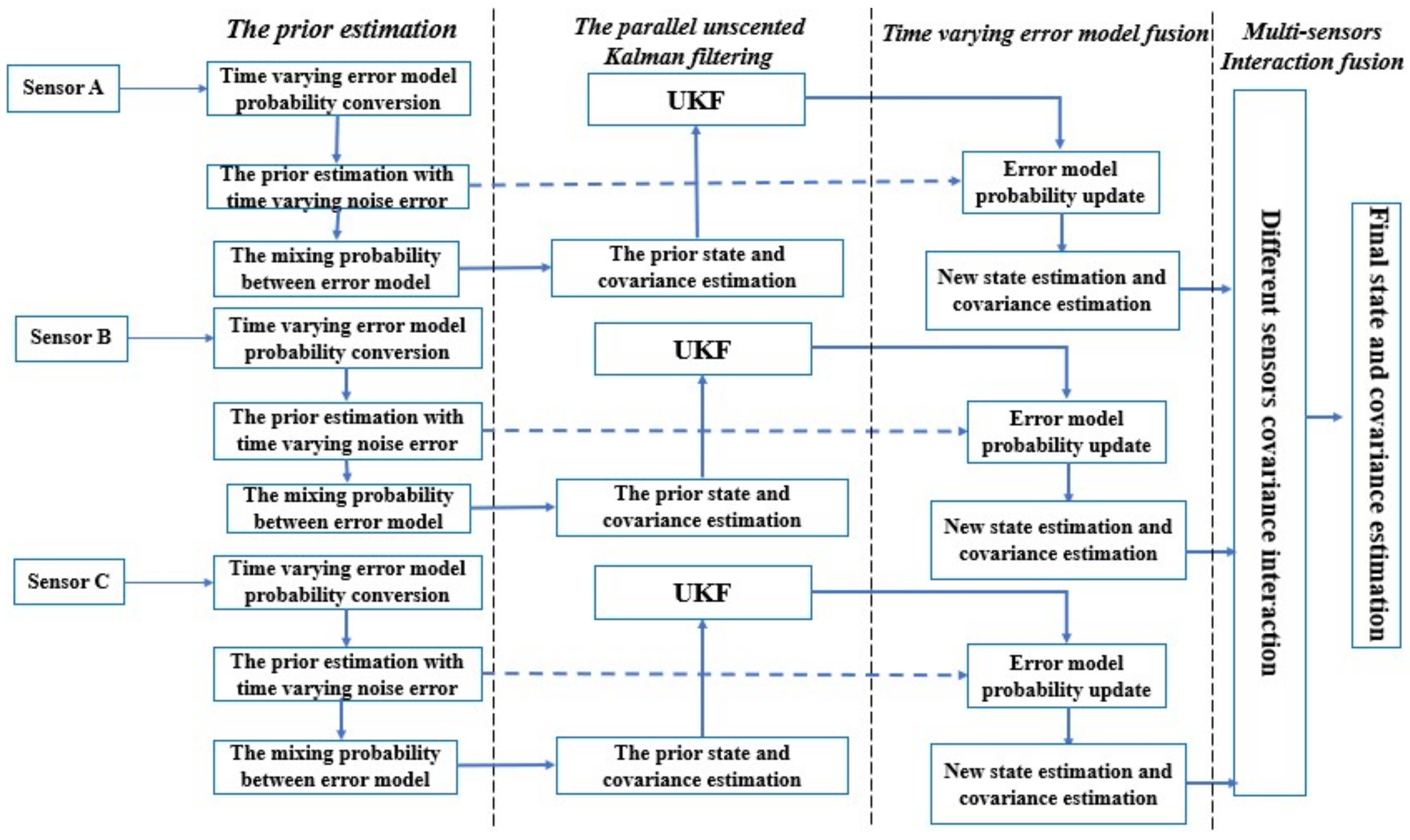
4.2. Multi-Sensor Interacted Vehicle Tracking Algorithm
4.2.1. The Prior Estimation
4.2.2. The Parallel Unscented Kalman Filters
4.2.3. Vehicle Tracking with Time-Varying Observation Error
4.2.4. Vehicle Tracking with Multi-Sensor Interaction
5. Simulation Results
5.1. Simulation Environment Settings
5.2. Simulation Results Analysis
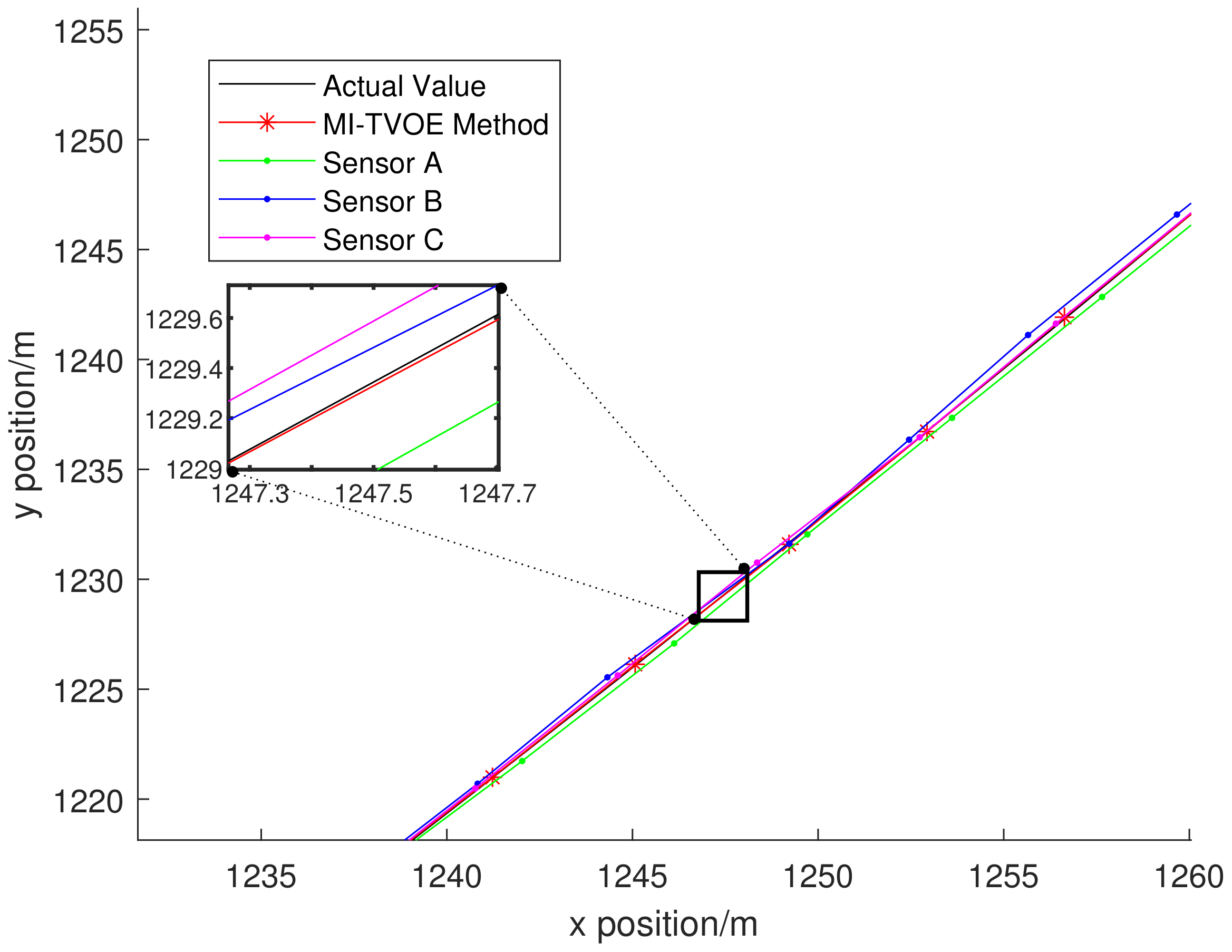
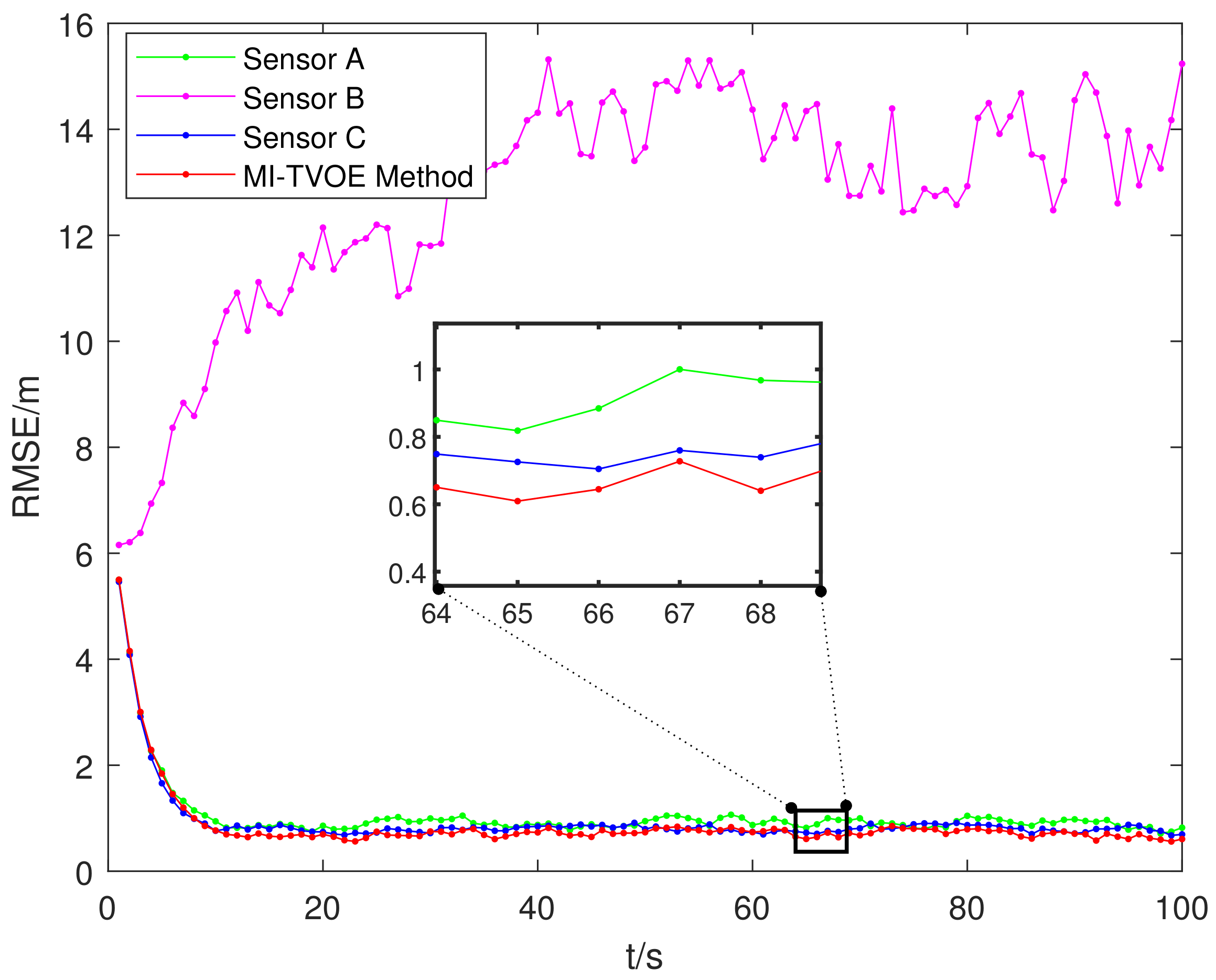
5.2.1. Tracking Result from Different Sensors
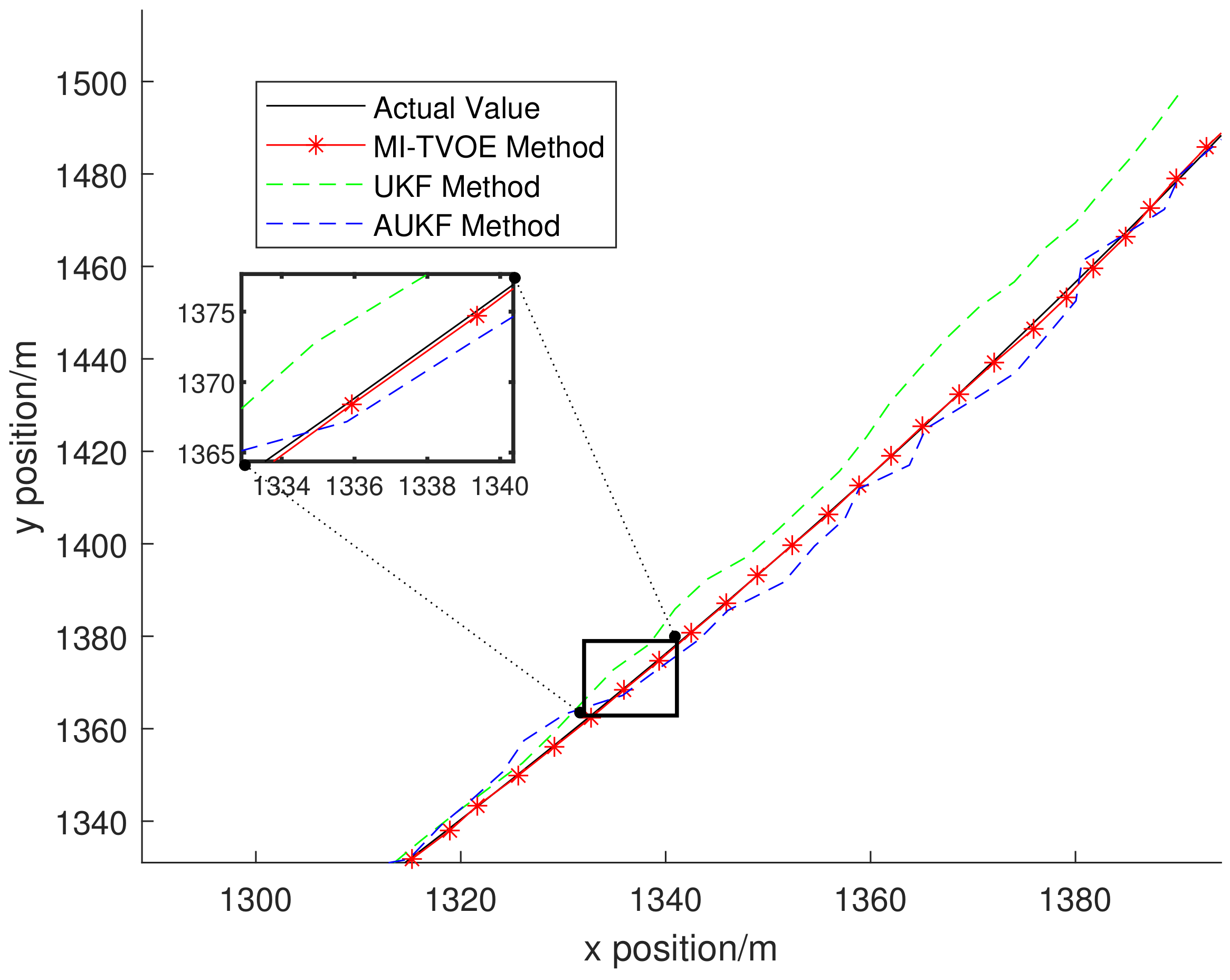
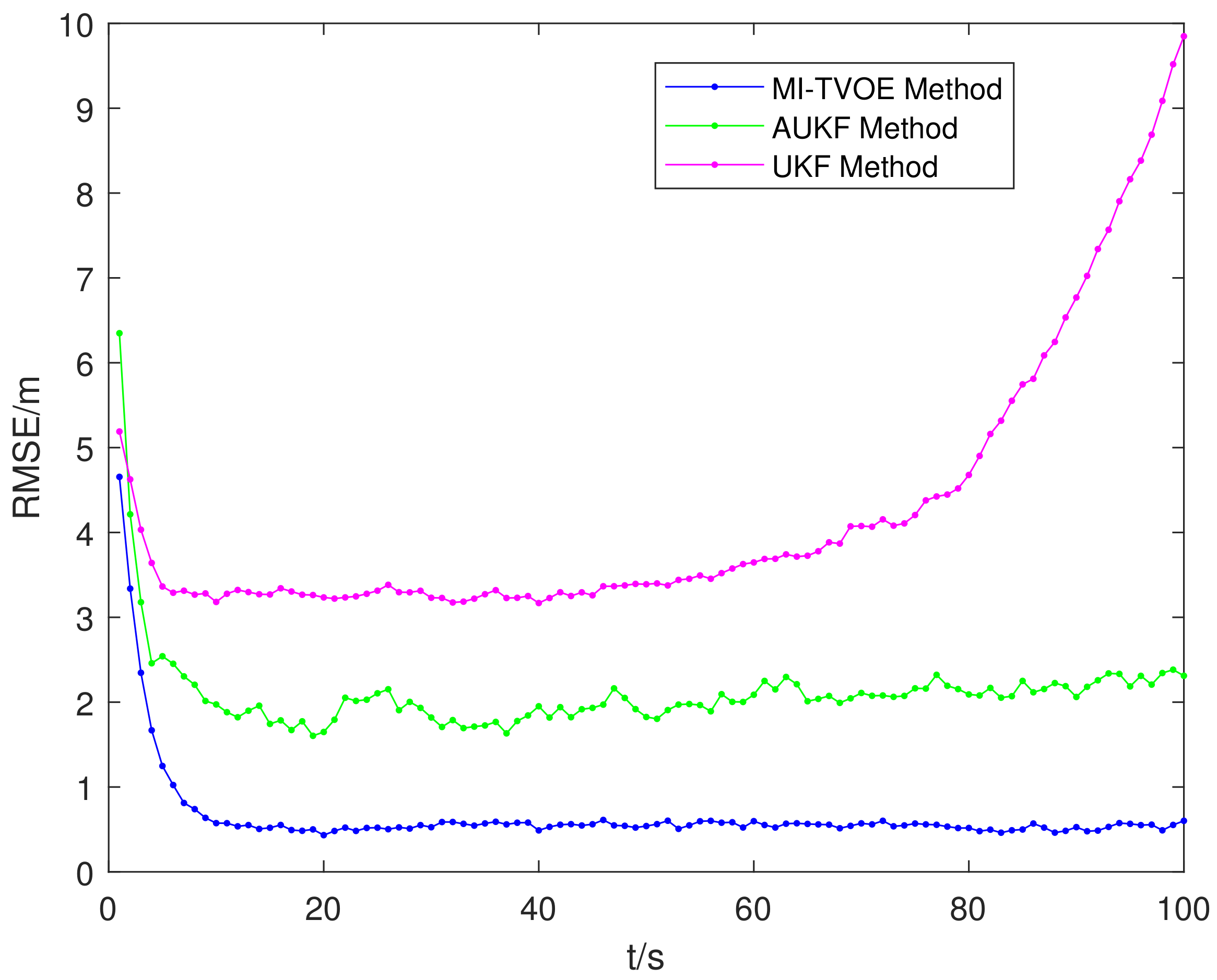
5.2.2. Tracking Result from Different Algorithm
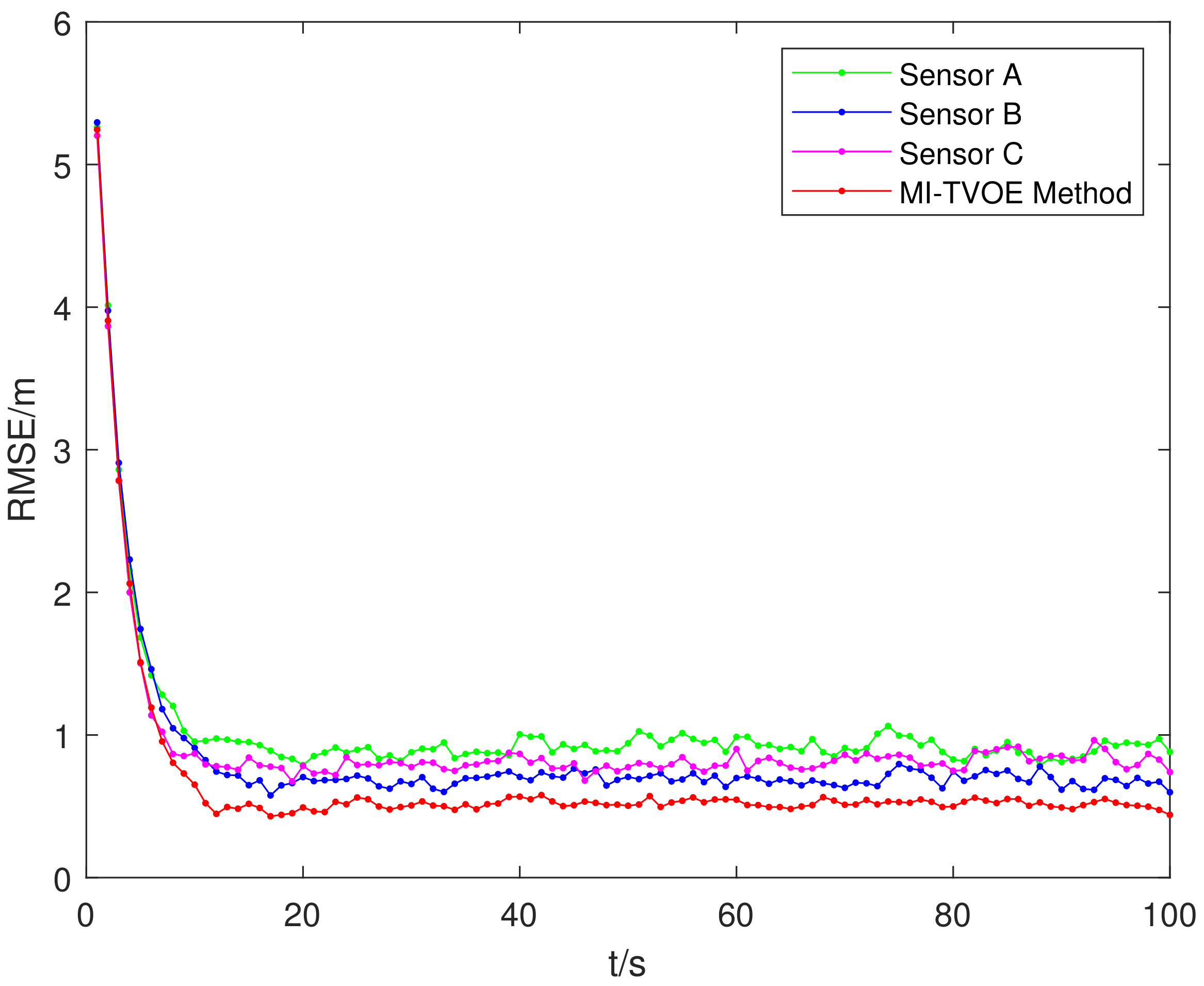
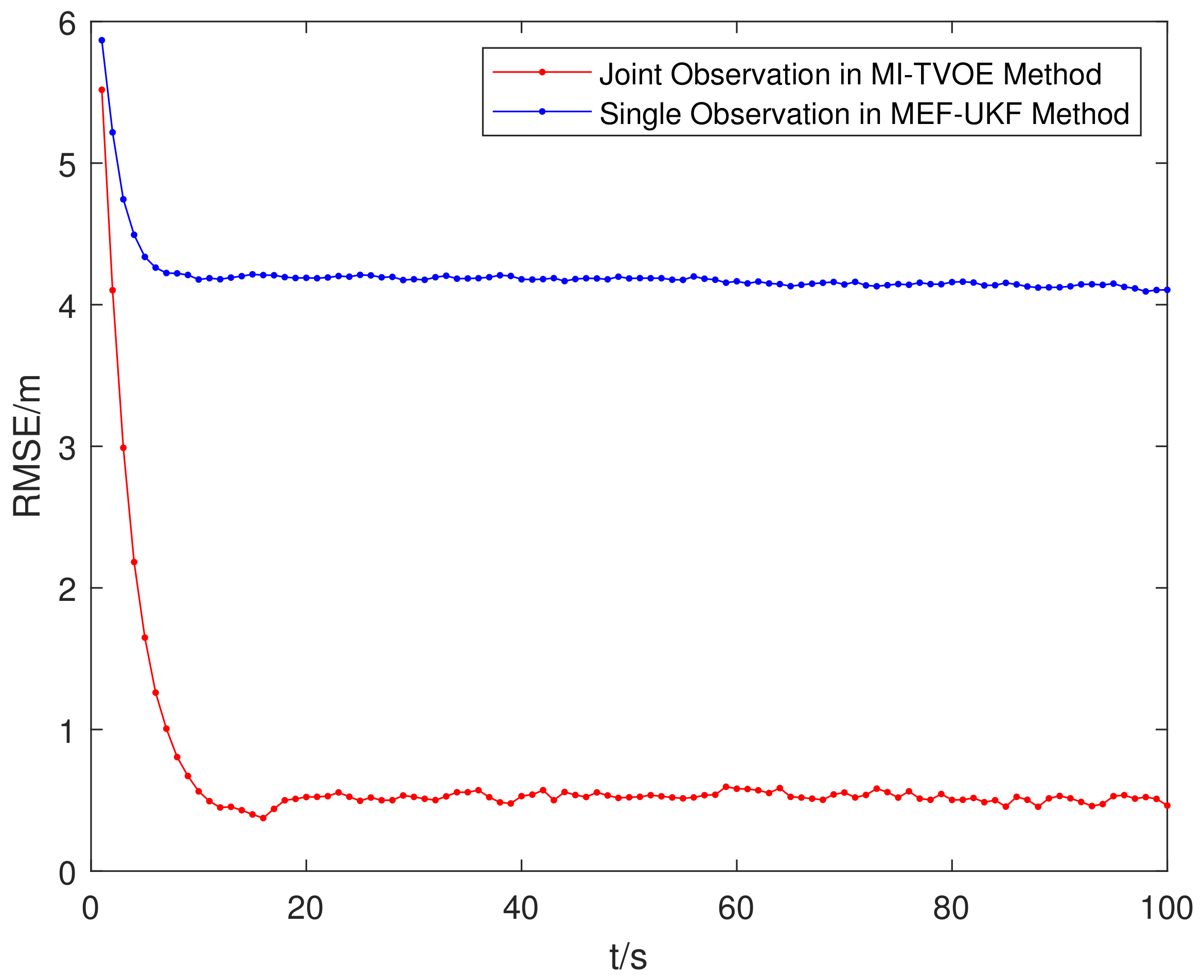
5.2.3. Tracking Performance Analysis
5.2.4. Computational Complexity Analysis
6. Experimental Result
6.1. Experiment Settings
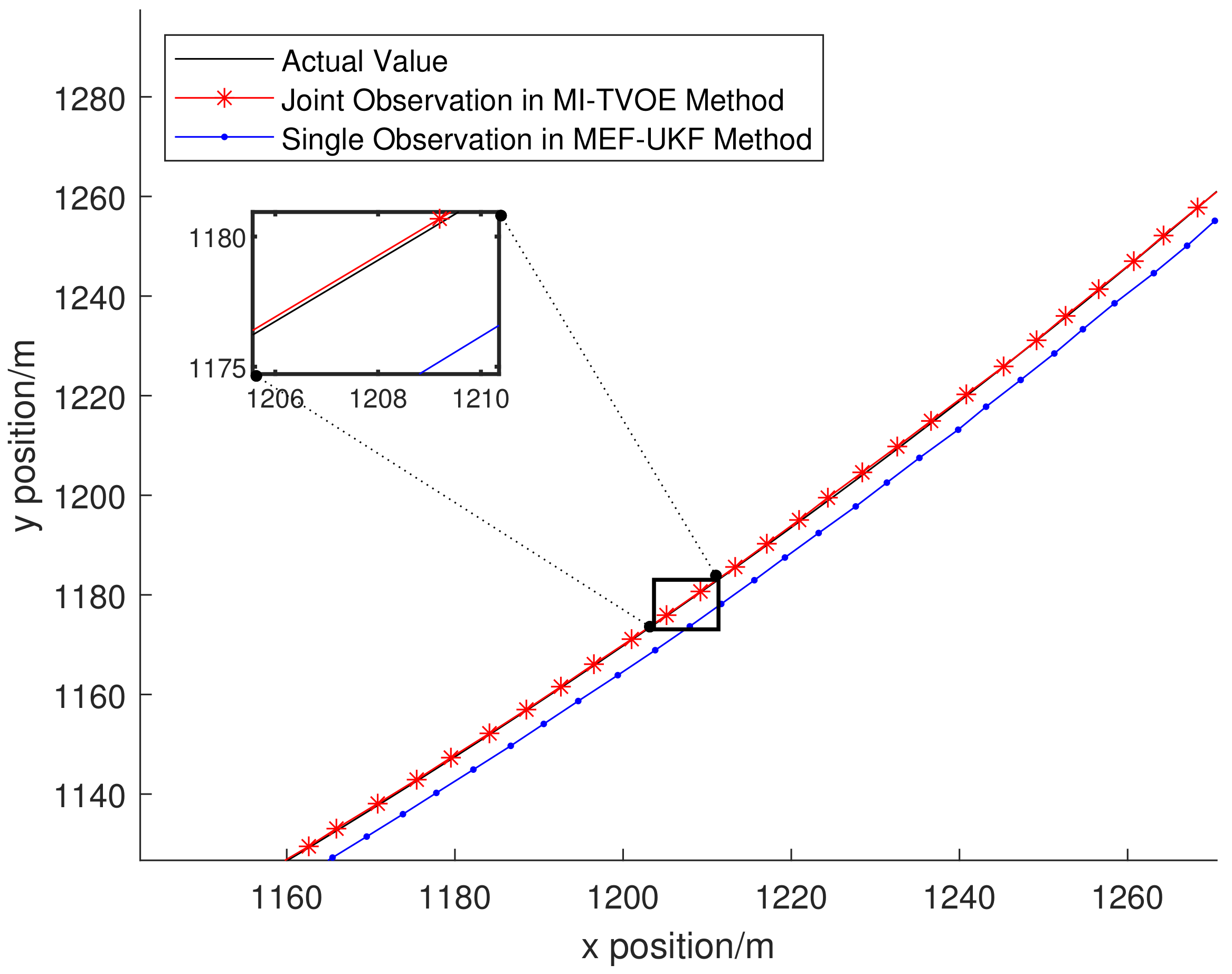
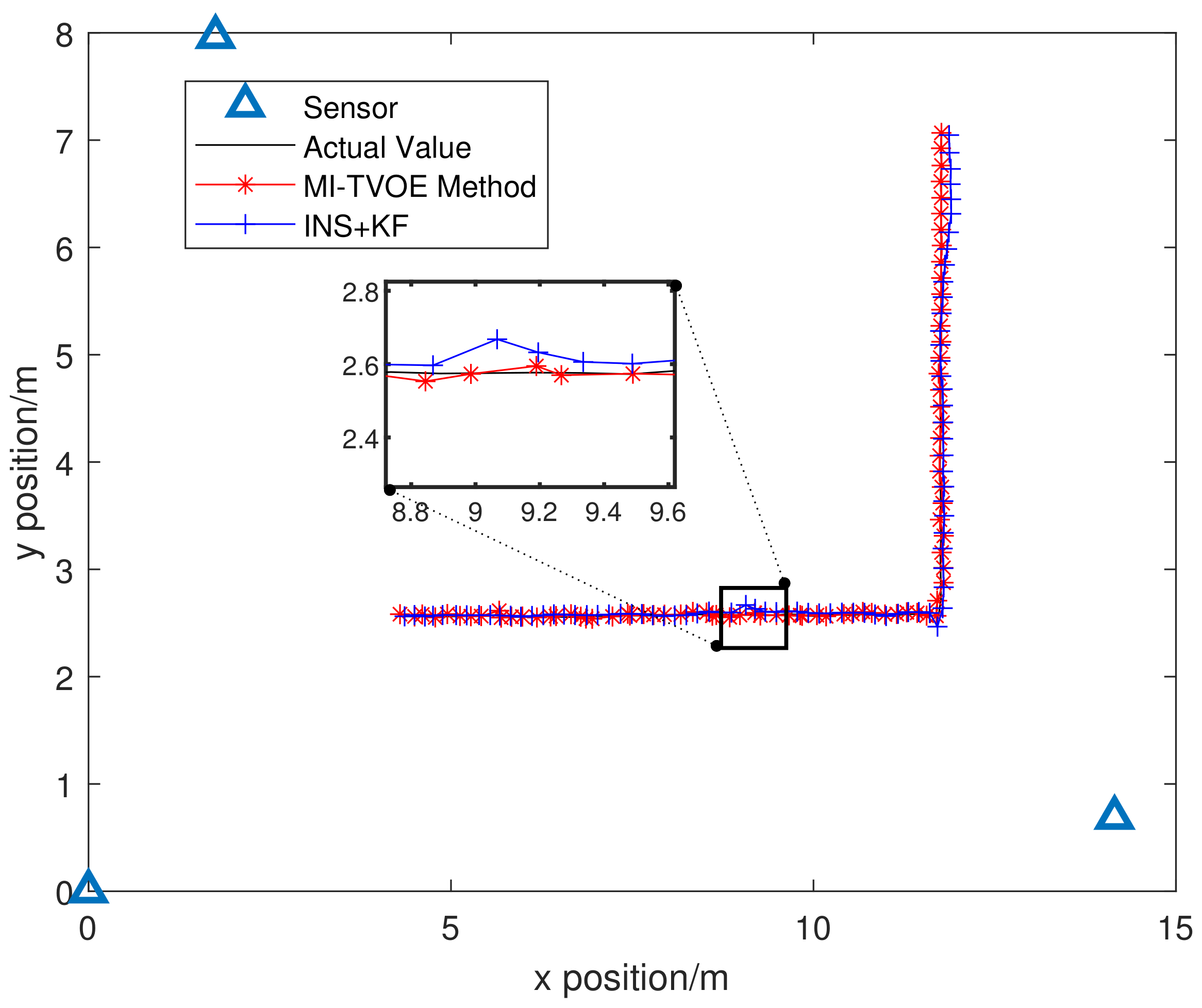
6.2. Experimental Results Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, Y.; Wang, W.; Yan, X.; Zhao, H.; Zha, H. On-Road Vehicle Tracking Using Part-Based Particle Filter. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4538–4552. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Zhou, Q.; Tian, Y. A Model Predictive Controller with Switched Tracking Error for Autonomous Vehicle Path Tracking. IEEE Access 2019, 7, 53103–53114. [Google Scholar] [CrossRef]
- Zhang, B.; Zong, C.; Chen, G.; Zhang, B. Electrical Vehicle Path Tracking Based Model Predictive Control with a Laguerre Function and Exponential Weight. IEEE Access 2019, 7, 17082–17097. [Google Scholar] [CrossRef]
- Scheunert, U.; Cramer, H.; Fardi, B.; Wanielik, G. Multi sensor based tracking of pedestrians: A survey of suitable movement models. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 774–778. [Google Scholar]
- Deming, R.; Schindler, J.; Perlovsky, L. Multi-Target/Multi-Sensor Tracking Using Only Range and Doppler Measurements. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 593–611. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Z.; Zhang, L.; Wang, C. Longitudinal Vehicle Speed Estimation for Four-Wheel-Independently-Actuated Electric Vehicles Based on Multi-Sensor Fusion. IEEE Trans. Veh. Technol. 2020, 69, 12797–12806. [Google Scholar] [CrossRef]
- Yang, P.; Duan, D.; Chen, C.; Cheng, X.; Yang, L. Multi-Sensor Multi-Vehicle (MSMV) Localization and Mobility Tracking for Autonomous Driving. IEEE Trans. Veh. Technol. 2020, 69, 14355–14364. [Google Scholar] [CrossRef]
- Tian, B.; Li, Y.; Li, B.; Wen, D. Rear-View Vehicle Detection and Tracking by Combining Multiple Parts for Complex Urban Surveillance. IEEE Trans. Intell. Transp. Syst. 2014, 15, 597–606. [Google Scholar] [CrossRef]
- Zheng, J.; Yu, H.; Wang, S.; Long, Y.; Meng, F. Distributed adaptive multi-sensor multi-target tracking algorithm. J. Chin. Inert. Technol. 2015, 23, 472–476. [Google Scholar]
- Yomchinda, T. A method of multirate sensor fusion for target tracking and localization using extended Kalman Filter. In Proceedings of the 2017 Fourth Asian Conference on Defence Technology—Japan (ACDT), Tokyo, Japan, 29 November–1 December 2017; pp. 1–7. [Google Scholar]
- Hu, F.; Wu, G. Distributed Error Correction of EKF Algorithm in Multi-Sensor Fusion Localization Model. IEEE Access 2020, 8, 93211–93218. [Google Scholar] [CrossRef]
- Yang, F.; Tang, W.; Wang, Y.; Chen, S. A RANSAC-Based Track Initialization Algorithm for Multi-Sensor Tracking System. In Proceedings of the 2018 International Conference on Control, Automation and Information Sciences (ICCAIS), Hangzhou, China, 24–27 October 2018; pp. 96–101. [Google Scholar]
- Shi, Y.; Yang, Z.; Zhang, T.; Lin, N.; Zhao, Y.; Zhao, Y. An Adaptive Track Fusion Method with Unscented Kalman Filter. In Proceedings of the 2018 IEEE International Conference on Smart Internet of Things (SmartIoT), Xi’an, China, 17–19 August 2018; pp. 250–254. [Google Scholar]
- Zhou, N.; Lau, L.; Bai, R.; Moore, T. A Genetic Optimization Resampling Based Particle Filtering Algorithm for Indoor Target Tracking. Remote Sens. 2021, 13, 132. [Google Scholar] [CrossRef]
- Niknejad, H.T.; Takeuchi, A.; Mita, S.; McAllester, D. On-road multivehicle tracking using deformable object model and particle filter with improved likelihood estimation. IEEE Trans. Intell. Transp. Syst. 2012, 13, 748–758. [Google Scholar] [CrossRef]
- Xu, H.; Bai, X.; Liu, P.; Shi, Y. Hierarchical Fusion Estimation for WSNs with Link Failures Based on Kalman-Consensus Filtering and Covariance Intersection. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5150–5154. [Google Scholar]
- Li, X.; Wu, P.; Zhang, X. An interacting multiple models probabilistic data association algorithm for maneuvering target tracking in clutter. Int. Symp. Comput. Inform. 2015, 13, 1685–1692. [Google Scholar]
- Zhu, L.; Cheng, X. High manoeuvre target tracking in coordinated turns. IET Radar Sonar Navig. 2015, 9, 1078–1087. [Google Scholar] [CrossRef]
- Choi, W.Y.; Kang, C.M.; Lee, S.H.; Chung, C.C. Radar accuracy modeling and its application to object vehicle tracking. Int. J. Control Autom. Syst. 2020, 18, 3146–3158. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.; Zhou, Q.; Che, H. An Adaptive Low-Cost INS/GNSS Tightly-Coupled Integration Architecture Based on Redundant Measurement Noise Covariance Estimation. Sensors 2017, 17, 2032. [Google Scholar] [CrossRef] [Green Version]
- Akhlaghi, S.; Zhou, N.; Huang, Z. Adaptive adjustment of noise covariance in Kalman filter for dynamic state estimation. In Proceedings of the 2017 IEEE Power $ Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Sun, Y.; Jing, F.; Liang, Z.; Tan, M. MMSE State Estimation Approach for Linear Discrete-Time Systems With Time-Delay and Multi-Error Measurements. IEEE Trans. Autom. Control 2017, 62, 1530–1536. [Google Scholar] [CrossRef]
- Jamroz, B.F.; Williams, D.F.; Rezac, J.D.; Frey, M.; Koepke, A.A. Accurate Monte Carlo Uncertainty Analysis for Multiple Measurements of Microwave Systems. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019; pp. 1279–1282. [Google Scholar]
- Lin, P.; Hu, C.; Lou, Y. Distributed Variational Bayes Based on Consensus of Probability Densities. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5013–5018. [Google Scholar]
- He, W.; Liu, Y.; Yao, H.; Mai, T.; Zhang, N.; Yu, F.R. Distributed Variational Bayes-Based In-Network Security for the Internet of Things. IEEE Internet Things J. 2021, 8, 6293–6304. [Google Scholar] [CrossRef]
- Kheirandish, A.; Fatehi, A.; Gheibi, M.S. Identification of Slow-Rate Integrated Measurement Systems Using Expectation–Maximization Algorithm. IEEE Trans. Instrum. Meas. 2020, 69, 9477–9484. [Google Scholar] [CrossRef]
- Peng, Y.; Panlong, W.; Shan, H. An IMM-VB Algorithm for Hypersonic Vehicle Tracking with Heavy Tailed Measurement Noise. In Proceedings of the 2018 International Conference on Control, Automation and Information Sciences (ICCAIS), Hangzhou, China, 24–27 October 2018; pp. 169–174. [Google Scholar]
- Li, Z.; Zhang, J.; Wang, J.; Zhou, Q. Recursive Noise Adaptive Extended Object Tracking by Variational Bayesian Approximation. IEEE Access 2019, 7, 151168–151179. [Google Scholar] [CrossRef]
- Byeon, M.; Lee, M.; Kim, K.; Choi, J.Y. Variational inference for 3-D localization and tracking of multiple targets using multiple cameras. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3260–3274. [Google Scholar] [CrossRef]
- Stauffer, C.; Grimson, W.E.L. Learning patterns of activity using real-time tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 747–757. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Wu, J.; Li, X.; Mo, R.; Zhang, M. A real-time tracking prediction for maneuvering target. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 3562–3566. [Google Scholar]
- Zhang, J.; Chen, T.; Shi, Z. A Real-Time Visual Tracking for Unmanned Aerial Vehicles with Dynamic Window. In Proceedings of the 2020 China Semiconductor Technology International Conference (CSTIC), Shanghai, China, 26 June–17 July 2020; pp. 1–3. [Google Scholar]
- Yan, X. Research and Design of Positioning Method of Small Unmanned Mobile Platform Based on UWB; Chang’an University: Xi’an, China, 2020. (In Chinese) [Google Scholar]
- Zhang, Q.; Gao, J.; Sun, H. The Unscented Kalman Filter Based Fusion Tracking Method with Multi-error Model. In Proceedings of the 2021 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 17–19 August 2021; pp. 1–5. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef] [Green Version]




| Symbol | Definition |
|---|---|
| F | State transition matrix |
| Input noise transition matrix | |
| H | Observation matrix |
| w, v | System noise and measurement noise vector |
| Q, R | System and measurement covariance matrix |
| T | Sample period |
| , , | The position, the velocity, and the acceleration of a moving vehicle |
| The position of sensor i | |
| , , | Distance, angle, and Doppler measurements of sensor i |
| , , | The jth observation variance of sensor i for distance, angle, Doppler |
| Markov probability transition matrix | |
| m | The number of different observation error models |
| N | The number of sensors |
| n | The dimension of the state vector |
| The prediction probability of the q th observation error model | |
| The mixing transition probability | |
| , | The prior state vector and covariance estimation |
| , | The prediction state vector and covariance estimation |
| , | A series of sigma points and corresponding weight |
| , | One-step prediction of the sigma points |
| Measurement (system output) vector | |
| , | State vector and covariance matrix for one filter update |
| K | Gain of Unscented Kalman Filter |
| , | The estimation with time-varying observation error of sensor i |
| tr | Trace of the matrix |
| diag | Diagonal of vector or matrix |
| Matrix inverse | |
| The fusion coefficient | |
| , | The estimated results of the sensors fusion |
| Parameter | Sensor A | Sensor B | Sensor C |
|---|---|---|---|
| Location | (1000 m, 1000 m) | (1200 m, 1300 m) | (1400 m, 1200 m) |
| Time-varying error model1 (distance, angle, Doppler noise) | |||
| Time-varying error model2 (distance, angle, Doppler noise) | |||
| Time-varying error model3 (distance, angle, Doppler noise) | |||
| Single-error model (distance, angle, Doppler noise) | |||
| Process noise | |||
| Model | Error Model1 | Error Model2 | Error Model3 |
|---|---|---|---|
| Parameter |
| Algorithm | Sensor A | Sensor B | Sensor C | Fusion |
|---|---|---|---|---|
| Traditional UKF method | 5.4794 | 5.1668 | 5.2910 | |
| MEF-UKF method | 4.3258 | 4..2050 | 4.2608 | |
| MI-TVOE method | 1.0331 | 0.8532 | 0.9146 | 0.6630 |
| Features | Parameter |
|---|---|
| Dimensions | 450 × 330 × 115 mm |
| Drive mode | Four-wheel independent drive |
| Rated load capacity | 20 kg |
| Maximum movement speed | 0.75 m/s |
| Maximum rotation speed | 215 °/s |
| Adapted terrain | Indoor and outdoor cement pavement with less pits |
| Feature | Parameter | Feature | Parameter |
|---|---|---|---|
| Input voltage | (4.5 V, 34 V) | Delay | <2 ms |
| Roll angle (static) | 0.2° | Roll angle (dynamic) | 0.3° |
| Sampling frequency | 10 kHz/ch (60 kS/s) | Speed accuracy | 0.05 m/s |
| Feature | Parameter |
|---|---|
| Size parameters | 6 cm × 5.3 cm |
| Quality | 12 g |
| Frequency Range | (3.5 GHz, 6.5 GHz) |
| Bit rate | Up to 6.8 Mbps |
| Sensor | X(m) | Y(m) |
|---|---|---|
| Sensor A | 14.1531 | 0.6864 |
| Sensor B | 1.7520 | 7.9625 |
| Sensor C | 0 | 0 |
| Algorithm | INS+KF | MI-TVOE Method |
|---|---|---|
| RMSE (m) | 0.0509 | 0.0314 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Zhang, Q.; Sun, H.; Wang, W. A Multi-Sensor Interacted Vehicle-Tracking Algorithm with Time-Varying Observation Error. Remote Sens. 2022, 14, 2176. https://doi.org/10.3390/rs14092176
Gao J, Zhang Q, Sun H, Wang W. A Multi-Sensor Interacted Vehicle-Tracking Algorithm with Time-Varying Observation Error. Remote Sensing. 2022; 14(9):2176. https://doi.org/10.3390/rs14092176
Chicago/Turabian StyleGao, Jingjie, Qian Zhang, Huachao Sun, and Wei Wang. 2022. "A Multi-Sensor Interacted Vehicle-Tracking Algorithm with Time-Varying Observation Error" Remote Sensing 14, no. 9: 2176. https://doi.org/10.3390/rs14092176
APA StyleGao, J., Zhang, Q., Sun, H., & Wang, W. (2022). A Multi-Sensor Interacted Vehicle-Tracking Algorithm with Time-Varying Observation Error. Remote Sensing, 14(9), 2176. https://doi.org/10.3390/rs14092176







