Calibration of Phased-Array High-Frequency Radar on an Anchored Floating Platform
Abstract
:1. Introduction
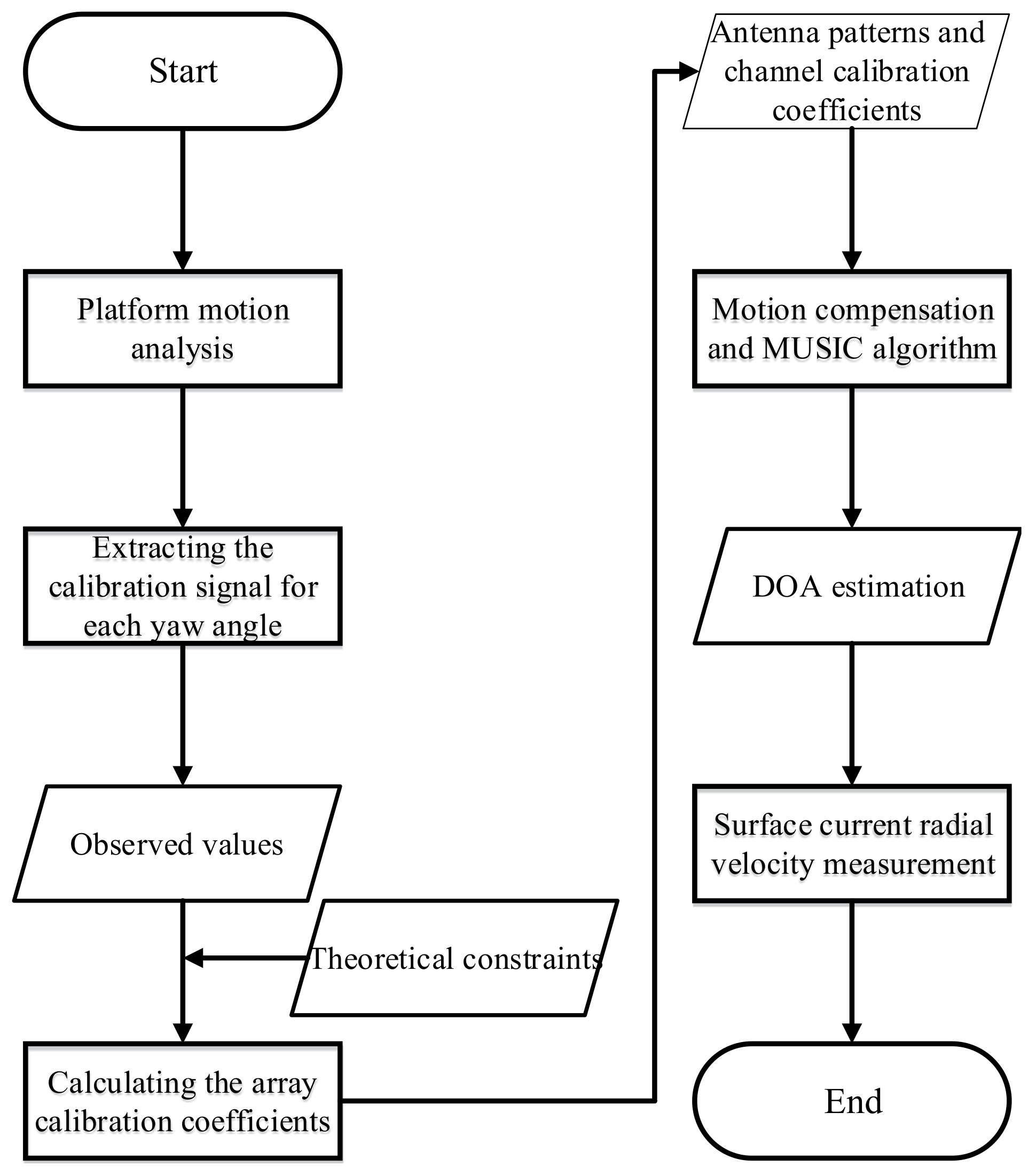
2. Materials and Methods
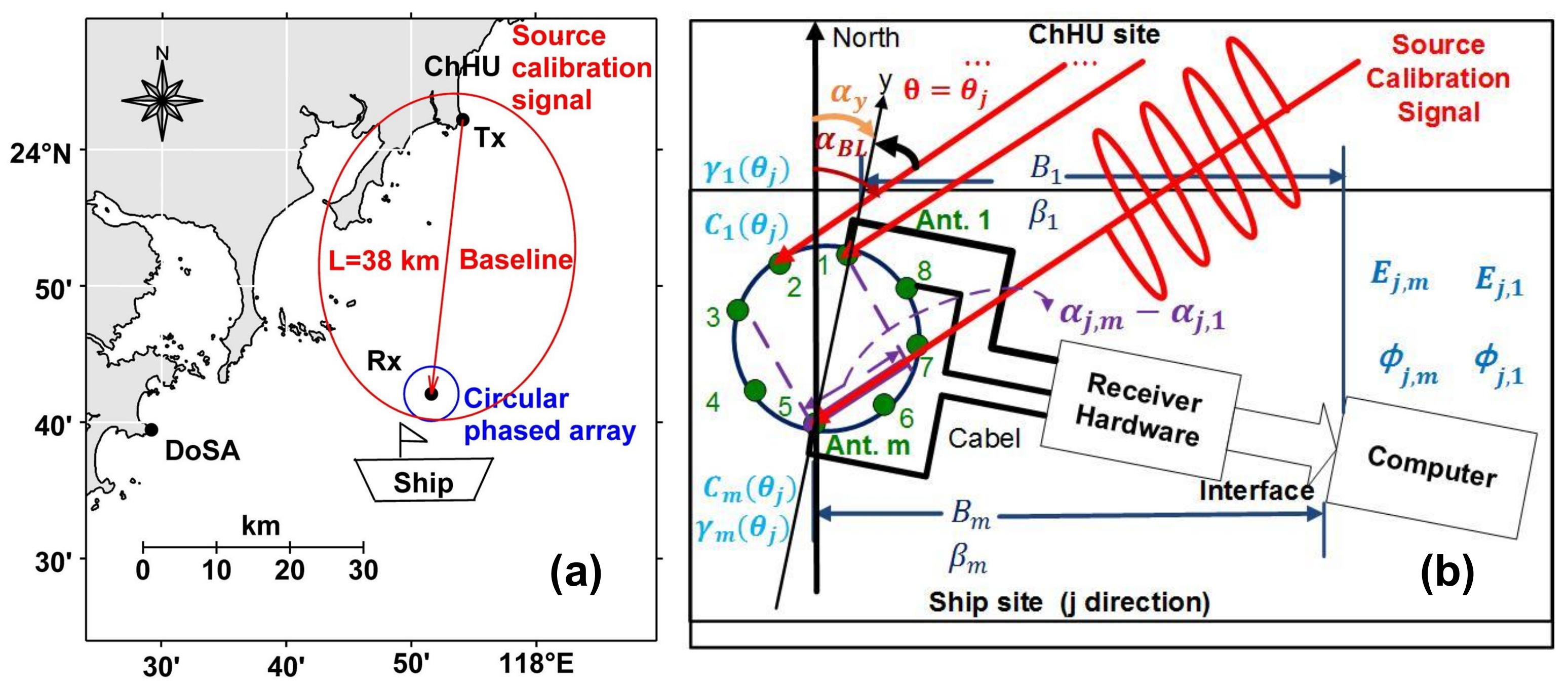
2.1. Introduction of the HF Radar Network
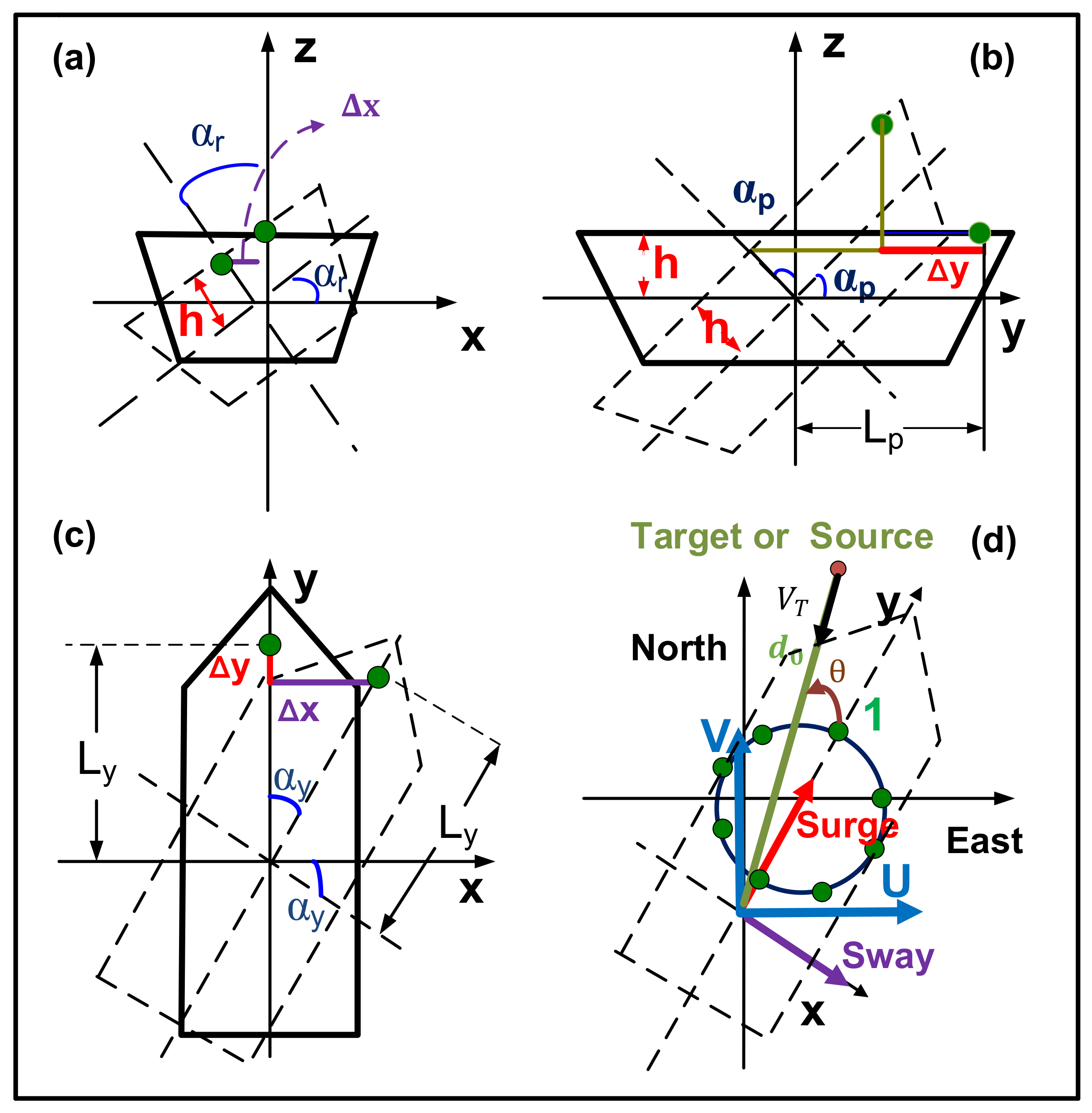
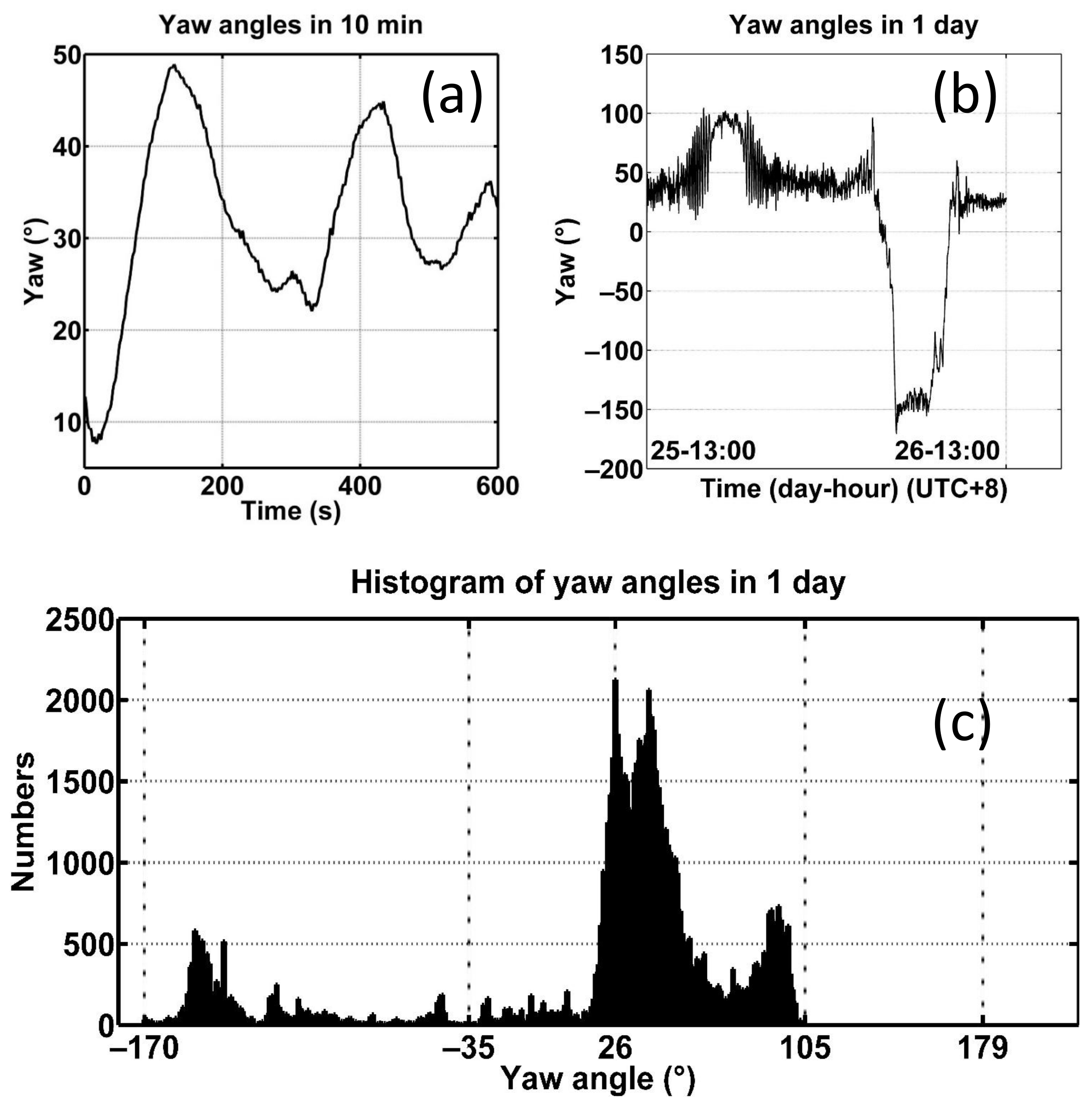
2.2. Platform Motion Analysis
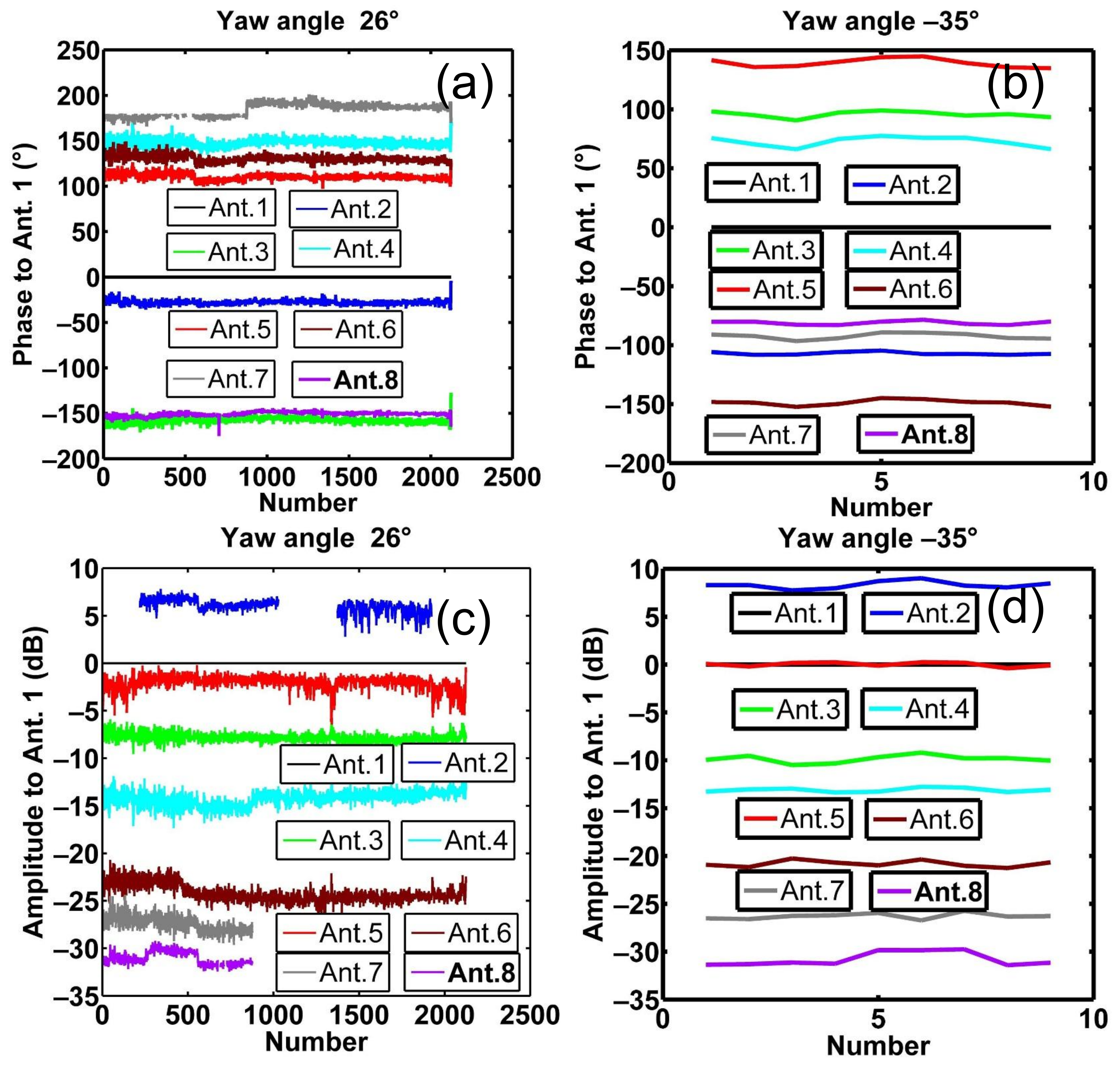
2.3. Extracting the Source Calibration Signal for Each Yaw Angle
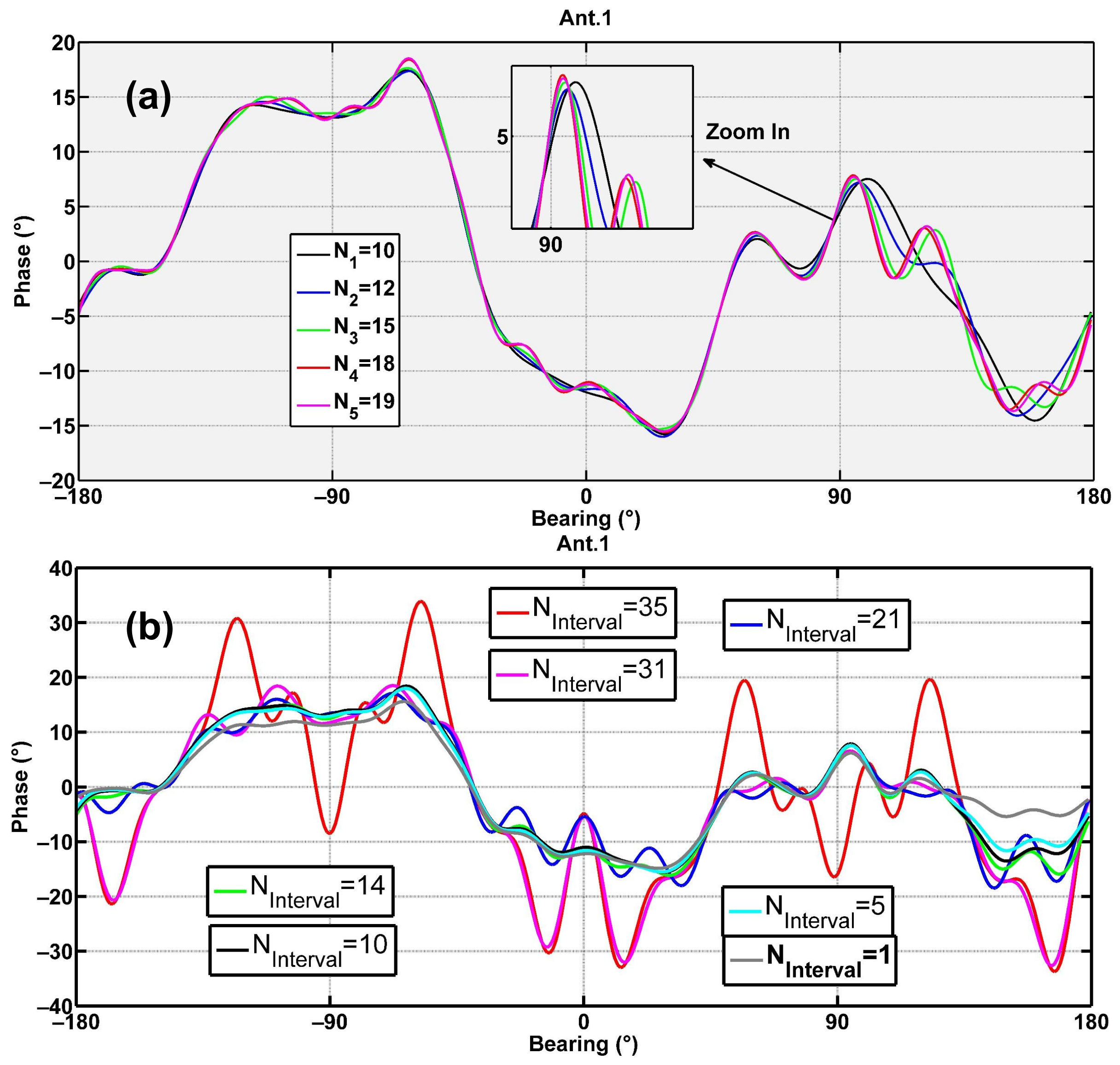
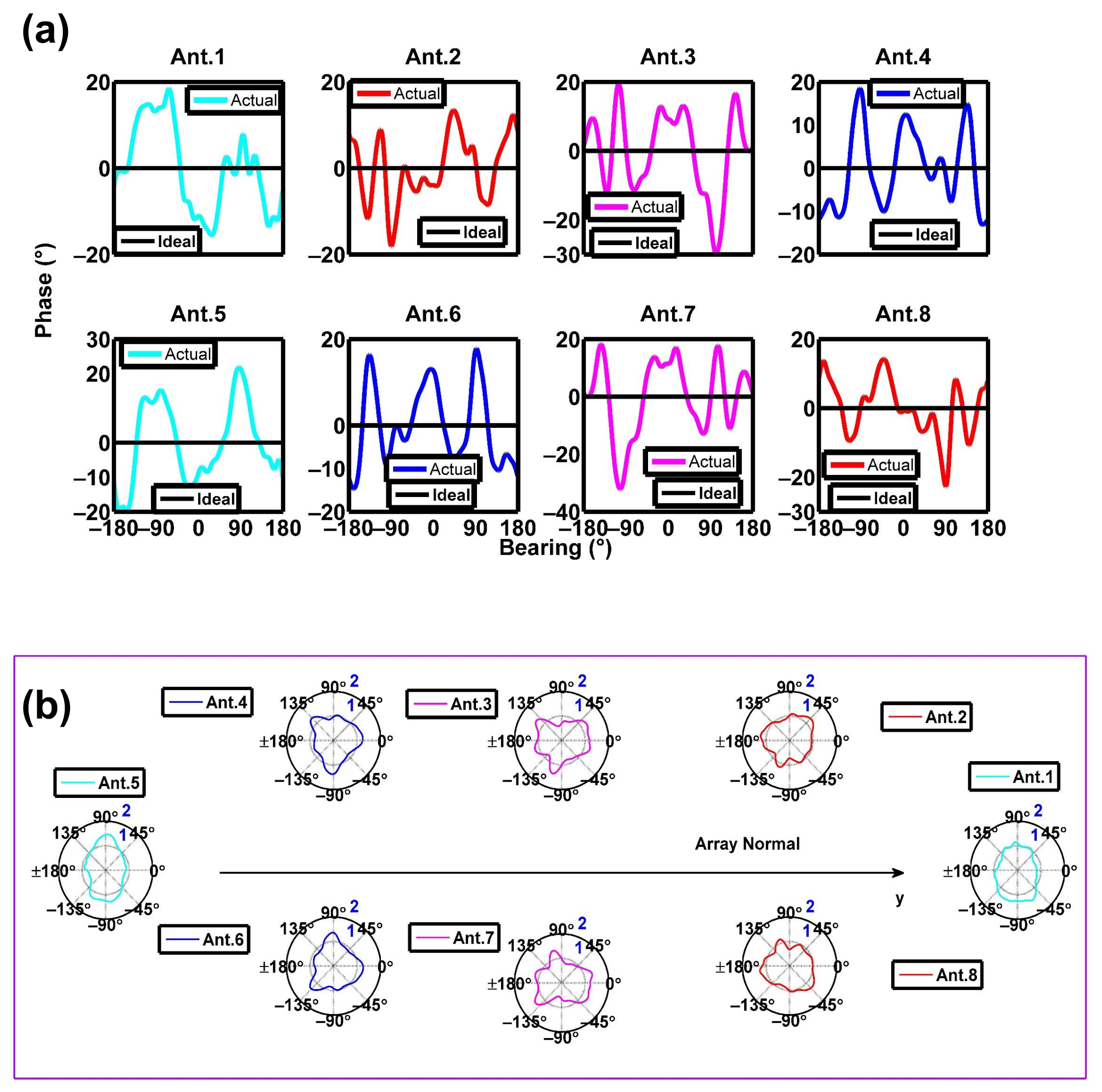
2.4. Calculating the Array Calibration Coefficients (Channel Calibration Coefficients and Calibrated Antenna Patterns)
3. Results
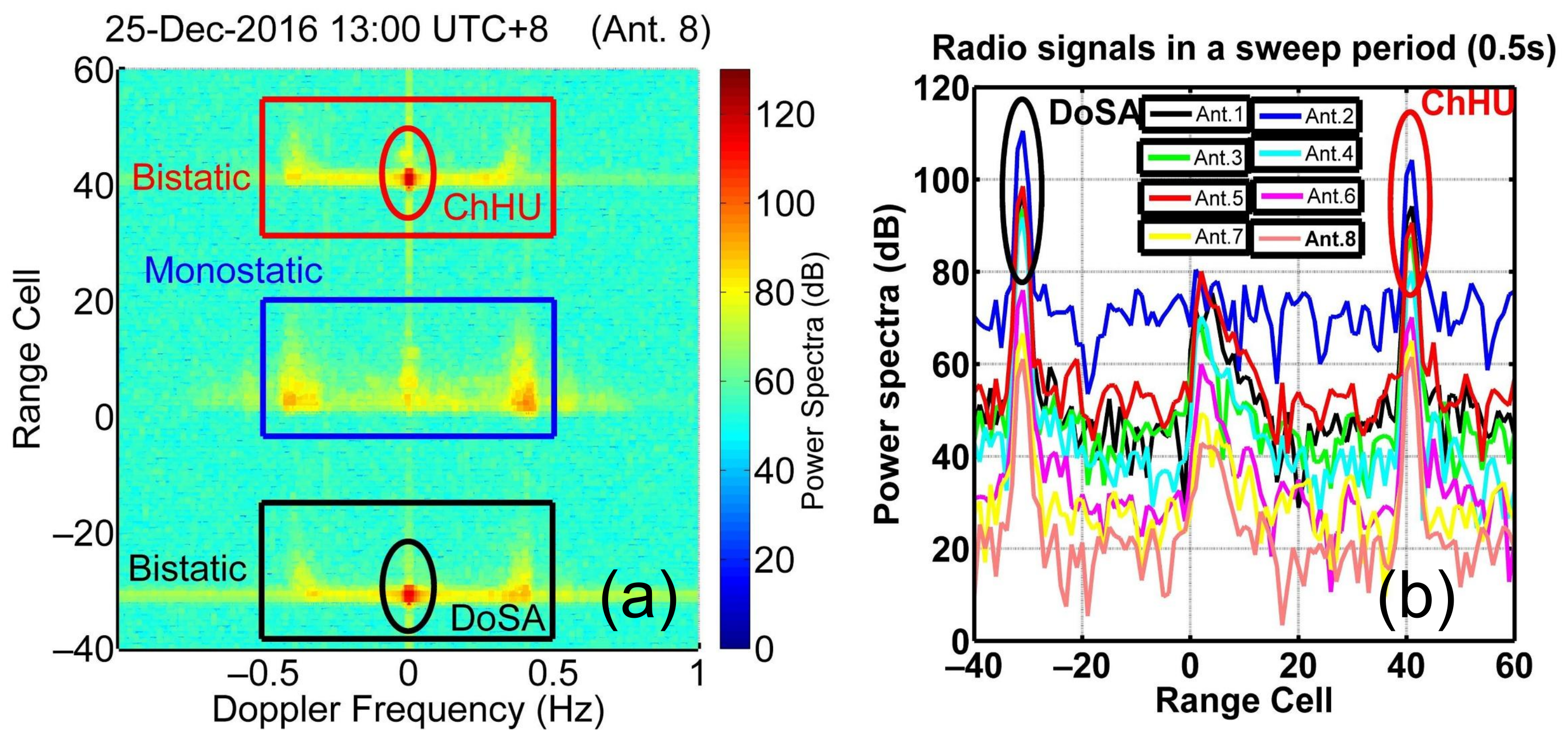
3.1. DOA
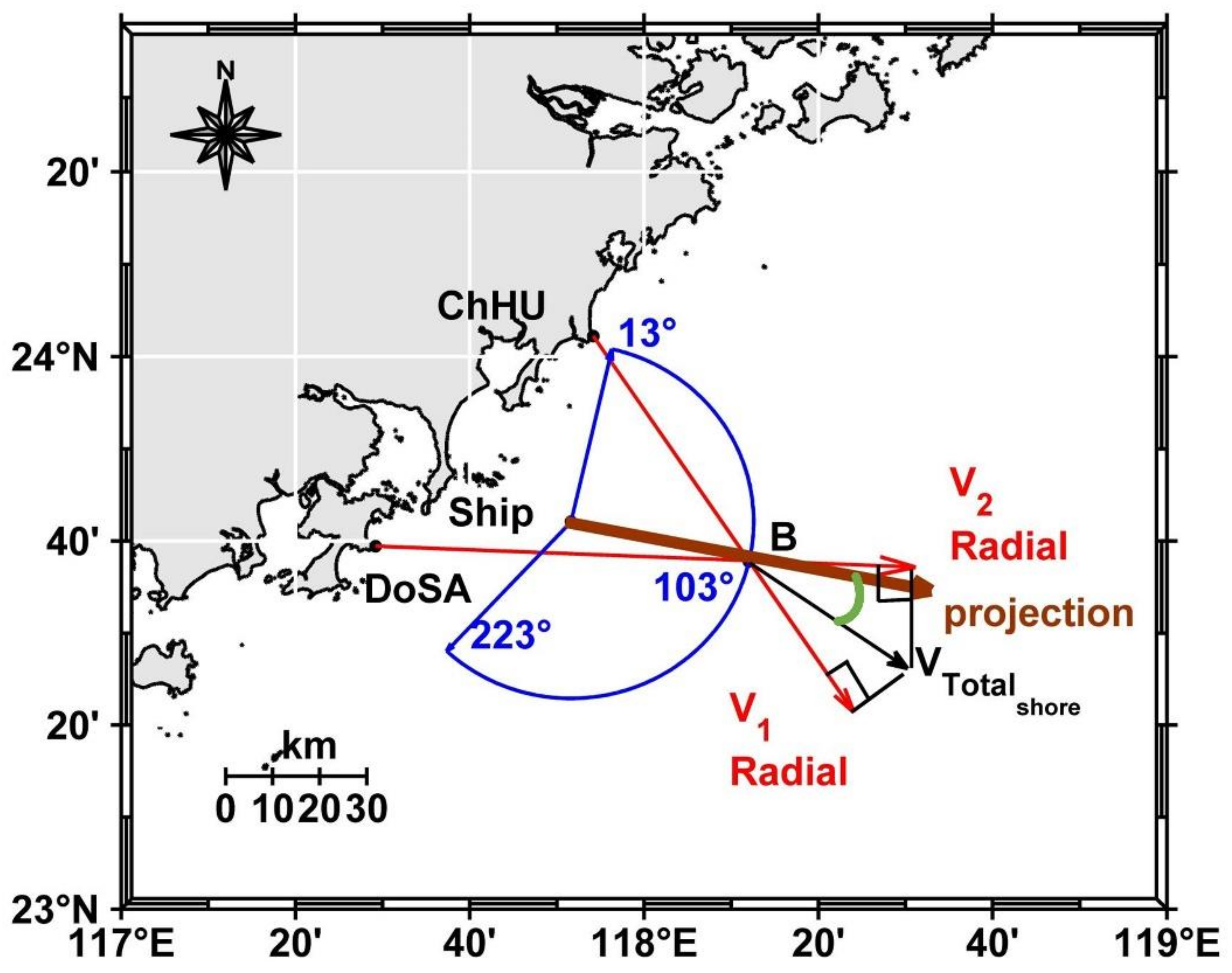
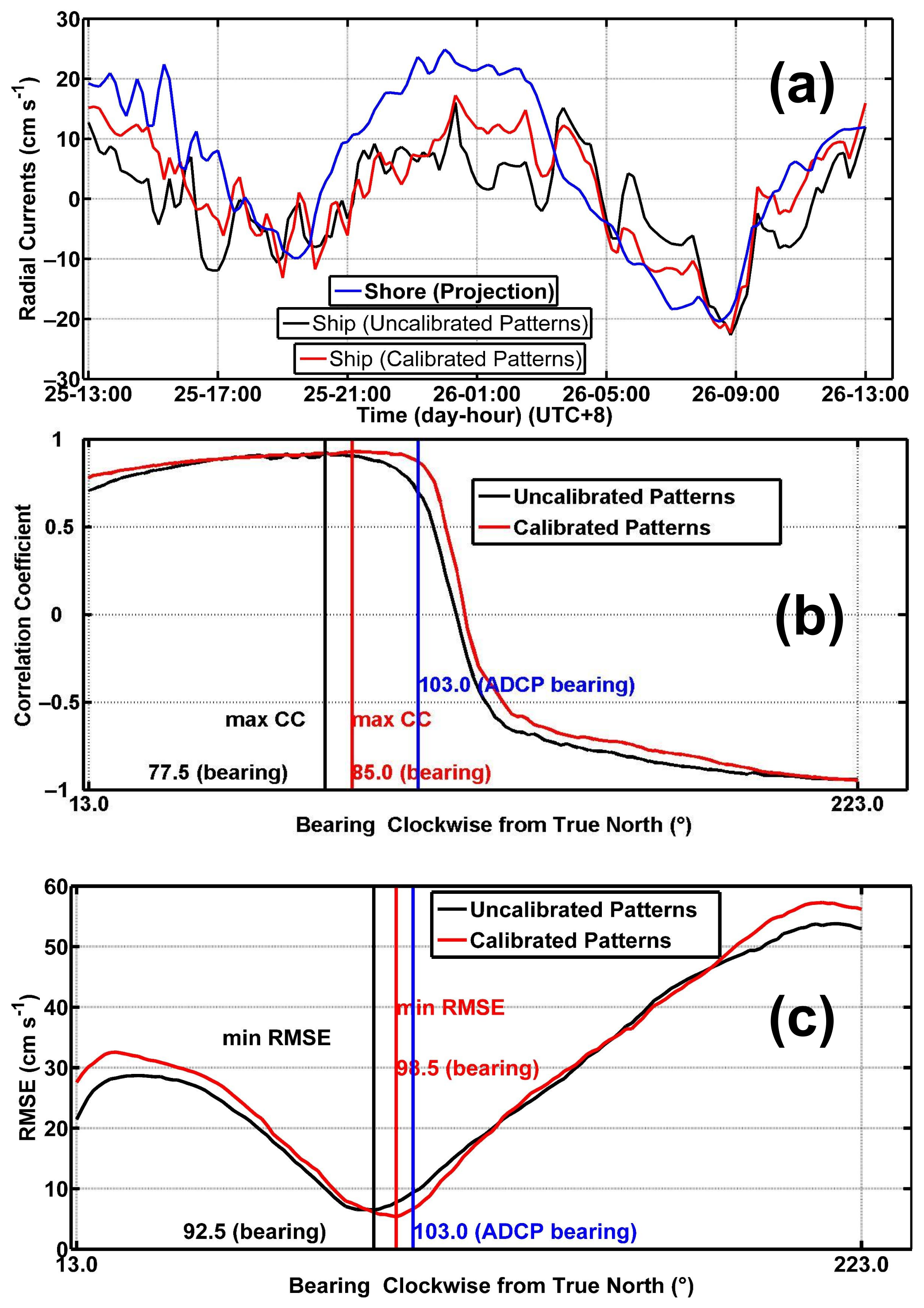
3.2. Radial Current and Bearing Offset
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Influence of Six-DOF Platform Motion

Appendix B. Analysis of the Least-Squares Solution
References
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Barrick, D.; Evans, M.; Weber, B. Ocean surface currents mapped by radar. In Proceedings of the 1978 IEEE First Working Conference on Current Measurement, Newark, DE, USA, 11–13 January 1978; Volume 1, pp. 59–65. [Google Scholar]
- Lipa, B.; Barrick, D. Least-squares methods for the extraction of surface currents from CODAR crossed-loop data: Application at ARSLOE. IEEE J. Ocean. Eng. 1983, 8, 226–253. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.E.; Diposaptono, S.; Isaacson, J.; Jena, B.K.; Nyden, B.; Rajesh, K.; Kumar, T.S. High Frequency (HF) Radar Detection of the Weak 2012 Indonesian Tsunamis. Remote Sens. 2012, 4, 2944–2956. [Google Scholar] [CrossRef] [Green Version]
- Lipa, B.; Isaacson, J.; Nyden, B.; Barrick, D.E. Tsunami Arrival Detection with High Frequency (HF) Radar. Remote Sens. 2012, 4, 1448–1461. [Google Scholar] [CrossRef] [Green Version]
- Guérin, C.A.; Grilli, S.T.; Moran, P.; Grilli, A.R.; Insua, T.L. Tsunami detection by high-frequency radar in British Columbia: Performance assessment of the time-correlation algorithm for synthetic and real events. Ocean Dyn. 2018, 68, 423–438. [Google Scholar] [CrossRef] [Green Version]
- Lipa, B.; Barrick, D.; Isaacson, J. Evaluating hf coastal radar site performance for tsunami warning. Remote Sens. 2019, 11, 2773. [Google Scholar] [CrossRef] [Green Version]
- Abascal, A.J.; Castanedo, S.; Fernandez, V.; Ferrer, M.I.; Medina, R. Oil spill trajectory forecasting and backtracking using surface currents from high-frequency (HF) radar technology. In Proceedings of the OCEANS 2011 IEEE—Spain, Santander, Spain, 6–9 June 2011; pp. 1–8. [Google Scholar]
- Bellomo, L.; Griffa, A.; Cosoli, S.; Falco, P.; Gerin, R.; Iermano, I.; Kalampokis, A.; Kokkini, Z.; Lana, A.; Magaldi, M.; et al. Toward an integrated HF radar network in the Mediterranean Sea to improve search and rescue and oil spill response: The TOSCA project experience. J. Oper. Oceanogr. 2015, 8, 95–107. [Google Scholar] [CrossRef]
- Abascal, A.J.; Sanchez, J.; Chiri, H.; Ferrer, M.I.; Cárdenas, M.; Gallego, A.; Castanedo, S.; Medina, R.; Alonso-Martirena, A.; Berx, B.; et al. Operational oil spill trajectory modelling using HF radar currents: A northwest European continental shelf case study. Mar. Pollut. Bull. 2017, 119, 336–350. [Google Scholar] [CrossRef]
- Choi, J.W.; Song, K.M.; Choi, J.Y. Accuracy improvement of particle tracking model using 2-D current measurement (HF-radar) data. J. Coast. Res. 2019, 91, 251–255. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Barrick, D.E.; Lipa, B.J. Evolution of bearing determination in HF current mapping radars. Oceanography 1997, 10, 72–75. [Google Scholar] [CrossRef] [Green Version]
- Laws, K.E.; Fernandez, D.M.; Paduan, J.D. Simulation-based evaluations of HF radar ocean current algorithms. IEEE J. Ocean. Eng. 2000, 25, 481–491. [Google Scholar] [CrossRef]
- Yang, S.; Ke, H.; Wu, X.; Tian, J.; Hou, J. HF radar ocean current algorithm based on MUSIC and the validation experiments. IEEE J. Ocean. Eng. 2005, 30, 601–618. [Google Scholar] [CrossRef]
- Emery, B.; Kirincich, A.; Washburn, L. Direction Finding and Likelihood Ratio Detection for Oceanographic HF Radars. J. Atmos. Ocean. Technol. 2022, 39, 223–235. [Google Scholar] [CrossRef]
- Barrick, D.; Lipa, B. Correcting for distorted antenna patterns in CODAR ocean surface measurements. IEEE J. Ocean. Eng. 1986, 11, 304–309. [Google Scholar] [CrossRef]
- Laws, K.; Paduan, J.D.; Vesecky, J. Estimation and assessment of errors related to antenna pattern distortion in CODAR SeaSonde high-frequency radar ocean current measurements. J. Atmos. Ocean. Technol. 2010, 27, 1029–1043. [Google Scholar] [CrossRef] [Green Version]
- Emery, B.; Washburn, L. Uncertainty estimates for SeaSonde HF radar ocean current observations. J. Atmos. Ocean. Technol. 2019, 36, 231–247. [Google Scholar] [CrossRef]
- Capodici, F.; Cosoli, S.; Ciraolo, G.; Nasello, C.; Maltese, A.; Poulain, P.; Drago, A.; Azzopardi, J.; Gauci, A. Validation of HF radar sea surface currents in the Malta-Sicily Channel. Remote Sens. Environ. 2019, 225, 65–76. [Google Scholar] [CrossRef]
- Xiongbin, W.; Feng, C.; Zijie, Y.; Hengyu, K. Broad Beam HFSWR Array Calibration Using Sea Echoes. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–3. [Google Scholar]
- Fernandez, D.M.; Vesecky, J.F.; Teague, C. Calibration of HF radar systems with ships of opportunity. In Proceedings of the IGARSS 2003: IEEE International Geoscience and Remote Sensing Symposium, International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volumes I–VII, pp. 4271–4273. [Google Scholar]
- Fernandez, D.; Vesecky, J.; Teague, C. Phase Corrections of Small-Loop HF Radar System Receive Arrays With Ships of Opportunity. IEEE J. Ocean. Eng. 2006, 31, 919–921. [Google Scholar] [CrossRef]
- Flores-Vidal, X.; Flament, P.; Durazo, R.; Chavanne, C.; Gurgel, K.W. High-frequency radars: Beamforming calibrations using ships as reflectors. J. Atmos. Ocean. Technol. 2013, 30, 638–648. [Google Scholar] [CrossRef]
- Emery, B.M.; Washburn, L.; Whelan, C.; Barrick, D.; Harlan, J. Measuring antenna patterns for ocean surface current HF radars with ships of opportunity. J. Atmos. Ocean. Technol. 2014, 31, 1564–1582. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, L.; Zhao, C.; Li, J. Calibration and Evaluation of a Circular Antenna Array for HF Radar Based on AIS Information. IEEE Geosci. Remote Sens. Lett. 2019, 17, 988–992. [Google Scholar] [CrossRef]
- Zhao, C.; Zong Chen, Z.; Li, J.; Ding, F.; Huang, W.; Gang Fan, L. Validation and Evaluation of a Ship Echo-Based Array Phase Manifold Calibration Method for HF Surface Wave Radar DOA Estimation and Current Measurement. Remote Sens. 2020, 12, 2761. [Google Scholar] [CrossRef]
- Sun, H.; Ji, Y.; Li, M.M.; Wang, Y.; Niu, J. Phase array amplitude and phase correction for HFSWR based on AIS information. In Proceedings of the IET International Radar Conference (IET IRC 2020), Online, 4–6 November 2021. [Google Scholar]
- Washburn, L.; Romero, E.; Johnson, C.; Emery, B.; Gotschalk, C. Measurement of Antenna Patterns for Oceanographic Radars Using Aerial Drones. J. Atmos. Ocean. Technol. 2017, 34, 971–981. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.; Isaacson, J.; Lilleboe, P. CODAR wave measurements from a North Sea semisubmersible. IEEE J. Ocean. Eng. 1990, 15, 119–125. [Google Scholar] [CrossRef]
- Peters, N.J.; Skop, R.A. Measurements of ocean surface currents from a moving ship using VHF radar. J. Atmos. Ocean. Technol. 1997, 14, 676–694. [Google Scholar] [CrossRef]
- Gurgel, K.W.; Essen, H.H. On the performance of a shipborne current mapping HF radar. IEEE J. Ocean. Eng. 2000, 25, 183–191. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, J.; Ji, Z.; Quan, T. Remote sensing of surface currents with single shipborne high-frequency surface wave radar. Ocean Dyn. 2016, 66, 27–39. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, J.; Wang, Y.; Yue, C.; Gong, W.; Liu, J.; Sun, H.; Yu, C.; Li, M. Coast–Ship Bistatic HF Surface Wave Radar: Simulation Analysis and Experimental Verification. Remote Sens. 2020, 12, 470. [Google Scholar] [CrossRef] [Green Version]
- Yao, G.; Xie, J.; Huang, W. First-order ocean surface cross-section for shipborne HFSWR incorporating a horizontal oscillation motion model. IET Radar Sonar Navig. 2018, 12, 973–978. [Google Scholar] [CrossRef]
- Yao, G.; Xie, J.; Huang, W. HF radar ocean surface cross section for the case of floating platform incorporating a six-DOF oscillation motion model. IEEE J. Ocean. Eng. 2020, 46, 156–171. [Google Scholar] [CrossRef]
- Yao, G.; Xie, J.; Huang, W. Ocean surface cross section for bistatic HF radar incorporating a six DOF oscillation motion model. Remote Sens. 2019, 11, 2738. [Google Scholar] [CrossRef] [Green Version]
- Barrick, D. Networking multiple HF radar systems with common coverage overlap. In Proceedings of the OCEANS’93, Victoria, BC, Canada, 18–21 October 1993. [Google Scholar]
- Roarty, H.; Glenn, S.; Kohut, J.; Gong, D.; Handel, E.; Rivera, E.; Garner, T.; Atkinson, L.; Brown, W.; Jakubiak, C.; et al. Operation and application of a regional high-frequency radar network in the Mid-Atlantic Bight. Mar. Technol. Soc. J. 2010, 44, 133–145. [Google Scholar] [CrossRef]
- Fujii, S.; Heron, M.L.; Kim, K.; Lai, J.W.; Lee, S.H.; Wu, X.; Wu, X.; Wyatt, L.R.; Yang, W.C. An overview of developments and applications of oceanographic radar networks in Asia and Oceania countries. Ocean Sci. J. 2013, 48, 69–97. [Google Scholar] [CrossRef]
- Whelan, C.; Hubbard, M. Benefits of multi-static on HF Radar networks. In Proceedings of the OCEANS 2015—MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; pp. 1–5. [Google Scholar]
- Harlan, J.; Terrill, E.; Hazard, L.; Otero, M.; Roarty, H. The integrated ocean observing system HF radar network. In Proceedings of the OCEANS 2015—MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Roarty, H.; Cook, T.; Hazard, L.; Harlan, J.; Cosoli, S.; Wyatt, L.; Alvarez Fanjul, E.; Terrill, E.; Otero, M.; Largier, J.; et al. The global high frequency radar network. Front. Mar. Sci. 2019, 6, 164. [Google Scholar] [CrossRef]
- Stewart, R.H.; Joy, J.W. HF radio measurements of surface currents. Deep. Sea Res. Oceanogr. Abstr. 1974, 21, 1039–1049. [Google Scholar] [CrossRef]
- Ha, E.C. Remote Sensing of Ocean Surface Current and Current Shear by HF Backscatter Radar. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 1979. [Google Scholar]
- Teague, C.; Vesecky, J.; Hallock, Z. A comparison of multifrequency HF radar and ADCP measurements of near-surface currents during COPE-3. IEEE J. Ocean. Eng. 2001, 26, 399–405. [Google Scholar] [CrossRef]
- Teague, C.; Vesecky, J.; Hallock, Z. Effective depth of HF current measurements: Observations from COPE-3. In Proceedings of the IGARSS IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; Volume 3, pp. 1134–1136. [Google Scholar]
- Wang, J.; Dizaji, R.; Ponsford, A. An analysis of phase array radar system on a moving platform. In Proceedings of the 2005 IEEE International Radar, Conference Record, Arlington, VA, USA, 9–12 May 2005; pp. 316–320. [Google Scholar]
- Chang, G.; Li, M.; Xie, J.; Zhang, L.; Yu, C.; Ji, Y. Ocean Surface Current Measurement Using Shipborne HF Radar: Model and Analysis. IEEE J. Ocean. Eng. 2016, 41, 970–981. [Google Scholar] [CrossRef]
- Strang, G. Linear Algebra and Its Application; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Barrick, D.; Lipa, B. Using antenna patterns to improve the quality of SeaSonde HF radar surface current maps. In Proceedings of the IEEE Sixth Working Conference on Current Measurement (Cat. No.99CH36331), San Diego, CA, USA, 13 March 1999; pp. 5–8. [Google Scholar]
- Emery, B.M.; Washburn, L.; Harlan, J.A. Evaluating Radial Current Measurements from CODAR High-Frequency Radars with Moored Current Meters. J. Atmos. Ocean. Technol. 2004, 21, 1259–1271. [Google Scholar] [CrossRef]
- Burke, G.J.; Pogio, A.J. Numerical Electromagnetics Code (NEC)-Method of Moments. A User-Oriented Computer Code for Analysis of the Electromagnetic Response of Antennas and Other Metal Structures. Part 1: Program Description-Theory. Part 2: Program Description-Code. Volume 1. Revised. STIN 1981, 81, 22263. [Google Scholar]
- Turetken, B.; Ustuner, F.; Demirel, E.; Dagdeviren, A. EMI/EMC analysis of shipboard HF antenna by moment method. In Proceedings of the 2006 International Conference on Mathematical Methods in Electromagnetic Theory, Kharkiv, Ukraine, 26–29 June 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 350–352. [Google Scholar]
- Shi, J.; Jin, Z.; Li, J.; Zuo, Y. Antenna Pattern Prediction for Ship-borne VHF Communication based on MOM/PO. In Proceedings of the 2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP), Auckland, New Zealand, 5–8 August 2018. [Google Scholar]
- Shi, X.; Xu, X.; Shi, Z.; Tang, Z. Measurements of the Cross-Loop Antenna Patterns in High-Frequency Surface Wave Radars. IEEE Geosci. Remote. Sens. Lett. 2015, 12, 1272–1276. [Google Scholar]
- Xie, J.; Yuan, Y.; Liu, Y. Experimental analysis of sea clutter in shipborne HFSWR. IEE Proc. Radar Sonar Navig. 2001, 148, 67–71. [Google Scholar] [CrossRef]
- Xie, J.; Sun, M.; Ji, Z. First-order ocean surface cross-section for shipborne HFSWR. Electron. Lett. 2013, 49, 1025–1026. [Google Scholar] [CrossRef]
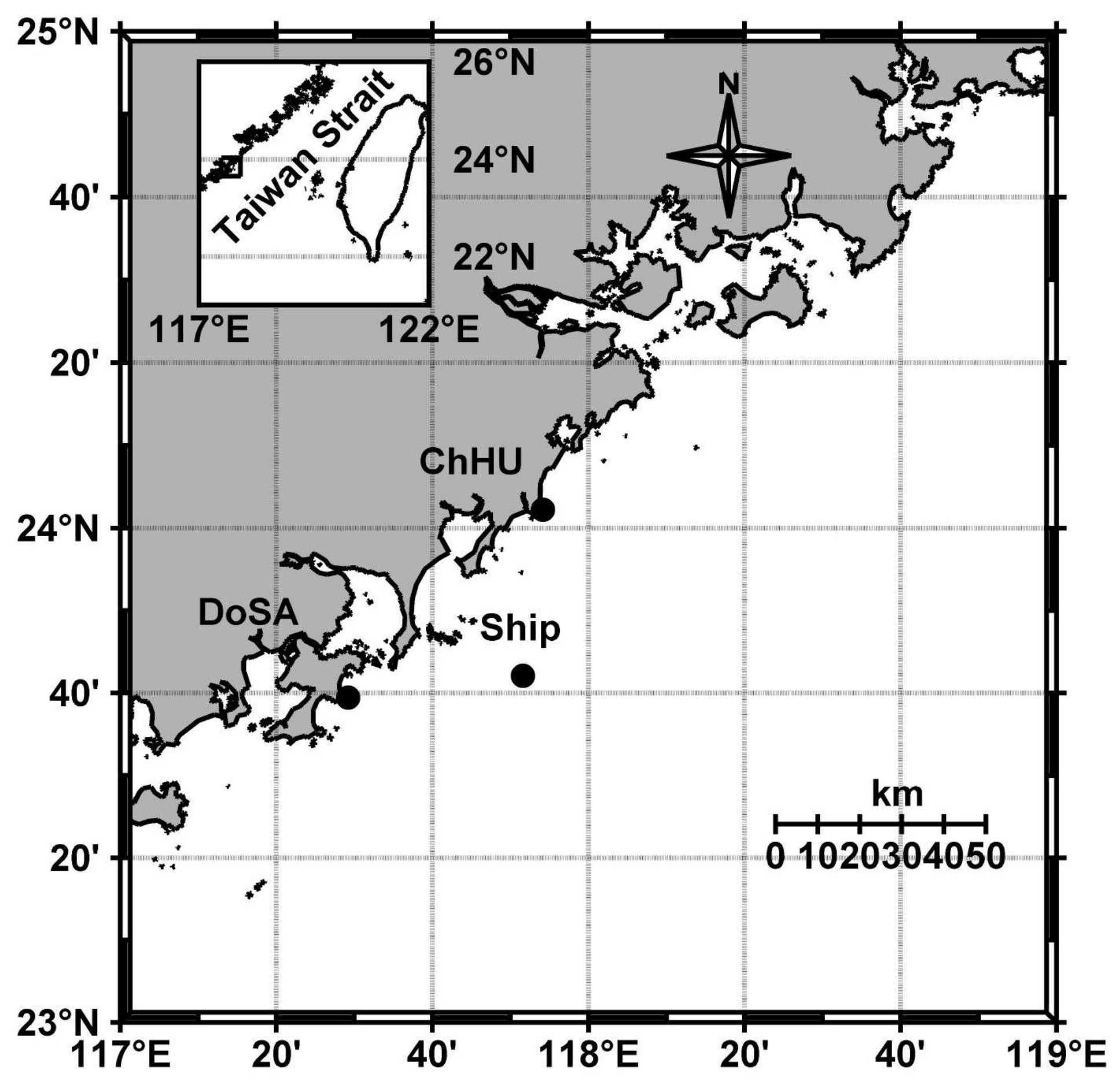



| Radar Site | Site 1 | Site 2 | Site 3 |
|---|---|---|---|
| Site Code | Ship | DoSA | ChHU |
| Latitude | 23°42′9″N | 23°39′25″N | 24°2′13″N |
| Longitude | 117°51′37″E | 117°29′2″E | 117°54′9″E |
| Operation Frequency | 13.15 MHz | ||
| Transmitted Wave Length | 22.8 m | ||
| Measurement Depth | 0.5∼0.9 m @ 13.15 MHz | ||
| Waveform | FMICW | ||
| Sweep Period | 0.5 s | ||
| Range Resolution | 5 km | ||
| Number of Transmitter Antenna Elements | 1 | ||
| Number of Receiver Antenna Elements (Phased-Array) | 8 | ||
| Technique for Azimuthal Resolution | Direction-finding | ||
| Doppler Coherent Integration Time (CIT) | 5 min or 10 min |
| DoSA DOA () | Mean (°) | Std. (°) | Max. (°) | Min. (°) | Med. (°) |
|---|---|---|---|---|---|
| Calibrated Channels and Uncalibrated Patterns | −95.0 | 6.3 | −83.6 | −113.9 | −94.1 |
| Calibrated Channels and Calibrated Patterns | −95.1 | 2.8 | −88.1 | −102.5 | −95.5 |
| Actual DoSA bearing () | −97.3 | ||||
| 725 Vessel-Target DOAs vs. True Directions | RMSE (°) | MAE (°) |
|---|---|---|
| Uncalibrated Channel and Uncalibrated Patterns | 56.5 | 43.2 |
| Calibrated Channels and Uncalibrated Patterns | 13.0 | 9.9 |
| Calibrated Channels and Calibrated Patterns | 7.9 | 5.1 |
| Ship () | Shore () | Shore (Bearing Offset) | ||
|---|---|---|---|---|
| RMSE (cm s−1) | CC | (°) | (°) | |
| Calibrated Channels and Uncalibrated Patterns | 9.40 | 0.69 | 10.5 | 25.5 |
| Calibrated Channels and Calibrated Patterns | 6.65 | 0.87 | 4.5 | 18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, B.; Wu, X.; Yue, X.; Zhang, L.; Wang, L. Calibration of Phased-Array High-Frequency Radar on an Anchored Floating Platform. Remote Sens. 2022, 14, 2174. https://doi.org/10.3390/rs14092174
Wan B, Wu X, Yue X, Zhang L, Wang L. Calibration of Phased-Array High-Frequency Radar on an Anchored Floating Platform. Remote Sensing. 2022; 14(9):2174. https://doi.org/10.3390/rs14092174
Chicago/Turabian StyleWan, Bin, Xiongbin Wu, Xianchang Yue, Lan Zhang, and Li Wang. 2022. "Calibration of Phased-Array High-Frequency Radar on an Anchored Floating Platform" Remote Sensing 14, no. 9: 2174. https://doi.org/10.3390/rs14092174
APA StyleWan, B., Wu, X., Yue, X., Zhang, L., & Wang, L. (2022). Calibration of Phased-Array High-Frequency Radar on an Anchored Floating Platform. Remote Sensing, 14(9), 2174. https://doi.org/10.3390/rs14092174








