Abstract
The spatial and temporal distribution of dust devils (DDs) in the two pre-selected landing regions (ZA and ZB) of the Tianwen-1 mission in southern Utopia Planitia have been investigated by using images from the Context Camera (CTX) of the Mars Reconnaissance Orbiter (MRO). From the images of the regions in 8 Martian years, no DD was found in ZA, while 77 DDs were found in ZB. The observed DDs are mainly distributed in the northeastern part of ZB. The temporal variation in the observed DDs shows a prominent two-peak pattern in their local early spring and late summer. The size and height of the observed DDs have also been evaluated from the images, and they show a similar temporal variation as the occurrence. To investigate the possible conditions pertinent to these observed patterns of DD distribution, some analysis based on the thermodynamic theory of heat engines was performed using the output of the Mars climate model, MarsWRF. The spatial and temporal distribution of the simulated DDs are generally consistent with the observation, with significantly more DDs in ZB. Analysis of the model results suggests that the spatial distributions of the predicted DDs are mainly related to the distribution of sensible heat flux, which, in turn, is mainly determined by the surface-to-air temperature difference. The difference in DDs between ZA and ZB (more DDs in ZB) is dominated by the difference in sensible heat flux, which, in turn, is mainly related to the spatial variation of surface albedo.
1. Introduction
Dust devils (DDs) are thermally driven columnar vortices and the smallest-scale dust-lifting events on Mars. Surface dust can be lifted into the atmosphere due to the strong surface wind and the suction effect of the low-pressure vortex core of a DD []. The dust-lifting process of DDs has been parameterized in many Mars climate models. Model results and observations suggest that DDs may make a significant contribution to the dust loading in the Martian atmosphere and so the observed annual dust cycle [,,,,], which, in turn, will affect the thermal structure and atmospheric circulation of Mars.
DDs were first identified on Mars by the Viking Orbiter [] and were first measured by the Viking Lander [], and subsequently observed by other missions, such as Mars Global Surveyor (MGS)/Mars Orbiter Camera (MOC) [,], Mars Express (MEX)/High-Resolution Stereo Camera (HRSC) [], Mars Reconnaissance Orbiter (MRO)/Context Camera (CTX) and High-Resolution Imaging Science Experiment (HiRISE) [,,]. In general, the appearance of DDs can be different in different types of images. From a rover (e.g., Opportunity, Curiosity), DDs always show a narrow base and a broader top. From orbiters, a typical active dust devil (ADD) is basically composed of a small bright cloud and a long tapered shadow []. Part of the vortex will leave light- or dark-surface tracks, ranging from 10 to 200 m in width and many tens to thousands of meters in length [,].
Dust devils can be observed at almost all latitudes and in all seasons, but always peak in their local spring and summer, when the solar radiation is relatively strong [,,,,]. In general, there are more DDs in the southern hemisphere [,]. One reasonable explanation is that the southern hemisphere receives more solar radiation in the local summer due to the orbital eccentricity. Haberle et al. [] and Stanzel et al. [] suggest that the ascending branch of Hadley circulation in southern summer is stronger than that in the northern summer and so leading to more DDs in the southern hemisphere. Whelley and Greeley [] suggest that fewer DDs in the northern hemisphere are owing to the lower thermal inertia of the surface. They infer that the lower-thermal-inertia regions in the northern hemisphere are generally dusty, so dust devil tracks (DDTs) in the northern hemisphere are not easy to observe. On the other hand, some regions have been considered to be particularly active in DDs, e.g., the Amazonis Planitia [,,], Casius [], Argyre Planitia [,] and the Hellas Basin [,]. Whelley and Greeley [] mapped the global distribution of DDs with the MOC images and found that most dust lifting by DDs is from the region near 60°N and 60°S in their corresponding spring and summer.
The relationship between DDs and their environments has been investigated in some previous studies. Balme [] compared the surface altitude and albedo with the distribution of DDs in the Aryer Planitia and the Hellas Basin, and suggests that the abundance of DDTs has no obvious relationship with altitude but is proportional to the albedo. Fisher et al. [] plotted the global map of surface temperature and boundary layer depth with TES data, but it cannot explain the especially active DDs in the Amazonis Planitia and they think mesoscale circulation may play a certain role. Similar to Balme [], Whelley and Greeley [] analyzed the environment pertinent to the occurrence of global DDTs and found that the elevation, slope, dust cover, or surface physical properties have little effect on the formation of DDTs. Based on the spatial distribution of DDs observed by the HRSC of MEX, Fenton and Lorenz [] measured and calculated the heights of active dust devils (ADDs) in 127 images (spanning about 3.6 Martian years (MY)), from the CTX of MRO in the northern Amazonis Planitia, and compared them with the heights of the planetary boundary layer (PBL) from observations (MEX and MGS) and the Mars Climate Database (MCD). They found that the PBL height is approximately 5-times the median height of ADDs. Newman et al. [] compared the pressure drop from the Rover Environmental Monitoring Station (REMS) on the Mars Science Laboratory (MSL) with the output from the general circulation model MarsWRF. They found that there is a good match between the predicted and observed DDs in the Gale crater, and the occurrence of DDs is basically proportional to the altitude of the topography (mainly attributed to the increased sensible heat flux as it climbs up the slope of Aeolis Mons).
Zhurong is the first Mars rover from China and is a major part of the Tianwen-1 mission. The candidate landing site, Utopia Planitia, is the largest recognized impact basin on Mars, where the Viking 2 lander landed in 1976. A good understanding of the characteristics of DDs in the landing region is important to the rover mission. However, the characteristics of DDs in the southern Utopia Planitia were generally not investigated in most previous studies. Wang et al. [] found 248 newly formed DDTs from 12 image pairs in the southern Utopia Planitia. Their main objective was to estimate the formation rate of DDs and the solar panel clearing recurrence interval in order to choose a suitable landing site for the Tianwen-1 mission. However, the environmental conditions for the occurrence of DDs in the southern Utopia Planitia were not analyzed in their study.
In this study, our basic objective was to investigate the characteristics of DDs in the landing region of the Tianwen-1 mission, and the environmental conditions pertinent to their occurrence. Our investigation focused on two particular regions with similar areas in southern Utopia, which are the two regions pre-selected for the landing of Zhurong (one region was finally chosen). Characteristics of DDs from CTX images in 8 MYs were investigated (Section 2). To investigate the environmental conditions pertinent to the occurrence of DDs in the target regions, DD activities simulated in the Mars climate model MarsWRF (Section 3) were analyzed. The main findings of this study will be summarized in Section 4, where the performance of the numerical model in simulating DD activities will also be discussed.
2. Observation of Dust Devils in the Target Landing Sites
2.1. Occurrence of Dust Devils
The main job of the CTX camera is to help provide the wider context for the high-resolution observations of HiRISE and CRISM (Compact Reconnaissance Imaging Spectrometer for Mars) at the MRO. Images from CTX are used in this study because of the relatively large spatial coverage (a typical image can be as wide as 30 km and as long as 160 km or more), long orbital time (from 2006 to now), and a pretty good resolution (~6 m/pixel). However, due to the limitation of the orbit, all images were taken at a local time (LT) around 15:00.
Before the landing of Zhurong, two target landing locations in southern Utopia Planitia were selected (private communication with the Chinese Academy of Space Technology), namely location A (center latitude: 25° N, longitude: 110° E), and location B (center latitude: 26.67° N, longitude: 131.67° E). Their locations are shown in Figure 1 (red stars). With locations A and B as the centers, the red boxes are set as our study regions (span ~10° in the latitude and longitude, Figure 1), and named as zone A (ZA, latitudes: 20–30° N, longitudes: 105–115° E) and zone B (ZB, latitudes: 21–32° N, longitudes: 126–137° E).
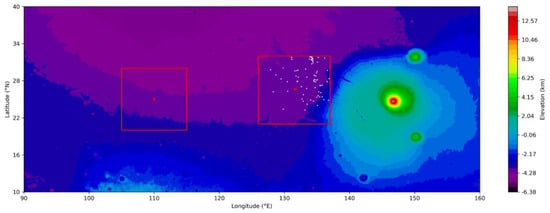
Figure 1.
Topography (shading) of regions ZA and ZB and the spatial distribution of ADDs (white dots) from CTX observations. Data of topography obtained from https://astrogeolo−gy.usgs.gov/search/map/Mars/Topography/HRSC_MOLA_Blend/Mars_HRSC_MOLA_BlendDE−M_Global_200mp_v2 (accessed on 20 July 2021).
From all available CTX images, a total of 258 images in ZA and 266 images in ZB can be obtained, which were then used to identify DDs from September 2006 to February 2021 (spanning ~8 MYs). As shown in Table 1, no ADD was found in the 258 images of ZA. On the other hand, 77 ADDs were found in ZB, and are mainly distributed in the northeast part of ZB (white dots in Figure 1). This result is interesting because, by intuition, ZA and ZB should have a similar number of DDs, since they are at similar latitudes and so receive a similar amount of downward solar radiation. In addition, the altitudes of ZA and ZB are similar (~4.28 km). In the light of some previous literature, it is speculated that different atmospheric conditions, topography, or surface properties of these two areas may explain the different distribution of ADDs. The terrain of ZA is relatively flat, and there are no large terrain undulations around it. In contrast, ZB is located at the northwestern foot of the Elysium Mons, and the terrain is more complex, and the surface roughness and slope in the southeast of ZB are higher. It is interesting to note that the geographical situation of ZB is similar to that of the Amazonis Planitia. Both regions have a mountain in their east. As mentioned before, Amazonis Planitia is the region particularly active in DD occurrence.

Table 1.
List of CTX images with ADDs in ZB including Martian Year (MY), solar longitude (Ls), incidence angle (INA), and the number of ADDs (NADDs). Images obtained from the website https://ode.rsl.wustl.edu/mars/indexproductsearch.aspx (accessed on 10 July 2021).
2.2. Dimension of Dust Devils
In addition to the occurrence of DDs, we also surveyed their sizes. Observed ADDs by orbiters are usually tens of meters to hundreds of meters in diameter, and hundreds of meters to thousands of meters in height, with a narrow base and broader top. A typical ADD is usually composed of a small bright cloud with long tapered shadows []. Although some small terrains may also show this feature, it can be ruled out by the images in the same location at a different time.
The CTX images are stretched by the ESRI ArcGIS software in ArcMap to increase the contrast, so that the ADDs can be easier to identify manually. To measure the diameters and shadow lengths of the ADDs, a simple cylindrical coordinate system of Mars is applied to all images imported into the ArcMap. Their measurement is not straightforward because of their variations in morphology during movement. At the base of the ADD, there is always a “dust skirt” that is usually larger than the vortex itself and so may overestimate the diameter of an ADD [,]. In addition, sometimes it is difficult to determine the edge of the shadow because of the variations in solar incidence angle. Besides, the DDs tend to lean in the direction of the ambient wind, which will affect the accurate measurement of diameter and shadow length.
Because of these uncertainties, a uniform standard is set for the measurements to minimize the subsequent analysis error (averaged error of ~20% in diameter, and ~11% in the height of ADDs). That is, the standard should be to draw a circle on the brightest part of the dust cloud and try to include the area where the brightest pixels are densely gathered. The diameter of the circle is then considered to be the diameter of the ADD. The distance from the center of the circle to the edge of the shadow line is then considered as the length of the shadow (see the example in Figure 2a,b). If the dust cloud is in a cone shape (probably due to the inclination of ADD by ambient wind []), the intersection of the shadow and the bright dust cloud is considered as the starting point for shadow measurement (see the example in Figure 2c,d). The height of an ADD is calculated by dividing the shadow length by the tangent of the local solar incidence angle.
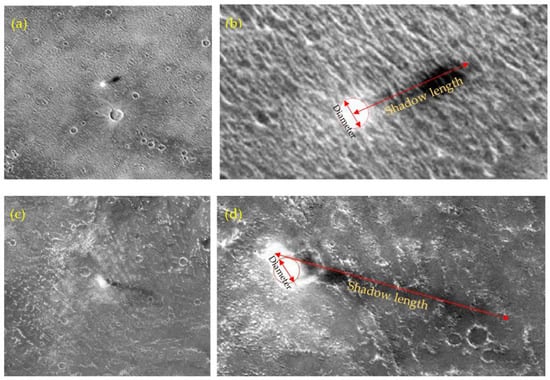
Figure 2.
Examples of measuring the diameter and shadow length of ADDs. (a,b) are from CTX image p15_006934_2076_xn_27n224w (Table 1). (c,d) are from CTX image p19_008503_2058_xn_25n227w.
2.3. Seasonal Variations in the Observed DDs
As can be seen from Figure 3 (left), the number of ADDs shows a prominent two-peak pattern in the temporal variation, with peaks in the local early spring (Ls: 0–30°) and late summer (Ls: 150–180°). This two-peak pattern of ADDs occurrence has also been found in other regions in some previous studies, such as the Argyre Planitia [], and the Amazonis Planitia []. Combining with the results from the previous research of [], based on dust devil tracks (DDTs) in the same study area (Figure 3, right), it can be seen that the sum of ADDs and DDTs still show a two-peak pattern, as before. However, the first peak came a little bit late.
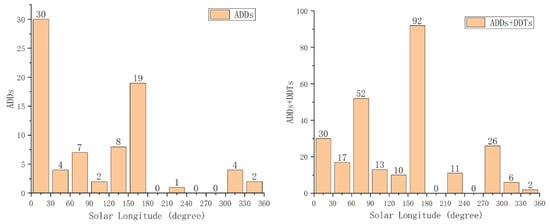
Figure 3.
Time series of the number of ADDs from CTX images in the study area (left), and the sum of ADDs and DDTs (Adapted from Ref. []) in the same area (right).
The median and mean values of the measured dimension of ADDs (Figure 4) show a similar pattern of seasonal variation as the ADDs number (Figure 3). During the two-peak periods, the sizes of ADDs reach their maximum when the number of occurrences reaches their maximum. In the second half of the year, it is clear that the size of ADDs is suppressed.
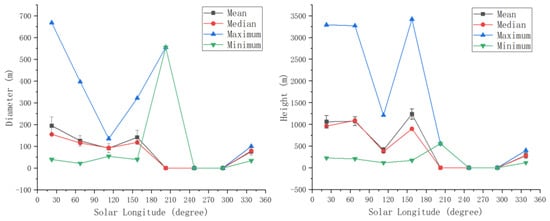
Figure 4.
Time series of diameter (left) and height (right) of ADDs from CTX images in the study area.
3. Numerical Simulations
From the observational results discussed above, some questions are worth exploring. For instance, why are DDs greater in ZB compared with ZA? Why are there two peaks for the occurrence of DDs in the temporal distribution? What are the possible factors that determine the spatial distribution of DDs in ZA and ZB (e.g., ADDs are mainly in the northeastern part of ZB)? To explore these questions, we conducted some analysis in ZA and ZB based on numerical simulations with the Mars climate model MarsWRF. The approach is basically similar to that in Newman et al. [] but the analyzed area is much larger compared with the Gale crater in Newman et al. [].
3.1. Numerical Model MarsWRF
MarsWRF is a Martian atmospheric model, which can perform multi-scale climate simulations of Mars [,]. MarsWRF includes most of the physical processes for simulating the Martian climate, such as the Carbon Dioxide cycle []. Short-wave and long-wave radiation is evaluated by the Wide Band Model (WBM), as described in Richardson et al. [] and Toigo et al. []. For dust radiative forcing, the so-called interactive approach is implemented in the simulations. In this approach, dust lifting is dependent on the atmospheric conditions (e.g., surface wind stress), while the suspending dust particles may change the atmospheric radiation and so the atmospheric conditions. The configuration in the MarsWRF is basically similar to that used in our previous studies (e.g., [,]), and it has been shown in these studies that the interactive dust approach could reasonably reproduce the observed dust climate on Mars.
Two simulations with different horizontal resolutions were performed in this study. The relatively low-resolution simulation (global domain, resolution: 3°) was used to study the seasonal variations in a Martian year. Another simulation has a higher resolution, which is used to study the spatial variations in the predicted DDs. In this simulation, a nested domain is used. The inner domain (Domain 2) has a resolution of about 1.67° (about 100 km in the equatorial region), which covers the two study regions, ZA and ZB, while the parent global domain has a resolution of about 5° (about 300 km). Because of the expensive computing cost, nested simulations were not performed for a whole Martian year but for a particular period (high season of DDs).
There are two parameterization schemes of dust-lifting processes in MarsWRF, one for DDs and the other for wind stress lifting []. Wind stress lifting occurs in cases when stress is greater than the threshold (0.043). See Richardson et al. [] and Xiao et al. [] for more details.
For DDs, most previous studies (e.g., [,]) interpreted them as convective vortices and the convective heat engine theory [], which is usually used to describe or parameterize the DD process. In this theory, the strength of DDs (and so the associated dust-lifting flux) is proportional to the sensible heat flux and the thermal efficiency, as follows:
where the strength is the dust-lifting flux by dust devils (DLIF), is thermal efficiency, given as Equation (2), and is sensible heat flux, given as Equation (4).
In the above, is the temperature at the top of the planetary boundary layer (PBL), is the surface temperature. The PBL top is defined by the PBL depth. There are certain conditions for DDs to occur in the model (Fs > 0, Tsurf − Tair > 27 K, Tsurf > 270 K), generally referred to as the condition of atmospheric instability near the surface.
The sensible heat flux is calculated by the bulk formula:
where is the exchange coefficient, depending on the stability of the near-surface atmosphere, is the near-surface air density, is drag velocity, is surface temperature, and is the near-surface air temperature (above the surface about 1.5 m).
3.2. Seasonal Variations in Predicted DDs
The predicted DDs from MarsWRF are reflected by DLIF. The time series of DLIF in ZB (Figure 5) shows that the temporal pattern of predicted DDs is generally consistent with observations. Obviously, the DLIF in ZB is higher than that in ZA in the first half of the year. In addition, in both ZA and ZB, there are two peaks of DLIF during their local early spring and late summer, which are in good agreement with the observations. After entering the dust season (the second half of the year), the generation of dust devils is very rare, which is also consistent with our observations and similar to those in previous studies []. To further understand why there are more DLIFs in ZB and the two-peak structure in temporal distribution, we analyzed the corresponding temporal variation in sensible heat flux and thermal efficiency, based on Equation (1).
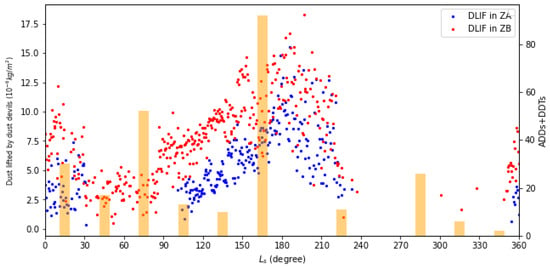
Figure 5.
Time series of total daily dust lifting by dust devils (DLIF) averaged in ZA (blue dots) and ZB (red dots). Orange bars are the observed number of DDs as shown in Figure 3.
Overall, in the first half of the year, the sensible heat flux and thermal efficiency in ZB (Figure 6) are always higher than those in ZA, and the difference in sensible heat flux between ZA and ZB (~5 W m−2) is generally larger than that of the thermal efficiency. Based on the DD theory of Rennó et al. [], it can be inferred that the difference in DLIF between ZA and ZB is mainly determined by sensible heat flux, which, in turn, is mainly related to the surface-to-air temperature difference (~2 K, Figure 7). The drag velocity plays a minor role in the difference (~0.2 m s−1). Besides, the mean albedo in ZA is about 0.229, while the mean albedo in ZB is around 0.205. This difference in albedo is also reflected in the net short-wave flux at the surface (short-wave flux at surface minus the reflected short-wave flux), which in ZB, is always stronger than ZA in their local spring and summer (Figure 8). By intuition, ZA and ZB are at similar latitudes and so should have similar solar radiation at the surface. The above results suggest that more DDs in ZB are mainly due to the relatively low albedo there.
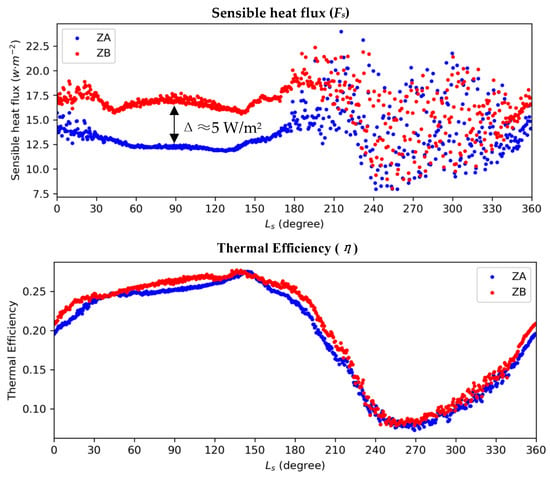
Figure 6.
Time series of daytime-mean sensible heat flux (top) and thermal efficiency (bottom) averaged in ZA (blue dots) and ZB (red dots). Δ is the difference between ZA and ZB.
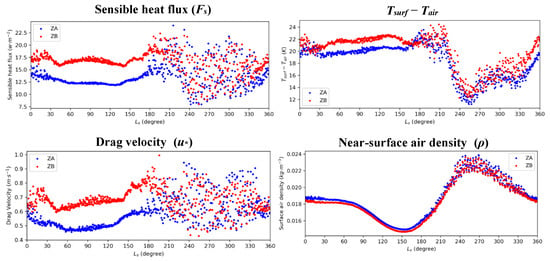
Figure 7.
Time series of daytime-mean sensible heat flux and its contributors (temperature difference between ground surface and near-surface air (Tsurf − Tair), drag velocity, and near-surface air density) averaged in ZA (blue dots) and ZB (red dots).
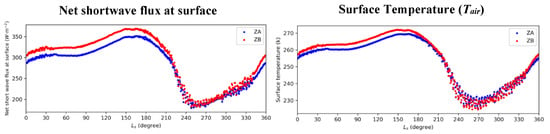
Figure 8.
Time series of daytime-mean net short-wave flux at the surface (left) and surface temperature (right) averaged in ZA (blue dots) and ZB (red dots).
The two-peak pattern can generally be seen in DLIF and its contributors (i.e., sensible heat flux, and thermal efficiency in Equation (1)). After entering the dust season in the second half of the year, the thermal efficiency and sensible heat flux drop sharply and so does the DLIF. Apparently, their net short-wave flux at surface and surface temperature (Figure 8) both reach their maximum at the two peak times (early spring and late summer). The results indicate that the two-peak structure in temporal distribution is related to the seasonal variation of solar radiation, and the pause between the two peaks corresponds to the period with relatively weaker solar radiation.
3.3. Spatial Distribution of Predicted DDs
This section focuses on the spatial distribution of DDs during their local summer (Ls = 150–180°), which is the time when solar forcing and the number of occurrences of DDs both reach their maximum, as discussed above. In the analysis of spatial distribution, we considered the day-time mean of the model results over the time period between ~11:00 and ~15:00 local time in the corresponding regions of ZA and ZB. This is the period when the dust lifting by dust devils occurs in the model simulations. Figure 9 (first column) clearly shows the completely different spatial distributions of predicted DDs in ZA and ZB. Predicted DDs are relatively active in ZB and are basically concentrated in the northwest part of ZB. There is a slight difference between the predicted and observed spatial distribution of DDs. This difference may be caused by the insufficient sample size or the inaccurate prediction by the model, which will be further discussed.
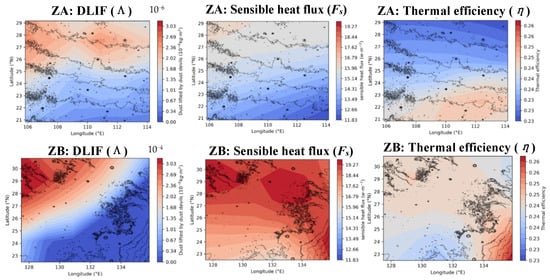
Figure 9.
Spatial distribution (shading) of daytime-mean DLIF (first column), sensible heat flux (second column), and thermal efficiency (third column) in ZA (top) and ZB (bottom) in northern summer (Ls: 150–180°). Black contours show the elevation.
According to Equation (1), we plotted the spatial distribution of sensible heat flux (Figure 9, second column) and thermal efficiency (Figure 9, third column) in their local summer (Ls: 150–180°). In ZA, the predicted DDs are mainly distributed in the north and this distribution is mainly determined by the sensible heat flux. The thermal efficiency in ZA has an opposite trend in the south–north direction. As mentioned above, the predicted DDs in ZB are mainly distributed in the northwest. In addition, the relatively large DLIF in the northwest of ZB is dominated by the sensible heat flux. The thermal efficiency may also play a positive role in the greater DLIF in the northwest of ZB, although the effect is much lower than that of the sensible heat flux. Notice that the DLIF in the southeast of ZB is nearly zero, while the sensible heat flux and thermal efficiency in the southeast are relatively large. This could be caused by the conditions for the occurrence of DD in the DD parameterization (discussed in Section 3.1), which will be further explained later. Overall, from the model results, we can see that the spatial distribution of DLIF both in ZA and ZB is dominated by sensible heat flux. To further understand the possible environmental conditions that contribute to the spatial distribution of sensible heat flux, we analyzed their contributors in ZA (Figure 10) and ZB (Figure 11), according to Equation (4).
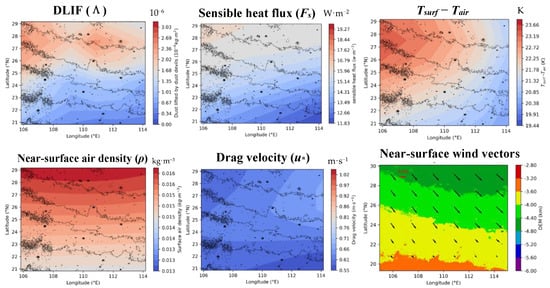
Figure 10.
Spatial distribution (shading) of daytime-mean DLIF, sensible heat flux and its main contributors: surface-to-air temperature difference, near-surface air density, drag velocity, and wind vectors (noon mean, shading is elevation) in their local summer (Ls: 150–180°) in ZA. Topography is depicted by the contours.
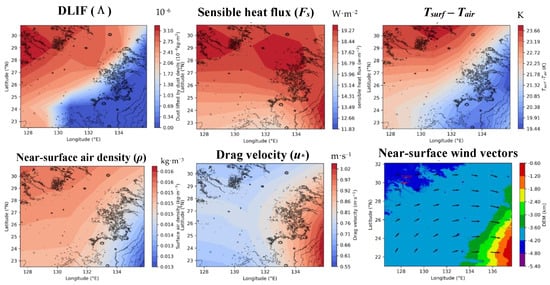
Figure 11.
Similar to Figure 10, but for ZB.
3.3.1. Sensible Heat Flux and Its Contributors
The predicted sensible heat flux in ZA (Figure 10) decreases from northwest to southeast, and so does the surface-to-air temperature difference (Tsurf − Tair). The variation in near-surface air density (~0.001 kg m−3) and drag velocity (~0.2 m s−1) shows a similar trend but the variation is very small. In addition, the wind direction basically corresponds to the Hadley circulation and thermal tide during their local summer. This indicates that the spatial distribution of sensible heat flux is mainly determined by the surface-to-air temperature difference. To better understand the surface-to-air temperature difference, the surface temperature, near-surface air temperature, net short-wave flux, and surface properties are further analyzed (Figure 12). The surface temperature decreases with increasing latitudes, and so does the net short-wave flux at the surface. On the other hand, the variation in the spatial distribution of albedo and thermal inertia is very small and, thus, shows little effect on the spatial distribution of surface temperature. The near-surface air temperature increases from northwest to southeast, which may be caused by thermal advection. These results show that the distribution of surface-to-air temperature difference is mainly determined by the solar radiation and thermal advection, which, in turn, determines the distribution of sensible heat flux and so the DLIF.
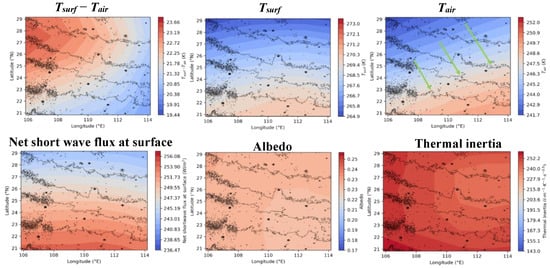
Figure 12.
Spatial distribution of day-time mean surface temperature, near-surface air temperature, net short-wave flux, and surface properties (albedo and thermal inertia) in ZA. Topography is depicted by contours. Green vectors show the ambient surface wind.
In ZB (Figure 11), the simulation results show that sensible heat flux in the northwestern part is mostly contributed by the surface-to-air temperature difference, while the horizontal variation in near-surface air density seems to be secondary. In the southwestern part, the sensible heat flux is mainly contributed by the relatively large drag velocity there, which is proportional to surface roughness and altitude. Notice that, although the drag velocity and sensible heat flux are relatively large in the southeastern part, the DLIF there is nearly zero. This is because, in our model, the occurrence of dust lifting by DDs requires three conditions (Section 3.1), as mentioned above. Both the surface temperature and sensible heat flux in the southeast of ZB meet the conditions for the occurrence of DDs, while the surface-to-air temperature difference does not. Therefore, the surface-to-air temperature difference is the most significant factor in determining the distribution of sensible heat flux and, hence, the DLIF. We also analyzed the spatial distribution of surface temperature, near-surface air temperature, net short-wave flux, and surface properties in ZB (Figure 13). The distribution of surface temperature is mostly controlled by the net short-wave flux at the surface, which is inversely proportional to the albedo. The surface temperature in the southeastern part of ZB is mostly related to the distribution of thermal inertia. Lower thermal inertia implies a faster heating rate at the surface. Besides, although surface temperature strongly controls the distribution of near-surface air temperature via radiative heating and sensible heat flux, the near-surface air could be mixed with the local wind (e.g., wind associated with local topography). Overall, our results suggest that the spatial distribution of sensible heat flux in ZB is mainly determined by the distribution of albedo, and the local topography may have a secondary effect.
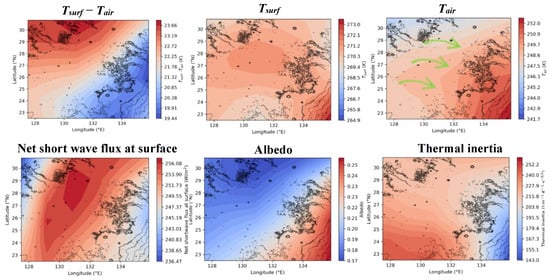
Figure 13.
Similar to Figure 12, but for ZB.
3.3.2. Thermal Efficiency and Its Contributors
Although DLIF is mainly determined by the sensible heat flux in both ZA and ZB, it is still worth analyzing the thermal efficiency. According to Equations (2) and (3), thermal efficiency is proportional to the temperature difference between the surface and the top of the convective vortex. Considering the spatial distribution of thermal efficiency (Figure 14), we can see that its pattern is dominated by the surface temperature in both ZA and ZB, and the distribution of surface temperature has been discussed before. Therefore, the distribution of thermal efficiency in ZA is mainly related to solar radiation, while it is mainly related to the distribution of albedo in ZB.
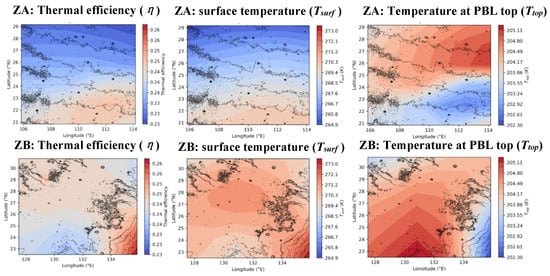
Figure 14.
Daytime-mean DLIF (first column), thermal efficiency (second column), and temperature at PBL top (third column) in ZA (top) and ZB (bottom) in their local summer (Ls: 150–180°). Topography is depicted by contours.
4. Summary and Discussion
4.1. Summary
This study focuses on the distribution and characteristics of DDs in the two pre-selected landing sites (ZA and ZB) of the Tianwen-1 mission (ZA was finally chosen for landing). A significant difference in the number of DDs occurring in these two regions was found in observations, which was also supported by the results of the numerical simulations with the MarsWRF model. Some questions have been put forward based on the observational results. In order to answer these questions, some analysis based on numerical simulations was performed from the perspective of atmospheric conditions and surface properties.
DDs are mainly concentrated in the first half of the year and there are more DDs in ZB than that in ZA. Based on the DD theory of Rennó et al. [], our analysis suggests that the difference in dust lifting by DDs (DLIF) between ZA and ZB is mainly dominated by the difference in sensible heat flux, which is mainly caused by the surface-to-air temperature difference. Thermal efficiency plays a relatively minor role. Furthermore, ZB has a stronger net short-wave radiative flux at the surface due to the lower albedo (~0.205) at the surface than ZA (~0.229). Overall, the results of the analysis suggest that more DDs in ZB are mainly caused by the lower albedo in ZB. However, it is worth mentioning that some of the differences could also be due to the difference in surface dust availability between the two regions, but there is a lack of observation and this is beyond the scope of the present study.
Both the observed and predicted DDs have a two-peak feature in their local early spring and late summer, and are generally coincident with the time of maximum solar radiation in their local time. This suggests that the temporal variation in solar radiation due to the revolution of Mars is primarily responsible for the two-peak pattern of temporal distribution. After entering the dust season in the second half of the year, the thermal efficiency and sensible heat flux drop sharply and so do the DD activities.
The spatial distributions of DDs, both in ZA and ZB, are mainly related to the distribution of sensible heat flux and surface-to-air temperature difference. In ZA, solar radiation at the surface dominates the spatial distribution of sensible heat flux, thus, causing the particular spatial distribution of DLIF. In ZB, our results suggest that the spatial distribution of surface-to-air temperature difference and sensible heat flux are mainly determined by the albedo, and so the resulting DLIF is concentrated in the northwest. The surrounding topography has little effect on the distribution of the predicted DDs. In the southeast corner of ZB, the surface-to-air temperature difference is relatively small, which is not favorable to the occurrence of DDs.
4.2. Discussion
As mentioned in Section 3.3, the predicted DDs are mainly concentrated in the northwest of ZB, while the observed DDs are mainly distributed in the northeast of ZB. The model’s prediction ability may be responsible for this discrepancy. First, the predicted DDs in the southeast are almost 0, but there are quite a few observed DDs here. According to the analysis of the sensible heat flux and its contributors, the threshold of surface-to-air temperature difference for DD occurrence is responsible for the no DLIF in the southeast. In fact, the distribution of sensible heat flux is more similar to that of the observed DDs. Besides, the distribution of surface temperature seems to be more similar to that of the sensible heat flux and so the predicted DDs, compared with the distribution of the surface-to-air temperature difference. Therefore, the role played by surface temperature should be more emphasized in the parameterization of DDs in the model.
From the simulation results, it is worth noting that there are more predicted DDs in the south of the Elysium Mons compared with that in ZA and ZB (Figure 15). However, from 518 CTX images (~8 MY), there are only 12 ADDs found in the south of Elysium Mons. The list of CTXs with ADDs in the south of Elysium Mons is shown in Table 2. In a similar geographical situation, there are only two DDs found in the south of the Olympus Mons, and a large number of DDs (9827) were found in the Amazonis Planitia from the global survey of DDs []. However, in our numerical simulations, DLIF in the south of Olympus is also greater than that in the Amazonis Planitia (Figure 16). Nevertheless, our simulations did very well in the time series of DDs in the Amazonis Planitia (Figure 17). The above discrepancy in DDs suggests that the present configuration of MarsWRF is likely not good enough to predict DDs in mountainous areas. There are two possible reasons for the discrepancy. One is the use of the unlimited dust source in our model, while in reality, there may be little dust on the hillside (most of which is blown away by the wind). The other one is that the parameterization of dust-lifting processes is not good enough for mountainous areas. Improving the simulation of DDs in mountainous areas is one important task of our future work.
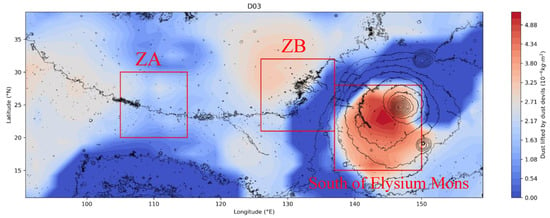
Figure 15.
DLIF (shading) in southern Utopia Planitia. Topography is depicted by contours.

Table 2.
List of CTX images with ADDs in ZC including Martian Year (MY), solar longitude (Ls), incidence angle (INA), and the number of ADDs (NADDs).
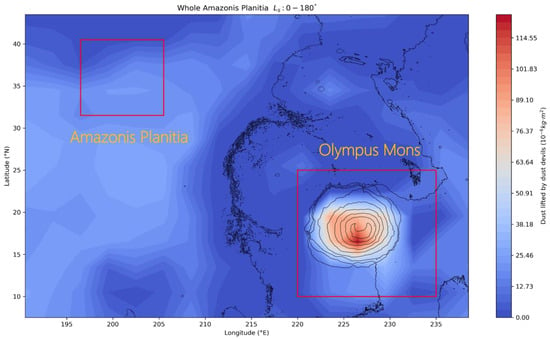
Figure 16.
DLIF (shading) in Amazonis Planitia and the Olympus Mons in their local spring and summer (the first half of the year, Ls: 0–180°). Topography is depicted by contours.
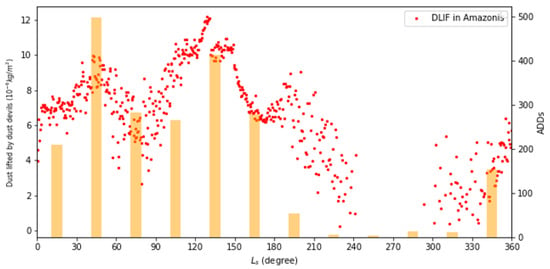
Figure 17.
Time series of dust devils in Amazonis Planitia (Adapted from Ref. []) (orange bar) and model-predicted dust devils averaged in the same study area (red dots).
Author Contributions
Conceptualization, K.-C.C., J.X., Y.-M.W. and Y.X.; methodology, K.-C.C., J.X. and Y.-M.W.; software, Y.-M.W.; validation, Y.-M.W. and K.-C.C.; formal analysis, Y.-M.W.; investigation, Y.-M.W.; resources, K.-C.C.; data curation, Y.-M.W.; writing—original draft preparation, Y.-M.W.; writing—review and editing, Y.-M.W. and K.-C.C.; visualization, Y.-M.W.; supervision, K.-C.C.; project administration, K.-C.C.; funding acquisition, K.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by grants from the FDCT of Macau (grant nos. 0088/2018/A3 and 0068/2019/A2). MarsWRF was obtained from Aeolis Research through the PlanetWRF modeling project, funded by numerous NASA grants.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Greeley, R. Martian dust devils: Laboratory simulations of particle threshold. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Stanzel, C.; Patzold, M.; Williams, D.; Whelley, P.; Greeley, R.; Neukum, G. Thehrsccoinvestigatorteam, Dust devil speeds, directions of motion and general characteristics observed by the Mars Express High Resolution Stereo Camera. Icarus 2008, 197, 39–51. [Google Scholar] [CrossRef] [Green Version]
- Newman, C.E.; Lewis, S.R.; Read, P.L.; Forget, F. Modeling the Martian dust cycle, 1. Representations of dust transport processes. J. Geophys. Res. Planets 2002, 107, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Basu, S. Simulation of the Martian dust cycle with the GFDL Mars GCM. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Kahre, M.A.; Murphy, J.R.; Haberle, R.M. Modeling the Martian dust cycle and surface dust reservoirs with the NASA Ames general circulation model. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Whelley, P.L.; Greeley, R. The distribution of dust devil activity on Mars. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Thomas, P.; Gierasch, P.J. Dust devils on Mars. Science 1985, 230, 175–177. [Google Scholar] [CrossRef]
- Ryan, J.A.; Lucich, R.D. Possible dust devils, vortices on Mars. J. Geophys. Res. 1983, 88, 11005–11011. [Google Scholar] [CrossRef]
- Fisher, J.A.; Richardson, M.I.; Newman, C.E.; Szwast, M.A.; Graf, C.; Basu, S.; Ewald, S.P.; Toigo, A.D.; Wilson, R.J. A survey of Martian dust devil activity using Mars Global Surveyor Mars Orbiter Camera images. J. Geophys. Res. Planets 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Cantor, B.A.; KKanak, M.; Edgett, K.S. Mars Orbiter Camera observations of Martian dust devils and their tracks (September 1997 to January 2006) and evaluation of theoretical vortex models. J. Geophys. Res. Planets 2006, 111. [Google Scholar] [CrossRef]
- Reiss, D.; Spiga, A.; Erkeling, G. The horizontal motion of dust devils on Mars derived from CRISM and CTX/HiRISE observations. Icarus 2014, 227, 8–20. [Google Scholar] [CrossRef]
- Choi, D.S.; Dundas, C.M. Measurements of Martian dust devil winds with HiRISE. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Perrin, C.; Rodriguez, S.; Jacob, A.; Lucas, A.; Spiga, A.; Murdoch, N.; Lorenz, R.; Daubar, I.J.; Pan, L.; Kawamura, T.; et al. Monitoring of Dust Devil Tracks Around the InSight Landing Site, Mars, and Comparison With In Situ Atmospheric Data. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Reiss, D.; Lorenz, R.D. Dust devil track survey at Elysium Planitia, Mars: Implications for the InSight landing sites. Icarus 2016, 266, 315–330. [Google Scholar] [CrossRef]
- Balme, M.R. Mars: Dust devil track survey in Argyre Planitia and Hellas Basin. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Fenton, L.K.; Lorenz, R. Dust devil height and spacing with relation to the martian planetary boundary layer thickness. Icarus 2015, 260, 246–262. [Google Scholar] [CrossRef]
- Whelley, P.L.; Greeley, R. Latitudinal dependency in dust devil activity on Mars. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Haberle, R.M.; Pollack, J.B.; Barnes, J.R.; Zurek, R.W.; Leovy, C.B.; Murphy, J.R.; Lee, H.; Schaeffer, J. Mars atmospheric dynamics as simulated by the NASA Ames General Circulation Model. I—The zonal-mean circulation. J. Geophys. Res. Planets 1993, 98, 3093–3123. [Google Scholar] [CrossRef]
- Newman, C.E.; Kahanpää, H.; Richardson, M.I.; Martínez, G.M.; Vicente-Retortillo, A.; Lemmon, M.T. MarsWRF Convective Vortex and Dust Devil Predictions for Gale Crater Over 3 Mars Years and Comparison With MSL-REMS Observations. J. Geophys. Res. Planets 2019, 124, 3442–3468. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, B.; Zhang, J.; Ling, Z.; Qiao, L.; Chen, S.; Qu, S. The Preliminary Study of Dust Devil Tracks in Southern Utopia Planitia, Landing Area of Tianwen-1 Mission. Remote Sens. 2021, 13, 2601. [Google Scholar] [CrossRef]
- Balme, M.; Greeley, R. Dust devils on Earth and Mars. Rev. Geophys. 2006, 44. [Google Scholar] [CrossRef]
- Greeley, R.; Whelley, P.L.; Arvidson, R.E.; Cabrol, N.A.; Foley, D.J.; Franklin, B.J.; Geissler, P.G.; Golombek, M.P.; Kuzmin, R.O.; Landis, G.A.; et al. Active dust devils in Gusev crater, Mars: Observations from the Mars Exploration Rover Spirit. J. Geophys. Res. Planets 2006, 111. [Google Scholar] [CrossRef]
- Maxworthy, T. A vorticity source for large-scale dust devils and other comments on naturally occurring columnar vortices. J. Atmos. Sci. 1973, 30, 1717–1722. [Google Scholar] [CrossRef] [Green Version]
- Richardson, M.I.; Toigo, A.D.; Newman, C.E. PlanetWRF: A general purpose, local to global numerical model for planetary atmospheric and climate dynamics. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Toigo, A.D.; Lee, C.; Newman, C.E.; Richardson, M.I.J.I. The impact of resolution on the dynamics of the martian global atmosphere: Varying resolution studies with the MarsWRF GCM. Icarus 2012, 221, 276–288. [Google Scholar] [CrossRef]
- Guo, X.; Lawson, W.G.; Richardson, M.I.; Toigo, A. Fitting the Viking lander surface pressure cycle with a Mars General Circulation Model. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Chow, K.-C.; Chan, K.-L.; Xiao, J. Dust activity over the Hellas basin of Mars during the period of southern spring equinox. Icarus Int. J. Sol. Syst. Stud. 2018, 311, 306–316. [Google Scholar] [CrossRef]
- Xiao, J.; Chow, K.-C.; Chan, K.-l. Dynamical processes of dust lifting in the northern mid-latitude region of Mars during the dust storm season. Icarus 2019, 317, 94–103. [Google Scholar] [CrossRef]
- Newman, C.E.; Richardson, M.I. The impact of surface dust source exhaustion on the martian dust cycle, dust storms and interannual variability, as simulated by the MarsWRF General Circulation Model. Icarus 2015, 257, 47–87. [Google Scholar] [CrossRef]
- Rennó, N.O.; Burkett, M.L.; Larkin, M.P. A simple thermodynamical theory for dust devils. J. Atmos. Sci. 1998, 55, 3244–3252. [Google Scholar] [CrossRef]
- Greeley, R.; Waller, D.A.; Cabrol, N.A.; Landis, G.A.; Lemmon, M.T.; Neakrase, L.D.V.; Hoffer, M.P.; Thompson, S.D.; Whelley, P.L. Gusev Crater, Mars: Observations of three dust devil seasons. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).