Analysis on Seasonal Variation and Influencing Mechanism of Land Surface Thermal Environment: A Case Study of Chongqing

Abstract

Rapid urbanization has brought about many problems in urban environments, including the deterioration of the thermal environment, which greatly affects the sustainable development of cities and the health of urban residents. Therefore, a comprehensive and thorough study of the thermal environment is necessary. In this study, quantitative and qualitative analyses of the interannual and seasonal variation of the thermal environment in the urban area of Chongqing were conducted using a combination of equal sector analysis, mathematical statistics, and principal component analysis. In addition, the mechanism by which multiple integrated human and natural factors affect the urban thermal environment in different seasons was explored. The thermal environment of the land surface has a clear spatial correlation with built-up areas. From 2010 to 2020, the Liangjiang New Area and the western high-tech zone were the main areas of thermal environment area expansion. From 2010 to 2020, a decrease in the area of low-temperature zones and an increase in the area of high-temperature zones were the main trends. In particular, during the summer of 2020, the low-temperature zones almost disappeared, and the area of high-temperature zones was nearly twice as large as in the other seasons. The combined influence of multiple factors on surface temperature has certain seasonal characteristics. The slope, elevation, normalized water body index, fractional vegetation cover, normalized imperviousness index, and nighttime light intensity were the main factors affecting the surface temperature, whereas landscape pattern indicators, as well as the population and points of interest (POI) density, had a low influence. The strength of the combined influence of these multiple factors of the different seasons exhibited the following order: winter > spring > summer > autumn.

1. Introduction

Rapid urbanization has brought about many problems in urban environments, including a deterioration of the thermal environment, which greatly affects the sustainable development of cities and the health of urban residents [1,2,3,4,5]. Therefore, a full study of variations in the thermal environment and their potential driving mechanisms can provide an effective basis for mitigating the effects of a thermal environment.

The term “thermal environment” refers to an environment that affects human perception and health caused by physical factors such as solar radiation, temperature, and relative humidity. The concept was proposed by experts and scholars in the field of meteorology and environmental research based on the concept of the urban heat island in recent years. For the past few years, scholars in China and abroad have conducted extensive research on thermal environments. First, some studies were conducted on the spatial distribution and variation in the thermal environment, which were fundamentally explorations of the current situation of the urban surface temperature and its spatiotemporal changes. This research was further developed using different models [6] and different types of data [7,8] at different spatial scales [9,10]. Since then, the focus has shifted to the identification of the driving factors and analysis of the driving mechanisms, such as analysis of the correlations between the urban thermal environment and nighttime light data [11], NDVI [12], land use [13], and impervious surfaces [14]. Moreover, with the deepening of such investigations, the comprehensive analysis of multiple driving factors has been enriched. The analysis of the roles of independent factors and interactions between factors [15], the investigation of multi-factor mechanisms of influence at the scale of functional areas and local climate zones [16,17,18], and the comparative study of source–sink landscapes have become mainstream topics in this research field [17]. As can be seen, the breadth and depth of the content of urban thermal environment research have continuously expanded.

However, there are still some deficiencies in the study of urban thermal environments. First of all, most studies have been conducted using annual summer temperature or annual average temperature data, although the thermal environment is also affected by the climatic characteristics of the study area and the seasonal differences [19,20]. The influence of climate characteristics and seasonal changes cannot be ignored. Secondly, the use of correlation analysis is still dominant in the current analysis of these driving mechanisms. For instance, geodetectors, geographically weighted regression (GWR), and other analysis techniques have some scientific validity, but the results of such methods only reveal single-factor correlations and two-factor interactions [20,21] and they do not allow for the exploration of the mechanism of multi-factor interactions. However, cities are complex systems [22], and the mechanisms driving their thermal environments are also controlled by the joint influences of various factors [23,24]. The use of scientific research methods to identify the mechanism by which multiple integrated factors affect urban thermal environments is an aspect that cannot be neglected in studies of thermal environments.

Therefore, the purpose of this study is to enrich and expand the research content of urban thermal environments, to make up for the shortcomings mentioned above, and to make the research results more scientific. On the one hand, the concept of four seasons is introduced in this study, which could make up for the deficiencies of previous studies based on summer and annual surface temperatures. On the other hand, principal component analysis is introduced in this study, which is rarely used in this field and which can identify the driving factors with a large influence on urban thermal environments. Based on the relationship between surface temperature and driving factors in different seasons, further linear fitting of the principal component analysis results of the original driving factors of thermal environments can enable the judgment of the comprehensive effects of multiple driving factors and can be used to analyze the temperature change in the study area under the joint action of multiple factors. Based on the study of seasonal variation in urban thermal environments and the comprehensive effect of seasonal driving factors, this study can provide an effective theoretical basis for urban construction and the optimization of urban human settlement environments.

2. Materials and Methods

2.1. Study Area

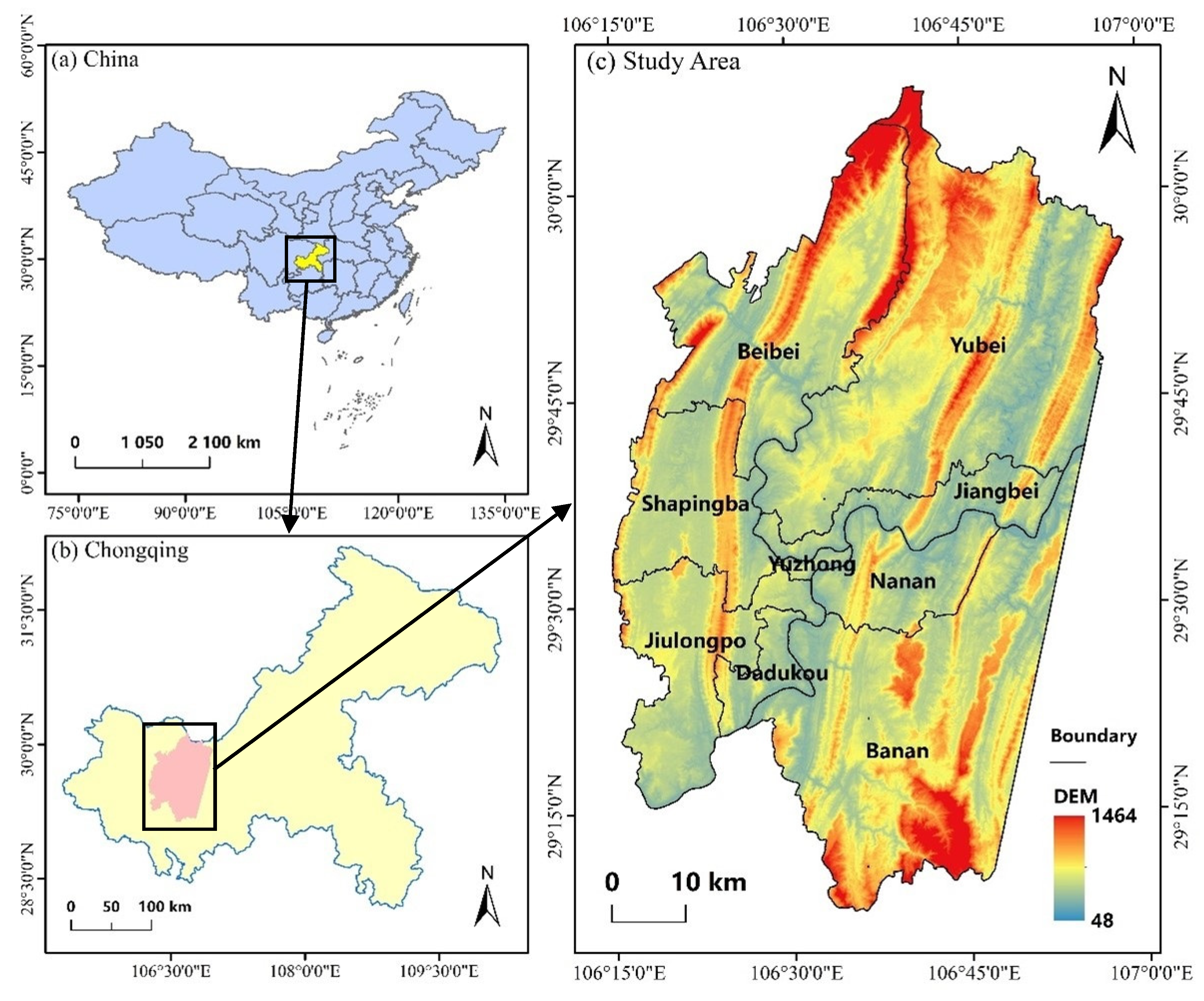
As one of the core cities of the Chengdu–Chongqing Economic Circle, Chongqing is located in southwest China and is the economic, scientific, technological innovation, trade, and logistics center in the upper reaches of the Yangtze River. According to the characteristics of urban distribution and remote sensing data, Figure 1 shows the study area selected for this paper. Located in the west of Chongqing, the area covers 4879.7 km². It is the main urban area and densely populated area of Chongqing, with a resident population of about 10.34 million in 2020. The topography is mainly mountainous and hilly, and the built-up area is multi-centered and grouped due to the mountainous barrier. With an annual average temperature of 16–18 °C, abundant precipitation, and an annual average relative humidity of 70–80%, a subtropical monsoonal humid climate is the main climate in the region. For the past few years, with the rapid economic development in Chongqing, the urban built-up area has been expanding. As a result of this urbanization, its own topographical features, its hot and humid climate, and its surface thermal environment have been intensified.

2.2. Datasets

Chongqing is located in a subtropical monsoon climate zone with four seasons—spring (March to May); summer (June to August); autumn (September to November); and winter (December to February). In this study, eight sets of Landsat data corresponding to the four season intervals with few clouds in similar years around 2010 and 2020 were obtained from the USGS (

Table 1. Remote sensing image data information.

Sensor	Date of Imaging	Path/Row
Landsat7 ETM+	29 April 2010	128/39, 128/40
	3 August 2010	128/39, 128/40
	22 October 2010	128/39, 128/40
	27 February 2011	128/39, 128/40
Landsat8 OLI/TIRS	29 March 2019	128/39, 128/40
	20 August 2019	128/39, 128/40
	10 November 2020	128/39, 128/40
	13 January 2021	128/39, 128/40

). The remote sensing data were pre-processed using ENVI. The land use data used were the first global geographic information public product provided by China to the United Nations (http://www.globeland30.org/home.html?type=data, accessed on 25 June 2021), and the overall accuracy of the data was determined to be 83.50% by a third party. The population density data were obtained from the world population density map published by WorldPop (https://www.worldpop.org/, accessed on 3 June 2021). The Chongqing POI data were obtained from the Gaode Map, which contains eight categories: food service, leisure and entertainment, medical facilities, shopping area, attractions, public facilities, transportation, and accommodations. In this paper, the POI density data were obtained through the kernel density analysis of ArcMap. The nighttime light data were obtained from the 2012–2020 Global Annual Nighttime Light Dataset (Annual VNL V2) produced by the NOAA-NGDC’s Earth Observation Group in 2021.

2.3. The Inversion of LST

The mono-window algorithm and the atmospheric correction method were used for the inversion of LST [25,26], and their accuracy was verified using data from meteorological stations in the central city. The overall accuracy of the atmospheric correction method was better than that of the mono-window algorithm, so it was chosen to invert the LST of the study area, as follows:

$$L=\left[\epsilon B\left(T_s\right)+\left(1-\epsilon \right)L_{down}\right]\tau +L_{up}$$

(1)

$$T_s=\frac{K_2}{ln\left(1+\frac{K_1}{B\left(T_s\right)}\right)}$$

(2)

where ε is the surface-specific emissivity, which was obtained using a previously published method [27,28]; and $B\left(T_S\right)$ is the blackbody thermal radiation brightness. $L_{up}$, $L_{down}$, and $\tau$ are the atmospheric upward and downward radiation and the atmospheric transmittance, respectively, which were obtained using the NASA atmospheric calculator. $K_1\mathrm{and}{K}_2$ are constants. Enhanced Thematic Mapper Plus (ETM+) data: $K_1$ = 666.09 and $K_2$ = 1282.71. Operational Land Imager (OLI) data: $K_1$= 774.89 and $K_2$ = 1321.08.

2.4. Spatial Pattern Analysis

2.4.1. Temperature Class Division

The ArcMap standard deviation method was used to classify the surface temperature into five classes: the low-temperature zone (T < u −1.5 std), sub-low-temperature zone (u −1.5 std ≤ T < u −0.5 std), medium-temperature zone (u −0.5 std ≤ T < u + 0.5 std), sub-high-temperature zone (u + 0.5 std ≤ T< u + 1.5 std), and high-temperature zone (T > u + 1.5 std). With the help of mathematical statistics, the classification more intuitively reflects the variations in, and distribution of, the LST in the study area.

2.4.2. Equal Sector Analysis Method

The equal sector analysis method involves taking the center of the study area as the center of a circle (the geometric center of the study area or the location that is important to the area in terms of the geographic location and economic activities), choosing a suitable radius to establish a circular buffer zone, dividing the buffer zone into a number of equal sectors according to the different directions, using the superposition analysis function of ArcMap to obtain the proportions of the areas that are the high and the sub-high-temperature zones within each sector during different periods, and quantitatively analyzing their spatial changes [29]. In this study, the location of Jiefangbei was used as the circular buffer area. The location of Jiefangbei was taken as the center of the circle, and the radius was set as 33 km, which basically covered the region of the study area with significant thermal environmental effects.

2.5. Analysis of Driving Mechanism

2.5.1. Selection of Driving Factors

In this study, based on the urban characteristics and socio-economic situation of Chongqing City, 12 associated factors were selected based on relevant research results [20,21,23] (

Table 2. Indicators of associated factors of Chongqing’s urban thermal environment.

First-Level Indicator	Second-Level Indicator	Third-Level Indicator
Natural factors	Vegetation and water bodies	FVC
		MNDWI
	Topography	DEM (m)
		Slope (°)
Human factors	Socio-economic activities	Population density (people/km2)
		Nighttime light intensity (nW/cm2/sr)
		POI density
	Landscape pattern	DIVISION
		CONTAG
		SHDI
		COHESION
	Urban built-up area	NDISI

). Some of the data needed to be calculated further, based on the remote sensing image data and land use data.

• The normalized difference impervious surface index (NDISI) was calculated as follows [30]:

  $$NDISI=\frac{TIRS-\left(MNDWI+NIR+SWIR1\right)/3}{TIRS+\left(MNDWI+NIR+SWIR1\right)/3}$$

  (3)
• The fractional vegetation cover (FVC) was calculated as follows:

  $$FVC=\frac{NDVI-NDV{I}_{min}}{NDV{I}_{max}-NDV{I}_{min}}$$

  (4)

  $$NDVI=\frac{NIR – Red}{NIR+Red}$$

  (5)
• The modified normalized difference water index (MNDWI) was calculated as follows [31]:

  $$MNDWI=\frac{Green-SWIR1}{Green+SWIR1}$$

  (6)

  where Green, Red, NIR, SWIR1, and TIRS1 correspond to bands 3, 4, 5, 6, and 10 in the Landsat 8 remote sensing imagery.
• SHDI, CONTAG, DIVISION, and COHESION are four indicators of landscape patterns, calculated by Fragstats, which provided the main characterization of the spatial structure of the landscape pattern and the characteristics of the distribution, enabling us to comprehensively reflect urban landscape pattern information [32].

2.5.2. Analysis of Driving Forces

Principal component analysis is a method of transforming the original multifaceted indicators into a few integrated indicators with good representativeness. These integrated indicators can reflect most of the information about the original indicators, and each indicator is independent of the others [33]. In this study, based on the principal component analysis, the results were linearly fit to achieve the quantitative output of the integrated influence of multiple factors [22].

The most suitable spatial scale for studying urban thermal environments is considered to be 500 to 650 m [34]; therefore, in this study, the research scale was chosen to be 500 m. Using ArcMap, the surface temperature data and the data for each associated factor were uniformly resampled into 500 × 500 m raster data. The sampling points in the study area were obtained using raster transcripts, and each sample point was obtained through multi-value extraction to the point. In order to eliminate the influences of the various parameters, the parameters were normalized using the fuzzy membership function of ArcMap, and SPSS was used for subsequent analysis.

3. Results

3.1. Spatiotemporal Evolution of the Thermal Environment

3.1.1. Seasonal Variation

Comparing the statistical data of the standard deviation of the surface temperature in the four seasons over two years (2010 and 2020) (

Table 3. Standard deviation of LST in all seasons (°C).

Season	Spring	Summer	Autumn	Winter
2010	2.64	4.39	2.82	1.73
2020	2.73	4.69	2.36	1.69

), the urban surface temperature in the different years was found to have the same distribution pattern; that is, the temperature varied more in summer, followed by spring and autumn, and it varied the least in winter.

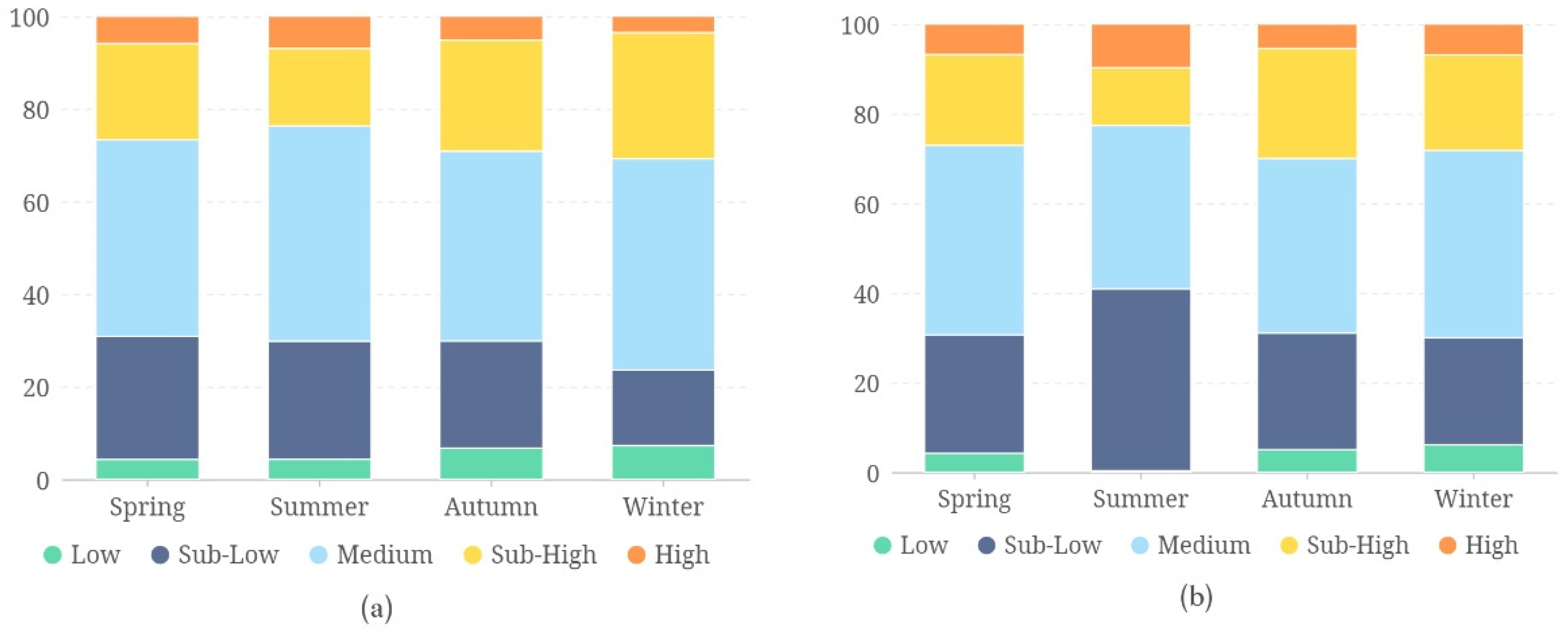
According to the stacked bar chart of the proportions of the areas of the temperature zones of all of the levels in the study area in all of the seasons (Figure 2), the proportion accounted for by the sub-low, medium, and sub-high-temperature zones was high, reaching 90% of the total study area. In contrast, the other two temperature zones only accounted for about 10%. The maximum area of the high-temperature zones and the minimum area of the low-temperature zones both occurred in summer, which showed that summer was the season with the maximum thermal environment effect. Compared with 2010, in 2020, the area of the low-temperature zones decreased, and the area of the high-temperature zones increased. This phenomenon was more significant in summer, with the high-temperature zones reaching 9.72% of the study area in summer and the proportion of low-temperature zones almost approaching zero. This shows that with the intensification of the thermal environment effect, the remaining seasons were able to maintain a stable proportion of each temperature zone, but the overall warming phenomenon in summer was obvious.

A comparison of the spatial distributions of the LST during the two years and four seasons is presented in Figure 3. In the same year, the overall distribution of different temperature ranges was similar, but the distribution varied greatly in different seasons. Comparison of the distributions of LST in the different seasons revealed that the distributions of the high-temperature zones were obvious and were concentrated in spring and summer, whereas they were more scattered in autumn and winter, indicating that the distribution pattern of the urban thermal environment exhibited seasonal differences. High-temperature and high-humidity climate conditions can intensify the effect of the thermal environment, whereas low-temperature and low-humidity conditions can alleviate the high-temperature phenomenon in the city to a certain extent. However, in the autumn and winter of 2020, clustering of the high and sub-high-temperature zones started to appear, which showed that, as the thermal environment effect in the city intensified, its influence gradually exceeded that of the climatic influence of the four seasons themselves.

3.1.2. Interannual Spatiotemporal Distribution

As can be seen in Figure 3, there was a very high degree of spatial correlation between the LST and the urban built-up area, that is, the high- and sub-high-temperature zones were located in the area where the population, buildings, and economic development were concentrated in the same period. Comparison of the distribution of the LST in the same season in the different years in the study area revealed that the sub-high- and high-temperature zones expanded with the urban built-up area from 2010 to 2020, and they had the same expansion direction as the urban built-up area. In 2010, the urban surface high-temperature zone was mainly concentrated in the urban built-up area between Zhongliang Mountain and Tongluo Mountain, and the establishment of the Liangjiang New Area in 2010 and the subsequent development of the Chongqing Western High-Tech Zone caused the central urban area to expand in this direction. The areas near Shuitu and Longxing around the city highway were subsequently developed and became industrial hotspots, and the sub-high- and high-temperature zones also expanded aggressively in this region.

Since Chongqing is a mountainous city, the topography of the central urban area of Chongqing plays an important role. As shown in Figure 3, the mountainous area is where the low- and sub-low-temperature zones were concentrated. Furthermore, the main mountains of the city served as obvious dividing lines of the thermal environment. With the increasing urbanization and the intensification of the thermal environment effect, their role as dividers became increasingly obvious.

The thermoregulatory capacity of the water bodies was obvious, but there were some changes over time. In 2010, the Yangtze and Jialing rivers—which run through the whole study area as the main water bodies—were representative low-temperature zones, especially in summer. In contrast, in 2020, the water bodies exhibited different temperature classes in all of the seasons. In spring, they represented a low-temperature zone; in summer, they represented a sub-low-temperature zone; in autumn, they contained sub-low- and medium-temperature zones; and in winter, they contained sub-high- and high-temperature zones.

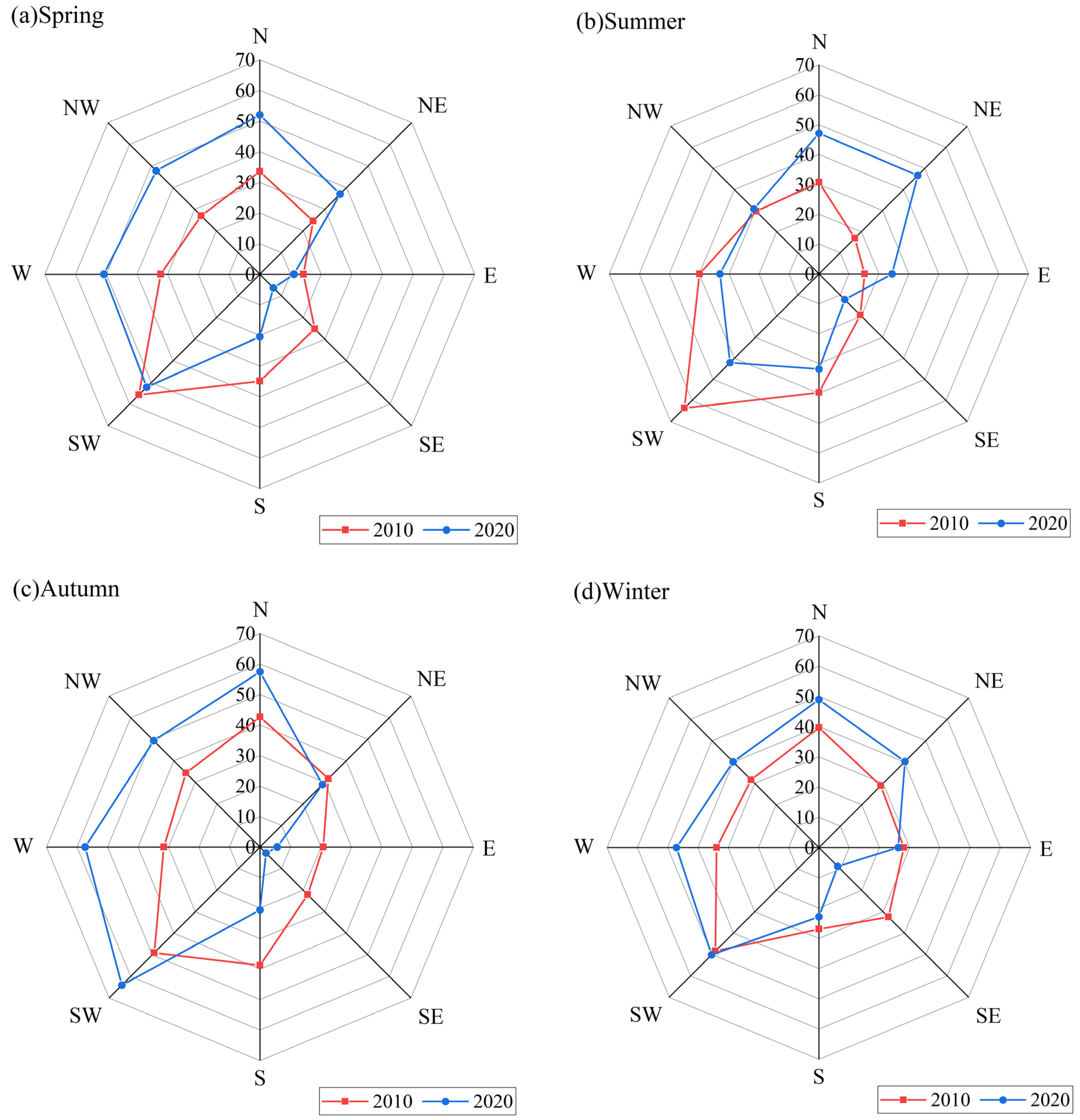
Because sub-high- and high-temperature zones were the areas where the effect of the urban thermal environment was more obvious, the equal sector analysis method was used to analyze the spatial distribution statistically, and the results are presented below (Figure 4). The interannual changes in the spring, autumn, and winter were basically the same, and the growth areas of the thermal environment were mainly located in the western, northwestern, northern, and northeastern of the study area, with an increase of more than 35%. There were obvious differences in summer, with the growth trend slowing down in the west and even with a negative growth phenomenon occurring in the northwest. The reason for this is that the built-up area was evenly distributed in these regions and the greening level was relatively high, so the heat island in summer did not exhibit the clustering that occurred in the other regions. These regions were mainly medium-temperature zones, which eventually resulted in a huge difference in the proportions of the areas in summer and the rest of the seasons. In terms of the multi-seasonal average changes, the growth points of Chongqing’s thermal environment were mainly located in the western high-tech zone and the northeastern Liangjiang New Area. The Nanan District and the Banan District—which are located in the southeastern and southern parts of the city—did not develop as quickly as the rest of the districts, relatively speaking, except for the main built-up areas, which remained in the high-temperature zone. The temperature zone levels of the rest of the urban areas decreased, and finally, the proportions of the areas of the sub-high- and the high-temperature zones decreased.

3.2. Analysis of Influencing Mechanisms

3.2.1. Spatialization of Driving Factors

Figure 5 shows the normalized results of each associated factor. It can be seen in Figure 5 that the distributions of the socio-economic activity indicator and the urban construction degree indicator were consistent with the distribution of the urban built-up areas and the sub-high- and high-temperature zones, and the population density, nighttime light intensity, and NDSI data were particularly significantly correlated. Second, the vegetation and water body indicators reflect the ecological environmental conditions of the study area. The FVC reflects the distribution of the vegetation. It was high in suburban areas and low in built-up areas, which was the opposite of the actual urban thermal environment’s distribution. The water body indicators did not exhibit strong variability in this area, except for the large water bodies, which was tentatively judged to be related to the local climate’s hot and humid characteristics. Third, for the topography and geomorphology indicators, the elevation data reflect the characteristics of the mountainous city of Chongqing. The barrier created by the mountains results in a polycentric city distribution, and it also affects the distribution of the urban thermal environment. Fourth, the landscape pattern indicated a high correlation between urban planning and land use, reflecting the diversity and dispersion of the landscape pattern within the city. Except for the patch cohesion indicator, the other indicators exhibited low clustering in the built-up area. It was found that the patch cohesion indicator was positively correlated with the LST, whereas the other indicators were negatively correlated.

3.2.2. Results of Principal Component Analysis of Driving Factors

The results of the PCA are presented in

Table 4. Eigenvalues and contribution rates of principal components.

Component	Initial Eigenvalue			Extraction of the Sum of Squares of Loads
	Total	Contribution (%)	Cumulative Contribution (%)	Total	Percentage of Variance (%)	Cumulative Contribution (%)
1	3.874	32.281	32.281	3.874	32.281	32.281
2	2.463	20.525	52.806	2.463	20.525	52.806
3	1.303	10.861	63.667	1.303	10.861	63.667
4	1.135	9.456	73.123	1.135	9.456	73.123
5	0.870	7.250	80.373
6	0.710	5.918	86.291
7	0.616	5.132	91.423
8	0.406	3.382	94.806
9	0.262	2.187	96.993
10	0.221	1.838	98.831
11	0.122	1.016	99.847
12	0.018	0.153	100.000

. The first four principal components have eigenvalues of greater than 1, which indicates that these four principal components can explain the spatial distribution characteristics of the urban thermal environment to some extent. The information loadings of each associated factor in each principal component were also obtained (

Table 5. Principal component score loading matrix.

Factor	First Principal Component	Second Principal Component	Third Principal Component	Fourth Principal Component
Population density	0.062	0.406	−0.045	0.065
POI density	0.060	0.435	−0.016	0.171
Nighttime light intensity	0.056	0.292	−0.042	−0.091
NDISI	0.056	0.099	−0.545	−0.059
MNDWI	−0.046	−0.029	0.512	0.027
FVC	−0.028	−0.040	−0.080	0.329
DEM	−0.024	0.133	−0.027	0.517
Slope	−0.071	0.117	0.146	0.555
DIVISION	0.367	0.059	−0.051	−0.047
CONTAG	0.036	−0.215	0.142	−0.124
SHDI	0.364	0.045	−0.035	−0.049
COHESION	−0.342	−0.048	0.039	0.010

). The larger the coefficient is, the greater the role of this factor in the principal component. This can be used to analyze the main types of principal components, and the main factors affecting the thermal environment of the study area were determined to be the landscape pattern, socio-economic conditions, impervious surfaces, water bodies, topography, and vegetation (Figure 6).

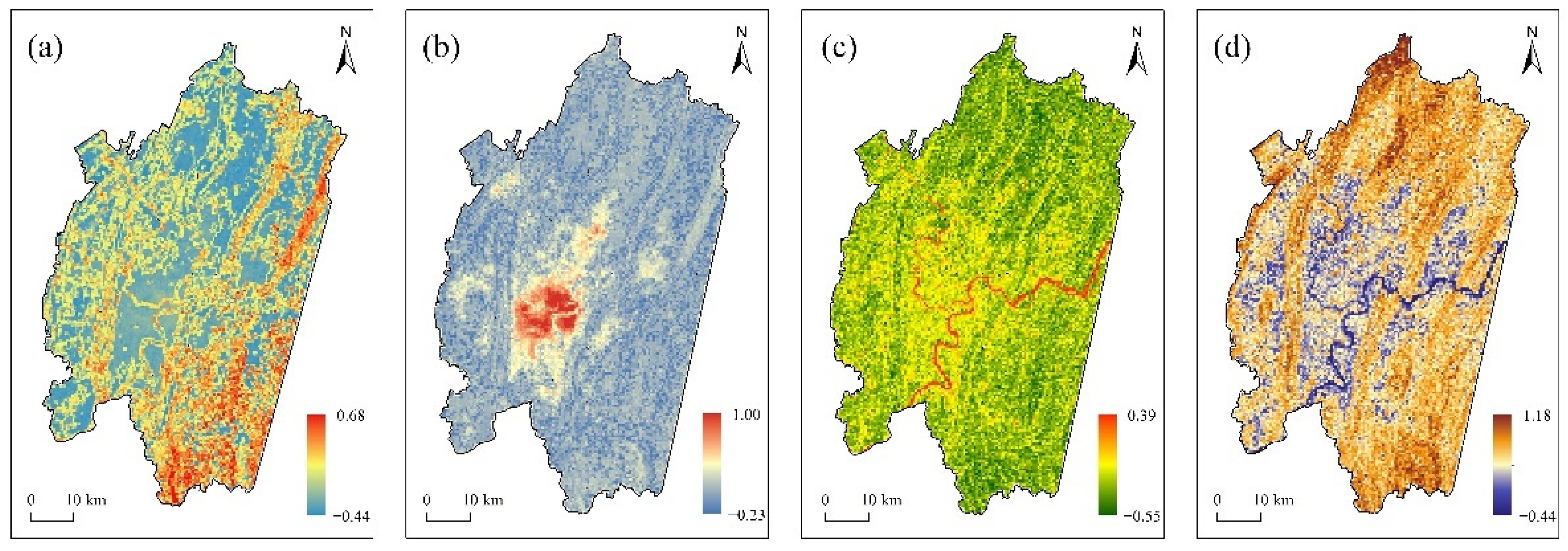
According to Figure 6, the first principal component was comprised of the influence of landscape characteristics, in which the landscape types were mainly construction land, forest land, arable land, grassland, bare land, and water bodies. The built-up area was the area with a concentration of high patch cohesion indicator values, whereas the values of the remaining indicators were low, indicating that the single and clustered land use types and sparse vegetation in the built-up area were the main reason for the increase in the surface temperature. In contrast, the cooling effect was obvious in the southeast due to the coexistence of green areas and various landscape types. The second principal component was comprised of the influence of socio-economic indicators, including the population density, POI density, and nighttime light intensity. The distribution pattern was highly consistent with the distributions of the thermal environment, indicating that a series of changes caused by socio-economic development was a major causal factor leading to the intensification of the urban thermal environment. The normalized water body indicator and the normalized imperviousness indicator were the main factors of the third principal component. The main influence of the water bodies was represented by the Yangtze River and the Jialing River, which are the main water bodies in the central urban area of Chongqing. The replacement of natural surfaces with impervious surfaces during urban construction was also a main cause of the intensification of the urban thermal environment. However, combined with the information loadings value, the degree of influence of the NDISI in terms of the principal component was higher than that of MNDWI to a certain extent. The fourth principal component was comprised of the influence of topography and vegetation. The mountainous features of the central urban area of Chongqing are obvious. The high mountain ranges are not conducive to air circulation, the heat diffusion rate of the flat land between the mountains was slow, and the gentle terrain resulted in these areas being the main clustering place for urban construction and the main area for heat production. Therefore, the topographic features of the mountainous city are an integral part of the thermal environment-associated factors. Among all principal components, CONTAG only exhibited a small degree of information loading in the first principal component, whereas it showed certain information loading in the other principal components, indicating that it had a potential influence on the mechanism and may require further research.

3.2.3. Simulation of the Relationships between the Surface Temperature and Driving Factors

In order to further study the fitness of each seasonal influencing factor in regard to the spatial distribution of LST, a linear fit analysis of each principal component to the surface temperature data was performed using SPSS, and the results are shown in

Table 6. Regression coefficients and test results.

Factor	Unstandardized Coefficient		Standardized Coefficient	T	p	Multicollinearity
	B	Standard Error	Beta			Tolerance	VIF
Spring	0.334	0.002	-	204.906	<0.001	-	-
First	−0.137	0.003	−0.285	−48.346	<0.001	0.988	1.012
Second	0.124	0.005	0.161	26.133	<0.001	0.906	1.104
Third	−0.433	0.008	−0.429	−51.608	<0.001	0.496	2.015
Fourth	−0.292	0.004	−0.645	−76.129	<0.001	0.478	2.093
Summer	0.296	0.002	-	142.899	<0.001	-	-
First	−0.128	0.004	−0.202	−35.642	0.000	0.988	1.012
Second	0.224	0.006	0.219	37.008	<0.001	0.906	1.104
Third	−0.311	0.011	−0.232	−29.122	<0.001	0.496	2.015
Fourth	−0.376	0.005	−0.627	−77.132	<0.001	0.478	2.093
Autumn	0.388	0.002	-	256.218	<0.001	-	-
First	−0.108	0.003	−0.255	−41.075	<0.001	0.988	1.012
Second	0.133	0.004	0.195	30.114	<0.001	0.906	1.104
Third	−0.258	0.008	−0.289	−32.995	<0.001	0.496	2.015
Fourth	−0.201	0.004	−0.503	−56.331	<0.001	0.478	2.093
Winter	0.479	0.001	-	374.281	<0.001	-	-
First	−0.103	0.002	−0.248	−46.193	<0.001	0.988	1.012
Second	0.048	0.004	0.071	12.734	<0.001	0.906	1.104
Third	−0.261	0.007	−0.299	−39.455	<0.001	0.496	2.015
Fourth	−0.304	0.003	−0.778	−100.750	<0.001	0.478	2.093

. In Table 6, the significance coefficients are less than 1%, and VIF is less than 10, so the model does not have multicollinearity. As a consequence, the four components are the main associated factors.

The normalized coefficients obtained from Table 6 were used to transform the principal component score loadings, and the results are presented in

Table 7. Specific effect coefficients of impact factors.

Factor	Spring	Summer	Autumn	Winter
Population density	0.025	0.046	0.044	−0.024
POI density	−0.051	−0.021	−0.012	−0.112
Nighttime light intensity	0.108	0.120	0.101	0.091
NDISI	0.272	0.174	0.192	0.202
MNDWI	−0.229	−0.133	−0.155	−0.165
FVC	−0.176	−0.191	−0.143	−0.228
DEM	−0.294	−0.284	−0.220	−0.379
Slope	−0.382	−0.342	−0.280	−0.449
DIVISION	−0.043	−0.019	−0.043	−0.035
CONTAG	−0.026	−0.009	−0.030	0.030
SHDI	−0.050	−0.025	−0.049	−0.038
COHESION	0.067	0.043	0.062	0.062
Total	−0.778	−0.642	−0.535	−1.045

, where the coefficients in the table indicate the unit amount of change in the surface temperature caused by each unit change in the corresponding associated factor. According to Table 7, among the 12 associated factors, the factors that had a high ability to influence LST in the study area were the slope, elevation, normalized imperviousness indicator, normalized water body indicator, fractional vegetation cover, and nighttime light intensity, whereas the landscape pattern indicator, population, and POI density showed a low influence. It can be seen that, under the combined effect of the multiple factors, the influence of some driving factors of LST begins to become less obvious, especially the driving factors of social attributes, whereas the factors of natural attributes can maintain a high capacity for influence.

By adding the coefficients of different driving factors corresponding to each season, the total effect value of the influence of various driving factors on temperature in this season can be obtained. A comprehensive analysis of the main influencing factors revealed that for each unit change of the 12 factors, the temperature changed by 0.778 units in spring, by 0.642 units in summer, by 0.535 units in autumn, and by 1.045 units in winter. Therefore, the combined influence of the positive associated factors identified in this study was lower than that of the negative factors. In addition, the strength of the combined effect of the driving factors had a certain seasonality, taking the following order: winter > spring > summer > autumn.

4. Discussion

In this study, the distribution pattern of the thermal environment in different seasons and years was analyzed. Based on the distribution of the urban high-temperature zones, the partitioning effect of the mountains and water bodies in mountainous cities also caused their thermal environments to appear polycentric and grouped [35]. The climatic characteristics of the different seasons affected the intensity and spatial distribution of the thermal environment. The high temperature and high humidity led to a more significant thermal environment effect in summer, whereas the low temperature and dryness in winter weakened the heat island effect. Through principal component analysis of multiple associated factors and linear fitting with respect to temperature, it was determined that only 6 of the 12 associated factors played an obvious role in the comprehensive influence: slope, elevation, the normalized imperviousness indicator, the normalized water body indicator, fractional vegetation cover, and nighttime light intensity. Natural factors played a more important role than human factors, and topographic factors were much more influential than the rest of the factors, reflecting the importance of topography in mountainous cities. Therefore, making full use of the topographic features of cities is necessary in order to improve the thermal environment in mountainous cities.

Compared to the results of previous studies, we found that the correlation between the landscape pattern indicator [22] and the thermal environment was not significant in the study area of Chongqing. According to our preliminary analysis, the mountainous barrier resulted in the distribution of the built-up areas being more dispersed, which weakened the influence of the landscape pattern within the city on the thermal environment. On the other hand, in this study we only analyzed its influence on the urban scale, mainly at the two-dimensional scale, whereas in recent years, studies of the relationship between landscape pattern and thermal environment have begun to focus on the three-dimensional scale and have achieved certain results [23,36,37]. Second, the coefficient of the topographic factor was higher under the combined effect of multiple factors, indicating that the role of topography is much greater than that of the other factors in mountainous cities [38]. Finally, the results of the comprehensive multi-factor analysis differed from the results of the simple correlation analysis. In previous correlation studies, the population density and POI density were found to be important correlation factors of the thermal environment [20], but the influence of both was determined to be low based on the comprehensive analysis conducted in this study, and we found that the nighttime light intensity can explain the influence of socioeconomic activities on the thermal environment more scientifically.

The main contribution of this study is the introduction of the concept of seasonal analysis and to analyze the combined effect of multiple factors. Most previous studies conducted on urban thermal environments were based on summer surface temperature or annual average surface temperature data [16,21,22,38,39]. In this study, a seasonal analysis method was used, which improved the comprehensiveness and scientific relevance of the research results to a certain extent. For instance, the effects of the water bodies were different in the different seasons in 2020 (see Section 3.1.2), and the results of the equal sector analysis in summer did not accurately reflect the spatial evolution of the thermal environment. In this study, PCA was used and the quantitative output of the comprehensive effect of multiple factors was achieved through linear fitting transformation in the comprehensive impact analysis of the multiple associated factors. Compared with one-sided correlation analysis [20,21], this method is superior in the comprehensive analysis of multiple factors and can be used as a reference for the study of the mechanisms by which multiple factors influence the urban thermal environment.

Further research can be conducted in the following aspects in the future. Firstly, the daily and nightly LST changes and their driving mechanisms can be analyzed on the basis of this study. Secondly, in the study of driving mechanisms, the selection of driving factors can be further enriched. For example, research on meteorological data such as wind and humidity with seasonal characteristics will also make the research results more significant and accurate. Thirdly, in this study, the differential characteristics of the water bodies in the four seasons during 2020 were also identified. The relationship between this feature and the urban surface temperature needs to be explored further to determine if the phenomenon is caused by the intensification of the thermal environment. Furthermore, this study was conducted at the scale of the whole city, and subsequent multi-scale analysis of this area of research can be carried out, such as further exploration of the distribution characteristics and the influencing mechanisms at the scale of functional areas and local climate zones, as well as the mechanisms by which the driving factors influence the urban thermal environment in order to obtain more comprehensive and thorough research results.

5. Conclusions

With the technical support of GIS, based on data from multiple sources, in this study, quantitative and qualitative analyses of the interannual and seasonal variation in the spatial distribution of the land surface thermal environment were conducted, using a combination of equal sector analysis, mathematical statistics, and principal component analysis. In addition, the mechanism by which multiple integrated human and natural factors affect the urban thermal environment in different seasons was explored.

The land surface thermal environment in the study area had a clear spatial correlation with the built-up area. From 2010 to 2020, with the continuous increase in the built-up area, the area of sub-high- and high-temperature zones also expanded, and the main growth points were located in the northeastern, northern, northwestern, and western parts of the study area—namely, the Liangjiang New Area and the western high-tech zone in Chongqing—with an increase of more than 35%.

The variation in the thermal environment exhibited interannual and seasonal differences. Regarding the distribution of the temperature zones of all of the levels in the different seasons, sub-low, medium, and sub-high temperatures were the major temperature ranges, accounting for nearly 90% of the total study area. From 2010 to 2020, a decrease in low-temperature zones and an increase in high-temperature zones were the main trends, with summer being the season with the most significant urban thermal environment effects, especially in 2020, in which the low-temperature zones almost disappeared and the areas of the high-temperature zones were nearly twice as large as in the other seasons.

The combined influence of multiple driving factors on the surface temperature exhibited certain seasonal characteristics. The slope, elevation, normalized water body indicator, fractional vegetation cover, normalized imperviousness indicator, and nighttime light intensity were the main factors affecting the surface temperature, whereas the landscape pattern indicator, population density, and POI density had a low level of influence. The strength of the combined influence of the multiple factors in each season exhibited the following order: winter > spring > summer > autumn.