The Potential of Sentinel-1A Data for Identification of Debris-Covered Alpine Glacier Based on Machine Learning Approach
Abstract
1. Introduction
2. Research Sites and Data
2.1. Research Sites
2.2. Data
2.2.1. Sentinel-1 Data
2.2.2. Landsat 8 OLI Data
2.2.3. ALOS Digital Surface Model Data
3. Methodology
3.1. Target Polarimetric Decomposition
3.2. SAR Interferometry
3.3. Texture Calculation
3.4. Data Suite Creation
3.5. Integrated Machine Learning Method
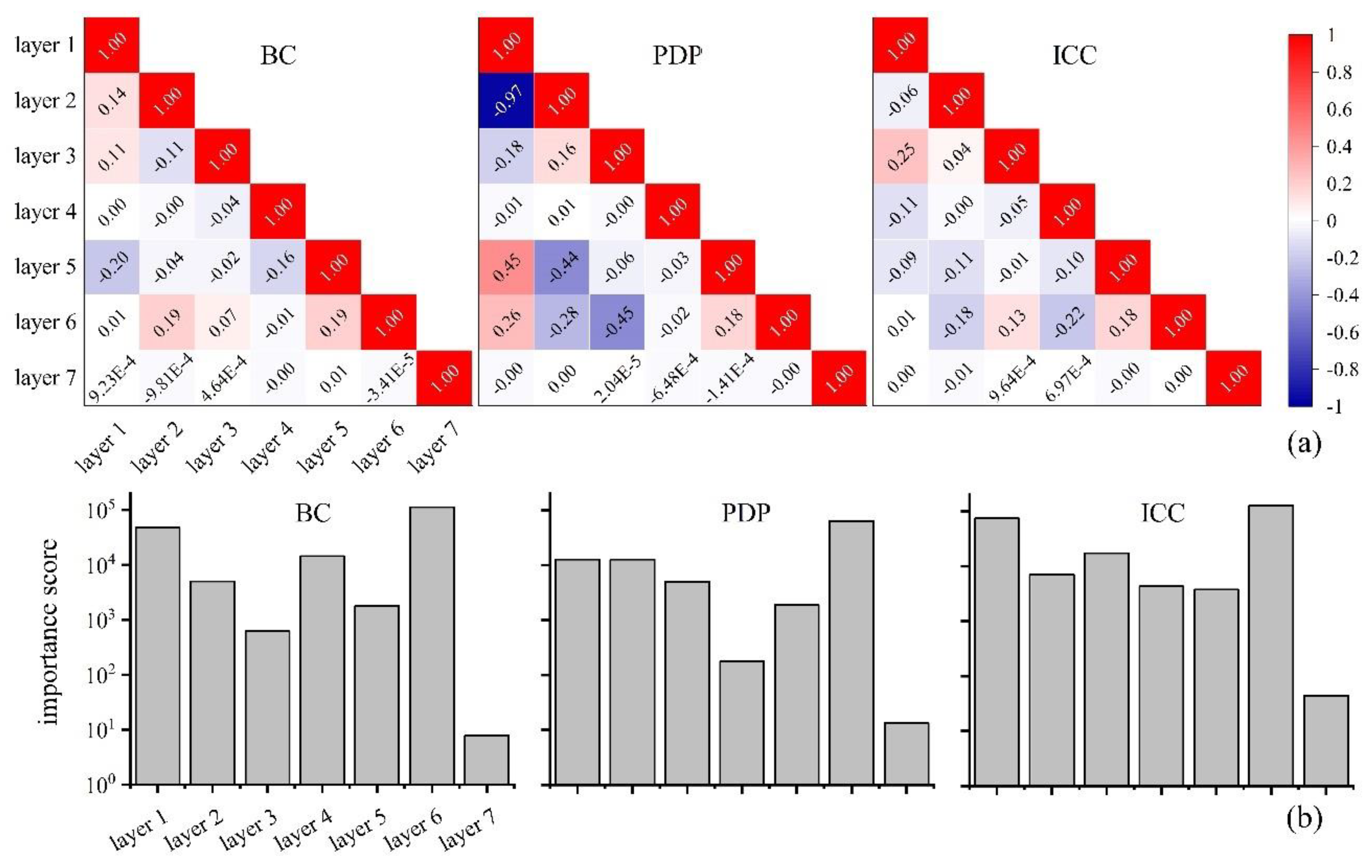
3.6. Feature Importance Calculation
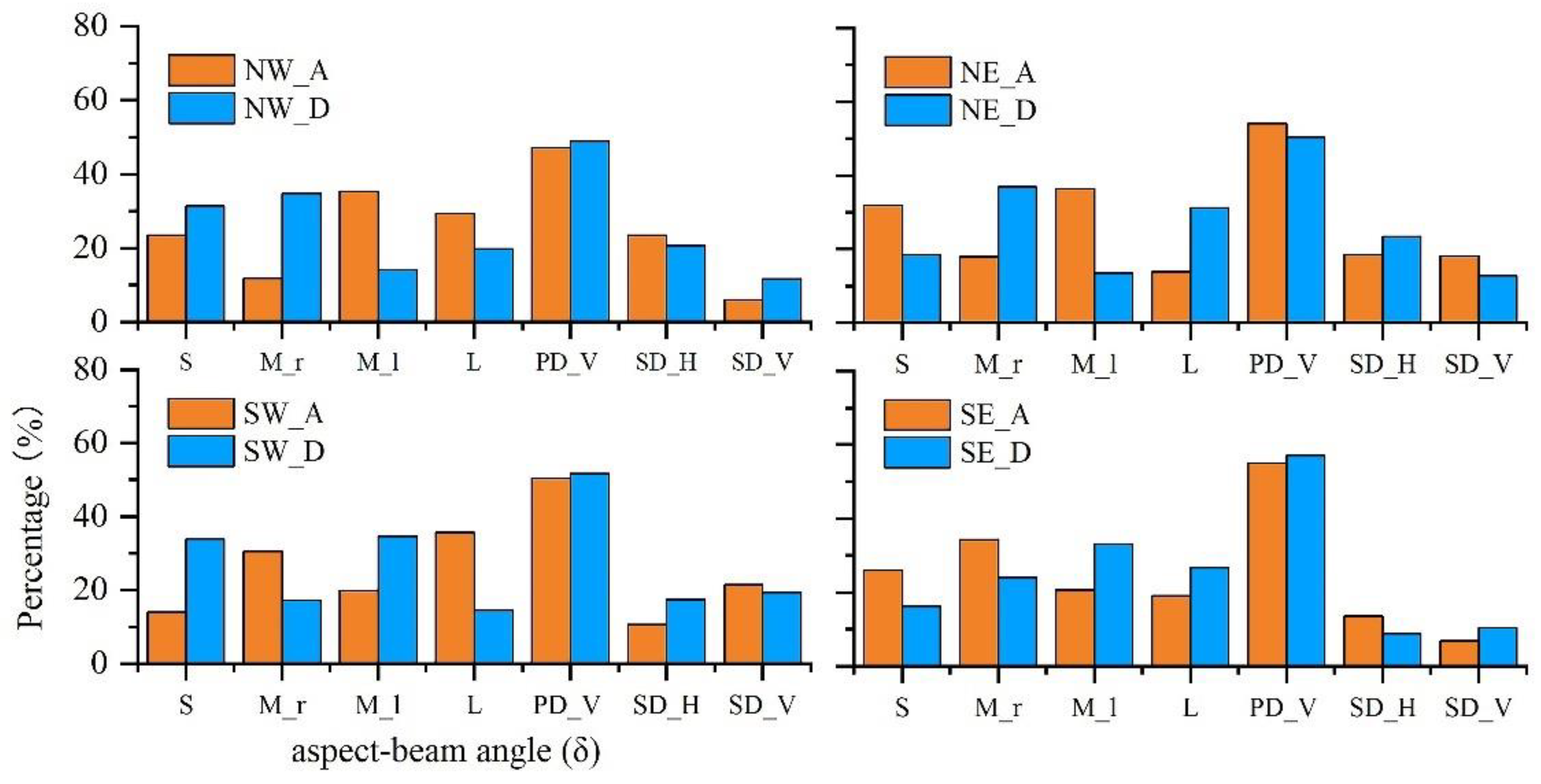
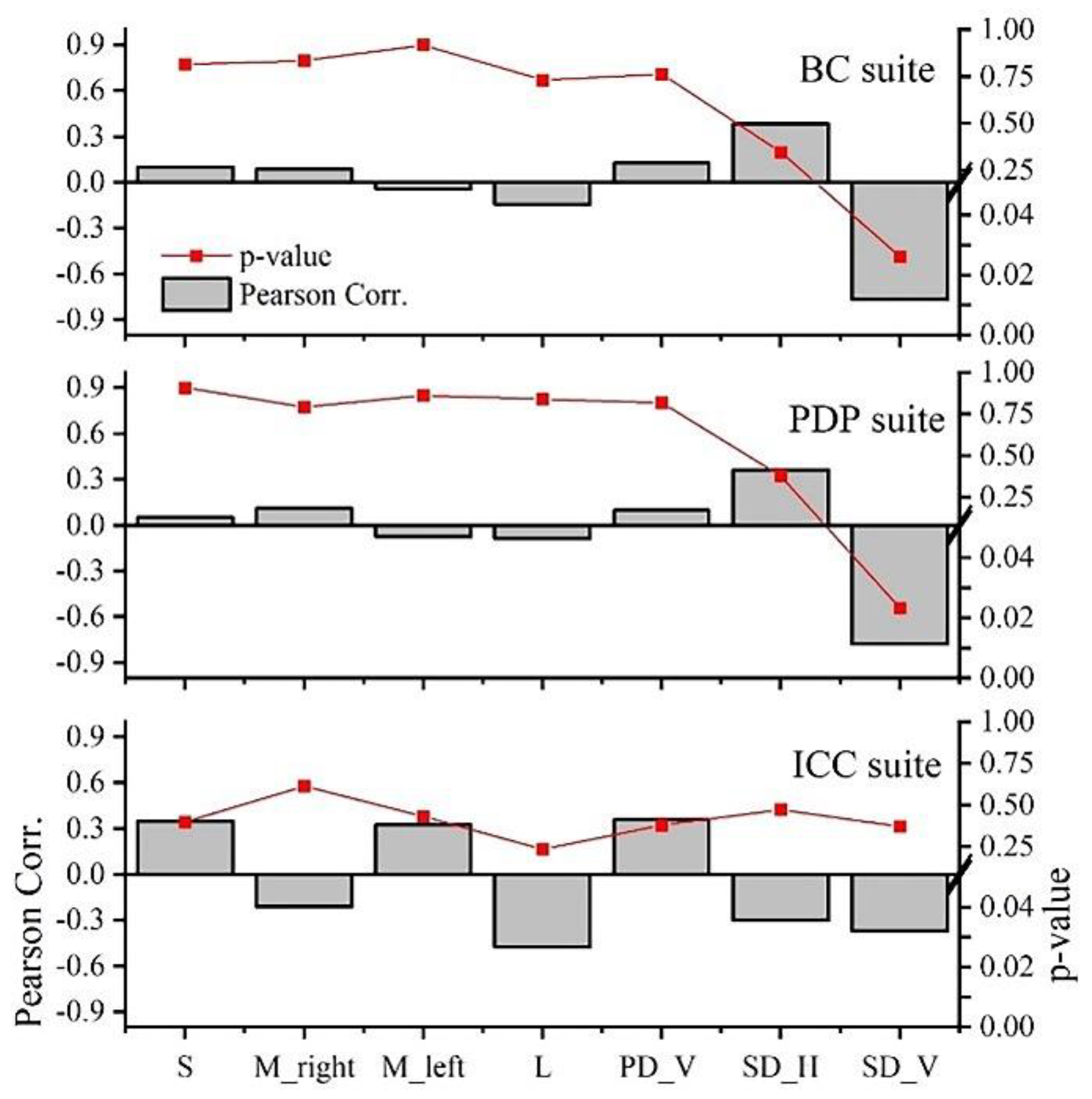
3.7. Aspect-Beam Angle
- S (small): δ values ranging from 0 to 45 degrees and 315 to 360 degrees, representing total forward scattering;
- M (medium): δ values ranging from 45 to 135 degrees and 225 to 315 degrees, with the former called M_r and the latter called M_l, since they are located on the right and left sides of the direction of the radar beam propagation; they both represent a mixture of forward and backscattering scattering;
- L (large): δ values ranging from 135 to 225 degrees, representing total backscattering.
4. Results
4.1. Aspect-Beam Angle in Four Glaciers
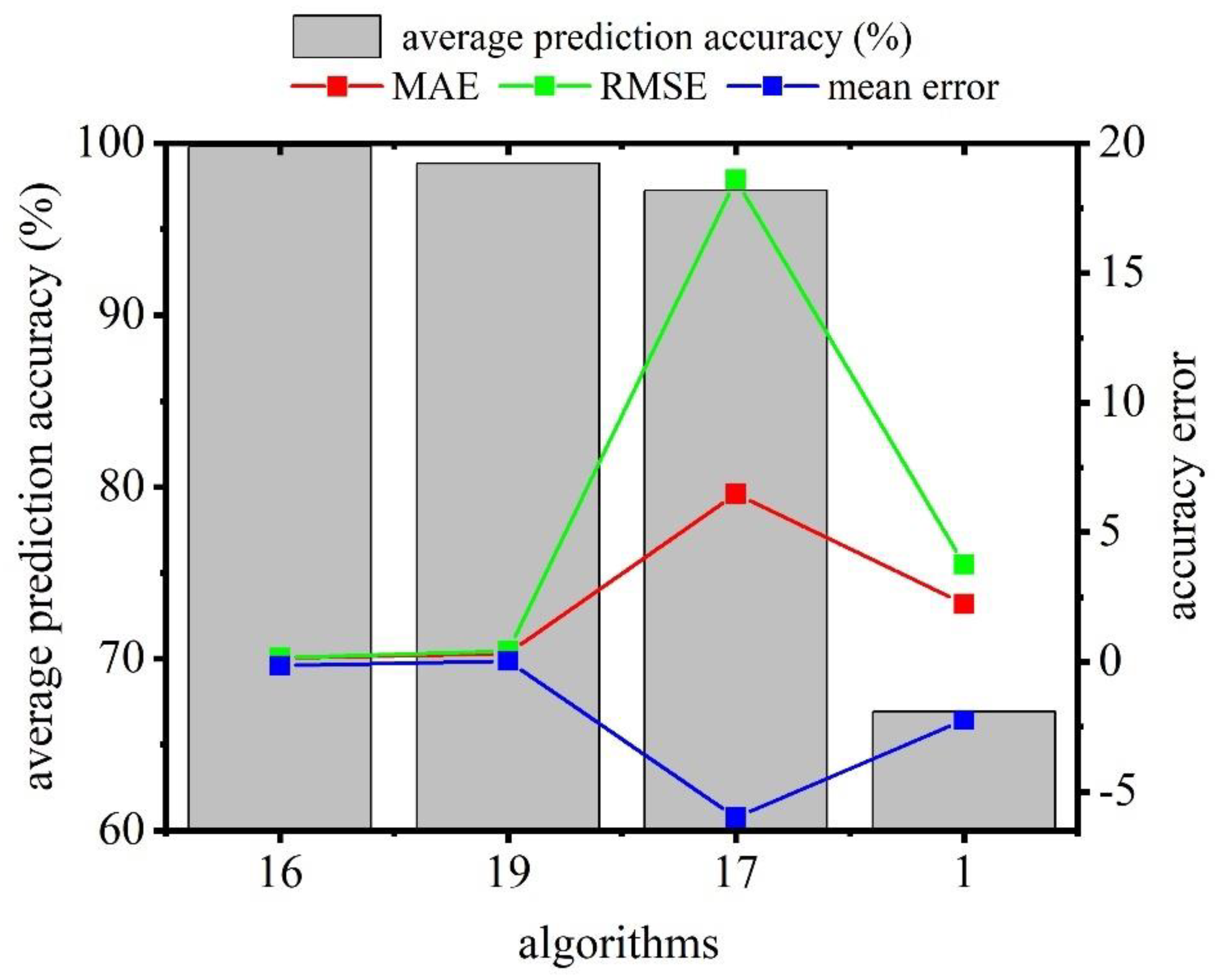
4.2. Machine Learning Classification Models
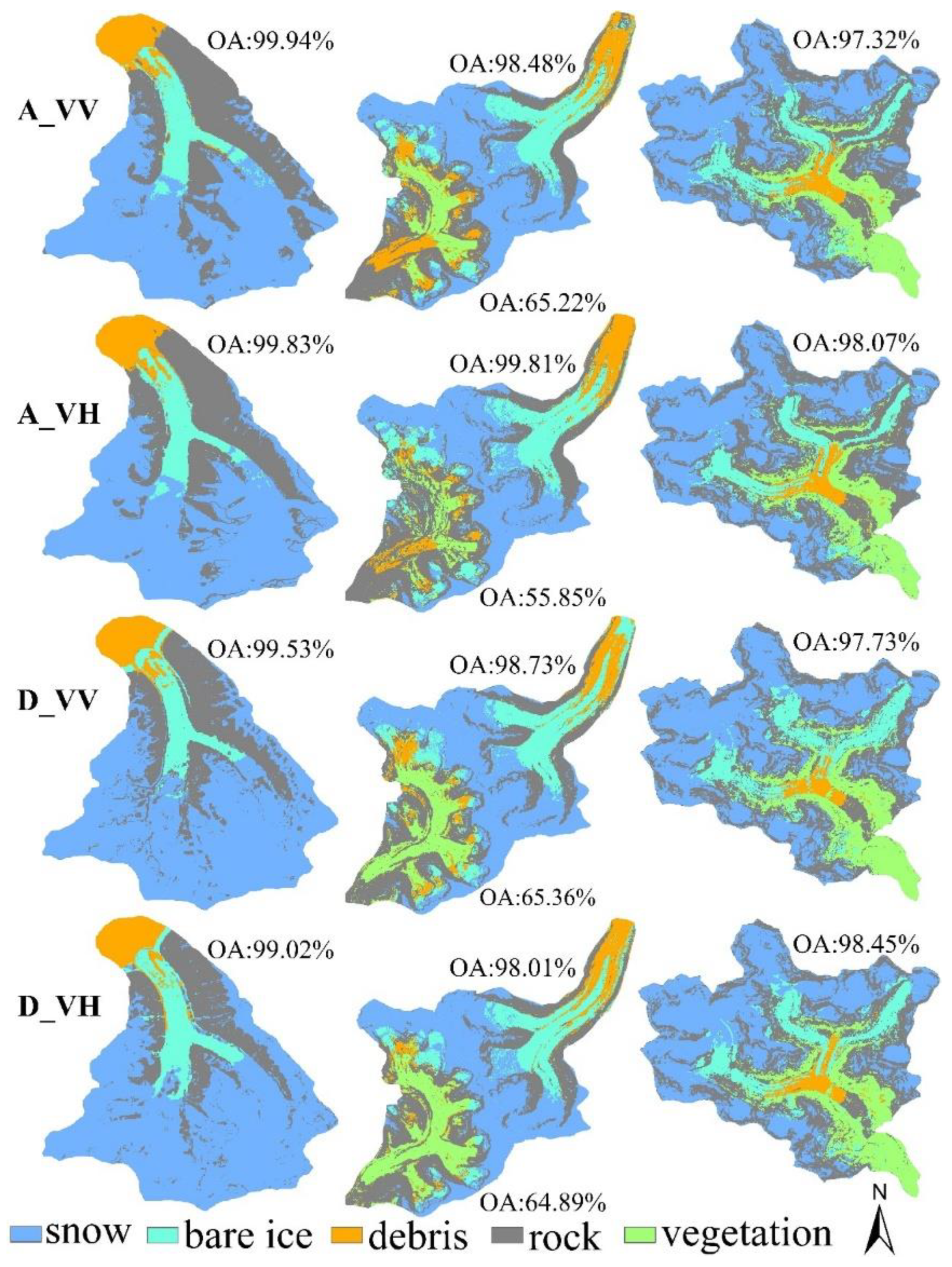
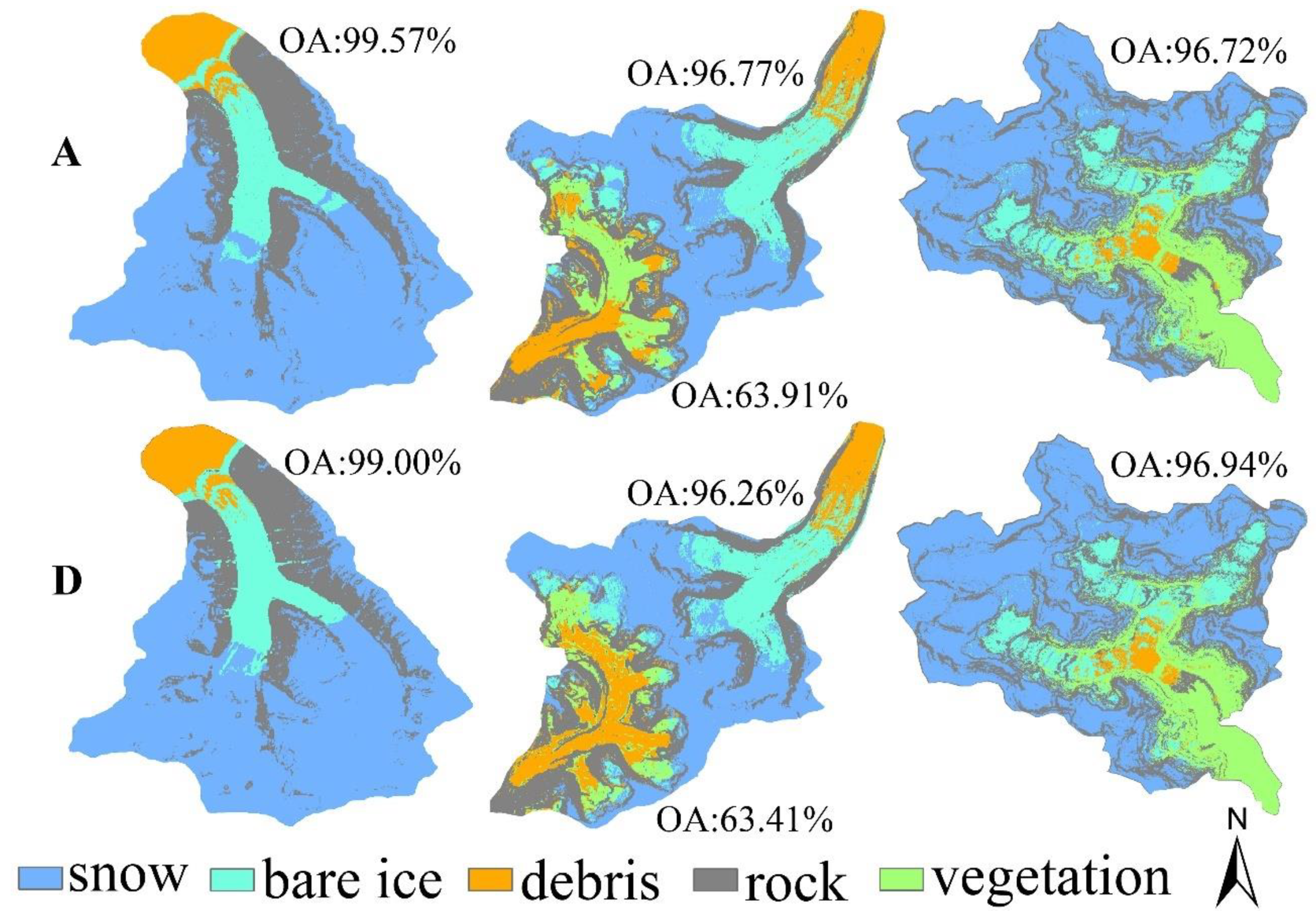
4.3. Classification Results from Different Data Suites
5. Discussion
5.1. Importance Analysis of Features
5.2. Impact of Data Suite on Glacier Identification
5.3. Impact of Glacial Aspect on Recognition
5.4. Uncertainties and Possible Transferability Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A_VH | The VH polarization mode under the ascending node |
| A_VV | The VV polarization mode under the ascending node |
| BC | Backscattering Coefficient |
| D_VH | The VH polarization mode under the descending node |
| D_VV | The VV polarization mode under the descending node |
| GLCM | Gray level co-occurrence matrix |
| ICC | Interference Coherence Coefficient |
| KNN | K-nearest neighbor |
| L | The angle between glacier surface orientation and radar beam propagation direction is between 135–225 degrees |
| M | The angle between glacier surface orientation and radar beam propagation direction is between 45–135 degrees or 225–315 degrees, the former is also called M_r, the latter is called M_l |
| NE | One of the four study sites, located in the middle of the Himalayas, the main orientation of the glacier is northeast |
| NW | One of the four study sites, located in the northwestern part of the TP, the main orientation of the glacier is northwest |
| OA | Overall Accuracy |
| PDP | Polarization Decomposition Parameter |
| PD_V | Percentage of the glacier surface orientation perpendicular to the radar beam direction |
| S | The angle between glacier surface orientation and radar beam propagation direction is between 0–45 degrees or 315–360 degrees |
| SD_H | Symmetry of the glacier surface orientation with respect to the plane parallel to the radar beam direction. |
| SD_V | Symmetry of the glacier surface orientation with respect to the plane perpendicular to the radar beam direction. |
| SE | One of the four study sites, located in the southeast part of the TP, the main orientation of the glacier is southeast |
| SLC | Single-Look Complex |
| SVM | support vector machine |
| SW | One of the four study sites, located in the middle of the Himalayas, the main orientation of the glacier is southwest |
| TP | Qinghai-Tibet Plateau |
References
- Cao, S.X.; Zhang, J.Z. Political risks arising from the impacts of large-scale afforestation on water resources of the Tibetan Plateau. Gondwana Res. 2015, 28, 898–903. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Immerzeel, W.W.; Van Beek, L.P.H.; Bierkens, M.F.P. Climate change will affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The Concept of Essential Climate Variables in Support of Climate Research, Applications, and Policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.W.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I.; et al. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef]
- Tapponnier, P.; Zhiqin, X.; Roger, F.; Meyer, B.; Arnaud, N.; Wittlinger, G.; Jingsui, Y. Oblique Stepwise Rise and Growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef]
- Molnar, P.; Boos, W.R.; Battisti, D.S. Orographic Controls on Climate and Paleoclimate of Asia: Thermal and Mechanical Roles for the Tibetan Plateau. Annu. Rev. Earth Planet. Sci. 2010, 38, 77–102. [Google Scholar] [CrossRef]
- Wijngaard, R.R.; Steiner, J.F.; Kraaijenbrink, P.D.A.; Klug, C.; Adhikari, S.; Banerjee, A.; Pellicciotti, F.; Van Beek, L.P.H.; Bierkens, M.F.P.; Lutz, A.F.; et al. Modeling the Response of the Langtang Glacier and the Hintereisferner to a Changing Climate Since the Little Ice Age. Front. Earth Sci. 2019, 7, 143. [Google Scholar] [CrossRef]
- Kääb, A. Combination of SRTM3 and repeat ASTER data for deriving alpine glacier flow velocities in the Bhutan Himalaya. Remote Sens. Environ. 2005, 94, 463–474. [Google Scholar] [CrossRef]
- Racoviteanu, A.E.; Williams, M.W.; Barry, R.G. Optical Remote Sensing of Glacier Characteristics: A Review with Focus on the Himalaya. Sensors 2008, 8, 3355–3383. [Google Scholar] [CrossRef]
- Rabatel, A.; Dedieu, J.-P.; Vincent, C. Using remote-sensing data to determine equilibrium-line altitude and mass-balance time series: Validation on three French glaciers, 1994–2002. J. Glaciol. 2005, 51, 539–546. [Google Scholar] [CrossRef]
- Alifu, H.; Vuillaume, J.-F.; Johnson, B.A.; Hirabayashi, Y. Machine-learning classification of debris-covered glaciers using a combination of Sentinel-1/-2 (SAR/optical), Landsat 8 (thermal) and digital elevation data. Geomorphology 2020, 369, 107365. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Tian, B.S.; Han, H.D.; Liu, Y.Q.; Zhou, J.M.; Chen, Q. Estimation of supraglacial debris thickness using a novel target decomposition on L-band polarimetric SAR images in the Tianshan Mountains. J. Geophys. Res. Earth Surf. 2017, 122, 925–940. [Google Scholar] [CrossRef]
- Huang, L.; Tian, B.-S.; Li, Z.; Zhou, J.-M. Scattering Property Analysis of Supraglacial Debris Using Target Decomposition on Polarimetric SAR Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1843–1852. [Google Scholar] [CrossRef]
- Zhang, G.; Cui, H.; Wang, T.; Li, Z.; Jiang, B.; Li, X.; Wang, H.; Zhu, Y. Random cross-observation intensity consistency method for large-scale SAR images mosaics: An example of Gaofen-3 SAR images covering China. ISPRS J. Photogramm. Remote Sens. 2019, 156, 215–234. [Google Scholar] [CrossRef]
- Wangchuk, S.; Bolch, T.; Zawadzki, J. Towards automated mapping and monitoring of potentially dangerous glacial lakes in Bhutan Himalaya using Sentinel-1 Synthetic Aperture Radar data. Int. J. Remote Sens. 2019, 40, 4642–4667. [Google Scholar] [CrossRef]
- Friedman, K.S.; Clemente-Colón, P.; Pichel, W.G.; Li, X. Routine Monitoring of Changes in the Columbia Glacier, Alaska, with Synthetic Aperture Radar. Remote Sens. Environ. 1999, 70, 257–264. [Google Scholar] [CrossRef]
- Richards, J.A. The technology of radar imaging. In Remote Sensing with Imaging Radar, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 81–85. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Akbari, V.; Doulgeris, A.P.; Eltoft, T. Monitoring Glacier Changes Using Multitemporal Multipolarization SAR Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3729–3741. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Tian, B.-S.; Chen, Q.; Liu, J.-L.; Zhang, R. Classification and snow line detection for glacial areas using the polarimetric SAR image. Remote Sens. Environ. 2011, 115, 1721–1732. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Tian, B.-S.; Zhou, J.-M.; Chen, Q. Recognition of supraglacial debris in the Tianshan Mountains on polarimetric SAR images. Remote Sens. Environ. 2014, 145, 47–54. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Minchew, B.M. Polarimetric SAR Decomposition of Temperate Ice Cap Hofsjökull, Central Iceland. Master’s Thesis, The University of Texas, Austin, TX, USA, 2010. [Google Scholar]
- Parrella, G.; Hajnsek, I.; Papathanassiou, K.P. Polarimetric Decomposition of L-Band PolSAR Backscattering Over the Austfonna Ice Cap. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1267–1281. [Google Scholar] [CrossRef]
- Yao, G.-H.; Ke, C.-Q.; Zhou, X.; Lee, H.; Shen, X.; Cai, Y. Identification of Alpine Glaciers in the Central Himalayas Using Fully Polarimetric L-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 691–703. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Tian, B.-S.; Chen, Q.; Zhou, J.-M. Monitoring glacier zones and snow/firn line changes in the Qinghai–Tibetan Plateau using C-band SAR imagery. Remote Sens. Environ. 2013, 137, 17–30. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Lippl, S.; Vijay, S.; Braun, M. Automatic delineation of debris-covered glaciers using InSAR coherence derived from X-, C- and L-band radar data: A case study of Yazgyl Glacier. J. Glaciol. 2018, 64, 811–821. [Google Scholar] [CrossRef]
- Wang, T.; Liao, M.S.; Perissin, D. InSAR Coherence-Decomposition Analysis. IEEE Geosci. Remote Sens. Lett. 2010, 7, 156–160. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Rott, H.; Moreira, A. Characterization of Snow Facies on the Greenland Ice Sheet Observed by TanDEM-X Interferometric SAR Data. Remote Sens. 2017, 9, 315. [Google Scholar] [CrossRef]
- Blaes, X.; Defourny, P. Retrieving crop parameters based on tandem ERS 1/2 interferometric coherence images. Remote Sens. Environ. 2003, 88, 374–385. [Google Scholar] [CrossRef]
- Capps, D.M.; Rabus, B.; Clague, J.J.; Shugar, D.H. Identification and characterization of alpine subglacial lakes using interferometric synthetic aperture radar (InSAR): Brady Glacier, Alaska, USA. J. Glaciol. 2010, 56, 861–870. [Google Scholar] [CrossRef]
- Li, S.S.; Benson, C.; Gens, R.; Lingle, C. Motion patterns of Nabesna Glacier (Alaska) revealed by interferometric SAR techniques. Remote Sens. Environ. 2008, 112, 3628–3638. [Google Scholar] [CrossRef]
- Dini, B.; Manconi, A.; Loew, S. Investigation of slope instabilities in NW Bhutan as derived from systematic DInSAR analyses. Eng. Geol. 2019, 259, 105111. [Google Scholar] [CrossRef]
- Frey, H.; Paul, F.; Strozzi, T. Compilation of a glacier inventory for the western Himalayas from satellite data: Methods, challenges, and results. Remote Sens. Environ. 2012, 124, 832–843. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Z.; Huang, L.; Tian, B.; Chen, Q. Extraction of glacier outlines and water-eroded stripes using high-resolution SAR imagery. Int. J. Remote Sens. 2016, 37, 1016–1034. [Google Scholar] [CrossRef]
- Chakraborty, M.; Panigrahy, S.; Kundu, S. Semi-automated Technique to Extract Boundary of Valley/mountain Glaciers using Glacio-morphological Information from Digital Elevation Model. In Proceedings of the ISPRS Technical Commission VIII Symposium, Hyderabad, India, 9–12 December 2014; Volume 40, pp. 511–516. [Google Scholar] [CrossRef][Green Version]
- He, G.; Feng, X.; Xiao, P.; Xia, Z.; Wang, Z.; Chen, H.; Li, H.; Guo, J. Dry and Wet Snow Cover Mapping in Mountain Areas Using SAR and Optical Remote Sensing Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2575–2588. [Google Scholar] [CrossRef]
- Paul, F.; Bolch, T.; Briggs, K.; Kääb, A.; McMillan, M.; McNabb, R.; Nagler, T.; Nuth, C.; Rastner, P.; Strozzi, T.; et al. Error sources and guidelines for quality assessment of glacier area, elevation change, and velocity products derived from satellite data in the Glaciers_cci project. Remote Sens. Environ. 2017, 203, 256–275. [Google Scholar] [CrossRef]
- Thakur, P.K.; Garg, V.; Nikam, B.; Chouksey, A.; Aggarwal, S.P.; Dhote, P.R. Cryospheric Studies in Indian Himalayan and Polar Region: Current Status, Advances and Future Prospects of Remote Sensing. Proc. Natl. Acad. Sci. India A 2017, 87, 593–616. [Google Scholar] [CrossRef]
- Fang, L.; Hoegner, L.; Stilla, U. Automatic mapping of glacier based on sar imagery by benefits of freely optical and thermal data. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 47–51. [Google Scholar] [CrossRef]
- Nagler, T.; Rott, H. Retrieval of wet snow by means of multitemporal SAR data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 754–765. [Google Scholar] [CrossRef]
- Tsai, Y.-L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. A Combination of PROBA-V/MODIS-based Products with Sentinel-1 SAR Data for Detecting Wet and Dry Snow Cover in Mountainous Areas. Remote Sens. 2019, 11, 1904. [Google Scholar] [CrossRef]
- Cai, Y.; Hu, S.; Lang, S.; Guo, Y.; Liu, J. End-to-End Classification Network for Ice Sheet Subsurface Targets in Radar Imagery. Appl. Sci. 2020, 10, 2501. [Google Scholar] [CrossRef]
- Robson, B.A.; Bolch, T.; MacDonell, S.; Hölbling, D.; Rastner, P.; Schaffer, N. Automated detection of rock glaciers using deep learning and object-based image analysis. Remote Sens. Environ. 2020, 250, 112033. [Google Scholar] [CrossRef]
- Fabijańska, A.; Feder, A.; Ridge, J. DeepVarveNet: Automatic detection of glacial varves with deep neural networks. Comput. Geosci. 2020, 144, 104584. [Google Scholar] [CrossRef]
- Blum, A.L.; Langley, P. Selection of relevant features and examples in machine learning. Artif. Intell. 1997, 97, 245–271. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Miles, K.E.; Willis, I.C.; Benedek, C.L.; Williamson, A.G.; Tedesco, M. Toward Monitoring Surface and Subsurface Lakes on the Greenland Ice Sheet Using Sentinel-1 SAR and Landsat-8 OLI Imagery. Front. Earth Sci. 2017, 5, 58. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E.; Scheuchl, B.; Millan, R. Comprehensive Annual Ice Sheet Velocity Mapping Using Landsat-8, Sentinel-1, and RADARSAT-2 Data. Remote Sens. 2017, 9, 364. [Google Scholar] [CrossRef]
- Zhou, C.; Zheng, L.; Sun, Q.; Liu, R. Amery Ice Shelf surface snowmelt detected by ASCAT and Sentinel-1. Remote Sens. Lett. 2019, 10, 430–438. [Google Scholar] [CrossRef]
- Han, H.; Lee, S.; Kim, J.-I.; Kim, S.H.; Kim, H.-C. Changes in a Giant Iceberg Created from the Collapse of the Larsen C Ice Shelf, Antarctic Peninsula, Derived from Sentinel-1 and CryoSat-2 Data. Remote Sens. 2019, 11, 404. [Google Scholar] [CrossRef]
- Howell, S.E.; Small, D.; Rohner, C.; Mahmud, M.S.; Yackel, J.J.; Brady, M. Estimating melt onset over Arctic sea ice from time series multi-sensor Sentinel-1 and RADARSAT-2 backscatter. Remote Sens. Environ. 2019, 229, 48–59. [Google Scholar] [CrossRef]
- Longepe, N.; Thibaut, P.; Vadaine, R.; Poisson, J.-C.; Guillot, A.; Boy, F.; Picot, N.; Borde, F. Comparative Evaluation of Sea Ice Lead Detection Based on SAR Imagery and Altimeter Data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4050–4061. [Google Scholar] [CrossRef]
- Yao, T.D.; Thompson, L.; Yang, W.; Yu, W.S.; Gao, Y.; Guo, X.J.; Yang, X.X.; Duan, K.Q.; Zhao, H.B.; Xu, B.Q.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Yao, T.; Masson-Delmotte, V.; Gao, J.; Yu, W.; Yang, X.; Risi, C.; Sturm, C.; Werner, M.; Zhao, H.; He, Y.; et al. A review of climatic controls on δ18O in precipitation over the Tibetan Plateau: Observations and simulations. Rev. Geophys. 2013, 51, 525–548. [Google Scholar] [CrossRef]
- Alganci, U.; Besol, B.; Sertel, E. Accuracy Assessment of Different Digital Surface Models. ISPRS Int. J. Geo-Inf. 2018, 7, 114. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G. Accuracy assessment of ALOS AW3D30 DSM and comparison to ALOS PRISM DSM created with classical photogrammetric techniques. Eur. J. Remote Sens. 2020, 53, 39–52. [Google Scholar] [CrossRef]
- ALOS@EORC Homepage. Available online: https://www.eorc.jaxa.jp/ALOS/en/index_e.htm (accessed on 15 September 2019).
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/ (accessed on 15 November 2019).
- Lee, J.-S.; Grunes, M.; De Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar] [CrossRef]
- Lee, J.-S.; Pottier, E. H/A/α polarimetric decomposition theorem. In Polarimetric Radar Imaging: From Basics to Applications; Thompson, B.J., Ed.; CRC Press: Boca Raton, FL, USA, 2009; pp. 153–165. [Google Scholar] [CrossRef]
- Guo, J.; Wei, P.-L.; Liu, J.; Jin, B.; Su, B.-F.; Zhou, Z.-S. Crop Classification Based on Differential Characteristics of H/α Scattering Parameters for Multitemporal Quad- and Dual-Polarization SAR Images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6111–6123. [Google Scholar] [CrossRef]
- Ji, K.; Wu, Y. Scattering Mechanism Extraction by a Modified Cloude-Pottier Decomposition for Dual Polarization SAR. Remote Sens. 2015, 7, 7447–7470. [Google Scholar] [CrossRef]
- Shan, Z.L.; Wang, C.; Zhang, H.; Chen, J.H. H-alpha decomposition and Alternative Parameters for Dual Polarization SAR Data. In Proceedings of the Progress in Electromagnetics Research Symposium, Suzhou, China, 12–16 September 2011; pp. 1386–1390. [Google Scholar]
- Cloude, S.R. The dual polarization entropy/alpha decomposition: A PALSAR case study. Sci. Appl. SAR Polarim. Polarim. Interferom. 2007, 644, 2. [Google Scholar]
- Wang, Z.; Li, Z.; Mills, J. A new approach to selecting coherent pixels for ground-based SAR deformation monitoring. ISPRS J. Photogramm. Remote Sens. 2018, 144, 412–422. [Google Scholar] [CrossRef]
- Galeana-Pizaña, J.M.; López-Caloca, A.; López-Quiroz, P.; Silván-Cárdenas, J.L.; Couturier, S. Modeling the spatial distribution of above-ground carbon in Mexican coniferous forests using remote sensing and a geostatistical approach. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 179–189. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Ren, B.; Hou, B.; Zhao, J.; Jiao, L. Unsupervised Classification of Polarimetirc SAR Image Via Improved Manifold Regularized Low-Rank Representation with Multiple Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 580–595. [Google Scholar] [CrossRef]
- Solberg, A.H.S.; Jain, A.K. A study of the invariance properties of textural features in SAR images. In Proceedings of the International Geoscience and Remote Sensing Symposium, Firenze, Italy, 10–14 July 1995; pp. 670–672. [Google Scholar] [CrossRef]
- Dos Reis, A.A.; Franklin, S.E.; de Mello, J.M.; Acerbi, F.W., Jr. Volume estimation in a Eucalyptus plantation using multi-source remote sensing and digital terrain data: A case study in Minas Gerais State, Brazil. Int. J. Remote Sens. 2019, 40, 2683–2702. [Google Scholar] [CrossRef]
- Moya, L.; Zakeri, H.; Yamazaki, F.; Liu, W.; Mas, E.; Koshimura, S. 3D gray level co-occurrence matrix and its application to identifying collapsed buildings. ISPRS J. Photogramm. Remote Sens. 2019, 149, 14–28. [Google Scholar] [CrossRef]
- Wurm, M.; Stark, T.; Zhu, X.X.; Weigand, M.; Taubenböck, H. Semantic segmentation of slums in satellite images using transfer learning on fully convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2019, 150, 59–69. [Google Scholar] [CrossRef]
- Barbat, M.M.; Rackow, T.; Hellmer, H.H.; Wesche, C.; Mata, M.M. Three Years of Near-Coastal Antarctic Iceberg Distribution from a Machine Learning Approach Applied to SAR Imagery. J. Geophys. Res. Oceans 2019, 124, 6658–6672. [Google Scholar] [CrossRef]
- Sonobe, R. Parcel-Based Crop Classification Using Multi-Temporal TerraSAR-X Dual Polarimetric Data. Remote Sens. 2019, 11, 1148. [Google Scholar] [CrossRef]
- Bangira, T.; Alfieri, S.M.; Menenti, M.; Van Niekerk, A. Comparing Thresholding with Machine Learning Classifiers for Mapping Complex Water. Remote Sens. 2019, 11, 1351. [Google Scholar] [CrossRef]
- Zerrouki, N.; Harrou, F.; Sun, Y.; Hocini, L. A Machine Learning-Based Approach for Land Cover Change Detection Using Remote Sensing and Radiometric Measurements. IEEE Sens. J. 2019, 19, 5843–5850. [Google Scholar] [CrossRef]
- Stothert, A. Diagnostic Feature Explorer. MATLB. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/69101-diagnostic-feature-explorer (accessed on 20 January 2022).
- Cai, J.; Wang, X.; Liu, G.; Yu, B. A Comparative Study of Active Rock Glaciers Mapped from Geomorphic- and Kinematic-Based Approaches in Daxue Shan, Southeast Tibetan Plateau. Remote Sens. 2021, 13, 4931. [Google Scholar] [CrossRef]
- Robson, B.A.; Nuth, C.; Dahl, S.O.; Hölbling, D.; Strozzi, T.; Nielsen, P.R. Automated classification of debris-covered glaciers combining optical, SAR and topographic data in an object-based environment. Remote Sens. Environ. 2015, 170, 372–387. [Google Scholar] [CrossRef]
- Winsvold, S.H.; Kääb, A.; Nuth, C.; Andreassen, L.M.; van Pelt, W.J.J.; Schellenberger, T. Using SAR satellite data time series for regional glacier mapping. Cryosphere 2018, 12, 867–890. [Google Scholar] [CrossRef]
- Lu, Y.J.; Zhang, Z.; Kong, Y.R.; Hu, H.K. Integration of optical, SAR and DEM data for automated detection of debris-covered glaciers over the western Nyainqentanglha using a random forest classifier. Cold Reg. Sci. Technol. 2021, 193, 103421. [Google Scholar] [CrossRef]
- Parrella, G.; Hajnsek, I.; Papathanassiou, K.P. Model-Based Interpretation of PolSAR Data for the Characterization of Glacier Zones in Greenland. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11593–11607. [Google Scholar] [CrossRef]
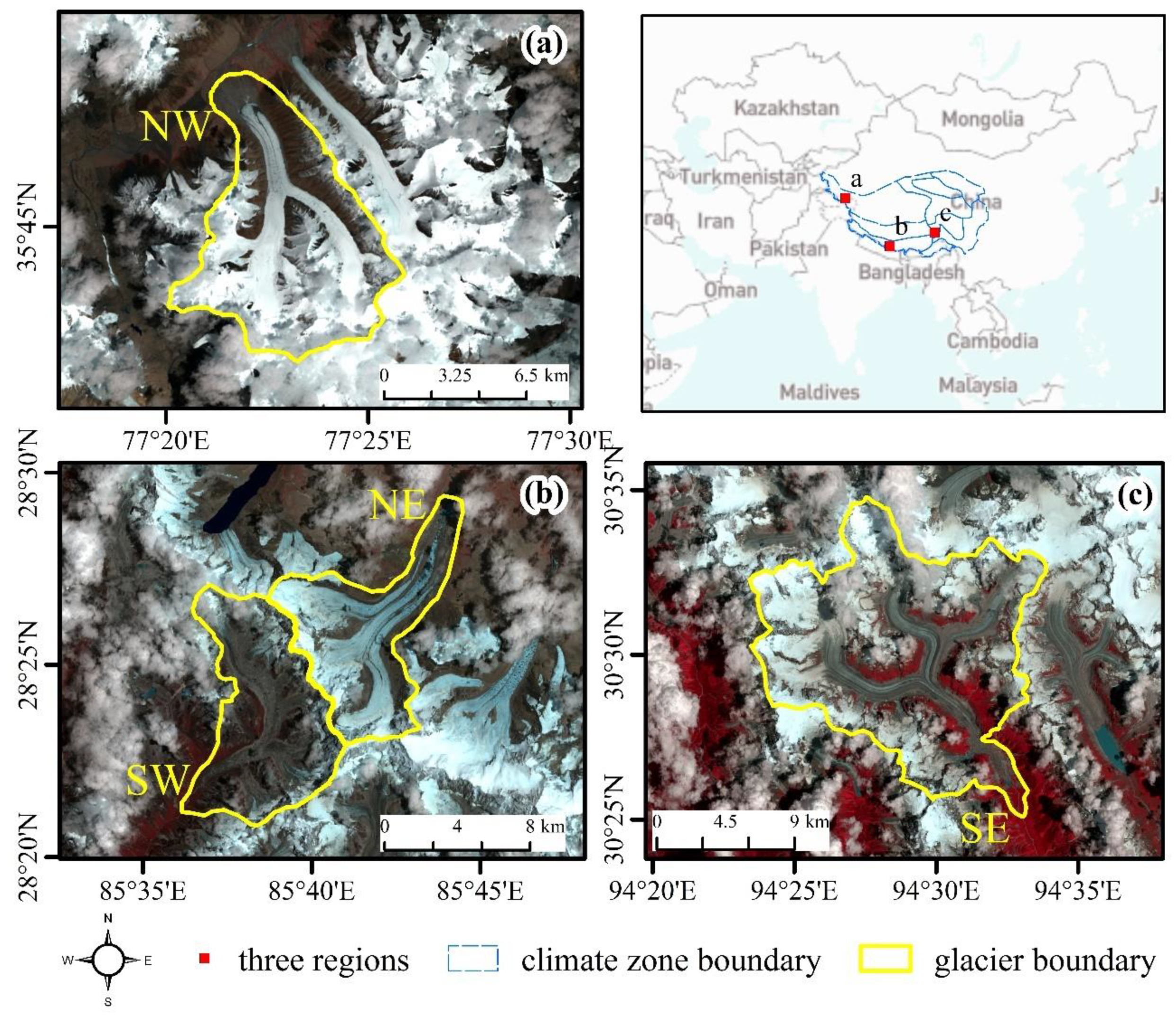

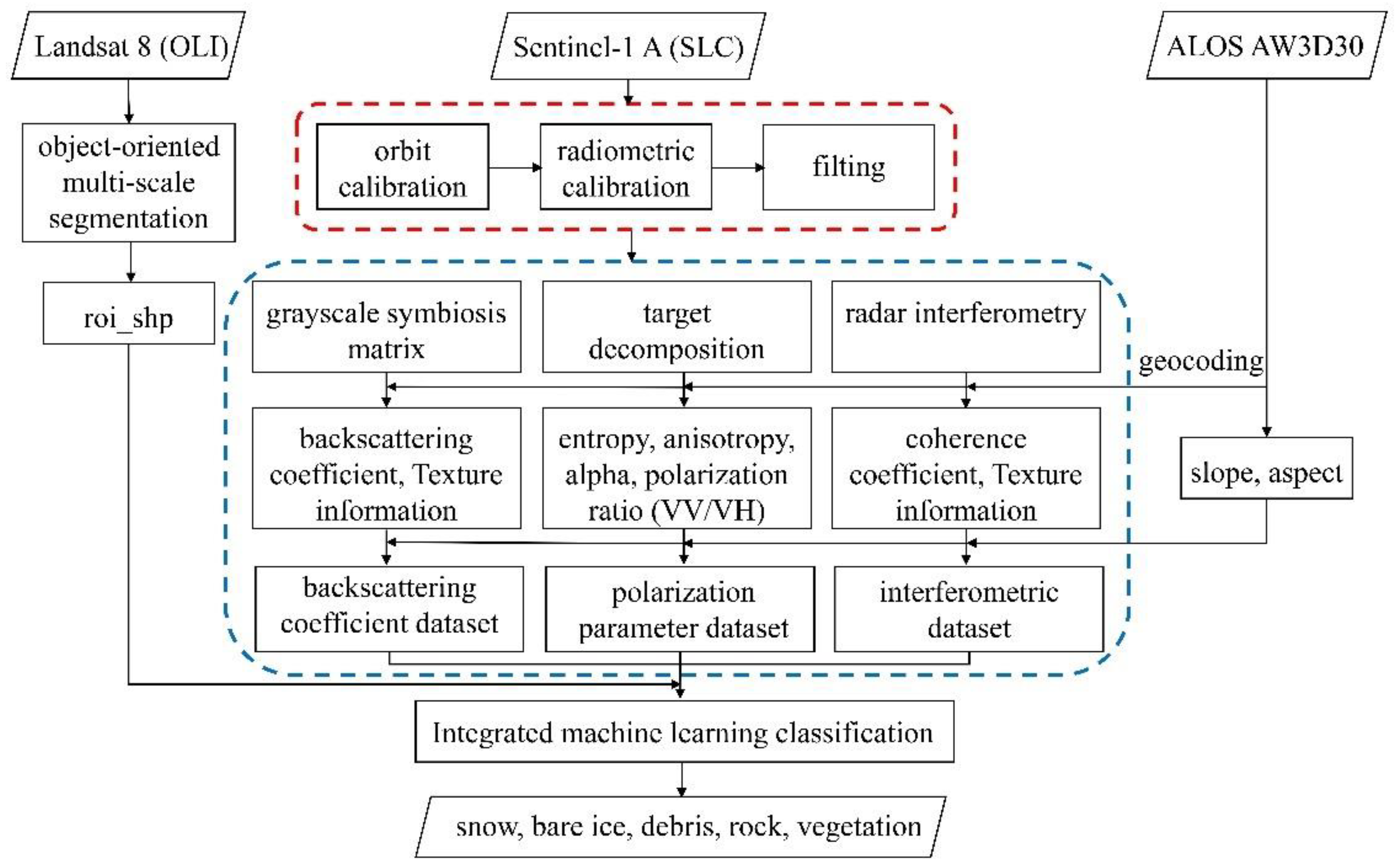
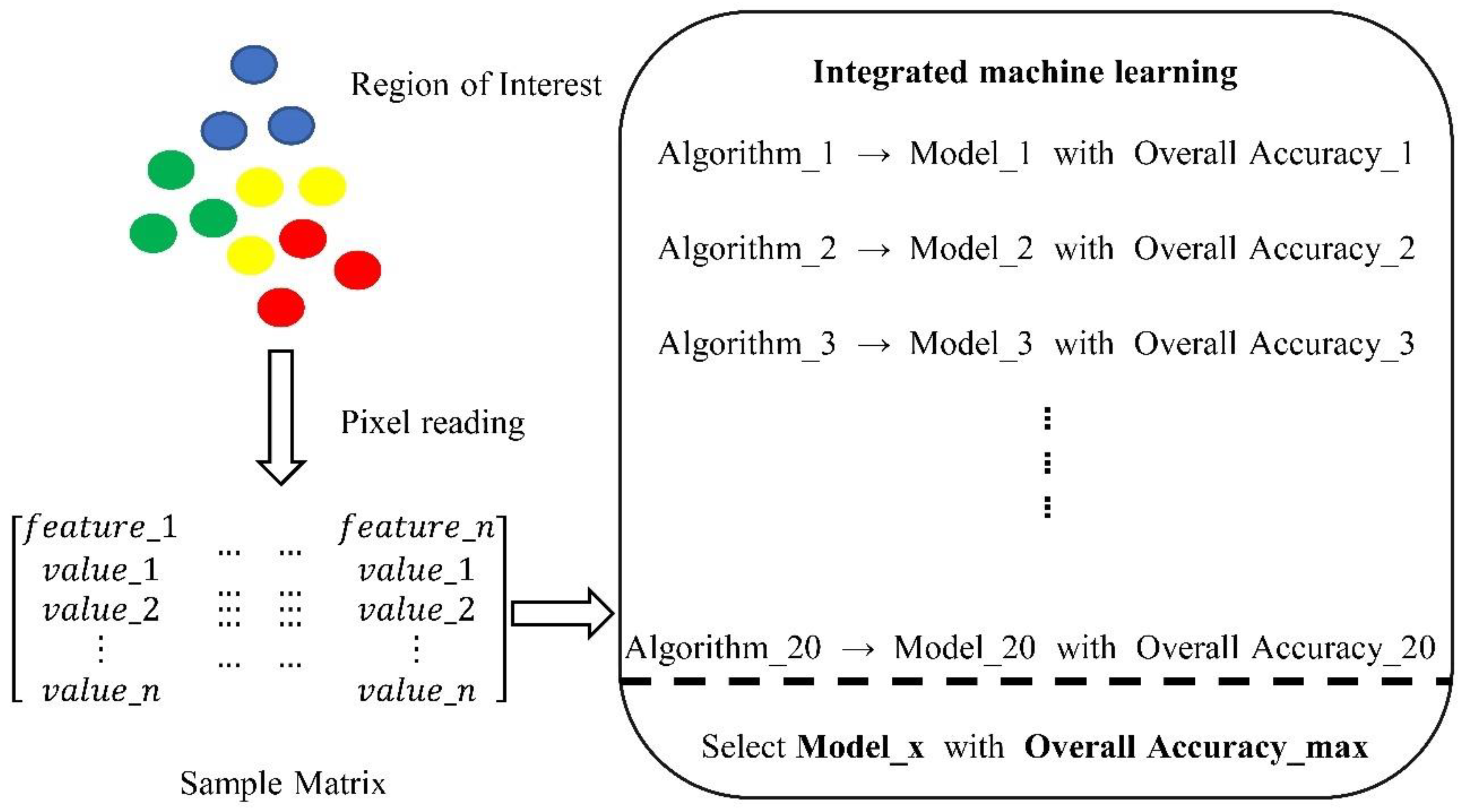
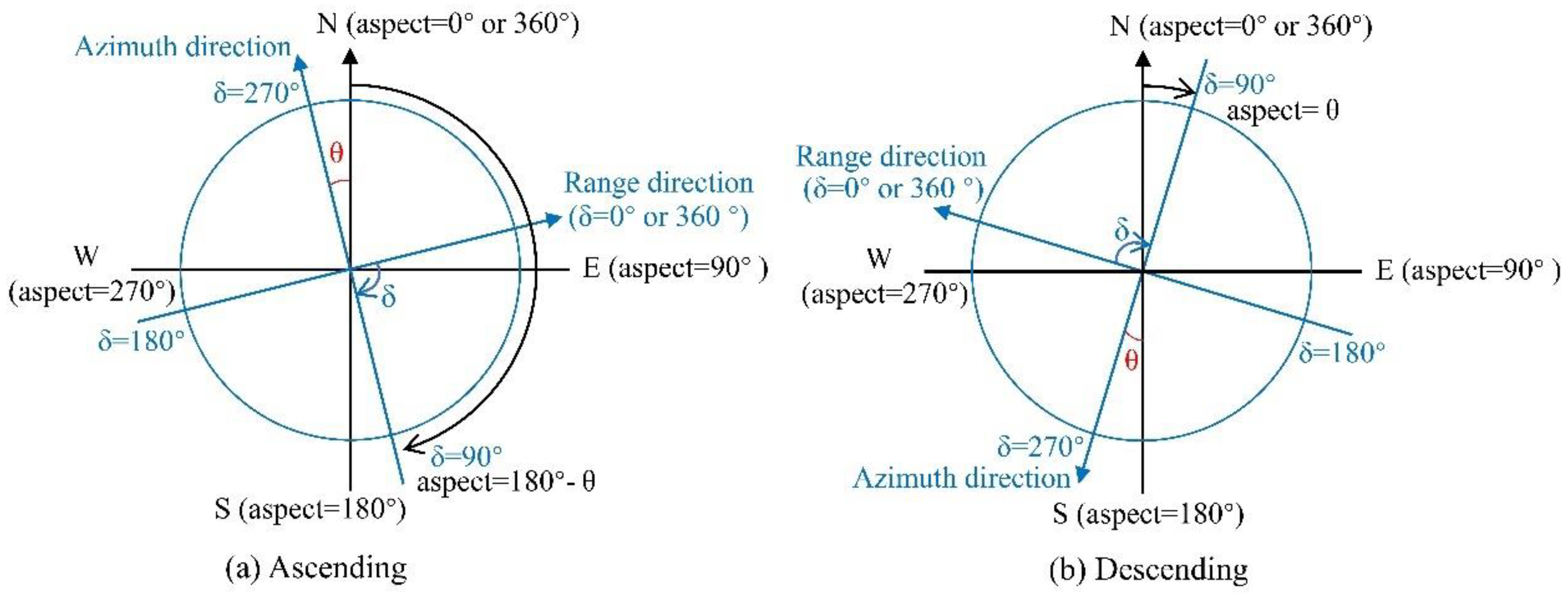

| No. | Glacier | Product Unique ID | Path | Frame | Incidence Angle (degree (°)) | Acquisition Time (MM/DD/2018 hh:mm) | Pass Direction |
|---|---|---|---|---|---|---|---|
| 1 | NW | 7BC9 | 129 | 112 | 31.19–54.04 | 25 July 12:48 | A |
| 2 | 2EF4 | 129 | 112 | 31.19–54.04 | 6 August 12:48 | A | |
| 3 | E522 | 136 | 471 | 30.74–53.95 | 26 July 0:49 | D | |
| 4 | 7647 | 136 | 471 | 30.74–53.95 | 7 August 0:49 | D | |
| 5 | NE & SW | 9671 | 85 | 88 | 30.71–54.09 | 22 July 12:22 | A |
| 6 | CA6A | 85 | 88 | 30.71–54.09 | 3 August 12:22 | A | |
| 7 | 479E | 121 | 496 | 31.49–53.96 | 25 July 0:10 | D | |
| 8 | 4E04 | 121 | 496 | 31.49–53.96 | 6 August 0:10 | D | |
| 9 | SE | DBB8 | 70 | 1282 | 31.24–54.13 | 21 July 11:41 | A |
| 10 | 20B8 | 70 | 1282 | 31.24–54.13 | 2 August 11:41 | A | |
| 11 | 9F69 | 77 | 490 | 31.33–54.05 | 21 July 23:45 | D | |
| 12 | C16C | 77 | 490 | 31.33–54.04 | 2 August 23:45 | D |
| BC Suite | PDP Suite | ICC Suite | |
|---|---|---|---|
| layer 1 | sigma naught | entropy | coherence coefficient |
| layer 2 | sigma naught_based texture_1 | anisotropy | coherence coefficient_based texture_1 |
| layer 3 | sigma naught_based texture_2 | alpha | coherence coefficient_based texture_2 |
| layer 4 | sigma naught_based texture_3 | VV/VH ratio | coherence coefficient_based texture_3 |
| layer 5 | local incident angle | local incident angle | local incident angle |
| layer 6 | elevation | elevation | elevation |
| layer 7 | slope | slope | slope |
| No. | Algorithm | Classifier Class |
|---|---|---|
| 1 | Fine Tree | Decision Trees |
| 2 | Medium Tree | |
| 3 | Coarse Tree | |
| 4 | Linear SVM | Support Vector Machines |
| 5 | Quadratic SVM | |
| 6 | Cubic SVM | |
| 7 | Fine Gaussian SVM | |
| 8 | Medium Gaussian SVM | |
| 9 | Coarse Gaussian SVM | |
| 10 | Fine KNN | Nearest Neighbor Classifiers |
| 11 | Medium KNN | |
| 12 | Coarse KNN | |
| 13 | Cosine KNN | |
| 14 | Cubic KNN | |
| 15 | Weighted KNN | |
| 16 | Boosted Trees | Ensemble Classifiers |
| 17 | Bagged Trees | |
| 18 | Subspace Discriminant | |
| 19 | Subspace KNN | |
| 20 | RUSBoosted Trees |
| Glacier | Algorithm | BC | PDP | ICC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A_VV | A_VH | D_VV | D_VH | A | D | A_VV | A_VH | D_VV | D_VH | ||
| NW | Coarse Gaussian SVM | 74.70 | |||||||||
| Boosted Trees | 99.80 | 99.80 | |||||||||
| Bagged Trees | 98.90 | ||||||||||
| Subspace KNN | 99.90 | 99.90 | 99.70 | 99.70 | 99.30 | 99.70 | |||||
| Error * | 0.04 | −0.07 | −0.17 | −0.68 | 0.27 | 0.10 | −3.59 | −0.30 | −0.23 | −0.06 | |
| NE | Bagged Trees | 98.40 | 98.60 | 98.50 | 97.00 | 96.10 | 96.50 | 96.50 | 96.60 | 96.70 | |
| Subspace KNN | 98.20 | ||||||||||
| Error | 0.08 | 0.6 | 0.13 | −0.49 | −0.23 | 0.16 | 0.74 | −0.08 | −54.90 | −56.64 | |
| SW | Fine Tree | 67.10 | 67.00 | 66.30 | 66.20 | 65.40 | 65.20 | 68.50 | 67.60 | 68.40 | 67.50 |
| Error | −1.88 | −11.15 | −0.94 | −1.31 | −1.49 | −1.79 | −1.08 | −0.66 | −1.18 | −0.92 | |
| SE | Bagged Trees | 97.10 | 98.00 | 97.30 | 98.10 | 96.90 | 96.30 | 96.70 | 96.40 | ||
| Subspace KNN | 96.80 | 96.20 | |||||||||
| Error | 0.22 | 0.07 | 0.43 | 0.35 | −0.08 | 0.74 | 0.70 | 0.65 | 0.58 | 0.27 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, G.; Zhou, X.; Ke, C.; Drolma, L.; Li, H. The Potential of Sentinel-1A Data for Identification of Debris-Covered Alpine Glacier Based on Machine Learning Approach. Remote Sens. 2022, 14, 1980. https://doi.org/10.3390/rs14091980
Yao G, Zhou X, Ke C, Drolma L, Li H. The Potential of Sentinel-1A Data for Identification of Debris-Covered Alpine Glacier Based on Machine Learning Approach. Remote Sensing. 2022; 14(9):1980. https://doi.org/10.3390/rs14091980
Chicago/Turabian StyleYao, Guohui, Xiaobing Zhou, Changqing Ke, Lhakpa Drolma, and Haidong Li. 2022. "The Potential of Sentinel-1A Data for Identification of Debris-Covered Alpine Glacier Based on Machine Learning Approach" Remote Sensing 14, no. 9: 1980. https://doi.org/10.3390/rs14091980
APA StyleYao, G., Zhou, X., Ke, C., Drolma, L., & Li, H. (2022). The Potential of Sentinel-1A Data for Identification of Debris-Covered Alpine Glacier Based on Machine Learning Approach. Remote Sensing, 14(9), 1980. https://doi.org/10.3390/rs14091980







