Multi-View Structural Feature Extraction for Hyperspectral Image Classification

Abstract

The hyperspectral feature extraction technique is one of the most popular topics in the remote sensing community. However, most hyperspectral feature extraction methods are based on region-based local information descriptors while neglecting the correlation and dependencies of different homogeneous regions. To alleviate this issue, this paper proposes a multi-view structural feature extraction method to furnish a complete characterization for spectral–spatial structures of different objects, which mainly is made up of the following key steps. First, the spectral number of the original image is reduced with the minimum noise fraction (MNF) method, and a relative total variation is exploited to extract the local structural feature from the dimension reduced data. Then, with the help of a superpixel segmentation technique, the nonlocal structural features from intra-view and inter-view are constructed by considering the intra- and inter-similarities of superpixels. Finally, the local and nonlocal structural features are merged together to form the final image features for classification. Experiments on several real hyperspectral datasets indicate that the proposed method outperforms other state-of-the-art classification methods in terms of visual performance and objective results, especially when the number of training set is limited.

1. Introduction

A hyperspectral image (HSI) is able to record hundreds of contiguous spectral channels, and thus provides an unique ability to identify different types of materials. Owing to this merit, hyperspectral imaging has been extensively applied in various aspects, such as land cover mapping [1,2], object detection [3,4], and environment monitoring [5,6]. Over the past few years, hyperspectral image classification has been made great progress because of its significance in mineral mapping, urban investigation, and precision agriculture. Nevertheless, object spectrum is usually affected by the imaging equipment and imaging environment, resulting in high spectrum mixture among different land covers.

To alleviate this problem, hyperspectral feature extraction methods have been widely studied to improve the class discrimination among different land covers. Some representative manifold learning tools [7,8,9,10] have been successfully used as feature extractor of HSIs, such as principal component analysis (PCA) [8], minimum noise fraction (MNF) [10], and independent component analysis (ICA) [9]. However, most of these techniques only utilize the spectral information of different objects, and thus fail to achieve satisfactory classification performance.

To fully exploit the spectral and spatial characteristics in HSIs, a mass of spectral–spatial feature extraction techniques have been developed [11,12,13,14,15]. For instance, Marpu et al. developed attribute profiles (APs) to extract discriminative features of HSIs by using morphological operations [12]. Mura et al. studied extended morphological attribute profiles (EMAP) to characterize HSIs by using a series of morphological attribute filters [13]. Kang et al. developed an edge-preserving filtering method for hyperspectral feature extraction to remove low-contrast details [14]. Duan et al. modeled hyperspectral image as a linear combination of structural profile and texture information, in which the structural profile was used as the spatial features [15]. After that, many improved approaches have been also studied for classification of HSIs, such as ensemble learning [16,17], semi-supervised learning [18,19], and active learning [20,21]. For instance, in [17], a random feature ensemble method was proposed by using ICA and edge-preserving filtering to boost the classification accuracy of HSIs. In [18], a rolling guidance filter-based semi-supervised classification method was developed in which an extended label propagation technique was utilized to expand the training set.

In addition, with the development of deep learning models, many deep learning models have been applied to extract the high-order semantic features of HSIs. For example, Chen et al. presented a 3D convolutional neural network (CNN)-based feature extraction technique in which the dropout and $L_2$ regularization were adopted to prevent overfitting for class imbalance [22]. Liu et al. proposed a Siamese CNN method with a margin ranking loss function to improve the discrimination of different objects [23]. Liu et al. designed a mixed deep feature extraction technique by combining the pixel frequency spectrum features obtained by fast Fourier transform and spatial features. Lately, all kinds of improved versions have been also investigated to increase the classification accuracy [24,25,26,27,28]. For example, Hang et al. designed an attention-guided CNN method to extract spectral–spatial information, in which a spectral attention module and a spatial attention module were considered to capture the spectral and spatial information, respectively [26]. Hong et al. improved the transformer network to characterize the sequence attributes of spectral information, where a cross-layer skip connection was used to fuse spatial features from different layers [27].

To better characterize spectral–spatial information, the multiview technique, which aims to reveal the data characteristics from diverse aspects and provide multiple features for model learning, has been applied in hyperspectral feature extraction [20,29,30]. In more detail, the raw data are first transformed into different views (e.g., attributes, feature subsets), and then, the complementary information of all views is integrated together to achieve a more accurate classification result. For example, in [20], Li et al. proposed a multi-view active learning method for hyperspectral image classification, where the subpixel-level, pixel-level, and superpixel-level information were jointly used to achieve a better identification ability. Xu et al. proposed multi-view attribute components for classification of HSIs, in which an intensity-based query scheme was used to expand the number of training set [29]. In general, these methods can increase the classification performance because of multi-view strategy. However, most of them only utilize the local neighboring information without considering the correlation of pixels in the nonlocal region. Based on the above analysis, it is necessary to develop a novel multi-view method to further boost the classification performance by jointly using the dependencies of pixels in the local and nonlocal regions.

In this work, we propose a novel multi-view structural feature extraction method for the first time, which consists of several key steps. First, the spectral dimension of the original data is reduced to increase the computational efficiency. Then, three multi-view structural features are constructed to characterize varying land covers from different aspects. Finally, different types of features are merged together to increase the discrimination of different land covers, and the fused feature is fed into a spectral classifier to obtain the classification results. Experiments are performed on three benchmark datasets to quantitatively and qualitatively validate the effectiveness of the proposed method. The experimental results verify that the proposed feature extraction method can significantly outperform other state-of-the-art feature extractors. More importantly, our method can obtain promising classification performance over other approaches in the case of limited training samples.

The remainder of this article is divided into four sections. Section 2 provides the proposed method. The experimental results are shown and analyzed in Section 3. Section 4 discusses the influence of different components. Finally, Section 5 concludes this work.

2. Method

Figure 1 shows the flowchart of the multi-view structural feature extraction method, which consists of three key steps. First, the spectral number of the raw data is reduced with the MNF method. Then, the multi-view structural features, i.e., local structural feature, intra-view, and inter-view structural features, are constructed based on the correlation of pixels in the local and nonlocal regions. Finally, the multi-view features are fused together with the kernel PCA (KPCA) method, and the fused feature is fed into the support vector machine (SVM) classifier to obtain the classification map.

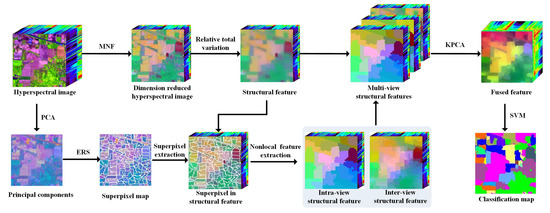
Figure 1. The flow chart of the proposed multi-view structural feature extraction method.

2.1. Dimension Reduction

To decrease the computing time and the influence of image noise, the maximum noise fraction (MNF) [31] is first exploited to decrease the spectral dimension of the original data. Specifically, assume $\mathbf{I}$ is the raw data, the MNF is to seek a transform matrix $\mathbf{W}$ to maximize the signal to noise ratio of transformed data.

$$\mathbf{R}={\mathbf{W}}^T\mathbf{I}$$

(1)

where $\mathbf{R}$ is the dimension-reduced data, and $\mathbf{W}$ is the transform matrix, which can be estimated as

$$\underset{\mathbf{W}}{argmax}\frac{{\mathbf{W}}^T{\sum }_S\mathbf{W}}{{\mathbf{W}}^T{\sum }_N\mathbf{W}}=\underset{\mathbf{W}}{argmax}\frac{{\mathbf{W}}^T{\sum }_I\mathbf{W}}{{\mathbf{W}}^T{\sum }_N\mathbf{W}}-1$$

(2)

where $\mathbf{I}$ is regarded as a linear combination of the uncorrelated signal $\mathbf{S}$ and noise matrix $\mathbf{N}$, and $\mathrm{cov}\left(\mathbf{I}\right)={\sum }_I={\sum }_S+{\sum }_N$, in which ${\sum }_S$ and ${\sum }_N$ denote the covariance of $\mathbf{S}$ and $\mathbf{N}$. In this work, the first L-dimensional components are preserved for the following feature extraction.

2.2. Multi-View Feature Generation

Since the imaging scene contains different types of land covers with different spatial size, a single structural feature cannot comprehensively characterize the spatial information of diverse objects. To alleviate this problem, a multi-view structural feature extraction method is proposed. Specifically, three different types of structural features are generated, including local structural feature, intra-view, and inter-view structural features.

(1) Local structural feature: The local structural feature aims to remove useless details (e.g., image noise and texture) and preserve the intrinsic spectral–spatial information. Specifically, a relative total variation technique [32] is performed on the dimension-reduced data $\mathbf{R}$ to construct local structural feature ${\mathbf{F}}_1$, which is expressed as

$$arg\underset{{\mathbf{F}}_1}{min}\sum _{i=1}^T{({\mathbf{F}}_{1i}-{\mathbf{R}}_i)}^2+\alpha ·(\frac{{\mathcal{D}}_x\left(i\right)}{{\mathcal{L}}_x\left(i\right)+\epsilon }+\frac{{\mathcal{D}}_y\left(i\right)}{{\mathcal{L}}_y\left(i\right)+\epsilon }),$$

(3)

where T represents the amount of pixels in total. ${\mathbf{F}}_1$ stands for the desired structural feature. $\alpha$ denotes a smoothing weight. $\epsilon$ is adopted to prevent dividing by zero. ${\mathcal{D}}_x$ and ${\mathcal{D}}_y$ indicate the variations in two directions. The solution of Equation (3) refers to [32].

$${\mathcal{D}}_x\left(i\right)=\sum _{j\in R\left(i\right)}{g}_{i,j}·\left|{\left({\partial }_x\mathbf{S}\right)}_j\right|$$

$${\mathcal{D}}_y\left(i\right)=\sum _{j\in R\left(i\right)}{g}_{i,j}·\left|{\left({\partial }_y\mathbf{S}\right)}_j\right|$$

(4)

where ${\partial }_x\mathbf{S}$ and ${\partial }_y\mathbf{S}$ stand for the partial derivatives in two directions, which mainly calculates the spatial similarity within a local window $R\left(i\right)$, and $g_{i,j}$ is a weight.

$$g_{i,j}=exp\left(-\frac{{(x_i-x_j)}^2+{(y_i-y_j)}^2}{2{\sigma }^2}\right).$$

(5)

where $\sigma$ denotes the window size.

(2) Intra-view structural feature: The intra-view structural feature is to reduce the spectral difference of pixels belonging to the same land cover and increase the spectral purity in the homogeneous regions. In order to extract the intra-view structural feature, first, an entropy rate superpixel (ERS) segmentation method [33] is adopted to obtain the homogeneous region of the same object. In more detail, the PCA scheme is first conducted on the local structural feature ${\mathbf{F}}_1$ to obtain the first three components ${\widehat{\mathbf{F}}}_1$, and then, the ERS segmentation scheme is utilized to obtain a 2D superpixel resulting map.

$$\mathbf{S}=ERS({\widehat{\mathbf{F}}}_1,T)$$

(6)

where $\mathbf{S}$ indicates the segmentation result, and T indicates the number of superpixels, which is determined by

$$T=⌊L\times \frac{\widehat{N}}{N}⌋$$

(7)

where L is empirically selected in this work, $\hat{N}$ represents the amount of nonzero pixels in the detected map obtained by performing Canny filter on the base image ${\widehat{\mathbf{F}}}_1$, and N represents the total amount of pixels in the base image. Based on the position indexes of pixels in each superpixel ${\mathbf{S}}_i$, we can obtain the corresponding 3D superpixels ${\mathbf{Y}}_i,i\in \{1,2,\dots ,T\}$.

Then, a mean filtering is conducted on each 3D superpixel ${\mathbf{Y}}_i$ to calculate the average value. Finally, we assign the pixels in each superpixel to the average value to obtain the intra-view structural feature ${\mathbf{F}}_2$.

(3) Inter-view structural feature: The intra-view structural feature is able to reduce the difference of pixels in each superpixel. However, the correlations of pixels for different superpixels are not considered. Thus, we construct an inter-view structural feature to improve the discrimination of different objects. Specifically, a weighted mean operation is performed on the neighboring superpixels ${\mathbf{Y}}_{i,j},\{j=1,2,\dots ,J\}$ of the current superpixel ${\mathbf{Y}}_i$ to obtain the inter-view structural feature ${\mathbf{F}}_3$.

$${\tilde{y}}_i=\sum _{j=1}^J{\omega }_{i,j}\times y_{i,j}$$

(8)

where ${\omega }_{i,j}$ denotes the neighboring superpixels of the ith superpixels. The obtained value ${\tilde{y}}_i$ is assigned to all pixels in the ith superpixel to produce the inter-view structural feature ${\mathbf{F}}_3$.

2.3. Feature Fusion

To make full use of multi-view structural features, the KPCA technique [34] is used to merge three types of features. Specifically, first, three structural features ${\mathbf{F}}_i,\{i=1,2,3\}$ are stacked together $\mathbf{F}=\{{\mathbf{F}}_1,{\mathbf{F}}_2,{\mathbf{F}}_3\}$. Then, the stacked data $\mathbf{F}$ is projected into a high-dimensional space $\mathcal{H}$ by using a Gaussian kernel function $\mathsf{\Phi }$. Finally, the fused feature $\widehat{\mathbf{F}}$ can be calculated:

$$\mathbf{K}\mathbf{\alpha }=\lambda \mathbf{\alpha }s.t.{∥\mathbf{\alpha }∥}_2=\frac{1}{\lambda }$$

(9)

where $\mathbf{K}$ indicates Gram matrix ${\mathsf{\Phi }}^T\left(\mathbf{S}\right)\mathsf{\Phi }\left(\mathbf{S}\right)$. In this paper, K-dimensional features are preserved in the fused feature. Once the fused feature is obtained, the spectral classifier, i.e., SVM, is considered to examine the classification performance. To clearly show the whole procedure of the proposed method, Algorithm 1 presents a pseudocode to summarize the key steps of our method.

Algorithm 1 Multi-view structural feature extraction

Input:  Input hyperspectral image I; Output:  Hyperspectral image feature $\widehat{\mathbf{F}}$  1: According to (1), reduce the spectral number of the raw data I to obtain the dimension reduced image R  2: According to (3), obtain the local structural feature ${\mathbf{F}}_1$ of the input image.  3: According to (6), obtain the 2-D superpixel segmentation map S  4: Obtain the corresponding 3-D superpixels Y based on the position indexes of pixels in each superpixels ${\mathbf{S}}_i$  5: Construct the intra-view structural feature ${\mathbf{F}}_2$ by performing the mean filtering on each 3-D superpixel  6: According to (8), construct the inter-view structural feature ${\mathbf{F}}_3$  7: According to (9), fuse the multi-view structural features ${\mathbf{F}}_i,\{i=1,2,3\}$ to obtain the final feature $\widehat{\mathbf{F}}$  8: Return$\widehat{\mathbf{F}}$

3. Experiments

3.1. Experimental Setup

(1) Datasets: In the experimental section, three hyperspectral datasets, i.e., Indian Pines, Salinas, and Honghu, are used to examine the classification performance of the proposed feature extraction method. All these datasets are collected from a public hyperspectral database.

The Indian Pines dataset was obtained by the Airborne Visible Infrared Imaging Spectrometer (AVIRIS) sensor over the Indian Pines test scene in northwestern Indiana, which is available online (http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes (accessed on 10 January 2022 )). This image is composed of 220 spectral bands spanning from 0.4 to 2.5 µm. The spatial size is 145 × 145 with a spatial resolution of 20 m. Twenty water absorption channels (No. 104-108, 150-163, and 220) are discarded before experiments. Figure 2a presents the false color composite image. Figure 2b shows the ground truth, which contains 16 different land covers. Figure 2c gives the class name.

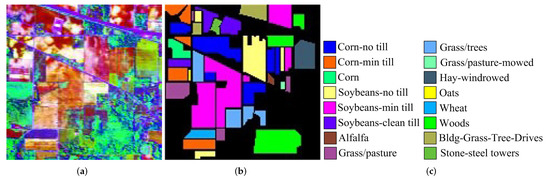
Figure 2. Indian Pines dataset. (a) False color composite. (b) Ground truth. (c) Label name.

The Salinas dataset was collected by the AVIRIS sensor over Salinas Valley, California, USA, which is available online (http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes (accessed on 10 January 2022)). This image consists of 224 spectral channels with spatial size of 512 × 217 pixels. The spatial resolution is of 3.7 m. This scene is an agricultural region, which includes different types of crops, such as vegetables, bare soils, and vineyard fields. Twenty spectral bands (No. 108-112, 154-167, and 224) are discarded before the following experiments. Figure 3a gives the false color composition. Figure 3b displays the ground truth, which consists of 16 different land covers. Figure 3c shows the class name.

Figure 3. Salinas dataset. (a) False color composite. (b) Ground truth. (c) Label name.

The Honghu dataset was captured by the a 17 mm focal length Headwall Nano-Hyperspec imaging sensor over Honghu City, Hubei province, China, which is available online (http://rsidea.whu.edu.cn/e-resource_WHUHi_sharing.htm (accessed on 10 January 2022)). This image consists of 270 spectral channels ranging from 0.4 to 1.0 µm. The spatial size is 940 × 475 pixels with a spatial resolution of 0.043 m. This scene is a complex agricultural area, including various crops and different cultivars of the same crop. Figure 4 gives the false color composition, ground truth, and class name. Table 1 presents the training and test samples of all used datasets for the following experiments.

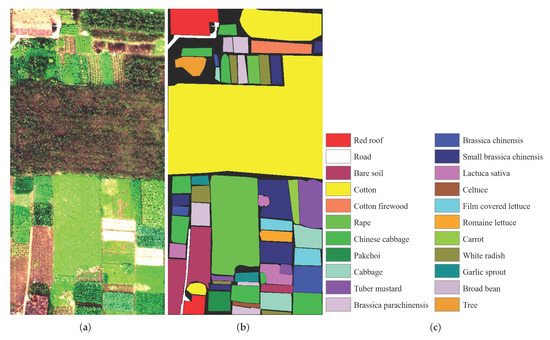
Figure 4. Honghu dataset. (a) False color composite. (b) Ground truth. (c) Label name.

Table 1. The number of training and test set. The colors represent different land covers in the classification map.

No.	Indian Pines Dataset			Salinas Dataset			Honghu Dataset
	Name	Train	Test	Name	Train	Test	Name	Train	Test
1	Alfalfa	6	40	Weeds_1	5	2004	Red roof	25	14,016
2	Corn_N	7	1421	Weeds_2	5	3721	Road	25	3487
3	Corn_M	6	824	Fallow	5	1971	Bare soil	25	21,796
4	Corn	6	231	Fallow_P	5	1389	Cotton	25	163,260
5	Grass_M	6	477	Fallow_S	5	2673	Cotton firewood	25	6193
6	Grass_T	6	724	Stubble	5	3954	Rape	25	44,532
7	Grass_P	6	22	Celery	5	3574	Chinese cabbage	25	24,078
8	Hay_W	7	471	Grapes	5	11,266	Packchoi	25	4029
9	Oats	6	14	Soil	5	6198	Cabbage	25	10,794
10	Soybean_N	7	965	Corn	5	3273	Tuber mustard	25	12,369
11	Soybean_M	8	2447	Lettuce_4	5	1063	Brassica parachinensis	25	10,990
12	Soybean_C	6	587	Lettuce_5	5	1922	Brassica chinensis	25	8929
13	Wheat	6	199	Lettuce_6	5	911	Small Brassica chinensis	25	22,482
14	Woods	6	1259	Lettuce_7	5	1065	Lactuca sativa	25	7331
15	Buildings	6	380	Vinyard_U	5	7263	Celtuce	25	977
16	Stone	7	86	Vinyard_T	5	1802	Film covered	25	7237
17	Total	102	10,147	Total	80	54,049	Romaine lettuce	25	2985
18							Carrot	25	3192
19							White radish	25	8687
20							Garlic sprout	25	3461
21							Broad bean	25	1303
22							Tree	25	4015
							Total	550	386,143

(2) Evaluation Indexes: To quantitatively calculate the classification accuracies of all considered techniques, four extensively used objective indexes [35,36,37], i.e., class accuracy (CA), overall accuracy (OA), average accuracy (AA), and Kappa coefficient, are used. The definitions of all objective indexes are shown as follows:

(1) CA: CA calculates the percentage of correctly classified pixels of each class in the total number of pixels.

$$CA=\frac{{\mathbf{M}}_{ii}}{{\displaystyle \sum _{j=1}^C}{\mathbf{M}}_{ij}}$$

(10)

where $\mathbf{M}$ is the confusion matrix obtained by comparing the ground truth with the predicted result, and C is the total number of categories.

(2) OA: OA assesses the proportion of correctly identified samples to all samples.

$$OA={\displaystyle \sum _{i=1}^C}{\mathbf{M}}_{ii}/N$$

(11)

where N is the total number of labeled samples, $\mathbf{M}$ is the confusion matrix, and C is the total number of categories.

(3) AA: AA represents mean of the percentage of the correctly identified samples.

$$AA=\frac{{\displaystyle \sum _{i=1}^C}\left({\mathbf{M}}_{ii}/\phantom{{\mathbf{M}}_{ii}{\displaystyle \sum _{j=1}^C}{\mathbf{M}}_{ij}}{\displaystyle \sum _{j=1}^C}{\mathbf{M}}_{ij}\right)}{C}$$

(12)

where C is the total number of categories, and $\mathbf{M}$ is the confusion matrix.

(4) Kappa: Kappa coefficient denotes the interrater reliability for categorical variables.

$$Kappa=\frac{N{\displaystyle \sum _{i=1}^C}{\mathbf{M}}_{ii}-{\displaystyle \sum _{i=1}^C}\left({\displaystyle \sum _{j=1}^C}{\mathbf{M}}_{ij}{\displaystyle \sum _{j=1}^C}{\mathbf{M}}_{ji}\right)}{N^2-{\displaystyle \sum _{i=1}^C}\left({\displaystyle \sum _{j=1}^C}{\mathbf{M}}_{ij}{\displaystyle \sum _{j=1}^C}{\mathbf{M}}_{ji}\right)}$$

(13)

where N is the total number of labeled samples, $\mathbf{M}$ is the confusion matrix, and C is the total number of categories.

3.2. Classification Results

To examine the effectiveness of the proposed feature extraction method, several state-of-the-art hyperspectral classification methods are selected as competitors, including (1) the spectral classifier, i.e., SVM on the original image (SVM) [38]; (2) the feature extraction methods, i.e., the image fusion and recursive filtering (IFRF) [14], the extended morphological attribute profiles (EMAP) [13], multi-scale total variation (MSTV) [15], the PCA-based edge-preserving features (PCAEPFs) [8]; (3) the spectral–spatial classification methods, i.e., the superpixel-based classification via multiple kernels (SCMK) [39] and the generalized tensor regression approach (GTR) [40]. These methods are adopted because they are either highly cited publications in the remote sensing field or are recently proposed classification methods with state-of-the-art classification performance on several hyperspectral datasets. For all considered approaches, the default parameters follow the corresponding publications for a fair comparison.

3.2.1. Indian Pines Dataset

The first experiment is performed on the Indian Pines dataset, in which 1% labeled samples are randomly selected from the reference image for training (see Table 1). Figure 5 presents the classification maps of all considered methods on the Indian Pines dataset. As shown in this figure, the SVM method yields very noisy visual effects in the classification result, exposing the disadvantages of the spectral classifier without considering the spatial information. By removing image details and preserving the strong edge structures, the IFRF method greatly improves the classification result over the spectral classifier. However, there are still obvious misclassified pixels around the boundaries. For the EMAP method, some homogeneous regions still contain “noise” such as mislabels in the resulting map. For the SCMK method, some obvious misclassified results appear in the edges and corners. The main reason is that the homogeneous region belonging to the same object cannot be accurately segmented. The MSTV method effectively removes the noisy labels. However, it tends to yield an oversmoothed classification map. The PCAEPFs method significantly boosts the classification performance with respect to the IFRF method, since multi-scale feature extraction strategy is adopted. However, some objects with small size fail to be well preserved in the classification map. The GTR method yields spot-like misclassification results since the tensor regression technique cannot fit the spectral curves of different objects well. By contrast, the proposed method obtains a better visual map by integrating multi-view spectral–spatial structural features, in which the edges of the classification map are more consistent with the real scene.

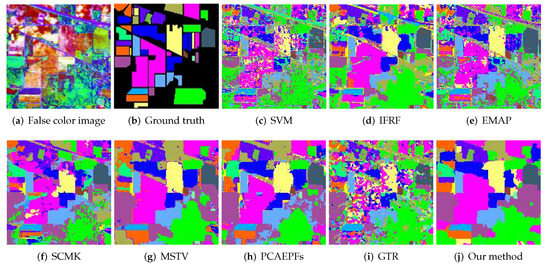
Figure 5. Classification results of all considered approaches on Indian Pines dataset. (a) False color image. (b) Ground truth. (c) SVM [33], OA = 55.30%. (d) IFRF [14], OA = 70.09%. (e) EMAP [13], OA = 67.70%. (f) SCMK [39], OA = 71.20%. (g) MSTV [15], OA = 88.25%. (h) PCAEPFs [8], OA = 85.58%. (i) GTR [40], OA = 63.25%. (j) Our method, OA = 90.32%.

For objective comparison, Table 2 lists the objective results of different approaches including CA, OA, AA, and Kappa. It is easily to observe that the proposed method is superior than all compared approaches in terms of OA, AA, and Kappa. For instance, OA value is increased from 53% to 90% obtained by the proposed method with respect to the SVM method on the original data. Moreover, the proposed feature extraction approach yields the highest classification accuracies for ten classes. This experiment illustrates that the proposed feature extraction method is more effective compared to other approaches.

Table 2. Classification accuracies of all methods on Indian Pines dataset. The bold denotes the best classification accuracy.

Class	SVM	IFRF	EMAP	SCMK	MSTV	PCAEPFs	GTR	Our Method
1	31.53 (9.74)	63.03 (27.93)	94.21 (9.19)	98.00 (1.05)	95.92 (10.41)	98.02 (4.65)	96.75 (2.06)	100.0 (0.00)
2	47.00 (6.00)	70.64 (15.98)	59.74 (8.25)	60.27 (11.34)	86.93 (5.35)	76.38 (7.21)	55.64 (8.15)	86.37 (5.87)
3	34.03 (14.66)	48.62 (12.35)	53.23 (13.54)	57.23 (13.07)	71.01 (8.26)	73.79 (13.56)	47.42 (8.58)	83.07 (16.27)
4	26.70 (6.66)	52.45 (11.34)	36.54 (6.17)	94.42 (4.94)	67.17 (9.51)	66.83 (7.53)	72.47 (11.74)	86.05 (10.51)
5	63.24 (9.75)	75.81 (10.59)	67.96 (10.27)	78.97 (12.76)	97.49 (3.45)	93.86 (6.29)	83.06 (9.97)	98.30 (3.94)
6	79.83 (8.04)	91.26 (4.32)	90.31 (3.84)	89.78 (11.19)	98.70 (2.05)	94.28 (3.29)	88.07 (5.81)	99.96 (0.13)
7	31.35 (14.53)	57.65 (21.85)	61.05 (20.27)	97.27 (2.35)	98.70 (2.10)	73.05 (31.40)	99.09 (2.87)	80.73 (25.62)
8	95.57 (2.12)	99.89 (0.27)	100.0 (0.00)	100.0 (0.00)	100.0 (0.00)	100.0 (0.00)	88.77 (7.52)	100.0 (0.00)
9	17.18 (8.59)	28.91 (13.60)	40.28 (10.36)	100.0 (0.00)	96.67 (10.54)	72.87 (21.18)	98.57 (4.52)	98.08 (4.27)
10	41.51 (5.35)	66.42 (8.13)	52.5 (10.53)	67.95 (13.90)	81.22 (9.40)	78.55 (10.42)	54.30 (8.60)	90.70 (8.08)
11	60.65 (8.31)	73.91 (6.22)	75.15 (9.85)	59.69 (9.88)	92.28 (4.04)	90.14 (4.52)	41.52 (11.20)	89.40 (6.90)
12	29.10 (5.43)	56.65 (9.17)	48.07 (5.31)	65.54 (9.57)	78.81 (12.25)	77.19 (12.22)	67.00 (8.52)	83.81 (15.76)
13	79.14 (3.12)	74.79 (12.60)	85.46 (9.48)	100.0 (0.00)	100.0 (0.00)	97.45 (4.78)	99.25 (1.09)	100.0 (0.00)
14	88.92 (5.36)	93.03 (4.09)	91.79 (4.98)	81.92 (9.64)	99.54 (0.65)	99.66 (0.45)	85.77 (9.36)	99.61 (0.24)
15	33.04 (7.36)	59.07 (13.37)	65.61 (14.81)	76.47 (11.34)	89.69 (10.56)	93.72 (5.04)	65.53 (11.80)	93.78 (6.94)
16	76.05 (19.59)	93.16 (5.08)	90.53 (7.63)	97.79 (0.37)	93.82 (3.82)	98.37 (1.07)	97.67 (4.17)	98.80 (0.02)
OA	53.30 (3.23)	70.09 (4.51)	67.70 (5.14)	71.20 (3.52)	88.25 (2.45)	85.58 (3.35)	63.25 (3.46)	90.32 (3.58)
AA	52.18 (2.78)	69.08 (4.43)	69.53 (3.88)	82.83 (1.89)	90.49 (1.93)	86.51 (2.53)	77.55 (1.61)	93.04 (2.75)
Kappa	47.57 (3.44)	66.35 (4.72)	63.67 (5.52)	67.50 (3.90)	86.63 (2.77)	83.65 (3.75)	58.79 (3.59)	88.96 (4.02)

Furthermore, the influence of the number of training set on all classification methods is discussed. Different numbers of samples varying from 1% to 10% are randomly chosen from the reference data to construct the training set. Figure 6 shows the change tendency of all studied methods with different numbers of training set. It is easily found that the classification performance of all methods tends to be improved when the amount of training set increases. In addition, the proposed method performs promising performance with respect to other methods especially when the number of training samples is limited.

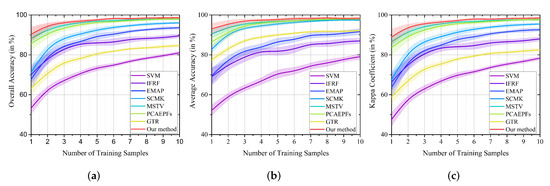
Figure 6. Classification performance of different approaches on the Indian Pines with different numbers of training samples. (a) OA. (b) AA. (c) Kappa. The widths of the line areas are the standard deviation of accuracies produced in ten experiments.

3.2.2. Salinas Dataset

The second experiment is conducted on the Salinas dataset, in which five samples per class are randomly selected from the reference image to constitute the training samples (see Table 1). Figure 7 shows the visual maps of all studied approaches. We can easily observe that the SVM method produces noisy classification performance. The reason is that the spatial priors are not considered in the spectral classifier. The IFRF method removes the noisy labels in some homogeneous regions. However, there are still serious misclassifications, such as Grapes_untrained and Vinyard_treils classes. The EMAP method also yields “pepper and noisy” appearance since this method is a pixel-level feature extraction method. For the SCMK method, some regions are misclassified into other classes due to the inaccurate segmentation. The MSTV method produces an oversmoothed visual resulting map. The main reason is that the feature extraction process removes the spatial information of land covers with low reflectivity. The PCAEPFs method produces noisy labels in the edges and boundaries. The GTR method yields a serious misclassification map since the tensor regression model fails to distinguish the similar spectral curves. Different from other methods, the proposed method provides the best visual classification effect in removing noisy labels and preserving the boundaries of different classes.

Figure 7. Classification results of all considered approaches on Salinas dataset. (a) False color image. (b) Ground truth. (c) SVM [33], OA = 80.08%. (d) IFRF [14], OA = 90.67%. (e) EMAP [13], OA = 85.54%. (f) SCMK [39], OA = 88.70%. (g) MSTV [15], OA = 94.46%. (h) PCAEPFs [8], OA = 95.12%. (i) GTR [40], OA = 85.59%. (j) Our method, OA = 98.13%.

Furthermore, Table 3 also verifies the effectiveness of the proposed method. Likewise, the proposed method obtains the highest classification accuracies with regard to OA, AA, and Kappa compared to other studied techniques. In addition, the influence of different numbers of training samples is presented in Figure 8. The number of training set for each class is varying from 5 to 50. It is shown that the increase of the training size is beneficial to the classification performance of all methods. Moreover, our method is always higher than other classification approaches.

Table 3. Classification performance of all methods on Salinas dataset. The bold denotes the best classification accuracy.

Classes	SVM	IFRF	EMAP	SCMK	MSTV	PCAEPFs	GTR	Our Method
1	99.13 (0.97)	99.95 (0.16)	99.98 (0.05)	97.53 (5.50)	100.0 (0.00)	100.0 (0.00)	97.33 (2.25)	100.0 (0.00)
2	98.74 (1.00)	98.66 (1.31)	99.75 (0.14)	98.90 (3.48)	99.97 (0.05)	99.95 (0.08)	99.84 (0.32)	100.0 (0.00)
3	79.50 (8.77)	98.34 (1.93)	94.55 (2.25)	96.40 (7.65)	97.87 (2.83)	97.72 (2.38)	85.58 (8.80)	99.47 (0.10)
4	96.00 (2.41)	91.59 (3.95)	95.93 (1.39)	90.01 (8.71)	96.90 (1.79)	93.19 (4.02)	99.83 (0.07)	97.03 (0.28)
5	94.01 (7.06)	97.08 (1.77)	96.66 (6.27)	97.93 (1.56)	96.86 (1.49)	98.98 (3.21)	90.12 (6.82)	99.96 (0.01)
6	99.79 (0.53)	100.0 (0.00)	99.41 (0.73)	99.75 (0.00)	98.34 (2.92)	99.98 (0.04)	98.89 (2.86)	99.97 (0.01)
7	95.27 (3.61)	97.43 (2.27)	96.27 (3.16)	99.85 (0.06)	96.23 (5.52)	99.92 (0.06)	99.18 (0.65)	99.83 (0.01)
8	64.94 (4.82)	91.99 (3.74)	80.00 (7.80)	69.96 (8.23)	92.73 (5.95)	93.66 (6.53)	69.49 (11.96)	98.22 (2.96)
9	98.66 (0.87)	98.95 (0.67)	98.99 (0.21)	99.91 (0.19)	98.61 (1.03)	99.58 (0.46)	98.84 (0.95)	99.33 (0.67)
10	77.21 (6.38)	97.51 (1.62)	87.98 (4.27)	82.44 (14.88)	95.02 (7.28)	99.31 (0.97)	80.51 (10.31)	98.98 (0.19)
11	82.43 (10.35)	93.20 (3.51)	79.41 (10.37)	94.93 (5.93)	99.65 (0.78)	95.04 (4.63)	96.43 (2.38)	97.42 (7.25)
12	89.11 (7.96)	94.98 (5.23)	88.64 (6.36)	91.05 (12.43)	99.11 (1.13)	94.71 (4.32)	98.12 (5.45)	98.62 (2.48)
13	79.04 (12.81)	83.39 (11.25)	92.32 (3.45)	93.94 (10.28)	95.32 (6.68)	91.81 (11.56)	98.79 (0.71)	81.85 (6.29)
14	85.09 (12.77)	84.15 (17.99)	97.23 (1.08)	88.92 (3.95)	89.54 (10.17)	92.54 (10.36)	91.01 (5.19)	94.81 (6.19)
15	46.93 (5.71)	70.34 (13.57)	56.84 (7.75)	82.66 (11.52)	84.53 (7.06)	84.52 (8.47)	65.16 (14.05)	95.59 (4.72)
16	93.27 (5.57)	99.12 (0.76)	96.43 (2.26)	93.83 (10.51)	97.68 (4.67)	99.96 (0.08)	86.38 (7.44)	100.0 (0.00)
OA	80.08 (1.96)	90.67 (3.33)	85.54 (2.57)	88.70 (2.84)	94.46 (1.47)	95.12 (1.37)	85.59 (3.54)	98.13 (0.59)
AA	86.19 (1.07)	93.54 (1.84)	91.27 (1.07)	92.38 (2.16)	96.14 (1.18)	96.30 (0.94)	90.96 (1.67)	97.57 (0.75)
Kappa	77.87 (2.15)	89.66 (3.65)	83.97 (2.81)	87.47 (3.15)	93.84 (1.64)	94.56 (1.53)	83.97 (3.94)	97.92 (0.67)

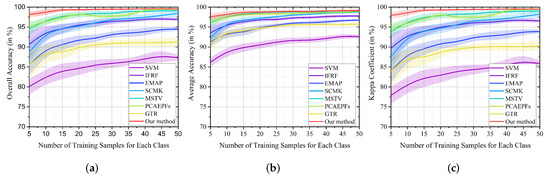
Figure 8. Classification performance of different approaches on the Salinas with different numbers of training samples. (a) OA. (b) AA. (c) Kappa. The widths of the line areas are the standard deviation of accuracies produced in ten experiments.

3.2.3. Honghu Dataset

The third experiment is performed on a complex crop scene with 22 crop classes, i.e., Honghu dataset, in which the benchmark training and test samples (http://rsidea.whu.edu.cn/e-resource_WHUHi_sharing.htm (accessed on on Jaunary 2022)) are adopted. The classification results of all methods are shown in Figure 9. Similarly, the SVM method produces a very noisy visual map since only the spectral information is used. The IFRF method greatly improves this problem by using the image filtering on the raw data, obtaining a better classification result over the SVM method. The EMAP method also obtains a noisy classification map. The reason is that this feature extraction method is in a pixel-wise pattern. For the SCMK method, the classification map has a small amount of misclassification labels for some classes. The MSTV method obtains a better classification map due to multi-scale technique. However, the edges of different classes still have misclassification appearance. The PCAEPFs method yields a similar classification effect to the MSTV method. For the GTR method, the classification result suffers from serious misclassification for this complex scene when the amount of training set is limited. By contrast, the proposed method yields the best visual map with respect to other studied approaches, since multi-view structural features are effectively merged to yield a complete characterization of different objects.

Figure 9. Classification results of all considered approaches on Honghu dataset. (a) False color image. (b) Ground truth. (c) SVM [33], OA = 64.43%. (d) IFRF [14], OA = 84.23%. (e) EMAP [13], OA = 76.11%. (f) SCMK [39], OA = 86.41%. (g) MSTV [15], 90.74%. (h) PCAEPFs [8], OA = 87.37%. (i) GTR [40], OA = 51.87%. (j) Our method, OA = 94.01%.

Furthermore, the objective results obtained by all considered approaches are listed in Table 4. It is obvious from Table 4 that our method still provides the highest classification accuracies concerning OA, AA, and Kappa coefficient. In addition, Figure 10 gives the OA, AA, and Kappa coefficient of all studied approaches as functions of the amount of training samples from 25 to 300. It should be mentioned that the training samples follow the benchmark dataset (http://rsidea.whu.edu.cn/e-resource_WHUHi_sharing.htm (accessed on 10 January 2022)). It is found that the classification accuracies of all methods tend to improve when the training size increases, and our method still produces the highest OA, AA, and Kappa coefficient.

Table 4. Classification performance of all methods on Honghu dataset. The bold denotes the best classification accuracy.

Classes	SVM	IFRF	EMAP	SCMK	MSTV	PCAEPFs	GTR	Our Method
1	88.17	98.22	91.04	86.91	97.73	89.84	75.41	89.69
2	54.73	67.79	64.54	86.23	73.31	78.28	57.36	57.95
3	88.51	96.16	92.62	93.44	93.27	96.64	61.13	97.83
4	96.12	99.31	98.30	87.64	99.50	99.56	44.66	99.72
5	17.85	57.84	23.49	98.66	63.24	52.07	55.53	79.29
6	85.18	90.83	89.97	89.74	93.78	93.26	69.41	99.40
7	74.00	89.38	81.95	77.24	89.62	88.44	50.93	95.81
8	6.09	16.05	10.73	90.02	43.87	31.39	42.74	97.99
9	91.60	99.21	89.67	94.61	90.23	86.79	90.75	97.82
10	49.29	73.45	73.62	76.59	91.88	83.72	32.99	99.44
11	28.17	58.82	41.50	77.43	69.88	64.28	21.36	79.63
12	43.33	61.20	52.56	93.64	64.18	61.54	43.77	96.26
13	50.58	77.54	70.86	70.73	79.52	81.99	30.38	78.44
14	43.35	70.73	60.01	86.77	90.14	78.77	61.29	80.40
15	3.97	31.73	23.46	97.24	57.05	51.69	82.80	91.99
16	80.93	93.51	87.57	94.53	99.01	98.66	82.34	98.37
17	54.39	72.82	62.17	93.10	85.53	92.66	73.80	97.09
18	21.83	32.85	39.27	95.08	72.90	67.53	74.91	68.77
19	48.88	64.45	51.52	64.06	83.41	58.41	56.23	74.37
20	38.00	54.19	59.34	99.86	79.59	65.60	46.06	88.71
21	11.04	24.32	38.85	100.00	86.11	43.46	71.14	91.70
22	21.50	47.34	25.73	99.55	82.90	76.21	73.23	89.30
OA	64.43	84.23	76.11	86.41	90.74	87.37	51.87	94.01
AA	49.88	67.17	60.39	88.18	81.21	74.58	59.01	88.64
Kappa	57.68	80.27	70.82	85.86	88.37	84.23	45.79	92.47

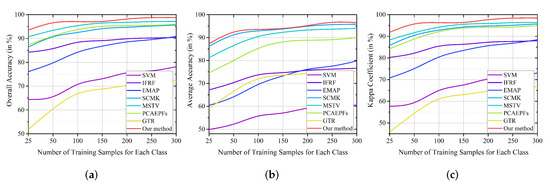
Figure 10. Classification performance of different approaches on the Honghu with different numbers of training samples. (a) OA. (b) AA. (c) Kappa.

4. Discussion

4.1. The Influence of Different Parameters

In this part, the influence of different free parameters, i.e., the number of dimension reduction L, the number of fused feature K, the smoothing weight $\alpha$, and the window size $\sigma$, on the classification accuracy of our method is analyzed. An experiment is performed on the three datasets with training set listed in Table 1. When L and K are discussed, $\alpha$ and $\sigma$ are fixed as 0.005 and 3, respectively. Similarly, when $\alpha$ and $\sigma$ are analyzed, L and K are set as 30 and 20, respectively. Figure 11 presents the classification accuracy OA of the proposed method with different parameter settings. It can be observed that the proposed method can yield satisfactory classification accuracy for all used datasets when L and K are set to be 30 and 20, respectively. Moreover, when L and K are relatively small, the classification performance tends to be decreased, since the limited number of features cannot well represent the spectral–spatial information in HSIs. Figure 11d–f shows the influence of different $\alpha$ and $\sigma$. It is shown that when $\alpha$ and $\sigma$ increase, the classification performance of the proposed method decreases. The reason is that the structural feature extraction technique smooths out the spatial structures of HSIs. When $\alpha$ and $\sigma$ are set to be 0.005 and 3, respectively, the proposed method obtains the highest classification accuracy. Based on this observation, L, K, $\alpha$, and $\sigma$ are set as 30, 20, 0.005, and 3, respectively.

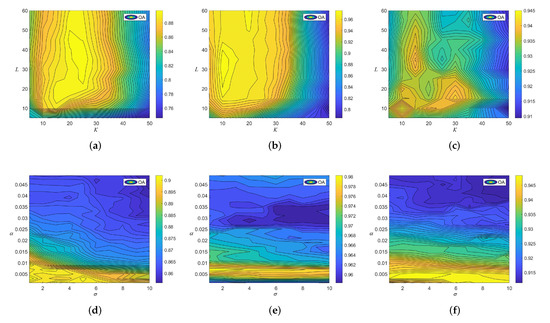
Figure 11. The influence of different parameters in the proposed method. The first row is the influence of the number of dimension reduction L and the number of fused feature K. The second row is the influence of the smoothing parameter $\alpha$ and the window size $\sigma$. (a) Indian Pines dataset; (b) Salinas dataset; (c) Honghu dataset; (d) Indian Pines dataset; (e) Salinas dataset; (f) Honghu dataset.

4.2. The Influence of Three Different Views

In this subsection, the influence of three different views on the classification accuracy is investigated. An experiment is conducted on the Indian Pines dataset. The classification performance obtained by the proposed framework with different views is shown in Table 5. It can be seen that the inter-view feature performs the best classification performance among three different views. Furthermore, the combination of two different views outperforms individual view in terms of classification accuracies. Overall, when three types of features are combined, the proposed method provides the highest classification results. The reason is that three different views have complementary information, which can be jointly utilized to improve the classification performance.

Table 5. Classification performance of three different views. The bold denotes the best classification performance.

Local-View	Intra-View	Inter-View	OA	AA	Kappa	Time (s)
✓			87.22	85.08	85.51	3.68
	✓		86.22	86.78	84.38	3.87
		✓	87.35	90.66	85.63	3.95
✓	✓		88.32	89.41	86.71	4.17
✓		✓	88.96	91.21	87.43	4.31
	✓	✓	88.25	92.07	86.58	4.48
✓	✓	✓	90.32	93.04	88.96	5.36

4.3. Effect of Different Hyperspectral Feature Methods

To demonstrate the advantage of the proposed feature extraction method, several widely used feature extraction methods for HSIs are selected as competitors, including extended morphological profiles (EMP) [41], extended morphological attribute profiles (EMAP) [13], Gabor filtering (Gabor) [42], image fusion and recursive filtering (IFRF) [14], intrinsic image decomposition (IID) [43], PCA-based edge-preserving filters (PCAEPFs) [8], invariant attribute profiles (IAPs) [44], low rank representation (LRR) [45], multi-scale total variation (MSTV) [15], and random patches network (RPNet) [46]. An experiment is performed on the Indian Pines dataset with 1% of training samples listed in Table 1. The classification accuracy of all considered approaches is shown in Figure 12. The EMP and EMAP methods only yield around 60% classification performance when the number of training samples is scarce. The classification performance obtained by the edge-preserving filtering-based feature extraction methods such as IFRF and PCAEPFs also tends to decrease when the number of training set is scarce. The RPNet-based deep feature extraction method also fails to achieve satisfactory performance. By contrast, it is found that the proposed feature method obtains the highest classification performance among all feature extraction techniques for three indexes, which further illustrates that the proposed method can better characterize the spectral–spatial information compared to other methods by fusing local and nonlocal multi-view structural features.

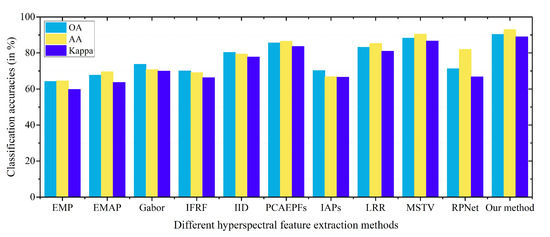
Figure 12. Classification accuracies of different hyperspectral feature extraction techniques on Indian Pines dataset.

4.4. Computing Time

The computing efficiency of all considered techniques for all datasets is provided in Table 6. All experiments are tested a laptop with 8 GB RAM and 2.6 GHz with Matlab 2018. We can observe from Table 6 that when the spatial and spectral dimensions of HSIs increase, the computing time of all methods tends to increases. Furthermore, the computing time of our method is quite competitive among all considered approaches (taking the Indian Pines dataset as an example, the running time of our method is around 5.36 s). The GTR method is the fastest as it is a regression model.

Table 6. The computing time of all considered approaches for all datasets. The bold denotes the best computing efficiency.

Datasets	SVM	IFRF	EMAP	SCMK	MSTV	PCAEPFs	GTR	Our Method
Indian Pines	5.53	2.32	3.25	4.49	4.35	2.67	2.04	5.36
Salinas	21.08	2.68	4.56	3.23	12.34	12.98	2.49	19.35
Honghu	128.26	16.55	69.94	15.75	45.67	20.79	9.37	102.23

5. Conclusions

In this work, a multi-view structural feature extraction method is developed for hyperspectral image classification, which consists of three key steps. First, the spectral number of the raw data is decreased. Then, the local structural feature, intra-view structural feature, and inter-view structural feature are constructed to characterize spectral–spatial information of diverse ground objects. Finally, the KPCA technique is exploited to merge multi-view structural features, and the fused feature is incorporated with the spectral classifier to obtain the classification map. Our experimental results on three datasets reveal that the proposed feature extraction method can consistently outperform other state-of-the-art classification methods even when the number of training set is limited. Furthermore, with regard to 10 other representative feature extraction methods, our method still produces the highest classification performance.